Water Quality Prediction Model Based Support Vector Machine Model for Ungauged River Catchment under Dual Scenarios
Abstract
:1. Introduction
1.1. Background
1.2. Problem Statement
1.3. Objectives
- (1)
- To provide effective methods of water-quality prediction to decision makers, towards better water resource planning and management.
- (2)
- To present a system-independent method of water-quality forecasting that utilises SVM in place of statistical modelling methods.
- (3)
- To provide recommendations to water-quality management agencies that accord with the research findings on the Langat River Basin, regarding how such findings may be integrated into ecological strategies for catchment management.
2. Materials and Methods
2.1. Case Study
2.2. Select Appropriate Inputs
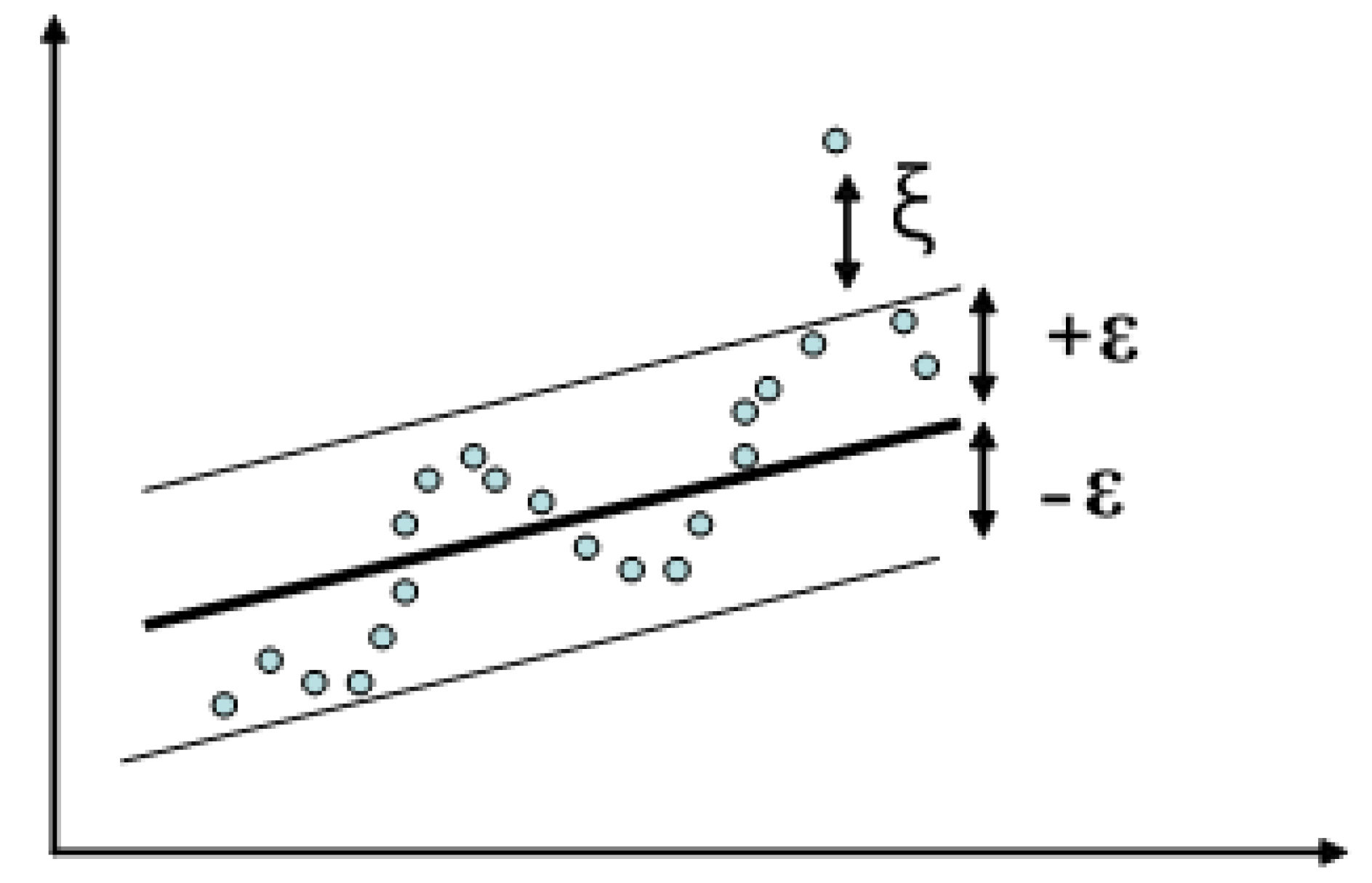
2.3. Structure of SVM
2.4. Statistical Indexes
2.4.1. Coefficient of Efficiency (CE)
2.4.2. Mean Square Error (MSE)
2.4.3. Coefficient of Correlation (CC)
2.5. Sensitivity Analysis
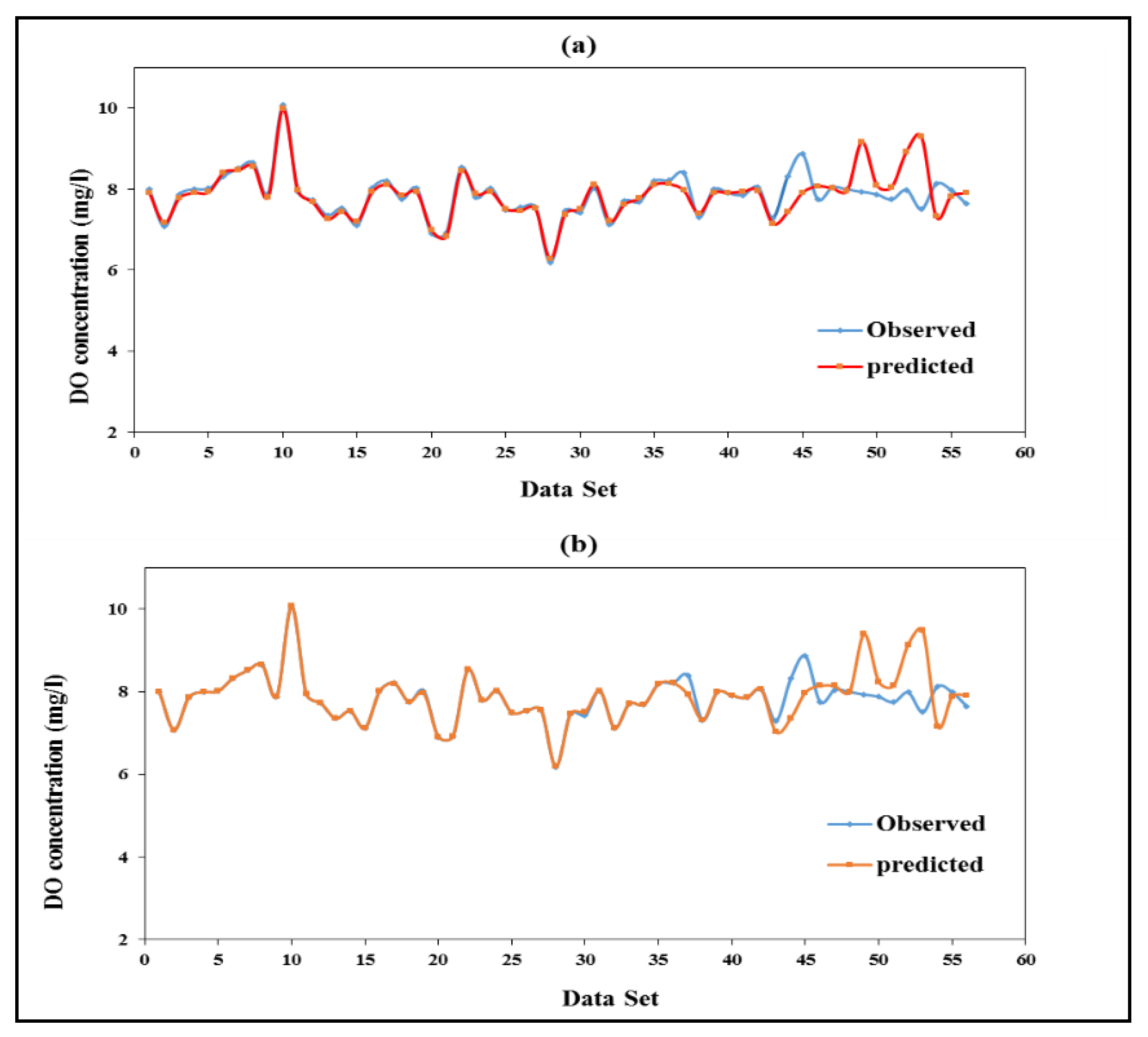
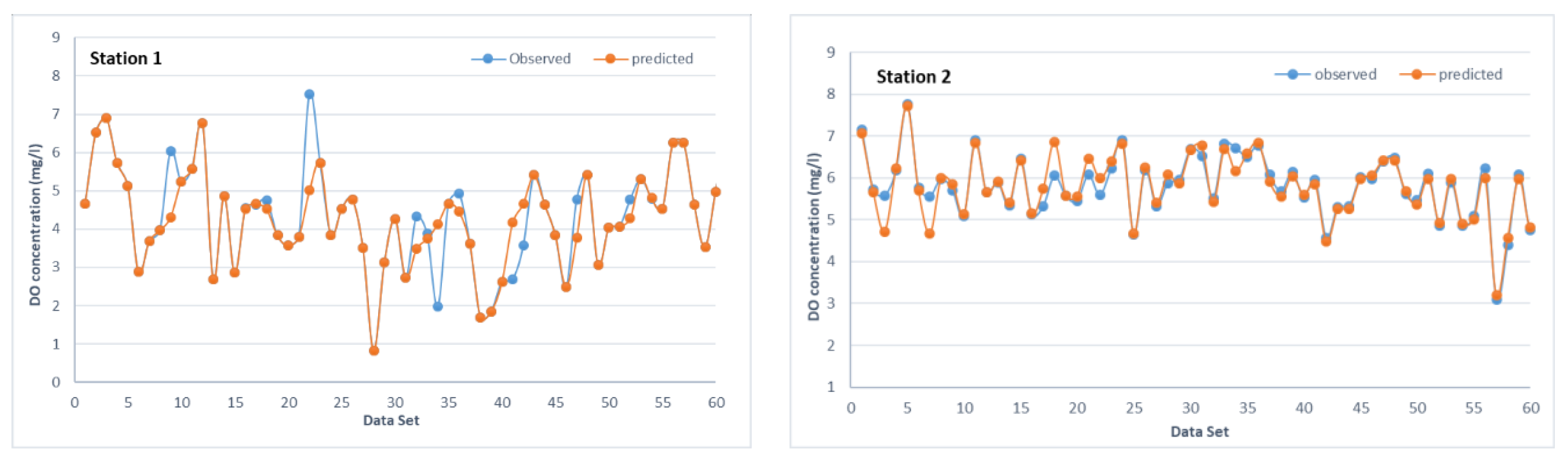
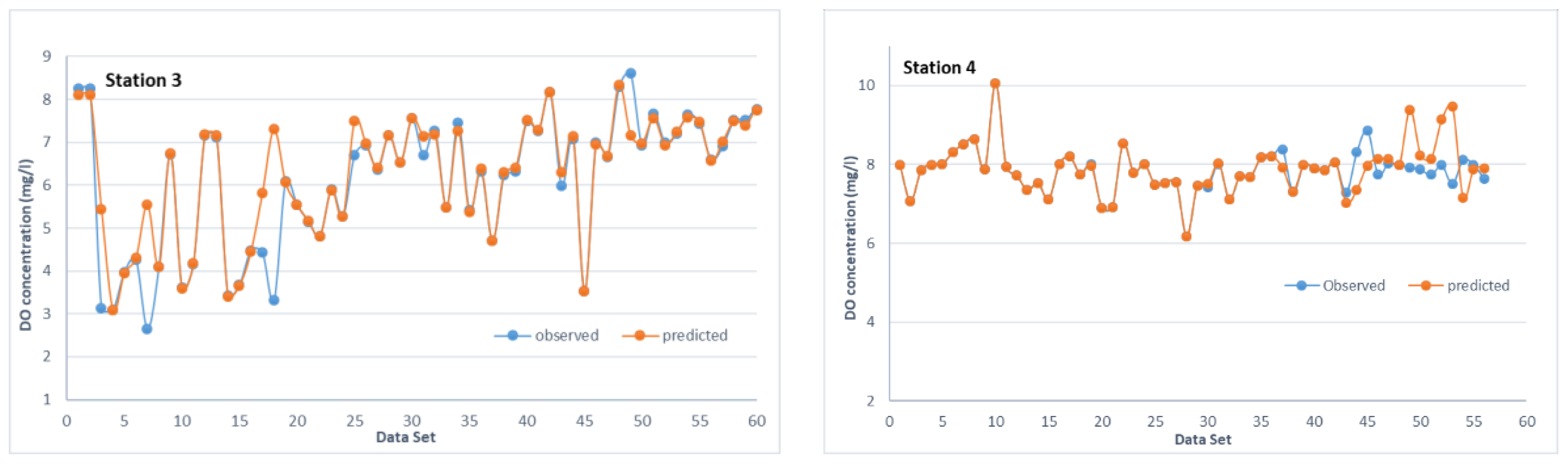
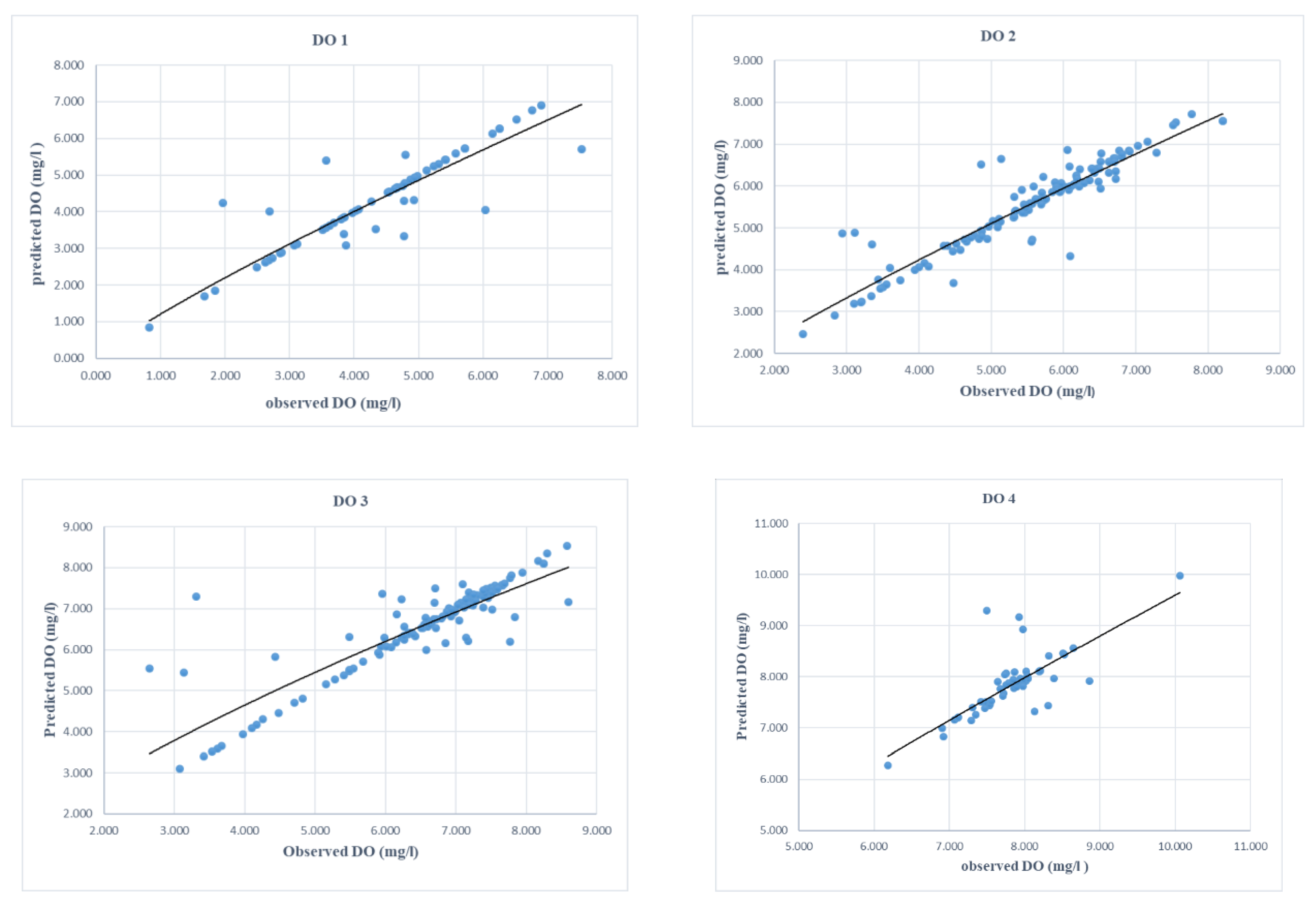
3. Results and Discussion
3.1. Kernel Functions of SVM
3.2. Epsilon-RBF Model and Nu-RBF Model
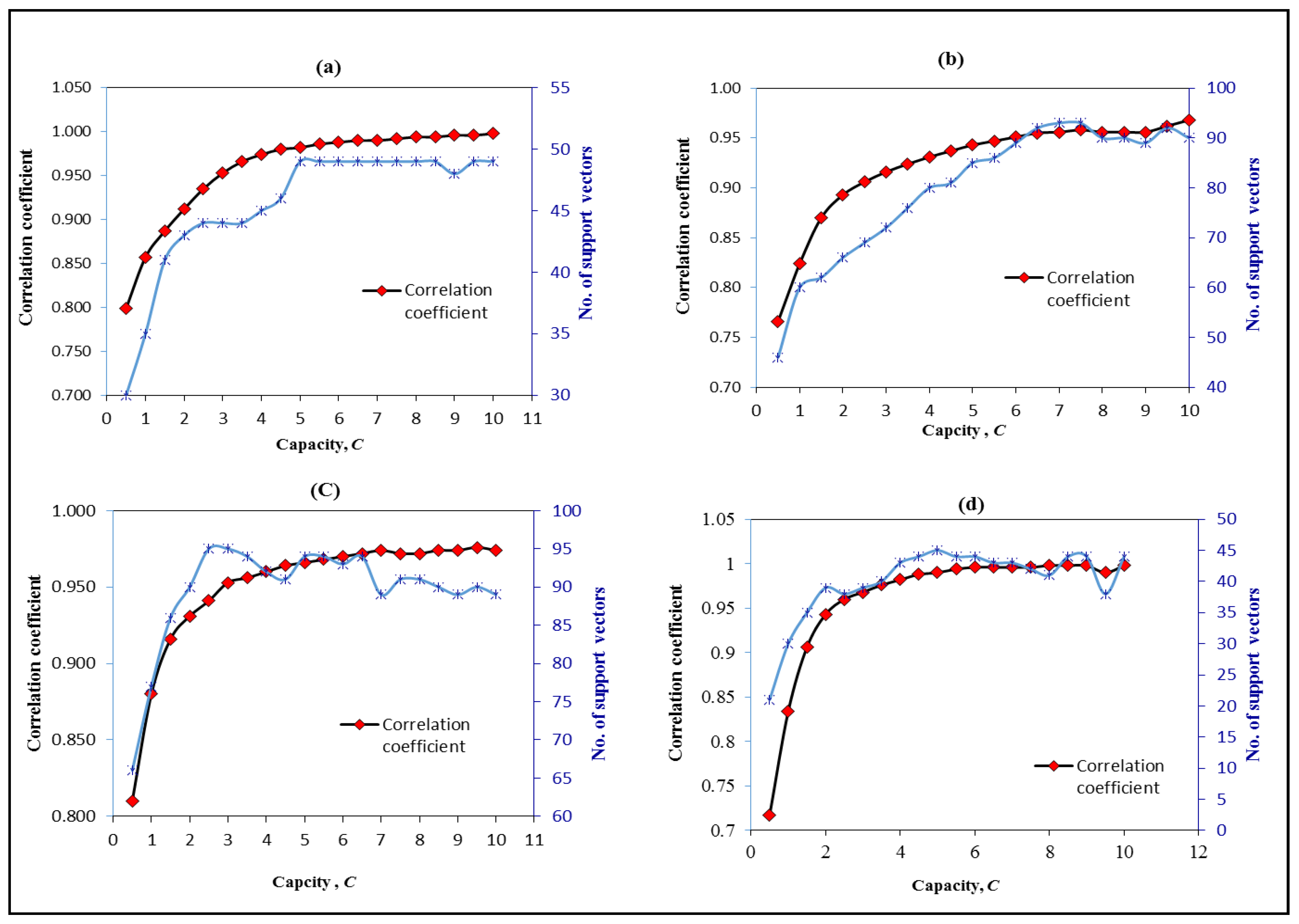
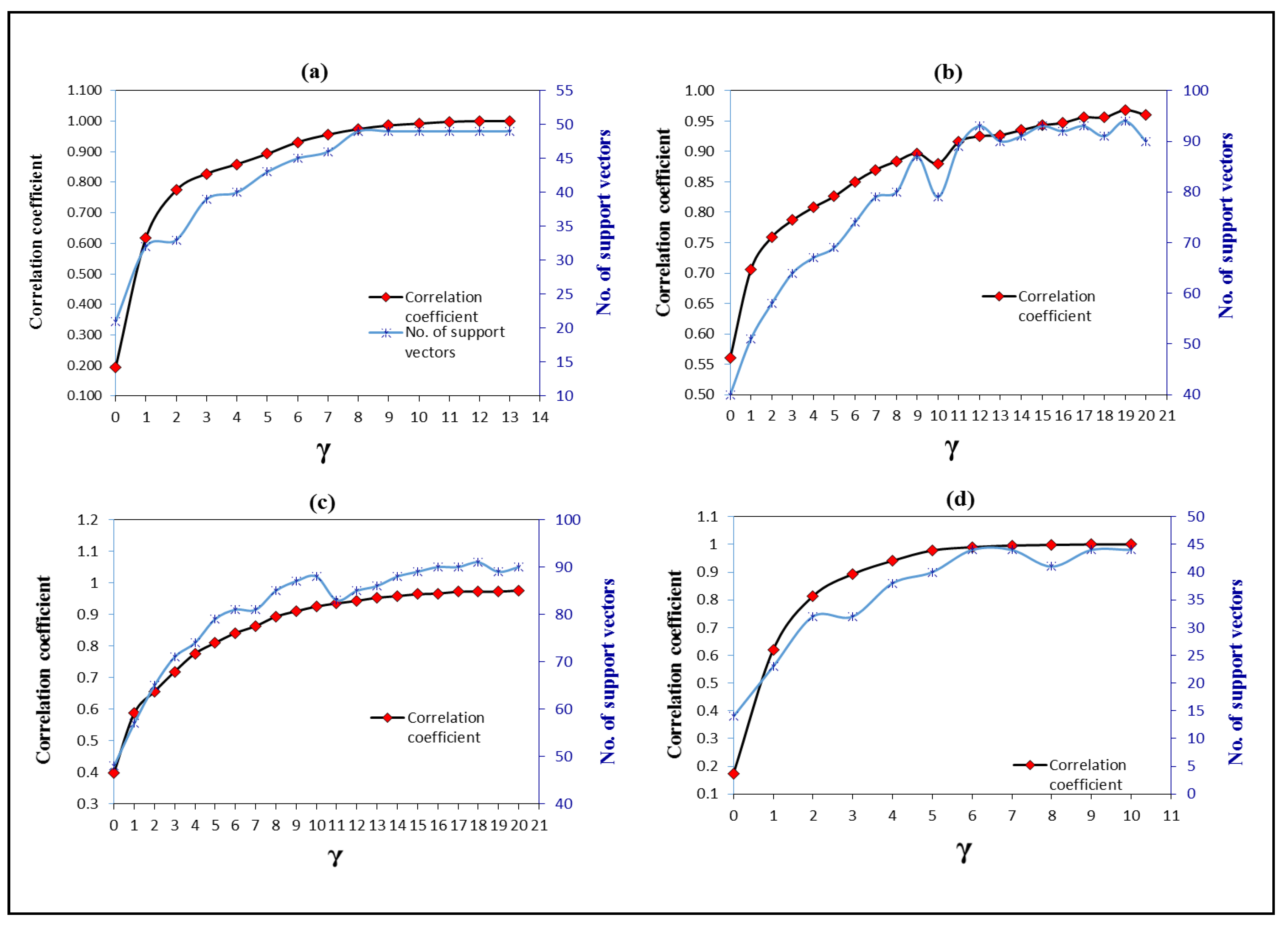
3.3. Optimising the Parameters of SVM
3.4. SVM Model Development
3.5. Compression between Scenario One and Two
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tarmizi, A.; Ahmed, A.N.; El-Shafie, A. Dissolved Oxygen Prediction Using Support Vector Machine in Terengganu River. Middle-East. J. Sci. Res. 2014, 21, 2182–2188. [Google Scholar]
- Behmel, S.; Damour, M.; Ludwig, R.; Rodriguez, M. Water quality monitoring strategies—A review and future perspectives. Sci. Total Environ. 2016, 571, 1312–1329. [Google Scholar] [CrossRef] [PubMed]
- Lumb, A.; Sharma, T.C.; Bibeault, J.-F. A Review of Genesis and Evolution of Water Quality Index (WQI) and Some Future Directions. Water Qual. Expo. Health 2011, 3, 11–24. [Google Scholar] [CrossRef]
- Najah, A.; El-Shafie, A.; Karim, O.A.; Jaafar, O. Integrated versus isolated scenario for prediction dissolved oxygen at progression of water quality monitoring stations. Hydrol. Earth Syst. Sci. Discuss. 2011, 8, 6069–6112. [Google Scholar] [CrossRef]
- Najah, A.; El-Shafie, A.; Karim, O.A.; El-Shafie, A.H. Performance of ANFIS versus MLP-NN dissolved oxygen prediction models in water quality monitoring. Environ. Sci. Pollut. Res. 2014, 21, 1658–1670. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, A.N.; El-Shafie, A.; Karim, O.A.; El-Shafie, A.H. An augmented wavelet de-noising technique with neuro-fuzzy inference system for water quality prediction. Int. J. Innov. Comput. Inf. Control 2012, 8, 7055–7082. [Google Scholar]
- Yoon, H.; Kim, Y.; Ha, K.; Lee, S.-H.; Kim, G.-P. Comparative Evaluation of ANN- and SVM-Time Series Models for Predicting Freshwater-Saltwater Interface Fluctuations. Water 2017, 9, 323. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, L.; Engel, B. Prediction of Sewage Treatment Cost in Rural Regions with Multivariate Adaptive Regression Splines. Water 2019, 11, 195. [Google Scholar] [CrossRef]
- Liu, C.; Hu, Y.; Yu, T.; Xu, Q.; Liu, C.; Li, X.; Shen, C. Optimizing the Water Treatment Design and Management of the Artificial Lake with Water Quality Modeling and Surrogate-Based Approach. Water 2019, 11, 391. [Google Scholar] [CrossRef]
- Elzwayie, A.; El-shafie, A.; Yaseen, Z.M.; Afan, H.A.; Allawi, M.F. RBFNN-based model for heavy metal prediction for different climatic and pollution conditions. Neural Comput. Appl. 2017, 28, 1–13. [Google Scholar] [CrossRef]
- El-Shafie, A.; Najah, A.; Alsulami, H.M.; Jahanbani, H. Optimized Neural Network Prediction Model for Potential Evapotranspiration Utilizing Ensemble Procedure. Water Resour. Manag. 2014, 28, 947–967. [Google Scholar] [CrossRef]
- Wang, K.; Wen, X.; Hou, D.; Tu, D.; Zhu, N.; Huang, P.; Zhang, G.; Zhang, H. Application of Least-Squares Support Vector Machines for Quantitative Evaluation of Known Contaminant in Water Distribution System Using Online Water Quality Parameters. Sensors 2018, 18, 938. [Google Scholar] [CrossRef] [PubMed]
- Chang, M.-J.; Chang, H.-K.; Chen, Y.-C.; Lin, G.-F.; Chen, P.-A.; Lai, J.-S.; Tan, Y.-C. A Support Vector Machine Forecasting Model for Typhoon Flood Inundation Mapping and Early Flood Warning Systems. Water 2018, 10, 1734. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, J.; Li, J.; Zhang, D.D. Multi-Spectral Water Index (MuWI): A Native 10-m Multi-Spectral Water Index for Accurate Water Mapping on Sentinel-2. Remote Sens. 2018, 10, 1643. [Google Scholar] [CrossRef]
- Yan, J.; Xu, Z.; Yu, Y.; Xu, H.; Gao, K. Application of a Hybrid Optimized BP Network Model to Estimate Water Quality Parameters of Beihai Lake in Beijing. Appl. Sci. 2019, 9, 1863. [Google Scholar] [CrossRef]
- Chen, Y.F. Influence and control strategies of agricultural nonpoint source pollution on water quality. China Resour. Compr. Utilization 2016, 34, 54–56. [Google Scholar]
- Akoteyon, I.S.; Omotayo, A.O.; Soladoye, O.; Olaoye, H.O. Determination of water quality index and suitability of urban river for municipal water supply in Lagos-Nigeria. Eur. J. Sci. Res. 2011, 54, 263–271. [Google Scholar]
- Malaysia.Jabatan Alam Sekitar. Malaysia Environmental Quality Report 2007; Department of Enviroment: Petaling Jaya, Malaysia, 2008; 84p, ISBN 9770127643008.
- River Water Quality (RWQ) | Malaysia Environmental Performance Index. Available online: http://www.epi.utm.my/v4/?page_id=102 (accessed on 5 April 2019).
- Heng, L.Y.; Abdullah, M.P.; Yi, C.S.; Mokhtar, M.; Ahmad, R. Development of Possible Indicators for Sewage Pollution for the Assessment Of Langat River Ecosystem Health. Malays. J. Anal. Sci. 2006, 10, 15–26. [Google Scholar]
- Aljanabi, Q.A.; Chik, Z.; Allawi, M.F.; El-Shafie, A.H.; Ahmed, A.N.; El-Shafie, A. Support vector regression-based model for prediction of behavior stone column parameters in soft clay under highway embankment. Neural Comput. Appl. 2018, 30, 1–11. [Google Scholar] [CrossRef]
- Afiq, H.; Ahmed, E.; Ali, N.; Othman, A.; Aini, K.; Mukhlisi, H.M. Daily forecasting of dam water levels: Comparing a support vector machine (SVM) model with adaptive neuro fuzzy inference system (ANFIS). Water Resour. Manag. 2013, 27, 3803–3823. [Google Scholar] [CrossRef]
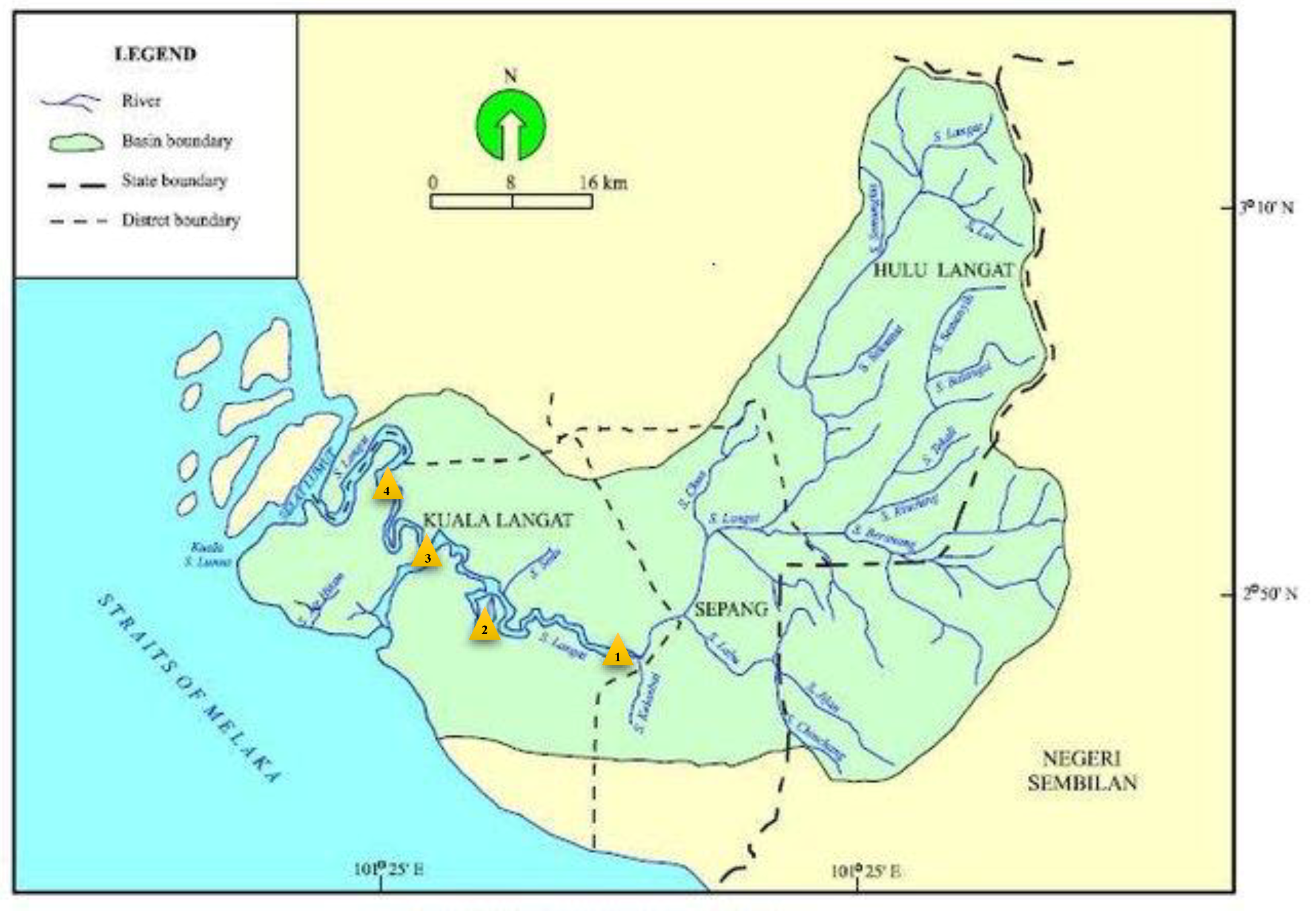
| Sampling Site | Basic Statistic | DO (mg/L) | BOD (mg/L) | COD (mg/L) | pH | SS (mg/L) | AN (mg/L) |
|---|---|---|---|---|---|---|---|
| Station 1 | Mean | 4.34 | 6.29 | 29.77 | 6.46 | 160.45 | 0.59 |
| Min | 0.83 | 1 | 4 | 2.41 | 0.1 | 0.01 | |
| Max | 7.53 | 23 | 99 | 7.36 | 1050 | 1.69 | |
| SD | 1.354 | 4.691 | 17.07 | 0.69 | 199 | 0.443 | |
| CV | 31.2 | 74.5 | 57.3 | 10.6 | 124 | 74.9 | |
| Station 2 | Mean | 4.34 | 5.77 | 25.54 | 6.58 | 121.3 | 0.96 |
| Min | 0.87 | 1 | 7 | 3.8 | 1 | 0.01 | |
| Max | 7.5 | 24 | 70 | 7.92 | 821 | 3.73 | |
| SD | 1.11 | 3.59 | 12.74 | 0.70 | 116.58 | 0.662 | |
| CV | 25.67 | 62.25 | 49.90 | 10.70 | 96.11 | 69.23 | |
| Station 3 | Mean | 5.81 | 5.29 | 23.72 | 7.01 | 182.9 | 1.11 |
| Min | 3.55 | 1 | 2 | 6.10 | 5 | 0.01 | |
| Max | 7.62 | 17 | 66 | 8.28 | 1400 | 5.75 | |
| SD | 0.77 | 2.50 | 11.87 | 0.323 | 202.94 | 0.995 | |
| CV | 13.2 | 47.34 | 50.06 | 4.61 | 110.96 | 90.01 | |
| Station 4 | Mean | 5.50 | 8.03 | 30.50 | 7.07 | 272.44 | 1.56 |
| Min | 2.39 | 2 | 5 | 5.84 | 3 | 0.01 | |
| Max | 8.2 | 27 | 84.10 | 7.91 | 1910 | 6.65 | |
| SD | 1.19 | 4.84 | 15.24 | 0.29 | 350.52 | 1.27 | |
| CV | 21.65 | 60.29 | 49.9 | 4.20 | 128.66 | 81.44 |
| Kernel Function | Mean Squared Error | Correlation Coefficient | ||
|---|---|---|---|---|
| Training | Testing | Training | Testing | |
| Linear | 0.229 | 0.189 | 0.564 | 0.438 |
| Polynomial | 0.177 | 0.217 | 0.732 | 0.496 |
| RBF | 0.177 | 0.322 | 0.998 | 0.801 |
| Sigmoid | 155.886 | 418.735 | 0.105 | 0.336 |
| ε | Mean Error Squared | Correlation Coefficient | No. of Support Vectors | |||
|---|---|---|---|---|---|---|
| (Train) | (Test) | (Train) | (Test) | (Overall) | ||
| 0.001 | 0.008 | 0.305 | 0.976 | 0.286 | 0.785 | 36 |
| 0.1 | 0.030 | 0.353 | 0.910 | 0.198 | 0.703 | 27 |
| 0.2 | 0.074 | 0.226 | 0.802 | 0.166 | 0.654 | 14 |
| 0.3 | 0.118 | 0.212 | 0.688 | 0.130 | 0.567 | 9 |
| 0.4 | 0.144 | 0.222 | 0.633 | 0.126 | 0.519 | 6 |
| 0.5 | 0.206 | 0.275 | 0.538 | 0.104 | 0.443 | 5 |
| Nu | Mean Error Squared | Correlation Coefficient | No. of Support Vectors | |||
|---|---|---|---|---|---|---|
| (Train) | (Test) | (Train) | (Test) | (Overall) | ||
| 0.001 | 0.357 | 0.363 | 0.416 | 0.057 | 0.339 | 2 |
| 0.1 | 0.018 | 0.340 | 0.946 | 0.241 | 0.743 | 33 |
| 0.2 | 0.003 | 0.302 | 0.992 | 0.306 | 0.802 | 41 |
| 0.3 | 0.001 | 0.326 | 0.998 | 0.272 | 0.797 | 41 |
| 0.4 | 0.001 | 0.321 | 0.998 | 0.278 | 0.801 | 44 |
| 0.5 | 0.001 | 0.331 | 0.998 | 0.268 | 0.795 | 42 |
| Statistical Evaluation | V-Fold | ||||
|---|---|---|---|---|---|
| 3 | 5 | 7 | 10 | 15 | |
| ε-RBF Model: | |||||
| RMSE | 0.458 | 0.164 | 0.167 | 0.164 | 0.164 |
| MAE | 0.393 | 0.538 | 0.530 | 0.538 | 0.538 |
| CR | 0.6050 | 0.933 | 0.933 | 0.933 | 0.933 |
| Nu-RBF model: | |||||
| RMSE | 0.089 | 0.070 | 0.089 | 0.089 | 0.077 |
| MAE | 0.648 | 0.646 | 0.646 | 0.648 | 0.632 |
| CR | 0.980 | 0.986 | 0.980 | 0.986 | 0.984 |
| Model | Input Parameters | Correlation Coefficient | Mean Square Error | ||||||
|---|---|---|---|---|---|---|---|---|---|
| DO 1 | DO 2 | DO 3 | DO 4 | DO 1 | DO 2 | DO 3 | DO 4 | ||
| 1 | DO, BOD, COD, SS, pH, AN | 0.99 | 0.99 | 0.93 | 0.95 | 0.004 | 0.044 | 0.035 | 0.001 |
| 2 | DO, BOD, COD, SS, pH | 0.92 | 0.85 | 0.64 | 0.72 | 0.141 | 0.281 | 0.212 | 0.008 |
| 3 | DO, BOD, COD, SS, AN | 0.90 | 0.82 | 0.82 | 0.73 | 0.175 | 0.131 | 0.203 | 0.071 |
| 4 | DO, BOD, COD, pH, AN | 0.97 | 0.94 | 0.88 | 0.92 | 0.058 | 0.084 | 0.052 | 0.009 |
| 5 | DO, BOD, SS, pH, AN | 0.95 | 0.91 | 0.83 | 0.85 | 0.081 | 0.124 | 0.105 | 0.040 |
| 6 | DO, COD, SS, pH, AN | 0.96 | 0.92 | 0.79 | 0.82 | 0.068 | 0.160 | 0.135 | 0.038 |
| Model | Input Parameters | CC | ||
|---|---|---|---|---|
| DO 2 | DO 3 | DO 4 | ||
| 1 | DO 1 | 0.279 | ||
| 2 | DO 1 | 0.236 | ||
| 3 | DO 2 | 0.258 | ||
| 4 | DO 1, DO2 | 0.571 | ||
| 5 | DO 1 | 0.503 | ||
| 6 | DO 2 | 0.344 | ||
| 7 | DO 3 | 0.361 | ||
| 8 | DO 1, DO2 | 0.746 | ||
| 9 | DO 1, DO3 | 0.656 | ||
| 10 | DO 2, DO3 | 0.701 | ||
| 11 | DO 1, DO2, DO 3 | 0.979 | ||
| Station | Maximum Residual Error | ||
|---|---|---|---|
| 1 Week | 2 Weeks | Month | |
| 1 | 2.264 | 2.068 | 1.409 |
| 2 | 1.924 | 0.634 | 0.525 |
| 3 | 3.992 | 3.04 | 2.559 |
| 4 | 0.994 | 1.129 | 0.450 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abobakr Yahya, A.S.; Ahmed, A.N.; Binti Othman, F.; Ibrahim, R.K.; Afan, H.A.; El-Shafie, A.; Fai, C.M.; Hossain, M.S.; Ehteram, M.; Elshafie, A. Water Quality Prediction Model Based Support Vector Machine Model for Ungauged River Catchment under Dual Scenarios. Water 2019, 11, 1231. https://doi.org/10.3390/w11061231
Abobakr Yahya AS, Ahmed AN, Binti Othman F, Ibrahim RK, Afan HA, El-Shafie A, Fai CM, Hossain MS, Ehteram M, Elshafie A. Water Quality Prediction Model Based Support Vector Machine Model for Ungauged River Catchment under Dual Scenarios. Water. 2019; 11(6):1231. https://doi.org/10.3390/w11061231
Chicago/Turabian StyleAbobakr Yahya, Abobakr Saeed, Ali Najah Ahmed, Faridah Binti Othman, Rusul Khaleel Ibrahim, Haitham Abdulmohsin Afan, Amr El-Shafie, Chow Ming Fai, Md Shabbir Hossain, Mohammad Ehteram, and Ahmed Elshafie. 2019. "Water Quality Prediction Model Based Support Vector Machine Model for Ungauged River Catchment under Dual Scenarios" Water 11, no. 6: 1231. https://doi.org/10.3390/w11061231
APA StyleAbobakr Yahya, A. S., Ahmed, A. N., Binti Othman, F., Ibrahim, R. K., Afan, H. A., El-Shafie, A., Fai, C. M., Hossain, M. S., Ehteram, M., & Elshafie, A. (2019). Water Quality Prediction Model Based Support Vector Machine Model for Ungauged River Catchment under Dual Scenarios. Water, 11(6), 1231. https://doi.org/10.3390/w11061231









