Towards Circular Water Neighborhoods: Simulation-Based Decision Support for Integrated Decentralized Urban Water Systems
Abstract
1. Introduction
2. Materials and Methods
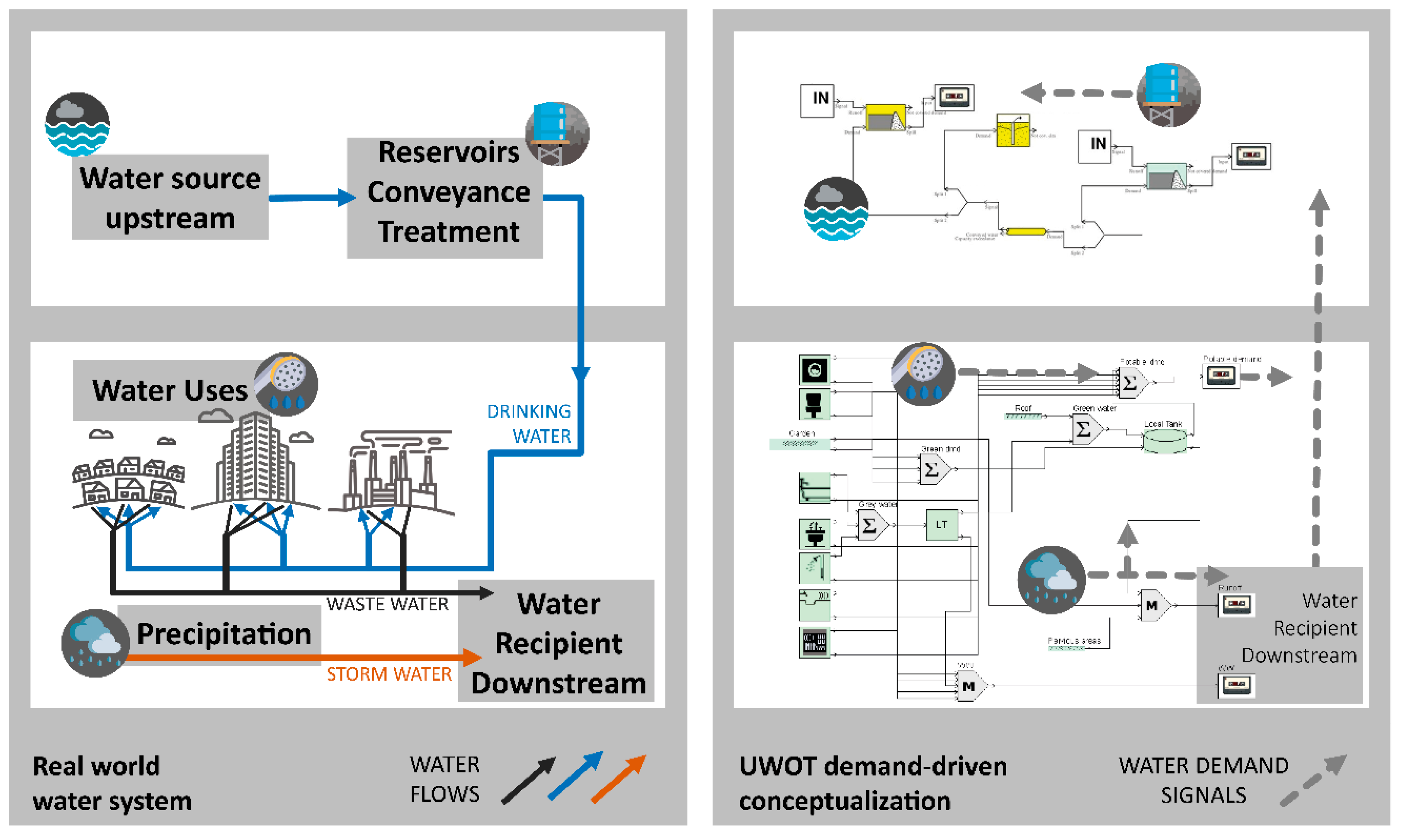
2.1. A Simulation-Based Approach Towards (Re-)designing Circular Water Neighborhoods
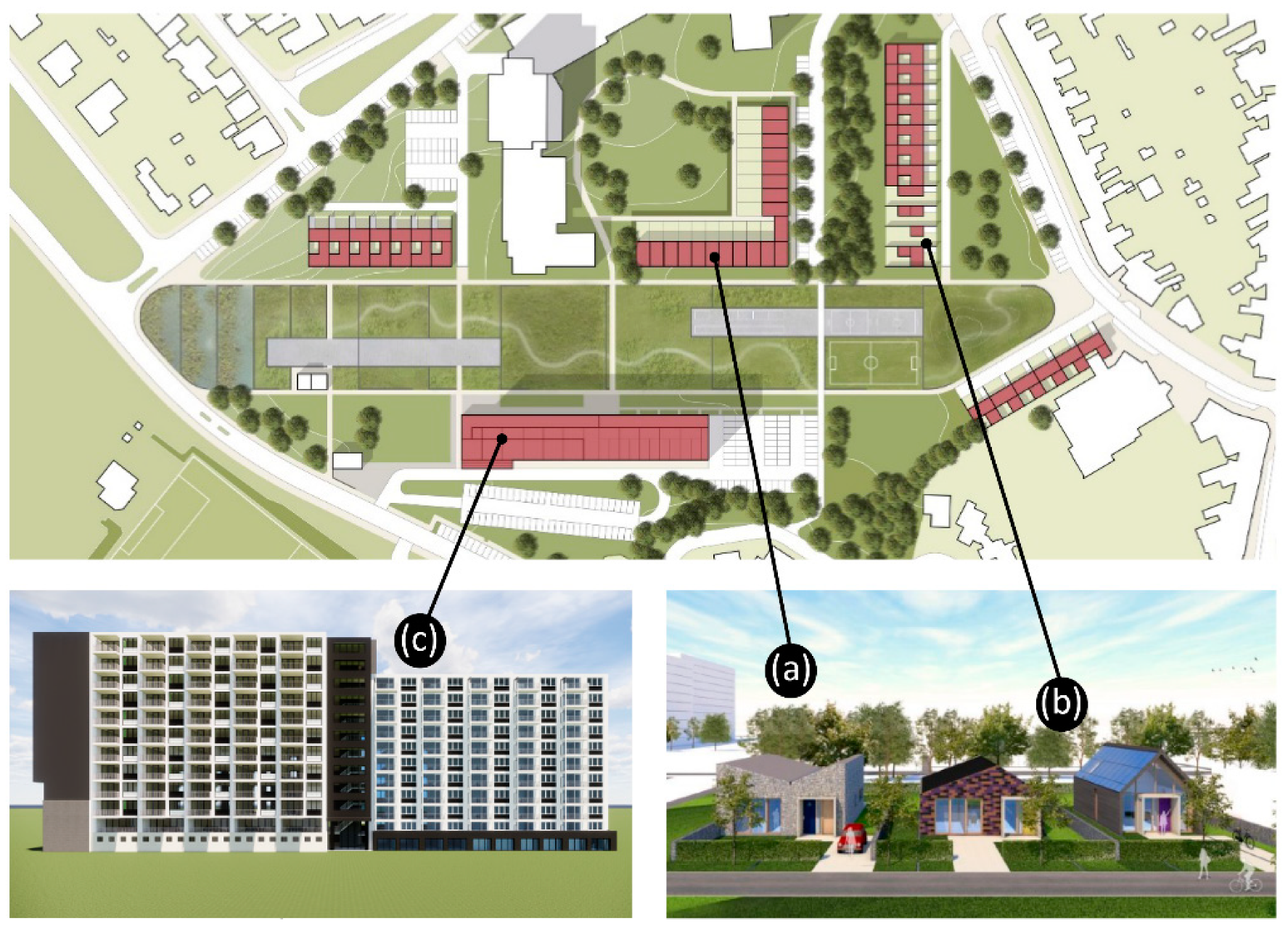
2.2. The Case Study: The Circular Water Neighborhood of SUPERLOCAL
- Installing water-saving household devices that have a reduced water footprint and lead to lower demands at a tap (household) level. A portfolio of technologies such as vacuum toilets, water-saving showers and recirculation showers are planned to be installed in different household types (Table 2).
- A rainwater harvesting (RWH) scheme at the neighborhood scale that collects water from household roofs and public (impervious) areas, purifies it and uses it to cover drinking water (DW) needs. Excess rainwater that is not captured is directed to a ‘water square’, a large infiltration basin designed to absorb rainwater through percolation. This measure constitutes a sustainable urban drainage system (SUDS) [30,31], aiming at capturing rainwater locally and not allowing it to reach the outlet of the neighborhood.
- A greywater recycling (GWR) scheme at the neighborhood scale that collects wastewater (WW) from selected uses such as the shower and handbasin, purifies it through a nature-based helophyte filter and redirects it in the urban water cycle, for instance to be used in certain common uses such as a shared laundry unit and car wash facility.
- A secondary (black water BW) sewage system processing water from vacuum toilets and food grinders in order to purify and reclaim resources and energy in a digester. This is an implementation of the ‘new sanitation’ concept, using the idea of separation of waste water at the source [32]. The inclusion of different sewage treatment options per (GW/BW) stream introduces a dual, parallel system that results in a higher GW quality and thus potential of reuse, as well as higher potential for energy and resource recovery in the BW stream rich in organic material. This concept requires the use of vacuum toilets (against other water-aware solutions), in order to maximize nutrient concentration in the BW stream and enable recovery.
2.3. Formulating the Performance Assessment Chain for Decentralized Urban Water Systems
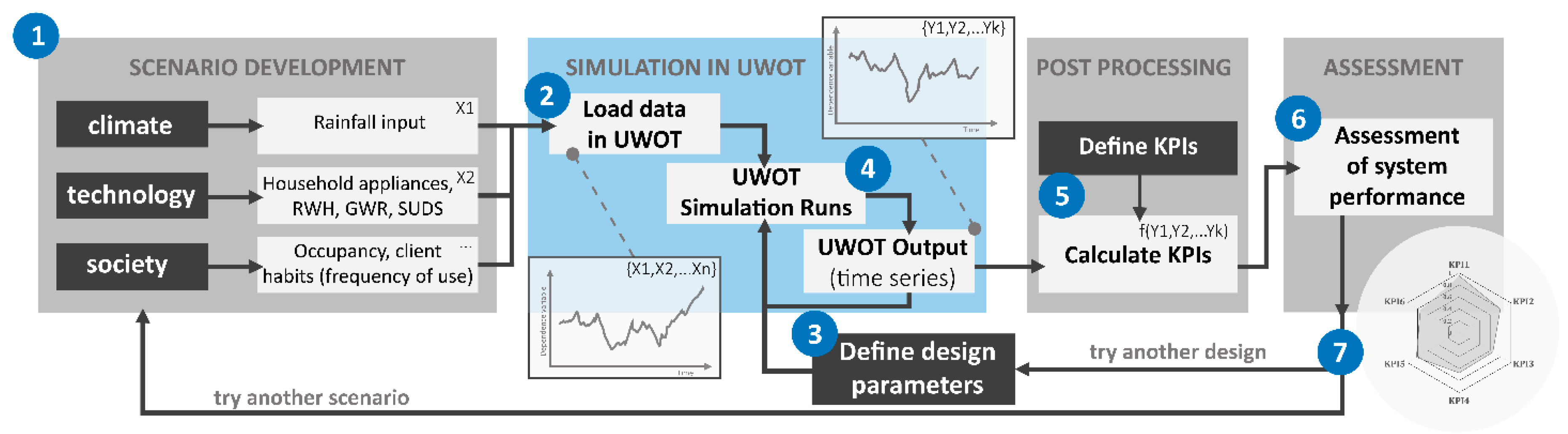
- Define the scenario (i.e., modeling reality) by deciding on climate, technological and social dimensions that affect model inputs.
- Convert this modeling reality to model input that comes in the form of n scalars or time-series that define the n-dimensional input space :In the case of UWOT and as aforementioned, assumptions on climate affect the rainfall time-series needed to calculate runoff, while assumptions on technology affect the choice of interventions at a neighborhood scale (household appliances, RWH, GWR).
- Define the design attributes of the given scenario. These attributes reflect design and operational characteristics for a given technological reality, such as the treatment capacity and buffer storage of a RWH/GWR design option, and come in the form of an m-dimensional model parameter space with m parameters :
- Perform model simulation using the input space and parameter space , in order to extract the system response in the form of time-series in the k-dimensional output space :In the case of UWOT, the output space includes water cycle streams that come as time-series of demands (i.e., requested DW), produced WW, simulated runoff etc.
- Reduce the complexity of output data by transforming model outputs to KPIs. This step can be also viewed as a statistical transformation process of the output time-series to scalars that represent system performance. Since KPIs aim to compare baseline with decentralized system performance, they can be considered a statistical transformation process across the output vectors and of two scenarios (a) and (b), where (a) is typically the baseline scenario and (b) is the decentralized scenario.
- Use the calculated KPIs to evaluate the performance of the system.
- In case the performance is not deemed adequate, two feedback options are possible—to return back to step (3) and try another design attribute (in order to increase the efficiency of the defined proposed decentralized system), or change the mixture of interventions altogether and try another scenario, thus going back to step (1).
2.4. Definition of KPIs for Decentralized Urban Water Systems
- The achieved reduction in household consumption RHC (or otherwise % household demand reduction):with denoting household DW demands averaged over time. This is DW KPI that can be viewed as a tap-level water demand management metric, describing the reduction in water requested at the household level before any upscaled measures such as RWH and GWR operate. The reduction at this household scale is caused by water-saving appliances, which reduce the water usage per appliance d.
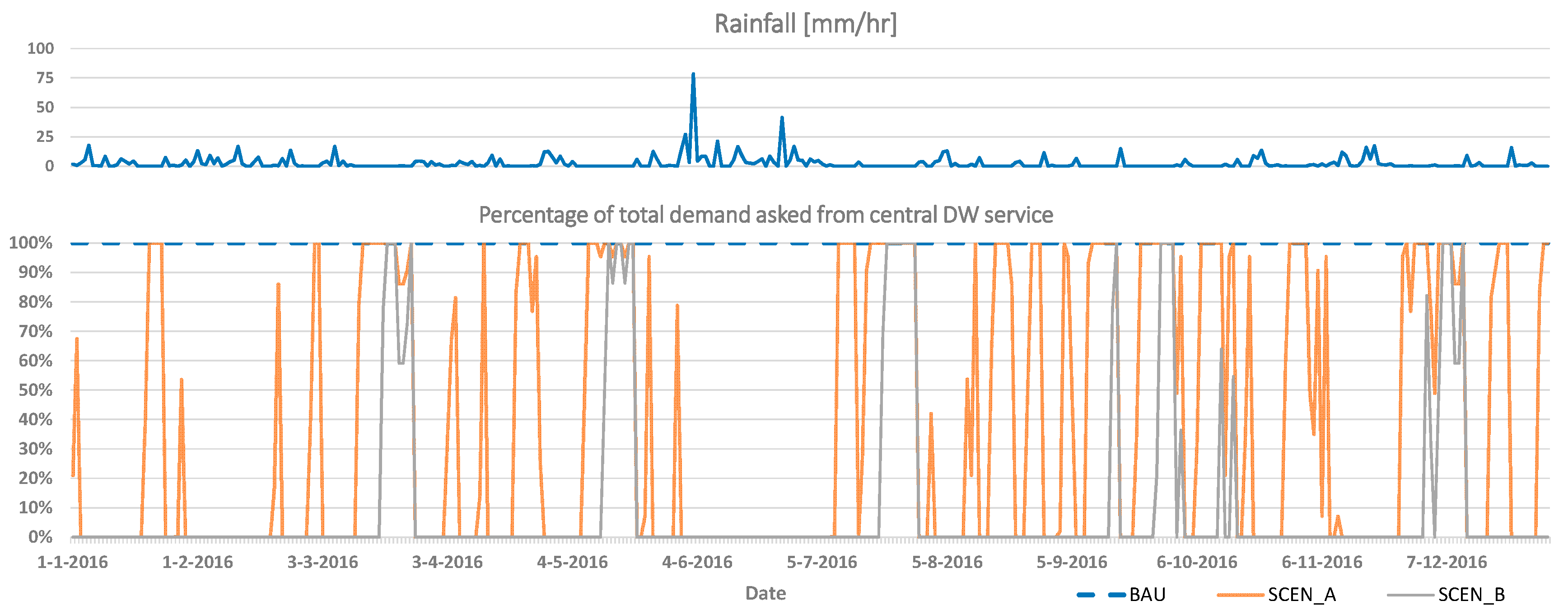
- The achieved reduction in clean DW (RDW) requested from the external, central service (or otherwise % reduction in the demand requested from central water utility):with denoting neighborhood DW demands averaged over time. This is a DW KPI that can be viewed as a more representative measure of the system autonomy, dependent on all decentralized technologies in place. Speaking the ‘signal language’ of UWOT, it represents the demand signal that cannot be covered by local (harvested or reused) DW supply and has to be met by the central utility through the connection to the mains.
- The achieved reduction in WW (RWW) that leaves the system (or otherwise % reduction of WW pushed to outlet):with denoting the volume of wastewater that leaves the neighborhood averaged over time. This is a WW KPI that constitutes another measure of neighborhood autonomy, now regarding the produced WW that cannot be stored or treated locally and is propagated externally (e.g., through the centralized sewer network).
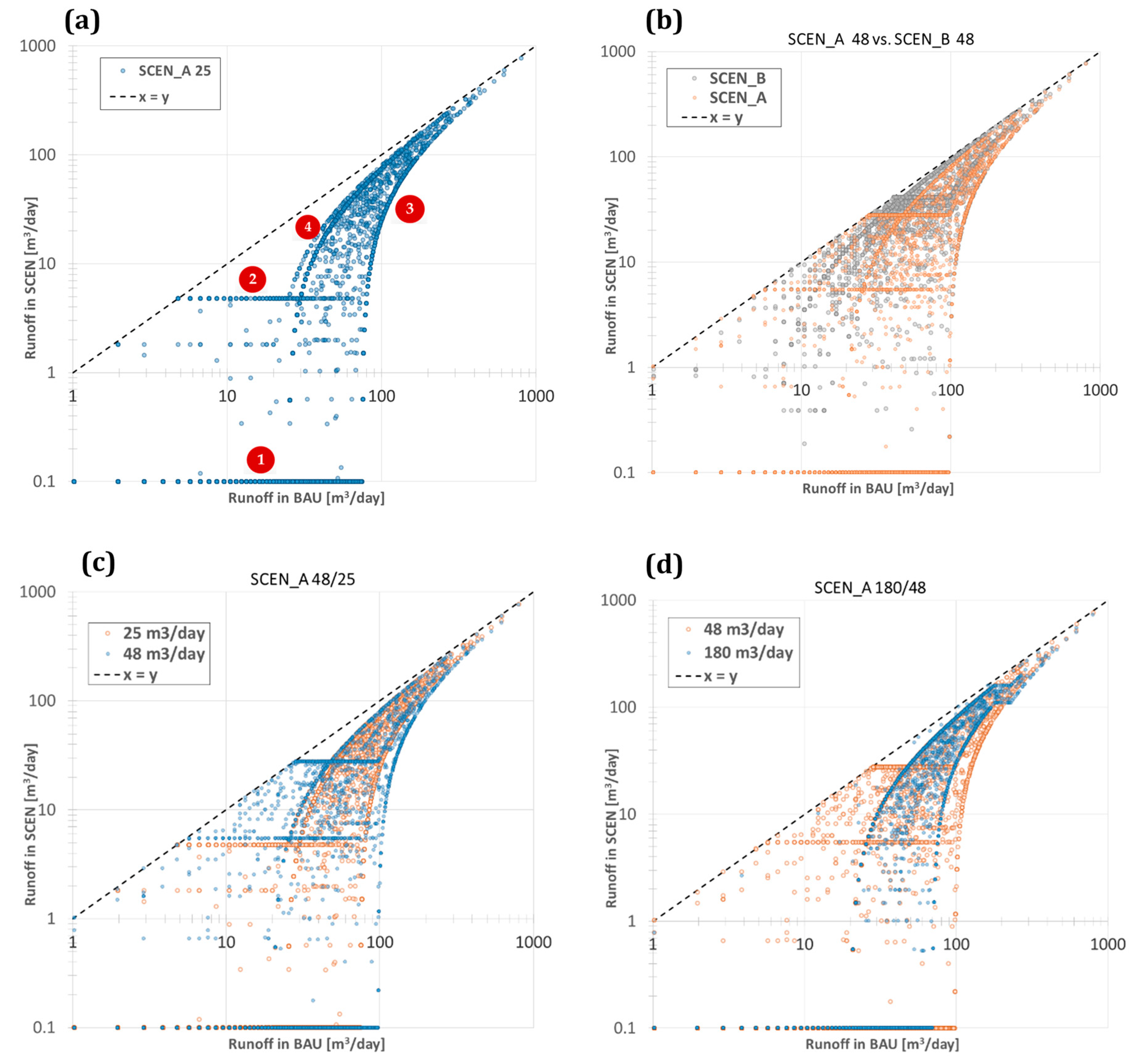
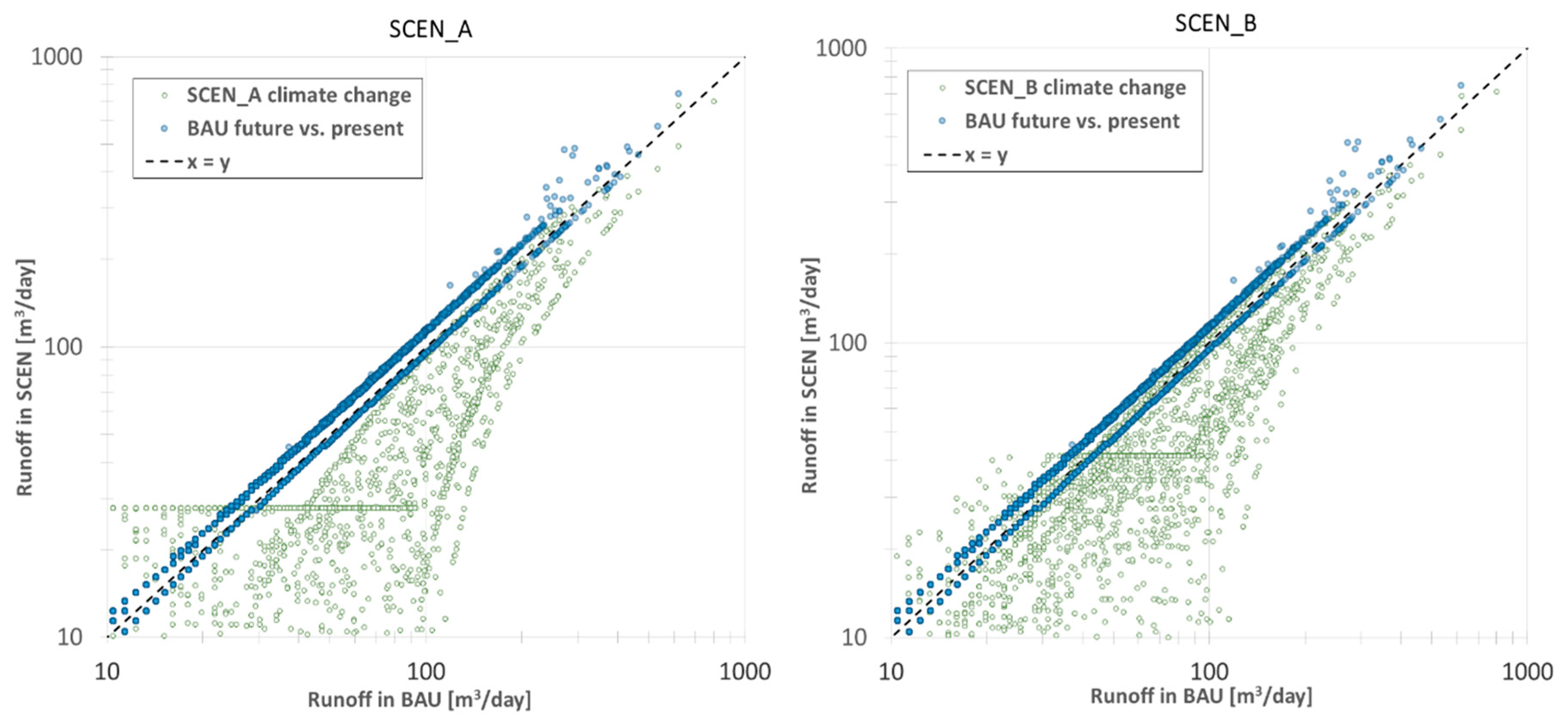
- The achieved runoff reduction RAR (or otherwise % reduction of runoff):where is the volume of runoff leaving the neighborhood, averaged annually or over the entire simulation time. This is a KPI related to runoff that measures the efficiency of the decentralized system to retain water in the long term.
- The achieved flood event reduction RER (or otherwise average % reduction of peak event runoff):which is the mean value of the runoff reduction observed at the event level, with denoting the peak runoff observed during a simulated flood event. This is a runoff-related KPI that is measured at a smaller timescale (i.e., on a per-event basis) and depicts the efficiency of the decentralized system in mitigating floods.
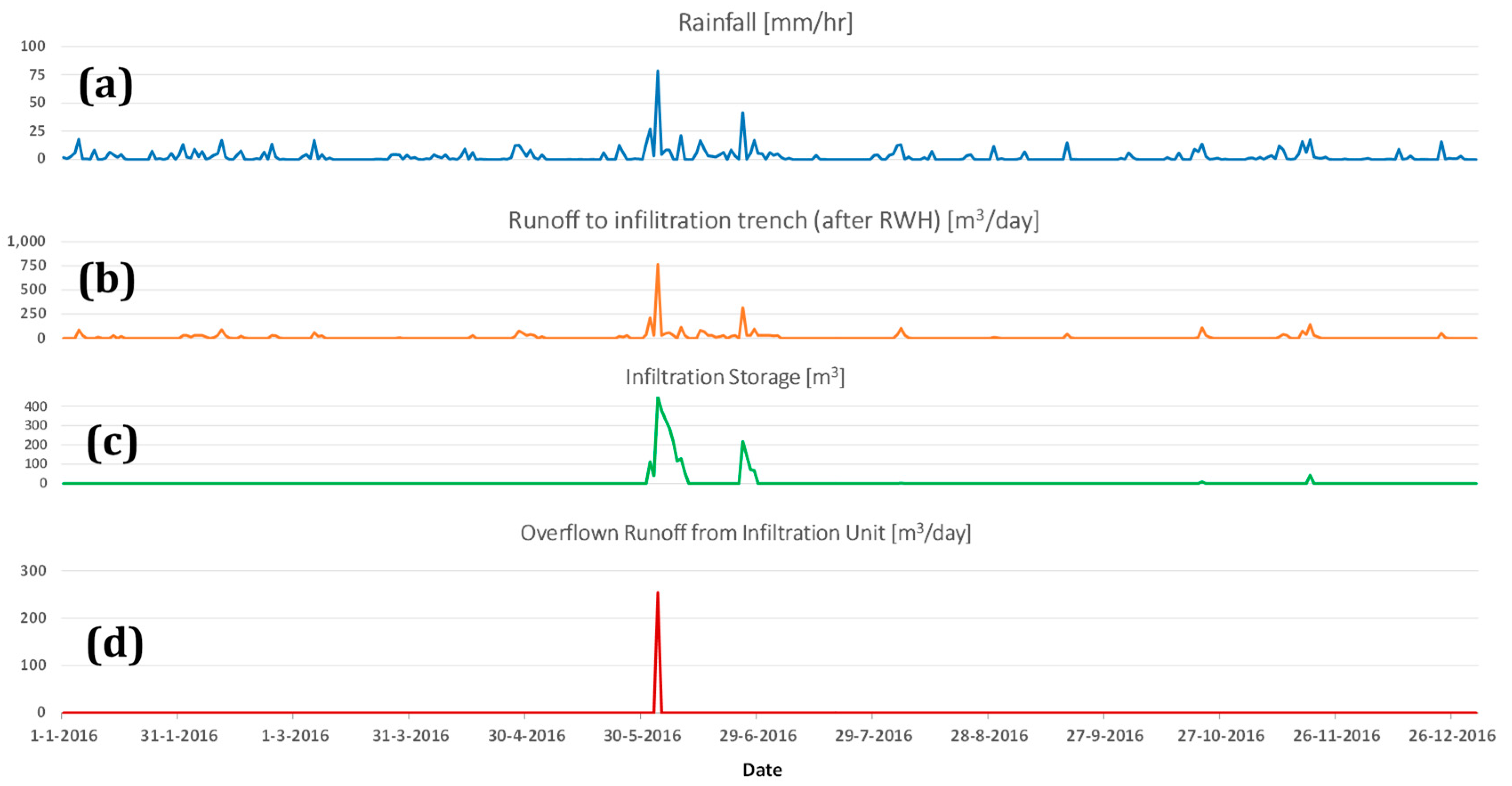
- The reliability of decentralized system design REL, which is defined in a simulation-based framework as the % of time steps that the system operated well. Reliability is a probabilistic concept with strong links to simulation modeling [41,42,43] generally defined as:with being the probability of either system failure or inefficiency. It is computed as the relative frequency of time steps with failure or inefficiency and with being a logical condition targeting the output space that is used to distinguish failed or inefficient time states from normal operational conditions during simulation. In this study, the focus is on the operational inefficiency for storage treatment systems, i.e., measured as the count of time steps during simulation when the storage capacity of these systems is full, the treatment capacity is inadequate and the incoming untreated water overflows from the treatment unit.
3. Analysis and Results
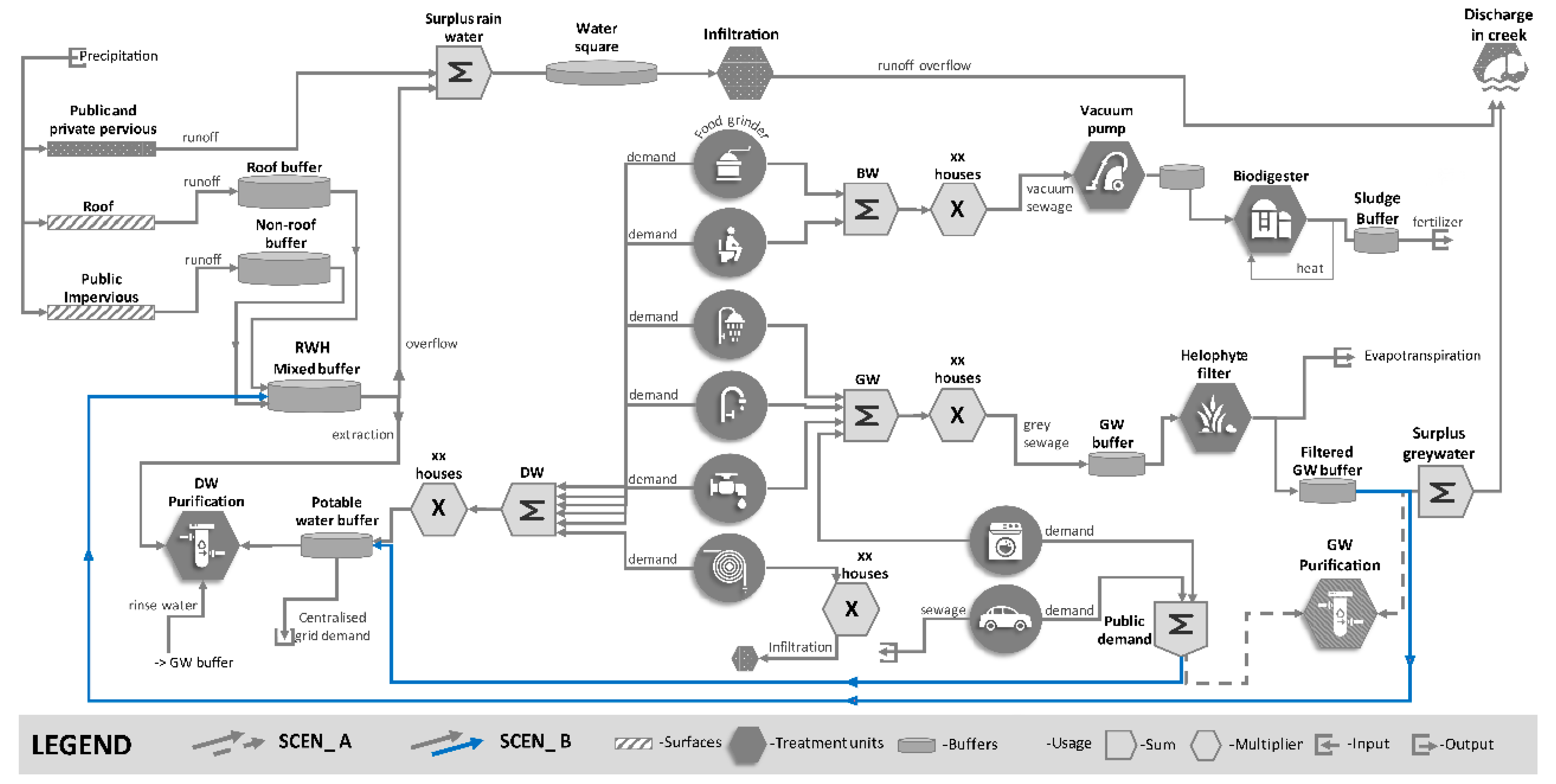
3.1. Bringing SUPERLOCAL to the UWOT Modeling Domain
3.2. Application of the framework in SUPERLOCAL
- The first baseline scenario corresponds to neighborhood equivalent to SUPERLOCAL (i.e., having the same household types, occupancy and spatial characteristics) that however features no decentralized technologies. This reality reflects a neighborhood that follows the centralized model of linear water management, where runoff and WW are propagated downstream (to the outlet and central stormwater or wastewater services), DW is requested from the central mains and conventional appliances are used in all house types. This reality serves as the baseline for comparison and has the abbreviation of business-as-usual (BAU).
- The second scenario is a neighborhood that features distinct recycling systems (RWH and GWR) that target different water uses. Treated RW covers all domestic uses, while treated GW covers common facilities, including a laundry and car wash. This decentralized reality has the abbreviation SCEN_A or “RWH|GWR”, to underline the distinct role of RWH and GWR.
- The third scenario is a neighborhood where GWR usability is extended; in that case, treated GW acts as light RW and is directed to the same buffer unit as RW, in order to create a common pool that targets all water uses. This reality has the abbreviation SCEN_B or “RWH + GWR”, to underline the combined role of RWH and GWR.
3.3. Model Validation
3.4. Performance Assessment of SUPERLOCAL Decentralized Design Options
3.5. Downscaling KPIs to Fit the Needs of Decision Support
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Disclaimer
Appendix A
| Technology | Drinking Water Usage | Discharge | ||||
|---|---|---|---|---|---|---|
| Water Usage d (L/use/day) | Frequency of Use ft (uses/day) | Per Capita Demand Request (L/person/day) | GW  | BW  | Soil (Pervious Areas)  | |
| Bathroom | ||||||
| Conventional shower | 8.7 | 8.1 | 70.5 | 100% | 0% | 0% |
| Watersaving shower | 6.9 | 8.1 | 55.9 | 100% | 0% | 0% |
| Recirculation shower | 2.5 | 8.1 | 20.3 | 100% | 0% | 0% |
| Sink | 2 | 2.5 | 5.0 | 100% | 0% | 0% |
| Toilet | ||||||
| Toilet | 6 | 6 | 36.0 | 100% | 0% | 0% |
| Vacuum toilet (silent and standard) | 1 | 6 | 6.0 | 0% | 100% | 0% |
| Kitchen | ||||||
| Food grinder | 3 | 0.33 | 1.0 | 0% | 100% | 0% |
| Cooking | 1 | 1.4 | 1.4 | 100% | 0% | 0% |
| Dishwashing by hand | 9.1 | 0.4 | 3.6 | 100% | 0% | 0% |
| Dishwasher | 17.4 | 0.3 | 5.2 | 100% | 0% | 0% |
| Household equipment | ||||||
| Washing machine (in house) | 52.9 | 0.29 | 15.3 | 100% | 0% | 0% |
| Washing machine (common launderette) | 50 | 0.25 | 12.5 | 100% | 0% | 0% |
| Car wash | 1 m3/day for the whole neighborhood | Sewer | Sewer | Sewer | ||
| Garden | ||||||
| Outdoor tap | 50 | 0.1 | 5 | 0% | 0% | 100% |
References
- Gleick, P.H. Water management: Soft water paths. Nature 2002, 418, 373. [Google Scholar] [CrossRef] [PubMed]
- Muller, M. Adapting to climate change: Water management for urban resilience. Environ. Urban. 2007, 19, 99–113. [Google Scholar] [CrossRef]
- Baird, G.M. A game plan for aging water infrastructure. J.-Am. Water Works Assoc. 2010, 102, 74–82. [Google Scholar] [CrossRef]
- Moe, C.L.; Rheingans, R.D. Global challenges in water, sanitation and health. J. Water Health 2006, 4, 41–57. [Google Scholar] [CrossRef] [PubMed]
- McDonald, R.I.; Green, P.; Balk, D.; Fekete, B.M.; Revenga, C.; Todd, M.; Montgomery, M. Urban growth, climate change, and freshwater availability. Proc. Natl. Acad. Sci. USA 2011, 108, 6312–6317. [Google Scholar] [CrossRef] [PubMed]
- McDonald, R.I.; Weber, K.; Padowski, J.; Flörke, M.; Schneider, C.; Green, P.A.; Gleeson, T.; Eckman, S.; Lehner, B.; Balk, D. Water on an urban planet: Urbanization and the reach of urban water infrastructure. Glob. Environ. Chang. 2014, 27, 96–105. [Google Scholar] [CrossRef]
- Iglesias, E.; Blanco, M. New directions in water resources management: The role of water pricing policies. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Koop, S.H.A.; van Leeuwen, C.J. The challenges of water, waste and climate change in cities. Environ. Dev. Sustain. 2017, 19, 385–418. [Google Scholar] [CrossRef]
- Daigger, G.T.; Crawford, G.V. Enhancing water system security and sustainability by incorporating centralized and decentralized water reclamation and reuse into urban water management systems. J. Environ. Eng. Manag. 2007, 17, 1. [Google Scholar]
- Newman, P. Sustainable urban water systems in rich and poor cities-steps towards a new approach. Water Sci. Technol. 2001, 43, 93–99. [Google Scholar] [CrossRef]
- Makropoulos, C.K.; Butler, D. Distributed Water Infrastructure for Sustainable Communities. Water Resour. Manag. 2010, 24, 2795–2816. [Google Scholar] [CrossRef]
- Geissdoerfer, M.; Savaget, P.; Bocken, N.M.P.; Hultink, E.J. The Circular Economy—A new sustainability paradigm? J. Clean. Prod. 2017, 143, 757–768. [Google Scholar] [CrossRef]
- EU Commission. Closing the Loop—An EU Action Plan for the Circular Economy; EU Commission: Brussels, Belgium, 2015. [Google Scholar]
- Hering, J.G.; Waite, T.D.; Luthy, R.G.; Drewes, J.E.; Sedlak, D.L. A Changing Framework for Urban Water Systems. Environ. Sci. Technol. 2013, 47, 10721–10726. [Google Scholar] [CrossRef] [PubMed]
- Wilderer, P.A.; Schreff, D. Decentralized and centralized wastewater management: A challenge for technology developers. Water Sci. Technol. 2000, 41, 1–8. [Google Scholar] [CrossRef]
- Makropoulos, C.K.; Natsis, K.; Liu, S.; Mittas, K.; Butler, D. Decision support for sustainable option selection in integrated urban water management. Environ. Model. Softw. 2008, 23, 1448–1460. [Google Scholar] [CrossRef]
- Peña-Guzmán, C.A.; Melgarejo, J.; Prats, D.; Torres, A.; Martínez, S. Urban water cycle simulation/management models: A review. Water 2017, 9, 285. [Google Scholar] [CrossRef]
- House-Peters, L.A.; Chang, H. Urban water demand modeling: Review of concepts, methods, and organizing principles. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Bacchin, T.K.; Ashley, R.; Sijmons, D.; Zevenbergen, C.; Van Timmeren, A. Green-blue multifunctional infrastructure: An urban landscape system design new approach. In Proceedings of the 13th International Conference on Urban Drainage, Sarawak, Malaysia, 7–12 September 2014; pp. 7–12. [Google Scholar]
- Rozos, E.; Makropoulos, C.; Maksimović, Č. Rethinking urban areas: An example of an integrated blue-green approach. Water Sci. Technol. Water Supply 2013, 13, 1534. [Google Scholar] [CrossRef]
- Nikolopoulos, D.; van Alphen, H.-J.; Vries, D.; Palmen, L.; Koop, S.; van Thienen, P.; Medema, G.; Makropoulos, C. Tackling the “New Normal”: A Resilience Assessment Method Applied to Real-World Urban Water Systems. Water 2019, 11, 330. [Google Scholar] [CrossRef]
- Corella-Barud, V.; Mena, K.D.; Gibbs, S.G.; Gurian, P.L.; Barud, A. Evaluation of neighborhood treatment systems for potable water supply. Int. J. Environ. Health Res. 2009, 19, 49–58. [Google Scholar] [CrossRef]
- Petit-Boix, A.; Leipold, S. Circular economy in cities: Reviewing how environmental research aligns with local practices. J. Clean. Prod. 2018, 195, 1270–1281. [Google Scholar] [CrossRef]
- Sokolowski, J.A.; Banks, C.M. Principles of Modeling and Simulation; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; ISBN 9780470403563. [Google Scholar]
- Makropoulos, C. Thinking platforms for smarter urban water systems: Fusing technical and socio-economic models and tools. Geol. Soc. Lond. Spec. Publ. 2017, 408, 201–219. [Google Scholar] [CrossRef]
- Rozos, E.; Makropoulos, C. Source to tap urban water cycle modelling. Environ. Model. Softw. 2013, 41, 139–150. [Google Scholar] [CrossRef]
- Bouziotas, D.; Rozos, V.; Makropoulos, C. Water and the City: Exploring links between urban growth and water demand management. J. Hydroinform. 2015, 17, 176–192. [Google Scholar] [CrossRef]
- Rozos, E.; Makropoulos, C.; Butler, D. Design Robustness of Local Water-Recycling Schemes. J. Water Resour. Plan. Manag. 2010, 136, 531–538. [Google Scholar] [CrossRef]
- Rozos, E.; Makropoulos, C. Assessing the combined benefits of water recycling technologies by modelling the total urban water cycle. Urban Water J. 2012, 9, 37–41. [Google Scholar] [CrossRef]
- Fletcher, T.D.; Shuster, W.; Hunt, W.F.; Ashley, R.; Butler, D.; Arthur, S.; Trowsdale, S.; Barraud, S.; Semadeni-Davies, A.; Bertrand-Krajewski, J.-L. SUDS, LID, BMPs, WSUD and more—The evolution and application of terminology surrounding urban drainage. Urban Water J. 2015, 12, 525–542. [Google Scholar] [CrossRef]
- Charlesworth, S.M.; Harker, E.; Rickard, S. A review of sustainable drainage systems (SuDS): A soft option for hard drainage questions? Geography 2003, 88, 99–107. [Google Scholar]
- Hegger, D.L.T.; Van Vliet, J.; Van Vliet, B.J.M. Niche Management and its Contribution to Regime Change: The Case of Innovation in Sanitation. Technol. Anal. Strateg. Manag. 2007, 19, 729–746. [Google Scholar] [CrossRef]
- Parmenter, D. Key Performance Indicators: Developing, Implementing, and Using Winning KPIs; John Wiley & Sons: Hoboken, NJ, USA, 2015; ISBN 1118925106. [Google Scholar]
- Chae, B. Developing key performance indicators for supply chain: An industry perspective. Supply Chain Manag. Int. J. 2009, 14, 422–428. [Google Scholar] [CrossRef]
- Del-Rey-Chamorro, F.M.; Roy, R.; van Wegen, B.; Steele, A. A framework to create key performance indicators for knowledge management solutions. J. Knowl. Manag. 2003, 7, 46–62. [Google Scholar] [CrossRef]
- Alegre, H.; Baptista, J.M.; Cabrera, E., Jr.; Cubillo, F.; Duarte, P.; Hirner, W.; Merkel, W.; Parena, R. Performance Indicators for Water Supply Services; IWA Publishing: London, UK, 2016; ISBN 1780406320. [Google Scholar]
- Lambert, A.O.; Brown, T.G.; Takizawa, M.; Weimer, D. A review of performance indicators for real losses from water supply systems. J. Water Supply Res. Technol. 1999, 48, 227–237. [Google Scholar] [CrossRef]
- Feingold, D.; Koop, S.; van Leeuwen, K. The City Blueprint Approach: Urban Water Management and Governance in Cities in the U.S. Environ. Manag. 2018, 61, 9–23. [Google Scholar] [CrossRef] [PubMed]
- Renouf, M.A.; Serrao-Neumann, S.; Kenway, S.J.; Morgan, E.A.; Low Choy, D. Urban water metabolism indicators derived from a water mass balance—Bridging the gap between visions and performance assessment of urban water resource management. Water Res. 2017, 122, 669–677. [Google Scholar] [CrossRef] [PubMed]
- Saary, M.J. Radar plots: A useful way for presenting multivariate health care data. J. Clin. Epidemiol. 2008, 61, 311–317. [Google Scholar] [CrossRef] [PubMed]
- Koutsoyiannis, D. Reliability Concepts in Reservoir Design. In Water Encyclopedia; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Hashimoto, T.; Stedinger, J.R.; Loucks, D.P. Reliability, resiliency, and vulnerability criteria for water resource system performance evaluation. Water Resour. Res. 1982, 18, 14–20. [Google Scholar] [CrossRef]
- Wagner, J.M.; Shamir, U.; Marks, D.H. Water distribution reliability: Simulation methods. J. Water Resour. Plan. Manag. 1988, 114, 276–294. [Google Scholar] [CrossRef]
- Van Alphen, H.-J.; van Duuren, D.; Koop, S. Decentrale Watersystemen: Potentie, Impact en Gevolgen Voor Drinkwaterbedrijven; BTO Speerpuntonderzoek: Nieuwegein, The Netherlands, 2018. [Google Scholar]
- VEWIN. Dutch Drinking Water Statistics 2017: From Source to Tap; VEWIN: Brussels, Belgium, 2017. [Google Scholar]
- Beven, K. Rainfall-Runoff Modelling; John Wiley & Sons Ltd.: Chichester, UK, 2012; ISBN 9781119951001. [Google Scholar]
- Blume, T.; Zehe, E.; Bronstert, A. Rainfall—Runoff response, event-based runoff coefficients and hydrograph separation. Hydrol. Sci. J. 2007, 52, 843–862. [Google Scholar] [CrossRef]
- Savenije, H.H.G. The runoff coefficient as the key to moisture recycling. J. Hydrol. 1996, 176, 219–225. [Google Scholar] [CrossRef]
- Thompson, D. The Rational Method. 2006. Available online: http://drdbthompson.net/writings/rational.pdf (accessed on 11 April 2019).
- Ndomba, P.M.; Wambura, F.J. Reliability of rainwater harvesting systems in suburbs. A case study of Changanyikeni in Dar es Salaam, Tanzania. Nile Basin Water Sci. Eng. 2010, 3, 72–85. [Google Scholar]
- Klein Tank, A.; Beersma, J.; Bessembinder, J.; van den Hurk, B.; Lenderink, G. KNMI ’14: Climate Scenarios for the Netherlands—A Guide for Professionals in Climate Adaption; KNMI: De Bilt, The Netherlands, 2014. [Google Scholar]
- Koutsoyiannis, D.; Economou, A. Evaluation of the parameterization-simulation-optimization approach for the control of reservoir systems. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Rani, D.; Moreira, M.M. Simulation-optimization modeling: A survey and potential application in reservoir systems operation. Water Resour. Manag. 2010, 24, 1107–1138. [Google Scholar] [CrossRef]
- Belaineh, G.; Peralta, R.C.; Hughes, T.C. Simulation/optimization modeling for water resources management. J. Water Resour. Plan. Manag. 1999, 125, 154–161. [Google Scholar] [CrossRef]
- Venkatesh, G.; Brattebø, H.; Sægrov, S.; Behzadian, K.; Kapelan, Z. Metabolism-modelling approaches to long-term sustainability assessment of urban water services. Urban Water J. 2017, 14, 11–22. [Google Scholar] [CrossRef]
- Tsoukalas, I.; Makropoulos, C.; Koutsoyiannis, D. Simulation of Stochastic Processes Exhibiting Any-Range Dependence and Arbitrary Marginal Distributions. Water Resour. Res. 2018, 54, 9484–9513. [Google Scholar] [CrossRef]
- Makropoulos, C.; Nikolopoulos, D.; Palmen, L.; Kools, S.; Segrave, A.; Vries, D.; Koop, S.; van Alphen, H.J.; Vonk, E.; van Thienen, P.; et al. A resilience assessment method for urban water systems. Urban Water J. 2018, 15, 316–328. [Google Scholar] [CrossRef]
- Abdulla, F.A.; Al-Shareef, A.W. Roof rainwater harvesting systems for household water supply in Jordan. Desalination 2009, 243, 195–207. [Google Scholar] [CrossRef]
- Rashidi Mehrabadi, M.H.; Saghafian, B.; Fashi, F.H. Assessment of residential rainwater harvesting efficiency for meeting non-potable water demands in three climate conditions. Resour. Conserv. Recycl. 2013, 73, 86–93. [Google Scholar] [CrossRef]
- Muthukumaran, S.; Baskaran, K.; Sexton, N. Quantification of potable water savings by residential water conservation and reuse—A case study. Resour. Conserv. Recycl. 2011, 55, 945–952. [Google Scholar] [CrossRef]
- Li, Z.; Boyle, F.; Reynolds, A. Rainwater harvesting and greywater treatment systems for domestic application in Ireland. Desalination 2010, 260, 1–8. [Google Scholar] [CrossRef]
- Ghisi, E.; Ferreira, D.F. Potential for potable water savings by using rainwater and greywater in a multi-storey residential building in southern Brazil. Build. Environ. 2007, 42, 2512–2522. [Google Scholar] [CrossRef]
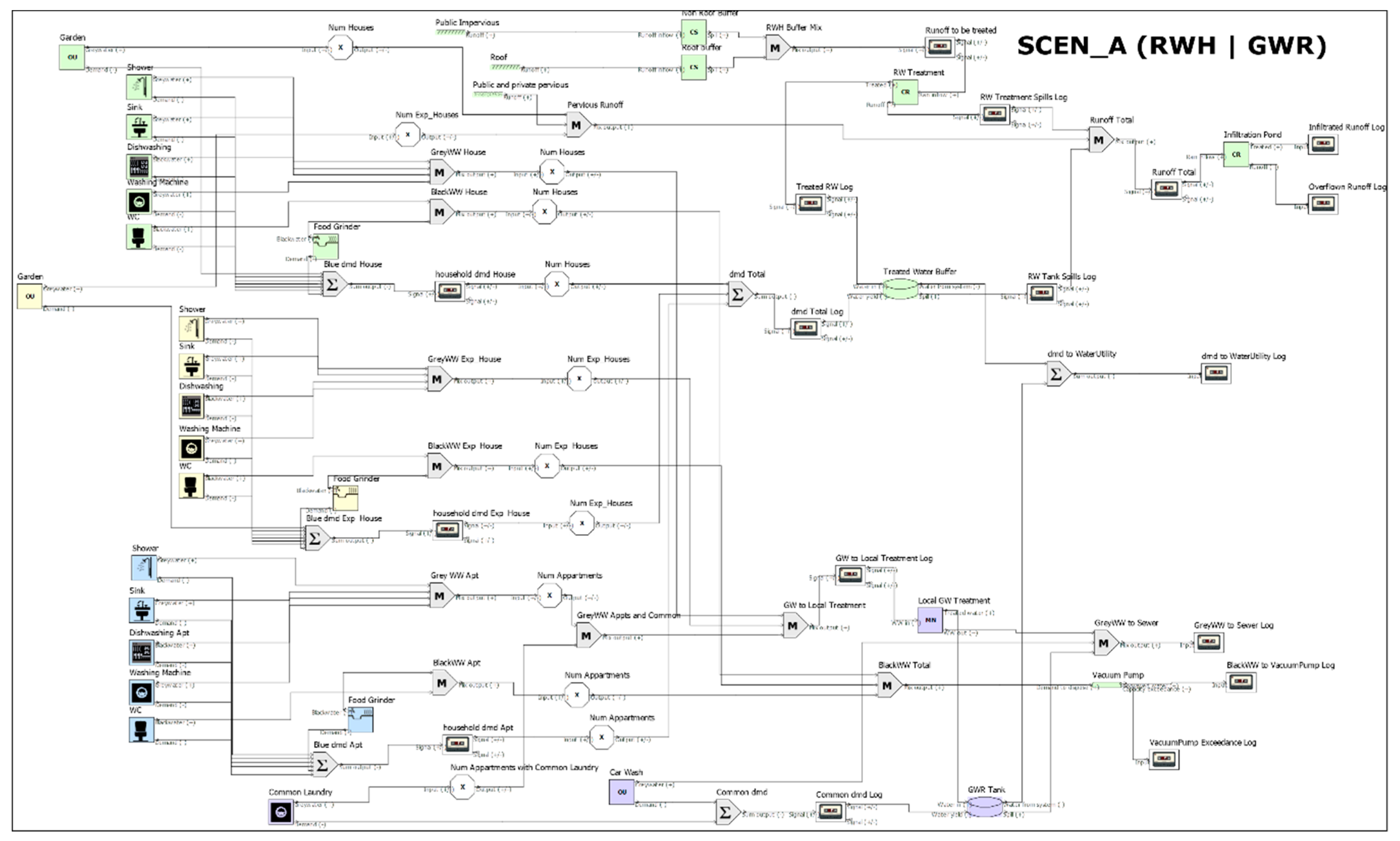
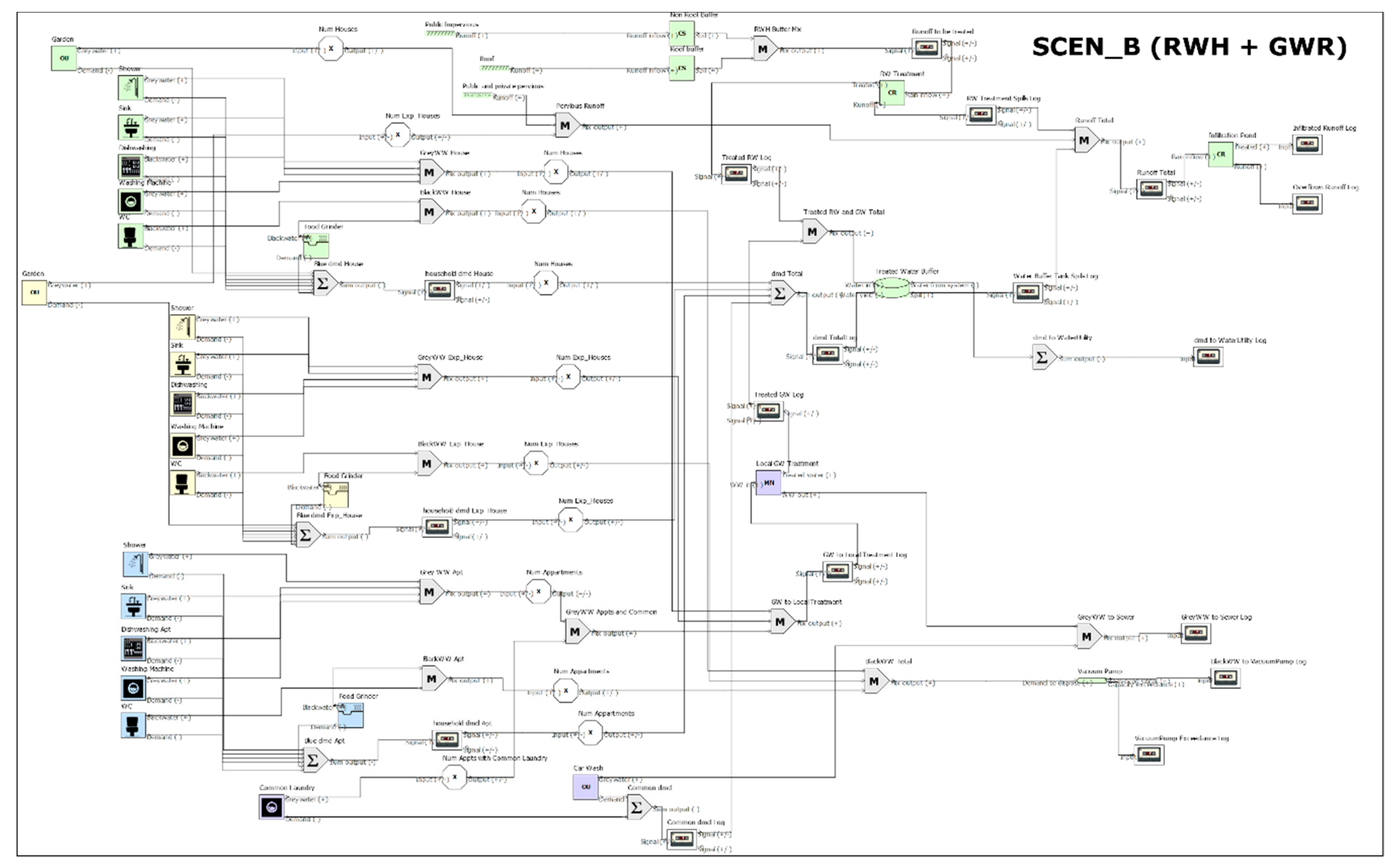
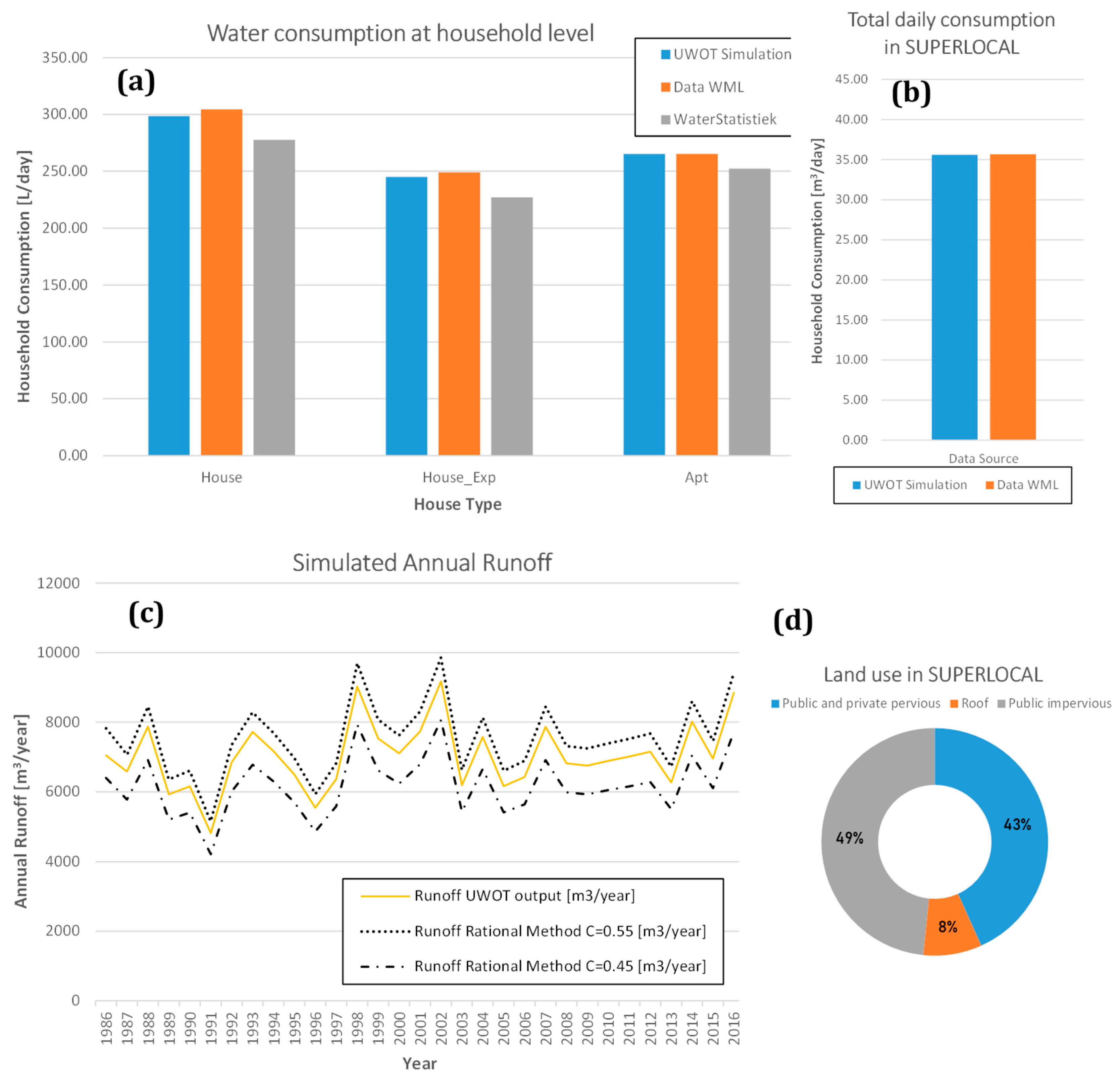
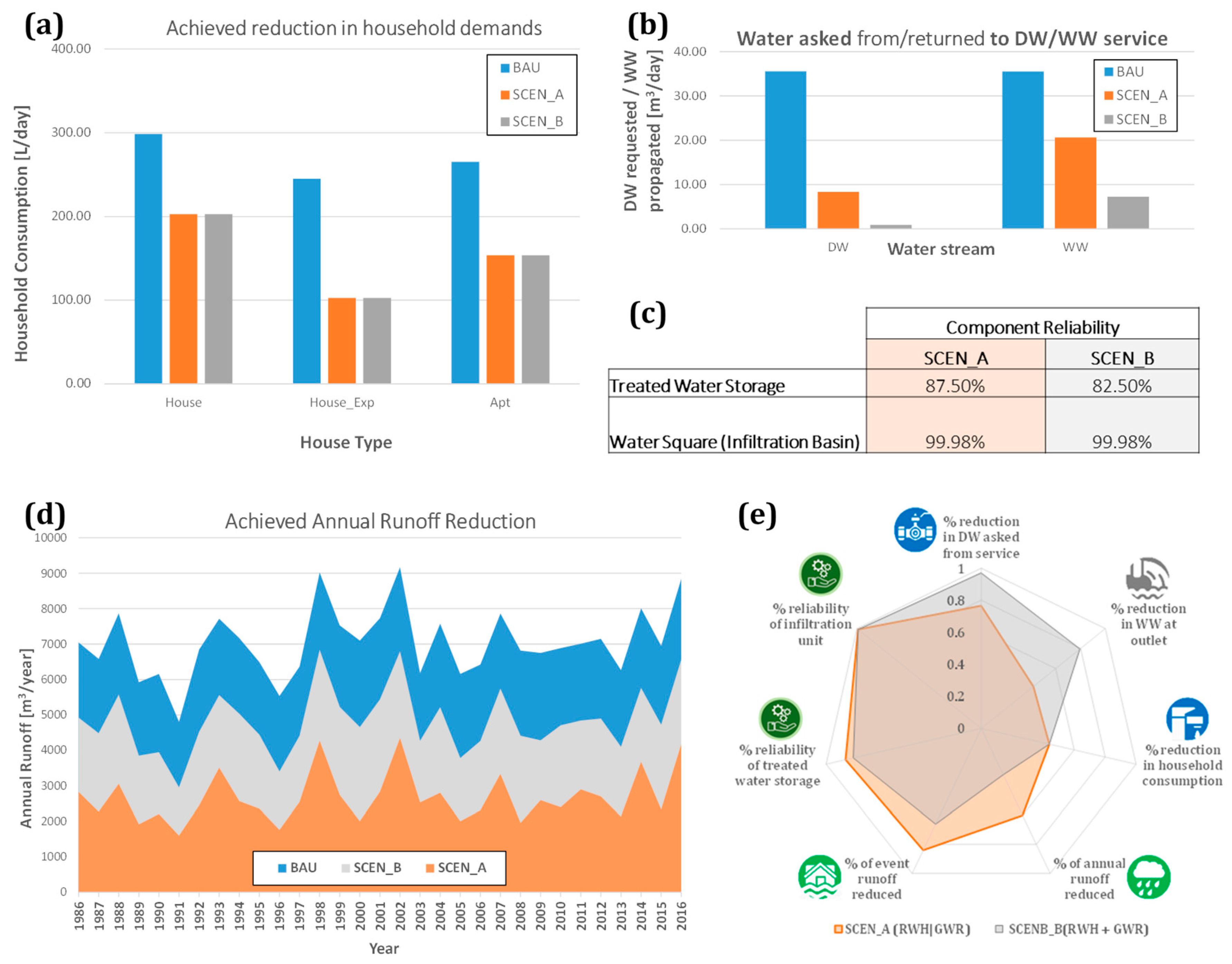
| Organization | Conventional Responsibilities | Decentralized Responsibilities (SUPERLOCAL) |
|---|---|---|
| Municipality (Kerkrade) | Rainwater management (incl. capturing, transport and discharge), sewage network (in cities) | Rainwater management (incl. capturing, transport and storage), public area development in regards rainwater harvesting, water square and infiltration services Operations: Vacuum station, sewage system (black and grey), and rainwater buffers |
| Drinking water company (WML) | Water extraction, production and distribution | Water extraction, production and distribution on a local scale Operations: connection between rainwater buffers and drinking water production (optimization) |
| Social housing corporation (HEEMwonen) | Installation of household technologies and inhouse piping | Installation of household technologies, inhouse piping and a second (vacuum) sewage system Operations: Common launderette, food grinders and car wash |
| Waste water company (WBL) | Sewage transport between municipalities and WWTP, and waste water treatment | Helophyte filter and buffers, and BW digestor Operations: pruning of helophyte filter, and residues transport |
| Unit | Houses | Experimental Houses | Apartments | Total |
|---|---|---|---|---|
| Abbreviation (Figure 2) | (a) | (b) | (c) | |
| Number of dwellings | 13 | 3 | 113 | 129 |
| Persons/dwelling (persons) | 2.2 (29) | 1.8 (5) | 2.0 (226) | 260 |
Type of toilet (n)  | Silent vacuum (13) | Standard vacuum (3) | Silent vacuum (113) | 129 |
Type of shower (n)  | Water saving (13) | Recirculation (3) | Water saving (113) | 129 |
Type washing machine (n)  | Regular (13) | Regular (3) | 50% regular (56); 50% use shared launderette (5) | 77 |
Food grinder (n)  | Water saving (13) | Water saving (3) | Large shared water saving on each level (9) | 25 |
Tap(s) (n)  | Regular (39) | Regular (6) | Regular (226) | 271 |
Outdoor tap (n)  | Regular (13) | Regular (3) | - (0) | 16 |
 = BW sewage,
= BW sewage,  = GW sewage,
= GW sewage,  = In soil
= In soil| KPI | Unit | Description | Stream | |
|---|---|---|---|---|
 1 1 | Achieved reduction in household consumption (RHC) | % of demand reduced | Tap-level WDM metric, reduction in water requested from households before RWH/GWR take place | DW—demands |
 2 2 | Reduction in (clean) water requested from central service (RDW) | % of reduction of demand requested from central service | Measure of system autonomy, dependent on al techs in place (appliances, RWH, GWR) | DW—demands |
 3 3 | Reduction in WW that leaves the system (RWW) | % of WW reduced | Measure of system autonomy or (vice versa) dependence on central services (sewer network) | Generated WW |
 4 4 | Achieved runoff reduction (RAR) | % of runoff reduced (annual) | Measure of the SUPERLOCAL ability to hold water | Runoff |
 5 5 | Achieved flood event reduction (RER) | % of event-based runoff reduced | Measure of the SUPERLOCAL ability to mitigate flood peaks | Runoff |
 6 6 | System design reliability (REL) | % of time steps that the system operated well | How reliable different parts of the system are against inefficiency (storage full, overflow) | Runoff |
| Overview | 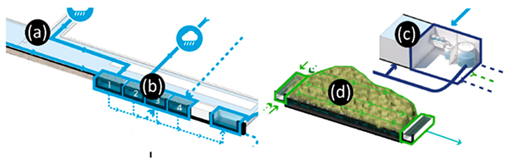 | |
|---|---|---|
| Surfaces | Area (m2) | Other Relevant Quantities |
| Public and private pervious | 8000 | Soil infiltration rate estimated at 0.10–0.15 m/day in all pervious areas |
| Roof | 1543 | |
| Public impervious (a) | 8942 | |
| Buffers | Storage (m3) | Other Relevant Quantities |
| RWH buffers (b) | 300 | Roof- 60 m3, non-roof- 190 m3, and mixed buffer 50 m3 |
| Potable water (DW) buffer | 50 | |
| Water square | 450 | Area 1000 m2, depth of 0.45 m, infiltration capacity 0.10–0.15 m/day |
| GW buffer | 27 | |
| Filtered GW buffer | 20 | |
| BW buffer | 40 | |
| Purification | Treatment Cap (m3/day) | Other Relevant Quantities |
| DW purification (c) | 30 (mean)/180 (max) | |
| Helophyte filter (vertical) (d) | 14.4 | Surface area of 400 m2 or smaller when aeration is added |
| Vacuum pump | 2.2 | |
| GW purification | 7.2 (mean)/15 (max) | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouziotas, D.; van Duuren, D.; van Alphen, H.-J.; Frijns, J.; Nikolopoulos, D.; Makropoulos, C. Towards Circular Water Neighborhoods: Simulation-Based Decision Support for Integrated Decentralized Urban Water Systems. Water 2019, 11, 1227. https://doi.org/10.3390/w11061227
Bouziotas D, van Duuren D, van Alphen H-J, Frijns J, Nikolopoulos D, Makropoulos C. Towards Circular Water Neighborhoods: Simulation-Based Decision Support for Integrated Decentralized Urban Water Systems. Water. 2019; 11(6):1227. https://doi.org/10.3390/w11061227
Chicago/Turabian StyleBouziotas, Dimitrios, Diederik van Duuren, Henk-Jan van Alphen, Jos Frijns, Dionysios Nikolopoulos, and Christos Makropoulos. 2019. "Towards Circular Water Neighborhoods: Simulation-Based Decision Support for Integrated Decentralized Urban Water Systems" Water 11, no. 6: 1227. https://doi.org/10.3390/w11061227
APA StyleBouziotas, D., van Duuren, D., van Alphen, H.-J., Frijns, J., Nikolopoulos, D., & Makropoulos, C. (2019). Towards Circular Water Neighborhoods: Simulation-Based Decision Support for Integrated Decentralized Urban Water Systems. Water, 11(6), 1227. https://doi.org/10.3390/w11061227







