Attribution Analysis of Dry Season Runoff in the Lhasa River Using an Extended Hydrological Sensitivity Method and a Hydrological Model
Abstract
1. Introduction
2. Methods
2.1. Preliminary Data Analysis
2.2. Statistical Methods
2.2.1. Trend Analysis Method
2.2.2. Abrupt Change Analysis
2.3. Coupled Water–Energy Balance Equation at an Arbitrary Time Scale
2.4. Extended Hydrological Sensitivity Method
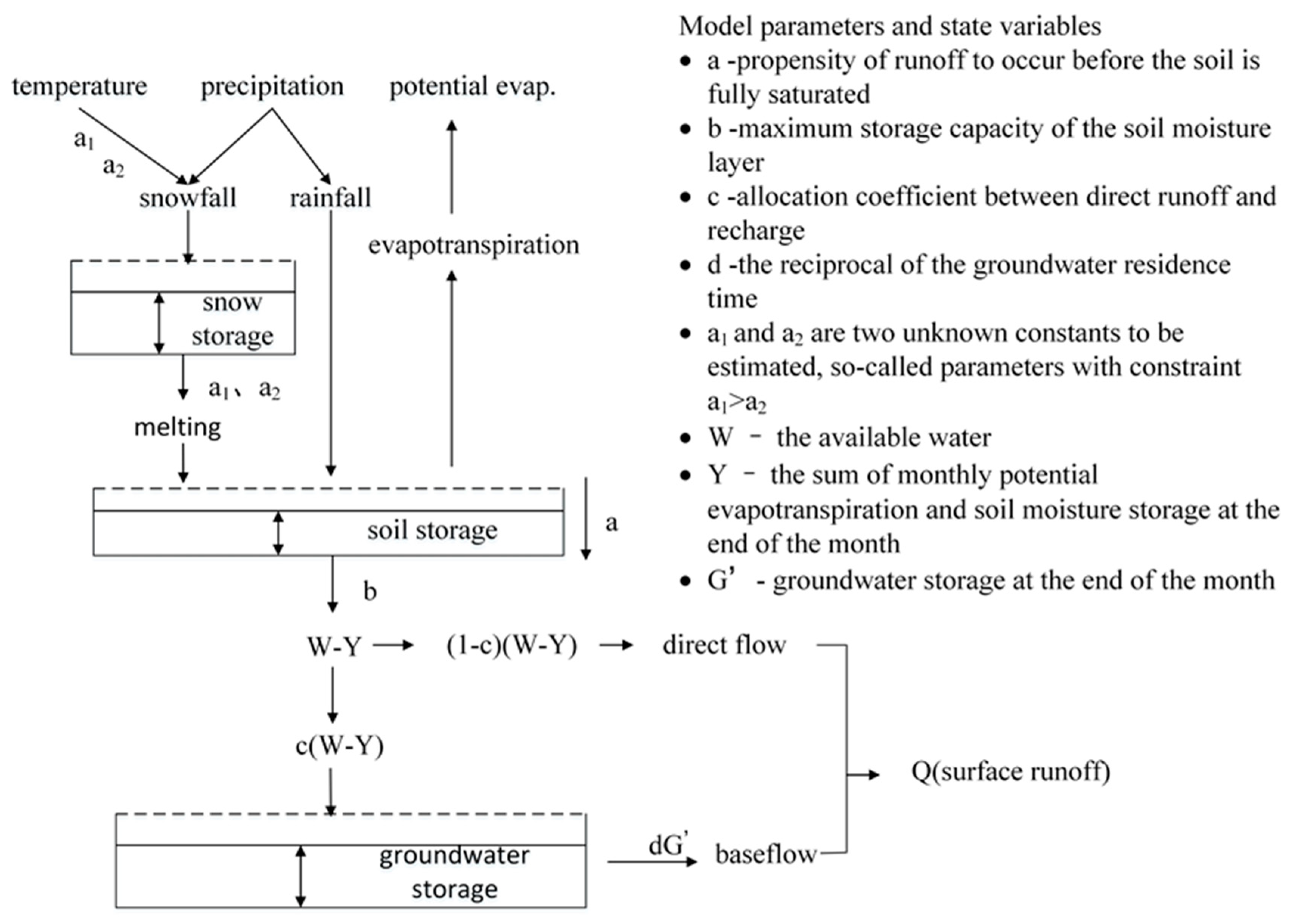
2.5. An Improved ABCD Model with a Snow Melt Module
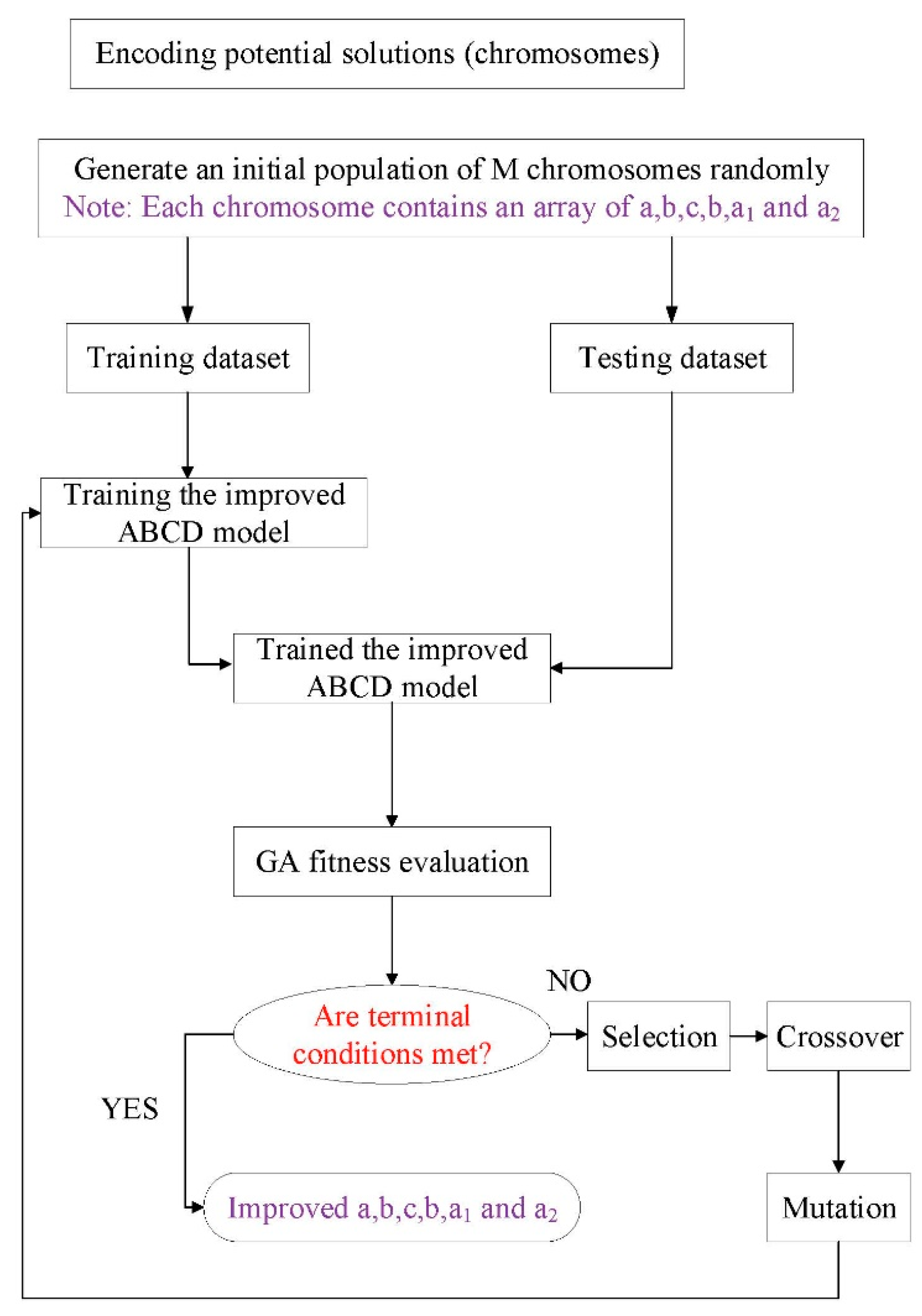
2.6. Genetic Algorithm Mehtod
3. Study Area and Data Sources
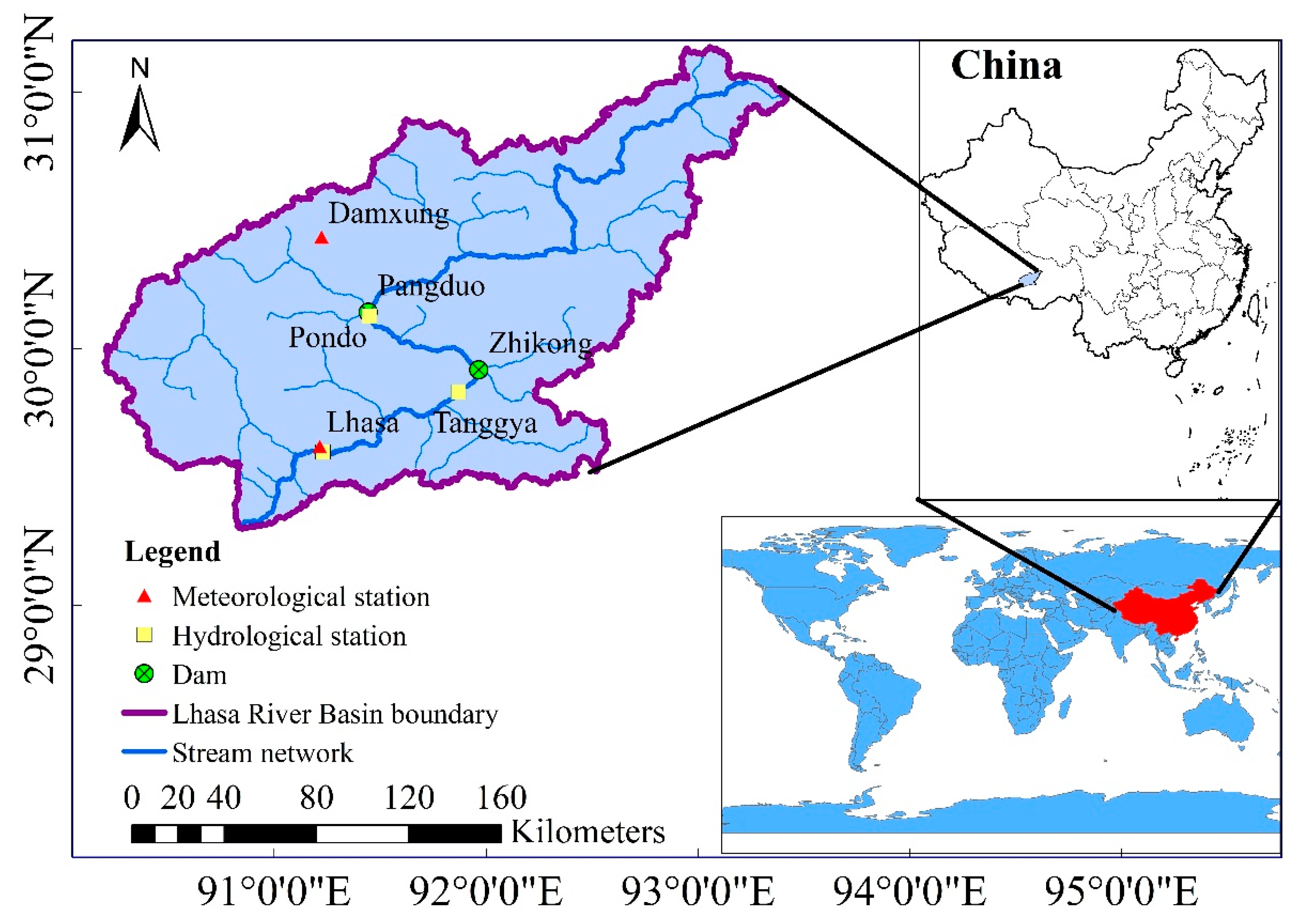
3.1. Study Area Description
3.2. Data
4. Results and Discussion
4.1. Preliminary Data Analysis
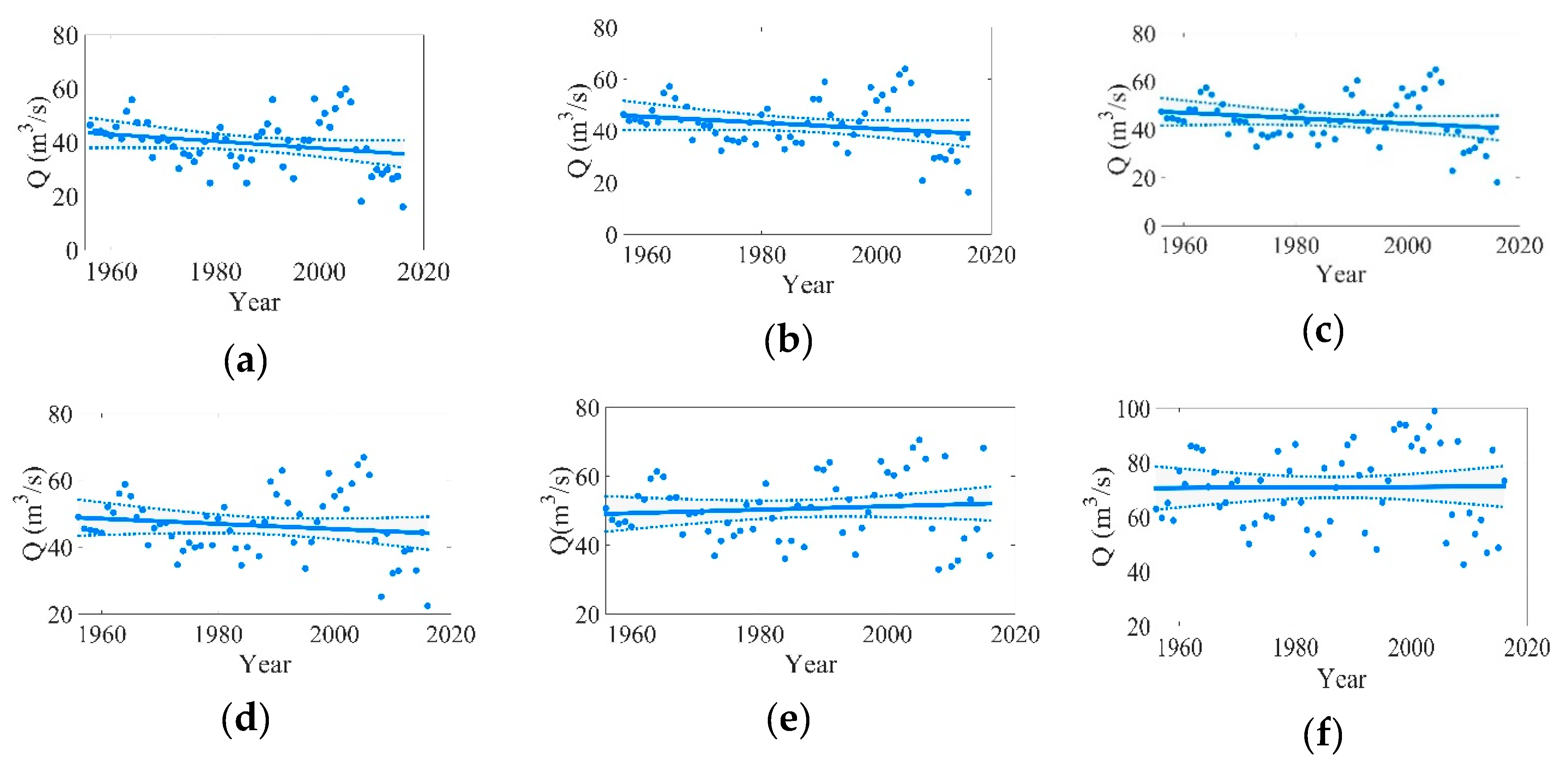
4.2. Trends for Runoff, Precipitation, and Potential Evapotranspiration during the Dry Season
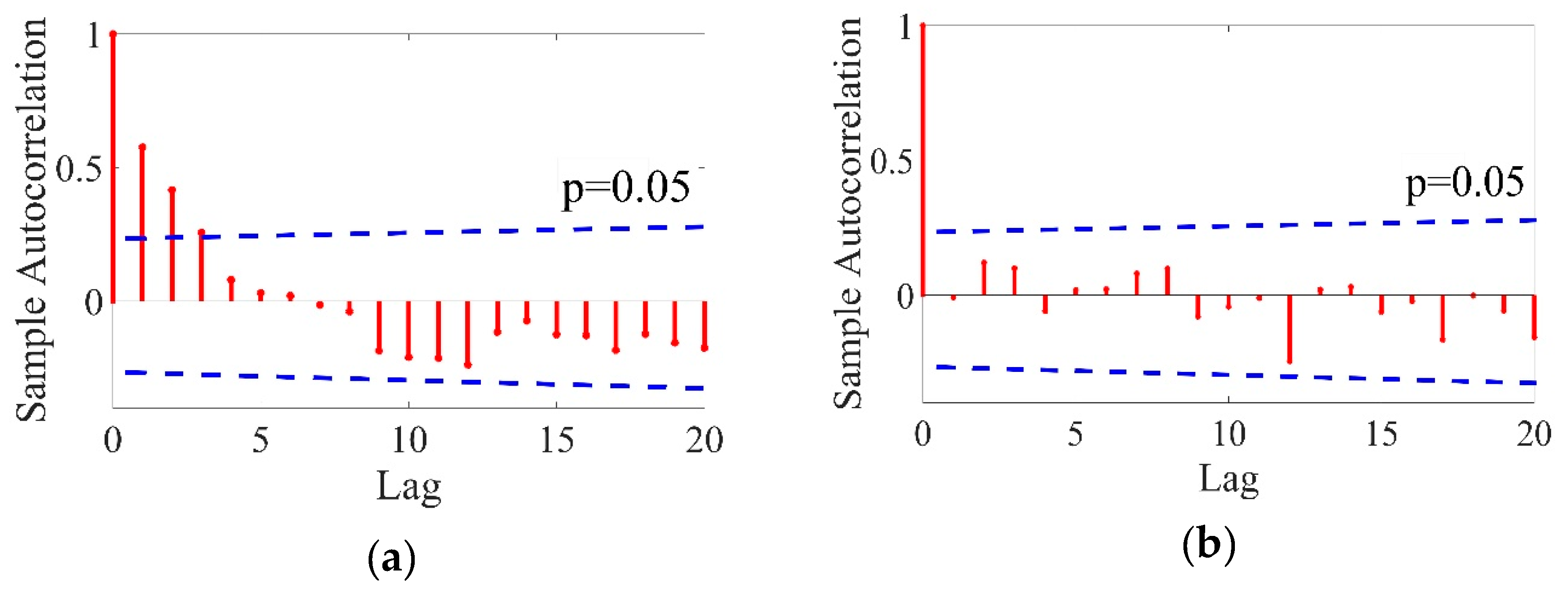
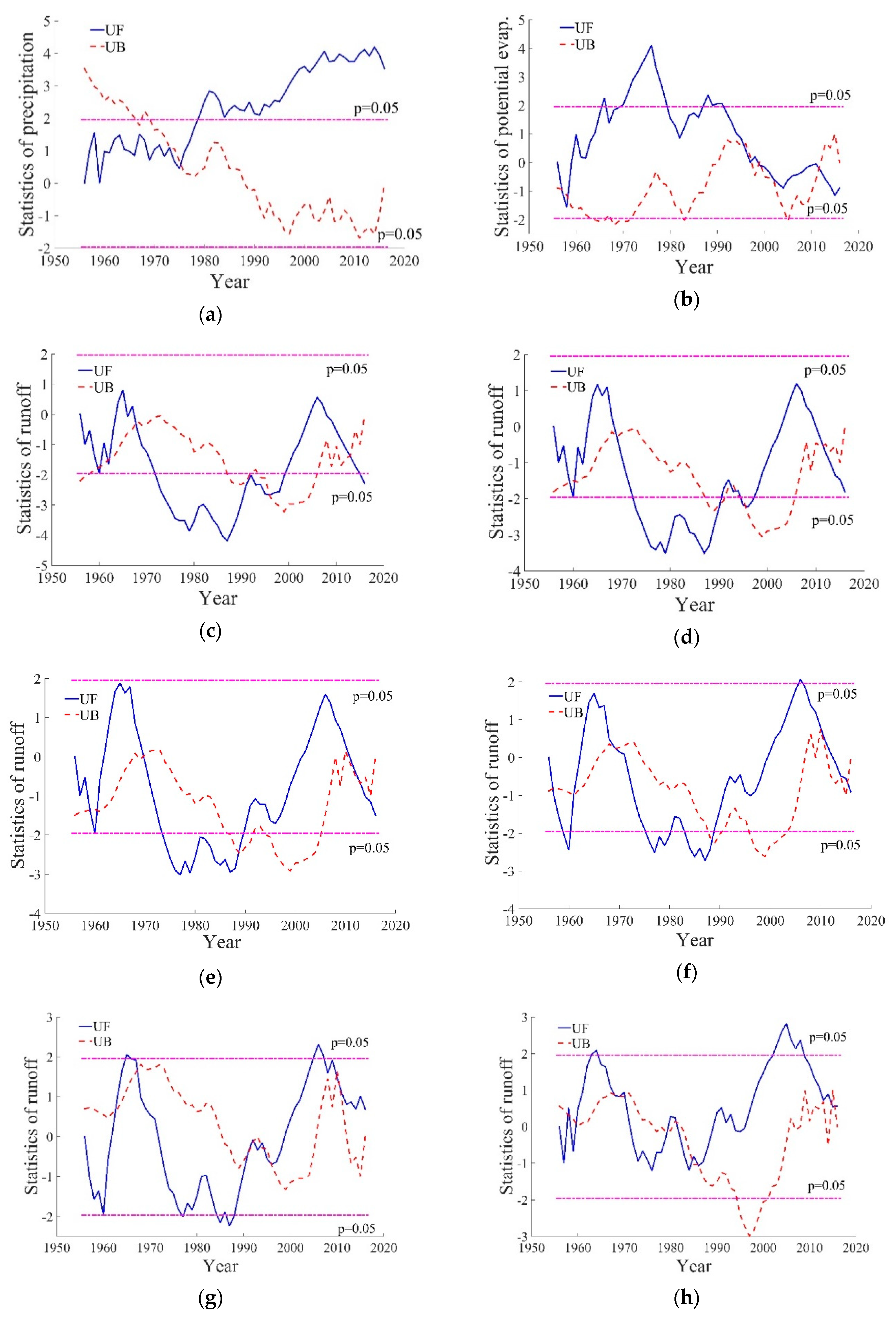
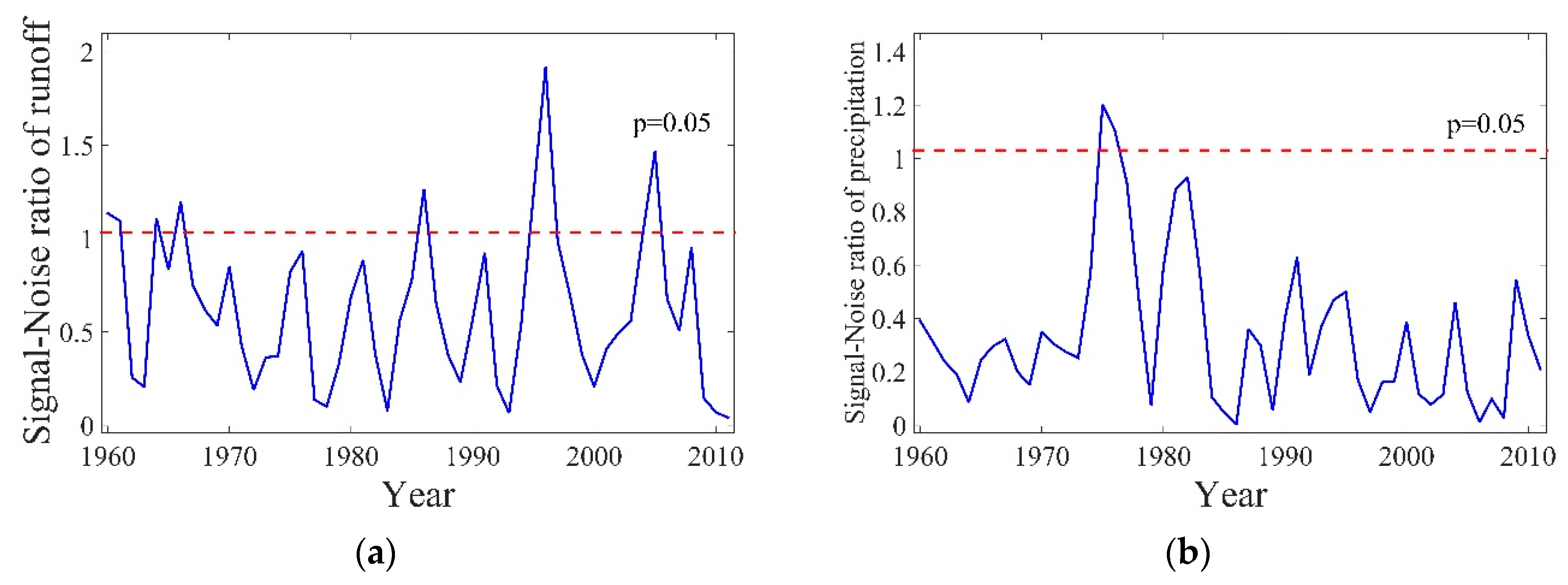
4.3. Change Point Identification of Hydro-Climatic Variables
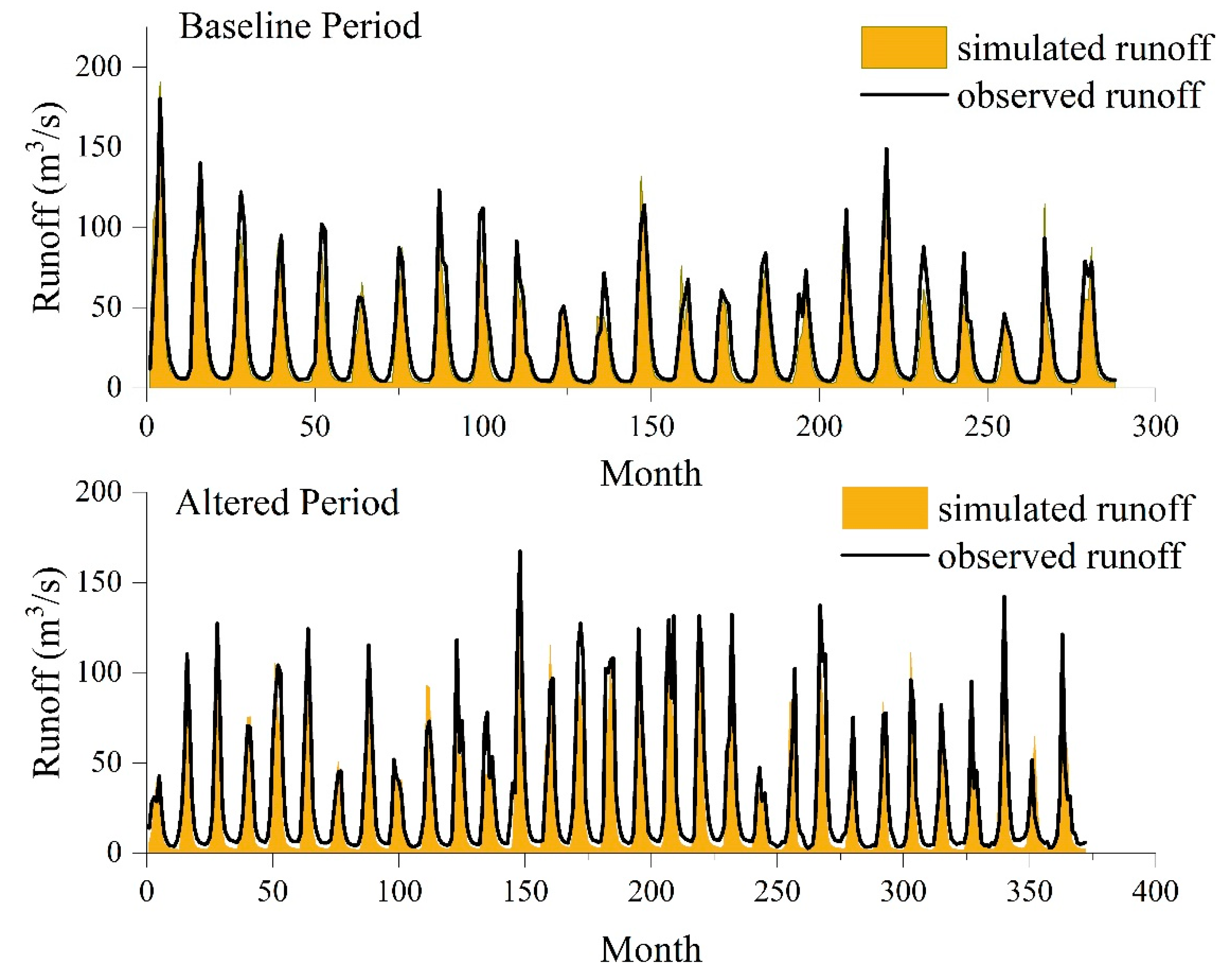
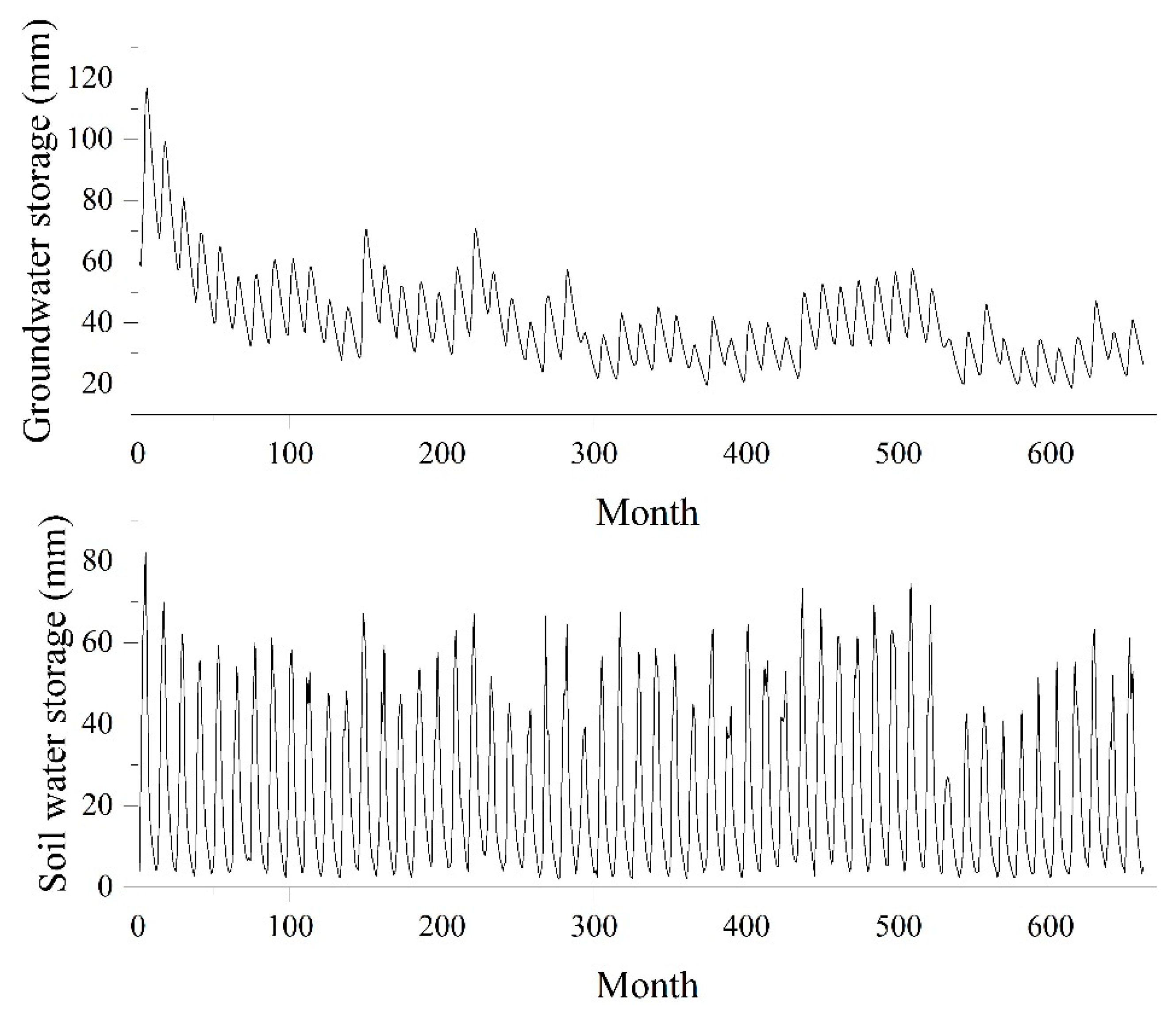
4.4. Modeling Dry Season Water Storage Change
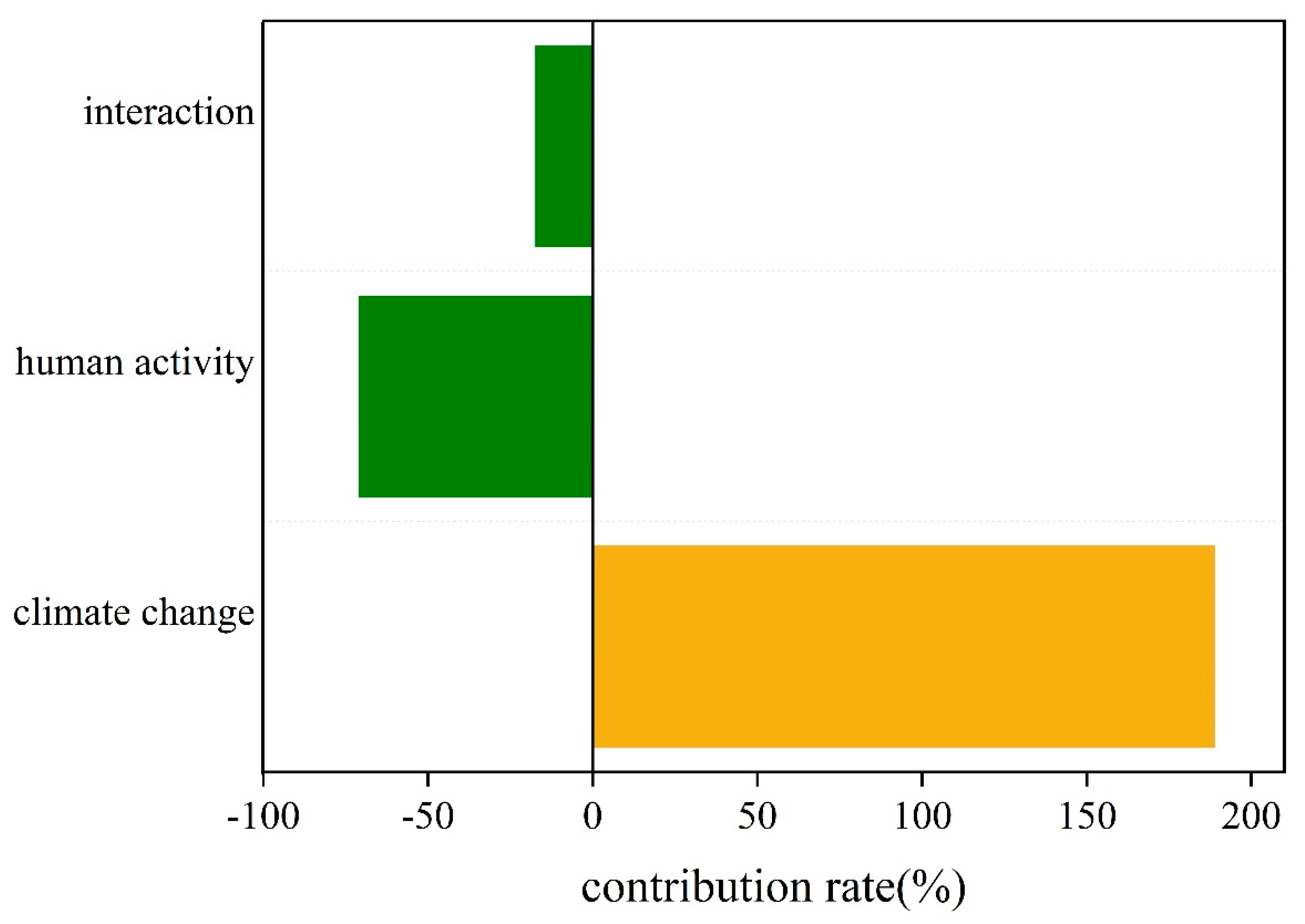
4.5. Quantitative Assessment of the Impacts of Climate Change and Anthropogenic Activities on Streamflow
4.6. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wu, X.; Li, Z.; Gao, P.; Huang, C.; Hu, T. Response of the Downstream Braided Channel to Zhikong Reservoir on Lhasa River. Water 2018, 10, 1144. [Google Scholar] [CrossRef]
- Fan, J.; Sun, W.; Zhao, Y.; Xue, B.; Zuo, D.; Xu, Z. Trend Analyses of Extreme Precipitation Events in the Yarlung Zangbo River Basin, China Using a High-Resolution Precipitation Product. Sustainability 2018, 10, 1396. [Google Scholar] [CrossRef]
- Makokha, G.O.; Wang, L.; Zhou, J.; Li, X.P.; Wang, A.H.; Wang, G.P.; Kuria, D. Quantitative drought monitoring in a typical cold river basin over Tibetan Plateau: An integration of meteorological, agricultural and hydrological droughts. J. Hydrol. 2016, 543, 782–795. [Google Scholar] [CrossRef]
- You, Q.; Kang, S.; Wu, Y.; Yan, Y. Climate change over the yarlung zangbo river basin during 1961–2005. J. Geogr. Sci. 2007, 17, 409–420. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, Y.; Yao, Z.; Gong, T.; Wang, H.; Chu, D.; Liu, L.; Zhang, F. The trend on runoff variations in the Lhasa River Basin. J. Geogr. Sci. 2008, 18, 95–106. [Google Scholar] [CrossRef]
- Liu, J.; Xie, J.; Gong, T.; Wang, H.; Xie, Y. Impacts of winter warming and permafrost degradation on water variability, upper Lhasa River, Tibet. Quat. Int. 2011, 244, 178–184. [Google Scholar] [CrossRef]
- Foulon, E.; Rousseau, A.N. Surface Water Quantity for Drinking Water during Low Flows—Sensitivity Assessment Solely from Climate Data. Water Resour. Manag. 2019, 33, 369–385. [Google Scholar] [CrossRef]
- Guzha, A.C.; Rufino, M.C.; Okoth, S.; Jacobs, S.; Nobrega, R. Impacts of land use and land cover change on surface runoff, discharge and low flows: Evidence from East Africa. J. Hydrol.-Reg. Stud. 2018, 15, 49–67. [Google Scholar] [CrossRef]
- Hanasaki, N.; Yoshikawa, S.; Pokhrel, Y.; Kanae, S. A global hydrological simulation to specify the sources of water used by humans. Hydrol. Earth Syst. Sci. 2018, 22, 789–817. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Kanae, S.; Seneviratne, S.I.; Handmer, J.; Nicholls, N.; Peduzzi, P.; Mechler, R.; Bouwer, L.M.; Arnell, N.; Mach, K.; et al. Flood risk and climate change: global and regional perspectives. Hydrol. Sci. J. 2014, 59, 1–28. [Google Scholar] [CrossRef]
- Mishra, V.; Cherkauer, K.A.; Niyogi, D.; Lei, M.; Pijanowski, B.C.; Ray, D.K.; Bowling, L.C.; Yang, G.X. A regional scale assessment of land use/land cover and climatic changes on water and energy cycle in the upper Midwest United States. Int. J. Climatol. 2010, 30, 2025–2044. [Google Scholar] [CrossRef]
- Napoli, M.; Massetti, L.; Orlandini, S. Hydrological response to land use and climate changes in a rural hilly basin in Italy. Catena 2017, 157, 1–11. [Google Scholar] [CrossRef]
- Tomer, M.D.; Schilling, K.E. A simple approach to distinguish land-use and climate-change effects on watershed hydrology. J. Hydrol. 2009, 376, 24–33. [Google Scholar] [CrossRef]
- Umar, D.A.; Ramli, M.F.; Aris, A.Z.; Jamil, N.R.; Abdulkareem, J.H. Runoff irregularities, trends, and variations in tropical semi-arid river catchment. J. Hydrol.-Reg. Stud. 2018, 19, 335–348. [Google Scholar] [CrossRef]
- Wu, J.; Miao, C.; Wang, Y.; Duan, Q.; Zhang, X. Contribution analysis of the long-term changes in seasonal runoff on the Loess Plateau, China, using eight Budyko-based methods. J. Hydrol. 2017, 545, 263–275. [Google Scholar] [CrossRef]
- Zhang, L.; Nan, Z.; Yu, W.; Zhao, Y.; Xu, Y. Comparison of baseline period choices for separating climate and land use/land cover change impacts on watershed hydrology using distributed hydrological models. Sci. Total Environ. 2018, 622–623, 1016–1028. [Google Scholar] [CrossRef] [PubMed]
- Bu, J.; Lu, C.; Niu, J.; Gao, Y. Attribution of Runoff Reduction in the Juma River Basin to Climate Variation, Direct Human Intervention, and Land Use Change. Water 2018, 10, 1775. [Google Scholar] [CrossRef]
- Li, C.; Wang, L.; Wanrui, W.; Qi, J.; Linshan, Y.; Zhang, Y.; Lei, W.; Cui, X.; Wang, P. An analytical approach to separate climate and human contributions to basin streamflow variability. J. Hydrol. 2018, 559, 30–42. [Google Scholar] [CrossRef]
- Yang, H.; Yang, D. Derivation of climate elasticity of runoff to assess the effects of climate change on annual runoff. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Dey, P.; Mishra, A. Separating the impacts of climate change and human activities on streamflow: A review of methodologies and critical assumptions. J. Hydrol. 2017, 548, 278–290. [Google Scholar] [CrossRef]
- Chen, X.; Alimohammadi, N.; Wang, D. Modeling interannual variability of seasonal evaporation and storage change based on the extended Budyko framework. Water Resour. Res. 2013, 49, 6067–6078. [Google Scholar] [CrossRef]
- Zhang, L.; Potter, N.; Hickel, K.; Zhang, Y.; Shao, Q. Water balance modeling over variable time scales based on the Budyko framework – Model development and testing. J. Hydrol. 2008, 360, 117–131. [Google Scholar] [CrossRef]
- Wang, D.B.; Alimohammadi, N. Responses of annual runoff, evaporation, and storage change to climate variability at the watershed scale. Water Resour. Res. 2012, 48, 5546. [Google Scholar] [CrossRef]
- Han, P.-F.; Wang, X.-S.; Istanbulluoglu, E. A Null-Parameter Formula of Storage–evapotranspiration Relationship at Catchment Scale and its Application for a New Hydrological Model. J. Geophys. Res. Atmospheres 2018, 123, 2082–2097. [Google Scholar] [CrossRef]
- Jiang, C.; Xiong, L.; Wang, D.; Liu, P.; Guo, S.; Xu, C.-Y. Separating the impacts of climate change and human activities on runoff using the Budyko-type equations with time-varying parameters. J. Hydrol. 2015, 522, 326–338. [Google Scholar] [CrossRef]
- Yang, H.; Yang, D.; Lei, Z.; Lei, H. Derivation and validation of watershed coupled water–energy balance equation at arbitrary time scale (in Chinese). J. Hydraul. Eng. 2008, 610–617. [Google Scholar]
- Wang, X. Advances in separating effects of climate variability and human activity on stream discharge: An overview. Adv. Water Resour. 2014, 71, 209–218. [Google Scholar] [CrossRef]
- Razali, N.M.; Wah, Y.B. Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests. J. Stat. Model. Anal. 2011, 2, 21–33. [Google Scholar]
- Kim, I.; Park, S. Likelihood ratio tests for multivariate normality. Commun. Stat. Theory Methods 2018, 47, 1923–1934. [Google Scholar] [CrossRef]
- Royston, P. Approximating the Shapiro–Wilk W-test for non-normality. Stat. Comput. 1992, 2, 117–119. [Google Scholar] [CrossRef]
- Buishand, T.A. Some methods for testing the homogeneity of rainfall records. J. Hydrol. 1982, 58, 11–27. [Google Scholar] [CrossRef]
- Pettitt, A.N. A Non-Parametric Approach to the Change-Point Problem. J. R. Stat. Soc. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Hirsch, R.M.; Slack, J.R.; Smith, R.A. Techniques of Trend Analysis for Monthly Water-Quality Data. Water Resour. Res. 1982, 18, 107–121. [Google Scholar] [CrossRef]
- Shadmani, M.; Marofi, S.; Roknian, M. Trend Analysis in Reference Evapotranspiration Using Mann–Kendall and Spearman’s Rho Tests in Arid Regions of Iran. Water Resour. Manag. 2012, 26, 211–224. [Google Scholar] [CrossRef]
- Poncela, P. Time series analysis by state space methods. Int. J. Forecast. 2004, 20, 139–141. [Google Scholar] [CrossRef]
- Haario, H.; Laine, M.; Mira, A.; Saksman, E. DRAM: Efficient adaptive MCMC. Stat. Comput. 2006, 16, 339–354. [Google Scholar] [CrossRef]
- Mikkonen, S.; Laine, M.; Mäkelä, H.M.; Gregow, H.; Tuomenvirta, H.; Lahtinen, M.; Laaksonen, A. Trends in the average temperature in Finland, 1847–2013. Stoch. Environ. Res. Risk Assess. 2015, 29, 1521–1529. [Google Scholar] [CrossRef]
- Laine, M.; Latva-Pukkila, N.; Kyrölä, E. Analysing time-varying trends in stratospheric ozone time series using the state space approach. Atmos. Chem. Phys. 2014, 14, 9707–9725. [Google Scholar] [CrossRef]
- Goossens, C.; Berger, A. How to Recognize an Abrupt Climatic Change? D. Reidel Publishing Company: Dordrecht, Holland, 1987. [Google Scholar]
- Mann, H.B. Nonparametric Tests against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Yamamoto, R.; Iwashima, T.; Sanga, N.K.; Hoshiai, M. An Analysis of Climatic Jump. J. Meteorol. Soc. Jpn. 1986, 64, 273–281. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C. Applicability of prewhitening to eliminate the influence of serial correlation on the Mann–Kendall test. WATER Resour. Res. 2002, 38. [Google Scholar] [CrossRef]
- Von Storch, H. Misuses of Statistical Analysis in Climate Research. In Analysis of Climate Variability: Applications of Statistical Techniques; von Storch, H., Navarra, A., Eds.; Springer: Berlin/Heidelberg, Germany, 1995; pp. 11–26. ISBN 978-3-662-03167-4. [Google Scholar]
- Salas, J.D. Applied Modeling of Hydrologic Time Series; Water Resources Publications: Littleton, CO, USA, 1980; Available online: https://www.researchgate.net/publication/243784685_Applied_Modeling_of_Hydrologic_Time_Series/ (accessed on 6 June 2019).
- Moraes, J.M.; Pellegrino, G.Q.; Ballester, M.V.; Martinelli, L.A.; Victoria, R.L.; Krusche, A.V. Trends in Hydrological Parameters of a Southern Brazilian Watershed and its Relation to Human Induced Changes. Water Resour. Manag. 1998, 12, 295–311. [Google Scholar] [CrossRef]
- Roderick, M.L.; Farquhar, G.D. A simple framework for relating variations in runoff to variations in climatic conditions and catchment properties. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Yang, H.; Yang, D.; Lei, Z.; Sun, F. New analytical derivation of the mean annual water–energy balance equation. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Konapala, G.; Valiya Veettil, A.; Mishra, A.K. Teleconnection between low flows and large-scale climate indices in Texas River basins. Stoch. Environ. Res. Risk Assess. 2018, 32, 2337–2350. [Google Scholar] [CrossRef]
- Ye, X.; Zhang, Q.; Liu, J.; Li, X.; Xu, C. Distinguishing the relative impacts of climate change and human activities on variation of streamflow in the Poyang Lake catchment, China. J. Hydrol. 2013, 494, 83–95. [Google Scholar] [CrossRef]
- Thomas, H.A., Jr. Improved Methods for National Water Assessment, Water Resources Contract: WR15249270; US Water Resources Council: Washington, DC, USA, 1981. Available online: https://pubs.er.usgs.gov/publication/70046351 (accessed on 6 June 2019).
- Alley, W.M. On The Treatment Of Evapotranspiration, Soil-Moisture Accounting, And Aquifer Recharge In Monthly Water-Balance Models. Water Resour. Res. 1984, 20, 1137–1149. [Google Scholar] [CrossRef]
- Pellicer Martinez, F.; Martínez Paz, J.M. Contrast and transferability of parameters of lumped water balance models in the Segura River Basin (Spain). Water Environ. J. 2015, 29, 43–50. [Google Scholar] [CrossRef]
- Shahid, M.; Cong, Z.; Zhang, D. Understanding the impacts of climate change and human activities on streamflow: A case study of the Soan River basin, Pakistan. Theor. Appl. Climatol. 2018, 134, 205–219. [Google Scholar] [CrossRef]
- Xu, C.Y.; Seibert, J.; Halldin, S.; Uppsala, U. Regional water balance modelling in the NOPEX area: Development and application of monthly water balance models. J. Hydrol. 1996, 180, 211–236. [Google Scholar] [CrossRef]
- Chang, F.-J.; Chen, L. Real-Coded Genetic Algorithm for Rule-Based Flood Control Reservoir Management. Water Resour. Manag. 1998, 12, 185–198. [Google Scholar] [CrossRef]
- Liu, P.; Li, L.; Guo, S.; Xiong, L.; Zhang, W.; Zhang, J.; Xu, C.-Y. Optimal design of seasonal flood limited water levels and its application for the Three Gorges Reservoir. J. Hydrol. 2015, 527, 1045–1053. [Google Scholar] [CrossRef]
- Farzin, S.; Singh, V.P.; Karami, H.; Farahani, N.; Ehteram, M.; Kisi, O.; Allawi, M.F.; Mohd, N.S.; El-Shafie, A. Flood Routing in River Reaches Using a Three-Parameter Muskingum Model Coupled with an Improved Bat Algorithm. Water 2018, 10, 1130. [Google Scholar] [CrossRef]
- Shi, H.; Fu, X.; Chen, J.; Wang, G.; Li, T. Spatial distribution of monthly potential evaporation over mountainous regions: case of the Lhasa River basin, China. Hydrol. Sci. J. 2014, 59, 1856–1871. [Google Scholar] [CrossRef]
- Luo, H.; Tang, Y.; Zhu, X.; Di, B.; Xu, Y. Greening trend in grassland of the Lhasa River Region on the Qinghai-Tibetan Plateau from 1982 to 2013. Rangel. J. 2016, 38, 591–603. [Google Scholar] [CrossRef]
- Ge, S.; Wu, Q.B.; Lu, N.; Jiang, G.L.; Ball, L. Groundwater in the Tibet Plateau, western China. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Smith, C.; Clark, M.; Broll, G.; Ping, C.L.; Kimble, J.M.; Luo, G. Characterization of selected soils from the Lhasa region of Qinghai-Xizang Plateau, SW China. Permafr. Periglac. Process. 1999, 10, 211–222. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.; Liu, C.; Bai, P.; Liu, X. A Flexible Framework HydroInformatic Modeling System—HIMS. Water 2018, 10, 962. [Google Scholar] [CrossRef]
- Liu, Z.; Yao, Z.; Huang, H.; Wu, S.; Liu, G. Land use and climate changes and their impacts on runoff in the Yarlung Zangbo River Basin, China. Land Degrad. Dev. 2014, 25, 203–215. [Google Scholar] [CrossRef]
| Linear Terms | Coupled Terms | Nonlinear Terms |
|---|---|---|
| Months | Jan. | Feb. | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sept. | Oct. | Nov. | Dec. | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Runoff (m3/s) | Maximum | 85.5 | 74.3 | 78.9 | 172 | 385 | 1020 | 1370 | 1800 | 1310 | 439 | 191 | 109 |
| Minimum | 33.6 | 26 | 31.4 | 36.3 | 38.8 | 121 | 309 | 203 | 141 | 87.3 | 59.5 | 41.1 | |
| Average | 57.5 | 51.1 | 50.2 | 62.1 | 124.6 | 398.0 | 749.0 | 849.9 | 630.0 | 265.8 | 125.1 | 77.9 | |
| Precipitation (mm) | Maximum | 5.5 | 18.9 | 19.3 | 26.2 | 78.3 | 192.5 | 258.9 | 283.2 | 147.2 | 38.4 | 22.4 | 12.7 |
| Minimum | 0 | 0 | 0 | 0 | 0.2 | 5.9 | 35.3 | 29 | 11 | 0 | 0 | 0 | |
| Average | 0.6 | 1.2 | 2.5 | 6.9 | 27.2 | 76.8 | 126.8 | 130.3 | 62.0 | 8.1 | 1.2 | 0.6 | |
| Series | Number of Years | Spearman’s Test | Mann–Kendall Test | ||||
|---|---|---|---|---|---|---|---|
| r | Threshold | Tendency | z | Threshold | Tendency | ||
| Annual minimum 1-day flow | 61 | −0.28 * | 0.25 |  | −2.24 * | 1.96 |  |
| Annual minimum 3-day flow | 61 | −0.23 | 0.25 | 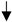 | −1.80 | 1.96 | 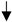 |
| Annual minimum 7-day flow | 61 | −0.20 | 0.25 | 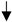 | −1.49 | 1.96 | 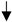 |
| Annual minimum 30-day flow | 61 | −0.14 | 0.25 |  | −0.89 | 1.96 |  |
| Annual minimum 90-day flow | 61 | 0.07 | 0.25 |  | 0.68 | 1.96 |  |
| Annual dry-seasonal flow* | 61 | 0.06 | 0.25 |  | 0.55 | 1.96 |  |
 represents a decreasing trend;
represents a decreasing trend;  represents an increasing trend. * Indicates significance at the 0.05 level. Annual dry season flow represents average seasonal runoff from November to April.
represents an increasing trend. * Indicates significance at the 0.05 level. Annual dry season flow represents average seasonal runoff from November to April.| Model | Calibration Method | Spin-Up Period | Baseline Period | Altered Period | ||
|---|---|---|---|---|---|---|
| Calibration Periods | Validation Periods | Calibration Periods | Validation Periods | |||
| Improved ABCD model | Genetic algorithm | 1956.5–1962.4 | 1962.5–1970.4 | 1970.5–1986.4 | 1986.5–1996.4 | 1996.5–2017.4 |
| Nash-Sutcliffe Efficiency | a | b | c | d | a1 | a2 | ||
|---|---|---|---|---|---|---|---|---|
| Range | / | 0~1 | 0~200 | 0~1 | 0~20 | 0~30 | −20~20 | |
| Baseline period | Calibration periods | 0.86 | 0.64 | 199.97 | 0.16 | 0.08 | 18.4 | 9.2 |
| Validation periods | 0.84 | |||||||
| Altered period | Calibration periods | 0.83 | 0.65 | 199.98 | 0.11 | 0.07 | 14.5 | 9.5 |
| Validation periods | 0.81 | |||||||
| Period | Pdry | Rdry | DSdry | Edry |
|---|---|---|---|---|
| Baseline period (1962–1985) | 454.3 | 799.8 | −1026.7 | 681.1 |
| Altered period (1986–2016) | 753.9 | 1100.7 | −1057.0 | 710.3 |
| Total period (1962–2016) | 1208.2 | 1900.5 | −2083.7 | 1391.4 |
| Variables | Baseline Period | Altered Period | Variability |
|---|---|---|---|
| (mm/month) | 33.33 | 35.51 | 2.18 |
| (mm/month) | 18.93 | 24.32 | 5.39 |
| (mm/month) | 489.24 | 465.04 | −24.20 |
| (mm/month) | −42.78 | −34.10 | 8.68 |
| 0.44 | 0.39 | −0.05 |
| 3.63 | 0.40 | −5.84 | 4.02 | 0.03 | 0.01 | 0.08 |
| 0.19 | 0.04 | −0.11 | 0.298 | −0.06 | −0.03 | −0.48 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Mei, Y.; Chen, J.; Hu, T.; Xiao, W. Attribution Analysis of Dry Season Runoff in the Lhasa River Using an Extended Hydrological Sensitivity Method and a Hydrological Model. Water 2019, 11, 1187. https://doi.org/10.3390/w11061187
Wu Z, Mei Y, Chen J, Hu T, Xiao W. Attribution Analysis of Dry Season Runoff in the Lhasa River Using an Extended Hydrological Sensitivity Method and a Hydrological Model. Water. 2019; 11(6):1187. https://doi.org/10.3390/w11061187
Chicago/Turabian StyleWu, Zhenhui, Yadong Mei, Junhong Chen, Tiesong Hu, and Weihua Xiao. 2019. "Attribution Analysis of Dry Season Runoff in the Lhasa River Using an Extended Hydrological Sensitivity Method and a Hydrological Model" Water 11, no. 6: 1187. https://doi.org/10.3390/w11061187
APA StyleWu, Z., Mei, Y., Chen, J., Hu, T., & Xiao, W. (2019). Attribution Analysis of Dry Season Runoff in the Lhasa River Using an Extended Hydrological Sensitivity Method and a Hydrological Model. Water, 11(6), 1187. https://doi.org/10.3390/w11061187






