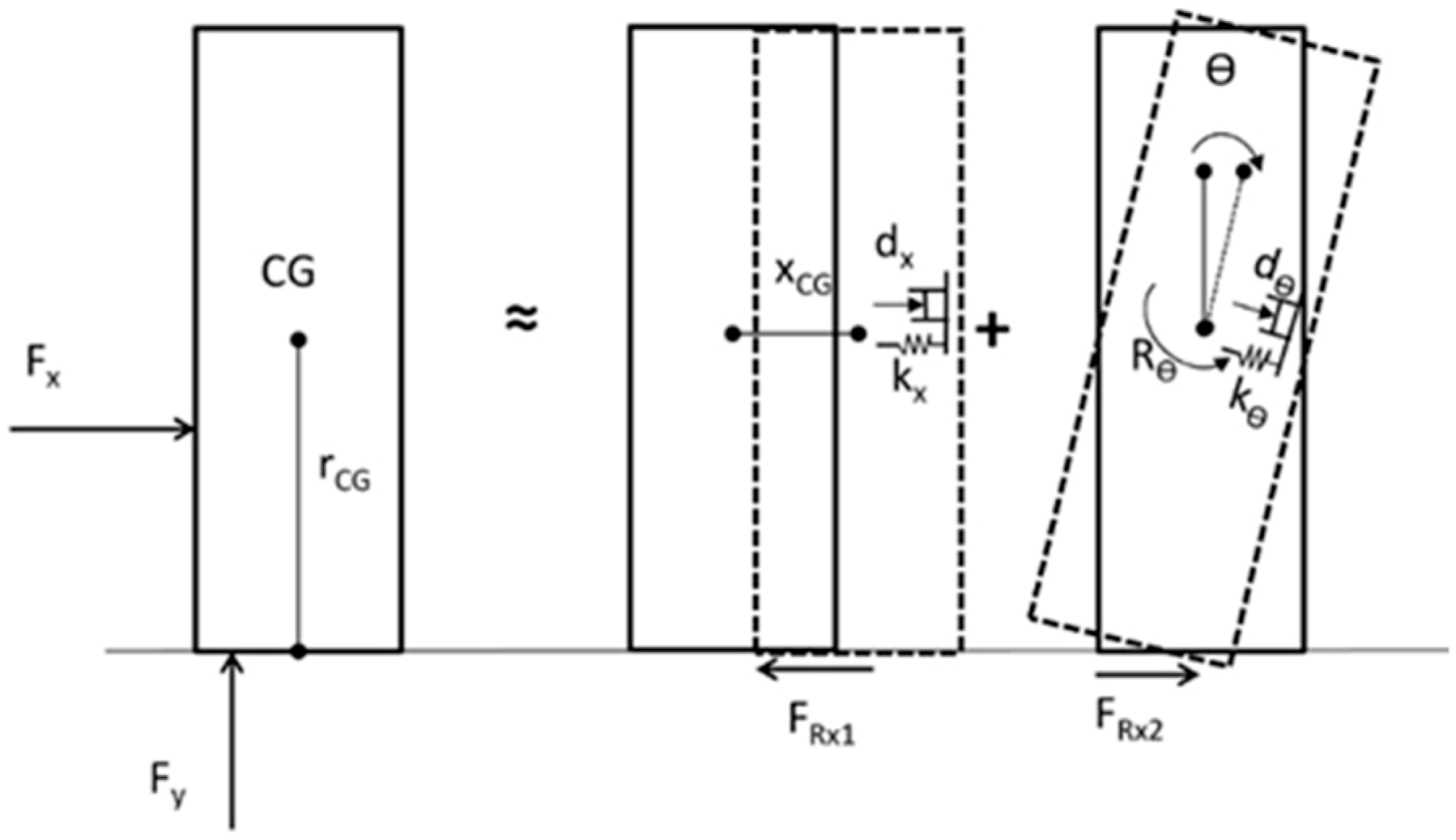
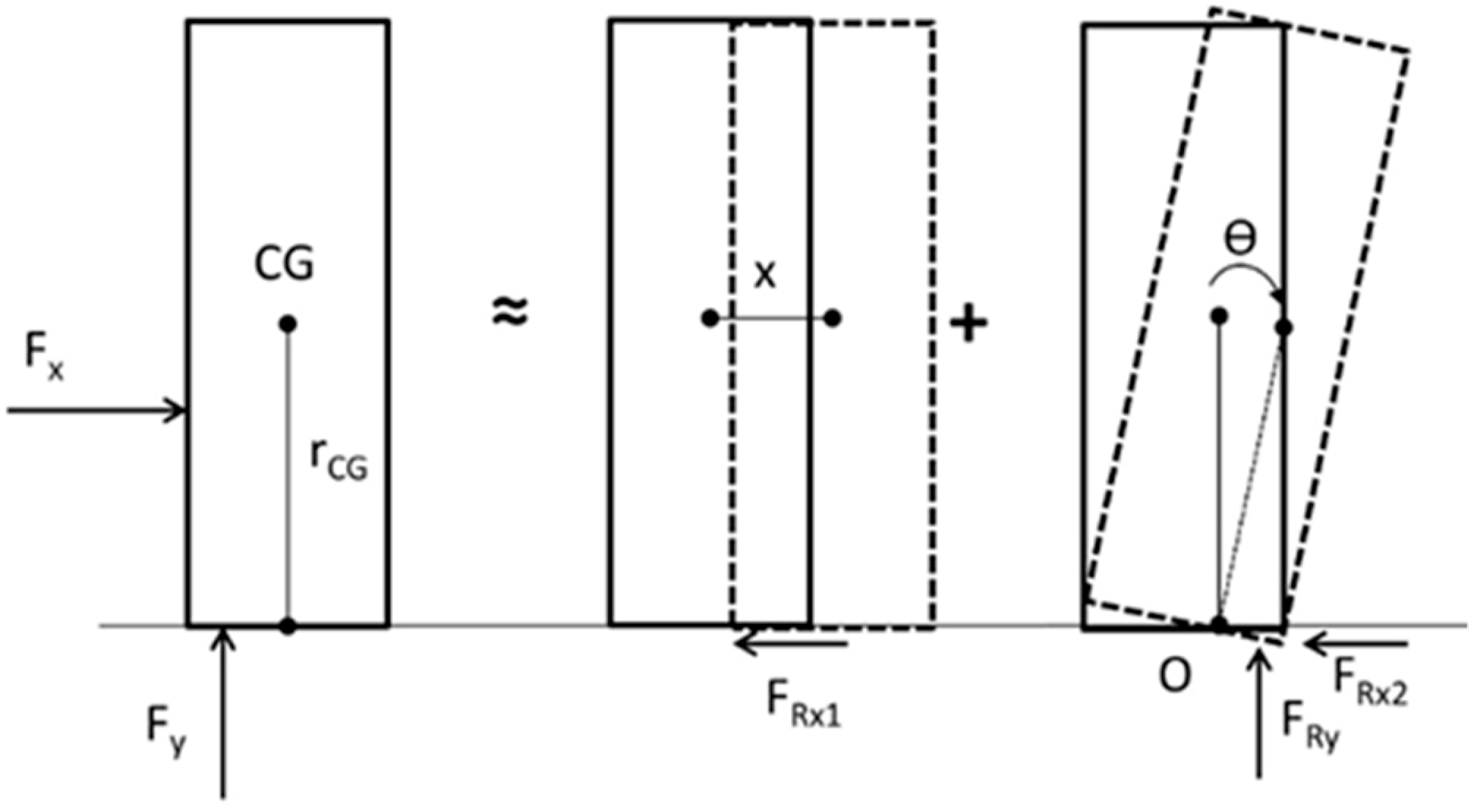
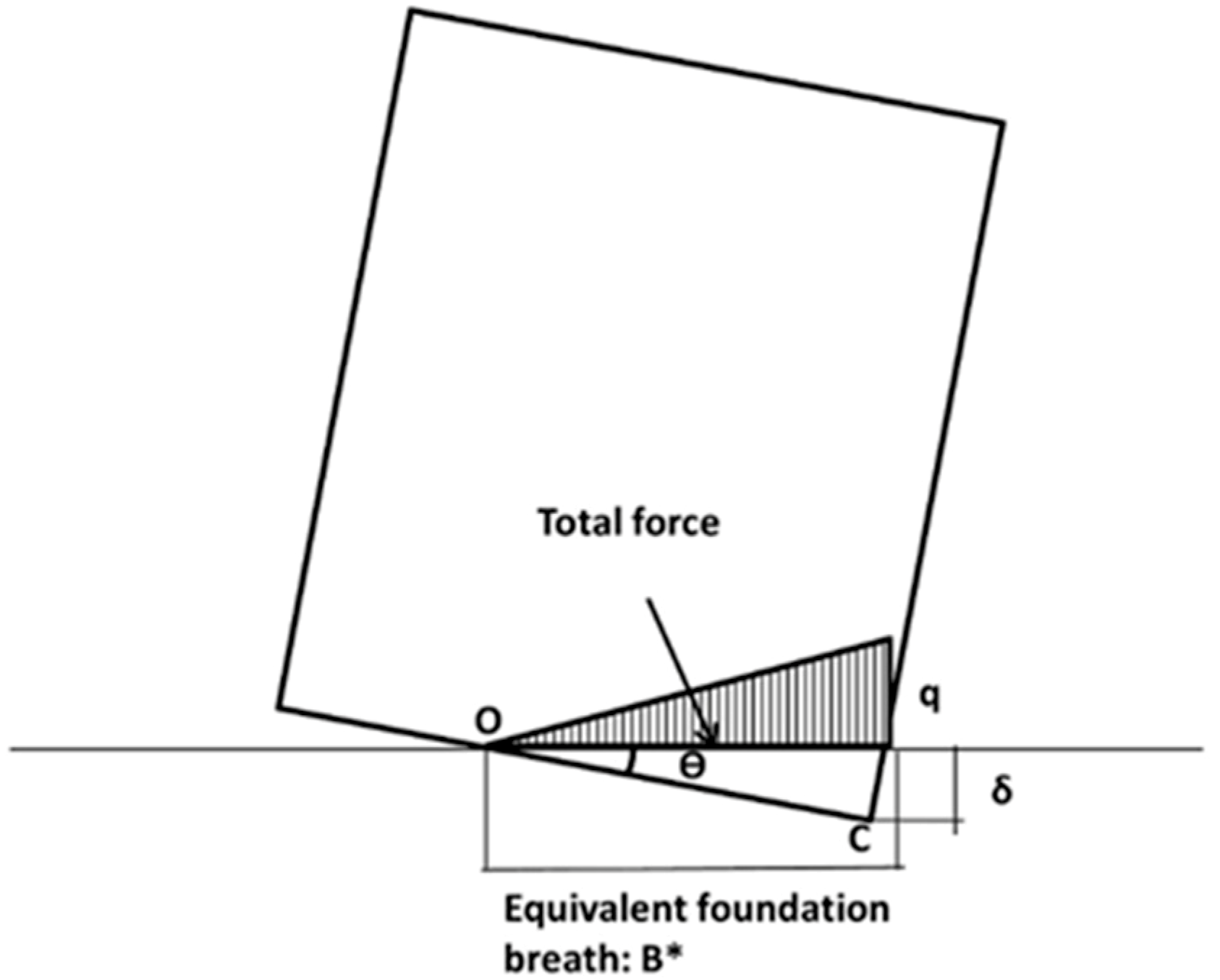
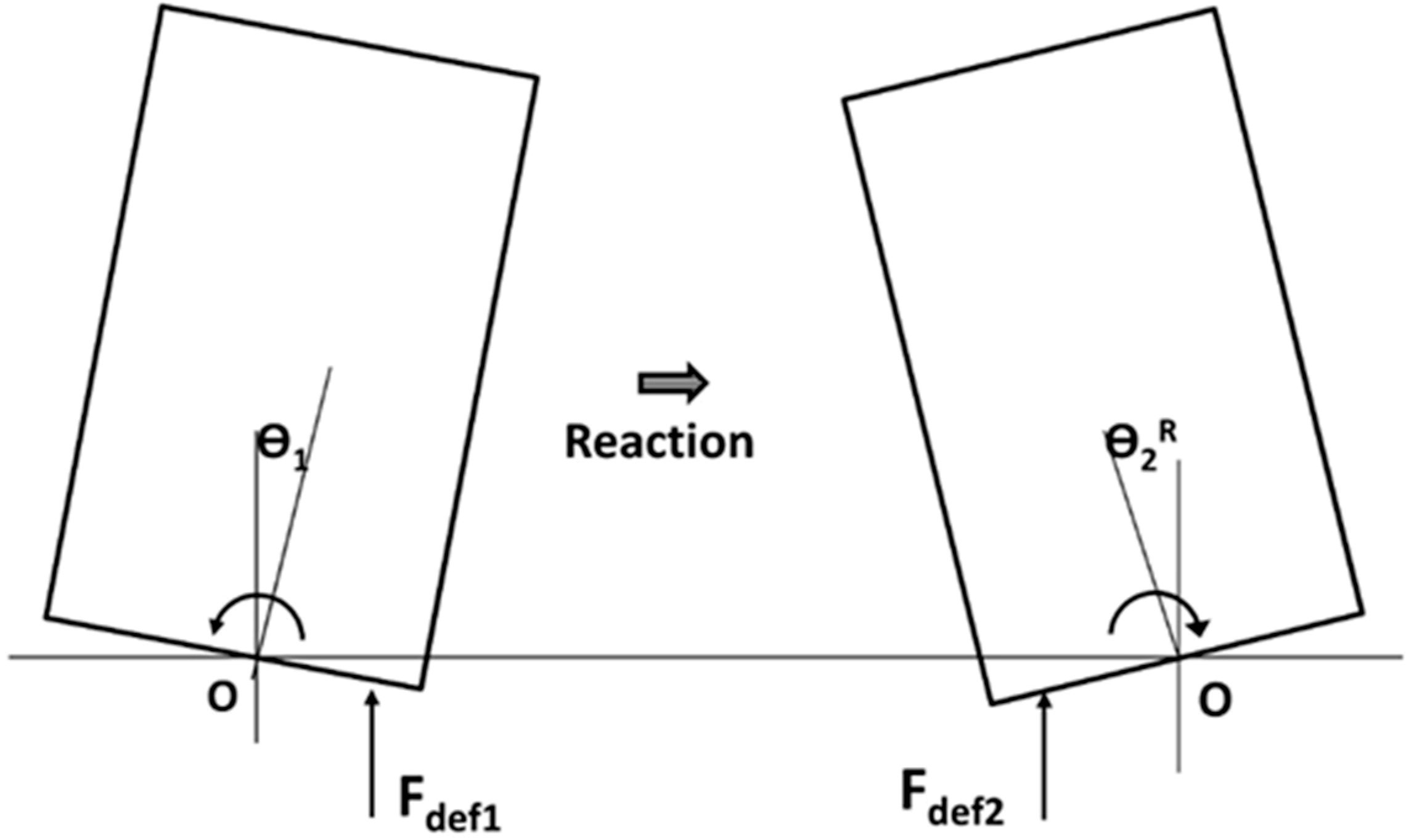
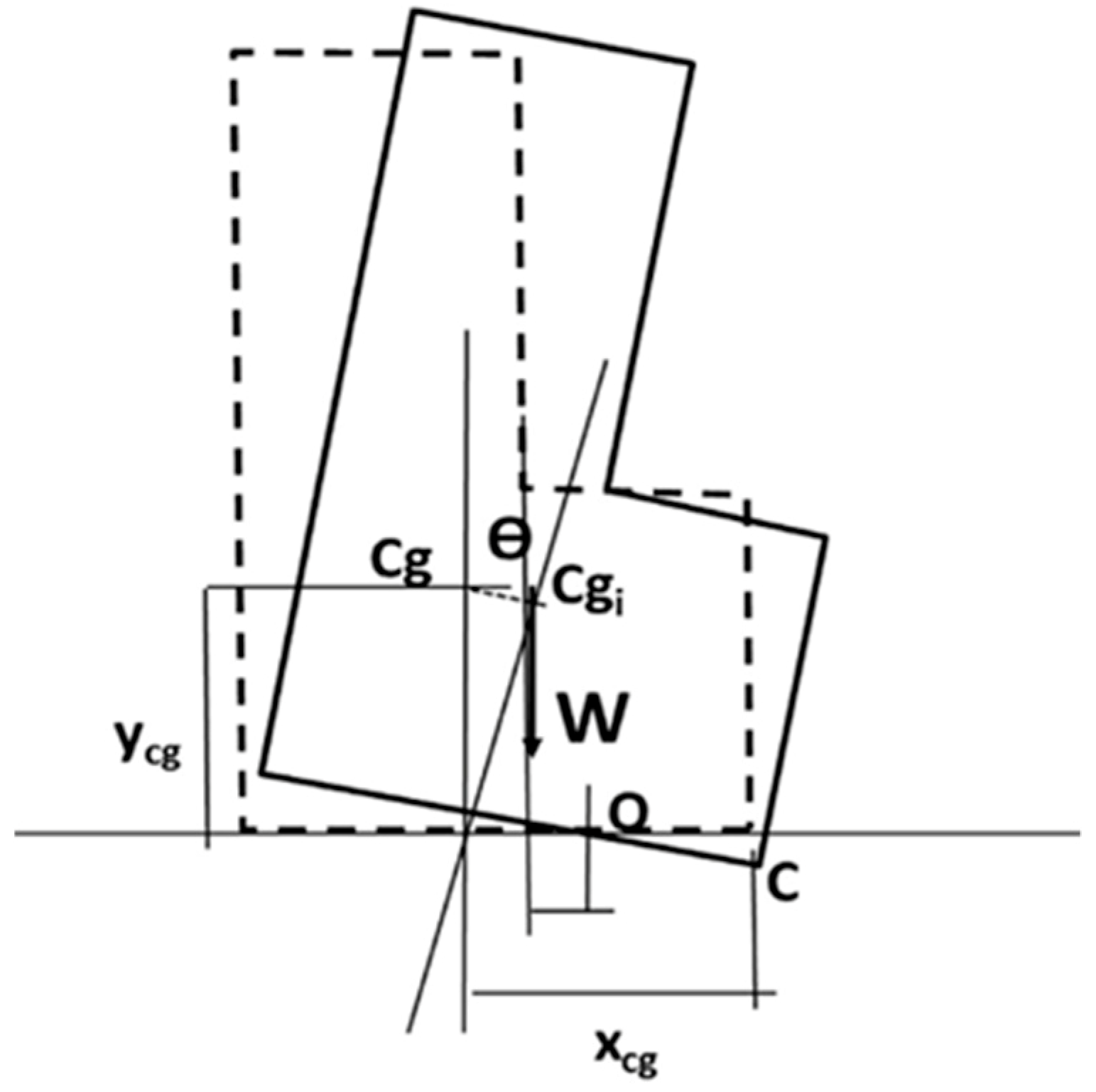
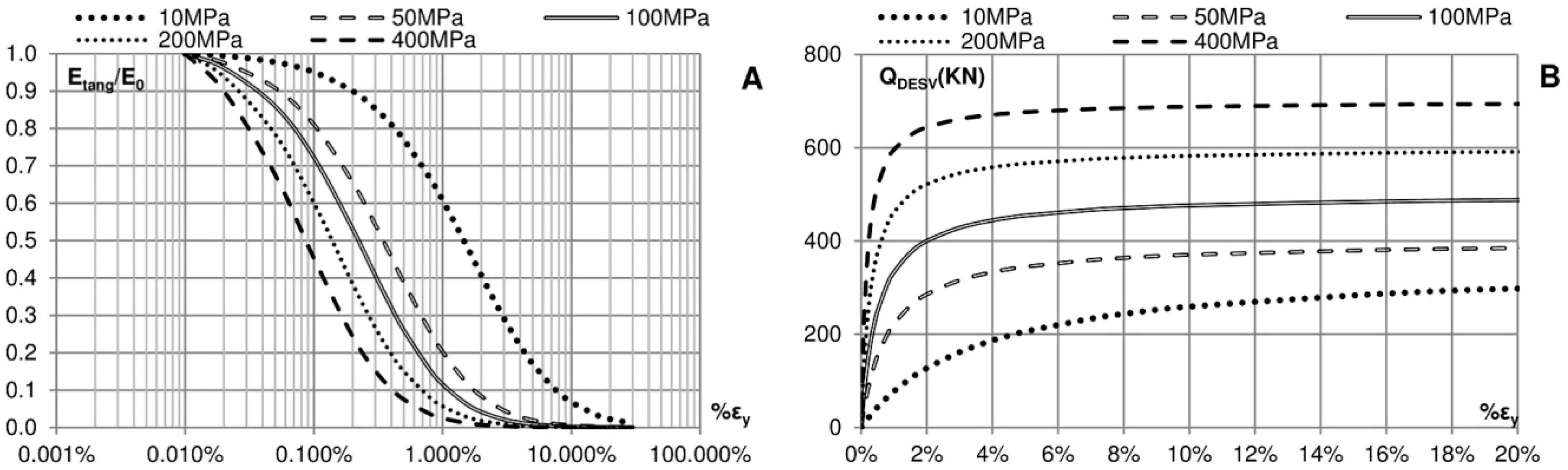
Figure 1.
Breakwater modes of failure (adapted from Pedersen [
2]).
Figure 1.
Breakwater modes of failure (adapted from Pedersen [
2]).
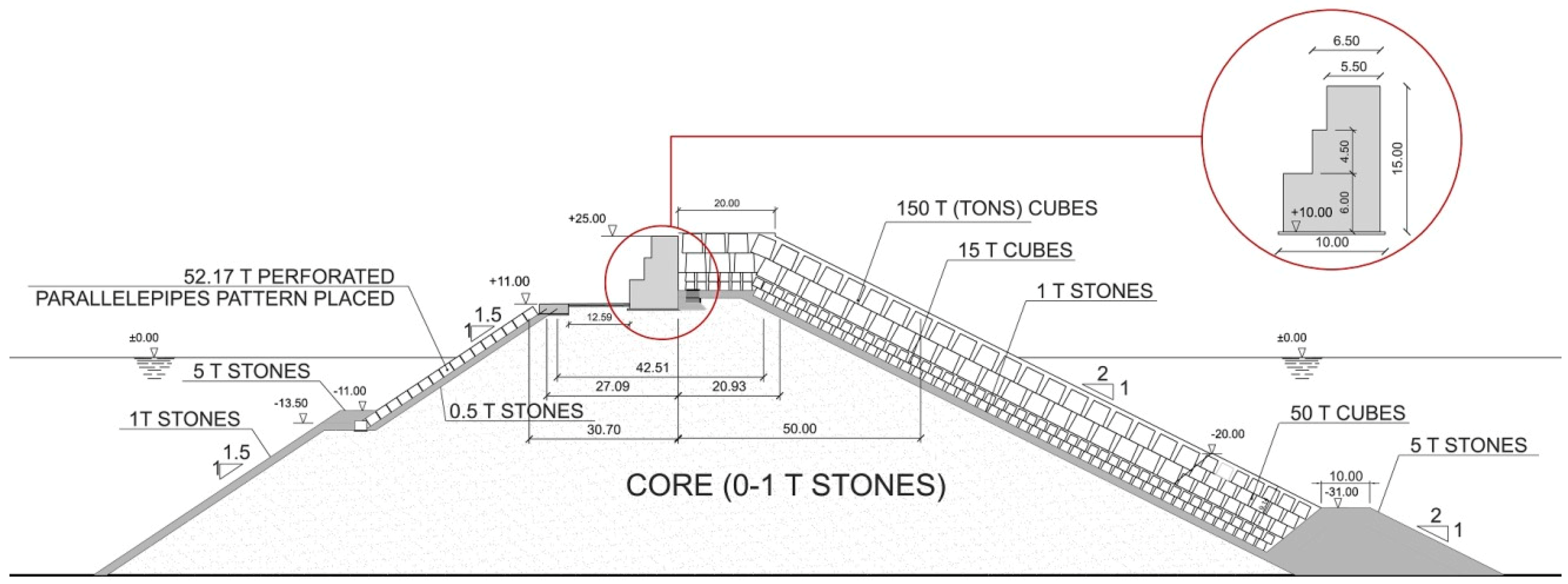
Figure 2.
Cross section of the main breakwater of the outer port of Punta Langosteira (A Coruña, Spain).
Figure 2.
Cross section of the main breakwater of the outer port of Punta Langosteira (A Coruña, Spain).
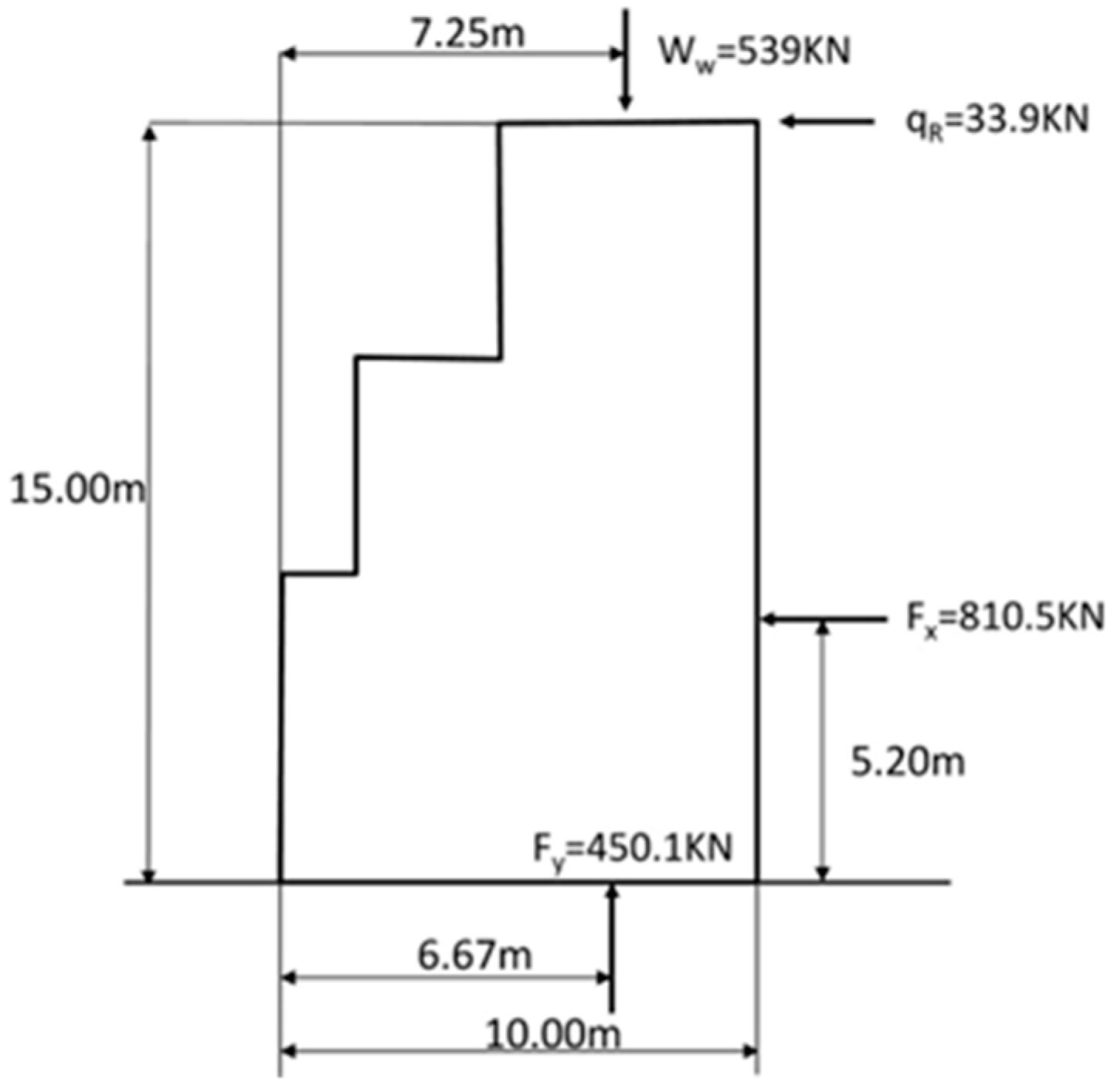
Figure 3.
Load state A, used for crown wall design (Wave height Hs (m) = 15.1; Peak period Tp (s) = 20), [
11].
Figure 3.
Load state A, used for crown wall design (Wave height Hs (m) = 15.1; Peak period Tp (s) = 20), [
11].
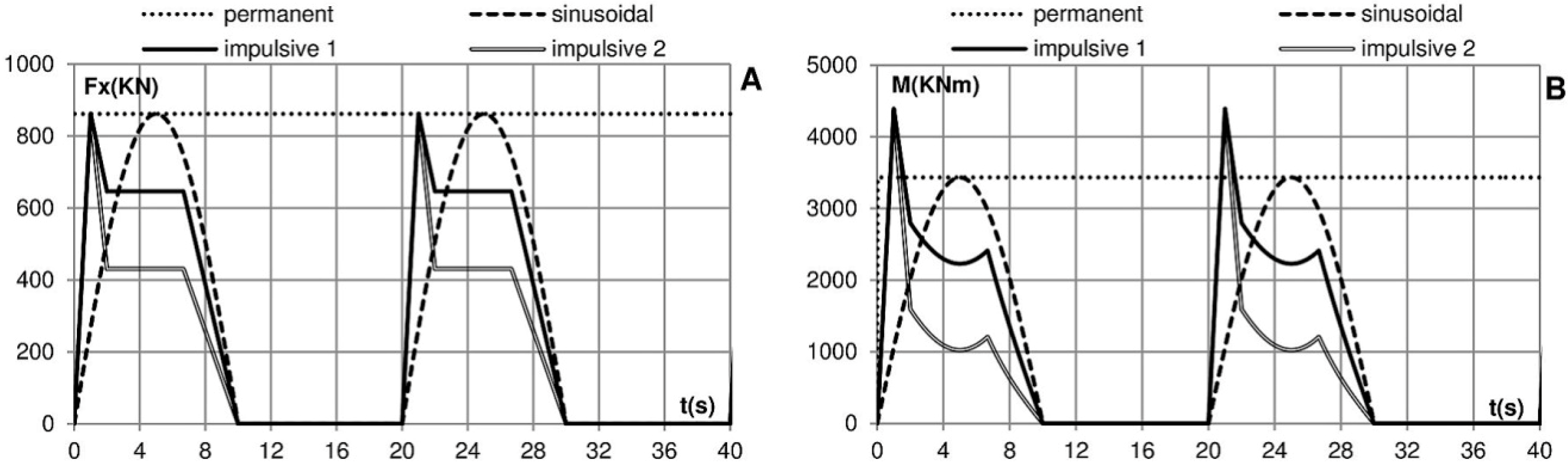
Figure 6.
Shape of the load state A in the time domain: (A) horizontal force (Fx); (B) overturning moment (M).
Figure 6.
Shape of the load state A in the time domain: (A) horizontal force (Fx); (B) overturning moment (M).
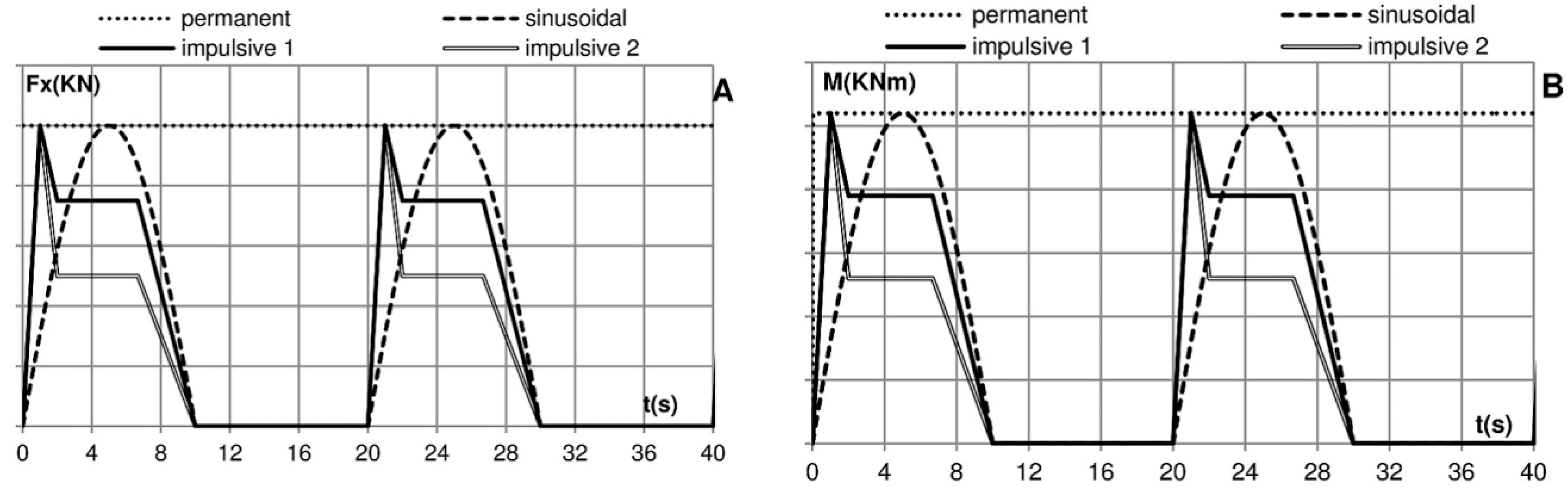
Figure 7.
Shape of the load states B and C in the time domain: (A) horizontal force (Fx); (B) overturning moment (M).
Figure 7.
Shape of the load states B and C in the time domain: (A) horizontal force (Fx); (B) overturning moment (M).
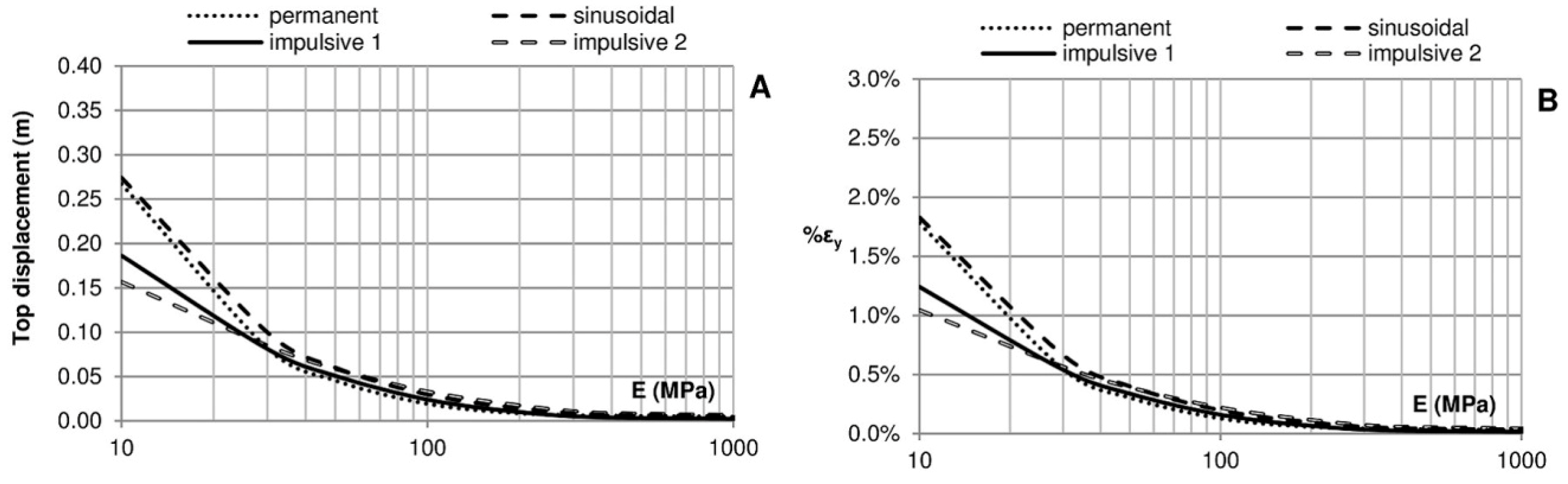
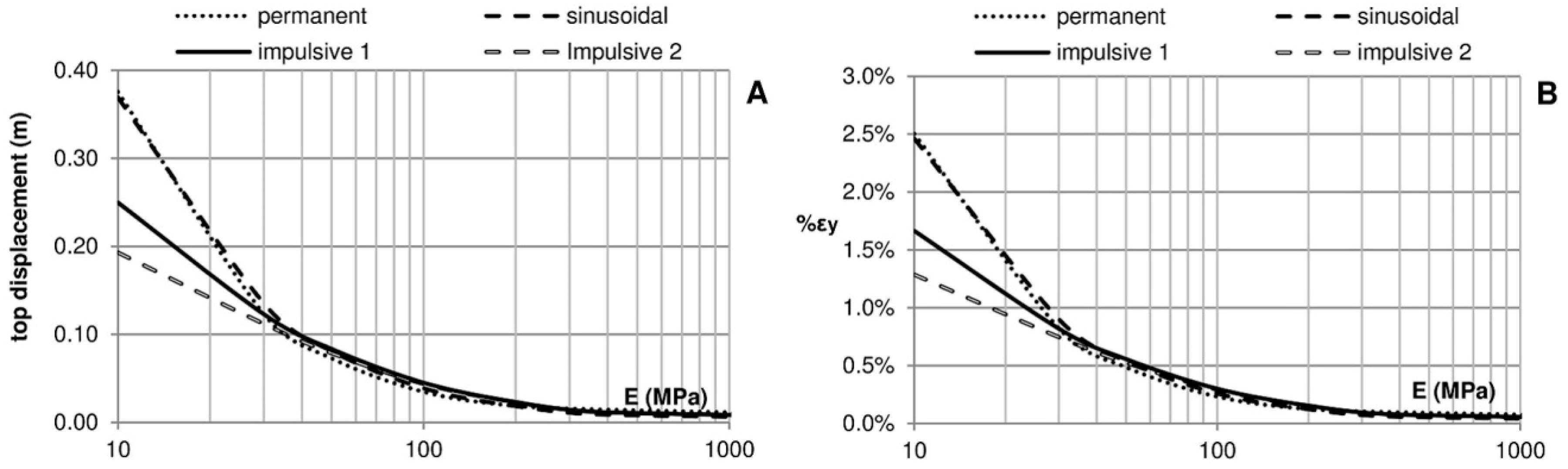
Figure 8.
(A) Movement on the top of the crown wall; (B) maximum vertical deformation of the foundation.
Figure 8.
(A) Movement on the top of the crown wall; (B) maximum vertical deformation of the foundation.
Figure 9.
Expected movement on the top of the foundation: E (MPa) = 10; 2 load cycles.
Figure 9.
Expected movement on the top of the foundation: E (MPa) = 10; 2 load cycles.
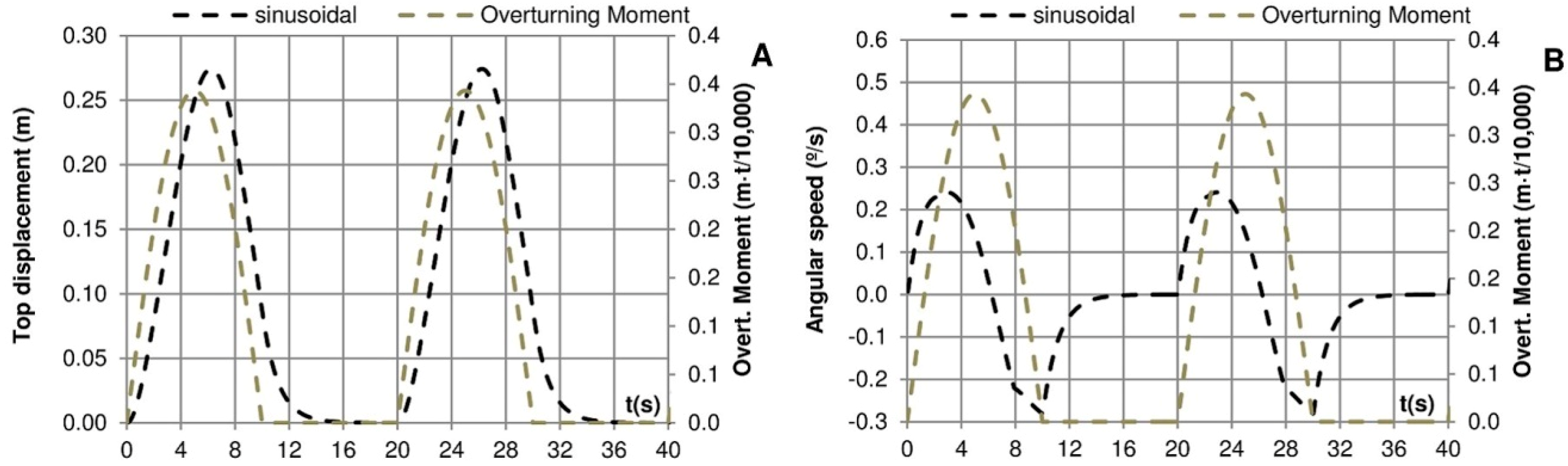
Figure 10.
Sinusoidal force. (A) Movement on the top of the crown wall; (B) angular velocity, related to the overturning moment. E (MPa) = 10; 2 load cycles.
Figure 10.
Sinusoidal force. (A) Movement on the top of the crown wall; (B) angular velocity, related to the overturning moment. E (MPa) = 10; 2 load cycles.
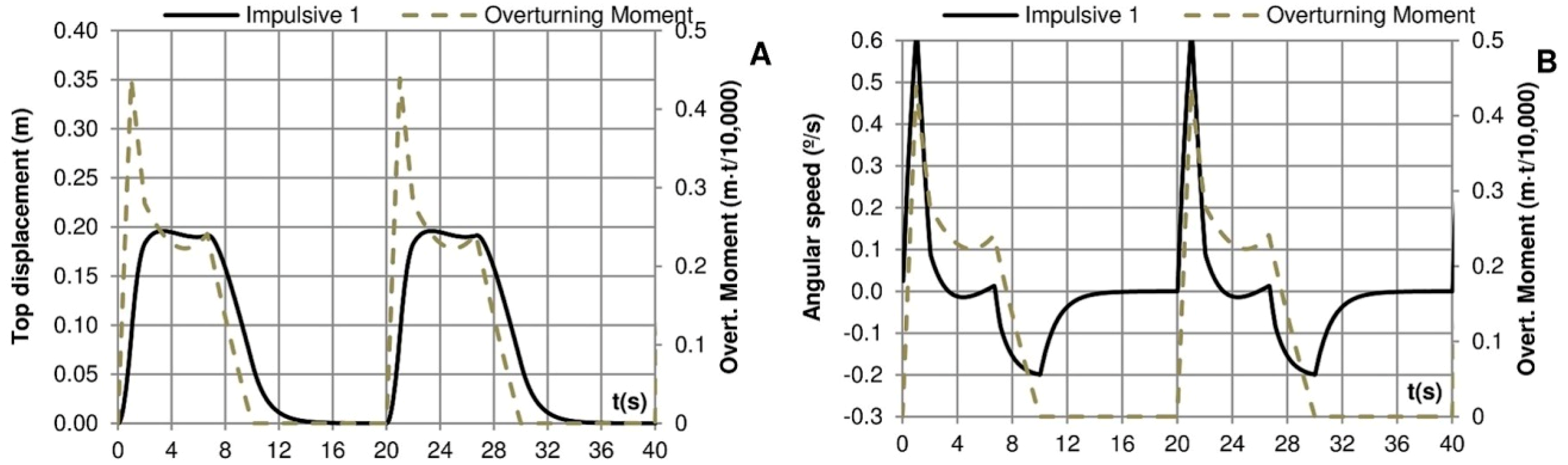
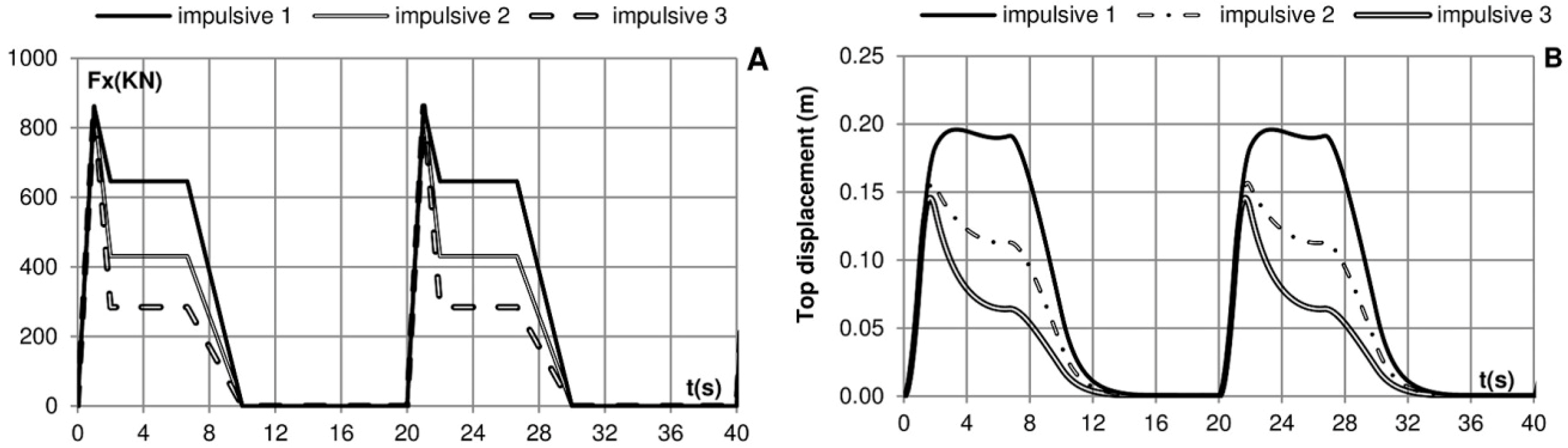
Figure 11.
Impulsive 1. (A) Movement on the top of the crown wall; (B) angular velocity, related to overturning moment. E (MPa) = 10; 2 load cycles.
Figure 11.
Impulsive 1. (A) Movement on the top of the crown wall; (B) angular velocity, related to overturning moment. E (MPa) = 10; 2 load cycles.
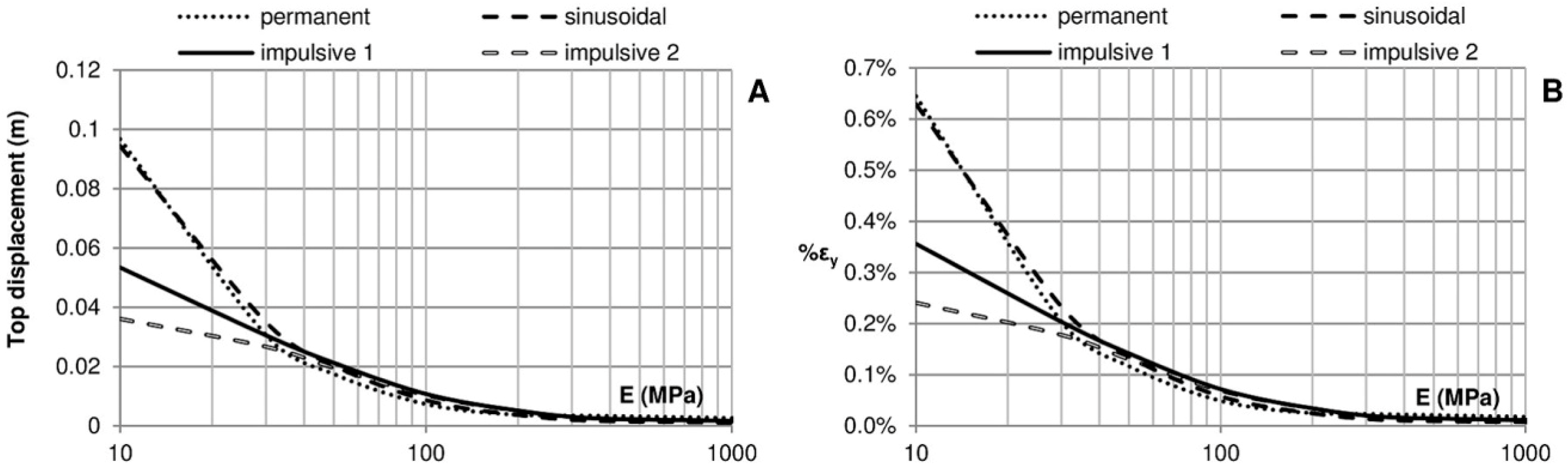
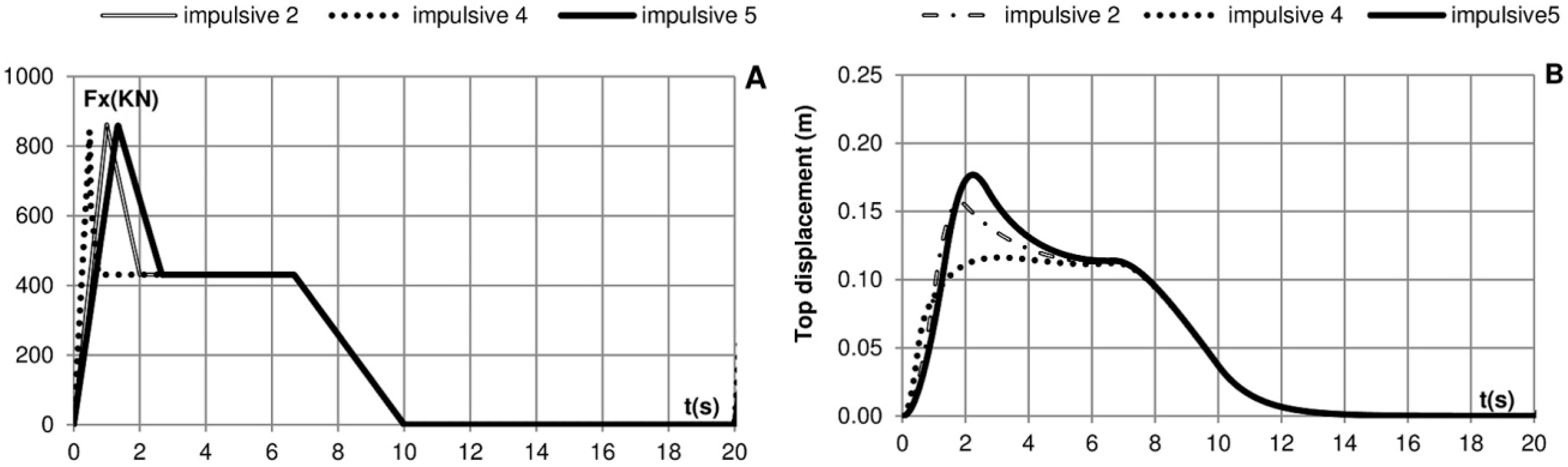
Figure 12.
(A) Movement on the top of the crown wall; (B) maximum vertical deformation of the foundation.
Figure 12.
(A) Movement on the top of the crown wall; (B) maximum vertical deformation of the foundation.
Figure 13.
(A) Residual movement on the top of the crown wall; (B) residual vertical deformation.
Figure 13.
(A) Residual movement on the top of the crown wall; (B) residual vertical deformation.
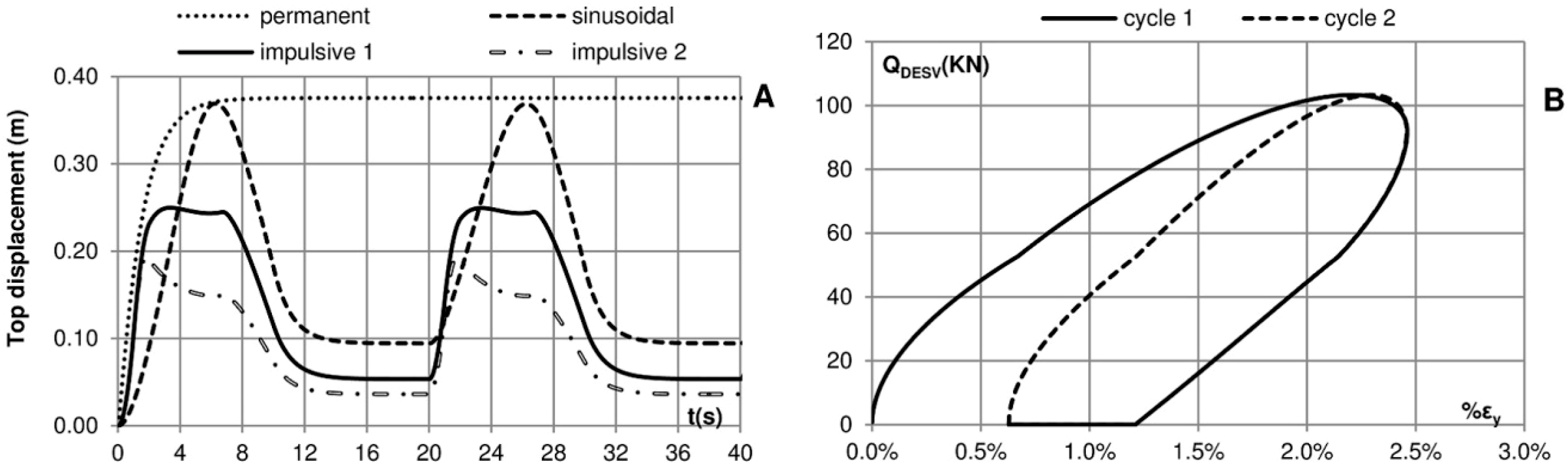
Figure 14.
(A) Movements on the top of the crown wall; (B) stress–strain graph showing the relationship between the load deviator and vertical deformation produced in the first and second cycles of loading.
Figure 14.
(A) Movements on the top of the crown wall; (B) stress–strain graph showing the relationship between the load deviator and vertical deformation produced in the first and second cycles of loading.
Figure 15.
Tip factor influence: (A) shape of the signals; (B) movements on the top of the foundation. 2 cycles.
Figure 15.
Tip factor influence: (A) shape of the signals; (B) movements on the top of the foundation. 2 cycles.
Figure 16.
Rise time influence: (A) shape of the signals; (B) movements on the top of the foundation.
Figure 16.
Rise time influence: (A) shape of the signals; (B) movements on the top of the foundation.
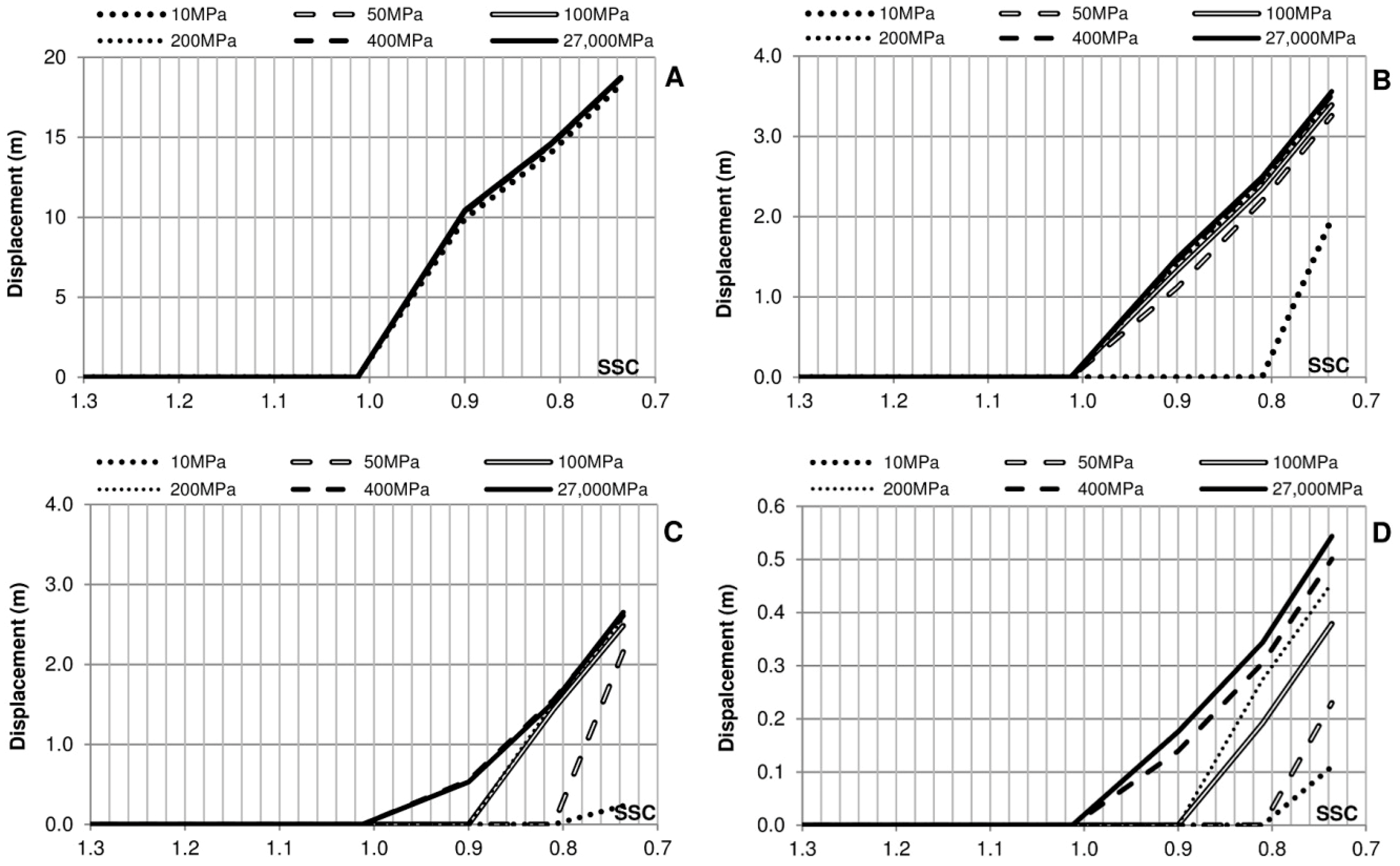
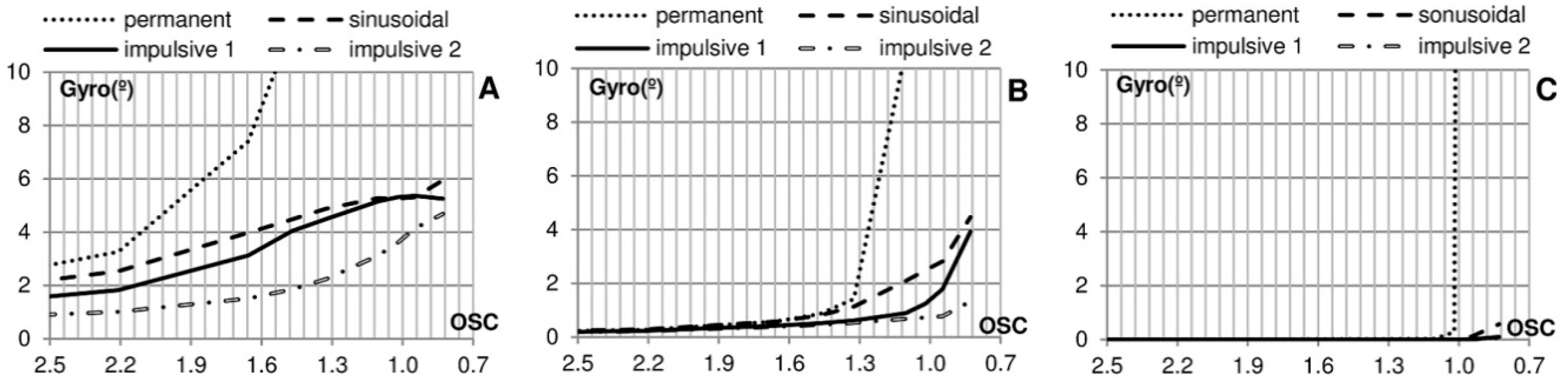
Figure 17.
Crown wall displacement as a function of Sliding Safety Coefficient (SSC) and Young’s modulus of the soil, assuming elastic soil, for the 4 different theoretical signals: (A) Permanent; (B) Sinusoidal; (C) Impulsive 1; (D) Impulsive 2.
Figure 17.
Crown wall displacement as a function of Sliding Safety Coefficient (SSC) and Young’s modulus of the soil, assuming elastic soil, for the 4 different theoretical signals: (A) Permanent; (B) Sinusoidal; (C) Impulsive 1; (D) Impulsive 2.
Figure 18.
Displacement of the upper part of the crown wall in the breakwater of A Garda, Spain (2017).
Figure 18.
Displacement of the upper part of the crown wall in the breakwater of A Garda, Spain (2017).
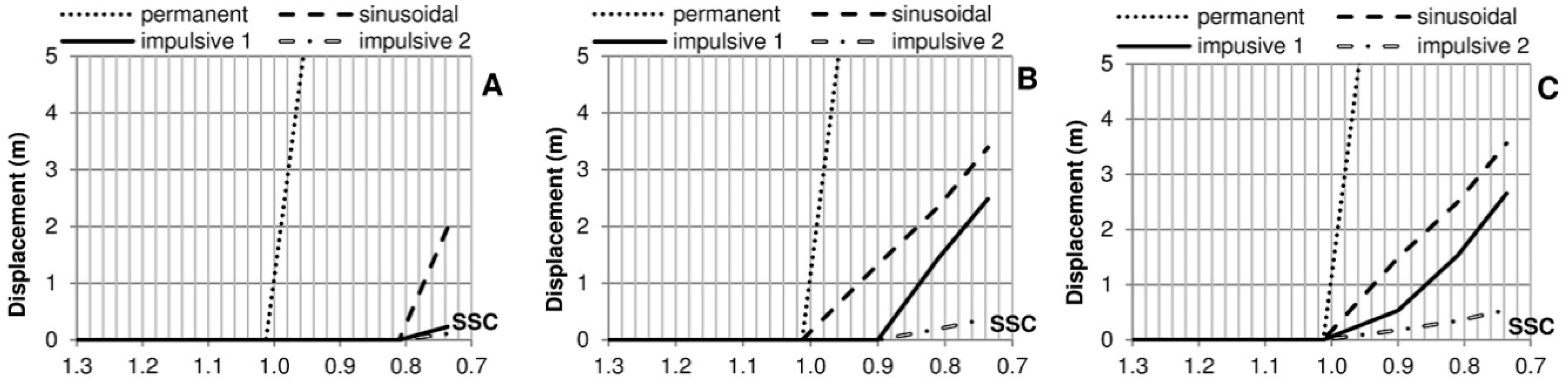
Figure 19.
Wall sliding as a function of SSC and the signal shape, assuming elastic soil. (A) E (MPa) = 10; (B); E (MPa) = 100; (C) E (MPa) = 27,000.
Figure 19.
Wall sliding as a function of SSC and the signal shape, assuming elastic soil. (A) E (MPa) = 10; (B); E (MPa) = 100; (C) E (MPa) = 27,000.
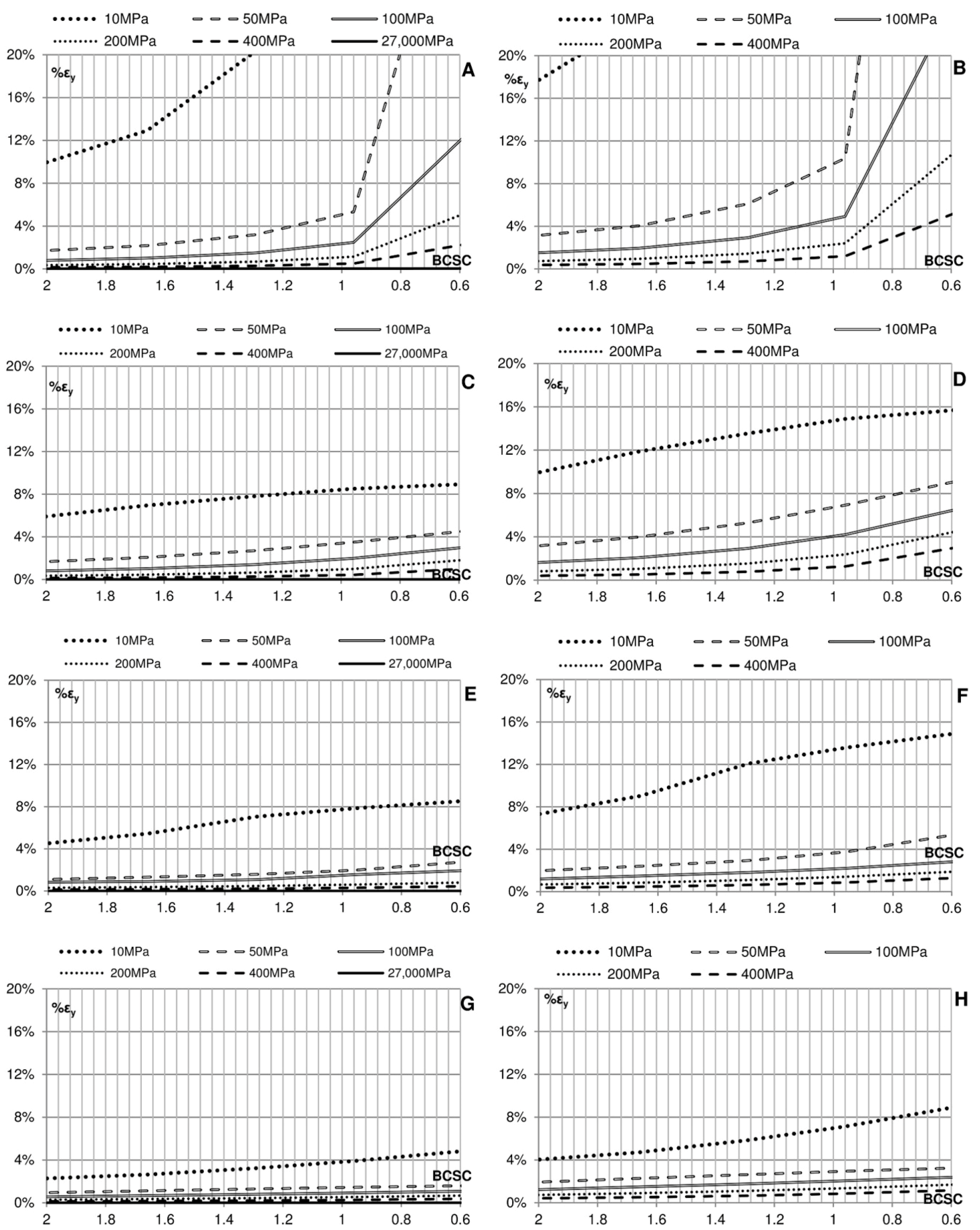
Figure 20.
Maximum deformation as a function of the bearing capacity safety coefficient (BCSC) and Young’s modulus of the soil, assuming elastic soil. (A) Permanent; (B) Sinusoidal; (C) Impulsive 1; (D) Impulsive 2.
Figure 20.
Maximum deformation as a function of the bearing capacity safety coefficient (BCSC) and Young’s modulus of the soil, assuming elastic soil. (A) Permanent; (B) Sinusoidal; (C) Impulsive 1; (D) Impulsive 2.
Figure 21.
Wall rotation as a function of Overturning Safety coefficient (OSC) and Young’s modulus, assuming elastic soil. (A) Permanent; (B) Sinusoidal; (C) Impulsive 1; (D) Impulsive 2.
Figure 21.
Wall rotation as a function of Overturning Safety coefficient (OSC) and Young’s modulus, assuming elastic soil. (A) Permanent; (B) Sinusoidal; (C) Impulsive 1; (D) Impulsive 2.
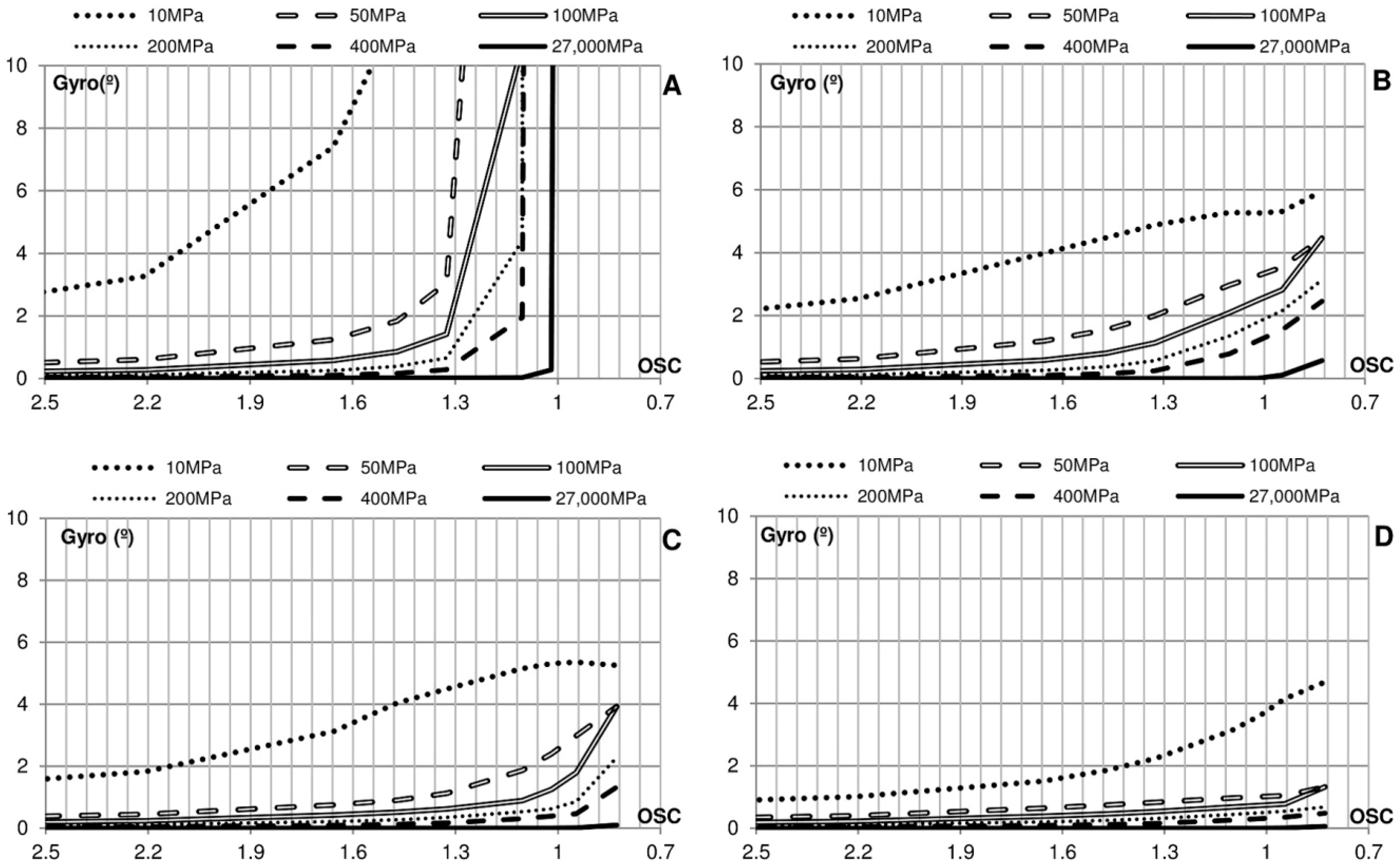
Figure 22.
Crown wall rotation as a function of OSC and the shape of the signal, assuming elastic soil (A) E (MPa) = 10; (B) E (MPa) = 100; (C); E (MPa) = 27,000.
Figure 22.
Crown wall rotation as a function of OSC and the shape of the signal, assuming elastic soil (A) E (MPa) = 10; (B) E (MPa) = 100; (C); E (MPa) = 27,000.
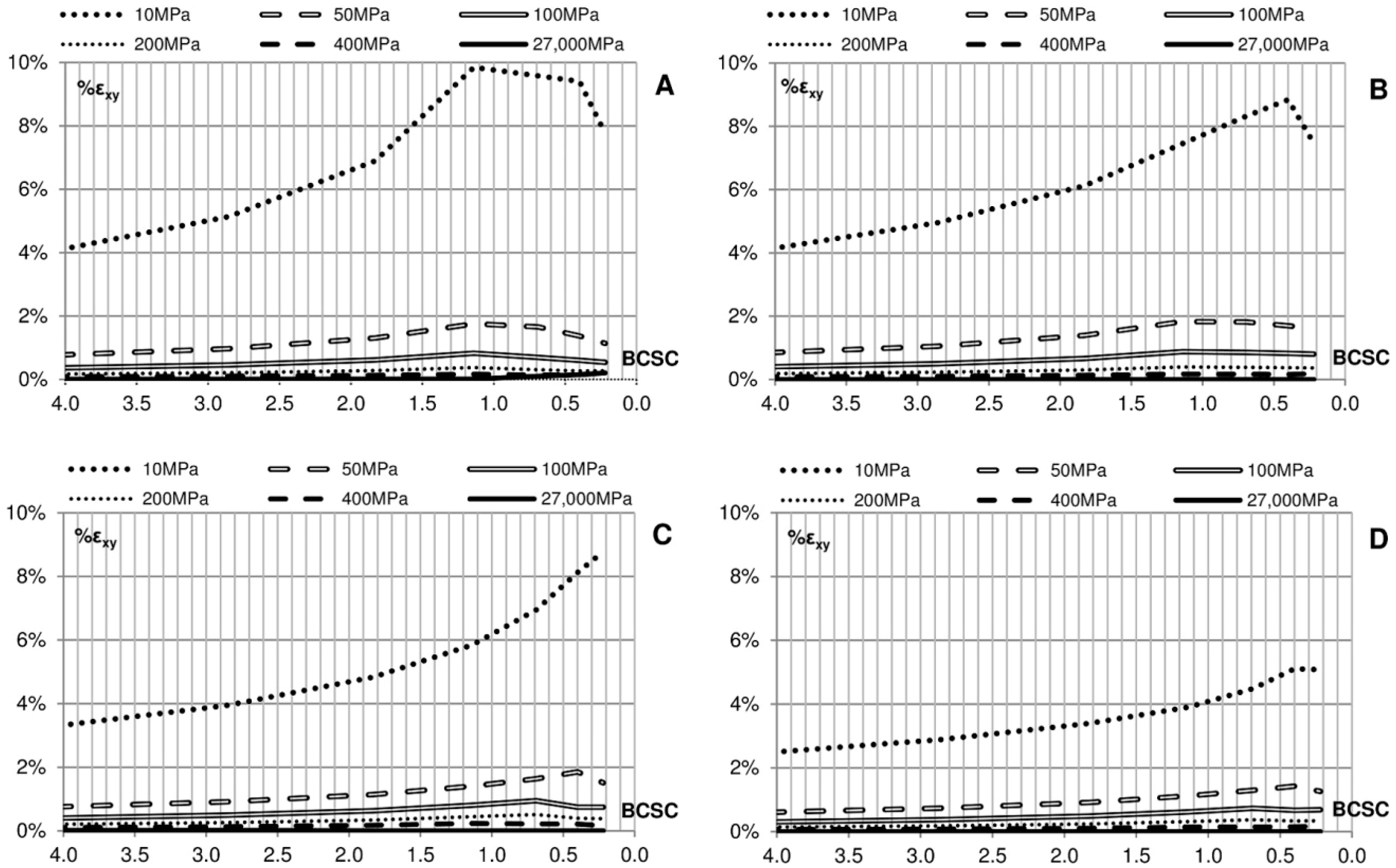
Figure 23.
Soil deformation as a function of Bearing Capacity Safety Coefficient (BCSC) and Young’s modulus. Permanent: (A) elastic soil; (B) elasto-plastic soil. Sinusoidal: (C) elastic soil; (D) elasto-plastic soil. Impulsive 1: (E) elastic soil; (F) elasto-plastic soil. Impulsive 2: (G) elastic soil; (H) elasto-plastic soil.
Figure 23.
Soil deformation as a function of Bearing Capacity Safety Coefficient (BCSC) and Young’s modulus. Permanent: (A) elastic soil; (B) elasto-plastic soil. Sinusoidal: (C) elastic soil; (D) elasto-plastic soil. Impulsive 1: (E) elastic soil; (F) elasto-plastic soil. Impulsive 2: (G) elastic soil; (H) elasto-plastic soil.
Table 1.
Safety coefficients obtained for load state A.
Table 1.
Safety coefficients obtained for load state A.
| Mode of Failure | Safety Coefficient | Verification |
|---|
| Sliding safety coefficient (SSC) | 1.93 | |
| Rigid overturning safety coefficient (OSC) | 4.61 | |
| Bearing capacity safety coefficient (BCSC) | 6.24 | Brinch-Jansen [15] |
Table 2.
Safety coefficients obtained for load state B.
Table 2.
Safety coefficients obtained for load state B.
| Fx (KN) (Horizontal Force) | 1000 | 1200 | 1400 | 1600 | 1800 | 2000 | 2200 |
| Sliding Safety Coefficient (SSC) | 1.62 | 1.35 | 1.16 | 1.01 | 0.90 | 0.81 | 0.74 |
| Overturning Safety Coefficient (OSC) | 3.27 | 2.55 | 2.18 | 1.91 | 1.70 | 1.53 | 1.39 |
| Bearing Capacity Safety Coefficient (BCSC) [15] | 4.34 | 2.86 | 1.83 | 1.14 | 0.69 | 0.40 | 0.22 |
Table 3.
Coefficients obtained for load state C.
Table 3.
Coefficients obtained for load state C.
| M (KNm) (Overturning Moment) | 4800 | 7200 | 9600 | 10,800 | 12,000 | 14,400 | 15,600 | 16,800 | 19,200 |
| Sliding Safety Coefficient (SSC) | 1.35 | 1.35 | 1.35 | 1.47 | 1.35 | 1.35 | 1.35 | 1.35 | 1.35 |
| Overturning Safety Coefficient (OSC) | 3.31 | 2.21 | 1.66 | 1.35 | 1.33 | 1.10 | 1.02 | 0.95 | 0.83 |
| Bearing Capacity Safety Coefficient (BCSC) [15] | 3.44 | 2.49 | 1.66 | 1.29 | 0.96 | 0.35 | 0.07 | 0.01 | 0 |
Table 4.
Results obtained with the simplified model and with FLAC2D 7.0 code, comparison without considering transverse deformation of the soil.
Table 4.
Results obtained with the simplified model and with FLAC2D 7.0 code, comparison without considering transverse deformation of the soil.
| E (MPa) Considering the Worst Values for the Core | Poisson Coefficient | Shape of the Load’s Signal | Simplified Model (Elastic) | FLAC2D 7.0 (Net Movements) |
|---|
| Top Displacement (m) | εy% | Top Displacement (m) | εy% |
|---|
| 10 | 0.30 | 1 | 0.27 | 1.8 | 0.30 | 2.0 |
| 30 | 0.30 | 1 | 0.08 | 0.5 | 0.07 | 0.5 |
Table 5.
Results obtained with the simplified model and with FLAC2D 7.0 code, comparison considering transverse deformation of the soil.
Table 5.
Results obtained with the simplified model and with FLAC2D 7.0 code, comparison considering transverse deformation of the soil.
| E (MPa) Considering the Worst Values for the Core | Poisson Coefficient | Shape of the Load’s Signal | Simplified Model (Elastic) | FLAC2D 7.0 (Total Movements) |
|---|
| Top Displacement (m) | εy% | εx% | Top Displacement (m) | εy% | εx% |
|---|
| 10 | 0.30 | 1 | 0.49 | 1.8 | 2.2 | 0.46 | 2.0 | 1.6 |
| 30 | 0.30 | 1 | 0.16 | 0.6 | 0.7 | 0.13 | 0.5 | 0.6 |
Table 6.
Crown wall sliding in simulations under load state B.
Table 6.
Crown wall sliding in simulations under load state B.
| Sliding Failure (m of Displacement, 10 Cycles of Load) |
|---|
| Sliding Safety Coefficient | 1.35 | 1.16 | 1.01 | 0.90 | 0.81 | 0.74 | 1.35 | 1.16 | 1.01 | 0.90 | 0.81 | 0.74 |
|---|
| Young’s Modulus | Signal | Elastic Soil | Elasto-Plastic Soil |
|---|
| E = 10 MPa | Permanent | - | - | - | 9.9 | 14.0 | 18.3 | - | - | - | 9.9 | 14.0 | 18.3 |
| Sinusoidal | - | - | - | - | - | 2.0 | - | - | - | - | - | 2.0 |
| Impulsive 1 | - | - | - | - | - | 0.2 | - | - | - | - | - | 0.2 |
| Impulsive 2 | - | - | - | - | - | 0.1 | - | - | - | - | - | 0.1 |
| E = 50 MPa | Permanent | - | - | - | 10.4 | 14.5 | 18.7 | - | - | - | 10.4 | 14.5 | 18.7 |
| Sinusoidal | - | - | - | 1.1 | 2.2 | 3.3 | - | - | - | 1.1 | 2.2 | 3.3 |
| Impulsive 1 | - | - | - | - | - | 2.2 | - | - | - | - | - | 2.2 |
| Impulsive 2 | - | - | - | - | - | 0.2 | - | - | - | - | - | 0.2 |
| E = 100 MPa | Permanent | - | - | - | 10.4 | 14.6 | 18.7 | - | - | - | 10.4 | 14.5 | 18.7 |
| Sinusoidal | - | - | - | 1.3 | 2.3 | 3.4 | - | - | - | 1.3 | 2.3 | 3.4 |
| Impulsive 1 | - | - | - | - | 1.4 | 2.5 | - | - | - | - | 1.4 | 2.5 |
| Impulsive 2 | - | - | - | - | 0.2 | 0.4 | - | - | - | - | 0.2 | 0.4 |
| E = 200 MPa | Permanent | - | - | - | 10.4 | 14.6 | 18.7 | - | - | - | 10.4 | 14.6 | 18.7 |
| Sinusoidal | - | - | - | 1.4 | 2.4 | 3.5 | - | - | - | 1.4 | 2.4 | 3.5 |
| Impulsive 1 | - | - | - | - | 1.5 | 2.6 | - | - | - | - | 1.5 | 2.6 |
| Impulsive 2 | - | - | - | - | 0.3 | 0.5 | - | - | - | - | 0.3 | 0.5 |
| E = 400 MPa | Permanent | - | - | - | 10.4 | 14.6 | 18.7 | - | - | - | 10.4 | 14.6 | 18.7 |
| Sinusoidal | - | - | - | 1.5 | 2.5 | 3.5 | - | - | - | 1.5 | 2.5 | 3.5 |
| Impulsive 1 | - | - | - | 0.6 | 1.6 | 2.6 | - | - | - | 0.5 | 1.5 | 2.6 |
| Impulsive 2 | - | - | - | 0.1 | 0.3 | 0.5 | - | - | - | 0.1 | 0.3 | 0.5 |
| E = 27,000 MPa | Permanent | - | - | - | 10.4 | 14.6 | 18.7 | | | | | | |
| Sinusoidal | - | - | - | 1.5 | 2.5 | 3.6 | | | | | | |
| Impulsive 1 | - | - | - | 0.5 | 1.5 | 2.7 | | | | | | |
| Impulsive 2 | - | - | - | 0.2 | 0.3 | 0.5 | | | | | | |
Table 7.
Vertical deformation in simulations under load state B.
Table 7.
Vertical deformation in simulations under load state B.
| Sliding Failure (% of Vertical Deformation) |
|---|
| Sliding Safety Coefficient | 1.35 | 1.16 | 1.01 | 0.90 | 0.81 | 0.74 | 1.35 | 1.16 | 1.01 | 0.90 | 0.81 | 0.74 |
|---|
| Young’s Modulus | Signal | Elastic Soil | Elasto-Plastic Soil |
|---|
| E = 10 MPa | Permanent | 4.1% | 5.9% | 8.9% | 8.4% | 7.8% | 7.8% | 6.5% | 9.7% | 15.6% | 14.5% | 13.4% | 13.3% |
| Sinusoidal | 3.5% | 4.5% | 5.8% | 6.4% | 6.6% | 5.4% | 5.4% | 7.3% | 9.6% | 10.9% | 11.1% | 8.9% |
| Impulsive 1 | 2.6% | 3.4% | 4.3% | 5.3% | 6.4% | 7.2% | 3.7% | 5.0% | 6.6% | 8.5% | 10.6% | 12.1% |
| Impulsive 2 | 1.5% | 1.8% | 2.1% | 2.5% | 3.0% | 3.5% | 2.6% | 3.1% | 3.7% | 4.5% | 5.4% | 6.4% |
| E = 50 MPa | Permanent | 0.7% | 1.1% | 1.5% | 1.4% | 1.3% | 1.1% | 1.3% | 1.9% | 2.8% | 2.6% | 2.2% | 1.9% |
| Sinusoidal | 0.8% | 1.1% | 1.6% | 1.6% | 1.5% | 1.4% | 1.4% | 2.0% | 2.9% | 2.9% | 2.7% | 2.6% |
| Impulsive 1 | 0.7% | 0.9% | 1.2% | 1.4% | 1.6% | 1.4% | 1.0% | 1.4% | 1.9% | 2.2% | 2.6% | 2.4% |
| Impulsive 2 | 0.5% | 0.7% | 0.9% | 1.1% | 1.2% | 1.1% | 1.1% | 1.4% | 1.8% | 2.2% | 2.3% | 2.1% |
| E = 100 MPa | Permanent | 0.3% | 0.5% | 0.7% | 0.7% | 0.6% | 0.5% | 0.6% | 0.9% | 1.3% | 1.3% | 1.0% | 0.9% |
| Sinusoidal | 0.3% | 0.5% | 0.7% | 0.7% | 0.7% | 0.7% | 0.7% | 1.0% | 1.5% | 1.5% | 1.4% | 1.4% |
| Impulsive 1 | 0.4% | 0.5% | 0.7% | 0.8% | 0.7% | 0.7% | 0.6% | 0.8% | 1.1% | 1.4% | 1.1% | 1.1% |
| Impulsive 2 | 0.3% | 0.4% | 0.5% | 0.6% | 0.6% | 0.6% | 0.7% | 0.9% | 1.2% | 1.4% | 1.2% | 1.2% |
| E = 200 MPa | Permanent | 0.1% | 0.2% | 0.3% | 0.3% | 0.3% | 0.2% | 0.3% | 0.4% | 0.7% | 0.6% | 0.5% | 0.4% |
| Sinusoidal | 0.1% | 0.2% | 0.3% | 0.3% | 0.3% | 0.3% | 0.3% | 0.5% | 0.7% | 0.7% | 0.7% | 0.7% |
| Impulsive 1 | 0.2% | 0.3% | 0.4% | 0.5% | 0.4% | 0.4% | 0.3% | 0.4% | 0.6% | 0.8% | 0.6% | 0.6% |
| Impulsive 2 | 0.1% | 0.2% | 0.3% | 0.3% | 0.3% | 0.3% | 0.4% | 0.5% | 0.7% | 0.8% | 0.7% | 0.7% |
| E = 400 MPa | Permanent | 0.1% | 0.1% | 0.1% | 0.1% | 0.1% | 0.1% | 0.2% | 0.2% | 0.3% | 0.3% | 0.3% | 0.2% |
| Sinusoidal | 0.1% | 0.1% | 0.1% | 0.1% | 0.1% | 0.2% | 0.2% | 0.2% | 0.4% | 0.4% | 0.4% | 0.4% |
| Impulsive 1 | 0.1% | 0.2% | 0.2% | 0.2% | 0.2% | 0.1% | 0.2% | 0.2% | 0.3% | 0.3% | 0.3% | 0.3% |
| Impulsive 2 | 0.1% | 0.1% | 0.1% | 0.1% | 0.1% | 0.1% | 0.2% | 0.3% | 0.4% | 0.4% | 0.4% | 0.4% |
| E = 27,000 MPa | Permanent | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | | | | | | |
| Sinusoidal | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | | | | | | |
| Impulsive 1 | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | | | | | | |
| Impulsive 2 | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | | | | | | |
Table 8.
Modes of failure in the simulations carried out under load state B and safety coefficients obtained at failure.
Table 8.
Modes of failure in the simulations carried out under load state B and safety coefficients obtained at failure.
| Failures Produced in Simulations under Load State B |
|---|
| Young’s Modulus | Signal | Elastic Soil | Elasto-Plastic Soil |
|---|
| Safety Coefficient at the Time of Failure | Mode of Failure | Safety Coefficient at the Time of Failure | Mode of Failure |
|---|
| SSC | BCSC | SSC | BCSC |
|---|
| E = 10 MPa | Permanent | 1.01 | 1.14 | SLIDING | 1.01 | 1.14 | SLIDING |
| Sinusoidal | 0.81 | 0.40 | SLIDING | 0.81 | 0.40 | SLIDING |
| Impulsive 1 | 0.81 | 0.40 | SLIDING | 0.81 | 0.40 | SLIDING |
| Impulsive 2 | 0.81 | 0.40 | SLIDING | 0.81 | 0.40 | SLIDING |
| E = 50 MPa | Permanent | 1.01 | 1.14 | SLIDING | 1.01 | 1.14 | SLIDING |
| Sinusoidal | 1.01 | 1.14 | SLIDING | 1.01 | 1.14 | SLIDING |
| Impulsive 1 | 0.81 | 0.40 | SLIDING | 0.81 | 0.40 | SLIDING |
| Impulsive 2 | 0.81 | 0.40 | SLIDING | 0.81 | 0.40 | SLIDING |
| E = 100 MPa | Permanent | 1.01 | 1.14 | SLIDING | 1.01 | 1.14 | SLIDING |
| Sinusoidal | 1.01 | 1.14 | SLIDING | 1.01 | 1.14 | SLIDING |
| Impulsive 1 | 0.90 | 0.69 | SLIDING | 0.90 | 0.69 | SLIDING |
| Impulsive 2 | 0.90 | 0.69 | SLIDING | 0.90 | 0.69 | SLIDING |
| E = 200 MPa | Permanent | 1.01 | 1.14 | SLIDING | 1.01 | 1.14 | SLIDING |
| Sinusoidal | 1.01 | 1.14 | SLIDING | 1.01 | 1.14 | SLIDING |
| Impulsive 1 | 0.90 | 0.69 | SLIDING | 0.90 | 0.69 | SLIDING |
| Impulsive 2 | 0.90 | 0.69 | SLIDING | 0.90 | 0.69 | SLIDING |
| E = 400 MPa | Permanent | 1.01 | 1.14 | SLIDING | 1.01 | 1.14 | SLIDING |
| Sinusoidal | 1.01 | 1.14 | SLIDING | 1.01 | 1.14 | SLIDING |
| Impulsive 1 | 1.01 | 1.14 | SLIDING | 1.01 | 1.14 | SLIDING |
| Impulsive 2 | 1.01 | 1.14 | SLIDING | 1.01 | 1.14 | SLIDING |
| E = 27,000 MPa | Permanent | 1.01 | | SLIDING | | | |
| Sinusoidal | 1.01 | | SLIDING | | | |
| Impulsive 1 | 1.01 | | SLIDING | | | |
| Impulsive 2 | 1.01 | | SLIDING | | | |
Table 9.
Crown wall turning in simulations under load state C. [The simulations with failure of the structure are highlighted in dark gray (failure due to rigid overturning) and in light gray (failure due to bearing capacity of the foundation)].
Table 9.
Crown wall turning in simulations under load state C. [The simulations with failure of the structure are highlighted in dark gray (failure due to rigid overturning) and in light gray (failure due to bearing capacity of the foundation)].
| Bearing Capacity and Overturning Failure (Rotation in Degrees) |
|---|
| Bearing Capacity Safety Coefficient | 2.49 | 1.66 | 1.29 | 0.96 | 0.35 | 0.07 | 0.01 | 2.49 | 1.66 | 1.29 | 0.96 | 0.35 | 0.07 | 0.00 |
|---|
| Overturning Safety Coefficient | 2.21 | 1.66 | 1.47 | 1.33 | 1.10 | 1.02 | 0.95 | 2.21 | 1.66 | 1.47 | 1.33 | 1.10 | 1.02 | 0.95 |
|---|
| Young’s Modulus | Signal | Elastic Soil | Elasto-Plastic Soil |
|---|
| 10 MPa | Permanent | 3.3 | 7.4 | 11.7 | 23.8 | 90.0 | 90.0 | 90.0 | 5.4 | 13.4 | 21.9 | 46.1 | 90.0 | 90.0 | 90.0 |
| Sinusoidal | 2.5 | 4.0 | 4.5 | 4.9 | 5.3 | 5.3 | 5.3 | 4.1 | 6.8 | 7.8 | 8.5 | 9.3 | 9.3 | 9.4 |
| Impulsive 1 | 1.8 | 3.1 | 4.0 | 4.5 | 5.2 | 5.3 | 5.4 | 2.8 | 5.2 | 6.9 | 7.8 | 9.0 | 9.3 | 9.4 |
| Impulsive 2 | 1.0 | 1.5 | 1.9 | 2.2 | 3.1 | 3.6 | 4.1 | 1.8 | 2.7 | 3.3 | 4.1 | 5.8 | 6.7 | 7.8 |
| 50 MPa | Permanent | 0.6 | 1.2 | 1.8 | 3.1 | 35.9 | 90.0 | 90.0 | 1.1 | 2.3 | 3.5 | 5.9 | 73.5 | 90.0 | 90.0 |
| Sinusoidal | 0.6 | 1.2 | 1.6 | 2.0 | 3.0 | 3.3 | 3.5 | 1.1 | 2.3 | 3.0 | 4.0 | 6.0 | 6.7 | 7.2 |
| Impulsive 1 | 0.4 | 0.8 | 0.9 | 1.1 | 1.9 | 2.4 | 3.0 | 0.8 | 1.4 | 1.7 | 2.1 | 3.7 | 4.8 | 6.0 |
| Impulsive 2 | 0.4 | 0.6 | 0.7 | 0.8 | 1.0 | 1.0 | 1.0 | 0.8 | 1.3 | 1.5 | 1.7 | 2.0 | 2.1 | 2.1 |
| 100 MPa | Permanent | 0.3 | 0.6 | 0.9 | 1.4 | 10.6 | 90.0 | 90.0 | 0.5 | 1.1 | 1.7 | 2.8 | 21.9 | 90.0 | 90.0 |
| Sinusoidal | 0.3 | 0.6 | 0.8 | 1.1 | 2.1 | 2.5 | 2.8 | 0.6 | 1.2 | 1.7 | 2.4 | 4.6 | 5.5 | 6.3 |
| Impulsive 1 | 0.2 | 0.4 | 0.5 | 0.6 | 0.9 | 1.2 | 1.8 | 0.5 | 0.8 | 1.0 | 1.3 | 1.9 | 2.7 | 3.9 |
| Impulsive 2 | 0.2 | 0.4 | 0.5 | 0.5 | 0.7 | 0.7 | 0.8 | 0.5 | 0.9 | 1.0 | 1.2 | 1.5 | 1.6 | 1.7 |
| 200 MPa | Permanent | 0.1 | 0.3 | 0.4 | 0.7 | 4.4 | 90.0 | 90.0 | 0.2 | 0.5 | 0.8 | 1.4 | 9.4 | 90.0 | 90.0 |
| Sinusoidal | 0.1 | 0.3 | 0.4 | 0.6 | 1.4 | 1.8 | 2.2 | 0.3 | 0.6 | 0.9 | 1.4 | 3.3 | 4.5 | 5.4 |
| Impulsive 1 | 0.1 | 0.2 | 0.3 | 0.3 | 0.5 | 0.6 | 0.9 | 0.2 | 0.5 | 0.6 | 0.8 | 1.3 | 1.5 | 2.1 |
| Impulsive 2 | 0.1 | 0.2 | 0.2 | 0.3 | 0.4 | 0.5 | 0.5 | 0.3 | 0.5 | 0.6 | 0.8 | 1.1 | 1.2 | 1.4 |
| 400 MPa | Permanent | 0.1 | 0.1 | 0.2 | 0.3 | 1.9 | 90.0 | 90.0 | 0.1 | 0.3 | 0.4 | 0.7 | 4.5 | 90.0 | 90.0 |
| Sinusoidal | 0.0 | 0.1 | 0.2 | 0.2 | 0.8 | 1.2 | 1.5 | 0.1 | 0.3 | 0.4 | 0.7 | 2.4 | 3.7 | 4.8 |
| Impulsive 1 | 0.0 | 0.1 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.1 | 0.3 | 0.4 | 0.5 | 0.9 | 1.1 | 1.4 |
| Impulsive 2 | 0.0 | 0.1 | 0.1 | 0.2 | 0.3 | 0.3 | 0.4 | 0.2 | 0.3 | 0.4 | 0.5 | 0.8 | 0.9 | 1.1 |
| 27,000 MPa | Permanent | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.3 | 90.0 | | | | | | | |
| Sinusoidal | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | | | | | | | |
| Impulsive 1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | | | | | | | |
| Impulsive 2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | | | | | | | |
Table 10.
Mode of failure in simulations under load state C and safety coefficients obtained at the time of failure of the crown wall.
Table 10.
Mode of failure in simulations under load state C and safety coefficients obtained at the time of failure of the crown wall.
| Failure Produced in Simulations under Load State C |
|---|
| Young’s Modulus | Signal | Maximum Acceptable Deformation | Elastic Soil | Elasto-Plastic Soil |
|---|
| Safety Coefficient at the Time of Failure | Mode of Failure | Safety Coefficient at the Time of Failure | Mode of Failure |
|---|
| BCSC | OSC | BCSC | OSC |
|---|
| E = 10 MPa | Permanent | 19.8% | 1.32 | 1.49 | bearing capacity | 1.88 | 1.80 | bearing capacity |
| Sinusoidal | no | no | no | no | no | no |
| Impulsive 1 | no | no | no | no | no | no |
| Impulsive 2 | no | no | no | no | no | no |
| E = 50 MPa | Permanent | 4.5% | 1.09 | 1.38 | bearing capacity | 1.58 | 1.62 | bearing capacity |
| Sinusoidal | 0.59 | 1.19 | bearing capacity | 1.51 | 1.58 | bearing capacity |
| Impulsive 1 | 0.05 | 1.00 | bearing capacity | 0.79 | 1.26 | bearing capacity |
| Impulsive 2 | no | no | no | 0.00 | 0.83 | bearing capacity |
| E = 100 MPa | Permanent | 2.8% | 0.95 | 1.32 | bearing capacity | 1.36 | 1.50 | bearing capacity |
| Sinusoidal | 0.66 | 1.22 | bearing capacity | 1.36 | 1.51 | bearing capacity |
| Impulsive 1 | 0.03 | 0.97 | bearing capacity | 0.61 | 1.20 | bearing capacity |
| Impulsive 2 | no | no | no | 0.09 | 1.03 | bearing capacity |
| E = 200 MPa | Permanent | 1.7% | 0.91 | 1.31 | bearing capacity | 1.20 | 1.43 | bearing capacity |
| Sinusoidal | 0.64 | 1.21 | bearing capacity | 1.22 | 1.44 | bearing capacity |
| Impulsive 1 | 0.01 | 0.95 | bearing capacity | 0.73 | 1.24 | bearing capacity |
| Impulsive 2 | no | no | no | 0.58 | 1.17 | bearing capacity |
| E = 400 MPa | Permanent | 1.0% | 0.85 | 1.29 | bearing capacity | 1.09 | 1.38 | bearing capacity |
| Sinusoidal | 0.59 | 1.19 | bearing capacity | 1.14 | 1.40 | bearing capacity |
| Impulsive 1 | 0.01 | 0.84 | bearing capacity | 0.84 | 1.25 | bearing capacity |
| Impulsive 2 | no | no | no | 0.79 | 1.24 | bearing capacity |
| E = 27,000 MPa | Permanent | | | 1.00 | overturning | | | |
| Sinusoidal | | no | no | | | |
| Impulsive 1 | | no | no | | | |
| Impulsive 2 | | no | no | | | |