Impact of Self-Cleansing Criteria Choice on the Optimal Design of Sewer Networks in South America
Abstract
1. Introduction
2. Methodology
2.1. Optimal Sewer Network Design
2.1.1. Design Cost
2.1.2. Design Constraints
- Minimum pipe diameter required for the cleaning and maintenance of the network;
- Maximum filling ratio that must be enabled to allow adequate aeration in the system;
- Minimum velocity and shear stress inside the pipes necessary to prevent particle sedimentation;
- Maximum velocity required to prevent problems such as cavitation and pipe wall erosion;
- Minimum and maximum depth below ground level necessary to protect the pipe structure from overloading and axial stresses, respectively.
2.2. Self-Cleansing Limits
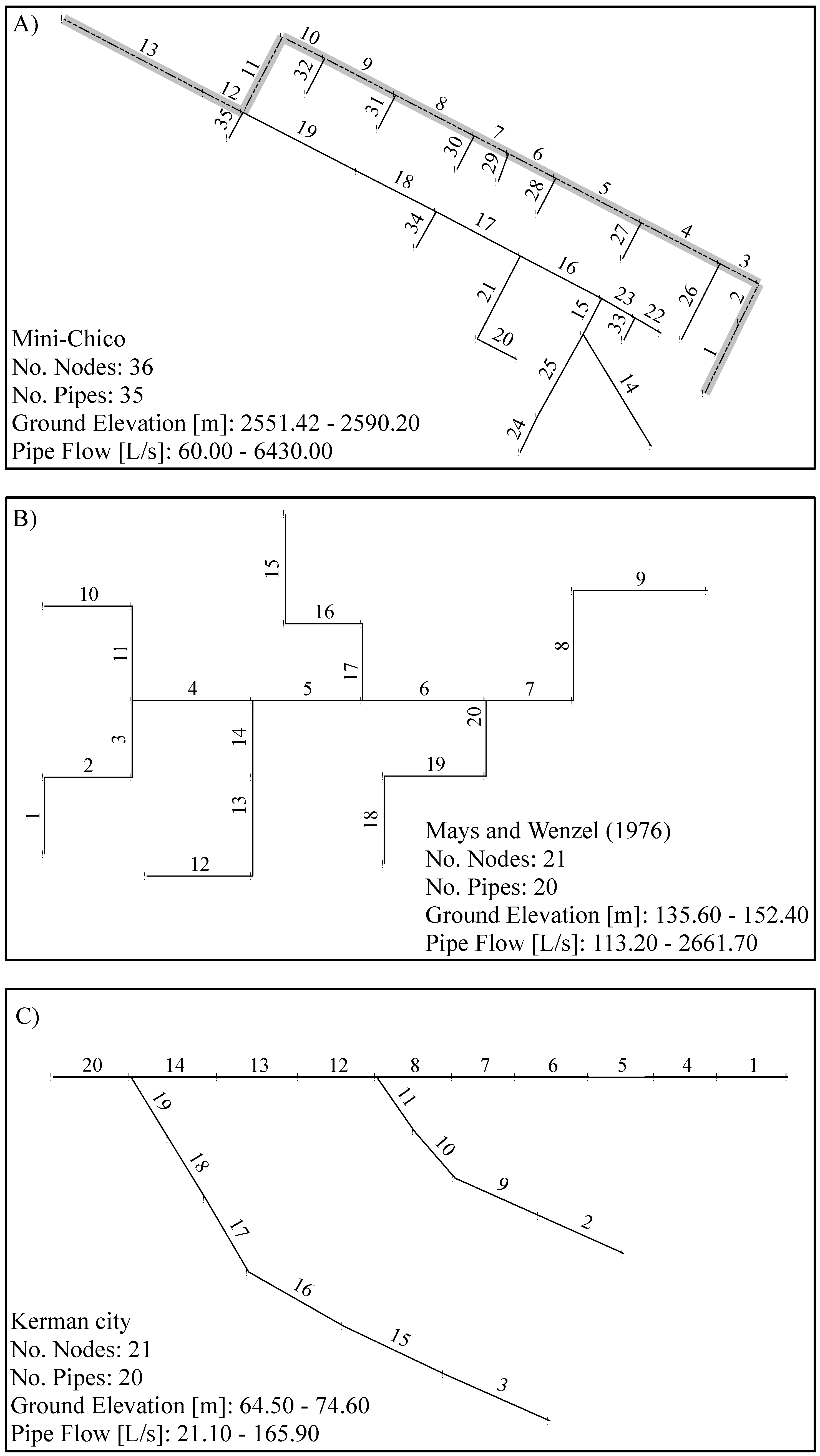
3. Case Studies
3.1. Description
3.2. Design Constraints
Self-Cleansing Limits
- Select a minimum velocity or minimum shear stress from Table 1;
- Select a pipe diameter;
- Define the filling ratio ;
- Solve Equation (3), for the minimum velocity, or Equation (4), for shear stress, to estimate the minimum self-cleansing slope;
- Move to the next pipe diameter and repeat step 4;
- Move to the next self-cleansing criterion in Table 1 and start the entire procedure over again.
3.3. Design Procedure
- Create a .txt file that includes the manholes of the main path of the network. Each manhole must include ground elevation and inflow information;
- Define design constraints and list of available commercial diameters;
- Create a graph with all the possible arcs (pipes). Each arc has an associated pipe diameter as well as upstream and downstream elevation to calculate the slope;
- Calculate the cost of each pipe using Equation (1);
- Calculate the hydraulic of each arc, i.e., determine flow, hydraulic radius, wetted area, and top width, amongst other hydraulic parameters, using the Manning equation using Equation (3). If the arc does not fulfill all the design constraints it will not be created;
- Use the Bellman–Ford algorithm to estimate the combination of arcs that minimize network cost;
- Report the results of the slope and diameter of each pipe in the network.
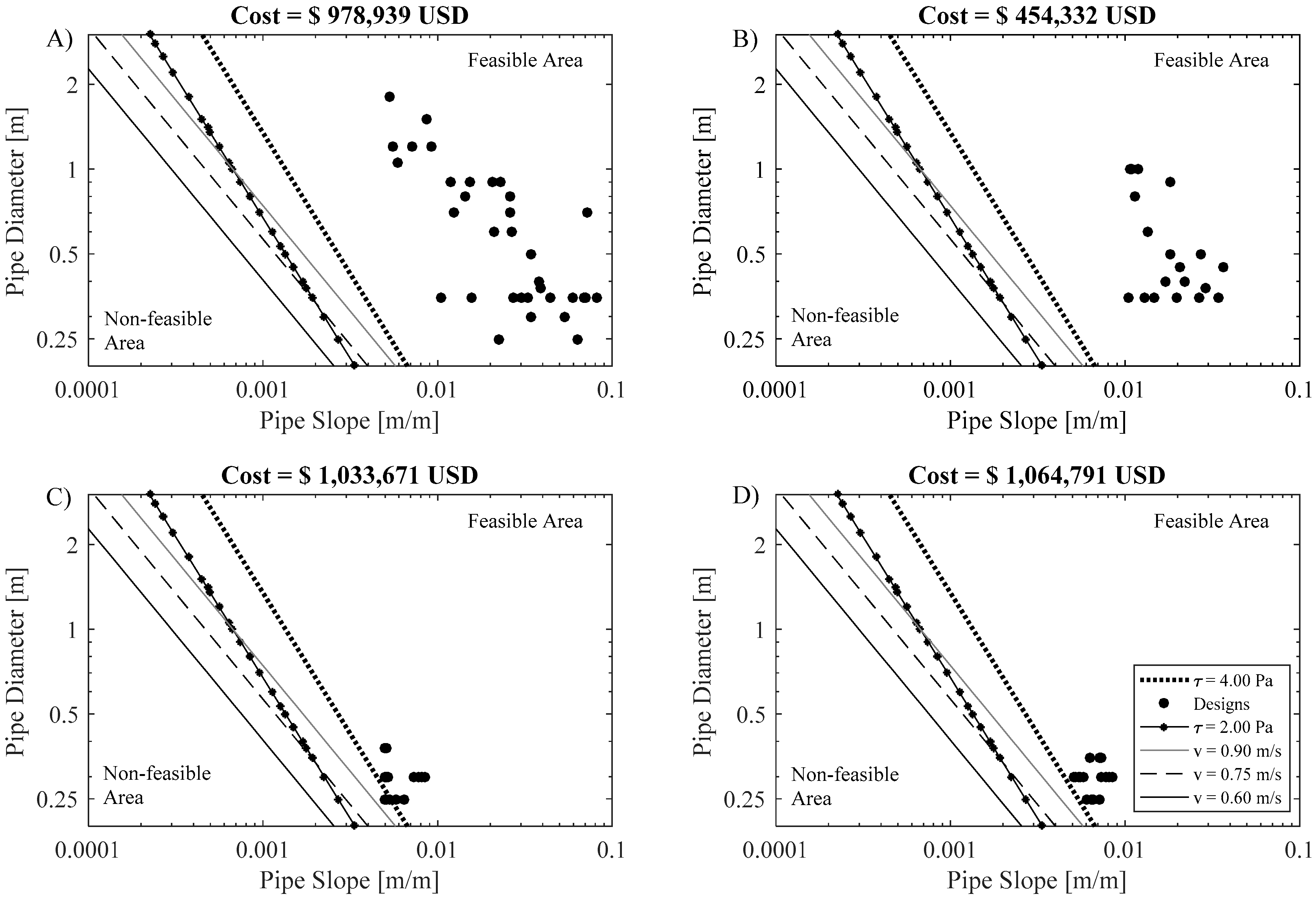
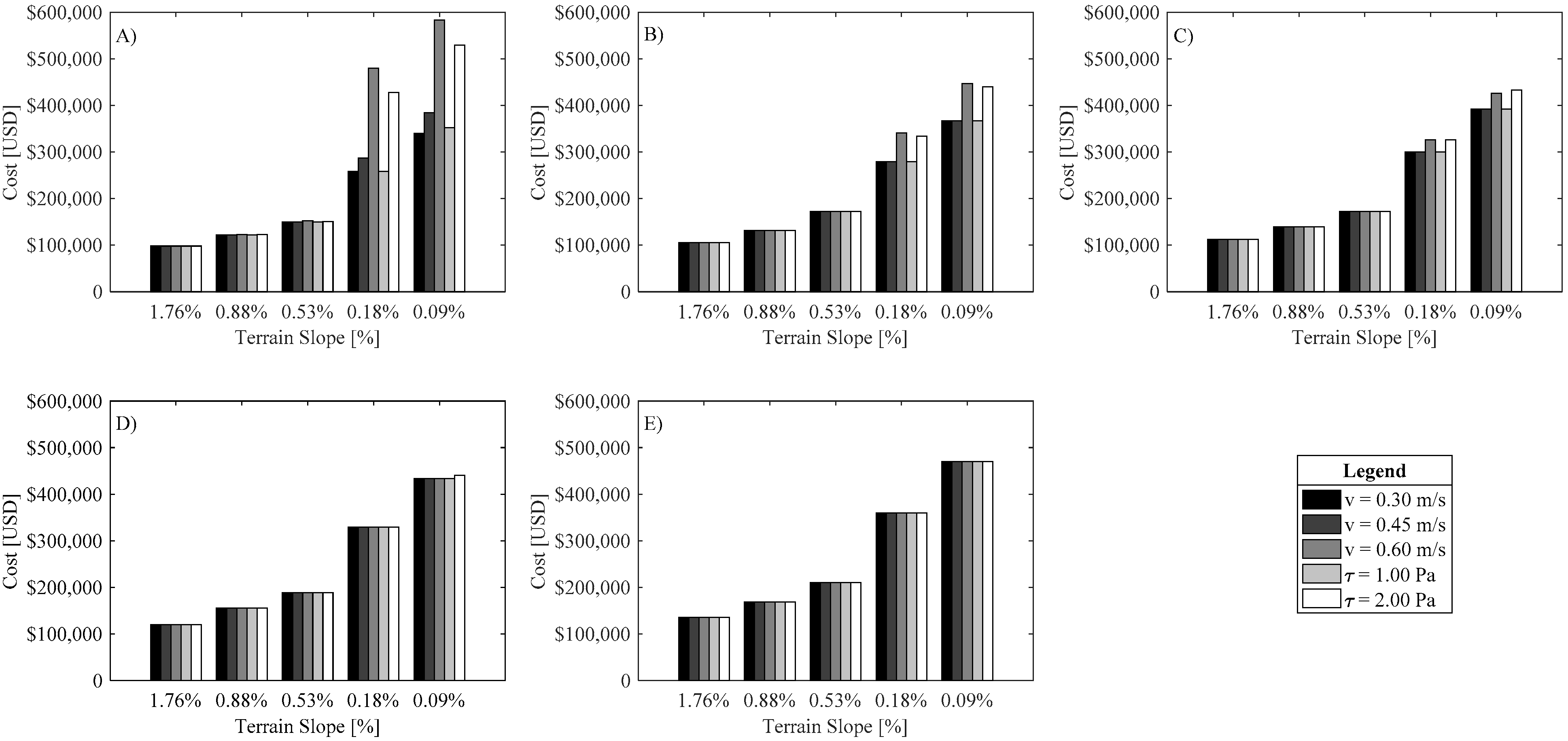
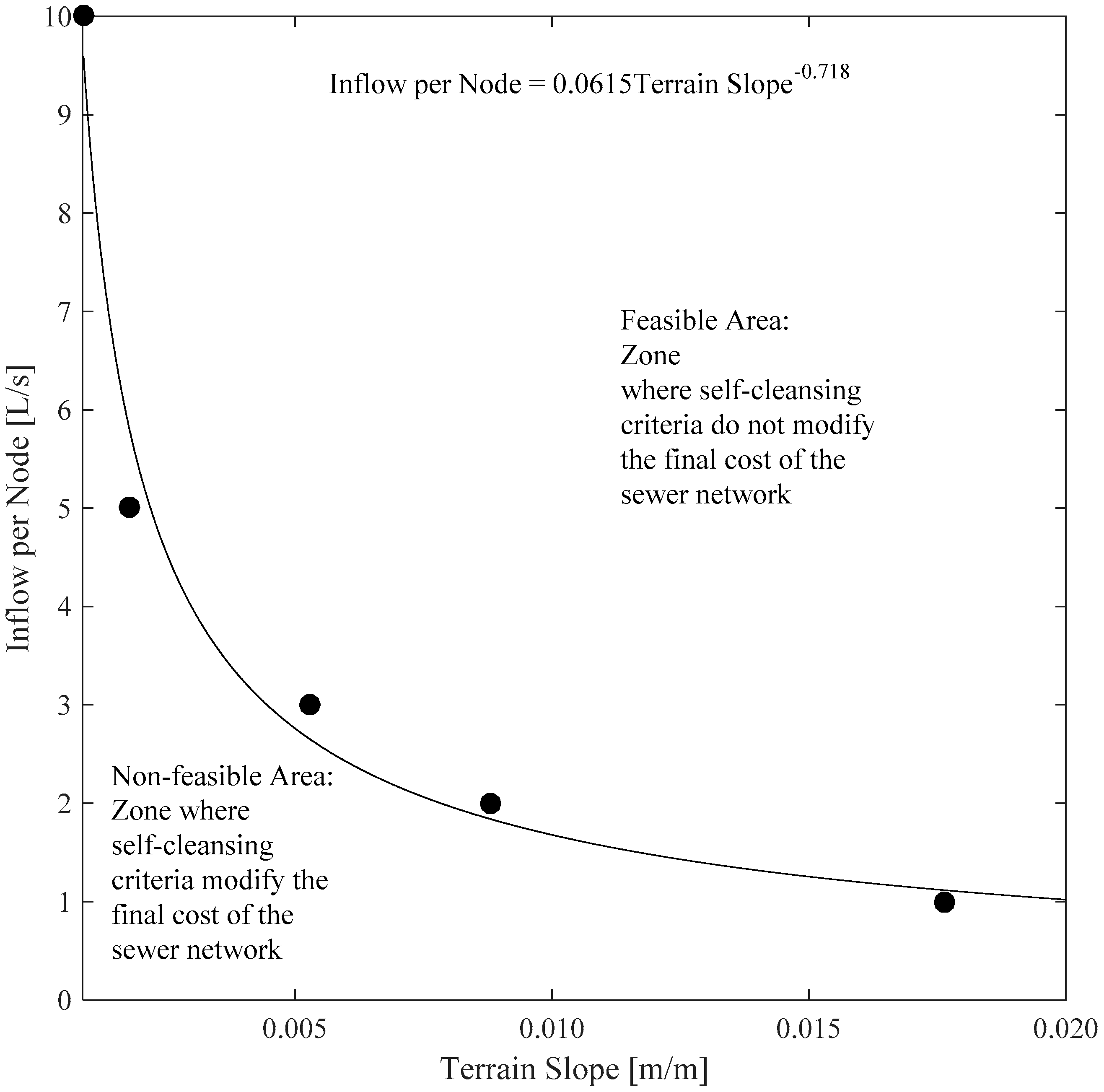
4. Results and Discussion
5. Sensitivity Analysis
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Argaman, Y.; Shamir, U.; Spivak, E. Design of Optimal Sewerage Systems. J. Environ. Eng. Div. 1973, 99, 703–716. [Google Scholar]
- Mein, W. Design of Sanitary Sewer Systems by Dynamic Programming. Master’s Thesis, McMaster University, Hamilton, ON, Canada, 1975. [Google Scholar]
- Li, G.; Matthew, R. New Approach for Optimization of Urban Drainage Systems. J. Environ. Eng. 1990, 116, 927–944. [Google Scholar] [CrossRef]
- Holland, M. Computer Models of Wastewater Collection Systems. Master’s Thesis, Harvard University, Cambridge, MA, USA, 1966. [Google Scholar]
- Elimam, A.A.; Charalambous, C.; Ghobrial, F.H. Optimum Design of Large Sewer Networks. J. Environ. Eng. 1989, 115, 1171–1190. [Google Scholar] [CrossRef]
- Walters, G.; Lohbeck, T. Optimal Layout of Tree Networks Using Genetic Algorithms. Eng. Optim. 1993, 22, 27–48. [Google Scholar] [CrossRef]
- Afshar, M. Application of a Genetic Algorithm to Storm Sewer Network Optimization. Sci. Iran. 2006, 13, 234–244. [Google Scholar]
- Cisty, M. Hybrid Genetic Algorithm and Linear Programming Method for Least-Cost Design of Water Distribution Systems. Water Resour. Manag. 2010, 24, 1–24. [Google Scholar] [CrossRef]
- Cozzolino, L.; Cimorelli, L.; Covelli, C.; Mucherino, C.; Pianese, D. An Innovative Approach for Drainage Network Sizing. Water 2015, 7, 546–567. [Google Scholar] [CrossRef]
- Hassan, W.; Jassem, M.; Mohammed, S. A GA-HP Model for the Optimal Design of Sewer Networks. Water Resour. Manag. 2018, 32, 865–879. [Google Scholar] [CrossRef]
- Shao, Z.; Zhang, X.; Li, S.; Deng, S.; Chai, H. A Novel SWMM Based Algorithm Application to Storm Sewer Network Design. Water 2017, 9, 747. [Google Scholar] [CrossRef]
- Duque, N.; Duque, D.; Saldarriaga, J. A New Methodology for the Optimal Design of Series of Pipes in Sewer Systems. J. Hydroinformatics 2016, 18, 757–772. [Google Scholar] [CrossRef]
- Mays, L.W.; Wenzel, H.G. Optimal Design of Multilevel Branching Sewer Systems. Water Resour. Res. 1976, 12, 913–917. [Google Scholar] [CrossRef]
- Ebtehaj, I.; Bonakdari, H.; Sharifi, A. Design Criteria for Sediment Transport in Sewers Based on Self-Cleansing Concept. J. Zhejiang Univ. Sci. A 2014, 15, 914–924. [Google Scholar] [CrossRef]
- ATV-DVWK-Regelwerk. Hydraulische Dimensionierung Und Leistungsnachweis von Abwasserkanalen Und-Leitungen; AVT-DVWK-A 110; Gesellschaft zur Förderung der Abwassertechnik e.V. (GFA): Hennef, Germany, 2001. [Google Scholar]
- Vongvisessomjai, N.; Tingsanchali, T.; Babel, M. Non-Deposition Design Criteria for Sewers with Part-Full Flow. Urban Water J. 2010, 7, 61–77. [Google Scholar] [CrossRef]
- Montes, C.; Bohórquez, J.; Borda, S.; Saldarriaga, J. Criteria of Minimum Shear Stress vs. Minimum Velocity for Self-Cleaning Sewer Pipes Design. Procedia Eng. 2017, 186, 69–75. [Google Scholar] [CrossRef]
- Lysne, D. Hydraulic Design of Self-Cleaning Sewage Tunnels. J. Sanit. Eng. Div. Am. Soc. Civ. Eng. 1969, 95, 17–36. [Google Scholar]
- American Society of Civil Engineers (ASCE). Water pollution control federation. Design and Construction of Sanitary and Storm Sewers. In American Society of Civil Engineers Manuals and Reports on Engineering Practices; ASCE: Reston, VA, USA, 1970. [Google Scholar]
- Yao, K. Sewer Line Design Based on Critical Shear Stress. J. Environ. Eng. Div. 1974, 100, 507–520. [Google Scholar]
- Minister of Interior. Instruction Technique Relative Aux Réseaux d’assainissement Des Agglomerations; Circulaire Interministerielle IT 77284 I; Minister of Interior: Paris, France, 1977. [Google Scholar]
- British Standard Institution. Sewerage-Guide to New Sewerage Construction BS8005 Part 1; British Standard Institution: London, UK, 1987. [Google Scholar]
- Instituto Ecuatoriano de Normalización. CPE INEN 005-9-1 (1992): Código Ecuatoriano de La Construcción C.E.C. Normas Para Estudio y Diseño de Sistemas de Agua Potable y Disposición de Aguas Residuales Para Poblaciones Mayores a 1 000 Habitantes; INEN: Quito, Ecuador, 1992. [Google Scholar]
- European Standard EN 752-4. Drain and Sewer System Outside Building: Part 4. Hydraulic Design and Environmental Considerations; European Comitte for Standardization (CEN): Brussels, Belgium, 1997. [Google Scholar]
- Great Lakes. Recommended Standars for Wastewater Facilities; Health Education Services Division, Health Research Inc.: Menands, NY, USA, 2004. [Google Scholar]
- Comisión Nacional del Agua. Manual de Agua Potable, Alcantarillado y Saneamiento; Comisión Nacional del Agua: Coyoacán, México, 2007. [Google Scholar]
- Instituto Boliviano de Normalización y Calidad. Diseño de Sistemas de Alcantarillado Sanitario y Pluvial (NB 688); Instituto Boliviano de Normalización y Calidad: La Paz, Bolivia, 2007. [Google Scholar]
- Empresas Públicas de Medellín. Guía Para El Diseño Hidráulico de Redes de Alcantarillado; Empresas Públicas de Medellín: Medellín, Colombia, 2009. [Google Scholar]
- Colombia, Ministerio de Vivienda, Ciudad y Territorio. Reglamento Técnico Del Sector de Agua Potable y Saneamiento Básico: TÍTULO D. Sistemas de Recolección y Evacuación de Aguas Residuales Domésticas y Aguas Lluvias; Colombia, Ministerio de Vivienda, Ciudad y Territorio: Bogotá, Colombia, 2012.
- Bellman, R. On a Routing Problem. Q. Appl. Math. 1958, 16, 87–90. [Google Scholar] [CrossRef]
- Maurer, M.; Scheidegger, A.; Herlyn, A. Quantifying Costs and Lengths of Urban Drainage Systems with a Simple Static Sewer Infrastructure Model. Urban Water J. 2013, 10, 268–280. [Google Scholar] [CrossRef]
- Moeini, R.; Afshar, M. Sewer Network Design Optimization Problem Using Ant Colony Optimization Algorithm and Tree Growing Algorithm. In Proceedings of the EVOLVE—A Bridge between Probability, Set Oriented Numerics, and Evolutionary Computation IV, Leiden, The Netherlands, 10–13 July 2013. [Google Scholar]
- Marchionni, V.; Lopes, N.; Mamouros, L.; Covas, D. Modelling Sewer Systems Costs with Multiple Linear Regression. Water Resour. Manag. 2014, 28, 4415–4431. [Google Scholar] [CrossRef]
- Afshar, M.; Shahidi, M.; Rohani, M.; Sargolzaei, M. Application of Cellular Automata to Sewer Network Optimization Problems. Sci. Iran. 2011, 18, 304–312. [Google Scholar] [CrossRef]
| Criterion No. | Source | Country | Sewer Type | [m/s] | [Pa] |
|---|---|---|---|---|---|
| (1) | Lysne [18] | USA | All | - | 2.0–4.0 |
| (2) | ASCE [19] | USA | WW | 0.6 | - |
| SW | 0.9 | - | |||
| (3) | Yao [20] | USA | SW | - | 3.0–4.0 |
| WW | - | 1.0–2.0 | |||
| (4) | Minister of Interior [21] | France | WW | 0.3 | - |
| C | 0.6 | - | |||
| (5) | British Standard BS 8001 [22] | UK | SW | 0.75 | - |
| C | 1 | - | |||
| (6) | Ecuadorian Normalization Institute (Instituto Ecuatoriano de Normalización) [23] | Ecuador | WW | 0.45 | - |
| SW | 0.9 | - | |||
| (7) | European Standard EN 752-4 [24] | Europe | All | 0.7 | - |
| (8) | ATV-DVWK-Regelwerk [15] | Germany | All | Depends on pipe diameter | - |
| (9) | Great Lakes [25] | USA | WW | 0.6 | - |
| (10) | National Water Commission (Comisión Nacional del Agua) [26] | Mexico | SW | 0.6 | - |
| WW | 0.3 | - | |||
| (11) | Bolivian Institute for Standarization and Quality (Instituto Boliviano de Normalización y Calidad) [27] | Bolivia | WW | - | 1 |
| SW and C | - | 1.5 | |||
| (12) | Medellin Public Enterprises (Empresas Públicas de Medellín) [28] | Colombia | WW | 0.45 | 1.5 |
| SW and C | 0.75 | 3 | |||
| (13) | Colombia. Ministry of Housing, City and Territory (Colombia. Ministerio de Vivienda, Ciudad y Territorio) [29] | Colombia | WW | 0.45 | 1.5 |
| SW and C | 0.75 | 3 |
| Design Constraint | Threshold Value |
|---|---|
| Minimum diameter | 200 mm |
| Maximum filling ratio | 0.85 |
| Minimum self-cleansing velocity | 0.6–0.9 m/s |
| Minimum shear stress | 2.0–4.0 Pa |
| Maximum velocity | 5.0 m/s |
| Minimum depth below ground level | 1.2 m |
| Maximum depth below ground level | 5.0 m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montes, C.; Kapelan, Z.; Saldarriaga, J. Impact of Self-Cleansing Criteria Choice on the Optimal Design of Sewer Networks in South America. Water 2019, 11, 1148. https://doi.org/10.3390/w11061148
Montes C, Kapelan Z, Saldarriaga J. Impact of Self-Cleansing Criteria Choice on the Optimal Design of Sewer Networks in South America. Water. 2019; 11(6):1148. https://doi.org/10.3390/w11061148
Chicago/Turabian StyleMontes, Carlos, Zoran Kapelan, and Juan Saldarriaga. 2019. "Impact of Self-Cleansing Criteria Choice on the Optimal Design of Sewer Networks in South America" Water 11, no. 6: 1148. https://doi.org/10.3390/w11061148
APA StyleMontes, C., Kapelan, Z., & Saldarriaga, J. (2019). Impact of Self-Cleansing Criteria Choice on the Optimal Design of Sewer Networks in South America. Water, 11(6), 1148. https://doi.org/10.3390/w11061148





