Stream Power Determination in GIS: An Index to Evaluate the Most ’Sensitive’Points of a River
Abstract
:1. Introduction
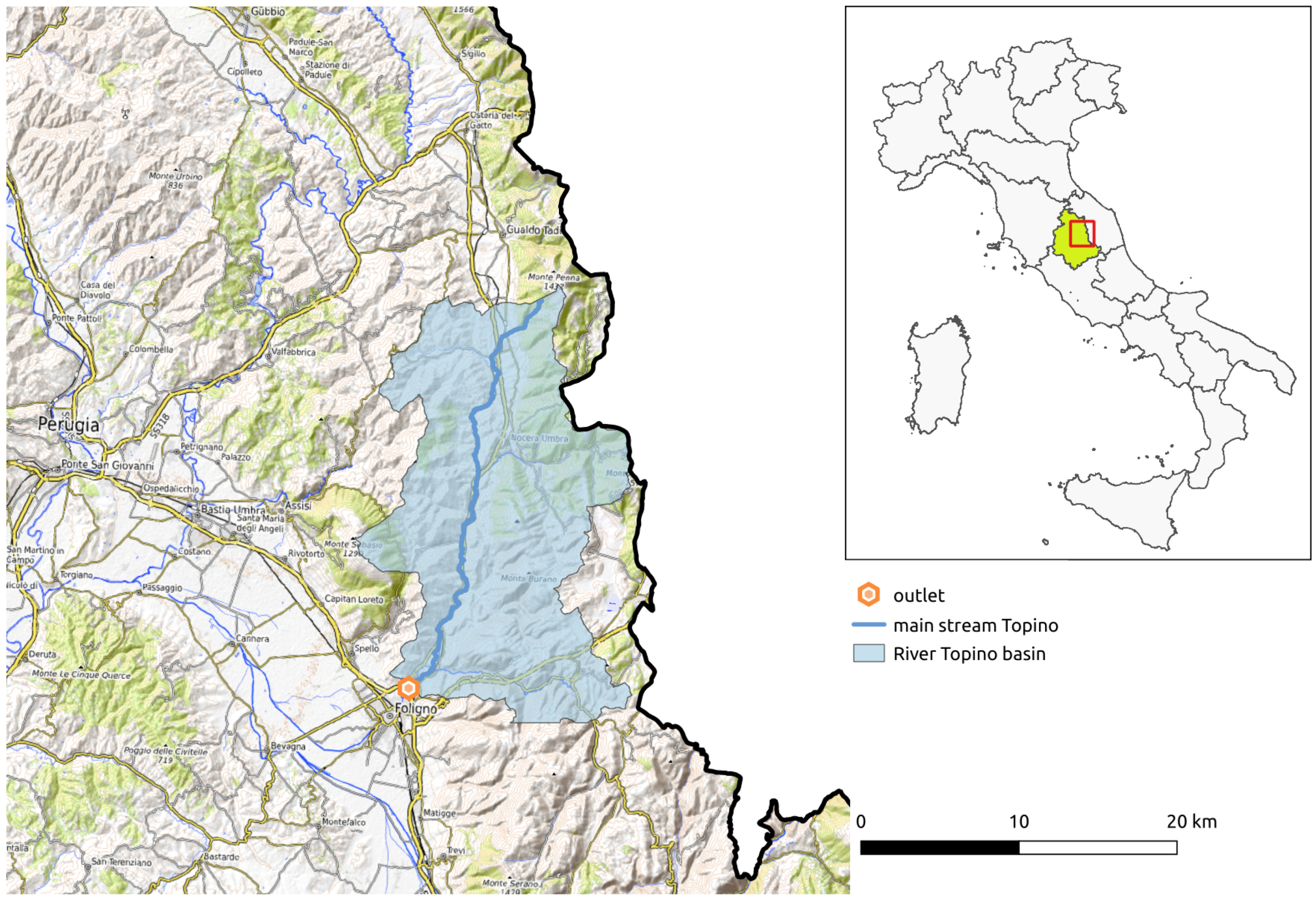
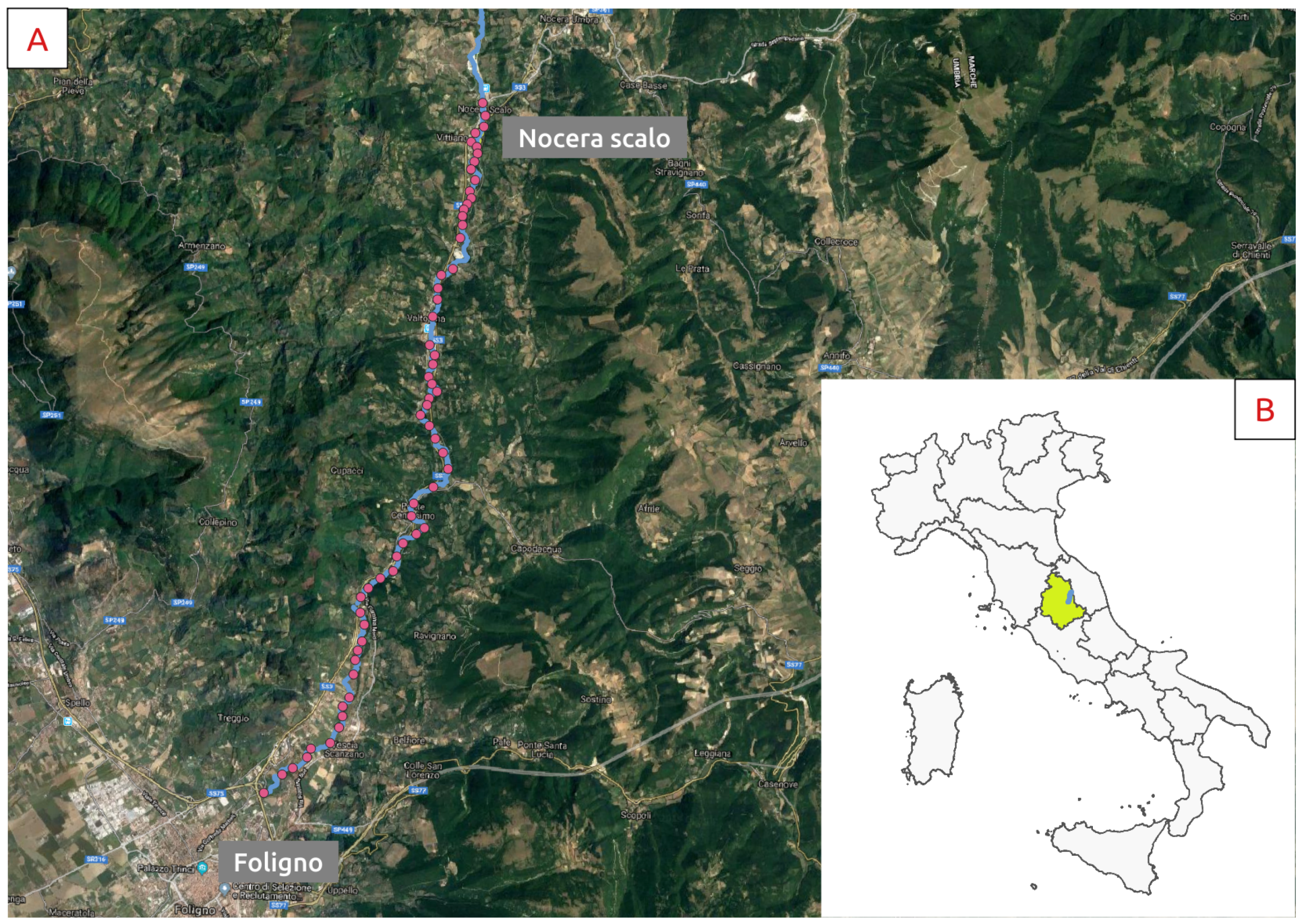
Study Area
2. Methods
2.1. Peak Flow Discharge
- Kirpich equation for basins smaller then 10 km2:withTc = run-off time (hours);L = main channel length (km);DH = drop in elevation of the main channel (m).
- Giandotti equation for basins larger than 10 km2:withTc = run-off time (hours);S = basin area (km2);L = main channel length (m);H = mean basin elevation (m a.s.l.).
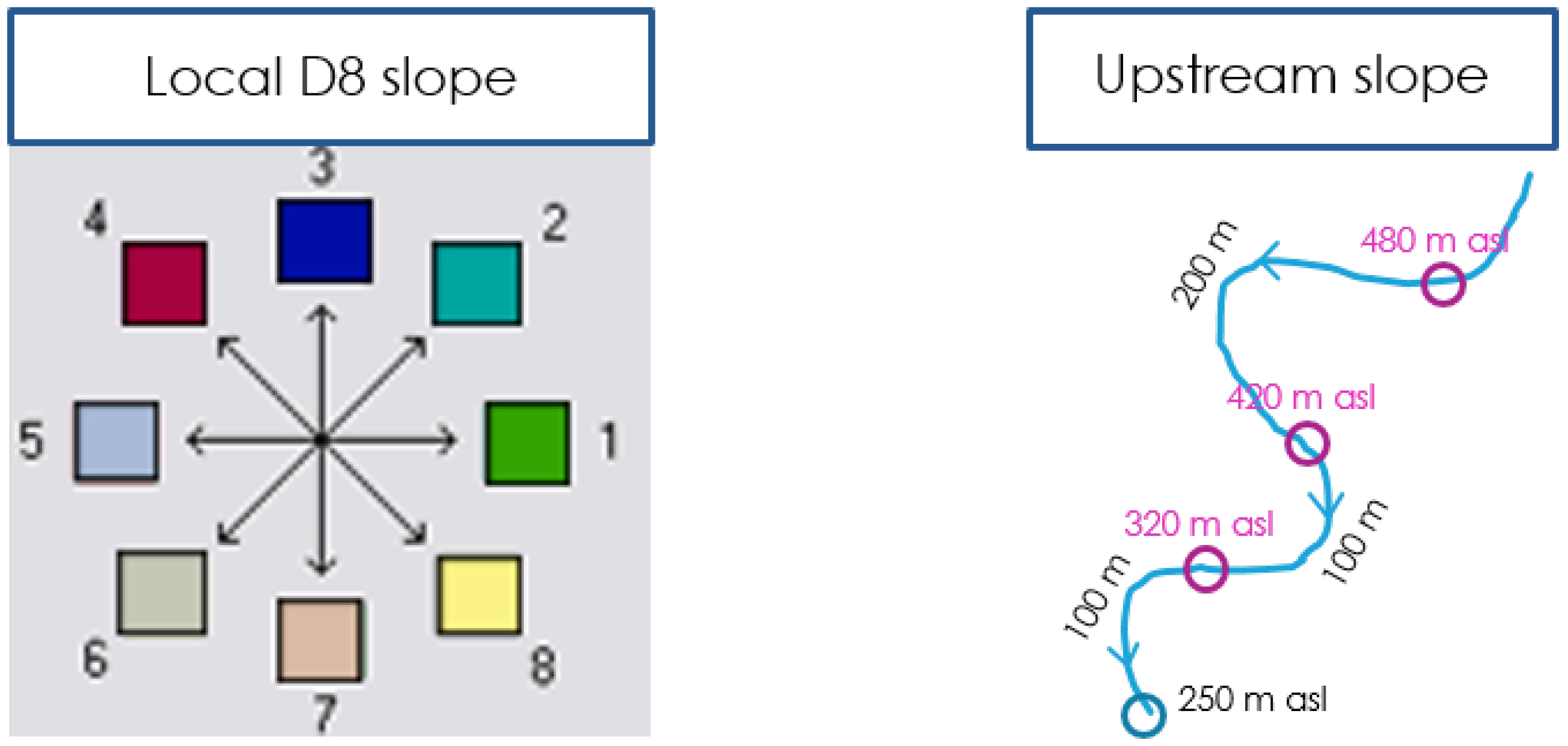
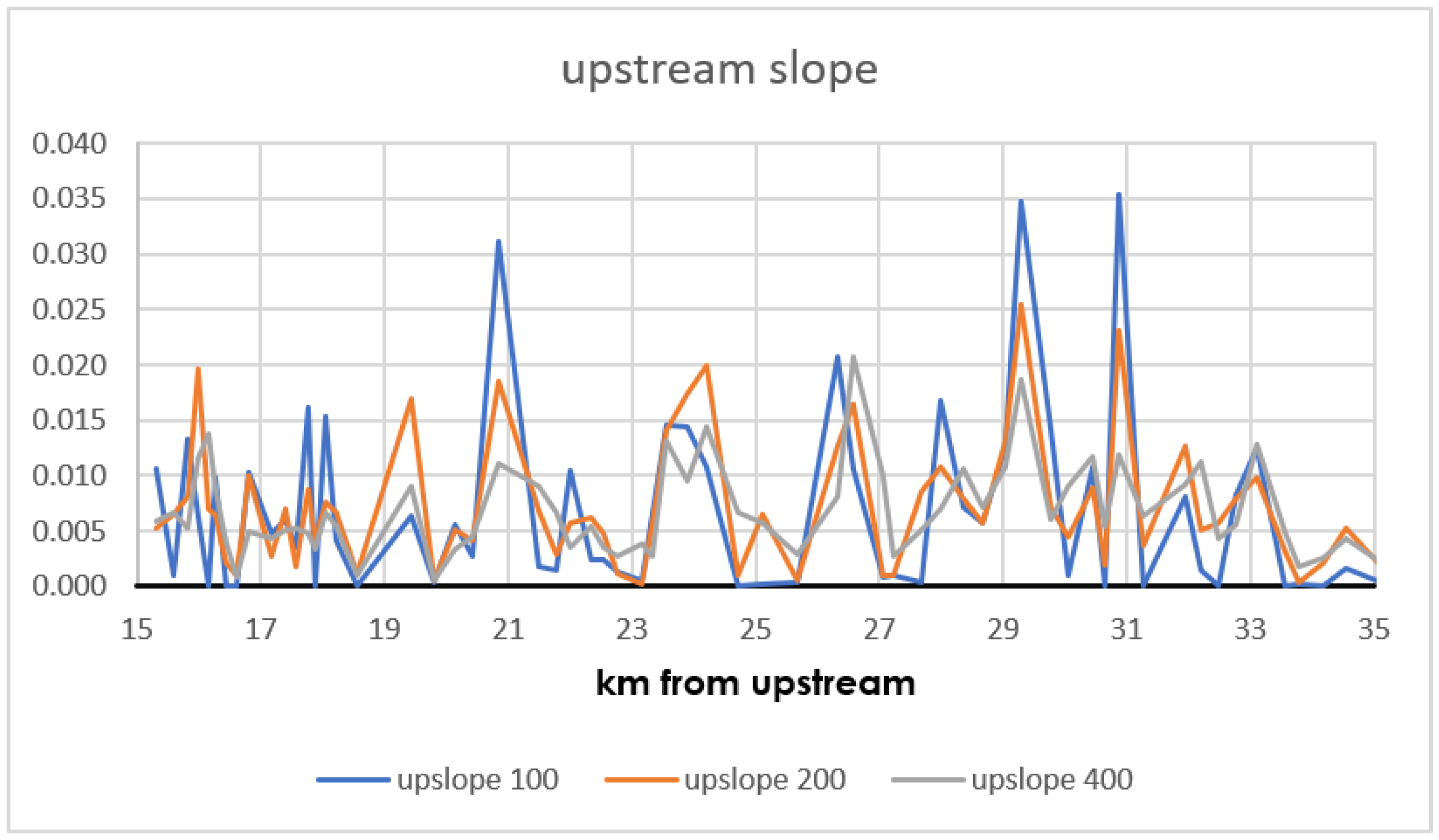
2.2. Slope Determination
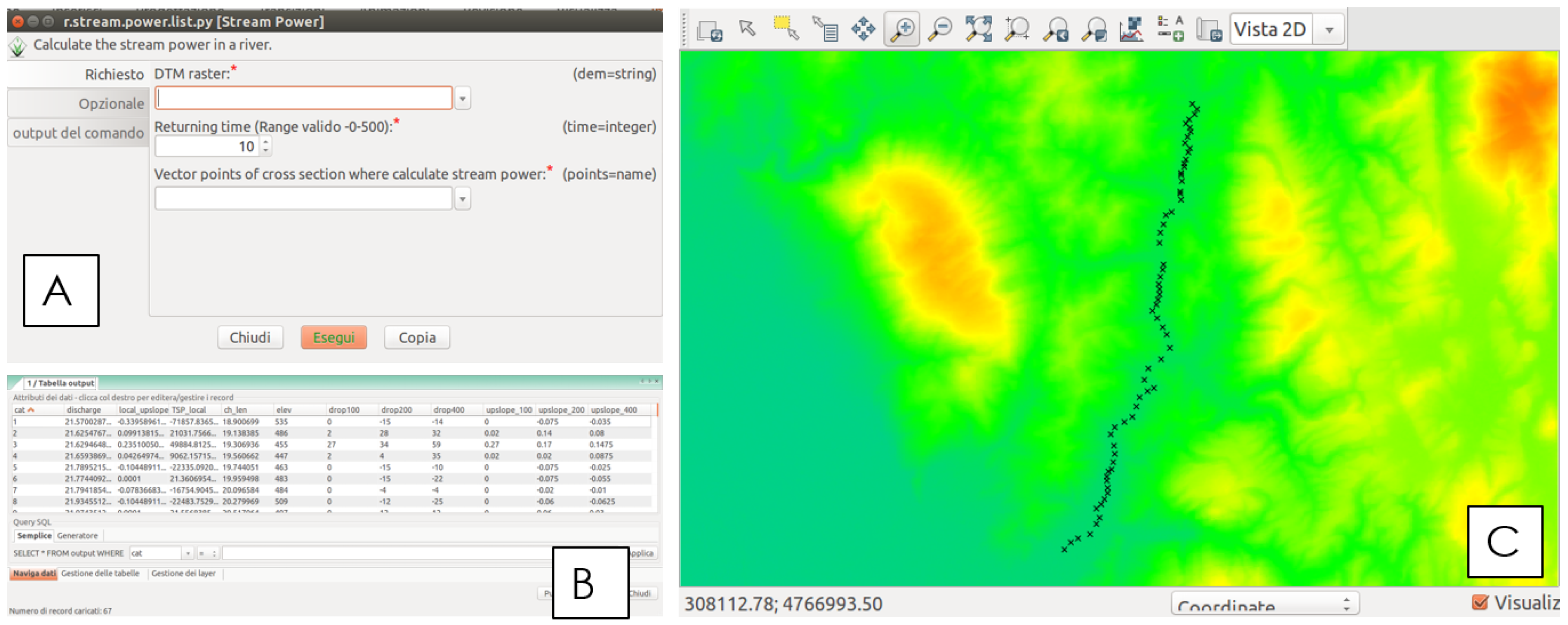
2.3. The Module r.stream.power
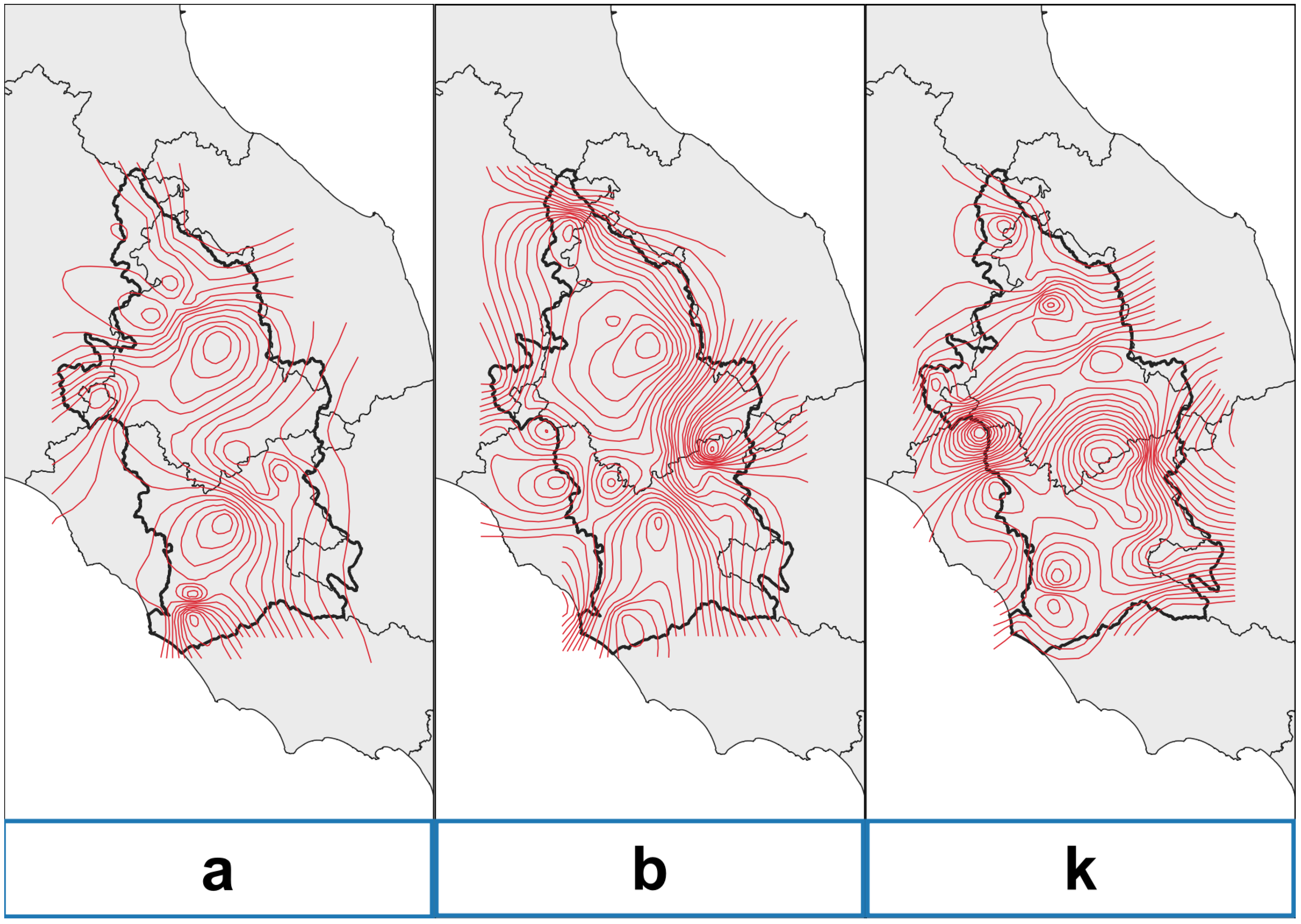
3. Results
4. Discussion
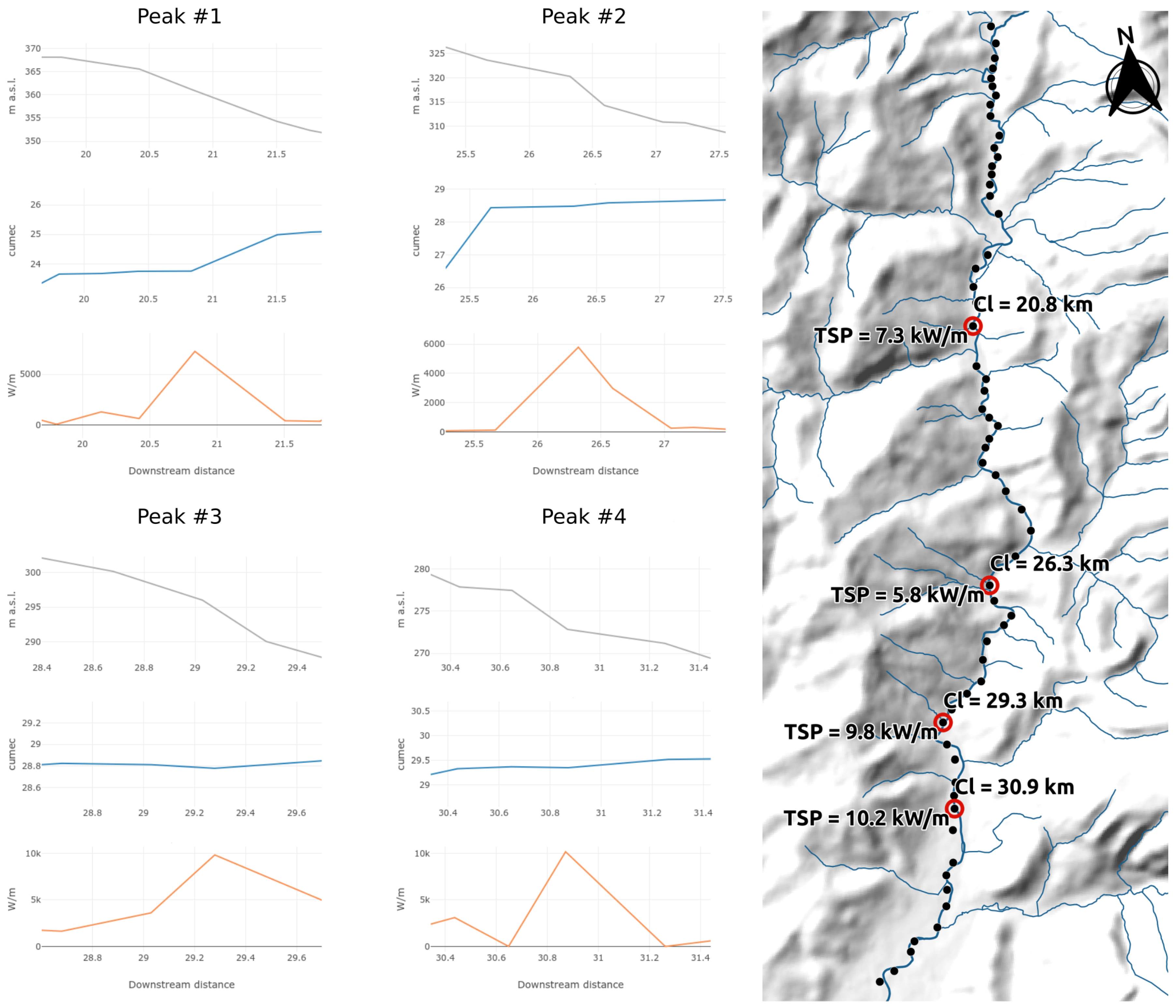
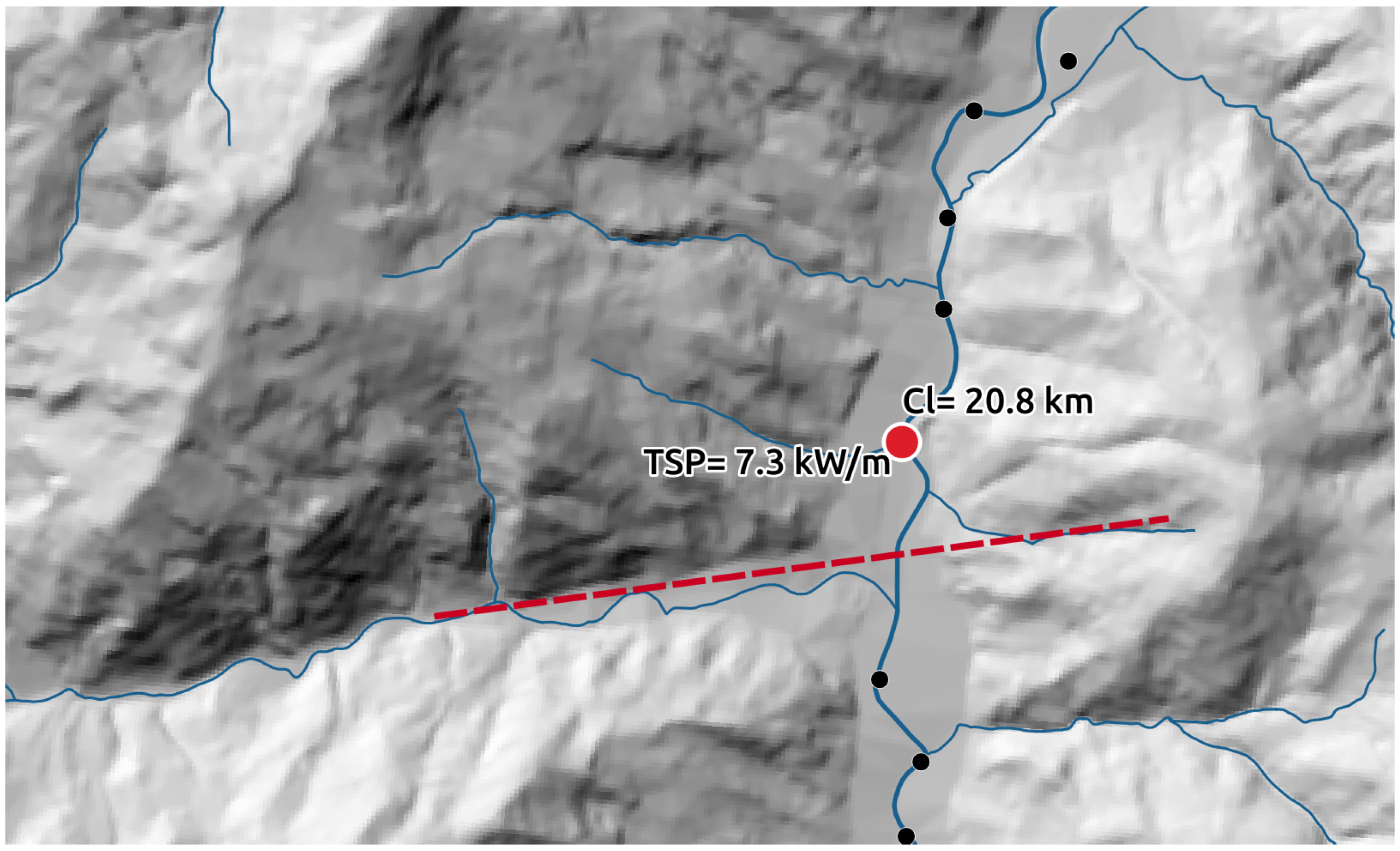
- Peak #1 is located 20.8 km downstream with a TSP value of 7250 W/m for an upslope distance of 100 m, 4295 W/m for an upslope distance of 200 m, and 2584 W/m for an upslope distance of 400 m. In this cross-section, the high value of the TSP was due to the local slope (about 1.8%) and discharge.
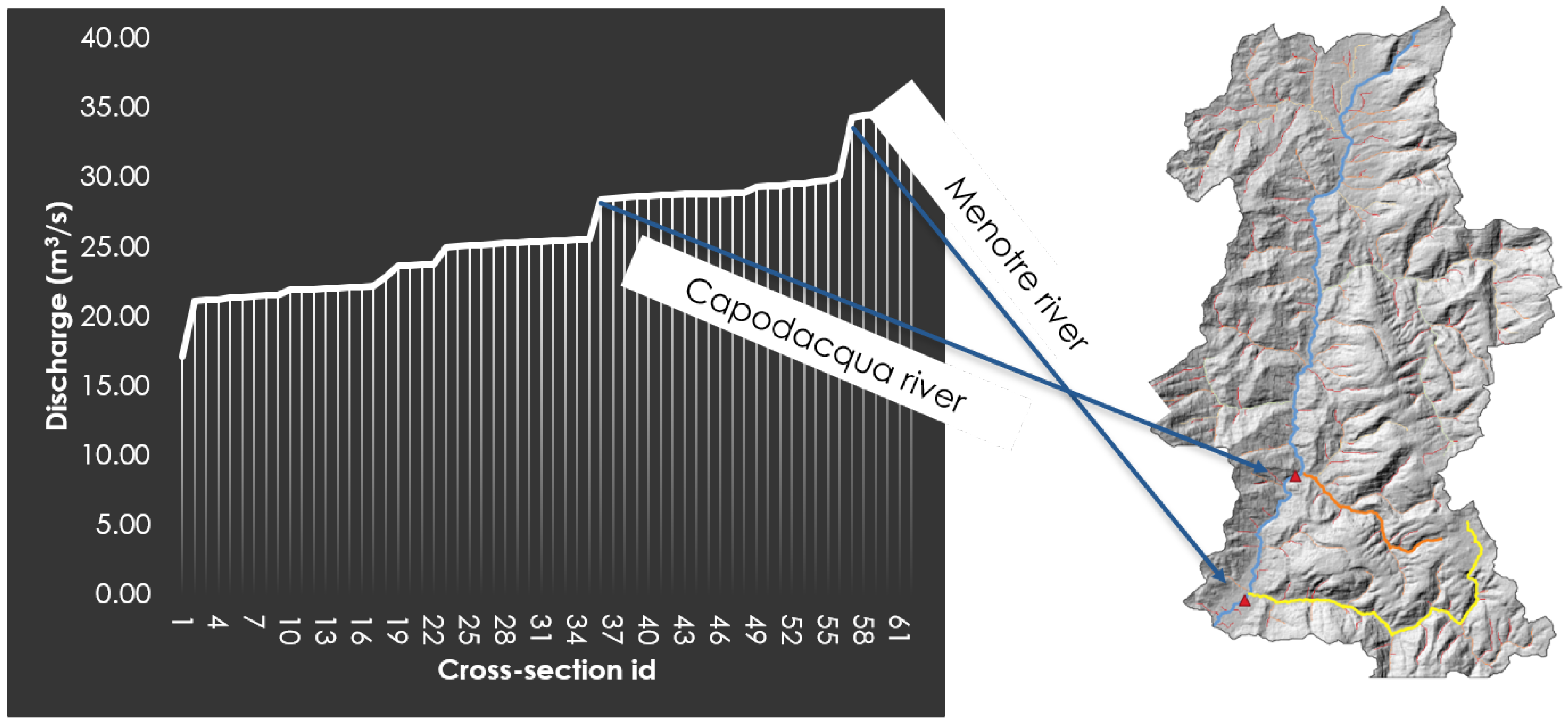
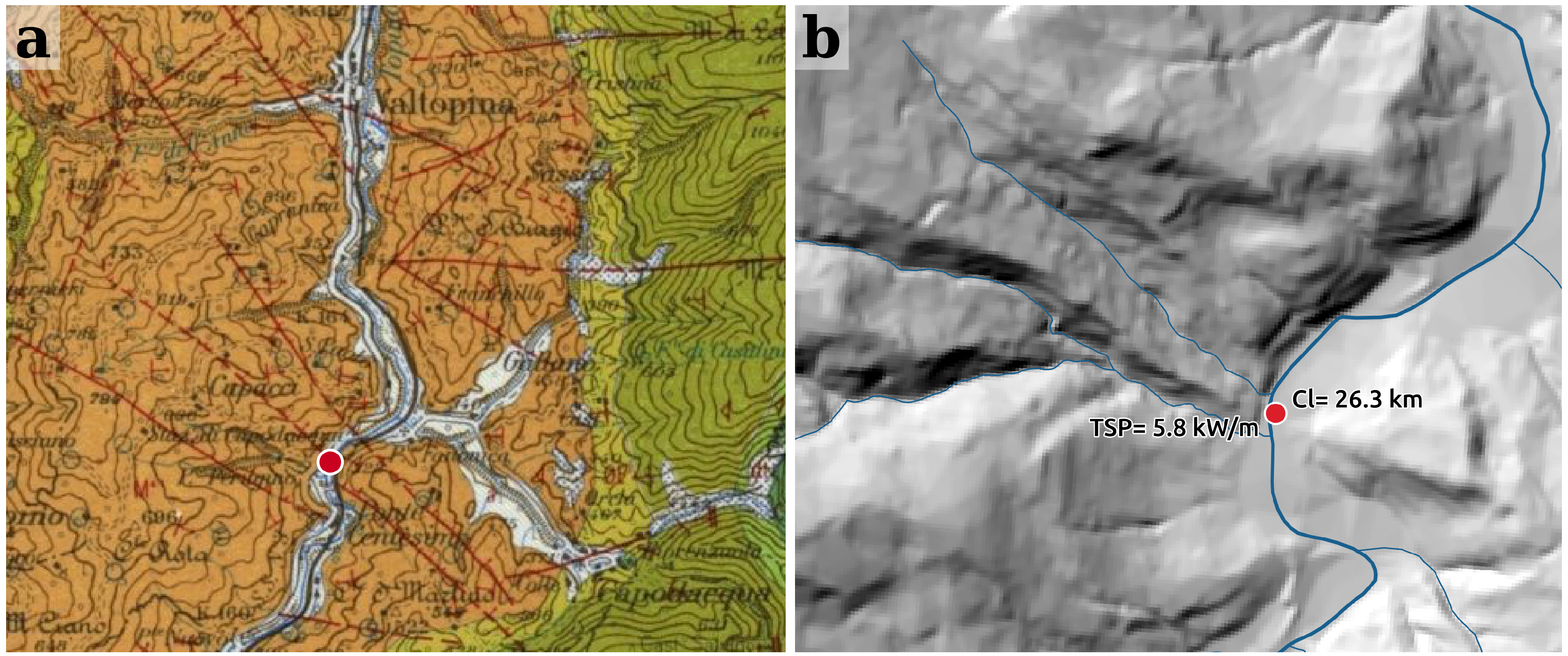
- Peak #2 is located 26.3 km downstream; the TSP ranged from 2270 W/m (for an upslope distance of 400 m) to 5796 W/m (for an upslope distance of 100 m). Even in this case, the increase in TSP was caused by high values of the discharge (the discharge increased from 25.5 m3/s–28.4 m3/s) and local slope (about 1–2%). In this section, in fact, the Rio Capodacqua, with its 35-km2 watershed, flows into the Topino River.
- Peak #3 is located 28.7 km downstream, with a TSP that ranged from 5286 W/m–9821 W/m. In this cross-section, the increase in the TSP was related to high values of the local slopes (about 3.5%).
- Peak #4 is located 29.3 km downstream with a TSP that ranged from 3429 W/m–10,164 W/m. Even here, the TSP increase was related to high values of the local slopes (about 3.5%).It is interesting to analyze the causes of a local gradient increase highlighted in Figure 10. Generally, high slope values are due to geological structural elements. For Peak # 1, the high value of SP was partially due to an increase in the flow discharge. Nevertheless, geological surveying demonstrated that this value of SP was due to the overall presence of a fault, which was evident by the alignment of the tributaries (on the right and on the left) of the Topino River (see Figure 11). The fault produced a clear increase in the Topino River slope as a consequence of the regressive erosion of the main channel that tried to re-establish its equilibrium profile. Furthermore, Peak # 2 is interesting because it showed the same situation: the increase in the slope was produced by a normal fault that caused a nick-point in the river longitudinal profile. It is likely that the fault activity was fairly recent because the river had not yet regulated the longitudinal profile to an equilibrium condition, resulting in a nick-point that was more evident than that in the previous case. Figure 12b shows the DEM, in which the fault appears clearly and produces an escarpment; this is also confirmed by the Geological Map of Italy (a), which displays a system of three faults in the same area. In order to determine the riverbed conditions in the locations of Peaks #3 and #4, a field survey was carried out. The survey revealed that the riverbed located upstream of these points is characterized by a step-pool morphology [27] that is related to the bedrock outcropping. Furthermore, in this reach, which is located at the entrance of a wide alluvial plain, the slope of the riverbed is controlled by the bedrock setting.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DEM | Digital Elevation Model |
| TSP | Total Stream Power |
| SP | Stream Power |
| IDF | Intensity-Duration-Frequency curve |
| TIN | triangulated irregular network |
References
- Bagnold, R.A. An Approach to the Sediment Transport Problem From General Physics; US Government Printing Office: Washington, DC, USA, 1966.
- Jain, V.; Preston, N.; Fryirs, K.; Brierley, G. Comparative assessment of three approaches for deriving stream power plots along long profiles in the upper Hunter River catchment, New South Wales, Australia. Geomorphology 2006, 74, 297–317. [Google Scholar] [CrossRef]
- Barker, D.M.; Lawler, D.M.; Knight, D.W.; Morris, D.G.; Davies, H.N.; Stewart, E.J. Longitudinal distributions of river flood power: the combined automated flood, elevation and stream power (CAFES) methodology. Earth Surf. Process. Landf. 2009, 34, 280–290. [Google Scholar] [CrossRef]
- Bagnold, R. Bed load transport by natural rivers. Water Resour. Res. 1977, 13, 303–312. [Google Scholar] [CrossRef]
- Nanson, G.; Croke, J. A genetic classification of floodplains. Geomorphology 1992, 4, 459–486. [Google Scholar] [CrossRef] [Green Version]
- Ferguson, R. Estimating critical stream power for bedload transport calculations in gravel-bed rivers. Geomorphology 2005, 70, 33–41. [Google Scholar] [CrossRef]
- Comiti, F.; Mao, L. Recent advances in the dynamics of steep channels. Gravel-Bed Rivers: Processes, Tools, Environments; John Wiley & Sons: Hoboken, NJ, USA, 2012; pp. 351–377. [Google Scholar]
- Knighton, A. Downstream variation in stream power. Geomorphology 1999, 29, 293–306. [Google Scholar] [CrossRef]
- Brierley, G.J.; Fryirs, K.A. Geomorphology and River Management: Applications of the River Styles Framework; Blackwell Publishing: Hoboken, NJ, USA, 2005. [Google Scholar]
- Church, M.; Hassan, M.A. Size and distance of travel of unconstrained clasts on a streambed. Water Resour. Res. 1992, 28, 299–303. [Google Scholar] [CrossRef]
- Tsutsumi, D.; Laronne, J.B. Gravel-Bed Rivers: Process and Disasters; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Bizzi, S.; Lerner, D. The use of stream power as an indicator of channel sensitivity to erosion and deposition processes. River Res. Appl. 2015, 31, 16–27. [Google Scholar] [CrossRef]
- Vocal Ferencevic, M.; Ashmore, P. Creating and evaluating digital elevation model-based stream-power map as a stream assessment tool. River Res. Appl. 2012, 28, 1394–1416. [Google Scholar] [CrossRef]
- De Rosa, P.; Fredduzzi, A.; Minelli, A.; Cencetti, C. Automatic Web Procedure for Calculating Flood Flow Frequency. Water 2019, 11, 14. [Google Scholar] [CrossRef]
- Cencetti, C. Morfotettonica ed evoluzione plio/pleistocenica del paesaggio nell’area appenninica compresa tra i monti di Foligno e la Val Nerina (Umbria centro-orientale). Boll. Soc. Geol. Ital. 1993, 112, 235–250. [Google Scholar]
- Albani, A. L’antico lago tiberino. L’Universo 1962, 52, 731–750. [Google Scholar]
- Robert, A. River Processes: An Introduction to Fluvial Dynamics; Routledge: Abingdon, UK, 2014. [Google Scholar]
- Autorita di Bacino del Fiume Tevere. Quaderno Idrologico del Fiume Tevere. Tevere 1996, 1, 64. [Google Scholar]
- Cronshey, R. Urban Hydrology for Small Watersheds, 2nd ed.; Technical Report; U.S. Dept. of Agriculture, Soil Conservation Service, Engineering Division: Washington, DC, USA, 1986.
- Strahler, A.N. Quantitative analysis of watershed geomorphology. Eos Trans. Am. Geophys. Union 1957, 38, 913–920. [Google Scholar] [CrossRef]
- De Rosa, P. r.stream.power: v1.0, Zenodo April 2019. Available online: https://zenodo.org/record/1463784#.XPCfZYh5tPY (accessed on 31 May 2019).
- Evans, I.S. General Geomorphometry, Derivatives of Altitude, and Descriptive Statistics; Chorley, R.J., Ed.; Spatial Analysis in Geomorphology: Methuen, MA, USA, 1972; pp. 17–90. [Google Scholar]
- Zevenbergen, L.W.; Thorne, C.R. Quantitative analysis of land surface topography. Earth Surf. Process. Landf. 1987, 12, 47–56. [Google Scholar] [CrossRef]
- Hengl, T.; Reuter, H. (Eds.) Geomorphometry: Concepts, Software, Applications; Elsevier: Amsterdam, The Netherlands, 2008; Volume 33, p. 772. [Google Scholar]
- Pérez-Peña, J.V.; Azañón, J.M.; Azor, A.; Delgado, J.; González-Lodeiro, F. Spatial analysis of stream power using GIS: SLk anomaly maps. Earth Surf. Process. Landf. 2009, 34, 16–25. [Google Scholar] [CrossRef]
- Finlayson, D.P.; Montgomery, D.R. Modeling large-scale fluvial erosion in geographic information systems. Geomorphology 2003, 53, 147–164. [Google Scholar] [CrossRef]
- Montgomery, D.R.; Buffington, J.M. Channel-reach morphology in mountain drainage basins. Geol. Soc. Am. Bull. 1997, 109, 596–611. [Google Scholar] [CrossRef]


| No Point | Q (m3/s) | No Point | Q (m3/s) | No Point | Q (m3/s) |
|---|---|---|---|---|---|
| 1 | 17.09 | 22 | 25.08 | 43 | 28.78 |
| 2 | 21.16 | 23 | 25.1 | 44 | 28.87 |
| 3 | 21.19 | 24 | 25.15 | 45 | 29.37 |
| 4 | 21.35 | 25 | 25.22 | 46 | 29.35 |
| 5 | 21.49 | 26 | 25.25 | 47 | 29.73 |
| 6 | 21.35 | 27 | 25.32 | 48 | 30.14 |
| 7 | 21.49 | 28 | 25.35 | 49 | 34.25 |
| 8 | 21.52 | 29 | 25.37 | 50 | 23.75 |
| 9 | 21.55 | 30 | 25.49 | 51 | 24.99 |
| 10 | 21.9 | 31 | 25.47 | 52 | 28.81 |
| 11 | 21.94 | 32 | 25.5 | 53 | 29.33 |
| 12 | 21.98 | 33 | 25.52 | 54 | 28.91 |
| 13 | 22.01 | 34 | 28.44 | 55 | 29.52 |
| 14 | 22.05 | 35 | 28.48 | 56 | 29.56 |
| 15 | 22.07 | 36 | 28.58 | 57 | 29.78 |
| 16 | 22.12 | 37 | 28.64 | 58 | 34.42 |
| 17 | 22.19 | 38 | 28.67 | 59 | 34.5 |
| 18 | 22.81 | 39 | 28.71 | 60 | 34.81 |
| 19 | 23.66 | 40 | 28.74 | 61 | 34.78 |
| 20 | 23.68 | 41 | 28.78 | 62 | 35.2 |
| 21 | 23.76 | 42 | 28.83 |
| ID | TSP Upslope Dist. 100 | TSP Upslope Dist. 200 | TSP Upslope Dist. 400 | ID | TSP Upslope Dist. 100 | TSP Upslope Dist. 200 | TSP Upslope Dist. 400 |
|---|---|---|---|---|---|---|---|
| 1 | 1775.82 | 887.91 | 995.82 | 32 | 3608.26 | 4333.66 | 2399.58 |
| 2 | 205.99 | 1369.75 | 1384.04 | 33 | 2693.06 | 4964.72 | 3617.26 |
| 3 | 2769.71 | 1689.04 | 1100.74 | 34 | 0 | 250.13 | 1671.12 |
| 4 | 1326.44 | 4088.01 | 2411.14 | 35 | 42.63 | 1630.99 | 1451.47 |
| 5 | 0 | 1471.07 | 2867.31 | 36 | 119.69 | 162.86 | 807.56 |
| 6 | 2067.75 | 1346.1 | 1824.74 | 37 | 5796.88 | 3530.41 | 2270.71 |
| 7 | 0 | 448.75 | 861.29 | 38 | 2983.37 | 4600.51 | 5792.17 |
| 8 | 0 | 211.09 | 175.19 | 39 | 246.54 | 304.04 | 2829.07 |
| 9 | 2169.69 | 2102.67 | 1051.34 | 40 | 304.25 | 273.83 | 772.59 |
| 10 | 1047.39 | 591.07 | 939.22 | 41 | 92.13 | 2409.56 | 1426.75 |
| 11 | 1307.58 | 1508.62 | 1095.74 | 42 | 4715.52 | 3019.24 | 1995.68 |
| 12 | 759.92 | 379.96 | 1124.67 | 43 | 2041.43 | 2245.54 | 2992.93 |
| 13 | 3487.96 | 1899.82 | 1050.22 | 44 | 1635.87 | 1635.79 | 2044.76 |
| 14 | 0 | 873.71 | 746.66 | 45 | 3603.57 | 3704.33 | 3031.84 |
| 15 | 3310.11 | 1655.06 | 1453.99 | 46 | 9821.8 | 7197.84 | 5286.04 |
| 16 | 914.71 | 1443.87 | 1189.17 | 47 | 4047.69 | 2050.47 | 1733.87 |
| 17 | 0 | 247.75 | 222.36 | 48 | 282.32 | 1285.76 | 2584.99 |
| 18 | 1429.41 | 3776.96 | 2036.58 | 49 | 3098.73 | 2560.6 | 3354.75 |
| 19 | 94.62 | 122.98 | 108.78 | 50 | 9.58 | 585.33 | 1574.71 |
| 20 | 1306.47 | 1197.6 | 795.25 | 51 | 10,164.98 | 6626.91 | 3429.73 |
| 21 | 655.28 | 982.88 | 1037.49 | 52 | 0 | 1086.14 | 1852.62 |
| 22 | 7250.18 | 4295.24 | 2584.58 | 53 | 2347.07 | 3659.51 | 2685.01 |
| 23 | 439.89 | 1691.53 | 2212.57 | 54 | 453.54 | 1496.99 | 3277.99 |
| 24 | 383.8 | 698.94 | 1648.99 | 55 | 0 | 1696.03 | 1249.72 |
| 25 | 2587.56 | 1424.29 | 888.19 | 56 | 2438.49 | 2342.2 | 1659.04 |
| 26 | 599.21 | 1527.07 | 1335.6 | 57 | 4187.26 | 3312.15 | 4336.91 |
| 27 | 618.92 | 1187.67 | 894.58 | 58 | 0 | 1092.1 | 1648.86 |
| 28 | 323.93 | 277.71 | 668.05 | 59 | 100.86 | 110.93 | 607.85 |
| 29 | 136.88 | 68.44 | 959.4 | 60 | 0 | 704.58 | 861.7 |
| 30 | 1615.29 | 1383.2 | 691.6 | 61 | 584.78 | 1793.74 | 1474.23 |
| 31 | 3611.47 | 3522.19 | 3252.77 | 62 | 0 | 378.64 | 589.71 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Rosa, P.; Fredduzzi, A.; Cencetti, C. Stream Power Determination in GIS: An Index to Evaluate the Most ’Sensitive’Points of a River. Water 2019, 11, 1145. https://doi.org/10.3390/w11061145
De Rosa P, Fredduzzi A, Cencetti C. Stream Power Determination in GIS: An Index to Evaluate the Most ’Sensitive’Points of a River. Water. 2019; 11(6):1145. https://doi.org/10.3390/w11061145
Chicago/Turabian StyleDe Rosa, Pierluigi, Andrea Fredduzzi, and Corrado Cencetti. 2019. "Stream Power Determination in GIS: An Index to Evaluate the Most ’Sensitive’Points of a River" Water 11, no. 6: 1145. https://doi.org/10.3390/w11061145





