Micromixing Efficiency of Particles in Heavy Metal Removal Processes under Various Inlet Conditions
Abstract
1. Introduction
2. Materials and Methods
2.1. Geometry and Simulation Parameters
2.2. Numerical Model
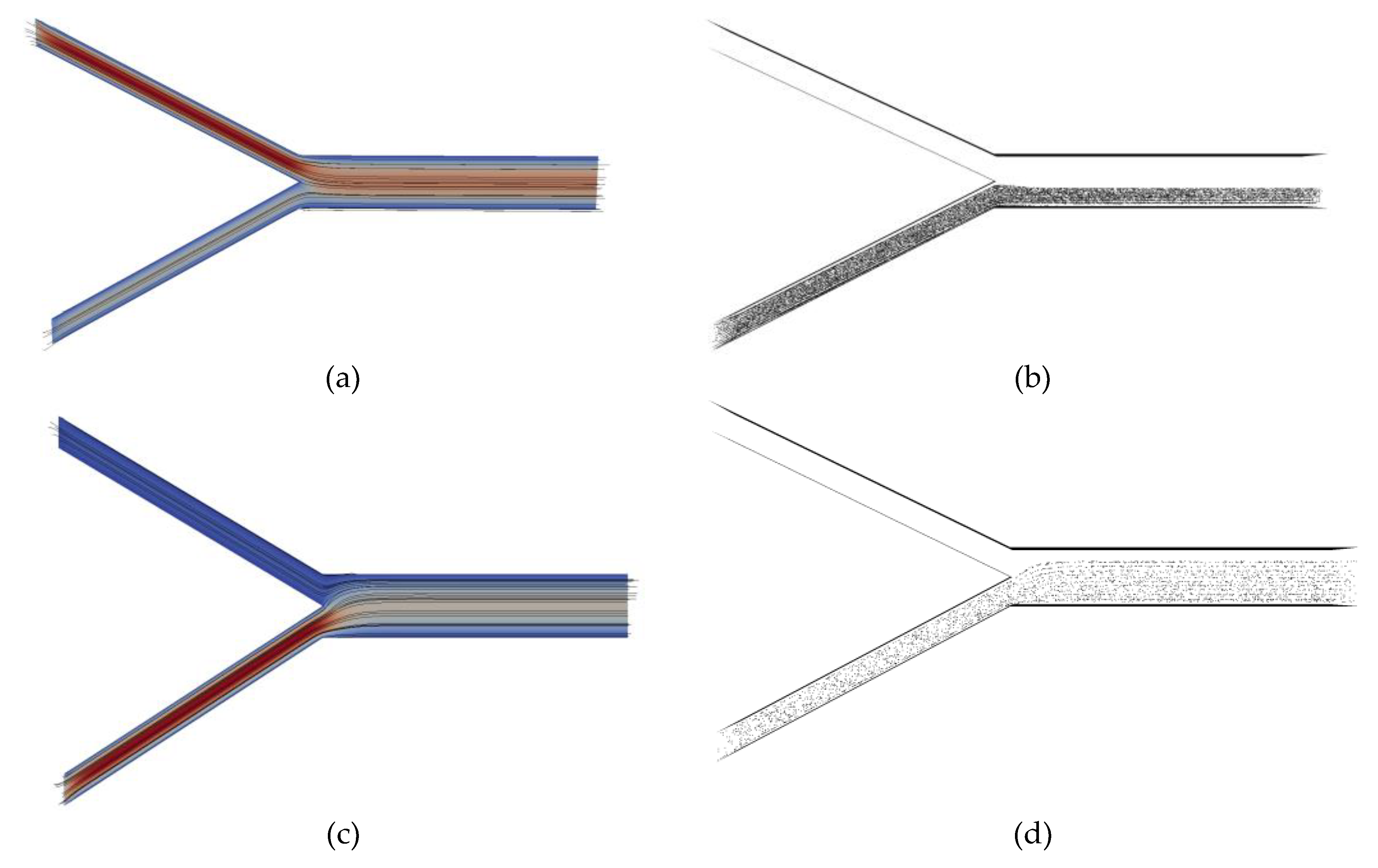
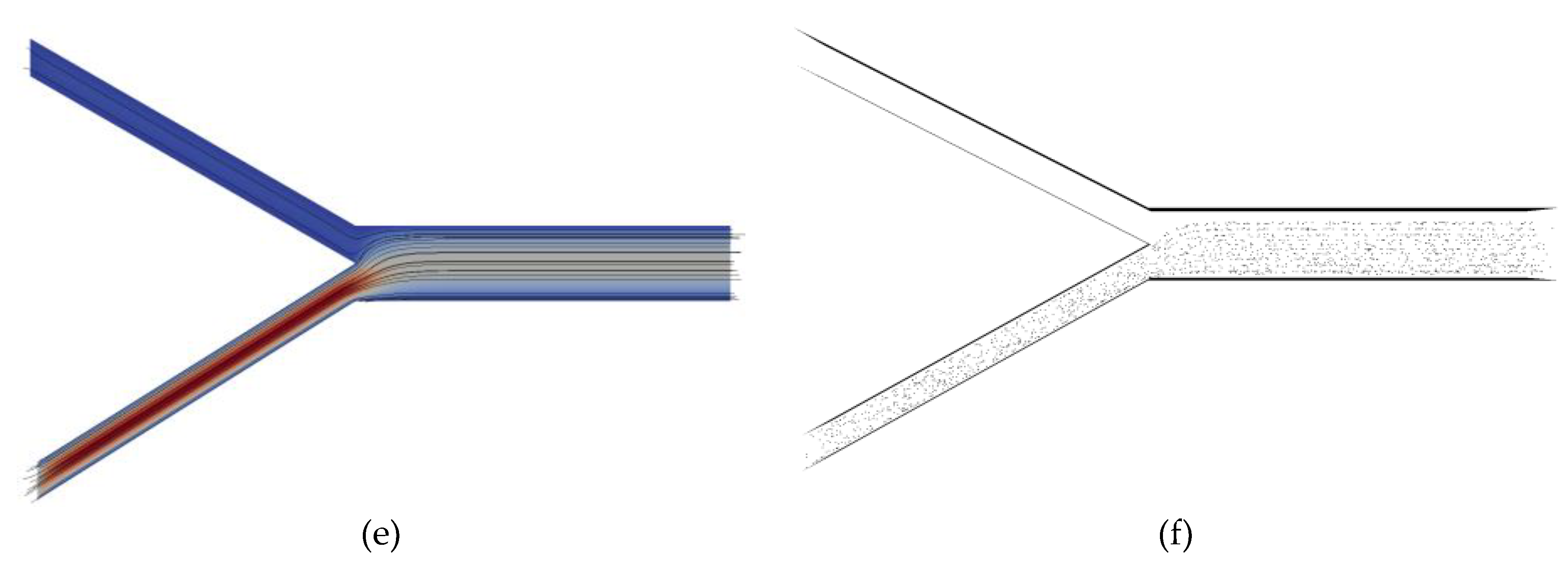
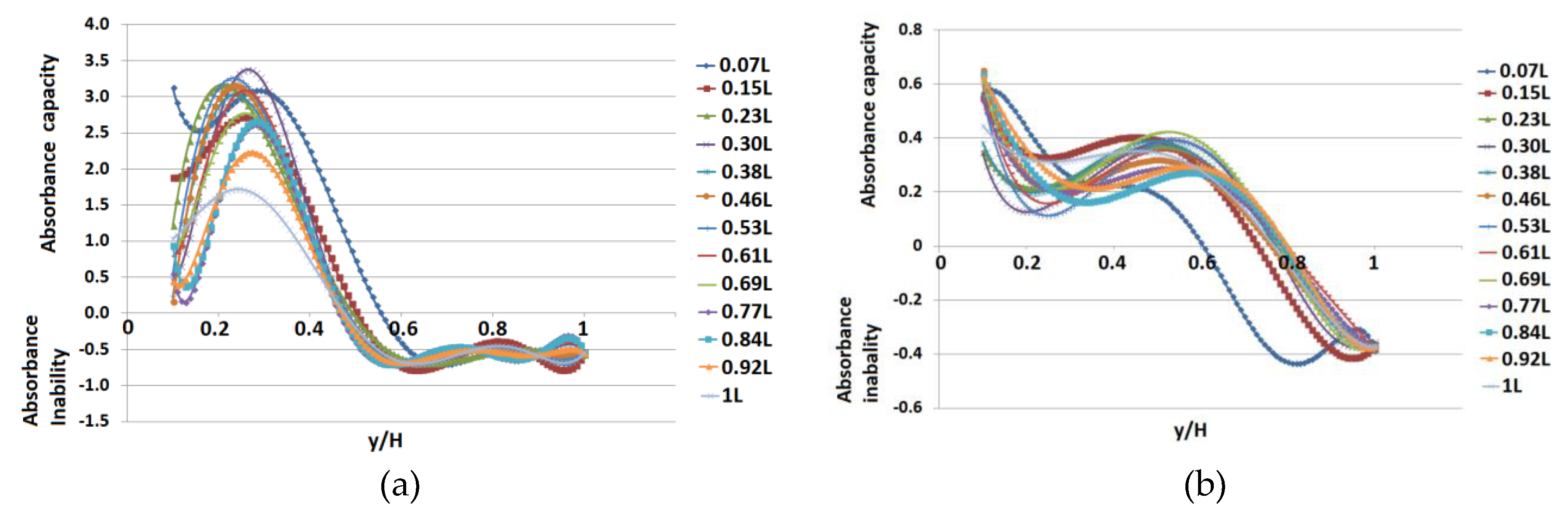
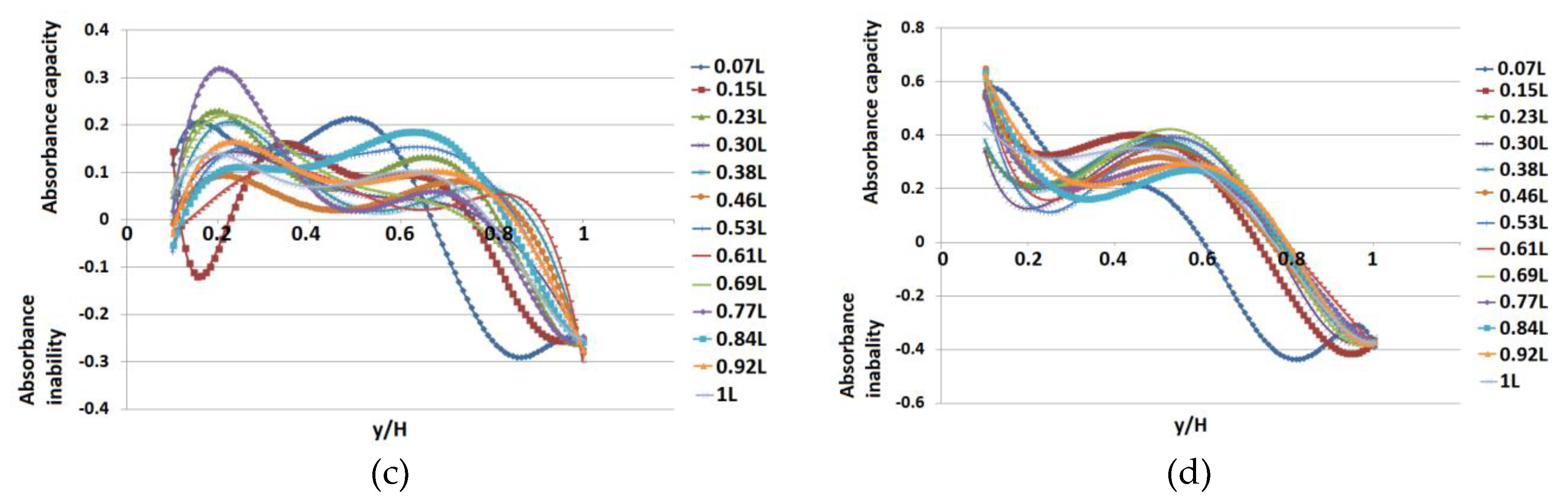
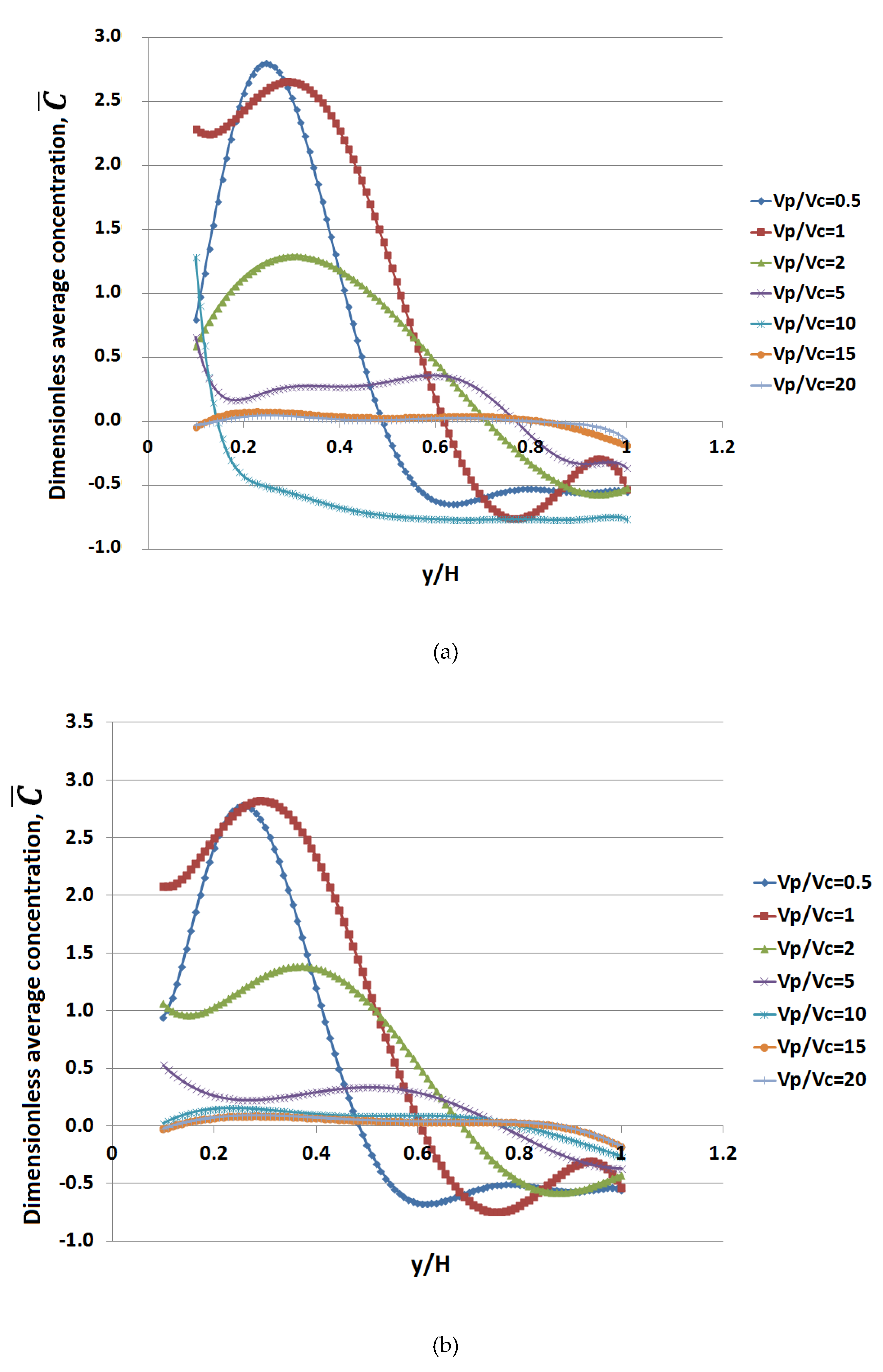
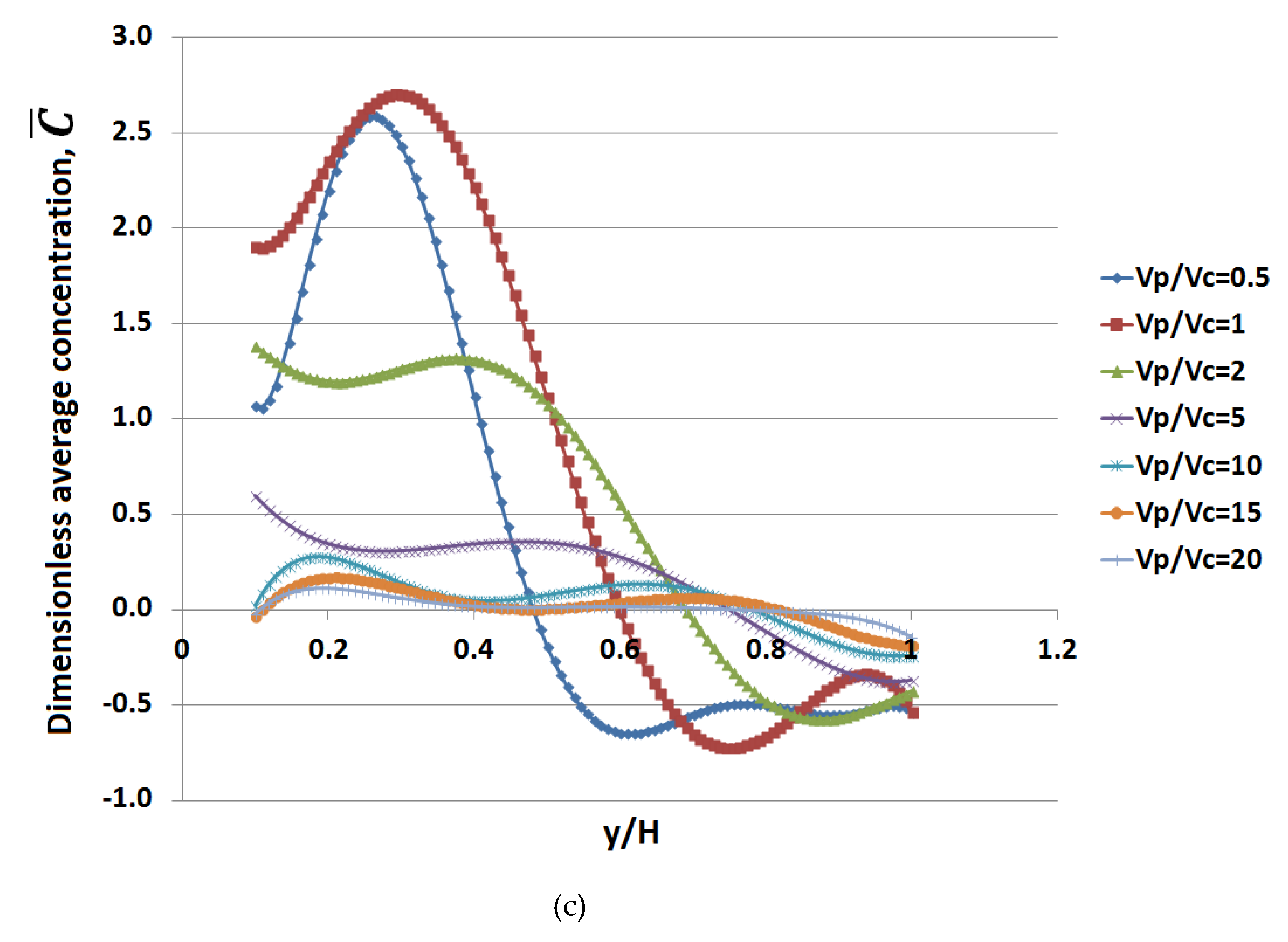
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mohmood, I.; Lopes, C.B.; Lopes, I.; Ahmad, I.; Duarte, A.C.; Pereira, E. Nanoscale materials and their use in water contaminants removal—A review. Environ. Sci. Pollut. Res. 2013, 20, 1239–1260. [Google Scholar] [CrossRef] [PubMed]
- Foley, A.J.; DeFries, R.; Asner, G.P.; Barford, C.; Bonan, G.; Carpenter, S.R.; Chapin, F.S.; Coe, M.T.; Daily, G.C.; Gibbs, H.K.; et al. Global consequences of land use. Science 2005, 309, 570–574. [Google Scholar] [CrossRef] [PubMed]
- Coetser, S.E.; Heath, R.G.M.; Ndombe, N. Diffuse pollution associated with the mining sectors in South Africa: A first-order assessment. Water Sci. Technol. 2007, 55, 9–16. [Google Scholar] [CrossRef]
- Sprenger, C.; Lorenzen, G.; Hülshoff, I.; Grützmacher, G.; Ronghang, M.; Pekdeger, A. Vulnerability of bank filtration systems to climate change. Sci. Total Environ. 2011, 409, 655–663. [Google Scholar] [CrossRef]
- Delpla, I.; Baurès, E.; Jung, A.V.; Clement, M.; Thomas, O. Issues of drinking water quality of small scale water services towards climate change. Water Sci. Technol. 2011, 63, 227–232. [Google Scholar] [CrossRef]
- Iaccarino, M. Water, population growth and contagious diseases. Water 2019, 11, 386. [Google Scholar] [CrossRef]
- Falcone, I.R.; Humpage, A.R. Health risk assessment of cyanobacterial (blue-green algal) toxins in drinking water. Int. J. Environ. Res. Public Health 2005, 2, 43–50. [Google Scholar] [CrossRef]
- Rozell, D.J.; Reaven, S.J. Water pollution risk associated with natural gas extraction from the marcellus shale. Risk Anal. 2011, 32, 1382–1393. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, J.; Ngo, H.H.; Guo, W.; Hu, W.; Liang, S.; Fan, J.; Liu, H. A review on the sustainability of constructed wetlands for wastewater treatment: Design and operation. Bioresour. Technol. 2015, 175, 594–601. [Google Scholar] [CrossRef] [PubMed]
- Gorgoglione, A.; Torretta, V. Sustainable management and successful application of constructed wetlands: A critical review. Sustainability 2018, 10, 3910. [Google Scholar] [CrossRef]
- Zhai, R.; Wan, Y.; Liu, L.; Zhang, X.; Wang, W.; Liu, J.; Zhang, B. Hierarchical MnO2 nanostructures: Synthesis and their application in water treatment. Water Sci. Technol. 2012, 65, 1054–1059. [Google Scholar] [CrossRef] [PubMed]
- Bottero, J.Y.; Rose, J.; Wiesner, M.R. Nanotechnologies: Tools for sustainability in a new wave of water treatment processes. Integr. Environ. Assess. Manag. 2009, 2, 391–395. [Google Scholar] [CrossRef]
- Warner, C.L.; Addleman, R.S.; Cinson, A.D.; Droubay, T.C.; Engelhard, M.H.; Nash, M.A.; Yantasee, W.; Warner, M.G. High-performance, superparamagnetic, nanoparticle-based heavy metal sorbents for removal of contaminants from natural waters. ChemSusChem 2010, 3, 749–757. [Google Scholar] [CrossRef]
- Chen, L.; Wang, T.; Tong, J. Application of derivatized magnetic materials to the separation and the preconcentration of pollutants in water samples. TrAC Trends Anal. Chem. 2011, 30, 1095–1108. [Google Scholar] [CrossRef]
- Sanchez, A.; Recillas, S.; Font, X.; Casals, E.; González, E.; Puntes, V. Ecotoxicity of, and remediation with, engineered inorganic nanoparticles in the environment. TrAC Trends Anal. Chem. 2011, 30, 507–516. [Google Scholar] [CrossRef]
- Li, F.B.; Li, X.Z.; Liu, C.S.; Liu, T.X. Effect of alumina on photocatalytic activity of iron oxides for bisphenol A degradation. J. Hazard. Mater. 2007, 149, 199–207. [Google Scholar] [CrossRef] [PubMed]
- Daniel-da-Silva, A.L.; Lóio, R.; Lopes-da-Silva, J.A.; Trindade, T.; Goodfellow, B.J.; Gil, A.M. Effects of magnetite nanoparticles on the thermorheological properties of carrageenan hydrogels. J. Colloid Interface Sci. 2008, 324, 205–211. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.F. Preparation and application of magnetic Fe3O4 nanoparticles for wastewater purification. Sep. Purif. Technol. 2009, 68, 312–319. [Google Scholar] [CrossRef]
- Indira, T.K.; Lakshmi, P.K. Magnetic Nanoparticles—A Review. Int. J. Pharm. Sci. Nanotechnol. 2010, 3, 1035–1042. [Google Scholar]
- Guo, L.; Li, J.; Zhang, L.; Li, J.; Li, Y.; Yu, C.; Shi, J.; Ruan, M.; Feng, J. A facile route to synthesize magnetic particles within hollow mesoporous spheres and their performance as separable Hg2+ adsorbents. J. Mater. Chem. 2008, 18, 2733–2738. [Google Scholar] [CrossRef]
- Atia, A.A.; Donia, A.M.; El-Enein, S.A.; Yousif, A.M. Effect of Chain Length of Aliphatic Amines Immobilized on a Magnetic Glycidyl Methacrylate Resin towards the Uptake Behavior of Hg(II) from Aqueous Solutions. Sep. Sci. Technol. 2007, 42, 403–420. [Google Scholar] [CrossRef]
- Li, H.; Li, Z.; Liu, T.; Xiao, X.; Peng, Z.; Deng, L. A novel technology for biosorption and recovery hexavalent chromium in wastewater by bio-functional magnetic beads. Bioresour. Technol. 2008, 99, 6271–6279. [Google Scholar] [CrossRef] [PubMed]
- Sheha, R.R.; El-Zahhar, A.A. Synthesis of some ferromagnetic composite resins and their metal removal characteristics in aqueous solutions. J. Hazard. Mater. 2008, 150, 795–803. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Chen, G.; Lo, I.M.C. Removal and recovery of Cr(VI) from wastewater by maghemite nanoparticles. Water Res. 2005, 39, 4528–4536. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.-S.; Ren, L.L.; Guo, Y.G.; Liang, H.P.; Cao, A.M.; Wan, L.J.; Bai, C.L. Mass Production and High Photocatalytic Activity of ZnS Nanoporous Nanoparticles. Angew. Chem. Int. Ed. 2005, 44, 1269–1273. [Google Scholar] [CrossRef]
- Borai, E.H.; El-Sofany, E.A.; Morcos, T.N. Development and optimization of magnetic technologies based processes for removal of some toxic heavy metals. Adsorption 2007, 13, 95–104. [Google Scholar] [CrossRef]
- Huang, C.; Hu, B. Silica-coated magnetic nanoparticles modified with γ-mercaptopropyltrimethoxysilane for fast and selective solid phase extraction of trace amounts of Cd, Cu, Hg, and Pb in environmental and biological samples prior to their determination by inductively coupled plasma mass spectrometry. Spect. Acta Part. B Atomic Spectrosc. 2008, 63, 437–444. [Google Scholar]
- Shin, S.; Jang, J. Thiol containing polymer encapsulated magnetic nanoparticles as reusable and efficiently separable adsorbent for heavy metal ions. Chem. Commun. 2007, 41, 4230–4232. [Google Scholar] [CrossRef]
- Karvelas, E.G.; Lampropoulos, N.K.; Karakasidis, T.E.; Sarris, I.E. A computational tool for the estimation of the optimum gradient magnetic field for the magnetic driving of the spherical particles in the process of cleaning water. Desalin. Water Treat. 2017, 99, 27–33. [Google Scholar] [CrossRef]
- Persson, J.; Wittgren, H.B. How hydrological and hydraulic conditions affect performance of ponds. Ecol. Eng. 2003, 21, 259–269. [Google Scholar] [CrossRef]
- Ranieri, E.; Gorgoglione, A.; Montanaro, C.; Iacovelli, A.; Gikas, P. Removal capacity of BTEX and metals of constructed wetlands under the influence of hydraulic conductivity. Desalin. Water Treat. 2015, 56, 1256–1263. [Google Scholar] [CrossRef]
- Hajiani, P.; Larachi, F. Magnetic-field assisted mixing of liquids using magnetic nanoparticles. Chem. Eng. Process. 2014, 84, 31–37. [Google Scholar] [CrossRef]
- Le, T.N.; Suh, Y.K.; Kang, S. Efficient Mixing in Microchannel by using Magnetic Nanoparticles. Int. J. Math. Models Methods Appl. Sci. 2009, 3, 58–67. [Google Scholar]
- Cao, Q.; Han, X.; Li, L. An active microfluidic mixer utilizing a hybrid gradient magnetic field. Int. J. Appl. Electomagn. Mech. 2015, 47, 583–592. [Google Scholar] [CrossRef]
- Wang, Y.; Zhe, J.; Chung, T.F.B.; Dutta, P. A rapid particle driven micromixer. Microfluid Nanofluid 2008, 4, 375–389. [Google Scholar] [CrossRef]
- Founiotis, N.T.; Horsch, G.M.; Lefteriotis, G.A. On the hydrodynamic geometry of the flow-through versus restricted lagoons. Water 2018, 10, 237. [Google Scholar] [CrossRef]
- Karvelas, E.G.; Liosis, C.; Karakasidis, T.; Sarris, I. Mixing of particles in Micromixers under different angles and Velocities of the incoming water. Proceedings 2018, 2, 577. [Google Scholar] [CrossRef]
- Karvelas, E.G.; Lampropoulos, N.K.; Sarris, I.E. A numerical model for aggregations formation and magnetic driving of spherical particles based on OpenFOAM®. Comput. Methods Progr. Biomed. 2017, 142, 21–30. [Google Scholar] [CrossRef]
- Tijskens, E.; Ramon, H.; Baerdemaeker, J. Discrete element modelling for process simulation in agriculture. J. Sound Vib. 2003, 266, 493–514. [Google Scholar] [CrossRef]
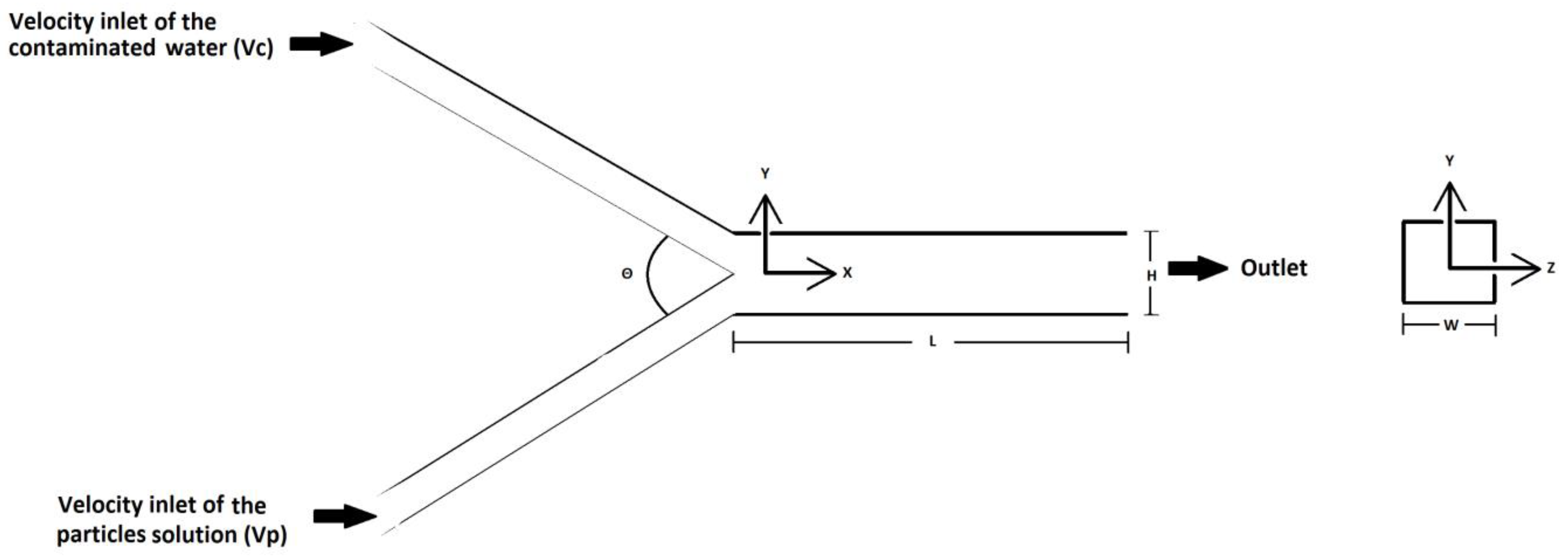

| Dimensions of the Micromixer Geometry | Angle between Streams (θ) | Computational Grid for Each Angle |
|---|---|---|
| Length (L): 5×10−4 m | 30° | 76,720 |
| Height (H): 1×10−4 m | 45° | 74,600 |
| Width (W): 1×10−4 m | 60° | 76,140 |
| Boundary | Velocity(U) (m/s) | Pressure(p) (pa) | Transport Scalar (φ) |
|---|---|---|---|
| Inlet of the contaminated water (Vc) | 0.001, 0.002 | zero gradient | 1 |
| Inlet of the particles solution (Vp) | 0.0001, 0.0002, 0.0005, 0.001, 0.0015, 0.002 | zero gradient | 0 |
| Outlet | zero gradient | 0 | zero gradient |
| Walls | 0 | zero gradient | zero gradient |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karvelas, E.; Liosis, C.; Benos, L.; Karakasidis, T.; Sarris, I. Micromixing Efficiency of Particles in Heavy Metal Removal Processes under Various Inlet Conditions. Water 2019, 11, 1135. https://doi.org/10.3390/w11061135
Karvelas E, Liosis C, Benos L, Karakasidis T, Sarris I. Micromixing Efficiency of Particles in Heavy Metal Removal Processes under Various Inlet Conditions. Water. 2019; 11(6):1135. https://doi.org/10.3390/w11061135
Chicago/Turabian StyleKarvelas, Evangelos, Christos Liosis, Lefteris Benos, Theodoros Karakasidis, and Ioannis Sarris. 2019. "Micromixing Efficiency of Particles in Heavy Metal Removal Processes under Various Inlet Conditions" Water 11, no. 6: 1135. https://doi.org/10.3390/w11061135
APA StyleKarvelas, E., Liosis, C., Benos, L., Karakasidis, T., & Sarris, I. (2019). Micromixing Efficiency of Particles in Heavy Metal Removal Processes under Various Inlet Conditions. Water, 11(6), 1135. https://doi.org/10.3390/w11061135








