A Quantitative Flood-Related Building Damage Evaluation Method Using Airborne LiDAR Data and 2-D Hydraulic Model
Abstract
:1. Introduction
2. Study Area and Dataset
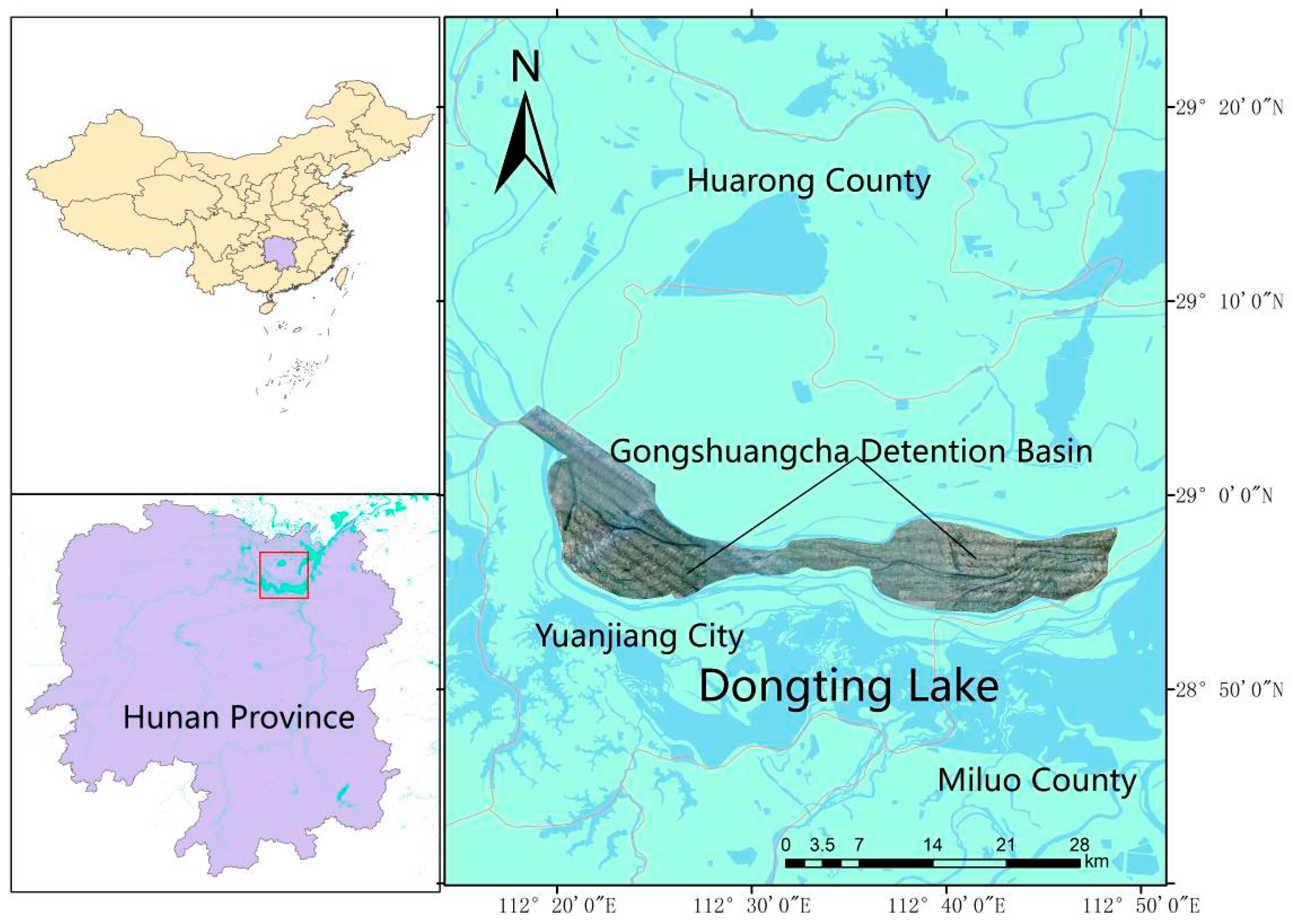
2.1. Study Area
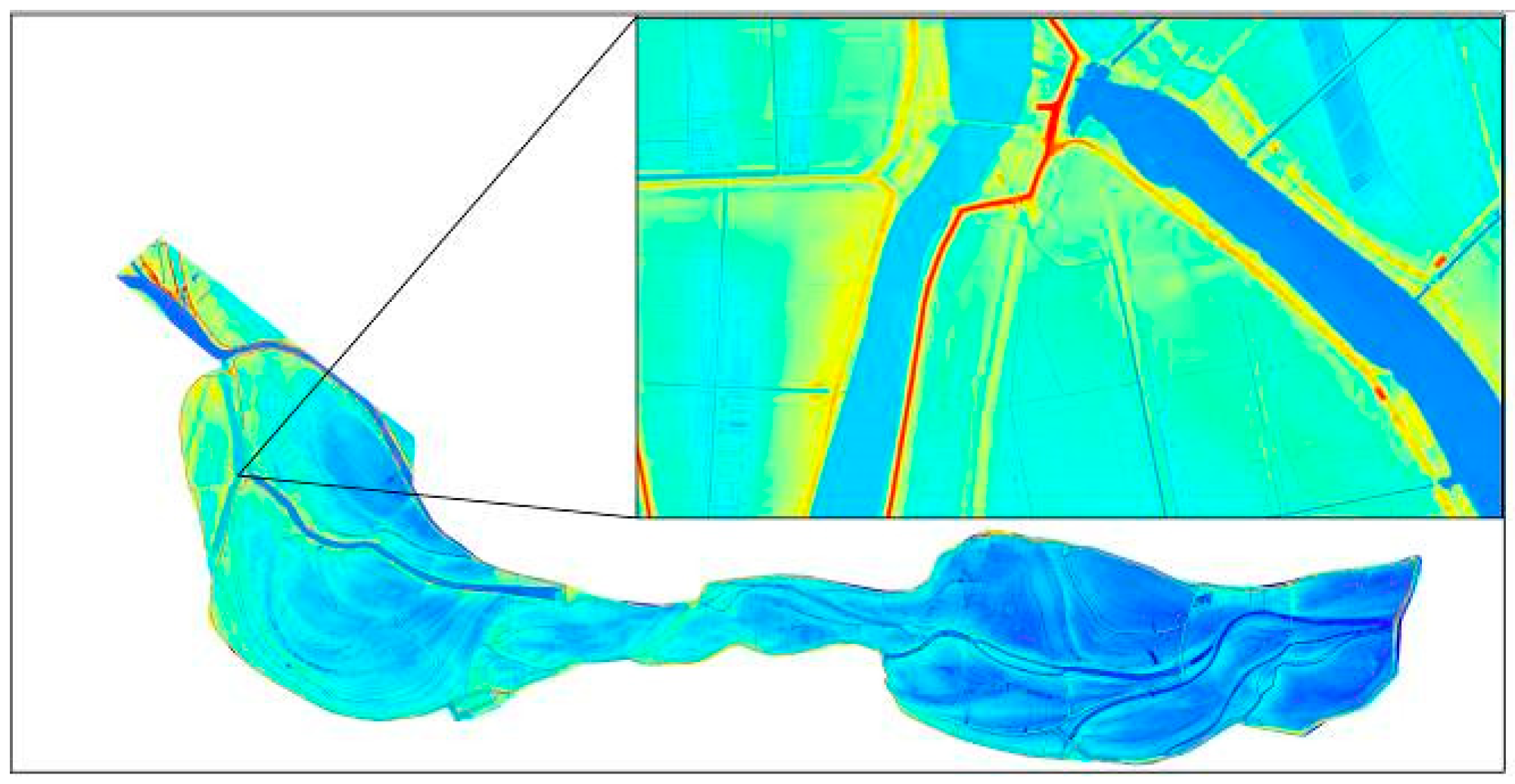
2.2. Dataset
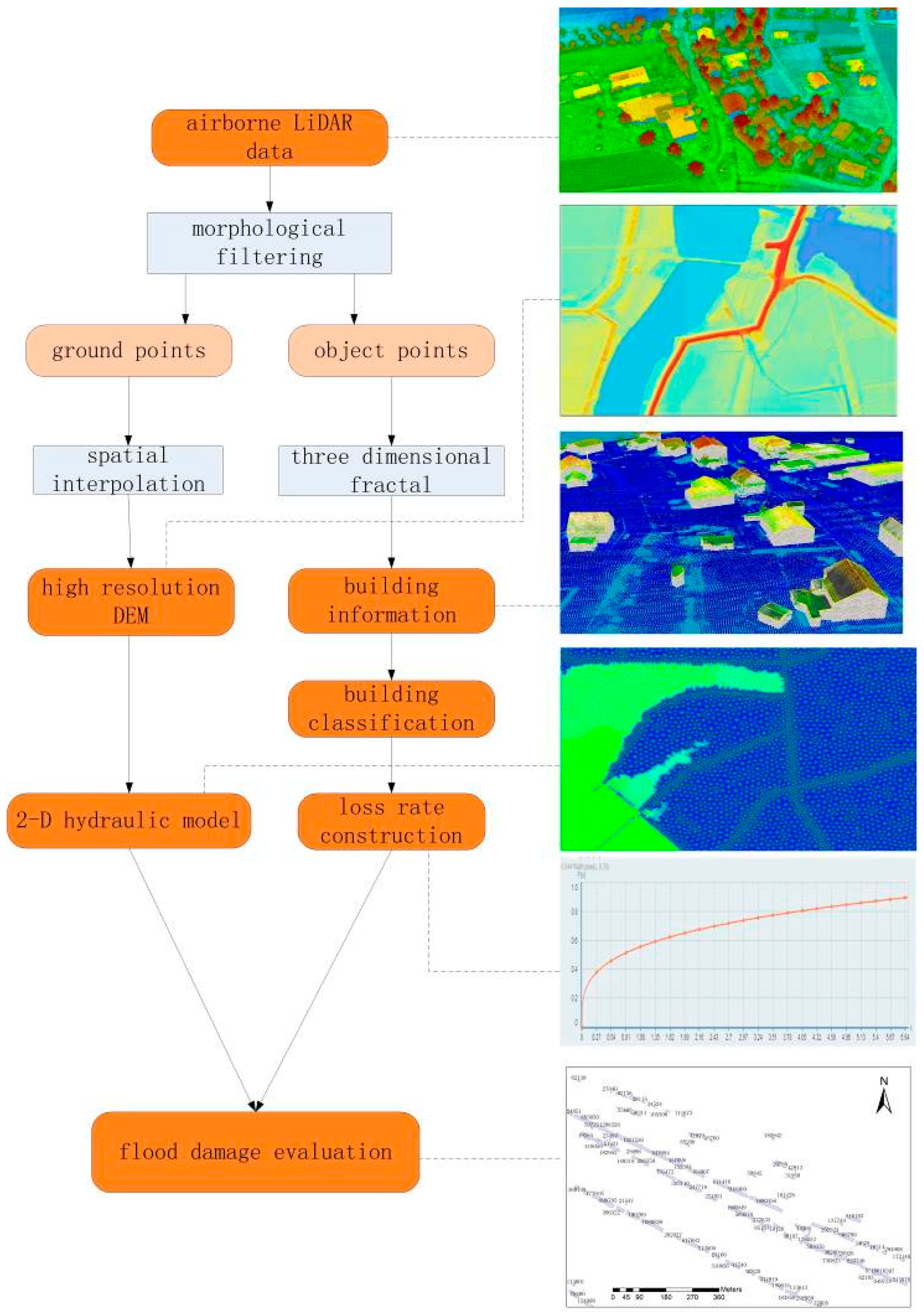
3. Methods
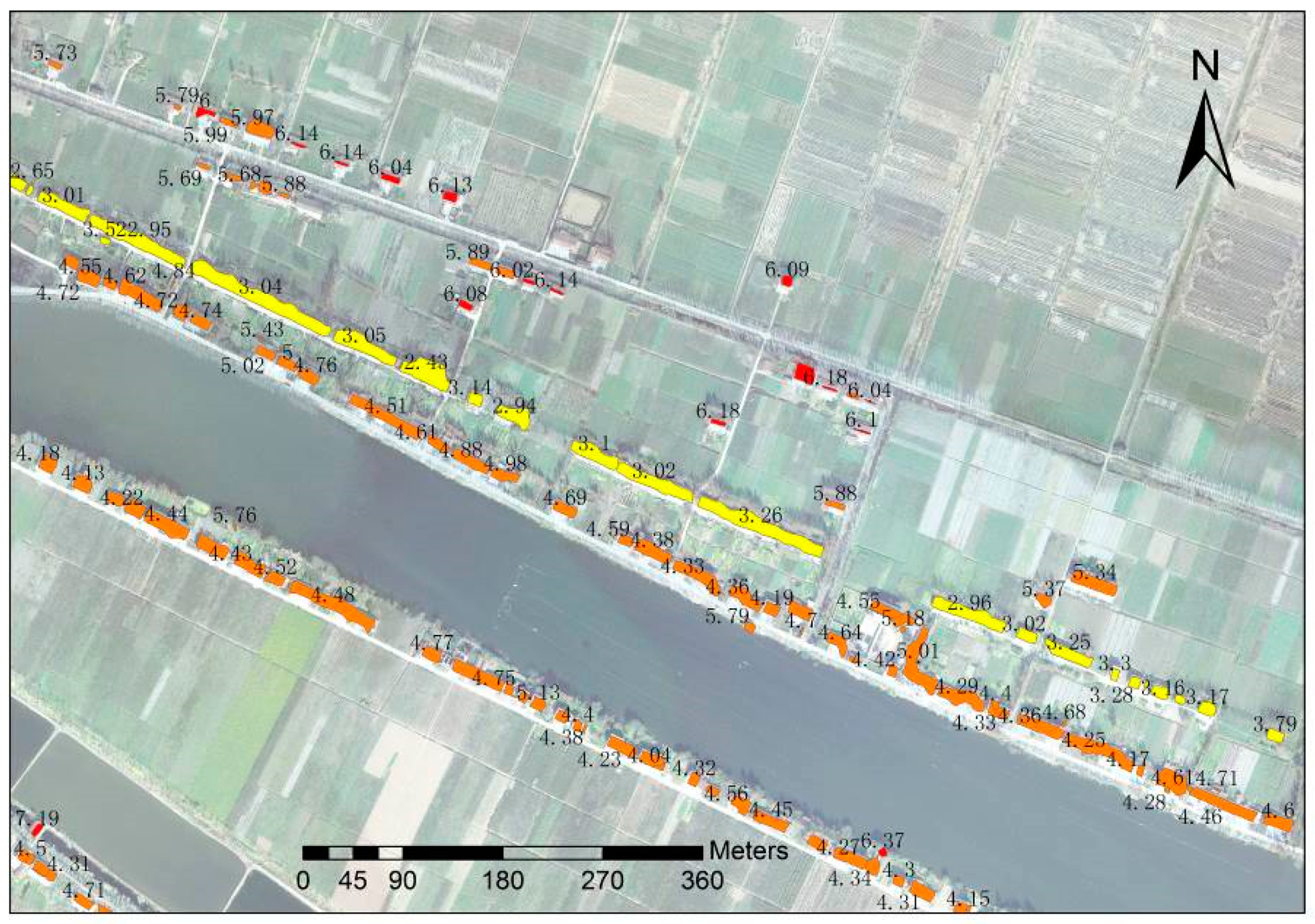
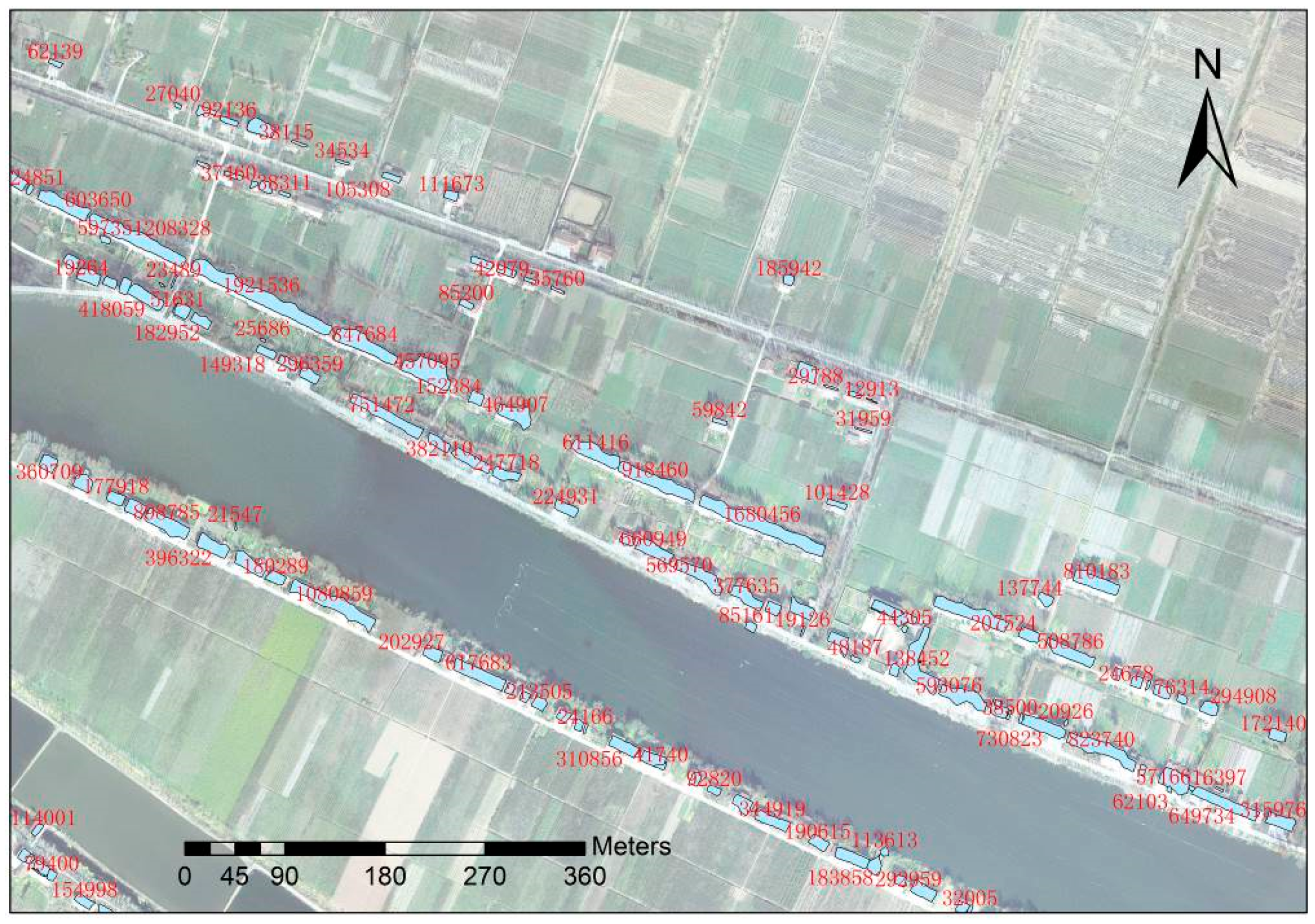
3.1. Building Extraction
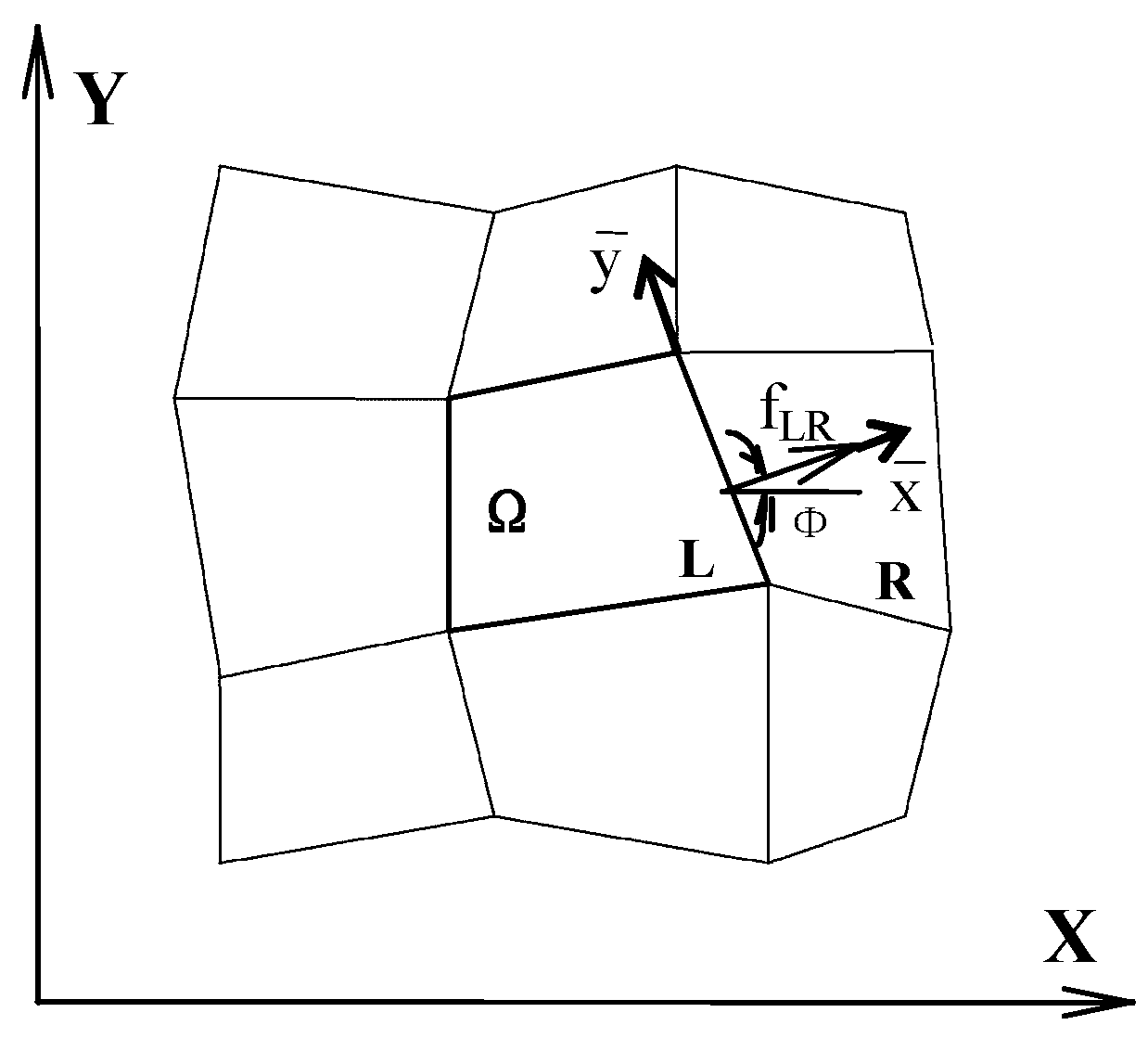
3.2. 2-D Hydraulic Model
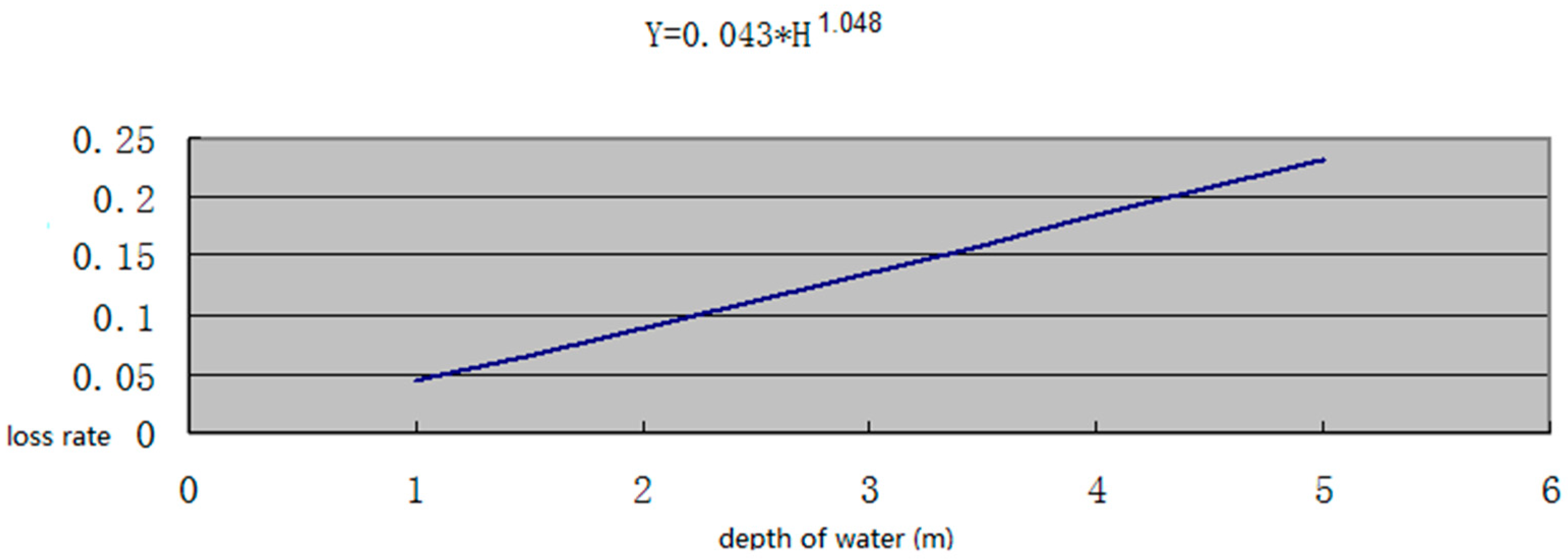
3.3. Construction of Building Flood Loss Rate Curves
3.3.1. Building Classification
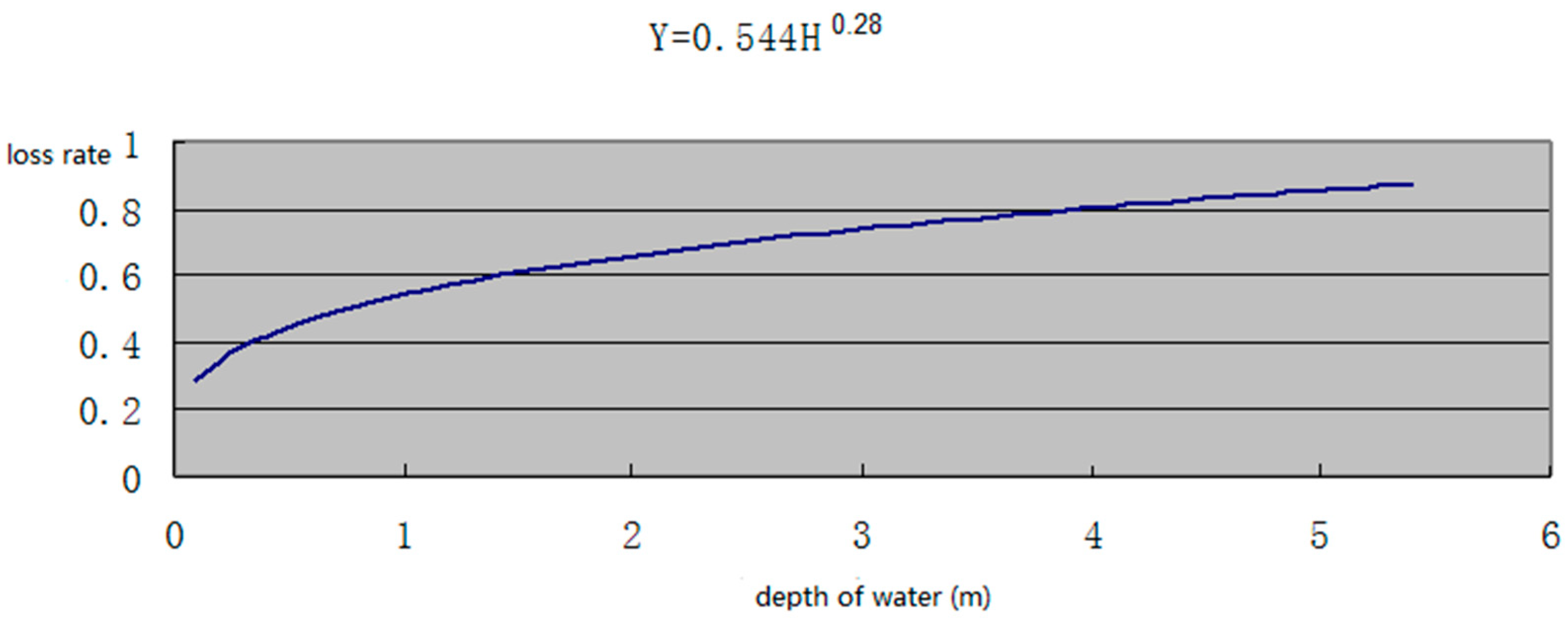
3.3.2. Establishment of Flood Loss Rate
3.4. Calculation of Building Replacement Cost
4. Results and Discussion
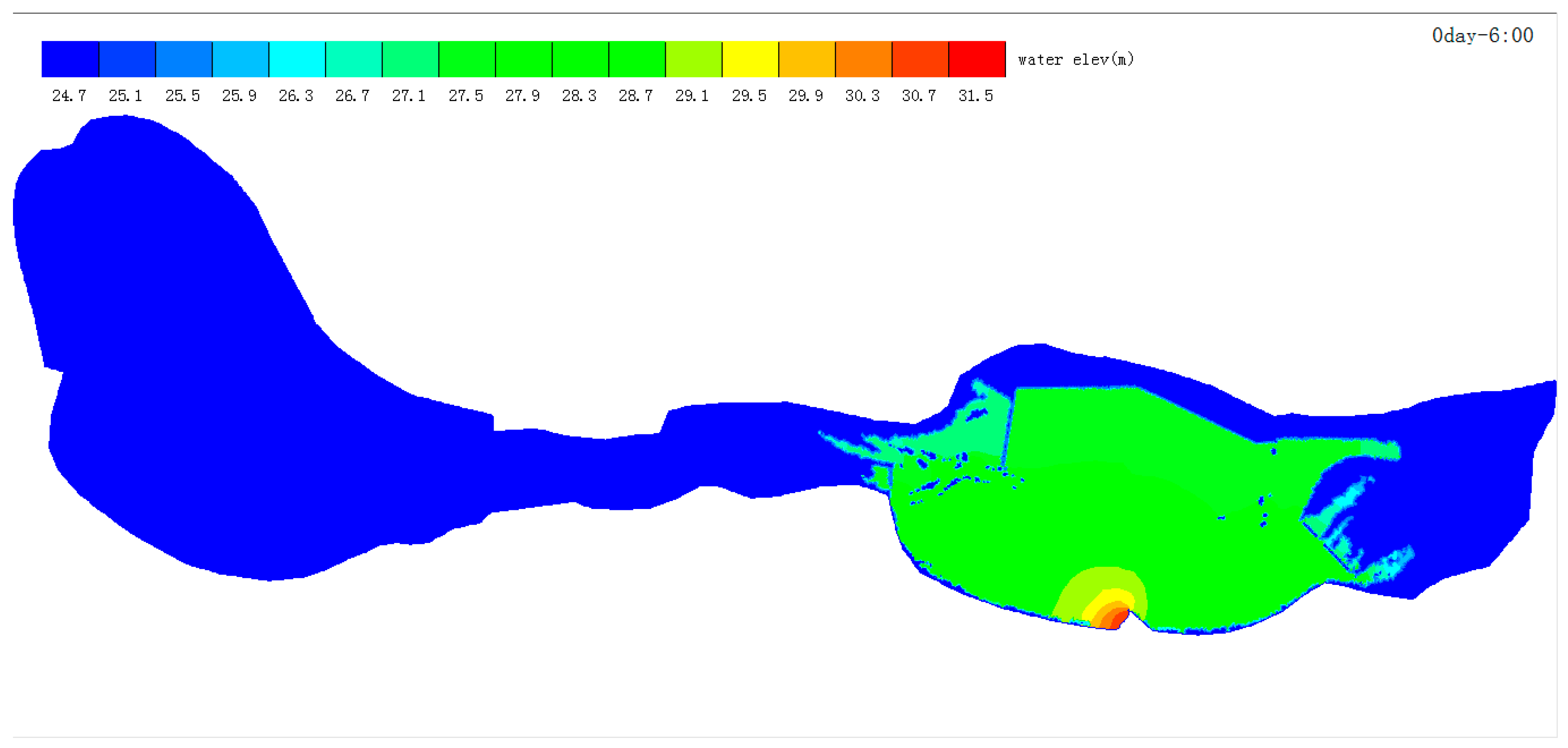
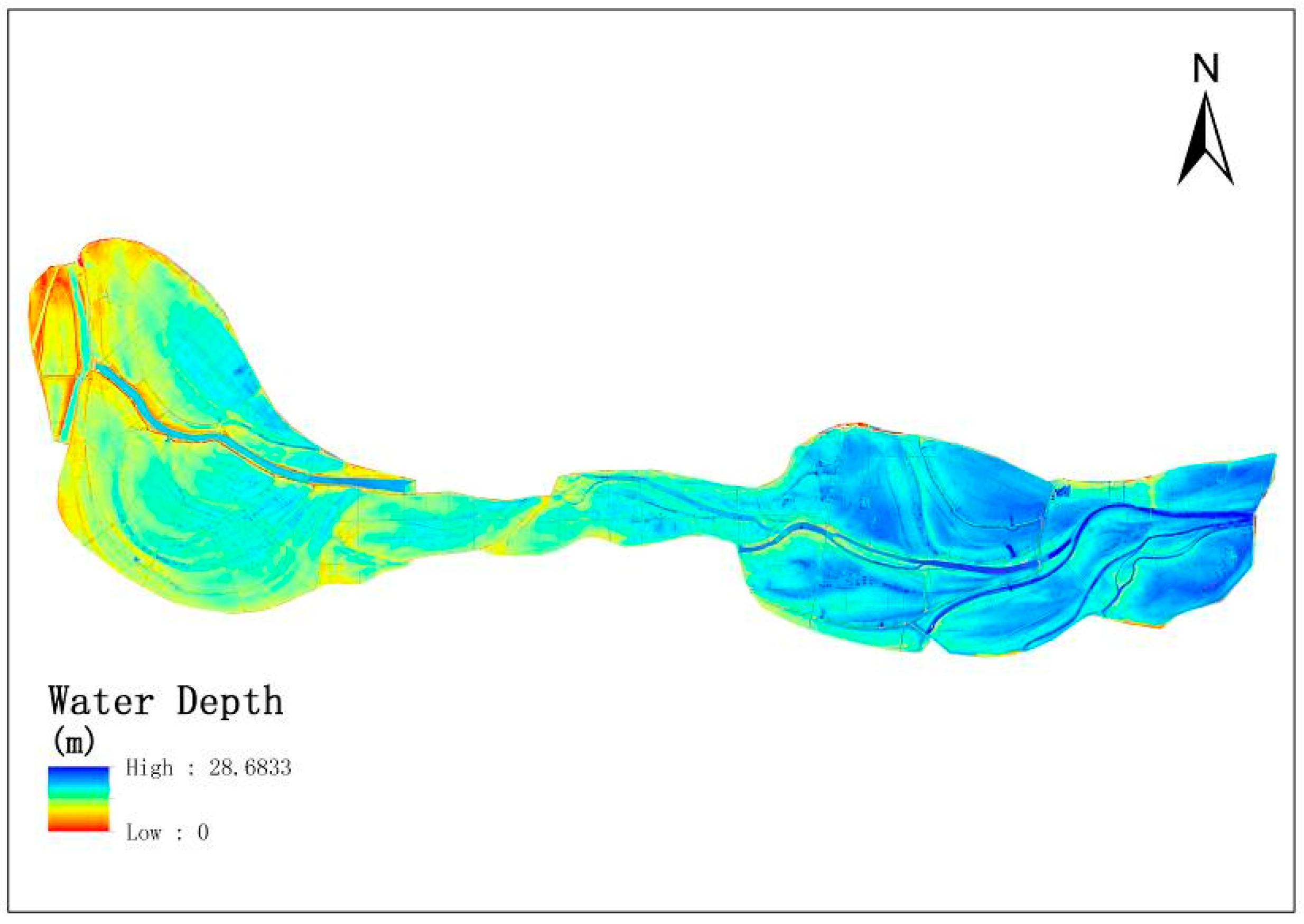
4.1. Results
4.2. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lekuthai, A.; Vongvisessomjai, S. Intangible Flood Damage Quantification. Water Resour. Manag. 2001, 15, 343–362. [Google Scholar] [CrossRef]
- Jonkman, S.N. Loss of Life Estimation in Flood Risk Assessment. Ph.D. Thesis, Delft University, Delft, The Netherlands, 2007. [Google Scholar]
- Tapsell, S.M.; Penning-Rowsell, E.C.; Tunstall, S.M.; Wilson, T.L. Vunerability to flooding: Health and social dimensions. Philos. Trans. R. Soc. A 2002, 360, 1511–1525. [Google Scholar] [CrossRef] [PubMed]
- Hajat, S.; Ebi, K.L.; Kovats, S.; Menne, B.; Edwards, S.; Haines, A. The human health consequnences of flooding in Europe and the implication for public health: A review of the evidence. Appl. Environ. Sci. Public Health 2003, 1, 13–21. [Google Scholar]
- Ahern, M.; Kovats, S.; Wilkinson, P.; Few, R.; Matthies, F. Global health impacts of floods: Epidemiologic evidence. Epidemiol. Rev. 2005, 27, 36–46. [Google Scholar] [CrossRef] [PubMed]
- Merz, B.; Kreibich, H.; Schwarze, R.; Thieken, A. Review article “Assessment of Economic Flood Damage”. Nat. Hazard. Earth Syst. 2010, 10, 1697–1724. [Google Scholar] [CrossRef]
- Moore, M.R. Development of a High-Resolution 1D/2D Coupled Flood Simulation of Charles City, Iowa. Master’s Thesis, University of Iowa, Iowa City, IA, USA, 2011; pp. 49–68. [Google Scholar]
- MURL (Ministerium fur Umwelt, Raumordnug und Land-wirtschaft des Landes Nordrhein-Westfalen). Potentielle Hochwasserschaden am Rhein in Nordrhein-Westfalen Dusseldorf; MURL: Düsseldorf, Germany, 2000. [Google Scholar]
- ICPR (International Commission for the Protection of the Rhine). Non Structural Flood Plain Management, Measures and Their Effectiveness; International Commission for the Protection of the Rhine: Koblenz, Germany, 2002. [Google Scholar]
- FEMA (Federal Emergency Management Agency). HAZUS: Multi-Hazard Loss Estimation Model Methodology-Flood Model; FEMA: Washington, WC, USA, 2003.
- Apel, H.; Aronica, G.T.; Kreibich, H.; Thieken, A.H. Flood risk analyses-how detailed do we need to be? Nat. Hazards 2009, 49, 79–98. [Google Scholar] [CrossRef]
- Huang, Z.; Zhou, J.; Song, L.; Lu, Y.; Zhang, Y. Flood disaster loss comprehensive evaluation model based on optimization support vector machine. Expert Syst. Appl. 2010, 37, 3810–3814. [Google Scholar] [CrossRef]
- Ranger, N.; Hallegatte, S.; Bhattacharya, S.; Bachu, M.; Priya, S.; Dhore, K.; Rafique, F.; Mathur, P.; Naville, N.; Henriet, F.; et al. An assessment of the potential impact of climate change on flood risk in Mumbai. Clim. Chang. 2011, 104, 139–167. [Google Scholar] [CrossRef]
- Van Dyck, J.; Willems, P. Probalistic flood risk assessment over large geographical regions. Water Resour. Res. 2013, 49, 3330–3344. [Google Scholar] [CrossRef]
- Prettenthaler, F.; Amrusch, P.; Habsburg-Lothringen, C. Estimation of an absolute flood damage curve based on an Austrian case study under a dam breach scenario. Nat. Hazards Earth Syst. 2010, 10, 881–894. [Google Scholar] [CrossRef] [Green Version]
- Bouwer, L.M.; Bubeck, P.; Wagtendonk, A.J.; Aerts, J.C.J.H. Iundation scenarios for flood damage evaluation in polder areas. Nat. Hazards Earth Syst. 2009, 9, 1995–2007. [Google Scholar] [CrossRef]
- Pistrika, A. Flood Damage Estimation based on Flood Simulation Scenarios and a GIS Platform. Eur. Water 2010, 30, 3–11. [Google Scholar]
- Ward, P.J.; Marfai, M.A.; Yulianto, F.; Hizbaron, D.R.; Aerts, J.C.J.H. Coastal inundation and damage exposure estimation: A case study for Jakarta. Nat. Hazards 2011, 56, 899–916. [Google Scholar] [CrossRef]
- Muhammad, M.; Takeuchi, K. Assessment of flood hazard, vulnerability and risk of mid-eastern Dhaka using DEM and 1D hydrodynamic model. Nat. Hazards 2012, 61, 757–770. [Google Scholar]
- Ernst, J.; Dewals, B.J.; Detrembleur, D.S.; Archambeau, P.; Erpicum, S.; Pirotton, M. Micro-scale flood rsik analysis based on detailed 2D hydraulic modeling and high resolution geographic data. Nat. Hazards 2010, 55, 181–209. [Google Scholar] [CrossRef]
- Mongkonkerd, S.; Hirunsalee, S.; Kanegae, H.; Denpaiboon, C. Comparison of Direct Monetary Flood Damage in 2011 to Pillar House and Non-Pillar House in Ayutthaya, Thailand. Procedia Environ. Sci. 2013, 17, 327–336. [Google Scholar] [CrossRef]
- Thieken, A.H.; Kreibich, H.; Muller, M.; Merz, B. Coping with floods: Preparedness, response and recovery of flood-affected residents in Germany in 2002. Hydrol. Sci. J. 2007, 52, 1016–1037. [Google Scholar] [CrossRef]
- Kreibich, H.; Piroth, K.; Seifert, I.; Maiwald, H.; Kunert, U.; Schwarz, J.; Merz, B.; Thieken, A.H. Is flow velocity a significant parameter in flood damage modelling? Nat. Hazards Earth Syst. 2009, 9, 1679–1692. [Google Scholar] [CrossRef] [Green Version]
- Boettle, M.; Kropp, P.; Reiber, L.; Roithmeier, O. About the influence of elevation model quality and small-sacle damage functions on flood damage estmation. Nat. Hazards Earth Syst. 2013, 11, 3327–3334. [Google Scholar] [CrossRef]
- Yang, Y.C.E.; Ray, P.A.; Brown, C.M.; Khalil, A.F.; Yu, W.H. Estimation of flood damage functions for river basin planning: A case study in Bangladesh. Nat. Hazards 2015, 75, 2773–2791. [Google Scholar] [CrossRef]
- Sanders, B.F. Evaluation of on-line DEMs for flood inundation modeling. Adv. Water Resour. 2007, 30, 1831–1843. [Google Scholar] [CrossRef]
- Sampson, C.C.; Fewtrell, T.J.; Duncan, A.; Shaad, K.; Horrit, M.S.; Bates, P.D. Use of terrestrial laser data to drive decimetric resolution urban inundation models. Adv. Water Resour. 2012, 14, 1–17. [Google Scholar] [CrossRef]
- Meesuk, V.; Vojinovic, Z.; Mynett, A.E.; Abdullah, A.F. Urban flood modelling combining top-view LiDAR data with ground-view SfM observations. Adv. Water Resour. 2015, 75, 105–117. [Google Scholar] [CrossRef]
- McCarthy, S.; Tunstall, S.; Parker, D.; Faulkner, H.; Howe, J. Risk communication in emergency response to a simulated extreme flood. Environ. Hazards 2007, 7, 179–192. [Google Scholar] [CrossRef] [Green Version]
- Leskens, J.G.; Brugnach, M.; Hoekstra, A.Y.; Schuurmans, W. Why are decisions in flood disaster management so poorly supported by information from flood models? Environ. Modell. Softw. 2014, 53, 53–61. [Google Scholar] [CrossRef]
- Gerl, T.; Bochow, M.; Kreibich, H. Flood Damage Modeling on the Basis of Urban Structure Mapping Using High-Resolution Remote Sesing Data. Water 2014, 6, 2367–2393. [Google Scholar] [CrossRef]
- Molinari, D.; Scorzini, A.R. On the Influence of Input Data Quality to Flood Damage Estimation: The Performance of the INSYDE Model. Water 2017, 9, 688. [Google Scholar] [CrossRef]
- Yang, H.; Chen, W.; Qian, T.; Shen, D.; Wang, J. The Extraction of Vegetation Points from LiDAR Using 3D Fractal Dimension Analyses. Remote Sens. 2015, 7, 10815–10831. [Google Scholar] [CrossRef] [Green Version]
- Liang, Q.; Borthwick, A.G.L. Adaptive quadtree simulation of shallow flows with wet–dry fronts over complex topography. Comput. Fluids 2009, 38, 221–234. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, Q.; Kresserwani, G.; Hall, J.W. A 2D shallow flow model for practical dam-break simulations. J. Hydraul. Res. 2011, 49, 307–316. [Google Scholar] [CrossRef]
- Design Code for Residential Buildings; GB 50096-2011; Ministry of Housing and Urban-Rural Development of China: Beijing, China, 2011.
- Ding, Z. A Study on the Technology and Method of Flood and Waterlogging Disaster Loss Assessment Based on RS and GIS. Ph.D. Thesis, China Institute of Water Resources and Hydropower Research, Beijing, China, 2004; pp. 63–80. [Google Scholar]
- Brunn, A.; Weidner, U. Hierarchical Bayesian nets for building extraction using dense digital surface models. ISPRS J. Photogramm. 1998, 53, 296–307. [Google Scholar] [CrossRef]
- Elberink, E.O.; Maas, H. The use of anisotropic height texture measures for the segmentation of airborne laser scanner data. Int. Arch. Photogram. Remote Sens. 2000, 33, 678–684. [Google Scholar]
- Tóvári, D.; Vögtle, T. Object Classification in Laser Scanning Data. Int. Arch. Photogramm. Remote Sens. 2012, 36, 45–49. [Google Scholar]
- Changjiang Water Resources Commission. Estimation of Flood Loss in Jingjiang Flood Diversion Area; Changjiang Water Resources Commission: Wuhan, China, 1983. [Google Scholar]
- Engineering Administration Bureau of Jingjiang Flood Diversion and Storage Area. Basic Data Collection of Jingjiang Flood Diversion Area; Engineering Administration Bureau of Jingjiang Flood Diversion and Storage Area: Jingzhou, China, 1991. [Google Scholar]
- Changjiang Water Resources Commission. A Brief Analysis of the Economic Loss of Flood Diversion and Storage in the Middle Reaches of the Yangtze River; Changjiang Water Resources Commission: Wuhan, China, 1987. [Google Scholar]
- Office of Flood Control and Drought Relief, Changjiang Water Resources Commission. Flood Storage and Detention Areas in the Middle and Lower Reaches of the Yangtze River; Office of Flood Control and Drought Relief, Changjiang Water Resources Commission: Wuhan, China, 1990. [Google Scholar]
- Changjiang Water Resources Commission. Investigation and Analysis of Economic Loss of Flood Distribution and Storage in the Middle Reaches of the Yangtze River; Changjiang Water Resources Commission: Wuhan, China, 1990. [Google Scholar]
- Hubei Provincial Water Resources and Hydropower Planning Survey and Design Institute. Benefit Calculation of Flood Control Project in Hanjiang Plain and Honghu Lake; Hubei Provincial Water Resources and Hydropower Planning Survey and Design Institute: Wuhan, China, 1989. [Google Scholar]



| Building Type | Height (m) | Count |
|---|---|---|
| Brick–wood | <3 | 1577 |
| 3–6 | 18,302 | |
| Brick–concrete | 6–9 | 6718 |
| 9–12 | 3259 | |
| 12–15 | 591 | |
| 15–18 | 90 | |
| 18–21 | 12 | |
| 21–24 | 2 |
| Submerged Water Depth (m) | <1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 |
|---|---|---|---|---|---|---|---|---|---|
| Rural house flood loss rate (%) | 33 | 38 | 43 | 48 | 55 | 62 | 70 | 80 | 92 |
| 33 | 38 | 42 | 49 | 55 | 70 | 70 | 70 | 70 | |
| 30 | 52 | 68 | 80 | 87 | 90 | 90 | 90 | 90 | |
| 46 | 60 | 80 | 80 | 80 | 80 | 80 | 80 | 80 | |
| 25 | 67 | 80 | 80 | 80 | 80 | 80 | 80 | 80 | |
| 27 | 53 | 86 | 86 | 86 | 86 | 86 | 86 | 86 | |
| Urban house flood loss rate (%) | 3 | 6 | 9 | 12 | 16 | 19 | 19 | 19 | 19 |
| Water Depth | Not Flooded | <1 m | 1–2 m | 2–3 m | 3–4 m | 4–5 m | 5–6 m | 6–7 m | 7–8 m | 8–9 m |
|---|---|---|---|---|---|---|---|---|---|---|
| Number of brick–concrete buildings | 0 | 197 | 413 | 1088 | 2046 | 3615 | 2568 | 677 | 59 | 9 |
| Number of brick–wood buildings | 0 | 336 | 787 | 1575 | 2717 | 5617 | 5672 | 3070 | 99 | 6 |
| Category | Items | Loss Rate of Assets | Average Loss Rate | ||||||
|---|---|---|---|---|---|---|---|---|---|
| [41] | [42] | [43] | [44] | [45] | [43] | [46] | |||
| Industries, commerce, and enterprises | Industrial assets | 60 | 38 | 54 | 80 | 60 | 60 | - | 58.7 |
| Commercial assets | 60 | 64 | 68 | 80 | 60 | 60 | - | 65.3 | |
| Post and telecommunication assets | 60 | 60 | 50 | 60 | - | 93 | 85 | 68 | |
| Rural power system assets | 50 | 90 | 80 | 80 | 100 | 89 | 85 | 82 | |
| Rural broadcasting assets | 100 | 100 | 80 | - | - | - | 85 | 91.3 | |
| Healthcare assets | - | 80 | 70 | - | - | - | 60 | 70 | |
| Culture and sports assets | - | 80 | 70 | - | - | 73 | 60 | 70.8 | |
| School assets | 80 | 80 | 70 | 80 | - | - | 60 | 70.8 | |
| Township assets | 70 | 70 | 60 | 60 | 70 | - | 60 | 65 | |
| Village team assets | - | 80 | 60 | 60 | 60 | - | 60 | 64 | |
| Township enterprise assets | 70 | 80 | 70 | 70 | - | - | - | 72.5 | |
| Transportation assets | 50 | 60 | 50 | - | - | 27.8 | 30 | 43.6 | |
| Residential property | Agricultural equipment | 60 | - | 50 | 60 | 50 | - | - | 55 |
| Private properties | 80 | 68 | 75 | 80 | 80 | 74 | 80 | 76.7 | |
| Cattles and horses | 10 | - | 20 | 10 | 10 | - | 30 | 16 | |
| Pigs | 30 | - | 40 | 30 | 30 | - | 60 | 38 | |
| Fowl | 100 | - | 100 | - | - | - | 90 | 96.7 | |
| Engineering facilities | Pump stations | 50 | 60 | - | - | - | - | - | 55 |
| Culverts and sluices | 50 | 20 | - | - | - | - | - | 35 | |
| Basic farmland facilities | 50 | - | 100 | - | - | - | - | 75 | |
| Roads and bridges | 50 | - | 50 | 50 | 50 | - | - | 50 | |
| Agriculture, forestry, and fisheries | Agriculture | 100 | 100 | 100 | 100 | 100 | 89.3 | 90 | 97 |
| Forestry | 20 | 57 | 52 | 25 | 20 | 51.9 | 37.7 | ||
| Fisheries | 100 | 89 | 68 | 100 | 100 | 68.1 | 80 | 86.4 | |
| Averages | 61.90 | 70.89 | 65.32 | 64.06 | 60.77 | 68.61 | 67.67 | 64.19 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, D.; Qian, T.; Chen, W.; Chi, Y.; Wang, J. A Quantitative Flood-Related Building Damage Evaluation Method Using Airborne LiDAR Data and 2-D Hydraulic Model. Water 2019, 11, 987. https://doi.org/10.3390/w11050987
Shen D, Qian T, Chen W, Chi Y, Wang J. A Quantitative Flood-Related Building Damage Evaluation Method Using Airborne LiDAR Data and 2-D Hydraulic Model. Water. 2019; 11(5):987. https://doi.org/10.3390/w11050987
Chicago/Turabian StyleShen, Dingtao, Tianlu Qian, Wenlong Chen, Yao Chi, and Jiechen Wang. 2019. "A Quantitative Flood-Related Building Damage Evaluation Method Using Airborne LiDAR Data and 2-D Hydraulic Model" Water 11, no. 5: 987. https://doi.org/10.3390/w11050987






