Response of Wetland Evapotranspiration to Land Use/Cover Change and Climate Change in Liaohe River Delta, China
Abstract
1. Introduction
2. Study Area and Data
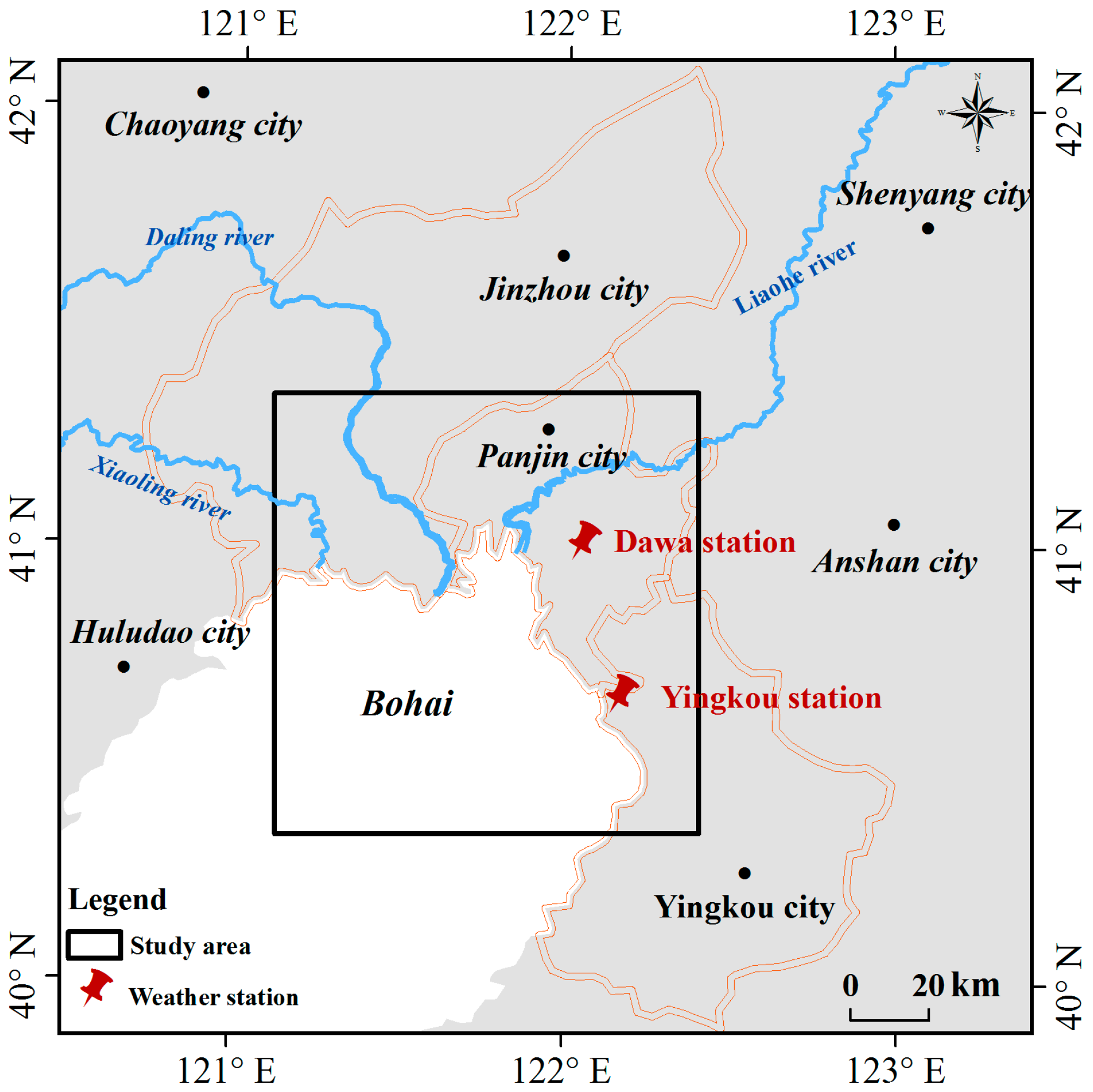
2.1. Study Area
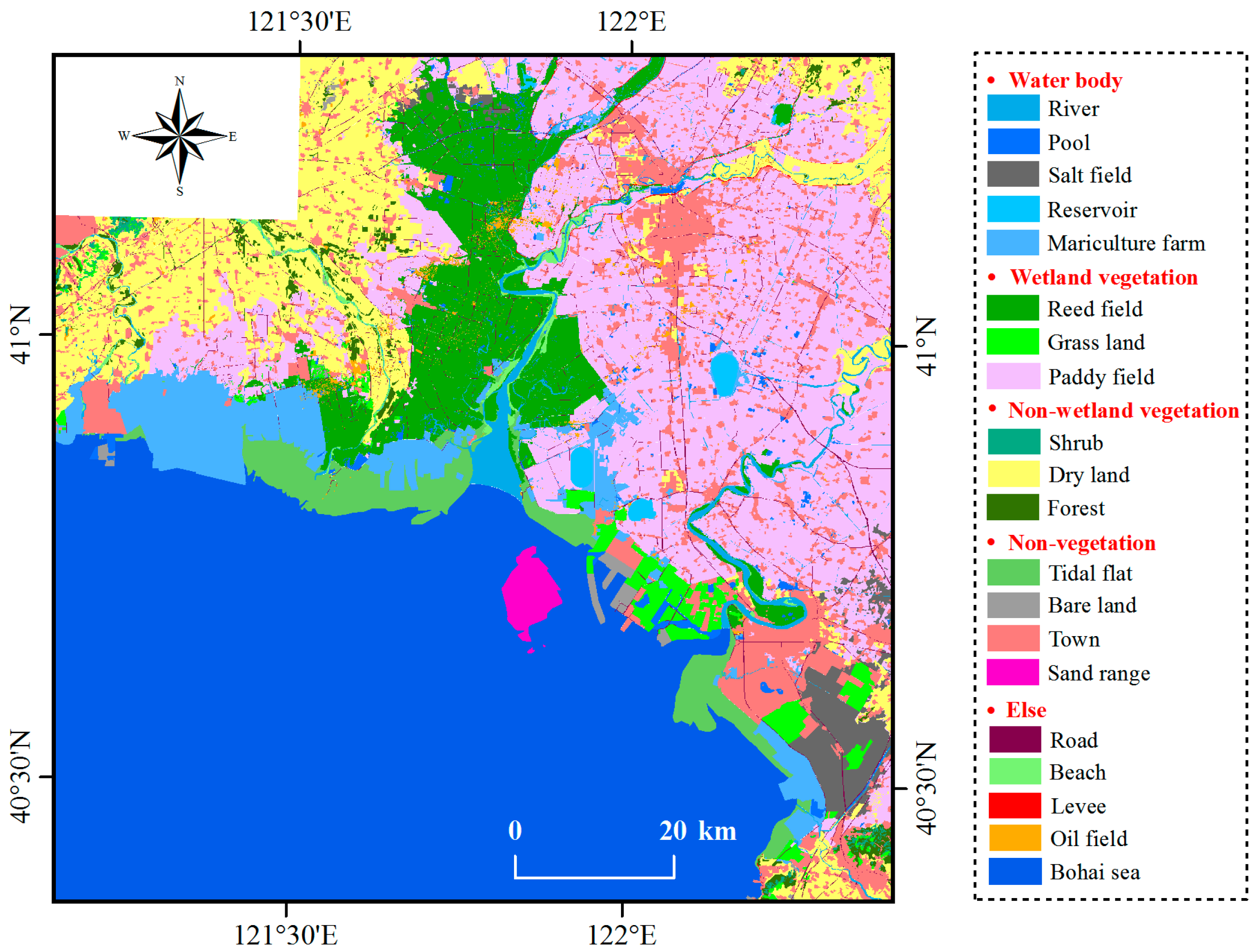
2.2. Data Acquisition and Pre-Processing
3. Methodology and Procedure
3.1. SEBAL Algorithm
3.2. Method for Analyzing the Influencing Factors of ET
4. Results
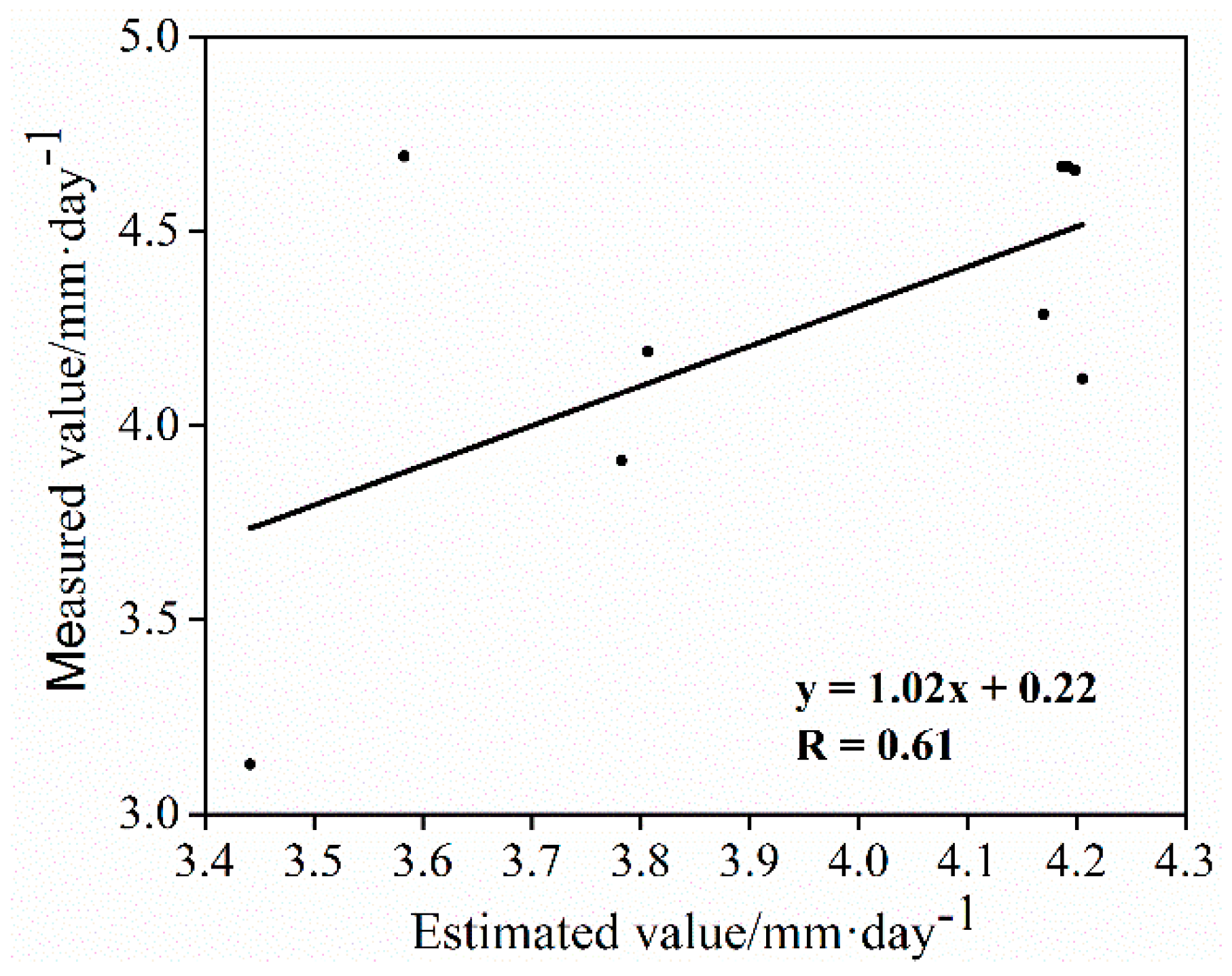
4.1. Validation of SEBAL Results
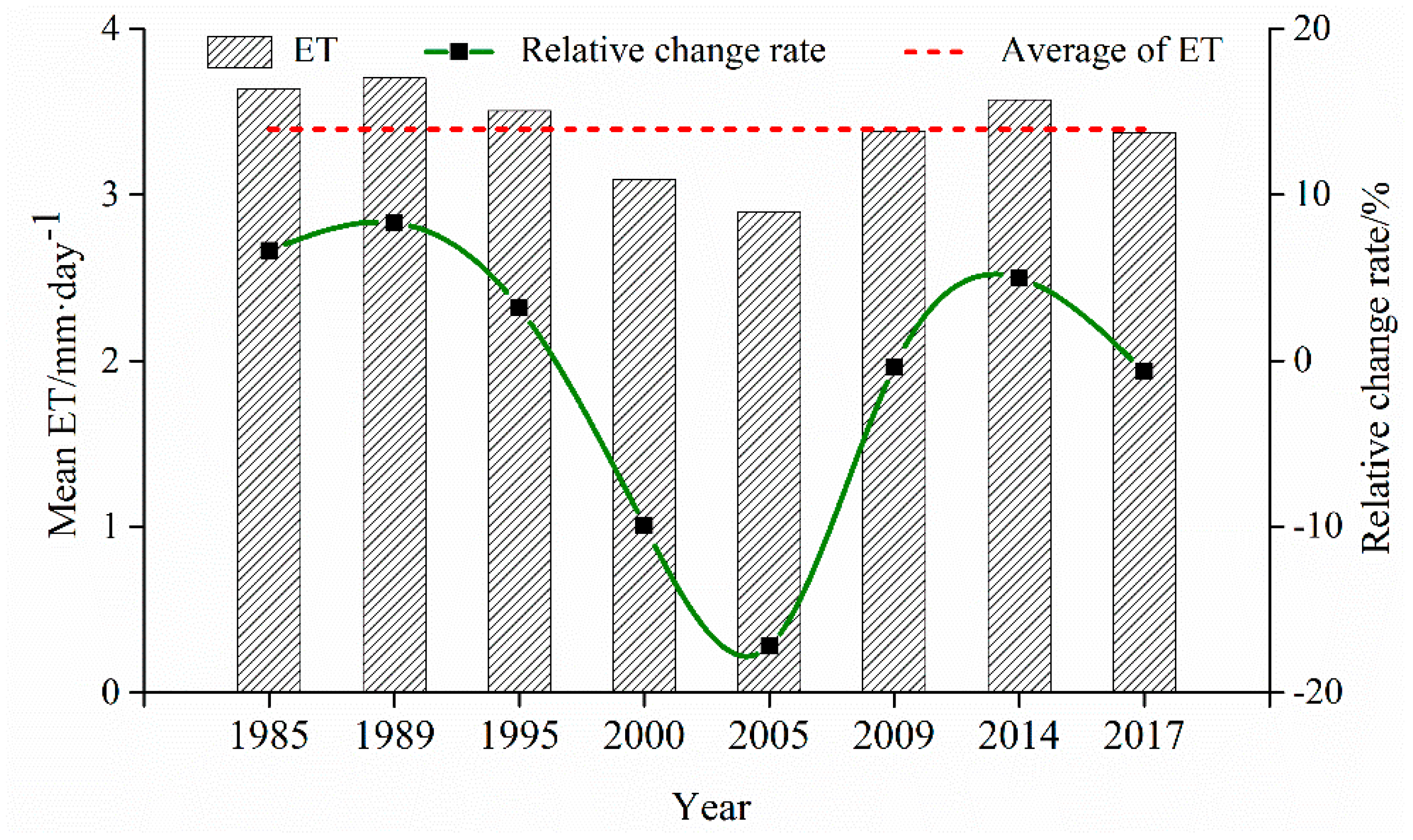
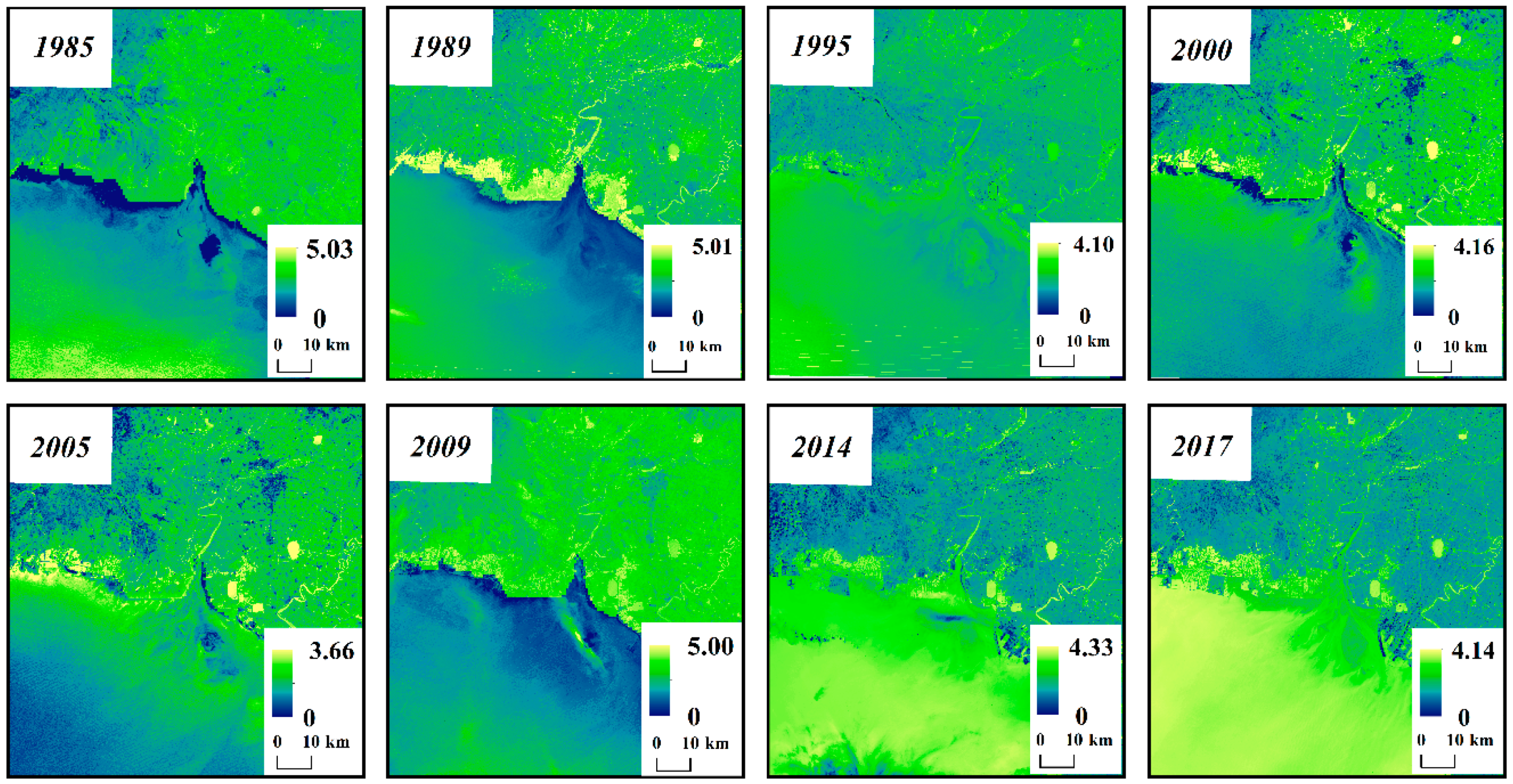
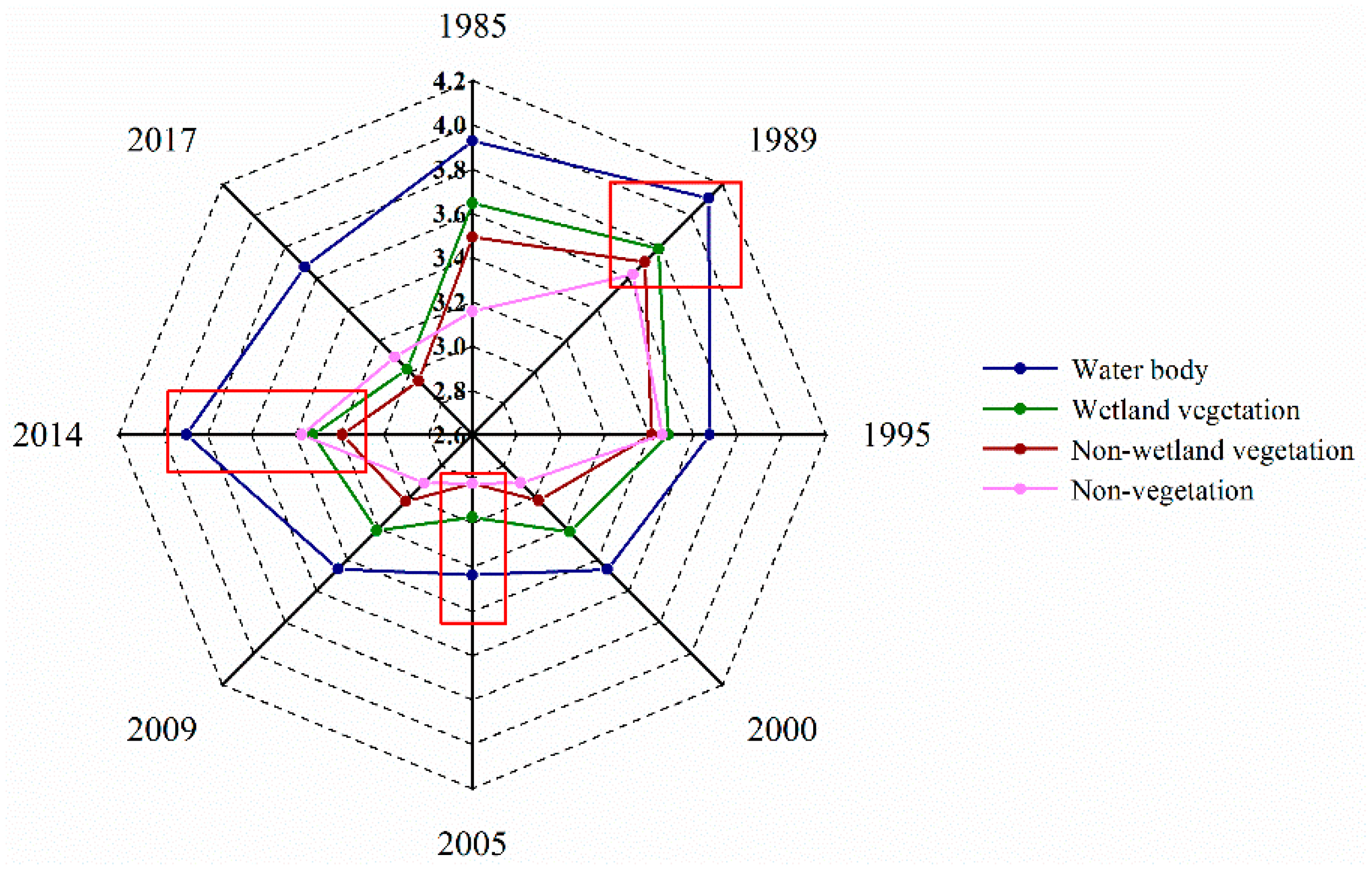
4.2. Spatial and Temporal Variations of ET
4.3. Dominant Factors of ET
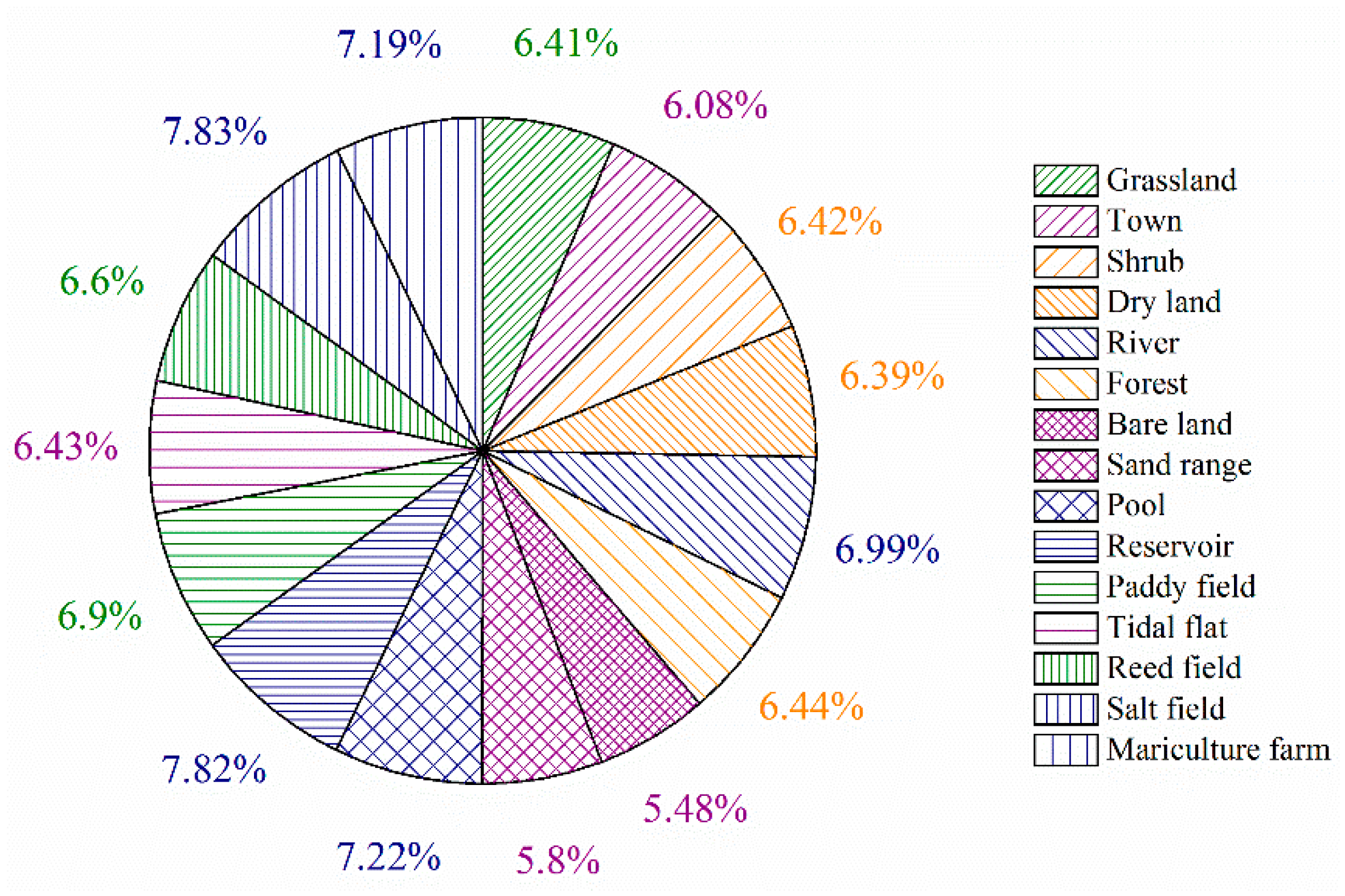
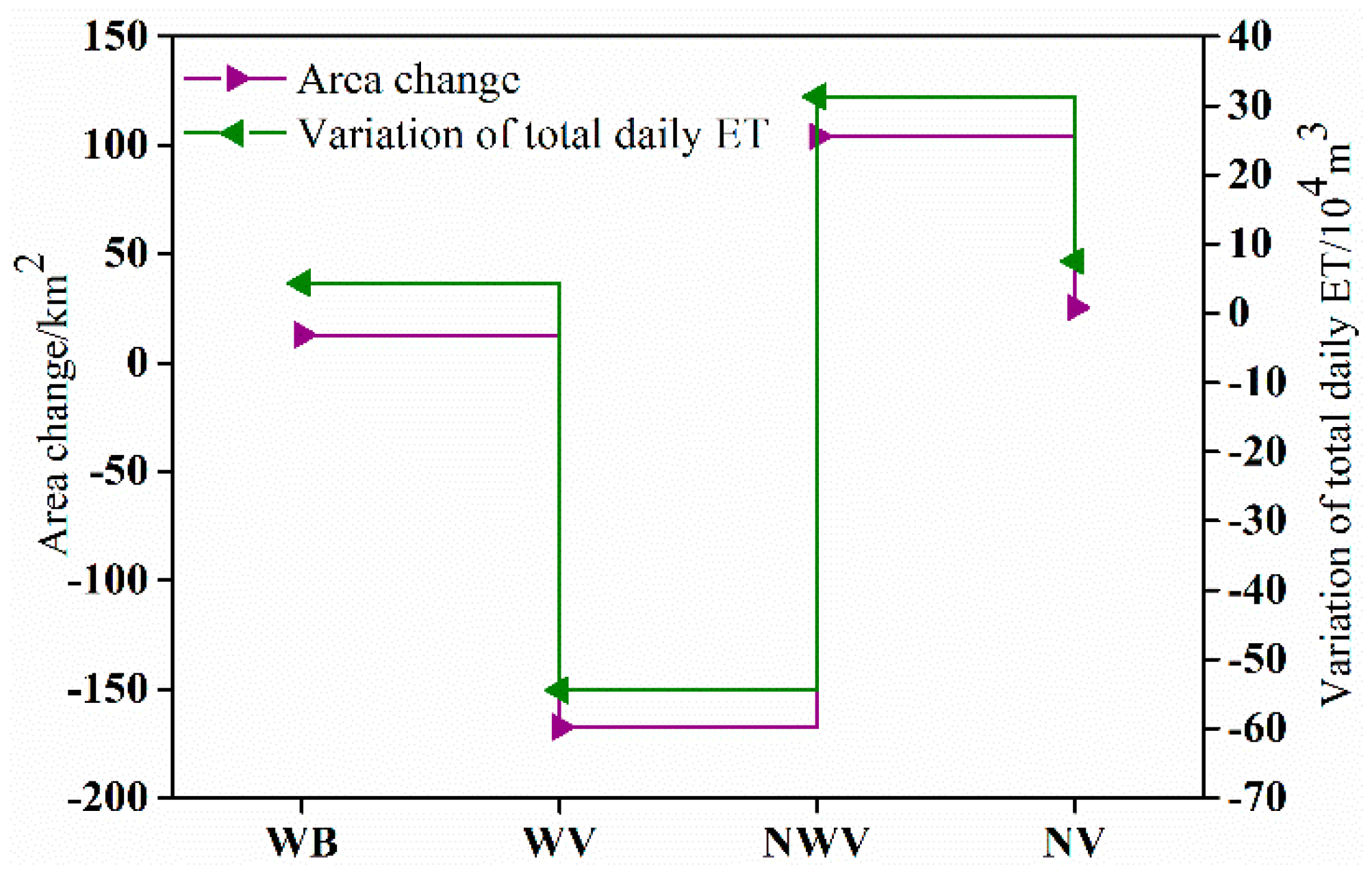
4.3.1. Effect of Land Cover on ET
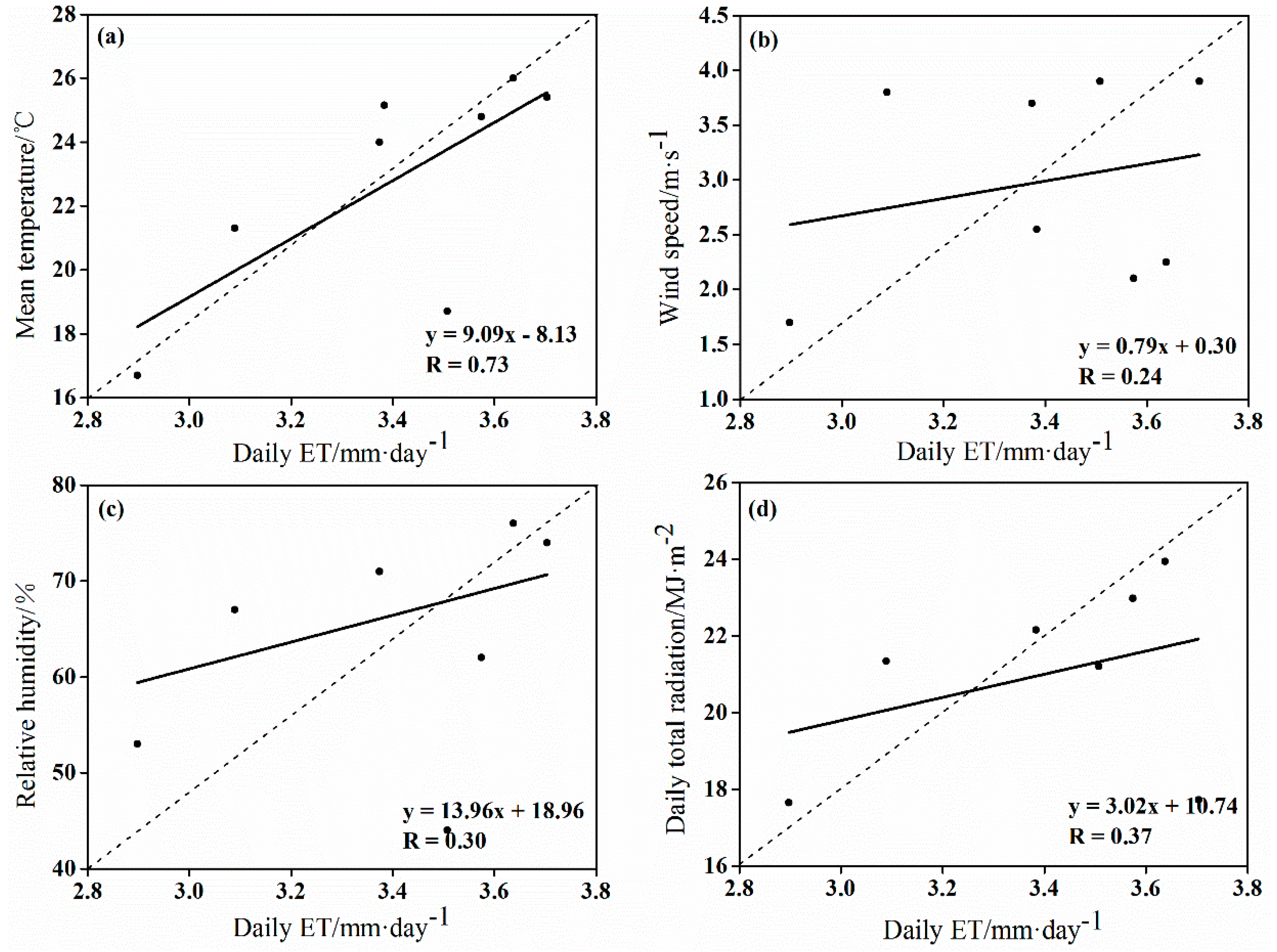
4.3.2. Effects of Meteorological Factors on ET
5. Discussion
6. Conclusions
- The results calculated by SEBAL were comparable with the values derived from pan observations, which indicated that the averaged relative error was 9.01%. The correlation analysis indicated that the estimated versus measured ET results were consistent, with a correlation coefficient of 0.61. Generally, the SEBAL model could be effectively used for estimating regional ET over the Liaohe River wetland.
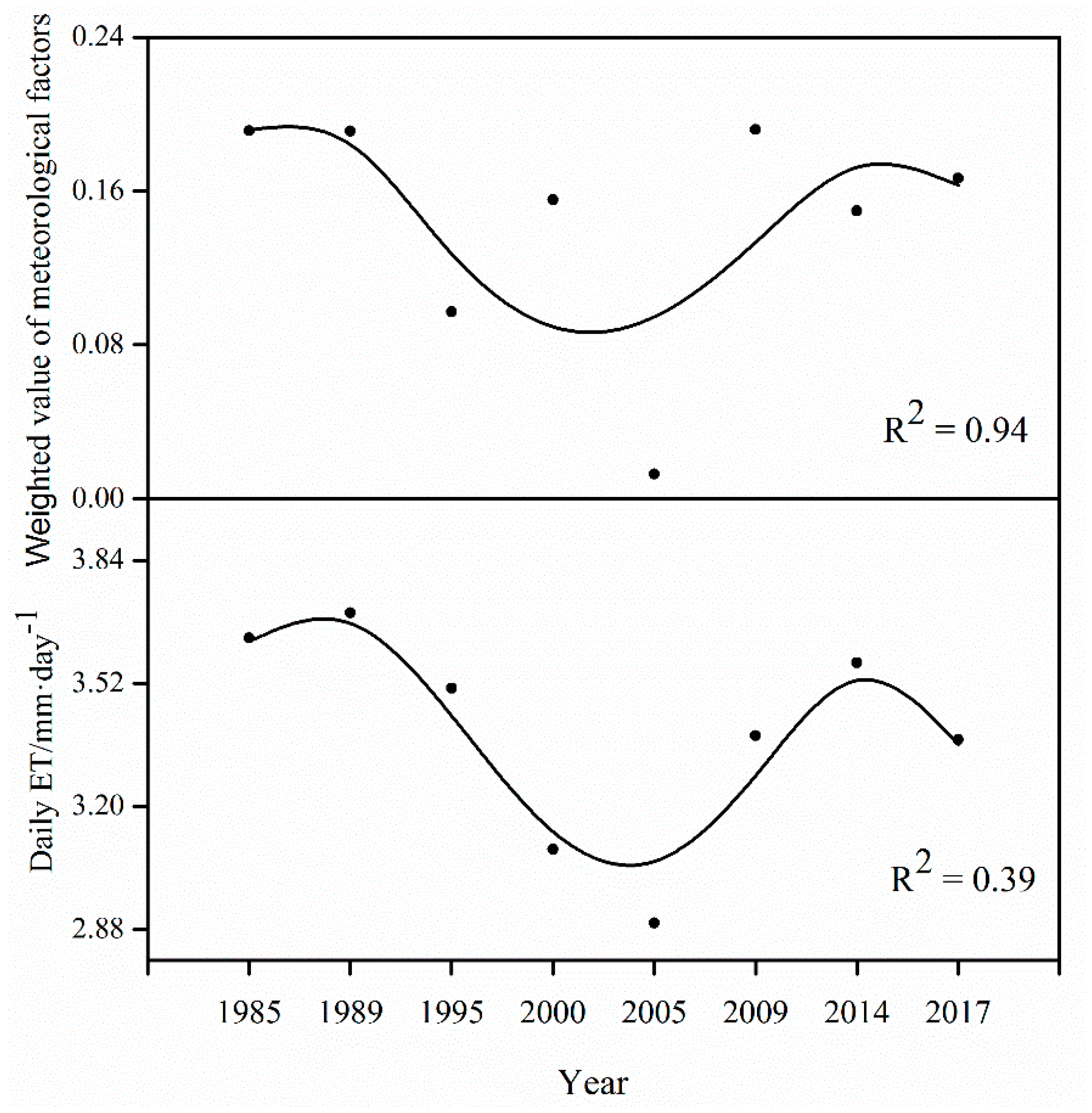
- From 1985 to 2017, the average value and relative change rate in ET showed bimodal characteristics in the study area, with the inflection points in 1989, 2005, and 2014; the average ET value was approximately 3.40 mm·day−1 for the entire area. A slightly decreasing trend of ET was also observed across the region. Local-scaled daily ET displayed highly heterogeneous spatial distribution, which was coherent with the land cover map to some extent.
- During the study period, the underlying surface and climate conditions were the dominant factors contributing to ET. The different land uses/cover types with ET were, in decreasing order: water body, wetland vegetation, non-wetland vegetation, and non-vegetation (except water body). Meanwhile, the variation of wetland ET was closely related to landscape transformation and meteorological factor change. This study also developed a new method of weighted comprehensive analysis for meteorological factors (e.g., solar radiation, air temperature, wind speed, and relative humidity), which could explain the temporal variation trend of ET to a certain extent.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wells, C.; Ketcheson, S.; Price, J. Hydrology of a wetland-dominated headwater basin in the Boreal Plain, Alberta, Canada. J. Hydrol. 2017, 547, 168–183. [Google Scholar] [CrossRef]
- Carol, E.; Kruse, E.; Mancuso, M.; Melo, M. Local and Regional Water Flow Quantification in Groundwater-dependent Wetlands. Water Resour. Manag. 2013, 27, 807–817. [Google Scholar] [CrossRef]
- Gharun, M.; Vervoort, R.W.; Turnbull, T.L.; Adams, M.A. A test of how coupling of vegetation to the atmosphere and climate spatial variation affects water yield modelling in mountainous catchments. J. Hydrol. 2014, 514, 202–213. [Google Scholar] [CrossRef]
- Suzuki, T.; Ohta, T.; Hiyama, T.; Izumi, Y.; Mwandemele, O.; Iijima, M. Effects of the introduction of rice on evapotranspiration in seasonal wetlands. Hydrol. Process. 2014, 28, 4780–4794. [Google Scholar]
- Gong, T.; Lei, H.; Yang, D.; Jiao, Y.; Yang, H. Monitoring the variations of evapotranspiration due to land use/cover change in a semiarid shrubland. Hydrol. Earth Syst. Sci. 2017, 21, 863–877. [Google Scholar] [CrossRef]
- Tao, B.O.; Tian, H.; Chen, G.; Ren, W.; Lu, C.; Alley, K.; Xu, X.; Liu, M.; Pan, S.; Virji, H. Terrestrial carbon balance in tropical Asia: Contribution from cropland expansion and land management. Glob. Planet. Chang. 2013, 100, 85–98. [Google Scholar] [CrossRef]
- Spera, S.A.; Galford, G.L.; Coe, M.T.; Mustard, J.F. Land-Use Change Affects Water Recycling in Brazil’s Last Agricultural Frontier. Glob. Chang. Biol. 2016, 22, 3405–3413. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Zhang, F.; Jing, Y.; Liu, Y.; Sun, G. Response of evapotranspiration to changes in land use and land cover and climate in China during 2001–2013. Sci. Total Environ. 2017, 596–597, 256–265. [Google Scholar] [CrossRef] [PubMed]
- Kousari, M.R.; Ahani, H.; Hakimelahi, H. An investigation of near surface wind speed trends in arid and semiarid regions of Iran. Theor. Appl. Climatol. 2013, 114, 153–168. [Google Scholar] [CrossRef]
- Drexler, J.Z.; Snyder, R.L.; Spano, D.; Tha Paw, U.K. A review of models and micrometeorological methods used to estimate wetland evapotranspiration. Hydrol. Process. 2010, 18, 2071–2101. [Google Scholar] [CrossRef]
- Dinpashoh, Y.; Jhajharia, D.; Fakheri-Fard, A.; Singh, V.P.; Kahya, E. Trends in reference crop evapotranspiration over Iran. J. Hydrol. 2011, 399, 422–433. [Google Scholar] [CrossRef]
- Glenn, E.P.; Mexicano, L.; Garcia-Hernandez, J.; Nagler, P.; Gomez-Sapiens, M.; Tang, D.; Lomeli, M.; Ramirez-Hernandez, J.; Zamora-Arroyo, F. Evapotranspiration and water balance of an anthropogenic coastal desert wetland: Responses to fire, inflows and salinities. Ecol. Eng. 2013, 59, 176–184. [Google Scholar] [CrossRef]
- Richardson, C.J.; Mccarthy, E.J. Effect of land development and forest management on hydrologic response in southeastern coastal wetlands: A review. Wetlands 1994, 14, 56–71. [Google Scholar] [CrossRef]
- Li, Z.; Liu, W.Z.; Zhang, X.C.; Zheng, F.L. Impacts of land use change and climate variability on hydrology in an agricultural catchment on the Loess Plateau of China. J. Hydrol. 2009, 377, 35–42. [Google Scholar] [CrossRef]
- Zhao, A.; Zhu, X.; Liu, X.; Pan, Y.; Zuo, D. Impacts of land use change and climate variability on green and blue water resources in the Weihe River Basin of northwest China. Catena 2016, 137, 318–327. [Google Scholar] [CrossRef]
- Kim, J.; Choi, J.; Choi, C.; Park, S. Impacts of changes in climate and land use/land cover under IPCC RCP scenarios on streamflow in the Hoeya River Basin, Korea. Sci. Total Environ. 2013, 452–453, 181–195. [Google Scholar] [CrossRef]
- Yin, J.; Ou, Z.; Fu, Q.; Liu, D.; Xing, Z. Review of Current Methodologies for Regional Evapotranspiration Estimation: Inversion and Data Assimilation. Sci. Geogr. Sin. 2018, 38, 448–456. [Google Scholar]
- Kool, D.; Agam, N.; Lazarovitch, N.; Heitman, J.; Sauer, T.; Ben-Gal, A. A review of approaches for evapotranspiration partitioning. Agric. For. Meteorol. 2014, 184, 56–70. [Google Scholar] [CrossRef]
- Mohamed, Y.A.; Bastiaanssen, W.G.; Savenije, H.H.; Van den Hurk, B.J.; Finlayson, C.M. Wetland versus open water evaporation: An analysis and literature review. Phys. Chem. Earth 2012, 47–48, 114–121. [Google Scholar] [CrossRef]
- Awada, H.; Ciraolo, G.; Maltese, A.; Provenzano, A.; Hidalgo, G.; Còrcoles, M.; Ignacio, J. Assessing the performance of a large-scale irrigation system by estimations of actual evapotranspiration obtained by Landsat satellite images resampled with cubic convolution. Int. J. Appl. Earth Obs. Geoinf. 2019, 75, 96–105. [Google Scholar] [CrossRef]
- Ortega-Farias, S.; Poblete-Echeverría, C.; Brisson, N. Parameterization of a two-layer model for estimating vineyard evapotranspiration using meteorological measurements. Agric. For. Meteorol. 2010, 150, 276–286. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.; Chen, K.; Jia, Y.; Li, C.; Sun, X. Spatial-scale effect on the SEBAL model for evapotranspiration estimation using remote sensing data. Agric. For. Meteorol. 2013, 174–175, 28–42. [Google Scholar] [CrossRef]
- Awan, U.K.; Ismaeel, A. A new technique to map groundwater recharge in irrigated areas using a SWAT model under changing climate. J. Hydrol. 2014, 519, 1368–1382. [Google Scholar] [CrossRef]
- Carrascobenavides, M.; Ortegafarías, S.; Lagos, L.; Kleissl, J.; Morales-Salinas, L.; Kilic, A. Parameterization of the Satellite-Based Model (METRIC) for the Estimation of Instantaneous Surface Energy Balance Components over a Drip-Irrigated Vineyard. Remote Sens. 2014, 6, 11342–11371. [Google Scholar] [CrossRef]
- Wang, X.G.; Wen, W.; Huang, D.; Yong, B.; Chen, X. Modifying SEBAL Model Based on the Trapezoidal Relationship between Land Surface Temperature and Vegetation Index for Actual Evapotranspiration Estimation. Remote Sens. 2014, 6, 5909–5937. [Google Scholar] [CrossRef]
- Mkhwanazi, M.; Chávez, J.; Andales, A. SEBAL-A: A Remote Sensing ET Algorithm that Accounts for Advection with Limited Data. Part I: Development and Validation. Remote Sens. 2015, 7, 15046–15067. [Google Scholar] [CrossRef]
- Brix, H.; Ye, S.; Laws, E.; Sun, D.; Li, G.; Ding, X.; Yuan, H.; Zhao, G.; Wang, J.; Pei, S. Large-scale management of common reed, Phragmites australis, for paper production: A case study from the Liaohe Delta, China. Ecol. Eng. 2014, 73, 760–769. [Google Scholar] [CrossRef]
- Du, J.; Song, K. Validation of global evapotranspiration product (MOD16) using flux tower data from Panjin coastal wetland, Northeast China. Chin. Geogr. Sci. 2018, 28, 420–429. [Google Scholar] [CrossRef]
- Liu, T.; Liu, X.; Du, J.; Song, K. Pattern and Change of Coastal Wetlands in the Liaohe River Delta for 5 Periods. Wetl. Sci. 2017, 15, 622–628. [Google Scholar]
- Zhuang, L.; Wang, S. Spatial interpolation methods of daily weather data in Northeast China. J. Appl. Meteorol. Sci. 2003, 24, 605–615. [Google Scholar]
- Bastiaanssen, W.; Mobin-ud-Din, A.; Chemin, Y. Satellite surveillance of evaporative depletion across the Indus Basin. Water Resour. Res. 2002, 38, 1273. [Google Scholar] [CrossRef]
- Zhan, C.; Yin, J.; Wang, H.; Chen, S. The regional evapotranspiration estimation using a two-layer model based on quantitative remote sensing in Shahe River Basin. J. Nat. Resour. 2013, 28, 161–170. [Google Scholar]
- Zeng, L.; Song, K.; Zhang, B.; Du, J. Applying Landsat Data and SEBAL Model to Inverse Regional Evapotranspiration and Its Parameters Estimation. Remote Sens. Technol. Appl. 2008, 23, 255–263. [Google Scholar]
- Liaqat, U.; Choi, M.; Awan, U. Spatio-temporal distribution of actual evapotranspiration in the Indus Basin Irrigation System. Hydrol. Process. 2015, 29, 2613–2627. [Google Scholar] [CrossRef]
- Jia, L.; Xi, G.; Liu, S.; Huang, C.; Yan, Y.; Liu, G. Regional estimation of daily to annual regional evapotranspiration with MODIS data in the Yellow River Delta wetland. Hydrol. Earth Syst. Sci. 2009, 13, 1775–1787. [Google Scholar] [CrossRef]
- Jassas, H.; Kanoua, W.; Merkel, B. Actual evapotranspiration in the Al-Khazir Gomal Basin (Northern Iraq) using the Surface Energy Balance Algorithm for Land (SEBAL) and water balance. Geosciences 2015, 5, 141–159. [Google Scholar] [CrossRef]
- Guo, S.; Cheng, Z. Estimation of catchment evapotranspiration by climatic approach. Hydrology 1994, 5, 16–22. [Google Scholar]
- Ren, Z.; Li, M.; Zhang, W. Conversion coefficient of small evaporation pan into E-601B pan in China. J. Appl. Meteorol. Sci. 2002, 13, 508–512. [Google Scholar]
- Eslamian, S.; Khordadi, M.J.; Abedi-Koupai, J. Effects of variations in climatic parameters on evapotranspiration in the arid and semi-arid regions. Glob. Planet. Chang. 2011, 78, 188–194. [Google Scholar] [CrossRef]
- Nam, W.H.; Hong, E.M.; Choi, J.Y. Has climate change already affected the spatial distribution and temporal trends of reference evapotranspiration in South Korea? Agric. Water Manag. 2015, 150, 129–138. [Google Scholar] [CrossRef]
- Zeng, L.; Song, K.; Zhang, B.; Wang, Z.; Du, J. Analysis of spatiotemporal variations in evapotranspiration and its influencing factors over the Songnen Plain in the growing season during the period 2000–2008. Resour. Sci. 2010, 32, 2305–2315. [Google Scholar]
- Han, S.; Tian, F.; Hu, H. Positive or negative correlation between actual and potential evaporation? Evaluating using a nonlinear complementary relationship model. Water Resour. Res. 2014, 50, 1322–1336. [Google Scholar] [CrossRef]
- Feng, C.; Zhang, Y.; Zhao, S.; Zhao, X.; Mi, Z. Correlation analysis between the evapotranspiration quantity and climatic factors of artificial grassland in Three River Sources areas. Agric. Sci. Technol. 2008, 9, 13–18. [Google Scholar]
- Xu, Y.; Zhao, Q.; Ba, Y.; Bai, S.; Sun, D. Spatio-temporal variations of land surface evapotranspiration of Bosten Lake basin based on MODIS data. Sci. Geogr. Sin. 2012, 32, 1353–1357. [Google Scholar]
- Shan, N.; Shi, Z.; Yang, X.; Gao, J.; Cai, D. Spatiotemporal trends of reference evapotranspiration and its driving factors in the Beijing-Tianjin Sand source control project region, China. Agric. For. Meteorol. 2015, 200, 322–333. [Google Scholar] [CrossRef]
- Xu, L.; Shi, Z.; Wang, Y.; Zhang, S.; Chu, X.; Yu, P.; Xiong, W.; Zuo, H.; Wang, Y. Spatiotemporal variation and driving forces of reference evapotranspiration in Jing river basin, northeast China. Hydrol. Process. 2015, 29, 4846–4862. [Google Scholar] [CrossRef]
- Han, J.; Wang, J.; Zhao, Y.; Wang, Q.; Zhang, B.; Li, H.; Zhai, J. Spatio-temporal variation of potential evapotranspiration and climatic drivers in the Jing-Jin-Ji region, North China. Agric. For. Meteorol. 2018, 256–257, 75–83. [Google Scholar] [CrossRef]
- Sun, G.; Caldwell, P.; Noormets, A.; Mcnulty, S.G.; Cohen, E.; Moore, M.J.; Domec, J.C.; Treasure, E.; Mu, Q.; Xiao, J. Upscaling key ecosystem functions across the conterminous United States by a water-centric ecosystem model. J. Geophys. Res. Biogeosci. 2011, 116, G00J05. [Google Scholar] [CrossRef]
- Xu, F.; Bao, H.; Li, H.; Kwan, M.P.; Huang, X. Land use policy and spatiotemporal changes in the water area of an arid region. Land Use Policy 2016, 54, 366–377. [Google Scholar] [CrossRef]
- Bronstert, A.; Niehoff, D.; Bürger, G. Effects of climate and land-use change on storm runoff generation: Present knowledge and modelling capabilities. Hydrol. Process. 2002, 16, 509–529. [Google Scholar] [CrossRef]
- Olchev, A.; Ibrom, A.; Priess, J.; Erasmi, S.; Leemhuis, C.; Twele, A.; Radler, K.; Kreilein, H.; Panferov, O.; Gravenhorst, G. Effects of land-use changes on evapotranspiration of tropical rain forest margin area in Central Sulawesi (Indonesia): Modelling study with a regional SVAT model. Ecol. Model. 2008, 212, 131–137. [Google Scholar] [CrossRef]
- Dias, L.; Macedo, M.; Costa, M.; Coe, M.; Neill, C. Effects of land cover change on evapotranspiration and streamflow of small catchments in the upper Xingu river basin, central Brazil. J. Hydrol. Reg. Stud. 2015, 4 Pt B, 108–122. [Google Scholar] [CrossRef]
- Douglas, E.M.; Jacobs, J.M.; Sumner, D.M.; Ray, R.L. A comparison of models for estimating potential evapotranspiration for Florida land cover types. J. Hydrol. 2009, 373, 366–376. [Google Scholar] [CrossRef]
- Li, B.; Chen, Y.; Li, W.; Cao, Z. Remote Sensing and the SEBAL model for estimating evapotranspiration in the Tarim River. Acta Geogr. Sin. 2011, 66, 1230–1238. [Google Scholar]
- Sánchez-Carrillo, S.; Angeler, D.G.; Sánchez-Andrés, R.; Alvarez-Cobelas, M.; Garatuza-Payána, J. Evapotranspiration in semi-arid wetlands: Relationships between inundation and the macrophyte-cover: Open-water ratio. Adv. Water Resour. 2004, 27, 643–655. [Google Scholar] [CrossRef]
| Date | Overpass Time (UTC) | Satellite | Sensor | Temporal Resolution |
|---|---|---|---|---|
| 13 July 1985 | 2:04 | Landsat-5 | TM | 16 day |
| 9 August 1989 | 2:01 | 16 day | ||
| 11 September 1995 | 1:37 | 16 day | ||
| 8 September 2000 | 2:12 | 16 day | ||
| 22 September 2005 | 2:22 | 16 day | ||
| 15 July 2009 | 2:23 | 16 day | ||
| 30 August 2014 | 2:43 | Landsat-8 | OLI/TIRS | 16 day |
| 7 September 2017 | 2:34 | 16 day |
| k | Monthly Average | Annually Average | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 0.56 | |
| / | / | / | 0.51 | 0.55 | 0.53 | 0.54 | 0.56 | 0.57 | 0.59 | / | / | ||
| Weather Station | Time | Estimated Value/mm | Measured Value/mm | Relative Error/% |
|---|---|---|---|---|
| Dawa station | 13 July 1985 | 4.20 | 4.66 | 9.85 |
| 9 August 19 | 4.20 | 4.66 | 10.13 | |
| 11 September 1995 | 3.81 | 4.19 | 9.14 | |
| 8 September 2000 | 3.78 | 3.91 | 3.28 | |
| 22 September 2005 | 3.44 | 3.13 | 10.02 | |
| 30 August 2014 | 4.21 | 4.12 | 2.04 | |
| Yingkou station | 8 September 1989 | 4.19 | 4.66 | 10.23 |
| 8 September 2000 | 3.58 | 4.69 | 23.64 | |
| Mean | -- | -- | -- | 9.01 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Hu, D. Response of Wetland Evapotranspiration to Land Use/Cover Change and Climate Change in Liaohe River Delta, China. Water 2019, 11, 955. https://doi.org/10.3390/w11050955
Liu M, Hu D. Response of Wetland Evapotranspiration to Land Use/Cover Change and Climate Change in Liaohe River Delta, China. Water. 2019; 11(5):955. https://doi.org/10.3390/w11050955
Chicago/Turabian StyleLiu, Manqing, and Deyong Hu. 2019. "Response of Wetland Evapotranspiration to Land Use/Cover Change and Climate Change in Liaohe River Delta, China" Water 11, no. 5: 955. https://doi.org/10.3390/w11050955
APA StyleLiu, M., & Hu, D. (2019). Response of Wetland Evapotranspiration to Land Use/Cover Change and Climate Change in Liaohe River Delta, China. Water, 11(5), 955. https://doi.org/10.3390/w11050955





