The Influence of Temperature on the Bulk Settling of Cohesive Sediment in Still Water with the Lattice Boltzmann Method
Abstract
:1. Introduction
2. Methods and Model
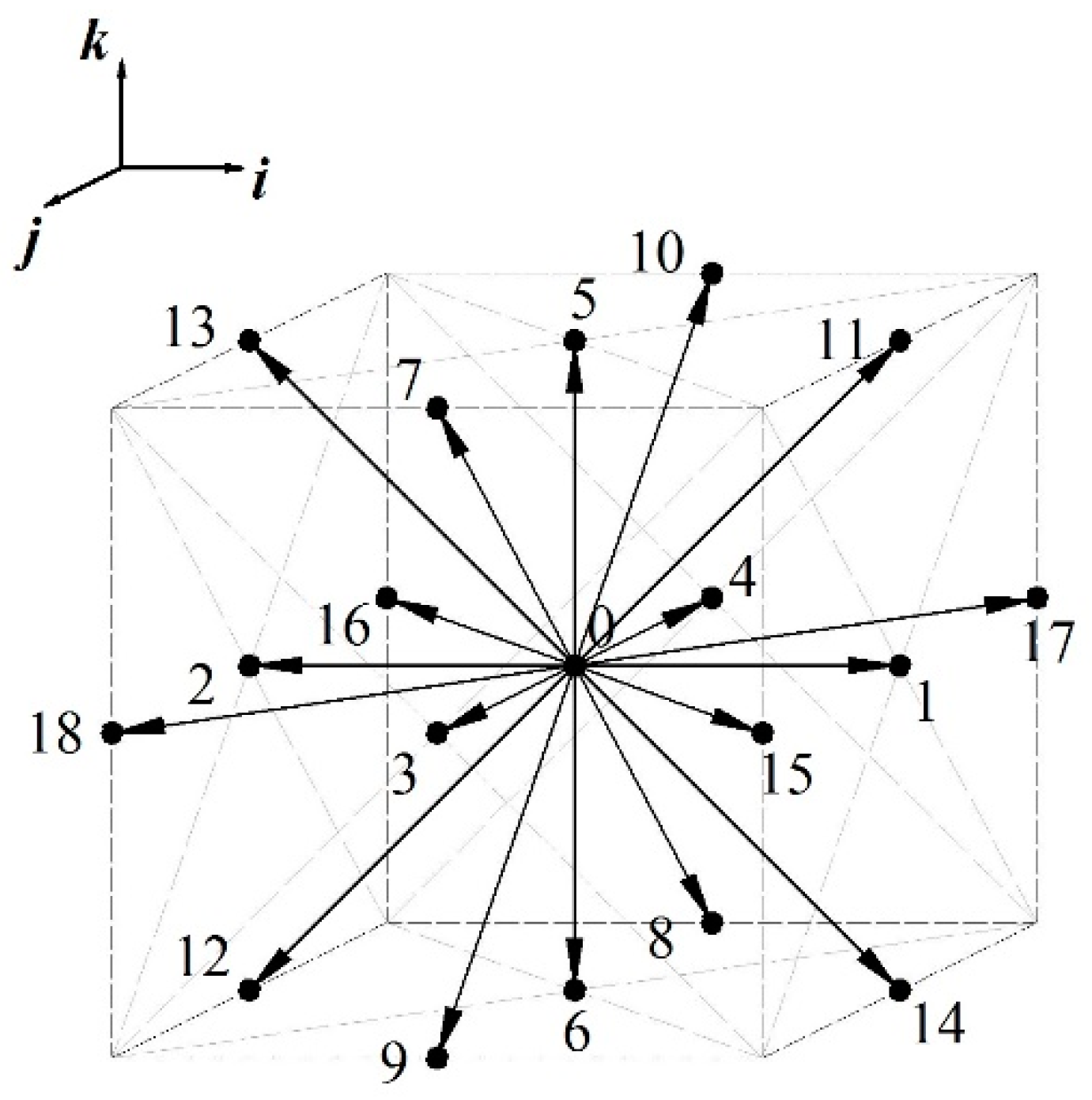
2.1. Lattice Boltzmann Method
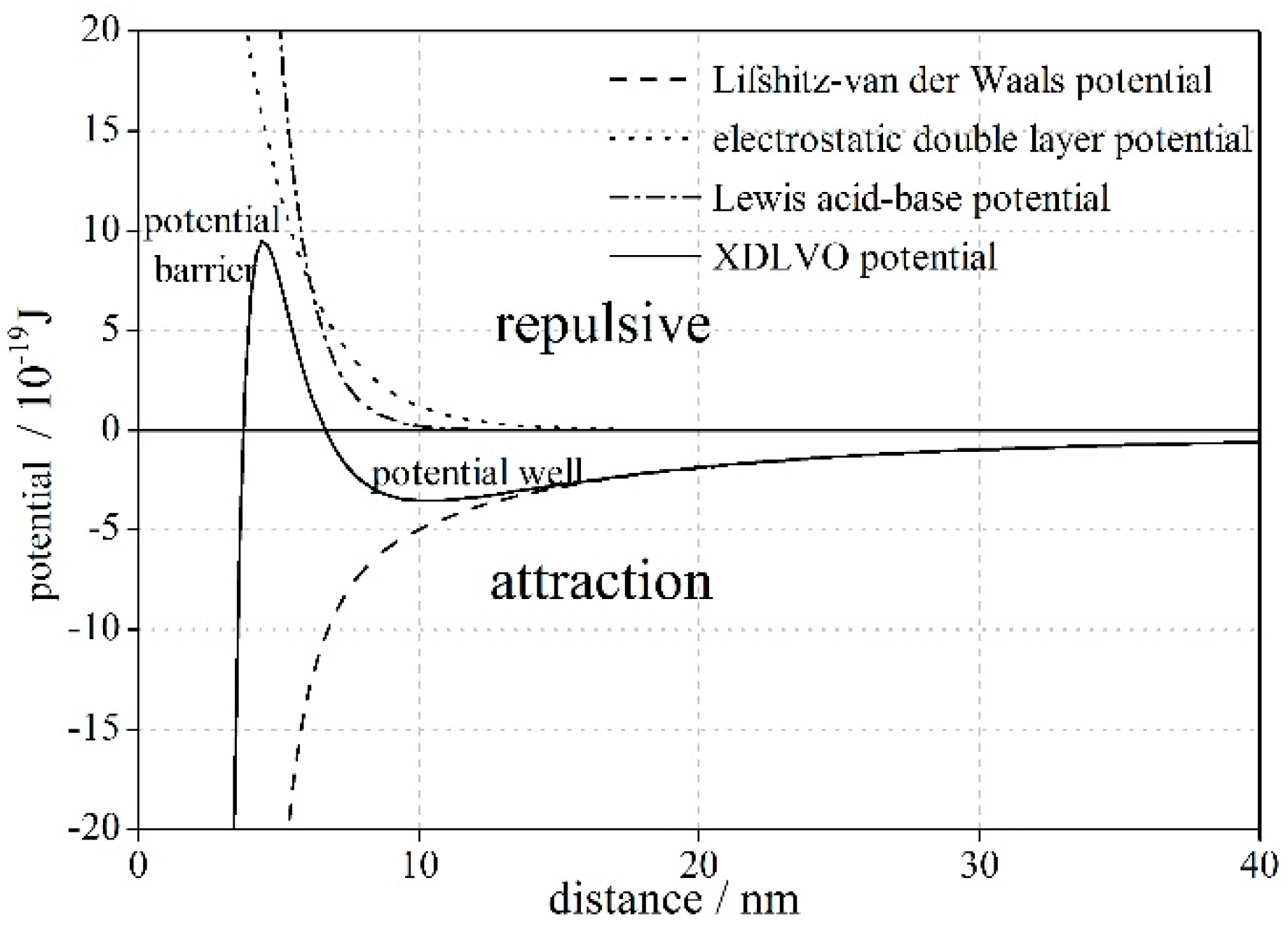
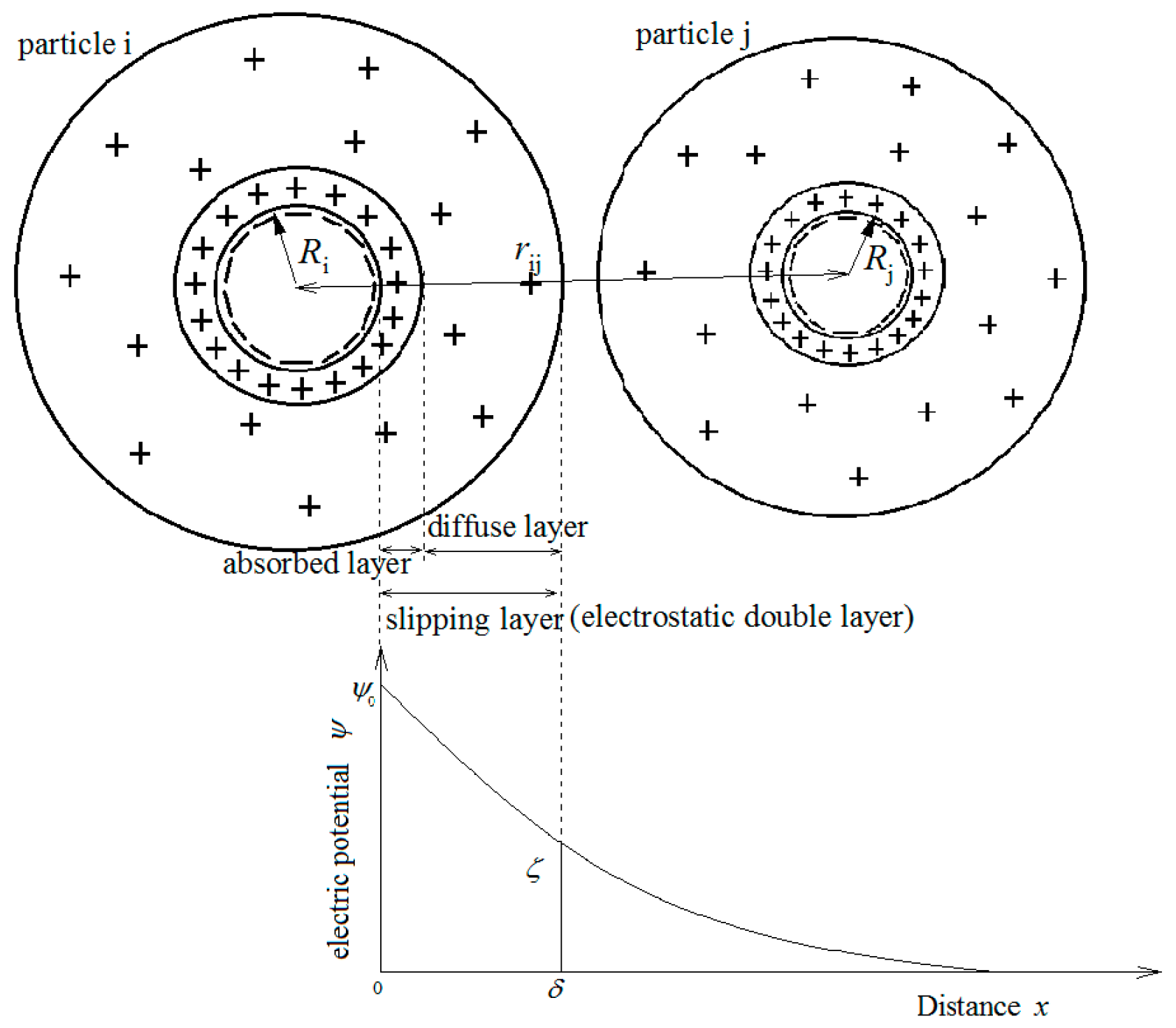
2.2. The Extended Derjaguin–Landau–Verwey–Overbeek Theory
2.3. Criterion Distance of Flocculation
3. Computational Conditions
4. Results
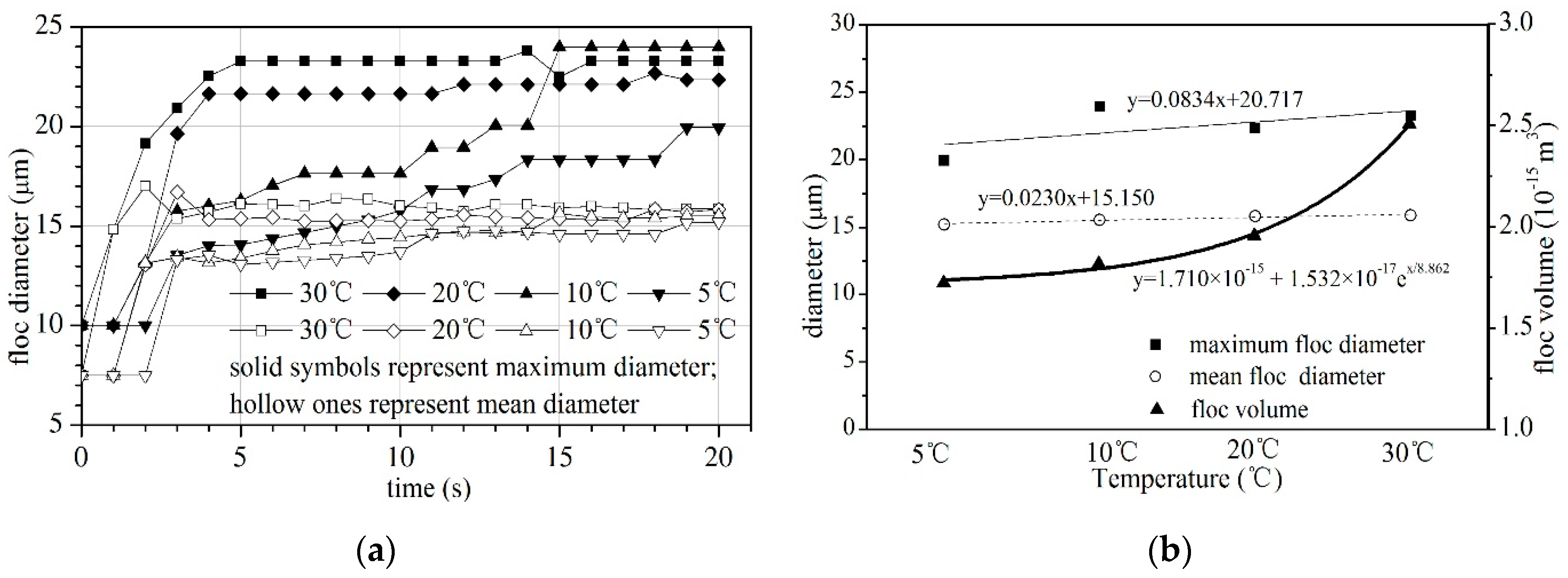
4.1. Floc Size and Floc Volume
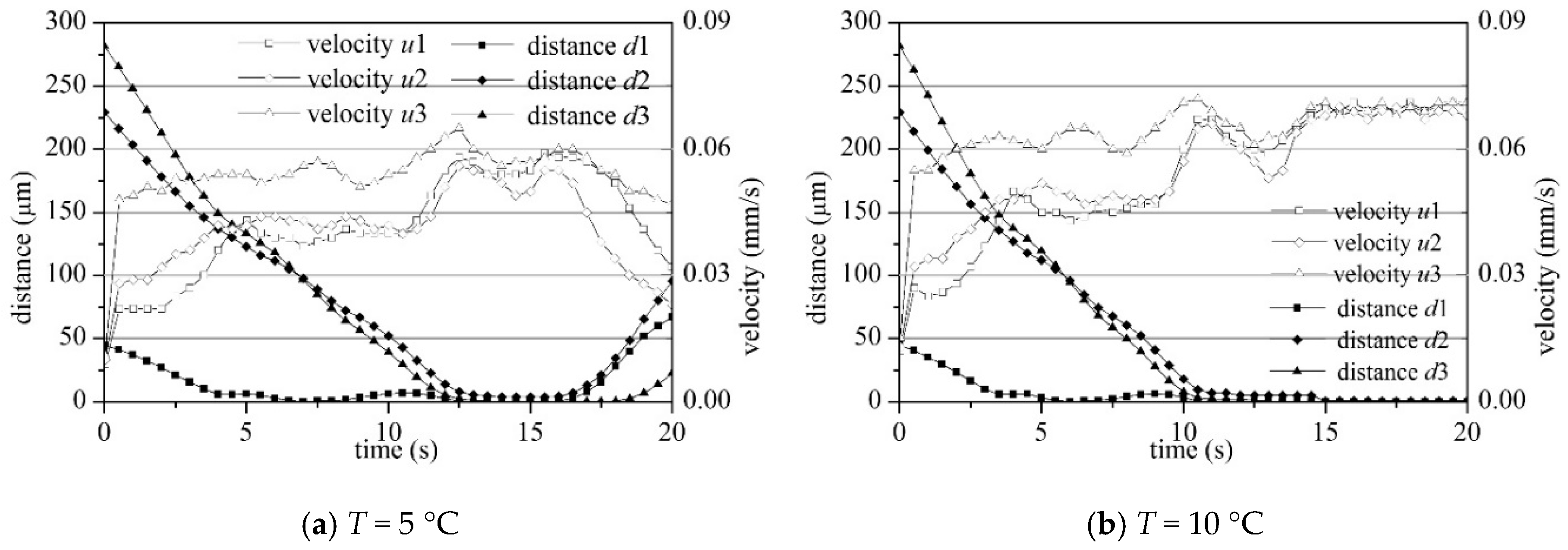
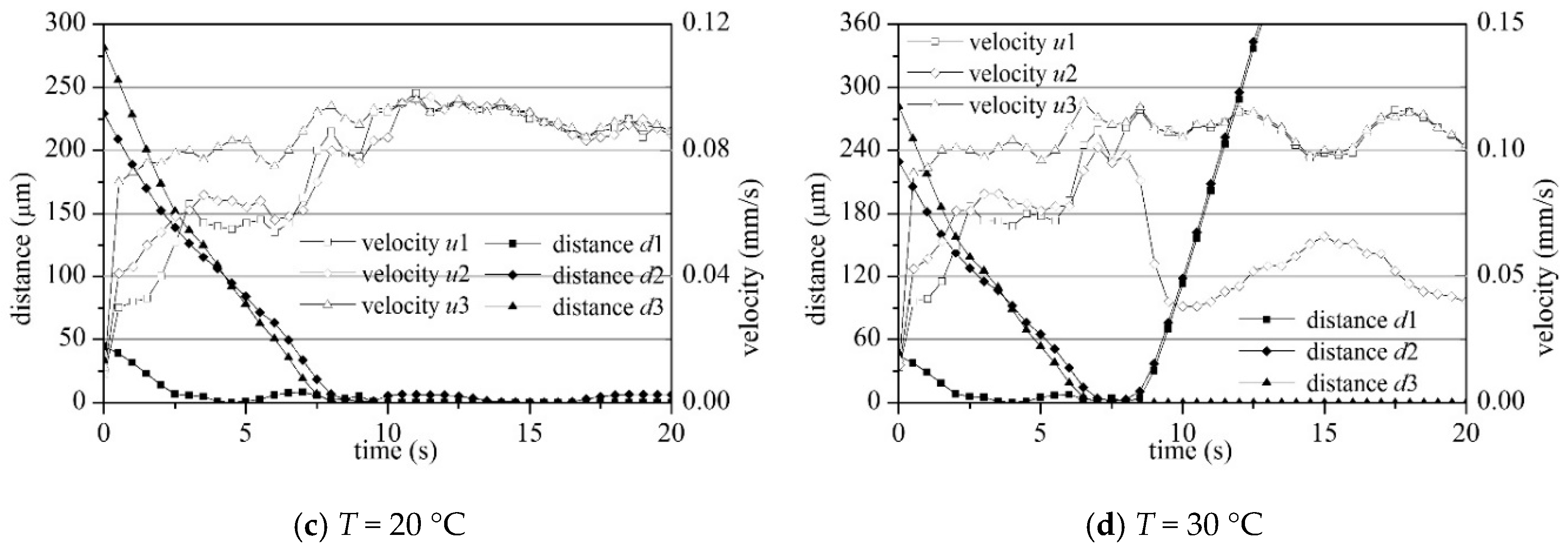
4.2. Settling and Flocculation Process
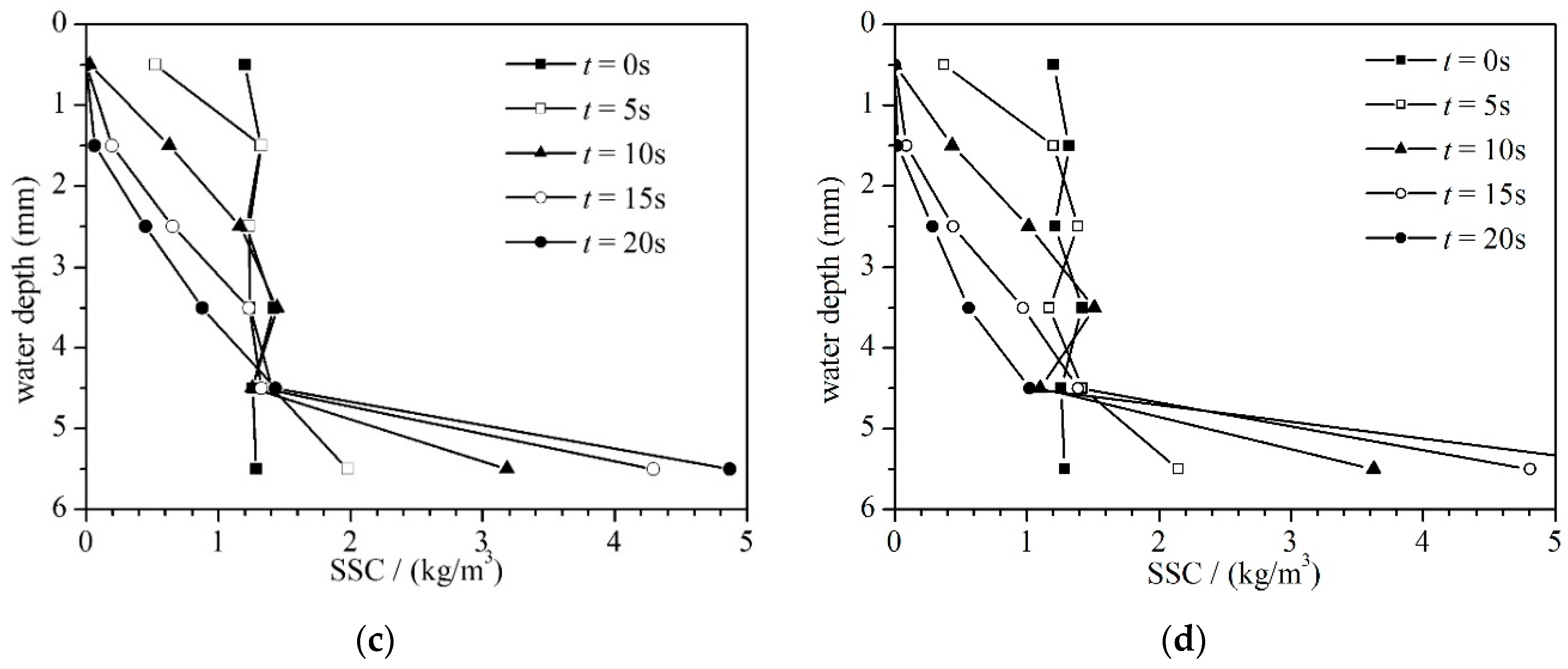
4.3. Suspended Sediment Concentration
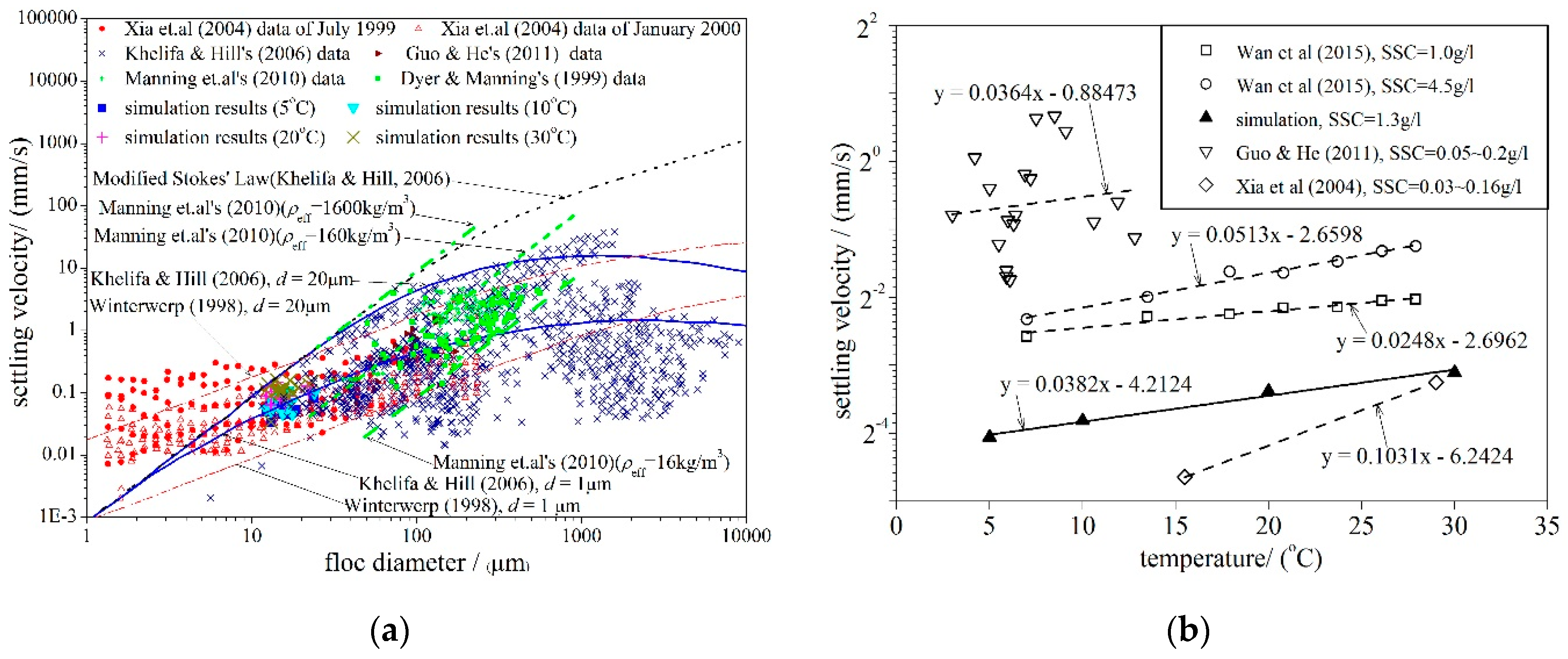
4.4. Sediment Settling Velocity
5. Discussion
6. Conclusions
- (1)
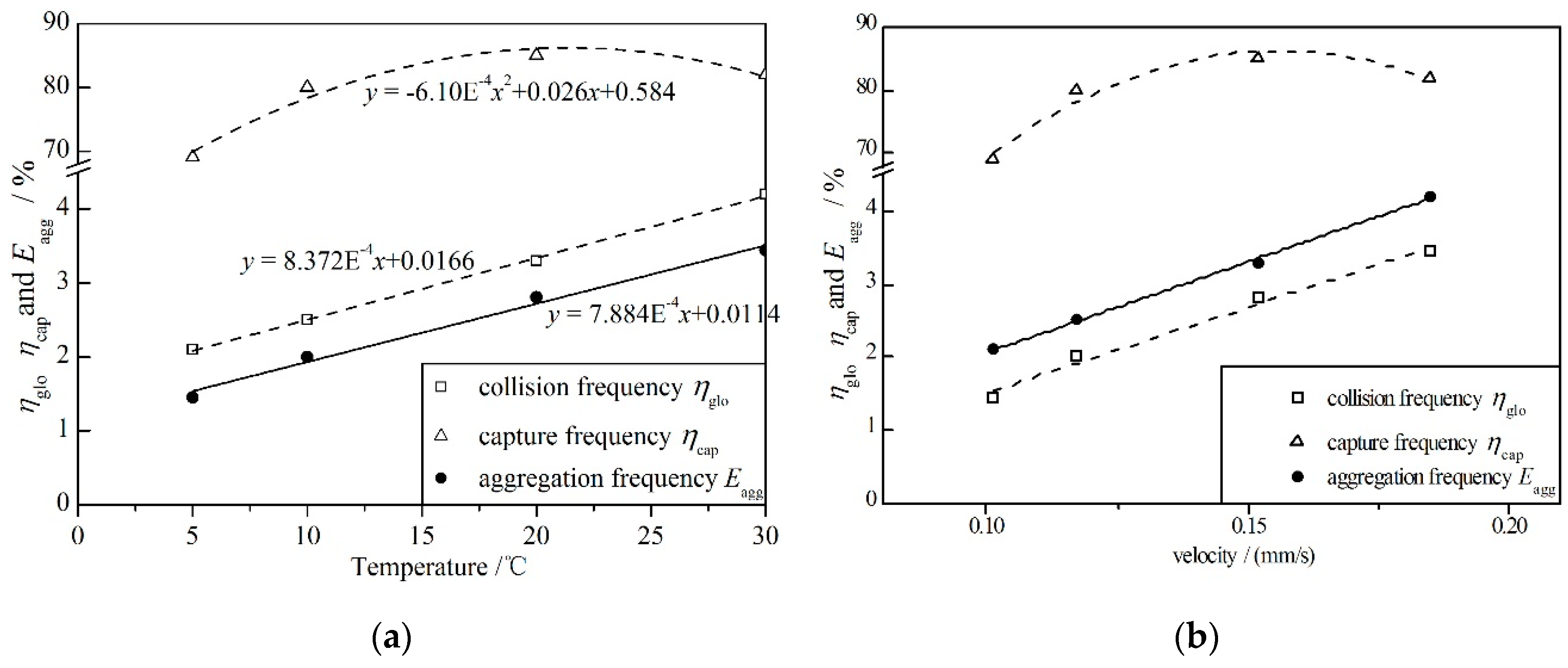
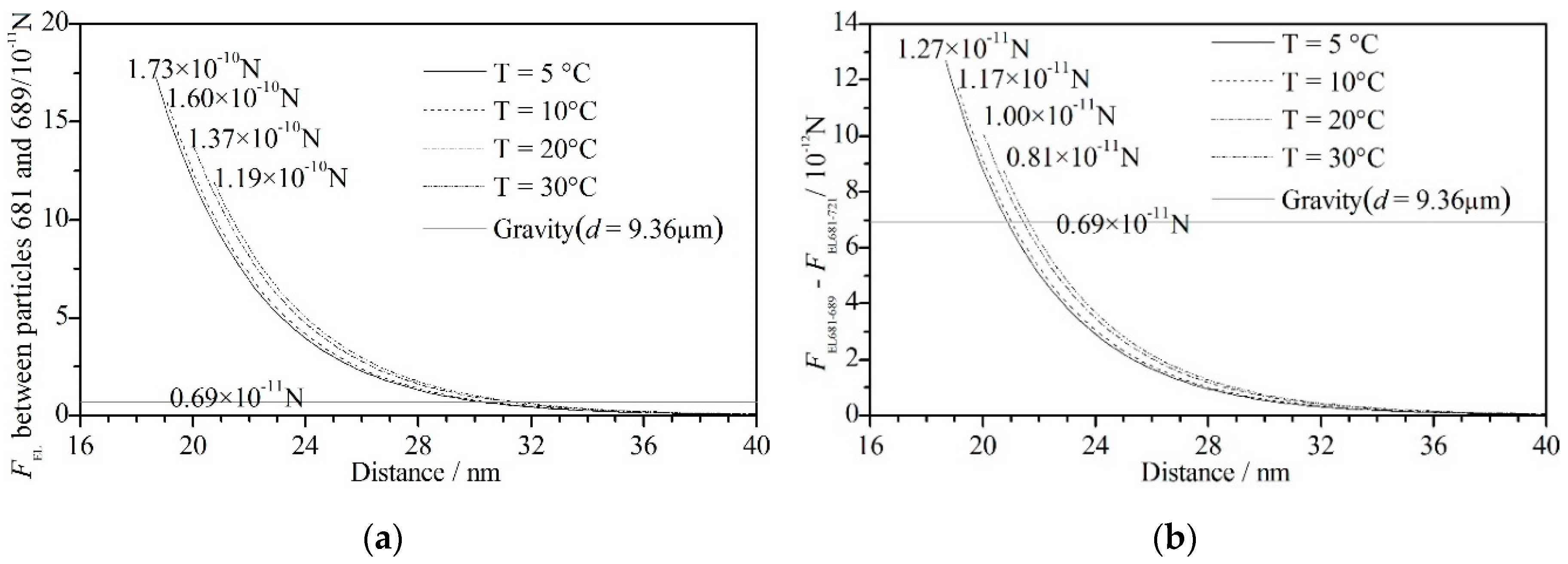
- The mean floc size and floc volume increased with increasing temperature. The maximum floc size initially increased and then decreased slightly with its peak at 10 °C and trough at 5 °C. The floc was not easily formed at low temperature but was unstable and cracked easily at high temperature. The aggregation process, aggregation frequency and forces between particles can be explained by the above. At low temperatures, the collision frequency ηglo and capture frequency ηcap were low, which meant the floc was not easily formed; at high temperatures, the large flocs were easily broken as the weighting of the macro force increased to have the same magnitude as the short-distance force.
- (2)
- During settling, the SSC time series curves fit well with the equation , from which the settlement half-life period and bulk setting velocity were deduced. Increasing the temperature had a negative effect on the settlement half-life, indicating a faster SSC incline at high temperatures than at low temperatures.
- (3)
- The macroscopic bulk velocity derived from the SSC change agreed well with the microscopic statistical settling velocity of each particle and floc. Both velocities agreed well with the existing physical test results, on-site observation data, and formulas, indicating that the LBM is a reasonable choice for simulating cohesive sediment bulk settling.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Winterwerp, J.C. On the flocculation and settling velocity of estuarine mud. Cont. Shelf Res. 2002, 22, 1339–1360. [Google Scholar] [CrossRef]
- Mietta, F.; Chassagne, C.; Manning, A.J.; Winterwerp, J.C. Influence of shear rate, organic matter content, ph and salinity on mud flocculation. Ocean Dyn. 2009, 59, 751–763. [Google Scholar] [CrossRef]
- Ha, H.K.; Maa, J.P.Y. Effects of suspended sediment concentration and turbulence on settling velocity of cohesive sediment. Geosci. J. 2010, 14, 163–171. [Google Scholar] [CrossRef]
- Jiang, G.; Zhou, H.; Ruan, W.; Yao, S.; Zhang, Z.; Zhao, L. Influence of water temperature on mud particle deposition—Laboratory tests. J. Coast. Res. 2004, 20, 59–66. [Google Scholar]
- Etemad-shahidi, A.; Shahkolahi, A.; Liu, W.C. Modeling of hydrodynamics and cohesive sediment processes in an estuarine system: Study case in Danshui river. Environ. Model. Assess. 2010, 15, 261–271. [Google Scholar] [CrossRef]
- Wan, Y.; Wu, H.; Roelvink, D.; Gu, F. Experimental study on fall velocity of fine sediment in the Yangtze Estuary, China. Ocean Eng. 2015, 103, 180–187. [Google Scholar] [CrossRef]
- Dickhudt, P.J.; Friedrichs, C.T.; Schaffner, L.C.; Sanford, L.P. Spatial and temporal variation in cohesive sediment erodibility in the York River estuary, eastern USA: A biologically influenced equilibrium modified by seasonal deposition. Mar. Geol. 2009, 267, 128–140. [Google Scholar] [CrossRef]
- Lau, Y.L. Temperature effect on settling velocity and deposition of cohesive sediments. J. Hydraul. Res. 1994, 32, 41–51. [Google Scholar] [CrossRef]
- Owen, M.W. The Effect of Temperature on the Settling Velocities of an Estuary Mud; Hydraulics Research Station Report, No. INT 106; Hydraulics Research Station: Wallingford, UK, 1972. [Google Scholar]
- Lee, B.J.; Fettweis, M.; Toorman, E.; Molz, F.J. Multimodality of a particle size distribution of cohesive suspended particulate matters in a coastal zone. J. Geophys. Res. Oceans. 2012, 117, C03014. [Google Scholar] [CrossRef]
- Andersen, T.J.; Pejrup, M. Biological mediation of the settling velocity of bed material eroded from an intertidal mudflat, the Danish Wadden Sea. Estuar. Coast. Shelf Sci. 2002, 54, 737–745. [Google Scholar] [CrossRef]
- Xia, X.M.; Li, Y.; Yang, H.; Wu, C.Y.; Sing, T.H.; Pong, H.K. Observations on the size and settling velocity distributions of suspended sediment in the Pearl River Estuary, China. Cont. Shelf Res. 2004, 24, 1809–1826. [Google Scholar] [CrossRef]
- Guo, L.; He, Q. Freshwater flocculation of suspended sediments in the Yangtze River, china. Ocean Dyn. 2011, 61, 371–386. [Google Scholar] [CrossRef]
- Winterwerp, J.C.; Van Kesteren, W.G.M. Introduction to the Physics of Cohesive Sediment in the Marine Environment; Elsevier: Amsterdam, The Netherlands, 2004; ISBN 0-444-51553-4. [Google Scholar]
- Grabowski, R.C.; Droppo, I.G.; Wharton, G. Erodibility of cohesive sediment: The importance of sediment properties. Earth Sci. Rev. 2011, 105, 101–120. [Google Scholar] [CrossRef]
- Khelifa, A.; Hill, P.S. Models for effective density and settling velocity of flocs. J. Hydraul. Res. 2006, 44, 390–401. [Google Scholar] [CrossRef]
- Manning, A.J.; Dyer, K.R. Mass settling flux of fine sediments in Northern European estuaries: Measurements and predictions. Mar. Geol. 2007, 245, 107–122. [Google Scholar] [CrossRef]
- Baugh, J.V.; Manning, A.J. An assessment of a new settling velocity parameterisation for cohesive sediment transport modeling. Cont. Shelf Res. 2007, 27, 1835–1855. [Google Scholar] [CrossRef]
- Markussen, T.N.; Andersen, T.J. A simple method for calculating in situ floc settling velocities based on effective density functions. Mar. Geol. 2013, 344, 10–18. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Q. Hydrodynamics of fractal flocs during settling. J. Hydrodyn. Ser. B 2009, 21, 347–351. [Google Scholar] [CrossRef]
- Tang, S.; Preece, J.M.; McFarlane, C.M.; Zhang, Z. Fractal morphology and breakage of DLCA and RLCA aggregates. J. Colloid Interface Sci. 2000, 221, 114–123. [Google Scholar] [CrossRef]
- Weber-Shirk, M.L.; Lion, L.W. Flocculation model and collision potential for reactors with flows characterized by high Peclet numbers. Water Res. 2010, 44, 5180–5187. [Google Scholar] [CrossRef] [PubMed]
- Maerz, J.; Verney, R.; Kai, W.; Feudel, U. Modeling flocculation processes: Intercomparison of a size class-based model and a distribution-based model. Cont. Shelf Res. 2011, 31, S84–S93. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, H.; Jiang, Z.; Huang, X.; Li, H.; Li, A.; Cheng, R. A new method for calculation of flocculation kinetics combining Smoluchowski model with fractal theory. Colloids Surf. A Physicochem. Eng. Asp. 2013, 423, 11–19. [Google Scholar] [CrossRef]
- Zhang, J.F.; Maa, P.Y.; Zhang, Q.H.; Shen, X.T. Direct numerical simulations of collision efficiency of cohesive sediments. Estuar. Coast. Shelf Sci. 2016, 178, 92–100. [Google Scholar] [CrossRef]
- Qiao, G.Q.; Zhang, J.F.; Zhang, Q.H. Study on the influence of temperature to cohesive sediment flocculation. J. Sediment Res. 2017, 42, 35–40. (In Chinese) [Google Scholar]
- Ladd, A.J.C. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J. Fluid Mech. 1994, 271, 285–310. [Google Scholar] [CrossRef]
- Ladd, A.J.C. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 2. Numerical results. J. Fluid Mech. 1994, 271, 311–339. [Google Scholar] [CrossRef]
- Ladd, A.J.C.; Verberg, R. Lattice-Boltzmann simulations of particle-fluid suspensions. J. Stat. Phys. 2001, 104, 1191–1251. [Google Scholar] [CrossRef]
- Nguyen, N.Q.; Ladd, A.J. Lubrication corrections for Lattice-Boltzmann simulations of particle suspensions. Phys. Rev. E. 2002, 66, 046708. [Google Scholar] [CrossRef]
- Zhang, J.F.; Zhang, Q.H. Lattice Boltzmann simulation of the flocculation process of cohesive sediment due to differential settling. Cont. Shelf Res. 2009, 31, S94–S105. [Google Scholar] [CrossRef]
- Zhang, J.F.; Zhang, Q.H.; Qiao, G.Q. A lattice Boltzmann model for the non-equilibrium flocculation of cohesive sediments in turbulent flow. Comput. Math. Appl. 2014, 67, 381–392. [Google Scholar]
- Van Oss, C.J. Interfacial Forces in Aqueous Media; CRC Press: Boca Raton, FL, USA, 1994; ISBN 978-1420015768. [Google Scholar]
- Hoek, E.M.V.; Agarwal, G.K. Extended DLVO interactions between spherical particles and rough surfaces. J. Colloid Interface Sci. 2006, 298, 50–58. [Google Scholar] [CrossRef] [PubMed]
- Qiao, G.Q.; Zhang, Q.H.; Zhang, J.F.; Cheng, H.J.; Lu, Z. Lattice Boltzmann model of cohesive sediment flocculation simulation based on the XDLVO theory. J. Tianjin Univ. 2013, 46, 232–238. (In Chinese) [Google Scholar]
- Vinogradov, J.; Jackson, M.D. Zeta potential in intact natural sandstones at elevated temperatures. Geophys. Res. Lett. 2015, 42, 6287–6294. [Google Scholar] [CrossRef]
- Yang, T.S.; Xiong, X.Z.; Zhan, X.L.; Yang, M.Q. The study on slipping water layers of cohesive sediment particles. J. Hydraul. Eng. 2002, 33, 20–26. (In Chinese) [Google Scholar]
- Sondi, I.; Bišćan, J.; Pravdić, V. Electrokinetics of pure clay minerals revisited. J. Colloid Interface Sci. 1996, 178, 514–522. [Google Scholar] [CrossRef]
- Tenth Report of the Joint Panel on Oceanographic Tables and Standards, Sidney, B.C. Canada, 1–5 September 1980; UNESCO Technical Papers in Marine Science No. 36; UNESCO: Paris, France, 1981.
- Chen, H.S.; Shao, M.A. Effect of NaCl concentration on dynamic model of fine sediment flocculation and settling in still water. J. Hydraul. Eng. 2002, 8, 63–67. (In Chinese) [Google Scholar]
- You, Z.J. The effect of suspended sediment concentration on the settling velocity of cohesive sediment in quiescent water. Ocean Eng. 2004, 31, 1955–1965. [Google Scholar] [CrossRef]
- Dyer, K.R.; Manning, A.J. Observation of the size, settling velocity and effective density of flocs, and their fractal dimensions. J. Sea. Res. 1999, 41, 87–95. [Google Scholar] [CrossRef]
- Manning, A.J.; Langston, W.J.; Jonas, P.J.C. A review of sediment dynamics in the Severn Estuary: Influence of flocculation. Mar. Pollut. Bull. 2010, 61, 37–51. [Google Scholar] [CrossRef]
- Winterwerp, J.C. A Simple Model for Turbulence Induced Flocculation of Cohesive Sediment. J. Hydraul. Res. 1998, 36, 309–326. [Google Scholar] [CrossRef]
- Kim, A.S.; Stolzenbach, K.D. Aggregate formation and collision efficiency in differential settling. J. Colloid Interface Sci. 2004, 271, 110–119. [Google Scholar] [CrossRef] [PubMed]
- Sterling, M.C., Jr.; Bonner, J.S.; Ernest, A.N.S.; Page, C.A.; Autenrieth, R.L. Application of fractal flocculation and vertical transport model to aquatic sol-sediment systems. Water Res. 2005, 39, 1818–1830. [Google Scholar] [CrossRef]


| Case ID | #1 | #2 | #3 | #4 |
|---|---|---|---|---|
| Temperature/(°C) | 5 | 10 | 20 | 30 |
| 2δ/(nm) | 18.7 | 19.1 | 20.0 | 20.7 |
| Water viscosity ν/(10−6 m2 s−1) | 1.52 | 1.31 | 1.00 | 0.80 |
| Temperature/(°C) | 5 | 10 | 20 | 30 |
|---|---|---|---|---|
| (1) velocity 1 v1/(mm/s) | 0.099 | 0.117 | 0.155 | 0.189 |
| (2) velocity 2 v2/(mm/s) | 0.101 | 0.117 | 0.152 | 0.185 |
| (3) ABS(1-2) |v1−v2|/(mm/s) | 0.002 | 0.000 | 0.003 | 0.004 |
| (4) |v1−v2|/(|v1+v2|/2)/(%) | 2.0% | 0.0% | 2.0% | 2.1% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, G.-q.; Zhang, J.-f.; Zhang, Q.-h.; Feng, X.; Lu, Y.-c.; Feng, W.-b. The Influence of Temperature on the Bulk Settling of Cohesive Sediment in Still Water with the Lattice Boltzmann Method. Water 2019, 11, 945. https://doi.org/10.3390/w11050945
Qiao G-q, Zhang J-f, Zhang Q-h, Feng X, Lu Y-c, Feng W-b. The Influence of Temperature on the Bulk Settling of Cohesive Sediment in Still Water with the Lattice Boltzmann Method. Water. 2019; 11(5):945. https://doi.org/10.3390/w11050945
Chicago/Turabian StyleQiao, Guang-quan, Jin-feng Zhang, Qing-he Zhang, Xi Feng, Yong-chang Lu, and Wei-bing Feng. 2019. "The Influence of Temperature on the Bulk Settling of Cohesive Sediment in Still Water with the Lattice Boltzmann Method" Water 11, no. 5: 945. https://doi.org/10.3390/w11050945
APA StyleQiao, G.-q., Zhang, J.-f., Zhang, Q.-h., Feng, X., Lu, Y.-c., & Feng, W.-b. (2019). The Influence of Temperature on the Bulk Settling of Cohesive Sediment in Still Water with the Lattice Boltzmann Method. Water, 11(5), 945. https://doi.org/10.3390/w11050945





