Impact of Urban Stormwater Runoff on Cyanobacteria Dynamics in A Tropical Urban Lake
Abstract
1. Introduction
2. Materials and Methods
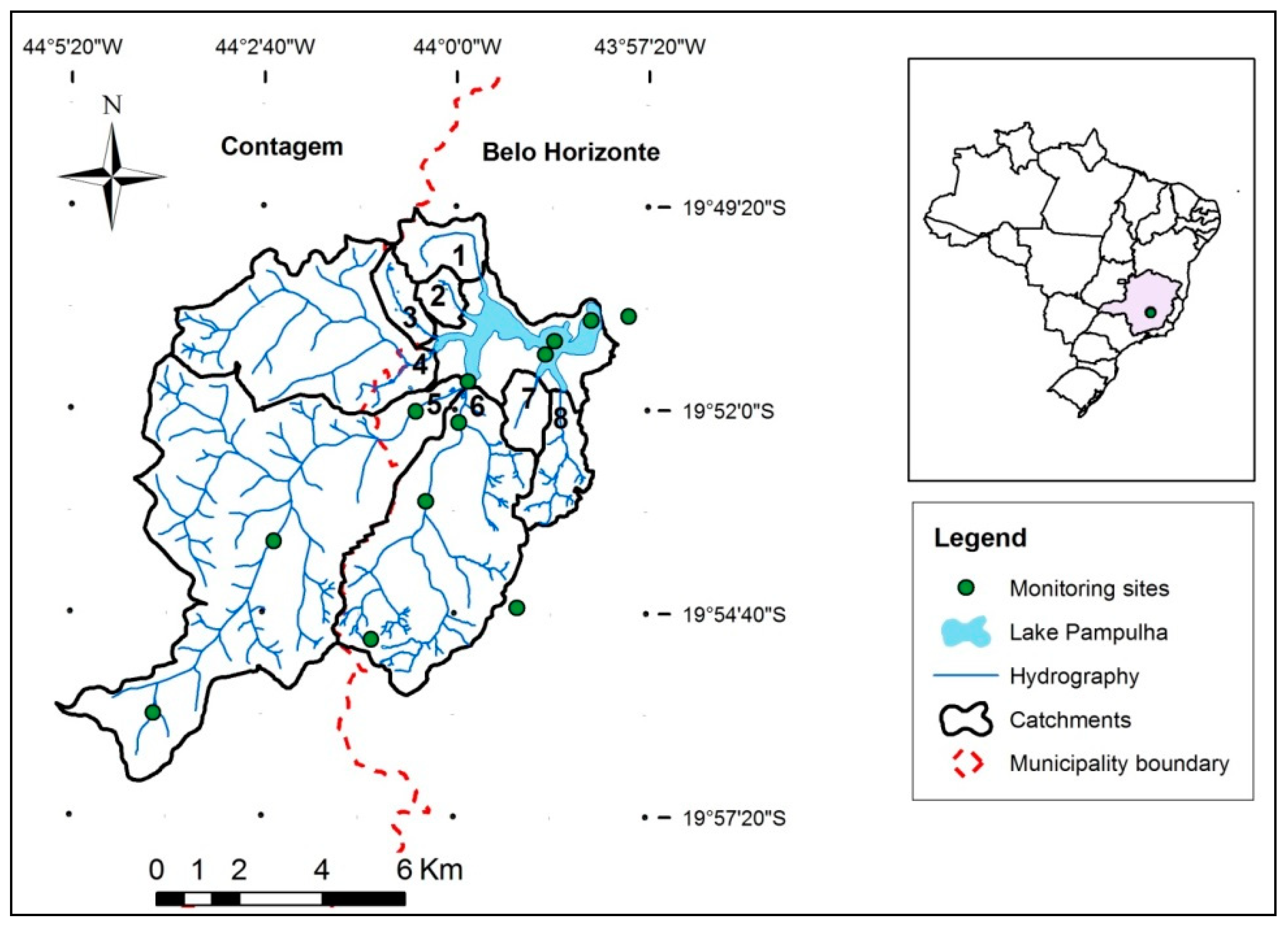
2.1. Study Site
2.2. Monitoring and Data Collection
2.2.1. Catchment Monitoring
2.2.2. Lake Monitoring
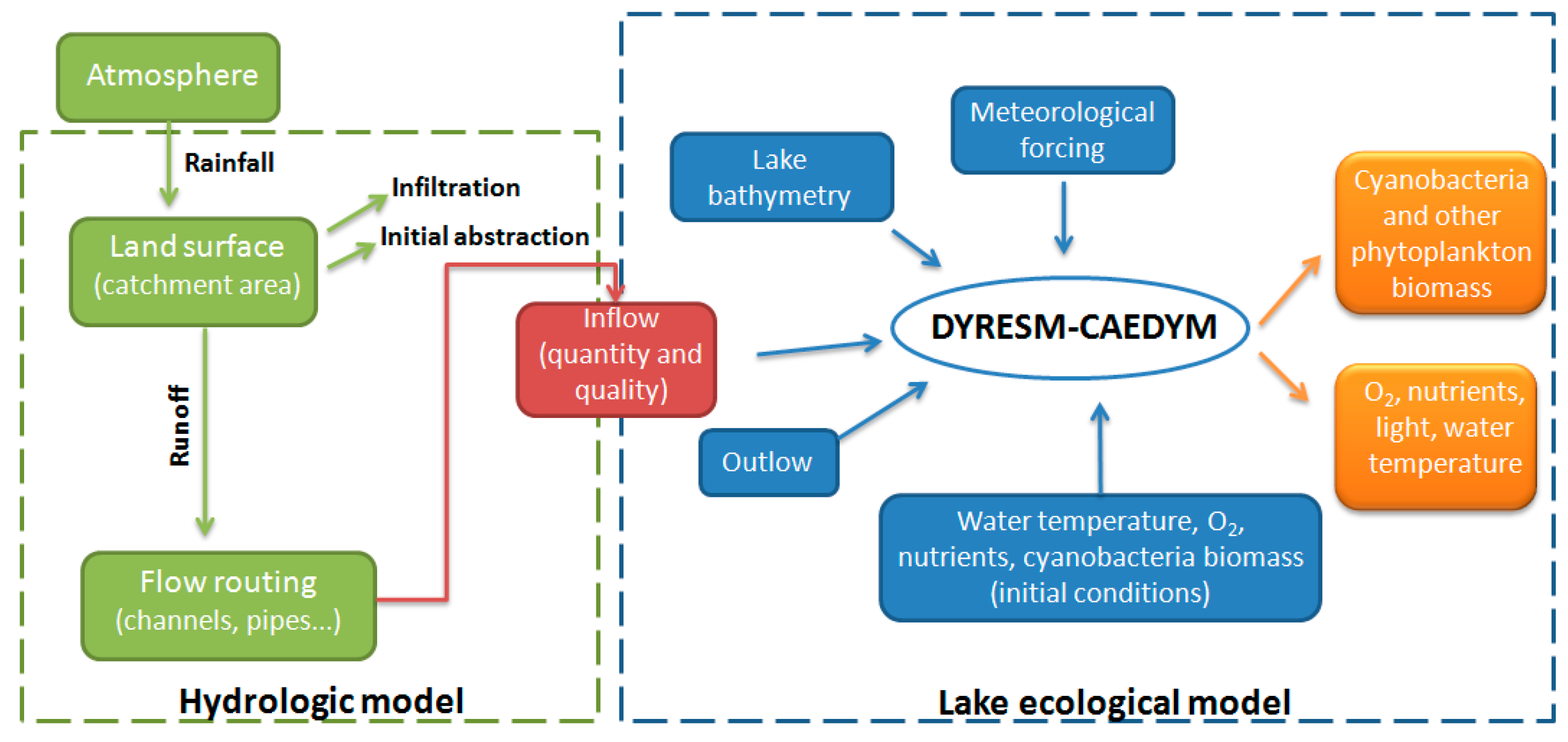
2.3. Catchment Model
2.4. Phytoplankton Dynamics Model
2.4.1. Configuration, Calibration and Validation of the Phytoplankton Dynamics Model
2.5. Integrating Catchment Model to Phytoplankton Dynamics Model
2.6. Scenarios of Catchment Changes
3. Results
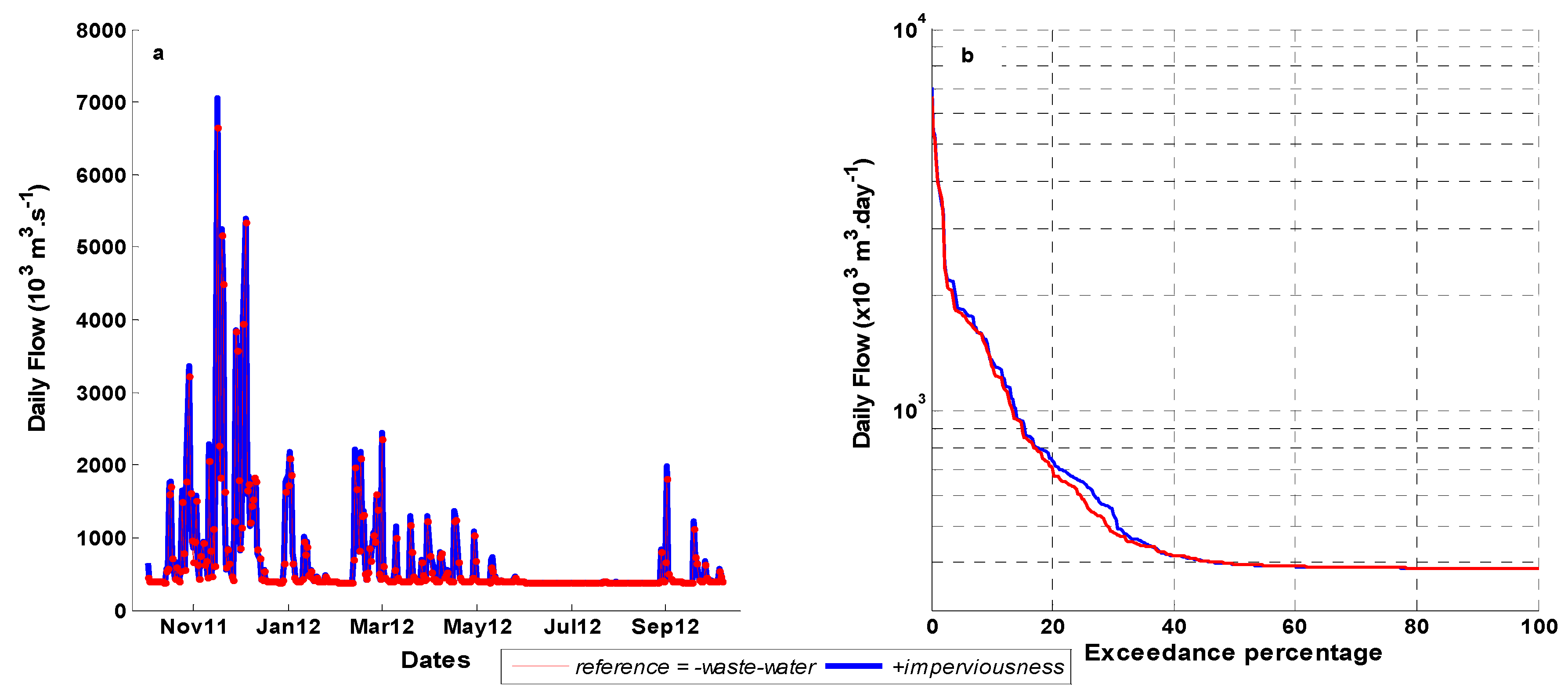
3.1. Runoff Water Quality Model
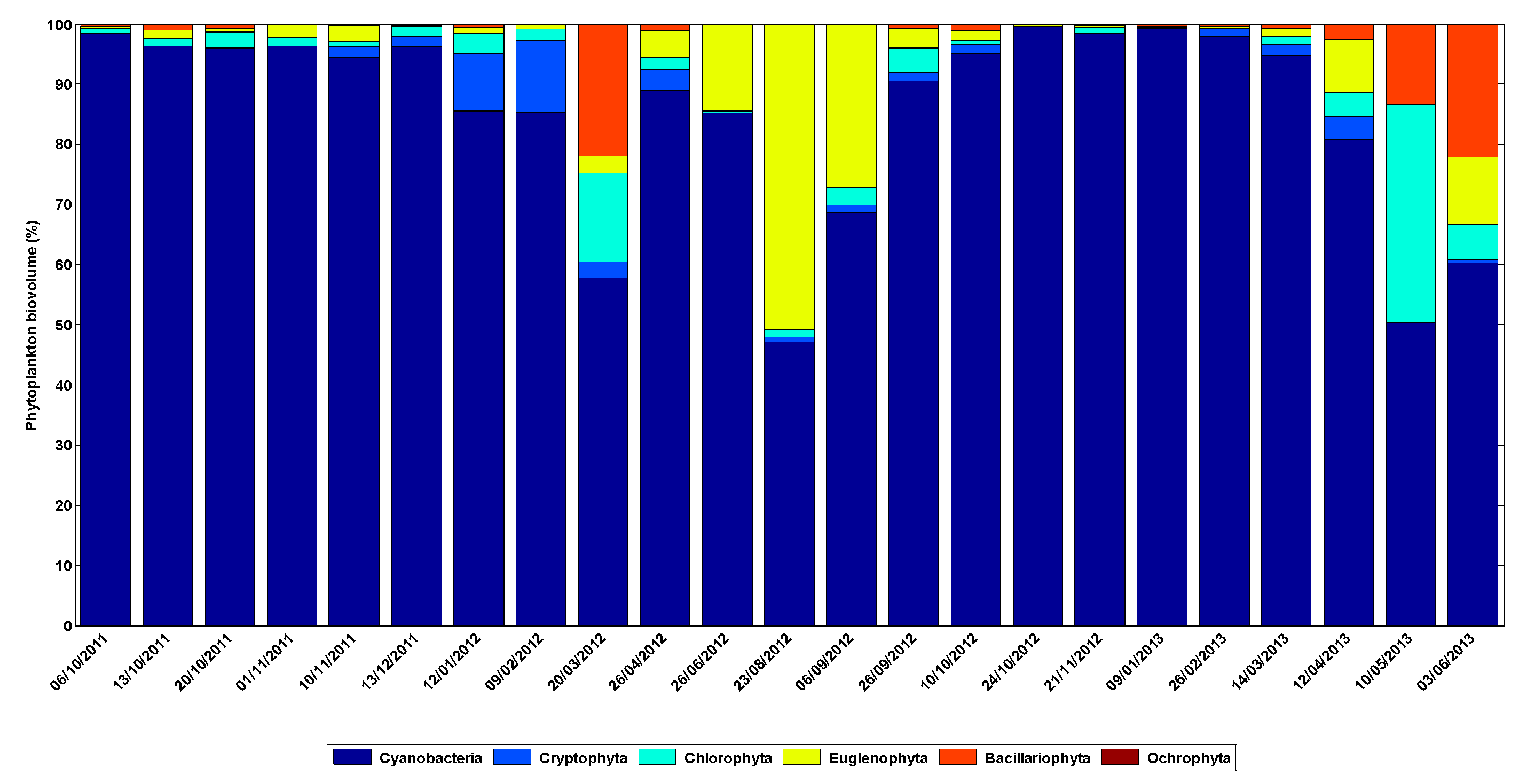
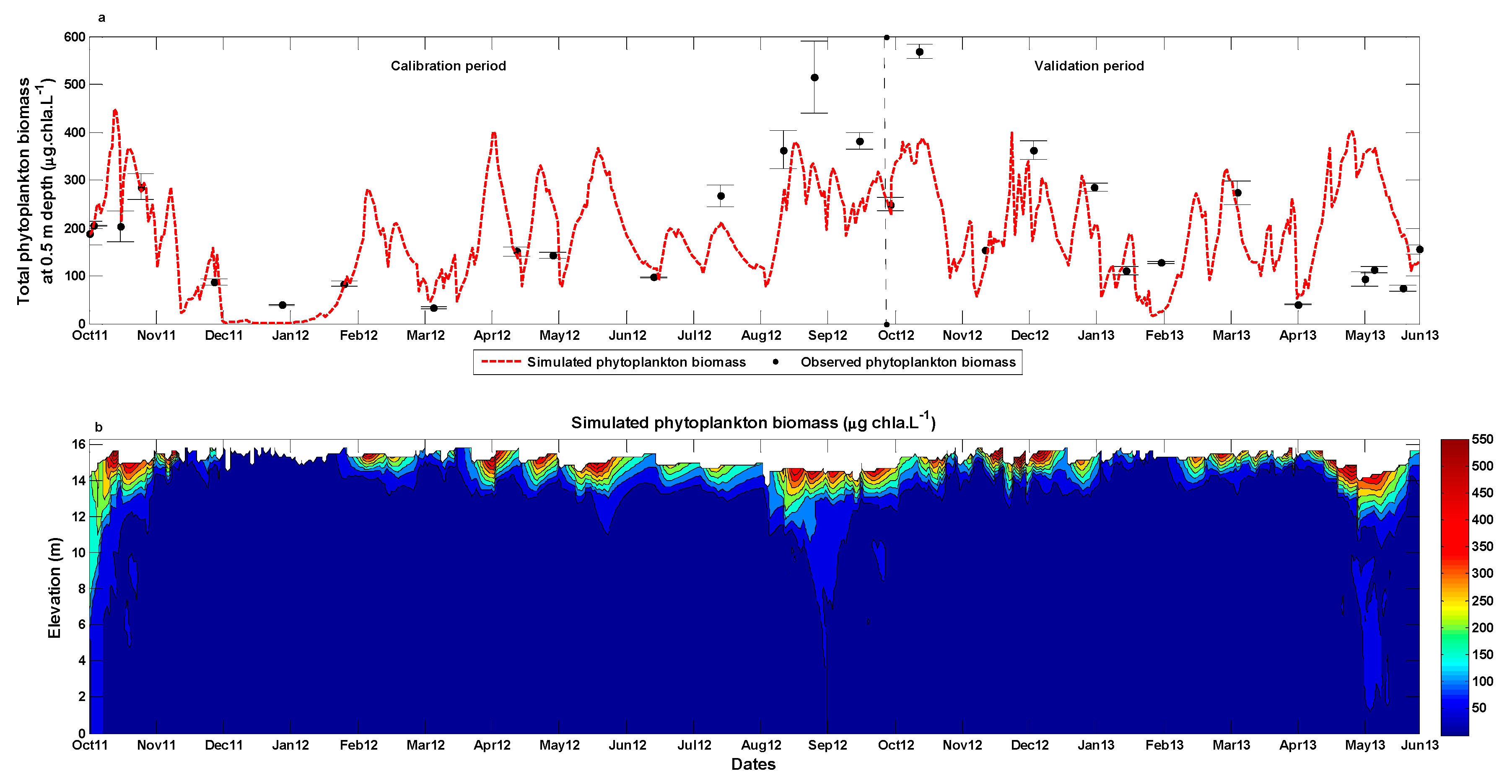
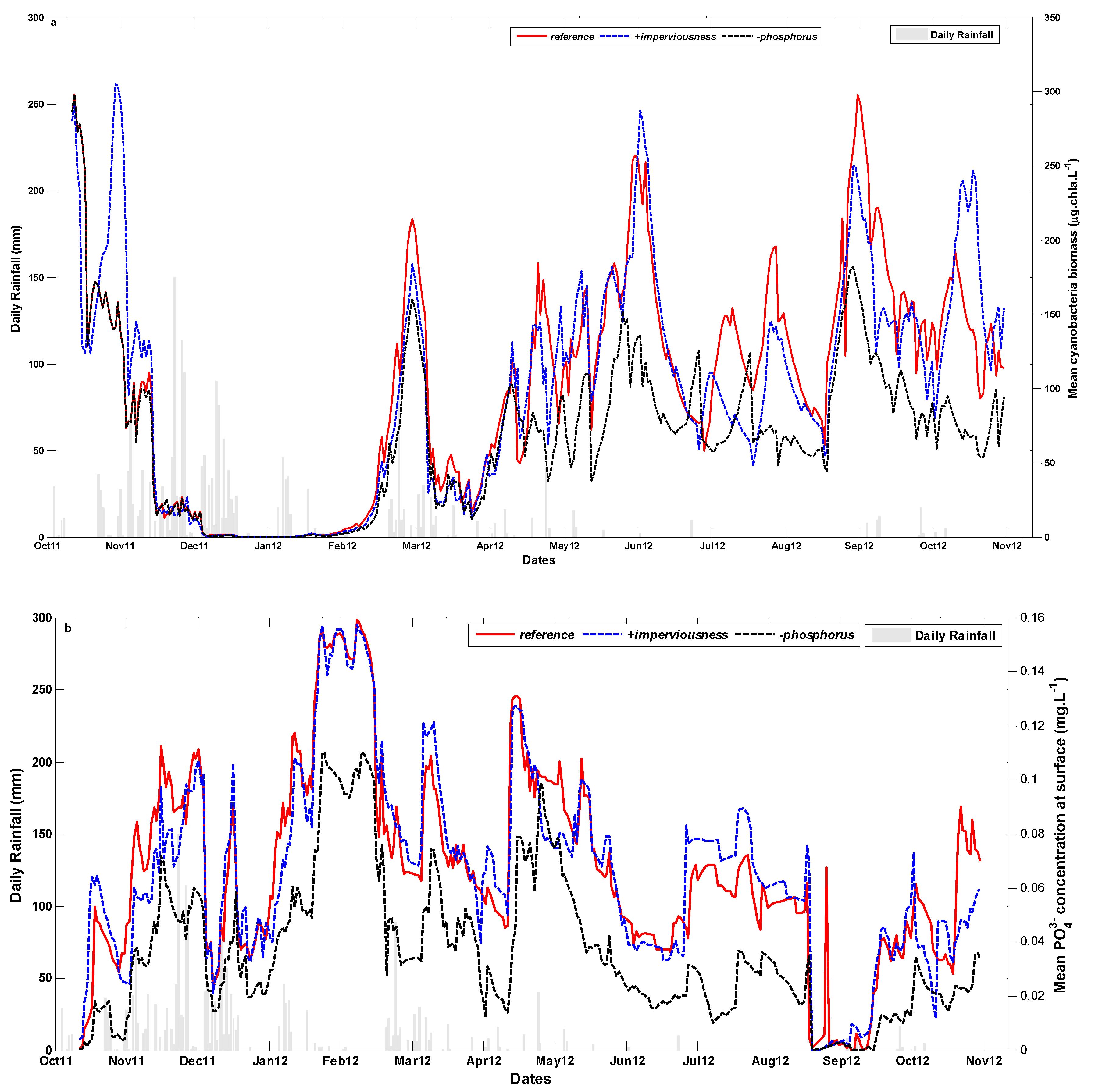
3.2. Phytoplankton Dynamics Modelling
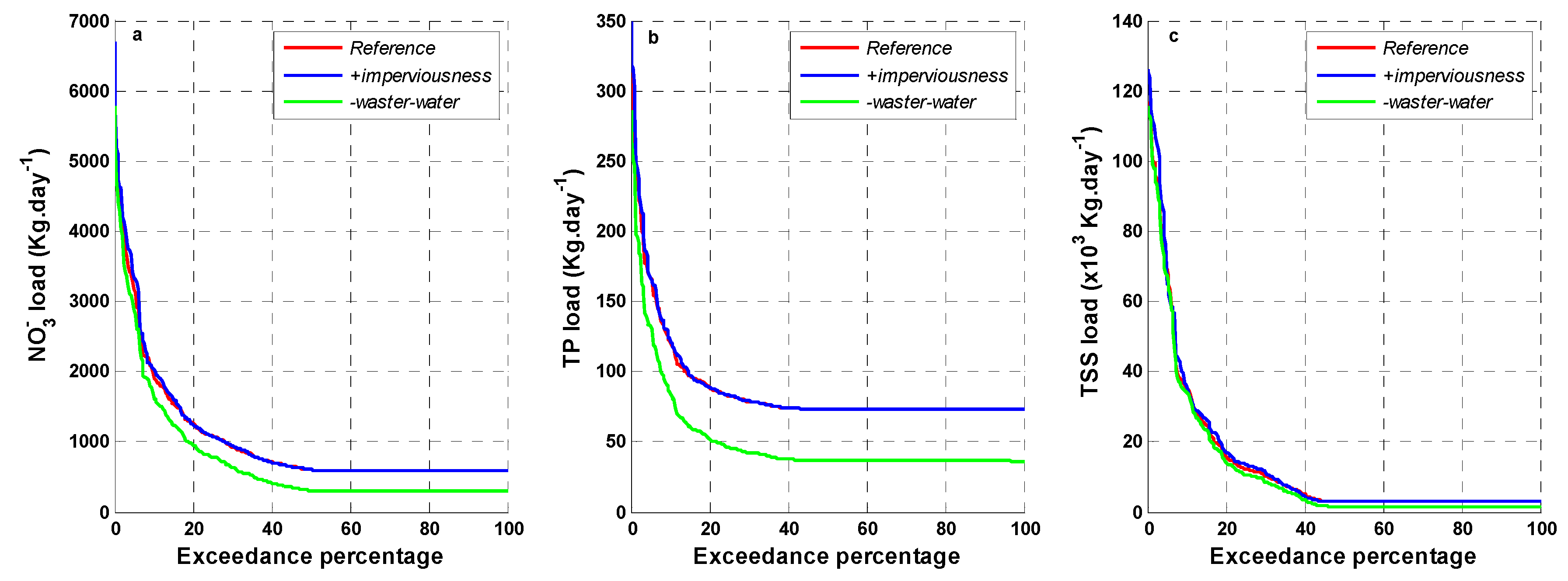
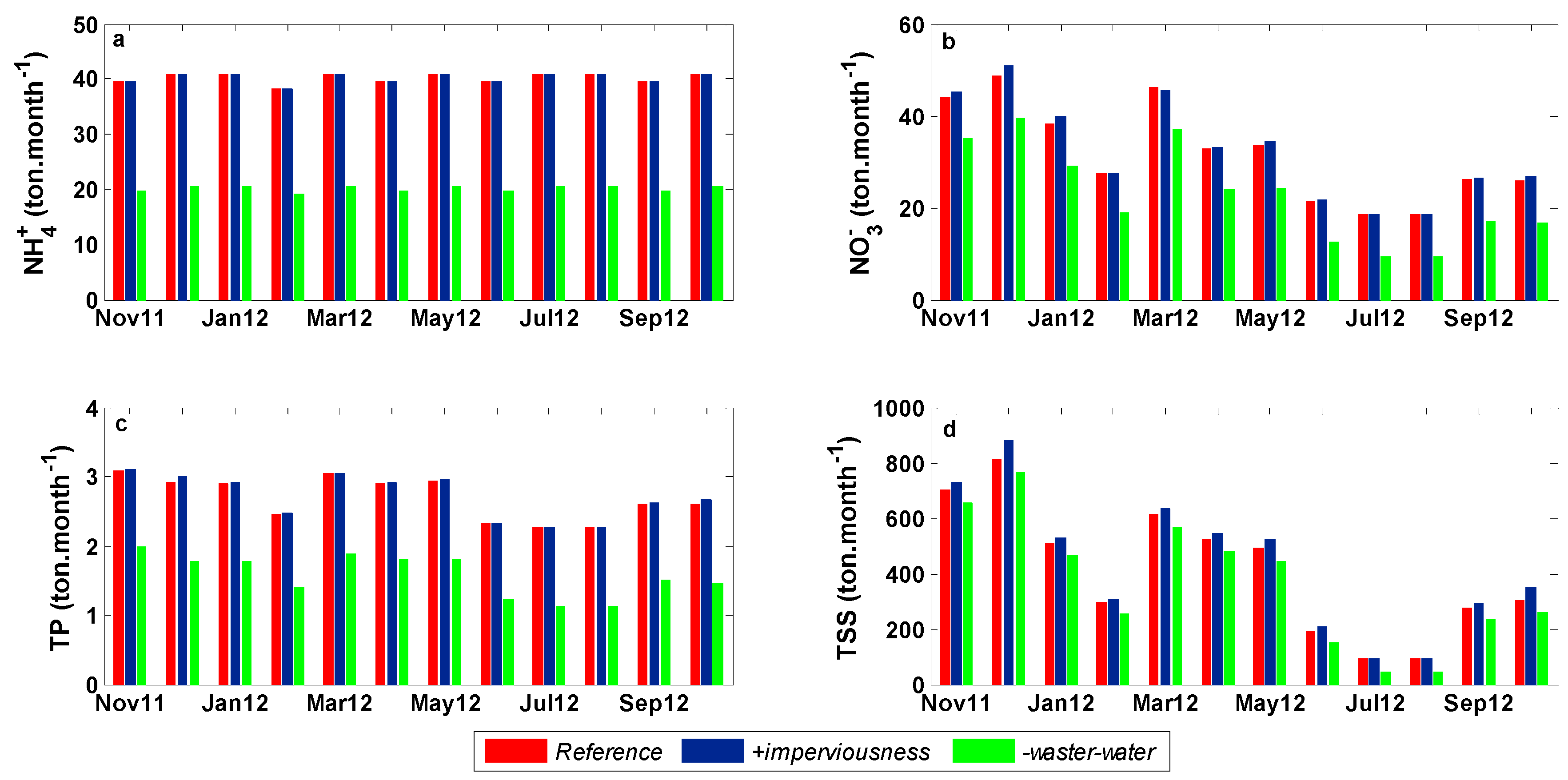
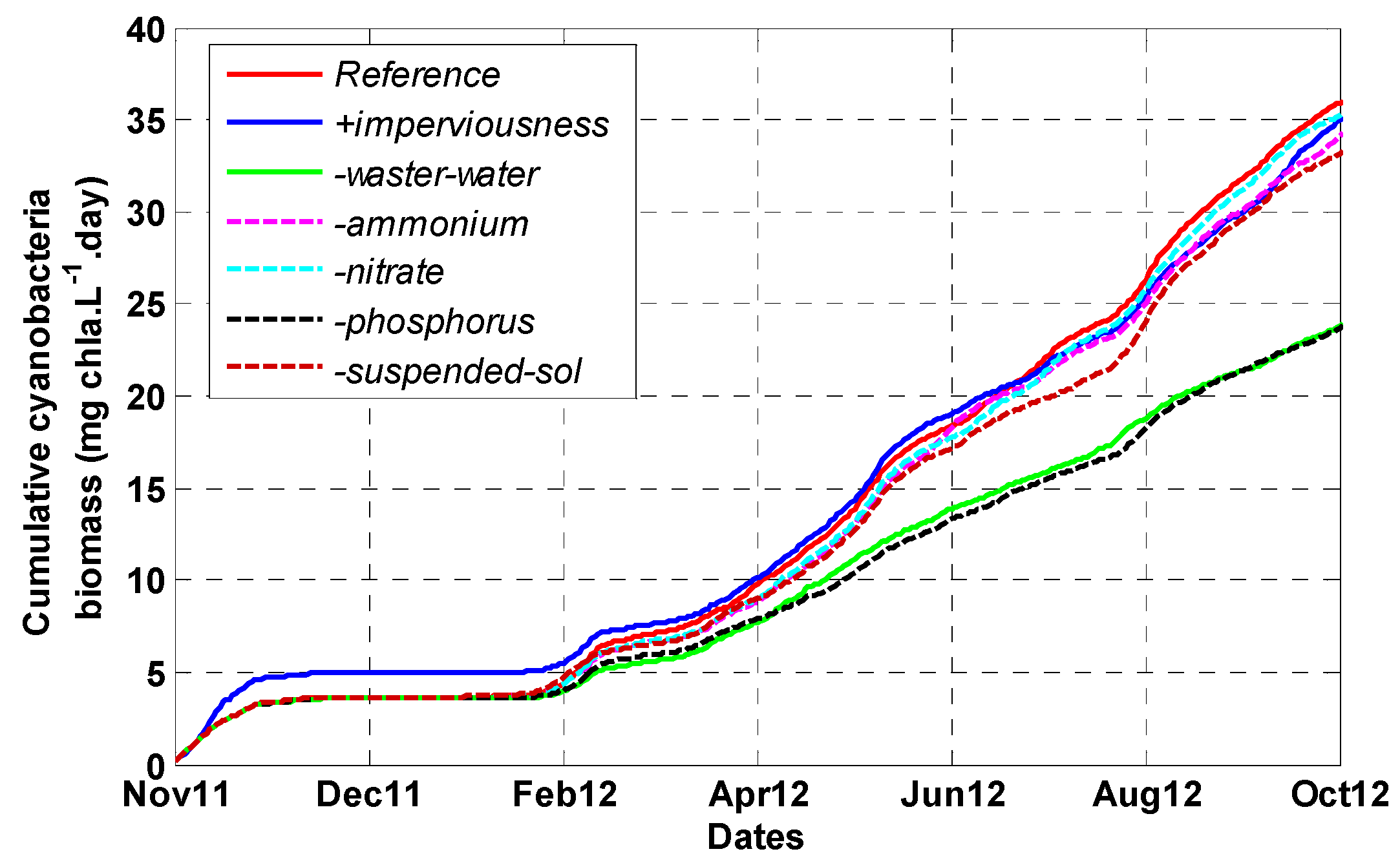
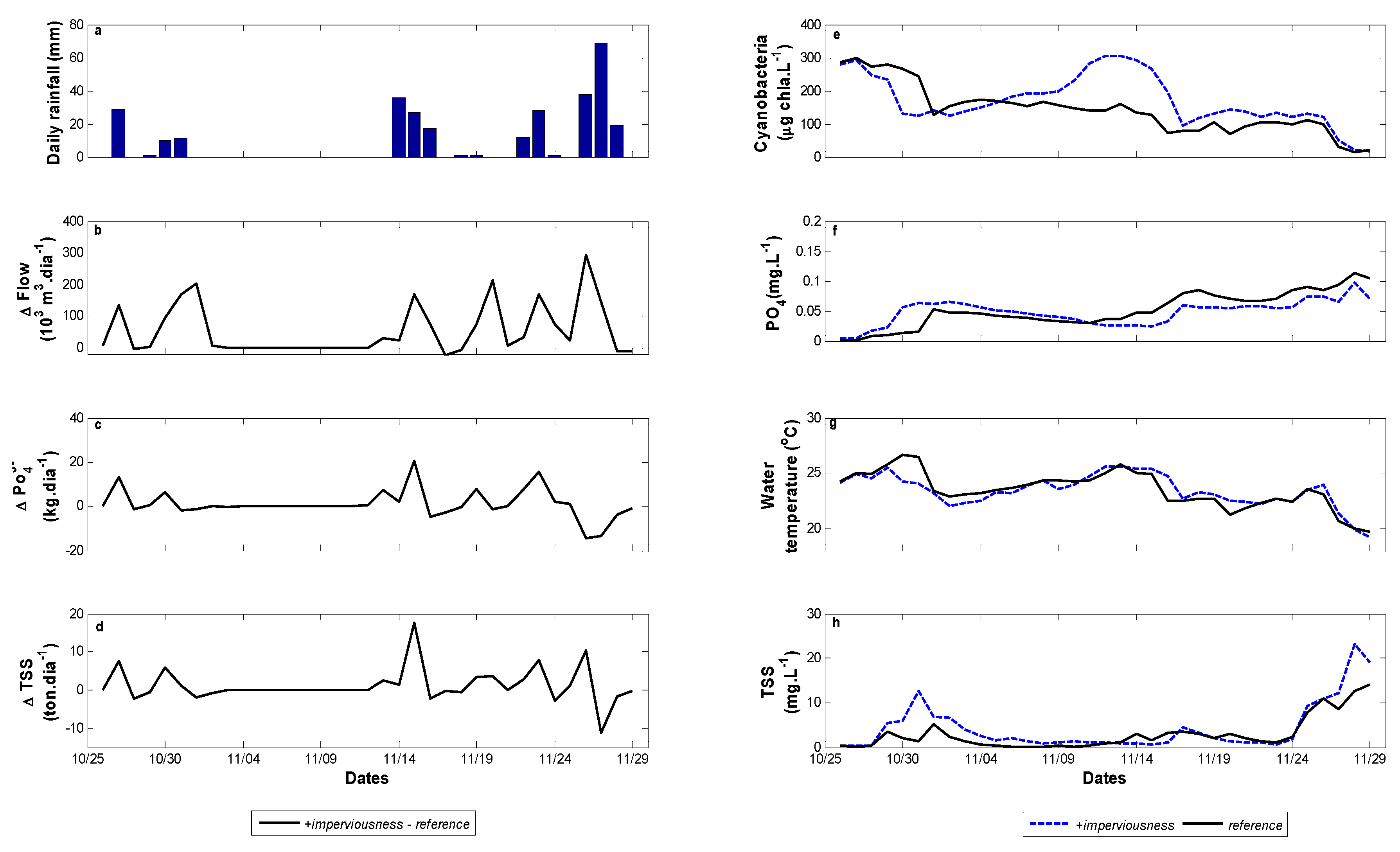
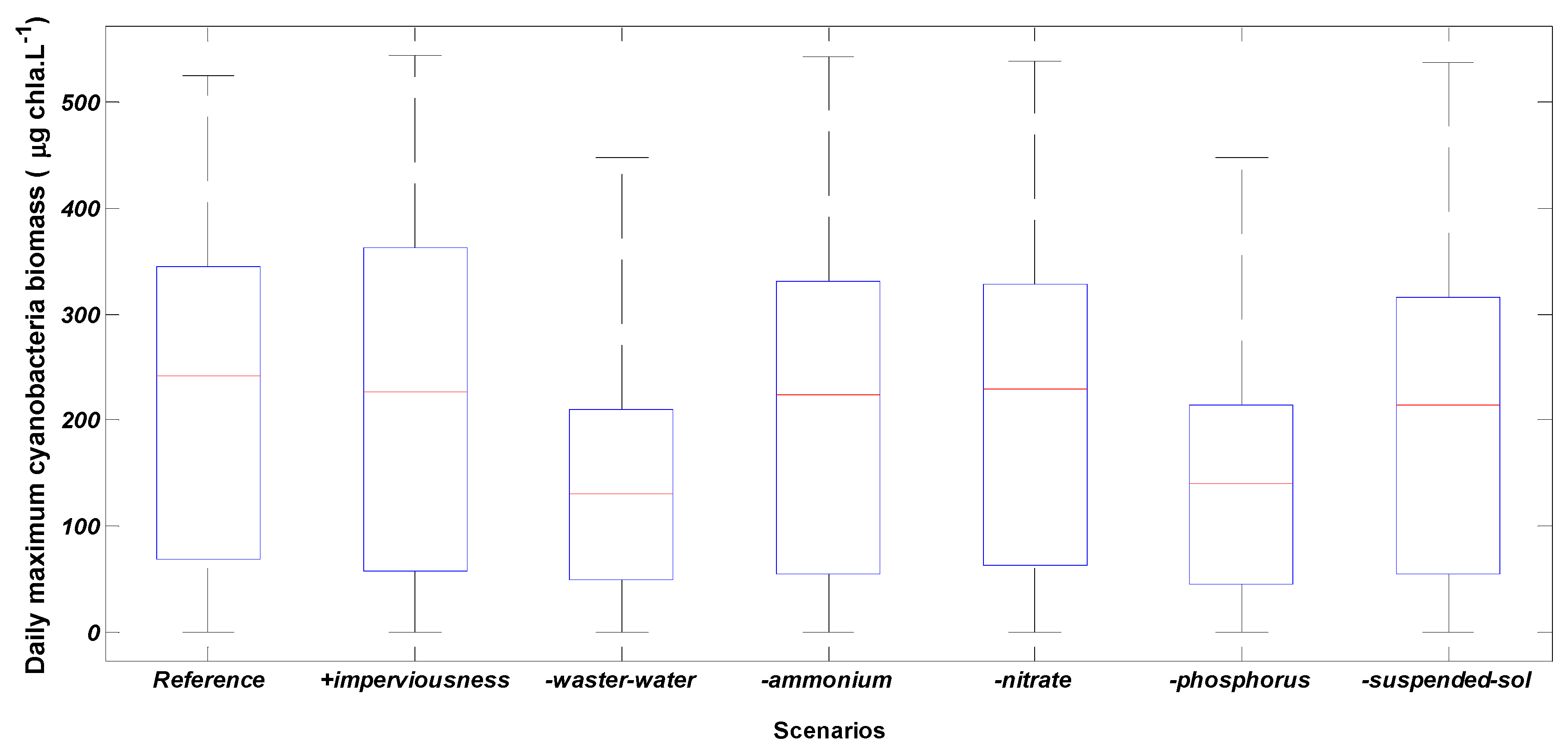
3.3. Scenarios of Catchment Changes
4. Discussion
4.1. Integrated Modelling Performance
4.2. Catchment Changes Impact on Cyanobacteria Dynamics
4.3. Mitigation Strategies
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Hydrological Model Parameters
| Parameter | Range | Unity | Calibrated Parameter |
|---|---|---|---|
| Fbuild-up TSS | 10–200 | kg ha−1 | 196 |
| dec TSS | 0–0.8 | day−1 | 0.77 |
| Fbuild-up NH4+ | 0–2 | kg ha−1 | 0 |
| dec NH4+ | 0–0.01 | day−1 | 0 |
| Fbuild-up NO3− | 0–6 | kg ha−1 | 5.95 |
| dec NO3− | 0–0.2 | day−1 | 0.19 |
| Fbuild-up TP | 0–10 | kg ha−1 | 0.78 |
| dec TP | 0–0.2 | day−1 | 0.19 |
| w TSS | 0–0.5 | mm−1 | 0.02 |
| wpo TSS (mean) | 0–2.5 | - | 1.38 |
| w NH4+ | 0–0.01 | mm−1 | 0 |
| wpo NH4+ | 0–2 | - | 0 |
| w NO3− | 0–0.3 | mm−1 | 0.005 |
| wpo NO3− (mean) | 0–2 | - | 0.93 |
| w TP | 0–0.1 | mm−1 | 0.02 |
| wpo TP (mean) | 0–2 | - | 1.08 |
Appendix B. Phytoplankton Model Equations
| Equation | |
|---|---|
| (a) Light | |
| (A1) | |
| (A2) | |
| (b) Temperature dependency (c, d and e are internally calculated) | |
| (A3) | |
| (A4) |
| Equation | |
|---|---|
| (a) Phytoplankton growth (µa) and loss due to mortality and respiration (La) and settling (MVa) | |
| (A5) | |
| (A6) | |
| (A7) | |
| (b) Carbon uptake through photosynthesis (U) and loss through respiration (R) and through mortality and excretion (E) | |
| (A8) | |
| (A9) | |
| (A10) | |
| (A11) | |
| (c) Light limitation | |
| (A12) | |
| Nitrogen limitation f(N), uptake U and loss E | |
| (A13) | |
| (A14) | |
| (A15) | |
| (A16) | |
| (A17) | |
| (A18) | |
| Phosphorus limitation f(P), uptake U and loss E | |
| (A19) | |
| (A20) | |
| (A21) | |
| (A22) |
| Description | Symbol |
|---|---|
| Ammonium | NH4+ |
| Computational time step | Δt |
| Depth | z |
| Detrital particulate organic carbon concentration | POC |
| Detrital particulate organic nitrogen concentration | PON |
| Detrital particulate organic phosphorus concentration | POP |
| Dissolved inorganic carbon | DIC |
| Dissolved organic carbon concentration | DOC |
| Dissolved organic matter | DOM |
| Dissolved organic nitrogen concentration | DON |
| Dissolved organic phosphorus concentration | DOP |
| Filterable reactive phosphorus | FRP |
| Light extinction coefficient | kD |
| Light intensity (photosynthetically active radiation - PAR) | I |
| Loss rate | La |
| Filterable reactive phosphorus | FRP |
| Time index | i |
| Incident shortwave intensity at water surface | I0 |
| Internal nitrogen concentration | AINa |
| Internal phosphorus concentration | AIPa |
| Nitrate | NO3− |
| Nitrogen | N |
| pH | pH |
| Phosphorus | P |
| Phytoplankton biomass | A |
| Phytoplankton group index | a |
| Phytoplankton loss due to settling | MVa |
| Suspended solids | SS |
| Vertical thickness of computational cell | Δz |
| Water temperature | T |
| Description | Symbol |
|---|---|
| (a) Light | |
| Fraction of incoming solar radiation which is photosynthetically active | Kpar |
| Specific light attenuation coefficient due to the action of pure water | KW |
| Specific light attenuation coefficient rate due to the action of DOC | KeDOC |
| Specific light attenuation coefficient rate due to the action of POC | KePOC |
| Specific light attenuation coefficient rate due to the action of SS | KeSS |
| Specific light attenuation coefficient rate due to Phytoplankton | KeA |
| (b) Temperature dependency | |
| Arrhenius constant | ϑ |
| Standard temperature | Tstd |
| Optimum temperature | Topt |
| Maximum temperature | Tmax |
| (c) Phytoplankton growth | |
| Maximum potential growth rate | µmaxa |
| Phytoplankton growth rate | µa |
| Metabolic loss rate coefficient | kra |
| Fraction of phytoplankton production lost due to photorespiration | krpa |
| Settling velocity | Vsa |
| (d) Carbon uptake and loss | |
| Stoichiometric ratio of C to chla | YC:chla |
| Fraction of respiration relative to total metabolic loss | fRES |
| Fraction of metabolic loss rate that goes to DOM | fDOMa |
| Fraction of photorespiration | kptr |
| (e) Light limitation | |
| Light intensity for maximum phytoplankton production | Ik |
| (f) Nitrogen uptake and loss | |
| Half saturation constant for nitrogen uptake | KNa |
| Maximum internal nitrogen concentration | AINmaxa |
| Maximum rate of nitrogen uptake | UNmax |
| Minimum internal nitrogen concentration | AINmina |
| Phytoplankton group preference for NH4+ | PNa |
| (g) Phosphorus uptake and loss | |
| Half saturation constant for phosphorus uptake | KPa |
| Maximum internal phosphorus concentration | AIPmaxa |
| Maximum rate of phosphorus uptake | UPmaxa |
| Minimum internal phosphorus concentration | AIPmina |
Appendix C. Phytoplankton Model Calibrated Parameters
| Parameter | Symbol | Unity | Range | Calibrated Value |
|---|---|---|---|---|
| (a) Cyanobacteria (index C) | ||||
| Maximum potential growth rate | µmaxC | day−1 | 0.25–1.60 | 1.60 |
| Metabolic loss rate coefficient | kRC | day−1 | 0.05–0.15 | 0.05 |
| Respiration temperature dependency | ϑRC | - | 1.04–1.10 | 1.05 |
| Maximum internal P concentration | AIPmaxC | mg P (mg chl-a)−1 | 0.92–3.80 | 0.92 |
| Maximum rate of P uptake | UPmaxC | mg P (mg chl-a)−1 day−1 | 0.4–54.4 | 24.4 |
| Maximum rate of N uptake | UNmaxC | mg N (mg chl-a)−1 day−1 | 0.2–4.8 | 0.71 |
| Optimum temperature | ToptC | °C | 25–35 | 29 |
| Specific attenuation coefficient | keC | (mg chl-a L−1) m−1 | 0.01–0.02 | 0.02 |
| Light intensity for maximum phytoplankton production | IkC | µEm−2 s−1 | 15–180 | 33 |
| (b) Other phytoplankton (index O) | ||||
| Maximum potential growth rate | µmaxO | day−1 | 0.50–1.84 | 0.50 |
| Metabolic loss rate coefficient | kRO | day−1 | 0.02–0.12 | 0.03 |
| Respiration temperature dependency | ϑRO | - | 1.04–1.12 | 1.10 |
| Maximum rate of P uptake | UPmaxO | mg P (mg chl-a)−1 day−1 | 1.0–4.5 | 3.3 |
| Optimum temperature | ToptO | °C | 21–29 | 26 |
| Maximum temperature | TmaxO | °C | 30–35 | 33 |
| Specific attenuation coefficient | keO | (mg chl-a L−1) −1 m−1 | 0.01–0.02 | 0.012 |
| Light intensity for maximum phytoplankton production | IkO | µEm−2 s−1 | 20–250 | 173 |
| (c) Sediment parameter | ||||
| Static sediment exchange rate | rSOS | g m−2 day−1 | 0.92–7.97 | 1.7 |
References
- Le Moal, M.; Gascuel-Odoux, C.; Ménesguen, A.; Souchon, Y.; Étrillard, C.; Levain, A.; Moatar, F.; Pannard, A.; Souchu, P.; Lefebvre, A.; et al. Eutrophication: A new wine in an old bottle? Sci. Total Environ. 2019, 651, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Vinçon-Leite, B.; Casenave, C. Modelling eutrophication in lake ecosystems: A review. Sci. Total Environ. 2019, 651, 2985–3001. [Google Scholar] [CrossRef] [PubMed]
- Rastogi, R.P.; Madamwar, D.; Incharoensakdi, A. Bloom Dynamics of Cyanobacteria and Their Toxins: Environmental Health Impacts and Mitigation Strategies. Front. Microbiol. 2015, 6, 1254. [Google Scholar] [CrossRef] [PubMed]
- Zurawell, R.W.; Chen, H.; Burke, J.M.; Prepas, E.E. Hepatotoxic Cyanobacteria: A Review of the Biological Importance of Microcystins in Freshwater Environments. J. Toxicol. Environ. Health Part B 2005, 8, 1–37. [Google Scholar] [CrossRef] [PubMed]
- O’Neil, J.M.; Davis, T.W.; Burford, M.A.; Gobler, C.J. The rise of harmful cyanobacteria blooms: The potential roles of eutrophication and climate change. Harmful Algae 2012, 14, 313–334. [Google Scholar] [CrossRef]
- Reichwaldt, E.S.; Ghadouani, A. Effects of rainfall patterns on toxic cyanobacterial blooms in a changing climate: Between simplistic scenarios and complex dynamics. Water Res. 2012, 46, 1372–1393. [Google Scholar] [CrossRef]
- Vilhena, L.C.; Hillmer, I.; Imberger, J. The role of climate change in the occurrence of algal blooms: Lake Burragorang, Australia. Limnol. Oceanogr. 2010, 55, 1188–1200. [Google Scholar] [CrossRef]
- Gkelis, S.; Papadimitriou, T.; Zaoutsos, N.; Leonardos, I. Anthropogenic and climate-induced change favors toxic cyanobacteria blooms: Evidence from monitoring a highly eutrophic, urban Mediterranean lake. Harmful Algae 2014, 39, 322–333. [Google Scholar] [CrossRef]
- Alberti, M.; Booth, D.; Hill, K.; Coburn, B.; Avolio, C.; Coe, S.; Spirandelli, D. The impact of urban patterns on aquatic ecosystems: An empirical analysis in Puget lowland sub-basins. Landsc. Urban Plan. 2007, 80, 345–361. [Google Scholar] [CrossRef]
- Hong, Y.; Li, C.; Lemaire, B.J.; Soulignac, F.; Martins, J.R.S.; Roguet, A.; Lucas, F.; Vinçon-Leite, B. An Integrated Approach for Assessing the Impact of Urban Stormwater Discharge on the Fecal Contamination in a Recreational Lake Near Paris. In New Trends in Urban Drainage Modelling; Springer: Cham, Switzerland, 2019; ISBN 978-3-319-99866-4. [Google Scholar]
- Starkl, M.; Brunner, N.; Stenström, T.A. Why do water and sanitation systems for the poor still fail? Policy analysis in economically advanced developing countries. Environ. Sci. Technol. 2013, 47, 6102–6110. [Google Scholar] [CrossRef] [PubMed]
- Van Drecht, G.; Bouwman, A.F.; Harrison, J.; Knoop, J.M. Global nitrogen and phosphate in urban wastewater for the period 1970 to 2050. Glob. Biogeochem. Cycles 2009, 23. [Google Scholar] [CrossRef]
- Khac, V.T.; Hong, Y.; Plec, D.; Lemaire, B.J.; Dubois, P.; Saad, M.; Vinçon-Leite, B. An Automatic Monitoring System for High-Frequency Measuring and Real-Time Management of Cyanobacterial Blooms in Urban Water Bodies. Processes 2018, 6, 11. [Google Scholar] [CrossRef]
- Carey, R.O.; Hochmuth, G.J.; Martinez, C.J.; Boyer, T.H.; Dukes, M.D.; Toor, G.S.; Cisar, J.L. Evaluating nutrient impacts in urban watersheds: Challenges and research opportunities. Environ. Pollut. 2013, 173, 138–149. [Google Scholar] [CrossRef] [PubMed]
- Silva, T.F.G.; Vinçon-Leite, B.; Giani, A.; Figueredo, C.C.; Petrucci, G.; Lemaire, B.; Sperling, E.V.; Tassin, B.; Seidl, M.; Khac, V.T.; et al. Modelling Lake Pampulha: A tool for assessing the catchment area impacts on the phytoplankton dynamics. Eng. Sanit. Ambient. 2016, 21, 95–108. [Google Scholar] [CrossRef]
- Couture, R.M.; Tominaga, K.; Starrfelt, J.; Moe, S.J.; Kaste, Y.; Wright, R.F. Modelling phosphorus loading and algal blooms in a Nordic agricultural catchment-lake system under changing land-use and climate. Environ. Sci. Process. Impacts 2014, 16, 1588–1599. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Godrej, A.N.; Grizzard, T.J. The hydrological calibration and validation of a complexly-linked watershed-reservoir model for the Occoquan watershed, Virginia. J. Hydrol. 2007, 345, 167–183. [Google Scholar] [CrossRef]
- Norton, L.; Elliott, J.A.; Maberly, S.C.; May, L. Using models to bridge the gap between land use and algal blooms: An example from the Loweswater catchment, UK. Environ. Model. Softw. 2012, 36, 64–75. [Google Scholar] [CrossRef]
- Hamilton, D.P.; Salmaso, N.; Paerl, H.W. Mitigating harmful cyanobacterial blooms: Strategies for control of nitrogen and phosphorus loads. Aquat. Ecol. 2016, 50, 351–366. [Google Scholar] [CrossRef]
- Munar, A.M.; Cavalcanti, J.R.; Bravo, J.M.; Fan, F.M.; da Motta-Marques, D.; Fragoso, C.R. Coupling large-scale hydrological and hydrodynamic modeling: Toward a better comprehension of watershed-shallow lake processes. J. Hydrol. 2018, 564, 424–441. [Google Scholar] [CrossRef]
- Frassl, M.A.; Abell, J.M.; Botelho, D.A.; Cinque, K.; Gibbes, B.R.; Jöhnk, K.D.; Muraoka, K.; Robson, B.J.; Wolski, M.; Xiao, M.; et al. A short review of contemporary developments in aquatic ecosystem modelling of lakes and reservoirs. Environ. Model. Softw. 2019, 117, 181–187. [Google Scholar] [CrossRef]
- Wu, J.; Yu, S.L.; Zou, R. A water quality-based approach for watershed wide BMP strategies. J. Am. Water Resour. Assoc. 2006, 42, 1193–1204. [Google Scholar] [CrossRef]
- Taner, M.U.; Carleton, J.N.; Wellman, M. Integrated model projections of climate change impacts on a North American Lake. Ecol. Model. 2011, 222, 3380–3393. [Google Scholar] [CrossRef]
- Markensten, H.; Moore, K.; Persson, I. Simulated lake phytoplankton composition shifts toward cyanobacteria dominance in a future warmer climate. Ecol. Appl. 2010, 20, 752–767. [Google Scholar] [CrossRef] [PubMed]
- Komatsu, E.; Fukushima, T.; Harasawa, H. A modeling approach to forecast the effect of long-term climate change on lake water quality. Ecol. Model. 2007, 209, 351–366. [Google Scholar] [CrossRef]
- Me, W.; Hamilton, D.P.; McBride, C.G.; Abell, J.M.; Hicks, B.J. Modelling hydrology and water quality in a mixed land use catchment and eutrophic lake: Effects of nutrient load reductions and climate change. Environ. Model. Softw. 2018, 109, 114–133. [Google Scholar] [CrossRef]
- Nobre, A.M.; Ferreira, J.G.; Nunes, J.P.; Yan, X.; Bricker, S.; Corner, R.; Groom, S.; Gu, H.; Hawkins, A.J.S.; Hutson, R.; et al. Assessment of coastal management options by means of multilayered ecosystem models. Estuar. Coast. Shelf Sci. 2010, 87, 43–62. [Google Scholar] [CrossRef]
- Bucak, T.; Trolle, D.; Tavşanoğlu, Ü.N.; Çakıroğlu, A.İ.; Özen, A.; Jeppesen, E.; Beklioğlu, M. Modeling the effects of climatic and land use changes on phytoplankton and water quality of the largest Turkish freshwater lake: Lake Beyşehir. Sci. Total Environ. 2018, 621, 802–816. [Google Scholar] [CrossRef]
- Scheffer, M.; Rinaldi, S.; Gragnani, A.; Mur, L.R.; van Nes, E. On the dominance of filamentous blue-green algae in shallow, turbid lakes. Ecology 1997, 78, 272–282. [Google Scholar] [CrossRef]
- Shimoda, Y.; Arhonditsis, G.B. Phytoplankton functional type modelling: Running before we can walk? A critical evaluation of the current state of knowledge. Ecol. Model. 2016, 320, 29–43. [Google Scholar] [CrossRef]
- Coutinho, W. Emprego da Flotação a ar Dissolvido no Tratamento de Cursos D’água: Avaliação do Desempenho da Estação de Tratamento dos Córregos Ressaca e Sarandi Afluentes à Lagoa da Pampulha. Master’s Thesis, Universidade Federal de Minas Gerais, Belo Horizonte, Brazil, 2007. [Google Scholar]
- Figueredo, C.C.; Pinto-coelho, R.M.; Lopes, A.M.M.B.; Lima, P.H.O.; Gücker, B.; Giani, A. From intermittent to persistent cyanobacterial blooms: Identifying the main drivers in an urban tropical reservoir. J. Limnol. 2016, 75, 445–454. [Google Scholar] [CrossRef]
- Resck, R.P.; Bezerra-Neto, J.; Coelho, R.M.P. Nova batimetria e avaliação de parâmetros morfométricos da Lagoa da Pampulha (Belo Horizonte, Brasil). Geografias 2007, 3, 24–37. [Google Scholar]
- Soares, L.M.V.; Silva, T.F.; das, G.; Vinçon-Leite, B.; Eleutério, J.; Lima, L.C.; de Nascimento, N.O. Modelling drought impacts on the hydrodynamics of a tropical water supply reservoir. Inl. Waters 2019. accepted. [Google Scholar]
- Beato, D.A.C.; Dutra, G.M.; Medeiros, M.J. Projeto Pampulha: Estudo Hidrogeológico da Bacia da Lagoa da Pampuha; CPRM: Belo Horizonte, Brazil, 2001; Volume I.
- Torres, I.C.; Resck, R.; Pinto-Coelho, R. Mass balance estimation of nitrogen, carbon, phosphorus and total suspended solids in the urban eutrophic, Pampulha reservoir, Brazil. Biologia 2007, 19, 79–91. [Google Scholar]
- Matos, A.; Lemos, R.; Silva, T.; Eleutério, J.; Nascimento, N. Evolução do uso e ocupação do solo em mananciais de abastecimento metropolitano na Região Metropolitana de Belo Horizonte, estado de Minas Gerais. In Proceedings of the Anais do XXI Simpósio Brasileiro de Recursos Hídricos, Florianópolis, Brazil, 26 November–1 December 2017. [Google Scholar]
- APHA. Standard Methods for the Examination of Water and Wastewater, 20th ed.; APHA: Washington, DC, USA, 2012. [Google Scholar]
- Nusch, E.A. Comparison of different methods for chlorophyll and phaeopigment determination. Arch. Hydrobiol. Beih 1980, 14, 14–36. [Google Scholar]
- Utermöhl, H. Zur Vervollkmnung der quantitativen Phytoplankton-Methodik. Int. Verh. Theor. Angew. Limnol. 1958, 9, 165–174. [Google Scholar]
- Rossman, L.A. Storm Water Management Model User’s Manual Version 5.1; EPA/600/R-; United States Environmental Protection Agency: Washington, DC, USA, 2015.
- Huber, W.C. Storm Water Management Model Version 4, 2nd ed.; United States Environmental Protection Agency: Washington, DC, USA, 1992.
- Silva, T. Suivi et modélisation de la Dynamique des Cyanobactéries dans les lacs Urbains au sein de leur Bassin Versant. Ph.D. Thesis, Universidade Federal de Minas Gerais, Paris, France, 2014. [Google Scholar]
- Petrucci, G.; Bonhomme, C. The dilemma of spatial representation for urban hydrology semi-distributed modelling: Trade-offs among complexity, calibration and geographical data. J. Hydrol. 2014, 517, 997–1007. [Google Scholar] [CrossRef]
- Bennett, N.D.; Croke, B.F.W.; Guariso, G.; Guillaume, J.H.A.; Hamilton, S.H.; Jakeman, A.J.; Marsili-libelli, S.; Newham, L.T.H.; Norton, J.P.; Perrin, C.; et al. Characterising performance of environmental models. Environ. Model. Softw. 2013, 40, 1–20. [Google Scholar] [CrossRef]
- Hamilton, D.P.; Schladow, S.G. Prediction of water quality in lakes and reservoirs. Part I—Model description. Ecol. Model. 1997, 96, 91–110. [Google Scholar] [CrossRef]
- Hipsey, M.R.; Romero, J.R.; Antenucci, J.P.; Hamilton, D.P. Computational Aquatic Ecosystem Dynamics Model—CAEDYM Science Manual; Centre for Water Research, University of Western Australia: Crawley, Australia, 2006. [Google Scholar]
- Gal, G.; Hipsey, M.R.; Parparov, A.; Wagner, U.; Makler, V.; Zohary, T. Implementation of ecological modeling as an effective management and investigation tool: Lake Kinneret as a case study. Ecol. Model. 2009, 220, 1697–1718. [Google Scholar] [CrossRef]
- Silva, T.; Giani, A.; Figueredo, C.; Viana, P.; Khac, V.T.; Lemaire, B.J.; Tassin, B.; Nascimento, N.; Vinçon-Leite, B. Comparison of cyanobacteria monitoring methods in a tropical reservoir by in vivo and in situ spectrofluorometry. Ecol. Eng. 2016, 97, 79–87. [Google Scholar] [CrossRef][Green Version]
- TVA. Heat and Mass Transfer between a Water Surface and the Atmosphere; Tennessee Valley Authority: Knoxville, TN, USA, 1972.
- Budai, P.; Clement, A. Estimation of nutrient load from urban diffuse sources: Experiments with runoff sampling at pilot catchments of Lake Balaton, Hungary. Water Sci. Technol. 2007, 56, 295–302. [Google Scholar] [CrossRef]
- Conley, D.J.; Paerl, H.W.; Howarth, R.W.; Boesch, D.F.; Seitzinger, S.P.; Havens, K.E.; Lancelot, C.; Likens, G.E. Controlling Eutrophication: Nitrogen and Phosphorus. Science 2009, 323, 1014–1015. [Google Scholar] [CrossRef]
- Paerl, H.W.; Hall, N.S.; Calandrino, E.S. Controlling harmful cyanobacterial blooms in a world experiencing anthropogenic and climatic-induced change. Sci. Total Environ. 2011, 409, 1739–1745. [Google Scholar] [CrossRef]
- Beaver, J.R.; Casamatta, D.A.; East, T.L.; Havens, K.E.; Rodusky, A.J.; James, R.T.; Tausz, C.E.; Buccier, K.M. Extreme weather events influence the phytoplankton community structure in a large lowland subtropical lake (Lake Okeechobee, Florida, USA). Hydrobiologia 2013, 709, 213–226. [Google Scholar] [CrossRef]
- Dotto, C.B.S.; Mannina, G.; Kleidorfer, M.; Vezzaro, L.; Henrichs, M.; McCarthy, D.T.; Freni, G.; Rauch, W.; Deletic, A. Comparison of different uncertainty techniques in urban stormwater quantity and quality modelling. Water Res. 2012, 46, 2545–2558. [Google Scholar] [CrossRef]
- Gaume, E.; Villeneuve, J.P.; Desbordes, M. Uncertainty assessment and analysis of the calibrated parameter values of an urban storm water quality model. J. Hydrol. 1998, 210, 38–50. [Google Scholar] [CrossRef]
- Bonhomme, C.; Petrucci, G. Should we trust build-up/wash-off water quality models at the scale of urban catchments? Water Res. 2017, 108, 422–431. [Google Scholar] [CrossRef] [PubMed]
- Baffaut, C.; Delleur, J.W. Calibration of SWMM runoff quality model with expert system. J. Water Resour. Plan. Manag. 1990, 116, 247–261. [Google Scholar] [CrossRef]
- Tsihrintzis, V.A.; Hamid, R. Runoff quality prediction from small urban catchments using SWMM. Hydrol. Process. 1998, 12, 311–329. [Google Scholar] [CrossRef]
- Chow, M.F.; Yusop, Z.; Toriman, M.E. Modelling runoff quantity and quality in tropical urban catchments using Storm Water Management Model. Int. J. Environ. Sci. Technol. 2012, 9, 737–748. [Google Scholar] [CrossRef]
- Dotto, C.B.S.; Kleidorfer, M.; Deletic, A.; Rauch, W.; McCarthy, D.T.; Fletcher, T.D. Performance and sensitivity analysis of stormwater models using a Bayesian approach and long-term high resolution data. Environ. Model. Softw. 2011, 26, 1225–1239. [Google Scholar] [CrossRef]
- Tuomela, C.; Sillanpää, N.; Koivusalo, H. Assessment of stormwater pollutant loads and source area contributions with storm water management model (SWMM). J. Environ. Manag. 2019, 233, 719–727. [Google Scholar] [CrossRef] [PubMed]
- Elliott, A.H.; Trowsdale, S.A. A review of models for low impact urban stormwater drainage. Environ. Model. Softw. 2007, 22, 394–405. [Google Scholar] [CrossRef]
- Liu, A.; Egodawatta, P.; Guan, Y.; Goonetilleke, A. Influence of rainfall and catchment characteristics on urban stormwater quality. Sci. Total Environ. 2013, 444, 255–262. [Google Scholar] [CrossRef] [PubMed]
- Zoppou, C. Review of urban storm water models. Environ. Model. Softw. 2001, 16, 195–231. [Google Scholar] [CrossRef]
- Obropta, C.C.; Kardos, J.S. Review of urban stormwater quality models: Deterministic, stochastic, and hybrid approaches. J. Am. Water Resour. Assoc. 2007, 43, 1508–1523. [Google Scholar] [CrossRef]
- Niazi, M.; Nietc, C.; Maghrebi, M.; Jackson, N.; Bennett, B.R.; Tryby, M.; Massoudieh, A. Storm Water Management Model: Performance Review and Gap Analysis Mehran. J. Sustain. Water Built Environ. 2017, 3, 04017002. [Google Scholar] [CrossRef]
- Trolle, D.; Hamilton, D.P.; Pilditch, C.A.; Duggan, I.C.; Jeppesen, E. Predicting the effects of climate change on trophic status of three morphologically varying lakes: Implications for lake restoration and management. Environ. Model. Softw. 2011, 26, 354–370. [Google Scholar] [CrossRef]
- Cui, Y.; Zhu, G.; Li, H.; Luo, L.; Cheng, X.; Jin, Y.; Trolle, D. Modeling the response of phytoplankton to reduced external nutrient load in a subtropical Chinese reservoir using DYRESM-CAEDYM. Lake Reserv. Manag. 2016, 32, 146–157. [Google Scholar] [CrossRef]
- Fenocchi, A.; Rogora, M.; Morabito, G.; Marchetto, A.; Sibilla, S.; Dresti, C. Applicability of a one-dimensional coupled ecological-hydrodynamic numerical model to future projections in a very deep large lake (Lake Maggiore, Northern Italy/Southern Switzerland). Ecol. Model. 2019, 392, 38–51. [Google Scholar] [CrossRef]
- Schindler, D.W. Recent advances in the understanding and management of eutrophication. Limnol. Oceanogr. 2006, 51, 356–363. [Google Scholar] [CrossRef]
- Søndergaard, M.; Jensen, J.P.; Jeppesen, E. Role of sediment and internal loading of phosphorus in shallow lakes. Hydrobiologia 2003, 506–509, 135–145. [Google Scholar] [CrossRef]
- Figueredo, C.C.; Von Rückert, G.; Cupertino, A.; Pontes, M.A.; Fernandes, L.A.; Ribeiro, S.G.; Maran, N.R. Lack of nitrogen as a causing agent of Cylindrospermopsis raciborskii intermittent blooms in a small tropical reservoir. FEMS Microbiol. Ecol. 2014, 87, 557–567. [Google Scholar] [CrossRef] [PubMed]
- Reichwaldt, E.S.; Sinang, S.; Ghadouani, A. Global warming, climate patterns and toxic cyanobacteria. In Climate Change and Marine and Freshwater Toxins; Botana, L.M., Louzao, M.C., Vilariño, N., Eds.; De Gruyter: Berlin, Germany, 2015; p. 490. [Google Scholar]
- Zhu, M.; Paerl, H.W.; Zhu, G.; Wu, T.; Li, W.; Shi, K.; Zhao, L.; Zhang, Y.; Qin, B.; Caruso, A.M. The role of tropical cyclones in stimulating cyanobacterial (Microcystis spp.) blooms in hypertrophic Lake Taihu, China. Harmful Algae 2014, 39, 310–321. [Google Scholar] [CrossRef]
- Havens, K.; Paerl, H.; Phlips, E.; Zhu, M.; Beaver, J.; Srifa, A. Extreme weather events and climate variability provide a lens to how shallow lakes may respond to climate change. Water 2016, 8, 229. [Google Scholar] [CrossRef]
- Rostami, S.; He, J.; Hassan, Q. Riverine Water Quality Response to Precipitation and Its Change. Environments 2018, 5, 8. [Google Scholar] [CrossRef]
- Friese, K.; Schmidt, G.; De Carvalho, J.L.; Nalini, A.H., Jr.; Zachmann, D.W. Anthropogenic influence on the degradation of an urban lake—The Pampulha reservoir in Belo Horizonte, Minas Gerais, Brazil. Limnologica 2010, 40, 114–125. [Google Scholar] [CrossRef]
- Fletcher, T.D.; Shuster, W.; Hunt, W.F.; Ashley, R.; Butler, D.; Arthur, S.; Trowsdale, S.; Barraud, S.; Semadeni-Davies, A.; Bertrand-Krajewski, J.L.; et al. SUDS, LID, BMPs, WSUD and more—The evolution and application of terminology surrounding urban drainage. Urban Water J. 2015, 12, 525–542. [Google Scholar] [CrossRef]
- Eckart, K.; McPhee, Z.; Bolisetti, T. Performance and implementation of low impact development—A review. Sci. Total Environ. 2017, 607–608, 413–432. [Google Scholar] [CrossRef] [PubMed]
- Ahiablame, L.M.; Engel, B.A.; Chaubey, I. Effectiveness of low impact development practices: Literature review and suggestions for future research. Water Air Soil Pollut. 2012, 223, 4253–4273. [Google Scholar] [CrossRef]
- Moore, T.L.C.; Hunt, W.F. Ecosystem service provision by stormwater wetlands and ponds—A means for evaluation? Water Res. 2012, 46, 6811–6823. [Google Scholar] [CrossRef] [PubMed]
- Voskamp, I.M.; Van de Ven, F.H.M. Planning support system for climate adaptation: Composing effective sets of blue-green measures to reduce urban vulnerability to extreme weather events. Build. Environ. 2015, 83, 159–167. [Google Scholar] [CrossRef]

| Morphological Characteristics | Water Quality | ||
|---|---|---|---|
| Altitude | 801 m | TP | 58–925 (207) μg P L−1 |
| Mean depth | 5.1 m | PO43− | 1.7–113.1 (22.1) μg P L−1 |
| Maximum depth | 16.2 m | NH4+ | 1.4–14.8 (5.7) mg N L−1 |
| Surface | 197 ha | NO3− | 3.1–460 (82.9) μg N L−1 |
| Volume | 9.9 × 106 m3 | Chlorophyll-a | 19.5–322.0 (113.0) μg L−1 |
| Term | S. I. Unity | Description | Term | S. I. Unity | Description |
|---|---|---|---|---|---|
| Q | mm h−1 | Runoff rate per unit area | TMbuild-up | kg | Pollutant total mass |
| Mbuild-Up | kg ha−1 | Pollutant mass per unit area | ML | kg h−1 | Wash-off pollutant mass per hour |
| t | day | Time | wpo | - | Exponent |
| Fbuild-Up | kg ha−1 | Maximum build-up per unit area | w | mm−1 | Wash-off empirical coefficient |
| dec | day−1 | Build-up rate constant |
| Name | Formula | Range | Ideal Value | Notes |
|---|---|---|---|---|
| Root Mean Square Error (RMSE) | (0, +∞) | 0 | RMSE express the error metric in the same units as the original data. Squaring the data causes bias towards large events. | |
| Normalized Root Mean Square Error (NRMSE) | (0, +∞) | 0 | RMSE is normalized by data range allowing comparison between study sites. | |
| Normalized Mean Absolute Error (NMAE) | (0, +∞) | 0 | NMAE reduces the bias towards large events and allows comparison between study sites. | |
| Pearson’s correlation coefficient (r) | (−1,1) | 1 | r measures the linear correlation of the measured and modelled values |
| Scenarios | Descriptions |
|---|---|
| reference | Current catchment condition |
| +imperviousness | +50% of imperviousness |
| -waste_water | −50% in TSS, NH4+, NO3− and TP concentration in dry weather flow |
| -ammonium | −50% in NH4+ concentration in dry weather flow |
| -nitrate | −50% in NO3− concentration in dry weather flow |
| -phosphorus | −50% in TP concentration in dry weather flow |
| -suspended_sol | −50% in TSS concentration in dry weather flow |
| Performance | TSS | NH4+ | NO3− | TP | ||||
|---|---|---|---|---|---|---|---|---|
| Cal | Val | Cal | Val | Cal | Val | Cal | Val | |
| n | 29 | 31 | 29 | 31 | 29 | 27 | 29 | 31 |
| r | 0.77 | 0.18 | 0.70 | 0.61 | 0.24 | −0.36 | 0.54 | −0.60 |
| RMSE (mg L−1) | 174 | 254 | 1.87 | 3.82 | 1.15 | 1.79 | 0.70 | 0.91 |
| NRMSE | 0.19 | 0.24 | 0.35 | 0.28 | 0.38 | 0.49 | 0.19 | 0.60 |
| NMAE | r | n | |
|---|---|---|---|
| Calibration | 0.24 | 0.89 | 16 |
| Validation | 0.55 | 0.54 | 43 |
| Water Body (Country) | Maximum Depth (m) | Model | Model Performance for Total Phytoplankton Biomass (chla-a) | Reference |
|---|---|---|---|---|
| Okareka (New Zealand) | 33.5 | DYRESM-CAEDYM | RE: 0.44 (cal); 0.28 (val) R2: 0.054 (cal); 0.45 (val) | [68] |
| Rotoehu (New Zealand) | 13.5 | DYRESM-CAEDYM | RE: 0.58 (cal); 0.57 (val) R2: 0.004 (cal); 0.00 (val) | [68] |
| Ellesmere (New Zealand) | 2.5 | DYRESM-CAEDYM | RE: 0.31 (cal); 0.61 (val) R2: 0.096 (cal); 0.18 (val) | [68] |
| Shahe reservoir (China) | 14 | DYRESM-CAEDYM | RE: 0.52 (cal); 0.73 (val) R2: 0.57 (cal); 0.21 (val) | [69] |
| Lake Maggiore (Italy) | 370 | GLM-AED2 | r: 0.69 (cal); 0.41 (val) NMAE: 0.38 (cal); 0.39 (val) | [70] |
| Lake Pampulha (Brazil) | 16 | DYRESM-CAEDYM | r: 0.88 (cal); 0.74 (val) NMAE: 0.26 (cal); 0.43 (val) | This study |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, T.F.G.; Vinçon-Leite, B.; Lemaire, B.J.; Petrucci, G.; Giani, A.; Figueredo, C.C.; Nascimento, N.d.O. Impact of Urban Stormwater Runoff on Cyanobacteria Dynamics in A Tropical Urban Lake. Water 2019, 11, 946. https://doi.org/10.3390/w11050946
Silva TFG, Vinçon-Leite B, Lemaire BJ, Petrucci G, Giani A, Figueredo CC, Nascimento NdO. Impact of Urban Stormwater Runoff on Cyanobacteria Dynamics in A Tropical Urban Lake. Water. 2019; 11(5):946. https://doi.org/10.3390/w11050946
Chicago/Turabian StyleSilva, Talita F. G., Brigitte Vinçon-Leite, Bruno J. Lemaire, Guido Petrucci, Alessandra Giani, Cléber C. Figueredo, and Nilo de O. Nascimento. 2019. "Impact of Urban Stormwater Runoff on Cyanobacteria Dynamics in A Tropical Urban Lake" Water 11, no. 5: 946. https://doi.org/10.3390/w11050946
APA StyleSilva, T. F. G., Vinçon-Leite, B., Lemaire, B. J., Petrucci, G., Giani, A., Figueredo, C. C., & Nascimento, N. d. O. (2019). Impact of Urban Stormwater Runoff on Cyanobacteria Dynamics in A Tropical Urban Lake. Water, 11(5), 946. https://doi.org/10.3390/w11050946





