Formulation and Implementation of Short-Term Optimal Reservoir Operation Schemes Integrated with Operation Rules
Abstract
1. Introduction
2. Comparative Analysis of the Three Implementation Modes of Optimal Operation Scheme
2.1. Implementation Mode of Optimal Operation Scheme
2.1.1. Water Level Control Mode
Difficulty in Accurate Implementation
Water Level Deviation or Discarded Water
Low Power Generation Efficiency
2.1.2. Outflow Control Mode
Beyond-Limit Water Level
The First-Type Discarded Water or Low Power Generation Efficiency
2.1.3. Output Control Mode
Beyond-Limit Water Level
Output Obstruction
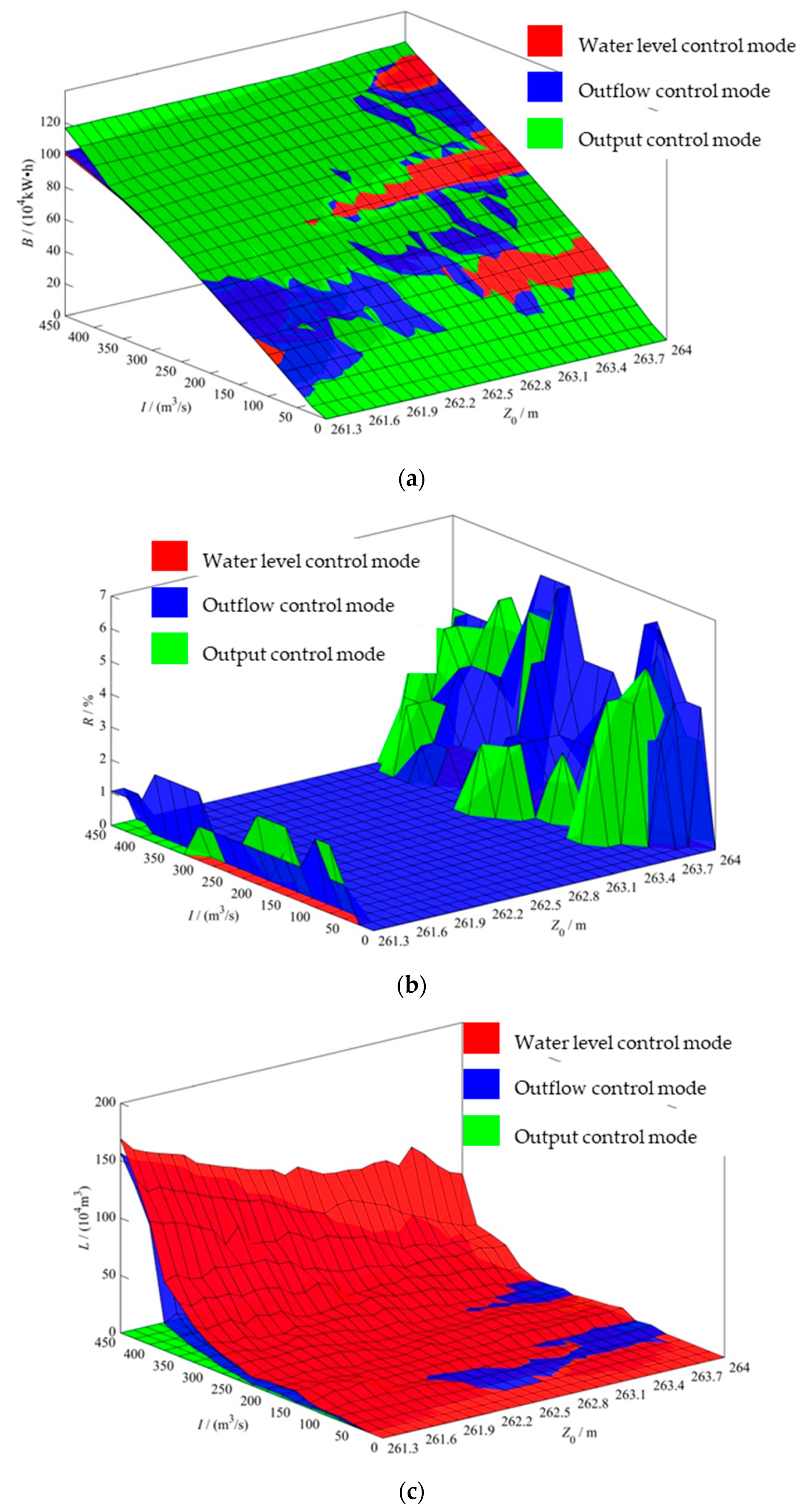
2.2. Post-Evaluation of Implementation Modes of Optimal Operation Scheme
2.2.1. Evaluation Index System
Power Generation Benefits
Risk Rate of Beyond-Limit Water Level
Discarded Water Quantity
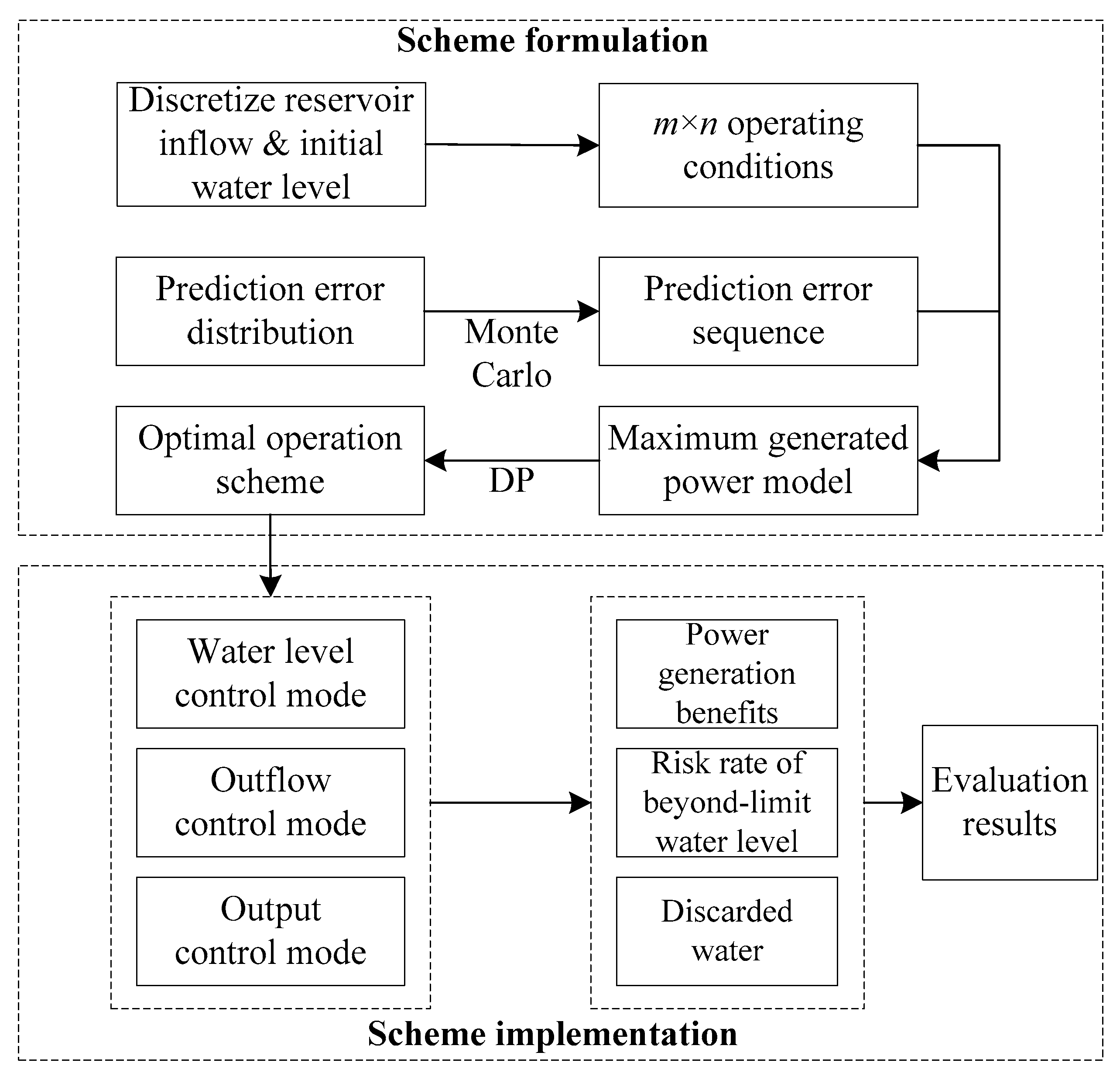
2.2.2. Evaluation Procedure
- Discretize the reservoir inflow I within its range [Imin, Imax] and get m discrete points; similarly, discretize the initial water level Z1 within its boundary [Zmin, Zmax] and get n discrete points. Combine the two sets of discrete points and obtain m × n operating conditions.
- Based on historical data, use the maximum entropy method [19] to fit the distribution of the inflow prediction error and obtain the maximum entropy distribution function. For a certain operating condition, use the Monte Carlo method [20] to randomly simulate a T-length sequence of prediction errors, and combine it with the actual inflow sequence to produce the predicted inflow sequence which is input to the foregoing maximum generated power model. Use DP to obtain the optimal operation scheme. Repeat this step until the optimal schemes for all operating conditions are formulated.
- With the actual inflow process, implement the optimal operation scheme under the water level control mode, the outflow control mode and the output control mode. Work out the index values of the three modes under all operating conditions, and obtain the evaluation results by comparative analysis.
2.3. Case Study: The 1st Scenario
3. Formulation of the Optimal Operation Scheme Integrated with Operation Rules
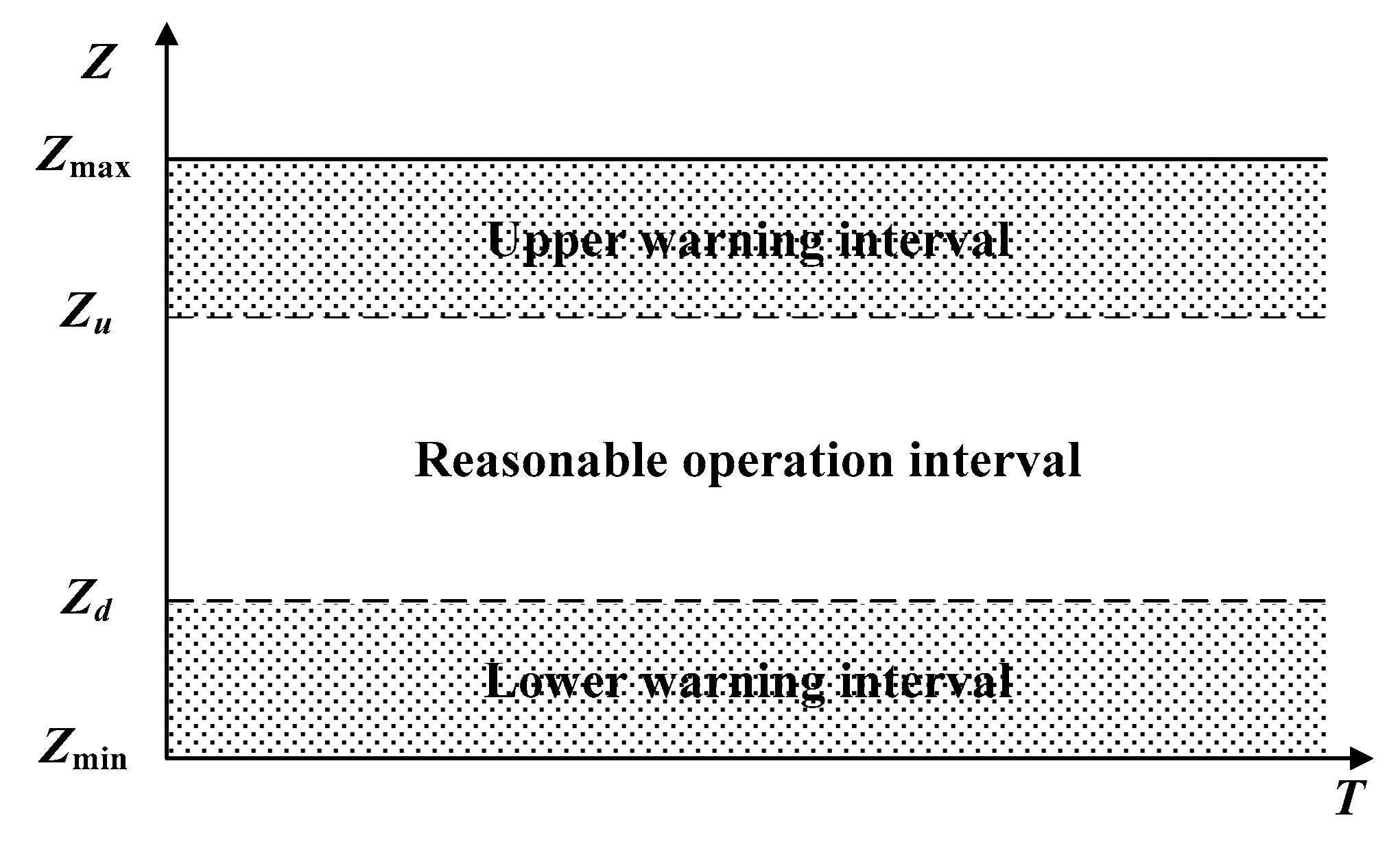
3.1. Operation Rules
3.2. Maximum Generated Power Model Integrated with Operation Rules
3.3. Case Study: The 2nd Scenario
3.3.1. The 1st Operating Condition
3.3.2. The 2nd Operating Condition
3.3.3. The 3rd Operating Condition
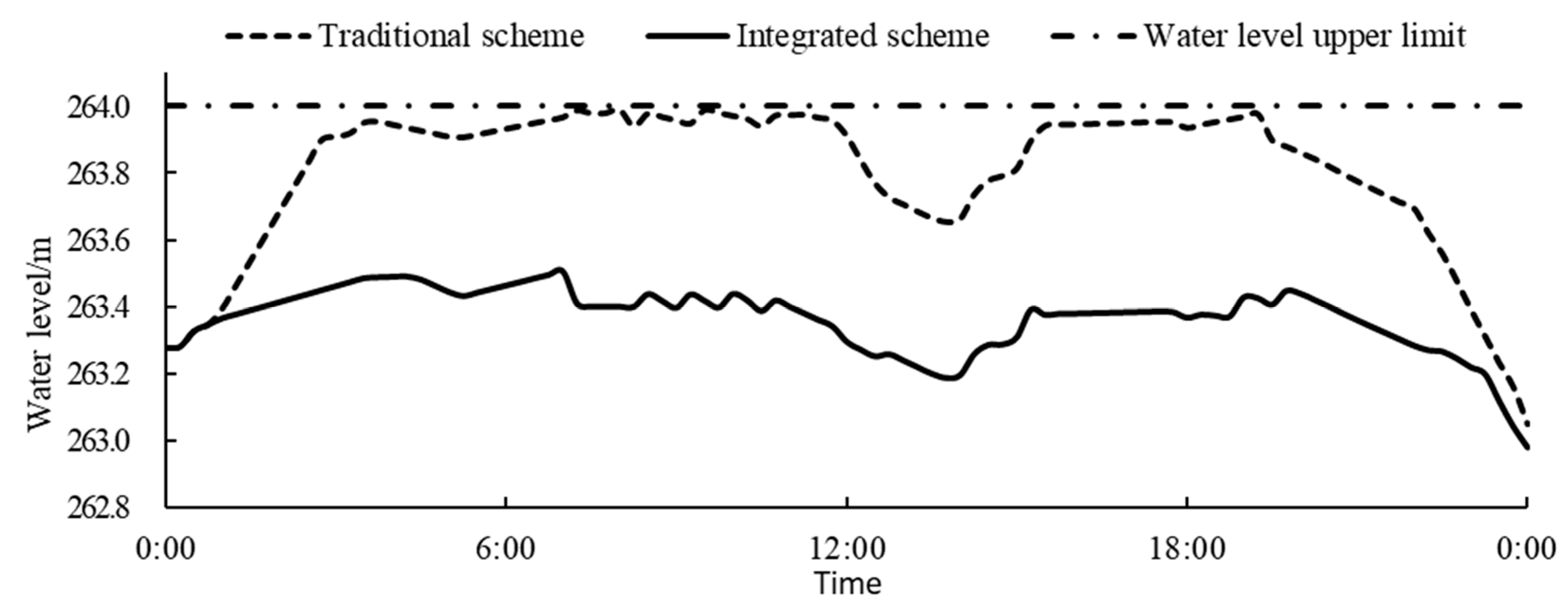
3.3.4. Result Discussions
4. Conclusions
- Compared with the water level control mode and the outflow control mode, the output control mode has the advantages of less discarded water and more power generation benefits with acceptable risk rate of beyond-limit water level, making it more suitable for the actual production of the Xiaoxuan Hydropower Station. Therefore, from the perspective of risk-benefit balance, it is recommended that the Xiaoxuan Reservoir adopt the output control mode in practical operation.
- With the setup of warning water levels, the optimal operation model integrated with operation rules combines the advantages of both conventional and optimal operation. Accordingly, the formulated operation scheme, along with the output control mode, significantly reduces the risk rate of beyond-limit water level and discarded water while maintaining the power generation benefits, which can effectively guide the safe and economic operation of the reservoir.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ma, L.; Wang, H.; Lu, B.; Qi, C. Application of Strongly Constrained Space Particle Swarm Optimization to Optimal Operation of a Reservoir System. Sustainability 2018, 10, 4445. [Google Scholar] [CrossRef]
- Xu, B.; Zhong, P.; Stanko, Z.; Zhao, Y.; Yeh, W.W.G. A multiobjective short-term optimal operation model for a cascade system of reservoirs considering the impact on long-term energy production. Water Resour. Res. 2015, 51, 3353–3369. [Google Scholar] [CrossRef]
- Ge, X.; Zhang, L.; Shu, J.; Xu, N. Short-term hydropower optimal scheduling considering the optimization of water time delay. Electr. Power Syst. Res. 2014, 110, 188–197. [Google Scholar] [CrossRef]
- Ji, C.; Li, C.; Wang, B.; Liu, M.; Wang, L. Multi-Stage Dynamic Programming Method for Short-Term Cascade Reservoirs Optimal Operation with Flow Attenuation. Water Resour. Manag. 2017, 31, 4571–4586. [Google Scholar] [CrossRef]
- Hossain, M.S.; El-Shafie, A.; Mahzabin, M.S.; Zawawi, M.H. System performances analysis of reservoir optimization–simulation model in application of artificial bee colony algorithm. Neural Comput. Appl. 2018, 30, 2101–2112. [Google Scholar] [CrossRef]
- Fu, X.; Liu, Q.; Wu, S. Risk assessment approach for reservoir operation performance. J. Hydraul. Eng. 2012, 43, 987–990. [Google Scholar]
- Ahmadi, A.; Karamouz, M.; Moridi, A. Robust Methods for Identifying Optimal Reservoir Operation Strategies Using Deterministic and Stochastic Formulations. Water Resour. Manag. 2010, 24, 2527–2552. [Google Scholar] [CrossRef]
- Karami, F.; Dariane, A.B. Many-Objective Multi-Scenario Algorithm for Optimal Reservoir Operation Under Future Uncertainties. Water Resour. Manag. 2018, 32, 3887–3902. [Google Scholar] [CrossRef]
- Zhou, T. Research of Reservoirs and Hydropower Stations Optimal Operation and Benefit Evaluation. Ph.D. Thesis, North China Electric Power University, Beijing, China, 2014. [Google Scholar]
- Ji, C.; Li, R.; Tian, K.; Zhang, Y.; Li, C. A coupling model of load adjustment for cascade hydropower stations based on inflow uncertainty: A case study of Jinping-guandi cascade hydropower stations. J. Hydraul. Eng. 2017, 48, 1–12. [Google Scholar]
- Yu, Y.; Wang, C.; Wang, P.; Hou, J.; Qian, J. Assessment of multi-objective reservoir operation in the middle and lower Yangtze River based on a flow regime influenced by the Three Gorges Project. Ecol. Inform. 2017, 38, 115–125. [Google Scholar] [CrossRef]
- Chen, D.; Li, R.; Chen, Q.; Cai, D. Deriving Optimal Daily Reservoir Operation Scheme with Consideration of Downstream Ecological Hydrograph Through A Time-Nested Approach. Water Resour. Manag. 2015, 29, 3371–3386. [Google Scholar] [CrossRef]
- Fu, X.; Li, A.; Wang, L.; Ji, C. Short-term scheduling of cascade reservoirs using an immune algorithm-based particle swarm optimization. Comput. Math. Appl. 2011, 62, 2463–2471. [Google Scholar] [CrossRef]
- Raso, L.; Malaterre, P.; Bader, J. Effective Streamflow Process Modeling for Optimal Reservoir Operation Using Stochastic Dual Dynamic Programming. J. Water Res. Plan. Man. 2017, 143, 4017003. [Google Scholar] [CrossRef]
- Ji, C.; Yu, H.; Wu, J.; Yan, X.; Li, R. Research on Cascade Reservoirs’ Short-Term Optimal Operation under the Effect of Reverse Regulation. Water 2018, 10, 808. [Google Scholar] [CrossRef]
- Wang, M.; Niu, D. Research on project post-evaluation of wind power based on improved ANP and fuzzy comprehensive evaluation model of trapezoid subordinate function improved by interval number. Renew. Energy 2019, 132, 255–265. [Google Scholar] [CrossRef]
- Wang, J. Short-term generation scheduling model of Fujian hydro system. Energ. Convers. Manag. 2009, 50, 1085–1094. [Google Scholar] [CrossRef]
- Ji, C.; Yu, H.; Yan, X.; Wei, X.; Li, J. Improved model of maximum energy storage increment based on progressive approximation. J. Hydroelectr. Eng. 2019, 38, 47–56. [Google Scholar]
- Zhang, Y.; You, J.; Ji, C.; Zhao, Y. Risk Analysis Method for Flood Control Operation of Cascade Reservoirs Considering Prediction Error. In AER-Advances in Engineering Research, Proceedings of the 3rd Annual International Conference on Sustainable Development, Tianjin, China, 14–16 July 2017; Haur, L., Tsang, Y., Dzikuc, M., Aziz, H., Psomopoulos, C., Eds.; Atlantis Press: Paris, France, 2017. [Google Scholar]
- Motevalli, M.; Zadbar, A.; Elyasi, E.; Jalaal, M. Using Monte-Carlo approach for analysis of quantitative and qualitative operation of reservoirs system with regard to the inflow uncertainty. J. Afr. Earth Sci. 2015, 105, 1–16. [Google Scholar] [CrossRef]
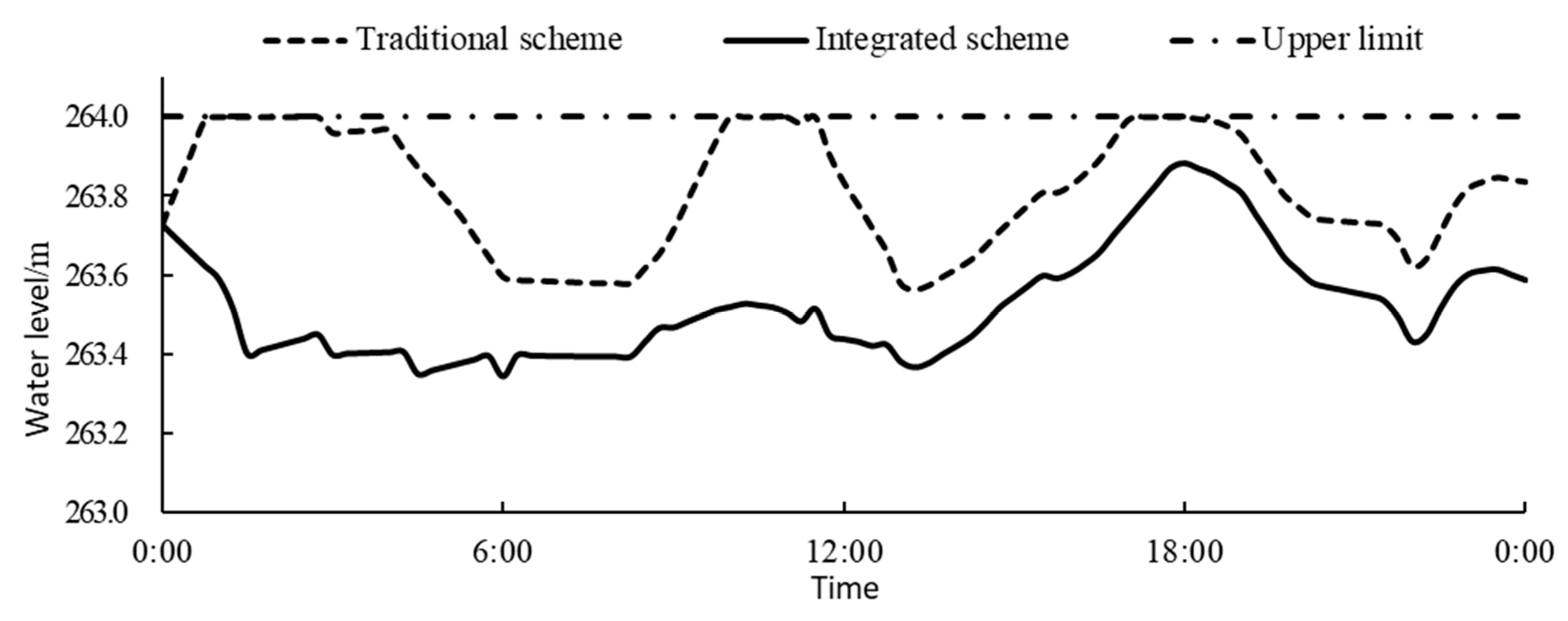
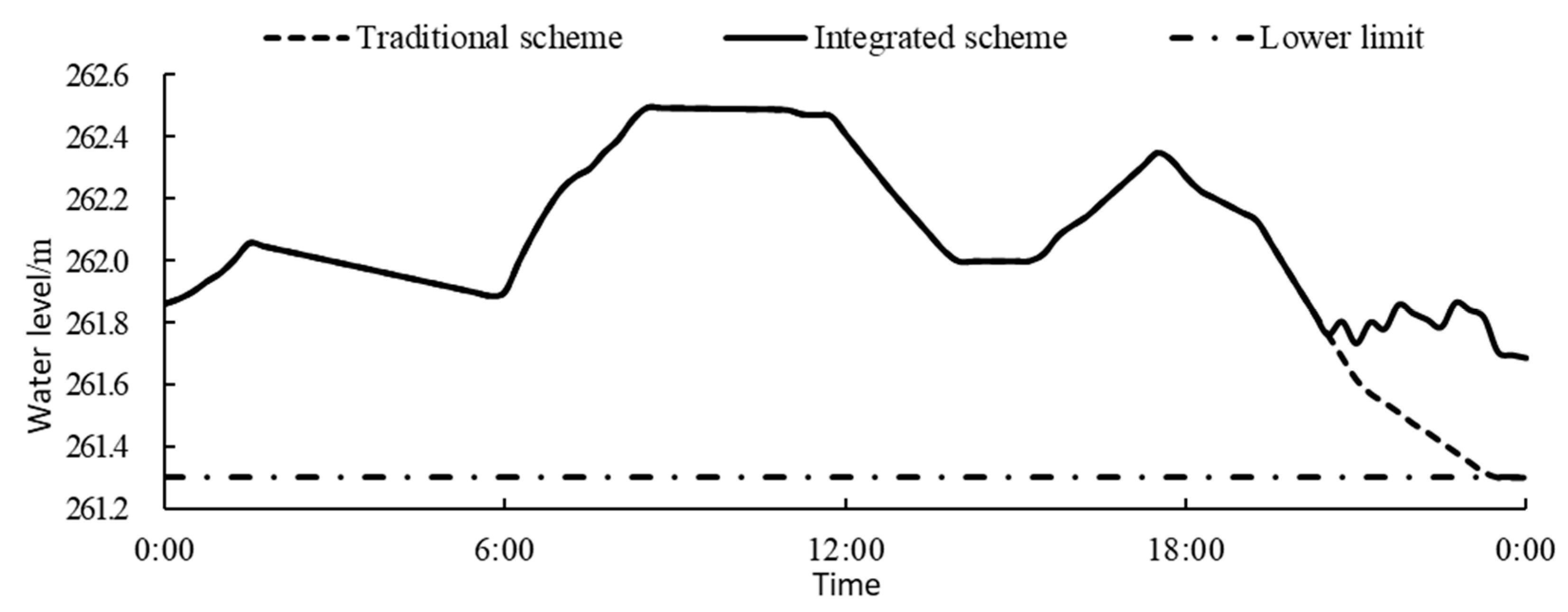
| Operating Condition | Daily Inflow of the Xiaoxuan Reservoir | Daily Initial Water Level/m | ||
|---|---|---|---|---|
| Predicted Value/(m3/s) | Actual Value/(m3/s) | Relative Error/% | ||
| 1st | 272.43 | 275.45 | −1.10 | 263.28 |
| 2nd | 348.91 | 383.62 | −9.05 | 263.73 |
| 3rd | 150.26 | 130.08 | 15.52 | 261.86 |
| Operation Scheme | Calculation Results | Evaluation Index | ||||
|---|---|---|---|---|---|---|
| Generated Power/104 kW·h | Reservoir Inflow Quantity/104 m3 | Reservoir Outflow Quantity/104 m3 | Power Generation Benefits/104 kW·h | Risk Rate of Beyond-Limit Water Level/% | Discarded Water Quantity/104 m3 | |
| (1) | (2) | (3) | (4) 1 | (5) | (6) | |
| Traditional scheme | 78.34 | 2379.87 | 2439.17 | 76.51 | 0 | 0 |
| Integrated scheme | 77.84 | 2379.87 | 2457.13 | 75.46 | 0 | 0 |
| Operation Scheme | Calculation Results | Evaluation Index | ||||
|---|---|---|---|---|---|---|
| Generated Power/104 kW·h | Reservoir Inflow Quantity/104 m3 | Reservoir Outflow Quantity/104 m3 | Power Generation Benefits/104 kW·h | Risk Rate of Beyond-Limit Water Level % | Discarded Water Quantity/104 m3 | |
| (1) | (2) | (3) | (4) 1 | (5) | (6) | |
| Traditional scheme | 93.84 | 3314.45 | 3286.17 | 94.71 | 18.75 | 130.90 |
| Integrated scheme | 98.28 | 3314.45 | 3350.65 | 97.17 | 0 | 0 |
| Operation Scheme | Calculation Results | Evaluation Index | ||||
|---|---|---|---|---|---|---|
| Generated Power/104 kW·h | Reservoir Inflow Quantity/104 m3 | Reservoir Outflow Quantity/104 m3 | Power Generation Benefits/104 kW·h | Risk Rate of Beyond-Limit Water Level/% | Discarded Water Quantity/104 m3 | |
| (1) | (2) | (3) | (4) 1 | (5) | (6) | |
| Traditional scheme | 36.66 | 1123.86 | 1259.38 | 32.49 | 3.125 | 0 |
| Integrated scheme | 34.49 | 1123.86 | 1166.16 | 33.19 | 0 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wu, J.; Yu, H.; Ji, C. Formulation and Implementation of Short-Term Optimal Reservoir Operation Schemes Integrated with Operation Rules. Water 2019, 11, 944. https://doi.org/10.3390/w11050944
Zhang Y, Wu J, Yu H, Ji C. Formulation and Implementation of Short-Term Optimal Reservoir Operation Schemes Integrated with Operation Rules. Water. 2019; 11(5):944. https://doi.org/10.3390/w11050944
Chicago/Turabian StyleZhang, Yanke, Jiajie Wu, Hongjie Yu, and Changming Ji. 2019. "Formulation and Implementation of Short-Term Optimal Reservoir Operation Schemes Integrated with Operation Rules" Water 11, no. 5: 944. https://doi.org/10.3390/w11050944
APA StyleZhang, Y., Wu, J., Yu, H., & Ji, C. (2019). Formulation and Implementation of Short-Term Optimal Reservoir Operation Schemes Integrated with Operation Rules. Water, 11(5), 944. https://doi.org/10.3390/w11050944




