A Numerical Study on Travel Time Based Hydraulic Tomography Using the SIRT Algorithm with Cimmino Iteration
Abstract
1. Introduction
2. Methodology
2.1. Discretization of the Line Integral
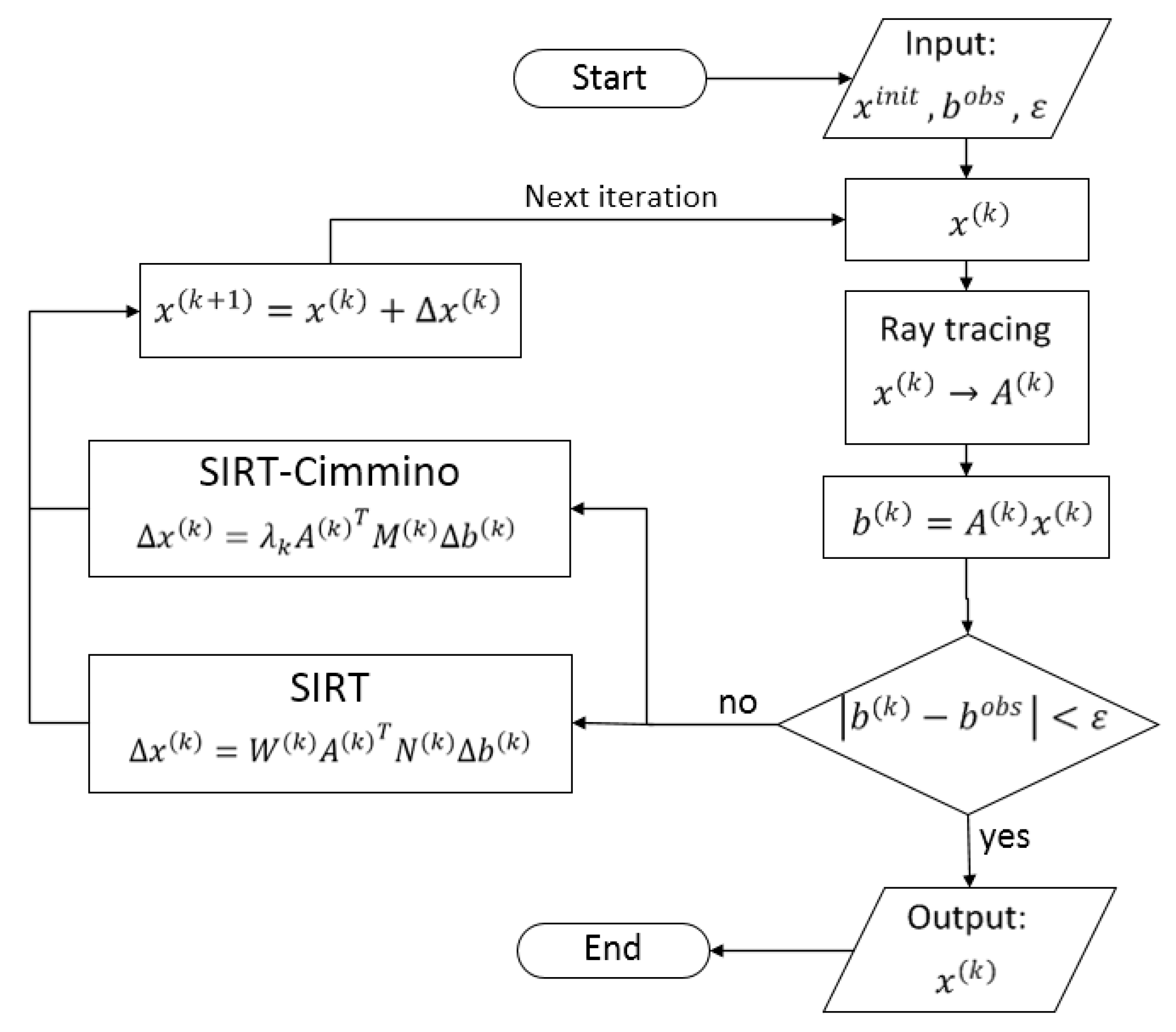
2.2. SIRT and SIRT-Cimmino Algorithms
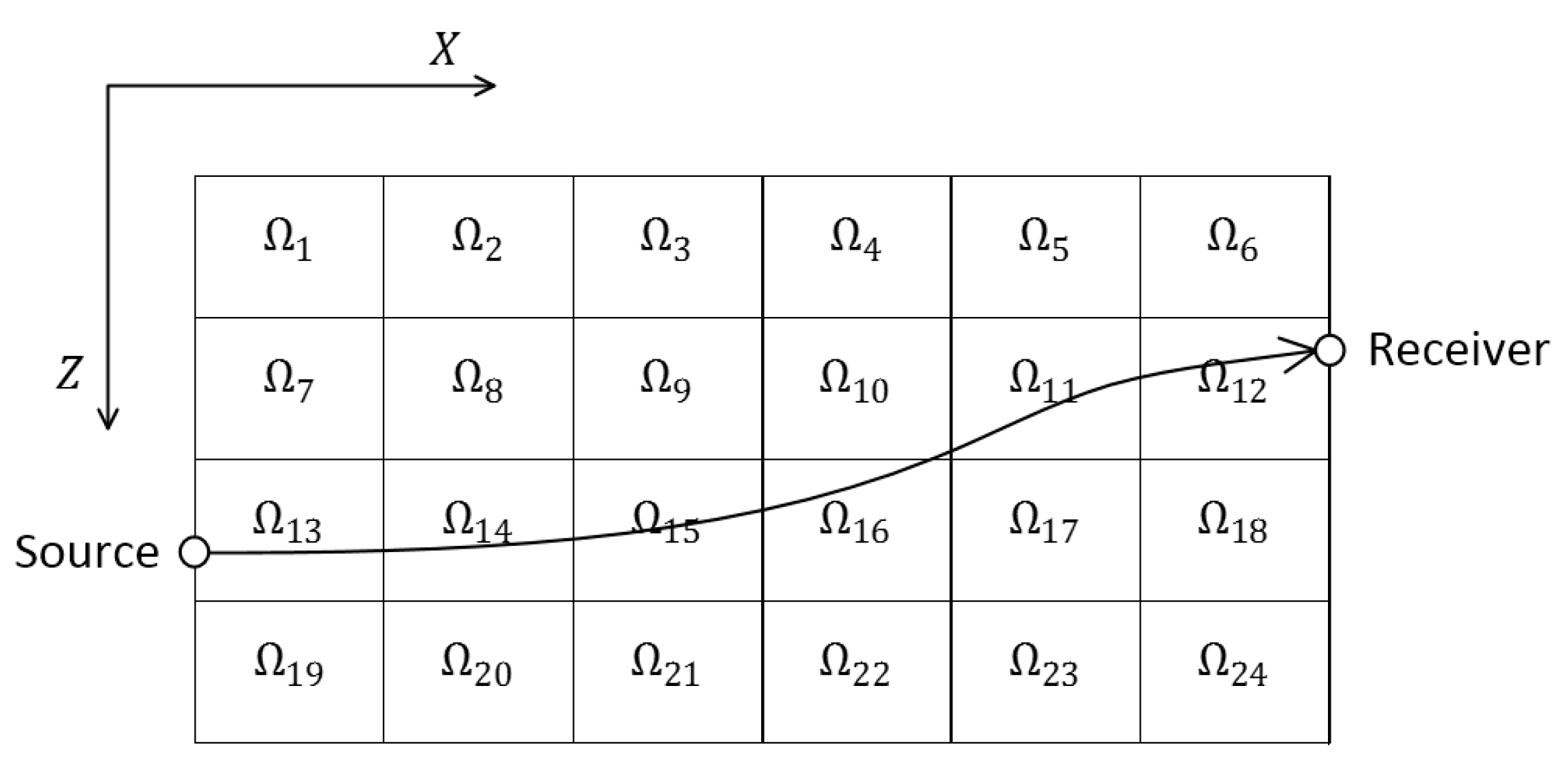
2.3. Ray-Tracing Technique
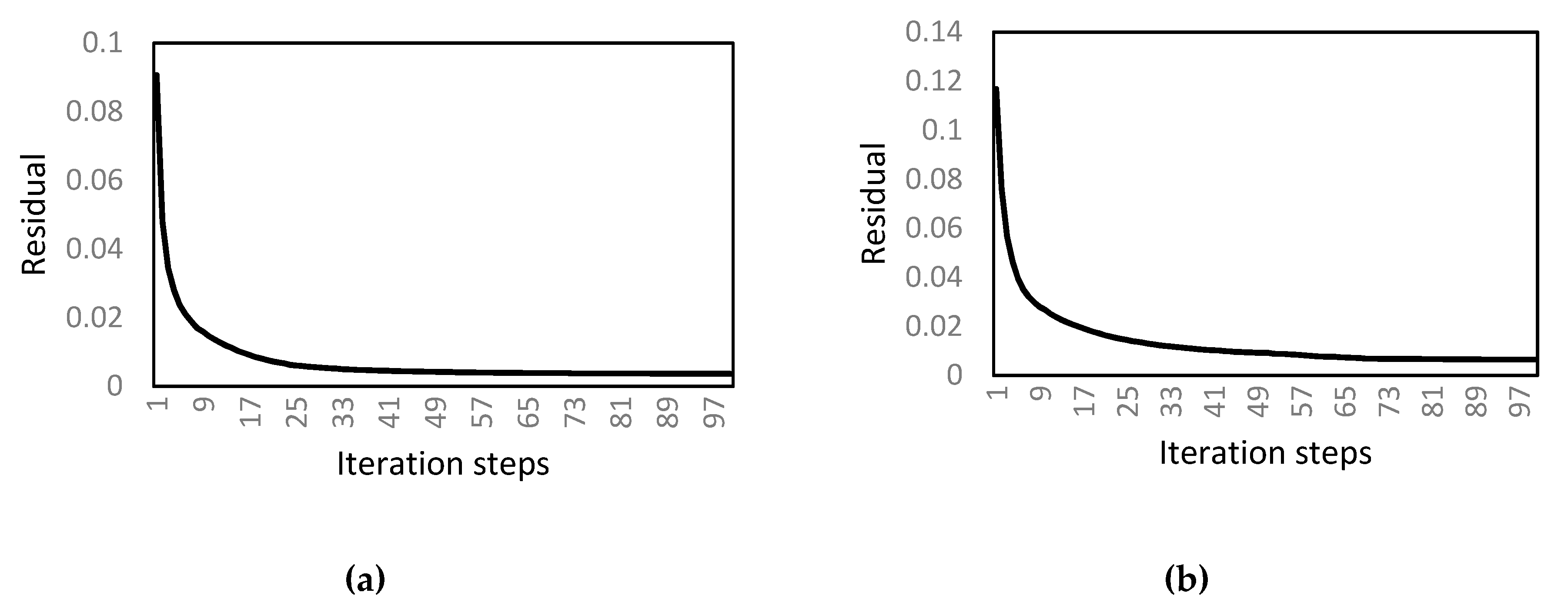
2.4. Residual, Root-Mean-Square Error and Correlation Coefficient
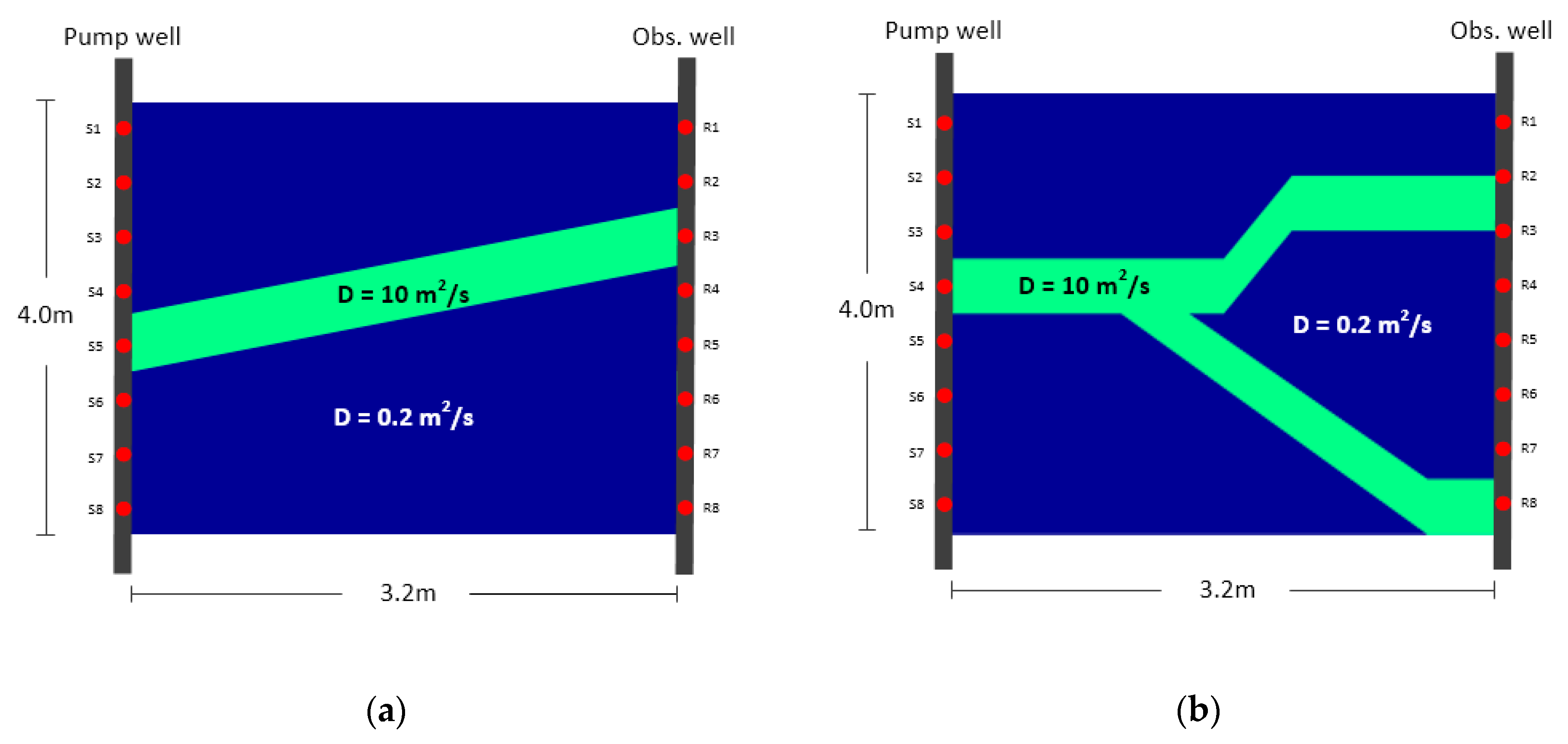
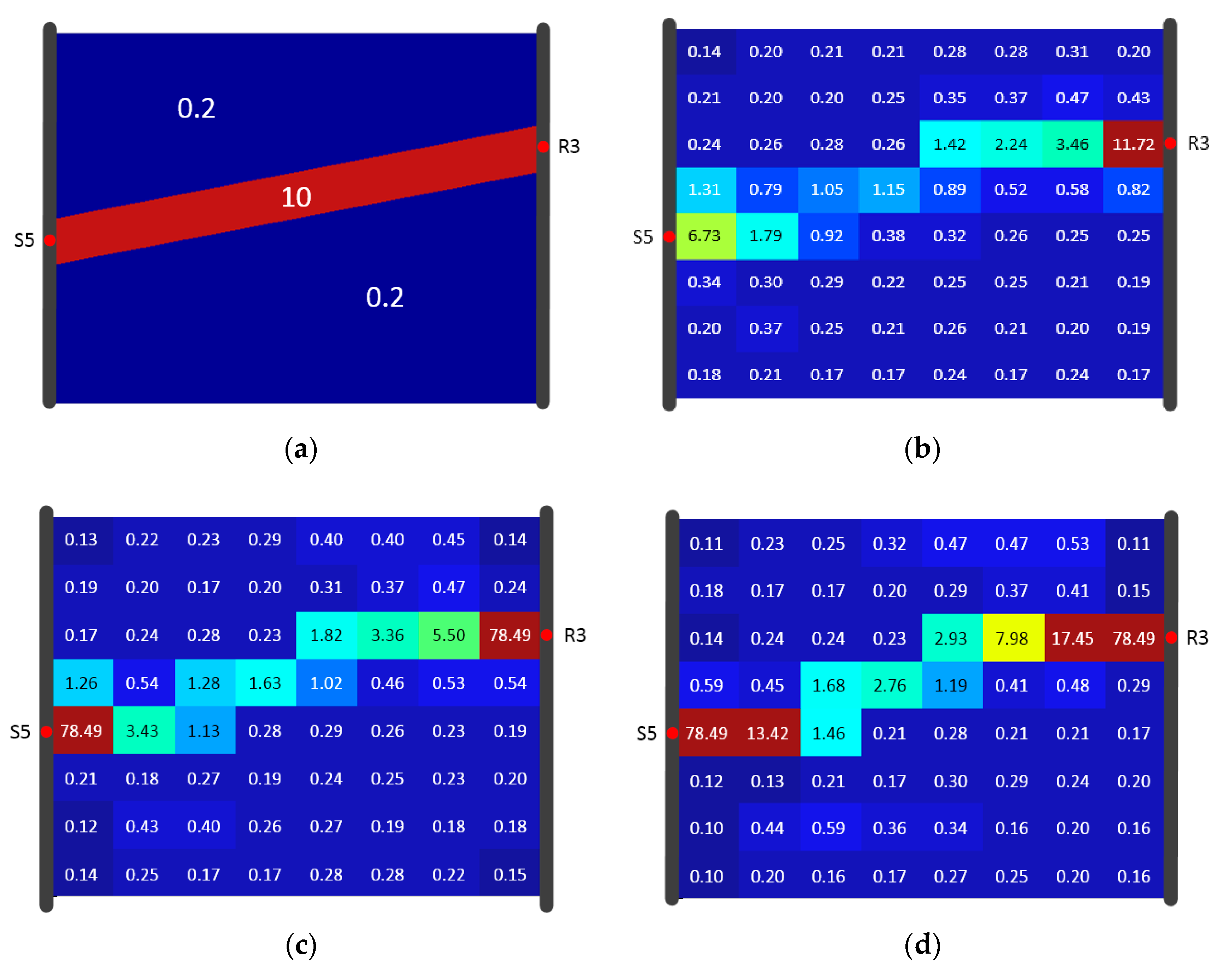
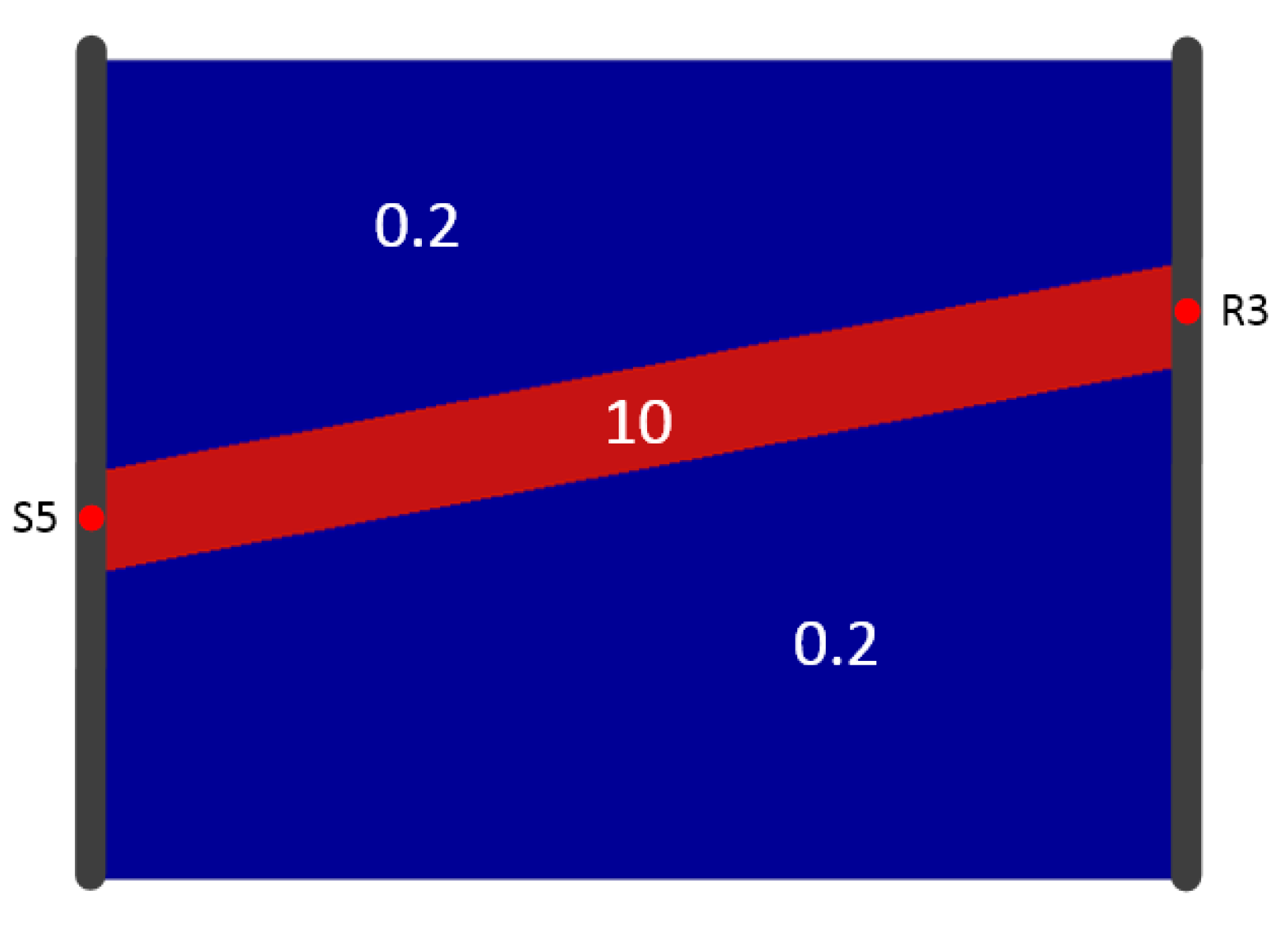
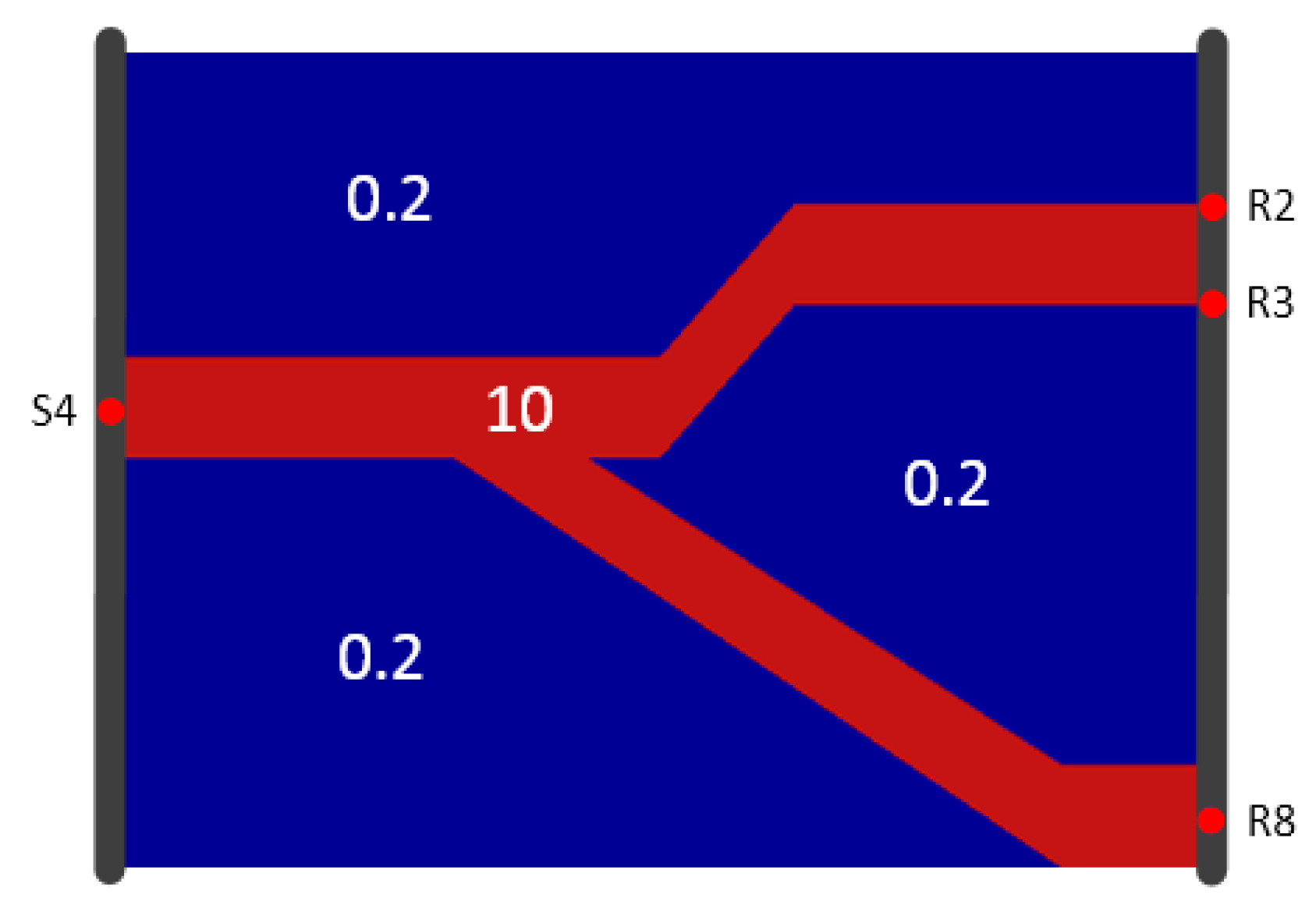
3. Numerical Study
4. Results
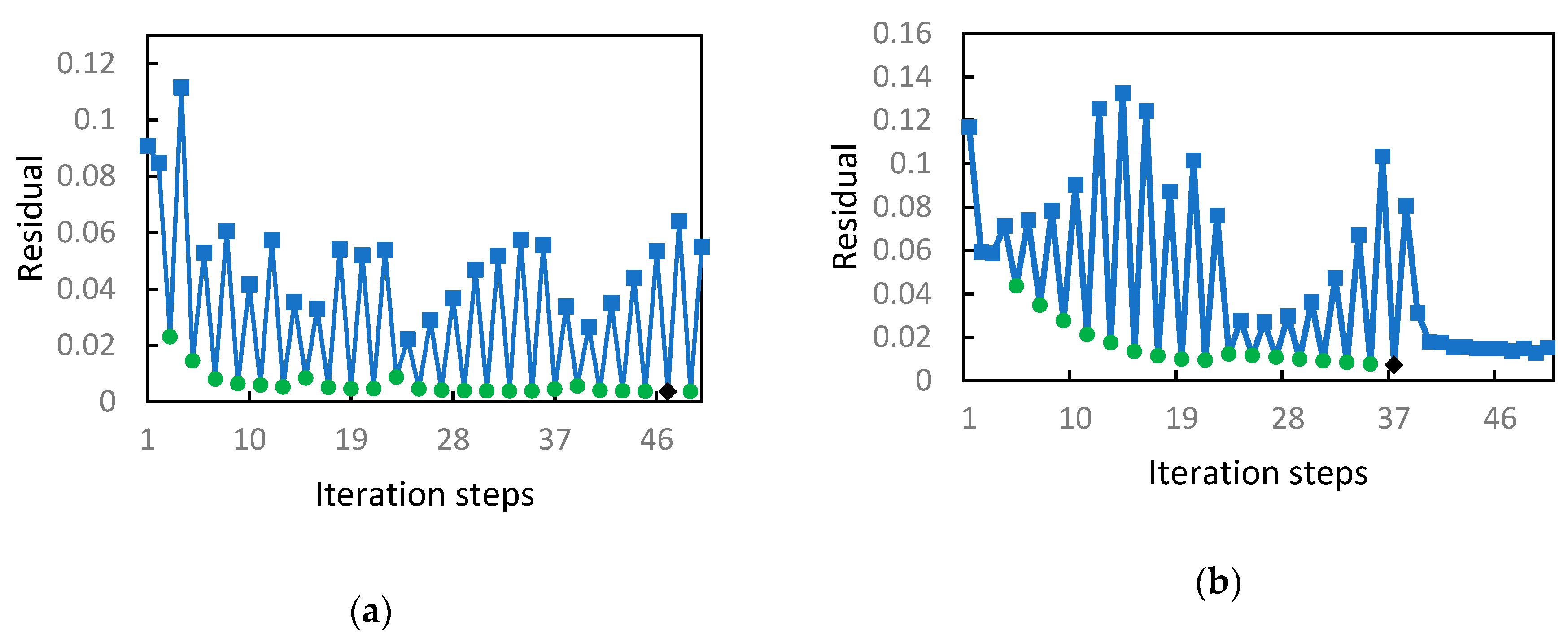
4.1. Result Selection Rule for SIRT
4.2. Result Selection Rule for SIRT-Cimmino
- (1)
- Calculating 50 steps of iteration (due to computational time);
- (2)
- Selecting a convergent subsequence with a low residual if convergent subsequences exist;
- (3)
- Choosing the step with the lowest residual in this convergent subsequence as the optimal NIS and the corresponding result as the SIRT-Cimmino reconstruction.
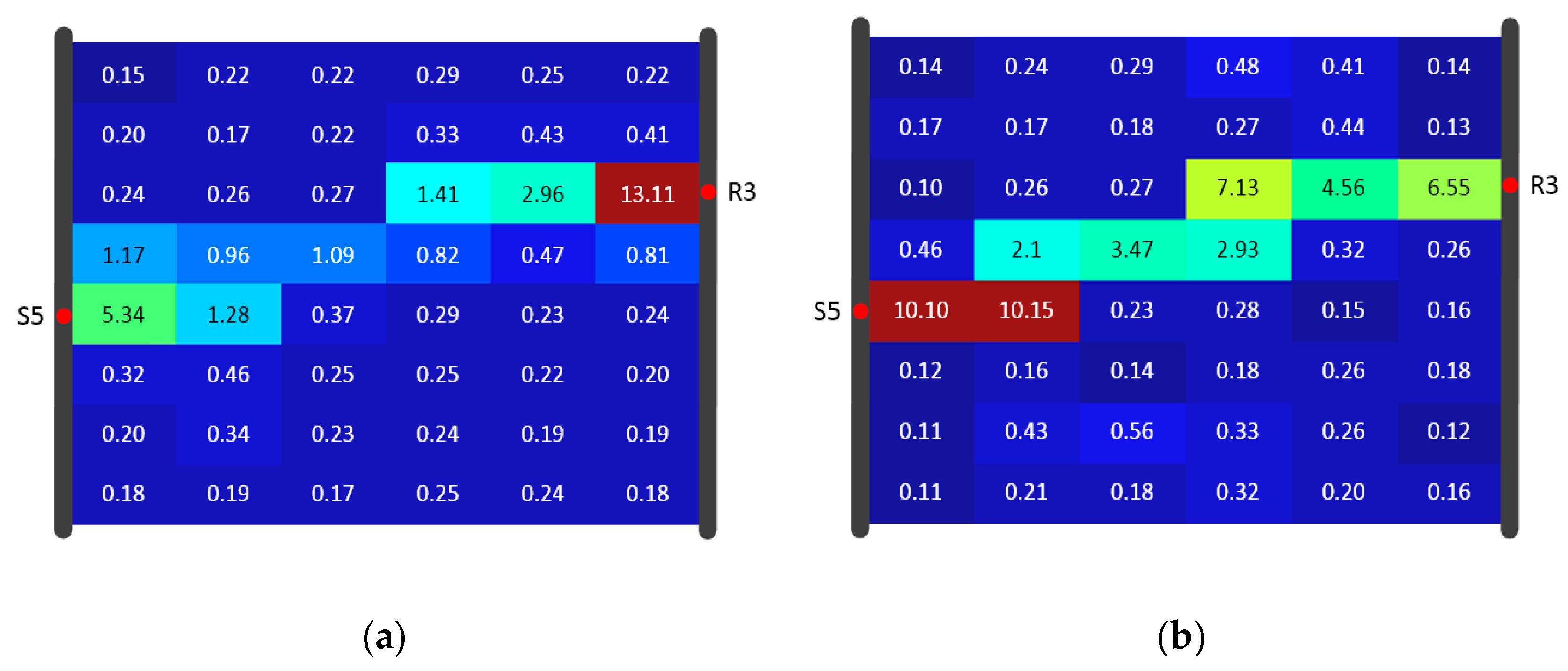
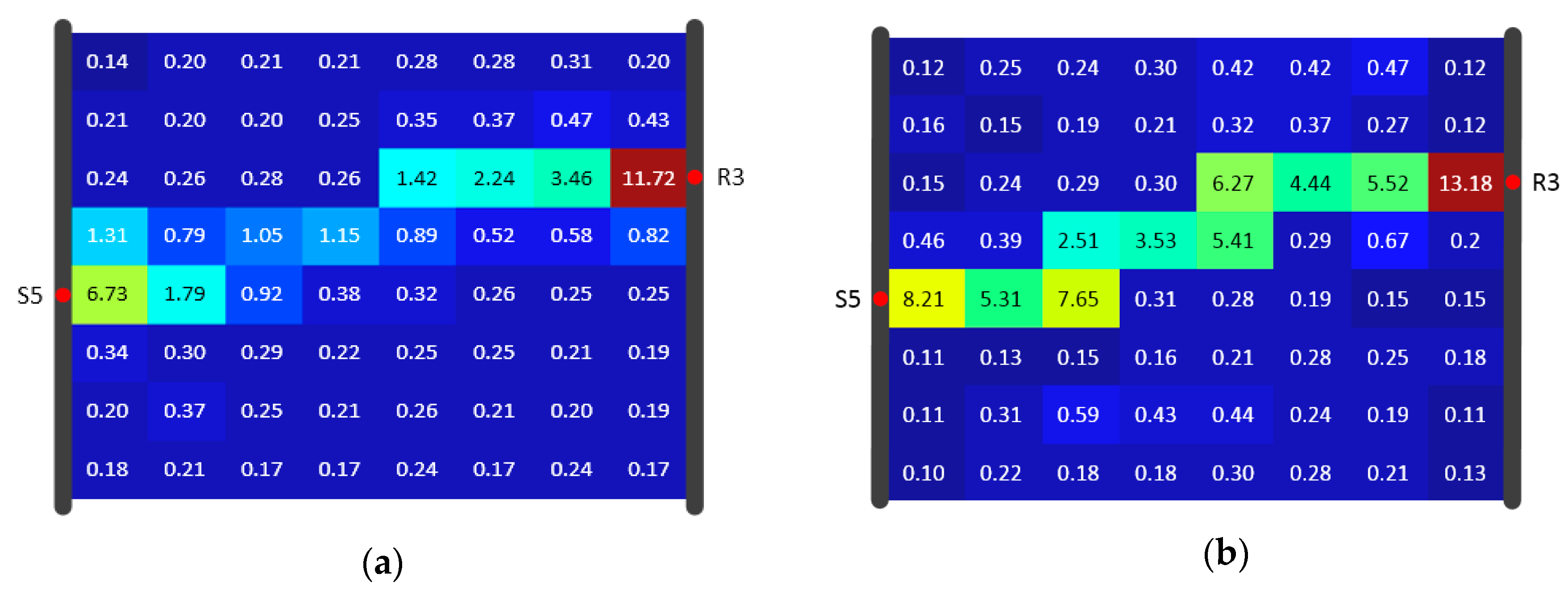
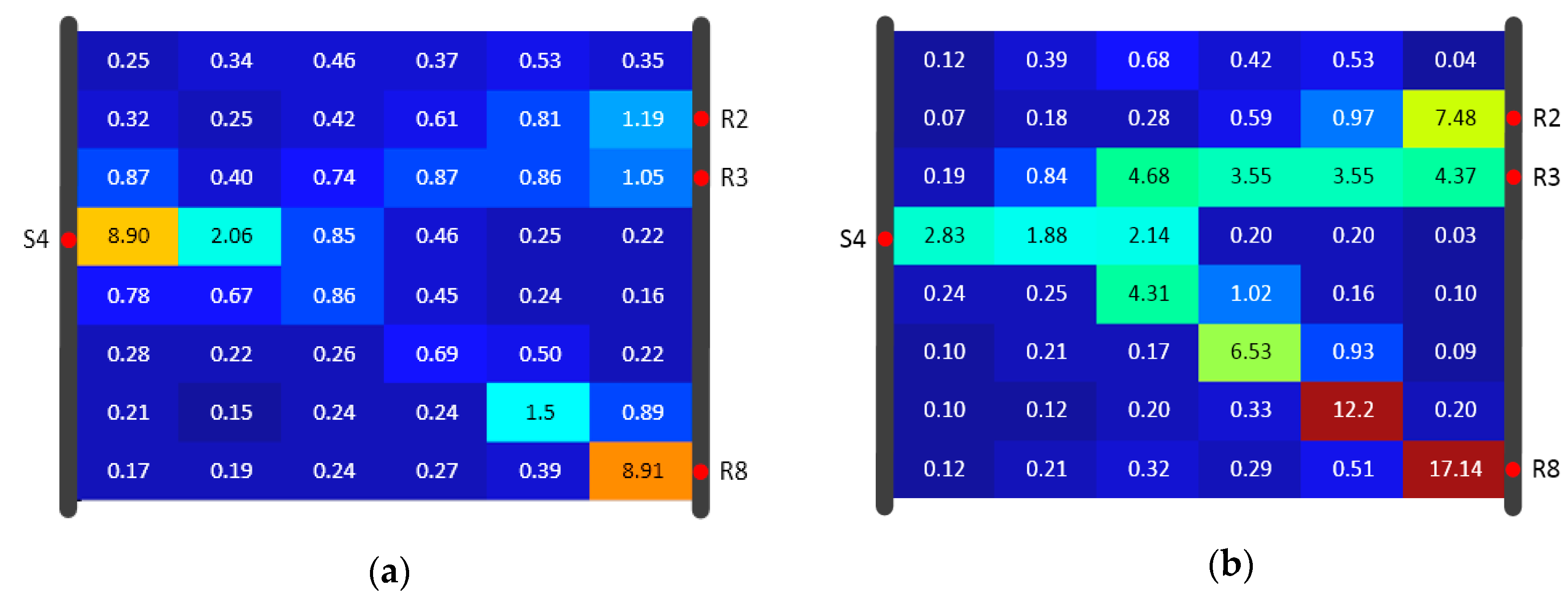
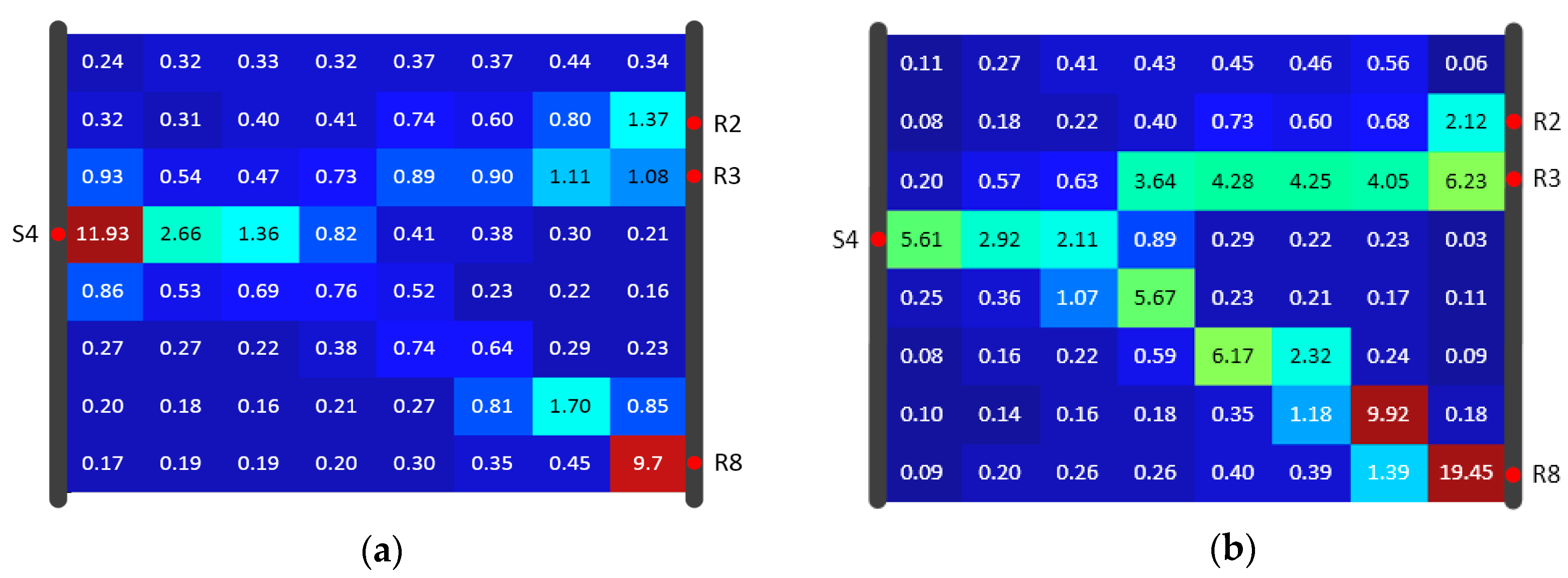
4.3. Reconstruction comparison of SIRT and SIRT-Cimmino for Model A
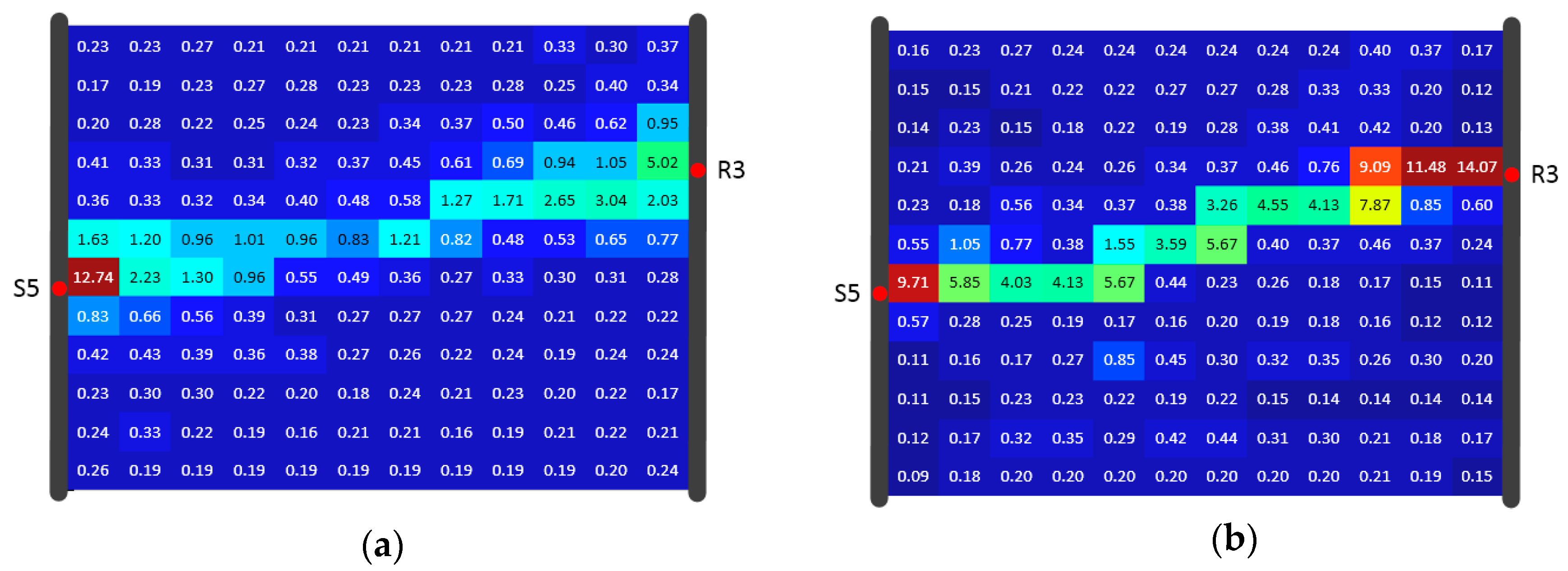
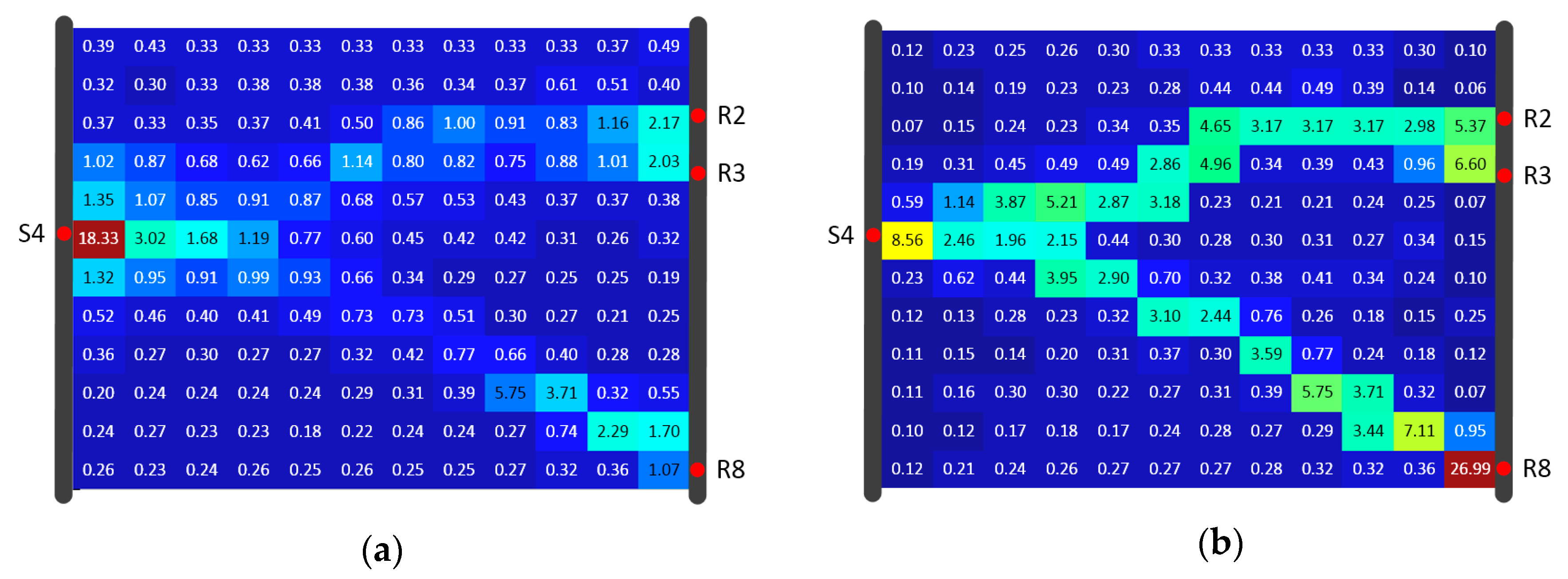
4.4. Reconstruction Comparison of SIRT and SIRT-Cimmino for Model B
5. Summary and Discussion
- (a)
- The overestimation of diffusivity occurs often in model cells near the source and receiver. The reason is the incremental correction built into every iteration step. The diffusivity in a cell is determined by the number of signals traveling through this cell. More signal trajectories in a cell lead to higher estimated diffusivity values, and the cells with a high signal trajectory density are always found at the joints of high diffusivity zones and wells. Depth orientated hydraulic tests (e.g., slug tests) are suggested for parameter estimation in the direct vicinity of the well to provide prior information and inversion constraints. This information could help delimit the inversion values.
- (b)
- Uniform grid setting within the study area affects the accuracy of the ray tracing approximation. Due to the non-uniqueness of the propagation path and the computational burden, the grid is not set to be very fine. An alternative is the adaptive mesh refinement method. With this method, the grid could be refined at the positions where the cells with a higher diffusivity gradient are detected. This method could not only reduce the computational burden but also improve the accuracy of the calculation.
- (c)
- Equal weight for all signals is utilized through the inversion in this study. In reality, an appropriate data subset could deliver better inversion result rather than the whole data set. For example, the inversion results from Hu et al. [14] have shown that pressure signals with a limited source–receiver angle could image horizontal features of the aquifer better. With the help of an appropriate weighting rule, more spatial features could be discovered.
- (d)
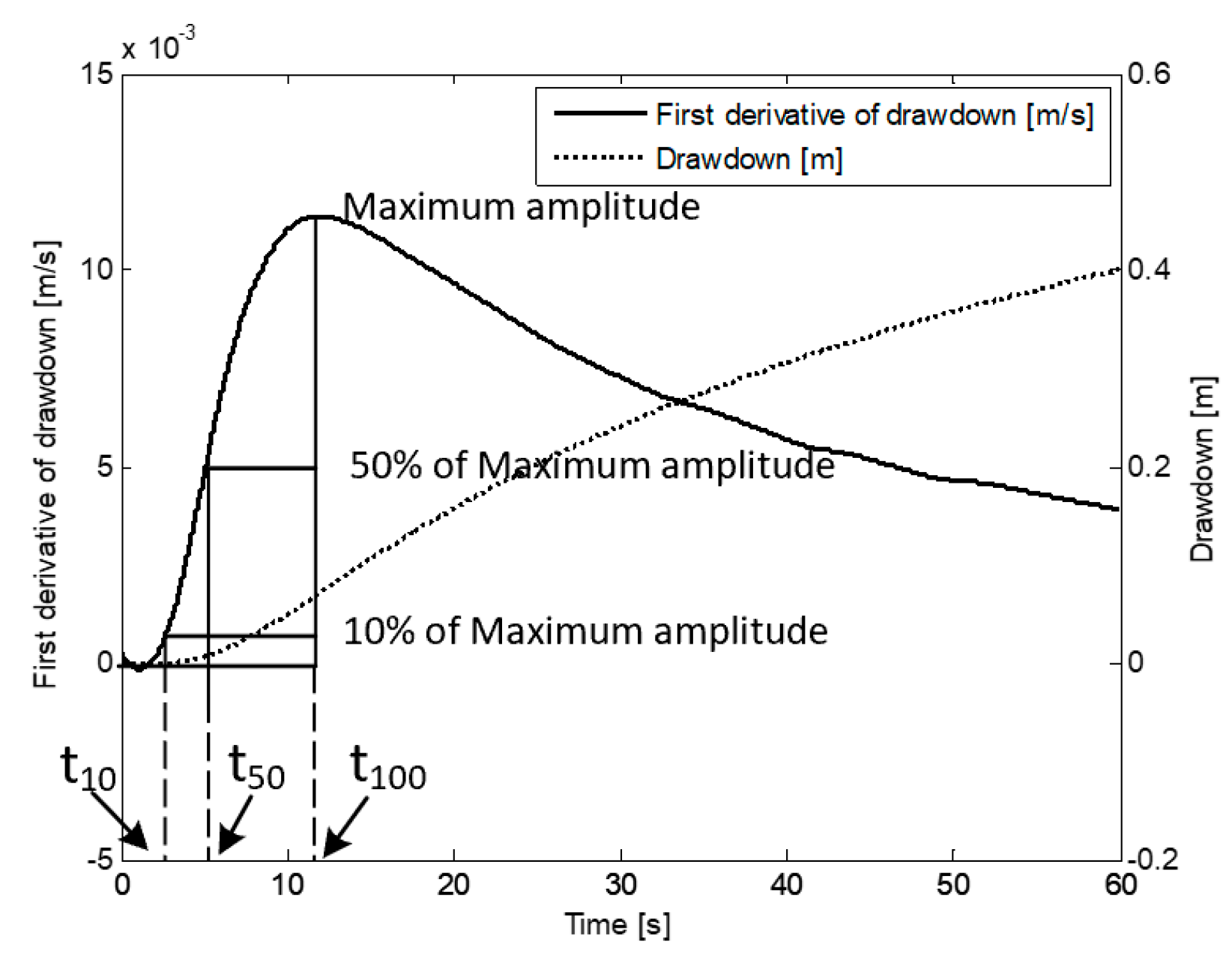
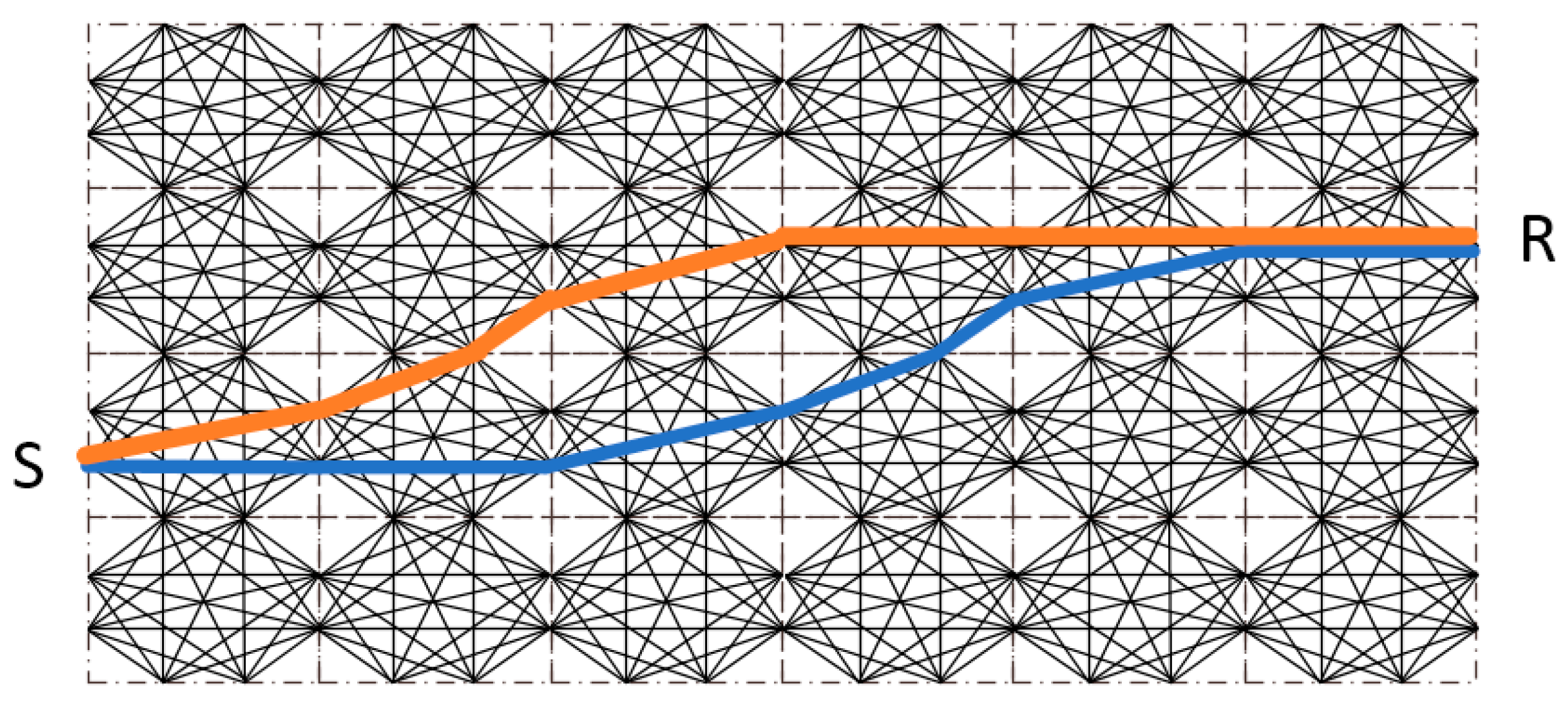
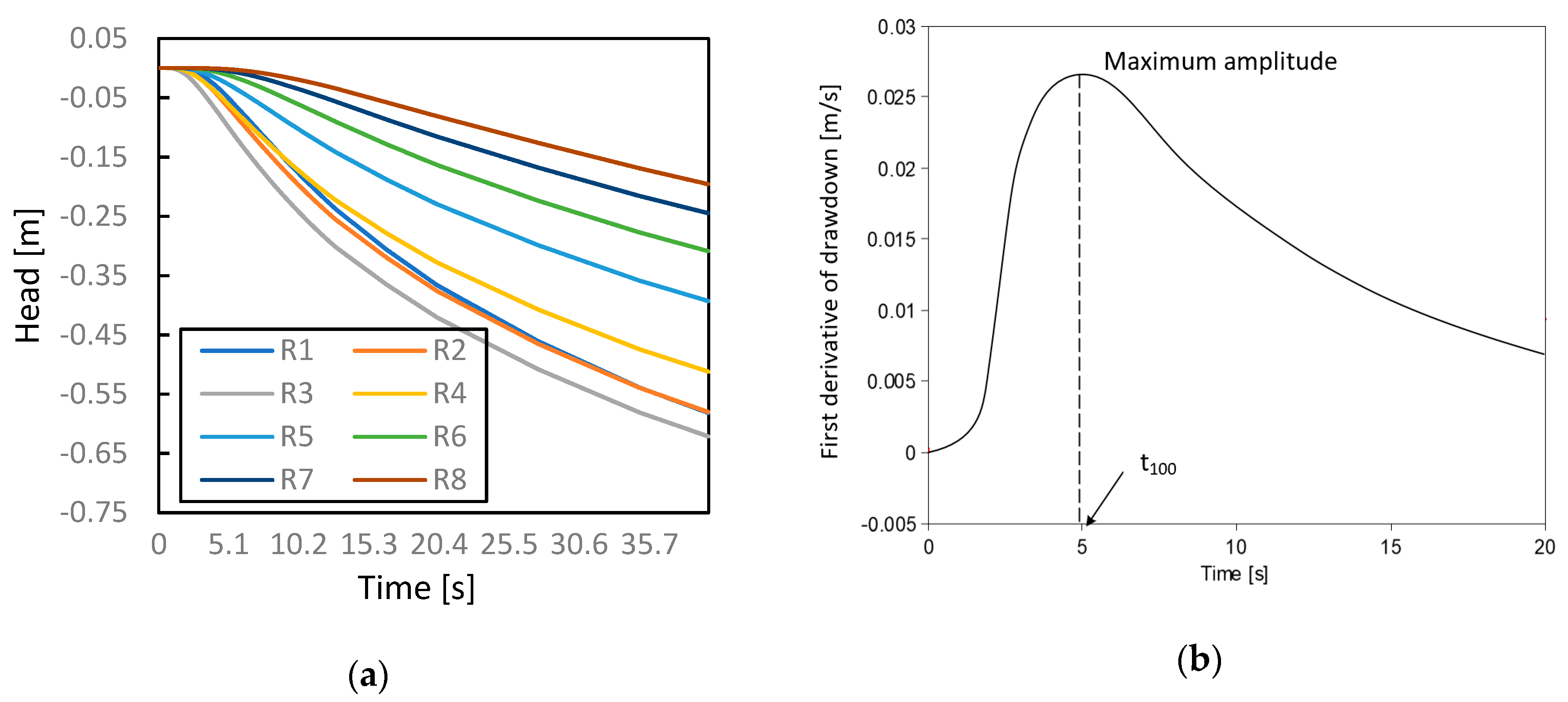
- Different types of travel time have different favorites on parameter characterization. Based on the Fermat principle, earlier arrival data reflect the path(s) of higher diffusivity. Hence, inversion results based on early travel times (e.g., or in Figure 1) could better reconstruct the connectivity of a high diffusivity zone. The late travel times (e.g., ) reflect more integral information of the entire aquifer, so a combination of different kinds of travel times could provide further characterization of aquifer properties.
Computer Code Availability
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Scudder, H.J. Introduction to Computer Aided Tomography. Proc. IEEE 1978, 66, 628–637. [Google Scholar] [CrossRef]
- Nolet, G. A Breviary of Seismic Tomography; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Tarantola, A. Inverse Problem Theory; Society of Industrial and Applied Mathematics: Philadelphia, PA, USA, 2005. [Google Scholar]
- Kaczmarz, S. Angenäherte Auflösung von Systemen linearer Gleichungen. Bull. Int. Acad. Pol. Sci. Lett. Cl. Sci. Math. Nat. 1937, 35, 355–357. [Google Scholar]
- Gilbert, P. Iterative Methods for the Three-Dimensional Reconstruction of An Object from Projections. J. Theor. Biol. 1972, 36, 105–117. [Google Scholar] [CrossRef]
- Gordon, R.; Bender, R.; Herman, G.T. Algebraic Reconstruction Techniques (ART) for Three-Dimensional Electron Microscopy and X-Ray Photography. J. Theor. Biol. 1970, 29, 471–481. [Google Scholar] [CrossRef]
- Qiao, L.; Li, L.; Chen, Z. Accelerated SIRT algorithm based on multigrid. CT Theory Appl. 2013, 22, 25–31. [Google Scholar]
- Berg, S.J.; Illman, W.A. Three-dimensional transient hydraulic tomography in a highly heterogeneous glaciofluvial aquifer-aquitard system. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Berg, S.J.; Illman, W.A. Comparison of hydraulic tomography with traditional methods at a highly heterogeneous site. Ground Water 2015, 53, 71–89. [Google Scholar] [CrossRef] [PubMed]
- Brauchler, R.; Böhm, G.; Leven, C.; Dietrich, P.; Sauter, M. A laboratory study of tracer tomography. Hydrogeol. J. 2013, 21, 1265–1274. [Google Scholar] [CrossRef]
- Cardiff, M.; Barrash, W. 3-D transient hydraulic tomography in unconfined aquifers with fast drainage response. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Hao, Y.; Yeh, T.C.; Han, B.; Xiang, J.; Zhu, F.; Ni, C. Imaging fracture connectivity hydraulic tomography. Hydrogeol. Eng. Geol. 2008, 6, 6–11. [Google Scholar]
- Hochstetler, D.L.; Barrash, W.; Leven, C.; Cardiff, M.; Chidichimo, F.; Kitanidis, P.K. Hydraulic Tomography: Continuity and Discontinuity of High-K and Low-K Zones. Ground Water 2016, 54, 171–185. [Google Scholar] [CrossRef] [PubMed]
- Hu, R.; Brauchler, R.; Herold, M.; Bayer, P. Hydraulic tomography analog outcrop study: Combining travel time and steady shape inversion. J. Hydrol. 2011, 409, 350–362. [Google Scholar] [CrossRef]
- Illman, W.A. Hydraulic Tomography Offers Improved Imaging of Heterogeneity in Fractured Rocks. Groundwater 2014, 52, 659–684. [Google Scholar] [CrossRef] [PubMed]
- Illman, W.A. Lessons Learned from Hydraulic and Pneumatic Tomography in Fractured Rocks. Procedia Environ. Sci. 2015, 25, 127–134. [Google Scholar] [CrossRef]
- Illman, W.A.; Craig, A.J.; Liu, X. Practical issues in imaging hydraulic conductivity through hydraulic tomography. Ground Water 2008, 46, 120–132. [Google Scholar] [CrossRef] [PubMed]
- Illman, W.A.; Liu, X.; Craig, A. Steady-state hydraulic tomography in a laboratory aquifer with deterministic heterogeneity: Multi-method and multiscale validation of hydraulic conductivity tomograms. J. Hydrol. 2007, 341, 222–234. [Google Scholar] [CrossRef]
- Illman, W.A.; Liu, X.; Takeuchi, S.; Yeh, T.-C.J.; Ando, K.; Saegusa, H. Hydraulic tomography in fractured granite: Mizunami Underground Research site, Japan. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Liu, X.; Illman, W.A.; Craig, A.J.; Zhu, J.; Yeh, T.C.J. Laboratory sandbox validation of transient hydraulic tomography. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Sanchez-Leon, E.; Leven, C.; Haslauer, C.P.; Cirpka, O.A. Combining 3D Hydraulic Tomography with Tracer Tests for Improved Transport Characterization. Ground Water 2016, 54, 498–507. [Google Scholar] [CrossRef]
- Sun, R.; Yeh, T.-C.J.; Mao, D.; Jin, M.; Lu, W.; Hao, Y. A temporal sampling strategy for hydraulic tomography analysis. Water Resour. Res. 2013, 49, 3881–3896. [Google Scholar] [CrossRef]
- Xiang, J.; Yeh, T.-C.J.; Lee, C.-H.; Hsu, K.-C.; Wen, J.-C. A simultaneous successive linear estimator and a guide for hydraulic tomography analysis. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Yeh, T.C.; Mao, D.; Zha, Y.; Hsu, K.C.; Lee, C.H.; Wen, J.C.; Lu, W.; Yang, J. Why hydraulic tomography works? Ground Water 2014, 52, 168–172. [Google Scholar] [CrossRef] [PubMed]
- Yeh, T.C.J.; Liu, S. Hydraulic tomography: Development of a new aquifer test method. Water Resour. Res. 2000, 36, 2095–2105. [Google Scholar] [CrossRef]
- Zha, Y.; Yeh, T.C.J.; Illman, W.A.; Zeng, W.; Zhang, Y.; Sun, F.; Shi, L. A Reduced-Order Successive Linear Estimator for Geostatistical Inversion and its Application in Hydraulic Tomography. Water Resour. Res. 2018, 54, 1616–1632. [Google Scholar] [CrossRef]
- Zha, Y.; Yeh, T.-C.J.; Illman, W.A.; Onoe, H.; Mok, C.M.W.; Wen, J.-C.; Huang, S.-Y.; Wang, W. Incorporating geologic information into hydraulic tomography: A general framework based on geostatistical approach. Water Resour. Res. 2017, 53, 2850–2876. [Google Scholar] [CrossRef]
- Zhu, J.; Yeh, T.-C.J. Characterization of aquifer heterogeneity using transient hydraulic tomography. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Hu, L.; Bayer, P.; Alt-Epping, P.; Tatomir, A.; Sauter, M.; Brauchler, R. Time-lapse pressure tomography for characterizing CO2 plume evolution in a deep saline aquifer. Int. J. Greenh. Gas Control 2015, 39, 91–106. [Google Scholar] [CrossRef]
- Hu, R.; Zhao, W.; Brauchler, R. An Aquifer Analogue Study of High Resolution Aquifer Characterization Based on Hydraulic Tomography. In Proceedings of the Geoshanghai 2010 International Conference, Shanghai, China, 3–5 June 2010. [Google Scholar]
- Fienen, M.N.; Clemo, T.; Kitanidis, P.K. An interactive Bayesian geostatistical inverse protocol for hydraulic tomography. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Lee, J.; Kitanidis, P.K. Large-scale hydraulic tomography and joint inversion of head and tracer data using the Principal Component Geostatistical Approach (PCGA). Water Resour. Res. 2014, 50, 5410–5427. [Google Scholar] [CrossRef]
- Liu, X.; Kitanidis, P.K. Large-scale inverse modeling with an application in hydraulic tomography. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Hu, R.; Liu, Q.; Xing, Y. Case Study of Heat Transfer during Artificial Ground Freezing with Groundwater Flow. Water 2018, 10, 1322. [Google Scholar] [CrossRef]
- Brauchler, R.; Doetsch, J.; Dietrich, P.; Sauter, M. Derivation of site-specific relationships between hydraulic parameters and p-wave velocities based on hydraulic and seismic tomography. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Brauchler, R.; Hu, R.; Dietrich, P.; Sauter, M. A field assessment of high-resolution aquifer characterization based on hydraulic travel time and hydraulic attenuation tomography. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Brauchler, R.; Liedl, R.; Dietrich, P. A travel time based hydraulic tomographic approach. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Hu, R. Hydraulic Tomography: A New Approach Coupling Hydraulic Travel Time, Attenuation and Steady Shape Inversions for High-Spatial Resolution Aquifer Characterization. Ph.D. Thesis, University of Goettingen, Goettingen, Germany, 2011. [Google Scholar]
- He, Z.; Datta-Gupta, A.; Vasco, D.W. Rapid inverse modeling of pressure interference tests using trajectory-based traveltime and amplitude sensitivities. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Schöniger, A.; Nowak, W.; Hendricks Franssen, H.J. Parameter estimation by ensemble Kalman filters with transformed data: Approach and application to hydraulic tomography. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Vasco, D.W.; Keers, H.; Karasaki, K. Estimation of reservoir properties using transient pressure data: An asymptotic approach. Water Resour. Res. 2000, 36, 3447–3465. [Google Scholar] [CrossRef]
- Lo, T.-W.; Inderwiesen, P.L. Fundamentals of Seismic Tomography. In Geophysical Monograph Series; Society of Exploration Geophysicists: Tulsa, OK, USA, 1994. [Google Scholar]
- Kulkarni, K.N.; Datta-Gupta, A.; Vasco, D.W. A Streamline Approach for Integrating Transient Pressure Data into High-Resolution Reservoir Models. In Proceedings of the 2000 SPE European Petroleum Conference, Dallas, TX, USA, 1–4 October 2000. [Google Scholar]
- Moser, T.J. Shortest Path Calculation of Seismic Rays. Geophysics 1991, 56, 59–67. [Google Scholar] [CrossRef]
- Elble, J.M.; Sahinidis, N.V.; Vouzis, P. GPU computing with Kaczmarz’s and other iterative algorithms for linear systems. Parallel Comput. 2010, 36, 215–231. [Google Scholar] [CrossRef]
- Cimmino, G. Calcolo approssimato per le soluzioni dei sistemi di equazioni lineari. La Ricerca Scientifica XVI 1938, 9, 326–333. [Google Scholar]
- Elfving, T.; Nikazad, T.; Hansen, P.C. Semi-Convergence and Relaxation Parameters for A Class of SIRT Algorithms. Electron. Trans. Numer. Anal. 2010, 37, 321–336. [Google Scholar]
- Santos, L.T.D. A parallel subgradient projections method for the convex feasibility problem. J. Comput. Appl. Math. 1987, 18, 307–320. [Google Scholar] [CrossRef]
- Jackson, M.J.; Tweeton, D.R. 3DTOM: Three-Dimensional Geophysical Tomography, Report of Investigations 9617; United States Department of the Interior: Washington, DC, USA, 1996.
- Dijkstra, E.W. A Note on Two Prblems in Connexion with Graphys. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Nakanishi, I.; Yamaguchi, K. A numerical experiment on nonlinear image reconstruction from first-arrival times for two-dimensional island arc structure. J. Phys. Earth 1986, 34, 195–201. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)? – Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Bayer, P.; Finkel, M. Evolutionary algorithms for the optimization of advective control of contaminated aquifer zones. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
| SIRT | |||
|---|---|---|---|
| 8 × 6 | 8 × 8 | 12 × 12 | |
| Model A () | 11 | 10 | 5 |
| Model B () | 5 | 5 | 3 |
| RMSE | Correlation Coefficient | |||||
|---|---|---|---|---|---|---|
| 8 × 6 | 8 × 8 | 12 × 12 | 8 × 6 | 8 × 8 | 12 × 12 | |
| SIRT | 4.04 | 3.55 | 6.41 | 0.70 | 0.70 | 0.77 |
| SIRT-Cimmino | 2.86 | 3.77 | 4.24 | 0.73 | 0.72 | 0.79 |
| RMSE | Correlation Coefficient | |||||
|---|---|---|---|---|---|---|
| 8 × 6 | 8 × 8 | 12 × 12 | 8 × 6 | 8 × 8 | 12 × 12 | |
| SIRT | 10.39 | 4.66 | 7.11 | 0.64 | 0.63 | 0.61 |
| SIRT-Cimmino | 7.51 | 8.04 | 10.77 | 0.65 | 0.66 | 0.66 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, P.; Hu, R.; Hu, L.; Liu, Q.; Xing, Y.; Yang, H.; Qi, J.; Ptak, T. A Numerical Study on Travel Time Based Hydraulic Tomography Using the SIRT Algorithm with Cimmino Iteration. Water 2019, 11, 909. https://doi.org/10.3390/w11050909
Qiu P, Hu R, Hu L, Liu Q, Xing Y, Yang H, Qi J, Ptak T. A Numerical Study on Travel Time Based Hydraulic Tomography Using the SIRT Algorithm with Cimmino Iteration. Water. 2019; 11(5):909. https://doi.org/10.3390/w11050909
Chicago/Turabian StyleQiu, Pengxiang, Rui Hu, Linwei Hu, Quan Liu, Yixuan Xing, Huichen Yang, Junjie Qi, and Thomas Ptak. 2019. "A Numerical Study on Travel Time Based Hydraulic Tomography Using the SIRT Algorithm with Cimmino Iteration" Water 11, no. 5: 909. https://doi.org/10.3390/w11050909
APA StyleQiu, P., Hu, R., Hu, L., Liu, Q., Xing, Y., Yang, H., Qi, J., & Ptak, T. (2019). A Numerical Study on Travel Time Based Hydraulic Tomography Using the SIRT Algorithm with Cimmino Iteration. Water, 11(5), 909. https://doi.org/10.3390/w11050909