Impact of Unsteady Flow Events on Bedload Transport: A Review of Laboratory Experiments
Abstract
1. Introduction
2. Experimental Conditions
3. Hydrodynamic Aspects of Sediment Transport
4. Impact of Unsteady Flow on Bed Structure and Composition
5. Total and Fractional Bedload Transport
6. The Impact of Flood History on Bedload Transport
7. Recapitulation, Open Questions, and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Fielding, C.R.; Alexander, J.; Allen, J.P. The role of discharge variability in the formation and preservation of alluvial sediment bodies. Sediment. Geol. 2018, 365, 1–20. [Google Scholar] [CrossRef]
- Millares, A.; Polo, M.J.; Monino, A.; Herrero, J.; Losada, M.A. Bed load dynamics and associated snowmelt influence in mountainous and semiarid alluvial rivers. Geomorphology 2014, 206, 330–342. [Google Scholar] [CrossRef]
- Aigner, J.; Kreisler, A.; Rindler, R.; Hauer, C.; Habersack, H. Bedload pulses in a hydropower affected alpine gravel bed river. Geomorphology 2017, 291, 116–127. [Google Scholar] [CrossRef]
- Mueller, E.R.; Schmidt, J.C.; Topping, D.J.; Shafroth, P.B.; Rodriguez-Burgueno, J.E.; Ramirez-Hernandez, J.; Grams, P.E. Geomorphic change and sediment transport during a small artificial flood in a transformed post-dam delta: The Colorado River delta, United States and Mexico. Ecol. Eng. 2017, 106, 757–775. [Google Scholar] [CrossRef]
- Hassan, M.A.; Egozi, R.; Parker, G. Experiments on the effect of hydrograph characteristics on vertical grain sorting in gravel bed rivers. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Billi, P. Flash flood sediment transport in a steep sand-bed ephemeral stream. Int. J. Sediment Res. 2011, 26, 193–209. [Google Scholar] [CrossRef]
- Reid, I.; Laronne, J.B.; Powell, D.M. Flash-flood and bedload dynamics of desert gravel-bed streams. Hydrol. Process. 1998, 12, 543–557. [Google Scholar] [CrossRef]
- Sui, J.; Koehler, G.; Krol, F. Characteristics of Rainfall, Snowmelt and Runoff in the Headwater Region of the Main River Watershed in Germany. Water Resour. Manag. 2010, 24, 2167–2186. [Google Scholar] [CrossRef]
- Kampf, S.K.; Lefsky, M.A. Transition of dominant peak flow source from snowmelt to rainfall along the Colorado Front Range: Historical patterns, trends, and lessons from the 2013 Colorado Front Range floods. Water Resour. Res. 2016, 52, 407–422. [Google Scholar] [CrossRef]
- Tabarestani, M.K.; Zarrati, A.R. Sediment transport during flood event: A review. Int. J. Environ. Sci. Technol. 2015, 12, 775–788. [Google Scholar] [CrossRef]
- Phillips, C.B.; Hill, K.M.; Paola, C.; Singer, M.B.; Jerolmack, D.J. Effect of Flood Hydrograph Duration, Magnitude, and Shape on Bed Load Transport Dynamics. Geophys. Res. Lett. 2018, 45, 8264–8271. [Google Scholar] [CrossRef]
- Guney, M.S.; Bombar, G.; Aksoy, A.O. Experimental Study of the Coarse Surface Development Effect on the Bimodal Bed-Load Transport under Unsteady Flow Conditions. J. Hydraul. Eng. 2013, 139, 12–21. [Google Scholar] [CrossRef]
- Lee, K.T.; Liu, Y.L.; Cheng, K.H. Experimental investigation of bedload transport processes under unsteady flow conditions. Hydrol. Process. 2004, 18, 2439–2454. [Google Scholar] [CrossRef]
- Muirhead, R.W.; Davies-Colley, R.J.; Donnison, A.M.; Nagels, J.W. Faecal bacteria yields in artificial flood events: Quantifying in-stream stores. Water Res. 2004, 38, 1215–1224. [Google Scholar] [CrossRef]
- Yager, E.M.; Kenworthy, M.; Monsalve, A. Taking the river inside: Fundamental advances from laboratory experiments in measuring and understanding bedload transport processes. Geomorphology 2015, 244, 21–32. [Google Scholar] [CrossRef]
- Rickenmann, D. Variability of Bed Load Transport during Six Summers of Continuous Measurements in Two Austrian Mountain Streams (Fischbach and Ruetz). Water Resour. Res. 2018, 54, 107–131. [Google Scholar] [CrossRef]
- Hallermeier, R.J. Oscillatory bedload transport: Data review and simple formulation. Cont. Shelf Res. 1982, 1, 159–190. [Google Scholar] [CrossRef]
- Ribberink, J.S.; Katopodi, I.; Ramadan, K.A.H.; Koelewijn, R.; Longo, S. Sediment transport under (non)-linear waves and currents. In Proceedings of the 24th International Conference on Coastal Engineering, Kobe, Japan, 23–28 October 1994. [Google Scholar] [CrossRef]
- Fang, H.W.; Chen, M.H.; Chen, Q.H. One-dimensional numerical simulation of non-uniform sediment transport under unsteady flows. Int. J. Sediment Res. 2008, 23, 316–328. [Google Scholar] [CrossRef]
- Caviedes-Voullieme, D.; Morales-Hernandez, M.; Juez, C.; Lacasta, A.; Garcia-Navarro, P. Two-Dimensional Numerical Simulation of Bed-Load Transport of a Finite-Depth Sediment Layer: Applications to Channel Flushing. J. Hydraul. Eng. 2017, 143. [Google Scholar] [CrossRef]
- Soares-Frazao, S.; Zech, Y. HLLC scheme with novel wave-speed estimators appropriate for two-dimensional shallow-water flow on erodible bed. Int. J. Numer. Methods Fluids 2011, 66, 1019–1036. [Google Scholar] [CrossRef]
- Gunsolus, E.H.; Binns, A.D. Effect of morphologic and hydraulic factors on hysteresis of sediment transport rates in alluvial streams. River Res. Appl. 2018, 34, 183–192. [Google Scholar] [CrossRef]
- Bombar, G.; Elci, S.; Tayfur, G.; Guney, S.; Bor, A. Experimental and Numerical Investigation of Bed-Load Transport under Unsteady Flows. J. Hydraul. Eng. 2011, 137, 1276–1282. [Google Scholar] [CrossRef]
- Mao, L. The effect of hydrographs on bed load transport and bed sediment spatial arrangement. J. Geophys. Res. Earth Surf. 2012, 117. [Google Scholar] [CrossRef]
- Mao, L. The effects of flood history on sediment transport in gravel-bed rivers. Geomorphology 2018, 322, 196–205. [Google Scholar] [CrossRef]
- Perret, E.; Berni, C.; Camenen, B.; Herrero, A.; Abderrezzak, K.E. Transport of moderately sorted gravel at low bed shear stresses: The role of fine sediment infiltration. Earth Surf. Process. Landf. 2018, 43, 1416–1430. [Google Scholar] [CrossRef]
- Humphries, R.; Venditti, J.G.; Sklar, L.S.; Wooster, J.K. Experimental evidence for the effect of hydrographs on sediment pulse dynamics in gravel-bedded rivers. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Wang, L.; Cuthbertson, A.J.S.; Pender, G.; Cao, Z. Experimental investigations of graded sediment transport under unsteady flow hydrographs. Int. J. Sediment Res. 2015, 30, 306–320. [Google Scholar] [CrossRef][Green Version]
- Li, Z.J.; Qian, H.L.; Cao, Z.X.; Liu, H.H.; Pender, G.; Hu, P.H. Enhanced bed load sediment transport by unsteady flows in a degrading channel. Int. J. Sediment Res. 2018, 33, 327–339. [Google Scholar] [CrossRef]
- Redolfi, M.; Bertoldi, W.; Tubino, M.; Welber, M. Bed Load Variability and Morphology of Gravel Bed Rivers Subject to Unsteady Flow: A Laboratory Investigation. Water Resour. Res. 2018, 54, 842–862. [Google Scholar] [CrossRef]
- Ferrer-Boix, C.; Hassan, M.A. Channel adjustments to a succession of water pulses in gravel bed rivers. Water Resour. Res. 2015, 51, 8773–8790. [Google Scholar] [CrossRef]
- Waters, K.A.; Curran, J.C. Linking bed morphology changes of two sediment mixtures to sediment transport predictions in unsteady flows. Water Resour. Res. 2015, 51, 2724–2741. [Google Scholar] [CrossRef]
- Wong, M.; Parker, G. One-dimensional modeling of bed evolution in a gravel bed river subject to a cycled flood hydrograph. J. Geophys. Res. Earth Surf. 2006, 111. [Google Scholar] [CrossRef]
- Mrokowska, M.M.; Rowinski, P.M.; Ksiazek, L.; Struzynski, A.; Wyrebek, M.; Radecki-Pawlik, A. Laboratory studies on bedload transport under unsteady flow conditions. J. Hydrol. Hydromech. 2018, 66, 23–31. [Google Scholar] [CrossRef]
- Curran, J.C.; Waters, K.A. The importance of bed sediment sand content for the structure of a static armor layer in a gravel bed river. J. Geophys. Res. Earth Surface 2014, 119, 1484–1497. [Google Scholar] [CrossRef]
- Orru, C.; Blom, A.; Uijttewaal, W.S.J. Armor breakup and reformation in a degradational laboratory experiment. Earth Surf. Dyn. 2016, 4, 461–470. [Google Scholar] [CrossRef]
- Curran, J.C.; Waters, K.A.; Cannatelli, K.M. Real time measurements of sediment transport and bed morphology during channel altering flow and sediment transport events. Geomorphology 2015, 244, 169–179. [Google Scholar] [CrossRef]
- Martin, R.L.; Jerolmack, D.J. Origin of hysteresis in bed form response to unsteady flows. Water Resour. Res. 2013, 49, 1314–1333. [Google Scholar] [CrossRef]
- Mrokowska, M.; Rowiński, P.; Książek, L.; Strużyński, A.; Wyrębek, M.; Radecki-Pawlik, A. Flume experiments on gravel bed load transport in unsteady flow—Preliminary results. In Hydrodynamic and Mass Transport at Freshwater Aquatic Interfaces; Rowiński, P., Ed.; Springer International Publishing Switzerland: Cham, Switzerland, 2016; pp. 221–233. [Google Scholar]
- Nelson, J.M.; Logan, B.L.; Kinzel, P.J.; Shimizu, Y.; Giri, S.; Shreve, R.L.; McLean, S.R. Bedform response to flow variability. Earth Surf. Process. Landf. 2011, 36, 1938–1947. [Google Scholar] [CrossRef]
- Piedra, M.M.; Haynes, H.; Hoey, T.B. The spatial distribution of coarse surface grains and the stability of gravel river beds. Sedimentology 2012, 59, 1014–1029. [Google Scholar] [CrossRef]
- Shvidchenko, A.B.; Kopaliani, Z.D. Hydraulic modeling of bed load transport in gravel-bed Laba River. J. Hydraul. Eng. 1998, 124, 778–785. [Google Scholar] [CrossRef]
- Ettema, R. Hydraulic modelling: Concepts and practice. In ASCE Manuals and Reports on Engineering Practice No. 97; American Society of Civil Engineers: Reston, VA, USA, 2000. [Google Scholar]
- Carbonneau, P.E.; Bergeron, N.E. The effect of bedload transport on mean and turbulent flow properties. Geomorphology 2000, 35, 267–278. [Google Scholar] [CrossRef]
- Nelson, J.M.; Shreve, R.L.; McLean, S.R.; Drake, T.G. Role of near-bed turbulence structure in bed-load transport and bed form mechanics. Water Resour. Res. 1995, 31, 2071–2086. [Google Scholar] [CrossRef]
- Dixit, S.; Patel, P. Stochastic nature of turbulence over mobile bed channels. J. Hydraul. Eng. 2018. [Google Scholar] [CrossRef]
- Dey, S.; Das, R.; Gaudio, R.; Bose, S.K. Turbulence in mobile-bed streams. Acta Geophys. 2012, 60, 1547–1588. [Google Scholar] [CrossRef]
- Bialik, R.J.; Nikora, V.I.; Karpinski, M.; Rowinski, P.M. Diffusion of bedload particles in open-channel flows: Distribution of travel times and second-order statistics of particle trajectories. Environ. Fluid Mech. 2015, 15, 1281–1292. [Google Scholar] [CrossRef]
- Spiller, S.M.; Ruther, N.; Friedrich, H. Dynamic Lift on an Artificial Static Armor Layer during Highly Unsteady Open Channel Flow. Water 2015, 7, 4951–4970. [Google Scholar] [CrossRef]
- Paiement-Paradis, G.; Marquis, G.; Roy, A. Effects of turbulence on the transport of individual particles as bedload in a gravel-bed river. Earth Surf. Process. Landf. 2011, 36, 107–116. [Google Scholar] [CrossRef]
- Song, T.; Chiew, Y.M.; Chin, C.O. Effect of bed-load movement on flow friction factor. J. Hydraul. Eng. 1998, 124, 165–175. [Google Scholar] [CrossRef]
- Hohermuth, B.; Weitbrecht, V. Influence of Bed-Load Transport on Flow Resistance of Step-Pool Channels. Water Resour. Res. 2018, 54, 5567–5583. [Google Scholar] [CrossRef]
- Campbell, L.; McEwan, I.; Nikora, V.; Pokrajac, D.; Gallagher, M.; Manes, C. Bed-load effects on hydrodynamics of rough-bed open-channel flows. J. Hydraul. Eng. 2005, 131, 576–585. [Google Scholar] [CrossRef]
- Recking, A.; Frey, P.; Paquier, A.; Belleudy, P.; Champagne, J.Y. Feedback between bed load transport and flow resistance in gravel and cobble bed rivers. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Ghimire, B.; Deng, Z. Event Flow Hydrograph-Based Method for Modeling Sediment Transport. J. Hydrol. Eng. 2013, 18, 919–928. [Google Scholar] [CrossRef]
- Graf, W.H.; Song, T. Bed-shear stresses in nonuniform and unsteady open-channel flows. J. Hydraul. Res. 1995, 33, 699–704. [Google Scholar] [CrossRef]
- Mrokowska, M.M.; Rowinski, P.M.; Kalinowska, M.B. A methodological approach of estimating resistance to flow under unsteady flow conditions. Hydrol. Earth Syst. Sci. 2015, 19, 4041–4053. [Google Scholar] [CrossRef]
- Rowinski, P.M.; Czernuszenko, W.; Pretre, J.M. Time-dependent shear velocities in channel routing. Hydrol. Sci. J. 2000, 45, 881–895. [Google Scholar] [CrossRef]
- Aberle, J.; Rowiński, P.M.; Henry, P.Y.; Detert, M. Auxiliary hydrodynamic variables. Bed shear stress. In Experimental Hydraulics, Volume 2: Methods, Instrumentation, Data Processing and Management; Aberle, J., Rennie, C., Admiraal, D., Muste, M., Eds.; CRC Press: Boca Raton, FL, USA, 2017; pp. 322–332. [Google Scholar]
- Tu, H.Z.; Graf, W.H. Friction in unsteady open-channel flow over gravel beds. J. Hydraul. Res. 1993, 31, 99–110. [Google Scholar] [CrossRef]
- Song, T.; Graf, W.H. Velocity and turbulence distribution in unsteady open-channel flows. J. Hydraul. Eng. 1996, 122, 141–154. [Google Scholar] [CrossRef]
- Nezu, I.; Nakagawa, H. Turbulence measurements in unsteady free-surface flows. Flow Meas. Instrum. 1995, 6, 49–59. [Google Scholar] [CrossRef]
- Ferreira, R.M.L.; Franca, M.J.; Leal, J.G.A.B.; Cardoso, A.H. Flow over rough mobile beds: Friction factor and vertical distribution of the longitudinal mean velocity. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Nikora, V.; McEwan, I.; McLean, S.; Coleman, S.; Pokrajac, D.; Walters, R. Double-averaging concept for rough-bed open-channel and overland flows: Theoretical background. J. Hydraul. Eng. 2007, 133, 873–883. [Google Scholar] [CrossRef]
- Mrokowska, M.M.; Rowinski, P.M.; Kalinowska, M.B. Evaluation of friction velocity in unsteady flow experiments. J. Hydraul. Res. 2015, 53, 659–669. [Google Scholar] [CrossRef]
- Bombar, G. Hysteresis and Shear Velocity in Unsteady Flows. J. Appl. Fluid Mech. 2016, 9, 839–853. [Google Scholar] [CrossRef]
- Ghimire, B.; Deng, Z.-Q. Event flow hydrograph-based method for shear velocity estimation. J. Hydraul. Res. 2011, 49, 272–275. [Google Scholar] [CrossRef]
- Meirovich, L.; Laronne, J.B.; Reid, I. The variation of water-surface slope and its significance for bedload transport during floods in gravel-bed streams. J. Hydraul. Res. 1998, 36, 147–157. [Google Scholar] [CrossRef]
- Frey, P.; Church, M. Bedload: A granular phenomenon. Earth Surf. Process. Landf. 2011, 36, 58–69. [Google Scholar] [CrossRef]
- Ferdowsi, B.; Ortiz, C.P.; Houssais, M.; Jerolmack, D.J. River-bed armouring as a granular segregation phenomenon. Nat. Commun. 2017, 8. [Google Scholar] [CrossRef]
- Reid, I.; Frostick, L.E.; Layman, J.T. The incidence and nature of bedload transport during flood flows in coarse-grained alluvial channels. Earth Surf. Process. Landf. 1985, 10, 33–44. [Google Scholar] [CrossRef]
- Bertin, S.; Friedrich, H. Effect of surface texture and structure on the development of stable fluvial armors. Geomorphology 2018, 306, 64–79. [Google Scholar] [CrossRef]
- Haschenburger, J.K.; Wilcock, P.R. Partial transport in a natural gravel bed channel. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Vericat, D.; Batalla, R.J.; Garcia, C. Breakup and reestablishment of the armour layer in a large gravel-bed river below dams: The lower Ebro. Geomorphology 2006, 76, 122–136. [Google Scholar] [CrossRef]
- Clayton, J.A.; Pitlick, J. Persistence of the surface texture of a gravel-bed river during a large flood. Earth Surf. Process. Landf. 2008, 33, 661–673. [Google Scholar] [CrossRef]
- Church, M.; Hassan, M.A. Mobility of bed material in Harris Creek. Water Resour. Res. 2002, 38. [Google Scholar] [CrossRef]
- Venditti, J.G.; Dietrich, W.E.; Nelson, P.A.; Wydzga, M.A.; Fadde, J.; Sklar, L. Mobilization of coarse surface layers in gravel-bedded rivers by finer gravel bed load. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Wilcock, P.R.; Kenworthy, S.T.; Crowe, J.C. Experimental study of the transport of mixed sand and gravel. Water Resour. Res. 2001, 37, 3349–3358. [Google Scholar] [CrossRef]
- Curran, J.C. The decrease in shear stress and increase in transport rates subsequent to an increase in sand supply to a gravel-bed channel. Sediment. Geol. 2007, 202, 572–580. [Google Scholar] [CrossRef]
- Church, M.; Ferguson, R.I. Morphodynamics: Rivers beyond steady state. Water Resour. Res. 2015, 51, 1883–1897. [Google Scholar] [CrossRef]
- Julien, P.Y.; Klaassen, G.J.; Ten Brinke, W.B.M.; Wilbers, A.W.E. Case study: Bed resistance of Rhine River during 1998 flood. J. Hydraul. Eng. 2002, 128, 1042–1050. [Google Scholar] [CrossRef]
- Reesink, A.J.H.; Parsons, D.R.; Ashworth, P.J.; Best, J.L.C.; Hardy, R.J.; Murphy, B.J.; McLelland, S.J.; Unsworth, C. The adaptation of dunes to changes in river flow. Earth-Sci. Rev. 2018, 185, 1065–1087. [Google Scholar] [CrossRef]
- Bloschl, G.; Hall, J.; Parajka, J.; Perdigao, R.A.P.; Merz, B.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; Bonacci, O.; Borga, M.; et al. Changing climate shifts timing of European floods. Science 2017, 357, 588–590. [Google Scholar] [CrossRef]
- Baynes, E.R.C.; van de Lageweg, W.I.; McLelland, S.J.; Parsons, D.R.; Aberle, J.; Dijkstra, J.; Henry, P.Y.; Rice, S.P.; Thom, M.; Moulin, F. Beyond equilibrium: Re-evaluating physical modelling of fluvial systems to represent climate changes. Earth-Sci. Rev. 2018, 181, 82–97. [Google Scholar] [CrossRef]
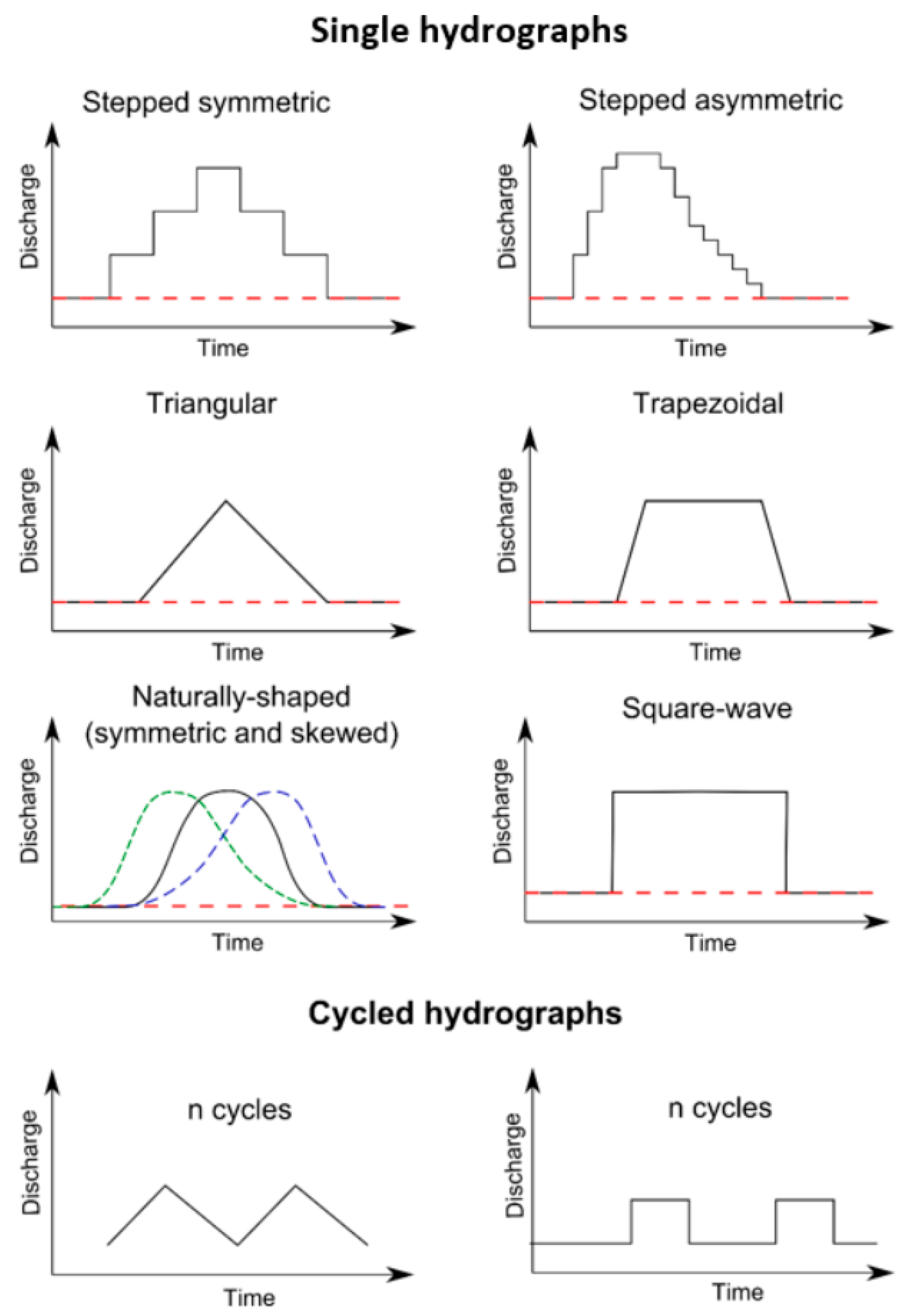
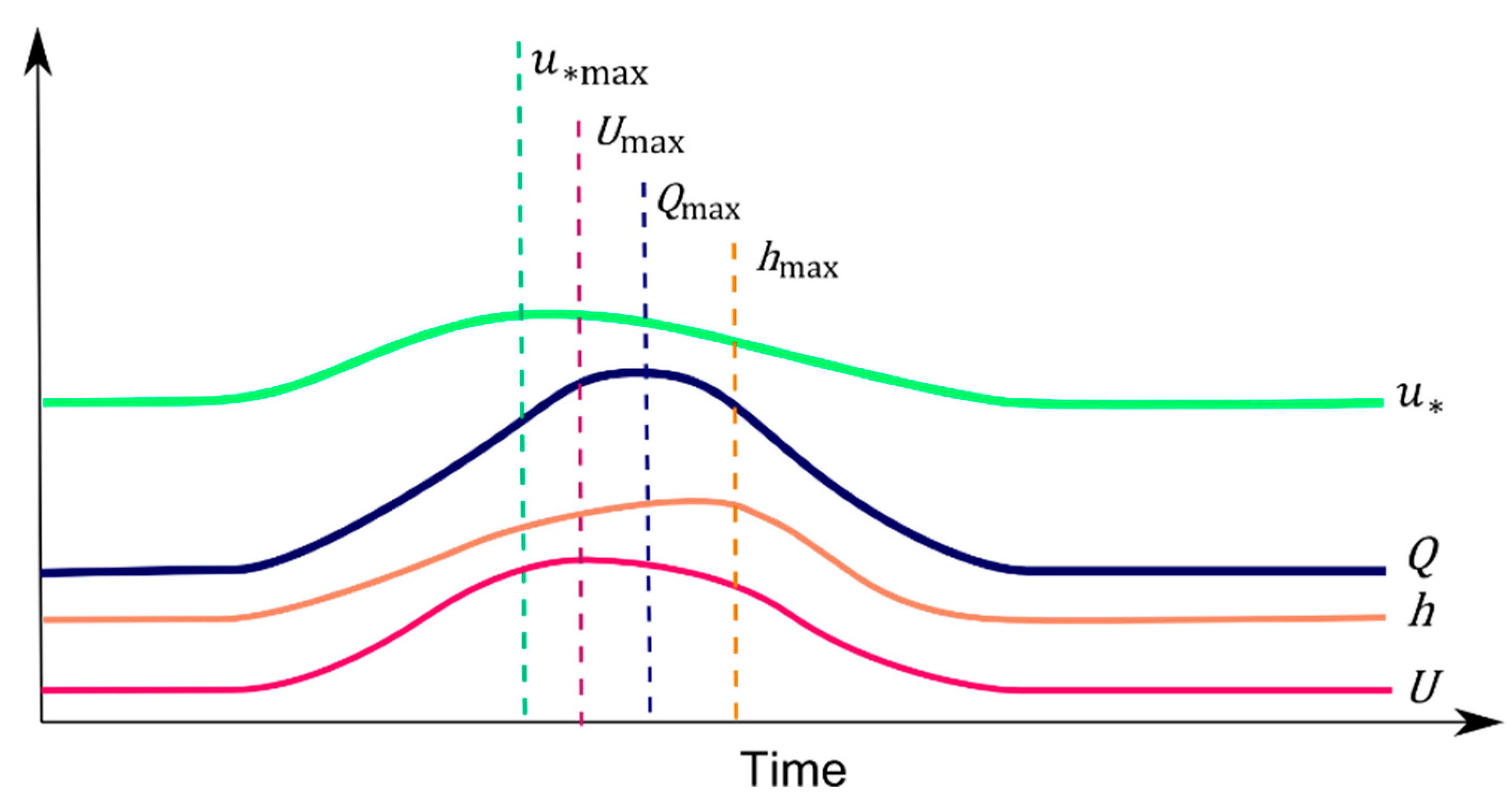
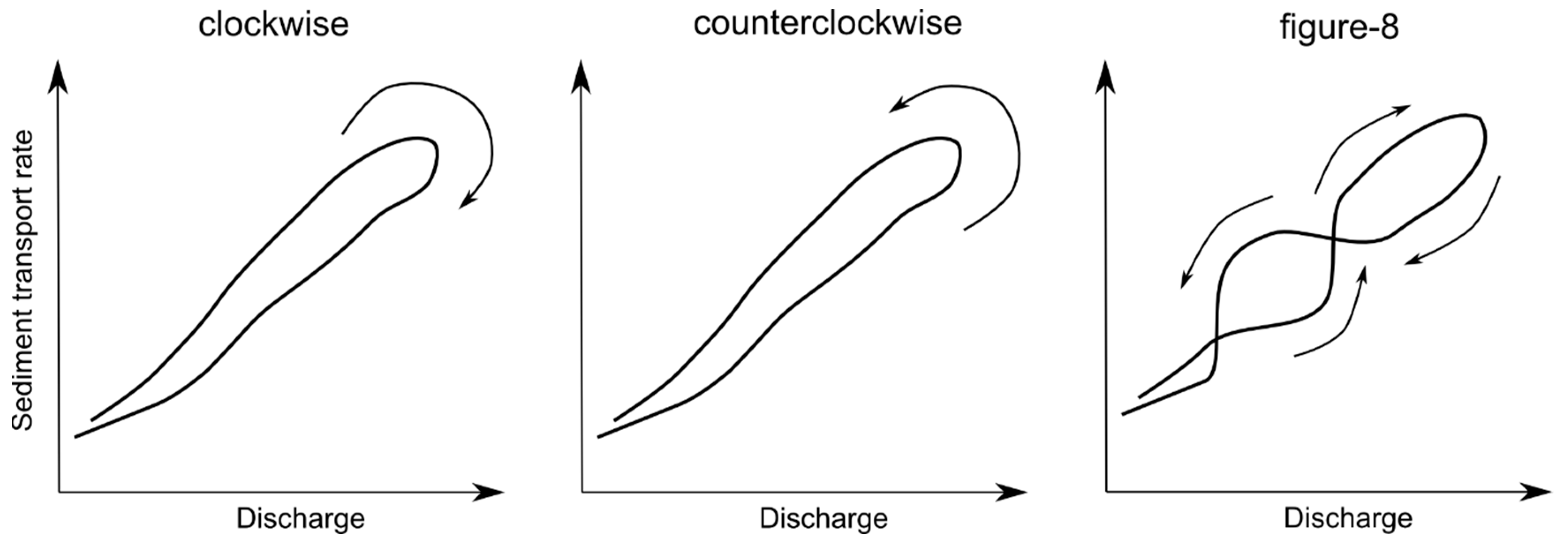
| Study | Type of Hydro-Graph 1 | Channel Dimensions 2 and Slope | Flow | Initial Bed Conditions | Sediment and Supply | Hyste-Resis 3 |
|---|---|---|---|---|---|---|
| Bombar et al., 2011 [23] | S, triangular, trapezoidal | 18.6 × 0.8 × 0.75 slope: 0.005 | peak about 80 L/s duration: 67–270 s | screeded and water-worked | gravel, d50 = 4.8 mm | N/A |
| Curran et al., 2015 [37] | S, stepped | 11 × 0.6 × 0.5 | duration: 76 min | well-mixed, screeded | 70% sand, 30% gravel; d50 = 0.5 mm; sediment recirculation | N/A |
| Ferrer-Boix, and Hassan. 2015 [31] | S, pulsed | 18 × 1 × 1 slope: 0.022 | variable duration (1–10 h) low flow 0.065 m2/s, followed by 1.5 h constant high flow pulse 0.091 m2/s | water-worked | dmean = 5.65 mm; 20% sand; constant feed rate 2.1 g/m/s | N/A |
| Guney et al., 2013 [12] | S, triangular | 18.6 × 0.8 slope: 0.006 | base flow: 9.5 L/s; peak flow: 49.6 L/s; duration: 10 min | well-mixed, water-worked | gravel/sand mixture; d50 = 3.4 mm, no supply | C, CC |
| Hassan et al., 2006 [5] | S, stepped triangular | 9 × 0.6 × 0.5 | 0.012–0.055 m3/s; duration: 0.83–64 h | water worked | range of grain size: 0.180–45 mm; no supply | N/A |
| Humphires et al., 2012 [27] | S, naturally-shaped (lognormal) | 28 × 0.86 × 0.86 | peak flow: 35 L/s, 25 L/s; duration: 14.5 h, 8.5 h | armored | d50 = 4.1 mm sediment pulses | S |
| Lee et al., 2004 [13] | S, triangular | 21 × 0.6 × 0.6 slope: 0.002 | base flow: 0.04 m2/s; peak flow 0.05–0.14 m2/s; duration: 21–80 min | d50 = 2.08 mm no supply | CC | |
| Li et al., 2018 [29] | S, naturally-shaped (smooth sinusoidal curves) | 35 × 1.2 × 0.8 slope: 0.003 | peak flow 0.018 m2/s and 0.038 m2/s | gravel (2–4 mm), sand (0.1–2 mm), 100% gravel; 100% sand; 53% gravel and 47% sand; 22% gravel and 78% sand; constant feed rate 2.1 g/(m s) | N/A | |
| Mao, 2012 [24] | S, stepped symmetrical | 8 × 0.3 slope: 0.01 | 0.024–0.085 m2/s | mixed and screeded sediment | 20% sand, 80% gravel, d50 = 6.2 mm, continuous recirculation | C |
| Mao, 2018 [25] | C, three types of stepped symmetrical | 8 × 0.3 slope: 0.01 | 0.024–0.085 m2/s | water-worked by steady antecedent flow | 20% sand, 80% gravel, d50 = 6.2 mm, supply | C, CC |
| Martin and Jerolmack, 2013 [38] | S, pulsed and triangular | 15 × 0.92 × 0.65 slope: 0 | peak flow: 81.4, 111.7 L/s; low flow: 39.1, 63.3 L/s, duration: several hours | water-worked by low flow | d50 = 0.37 mm no supply | N/A |
| Mrokowska et al., 2018 [34] Mrokowska et al., 2016 [39] | S, triangular | 12 × 0.49 × 0.6 slope: 0.0083 | base flow: 0.0035–0.0131 m3/s; peak flow: 0.0387–0.0456 m3/s; duration: 400–800 s | well-mixed, screeded, without and with antecedent flow | dmean = 4.93 mm supply | C |
| Nelson et al., 2011 [40] | S, square-wave | 6 × 0.25 × 0.4 slope: 0.002 | peak: 0.02 m3/s | well-sorted | sand d50 = 0.58 mm no supply | N/A |
| Orru et al., 2016 [36] | S, one step | 14 × 0.4 × 0.45 slope: 0.0022 | stepped increase form 0.0465 m3/s to 0.0547 m3/s | water-worked | tri-modal sediment mixture d50 = 1 mm, d50 = 6 mm, d50 = 10 mm; no supply | no |
| Perret et al., 2018 [26] | C, stepped symmetrical | 18 × 1 × 0.8 slope: 0.01 | - | loose and packed gravel beds, infiltrated with fine grains | gravel d50 = 6.8 mm and bimodal gravel–sand and gravel–silt | N/A |
| Phillips et al., 2018 [11] | C, four different shapes: triangular and rectangular | 30 × 0.5 | - | - | unimodal well-mixed, dmean = 7.2 mm | N/A |
| Piedra et al., 2012 [41] | S, stepped, increasing discharge | 7 × 0.9 slope: 1/150 | peak: 29–34 L/s | - | gravel d50 = 6.6 mm no supply | No |
| Redolfi et al., 2018 [30] | C, square-wave and triangular | 24 × 2.9, 24 × 0.8 slope: 1.0% | square-wave: 1.2–2.5 L/s, 1.5–2.5 L/s;triangular: 0.5–2.5 L/s | well-sorted sand, water-worked by antecedent low flow | sand d50 = 1 mm supply | C |
| Shvidchenko and Kopaliani, 1998 [42] | S, stepped | outdoor plot: 84 × 10; flume: 100 × 1; recirculating tilting flume: 18 × 2.46 | - | braided channel | dmean = 0.69 mm dmax = 5–8 mm recirculating flume: d50 = 4.3 mm | No |
| Waters and Curran, 2015 [32] | C, stepped | 9 × 0.6 × 0.5 | duration: 76 min, cycled with 2 h base flow between, peak flow: 0.073, 0.131 m2/s, base flow 0.029 m2/s | well mixed screeded flat, antecedent low flow | 70% sand, 30% gravel, d50 = 0.55 mm and 70% sand, 30% silt, clay d50 = 0.27 mm no supply | F8, CC most frequent |
| Wang et al., 2015 [28] | S, natural-shaped | 8 × 0.3 × 0.3 slope: 0.0083 | base flow 8 L/s, peak flow 13.5–18 L/s; duration: 120–141 s | screeded, antecedent flow | range of grain size: 1–16 mm; d50 = 5 mm, unimodal and bimodal | C |
| Wong and Parker, 2006 [33] | C, triangular | 22.5 × 0.5 | peak flow: 0.065–0.102 m3/s; duration 15–60 min | well-sorted | gravel, d50 = 7.1 mm, constant feed | N/A |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mrokowska, M.M.; Rowiński, P.M. Impact of Unsteady Flow Events on Bedload Transport: A Review of Laboratory Experiments. Water 2019, 11, 907. https://doi.org/10.3390/w11050907
Mrokowska MM, Rowiński PM. Impact of Unsteady Flow Events on Bedload Transport: A Review of Laboratory Experiments. Water. 2019; 11(5):907. https://doi.org/10.3390/w11050907
Chicago/Turabian StyleMrokowska, Magdalena M., and Paweł M. Rowiński. 2019. "Impact of Unsteady Flow Events on Bedload Transport: A Review of Laboratory Experiments" Water 11, no. 5: 907. https://doi.org/10.3390/w11050907
APA StyleMrokowska, M. M., & Rowiński, P. M. (2019). Impact of Unsteady Flow Events on Bedload Transport: A Review of Laboratory Experiments. Water, 11(5), 907. https://doi.org/10.3390/w11050907






