Flow over a gravel-bed is spatially heterogeneous and this affects the entire turbulence structure in the flow. The continuous fluid–particle interaction causes a more complex near-bed flow field, making difficult to estimate the sediment transport, the resistance to flow and important turbulence parameters in the flow. It implies that the bed topography is the primary cause to have such a complex flow field. Thus far, several studies show that the bed topography in a WGB is fairly different from that in an SGB, as mentioned in the preceding section, suggesting that the impacts of both the beds on the turbulence characteristics are different. Considering this, several researchers analyzed the effects of the WGB roughness structures on the turbulence parameters for various flow conditions.
3.1. Effects of Water-Work on Streamwise Velocity
Barison et al. [
24] analyzed the time-averaged flow field over a WGB and found that the flow field is drastically affected by the roughness structure owing to the action of water-work. However, in their study, they did not analyze the bed topography precisely. Later, Buffin-Bélanger et al. [
11] analyzed the spatial heterogeneity in the flow parameters, especially at the near-bed flow zone, considering three different Reynolds numbers (1.7 × 10
5, 2.2 × 10
5 and 2.9 × 10
5) in a WGB. They observed that the spatial heterogeneity of the time-averaged velocity decreases with a decrease in the vertical distance, but it increases with an increase in Reynolds number. At a high Reynolds number, the spatial heterogeneity was found to be maximum in the near-bed flow zone. Further, they analyzed the mean and skewness maps of the time-averaged streamwise velocity on the horizontal plane at two different vertical distances: one near the bed and the other in the main flow layer. They observed that the mean and skewness maps for the near-bed case were more complex than those for the main flow layer case. The skewness values suggested that the shapes of the velocity distributions are different for these cases. In the near-bed flow zone, the skewness is mostly positive, while in the main flow layer, the skewness is almost negative. Buffin-Bélanger et al. [
11] argued that the positive skewness values in the near-bed flow zone possibly reflect incursions of high-speed fluid streaks, while the negative values in the main flow layer indicate the incursions of low-speed fluid streaks. To be explicit, the low-speed and high-speed fluid streaks refer to the ejections and sweeps.
To understand the effects of the bed roughness structure on the spatial organization of the flow structure, Cooper et al. [
25] conducted experiments on two WGBs, where the bed structure was created using unimodal and bimodal gravel mixtures. They analyzed the streamwise velocities in both the beds and found that, although the bed roughness structures are different, the spatial organization of streamwise velocities in both the beds are almost the same. Further, Cooper et al. [
25] also studied the effects of relative submergence (1.2–1.9 for unimodal gravel-bed and 1.3–2 for bimodal gravel-bed) on the spatial pattern of streamwise velocity showing them in the form of contour plots. They found that, with an increase in relative submergence, the number of high-speed fluid streaks decreases, but the number of low-speed fluid streaks increases. It implies that, as relative submergence increases, the streamwise velocity distribution becomes spatially homogeneous, which is in conformity with the observations of Legleiter et al. [
26]. In both unimodal and bimodal gravel-beds, they also found that, for a given slope and bed shear stress, the relative submergence provides a more significant impact on the spatial distribution of the streamwise velocity than the bed topography. Later, Hardy et al. [
27] performed a time series analysis to visualize the instantaneous velocity field through a series of consecutive images in WGBs, for three different Reynolds numbers (1.3 × 10
5, 2.5 × 10
5 and 2.7 × 10
5). They observed that, for all Reynolds numbers, the flows are highly inconsistent in the near-bed flow zone. Further, the turbulent structures that originate from the near-bed zone are to intrude into the main flow layer. These structures change their form and magnitude at higher Reynolds numbers, becoming more distinct, having a clearer velocity signature and a steeper upstream-dipping slope.
Thereafter, Koll et al. [
28] studied the near-bed turbulent flow field over two WGBs. They kept the statistical distribution of the surface gravels identical in both the beds, but with different gravel orientations. In the first phase, they created a WGB and took the flow measurements over it. Subsequently, they rotated the surface gravels in a WGB by 90° and measured the flow field in the newly created WGB. Analysis of the double averaged (DA) streamwise velocity 〈
ū〉 profiles in both the beds showed that a higher flow retardation occurs in the WGB with rotated gravels than in the original WGB. They identified that the difference in magnitude of 〈
ū〉 is mainly caused by the change in near-bed turbulence rather than by the spatial distribution of time-averaged velocity.
Besides, after Nezu et al. [
29], the bed topography can be considered as one of the most influencing factors in estimating the turbulence parameters. Therefore, to quantify the impact of the bed topography on the flow velocity, Pu et al. [
30] carried out experiments over three different beds (a smooth bed, a WGB and an SGB), using an Acoustic Doppler Velocimeter (ADV), and compared the results. They used the following equations of log-wake laws for velocity profiles:
For smooth flow,
and for rough (SGB and WGB) flows,
where
u* is the frictional velocity,
z is the vertical distance,
ν is the kinematic viscosity,
Br is the constant of integration,
κ is the von Kármán coefficient, Π is the Coles’ wake parameter, Δ
z is the virtual bed level (≈0.25
ks, according to Dey et al. [
31]),
z0 is the zero velocity level,
ks is the average roughness height, and
h is the flow depth.
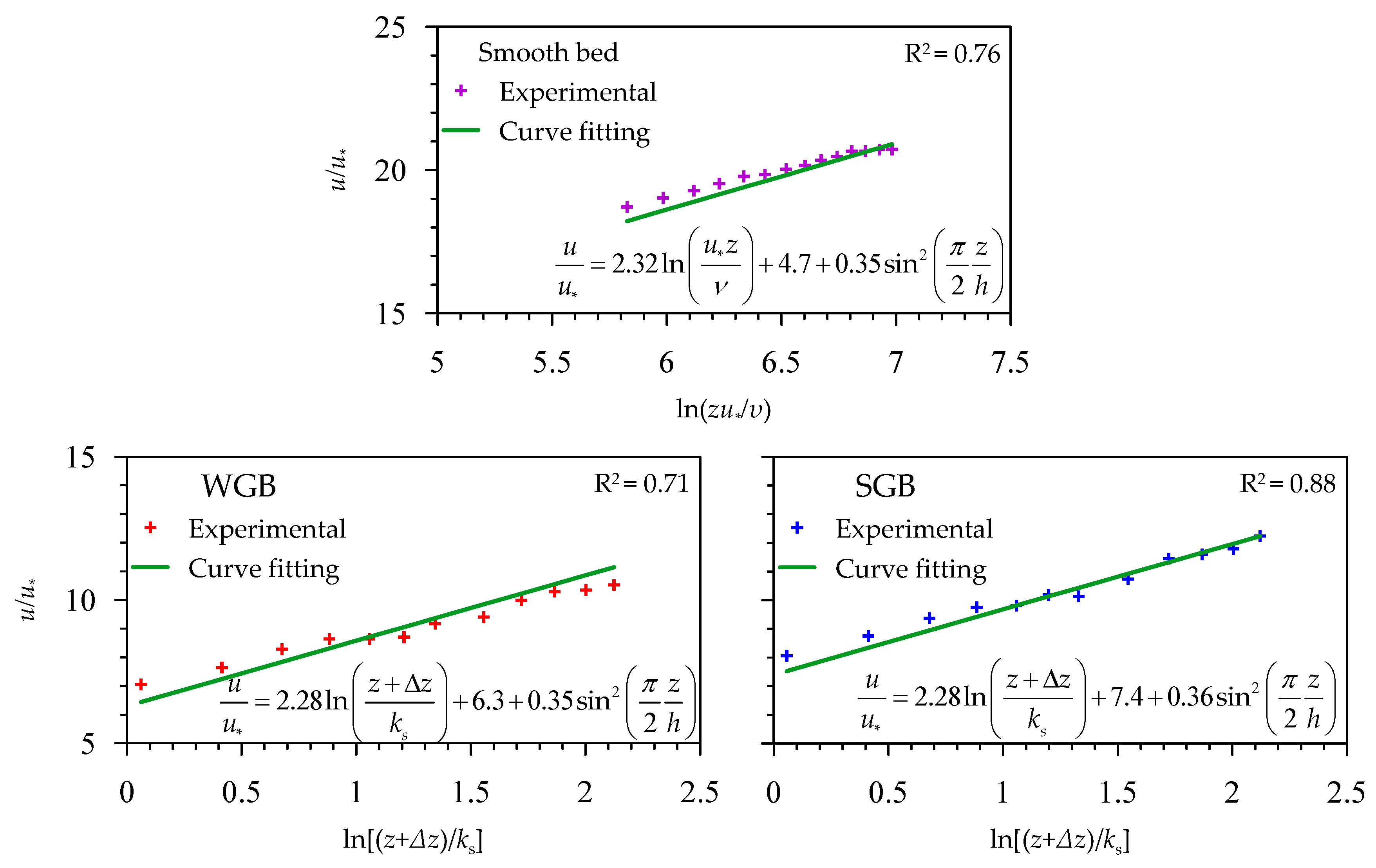
Pu et al. [
30] used the velocity data of each bed to obtain the fitted curves for the log-wake laws (
Figure 7). Interestingly, the values of
Br are lower in both the smooth and the rough (WGB and SGB) beds than the traditional values:
Br = 5.5 and 8.5 for the smooth and rough beds, respectively. Further, even though the flow conditions of both the WGB and SGB were identical, they observed that the
Br in the WGB was smaller than that in the SGB. It implies that, in the near-bed flow zone, a WGB roughness structure affects
Br and, in turn, the velocity profile. In addition, the comparison of Π values in the WGB and SGB revealed that the values of Π remain the same in the velocity profiles of both the beds, suggesting that the water-work has an insignificant impact on the Π, which mainly governs the velocity profile in the outer layer.
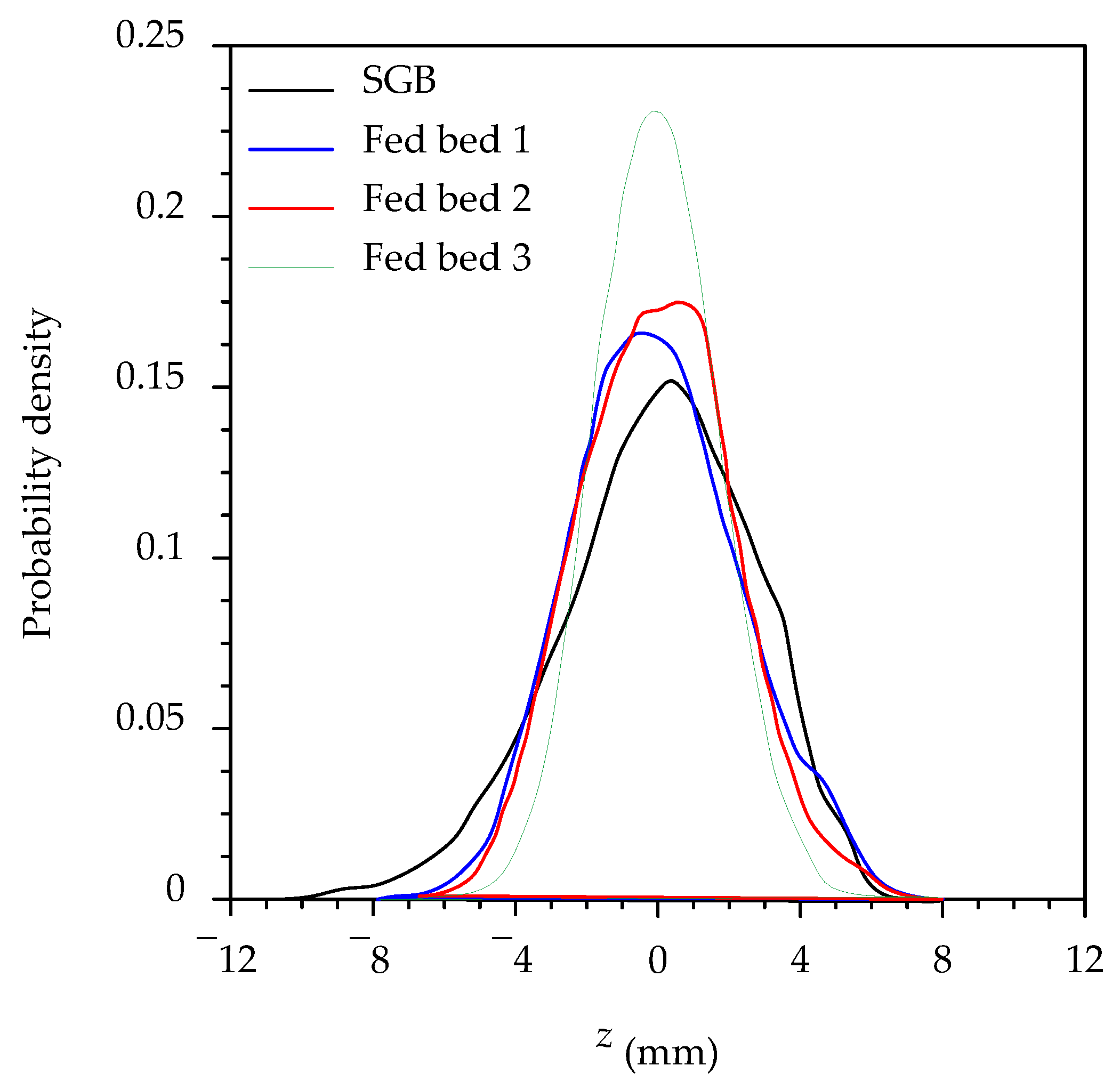
To ascertain the impact of the water-work on streamwise velocity more precisely, using a unimodal sediment mixture, Padhi et al. [
32] measured streamwise velocity in a WGB using a Particle Image Velocimetry (PIV) system and compared it with that in an SGB (
Figure 8). In their study, owing to the water action, the WGB roughness structure was observed to be better organized than the SGB roughness structure, where gravels were randomly sorted. Akin to other rough-flow, in the study by Padhi et al. [
32], owing to the presence of gravels, the values of 〈
ū〉 in both the WGB and SGB are small in the near-bed flow zone. However, they gradually increase with an increase in vertical distance, reaching a maximum at the free surface. Moreover, Padhi et al. [
32] found that, close to the bed, the 〈
ū〉 in the WGB is higher than that in the SGB, although the flow conditions in both the beds were alike. They argued that the well-organized roughness structure in a WGB makes the near-bed flow more streamlined than that in an SGB, inducing the 〈
ū〉 to attain a higher magnitude in the former than in the latter. However, the difference in magnitudes of 〈
ū〉 between a WGB and an SGB gradually diminishes, as the vertical distance increases.
3.2. Effects of Water-Work on Reynolds Shear Stresses and Form-Induced Shear Stresses
For steady, uniform flow over a macro-rough bed, the spatially averaged (SA) total fluid shear stress 〈
〉 can be expressed as follows:
where 〈
τf〉 is the SA form-induced shear stress (= −
ρ〈
〉),
ρ is the mass density of fluid,
ũ and
are the spatial velocity fluctuations in the streamwise and vertical directions, respectively, 〈
〉 is the SA Reynolds shear stress (= −
ρ〈
〉),
u′ and
w′ are the temporal velocity fluctuations in the streamwise and vertical directions, respectively, and 〈
〉 is the SA viscous shear stress (= −
ρνd〈
ū〉/d
z).
Although the 〈
〉 remains the prevailing stress in a turbulent flow across the flow depth, the 〈
τf〉 is the governing stress near the gravel-bed [
33]. Aberle et al. [
34] focused on the 〈
τf〉 profile influenced by the roughness elements. They analyzed the spatial flow heterogeneity in terms of the 〈
τf〉 in WGBs for different discharges. Their results infer that the magnitude of 〈
τf〉 is small away from the crest. However, the 〈
τf〉 increases as one moves toward the crest in the downward direction. It indicates that the
ũ and
near the bed are higher than those away from the bed, resulting in a higher magnitude of 〈
τf〉. Further, they found that the 〈
τf〉 profiles are similar for different discharges. Interestingly, the similarity in 〈
τf〉 profiles is not preserved for different bed slopes. It suggests that for a given bed slope, the 〈
τf〉 profile is independent of discharge.
Then, to study the effects of different sediment mixtures on both the 〈
〉 and 〈
τf〉, Cooper and Tait [
35] analyzed all the terms of Equation (9) in two WGBs created by the unimodal and bimodal sediment mixtures. For the unimodal sediment mixture, the relative submergences varied within the range of 1.2–1.9, while, for bimodal sediment mixture, they varied within 1.3–2. They analyzed the results in terms of forces caused by the shear stresses. In doing so, they considered the fluid force caused by the 〈
〉 at a given vertical distance as 〈
〉
ϕA0, where
ϕ is the roughness geometric function (=
Af/
A0, where
Af is the area of fluid in the averaging domain at a given elevation within the total area
A0). Above the roughness crest,
ϕ = 1. Similarly, the fluid force caused by the 〈
τf〉 at given vertical distance was obtained as 〈
τf〉
ϕA0. They further argued that in addition to these two forces, there exists an additional force called the form drag 〈
τd〉, which can be computed as
, where
Cd is the drag coefficient and
Ae is the exposed frontal area of the grain to the fluid. However, in the analysis, they neglected the force caused by the 〈
〉 term considering that it has minimal impact on the turbulent flow. It is pertinent to mention that their analysis mainly focused on the zone below the roughness crest. Analyzing the forces, they inferred that within this zone, the vertical variations of the forces contributed from 〈
〉, 〈
τf〉 and 〈
τd〉 with
ϕ are similar and thus controlled by the geometry of the roughness elements. Moreover, they observed that with a decrease in vertical distance, the reduction in the force caused by a damping of 〈
〉 is compensated by the addition of the force caused by 〈
τd〉. Furthermore, their results showed that as the relative submergence increases, the forces contributed from the 〈
〉, 〈
τf〉, and 〈
τd〉 increase. It suggests that for a given bed surface topography, the mechanism of momentum transfer between the fluid and particle fairly changes with an increase in relative submergence. When the results of unimodal and bimodal WGBs were compared, they found that for a given vertical distance and relative submergence, the force contributed from the 〈
〉 and 〈
τd〉 in the unimodal WGB is less than that in the bimodal WGB in the upper portion of the roughness layer and vice versa. Interestingly, in the lower portion of the roughness layers of both beds, the force caused by the 〈
τf〉 was observed to have different vertical distributions. It indicates that for a given relative submergence, the mechanism of momentum transfer differs owing to the difference in roughness structure.
Later, Cooper et al. [
36] used the experimental data of Aberle et al. [
34] to quantify the spatial flow variance and the 〈
τf〉 for different flow submergence conditions and for gravel-beds with different roughness structures. They observed that the spatial flow variance within the roughness layer is typically 4–5 times higher than that above the roughness layer. In fact, it becomes invariant to the vertical distance at a distance twice the roughness height above the crest. Owing to the increase in relative submergence, the spatial flow variance with respect to 〈
τf〉 decreases within and above the roughness layer. However, the flow submergence does not have a significant impact on the spatial flow variance with respect to 〈
〉. Further, their study infers that for different bed surface topographies, the spatial flow variance and the 〈
τf〉 profiles vary, suggesting that the bed geometry possesses a strong control on the spatial flow variance profiles and the vertical organization of the time-averaged flow within the roughness layer.
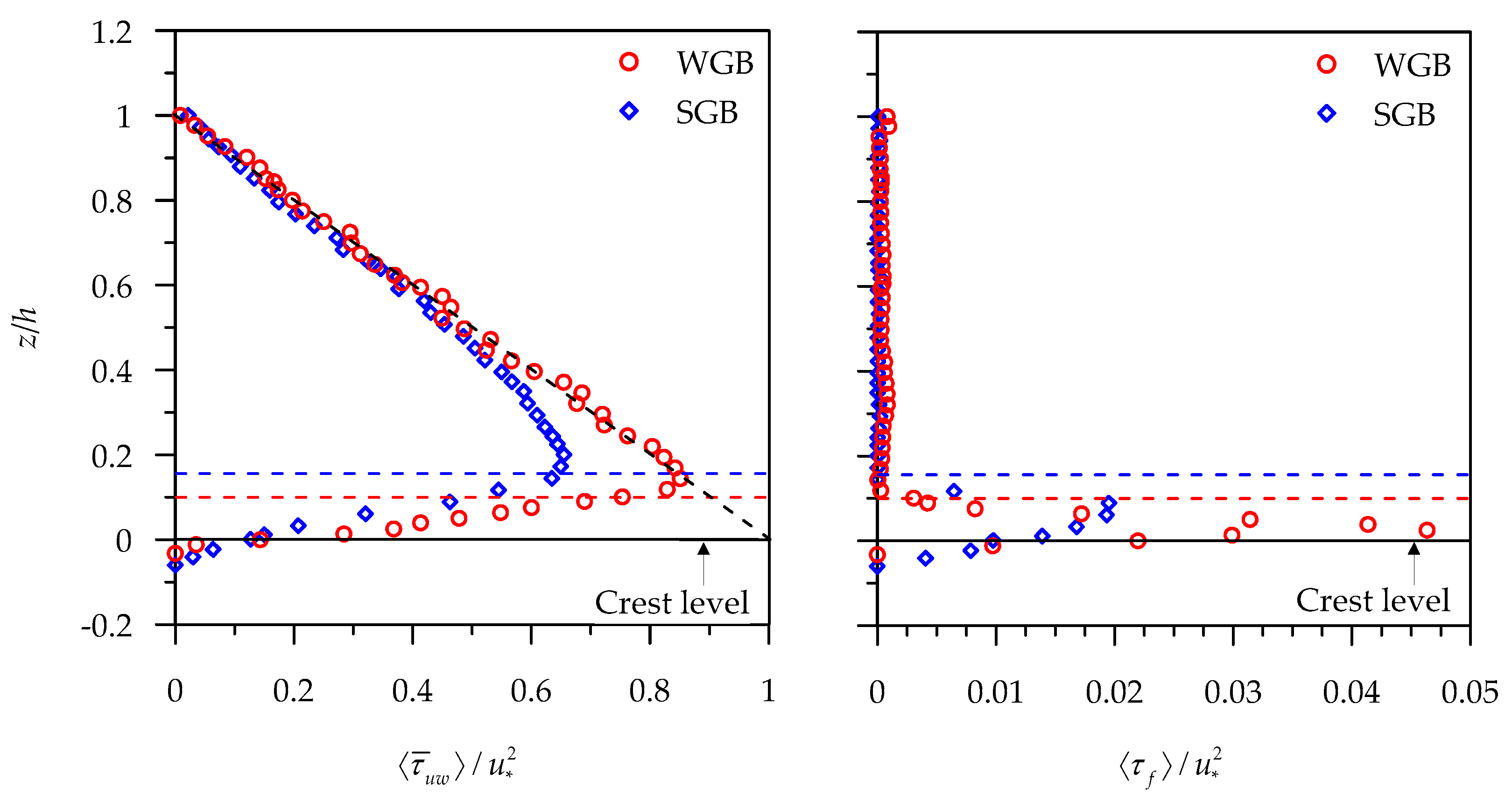
Pu et al. [
30] compared the 〈
〉 profiles in a smooth bed with those in the WGB and SGB. They showed that the 〈
〉 profile in the smooth bed converges with the gravity line at a shorter vertical distance than those in the WGB and SGB. Between these two rough beds, the 〈
〉 profile in the WGB takes longer vertical distance to collapse on the gravity line than that in the SGB. They argued that as the WGB possesses higher roughness among all the beds, it causes the flow to have the thickest unsettled turbulence mixing layer in the near-bed flow zone, although the effects of roughness do not persist in the main flow layer. Further, regarding the magnitude of 〈
〉 profile, they showed that the 〈
〉 profile in a smooth bed attains the highest magnitude among all, but no explanation was given for that. Moreover, although they showed the effects of roughness on the 〈
〉, the impact of roughness on the 〈
τf〉 were not taken into consideration.
Recently, Padhi et al. [
32] examined the effects of roughness on the 〈
〉 and 〈
τf〉 profiles in a WGB and an SGB. Akin to Pu et al. [
30], Padhi et al. [
32] found that the roughness height in the WGB was also higher than that in the SGB. However, the results of Padhi et al. [
32] do not correspond to those of Pu et al. [
30]. In the study by Padhi et al. [
32], the 〈
〉 profile in the WGB is higher than that in the SGB owing to a higher roughness height in the former than in the latter (
Figure 9). They stated that a higher roughness in the WGB than in the SGB enhances the
u′ and
w′ values, causing an increased magnitude of 〈
〉 in the WGB. The results are in agreement with those reported in Nezu and Nakagawa [
29], Nikora et al. [
33], Mignot et al. [
37] and Dey and Das [
38]. Moreover, the 〈
〉 profile in the WGB collapses on the gravity line at a shorter distance than that in the SGB. It implies that, although the WGB exhibits a higher roughness height than the SGB, owing to the well-organized roughness structure in the WGB, intense flow mixing is restricted to a shorter vertical distance. Further, the 〈
τf〉 profiles in the WGB and SGB showed that a higher roughness in the WGB than in the SGB produces large values of
ũ and
causing an increased magnitude of 〈
τf〉 in the former than that in the latter (
Figure 9). This suggests that in the near-bed flow zone, the flow is more heterogeneous in the WGB than in the SGB.
3.3. Effects of Water-Work on Reynolds Normal Stresses and Form-Induced Normal Stresses
For a heterogeneous turbulent flow, the SA streamwise and vertical Reynolds normal stresses are expressed as 〈σuu〉 = ρ〈〉, and 〈σww〉 = ρ〈〉, respectively. Similarly, the streamwise and vertical form-induced normal stresses are 〈σfuu〉 = ρ〈〉 and 〈σfww〉 = ρ〈〉, respectively.
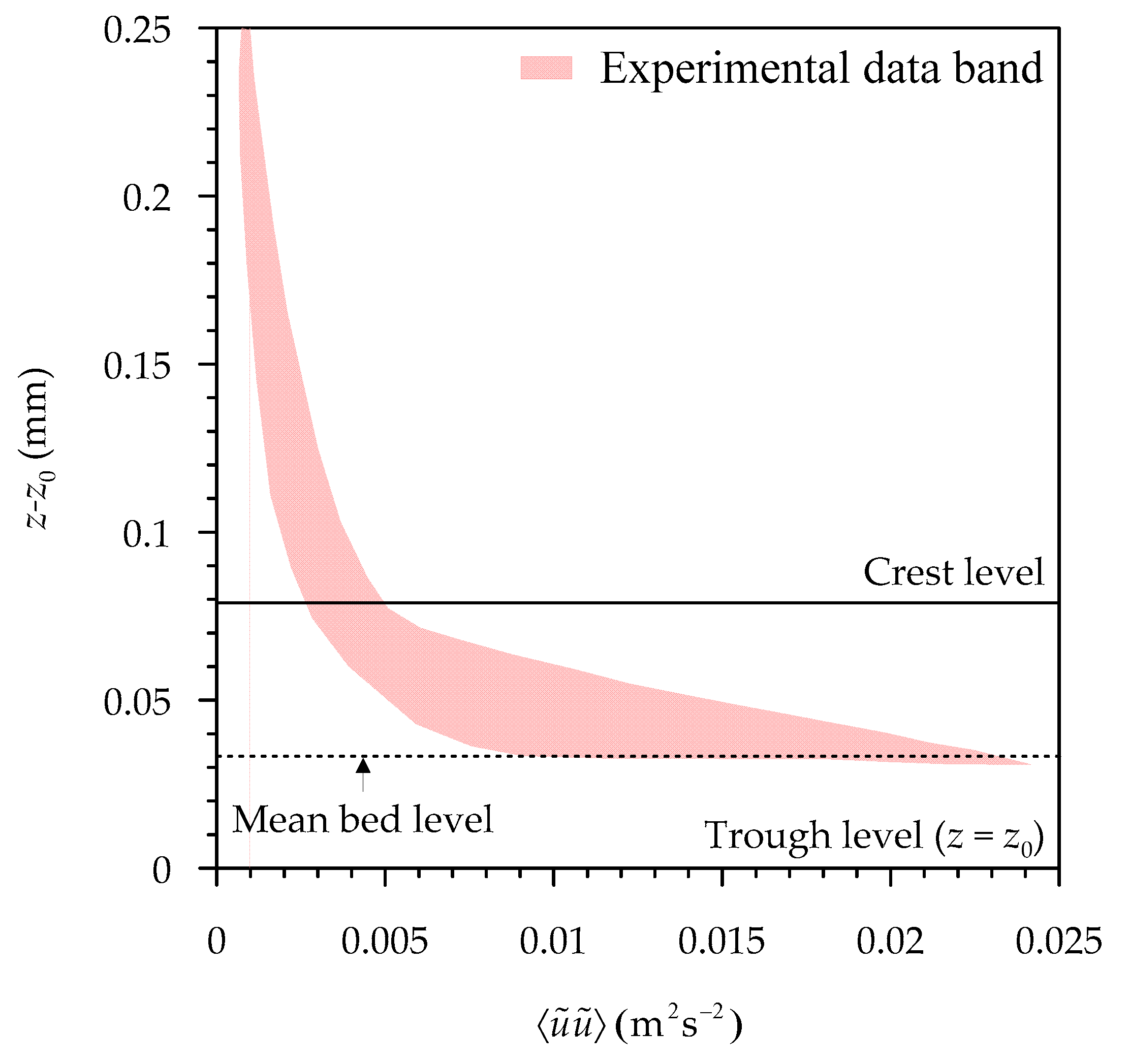
According to Aberle et al. [
34], the effects of the spatial heterogeneity in bed roughness on the streamwise time-averaged velocity can be ascertained by analyzing the 〈
σfuu〉 (
Figure 10). They observed that, akin to the 〈
τf〉 profile, the 〈
σfuu〉 profile is small away from the crest and gradually increases, as one moves downward toward the crest. Interestingly, they found that for a given bed slope and bed roughness structure, the 〈
σfuu〉 profiles are almost identical for all the discharges. It implies that the shape of the 〈
σfuu〉 profiles are independent of discharge. Further, they compared the 〈
σfuu〉 profiles obtained for different roughness structures, but for a constant bed slope. They argued that the shapes of all the 〈
σfuu〉 profiles are similar, although their absolute magnitudes are different. This suggests that the magnitude of 〈
σfuu〉 profiles is governed by the roughness structure. Then, they analyzed the 〈
σfuu〉 profiles for different bed slopes, keeping the roughness structure identical. The comparison of 〈
σfuu〉 profiles revealed that the variation of bed slope (
S0 = 0.001 to 0.01) has a significant impact on the shape of the 〈
σfuu〉 profiles.
The spatial velocity fluctuations
ũ and
are highly affected by the relative submergence [
34]. Hence, to understand the behavioral features of the
ũ with respect to the relative submergence, Koll et al. [
28] studied the 〈
σfuu〉 profiles over the original and rotated WGBs. They tested two relative submergences for each bed type: for the original WGB, the relative submergences were taken as 4.4 and 3.2, while, for the rotated WGB, they were 4.5 and 3.3. They noticed that, in the near-bed flow zone, the 〈
σfuu〉 profile increases with an increase in relative submergence. However, away from the bed, the effects of relative submergence diminish. Cooper et al. [
36] examined the impact of the relative submergence on both the 〈
σfuu〉 and 〈
σfww〉 profiles in a WGB. In fact, they carried out the analysis for form-induced intensities, 〈
σfuu〉
0.5 and 〈
σfww〉
0.5. They showed that the SA streamwise form-induced intensity 〈
σfuu〉
0.5 profiles exhibit similar shape for all the values of relative submergences. The spatial flow variance is maximum at the middle of the interfacial sublayer, gradually diminishing away from the crest and continuing up to a vertical distance equaling twice the roughness height above the crest. Further, they observed that between the crest and the vertical distance of twice the roughness height above the crest, the spatial variance is half of its peak value in all the 〈
σfuu〉
0.5 profiles, irrespective of the bed roughness. Analysis of the impact of relative submergence on the 〈
σfuu〉
0.5 profiles revealed that, for a given vertical distance, the magnitude of 〈
σfuu〉
0.5 profile is inversely proportional to the relative submergence. Thus, it confirms that the relative submergence governs the 〈
σfuu〉
0.5 profile. By contrast, the results of SA vertical form-induced intensity 〈
σfww〉
0.5 profiles inferred that although the shapes of 〈
σfww〉
0.5 profiles are similar to those of 〈
σfuu〉
0.5 profiles, there is an insignificant difference in the magnitudes of 〈
σfuu〉
0.5 profiles owing to the difference in relative submergences. Additionally, they analyzed the 〈
σuu〉
0.5 and 〈
σww〉
0.5 profiles for different relative submergences. Akin to 〈
σfuu〉
0.5 profiles, the magnitudes of 〈
σuu〉
0.5 profiles reduce with an increase in relative submergence, confirming that these profiles are also affected by the relative submergence. Further, they found that the spatial variance in 〈
σuu〉
0.5 profiles is approximately half of the spatial variance in the time-averaged streamwise velocity profiles. Moreover, a small variation in 〈
σww〉
0.5 profiles was observed owing to the change in relative submergence. It is important to mention that the spatial variance in 〈
σww〉
0.5 profiles is approximately half of the spatial variance in 〈
σuu〉
0.5 profiles and equals the spatial variance in time-averaged vertical velocity profiles. This implies that the spatial flow variance in the streamwise direction is higher than that in the vertical direction.
Considering three types of beds (smooth bed, WGB and SGB), Pu et al. [
30] measured the turbulence intensities in streamwise, spanwise and vertical directions. As traditionally found, the turbulence intensities are higher in the rough beds (WGB and SGB) than in the smooth bed. Further, their observations revealed that between the WGB and SGB, the WGB possesses a less even bed roughness structure than that in the SGB. It causes to have larger turbulence intensities and velocity fluctuations in the former than in the latter. It indicates that the WGB can modify the flow turbulence intensity distribution and in turn, the Reynolds normal stresses with respect to the SGB.
Recently, Padhi et al. [
32] examined the 〈
σuu〉, 〈
σww〉, 〈
σfuu〉 and 〈
σfww〉 profiles in a WGB and an SGB. Their analysis showed that owing to the higher WGB roughness height, both
u′ and
w′ enhance, resulting in higher values of 〈
σuu〉 and 〈
σww〉, respectively. Moreover, they also observed that in both the beds, the effects of roughness height are more prominent in the streamwise direction than in the vertical direction. Therefore, the magnitude of 〈
σuu〉 profile, for a given vertical distance, is greater than that of 〈
σww〉 profile. While comparing the 〈
σfuu〉 and 〈
σfww〉 profiles in both the beds, they found that a higher roughness in the WGB than that in the SGB enhances the
ũ and
. As a result, for a given vertical distance, the 〈
σfuu〉 and 〈
σfww〉 profiles in the WGB appear to have higher magnitudes than those in the SGB.
3.4. Effects of Water-Work on Conditional Turbulent Events
Quadrant analysis of two-dimensional velocity fluctuations (
u′ and
w′) is usually performed to understand the dynamics of the coherent flow structure in a turbulent flow. In general, in a turbulent boundary-layer flow, the turbulent events generated from the second and the fourth quadrants, termed ejections
Q2 (−
u′ and +
w′) and sweeps
Q4 (+
u′ and −
w′), respectively, are the dominating events, which govern the turbulence mechanism in the flow. On the other hand, those generated from the first and the third quadrants, termed outward interactions
Q1 (+
u′ and +
w′) and inward interactions
Q3 (−
u′ and −
w′), respectively, are the weak events, but they can be effective in the context of sediment entrainment [
39].
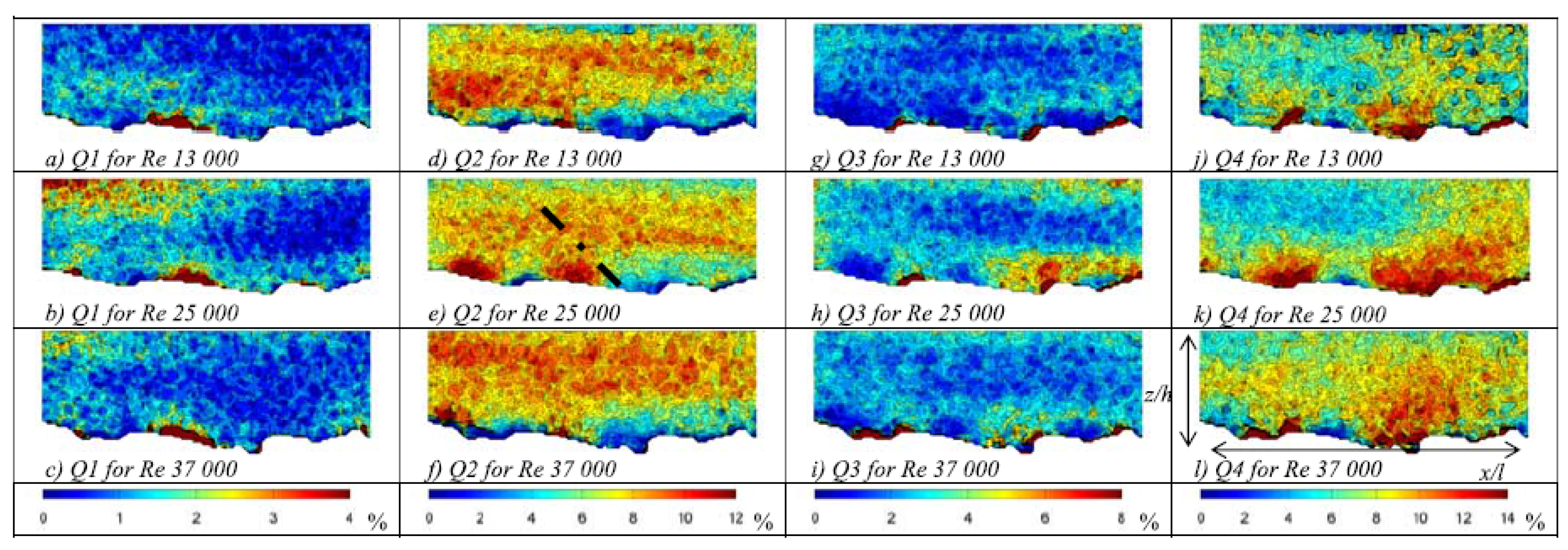
In a WGB, Hardy et al. [
27] performed the quadrant analysis to study the relative contribution from each event to the total Reynolds shear stress in governing the turbulent flow. As traditionally observed, their analysis also depicted that the sweeps in the near-bed flow zone are the prevailing events, while the ejections govern in the main flow layer. They however observed more localized flow patterns close to the bed. Near the bed, the ejections and sweeps occur in an alternative manner. In the leeside of a bed undulation, the sweeps govern the flow, while, in the stoss-side of the bed undulation, the ejections are ascendant, as shown in
Figure 11. This suggests that the shape of the localized bed topography influences the turbulence characteristics. Furthermore, regarding the outward and inward interactions, they found that the occurrence of these events follows the alternative pattern, as observed for the sweeps and ejections. In the stoss-side of a particle, the outward interactions occur, while in the leeside of a particle, inward interactions prevail. Therefore, as the flow approaches the particle, it decelerates close to the bed; otherwise, it accelerates over or around the particle.