Analysis of Floodplain Dynamics in the Atrato River Colombia Using SAR Interferometry
Abstract
:1. Introduction
2. Materials and Methods
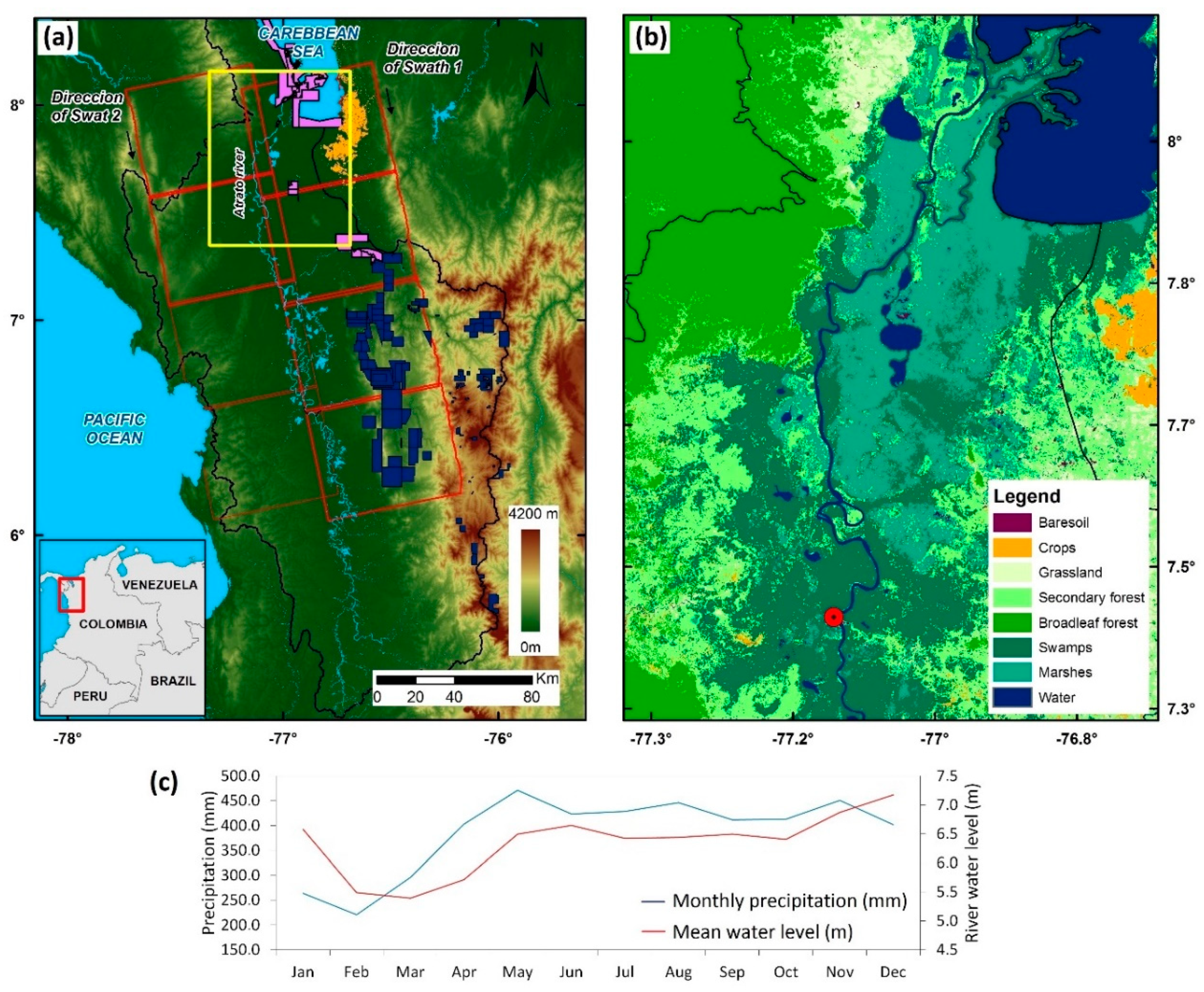
2.1. Study Area
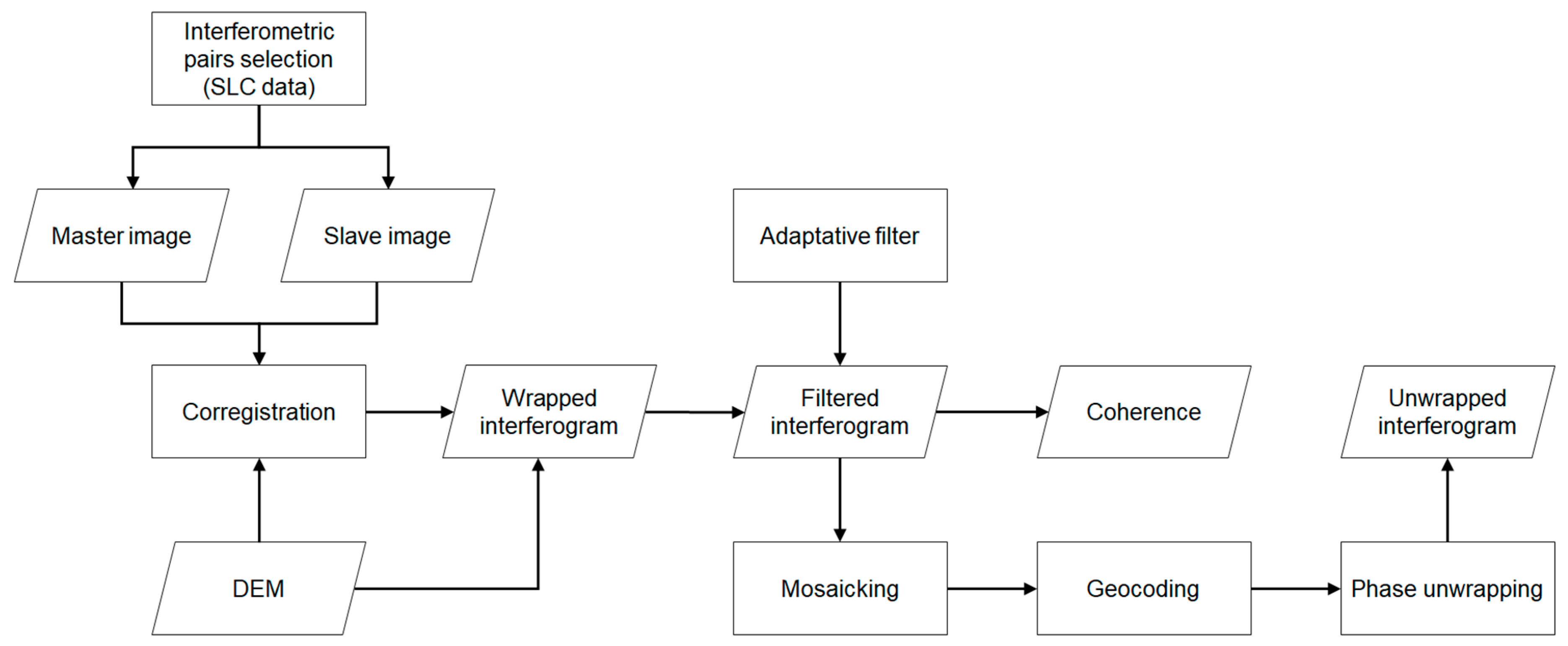
2.2. Data and Pre-processing
2.3. Surface Water Flow Analysis in the Atrato River Floodplains
3. Results and Discussion
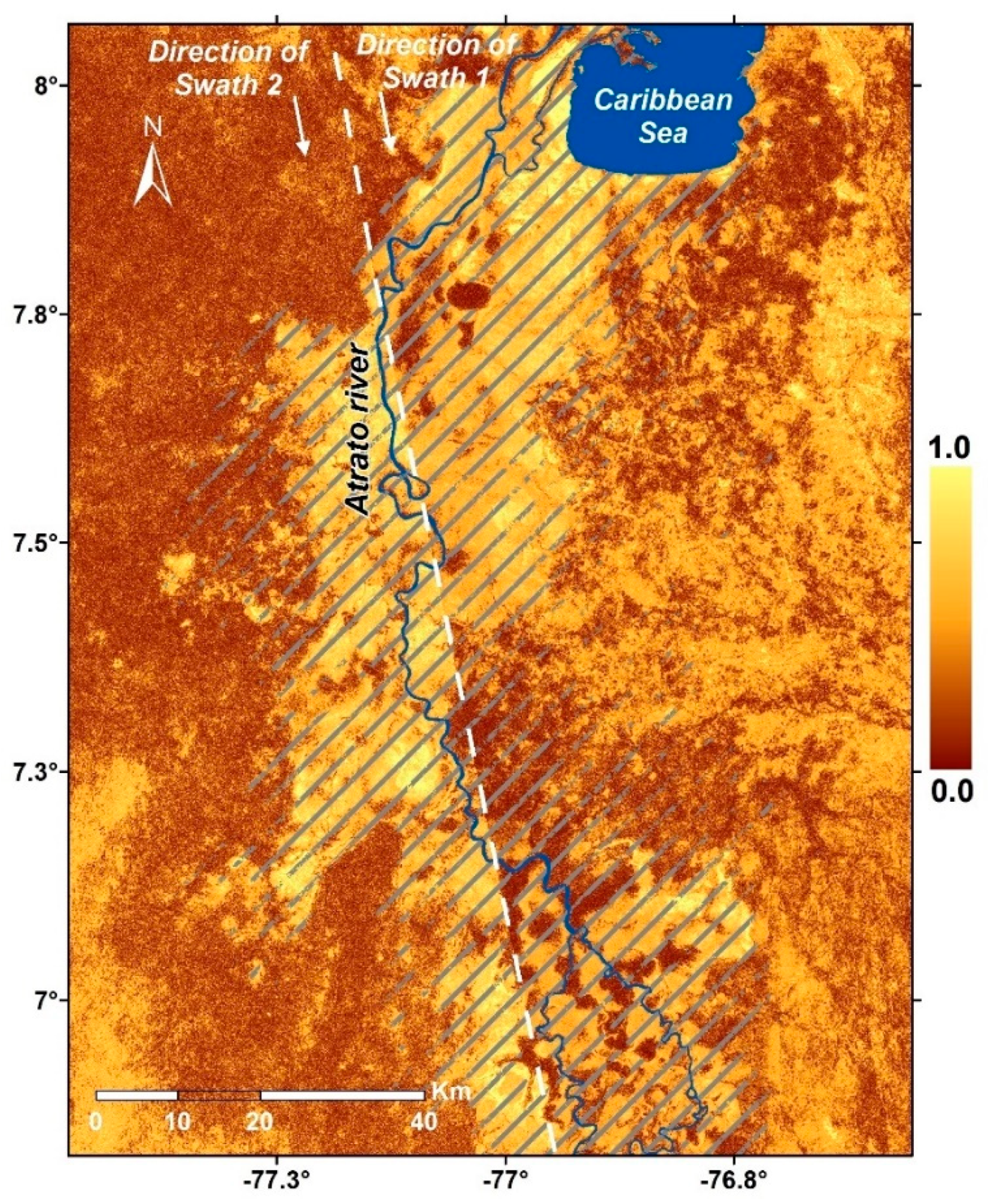
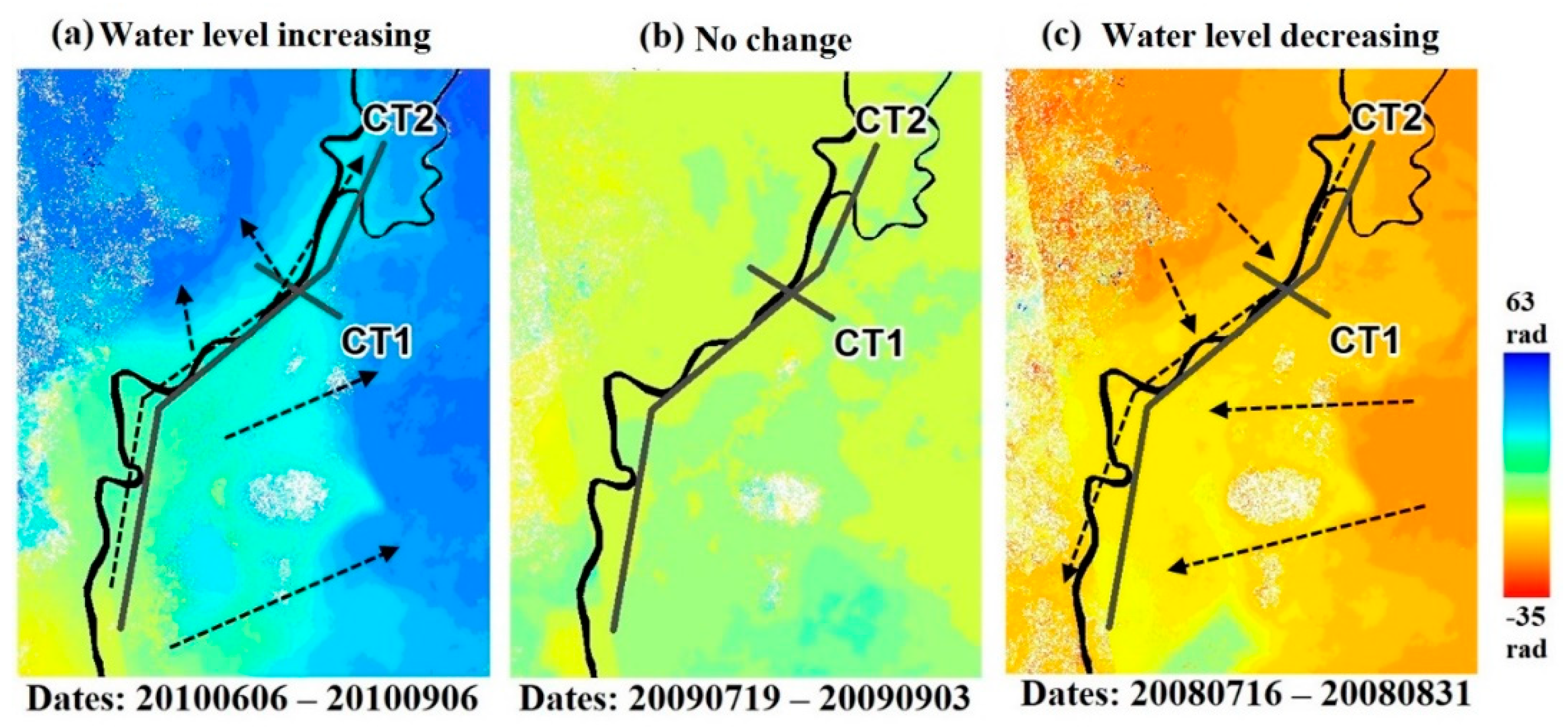
3.1. Spatial Distribution of DInSAR Phase Patterns
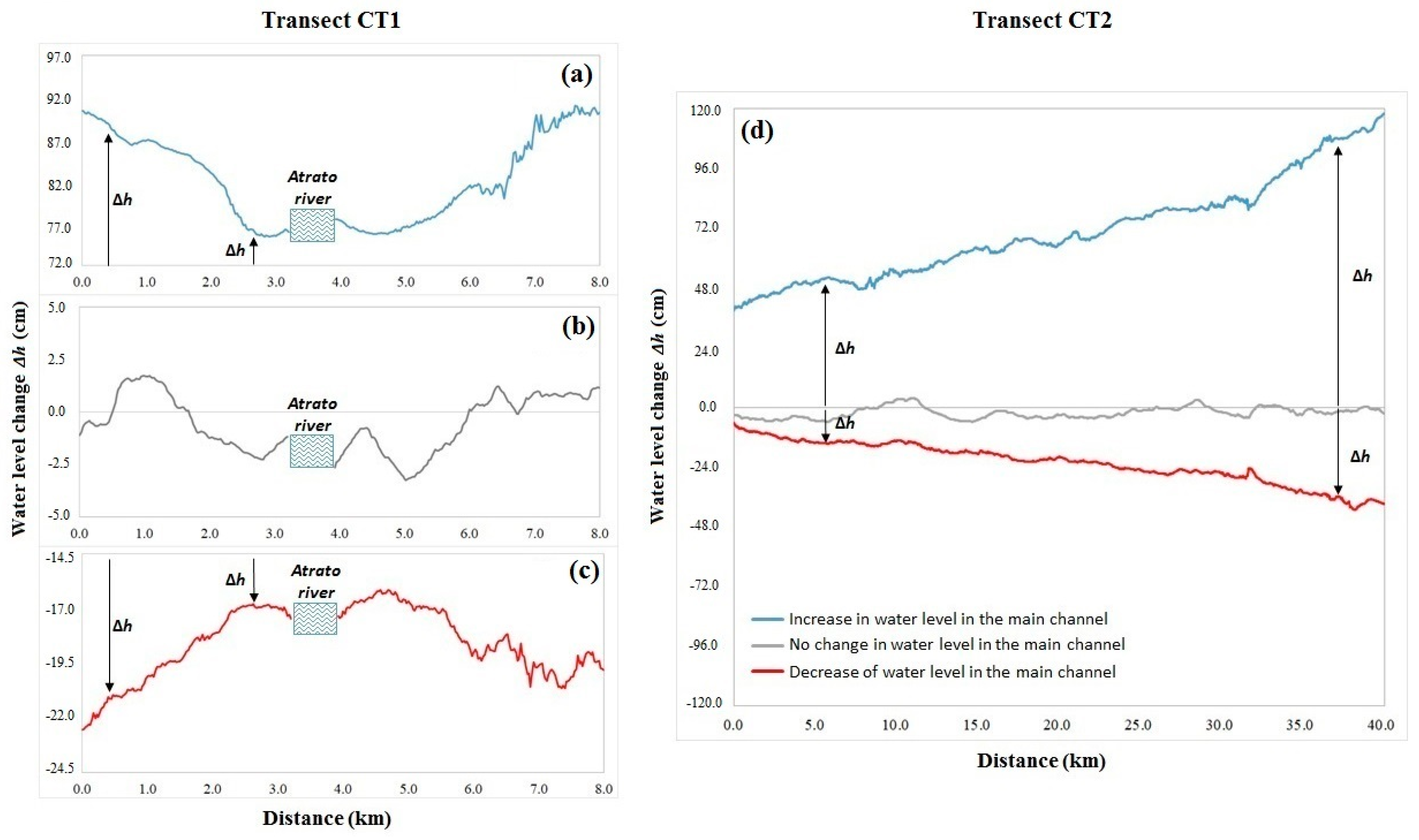
3.2. Temporal Fluctuations in the DInSAR Phase Patterns
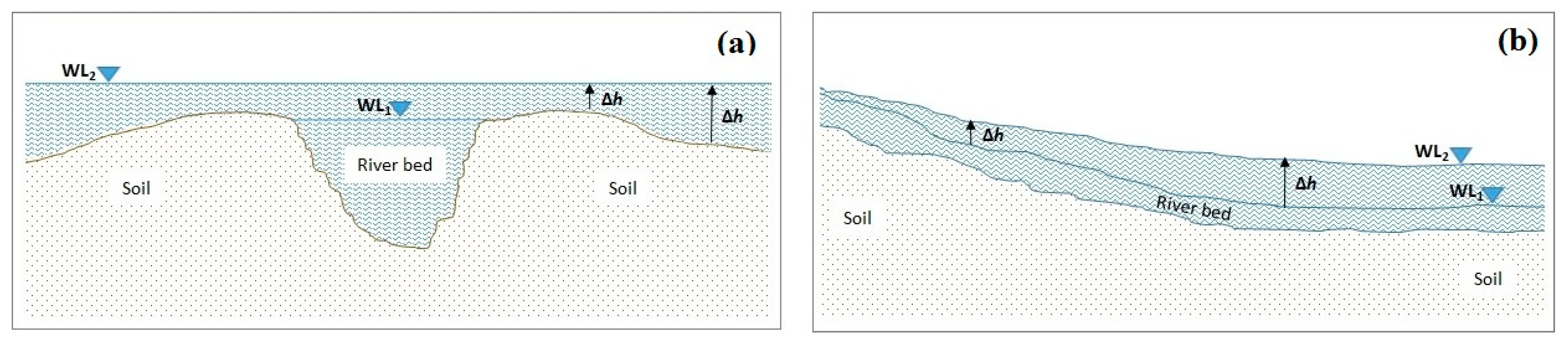
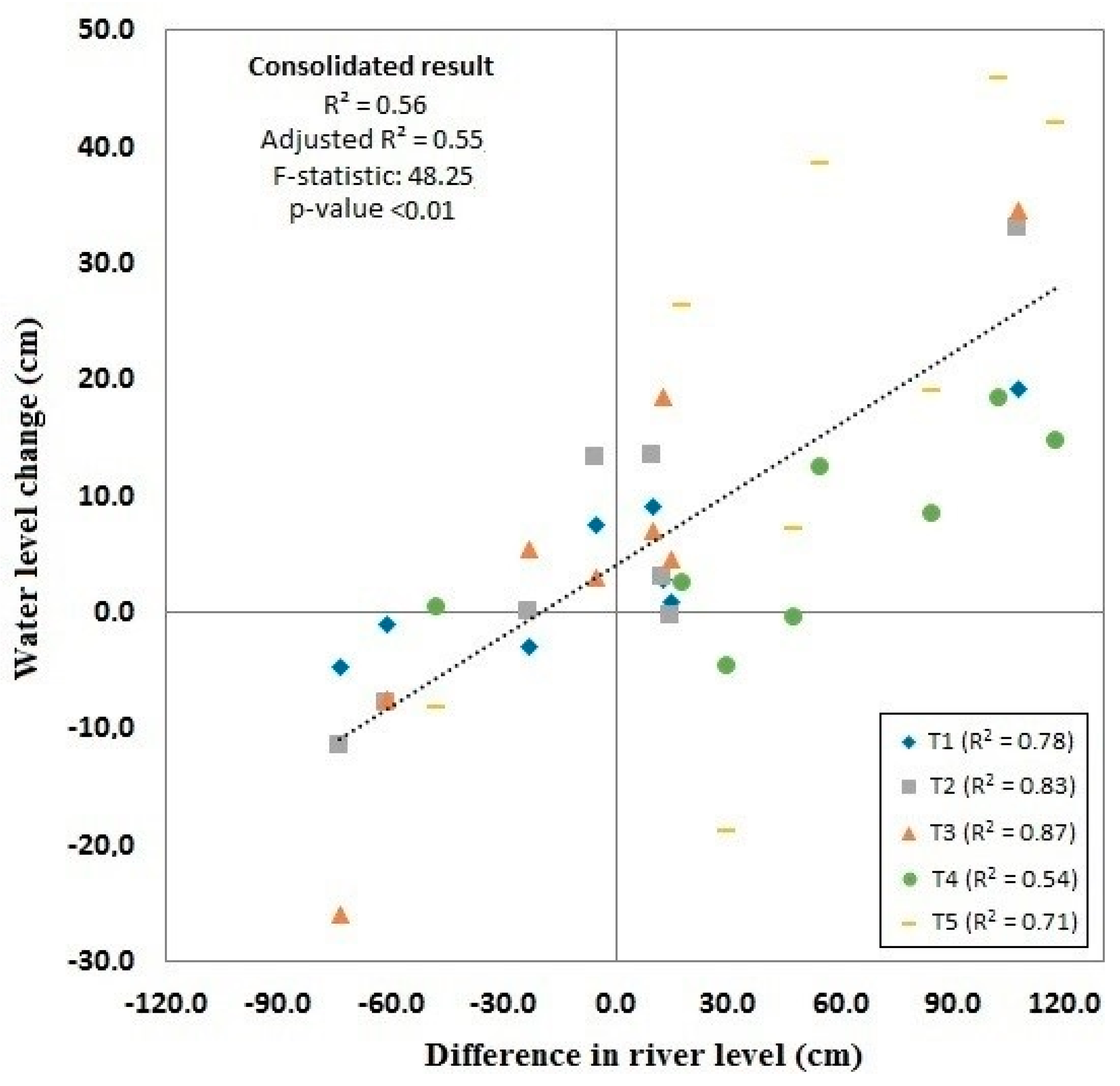
3.3. Relationship between Water Changes in the Main Channel Upstream and Floodplain
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hamilton, S.K.; Sippel, S.J.; Melack, J.M. Comparison of inundation patterns among major South American floodplains. J. Geophys. Res. Atmos. 2002, 107, 8038. [Google Scholar] [CrossRef]
- Melack, J.M. Interactions between Biosphere, Atmosphere and Human Land Use in the Amazon Basin; Nagy, L., Forsberg, B., Artaxo, P., Eds.; Springer: Berlin, Germany, 2016; pp. 117–145. [Google Scholar]
- Thorslund, J.; Jarsjo, J.; Jaramillo, F.; Jawitz, J.W.; Manzoni, S.; Basu, N.B.; Chalov, S.R.; Cohen, M.J.; Creed, I.F.; Goldenberg, R.; et al. Wetlands as large-scale nature-based solutions: Status and challenges for research, engineering and management. Ecol. Eng. 2017, 108, 489–497. [Google Scholar] [CrossRef]
- Audesirk, T.; Audesirk, G.; Bruce, E. Biología: La vida en la Tierra; Prentice Hall Inc.: Upper Saddle River, NJ, USA, 2008. [Google Scholar]
- Melack, J.M.; Engle, D. An organic carbon budget for an Amazon floodplain lake. Int. Ver. Theor. Angew. Limnol. Verh. 2009, 30, 1179–1182. [Google Scholar] [CrossRef]
- Richey, J.E.; Melack, J.M.; Aufdenkampe, A.K.; Ballester, V.M.; Hess, L.L. Outgassing from Amazonian rivers and wetlands as a large tropical source of atmospheric CO2. Nature 2002, 416, 617. [Google Scholar] [CrossRef] [PubMed]
- Pontes, P.R.M.; Fan, F.M.; Fleischmann, A.S.; de Paiva, R.C.D.; Buarque, D.C.; Siqueira, V.A.; Jardim, P.F.; Sorribas, M.V.; Collischonn, W. MGB-IPH model for hydrological and hydraulic simulation of large floodplain river systems coupled with open source GIS. Environ. Model. Softw. 2017, 94, 1–20. [Google Scholar] [CrossRef]
- Jaramillo, F.; Brown, I.; Castellazzi, P.; Espinosa, L.; Guittard, A.; Hong, S.-H.; Rivera-Monroy, V.H.; Wdowinski, S. Assessment of hydrologic connectivity in an ungauged wetland with InSAR observations. Environ. Res. Lett. 2018, 13, 24003. [Google Scholar] [CrossRef] [Green Version]
- Wemple, B.C.; Browning, T.; Ziegler, A.D.; Celi, J.; Chun, K.P.; Jaramillo, F.; Leite, N.K.; Ramchunder, S.J.; Negishi, J.N.; Palomeque, X.; et al. Ecohydrological disturbances associated with roads: Current knowledge, research needs, and management concerns with reference to the tropics. Ecohydrology 2018, 11, e1881. [Google Scholar]
- Van Meter, K.J.; Basu, N.B. Signatures of human impact: Size distributions and spatial organization of wetlands in the Prairie Pothole landscape. Ecol. Appl. 2015, 25, 451–465. [Google Scholar] [CrossRef]
- Quin, A.; Jaramillo, F.; Destouni, G. Dissecting the ecosystem service of large-scale pollutant retention: The role of wetlands and other landscape features. Ambio 2015, 44, 127–137. [Google Scholar] [CrossRef] [Green Version]
- Alsdorf, D.E.; Lettenmaier, D.P. Tracking Fresh Water from Space. Science 2003, 301, 1491–1494. [Google Scholar] [CrossRef]
- Cao, N.; Lee, H.; Jung, C.H.; Yu, H. Estimation of Water Level Changes of Large-Scale Amazon Wetlands Using ALOS2 ScanSAR Differential Interferometry. Remote Sens. 2018, 10, 966. [Google Scholar] [CrossRef]
- Schulz, J.; Albert, P.; Behr, H.-D.; Caprion, D.; Deneke, H.; Dewitte, S.; Dürr, B.; Fuchs, P.; Gratzki, A.; Hechler, P.; et al. Operational climate monitoring from space: The EUMETSAT satellite application facility on climate monitoring (CM-SAF). Atmos. Chem. Phys. 2008, 8, 8517–8563. [Google Scholar] [CrossRef]
- Wdowinski, S.; Hong, S. Wetland InSAR: A review of the technique and applications. In Remote Sensing of Wetlands; CRC Press: Boca Raton, FL, USA, 2015; pp. 154–171. [Google Scholar]
- Xie, C.; Shao, Y.; Xu, J.; Wan, Z.; Fanga, L. Analysis of ALOS PALSAR InSAR data for mapping water level changes in International Journal of Remote Analysis of ALOS PALSAR InSAR data for mapping water level changes in Yellow River Delta wetlands. Int. J. Remote Sens. 2013, 34, 2047–2056. [Google Scholar] [CrossRef]
- Alsdorf, D.E.; Smith, L.C.; Melack, J.M. Amazon floodplain water level changes measured with interferometric SIR-C radar. IEEE Trans. Geosci. Remote Sens. 2001, 39, 423–431. [Google Scholar] [CrossRef]
- Poncos, V.; Teleaga, D.; Bondar, C.; Oaie, G. A new insight on the water level dynamics of the Danube Delta using a high spatial density of SAR measurements. J. Hydrol. 2013, 482, 79–91. [Google Scholar] [CrossRef]
- Jung, H.C.; Hamski, J.; Durand, M.; Alsdorf, D.; Hossain, F.; Lee, H.; Hossain, K.; Hasan, A.K.M.A.; Khan, A.S.; Hoque, A.K.M.Z. Characterization of complex fluvial systems using remote sensing of spatial and temporal water level variations in the Amazon, Congo, and Brahmaputra Rivers. Earth Surf. Process. Landf. 2010, 35, 294–304. [Google Scholar] [CrossRef]
- Yuan, T.; Lee, H.; Jung, H.C. Congo Floodplain Hydraulics using PALSAR InSAR and Envisat Altimetry Data. In Remote Sensing of Hydrological Extremes; Lakshmi, V., Ed.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Oliver-Cabrera, T.; Wdowinski, S. InSAR-Based Mapping of Tidal Inundation Extent and Amplitude in Louisiana Coastal Wetlands. Remote Sens. 2016, 8, 393. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef] [Green Version]
- Arnesen, A.S.; Silva, T.; Hess, L.; Novo, E.; Rudorff, C.M.; Chapman, B.; McDonald, K.C. Monitoring flood extent in the lower Amazon River floodplain using ALOS/PALSAR ScanSAR images. Remote Sens. Environ. 2013, 130, 51–61. [Google Scholar] [CrossRef]
- Evans, T.; Costa, M.; Telmer, K.; Silva, T. Using ALOS/PALSAR and RADARSAT-2 to Map Land Cover and Seasonal Inundation in the Brazilian Pantanal. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 4, 560–575. [Google Scholar] [CrossRef]
- Hoekman, D.; Vissers, M.A.A.; Wielaard, N. PALSAR Wide-Area Mapping of Borneo: Methodology and Map Validation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 605–617. [Google Scholar] [CrossRef]
- Alsdorf, D.E.; Melack, J.M.; Dunne, T.; Mertes, L.A.K.; Hess, L.L.; Smith, L.C. Interferometric radar measurements of water level changes on the Amazon flood plain. Nature 2000, 404, 174. [Google Scholar] [CrossRef] [PubMed]
- Reiche, J.; Lucas, R.; Mitchell, A.L.; Verbesselt, J.; Hoekman, D.H.; Haarpaintner, J.; Kellndorfer, J.M.; Rosenqvist, A.; Lehmann, E.; Woodcock, C.E.; et al. Combining satellite data for better tropical forest monitoring. Nat. Clim. Chang. 2016, 6, 120–122. [Google Scholar] [CrossRef]
- Kovacs, J.M.; Lu, X.X.; Flores-Verdugo, F.; Zhang, C.; Flores de Santiago, F.; Jiao, X. Applications of ALOS PALSAR for monitoring biophysical parameters of a degraded black mangrove (Avicennia germinans) forest. ISPRS J. Photogramm. Remote Sens. 2013, 82, 102–111. [Google Scholar] [CrossRef]
- Gudmundsson, S.; Sigmundsson, F. Three-dimensional surface motion maps estimated from combined interferometric synthetic aperture radar and GPS data. J. Geophys. Res. 2002, 107, 1–14. [Google Scholar] [CrossRef]
- Farolfi, G.; Bianchini, S.; Casagli, N. Integration of GNSS and Satellite InSAR Data: Derivation of Fine-Scale Vertical Surface Motion Maps of Po Plain, Northern Apennines, and Southern Alps, Italy. IEEE Trans. Geosci. Remote Sens. 2019, 57, 319–328. [Google Scholar] [CrossRef]
- McGlynn, B.L.; Blöschl, G.; Borga, M.; Bormann, H.; Hurkmans, R.; Komma, J.; Nandagiri, L.; Uijlenhoet, R.; Wagener, T. A data acquisition framework for predictions of runoff in ungauged basins. In Run-Off Prediction in Ungauged Basins: Synthesis Across Processes, Places and Scales; Cambridge University Press: Cambridge, UK, 2013; pp. 29–51. [Google Scholar]
- Hidayat, H.; Teuling, A.J.; Vermeulen, B.; Taufik, M.; Kastner, K.; Geertsema, T.J.; Bol, D.C.C.; Hoekman, D.H.; Haryani, G.S.; Van Lanen, H.A.J.; et al. Hydrology of inland tropical lowlands: The Kapuas and Mahakam wetlands. Hydrol. Earth Syst. Sci. 2017, 21, 2579–2594. [Google Scholar] [CrossRef]
- Myers, N.; Mittermeier, R.A.; Mittermeier, C.G.; da Fonseca, G.A.B.; Kent, J. Biodiversity hotspots for conservation priorities. Nature 2000, 403, 853–858. [Google Scholar] [CrossRef] [PubMed]
- Anaya-Acevedo, J.A.; Escobar-Martínez, J.F.; Massone, H.; Booman, G.; Quiroz-Londoño, O.M.; Cañón-Barriga, C.C.; Montoya-Jaramillo, L.J.; Palomino-Ángel, S. Identification of wetland areas in the context of agricultural development using remote sensing and GIS. DYNA 2017, 84, 201. [Google Scholar]
- Patino, J.E.; Estupinan-Suarez, L. Hotspots of Wetland Area Loss in Colombia. Wetlands 2016, 36, 935–943. [Google Scholar] [CrossRef]
- Survey of Territories Affected by Illicit Crops-2016. Available online: https://www.unodc.org/documents/crop-monitoring/Colombia/Colombia_Coca_survey_2016_English_web.pdf (accessed on 9 April 2019).
- Gómez, L.F.; Suárez, C.F.; Trujillo, A.F.; Bravo, A.M.; Rojas, V.; Hernandez, N.; Vargas, M.C. Landscape Management in Chocó-Darién Priority Watersheds; WWF-Colombia: Bogotá, Colombia, 2014. [Google Scholar]
- Hurtado, A.; Santamaría, M.; Matallana-Tobón, C.L. Plan de Investigación y Monitoreo del Sistema Nacional de Áreas Protegidas (Sinap): Avances Construidos desde la Mesa de Investigación y Monitoreo Entre 2009 y 2012; Instituto de Investigación de Recursos Biológicos Alexander von Humboldt: Bogotá, Colombia, 2013. [Google Scholar]
- Klemas, V. Remote sensing of emergent and submerged wetlands: An overview. Int. J. Remote Sens. 2013, 34, 6286–6320. [Google Scholar] [CrossRef]
- King, B.; Yurco, K.; Young, K.R.; Crews, K.A.; Shinn, J.E.; Eisenhart, A.C. Livelihood Dynamics Across a Variable Flooding Regime. Hum. Ecol. 2018, 46, 865–874. [Google Scholar] [CrossRef]
- Estupinan-Suarez, L.M.; Florez-Ayala, C.; Quinones, M.J.; Pacheco, A.M.; Santos, A.C. Detection and characterization of Colombian wetlands: Integrating geospatial data with remote sensing derived data. Using ALOS PALSAR and MODIS imagery. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2015, 40, 375–382. [Google Scholar] [CrossRef]
- Mosquera-Machado, S.; Ahmad, S. No TitleFlood hazard assessment of Atrato River in Colombia. Water Resour. Manag. 2007, 21, 591–609. [Google Scholar] [CrossRef]
- Martinez-Ortega, E.F.; Mena, D.; Bernal, F. Modelación Hidrológica de la Cuenca alta del rio Atrato Mediante HEC-HMS, para la Determinación de Caudales Máximos; IDEAM: Bogotá, Colombia, 2014.
- Palomino-Ángel, S.; Anaya-Acevedo, J.A.; Botero, B.A. Evaluation of 3B42V7 and IMERG daily-precipitation products for a very high-precipitation region in northwestern South America. Atmos. Res. 2019, 217, 37–48. [Google Scholar] [CrossRef]
- Chen, M.; Xie, P.; Janowiak, J.E.; Arkin, P.A. Global Land Precipitation: A 50-yr Monthly Analysis Based on Gauge Observations. J. Hydrometeorol. 2002, 3, 249–266. [Google Scholar] [CrossRef]
- Adler, R.F.; Huffman, G.J.; Chang, A.; Ferraro, R.; Xie, P.; Janowiak, J.; Rudolf, B.; Schneider, U.; Curtis, S.; Bolvin, D.; et al. The Version-2 Global Precipitation Climatology Project (GPCP) Monthly Precipitation Analysis (1979–Present). J. Hydrometeorol. 2003, 4, 1147–1167. [Google Scholar] [CrossRef] [Green Version]
- Bamler, R.; Hartl, P. Synthetic aperture radar interferometry. Inverse Probl. 1998, 14, 55. [Google Scholar] [CrossRef]
- Massonnet, D.; Feigl, K.L. Radar interferometry and its application to changes in the Earth’s surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef]
- Gray, A.L.; Mattar, K.E.; Sofko, G. Influence of Ionospheric Electron Density Fluctuations on Satellite Radar Interferometry streaking’ and the ionosphere. Geophys. Res. Lett. 2000, 27, 1451–1454. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Chen, C. Measurement and mitigation of the ionosphere in L-band Interferometric SAR data. In Proceedings of the 2010 IEEE Radar Conference, Washington, DC, USA, 10–14 May 2010; pp. 1459–1463. [Google Scholar]
- Meyer, F.; Bamler, R.; Jakowski, N.; Fritz, T. The Potential of Low-Frequency SAR Systems for Mapping Ionospheric TEC Distributions. IEEE Geosci. Remote Sens. Lett. 2006, 3, 560–564. [Google Scholar] [CrossRef]
- Zolesi, B.; Cander, L.R. Ionospheric Prediction and Forecasting; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Rignot, E.J.M. Effect of Faraday rotation on L-band interferometric and polarimetric synthetic-aperture radar data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 383–390. [Google Scholar] [CrossRef] [Green Version]
- Chen, A.C.; Zebker, H.A. Reducing Ionospheric Effects in InSAR Data Using Accurate Coregistration. IEEE Trans. Geosci. Remote Sens. 2014, 52, 60–70. [Google Scholar] [CrossRef]
- Fattahi, H.; Simons, M.; Agram, P. InSAR Time-Series Estimation of the Ionospheric Phase Delay: An Extension of the Split Range-Spectrum Technique. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5984–5996. [Google Scholar] [CrossRef]
- Rosen, P.A.; Gurrola, E.; Sacco, G.F.; Zebker, H. The InSAR scientific computing environment. In Proceedings of the EUSAR 2012 9th European Conference on Synthetic Aperture Radar, Nürnberg, Germany, 23–26 April 2012; pp. 730–733. [Google Scholar]
- Shim, J.S. Analysis of Total Electron Content (TEC) Variations in the Low- and Middle-Latitude Ionosphere; Utah State University: Logan, UT, USA, 2009. [Google Scholar]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1997, 25, 4035–4038. [Google Scholar] [CrossRef]
- Song, R.; Guo, H.; Liu, G.; Perski, Z.; Fan, J. Improved Goldstein SAR interferogram filter based on empirical mode decomposition. IEEE Geosci. Remote Sens. Lett. 2014, 11, 399–403. [Google Scholar] [CrossRef]
- Lu, Z.; Kwoun, O. Radarsat-1 and ERS InSAR Analysis Over Southeastern Coastal Louisiana: Implications for Mapping Water-Level Changes Beneath Swamp Forests. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2167–2184. [Google Scholar] [CrossRef]
- Woodhouse, I.H. Introduction to Microwave Remote Sensing; Taylor & Francis Group: Boca Raton, FL, USA, 2006. [Google Scholar]
- Costantini, M. A novel phase unwrapping method based on network programming. IEEE Trans. Geosci. Remote Sens. 1998, 36, 813–821. [Google Scholar] [CrossRef]
- Alsdorf, D.; Bates, P.; Melack, J.; Wilson, M.; Dunne, T. Spatial and temporal complexity of the Amazon flood measured from space. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef] [Green Version]
| Swath 1 | Swath 2 | ||||
|---|---|---|---|---|---|
| Master-Slave Dates (year-month-day) | Time Difference (days) | Baseline (m) | Master-Slave Dates (year-month-day) | Time Difference (days) | Baseline (m) |
| 20080531–20080716 | 46 | 682 | 20080502–20080617 | 46 | 3547 |
| 20080531–20080831 | 92 | 1479 | 20090620–20090805 | 46 | 737 |
| 20080716–20080831 | 46 | 798 | 20100508–20100623 | 46 | 118 |
| 20080831–20090719 | 322 | 948 | 20100508–20100808 | 92 | 286 |
| 20090719–20090903 | 46 | 279 | 20100508–20100923 | 138 | 278 |
| 20090719–20100606 | 322 | 589 | 20100623–20100808 | 46 | 404 |
| 20090903–20100606 | 276 | 373 | 20100623–20100923 | 92 | 388 |
| 20100606–20100906 | 92 | 93 | 20100808–20100923 | 46 | 90 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palomino-Ángel, S.; Anaya-Acevedo, J.A.; Simard, M.; Liao, T.-H.; Jaramillo, F. Analysis of Floodplain Dynamics in the Atrato River Colombia Using SAR Interferometry. Water 2019, 11, 875. https://doi.org/10.3390/w11050875
Palomino-Ángel S, Anaya-Acevedo JA, Simard M, Liao T-H, Jaramillo F. Analysis of Floodplain Dynamics in the Atrato River Colombia Using SAR Interferometry. Water. 2019; 11(5):875. https://doi.org/10.3390/w11050875
Chicago/Turabian StylePalomino-Ángel, Sebastián, Jesús A. Anaya-Acevedo, Marc Simard, Tien-Hao Liao, and Fernando Jaramillo. 2019. "Analysis of Floodplain Dynamics in the Atrato River Colombia Using SAR Interferometry" Water 11, no. 5: 875. https://doi.org/10.3390/w11050875
APA StylePalomino-Ángel, S., Anaya-Acevedo, J. A., Simard, M., Liao, T.-H., & Jaramillo, F. (2019). Analysis of Floodplain Dynamics in the Atrato River Colombia Using SAR Interferometry. Water, 11(5), 875. https://doi.org/10.3390/w11050875






