A Greedy Algorithm for Optimal Sensor Placement to Estimate Salinity in Polder Networks
Abstract
1. Introduction
2. Methodology
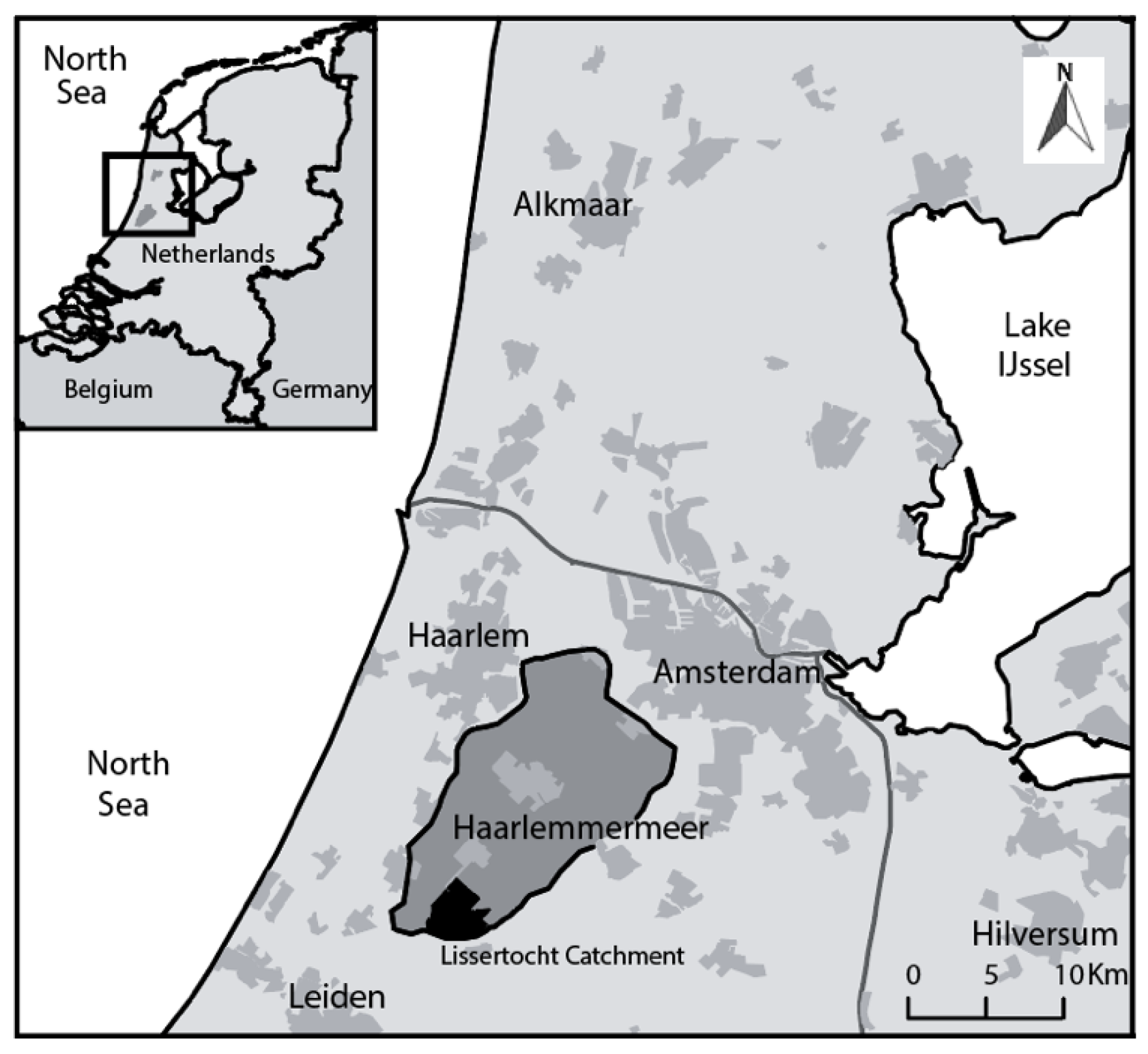
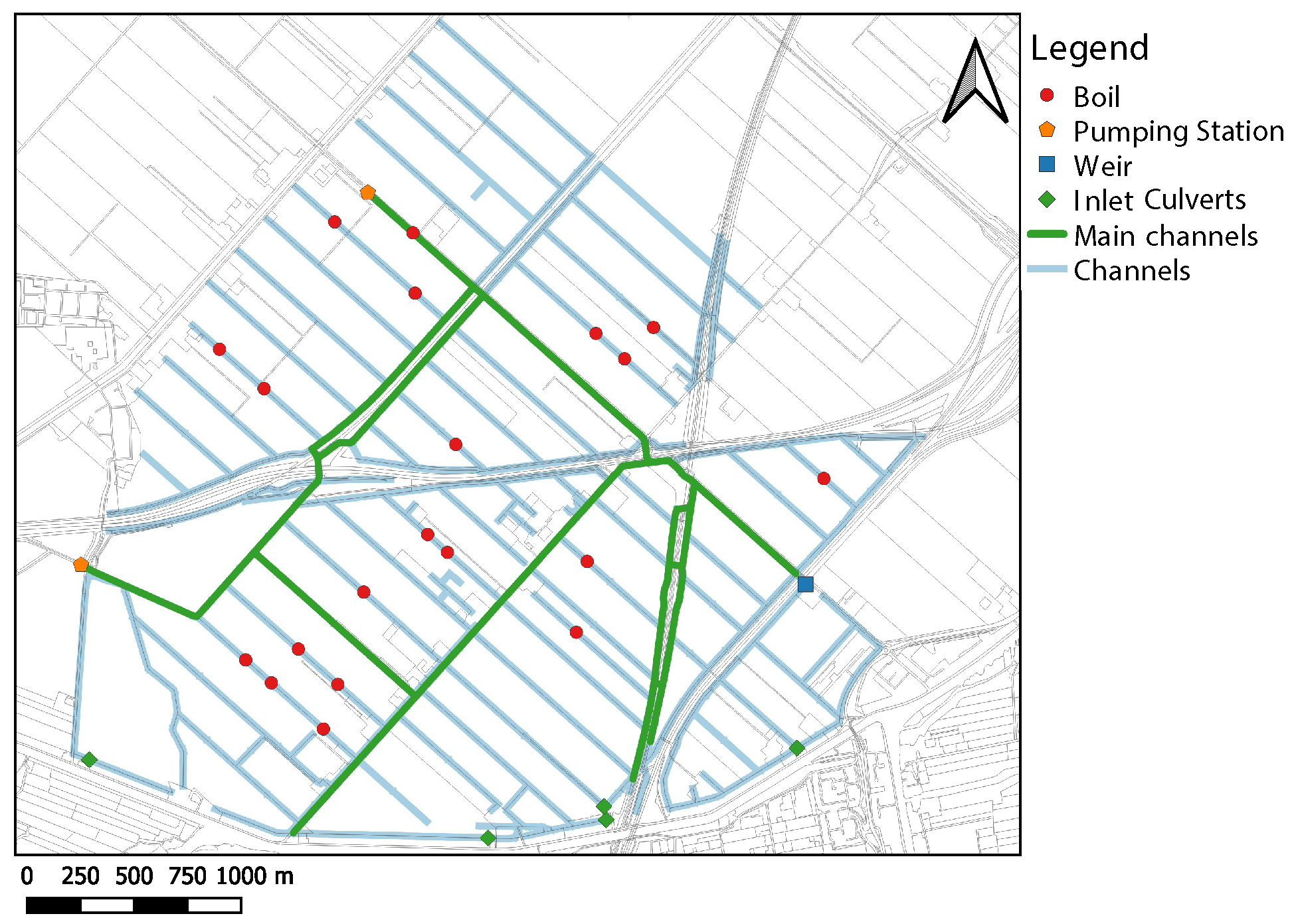
2.1. Case Study Area and Salinization Problem
2.2. Modeling Spatial and Temporal Salinity Distributions
2.3. Principal Component Analysis for Estimating Salinity
2.4. Sensor Placement Using a Greedy Algorithm
| Algorithm 1: Pseudo code of sensor placement. |
 |
3. Results and Discussions
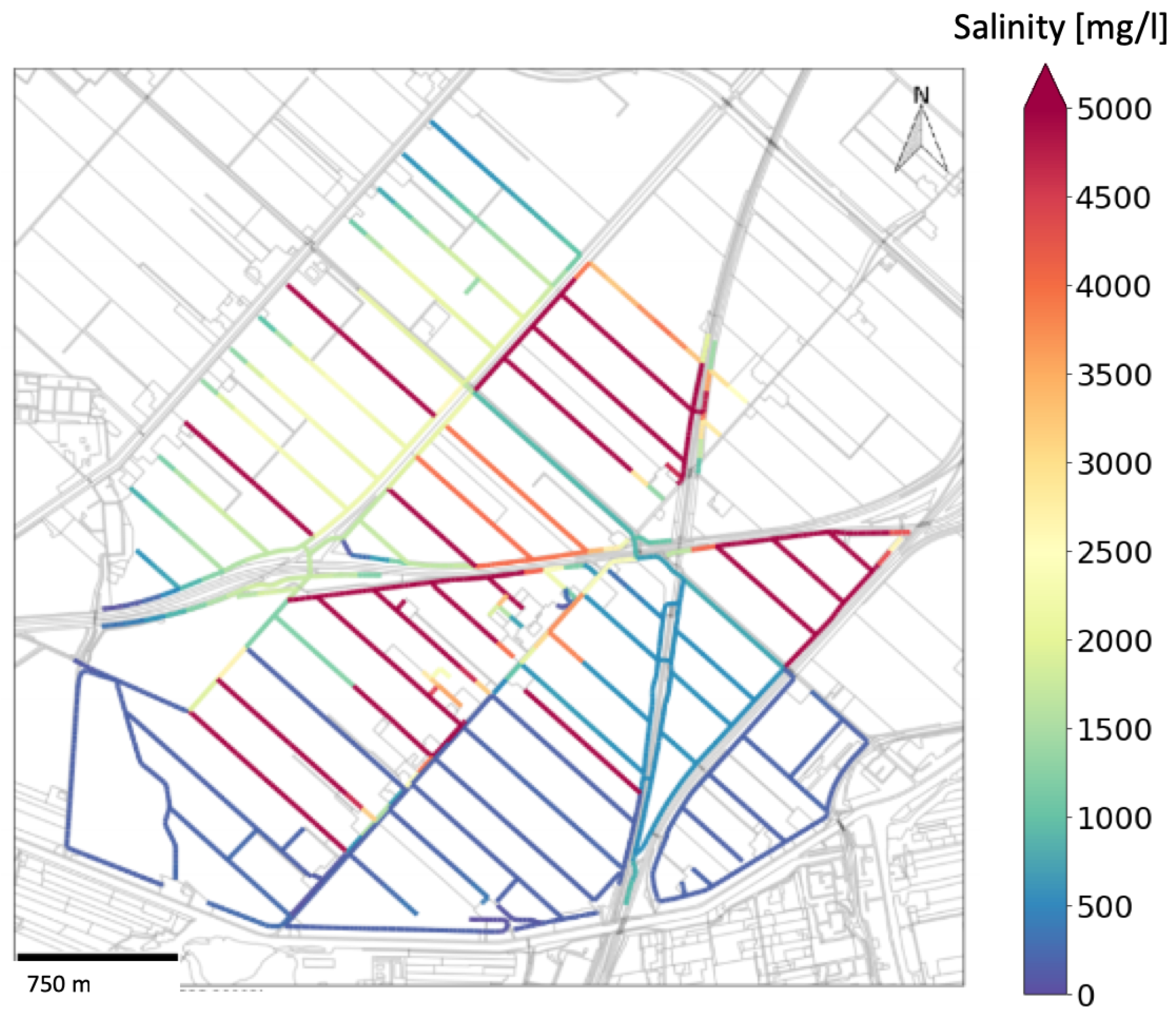
3.1. Reference Scenario
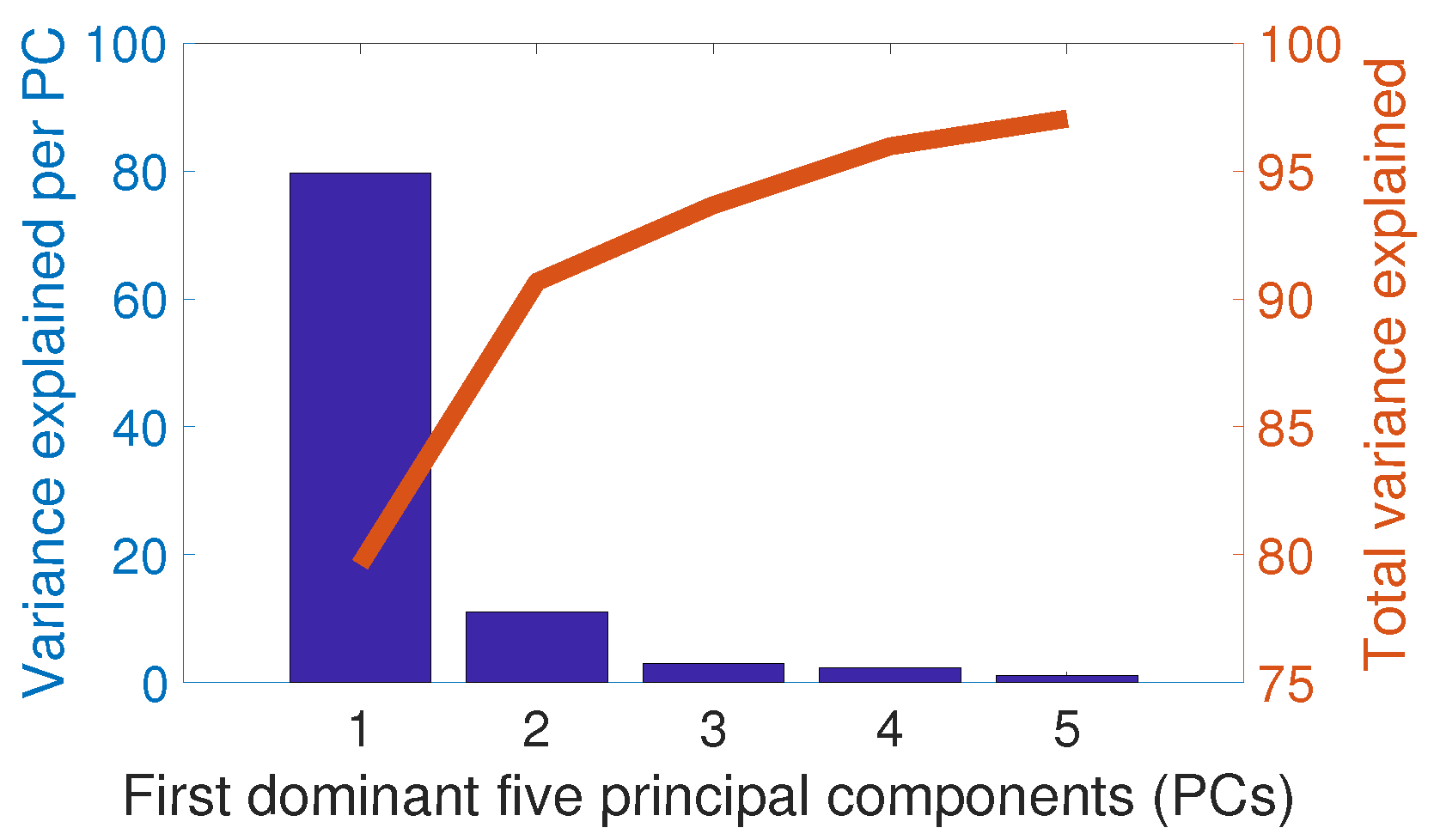
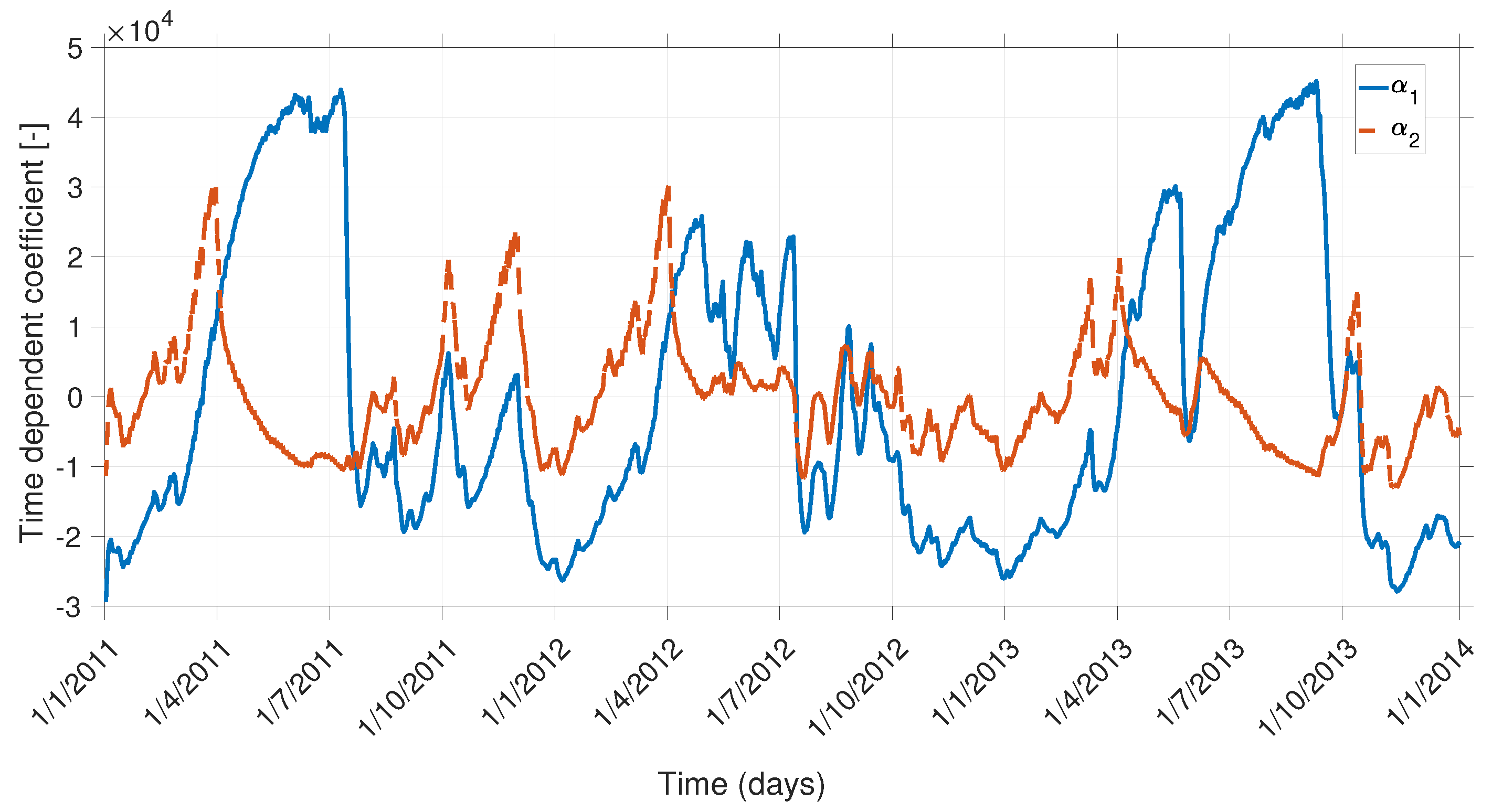
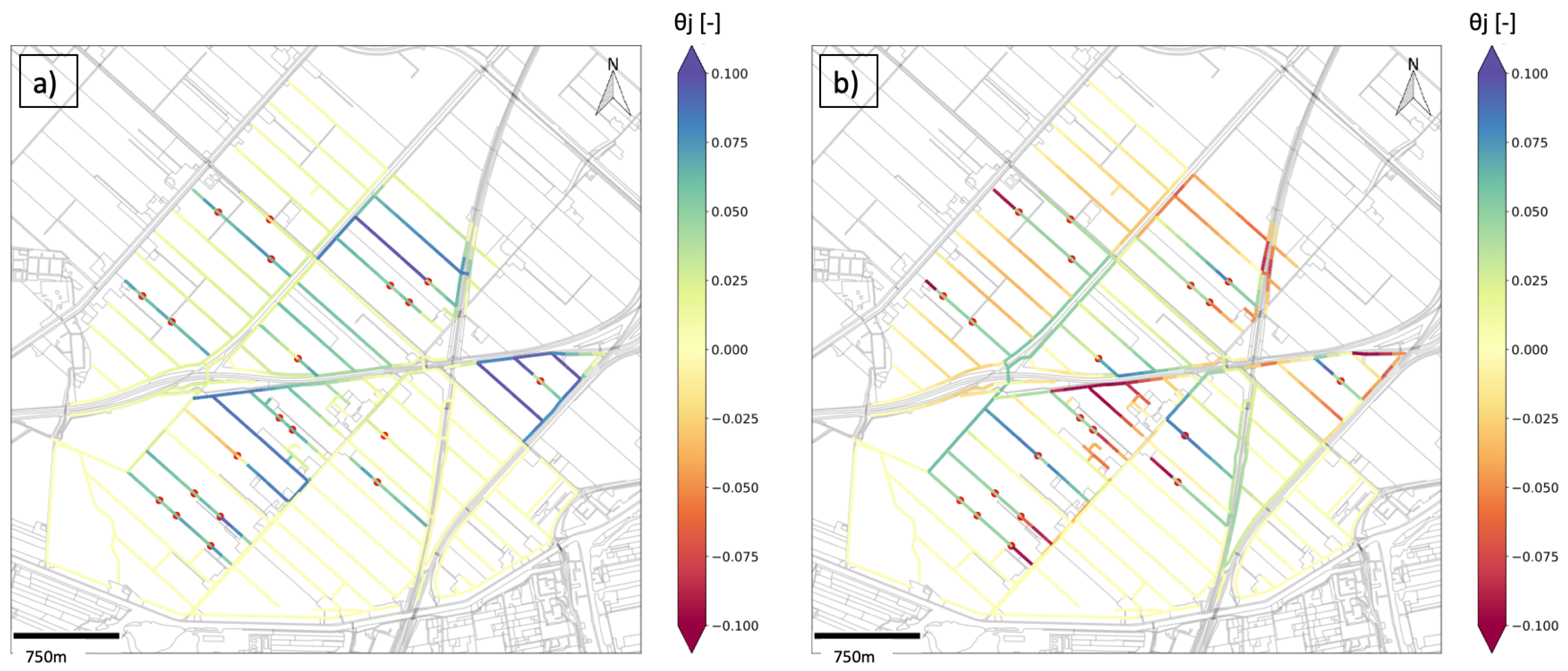
3.2. Principal Component Analysis
3.3. Optimum Sensor Placement Based on the Low-Order PCA Model
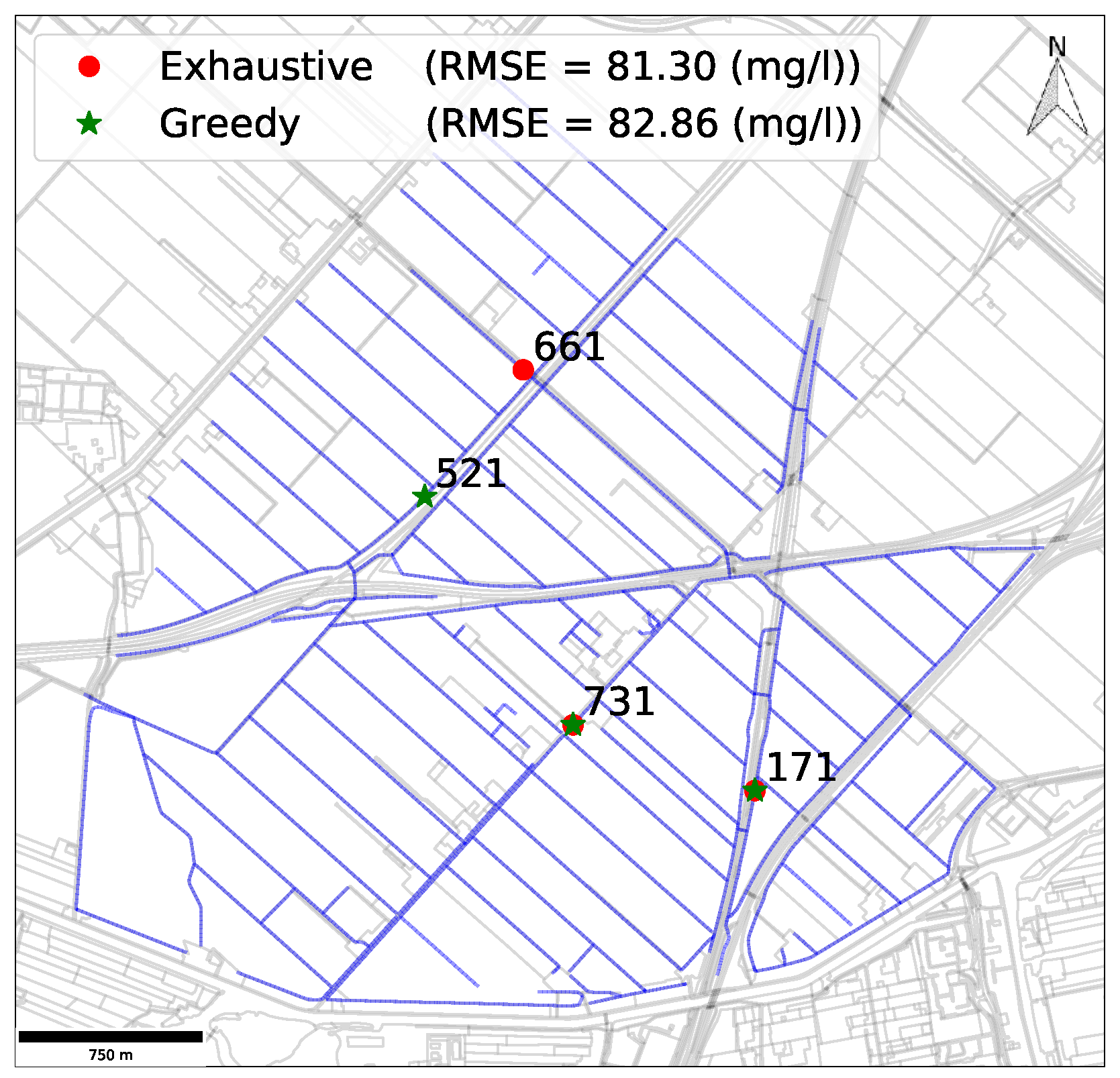
3.4. Optimality of Placements Using Greedy Algorithm
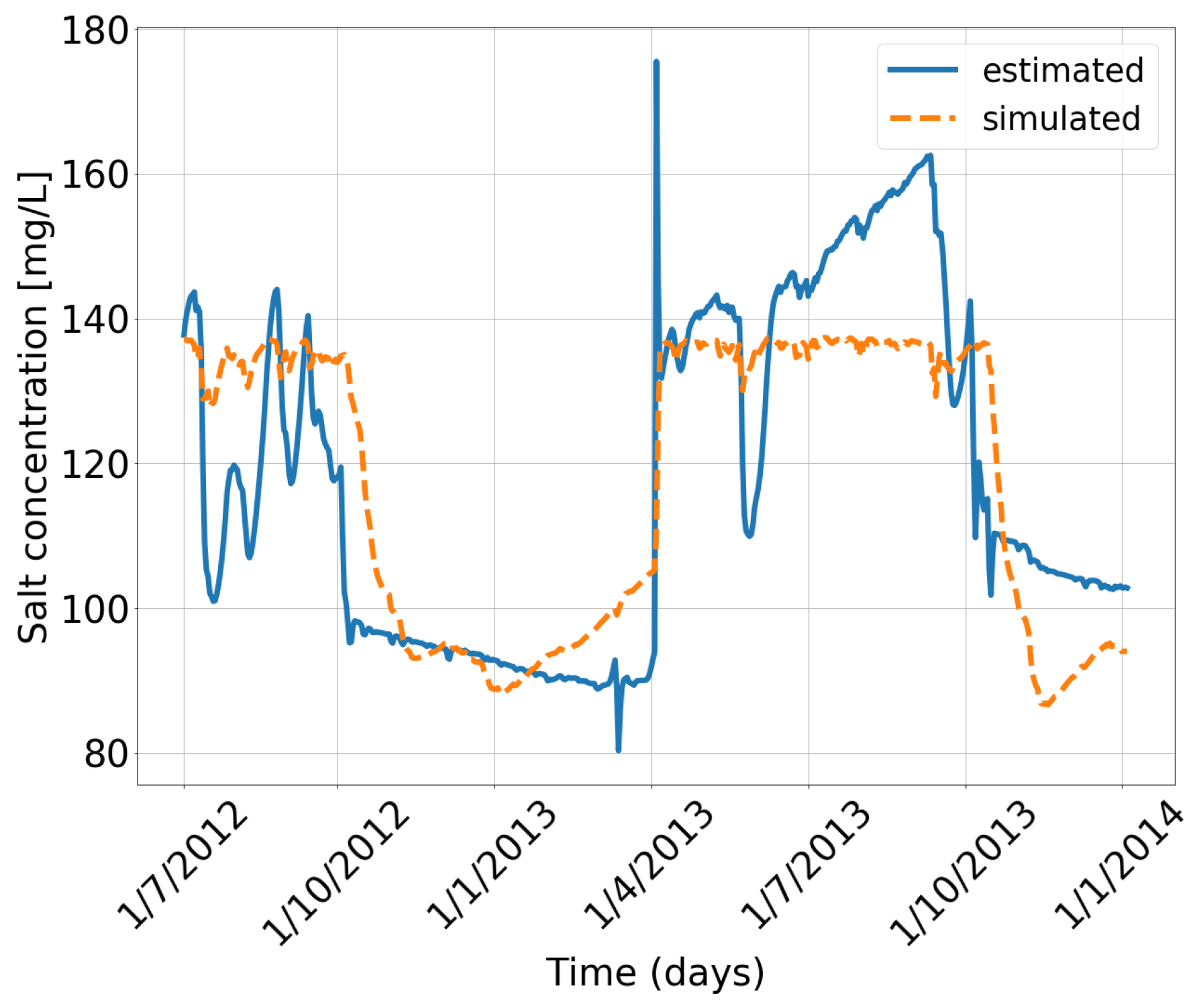
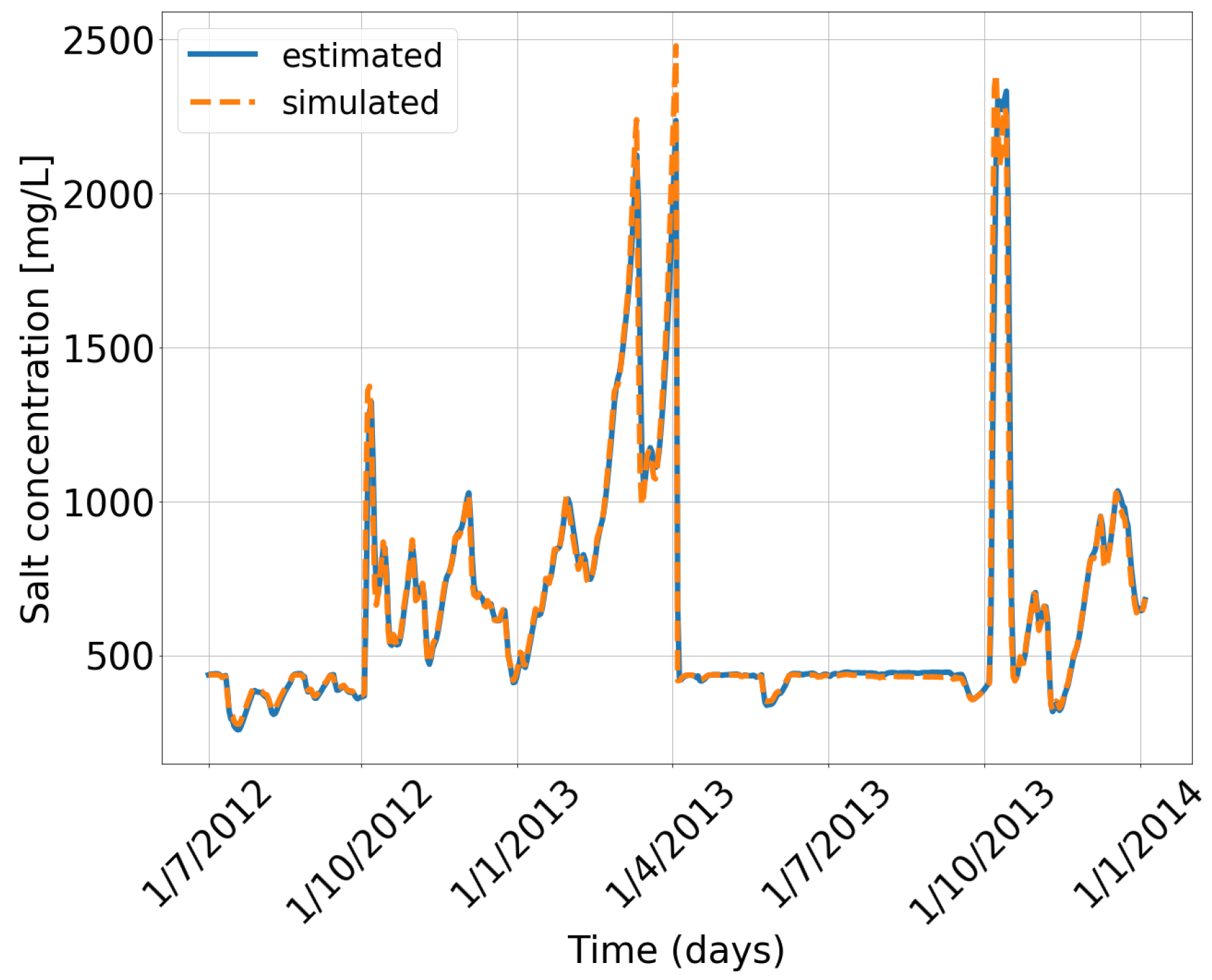
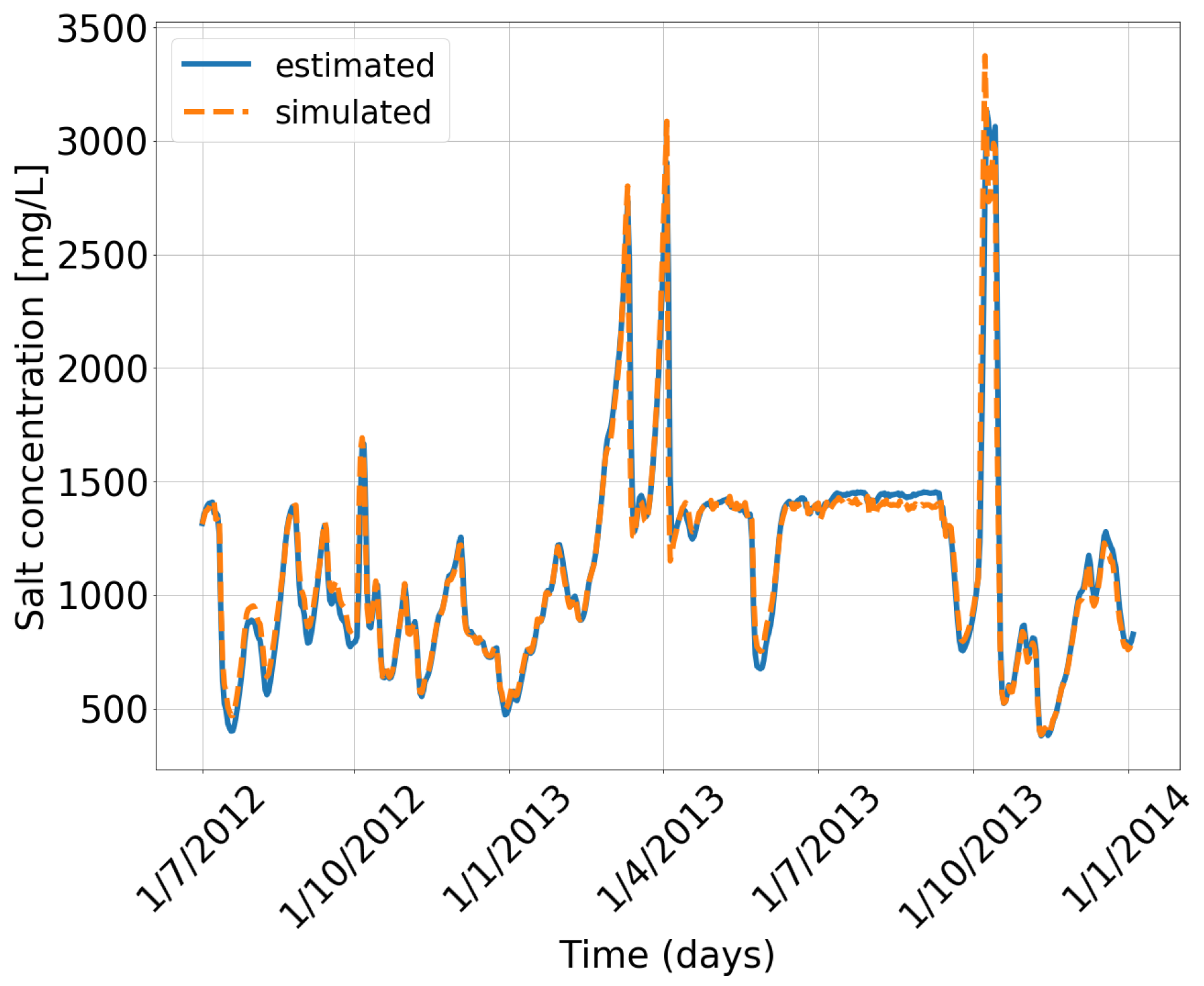
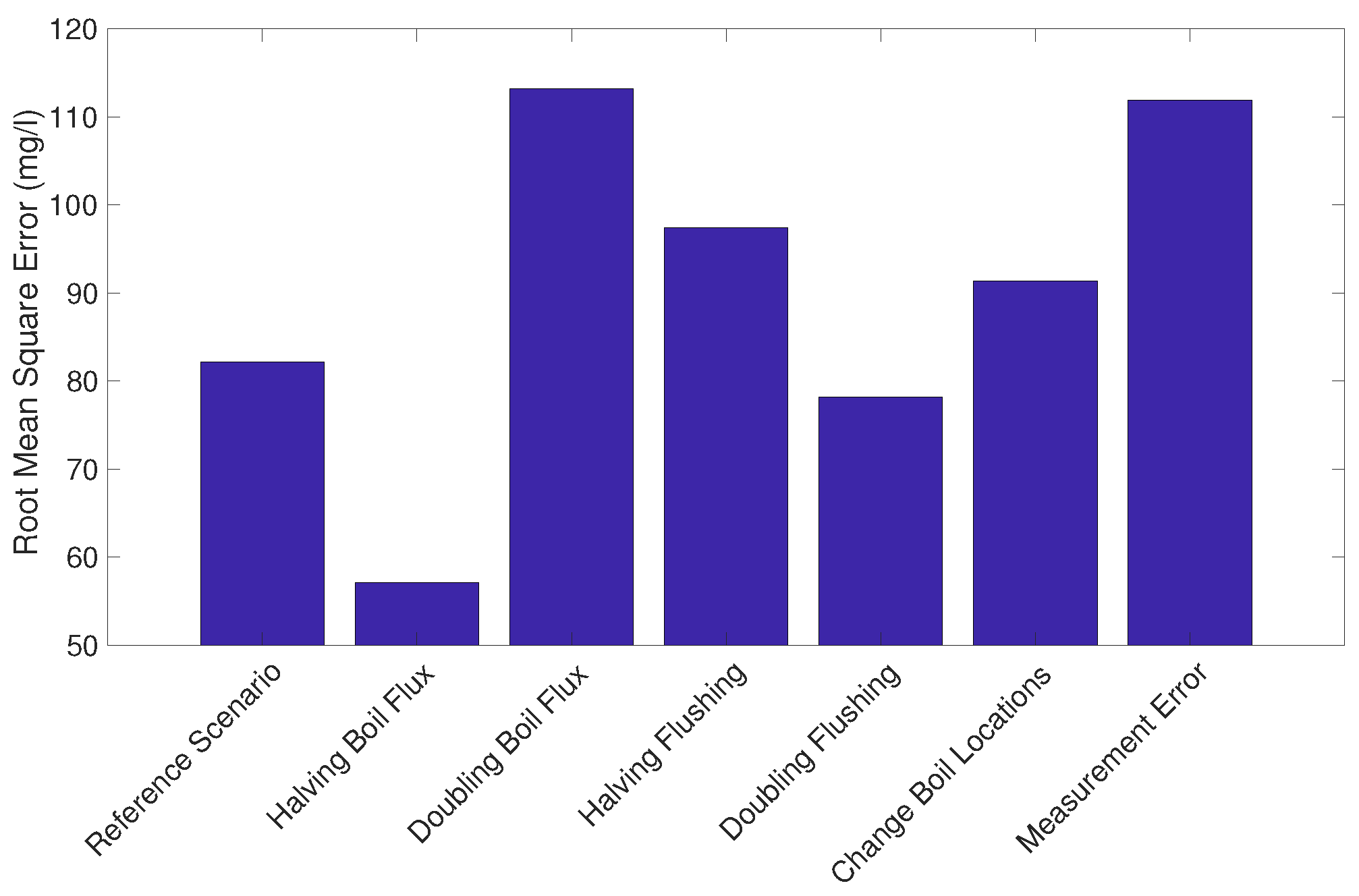
3.5. A Posteriori Assessment of Robustness of Sensor Placement to Measurement and Modeling Errors
4. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Delsman, J.R.; Waterloo, M.J.; Groen, M.M.; Groen, J.; Stuyfzand, P.J. Investigating summer flow paths in a Dutch agricultural field using high frequency direct measurements. J. Hydrol. 2014, 519, 3069–3085. [Google Scholar] [CrossRef]
- Delsman, J.R.; Oude Essink, G.H.P.; Beven, K.J.; Stuyfzand, P.J. Uncertainty estimation of end-member mixing using generalized likelihood uncertainty estimation (GLUE), applied in a lowland catchment. Water Resour. Res. 2013, 49, 4792–4806. [Google Scholar] [CrossRef]
- De Louw, P.; Oude Essink, G.; Stuyfzand, P.; van der Zee, S. Upward groundwater flow in boils as the dominant mechanism of salinization in deep polders, The Netherlands. J. Hydrol. 2010, 394, 494–506. [Google Scholar] [CrossRef]
- Oude Essink, G.H.P.; Van Baaren, E.S.; De Louw, P.G.B. Effects of climate change on coastal groundwater systems: A modeling study in the Netherlands. Water Resour. Res. 2010, 46, W00F04. [Google Scholar] [CrossRef]
- Delsman, J.R. Saline Groundwater-Surface Water Interaction in Coastal Lowlands; IOS Press, Inc.: Amsterdam, The Netherlands, 2015; pp. 1–188. [Google Scholar]
- Aydin, B.E.; Tian, X.; Delsman, J.; Oude Essink, G.H.; Rutten, M.; Abraham, E. Optimal salinity and water level control of water courses using Model Predictive Control. Environ. Model. Softw. 2019, 112, 36–45. [Google Scholar] [CrossRef]
- Mahjouri, N.; Kerachian, R. Revising river water quality monitoring networks using discrete entropy theory: The Jajrood River experience. Environ. Monit. Assess. 2011, 175, 291–302. [Google Scholar] [CrossRef]
- Noori, R.; Sabahi, M.S.; Karbassi, A.R.; Baghvand, A.; Zadeh, H.T. Multivariate statistical analysis of surface water quality based on correlations and variations in the data set. Desalination 2010, 260, 129–136. [Google Scholar] [CrossRef]
- Ouyang, Y. Evaluation of river water quality monitoring stations by principal component analysis. Water Res. 2005, 39, 2621–2635. [Google Scholar] [CrossRef]
- Alfonso, L.; Lobbrecht, A.; Price, R. Optimization of water level monitoring network in polder systems using information theory. Water Resour. Res. 2010, 46, 595–612. [Google Scholar] [CrossRef]
- Alfonso, L.; He, L.; Lobbrecht, A.; Price, R. Information theory applied to evaluate the discharge monitoring network of the Magdalena River. J. Hydroinform. 2013, 15, 211. [Google Scholar] [CrossRef]
- Raso, L.; Weijs, S.V.; Werner, M. Balancing Costs and Benefits in Selecting New Information: Efficient Monitoring Using Deterministic Hydro-economic Models. Water Resour. Manag. 2018, 32, 339–357. [Google Scholar] [CrossRef]
- Cohen, K.; Siegel, S.; McLaughlin, T. A heuristic approach to effective sensor placement for modeling of a cylinder wake. Comput. Fluids 2006, 35, 103–120. [Google Scholar] [CrossRef]
- Yildirim, B.; Chryssostomidis, C.; Karniadakis, G.E. Efficient sensor placement for ocean measurements using low-dimensional concepts. Ocean Model. 2009, 27, 160–173. [Google Scholar] [CrossRef]
- Gangopadhyay, S.; Das Gupta, A.; Nachabe, M. Evaluation of Ground Water Monitoring Network by Principal Component Analysis. Ground Water 2001, 39, 181–191. [Google Scholar] [CrossRef] [PubMed]
- Mishra, A.K.; Coulibaly, P. Developments in hydrometric network design: A review. Rev. Geophys. 2009, 47, RG2001. [Google Scholar] [CrossRef]
- Keum, J.; Kornelsen, K.C.; Leach, J.M.; Coulibaly, P. Entropy applications to water monitoring network design: A review. Entropy 2017, 19, 613. [Google Scholar] [CrossRef]
- Hart, W.E.; Murray, R. Review of Sensor Placement Strategies for Contamination Warning Systems in Drinking Water Distribution Systems. J. Water Resour. Plan. Manag. 2010, 136, 611–619. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Lee, C.; Paik, K.; Yoo, D.G.; Kim, J.H. Efficient method for optimal placing of water quality monitoring stations for an ungauged basin. J. Environ. Manag. 2014, 132, 24–31. [Google Scholar] [CrossRef]
- Memarzadeh, M.; Mahjouri, N.; Kerachian, R. Evaluating sampling locations in river water quality monitoring networks: Application of dynamic factor analysis and discrete entropy theory. Environ. Earth Sci. 2013, 70, 2577–2585. [Google Scholar] [CrossRef]
- Boroumand, A.; Rajaee, T. Discrete entropy theory for optimal redesigning of salinity monitoring network in San Francisco bay. Water Sci. Technol. Water Supply 2017, 17, 606–612. [Google Scholar] [CrossRef]
- Banik, B.K.; Alfonso, L.; Torres, A.S.; Mynett, A.; Di Cristo, C.; Leopardi, A. Optimal placement of water quality monitoring stations in sewer systems: An information theory approach. Procedia Eng. 2015, 119, 1308–1317. [Google Scholar] [CrossRef]
- Lee, J.H. Determination of optimal water quality monitoring points in sewer systems using entropy theory. Entropy 2013, 15, 3419–3434. [Google Scholar] [CrossRef]
- Masoumi, F.; Kerachian, R. Assessment of the groundwater salinity monitoring network of the Tehran region: Application of the discrete entropy theory. Water Sci. Technol. 2008, 58, 765–771. [Google Scholar] [CrossRef]
- Mogheir, Y.; Singh, V.P. Application of information theory to groundwater quality monitoring networks. Water Resour. Manag. 2002, 16, 37–49. [Google Scholar] [CrossRef]
- Owlia, R.R.; Abrishamchi, A.; Tajrishy, M. Spatial-temporal assessment and redesign of groundwater quality monitoring network: A case study. Environ. Monit. Assess. 2011, 172, 263–273. [Google Scholar] [CrossRef] [PubMed]
- Banik, B.K.; Alfonso, L.; Di Cristo, C.; Leopardi, A. Greedy algorithms for sensor location in sewer systems. Water 2017, 9, 856. [Google Scholar] [CrossRef]
- Banik, B.K.; Alfonso, L.; Di Cristo, C.; Leopardi, A.; Mynett, A. Evaluation of Different Formulations to Optimally Locate Sensors in Sewer Systems. J. Water Resour. Plan. Manag. 2017, 143, 04017026. [Google Scholar] [CrossRef]
- Uber, J.; Janke, R.; Murray, R.; Meyer, P. Greedy Heuristic Methods for Locating Water Quality Sensors in Distribution Systems. In Critical Transitions in Water and Environmental Resources Management; American Society of Civil Engineers: Reston, VA, USA, 2004; Volume 40737, pp. 1–9. [Google Scholar]
- Krause, P.; Boyle, D.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Hoes, O.; Luxemburg, W.; Westhof, M.C.; van de Giesen, N.; Selker, J. Identifying seepage in ditches and canals in polders in The Netherlands by Distributed Temperature Sensing. Lowl. Technol. Int. 2009, 11, 21–26. [Google Scholar]
- Delsman, J.R.; de Louw, P.G.; de Lange, W.J.; Oude Essink, G.H. Fast calculation of groundwater exfiltration salinity in a lowland catchment using a lumped celerity/velocity approach. Environ. Model. Softw. 2017, 96, 323–334. [Google Scholar] [CrossRef]
- Kelderman, I. Slimmer Inlaten in de Haarlemmermeerpolder. Technical Report, Deltares. 2015. Available online: https://publicwiki.deltares.nl/display/ZOETZOUT/Slimmer+doorspoelen (accessed on 24 March 2019).
- Hof, A.; Schuurmans, W. Water quality control in open channels. Water Sci. Technol. 2000, 42, 153–159. [Google Scholar] [CrossRef]
- Udell, M.; Horn, C.; Zadeh, R.; Boyd, S. Generalized low rank models. Found. Trends® Mach. Learn. 2016, 9, 1–118. [Google Scholar] [CrossRef]

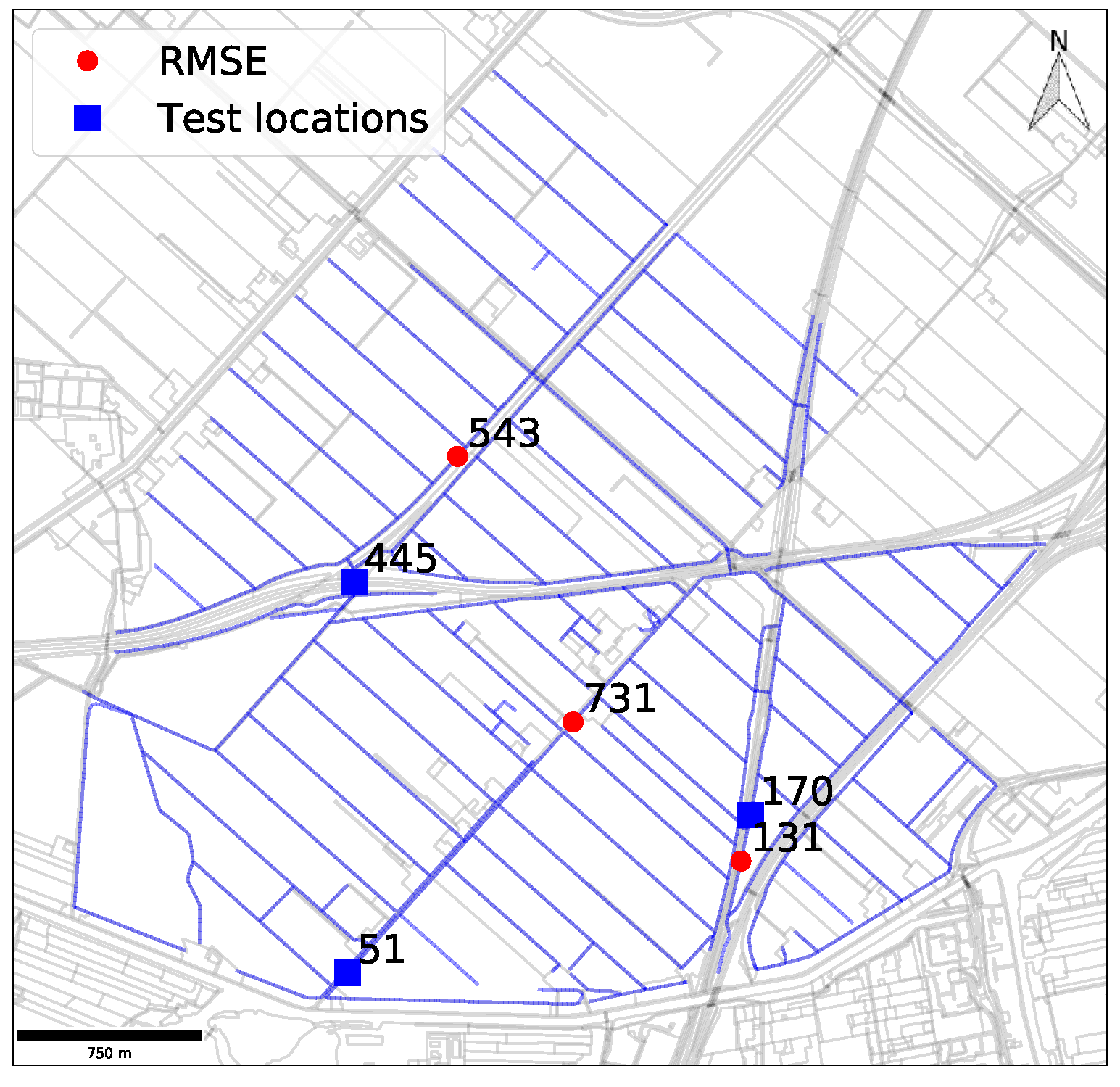
| Node Number(s) | RMSE (mg/L) |
|---|---|
| 543 | 140.02 |
| 543, 131 | 84.31 |
| 543, 131, 731 | 82.18 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aydin, B.E.; Hagedooren, H.; Rutten, M.M.; Delsman, J.; Oude Essink, G.H.P.; van de Giesen, N.; Abraham, E. A Greedy Algorithm for Optimal Sensor Placement to Estimate Salinity in Polder Networks. Water 2019, 11, 1101. https://doi.org/10.3390/w11051101
Aydin BE, Hagedooren H, Rutten MM, Delsman J, Oude Essink GHP, van de Giesen N, Abraham E. A Greedy Algorithm for Optimal Sensor Placement to Estimate Salinity in Polder Networks. Water. 2019; 11(5):1101. https://doi.org/10.3390/w11051101
Chicago/Turabian StyleAydin, Boran Ekin, Hugo Hagedooren, Martine M. Rutten, Joost Delsman, Gualbert H. P. Oude Essink, Nick van de Giesen, and Edo Abraham. 2019. "A Greedy Algorithm for Optimal Sensor Placement to Estimate Salinity in Polder Networks" Water 11, no. 5: 1101. https://doi.org/10.3390/w11051101
APA StyleAydin, B. E., Hagedooren, H., Rutten, M. M., Delsman, J., Oude Essink, G. H. P., van de Giesen, N., & Abraham, E. (2019). A Greedy Algorithm for Optimal Sensor Placement to Estimate Salinity in Polder Networks. Water, 11(5), 1101. https://doi.org/10.3390/w11051101






