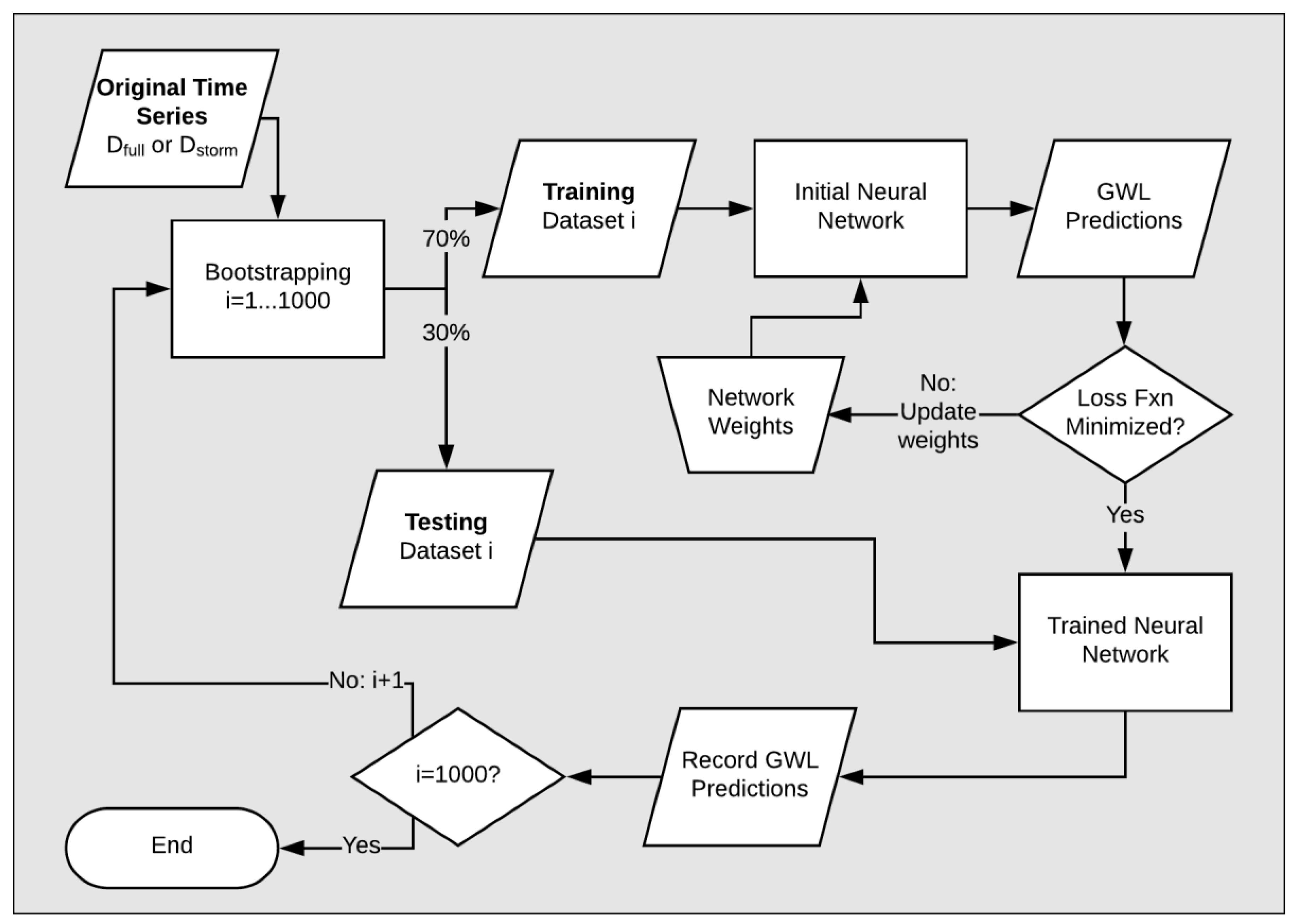
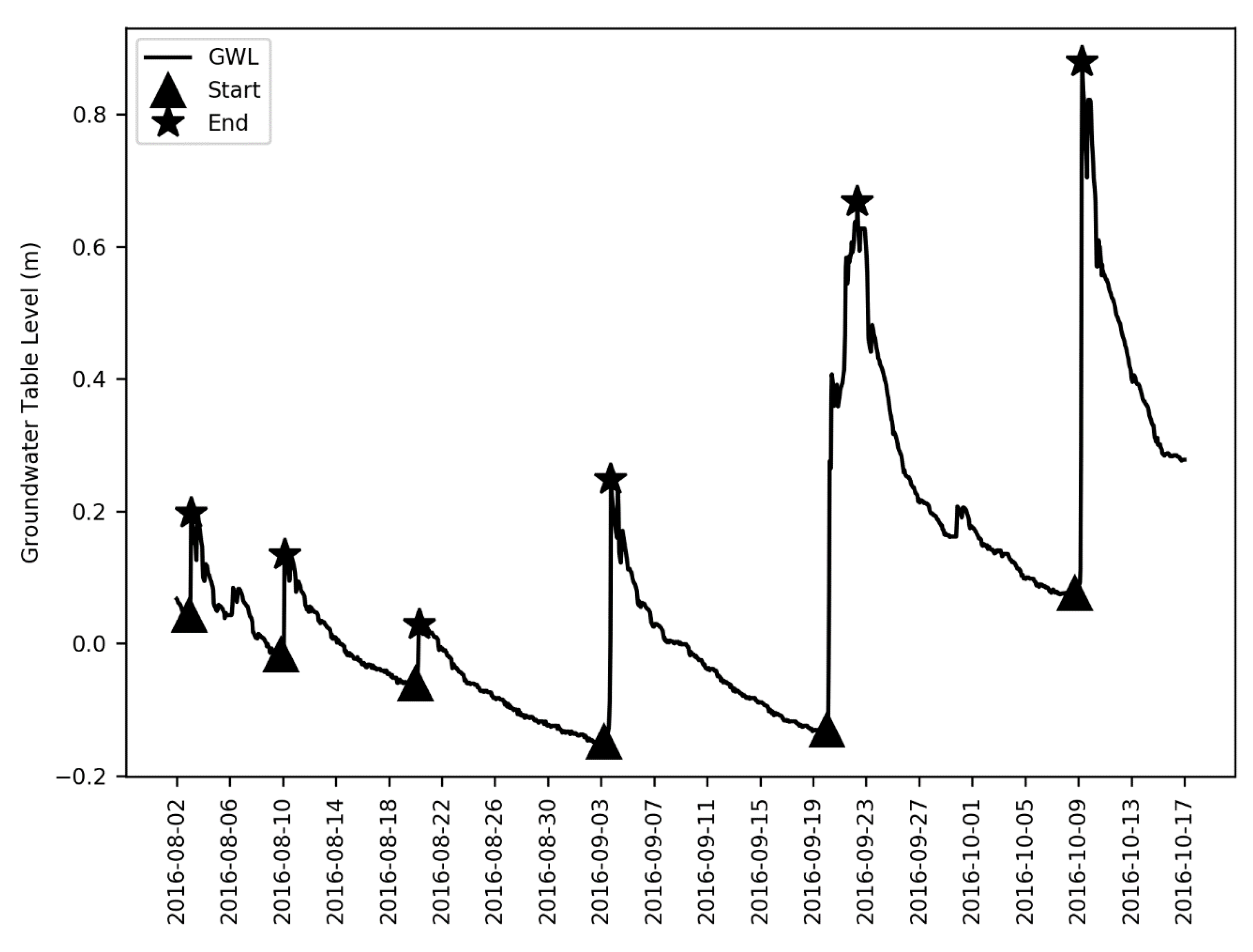
1. Introduction
Storm events in low relief coastal areas can quickly raise the groundwater table, which is often relatively shallow [
1,
2]. During these events, infiltration and groundwater table response decrease the volume available for stormwater storage, therefore increasing runoff and, by extension, loads on stormwater systems [
3]. Many coastal urban areas are also experiencing increased flooding due to land subsidence and climate change effects, such as sea level rise [
4], increased precipitation, and more frequent extreme climactic events [
5]. While there are several causes of flooding in coastal cities [
6], the groundwater table level is a largely unrepresented factor and forecasting its variations can provide valuable information to aid in planning and response to storm events. Furthermore, because the groundwater table will rise as sea level rises [
3,
7,
8,
9], stormwater storage capacity will continue to decrease and inundation from groundwater may occur. Damage from groundwater inundation, which occurs through different mechanisms than overland flooding, can have significant impacts on subsurface structures [
10,
11]. Even if groundwater inundation does not regularly reach the land surface, increased duration of high groundwater table levels could have significant impacts on infrastructure [
8,
12,
13,
14] making groundwater table forecasting an increasingly important part of effectively modeling and predicting coastal urban flooding.
In the field of groundwater hydrology, models based on the physical principles of groundwater flow have traditionally been some of the main tools for understanding the mechanics of these systems [
9,
15,
16,
17,
18,
19,
20]. Developing these models, however, requires extensive details about aquifer properties. In urban areas, this level of detail is hard to achieve at high resolutions because the subsurface is a complex mix of natural and anthropogenic structures such as varied geologic deposits, buried creeks or wetlands, roadbeds, building foundations, and sanitary and stormwater pipes. These factors should be considered when developing a physics-based model; if the necessary data are not available then assumptions and estimations must be substituted based on domain knowledge. Even if the data necessary to build a physics-based model are available, there is still the challenge of calibrating the model to adequately reflect reality.
Machine learning approaches are being increasingly used by hydrologists in order to mitigate the difficulties associated with physics-based models [
6,
21,
22,
23,
24,
25,
26,
27]. The advantage of such data-driven modeling is that physical relationships and the physical parameters needed to describe the physical environment do not need to be explicitly defined; the machine learning algorithm approximates the relationship between model inputs and outputs through an iterative learning process [
28]. Neural networks (NN) have been used to model and predict nonlinear time series data, such as the groundwater table, and have been found to perform as well as, and in some cases, better than physics-based models [
29,
30]. Several studies have applied NN models on a daily or monthly time step to aquifers used for water supply in order to make forecasts appropriate for groundwater management. [
31,
32,
33,
34,
35,
36]. Few studies, however, have used NNs for predicting the groundwater table in unconfined surficial coastal aquifers where flooding is a major concern and a finer time scale is needed to capture the impacts of storm events [
2].
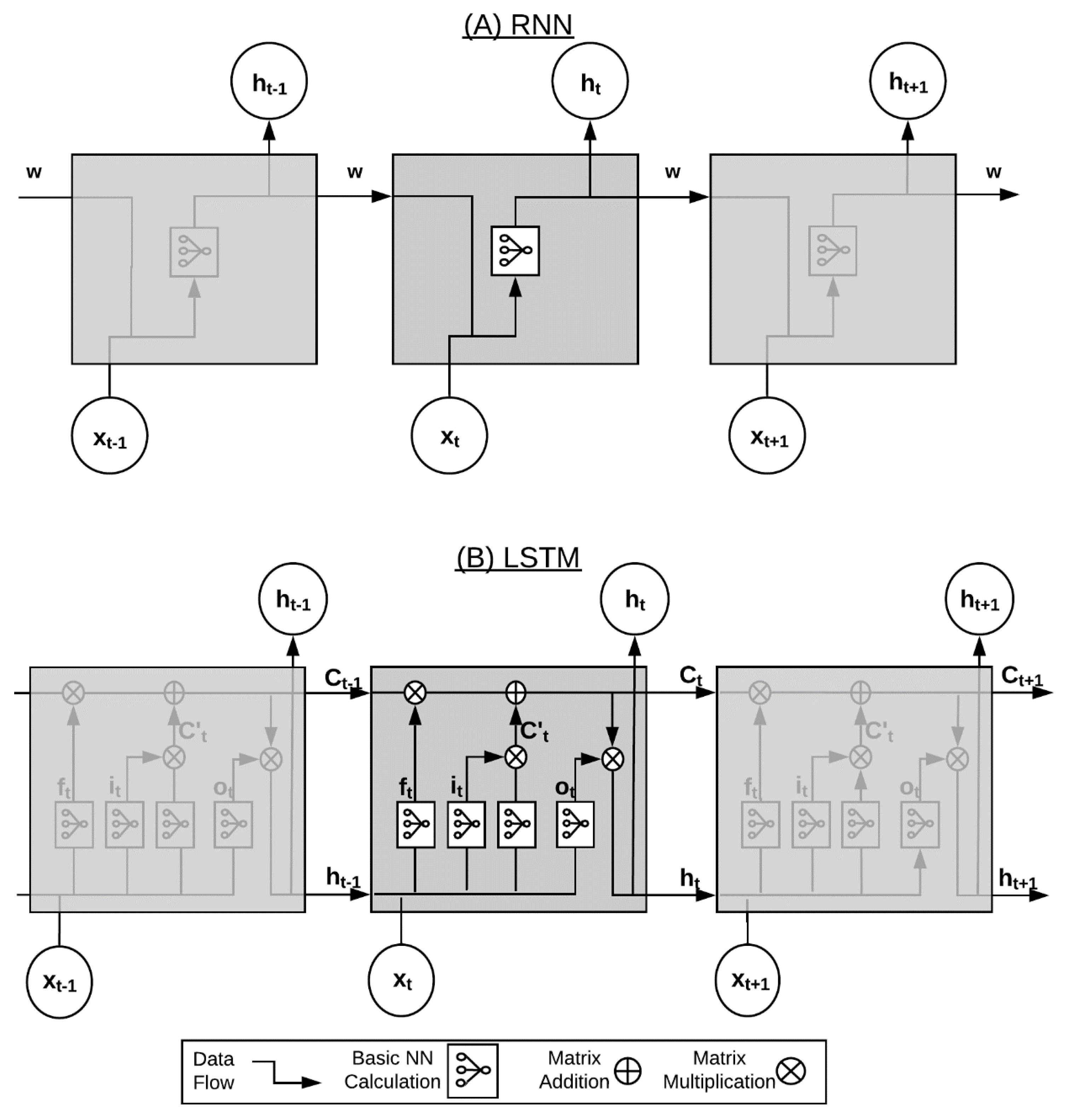
Recurrent neural networks (RNNs) have been a popular choice for modeling groundwater time series data because they attempt to retain a memory of past network conditions. While RNNs have been successfully applied to groundwater modeling [
31,
32,
33,
34], it’s been found that standard RNN architectures have difficulty capturing long term dependencies between variables [
37]. This is due to two problems, (i) vanishing and (ii) exploding gradient, where weights in the network go to zero or become extremely large during model training. These two problems occur because the error signal can only be effectively backpropagated for a limited number of steps [
38].
One of the most successful approaches to avoiding the vanishing and exploding gradient problems has been the long short-term memory (LSTM) variant of standard RNNs [
38]. LSTM is able to avoid these training problems by eliminating unnecessary information being passed to future model states, while retaining a memory of important past events. In the field of natural language processing, LSTM has become a popular choice of neural network because of its ability to retain context over long spans [
39]. LSTM has also been effective for financial time series prediction [
40] and for short-term traffic and travel time predictions [
41,
42] Despite the wide variety of applications, however, LSTM has only recently been used for hydrologic time series prediction [
43,
44]. For example, LSTM was found to outperform two simpler RNN architectures for predicting streamflow [
45]. LSTM networks have also recently been used to model the groundwater table on a monthly time step in an inland agricultural area of China [
46]. This agriculture focused study provides valuable information on the advantages of LSTM for groundwater level prediction over a basic feed-forward neural network (FFNN), but only presents predictions for one time step ahead. In a real-time flood forecasting application, however, longer forecasts of the groundwater table at short time intervals would be needed [
2] and should include the use of forecast input data. LSTM models have yet to be evaluated for this type of application.
With the growing availability of large datasets and high performance computing, data-driven modeling techniques can now be evaluated for groundwater table forecasting. The objective of this study, therefore, is to compare RNN and LSTM neural networks for their ability to model and predict groundwater table changes in an unconfined coastal aquifer system with an emphasis on capturing groundwater table response to storm events. Based on prior research on this topic, it is expected that LSTM will outperform RNN for forecasting groundwater table levels. In this study, LSTM and RNN models were built for seven sites in Norfolk, Virginia USA, a flood prone coastal city. The models were trained and tested using observed groundwater table, sea level, and rainfall data as input. In addition to comparing RNN and LSTM neural networks, the effect of different training methods on model accuracy was evaluated by creating two unique datasets, one of the complete time series and one containing only periods identified as storms. The two types of datasets were bootstrapped and a statistical comparison of the two model types was made with t-tests to determine if differences in the results were significant. To ensure fair comparison, the hyperparameters of the RNN and LSTM networks were individually optimized with an advanced tuning technique instead of traditional ad-hoc methods. Once trained and evaluated, the RNN and LSTM models were tested with forecast sea level and rainfall input data to quantify the accuracy that could be expected in a real-time forecasting scenario.
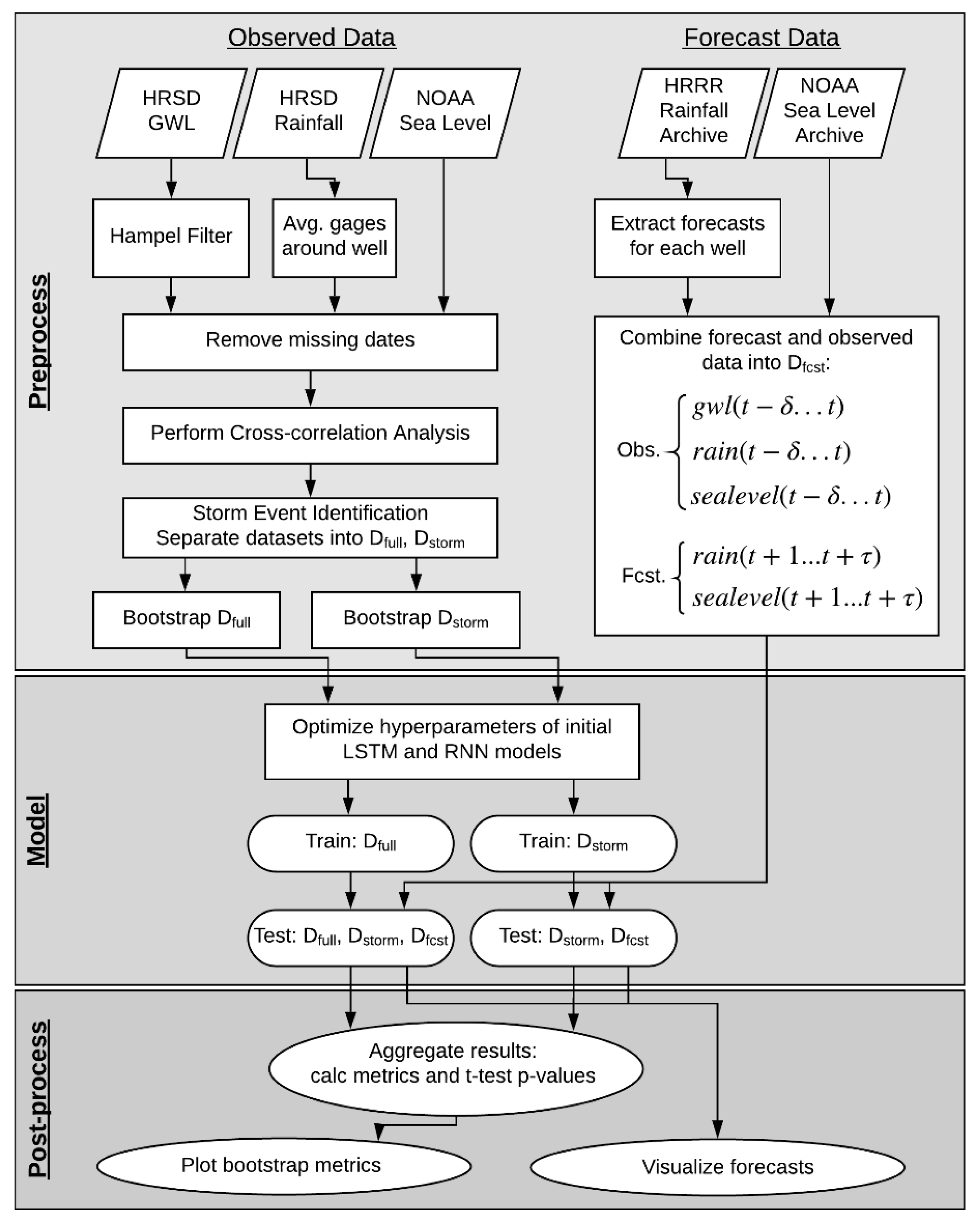
This paper is structured as follows: First, a description of the study area, data and methodology used is given in
Section 2. The methodology includes a description of the RNN and LSTM networks, input data preprocessing, and how models are trained and evaluated. The results of data preprocessing and modeling are then presented in
Section 3 and discussed in
Section 4. Conclusions are drawn in
Section 5.
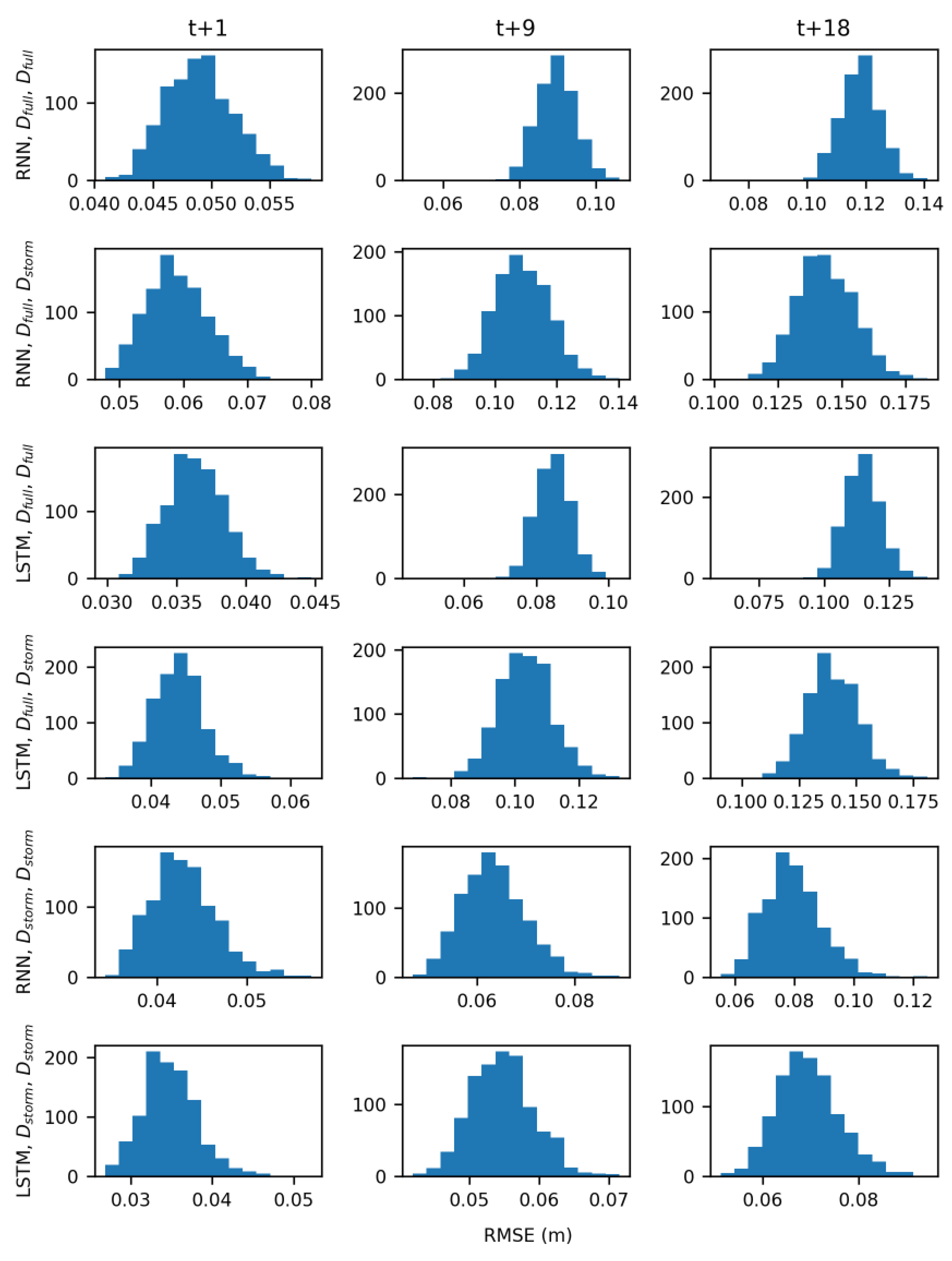
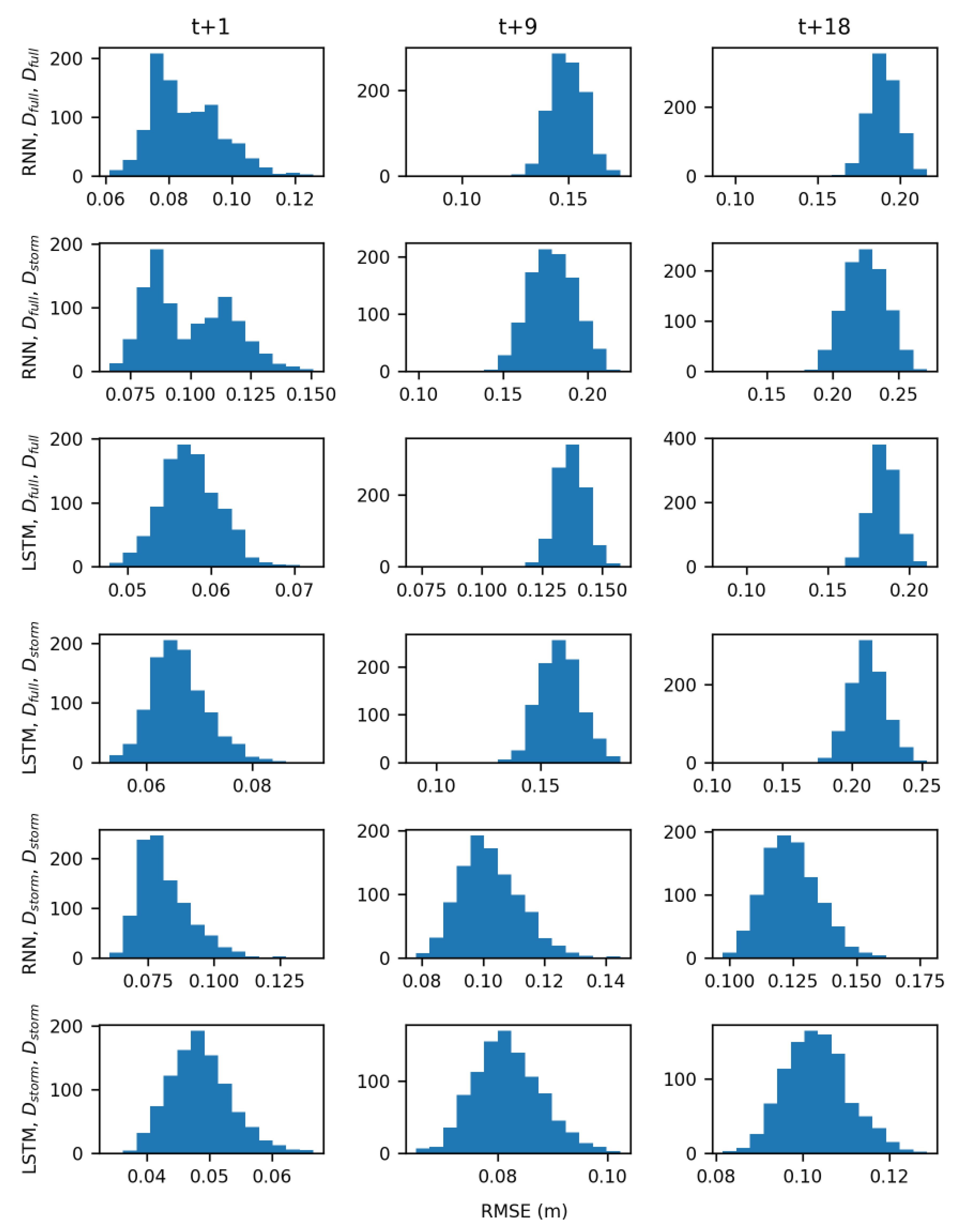
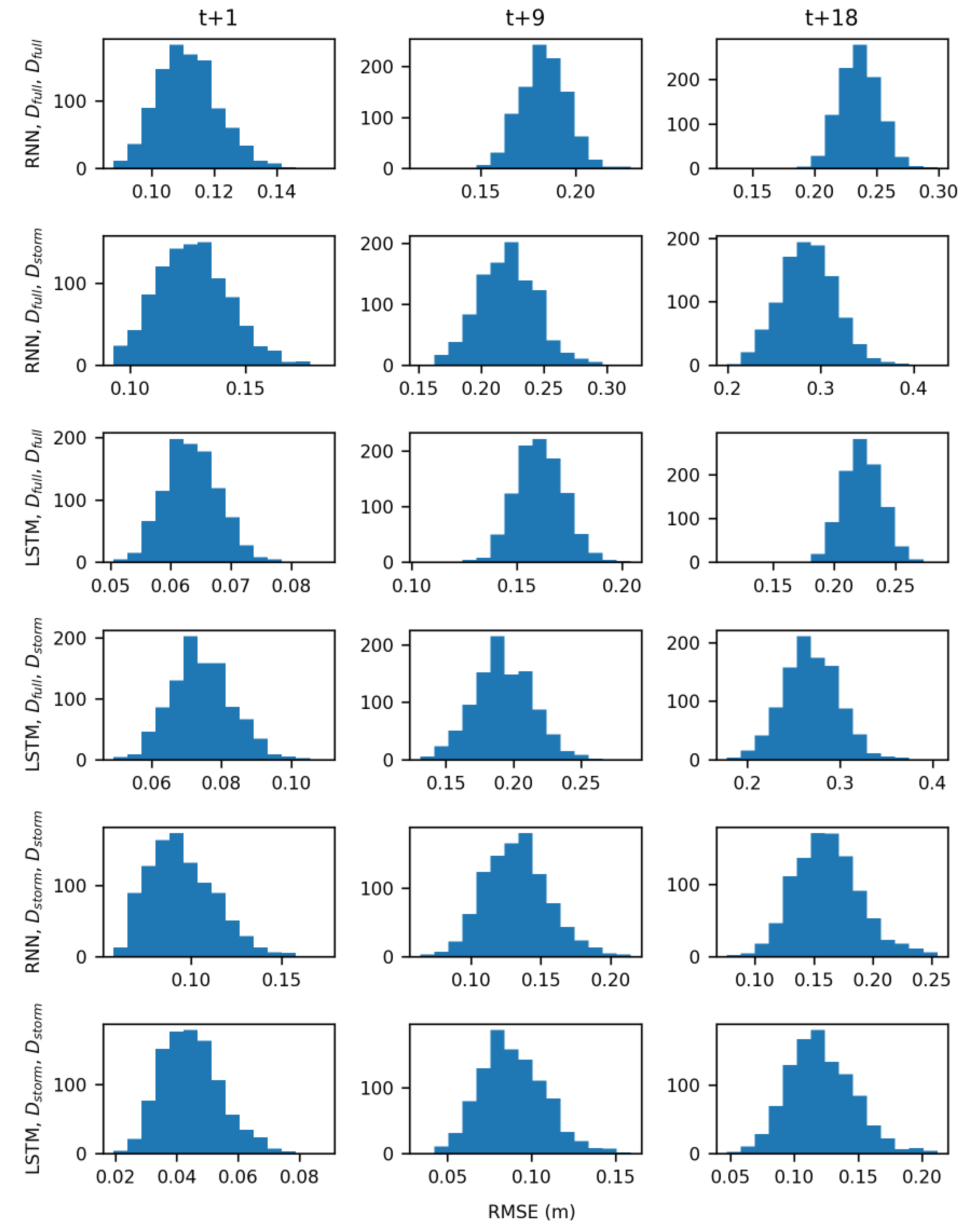
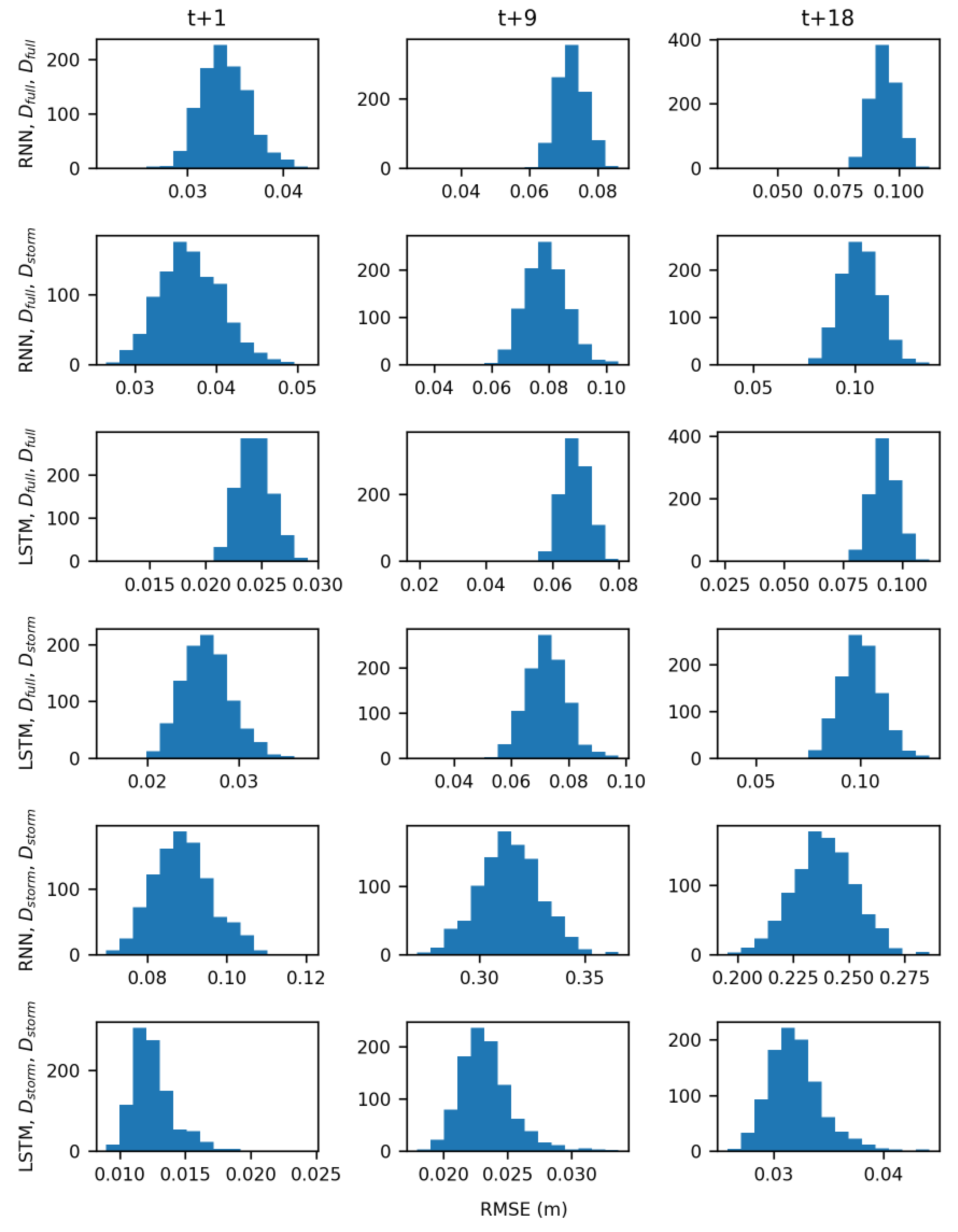
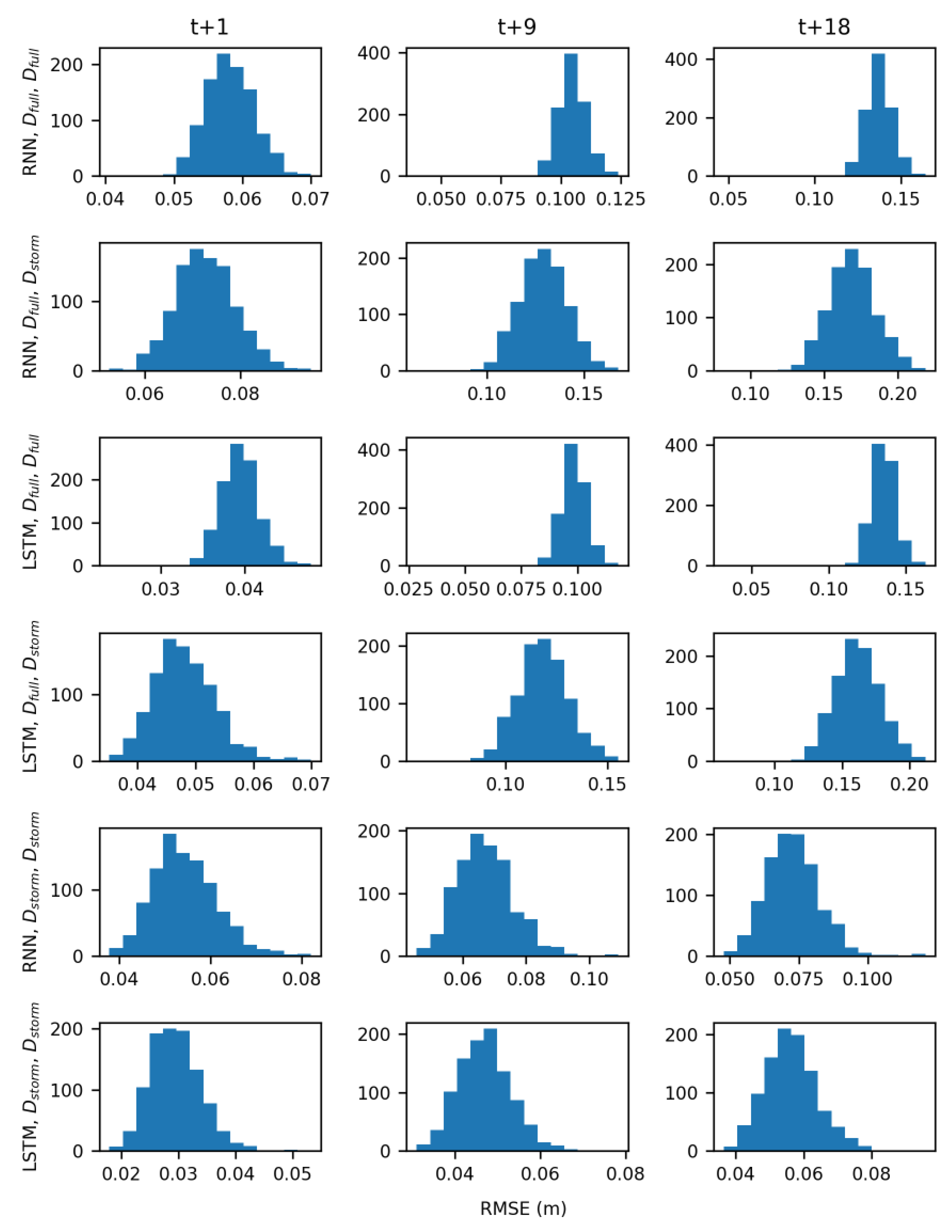
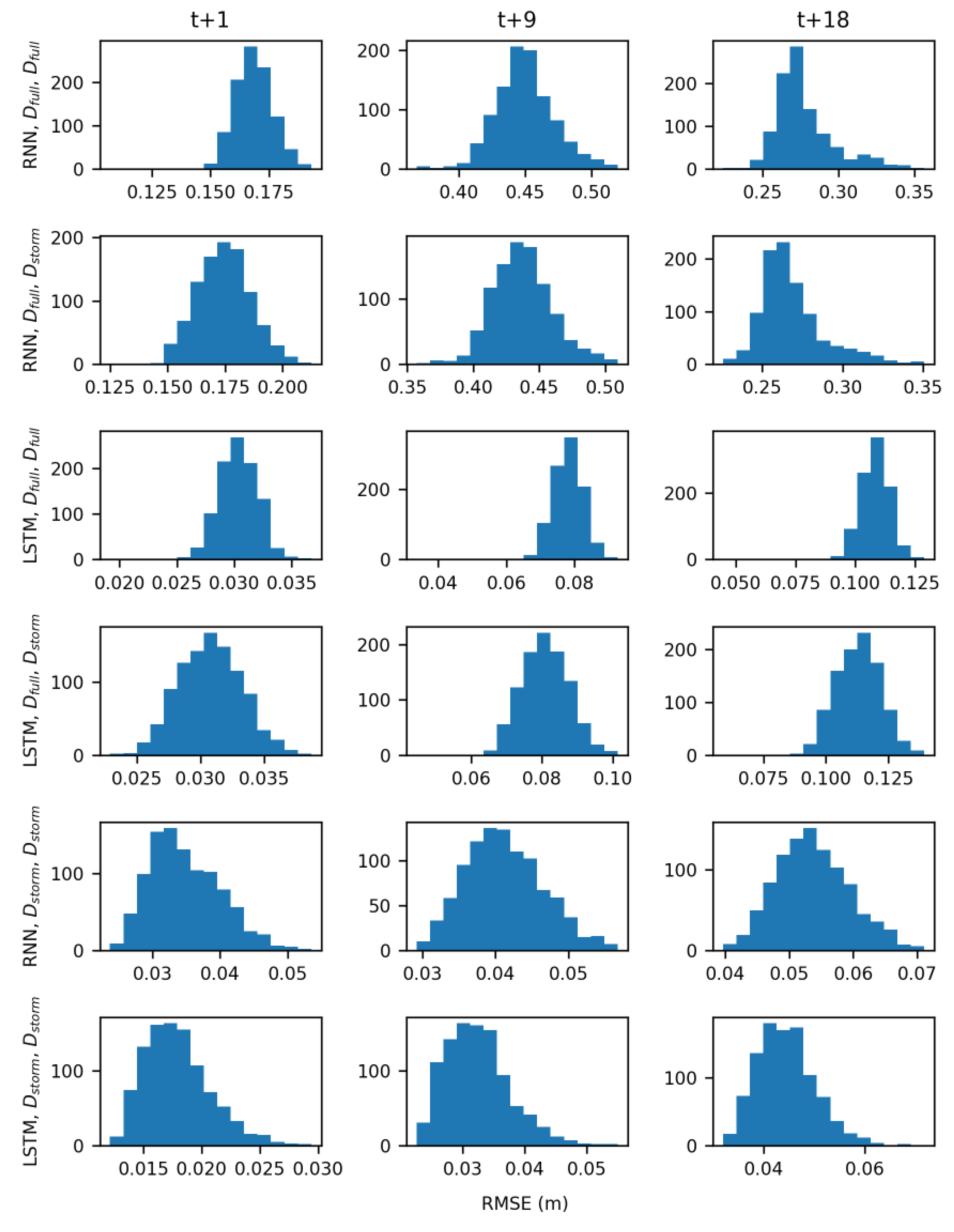
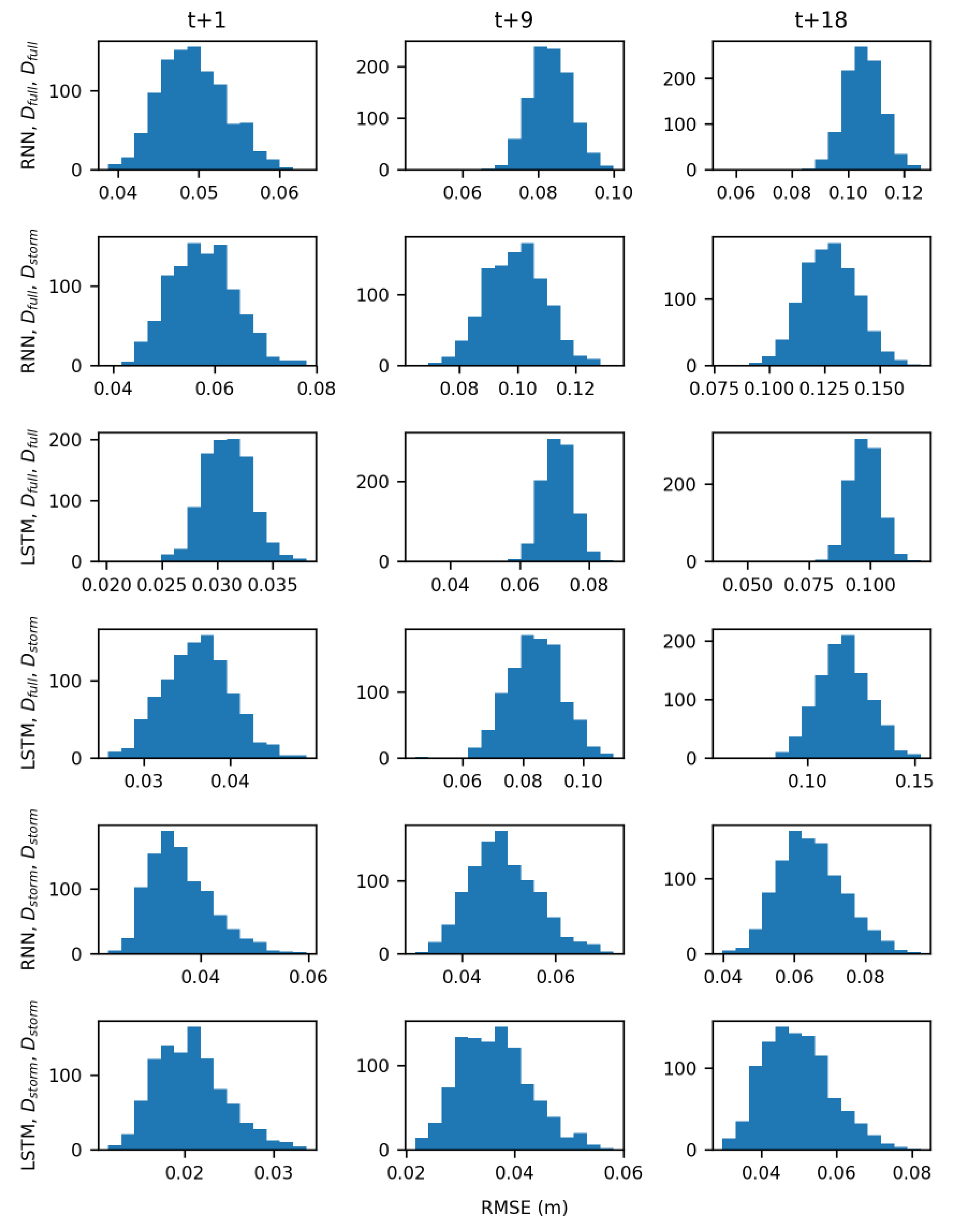
4. Discussion
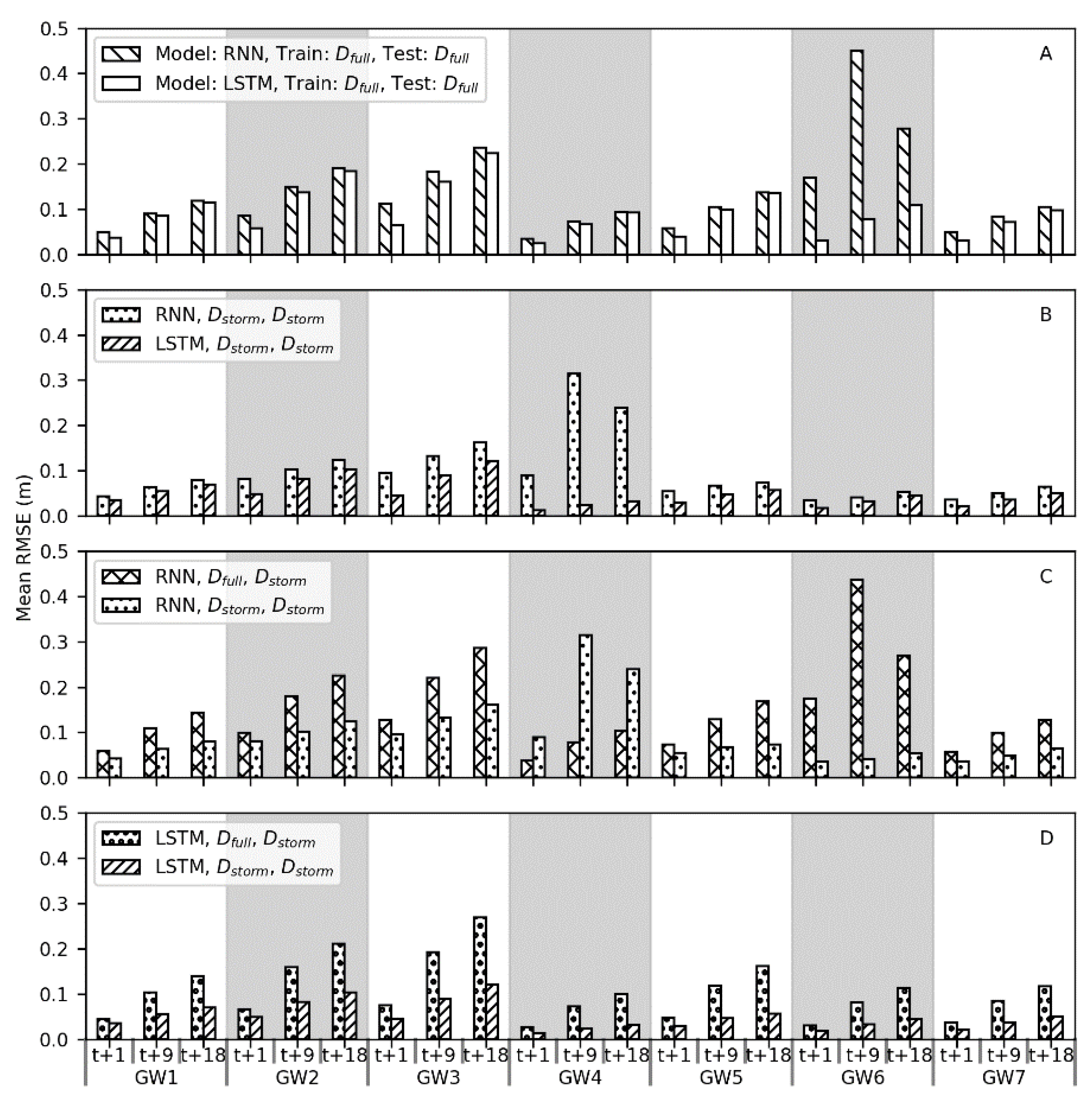
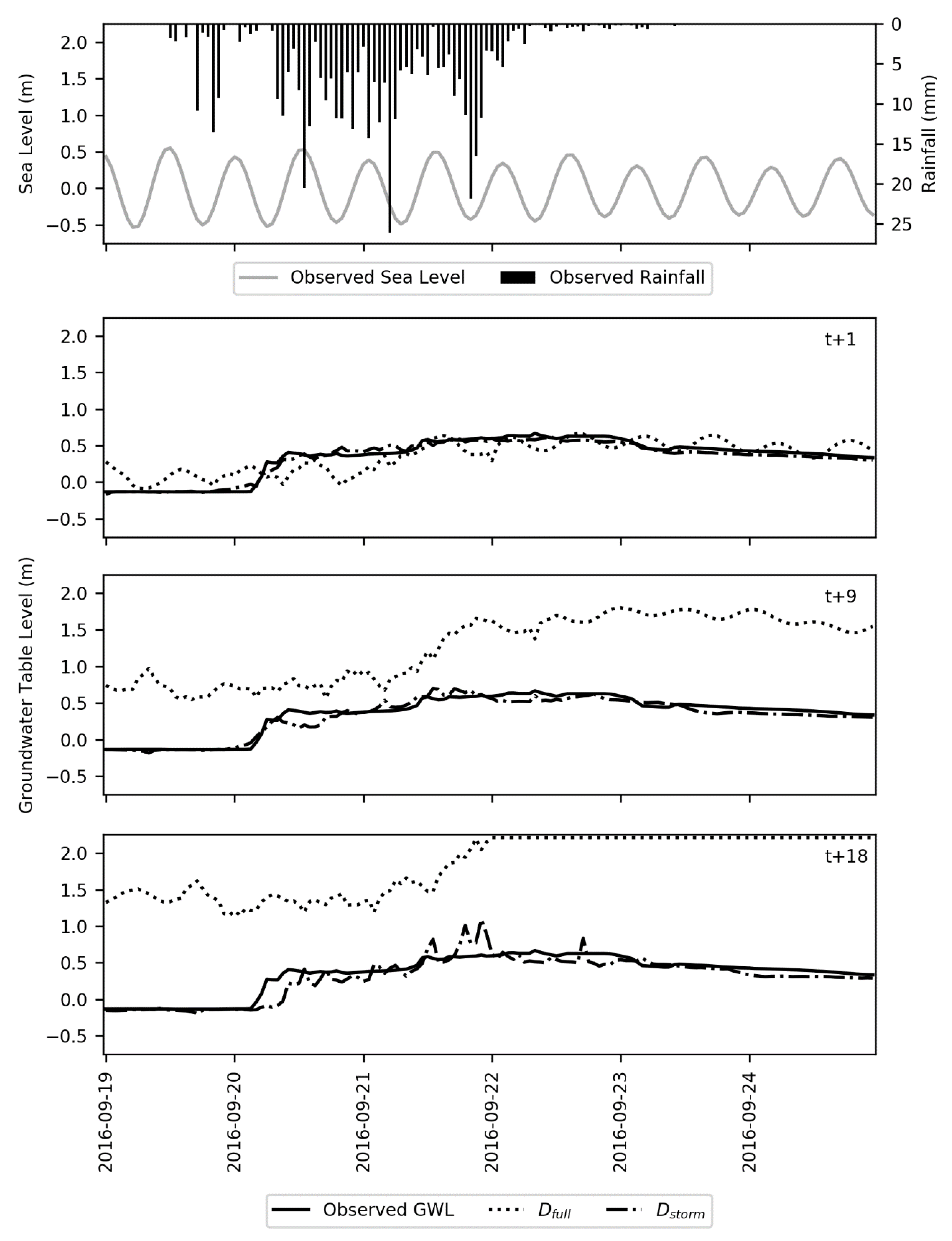
The results of hypothesis testing (
Table 5) indicate that both model type and the training data influenced the accuracy of groundwater table forecasts. The LSTM architecture was better able to learn the relationships between groundwater table, rainfall, and sea level than the simpler RNN. Additionally, models trained with storm data D
storm outperformed models trained with the full dataset D
full when tested on either observed for forecast data. In the real-time scenario one reason for this difference in performance could be the structure of the test set D
fcst. These results indicate that the structure of the time series data in D
storm and D
fcst are more closely aligned, as opposed to the time series structure of D
full and D
fcst. The models trained on D
full also have to learn groundwater table response with many observations where no rainfall occurred. In contrast, models trained on D
storm, which have a higher proportion of observations with rainfall, may have a clearer pattern to learn.
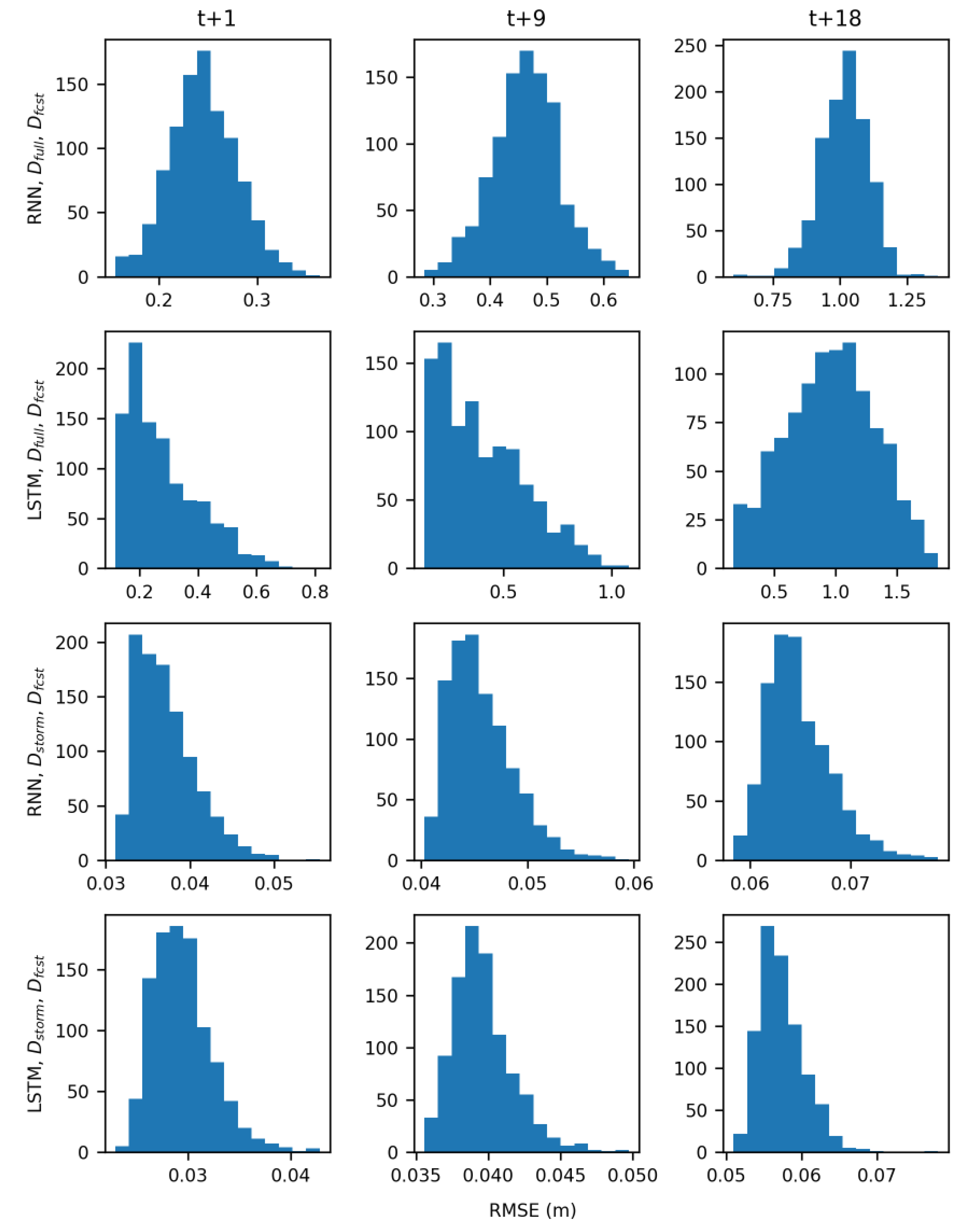
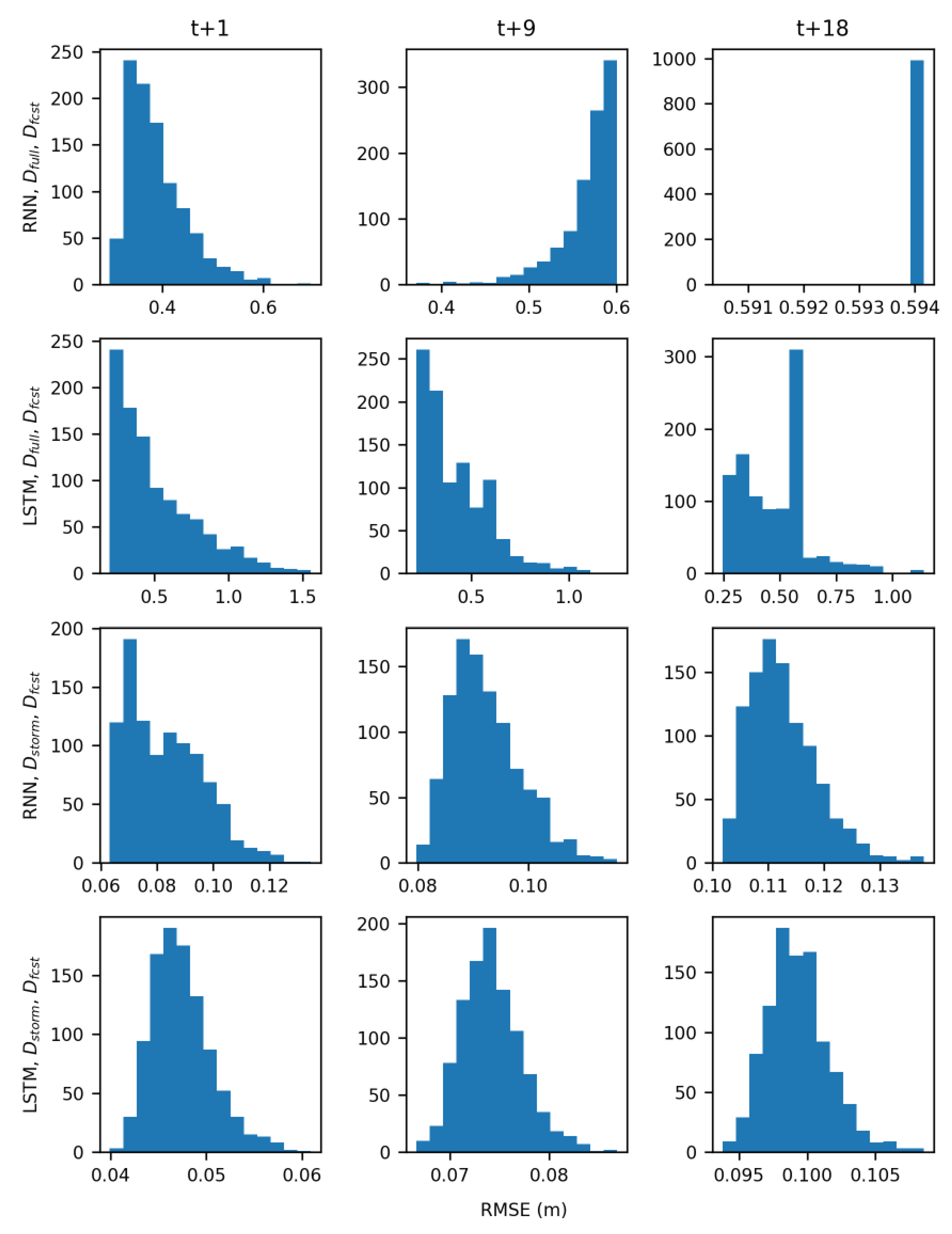
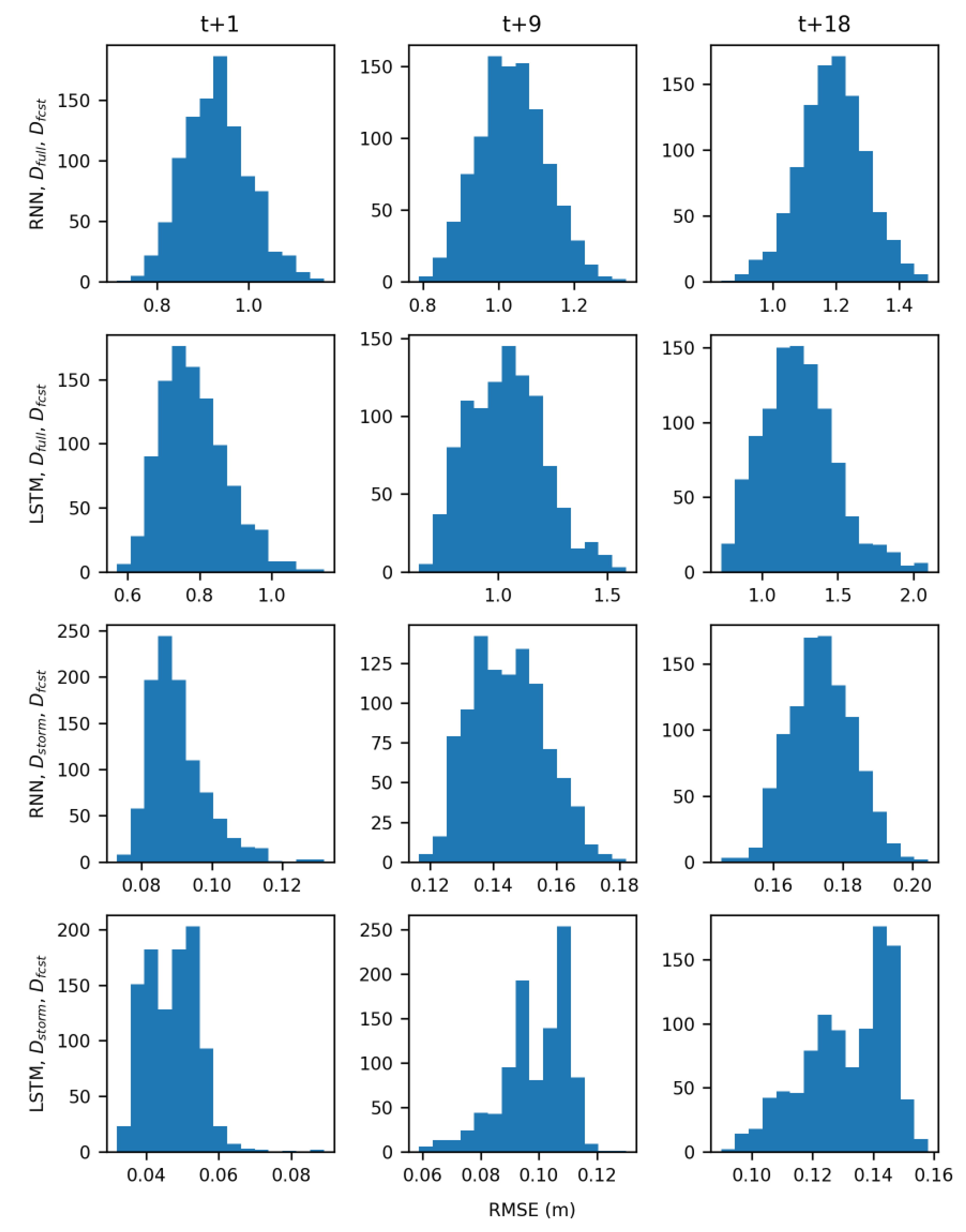
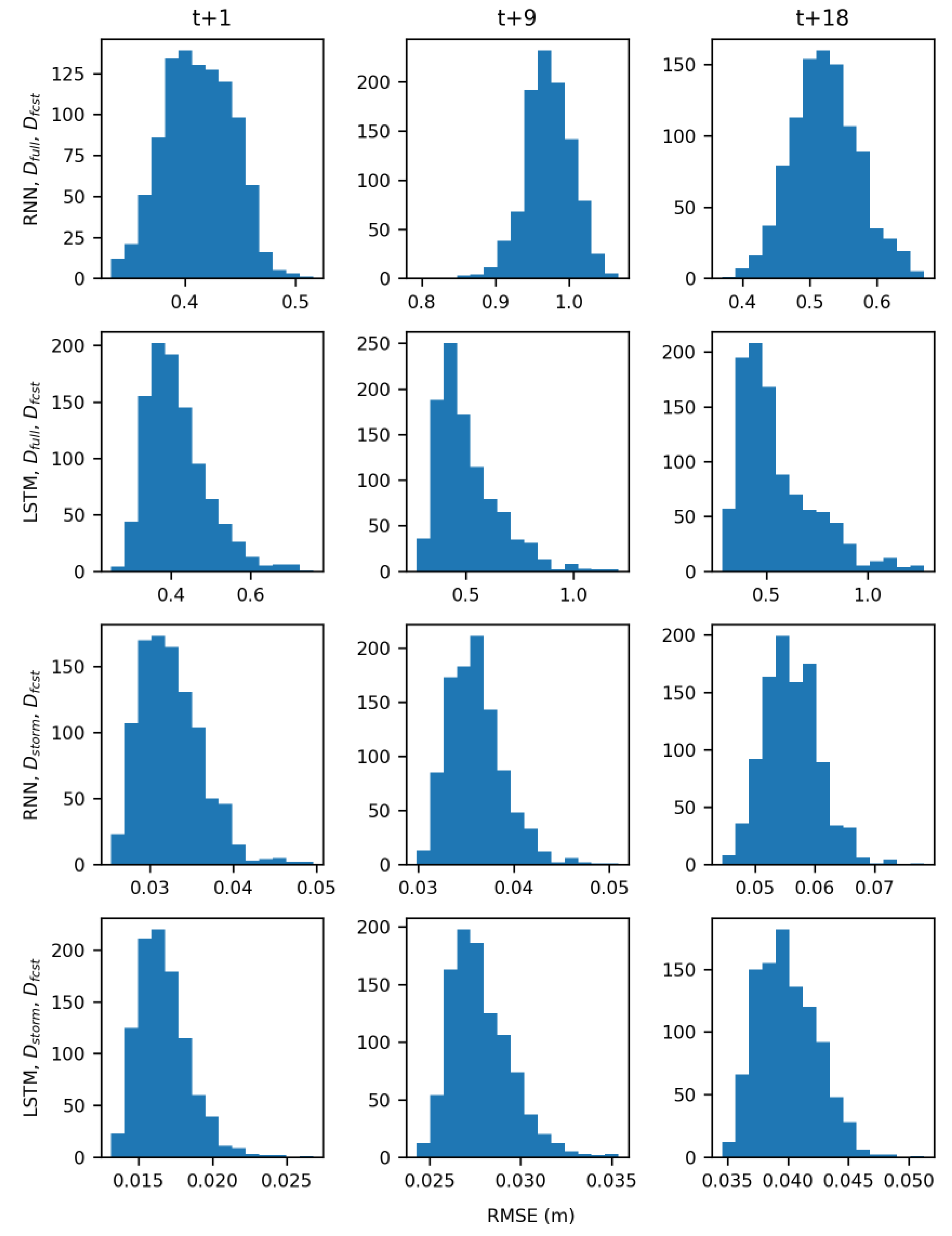
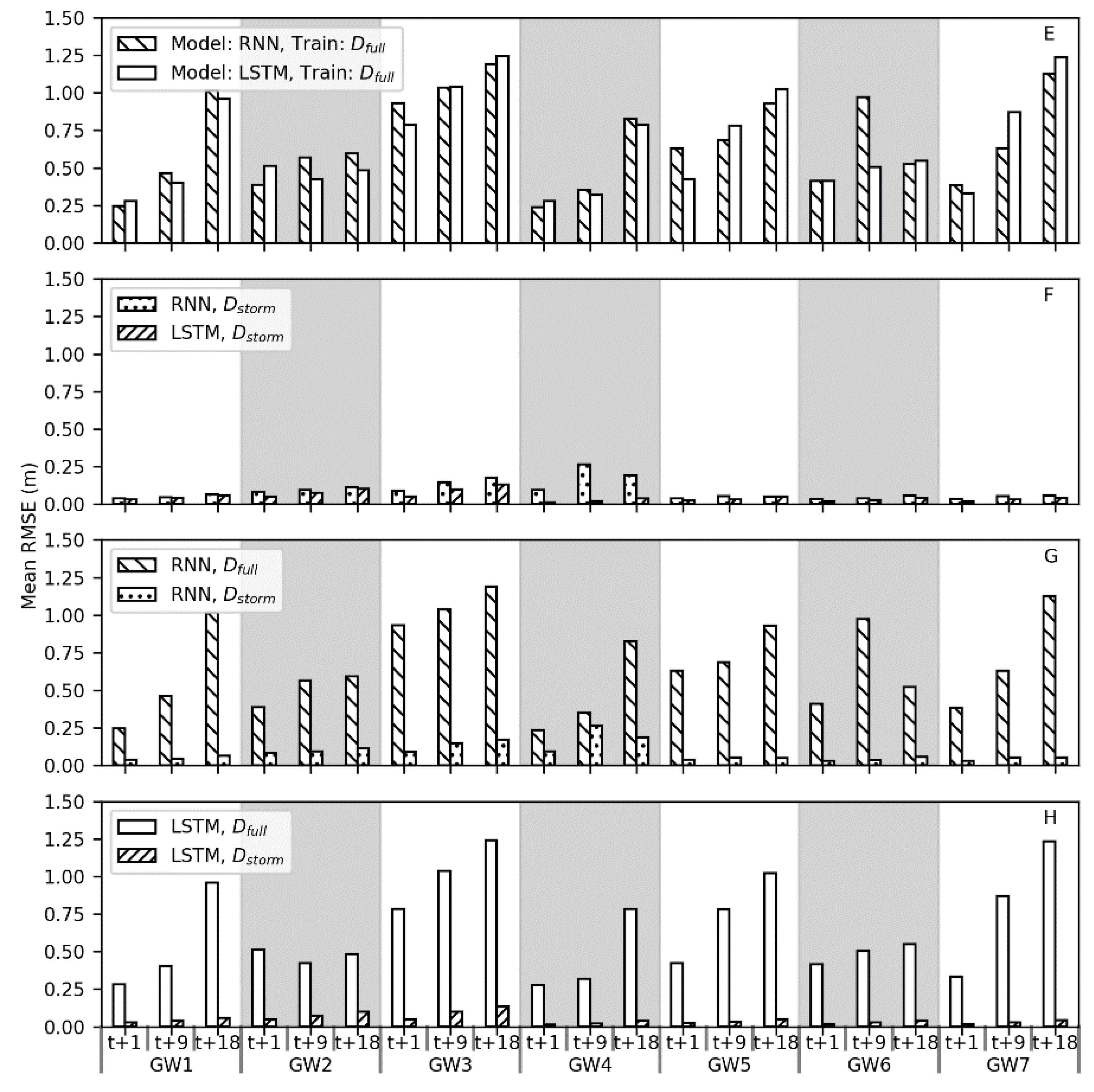
In the real-time forecasting scenario, both RNN and LSTM models trained with D
storm demonstrated predictive skill, forecasting groundwater table levels with low RMSE values (
Figure 8F). Models trained with D
full however performed much worse because of the noisier signal they had to learn (
Figure 9) and are not suitable for use in a real-time forecasting scenario. Across all wells, averaged RMSE values for the RNN models were 0.06 m, 0.1 m, and 0.1 m for the t + 1, t + 9, and t + 18 predictions, respectively. Averaged RMSE values for the LSTMs were slightly lower at 0.03 m, 0.05 m, and 0.07 m for the t+1, t+9, and t+18 predictions, respectively. While there is limited research on the use of LSTMs for forecasting groundwater table, these results are comparable with the work of J. Zhang et al. [
46], who reported RMSE values for one-step ahead prediction of monthly groundwater table at six sites ranging from 0.07 m to 0.18 m. The current work makes advances by showing that both LSTM and RNN can accurately forecast groundwater table response to storm events at an hourly time step, with forecast input data, and at longer prediction horizons all of which are necessary in a coastal urban environment.
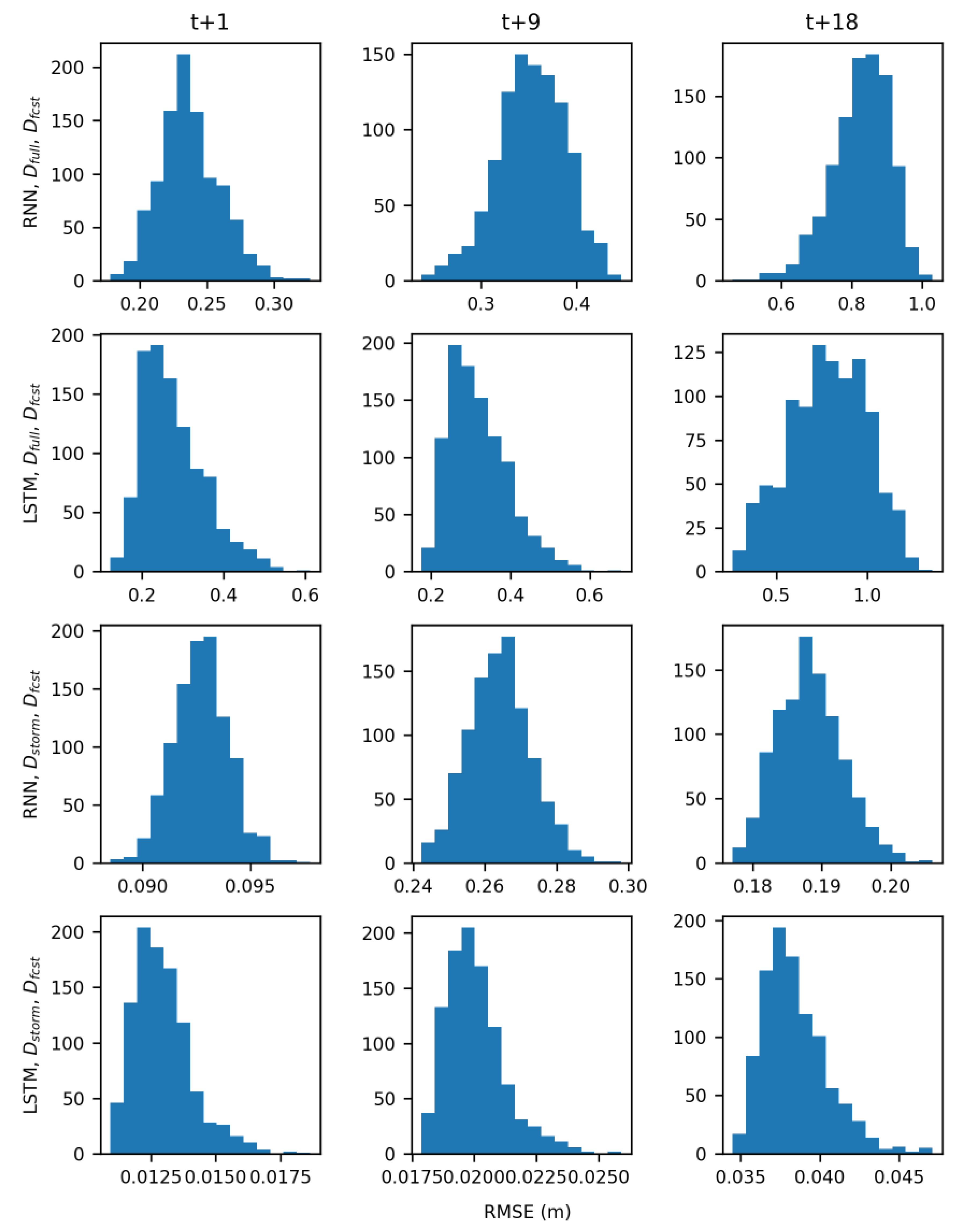
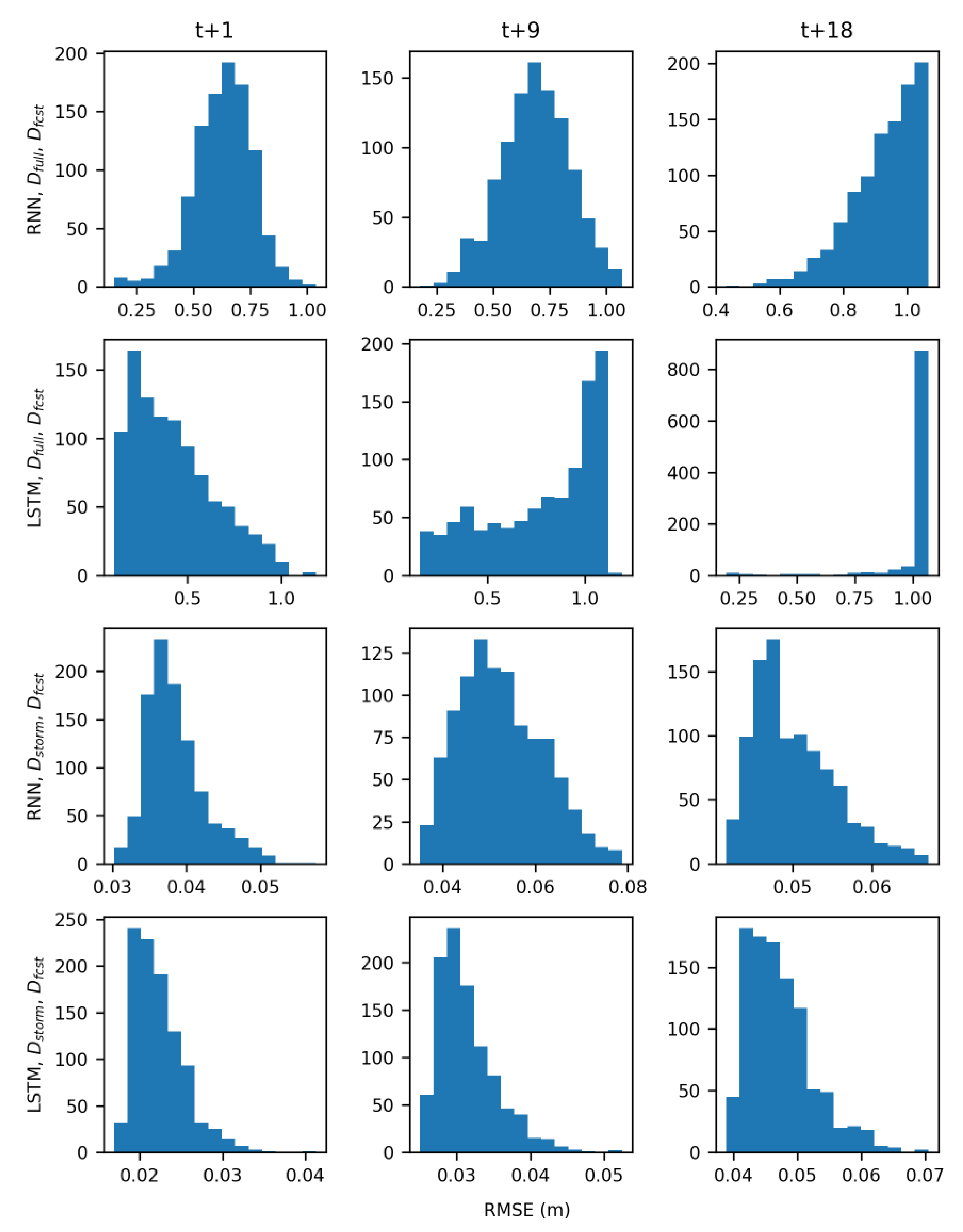
Because the effect of sea level on the groundwater table is heavily dependent on well location and soil characteristics not included in this study, a sensitivity analysis was performed by removing sea level from the D
full and D
storm data sets and retraining and retesting the models. Of the wells that were not correlated with sea level, GW3 and GW6 performed better without sea level data. Using RNN models trained with D
full, there was an average decrease in RMSE of 12% for GW3 and 41% for GW6. The only exception to this is the GW6 RNN trained with D
storm which performed much worse without sea level. For LSTM models trained with D
full however, there was only a 3% decrease in RMSE for GW3 and a 2% decrease for GW6. The third well that was not correlated with sea level, GW5, was worse without sea level for the RNN trained with D
full; the average increase in RMSE was 17%. Removing sea level at this well had no change in RMSE for the LSTM models trained with D
full. This particular well is only 32 m from the coast so the influence of sea level seems reasonable. When models were trained with D
storm excluding sea level, across all well there was an average increase in RMSE of 8% for RNN models and no change for LSTM models. This demonstrates that sea level data is important for groundwater table prediction during storms for wells close to the coast and this is captured effectively by the D
storm datasets (
Table 7). This analysis indicated that RNN models were much more sensitive to the inputs used than LSTM models. As designed, the structure of LSTM models allowed them to filter out noisy data and have little to no change in RMSE if sea level data was removed, especially when using the best performing combination of LSTM and D
storm training data.
The results of this study illustrate the trade-off between model complexity and performance that has implications beyond creating forecasts. The increased complexity of LSTM models, in terms of gates that learn and the constant error pathway, allowed them to have more predictive skill than the RNN models for forecasting groundwater table response to storm events. Additionally, the structure of LSTM models allowed them to filter out noise from the sea level signal which RNN struggled to do. Most of the comparisons presented in the Results had significant p-values; because of the large sample size (1000) however, even a very small difference in RMSE values between two models was considered significant. For example, the differences between LSTM and RNN models trained with D
storm in the real-time forecasting scenario were statistically significant (
Figure 8F). The average difference in the RNN and LSTM RMSE values, however, was only 0.03 m, 0.05 m, and 0.03 m for the t + 1, t + 9, and t + 18 predictions, respectively. If these groundwater table forecasts were to be used as additional input to a rainfall-runoff model to predict flooding, it seems unlikely that the small differences between RNN and LSTM models would have a large impact, especially when compared to other factors like rainfall variability and storm surge timing.
The increased complexity of the LSTM models, while they had better performance than the RNN models, also increased their computational cost. The main difference in computational cost of the LSTM and RNN in this study was the length of training time. When trained on an HPC with either an NVIDIA Tesla K80 or P100 GPU or a smaller NVIDIA Quadro P2000 GPU on a desktop computer, wall-clock training time for LSTM models was approximately three times that of RNN models. Factors in training time include hyperparameters, such as the number of neurons in the hidden layer, which were relatively similar between model types. Once models are trained, groundwater table forecasts are obtained by a forward pass of input data through the network; this time was short and comparable for both models. For this groundwater table forecasting application training time was not a major concern, but if the application was time sensitive and the models were frequently retrained, RNNs could be an appropriate choice that does not sacrifice much in terms of accuracy.
Because forecast data were used as model input in the real-time scenario, it’s important to note some of the uncertainties that dataset might introduce. HRRR rainfall data are a product of a numerical forecast model and as such is subject to the uncertainty of that model, which includes the transformation of radar reflectivity data into precipitation amounts [
74]. Additionally, the uncertainty of HRRR forecasts will increase the farther into the future they are. NOAA sea level forecasts, as previously mentioned, are based only on the harmonic constituents of the astronomical tide cycle. For rainfall-dominated storm events this type of forecast may be accurate enough as a model input, but any storm surge from hurricanes or nor’easters would not be included. This could result in under prediction of groundwater table levels. While archived storm surge predictions were not available for this study, in a real scenario predictions of storm surge could be incorporated into the model input.
The neural networks and data processing techniques presented in this paper are applicable to other coastal cities facing sea level rise and recurrent flooding. Because there is a lack of groundwater table data in most locations however, the direct transferability of the models created for Norfolk should be explored in other locations were observational data are not available. Even in Norfolk, questions still remain about how much data, both temporally and spatially, is needed to accurately forecast groundwater table levels using the methods presented in this study. In this study, at least eight years of data were available for each well, but other researchers have found acceptable results when training neural networks with more [
32,
33] and less [
2,
71] time series data. Based on our sensitivity analysis, rainfall is the most important input for the models. However, sea level data was from a single station; if there were more sea level gauges throughout the city it could provide a more accurate input for these models to learn from. The groundwater table monitoring network in Norfolk consists of only seven wells; while this network is a valuable source of data, it may not be dense enough to accurately represent the groundwater table across the complex urban landscape. The city is divided by many tidal rivers and stormwater conveyances and the effects these features have on the groundwater table maybe highly localized. Areas where groundwater table level is important to flooding are likely not well represented by a distant monitoring well. Research has been done with kriging to determine potential densities of groundwater monitoring [
75] and rain gauge networks [
76]. A similar approach may be valuable in Norfolk or comparable cities to determine the optimal density of monitoring networks when planning for and adapting to climate change and sea level rise.
5. Conclusions
The objective of this study was to compare two types of neural networks, RNN and LSTM, for their ability to predict groundwater table response to storm events in a coastal environment. The study area was the city of Norfolk, Virginia where time series data from 2010–2018 were collected from seven shallow groundwater table wells distributed throughout the city. Two sets of observed data, the full continuous time series Dfull and a dataset of only time periods with storm events Dstorm, were bootstrapped and used to train and test the models. An additional dataset Dfcst including forecasts of rainfall and sea level was used to evaluate model performance in a simulation of real-time model application. Statistical significance in model performance was evaluated with t-tests.
Major conclusions from this study, in light of the hypotheses described in
Table 4 are:
Both model type and training data are important factors in creating skilled predictions of hourly groundwater table using observed data:
Using Dfull, LSTM had a lower average RMSE than RNN (0.09 m versus 0.14 m, respectively)
Using Dstorm, LSTM had a lower average RMSE than RNN (0.05 m versus 0.10 m, respectively)
The best predictive skill was achieved using LSTM models trained with Dstorm (average RMSE = 0.05 m) versus RNN models trained with Dstorm (average RMSE = 0.10 m)
LSTM has better performance than RNN but requires approximately 3 times more time to train
In a real-time scenario using observed and forecasted input data, accurate forecasts of groundwater table were created with an 18 h horizon:
LSTM: Average RMSE values of 0.03, 0.05, and 0.07 m, for the t + 1, t + 9, and t + 18h forecasts, respectively
RNN: Average RMSE values of 0.06, 0.10, and 0.10 m, for the t + 1, t + 9, and t + 18h forecasts, respectively
Forecasts of groundwater table levels are not common; in many locations even direct measurements of the groundwater table are not widely available. As sea levels rise and storms become more extreme, however, forecasts of groundwater table will become an increasingly important part of flood modeling. In low-lying coastal areas, sea level rise, stormwater infiltration, and storm surge could cause groundwater inundation. Even if groundwater inundation does not occur, increased duration of high groundwater table levels could have significant impacts on infrastructure. Forecasts of groundwater table, an often overlooked part of coastal urban flooding, can provide valuable information on subsurface storage available for stormwater and help inform infrastructure management and planning.