Achieving Urban Stormwater Mitigation Goals on Different Land Parcels with a Capacity Trading Approach
Abstract
1. Introduction
- Existing GI projects are mainly supported by public funds on public domains, or on private properties with some government subsidies; many of these projects are research oriented, or for demonstration purposes. This to a great extent has made the economic concerns less pressing than it should be;
- Many studies that were conducted at watershed scale or over large areas used mathematical models to evaluate hydrological and environmental impact of GIs; these modeling studies generally dealt with physical delineation lines, such as rivers, roads, and watershed boundaries, economical responsibilities were seldom considered [3,26].
2. Materials and Methods
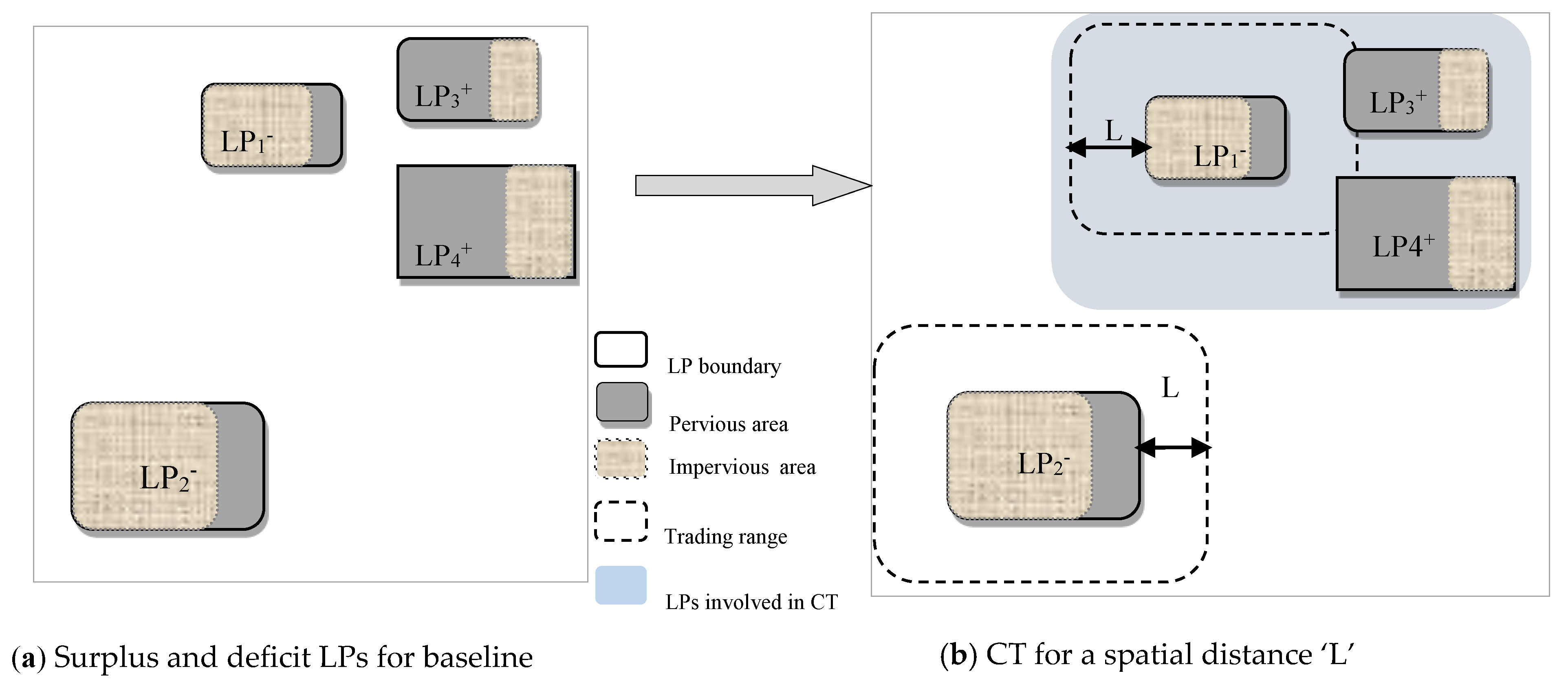
2.1. Procedure for GI Capacity Trading (CT) and Significance of Trading Scales
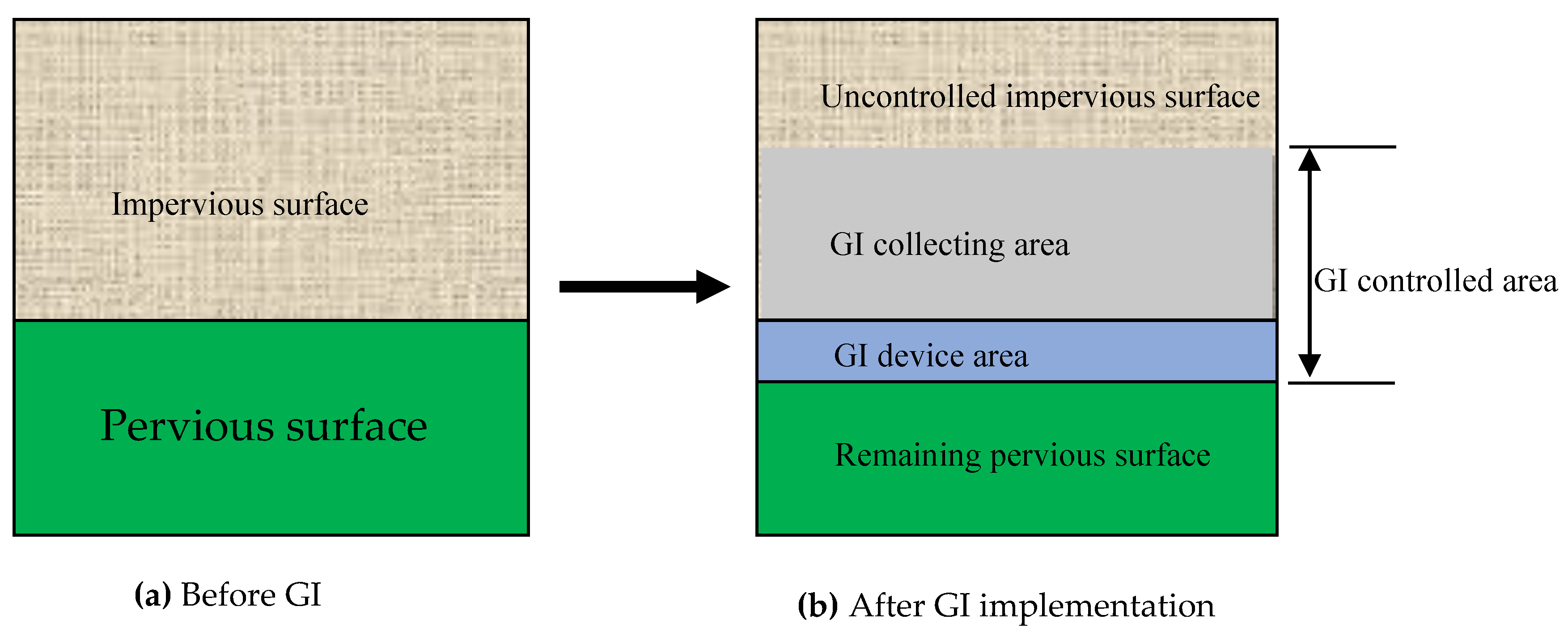
2.1.1. Step 1: Determining Runoff Coefficient (RC) before and after GI Implementation
2.1.2. Step 2: Determining the Baseline Condition and the Trading Capacity
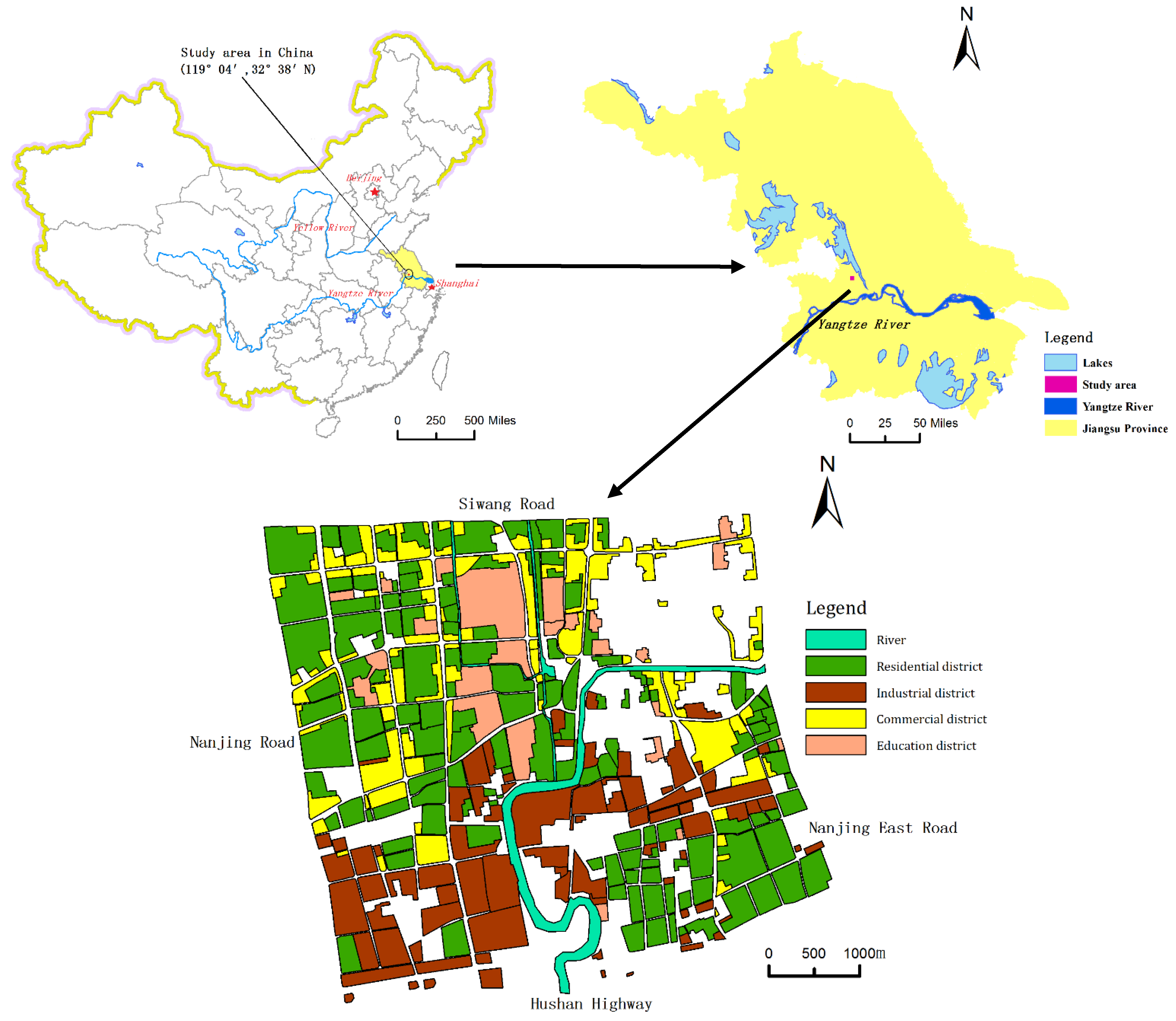
2.2. Study Area and Proposed CT Scenarios
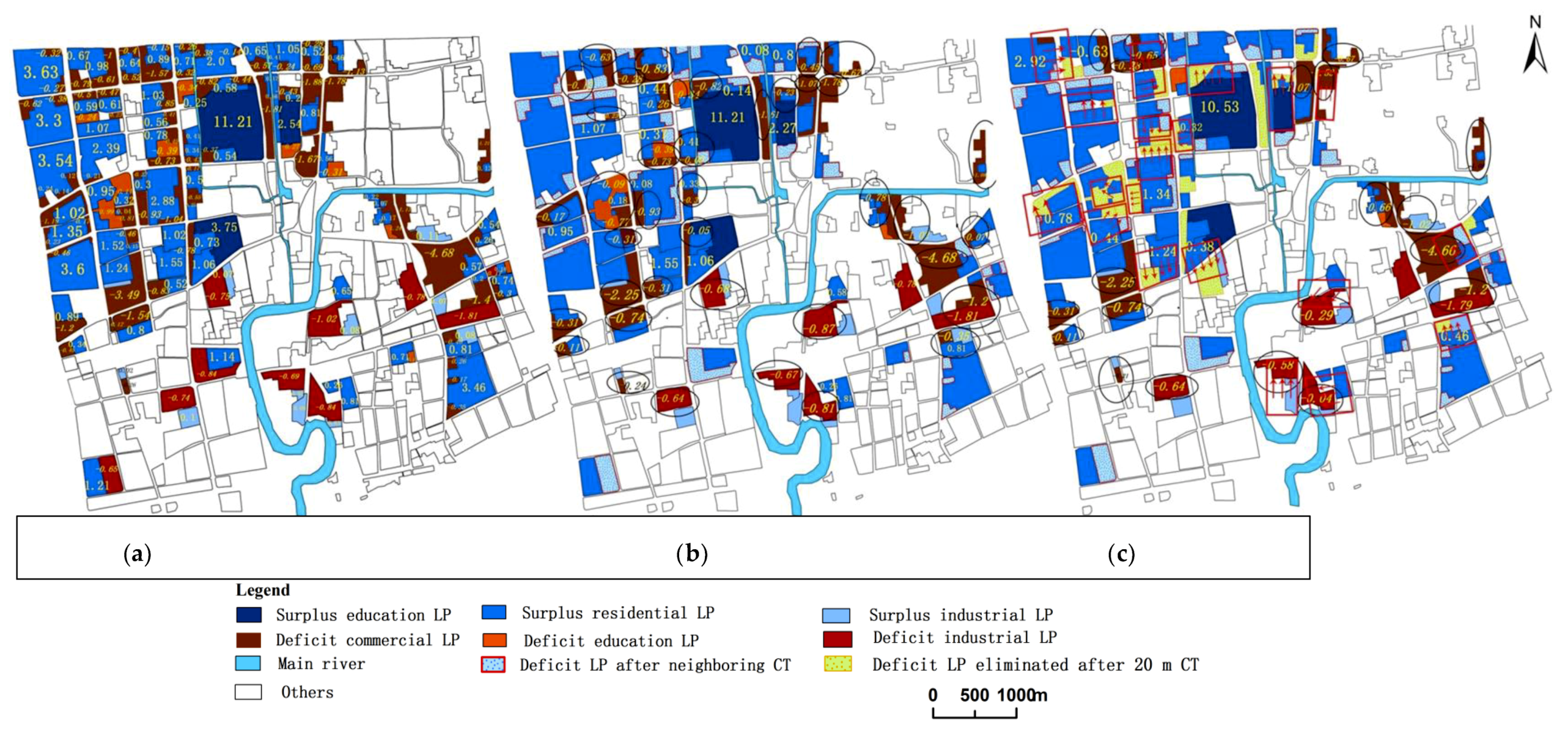
3. Results
- No capacity trading (No-CT),
- Trading with neighboring LPs (Neighboring CT),
- Trading with surplus LPs within 20 m range (20 m radius CT), and
- Baseline condition, which is equivalent to overall trading (Overall CT).
4. Discussion
4.1. The Impact of Trading Scales on CT Effectiveness
4.2. Economic Incentives for Capacity Trading and Limitations of the Current Study
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fletcher, T.D.; Shuster, W.; Hunt, W.F.; Ashley, R.; Butler, D.; Arthur, S.; Trowsdale, S.; Barraud, S.; Semadeni-Davies, A.; Bertrand-Krajewski, J.L.; et al. SUDS, LID, BMPs, WSUD and more e the evolution and application of terminology surrounding urban drainage. Urban Water J. 2014, 12, 525–542. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Ngo, H.H.; Guo, W.; Wang, X.C.; Ren, N.; Li, G.; Ding, J.; Liang, H. Implementation of a specific urban water management—Sponge City. Sci. Total. Environ. 2019, 652, 147–162. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Chui, T.F.M. Integrated hydro-environmental impact assessment and alternative selection of low impact development practices in small urban catchments. J. Environ. Manag. 2018, 223, 324–337. [Google Scholar] [CrossRef] [PubMed]
- Ministry of Resident and Contruction (MORC). Technical Guide of Sponge City Construction; Ministry of Resident and Contrction: Beijing, China, 2014. (In Chinese)
- Rowe, A.A.; Rector, P.; Bakacs, M. Survey Results of Green Infrastructure Implementation in New Jersey. J. Sustain. Water Built Environ. 2016, 2, 04016001. [Google Scholar] [CrossRef]
- Ashley, R.; Gersonius, B.; Digman, C.; Horton, B.; Smith, B.; Shaffer, P. Including uncertainty in valuing blue and green infrastructure for stormwater management. Ecosyst. Serv. 2018, 33, 237–246. [Google Scholar] [CrossRef]
- Mell, I.C.; Henneberry, J.; Hehl-Lange, S.; Keskin, B. To green or not to green: Establishing the economic value of green infrastructure investments in The Wicker, Sheffield. Urban For. Urban Green. 2016, 18, 257–267. [Google Scholar] [CrossRef]
- Mell, I.C.; Henneberry, J.; Hehl-Lange, S.; Keskin, B. Promoting urban greening: Valuing the development of green infrastructure investments in the urban core of Manchester, UK. Urban For. Urban Green. 2013, 12, 296–306. [Google Scholar] [CrossRef]
- Palla, A.; Gnecco, I.; La Barbera, P. Assessing the Hydrologic Performance of a Green Roof Retrofitting Scenario for a Small Urban Catchment. Water 2018, 10, 1052. [Google Scholar] [CrossRef]
- Zhang, K.; Chui, T.F.M. Linking hydrological and bioecological benefits of green infrastructures across spatial scales—A literature review. Sci. Total Environ. 2018, 646, 1219–1231. [Google Scholar] [CrossRef]
- Coleman, S.; Hurley, S.; Rizzo, D.; Koliba, C.; Zia, A. From the household to watershed: A cross-scale analysis of residential intention to adopt green stormwater infrastructure. Landsc. Urban Plan. 2018, 180, 195–206. [Google Scholar] [CrossRef]
- Eckart, K.; McPhee, Z.; Bolisetti, T. Performance and implementation of low impact development—A review. Sci. Total Environ. 2017, 607, 413–432. [Google Scholar] [CrossRef] [PubMed]
- Tang, S.C.; Luo, W.; Jia, Z.H.; Li, S.; Wu, Y.; Zhou, M. Effect of rain gardens on storm runoff reduction. Adv. Water Sci. 2015, 26, 787–794. [Google Scholar]
- Sharma, A.K.; Pezzaniti, D.; Myers, B.; Cook, S.; Tjandraatmadja, G.; Chacko, P.; Chavoshi, S.; Kemp, D.; Leonard, R.; Koth, B.; et al. Water Sensitive Urban Design: An Investigation of Current Systems, Implementation Drivers, Community Perceptions and Potential to Supplement Urban Water Services. Water 2016, 8, 272. [Google Scholar] [CrossRef]
- Baptiste, A.K.; Foley, C.; Smardon, R. Understanding urban neighborhood differences in willingness to implement green infrastructure measures: A case study of Syracuse, NY. Landsc. Urban Plan. 2015, 136, 1–12. [Google Scholar] [CrossRef]
- Keeley, M.; Koburger, A.; Dolowitz, D.P.; Medearis, D.; Nickel, D.; Shuster, W. Perspectives on the Use of Green Infrastructure for Stormwater Management in Cleveland and Milwaukee. Environ. Manag. 2013, 51, 1093–1108. [Google Scholar] [CrossRef]
- Thurston, H.W. Opportunity Costs of Residential Best Management Practices for Stormwater Runoff Control. J. Water Res. Plan. Manag. 2006, 132, 89–96. [Google Scholar] [CrossRef]
- Thurston, H.W.; Goddard, H.C.; Szlag, D.; Lemberg, B. Controlling Storm-Water Runoff with Tradable Allowances for Impervious Surfaces. J. Water Res. Plan. Manag. 2003, 129, 409–418. [Google Scholar] [CrossRef]
- City of Richmond Department of Public Utilities (CRDOPT). Stormwater Management Program—Single Family Residential Property Credit Manual. Available online: http://www.richmondgov.com/PublicUtilities/StormwaterCredits.aspx (accessed on 20 April 2019).
- ECORI. Somehow Stormwater Runoff Needs to Be Taxed. Available online: https://www.ecori.org/pollution-contamination/2014/12/1/somehow-stormwater-runoff-needs-to-be-taxed.html (accessed on 20 April 2019).
- Matthews, T.; Lo, A.Y.; Byrne, J.A. Reconceptualizing green infrastructure for climate change adaptation: Barriers to adoption and drivers for uptake by spatial planners. Landsc. Urban Plan. 2015, 138, 155–163. [Google Scholar] [CrossRef]
- Vandermeulen, V.; Verspecht, A.; Vermeire, B.; Van Huylenbroeck, G.; Gellynck, X. The use of economic valuation to create public support for green infrastructure investments in urban areas. Landsc. Urban Plan. 2011, 103, 198–206. [Google Scholar] [CrossRef]
- Hoghooghi, N.; Golden, H.E.; Bledsoe, B.P.; Barnhart, B.L.; Brookes, A.F.; Djang, K.S.; Halama, J.J.; McKane, R.B.; Nietch, C.T.; Pettus, P.P. Cumulative Effects of Low Impact Development on Watershed Hydrology in a Mixed Land-Cover System. Water 2018, 10, 991. [Google Scholar] [CrossRef]
- Pigou, A.C. The Economics of Welfare, 4th ed.; Macmillan: London, UK, 1962. [Google Scholar]
- Fullerton, D.; Wolverton, A. Two Generalizations of a Deposit–Refund System. Am. Econ. 2000, 90, 238–242. [Google Scholar] [CrossRef]
- Li, C.; Fletcher, T.D.; Duncan, H.P.; Burns, M.J. Can stormwater control measures restore altered urban flow regimes at the catchment scale? J. Hydrol. 2017, 549, 631–653. [Google Scholar] [CrossRef]
- Ando, A.W.; Freitas, L.P.C. Consumer demand for green stormwater management technology in an urban setting: The case of Chicago rain barrels. Water Resour. Res. 2011, 47, 1–11. [Google Scholar] [CrossRef]
- Martin-Mikle, C.J.; de Beurs, K.M.; Julian, J.P.; Mayer, P.M. Identifying priority sites for low impact development (LID) in a mixed-use watershed. Landsc. Urban Plann. 2015, 140, 29–41. [Google Scholar] [CrossRef]
- Xu, J.H.; Yue, W.Z.; Tan, W.Q. A statistical study on spatial scaling effects of urban landscape pattern: A case study of the central area of the External Circle Highway in Shanghai. Acta Geogr. Sin. 2004, 59, 32–34. [Google Scholar]
- Liu, Y.Q.; Ge, J.F.; Li, C.; Liu, X. Spatial differentiation characteristics of urban residential land prices of Shijiazhuang City based on spatial autocorrelation. J. Arid Land Resour. Environ. 2018, 32, 55–62. [Google Scholar]
| LP types | Education Organizations | Commercial Plazas | Residential Area | Industrial Areas | Total | ||
|---|---|---|---|---|---|---|---|
| Colleges | Schools | Large | Small | ||||
| No. of LPs | 4 | 18 | 100 | 152 | 21 | 60 | 355 |
| Area (ha) | 107.0 | 64.5 | 312.6 | 815.9 | 272.1 | 150.6 | 1722.7 |
| αimp (/%) | 24–42 | 24–52 | 75–86 | 54–61 | 71–80 | 66–76 | 49~68 |
| LP types | Education Organizations | Commercial Plazas | Residential Area | Industrial Areas | Total | ||
|---|---|---|---|---|---|---|---|
| Colleges | Schools | Large | Small | ||||
| Present (RC) | 0.54 | 0.76 | 0.82 | 0.60 | 0.75 | 0.69 | 0.67 |
| Baseline CT (RC’) | 0.22 b | 0.59 c | 0.70 c | 0.36 b | 0.58 c | 0.48 b | 0.50 d |
| Changes of the Deficit LPs | No. of LPs with Deficit | Area of LPs with Deficit (ha) | Left Deficit Area (ha) |
|---|---|---|---|
| No-CT | 139 | 649.2 | −90.1 |
| Neighboring CT | 97 | 558.4 | −75.5 |
| 20 m radius CT | 78 | 478.2 | −59.9 |
| Overall CT † | 0 | 0 | 0 |
| LP Types | Commercial Area | Industrial Area | Education Area | Total |
|---|---|---|---|---|
| No-CT | 100 | 21 | 18 | 139 |
| Neighboring CT | 66 | 18 | 13 | 97 |
| 20 m radius CT | 48 | 18 | 12 | 78 |
| Overall CT † | 0 | 0 | 0 | 0 |
| Trading Range | Involved | Eliminated |
|---|---|---|
| Neighboring | 86 | 42 |
| 20 m radius | 117 | 61 |
| LP types | Commercial | Industrial | Education |
|---|---|---|---|
| Neighboring CT | 68 a/100 b | 10/21 | 8/18 |
| 20 m radius CT | 94/100 | 13/21 | 10/18 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Q.; Jia, Z.; Tang, S.; Luo, W.; Xu, C. Achieving Urban Stormwater Mitigation Goals on Different Land Parcels with a Capacity Trading Approach. Water 2019, 11, 1091. https://doi.org/10.3390/w11051091
Xu Q, Jia Z, Tang S, Luo W, Xu C. Achieving Urban Stormwater Mitigation Goals on Different Land Parcels with a Capacity Trading Approach. Water. 2019; 11(5):1091. https://doi.org/10.3390/w11051091
Chicago/Turabian StyleXu, Qing, Zhonghua Jia, Shuangcheng Tang, Wan Luo, and Chengxuan Xu. 2019. "Achieving Urban Stormwater Mitigation Goals on Different Land Parcels with a Capacity Trading Approach" Water 11, no. 5: 1091. https://doi.org/10.3390/w11051091
APA StyleXu, Q., Jia, Z., Tang, S., Luo, W., & Xu, C. (2019). Achieving Urban Stormwater Mitigation Goals on Different Land Parcels with a Capacity Trading Approach. Water, 11(5), 1091. https://doi.org/10.3390/w11051091





