1. Introduction
Water pump control, which is widely used in various chemical industries [
1,
2,
3], such as in regenerative heaters [
4] and drum boilers [
5], petrochemical processes [
6], open channels [
7], surge tanks of hydropower stations [
8], and steam generators [
9,
10,
11,
12], plays a significant role in maintaining economic efficiency and stable plant operation. For instance, in thermal power plants, the drum boiler water level is a key parameter in monitoring boiler operational conditions, which indirectly reflects the balance between the steam load and water supply. An appropriate pump control design is able to maintain the water level and thus guarantee the safe operation of the boiler [
13]. Furthermore, for nuclear steam supply systems, one of the most important control strategies of such a system is steam generator water level regulation to preserve the level around programmed setpoint, because the reduction of the water level jeopardizes the heat removal from the reactor, and increasing the level will cause the humidity of the generated steam to rise, causing severe erosion of the turbine blades [
11].
However, water control is challenging due to slow dynamics, strong nonlinearity, and various disturbances. There are many proposed control strategies in the literature to design water level control systems (see e.g., [
14,
15,
16]). Among the most widely used techniques are simple fixed gain proportional-integral (PI) controllers. A model-free control has also been proposed to address the multivariable nonlinear finite-dimension and important unknown disturbances and to ensure that the water level reaches the setpoint [
7]. Additionally, a new global water level control of horizontal steam generator was designed using the quantitative feedback theory [
9]. A gain scheduled fractional-order proportional-integral-derivative (PID) control system has also been used to control steam generator levels over an entire operating range [
11]. Moreover, an adaptive estimator-based dynamic sliding mode control method was developed to address the level control problem [
10].
It is regrettable that none of the above controllers combine model information with real-time input and output data, such that disturbances affecting these models cannot be compensated by real-time data. In addition, it is well known that noise has a negative impact on the executing agencies in industrial processes, but the noise generated by fluctuations in water level has not drawn much attention in the above literature. Therefore, this paper introduces a new controller with the above two problems taken into account. The proposed controller can compensate for disturbances in real time so as to control the water level accurately and suppress the influence of noise in the system.
The current process control strategies can be categorized in two aspects. One branch utilizes model-based control design, in which much effort is put into developing a class of accurate models under different operation conditions. Then, the controller is designed by taking into consideration the detailed dynamics, nonlinearity, and uncertainty information. To overcome the robustness deficiency of the model-based design, the other branch chooses to avoid the tough modeling work and adopts a data-driven method, such as active disturbance rejection control (ADRC) [
17]. Under this data-driven paradigm, the unknown dynamics, nonlinearity, and uncertainty are treated as a lumped disturbance term that can be estimated and mitigated by analyzing real-time data. A combination of two data-driven techniques—the virtual reference feedback tuning and model-free control—was proposed to serve as a control system [
18]. A novel multi-agent-based data-driven distributed adaptive cooperative control method was also investigated for multi-direction queuing strength balance with changeable cycles in urban traffic signal timing [
19]. Two new control structures referred to as second-order, data-driven active disturbance rejection control combined with proportional-derivative Takagi-Sugeno fuzzy control are proposed, which consists of a second-order, data-driven active disturbance rejection control and a proportional-derivative Takagi-Sugeno fuzzy logic controller [
20].
Although robust, this new method may suffer from strong sensitivity to the measurement noise, which is harmful for the actuator. Relatively large inertia and strong measurement noise are often encountered in industrial water pump control processes that challenge the precision and stability of industrial water pump control, especially in terms of the following aspects:
For a large inertia of the system, it is difficult for the conventional proportional–integral–derivative (PID) controller to achieve good control performance. Specifically, for the reference tracking control, the conventional PID control suffers from integral saturation, which leads to large overshoot and even sustained oscillation.
The measurement noise will directly influence the output control variable in the closed-loop control. In particular, the high-frequency noise caused by the low resolution of the measurement device in the industrial process will cause large fluctuation to the control variables, which may cause irreversible damage and shorten the life span of the actuator under serious conditions.
In order to solve the second problem mentioned above, a low-pass filter is usually added at the output terminal to reduce the fluctuation of output control variables and protect the actuators. However, it is well known that the introduction this filter will attenuate the control variables and thus weaken the controller performance.
Simple yet effective, the PID controller has flourished in industry in recent years [
21]. However, the ever-increasing demands on accuracy, robustness, and efficiency, coupled with the inherent limitations of the PID, have driven engineers to seek better control methods elsewhere. In recent years, the ADRC as a promising new control design framework has emerged as a viable alternative. It offers a timely, if not conventional, solution to practical problems [
22]. The essence of the ADRC is an effective control strategy for dealing with unknown disturbances and uncertainties. Its robustness property to changes in dynamics and external disturbances has been repeatedly demonstrated in practical applications [
23,
24].
In the ADRC application, the influence of the model uncertainty and the external unknown disturbances is observed by the extended state observer (ESO) based on the input-output data of the system. The control is then given to compensate for these disturbances, thereby greatly reducing the effect of the disturbance. From the frequency domain point of view, such a control method is far ahead of the general “error-based” controller in terms of phase, namely, the control function is ahead of the ordinary PID control, thereby having a better control effect.
The flourishing achievements in both academia and industry applications of the ADRC, for instance, in motion control [
25,
26] and process control [
27,
28], can be attributed to its simple structure, ease of tuning, and excellent control performance [
29].
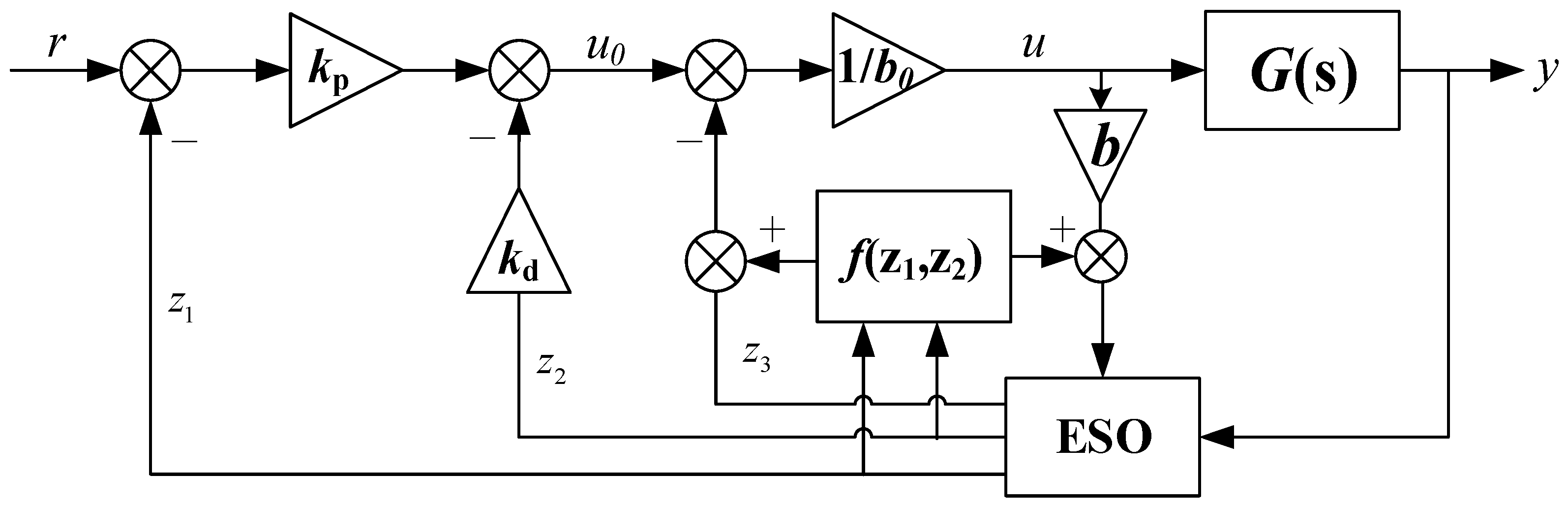
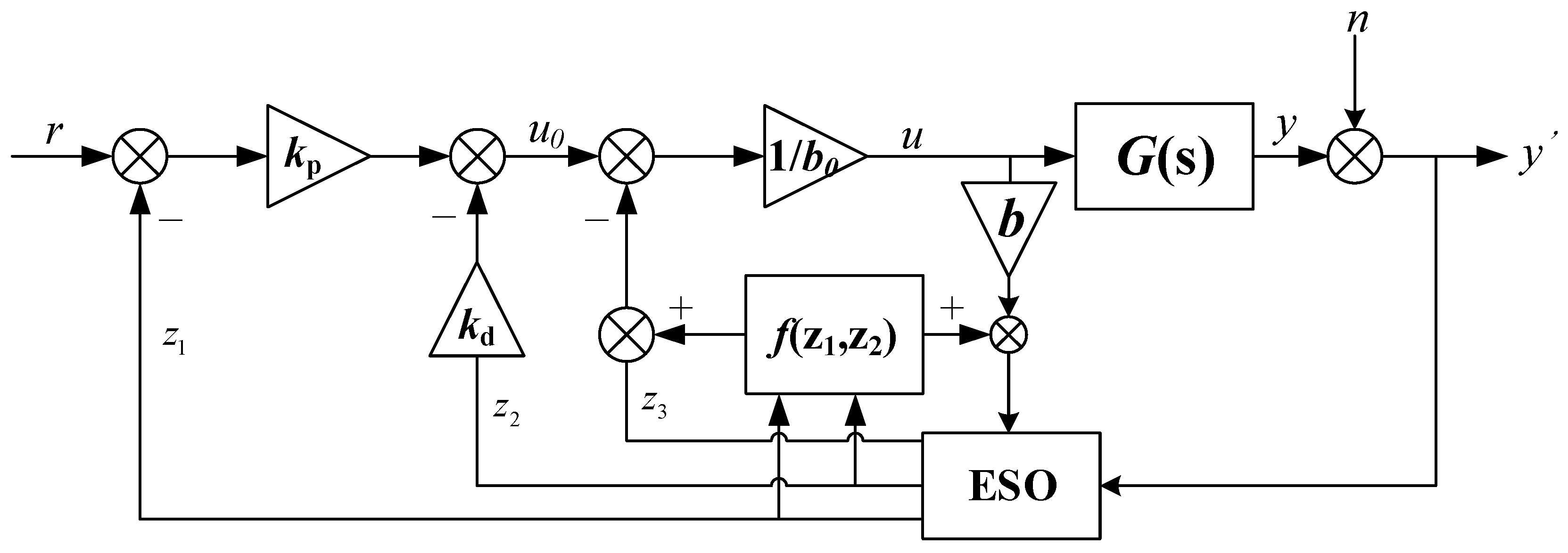
A combined structure of the feedforward and the ADRC is proposed in [
30] to address the difficulties in controlling the non-minimum phase (NMP) systems. Inspired by this, along with the characteristics of practical controlled systems, the information on the system model is added to the ESO, resulting in an improved ESO for the ADRC. Compared with the conventional ADRC, the modified ADRC (MADRC) proposed in this paper features as the following itemized points:
The estimation accuracy is improved by incorporating the model information;
The control performance is improved in terms of both set-point tracking and disturbance rejection;
The control action is experimentally demonstrated to be less sensitive to the measurement noise.
In this paper, on the basis of theoretical deduction, we will verify two remarkable performances of the proposed MADRC compared with ADRC and PID through experiments: (1) excellent set-point tracking ability and (2) noise suppression ability. It is worth noting that in this paper, we first deduce a theoretical noise reduction condition for the controller and then verify it in simulation experiments and practical experiments. The remainder of the paper is organized as follows:
Section 2 presents the structure of the modified ESO and the MADRC. The noise problem in the close-loop is formulated in
Section 3, and the noise suppression ability of the MADRC is analyzed. The controller design and simulation experiment are given in
Section 4. A comparative study is carried out by hardware experiment in
Section 5, and the conclusions are reached in
Section 6.
3. The Noise Reduction Performance of MADRC
As mentioned above, strong fluctuation of control variables is caused by measurement noise. However, introducing the filter will attenuate the control variables, thus weakening the control strength. On this basis, this paper will show that the MADRC has depressing capacity to some extent.
3.1. Problem Formulation
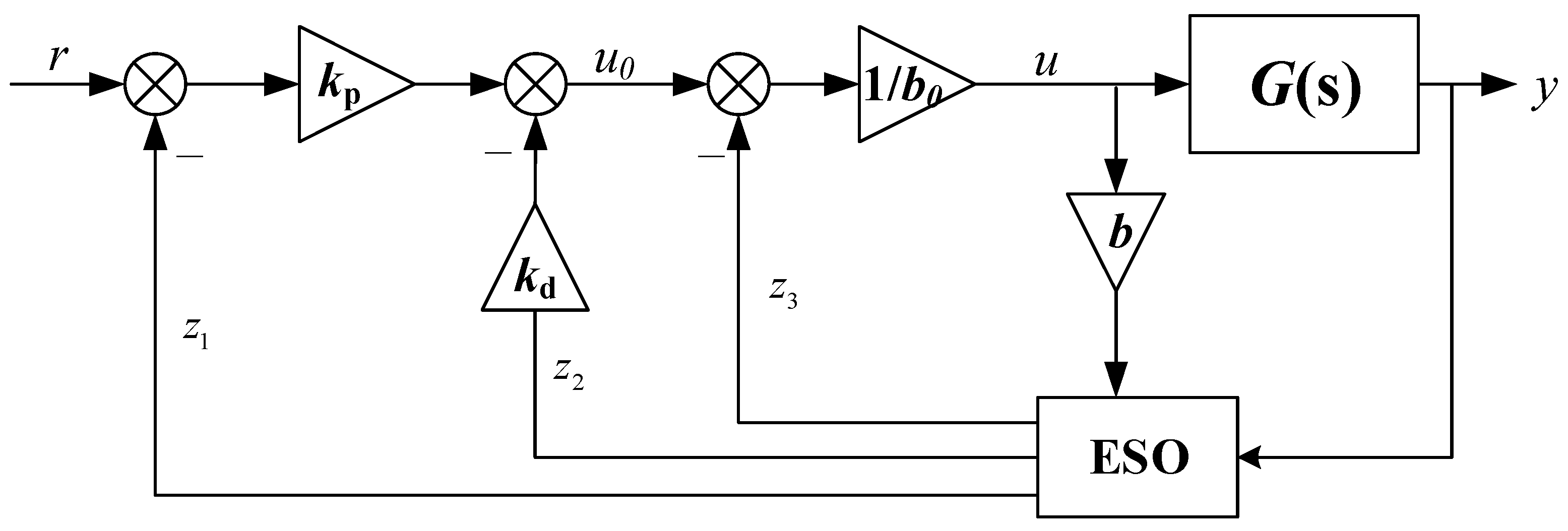
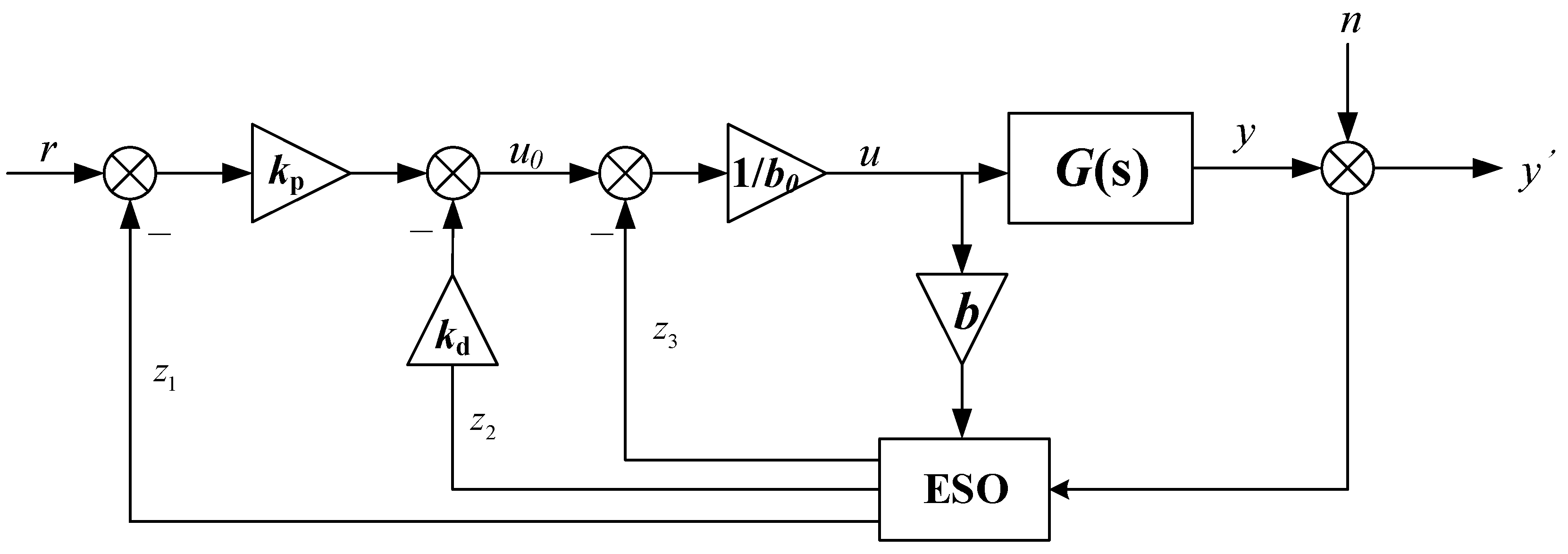
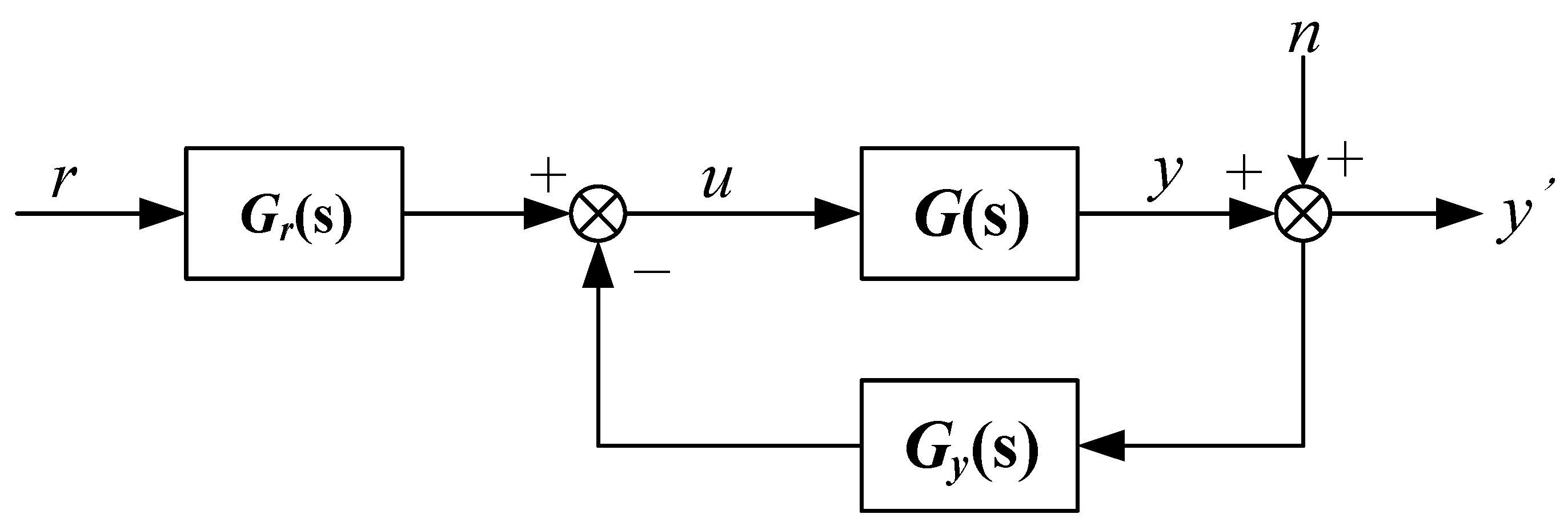
Figure 3 and
Figure 4 show the ADRC structure in the presence of measurement noise at the measurement end, where
y denotes the real output and
y′ is the measurement. As we can see from figures, there are two inputs in the whole closed-loop systems: reference
r and noise
n. The factors affecting the control variables
u are
r and
n. Besides, it is revealed in [
34,
35] that the ADRC is actually of two-degrees-of-freedom structure; therefore, we converted the above structure to the structure shown in
Figure 5. For simplicity and generality, we define the transfer function from
y to
u as
Gy(
s) and the transfer function from
r to
u as
Gr(
s).
Converting the ADRC equations to the frequency domain using the Laplace transform, the control variable is
As
Figure 5 shows, the transfer function from
n to
u is equivalent to the transfer function from
y to
u. The comparison in noise reduction performance will be given by discussing the polynomials of
Gy(
s) between ADRC and MADRC.
3.2. Derivation of Transfer Function for ADRC
Based on the introduction of
Section 3.1, this section will derive the transfer function from
y to
u for ADRC. Same as the controller described above, for the sake of universality and verifiability, the noise reduction conditions deduced later are not specific to any system or object. For clarity and simplicity, we will introduce the derivation process step by step.
(1) Structural transformation for ESO:
As defined in (4), the conventional ESO structure is
represented in matrix format,
where
(2) Laplace transformation for ESO, as follows:
The observer gain
β are calculated from (6), as follows:
and the estimates
z1,
z2, and
z3 are then deduced using the Laplace transform of (25) to yield
where
(3) Transfer function acquisition, as follows:
According to the control variable
u expressed in (7) and (9),
where the controller gain
kp and
kd are calculated from (20), as follows:
Meanwhile, from (20),
u is deduced, as follows:
where
Gr1(
s) and
Gy1(
s) stand for transfer functions for ADRC with respective polynomials. Furthermore,
Gy1(
s) can be simplified as
The detailed expression of the polynomials
N1,
n1,
n2,
d1, and
d2 in the transfer functions are given in
Appendix A.
3.3. Derivation of Transfer Function for MADRC
The derivation of transfer function for MADRC is generally similar to that of ADRC; this section gives a brief description in order to avoid repetition and redundancy.
(1) Structural transformation and Laplace transformation for ESO, as follows:
Similarly, the modified ESO structure (13) is
The observer gain
β are calculated from (15), as follows:
The estimates
z1,
z2, and
z3 are then deduced using the Laplace transform of (35) to yield:
(2) Transfer function acquisition, as follows:
The control variable
u is expressed in (9) and (16), as follows:
which is deduced as follows:
where
Gr2(
s) and
Gy2(
s) stand for transfer functions for MADRC. Furthermore,
Gy2(
s) can be simplified as
The detailed expression of the polynomials
N2,
n3,
n4,
n5,
n6,
d3, and
d4 of the transfer functions are given in
Appendix A.
3.4. Analysis of Noise Reduction Conditions
Before the analysis and proof on noise reduction performance, we have to clarify the following aspects:
The noise discussed in this paper is usually the high-frequency noise in industrial applications, namely, ω is set to infinite;
We consider the second-order system as a stable system, namely, a1 > 0, a2 > 0;
The subject discussed in this paper is based on the condition that the observer and the controller bandwidths of the two types of ADRC (ωo and ωc) are equal.
According to explicit point 1, when discussing the gain of the two kinds of ADRC with high-frequency noise, on the basis of the corresponding relation between frequency domain and complex domain G(jω) = G(s)|s = jω, it becomes clear that the discussion focuses on the higher order terms of the transfer function, namely, the N1 and N2 in Formula (34) and (40).
Assuming that the MADRC has the capability of noise reduction, N2 must be less than N1, that is to say, the inequality should be proved.
Since both a1 and a2 are positive, only f1 and f2 need to be discussed.
Note that
f1 > 0 as long as the following condition is satisfied:
Similarly,
f2 > 0, as long as the following condition is satisfied:
Combining condition (44) and condition (45), we get the following:
That is to say, as long as the condition ωo ≥ ωc ≥ 0.4a2 is satisfied, the MADRC has a better noise reduction ability compared to the ADRC. For simplicity and generality, the condition is called the noise reduction condition hereinafter.
3.5. Reflections on the Condition
As shown in (46), the simplicity of the condition is beyond one’s expectation. Moreover, this is a very conservative or even stricter condition obtained by mathematical deduction. In other words, in practical control applications, this condition is extremely easy to meet:
- (a)
In general, the observer bandwidth ωo must be greater than the controller bandwidth ωc, that is, the observer frequency must be greater than the controller operating frequency. Even in most ADRC applications, ωo is ten times or even larger than ωc;
- (b)
On the other hand, the ADRC closed-loop characteristic polynomial is as follows:
and the open-loop characteristic polynomial of the plant is as follows:
Obviously, since the closed-loop control response must be faster than the open-loop, namely, ωc ≥ 0.5a2. Even in the actual control, the closed-loop response is required to be much faster than the open-loop response: ωc ≫ 0.5a2.
To sum up, the strict condition obtained under the rigorous mathematical derivation is extremely easy to be satisfied in most control applications, and the margin of satisfaction is quite large.
This section completed the derivation of noise reduction condition of MADRC, and obtained a “strict noise reduction condition” that can be easily met in application. Through the theoretical parts of the
Section 2 and
Section 3, we have a preliminary understanding of the structure and noise reduction ability of MADRC. The next section will verify control quality of MADRC and noise reduction ability compared with ADRC through simulations and experiments.
4. Controller Design and Simulation
4.1. Model-Based System Identification
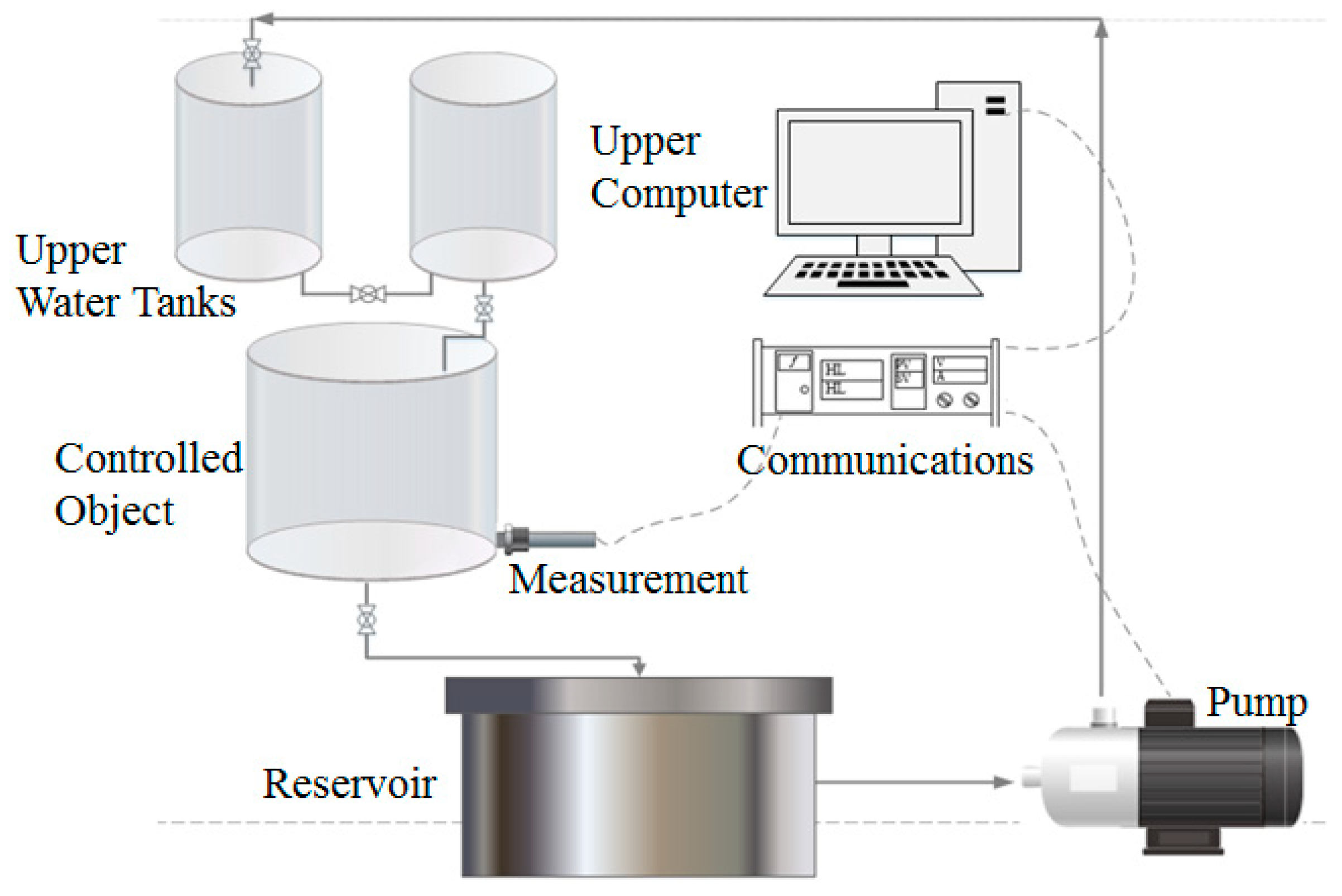
As introduced in the previous section, the water tank systems in industrial applications usually have large inertia. To this end, we have developed an experimental platform consisting of three water tanks whose structural diagram is shown in
Figure 6. In order to emulate the large inertia, we have made full use of the inertia of the tank by making water flow through three water tanks in cascade.
The upper computer receives the signal of the communicator through the data bus. The communicator receives the signal of the pressure transducer and outputs the control signal to the frequency converter to adjust the rotational speed of the pump. The steady-state range of the controlled water level is obtained by testing at an operating point. Thus, the step-input experiment and the control experiment are carried out in the steady-state range. For simplicity and generality, the voltage signal received by the inverter is used as a control variable in the following description.
The form of transfer function of the platform is denoted as
As mentioned above,
U is the voltage signal received by the inverter and
Y is the water level of the controlled plant.
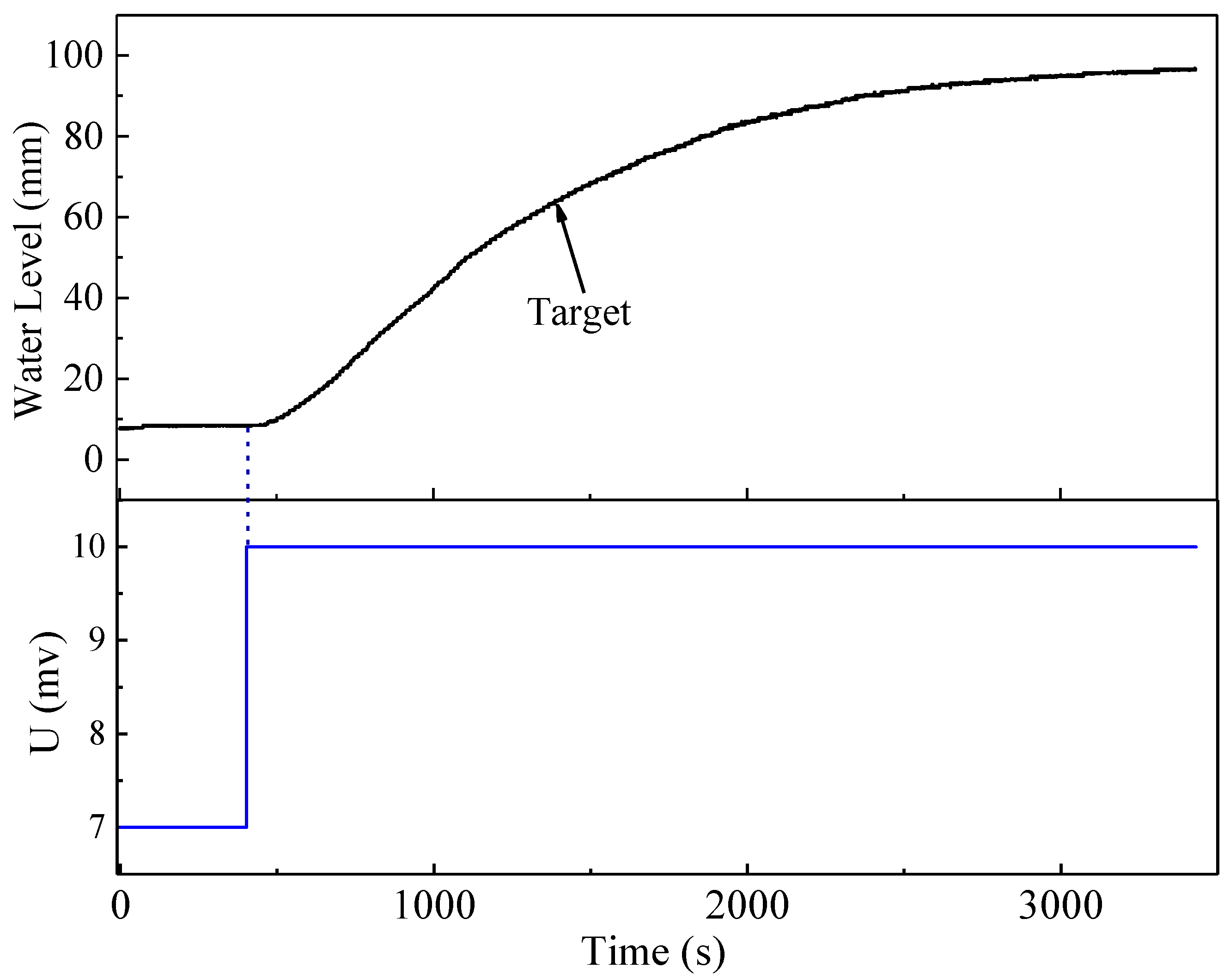
Figure 7 depicts the open-loop water level step response in the steady-state range, based on which the following transfer function was identified by using MATLAB System Identification Tool Box:
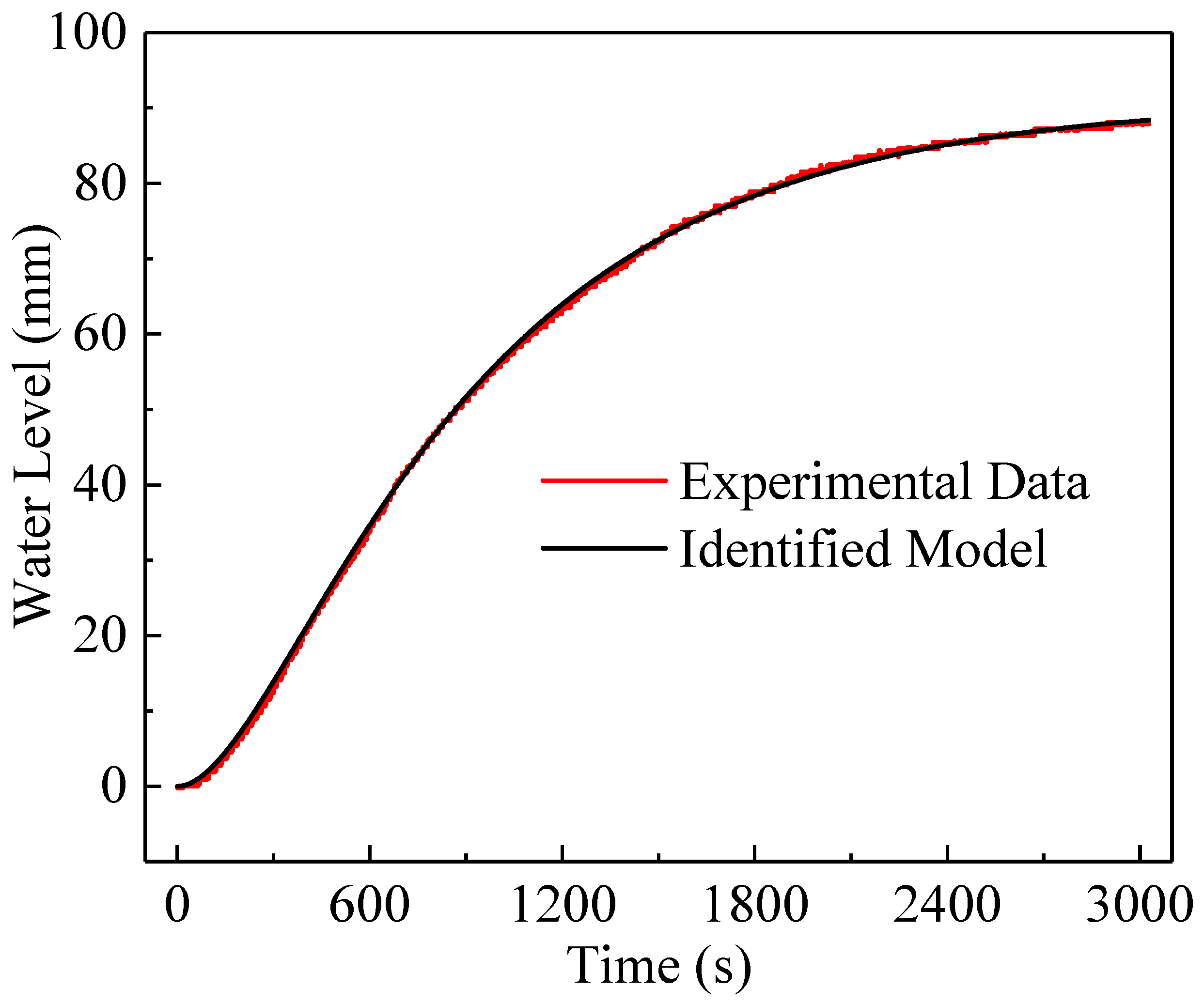
Figure 8 shows the fitting of the experimental data with the identified model. According to the degree of fitting shown in the figure, it can be concluded that the identified transfer function represents the system very well. In addition, by comparing (10) and formula (50), it can be obtained that
b = 1.77176 × 10
−4,
a1 = 5.8397 × 10
−6, and
a2 = 5.8401 × 10
−3.
4.2. PI Controller Parameters Tuning
As empirical setting, the proportional-integral (PI) controller without differentiation is adequate to control the second-order system in industrial processes. Accordingly, we applied PI controller to the experiments. The form of PI controller is denoted as
In order to design an engineering friendly controller for the system, we tuned the parameters based on the following method: SIMC-PID tuning rules widely used in industry, here SIMC means “Simple Internal Model Control” [
36]. According to the identified result, the PI parameters are tuned as
The PI control performance has fast response with good robustness, namely, fast transient period and reasonable overshoot, which will be further exhibited in
Section 4.4.
4.3. ADRC Controller Parameters Tuning
According to the theoretical deduction above for ADRC, there is a quantitative relationship between derivative gain kd and the damping factor ζ as shown in (23). Moreover, in order to compare the control performance between ADRC and MADRC, we set the ωo and ωc of the two types of ADRC to be equal to satisfy the unique variable principle.
In this experiment, the value of
ωo and
ωc are tuned as
On this basis, the parameters of ADRC and MADRC are as follows:
- (1)
ADRC: β1 = 0.09, β2 = 2.7 × 10−3, β3 = 2.7 × 10−5, kp = 1.225 × 10−5, kd = 7 × 10−3;
- (2)
MADRC: β1 = 0.08416, β2 = 2.2026 × 10−3, β3 = 2.7 × 10−5, kp = 1.225 × 10−5, kd = 7 × 10−3.
Obviously, since the improvement of ADRC mainly focuses on the ESO, the difference of parameters setting between ADRC and MADRC is mainly concentrated on the observer parameters β1 and β2, while the controller parameters are identical.
The superiority of MADRC is fully explicated in the following sections.
4.4. Simulation Comparison on Control Effects
To evaluate and compare the robustness against parameter perturbation, PI, ADRC, and MADRC are simulated based on the identified model. Several sets of step-input experiments of water level are given to prove the validity of tuned parameters and the control effect of the MADRC compared with the ADRC and PI controller. The amplitude of control variable is limited within [0, 10], which considers the working voltage of actuator used in the experiment.
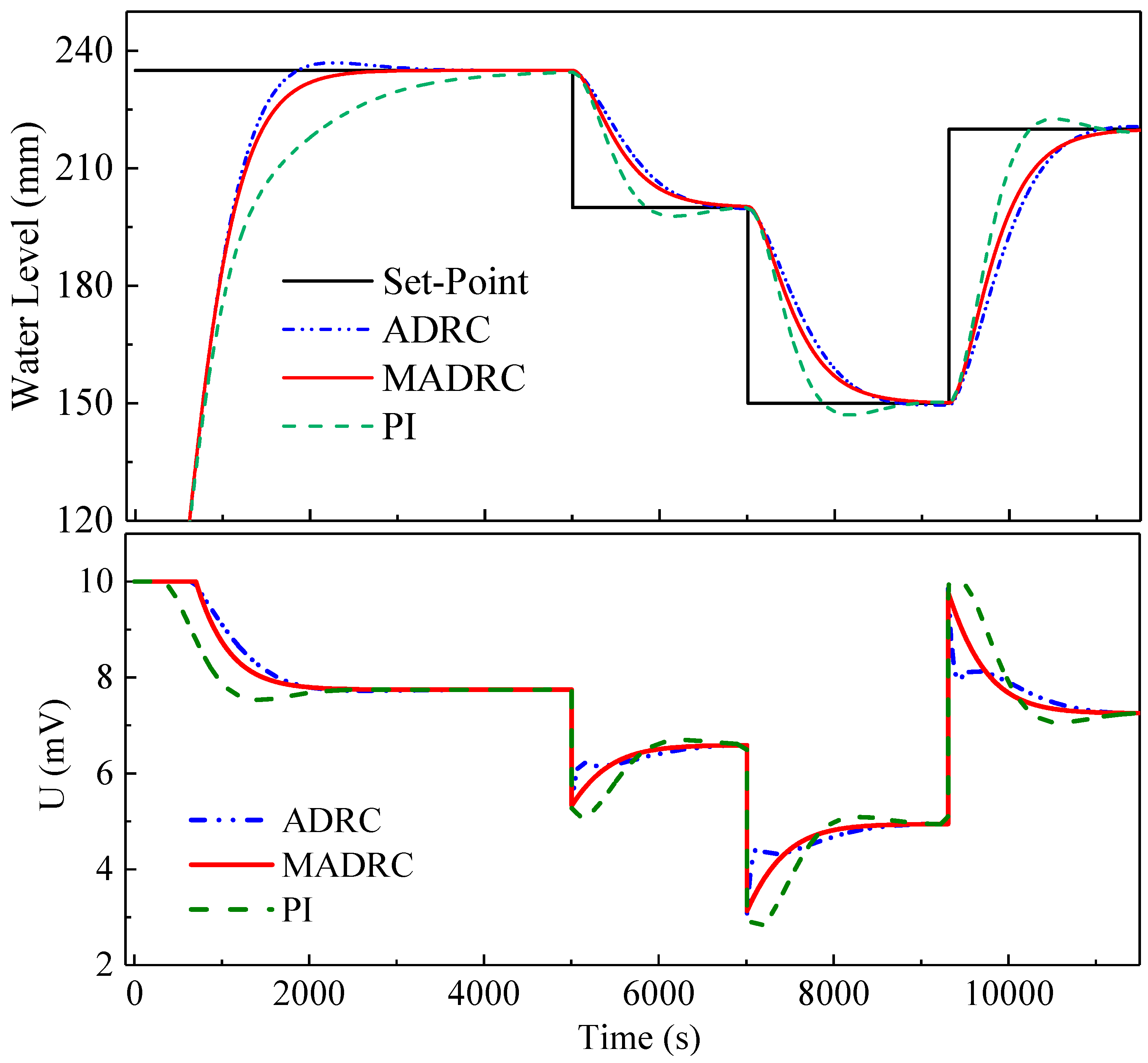
Figure 9 shows the result of reference tracking control. The step-changes in the water-level reference happened at 0 s, 5003 s, 7009 s, and 9310 s with amplitudes of +235, −35, −50, and +70, respectively. Compared with the PI and ADRC controller, the MADRC controller yields shorter transient period and smaller overshoot. It is generally known that such control performance is the goal of industrial control processes. From this point of view, the simulation results validate one of the capabilities of the MADRC mentioned above.
4.5. Noise Reduction Simulation Comparison
To compare and verify the capability of noise reduction, the ADRC and MADRC are simulated based on the identified model. High-frequency white noise is introduced into the close-loop to explore the influence of noise on the control variable. As mentioned above, the identified model is (50)
namely, the system parameter
a2 = 5.84 × 10
−3 in the second-order system (10). We adopted the same controller parameters of ADRC and MADRC, i.e.,
ωo = 0.03 and
ωc = 0.0035, which satisfy the noise reduction condition
ωo ≥
ωc ≥ 0.4
a2.
Figure 10 and
Figure 11 show the result of noise-reduction simulation experiments.
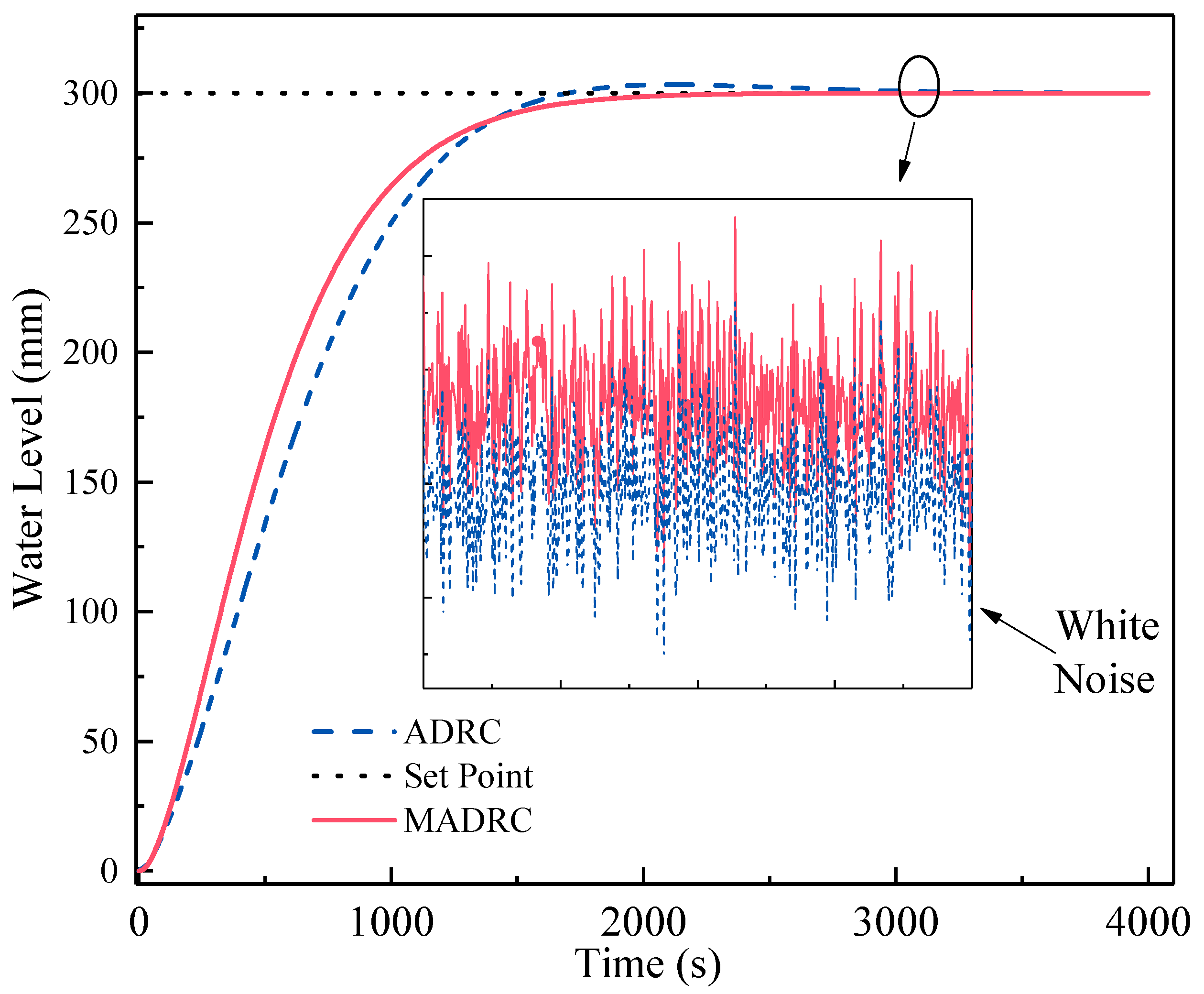
Figure 10 shows the output values of the two ADRC step experiments in the presence of noise, and highlights the fluctuation of output values after introducing white noise.
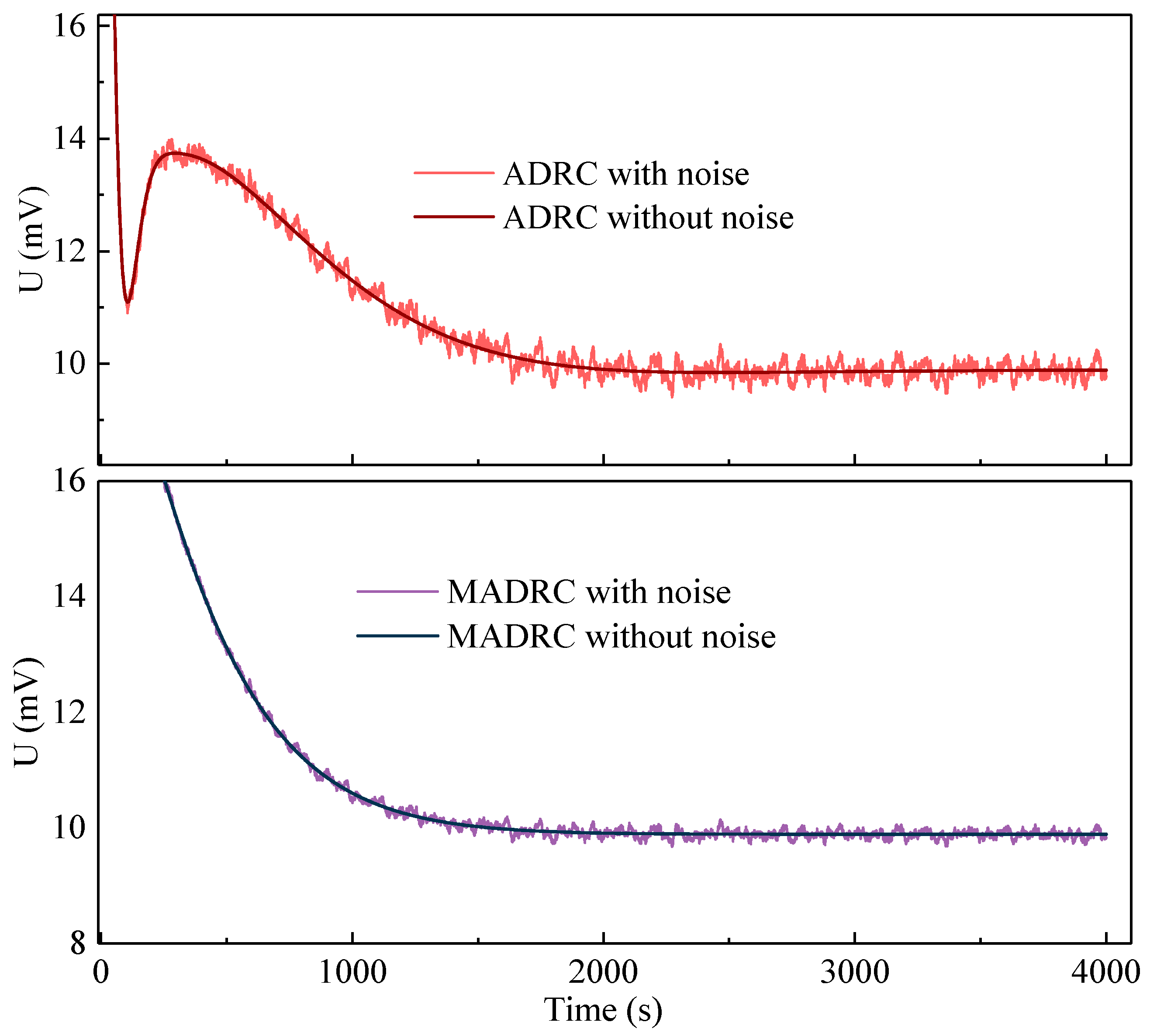
Figure 11 shows the fluctuation of control variables of the two ADRC relative to their noise-free conditions. Since the settings of the horizontal and vertical coordinates of the two figures are the same, it can be seen intuitively that the fluctuation of output control variable is much smaller in the MADRC than in the ADRC. This preliminarily verifies the idea proposed in this paper, that is, the MADRC has a better noise reduction ability compared with the ADRC under the same noise interference and the same bandwidth settings.
In order to demonstrate the noise reduction ability of the MADRC quantitatively, we introduced the integral absolute error (
IAE) to evaluate the fluctuations of control variable, which is defined as
In this experiment, y denotes the control variable under noise and r denotes noise-free reference. Obviously, the smaller the IAE, the smaller the fluctuation. Calculation results of the two ADRC are as follows:
By comparing (56) and (57), IAEMADRC < IAEADRC, and we can draw the same conclusion that MADRC indeed has a better noise reduction ability.
So far, the validity and feasibility of the proposed MADRC have been demonstrated by simulation experiments with the identified model. Therefore, the prerequisite for the hardware experiment is readily met. The water pump control experiment in hardware will be carried out in the next section.
5. Experimental Results
5.1. Experimental Setup
The picture of water pump control experimental platform is shown in
Figure 12, where some critical equipments are labeled. To avoid distraction, some irrelevant components in the experiment, such as lift of pump, pipe diameter, relays, and opening of each valve, are not detailed in the figure, but they are indispensable for the experiment.
The experimental scheme is to change the rotational speed of the pump by adjusting the input control signal of the variable frequency pump, so as to adjust the flow of water, and then adjust the water level of the tank. It needs to be emphasized that the factors affecting the water level of the tank are not only the inlet water volume but also its own water level, because the increase of the water level will lead to the increase of the output water yield.
The host computer controls the system, and the control algorithm is realized by building control module structures and tuning parameters. The communication between the platform and the host computer is via MODBUS module.
5.2. Experimental Results
Based on the previous simulation work in
Section 4, we applied the well-tuned controller parameters to control the water level of the experimental platform. In order to verify the quantitative relationship between
kd and
ζ and take
Ts into account,
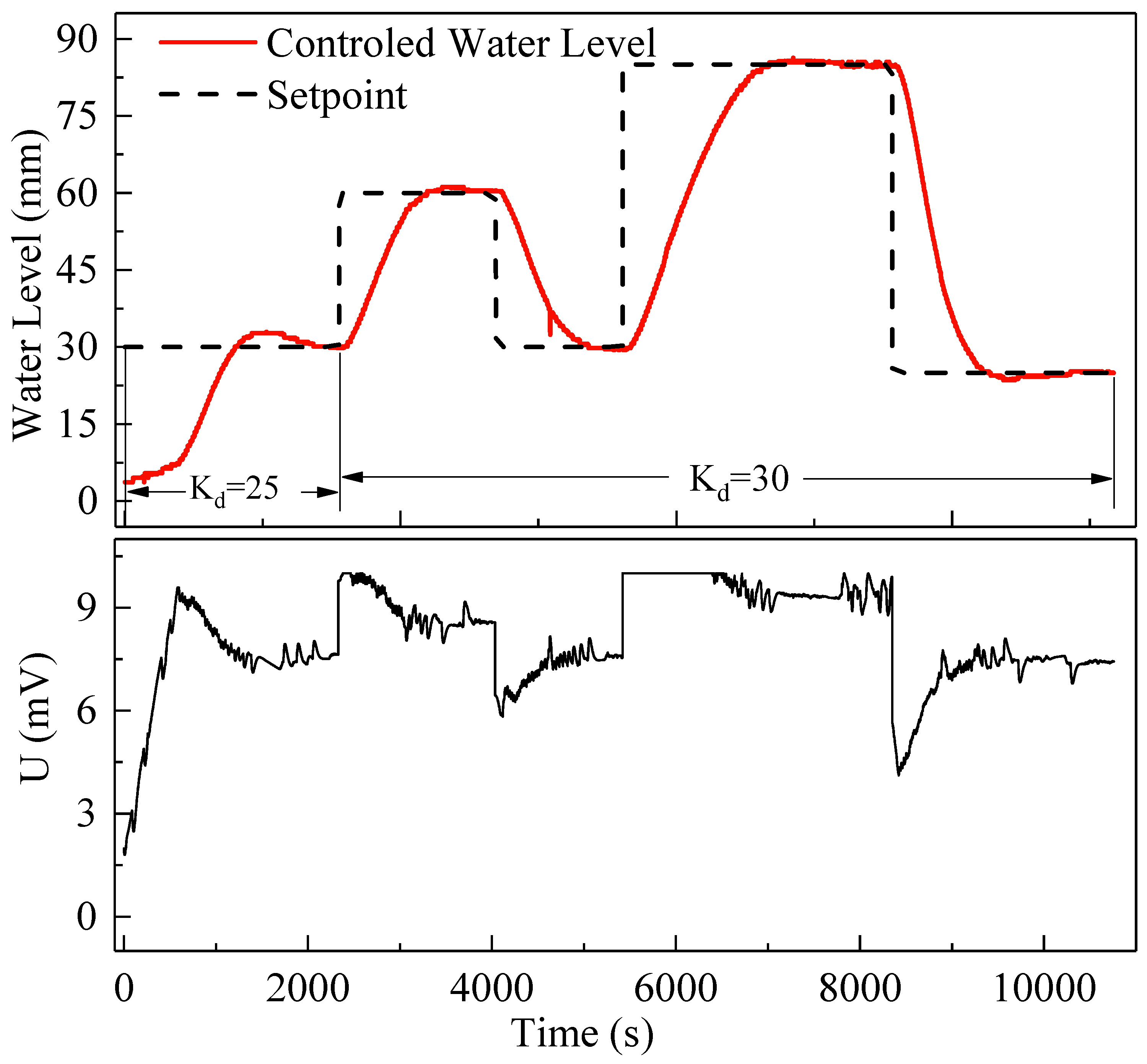
kd is set in discrete steps. The other parameters and the structure of the controllers are the same as mentioned in the simulation experiment. In order to fully reflect the effect of the controller, the experiments were set up with multiple groups of positive/negative steps in different amplitudes.
Figure 13 and
Figure 14 represent the water level tracking performance of ADRC and MADRC controllers, respectively.
Similarly, in order to demonstrate the control effect more quantitatively, we introduced some evaluation indices, such as integral absolute error per time, IAET, overshoot O, and transient time Ts with 2% error band.
The definition of
IAET is
where
y and
r denote the actual water level and set point, respectively.
The overshoot is defined as
where
ymax denotes maximum output value and
yt = ∞ is the stable value.
The definition of transient time is the time required for the response curve to reach and stay within a range of certain percentage (usually 2% or 5%) of the final value [
34]. The error band is the range between the ±2%/±5% amplitude around the reference value.
Each of the three evaluation indices focuses on different aspects. The transient time Ts is a comprehensive index reflecting the response speed and damping degree of the system. Simply speaking, it can be considered as the minimum time required to complete the specified control function. The overshoot is the most commonly used control index to partially depict the robustness of a controller. In some specific industrial processes, the overshoot is strictly restricted to nearly zero; IAET is an auxiliary evaluation index in this paper. It represents the real-time error between the actual output value and the reference value, which is used to indicate the accuracy of the control performance.
The calculation results of evaluation indices are tabulated in
Table 1. In the next section, the analysis will be carried out according to the evaluation indicators in the table.
5.3. Result Analysis
According to the values in
Table 1, it is obvious that
Ts and overshoot is smaller in MADRC than in ADRC in each step experiment, which reflects the excellent control performance of the MADRC compared with the ADRC in terms of water pump control. As for
IAET, the
IAET of the ADRC is less than that of the MADRC in smaller steps and almost equal in larger steps. Reasons for this can be the overshoot of the ADRC is similar to that of the MADRC when the step is small, but the rising speed of the ADRC controlled signal is faster than that of the MADRC, thus leading to smaller real-time error. During large steps, although the ADRC is more powerful than the MADRC, the overshoot of the ADRC is also larger than that of the MADRC, so the
IAET of the ADRC and the MADRC become almost the same.
The comparison of control performance in the above analysis can be observed in the figures. Overall, the MADRC has an excellent control performance compared to the ADRC in terms of water pump control, showing great potential in its application to water pump control in industrial processes.
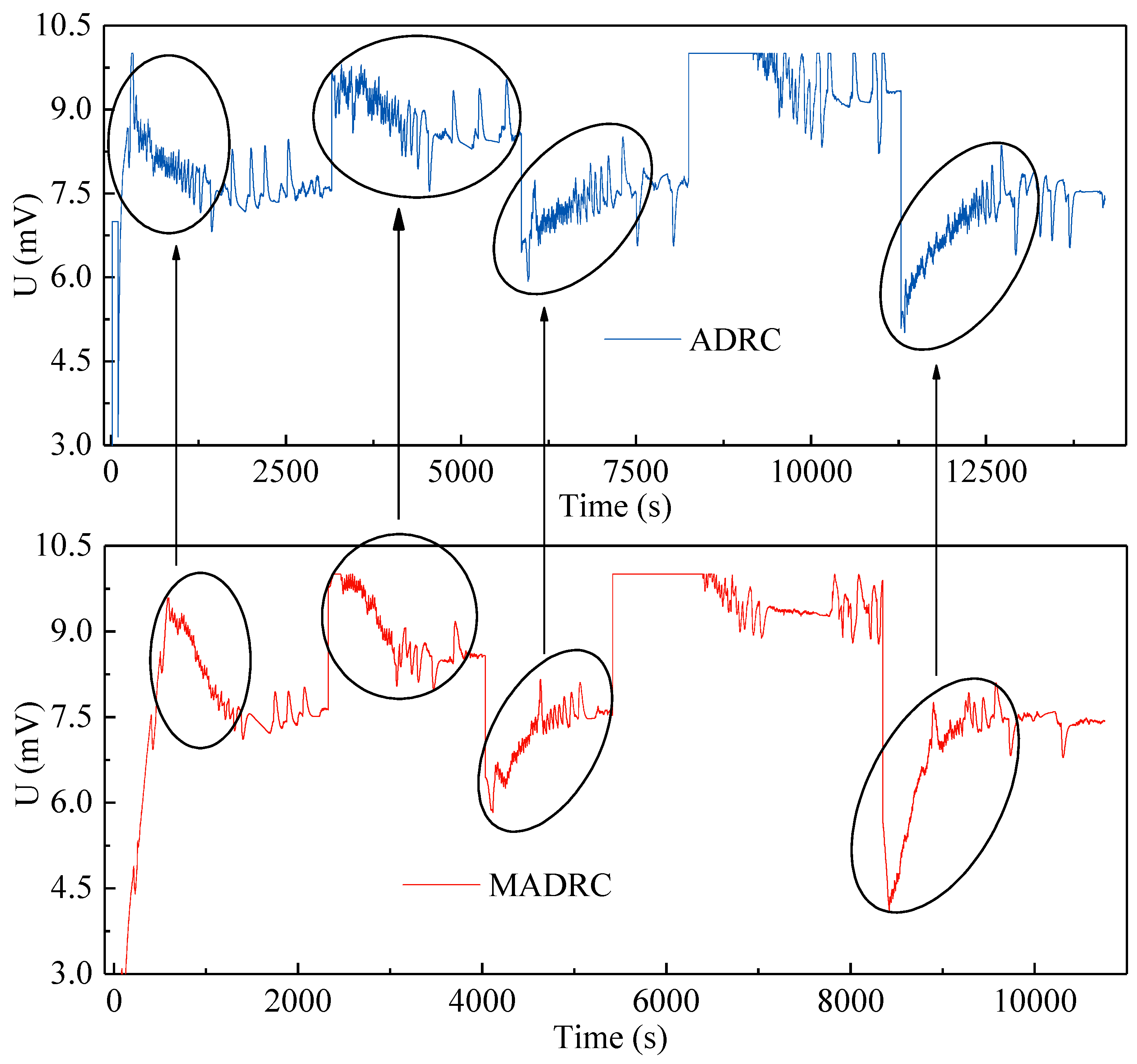
Noise reduction analysis is achieved mainly through the comparison of the ADRC and MADRC control variables, namely, the output signal of the pump speed. Since the two sets of experiments have the same step amplitudes, it is feasible to compare the control variables.
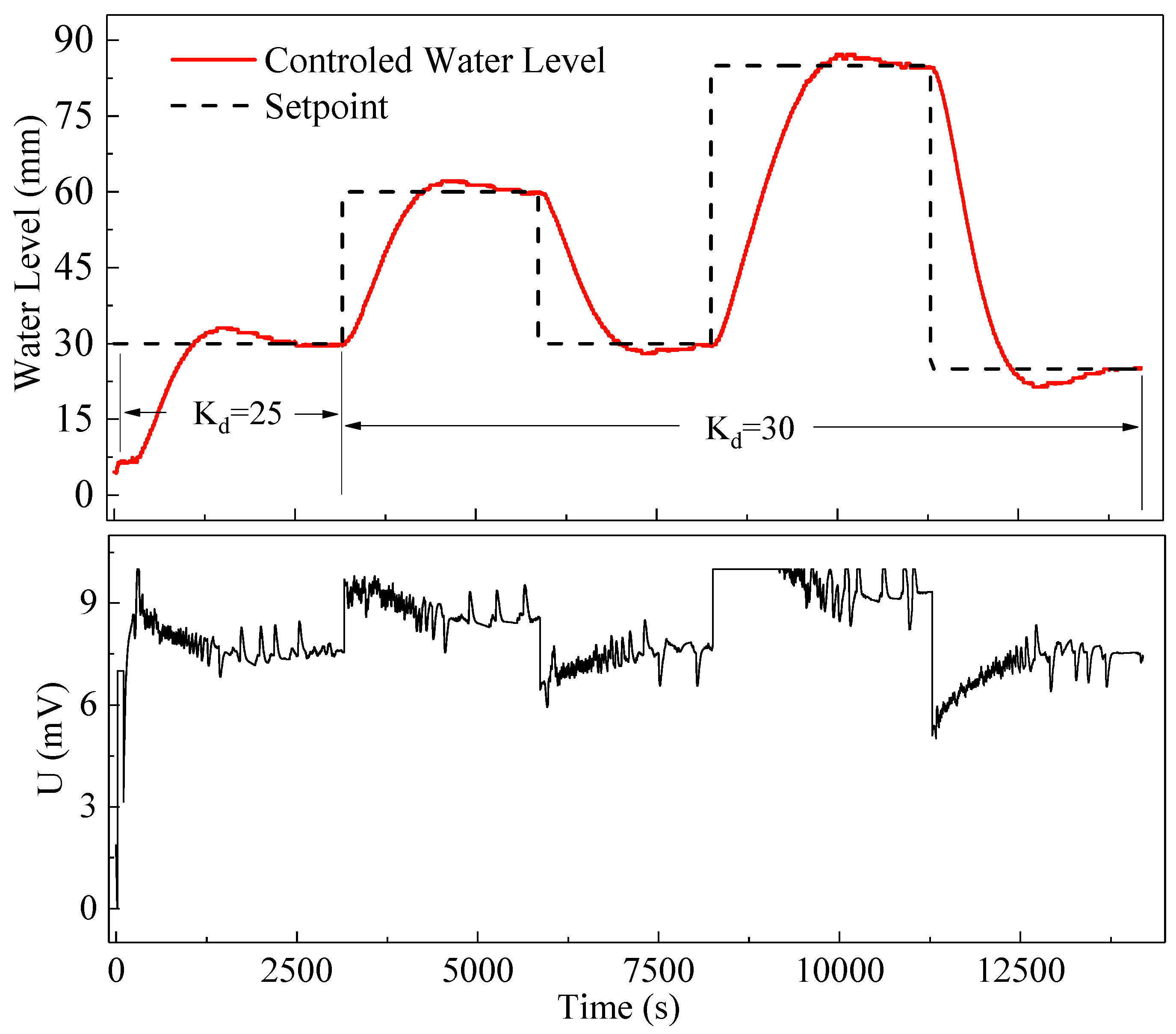
Figure 15 shows the comparison of control variables.
Valuable insights can be obtained from the experimental results: when we have to deal with some objects with the attributes of slow dynamics, strong nonlinearity, and various disturbances, MADRC is indeed a trustworthy choice, which can effectively deal with various uncertainties. Meanwhile, its noise reduction performance is advantageous to various executing agencies in industry, especially mechanical equipment. All in all, MADRC has excellent application prospects in the field of industrial process control.
It clearly depicted in
Figure 15 that when control variable undergoes a large numerical change, severe fluctuation will occur. However, according to the corresponding circled plots, it is obvious that the fluctuation of control variable is smaller for the MADRC than for the ADRC. Moreover, on the basis of model information and controller parameters, the parameters satisfy the noise reduction conditions mentioned in this paper:
ωo ≥
ωc ≥ 0.4
a2. This shows that the MADRC indeed has a better noise reduction capability compared with the ADRC under the same noise reduction condition. As in the simulation experiments, the feasibility of the noise reduction condition is also demonstrated, which is quite useful in industrial applications for its friendliness to actuators.
6. Conclusions
This paper verifies the promising application of the modified model-assisted ADRC control methodology on a practical water pump control system by analysis, simulation, and well-designed hardware experiment. This paper focuses on the tracking performance and noise reduction capability of the MADRC. The superiority of the MADRC in these two aspects has been verified by simulation and practical hardware experiment.
On the one hand, the MADRC has better control performance, especially in the reference tracking with large step changes. It can be clearly seen from the simulation results in
Figure 9 and the actual experimental results in
Table 1 that MADRC is superior to ADRC and PID in both overshoot and transient time. Specifically, in the case of a smaller overshoot, it also has faster transient time, which is essential for the control process under specific requirements.
On the other hand, the MADRC has better noise reduction capability compared to the ADRC under the same noise reduction condition. Furthermore, the strict condition derived under the rigorous mathematical analysis is extremely easy to satisfy in the most practical control processes, and the satisfactory margin is quite large. The control variables with weakened fluctuation after noise reduction will benefit the actuator and prolong its life, which is especially critical for systems with complex installation procedure.
To sum up, the proposed MADRC method is able to achieve a better control performance and better noise reduction capability by sacrificing some structure conciseness and ease of use.
This paper provides a hybrid data-driven and model-assisted active disturbance rejection control for precise control of water level in industrial process, and it could even be carried out in extensive industrial control problems. More importantly, this paper provides an idea of designing control algorithm: by combining model information with real-time input and output data, better control effects could be achieved by using both steady state data and dynamic data in the control process. Moreover, the best disturbance-rejection performance of the MADRC control approach can contribute to pumped-storage distributed energy-supply systems like combined cooling, heating and power-generating systems [
37] and also to a study on robust optimization of the distributed generating units [
38] in the future.