A River Temperature Model to Assist Managers in Identifying Thermal Pollution Causes and Solutions
Abstract
1. Introduction
2. Methods
2.1. Heat Flux Formulation
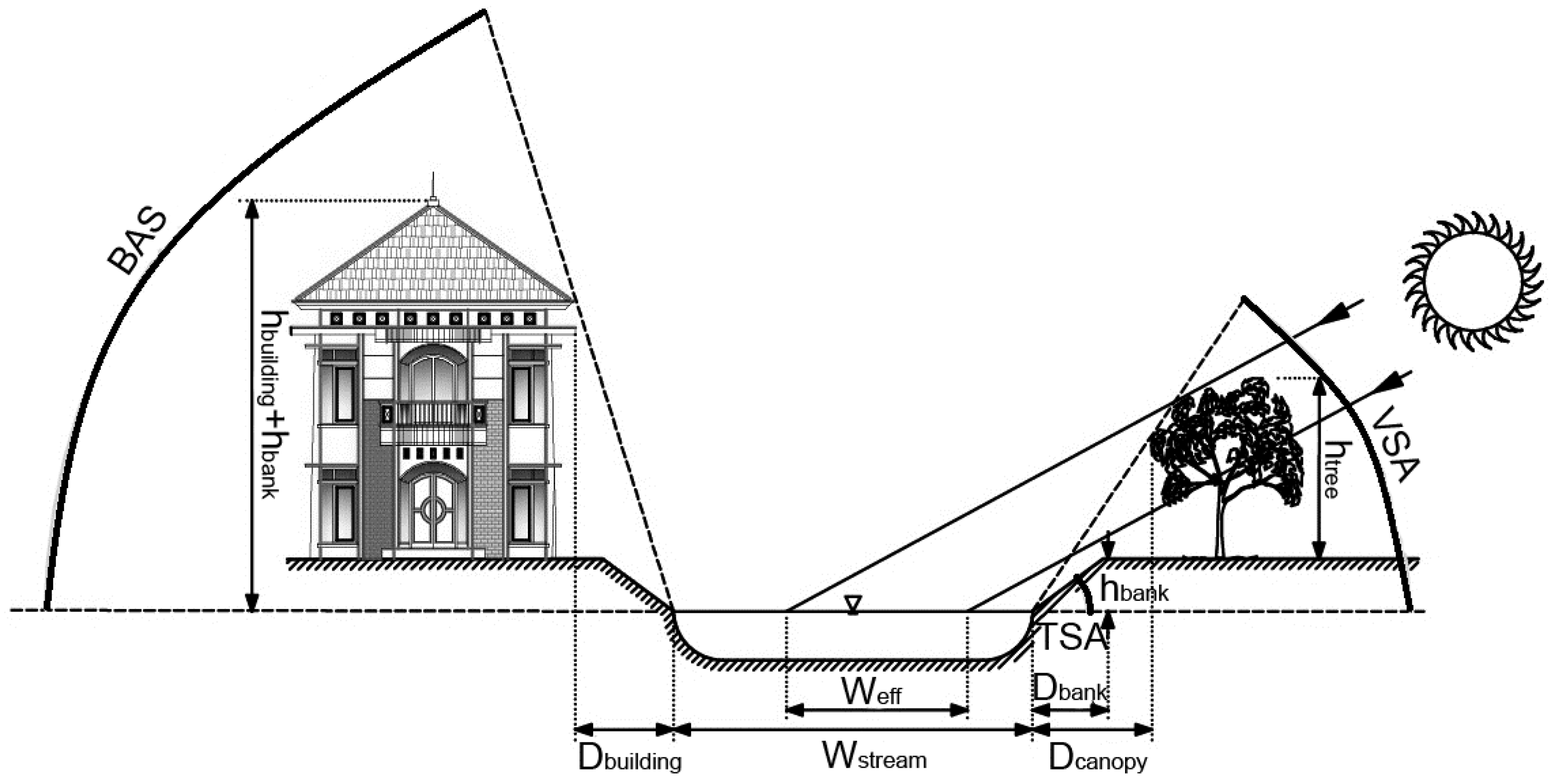
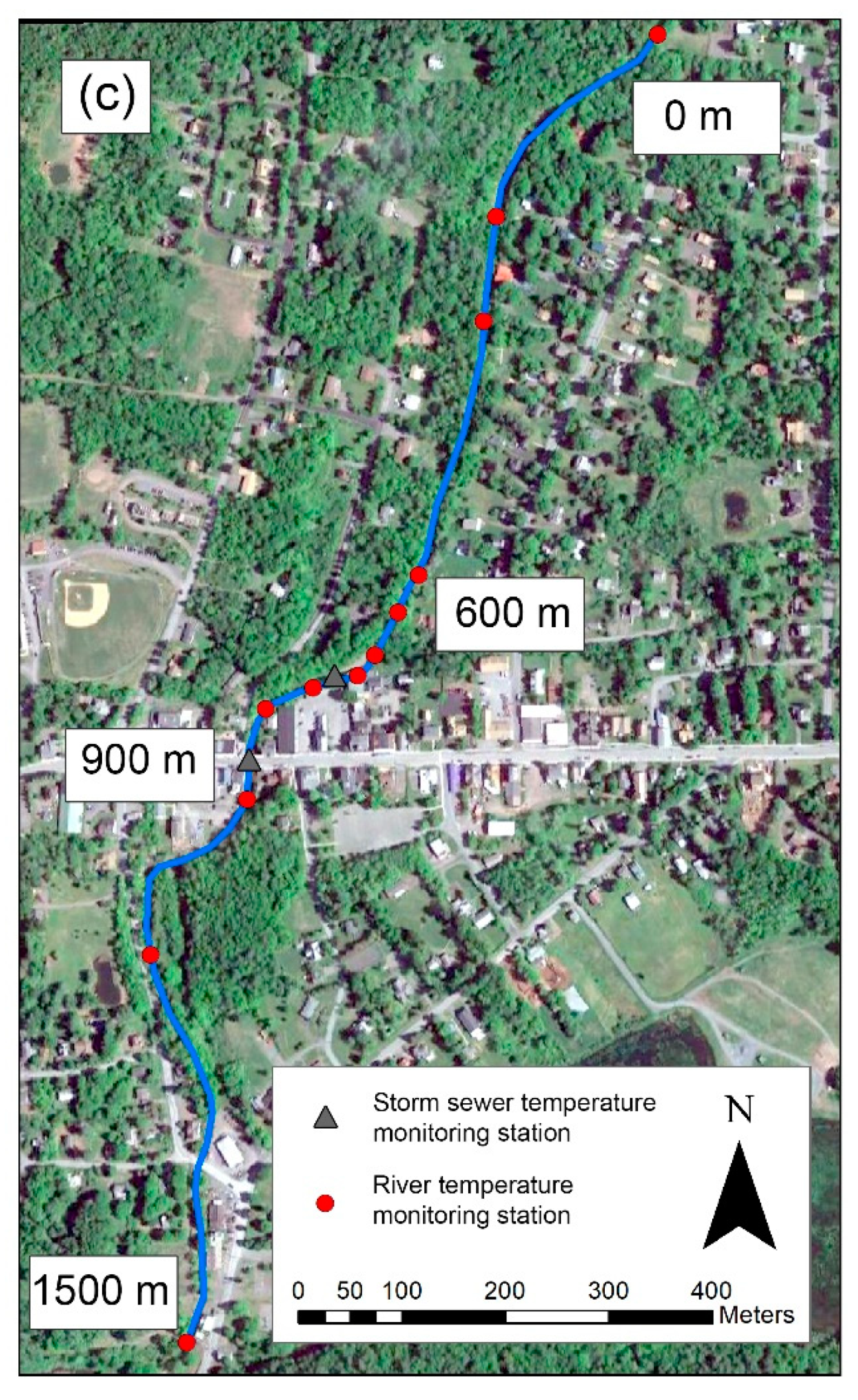
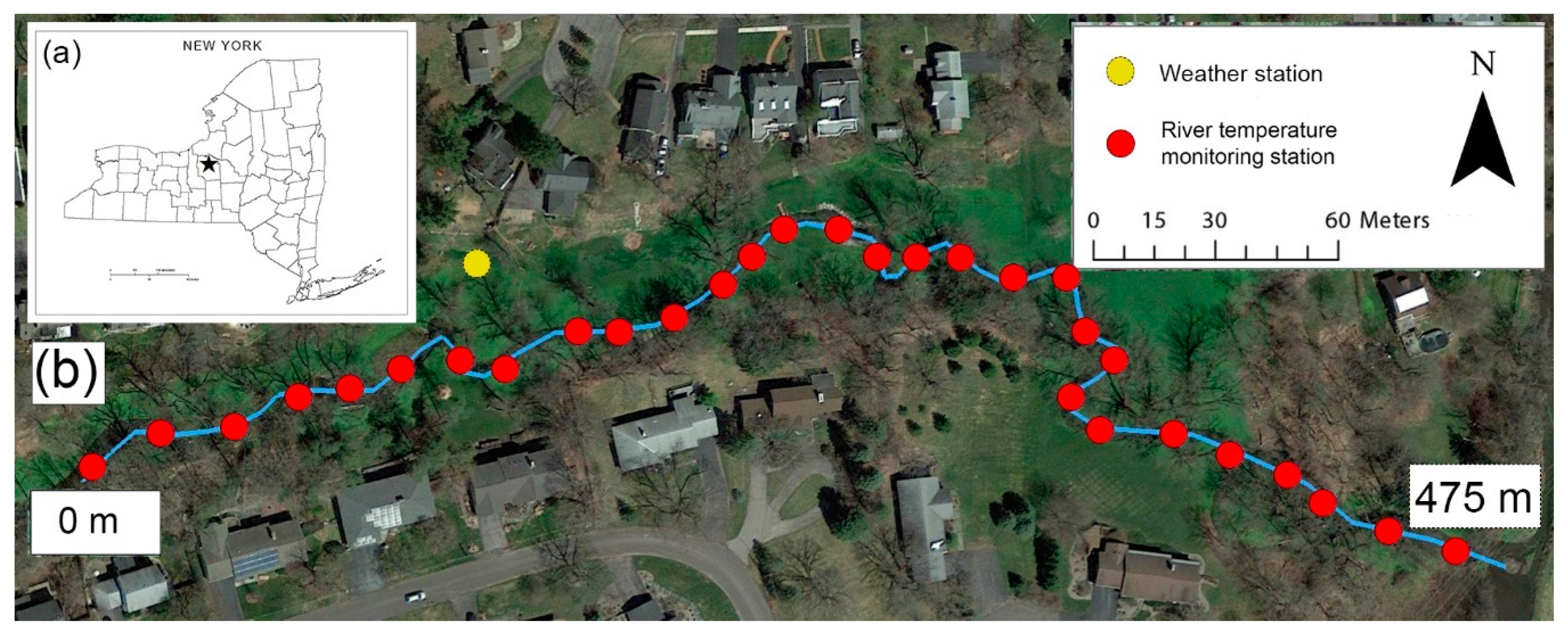
2.2. Study Area and Model Inputs
3. Results
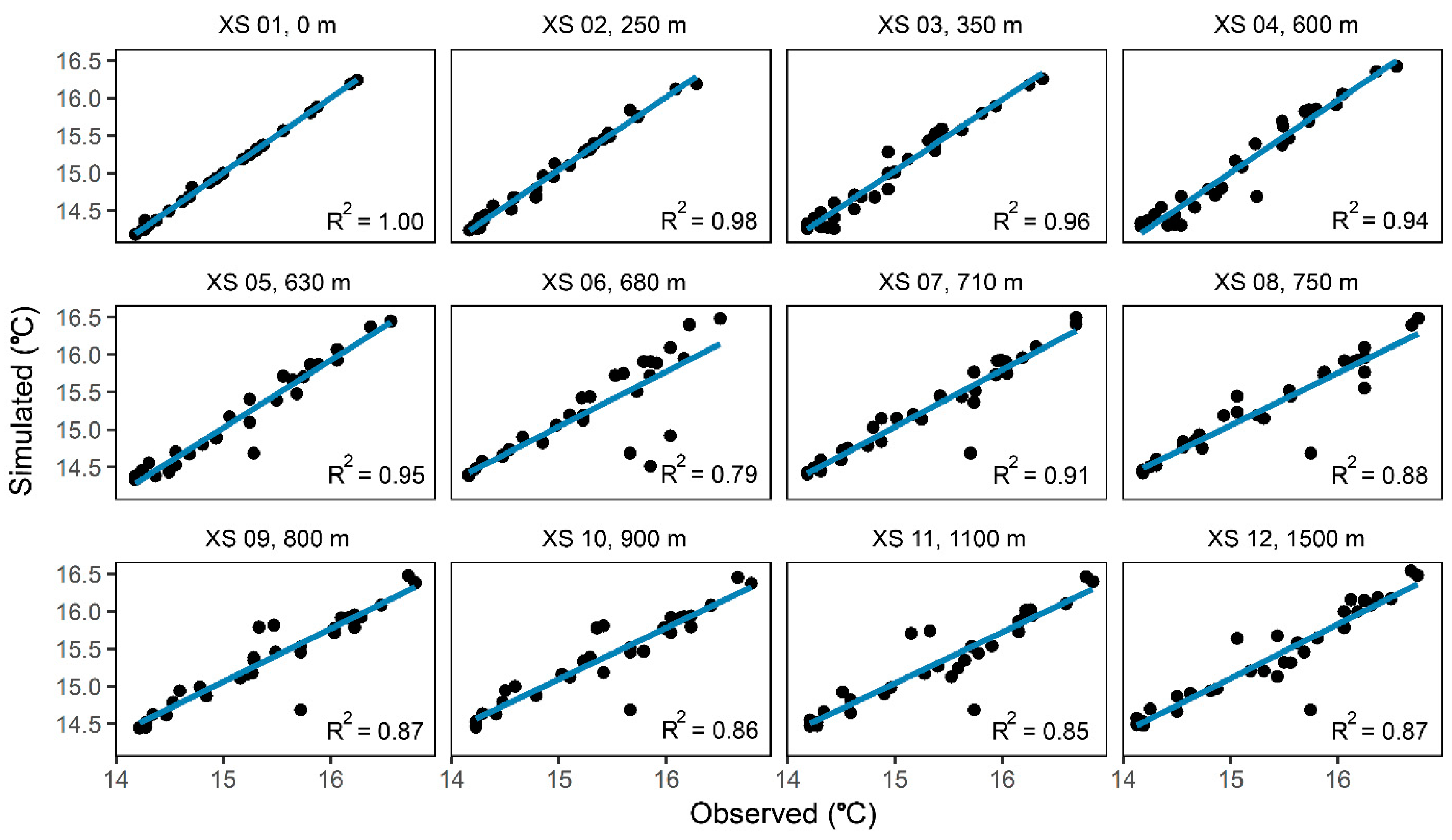
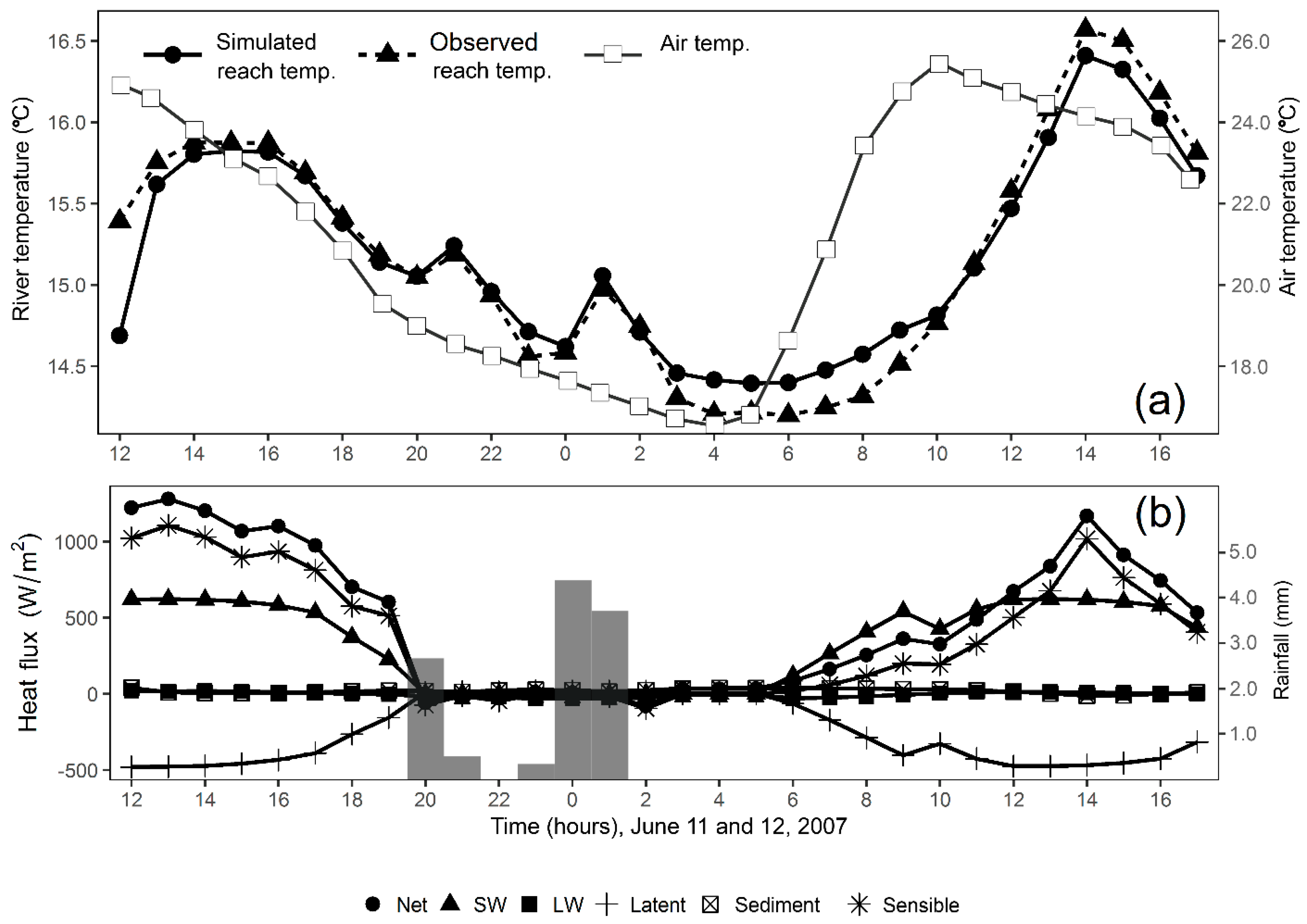
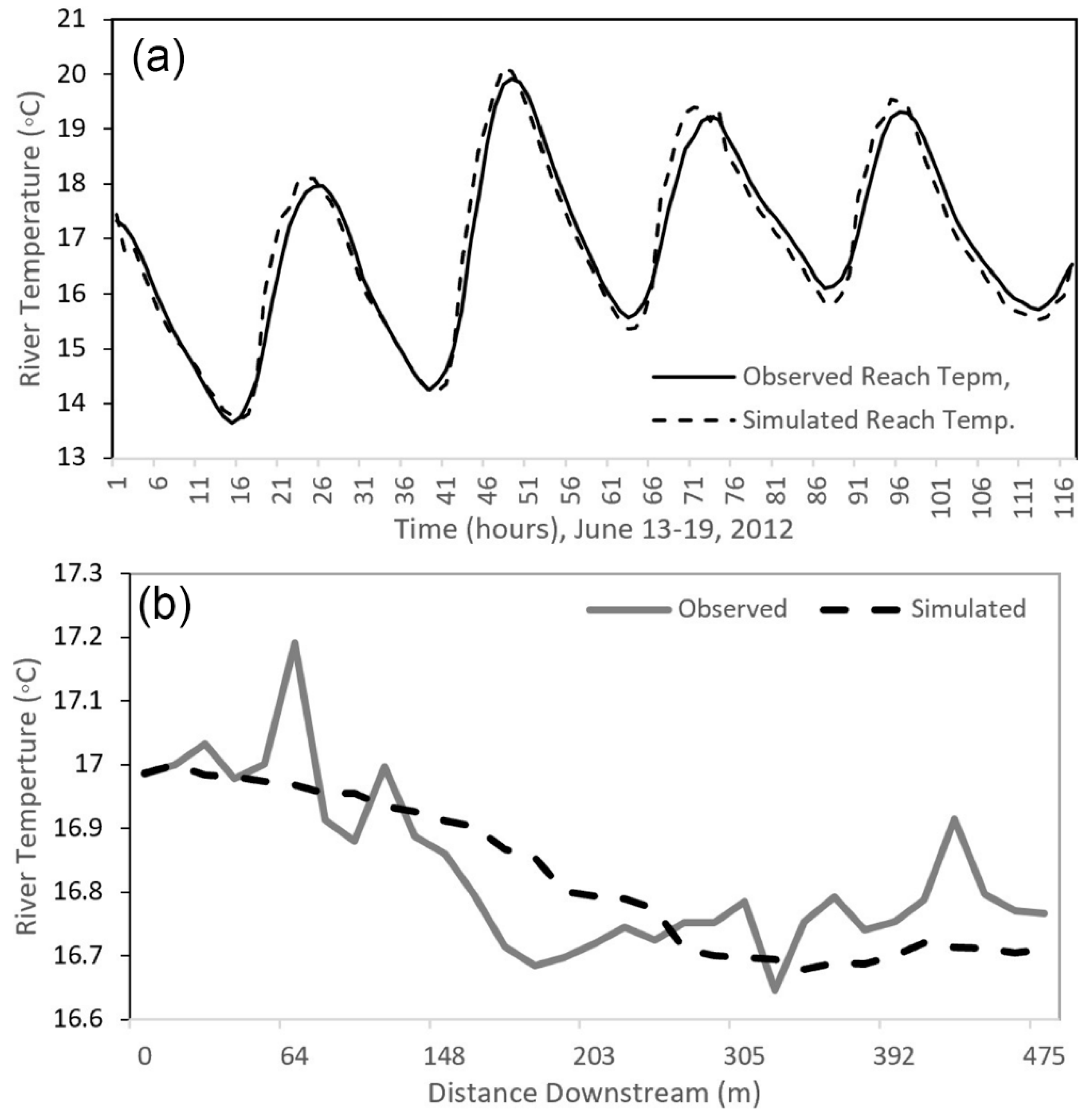
3.1. Model Evaluation
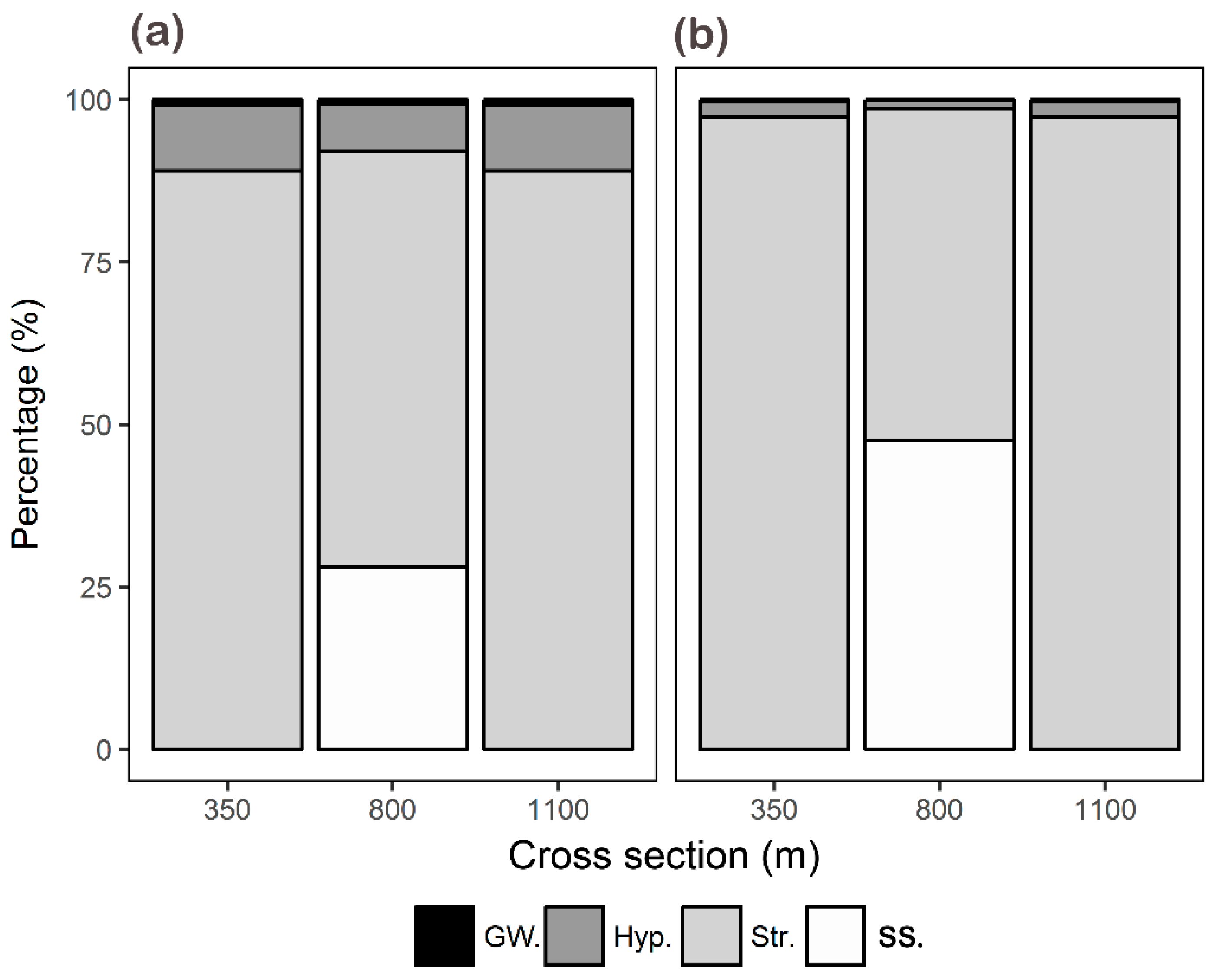
3.2. Sensitivity Analysis
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Herb, W.R.; Janke, B.; Mohseni, O.; Stefan, H.G. Thermal pollution of streams by runoff from paved surfaces. Hydrol. Process. 2008, 22, 987–999. [Google Scholar] [CrossRef]
- Parker, F.L.; Krenkel, P.A. Thermal Pollution: Status of the Art; Report 3; Department of Environmental and Resource Engineering, Vanderbilt University: Nashville, TN, USA, 1969. [Google Scholar]
- Wunderlich, T.E. Heat and Mass Transfer between a Water Surface and the Atmosphere; Report No. 14; Water Resources Research Laboratory, Tennessee Valley Authority: Norris Tennessee, TN, USA, 1972. [Google Scholar]
- Poshtiri, M.P.; Pal, I. Patterns of hydrological drought indicators in major U.S. River basins. Clim. Chang. 2016, 134, 549–563. [Google Scholar] [CrossRef]
- Deas, M.L.; Orlob, G.T. Klamath River Modeling Project and Appendices, Report No. 99–04; University of California: Davis, CA, USA, 1999; 376p. [Google Scholar]
- Langan, S.J.; Johnston, L.; Donaghy, M.J.; Youngson, F.; Hay, D.W.; Soulsby, C. Variation in river water temperatures in an upland stream over a 30-years period. Sci. Total Environ. 2001, 265, 195–207. [Google Scholar] [CrossRef]
- Abdi, R.; Yasi, M. Evaluation of environmental flow requirements using eco-hydrologic-hydraulic methods in perennial rivers. Water Sci. Technol. 2015, 72, 354–363. [Google Scholar] [CrossRef] [PubMed]
- Sand-Jensen, K.; Pedersen, N.L. Differences in temperature, organic carbon and oxygen consumption among lowland streams. Freshw. Biol. 2005, 50, 1927–1937. [Google Scholar] [CrossRef]
- Ficke, A.D.; Myrick, C.A.; Hansen, L.J. Potential impacts of global climate change on freshwater fisheries. Rev. Fish Biol. Fish. 2007, 17, 581–613. [Google Scholar] [CrossRef]
- Segura, C.; Caldwell, P.; Sun, G.; Mcnulty, S.; Zhang, Y. A model to predict stream water temperature across the conterminous USA. Hydrol. Process. 2015, 29, 2178–2195. [Google Scholar] [CrossRef]
- Elliott, J.M.; Hurley, M.A.; Fryer, R.J. A new, improved growth model for brown trout, Salmo trutta. Funct. Ecol. 1995, 9, 290–298. [Google Scholar] [CrossRef]
- Ahmadi-Nedushan, B.; St-Hilaire, A.; Quarda, T.B.M.J.; Bilodeau, L.; Robichaud, E.; Thiemonge, N.; Bobee, B. Predicting river water temperatures using stochastic models: Case study of the Moisie River (Quebec, Canada). Hydrol. Process. 2007, 21, 21–34. [Google Scholar] [CrossRef]
- LeBlanc, R.T.; Brown, R.D.; FitzGibbon, J.E. Modeling the effects of land use change on the water temperature in unregulated urban streams. Environ. Manag. 1997, 49, 445–469. [Google Scholar] [CrossRef]
- Chen, Y.D.; Carsel, R.F.; McCutcheon, S.C.; Nutter, W.L. Stream temperature simulation of forested riparian areas: I. Watershed-Scale model development. J. Environ. Eng. 1998, 124, 304–315. [Google Scholar] [CrossRef]
- Van Buren, M.; Watt, W.E.; Marsalek, J.; Anderson, B.C. Thermal enhancement of stormwater runoff by paved surfaces. Water Res. 2000, 34, 1359–1371. [Google Scholar] [CrossRef]
- Sridhar, V.; Sansone, A.L.; LaMarche, J.; Dubin, T.; Lettenmaier, D.P. Prediction of stream temperature in forested watersheds. J. Am. Water Resour. Assoc. 2004, 40, 197–213. [Google Scholar] [CrossRef]
- Herb, W.R.; Janke, B.; Mohseni, O.; Stefan, H.G. Runoff temperature model for paved surfaces. J. Hydrol. Eng. 2009, 14, 1146–1155. [Google Scholar] [CrossRef]
- Sun, N.; Yearsley, J.; Voisin, N.; Lettenmaier, D.P. A spatially distributed model for the assessment of land use impacts on stream temperature in small urban watersheds. Hydrol. Process. 2015, 29, 2331–2345. [Google Scholar] [CrossRef]
- Jones, M.P.; Hunt, W.F.; Winston, R.J. Effect of urban catchment composition on runoff temperature. J. Environ. Eng. 2012, 138, 1231–1236. [Google Scholar] [CrossRef]
- Hester, E.T.; Bauman, K.S. Stream and retention pond thermal response to heated summer Runoff from urban impervious surfaces. J. Am. Water Resour. Assoc. 2013, 49, 328–342. [Google Scholar] [CrossRef]
- Guzy, M.; Richardson, K.; Lambrinos, J.G. A tool for assisting municipalities in developing riparian shade inventories. Urban For. Urban Green. 2015, 14, 345–353. [Google Scholar] [CrossRef]
- Edinger, J.E.; Duttweil, D.; Geyer, J.C. Response of water temperatures to meteorological conditions. Water Resour. Res. 1968, 4, 1137–1143. [Google Scholar] [CrossRef]
- Aboelnour, M.; Engel, B.A. Application of remote sensing techniques and geographic information systems to analyze land surface temperature in response to land use/land cover change in greater Cairo region, Egypt. J. Geogr. Inf. Syst. 2018, 10, 57–88. [Google Scholar] [CrossRef]
- Caissie, D. The thermal regime of rivers: A review. Freshw. Biol. 2006, 51, 1389–1406. [Google Scholar] [CrossRef]
- Webb, B.; Zhang, Y. Spatial and seasonal variability in the components of the river heat budget. Hydrol. Process. 1997, 11, 79–101. [Google Scholar] [CrossRef]
- Nelson, K.; Palmer, M.A. Stream temperature surges under urbanization and climate change: Data, models, and responses. J. Am. Water Resour. Assoc. 2007, 43, 440–452. [Google Scholar] [CrossRef]
- Boyd, M.; Kasper, B. Analytical Methods for Dynamic Open Channel Heat and Mass Transfer: Methodology for Heat Source Model Version 7.0; Watershed Sciences Inc.: Portland, OR, USA, 2003. [Google Scholar]
- Yearsley, J.R. A semi-Lagrangian water temperature model for advection-dominated river systems. Water Resour. Res. 2009, 45, W12405. [Google Scholar] [CrossRef]
- Crispell, J.K. Hyporheic Exchange Flow around Stream Restoration Structures and the Effect of Hyporheic Exchange Flow on Stream Temperature. Master’ Thesis, College of Environmental Science and Forestry, State University of New York, Syracuse, NY, USA, 2008; 63p. [Google Scholar]
- Mohseni, O.; Stefan, H.G.; Erickson, T.R. A nonlinear regression model for weekly stream temperatures. Water Resour. Res. 1998, 34, 2685–2692. [Google Scholar] [CrossRef]
- Glose, A.; Lautz, L.K.; Baker, E.A. Stream heat budget modeling with HFLUX: Model development, evaluation, and applications across contrasting sites and seasons. Environ. Model. Softw. 2017, 92, 213–228. [Google Scholar] [CrossRef]
- Martin, J.L.; McCutcheon, S.C. Hydrodynamics and Transport for Water Quality Modeling; Lewis Publishers: New York, NY, USA, 1999. [Google Scholar]
- Kustas, W.P.; Rango, A.; Uijlenhoet, R. A simple energy budget algorithm for the snowmelt runoff model. Water Resour. Res. 1994, 30, 1515–1527. [Google Scholar] [CrossRef]
- Dingman, S.L. Physical Hydrology; Prentice-Hall Inc.: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- Westhoff, M.C.; Savenije, H.H.G.; Luxemburg, W.M.J.; Stelling, G.S.; Van De Giesen, N.C.; Selker, J.S. Sciences A distributed stream temperature model using high-resolution temperature observations. Hydrol. Earth Syst. Sci. 2007, 11, 1469–1480. [Google Scholar] [CrossRef]
- Benyahya, L.; Caissie, D.; El-jabi, N.; Satish, M.G. Comparison of microclimate vs. remote meteorological data and results applied to a water temperature model (Miramichi River, Canada). J. Hydrol. 2010, 380, 247–259. [Google Scholar] [CrossRef]
- Wolman, M.G. A method of sampling coarse bed material. Trans. Am. Geophys. Union 1954, 35, 951–956. [Google Scholar] [CrossRef]
- Yang, Y.; Endreny, T.A.; Nowak, D.J. iTree-Hydro: Snow hydrology update for the urban forest hydrology model. J. Am. Water Resour. Assoc. 2011, 47, 1211–1218. [Google Scholar] [CrossRef]
- Memon, R.A.; Leung, D.Y.C.; Liu, C.H.; Leung, M.K.H. Urban heat island and its effect on the cooling and heating demands in urban and suburban areas of Hong Kong. Theor. Appl. Climatol. 2011, 103, 441–450. [Google Scholar] [CrossRef]
- Hathaway, J.M.; Winston, R.J.; Brown, R.A.; Hunt, W.F.; McCarthy, D.T. Temperature dynamics of stormwater runoff in Australia and the USA. Sci. Total Environ. 2016, 559, 141–150. [Google Scholar] [CrossRef]
- Somers, K.A.; Bernhardt, E.S.; Grace, J.B.; Hassett, B.A.; Sudduth, E.B.; Wang, S.; Urban, D.L. Streams in the urban heat island: Spatial and temporal variability in temperature. Freshw. Sci. 2013, 32, 309–326. [Google Scholar] [CrossRef]
- Beven, K. So how much of your error is epistemic? Lessons from Japan and Italy. Hydrol. Process. 2013, 27, 1677–1680. [Google Scholar] [CrossRef]
- Crispell, J.K.; Endreny, T.A. Hyporheic exchange flow around constructed in-channel structures and implications for restoration design. Hydrol. Process. 2009, 23, 2267–2274. [Google Scholar] [CrossRef]
- Hester, E.T.; Doyle, M.W.; Poole, G.C. The influence of in-stream structures on summer water temperatures via induced hyporheic exchange. Limnol. Oceanogr. 2009, 54, 355–367. [Google Scholar] [CrossRef]
- Loheide, S.P.; Gorelick, S.M. Quantifying stream−Aquifer interactions through the analysis of remotely sensed thermographic profiles and in situ temperature histories. Environ. Sci. Technol. 2006, 40, 3336–3341. [Google Scholar] [CrossRef]
- Risley, J.C.; Constantz, J.; Essaid, H.; Rounds, S. Effects of upstream dams versus groundwater pumping on stream temperature under varying climate conditions. Water Resour. Res. 2010, 46, W06517. [Google Scholar] [CrossRef]
- Kurylyk, B.L.; Moore, R.D.; Macquarrie, K.T.B. Scientific briefing: Quantifying streambed heat advection associated with groundwater-surface water interactions. Hydrol. Process. 2016, 30, 987–992. [Google Scholar] [CrossRef]
- Poole, G.C.; Berman, C.H. An ecological perspective on in-stream temperature: Natural heat dynamics and mechanisms of human-caused thermal degradation. Environ. Manag. 2001, 27, 787–802. [Google Scholar] [CrossRef]
- Roth, T.R.; Westhoff, M.C.; Huwald, H.; Huff, J.A.; Rubin, J.F.; Barrenetxea, G.; Vetterli, M.; Parriaux, A.; Selker, S.; Parlange, M.B. Stream temperature response to three riparian vegetation scenarios by use of a distributed temperature validated model. Environ. Sci. Technol. 2010, 44, 2072–2078. [Google Scholar] [CrossRef] [PubMed]
- Guoyuan, L.; Jackson, C.; Kraseski, K. Modeled riparian stream shading: Agreement with field measurements and sensitivity to riparian conditions. J. Hydrol. 2012, 428, 142–151. [Google Scholar]
- Lee, T.Y.; Huang, J.C.; Kao, S.J.; Liao, L.Y.; Tzeng, C.S.; Yang, C.H.; Kalita, P.K.; Tung, C.P. Modeling the effects of riparian planting strategies on stream temperature: Increasing suitable habitat for endangered Formosan Landlocked Salmon in Shei-Pa National Park, Taiwan. Hydrol. Process. 2012, 26, 3635–3644. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdi, R.; Endreny, T. A River Temperature Model to Assist Managers in Identifying Thermal Pollution Causes and Solutions. Water 2019, 11, 1060. https://doi.org/10.3390/w11051060
Abdi R, Endreny T. A River Temperature Model to Assist Managers in Identifying Thermal Pollution Causes and Solutions. Water. 2019; 11(5):1060. https://doi.org/10.3390/w11051060
Chicago/Turabian StyleAbdi, Reza, and Theodore Endreny. 2019. "A River Temperature Model to Assist Managers in Identifying Thermal Pollution Causes and Solutions" Water 11, no. 5: 1060. https://doi.org/10.3390/w11051060
APA StyleAbdi, R., & Endreny, T. (2019). A River Temperature Model to Assist Managers in Identifying Thermal Pollution Causes and Solutions. Water, 11(5), 1060. https://doi.org/10.3390/w11051060





