Physical Modeling of Spatial and Temporal Development of Local Scour at the Downstream of Bed Protection for Low Froude Number
Abstract
:1. Introduction
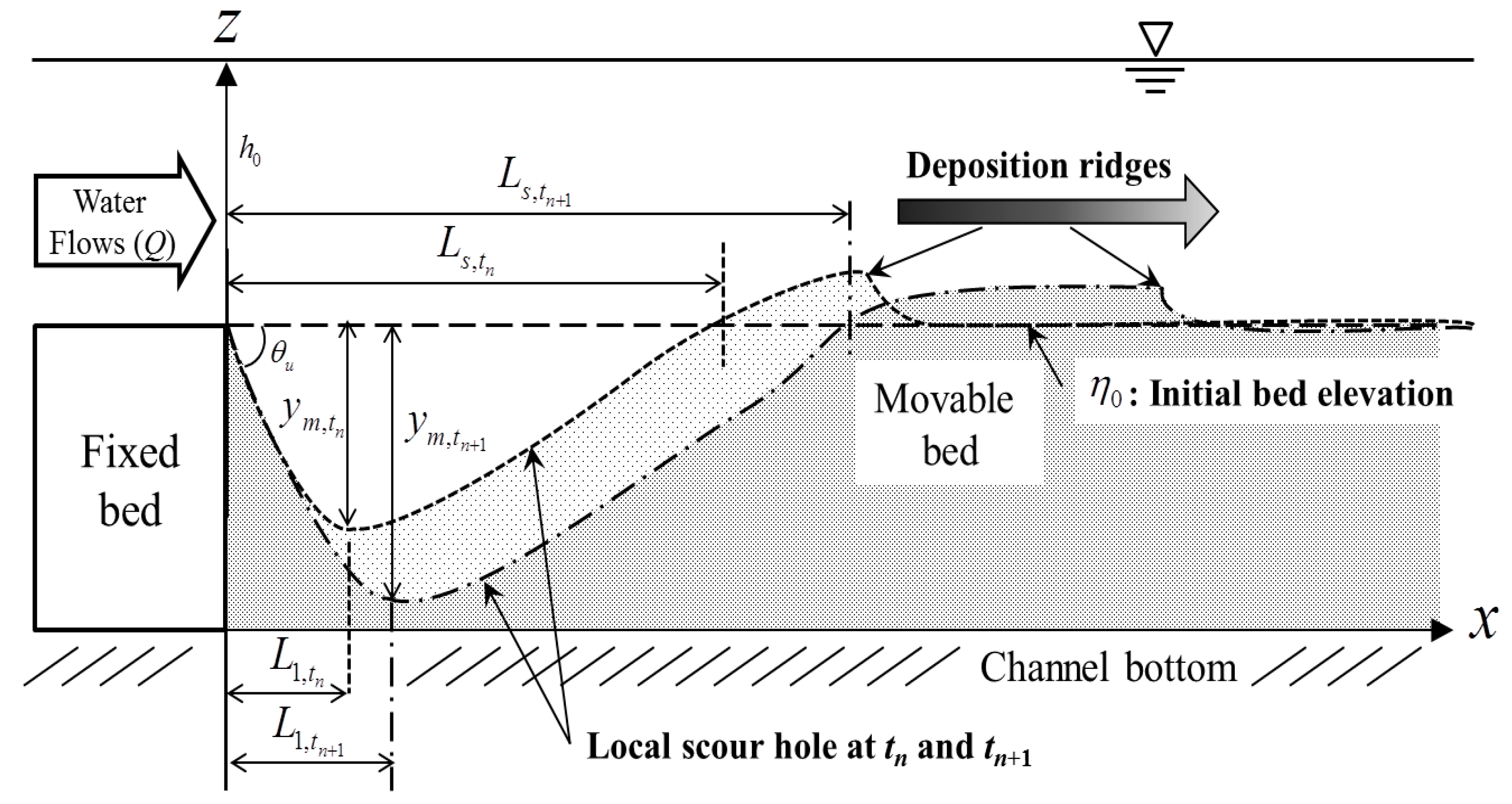
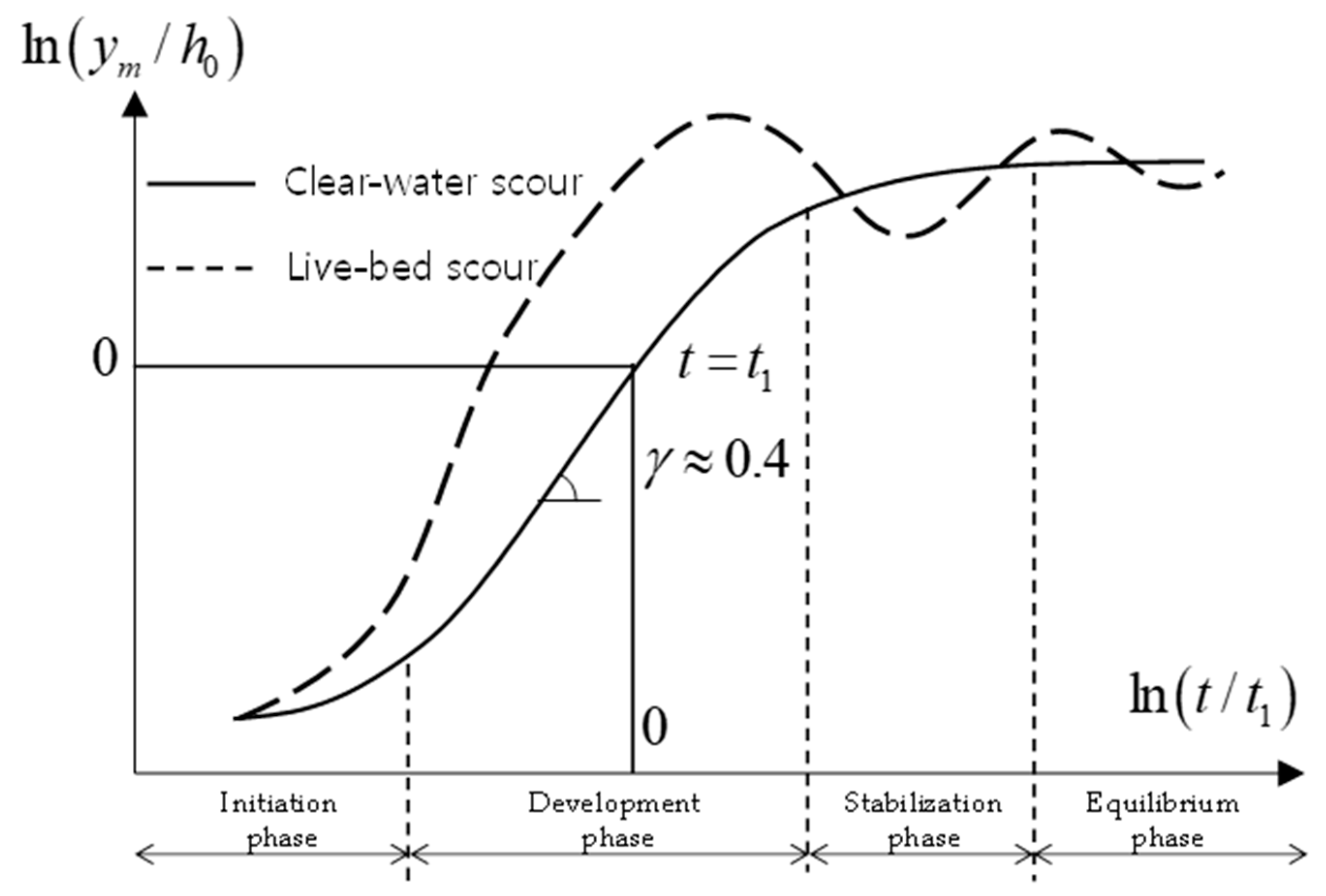
2. Local Scouring and Its Process
3. Materials and Methods
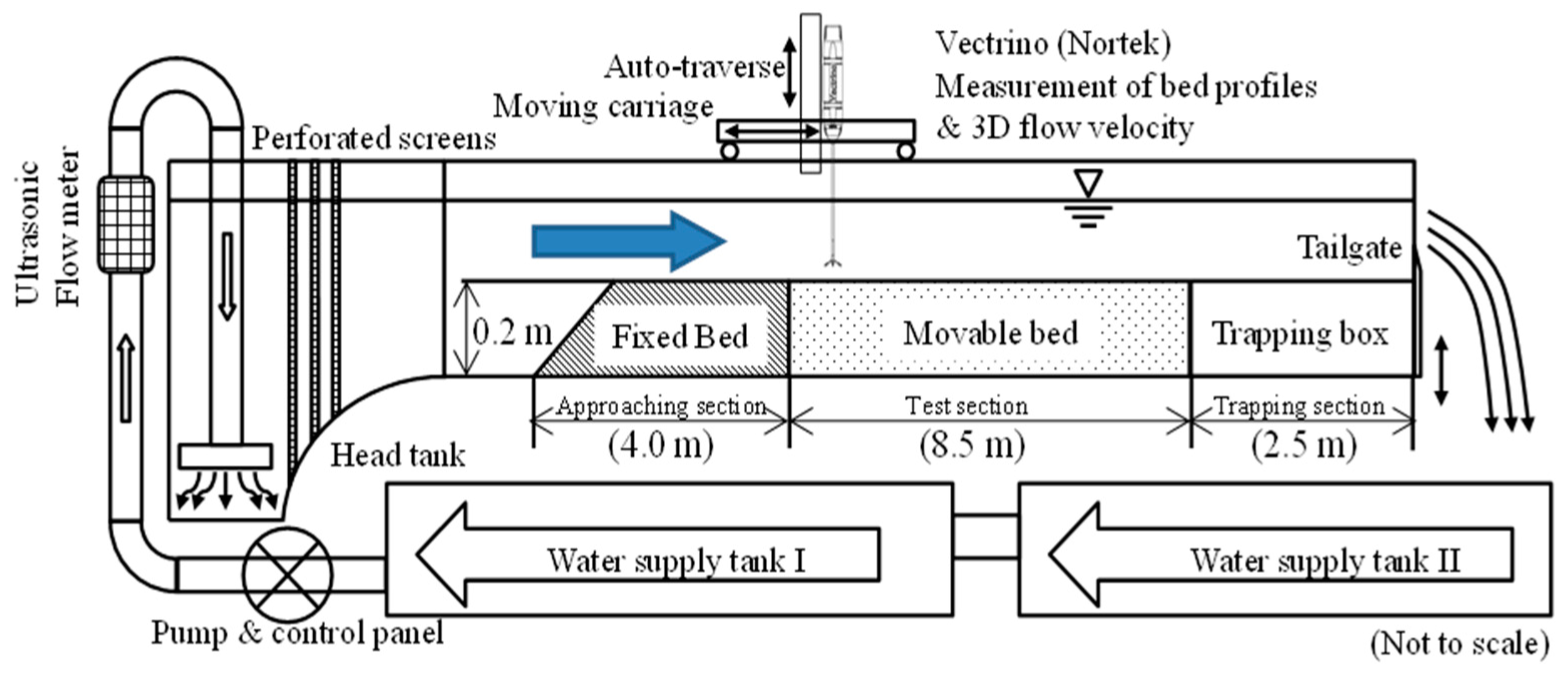
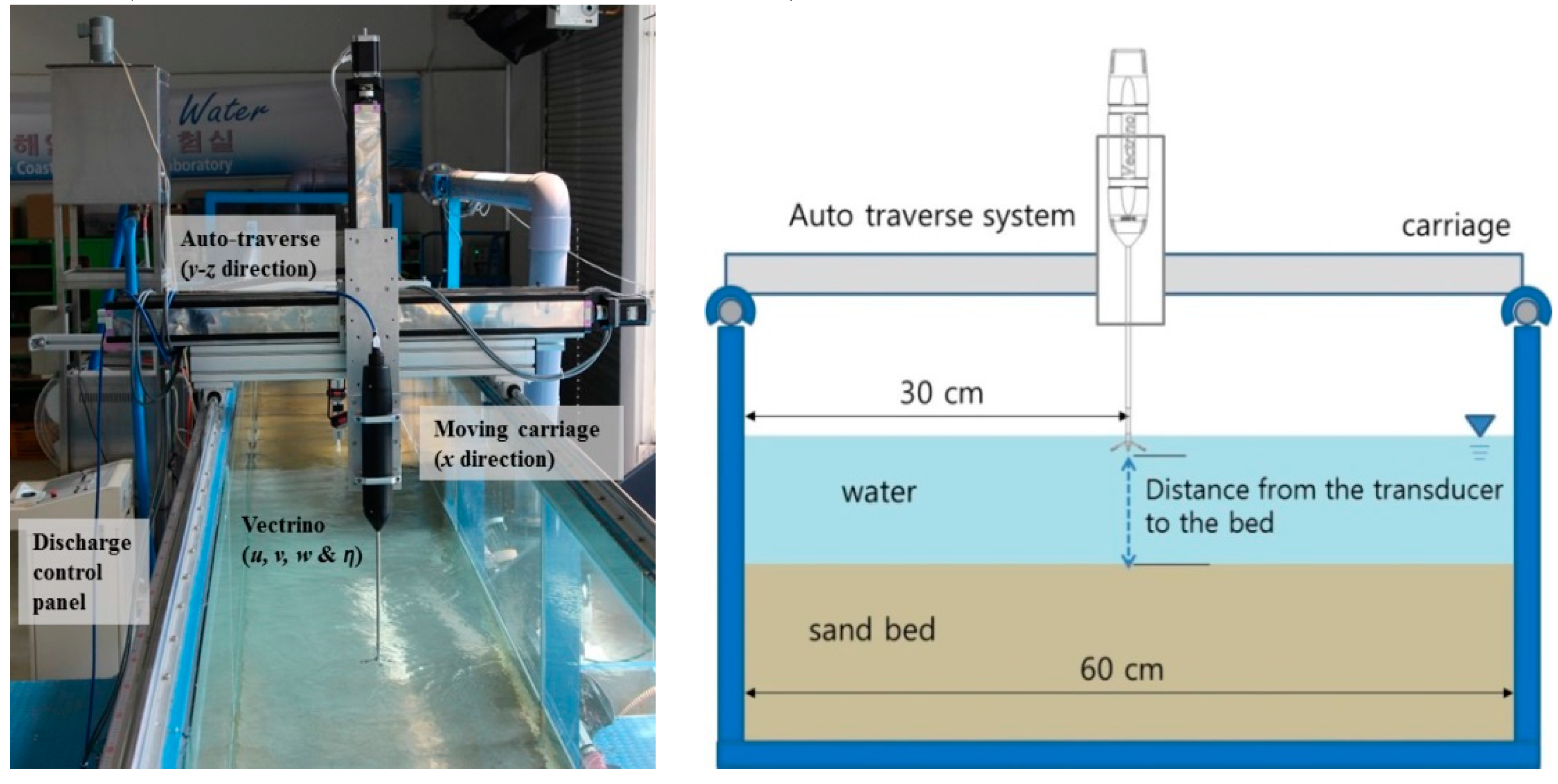
3.1. Laboratory Flume and Measurement Devices
3.2. Test Procedures and Hydraulic Conditions
4. Experimental Results
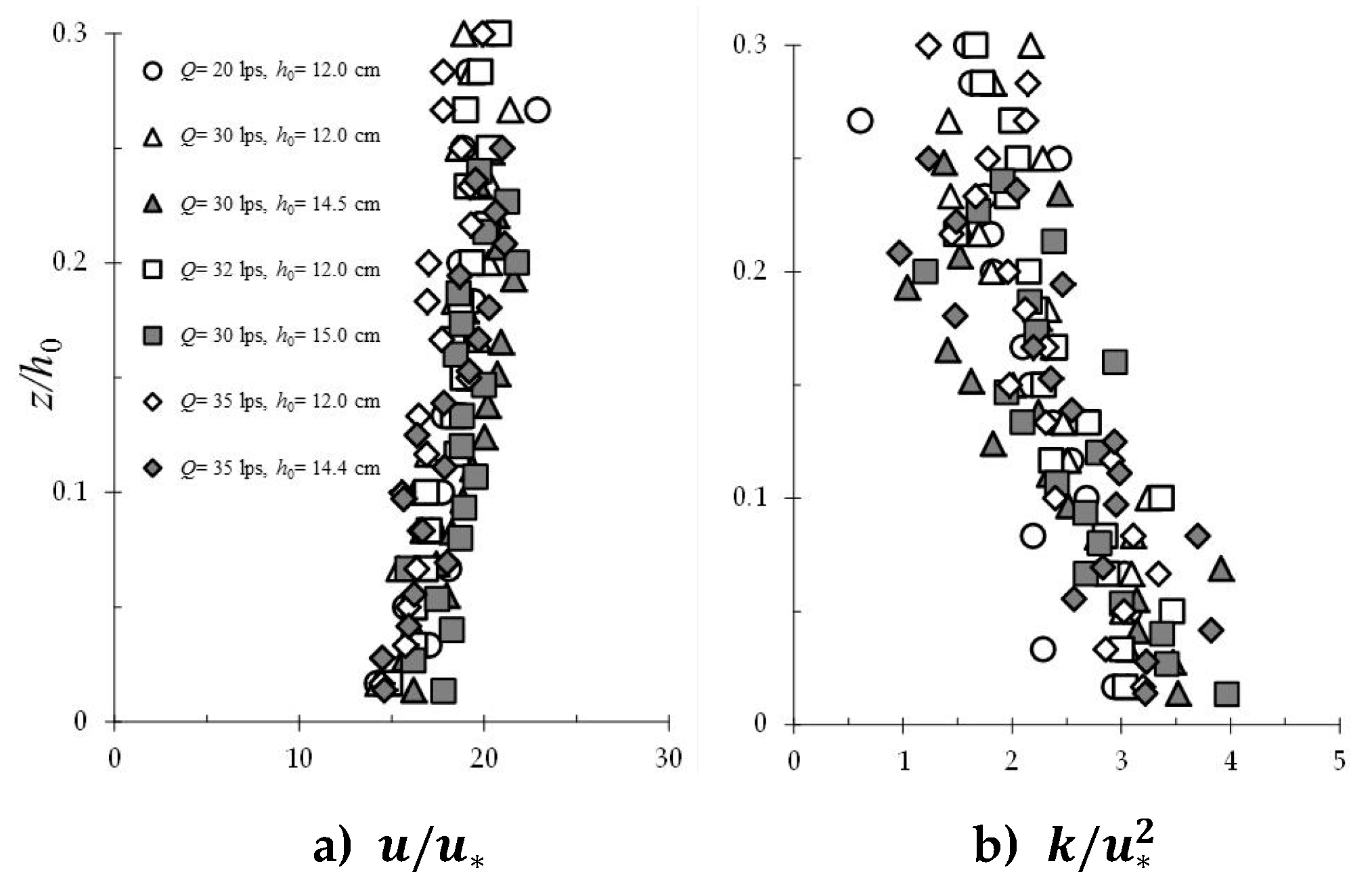
4.1. Flow and Sediment Characteristics
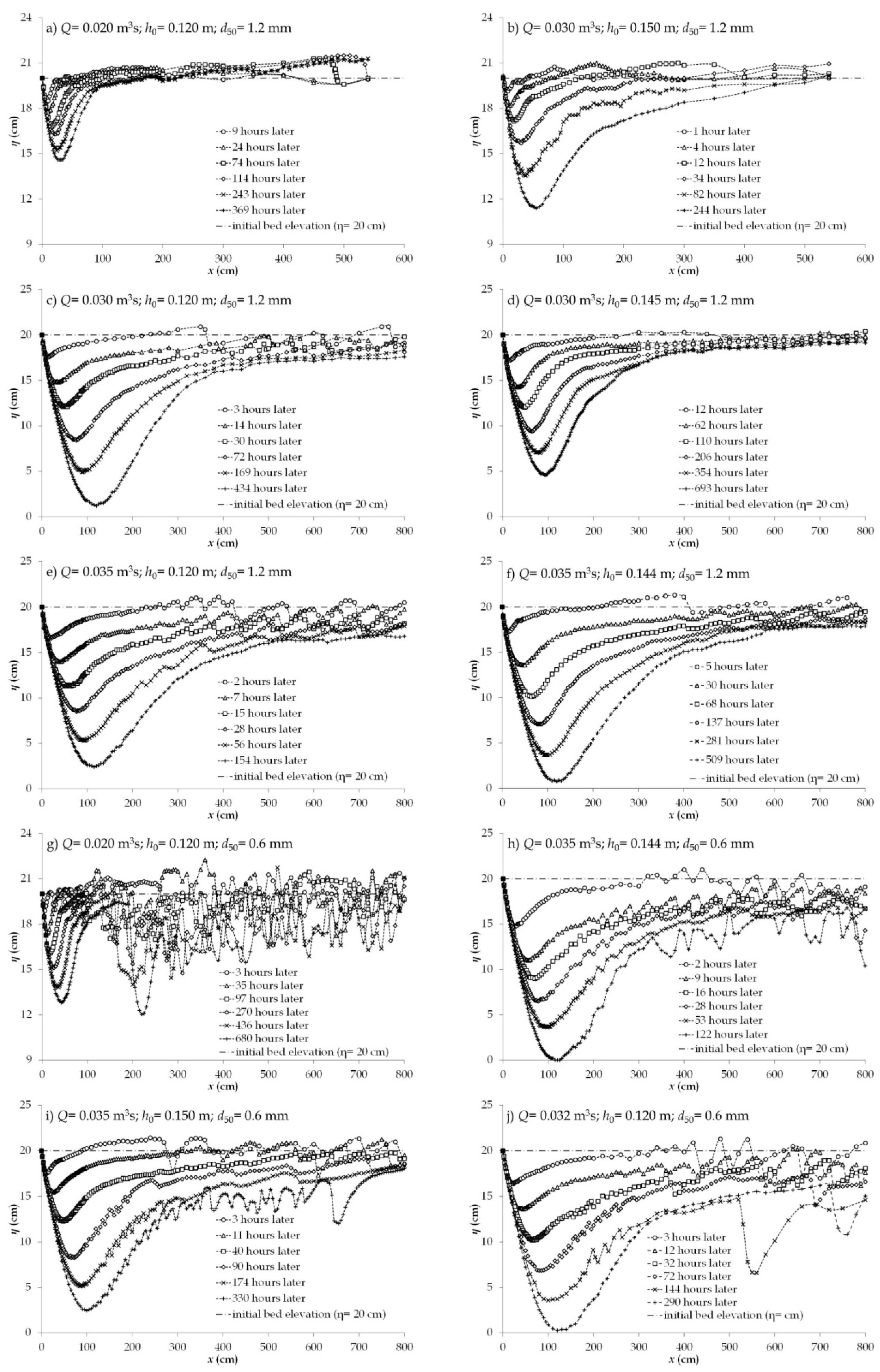
4.2. Development of Scour Hole and Maximum Scour Depth
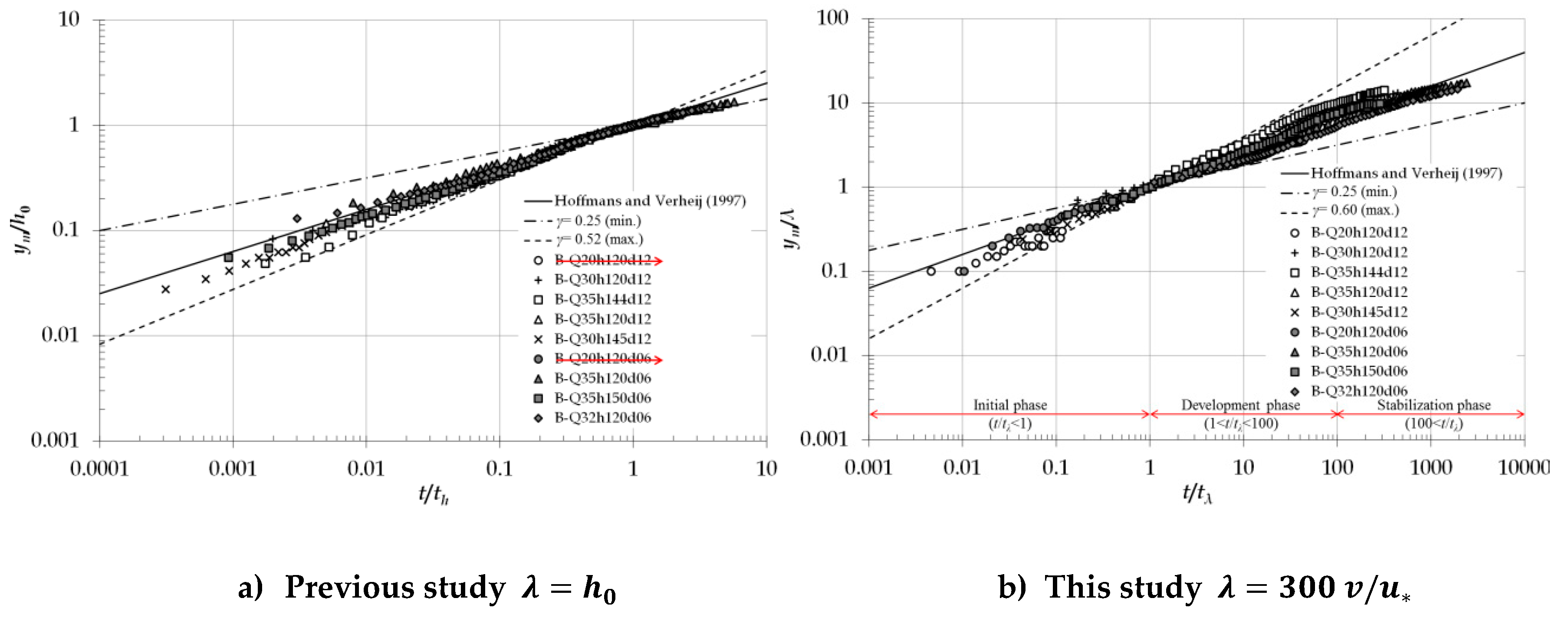
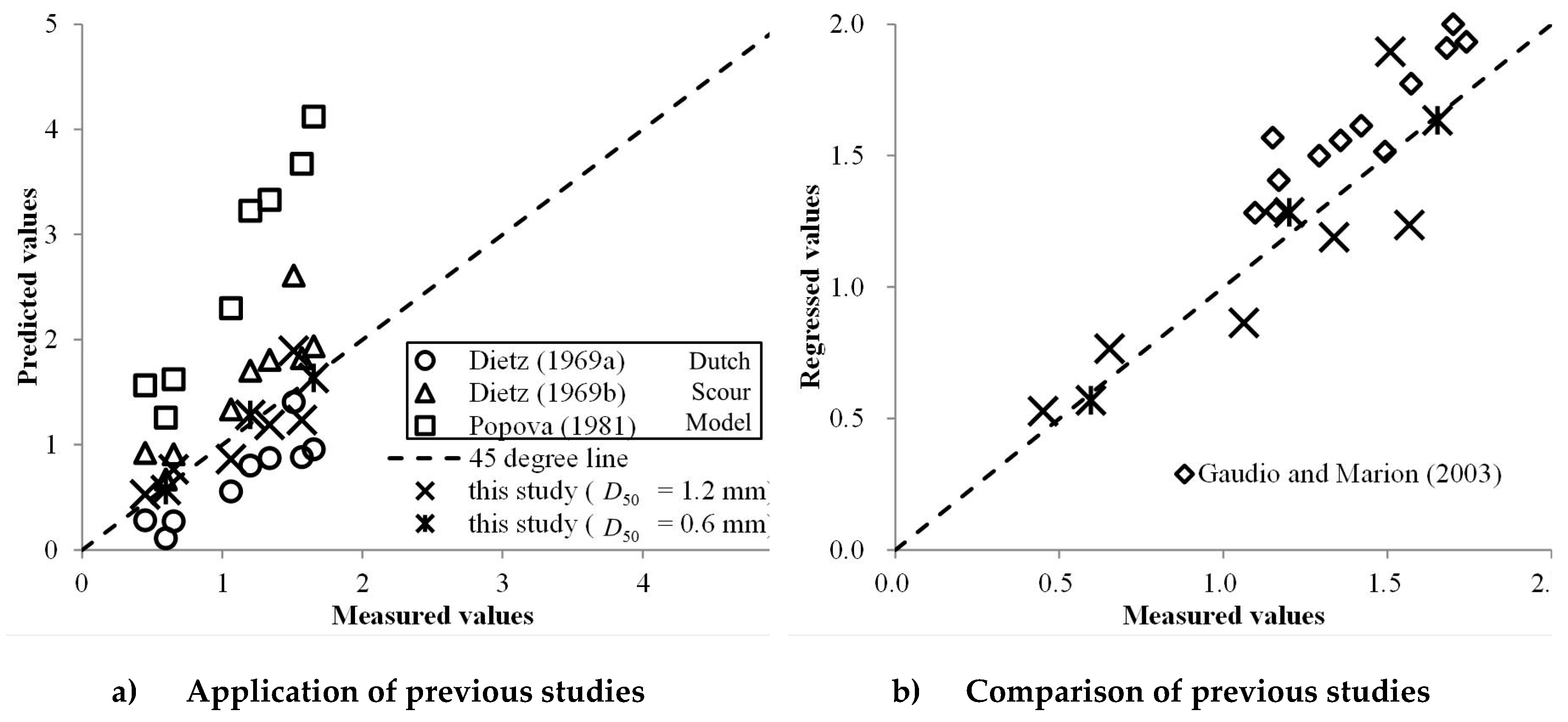
4.3. Equilibrium Maximum Scour Depth
5. Conclusions and Remarks
- Laboratory experiments on local scouring at the downstream of fixed bed model were carried out with relatively lower Froude number (less than 0.5) than those of the previous study by Gaudio and Marion [16] and therefore, the total duration of the experiments have exceeded 700 hours. As previous researches have suggested, dominant shapes of local scouring at the downstream of the fixed bed were characterized with time. The upstream scour slope at the downstream of fixed bed reached its equilibrium value earlier than other dimensions and the developments of the scoured hole were gradually increased with time and reached to the equilibrium state. At downstream of the scoured hole, eroded sediment particles were deposited and propagated toward downstream.
- Temporal development of maximum scour depth, which should have dominantly been considered for the design of the various hydraulic structures in rivers and streams, was analyzed with more reasonable dimensionless time and length scales and classified into the four-time step of the local scour development with revision of previous studies. And the relationship between dimensionless time and length scale of the maximum scour depth in development phase was revealed as the exponential function with exponent equals approximately 0.4. Also, with this modified relationship is applicable to both deep and shallow water depth cases.
- Values of scouring rates of finer sediment cases were larger than those of coarser cases. Therefore, design and construction of hydraulic structures in the rivers and streams near the finer bed materials should be considered with excessive local scouring in short time. Additional experimental researches about various Froude number and sediment size will be compared with this research and empirical equation can be modified.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hoffmans, G.J.C.M. A Study Concerning the Influence of the Relative Turbulence Intensity on Local-Scour Holes; Report W-DWW-93-251; Delft Hydraulics: Delft, The Netherlands, 1993. [Google Scholar]
- Breusers, H.N.C. Time scale of two-dimensional local scour. In Proceedings of the 12th IAHR-Congress, Fort Collins, CO, USA, 11–14 September 1967; pp. 275–282. [Google Scholar]
- Dietz, J.W. Kolkbildung in Feinen Oder Leichten Sohlmaterialien bei Strömendem Abfluβ; Mitteilungen, Heft 155; Universität Fridericiana Karlsruhe: Karlsruhe, Germany, 1969. [Google Scholar]
- Van der Meulen, T.; Vinjé, J.J. Three-dimensional local scour in non-cohesive sediments. In Proceedings of the 16th IAHR-Congress, San Paulo, Brasil, 27 July–1 August 1975. [Google Scholar]
- Buchko, M.; Kolkman, P.; Pilarczyk, K. Investigation of local scour in cohesionless sediments using a tunnel-model. In Proceedings of the IAHR-Congress, Topics in Hydraulic Modeling, Lausanne, Switzerland, 31 August–4 September 1987; pp. 233–239. [Google Scholar]
- Hoffmans, G.J.C.M.; Verheij, H.J. Scour Manual; Taylor and Francis Group: Milton, Abingdon, UK, 1997. [Google Scholar]
- Balachandar, R.; Kells, J.A. Local channel scour in uniformly graded sediments: The time-scale problem. Can. J. Civ. Eng. 1997, 24, 799–807. [Google Scholar] [CrossRef]
- Lenzi, M.A.; Marion, A.; Comiti, F. Interference processes on scouring at bed sills. Earth Surf. Process Landf. 2003, 28, 99–110. [Google Scholar] [CrossRef]
- Amoudry, L.O.; Liu, P.L.-F. Two-dimensional, two phase granular sediment transport model with applications to scouring downstream of an apron. Coast. Eng. 2009, 56, 693–702. [Google Scholar] [CrossRef]
- Termini, D. Bed Scouring downstream of hydraulic structures under steady flow conditions: Experimental analysis of space and time scales and implications for mathematical modeling. CATENA 2011, 84, 125–135. [Google Scholar] [CrossRef]
- Meftah, M.B.; Mossa, M. Scour holes downstream of bed sills in low-gradient channels. J. Hydraul. Res. 2006, 44, 497–509. [Google Scholar] [CrossRef]
- Hoffmans, G.J.C.M.; Pilarczyk, K.W. Local scour downstream of hydraulic structures. J. Hydraul. Eng. 1995, 121, 326–340. [Google Scholar] [CrossRef]
- Mosonyi, E.; Schoppmann, B. Ein Beitrag zur Erforschung von Örtlichen Auskolkungen Hinter Geneigten Befestigungsstrecken in Abhängigkeit der Zeit, Mit-Teilungen des Teodor-Rehbock-Fluβbaulaboratoriums; Universität Karlsruhe: Karlsruhe, Germany, 1968. [Google Scholar]
- Popova, K.S. Recommendations on Computations of Local Erosiocn in Channels Consisting of Non-Rock Soil, Downstream of Revetments on Medium-Head Spillway Dams; VNIIG, Hydraulic Laboratory: St. Petersburg, Russia, 1981. [Google Scholar]
- Gaudio, R.; Marion, A.; Bovolin, V. Morphological effects of bed sills in degrading rivers. J. Hydraul. Res. 2000, 38, 89–96. [Google Scholar] [CrossRef]
- Gaudio, R.; Marion, A. Time evolution of scouring downstream of bed sills. J. Hydraul. Res. 2003, 41, 271–284. [Google Scholar] [CrossRef]
- Park, S.W. Experimental Study of Local Scouring at the Downstream of River Bed Protection. Ph.D. Thesis, Seoul National University, Seoul, Korea, 2016. [Google Scholar]
- Kundu, P.K.; Cohen, I.M. Fluid Mechanics, 4th ed.; Academic Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Graf, W.H. Fluvial Hydraulics: Flow and Transport Processes in Channels of Simple Geometry; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]

| Case Number | Q (m3/s) | h0 (m) | d50 (mm) | U0 (m/s) | Fr (-) | Rh (m) | Re (×105) |
|---|---|---|---|---|---|---|---|
| Q20h120d12 | 0.020 | 0.120 | 1.2 | 0.278 | 0.256 | 0.086 | 0.333 |
| Q30h150d12 | 0.030 | 0.150 | 0.333 | 0.275 | 0.100 | 0.500 | |
| Q30h120d12 | 0.030 | 0.120 | 0.417 | 0.384 | 0.086 | 0.500 | |
| Q35h120d12 | 0.035 | 0.120 | 0.486 | 0.448 | 0.086 | 0.583 | |
| Q35h144d12 | 0.035 | 0.144 | 0.405 | 0.341 | 0.097 | 0.583 | |
| Q30h145d12 | 0.030 | 0.145 | 0.345 | 0.289 | 0.098 | 0.500 | |
| Q20h120d06 | 0.020 | 0.120 | 0.6 | 0.278 | 0.256 | 0.086 | 0.333 |
| Q35h120d06 | 0.035 | 0.120 | 0.486 | 0.448 | 0.086 | 0.583 | |
| Q35h150d06 | 0.035 | 0.150 | 0.389 | 0.321 | 0.100 | 0.583 | |
| Q32h120d06 | 0.032 | 0.120 | 0.445 | 0.410 | 0.086 | 0.533 |
| Case Number | (-) | (-) | (m/s) | (Pa) | Re∗(-) | T (hr.) | (Observed, m) |
|---|---|---|---|---|---|---|---|
| Q20h120d12 | 0.073 | 2.55 | 0.015 | 0.29 | 18.0 | 369 | 0.054 |
| Q30h150d12 | 0.054 | 3.03 | 0.018 | 0.23 | 20.4 | 314 | 0.098 |
| Q30h120d12 | 0.055 | 3.12 | 0.021 | 0.44 | 25.2 | 434 | 0.188 |
| Q35h120d12 | 0.054 | 3.34 | 0.026 | 0.68 | 31.2 | 154 | 0.181 |
| Q35h144d12 | 0.056 | 3.21 | 0.022 | 0.48 | 26.4 | 509 | 0.193 |
| Q30h145d12 | 0.059 | 3.16 | 0.018 | 0.32 | 21.6 | 717 | 0.154 |
| Q20h120d06 | 0.073 | 3.07 | 0.015 | 0.23 | 9.0 | 700 | 0.072 |
| Q35h120d06 | 0.054 | 2.92 | 0.026 | 0.68 | 15.6 | 120 | 0.200 |
| Q35h150d06 | 0.057 | 2.89 | 0.020 | 0.40 | 12.0 | 358 | 0.173 |
| Q32h120d06 | 0.057 | 3.08 | 0.022 | 0.48 | 13.2 | 289 | 0.198 |
| Case Number | λ (m) | tλ (Hour) | γ (-) | (m/s) | (m/s) | (Calculated, m) |
|---|---|---|---|---|---|---|
| Q20h120d12 | 0.020 | 18.0 | 0.439 | 0.021 | 0.26 | 0.12 |
| Q30h150d12 | 0.017 | 3.80 | 0.400 | 0.023 | 0.30 | 0.18 |
| Q30h120d12 | 0.014 | 0.98 | 0.425 | 0.022 | 0.28 | 0.31 |
| Q35h120d12 | 0.012 | 0.10 | 0.458 | 0.019 | 0.24 | 0.51 |
| Q35h144d12 | 0.014 | 1.60 | 0.463 | 0.023 | 0.30 | 0.29 |
| Q30h145d12 | 0.016 | 3.80 | 0.408 | 0.023 | 0.30 | 0.19 |
| Q20h120d06 | 0.020 | 16.0 | 0.366 | 0.018 | 0.26 | 0.11 |
| Q35h120d06 | 0.012 | 0.05 | 0.356 | 0.016 | 0.23 | 0.55 |
| Q35h150d06 | 0.018 | 1.25 | 0.425 | 0.018 | 0.27 | 0.32 |
| Q32h120d06 | 0.014 | 0.15 | 0.378 | 0.017 | 0.24 | 0.42 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.W.; Hwang, J.H.; Ahn, J. Physical Modeling of Spatial and Temporal Development of Local Scour at the Downstream of Bed Protection for Low Froude Number. Water 2019, 11, 1041. https://doi.org/10.3390/w11051041
Park SW, Hwang JH, Ahn J. Physical Modeling of Spatial and Temporal Development of Local Scour at the Downstream of Bed Protection for Low Froude Number. Water. 2019; 11(5):1041. https://doi.org/10.3390/w11051041
Chicago/Turabian StylePark, Sung Won, Jin Hwan Hwang, and Jungkyu Ahn. 2019. "Physical Modeling of Spatial and Temporal Development of Local Scour at the Downstream of Bed Protection for Low Froude Number" Water 11, no. 5: 1041. https://doi.org/10.3390/w11051041
APA StylePark, S. W., Hwang, J. H., & Ahn, J. (2019). Physical Modeling of Spatial and Temporal Development of Local Scour at the Downstream of Bed Protection for Low Froude Number. Water, 11(5), 1041. https://doi.org/10.3390/w11051041





