Abstract
Wave overtopping—i.e., excess of water over the crest of a coastal protection infrastructure due to wave run-up—of a smooth slope can be reduced by introducing slope roughness. A stepped revetment ideally constitutes a slope with uniform roughness and can reduce overtopping volumes of breaking waves up to 60% compared to a smooth slope. The effectiveness of the overtopping reduction decreases with increasing Iribarren number. However, to date a unique approach applicable for a wide range of boundary conditions is still missing. The present paper: (i) critically reviews and analyzes previous findings; (ii) contributes new results from extensive model tests addressing present knowledge gaps; and (iii) proposes a novel empirical formulation for robust prediction of wave overtopping of stepped revetments for breaking and non-breaking waves. The developed approach contrasts a critical assessment based on parameter ranges disclosed beforehand between a smooth slope on the one hand and a plain vertical wall on the other. The derived roughness reduction coefficient is developed and adjusted for a direct incorporation into the present design guidelines. Underlying uncertainties due to scatter of the results are addressed and quantified. Scale effects are highlighted.
1. Introduction
Traditionally, the main purpose of a coastal structure is to provide coastal safety, taking into account constraints from urban development, environmental compatibility and costs. However, in recent years, increasing emphasis has been placed on the secondary purposes of coastal structures, e.g., tourism and recreation [1,2]. As a result, a coastal protection system ideally combines secondary purposes without affecting its main purpose of providing protection against storm surges. A stepped revetment can be built with steep slopes and thus could have a relatively small footprint. These steep slopes can be easily and safely accessed, thus shaping the concept and realization of stepped revetments an appealing multi-functional coastal structure.
A number of scientific studies has proven the ability of a stepped revetment to reduce wave run-up and wave overtopping [3,4,5,6,7,8,9,10,11]. The results of these studies are partly inconclusive, mainly due to the variable hydraulic- and geometric boundary conditions from which conclusions on reduction were determined. The present paper is mainly based on findings from [8] incorporating findings from more recent studies [9,12].
To the authors’ knowledge this paper embraces the first systematic comparison of the influence of stepped revetments to reduce wave overtopping. The study considers a broad range of hydraulic and structure-related parameters, i.e., breaking and non-breaking wave conditions, slope gradients between 1:1 to 1:6 and step heights much smaller and much larger than the spectral significant wave height. In addition to the data sets collected in physical modelling studies at the Ludwig Franzius Institute, data sets from two other laboratories are included in the analysis and results. These data sets are based on comparable experimental setups, and model effects of individual studies are, therefore, incorporated.
The aim of the present paper is the empirical derivation of a roughness reduction coefficient for wave overtopping on stepped revetments in relation to a smooth slope for breaking and non-breaking wave conditions following [13].
The paper is structured as follows: first the influence and determination of the roughness of a revetment with special focus to stepped slopes is presented and discussed. In Section 2 the experimental set-up, test procedure and conditions of the conducted model tests are described. Section 3 follows with the documentation of the results gained. The analysis of the overtopping performance of stepped revetments in comparison to smooth slopes is conducted in Section 4. The governing processes of the energy dissipation over stepped slopes are discussed in Section 5 in the context of findings from existing literature. Model and scale-effects are discussed. In conclusion, Section 6 summarizes the main findings and gives an outlook of future research. A brief description of the technical background on the harmonization of data sets, parameter definitions and the wave overtopping prediction according to EurOtop (2018) [13] under consideration of the surface roughness is provided in Appendix A.
1.1. Surface Roughness of Stepped Revetments
Drivers and processes of wave-induced responses of stepped revetments have been studied in the discipline of coastal engineering over the last 100 years. A comprehensive literature review on hydraulic model tests related to stepped revetments with focus on wave run-up, wave overtopping and scour development at the toe of such revetments is provided by Kerpen and Schlurmann (2016) [14]. The review includes the main findings from numerous studies [3,4,5,6,7,15] and others. For regular waves, a prediction of the mean overtopping discharges on stepped revetments is derived [16]. Literature studies, focusing particularly on physical model tests on the wave run-up or wave overtopping by irregular waves at stepped revetments (without influence of parapets as data sets provided [7,11,17]) are summarized hereafter.
Overtopping data for a stepped revetment was provided by Goda and Kishira (1976) [6] with a revetment slope of with foreshores of two different gradients (1:10 and 1:30). The still water level (SWL) of the set-up was located at the toe of the stepped revetment (i.e., at the end of the inclined foreshore with smooth surface). Hence, only broken waves reached the stepped revetment and caused overtopping. This study provided data for relatively large dimensionless step heights (with as spectral wave height and depicting the step height of the revetment), and therefore it was included in the analysis after being corrected for the effect of broken waves. A roughness influence factor of for relatively large dimensionless step heights and broken waves with a narrow band of deep water Iribarren number in the range of was provided. As the step heights Sh {0.006 m, 0.009 m} in the model tests were relatively small induced by the scale of 1:33.3 these data are influenced by scale effects. Data for the mean wave period were converted for the present analysis according to Equations (7) and (8) to ensure that this data set was comparable. The wave data was then further processed with Equation (A1).
A data set of wave overtopping at stepped revetment with smaller dimensionless step heights was provided by Melby et al. (2009) [18]. Below the SWL (with the vertical coordinate ) the stepped revetment continued up to a distance of . Below this value, the slope is modelled as smooth slope. The freeboard height in the tests was gradually increased by adding additional steps on the crest, until an overtopping volume less than a certain target was measured. The corresponding roughness reduction coefficient of this study was .
A comprehensive study and comparison of different data sets of wave run-up and wave overtopping in regular and irregular waves was provided by Kerpen (2017) [8]. This data set covered a wide range of application (). However, because of slightly better coefficients of determination, the roughness influence factors for the wave run-up were calculated relative to the smooth slope prediction by Schüttrumpf (2001) [19]. To enable a standardized implementation of the roughness influence factor in the EurOtop (2018) formulae [13], the present paper incorporates the measured overtopping values accordingly.
The work of Van Steeg et al. (2018) [9] was based on an internal project report [15] and provided data for stepped revetments with . Compared to the before described studies ([6,18]) the analyzed dimensionless step heights were smaller and plunging and surging wave breaking were covered . The provided roughness reduction coefficients were in a range of for small steps and reduced values in a range of for steps with a doubled height . They derived a correlation between the roughness reduction coefficient and the step height and the slope, related to the wave height and weighted by the dimensionless overtopping discharge which follows the form:
Gallach-Sánchez (2018) [10] discussed overtopping data for stepped revetments for steep slopes and the impact of surging waves . The author provided a formula to predict the roughness reduction coefficient which is applicable for configurations in a range of . The author compares his findings with Kerpen (2017) [8] and found lower values for equal Iribarren numbers.
Schoonees et al. (2018) [12] provided overtopping data for stepped revetments over gentle slopes . The tests were conducted in the same wave flume as the tests of the present study. They covered dimensionless step heights in a range of for plunging waves . The derived roughness reduction coefficient for gentle slopes—compared to the other studies—was with a corresponding goodness of fit of and a root mean square error of .
Table 1 gives a summary of the values for wave run-up and overtopping on plain stepped revetments as reported by various authors. The dimensionless step heights, Iribarren numbers and slopes indicate the ranges for which the roughness factors are applicable. Only studies with irregular wave conditions are included in the table. Reliable data for further analysis in this paper is extracted from appropriate literature [6,8,9,12].

Table 1.
Influence factors for roughness for plain stepped revetments by various authors.
From Table 1 it is evident that individual studies mostly considered stepped revetments with limited parameter ranges. In order to draw more general conclusions regarding the overtopping performance of stepped revetments, this paper considers data sets of a number of studies and by this means covers a wider range of dimensionless step heights, slopes and wave-breaking conditions in order to achieve a greater understanding of the reduction of wave overtopping on stepped revetments. The influence factor for roughness was initially derived for a breaking wave condition [20] and should, therefore, be adapted to the friction reduction for non-breaking waves or surging (). Currently, only a single study [9] considered this adaptation, and thus the other data [6,8] were recalculated according to Equation (A10). Solely breaking wave conditions were provided by Schoonees et al. (2018) [12] and thus no adaptation is required.
2. Experimental Set-Up and Test Conditions
2.1. Model Set-Up
Hydraulic model tests were conducted in a wave flume with a length of 110 m, a width of 2.2 m and an overall depth of 2.0 m. The water depth can be varied from 0.0 m to 1.2 m. The flume is equipped with a hydraulic-driven piston type wave maker (wet-back). Waves can be generated with a total stroke of 0.6 m and a maximum velocity of 1.2 m/s. Hence, depending on the water depth , significant wave heights up to and wave periods larger than can be generated. A 1:10 inclined rubble mound slope is located at the end of the flume to serve as a passive wave absorber. The models, constructed from composite timber sheets, are placed on the horizontal flume bed at a distance of 85 m from the wave board with respect to the model’s crest. Further details of the model set-up are provided in literature [8,21]. An impression of the model set-ups is given in Figure 1.
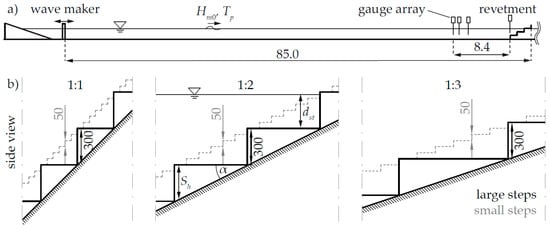
Figure 1.
(a) Side view of the model set-up with wave gauge positions (units in meter). (b) Side view of the tested step geometries (units in millimeter).
For each test, standard JONSWAP spectra were generated with a peak enhancement factor of 3.3 and a relative peak width of 0.07 and 0.09 for frequencies below and above the peak frequency respectively. The wave overtopping volume was collected in a reservoir behind the crest of the structure equipped with weighting cells enabling the calculation of the mean overtopping volume. For statistical validity, long test durations with more than 1000 waves were simulated [22]. Wave conditions in front of the model have been analyzed by a set of 3 gauges [23]. The gauge array had a minimum distance of from the structure, where is defined as the peak wave length, to avoid evanescent mode effects [24]. Wave data was analyzed with the Matlab toolbox WAFO [25]. Wave parameters were calculated according to Section 1.1 for further analysis. After initial reference tests with a plain slope (), tests for small () and large step heights () were conducted. The wave overtopping was analyzed for three different slopes and three freeboard heights Additional measurements of horizontal and vertical pressures on the step face were taken and reported [21]. To allow visual interpretation of the results, all tests were documented by video.
2.2. Test Conditions
The test conditions were based on the findings of a thorough dimensional analysis [26], which resulted in the dimensionless notation for the wave overtopping analysis of stepped revetments:
with defined as spectral wave length and the mean overtopping discharge per meter crest length and second. As most dimensionless values were already covered by Equations (A4) and (A5) the roughness reduction coefficient to be derived for stepped revetments should be based only on the remaining dimensionless step height . The test program was selected to cover a wide range of boundary conditions (, , , ), including the boundary conditions of the presented literature [6,8,9,12]. An overview of the boundary conditions is given together with the results for each test in Table 3.
3. Results
3.1. Calibration
The overtopping reduction coefficient for the stepped revetments , interpreted as a roughness coefficient, was calculated in relation to the wave overtopping on a smooth slope following Equation (A8). The overtopping discharge measured for a rough slope () was correlated with the corresponding value from a regression analysis through the smooth slope data () [13]. The fitted curves for the smooth slopes of the present study (Equation (A4) and (A5) with regression coefficients a and b according to Table 2) are plotted in Figure 2.

Table 2.
Regression coefficients a and b according to Equations (A4) and (A5) for corresponding smooth slopes.
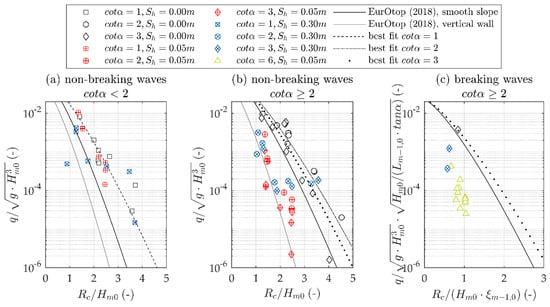
Figure 2.
Dimensionless overtopping discharge over the dimensionless freeboard height for smooth and stepped surfaces with different slope angles. Overtopping prediction formulae according to EurOtop (2018) [13] for smooth slopes and vertical walls are given as reference. Determined best fits for smooth slopes of the present study are given for (a) steep slopes with and non-breaking wave conditions, (b) milder slopes with and non-breaking wave conditions and (c) mild slopes with and breaking wave conditions.
Figure 2 provides an overview of measured dimensionless overtopping volumes versus the dimensionless freeboard height for smooth and stepped slope conditions. The results are separated into breaking and non-breaking wave conditions. As a reference, predictions for smooth slopes (Equation (A4) and (A5)) and vertical wall conditions are given. The mean wave overtopping at a vertical wall—a hypothetical adopted single vertical step face—is predicted by Equation (A5) and corresponding regression coefficients and .
Figure 2a provides steep slope conditions for non-breaking waves. The measured dimensionless overtopping discharge for the smooth slope is larger than the prediction with Equation (A5) but the deviations are covered with the corresponding 90% confidence band representing a 5%-exceedance from the prediction. The dimensionless overtopping discharge decreases only slightly with increasing step height. For the largest tested step height data scatters significantly.
For milder slopes and non-breaking wave conditions (Figure 2b) the mean overtopping discharge for smooth slope conditions is also larger than the prediction with Equation (A5). The mean overtopping discharge decreases for an increased surface roughness but is mostly larger than the predicted overtopping for a plain vertical wall.
For breaking wave conditions and mild slopes (Figure 2c) only a single test for smooth slopes is available. Nevertheless, the mean overtopping discharge of this test is also larger than predicted according to Equation (A4).
The values a and b in Equation (A4) and (A5) as derived from the regression of the smooth slope data given in Figure 2, are given in Table 2. For a 1:6 slope no data for a smooth slope is available, but the tests were conducted in the same wave flume as the present study. A comparably larger mean overtopping rate relative to the prediction is assumed and, therefore, applied in further calculations.
3.2. Measured and Determined Values
The regression coefficients listed in Table 2 are empirically derived and applied to the prediction formulae (Equation (A4) and (A5)) and set in proportion to the mean overtopping volumes obtained from the stepped surface tests. The influence factor for roughness was calculated by applying Equation (A8). The derived values for for non-breaking waves were corrected according to Equation (A10). Table 3 provides an overview of the measured parameters of the conducted model tests. The mean overtopping discharge , the calculated () and corrected ) friction reduction coefficients for stepped revetments are also given.

Table 3.
Overview of model test parameter, including calculated () and corrected () roughness reduction coefficients for stepped revetments.
4. Analysis
Figure 2 indicates that at a stepped revetment the wave overtopping volume is lower than at a smooth slope and larger than at a vertical wall. The reduction is caused by the geometry of the stepped revetment, that reduces run-up and overtopping by dissipating and reflecting incoming wave energy. In analogy to stepped spillways the step diameter is introduced to describe the surface roughness of a stepped revetment [27]. It is defined as the perpendicular distance between the step niche and the straight connection between the two adjacent step edges (Figure 3). The step diameter can be calculated with the step height and the slope angle of the revetment :
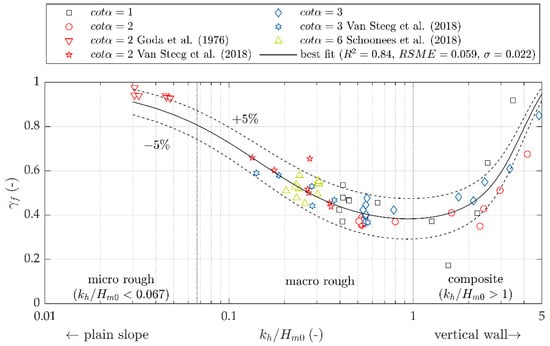
Figure 3.
Reduction coefficient versus the step ratio for varying slopes including a best fit regression line and the 90% confidence band.
Figure 3 gives the calculated correlation between the reduction coefficients for roughness of a stepped revetment against the corresponding step ratio . The given values for refer to the corrected values for surging waves according to Equation (A10). Data of the present study were combined with previous findings [6,9,12] to extend the range of validity as the additional data sets include different slopes and step ratios. Data for four different slopes () and a wide range of step ratios () are given.
A plain slope has a step ratio of 0.0 and, therefore, a corresponding reduction coefficient for roughness equal to 1.0. A vertical wall can be interpreted as a single vertical step face and therefore in analogy as a large step ratio. These two extremes define the outer boundary conditions. In between these values the surface roughness of the stepped revetment influences the wave overtopping discharge. The regression analysis of the data results in a double arctangent function:
The function describes the relation between the reduction coefficient for roughness of a stepped revetment and the corresponding step ratio with a goodness of fit of , a root mean square error of and a standard deviation . Starting from the derived prediction for decreases up to a minimum value of 0.38 for and increases again for . The minimum represents the maximum efficiency of wave overtopping reduction and is in a range of .5.
The quality of the derived prediction according to Equation (4) is given for the individual test series in Table 4. Data from the present study show an appropriate goodness of fit for milder slopes ). The goodness of fit is lower for the steep 1:1 slope ) which is mainly caused by two outliers for step ratio large 1.0. The low outlier was a test with a high wave steepness (, the upper outlier a test with large freeboard height () and therefore a low corresponding overtopping volume. Several data [6,12] covers only a narrow range of step ratios which explains the comparably low goodness of fit for the prediction. Furthermore, increased standard deviations are present. Data from Van Steeg et al. (2018) [9] follow the trends observed in the present study. According to the authors, the outlier corresponding to the 1:2 slope is caused by a relatively large amount of wave overtopping. Equation (4) gives fairly comparable results for compared to the prediction provided by Equation (1) for . Hence, the new approach incorporates the findings from [9] and provides an extension of its coverage.

Table 4.
Goodness of fit ), root mean square error () and standard deviation () for data given in Figure 3 according to Equation (4).
A validation of the applicability of the presented approach to the prediction according to EurOtop (2018) [13] is given in Figure 4. The reduction coefficients for the roughness of stepped revetment derived by Equation (4) was applied to the available data with Equation (A4) and (A5). As all studies showed minor deviations in the mean wave overtopping on smooth slopes between measurement and prediction, the presented results were corrected to this deviation by applying the regression coefficients according to Table 2 (). Similar regression coefficients were provided by Van Steeg et al. (2018) [9] by which the presented results were corrected. For Goda and Kishira (1976) [6] the effect of broken waves over the shallow foreshore () was calculated in a simplified way with Equation (A5) and regression coefficients (for ) and (for ). The mean overtopping discharge for breaking and non-breaking waves at steep and gentle sloped stepped revetments was predicted within the 90% confidence bands given by EurOtop (2018) [13]. Therefore, it is recommended to increase the average discharge by about one standard deviation for a design or assessment approach. The applicability of the approach for steep slopes () in combination with large step ratios () is limited. For these composite-like boundary conditions the position of the relative to the step edge becomes important and a prediction in analogy to a composite wall should be considered.
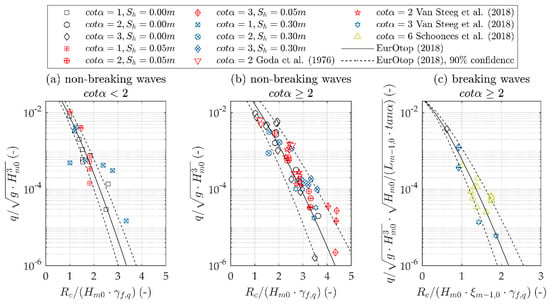
Figure 4.
Dimensionless overtopping discharge against the dimensionless freeboard height including a roughness coefficient for stepped revetments. Overtopping prediction formulae according to EurOtop (2018) [13] are given for smooth slopes and 90% confidence bands. Data for (a) steep slopes with and non-breaking wave conditions, (b) milder slopes with and non-breaking wave conditions and (c) mild slopes with and breaking wave conditions.
5. Discussion
In the analysis, data sets from different studies were gathered and combined to determine the overtopping reduction performance of stepped revetments with varying slopes and step ratio. In this way, a basis for comprehensive analysis on the performance of overtopping of stepped revetments was created. Previous findings were based on individual experimental set-up and analysis, and both consistencies and contradictions in the findings and interpretation exist.
Data displayed in the present study are based on hydraulic model tests [8]. The corresponding data analysis did not account for the correction of the roughness reduction coefficient for as required [20], which serves as basis for the present wave run-up and overtopping prediction in EurOtop (2018) [13]. Hence, the roughness reduction coefficient derived by Kerpen (2017) [8] was a function of the Iribarren number. The correction of the roughness reduction coefficient for non-breaking waves was already accounted for by Van Steeg et al. (2018) [9]. Besides the dependency of on the step ratio, Van Steeg et al. (2018) [9] refined the correlation by introducing an additional dependency on the dimensionless overtopping discharge. This approach was not followed in the present study as no significant improvement was observed for the extended parameter range. Conveniently, the iteration of is avoided and for clarity the dependencies of are based only on the key variable step ratio.
In Figure 3, data from Goda and Kishira (1976) [6] show comparably low values for the reduction coefficient (). Evidently, the corresponding low step ratios () have only a minor influence on the wave overtopping reduction due to the small energy dissipation rates. This phenomenon was already observed on dikes covered with grass meadows. It is recommended to neglect the roughness of grass cover of sloping coastal protecting structures for wave heights larger than in the calculation of wave run-up due to underlying hydraulic insignificance [20]. Assuming that the mean grass height is about and that this roughness value is comparable with the step diameter a limit of
was derived. The space in the step niches (porosity) is relatively low compared to the water volume in the wave run-up and run-down. Below this value, the roughness can be defined as micro-rough with negligible influence on the wave run-up and overtopping reduction due to marginal energy dissipation rates.
For the step geometry becomes the governing parameter and scatter increases between the prediction of Equation (4) and the achieved reduction coefficient. The position of the relative to the step edge becomes important (Figure 3). For step ratios it is therefore advised to include the overtopping prediction for composite walls given in EurOtop (2018) [13].
Nonetheless, there is still an uncertainty in the prediction of the reduction coefficient for roughness of stepped revetments. The uncertainty of the currently available data is covered within the 90% confidence band given in EurOtop (2018) [13].
5.1. Governing Process Description
The number of steps as well as the step ratio influence the energy dissipation at stepped revetments significantly. The intensity of the wave-induced turbulence due to the presence of the steps is dependent on the roughness elements (shape and dimensions) and the flow velocity [28]. The dependence between the geometrical parameters of the stepped revetment and the hydraulic boundary conditions is presented in Section 4. The following process description is based on these findings and graphically summarized in Figure 5.
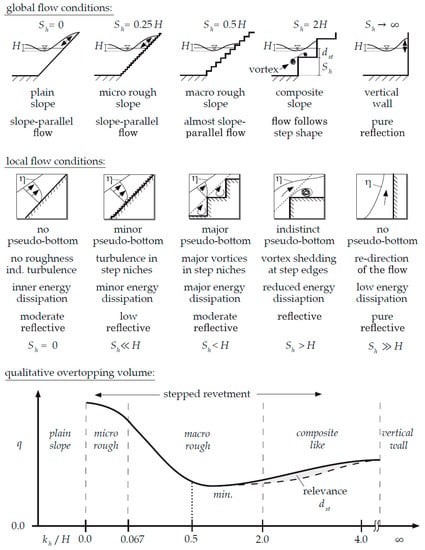
Figure 5.
Dependence of the step ratio on the wave run-up and wave overtopping.
A step ratio equal to zero () represents a smooth slope. The highest overtopping volumes were measured for smooth slopes due to relatively low energy dissipation on their surfaces in comparison to the macro roughness surfaces of stepped revetments. As a consequence, the shear stresses on the smooth slope are also low and, thus, induce relatively low shear stresses on the structure. Most of the kinetic wave energy converts into potential energy in the run-up process. With increasing step height, the roughness and turbulence increase, leading to decreasing overtopping volumes. A minor part of the kinetic energy of the incident waves is converted to potential energy as some energy is dissipated by increasing turbulence.
As discussed, it was found that the step geometry has little influence on the energy dissipation for very small step heights (). The flow direction of the wave run-up was still slope-parallel. Consequently, these small steps can be considered as micro roughness and are, therefore, comparable in terms of run-up reduction effectiveness to any other impermeable micro-rough surface.
With increasing step height () the slope-parallel wave run-up is disturbed by means of the step edges more effectively. The flow processes on a single step become more important as induced vorticity diminishes kinetic energy. Likewise, vortex shedding occurs at the step edges in dependence of the relative step to wave height and period of the run-up process. In relation to smooth slopes, smaller amounts of kinetic energy of the incident wave are converted into potential energy as wave-induced energy is dissipated by the production of step-induced vortices, stronger turbulence and non-linear wave transformation processes over the steps. The vortex shedding on stepped revetments is discussed elsewhere [29]. In effect, a maximum in total energy dissipation leads to the lowest overtopping volumes at stepped revetments with step ratios of . Step ratios appear to mimic conditions for vertical walls. For a low step ratio, the influence of the offshore located steps decreases due to less energy dissipation in increasing water depth. With increasing step ratio the revetment becomes more reflective and the wave breaking is affected by the step geometry itself. Therefore, the water depth over the step () also influences the wave overtopping. This system performance is comparable to composite walls (). If the step height is significantly larger than the wave height () the wave overtopping tends to mimic the physical conditions of vertical walls. The kinetic energy of the incident wave is converted to potential energy and most of the incoming wave energy is reflected at the wall.
5.2. Model and Scale Effects
In most coastal engineering applications, the Froude scaling law is applied when tests are not conducted under prototype conditions. The parameter study presented has no particular scale but wave conditions are certainly lower than in prototype. Therefore, predominantly inertial forces and gravity are considered, while viscosity, elasticity, and surface tension are incorrectly represented. In the EC Mast III Opticrest research project results from scaled model tests were compared to prototype tests to identify scale effects. About 50% higher run-up heights were observed for a rubble mound breakwater in prototype conditions than predicted by empirical formulae [30].
In the present study, all friction effects—especially on the boundary layer—are overestimated. For friction, the Reynolds law is better suited since it considers viscosity. With wave breaking the Weber, Reynolds and Cauchy law should be applied. Therefore, by applying the Froude law, the effects of wave breaking are only idealized. Furthermore, to the wave run-up process Reynolds and Weber law are important.
The surface roughness of the tested revetments was very smooth as it is constructed by wooden planks with a surface comparable to glass. For the smooth slopes—used as a reference—the surface is not ideally smooth and the run-up is, therefore, slightly reduced due to surface friction. For the stepped slopes a slightly higher run-up is expected in the model tests as the surface is much smoother than e.g., concrete and, therefore, less friction is expected in the interface of step and water. Nevertheless, both boundaries result in conservative reduction coefficients. Overall, the effect of the surface roughness of the construction material is of minor importance.
It is expected that the inability to scale the air entrainment will have a more significant effect. The importance of the air entrainment for the energy dissipation is known [31]. The influence of scale effects affecting the air entrainment with Froude similitude proven for hydraulic jumps [32]. It is assumed that the described principle processes are comparable with the process of the wave run-up over stepped revetments. The aeration is significantly lower in smaller scales and cannot be achieved under Froude similitude [32]. Since the presented results are based on small scale model tests, the effectiveness of stepped revetments with respect to wave run-up heights and wave overtopping volumes is overestimated [30]. Full scale tests can, therefore, contribute to reduce uncertainties.
6. Conclusions
The objective of the present study was to derive a reduction coefficient for the roughness of a stepped revetment for a wide range of application. Previous literature highlights the importance of the dimensionless step height on the energy dissipation in the wave run-up and, as a consequence, the reduction of the mean overtopping discharge. Knowledge gaps from previous studies covering different parameter ranges and differences in the post-processing of data were identified.
The present study combined available data sets for the wave overtopping on stepped revetments. A new set of hydraulic model tests extended the range of parameters to cover the full range of step ratios between the two defined extreme conditions, a plain slope and a vertical wall. The experimental work included 69 individual tests with irregular waves covering steep and gentle slopes (), breaking and non-breaking wave conditions (), and dimensionless freeboard heights of . The corresponding mean overtopping discharge was in the range of .
Processes that govern the energy dissipation of a stepped revetment are discussed in relation to the step ratio. Three different zones of energy dissipation are identified, namely micro rough, macro rough and composite-like roughness. An optimum in the reduction of the mean overtopping discharge (by about 60% for breaking waves compared to a smooth slopes) was identified for step ratios in the range of . For non-breaking waves the influence of decreases for increasing Iribarren numbers as the step niches are filled by water from the previous wave run-up and the macro roughness of the revetment is thereby reduced. In an analogy to grass slopes, it is shown that the wave overtopping reduction for step ratios smaller than is negligible. An application of the derived prediction formula for the roughness coefficient of a stepped revetment to the design approach ([13]) results in accordance with the given 90% confidence band. The new formula comprises only the step ratio. Influences of wave breaking on the slope are considered by the standard design approach according to EurOtop (2018) [13].
The derived roughness coefficient for stepped revetments is not based on prototype scale. Hence, it is likely influenced by scale effects. If a correction for scale effects, such as provided by De rouck et al. (2005) [33], is applicable for stepped revetments has to be determined by further research.
Author Contributions
T.S. (Torsten Schlurmann) and N.B.K. developed the presented idea and designed the research project “waveSTEPS”. N.B.K. developed the theory, conducted the hydraulic model tests, analyzed and verified the results from physical model tests and compared the findings with the literature. T.S. (Talia Schoonees) provided data and insights from 1:6 slope tests. All authors discussed the results and contributed to the final manuscript.
Funding
The publication of this article was funded by the Open Access fund of Leibniz Universität Hannover.
Acknowledgments
Valuable discussions with K.-F. Daemrich throughout the entire project are appreciated.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Technical Background
In the following, fundamentals and definitions for the data preparation and analysis related to wave overtopping are summarized. The described methods are applied to data from different authors in the results and analysis section.
Appendix A.1. Harmonization of Data Sets
Studies with different decade of origin and from diverse laboratories demand for a sound processing and harmonization of certain values that are applied in the present design assessment. The Iribarren number applied in wave run-up and overtopping predictions is based on the fictitious wave steepness [34]. This fictitious wave steepness is a function of the spectral significant wave height and the mean energy wave period , both measured at the toe of the structure as follows:
The mean wave period of the irregular wave train is derived from the quotient of the 1st negative moment and the zeroth moment of the corresponding wave energy density spectrum which is designated in the indices of the parameter . A detailed discussion about the practicality and suitability of this dedicated parameter in the context of the overtopping prediction is given in EurOtop (2018) [13].
The peak wave period for a wave spectrum following Bretschneider’s distribution is correlated to the mean wave period [35] by:
and the mean spectral wave period is correlated to the peak wave period [36] by
Appendix A.2. Wave Overtopping Prediction
Wave overtopping is caused by waves running up the face of a dike or seawall [13]. If the wave run-up is higher than the freeboard height of the structure water will reach and pass over the crest. Also splash and spray induced from waves breaking on the face of the structure cause overtopping. The general equations for the relative overtopping discharge prediction under breaking waves for relatively gentle slopes is given by the mean value approach
with depicting the mean overtopping volume per meter crest width and second, and represent regression coefficients, is the freeboard height defined as the crest height of a structure relative to the still water line () and the reduction coefficient for friction. The influence factors for the presence of a berm (), oblique wave attack () and a vertical wall on the crest of the structure () are not relevant for the present study and, therefore, set to 1.0 in subsequent equations. For non-breaking waves under the same boundary conditions by:
For very steep slopes and non-breaking waves EurOtop (2018) [13] is referring to the work by Victor (2012) [37] who provides the coefficients:
for Equation (A5). But, this formula is valid only for smooth slopes, hence, the friction reduction coefficient has to be set to . For breaking waves, Equation (A4) shall be used.
The slope roughness is represented in the empirical formulae by the roughness influence factor , representing the permeability and roughness of or on the slope. The mean value approach [13] to predict the mean wave overtopping discharge on coastal dikes and embankments is derived originally by Van der Meer and Bruce (2014) [38].
Appendix A.3. The Influence of Roughness
The influence factor for the permeability or roughness of or on the slope is defined for the wave run-up as
with defined as the wave run-up level, measured vertically from the which is exceeded by of the number of incident waves. For wave overtopping, the roughness reduction factor is defined as
The roughness reduction coefficient is derived for a method described in TAW (2002) [20] and is valid only for breaking waves [9]. For Iribarren numbers larger than (with in the present study) the roughness reduction coefficient has to be corrected by linear extrapolation between its value at 1.8 along to
Although this approach is based on findings from tests with impermeable rock slopes, it is advised to also apply Equation (A9) for cases with roughness elements [20]. The results of hydraulic model tests already incorporate the reduced influence of friction for surging waves . Hence, an adjusted roughness factor has to be determined by a rearrangement of Equation (A9) to
References
- Pranzini, E.; Wetzel, L.; Williams, A.T. Aspects of coastal erosion and protection in Europe. J. Coast. Conserv. 2015, 19, 445–459. [Google Scholar] [CrossRef]
- Schoonees, T.; Gijón Mancheño, A.; Scheres, B.; Bouma, T.J.; Silva, R.; Schlurmann, T.; Schüttrumpf, H. Hard Structures for Coastal Protection, Towards Greener Designs. Estuar. Coasts 2019, 1–22. [Google Scholar] [CrossRef]
- Saville, T. Wave Run-Up on Shore Structures. Proc. Am. Soc. Civ. Eng. 1956, 82, 1–14. [Google Scholar]
- Wassing, F. Model Investigation on Wave Run-Up Carried out in the Netherlands during the Past Twenty Years. In Proceedings of the 6th Conference on Coastal Engineering, Hydraulics Laboratory Delft, Gainesville, FL, USA, 1957; Volume 6, pp. 700–714. Available online: https://journals.tdl.org/icce/index.php/icce/issue/view/128 (accessed on 31 January 2019).
- Jachowski, R.A. Interlocking Precast Concrete Block Seawall. In Proceedings of the 9th International Conference on Coastal Engineering, Lisbon, Portugal, 1964; pp. 504–517. Available online: https://ascelibrary.org/doi/10.1061/9780872620056.032 (accessed on 31 January 2019).
- Goda, Y.; Kishira, X. Experiments on Irregular Wave Overtopping Characteristics of Seawall of Low Crest Types; Technical Note of PARI; Port and Airport Research Institute: Yokosuka, Japan, 1976; pp. 1–29. [Google Scholar]
- Heimbaugh, M.S. Coastal Engineering Studies in Support of Virginia Beach, Virginia, Beach Erosion Control and Hurricane Protection Project: Report 1, Physical Model Tests of Irregular Wave Overtopping and Pressure Measurements; CERC U.S. Army Corps of Engineers: Springfield, VA, USA, 1988; Volume 88-1. [Google Scholar]
- Kerpen, N.B. Wave-Induced Responses of Stepped Revetments. Ph.D. Thesis, Gottfried Wilhelm Leibniz University, Hannover, Germany, 2017. [Google Scholar]
- Van Steeg, P.; Joosten, R.A.; Steendam, G.J. Physical model tests to determine the roughness of stair shaped revetments. In Proceedings of the 3rd International Conference on Protection against Overtopping, Grange-over-Sands, UK, 6–8 June 2018; p. 8. [Google Scholar]
- Gallach-Sánchez, D. Experimental Study of Wave Overtopping Performance of Steep Low-Crested Structures. Ph.D. Thesis, Ghent University, Zwijnaarde, Belgium, 2018. [Google Scholar]
- Ward, D.L. Overtopping Studies of a Stepped Revetment for City of Chicago, Illinois; Final Report ERDC/CHLTR-03-14; Defense Technical Information Center: Fort Belvoir, VA, USA, 2003; p. 48.
- Schoonees, T.; Kerpen, N.B.; Liebisch, S.; Schlurmann, T. Wave overtopping prediction of a gentle sloped stepped revetment. Coast. Eng. Proc. 2018, 1, 99. [Google Scholar] [CrossRef]
- EurOtop. Manual on Wave Overtopping of Sea Defences and Related Structures. An Overtopping Manual Largely Based on European Research, but for Worldwide Application, 2nd ed.; Van der Meer, J.W., Allsop, N.W.H., Bruce, T., De Rouck, J., Kortenhaus, A., Pullen, T., Schüttrumpf, H.F.R., Troch, P., Zanuttigh, B., Eds.; 2018; Available online: www.overtopping-manual.com (accessed on 31 January 2019).
- Kerpen, N.B.; Schlurmann, T. Stepped revetments–Revisited. In Proceedings of the 6th International Conference on the Application of Physical Modelling in Coastal and Port Engineering and Science, Ottawa, ON, Canada, 10–13 May 2016; p. 10. [Google Scholar]
- Van Steeg, P.; Wolters, G.; Van Gent, M.R.A. Invloedsfactor voor Ruwheid van een Getrapt talud bij Golfoverslag bij Dijken: Verslag Fysieke Modeltesten en Analyse; Project Report 1206984-000-HYE-0006; Deltares: Delft, The Netherlands, 2012. (In Dutch) [Google Scholar]
- Kerpen, N.B.; Goseberg, N.; Schlurmann, T. Experimental Investigations on Wave Overtopping on Stepped Embankments. In Proceedings of the 5th International Conference on Application of Physical Modelling to Port and Coastal Protection (Coastlab14), Varna, Bulgaria, 29 September–2 October 2014; Volume 1, pp. 226–269. [Google Scholar]
- Ward, D.L.; Ahrens, J.P. Overtopping Rates for Seawalls; Miscellaneous Paper CERC-92-3; Coastal Engineering Research Center: Washington, DC, USA, 1992; p. 64. [Google Scholar]
- Melby, J.A.; Burg, E.C.; McVan, D.; Henderson, W. South Florida Reservoir Embankment Study; ERDC/CHL-TR-09-3; Engineer Research and Development Center Vicksburg MS Coastal and Hydraulic Lab: Vicksburg, MS, USA, 2009; p. 46.
- Schüttrumpf, H.F.R. Wellenüberlaufströmung bei Seedeichen: Experimentelle und theoretische Untersuchungen. Ph.D. Thesis, Mitteilungen aus dem Leichtweiss Institut für Wasserbau, Technischen Universität Carlo-Wilhelmina zu Braunschweig, Braunschweig, Germany, 2001; p. 173. (In German). [Google Scholar]
- TAW. Technisch Rapport Golfoploop en Golfoverslag Bij Dijken; Technical Report; Technische Adviescommissie voor de Waterkeringen (TAW): Delft, The Netherlands, 2002; p. 42. (In Dutch) [Google Scholar]
- Kerpen, N.B.; Schoonees, T.; Schlurmann, T. Wave Impact Pressures on Stepped Revetments. J. Mar. Sci. Eng. 2018, 6, 156. [Google Scholar] [CrossRef]
- Daemrich, K.-F.; Mai, S.; Kerpen, N.B. On the reasons of scatter in data for design formula evolution. In Proceedings of the 6th CG Joint Symposium on Hydraulic and Ocean Engineering, Keelung, Taiwan, 23–29 September 2012; p. 6. [Google Scholar]
- Mansard, E.P.D.; Funke, E.R. The Measurement of Incident and Reflected Spectra Using a Least Squares Method; Coastal Engineering; ASCE—Texas Digital Library: Sydney, Australia, 1980; pp. 154–172. [Google Scholar]
- Klopman, G.; Van der Meer, J.W. Random Wave Measurements in Front of Reflective Structures. J. Water Port Coast. Ocean Eng. 1999, 125, 39–45. [Google Scholar] [CrossRef]
- Brodtkorb, P.A.; Johannesson, P.; Lindgren, G.; Rychlik, I.; Rydén, J.; Sjö, E. WAFO—A Matlab Toolbox for the Analysis of Random Waves and Loads. In Proceedings of the 10th ISOPE 2000, Seattle, WA, USA, 28 May–2 June 2000; Volume 3, pp. 343–350. [Google Scholar]
- Buckingham, E. On Physically Similar Systems; Illustrations of the Use of Dimensional Equations. Phys. Rev. 1914, 4, 345–376. [Google Scholar] [CrossRef]
- Chanson, H. Stepped spillway flows and air entrainment. Can. J. Civ. Eng. 1993, 20, 422–435. [Google Scholar]
- Von Kármán, T. Mechanical Similitude and Turbulence. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen 1930, 5, 58–76. [Google Scholar]
- Kerpen, N.B.; Bung, D.B.; Valero, D.; Schlurmann, T. Energy dissipation within the wave run-up at stepped revetments. J. Ocean Univ. China 2017, 16, 649–654. [Google Scholar] [CrossRef]
- Troch, P.; De Rouck, J.; Van Damme, L. Instrumentation and prototype measurements at the Zeebrugge rubble mound breakwater. Coast. Eng. 1998, 35, 141–166. [Google Scholar] [CrossRef]
- Führböter, A. Über die Bedeutung des Lufteinschlages für die Energieumwandlung in Brandungszonen; Die Küste; Boyens: Heide, Germany, 1971; Volume 21, pp. 34–42. (In German) [Google Scholar]
- Chanson, H.; Murzyn, F. Froude Similitude and Scale Effects Affecting Air Entrainment in Hydraulic Jumps. In Proceedings of the World Environmental and Water Resources Congress 2008, Honolulu, HI, USA, 12–16 May 2008; Babcock, R.W., Jr., Walton, R., Eds.; pp. 1–10. [Google Scholar]
- De Rouck, J.; Geeraerts, J.; Troch, P.; Kortenhaus, A.; Pullen, T.; Franco, L. New results on scale effects for wave overtopping at coastal structures. In International Conference on Coastlines, structures and breakwaters 2005; Allsop, N.W.H., Ed.; Thomas Telford: London, UK, 2005; pp. 29–43. [Google Scholar]
- Heineke, D.; Verhagen, H.J. On the use of the fictitious wave steepness and related surf-similarity parameter in methods that describe the hydraulic and structural response to waves. In Proceedings of the Coastal Structures 2007, Venice, Italy, 2–4 June 2007; World Scientific Publishing Company: Venice, Italy, 2009; pp. 1057–1066. [Google Scholar]
- Goda, Y. Random Seas and Design of Maritime Structures, 3rd ed.; Advanced Series on Ocean Engineering; World Scientific Publ.: Singapore, 2010; Volume 33, ISBN 978-981-4282-40-6. [Google Scholar]
- Bretschneider, C.L. Revisions in Wave Forecasting: Deep and Shallow Water. Coast. Eng. Proc. 1957, 1, 3. [Google Scholar] [CrossRef]
- Victor, L. Optimization of the Hydrodynamic Performance of Overtopping Wave Energy Converters: Experimental Study of Optimal Geometry and Probability Distribution of Overtopping Volumes. Ph.D. Thesis, Ghent University, Zwijnaarde, Belgium, 2012. [Google Scholar]
- Van der Meer, J.W.; Bruce, T.P. New Physical Insights and Design Formulas on Wave Overtopping at Sloping and Vertical Structures. J. Waterw. Port Coast. Ocean Eng. 2014, 140, 04014025. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).