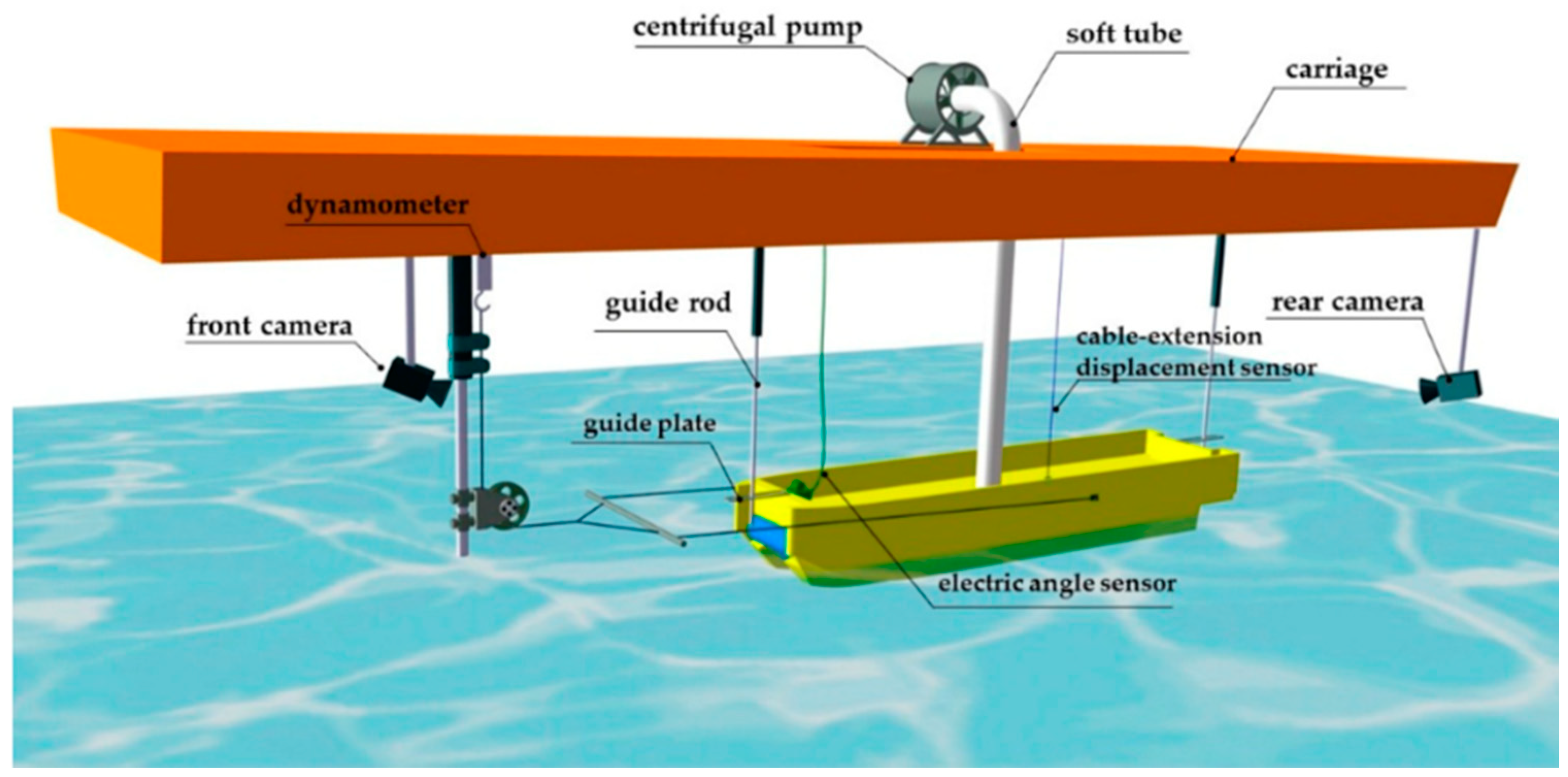
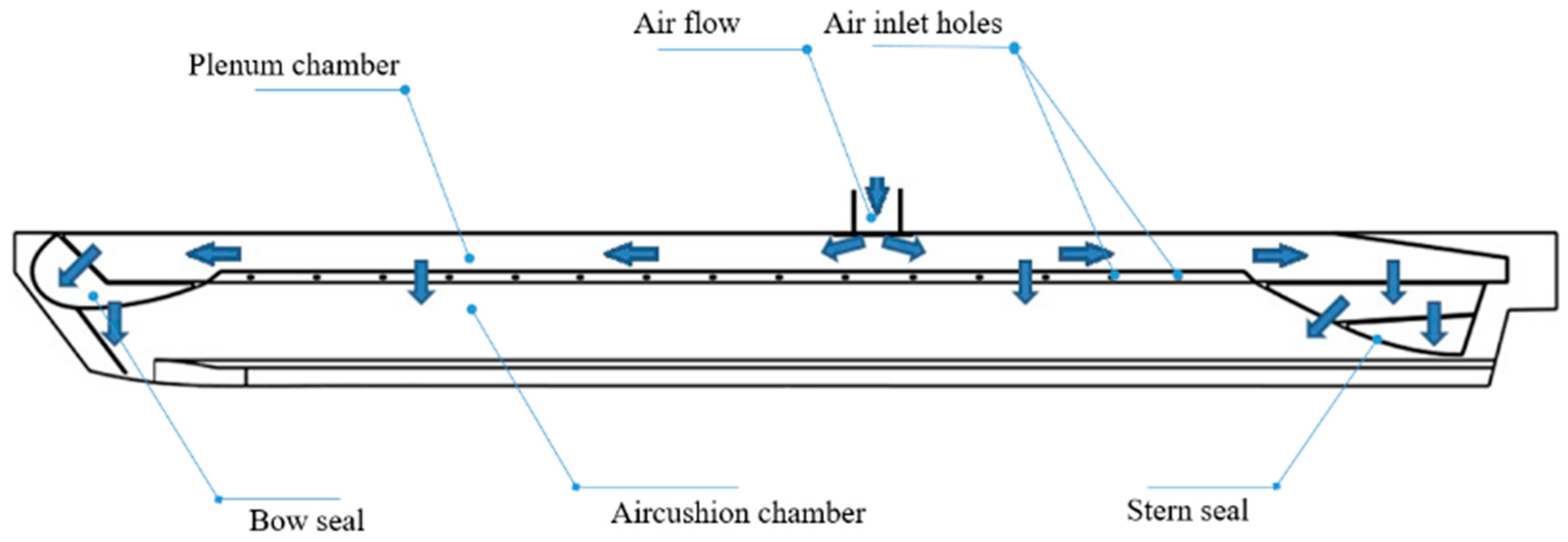
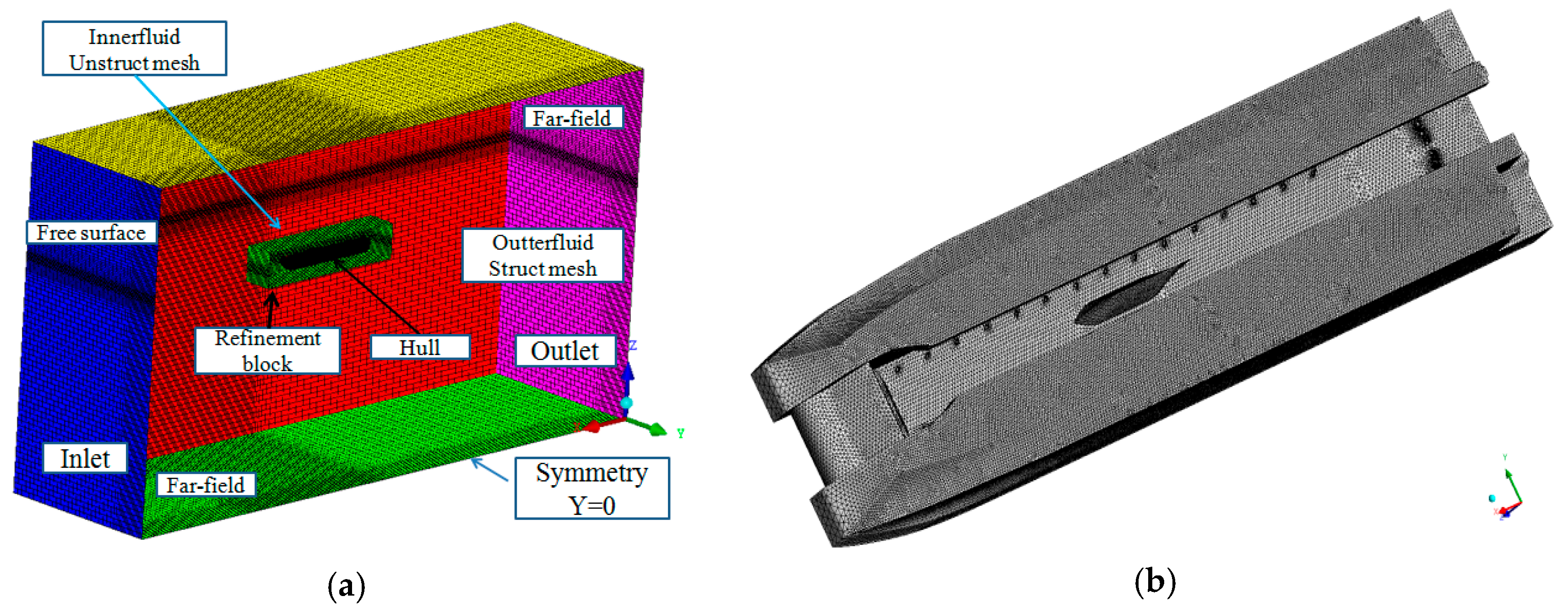
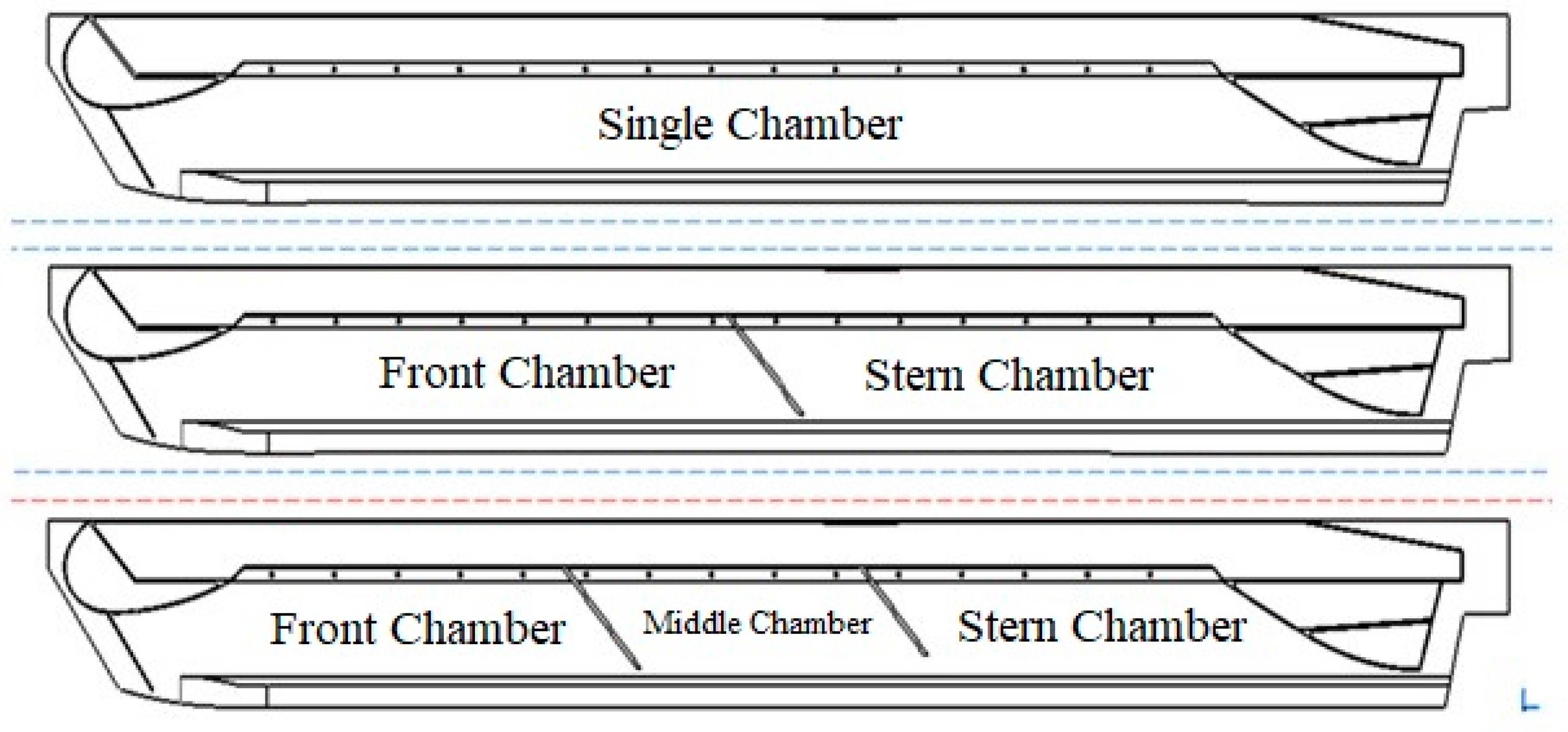
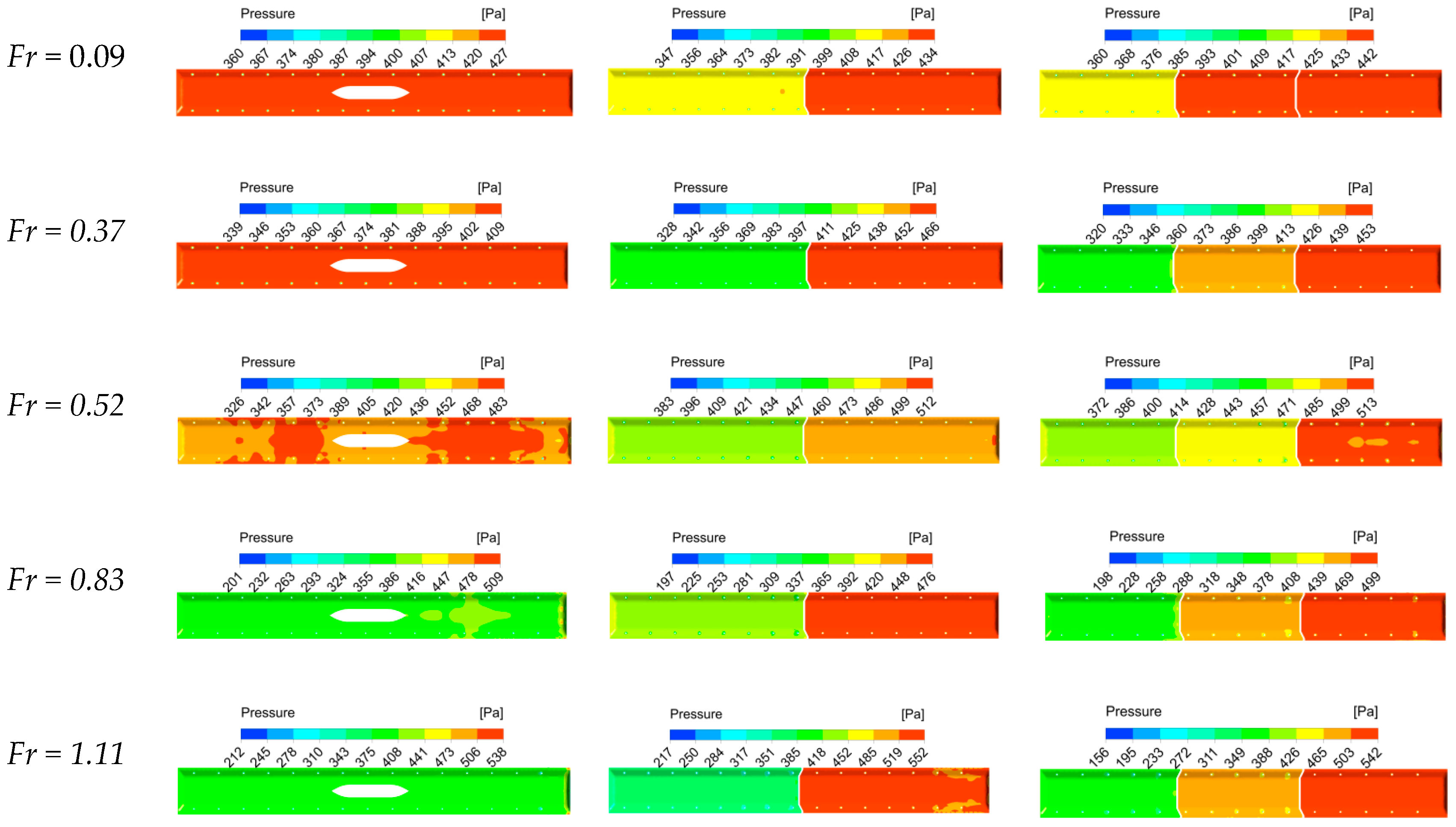
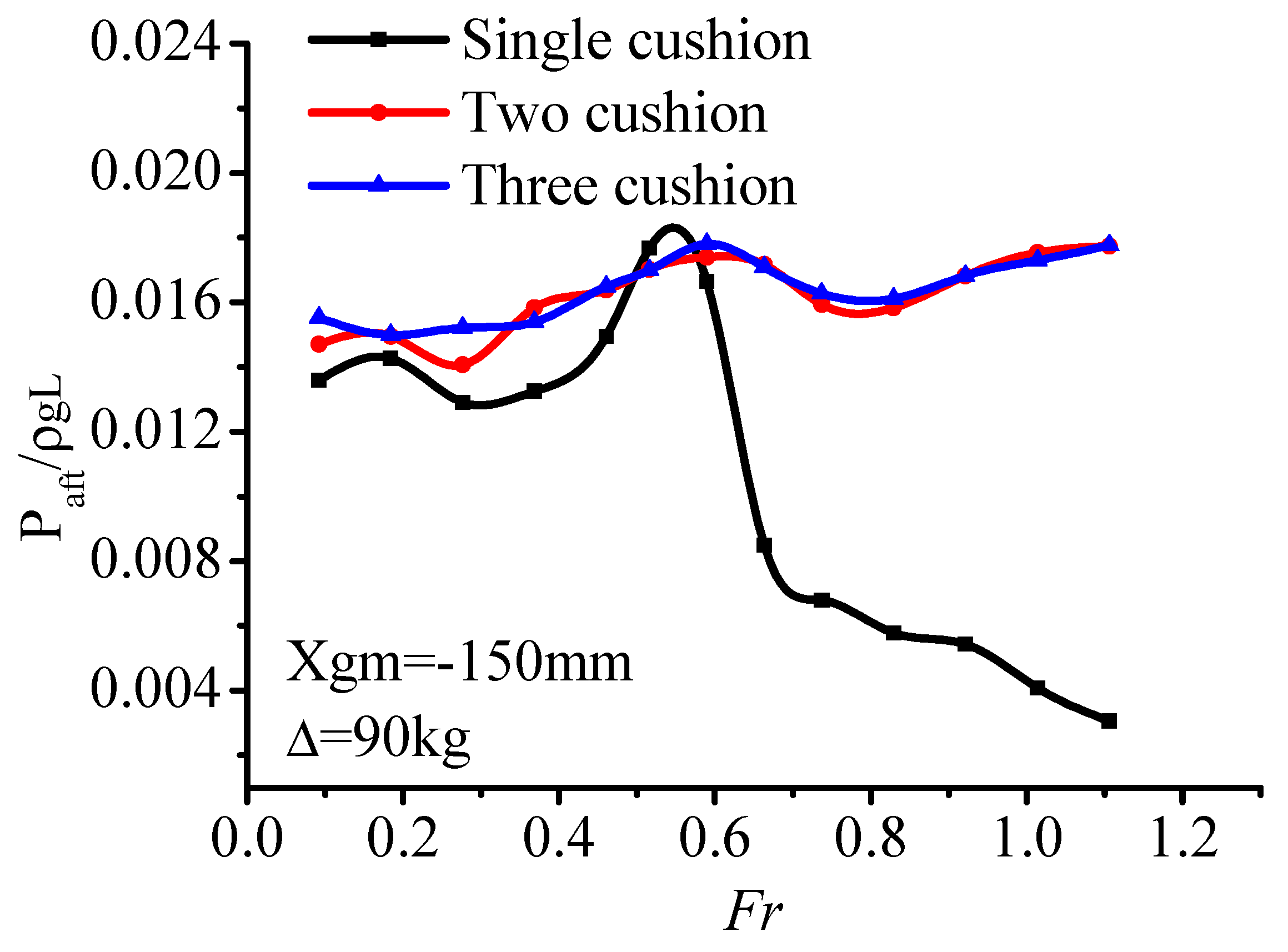
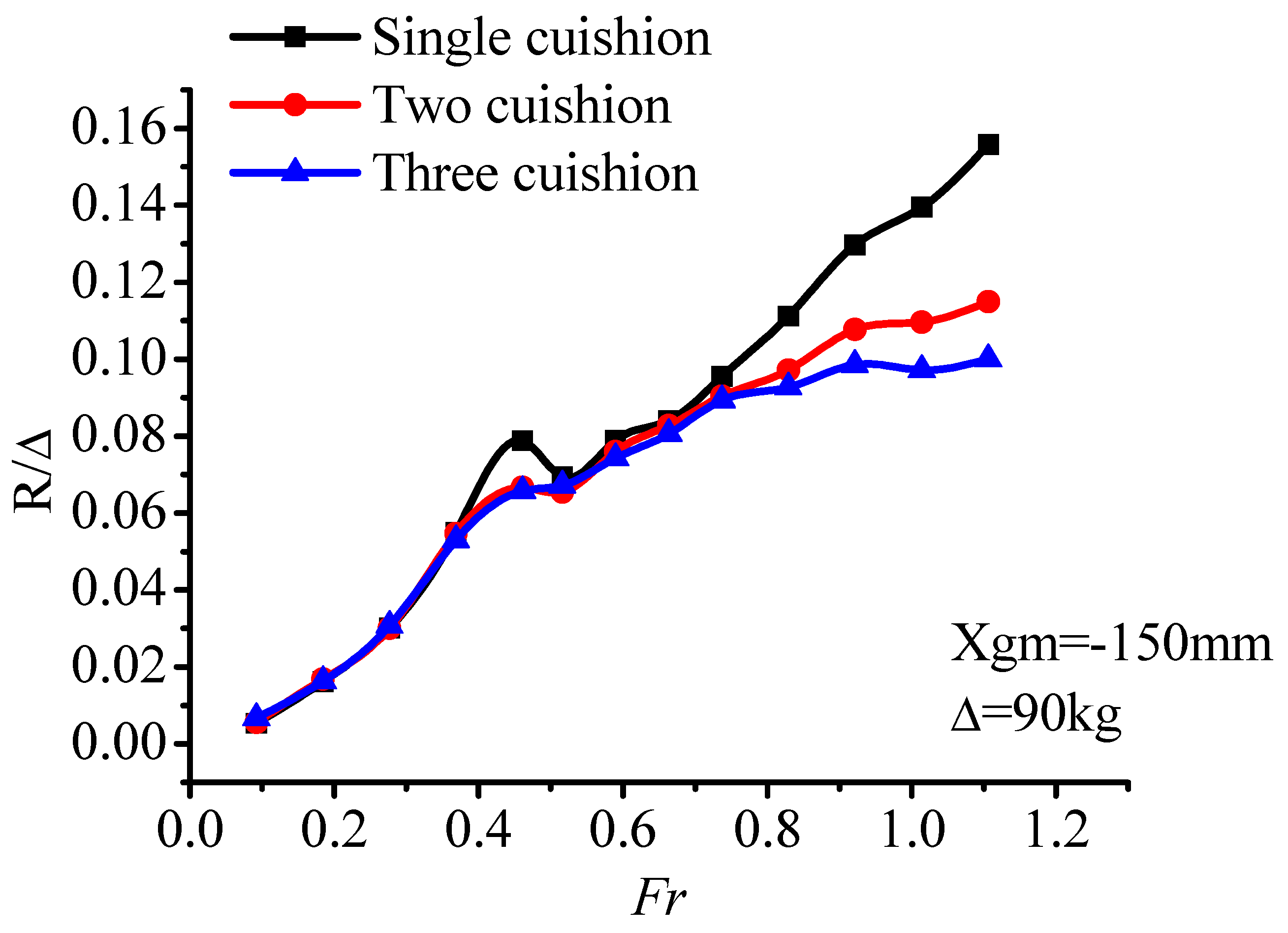
In this section, experimental and numerical results data are extracted and analyzed. The relationship among parameters, such as air cushion pressure, trim angle, heave, and resistance is preliminarily analyzed. In addition, the components of total resistance is divided.
3.1. Results of Towing Test
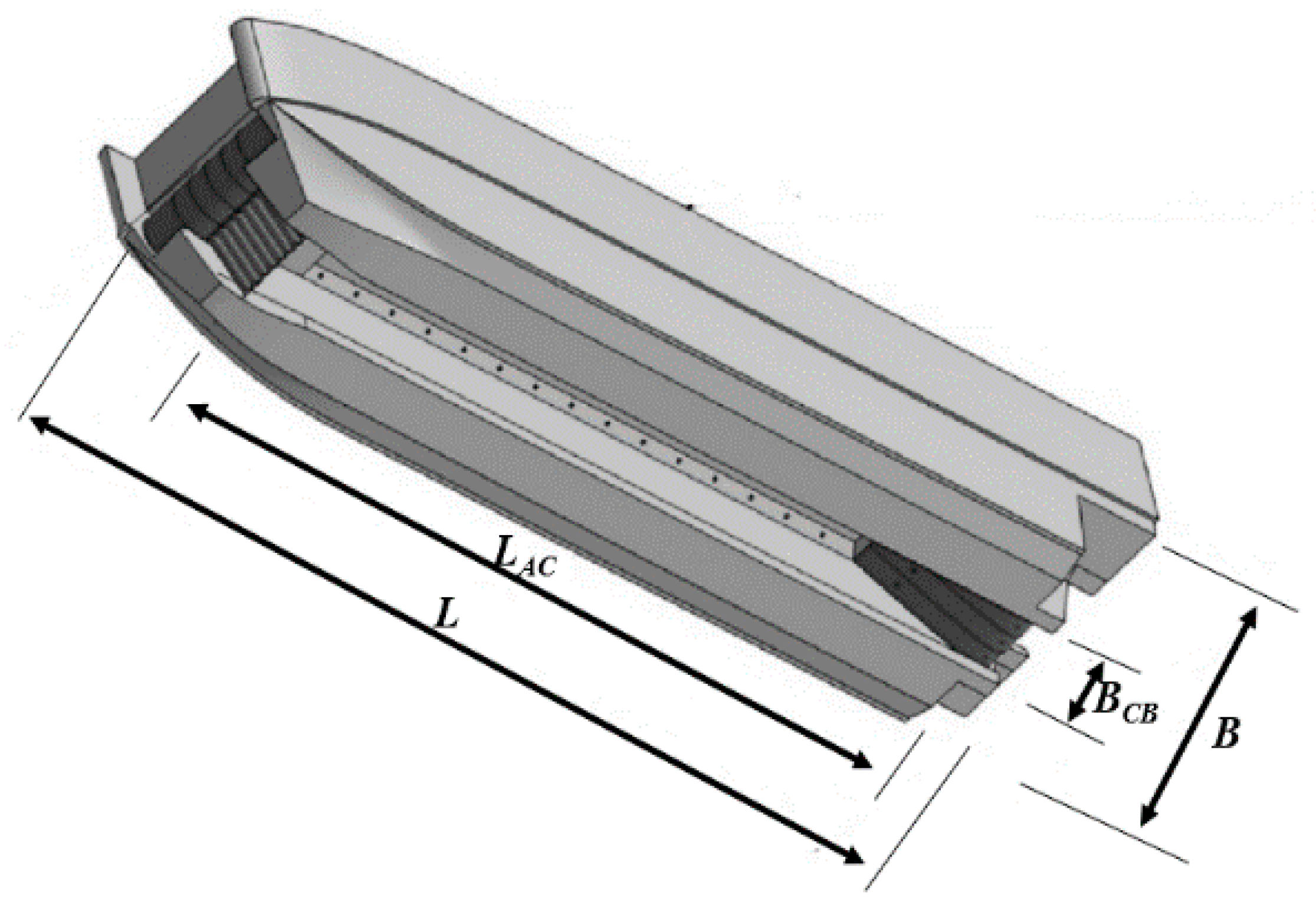
Main parameters dimensionless have been proceed under dimensionless expressions shown in
Table 3. In
Figure 8,
Figure 9 and
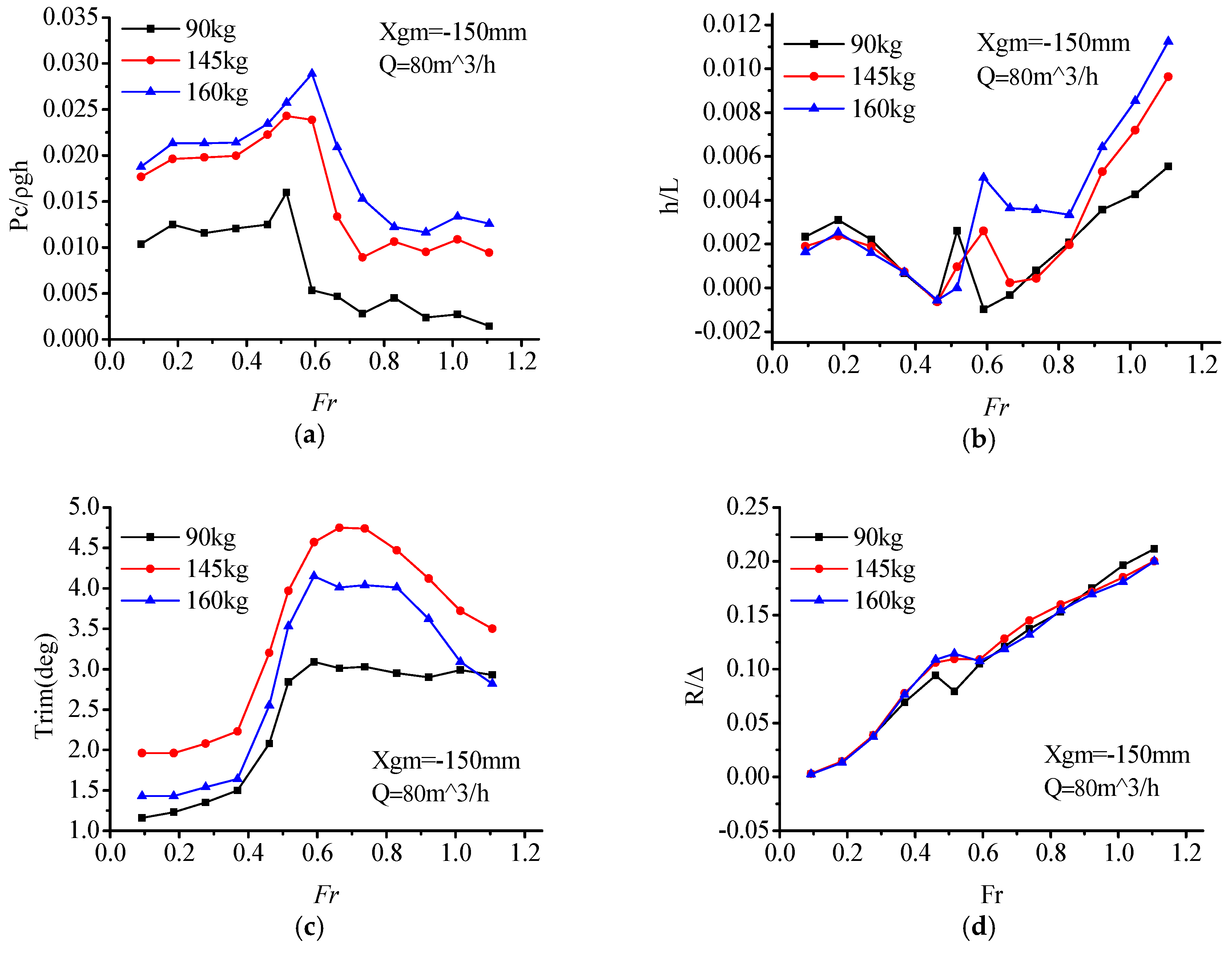
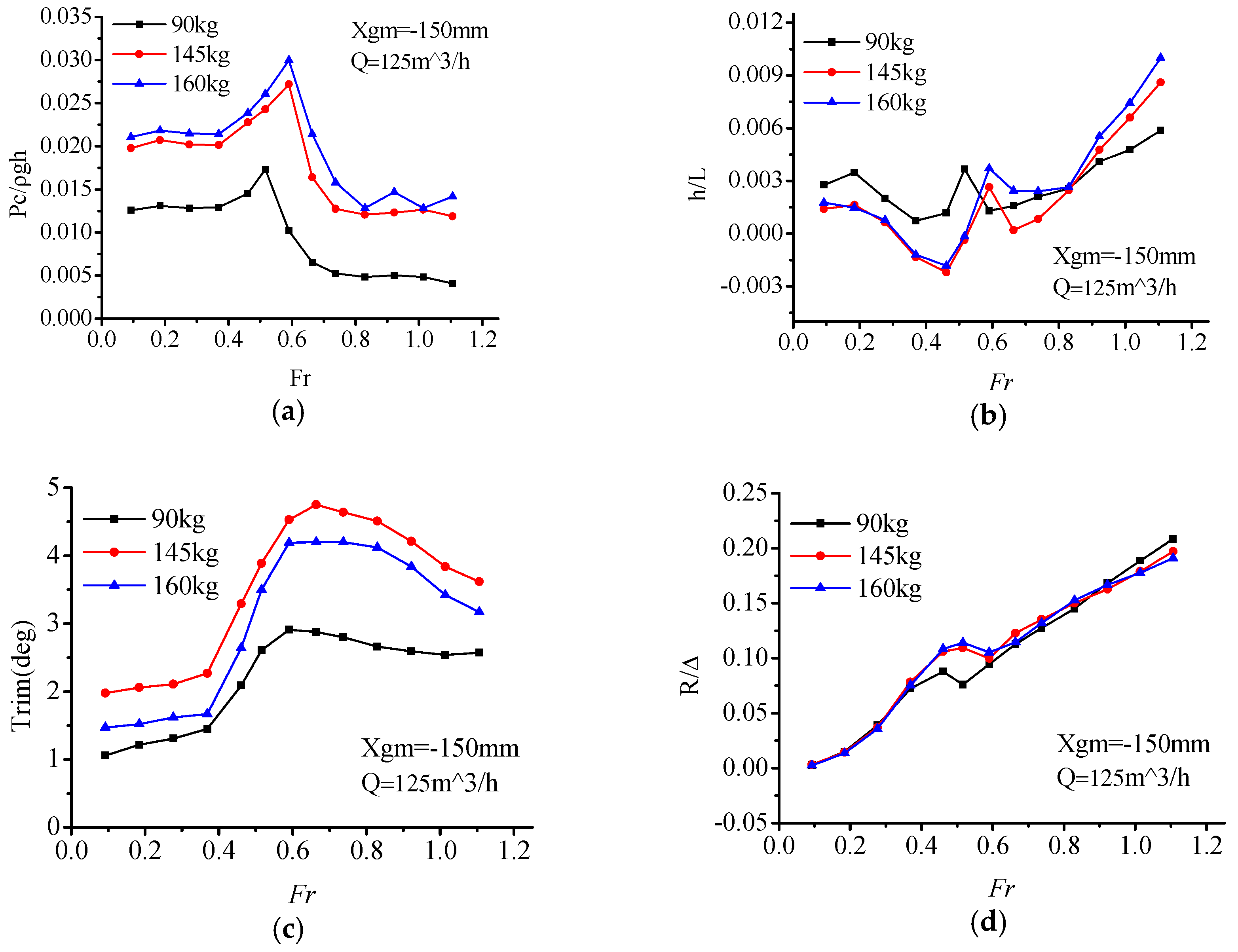
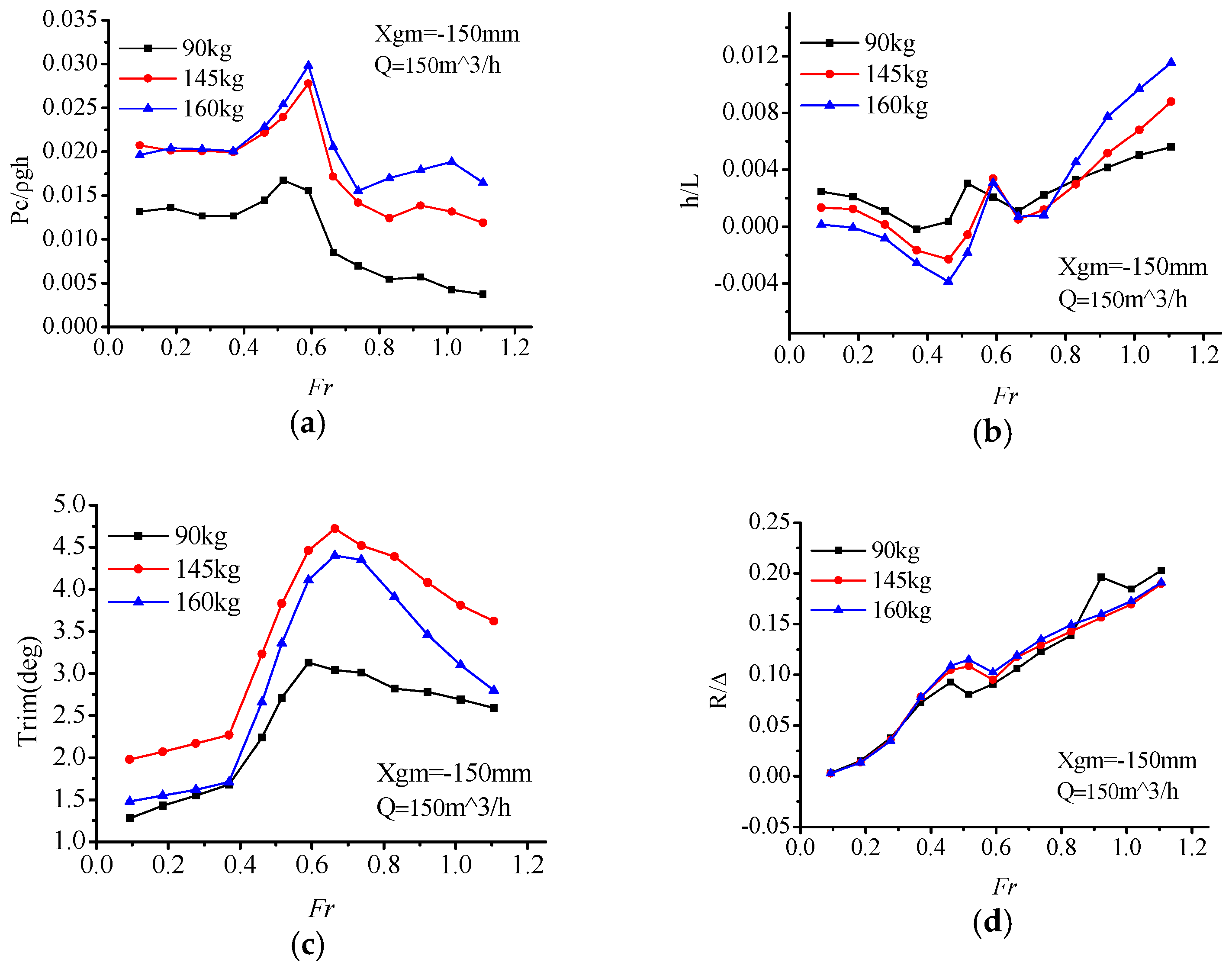
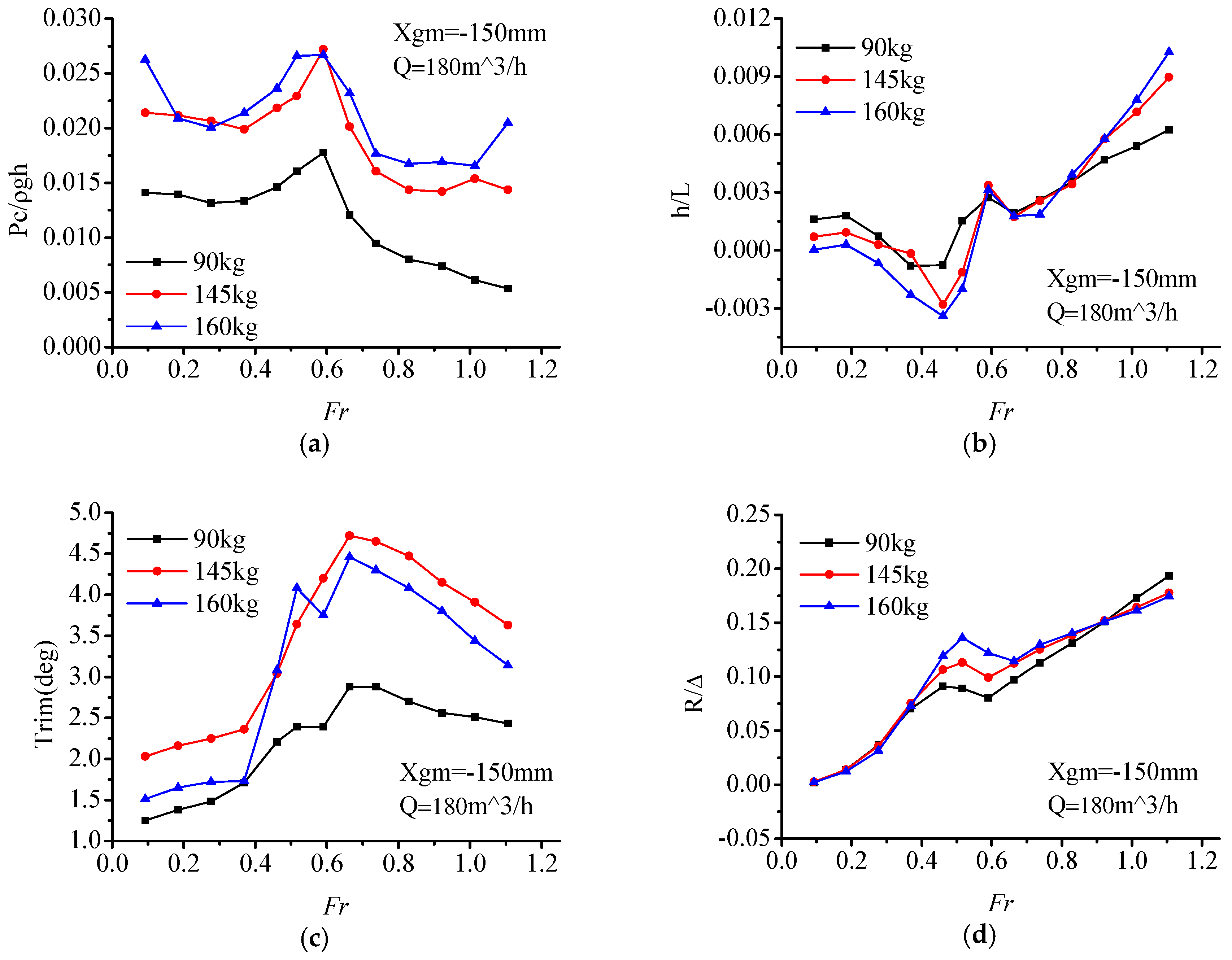
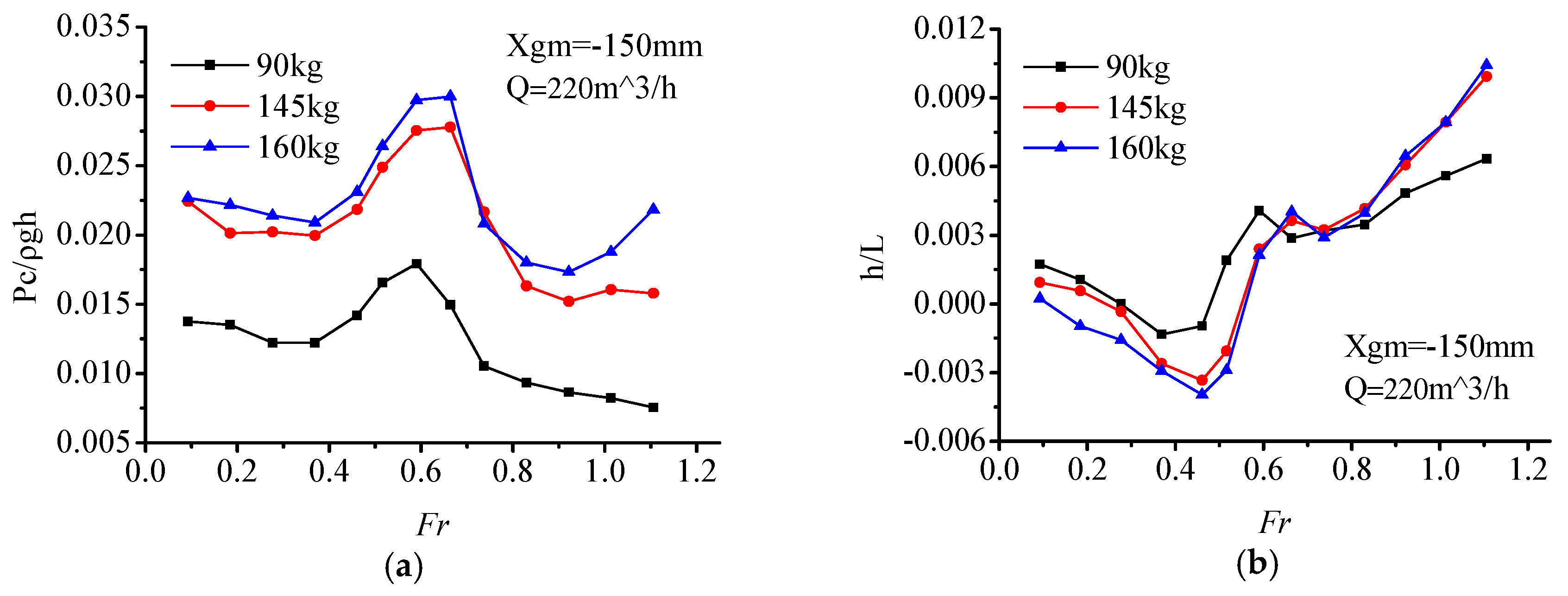
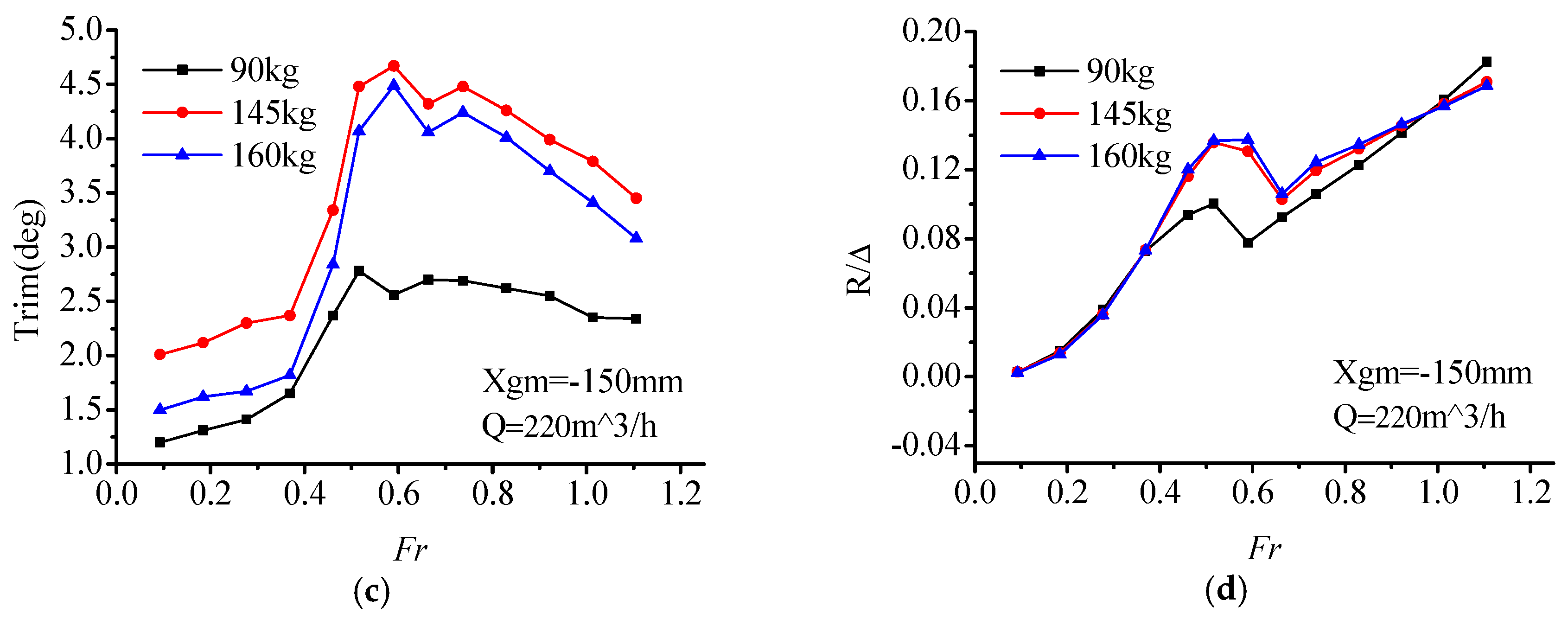
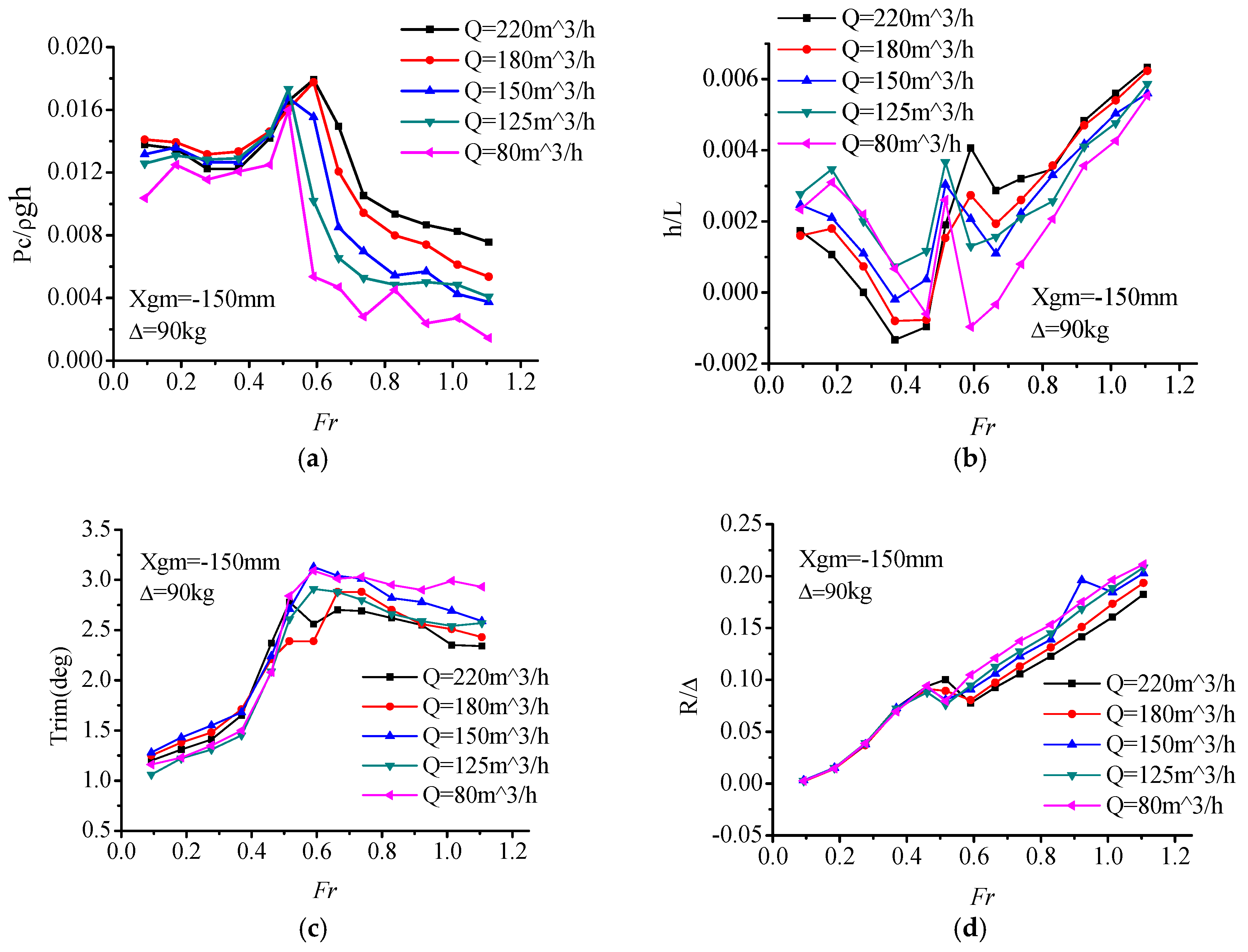
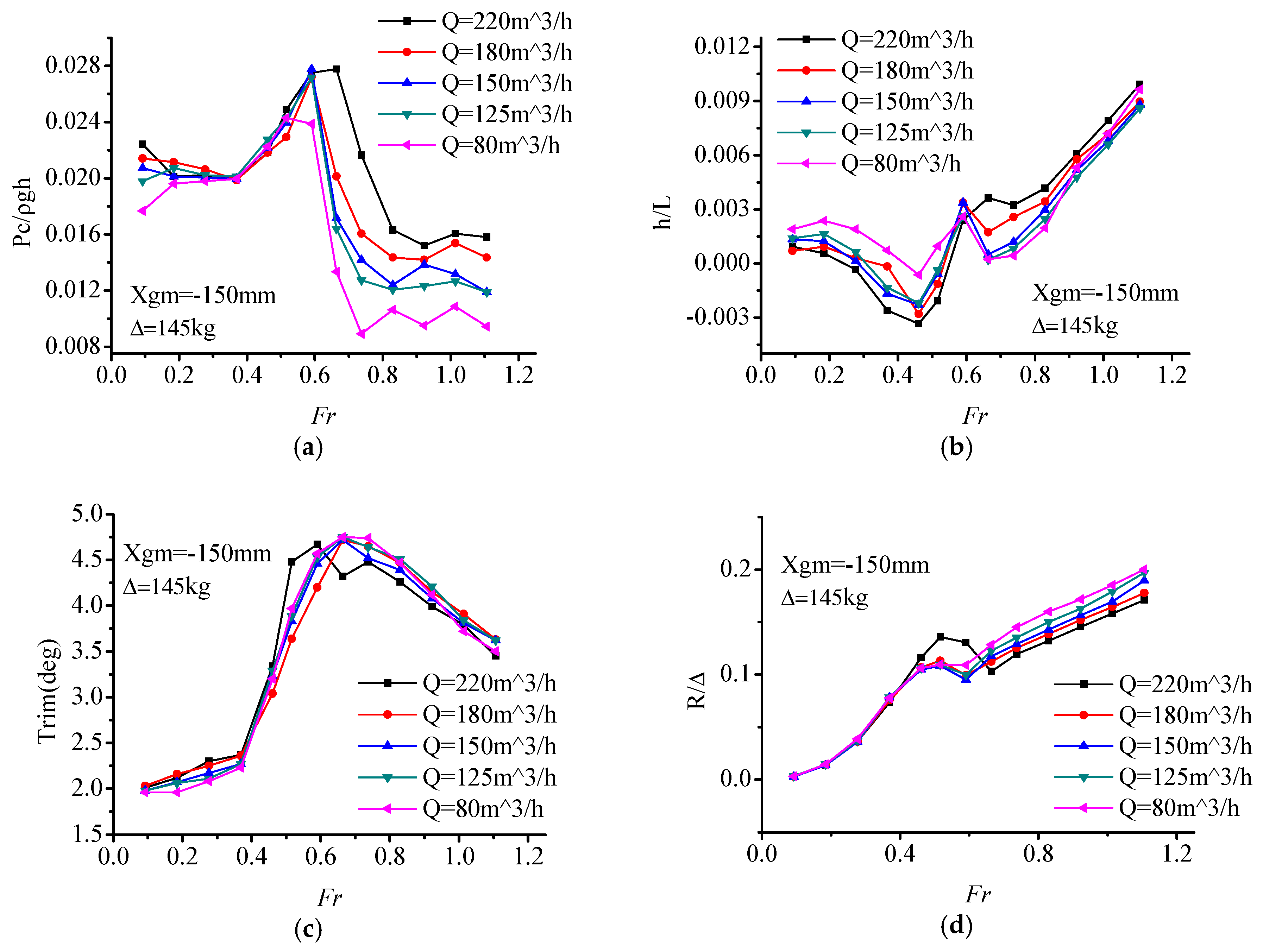
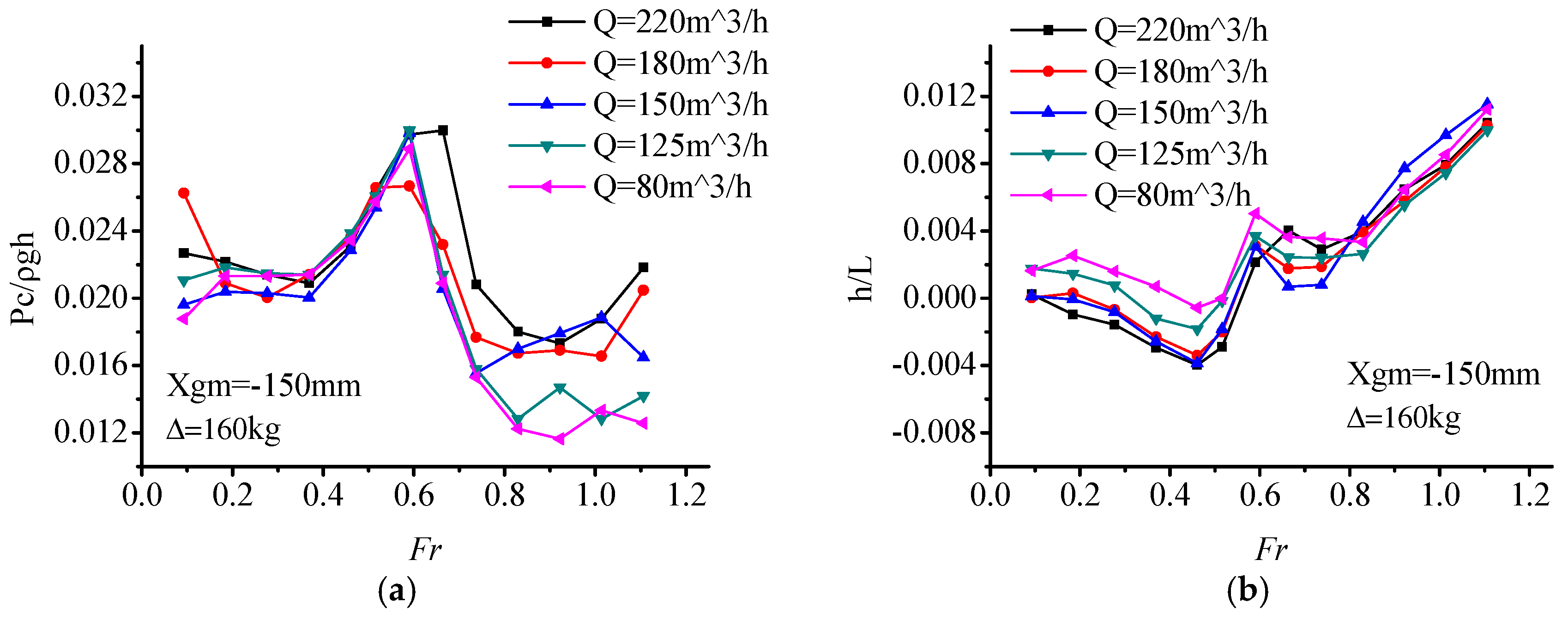
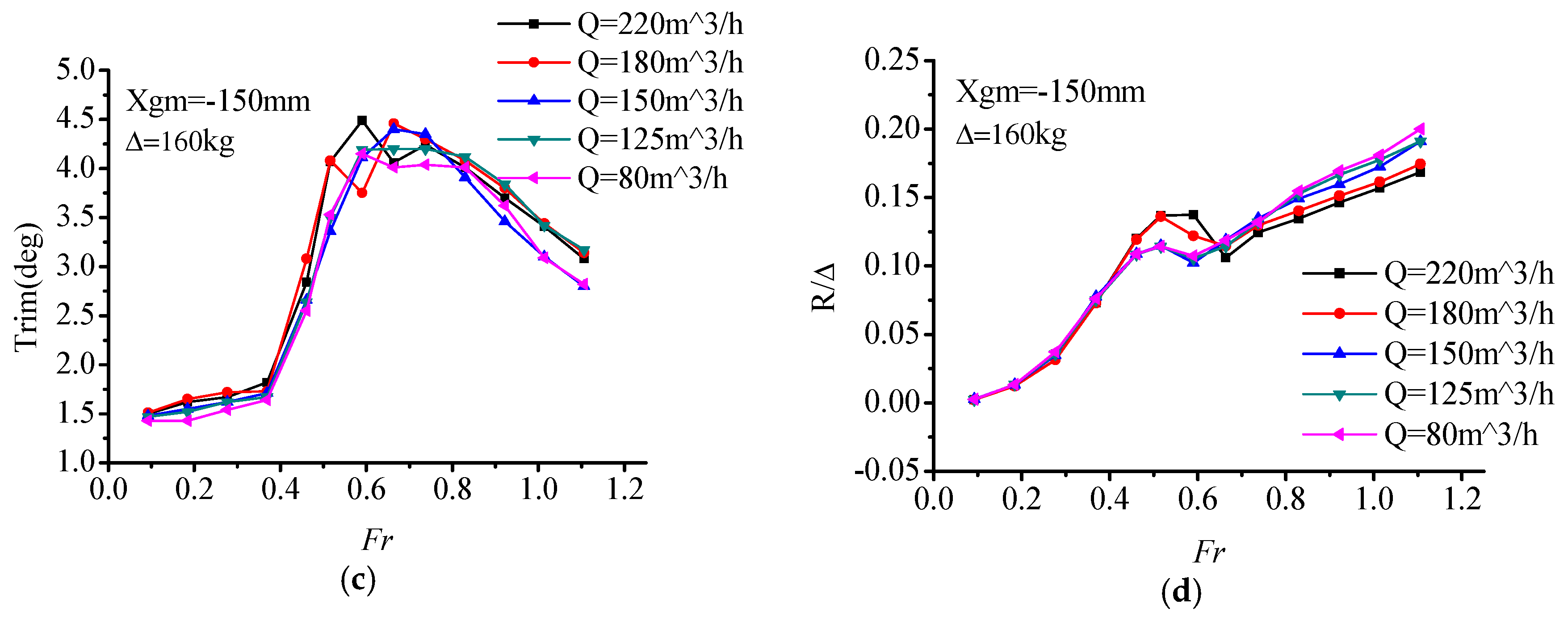
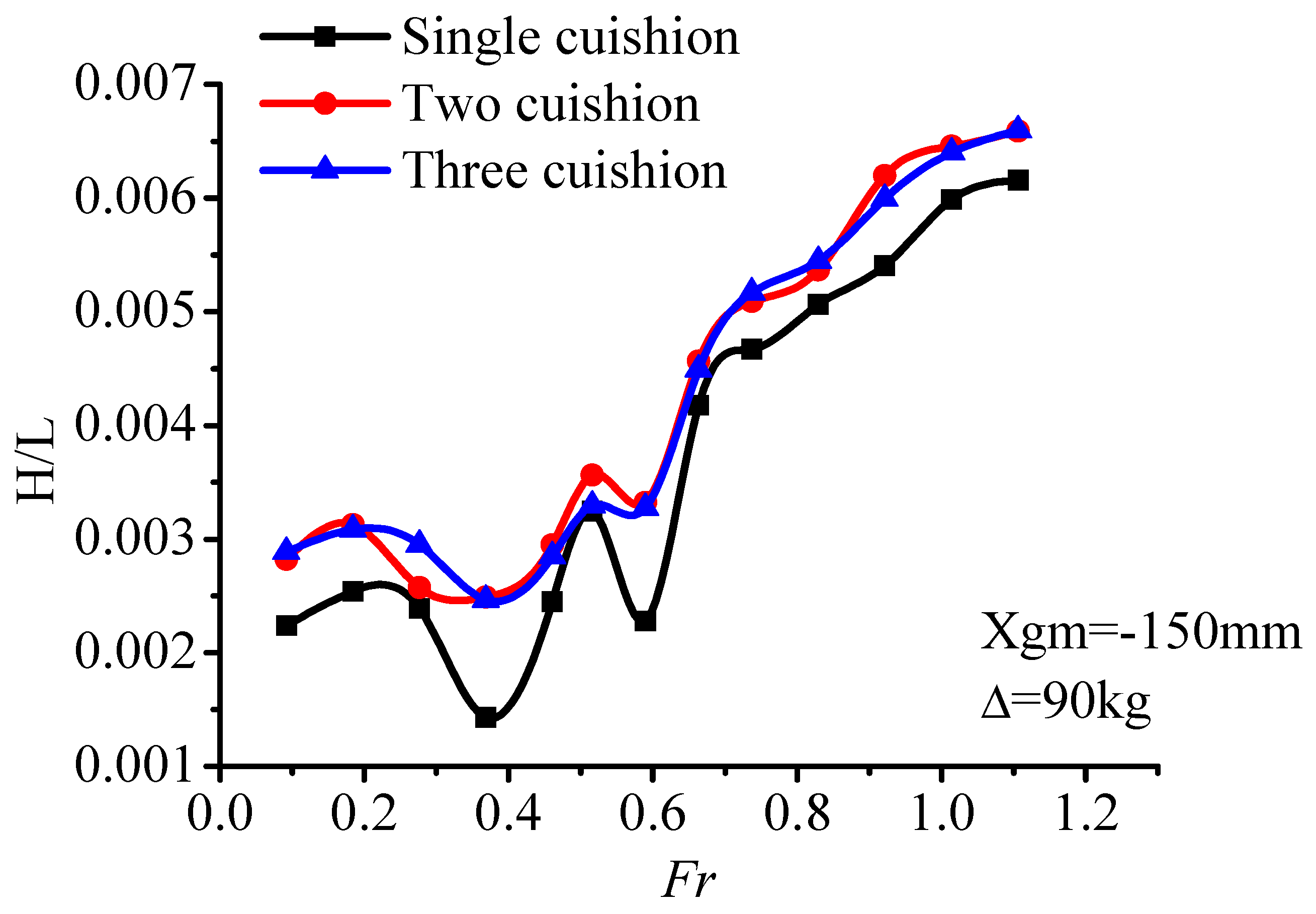
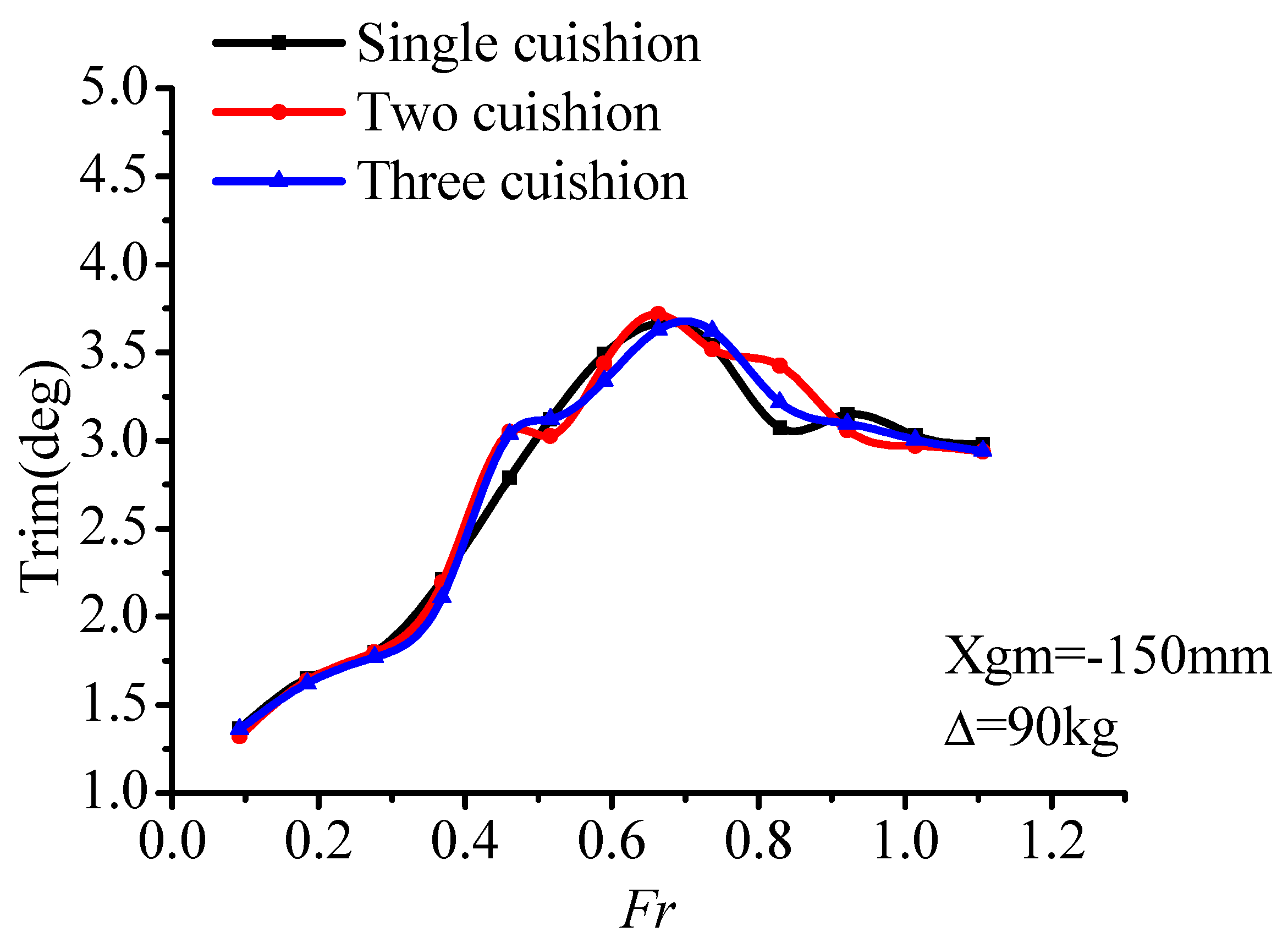
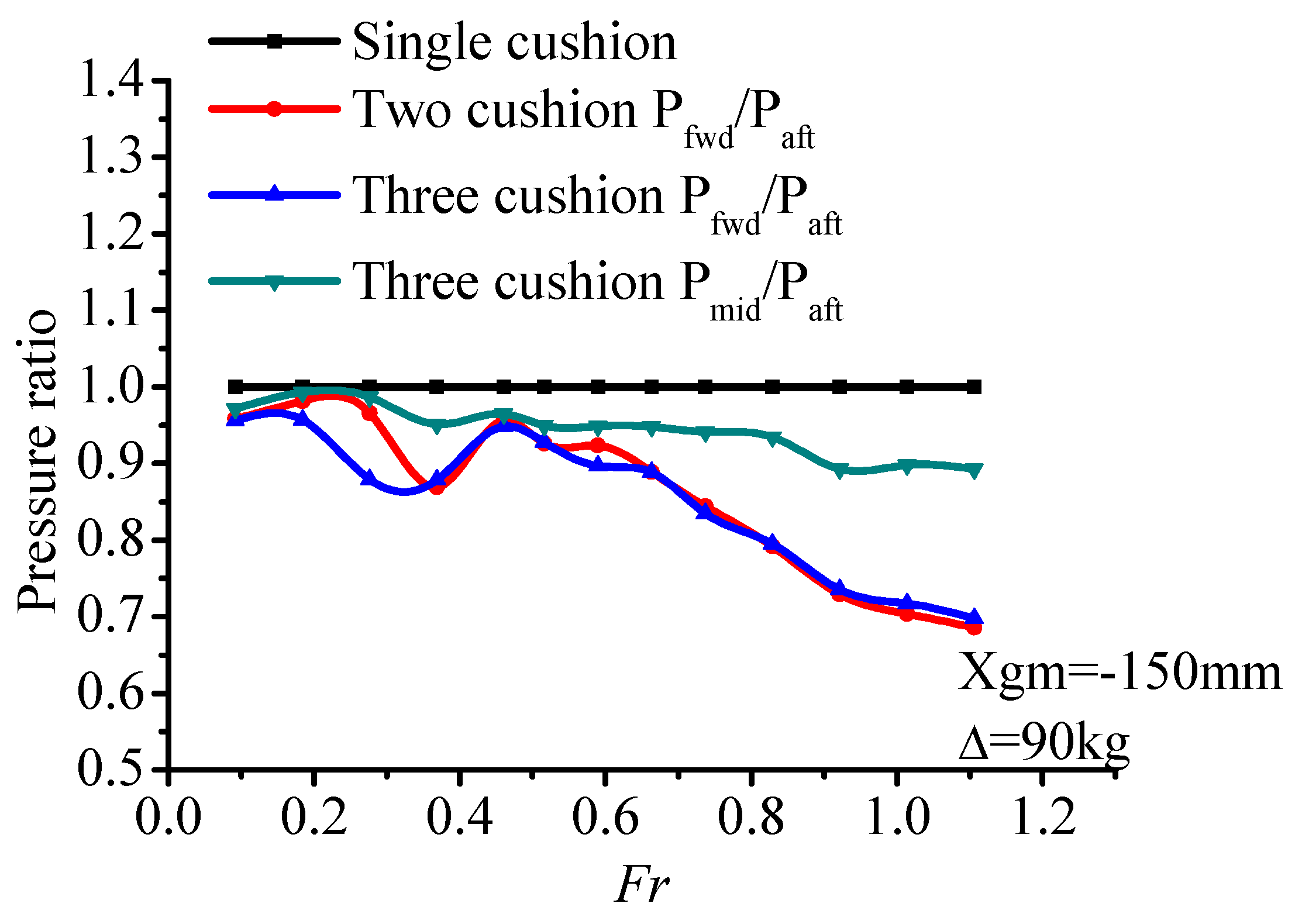
Figure 10, it can be seen that with the change of load displacement (90 kg, 145 kg, 160 kg), the variations of air cushion pressure P
c are consistent with each other. At light displacement 90 kg, with the increase of air flow, the air cushion pressure increased. Within the range of
Fr = 0.59–0.66, the pressure curve reached its pressure peak, which was slightly later than the resistance peak (
Fr = 0.46–0.66).
Within the range of the whole-speed segment, interaction of the air cushion pressure, and hydrodynamic force act on the model. Air cushion pressure had a small influence on the trim angle, but a great relationship with the heave. In the low-speed segment (Fr < 0.46), with the increase of speed, the air cushion pressure was stable within a certain range while the trim angle increased, thereupon, the center of gravity position decreased, and the value of heave went down. In this speed segment, the hull met the characteristics of conventional displacement ship, and the resistance increased sharply.
Within the resistance peak segment (Fr = 0.46–0.66), the cushion pressure gradually increased, the heave height increased, and the trim angle also increases continuously. Under the combined action of these three factors, the total resistance of the ship increased sharply up to the peak.
In the high-speed segment (Fr > 0.66), the air cushion pressure reached a peak, so did the heave height. The trim maintained at a high angle level with a slightly reducing trend. Furthermore, on account of the high value of trim angle, the bow-flow-discharge increased, and air cushion pressure also reduced gradually, which caused the air cushion lift to have a decreasing trend. Total resistance increased gradually due to catamaran hull high-speed planing hydrodynamic factors.
To sum up, during the low and high-speed segment, the influence of cushion pressure on the PACSCAT sailing state is not obvious, and the response pattern is consistent with the hydrodynamic influence trend. While in the range of the resistance peak, cushion pressure affects the resistance peak by changing the motion attitude. This phenomenon may be caused by the interaction of cushion pressure and the motion state. At lower speed, the cushion influence is limited. The total resistance is similar to a displacement hull. While the cushion pressure and trim make the heave decrease gradually. But in the resistance peak-speed segment, the cushion chamber remains at a high-pressure level which generates a high lift ratio and moment, the uppitch degree increases rapidly. At the same time, the high lift ratio causes an increase of the heave. At the high-speed segment, the influence of the cushion pressure weakens; the response pattern is consistent with the hydrodynamic influence trend again.
As for the total resistance of PACSCAT, the influence of the air flow supply rate in the low-speed segment is finite, with a narrow resistance difference between each condition. In the resistance peak segment, the large air flow rate causes a large resistance peak. However, in the high-speed segment, the larger air flow rate matches a smaller resistance. That means the whole-speed segment’s optimal resistance curve can only be obtained by selecting suitable air flow rate schemes for specific speeds, respectively.
In another form, the experimental data are organized to clarify the comparison of the air cushion pressure, heave, trim, and resistance under various displacements at the same air flow rate, respectively (On account of five different air flow rate condition, the figures are summarized in five groups, and the number plot is up to 20. Considering a better continuity and readability of the main text, the plots are attached in
Appendix A). From
Figure A1,
Figure A2,
Figure A3,
Figure A4 and
Figure A5, it can be seen that the demihull draft increases with the displacement, so does the trend of air cushion pressure and trim angle. As for the total resistance, the displacement has a significant influence on total resistance peak value, with a positive correlation trend; the increase of displacement corresponds to the increase of the resistance peak while there is no obvious resistance difference at high speed.
3.2. Test Phenomena and Resistance Components Analysis
Due to the resistance, components of PACSCAT are complex, both the wider demihull and air cushion have a significant influence on the sailing performance, which distinguishes it from traditional hovercraft. Using the estimation formula to extract air cushion and hull resistance (air cushion wave-making resistance, air seal resistance, air resistance, friction resistance, and so on), respectively, the composition and proportion of the resistance along the whole-speed segment were obtained.
The air cushion wave-making resistance of a hovercraft can be expressed as:
where
represents Newman cushion wave resistance coefficient valuing from the resistant coefficients atlas [
12].
The total resistance generated by the hull can be expressed as:
where,
Rhw,
Rair,
, and
represent hull wave-making resistance, air friction, friction, and total seal resistance of bow and stern, respectively.
Further, hull wave-making resistance and air friction can be obtained by
where
: air density,
: coefficient of air resistance,
: speed,
: model maximum cross-sectional area.
: water density,
: frictional resistance coefficient, adopting the 1957 ITTC (The International Towing Tank Conference) formula,
: wetted surface.
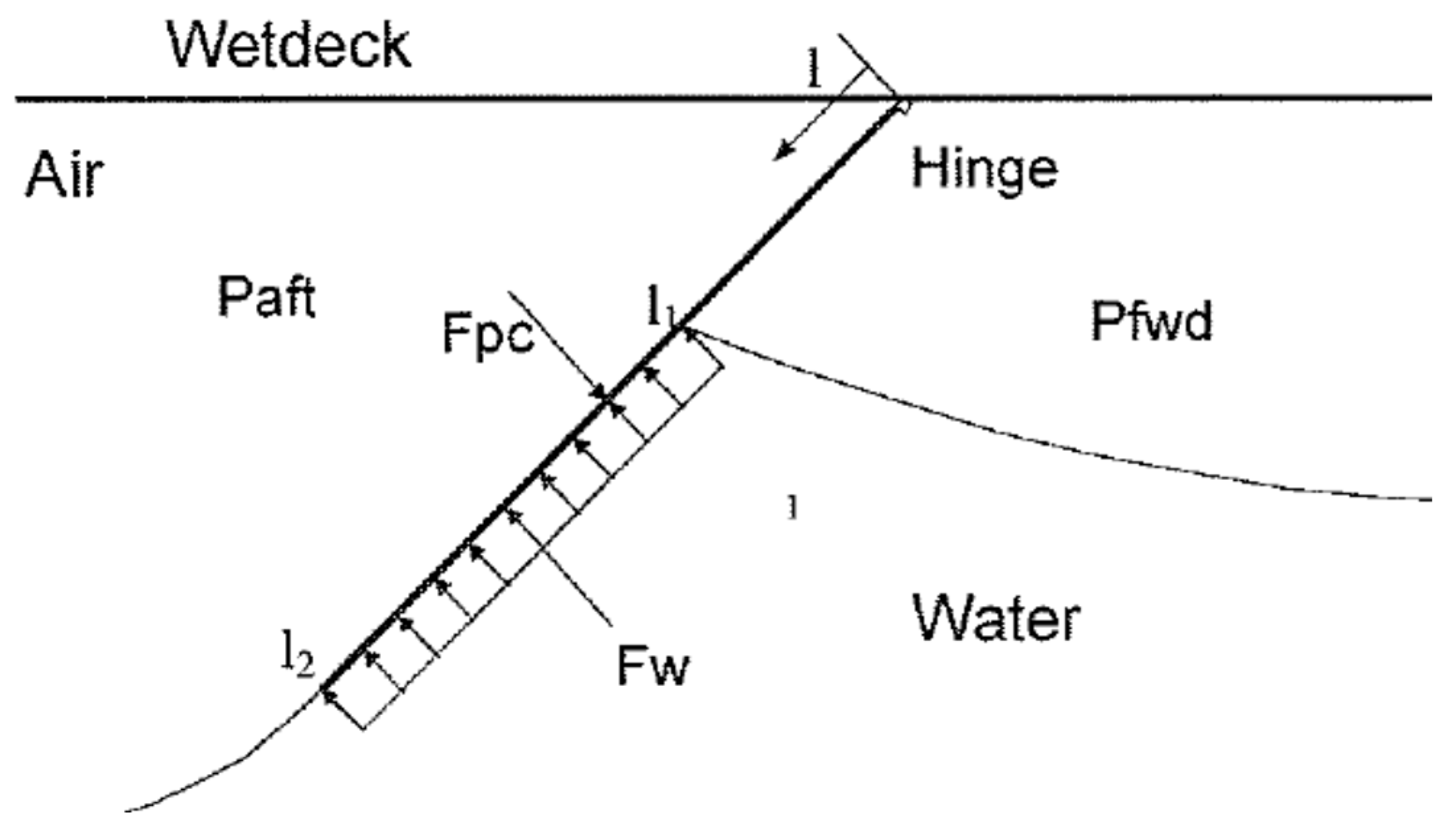
And, air seal resistance can be calculated by formula [
13]
where,
: rear side pressure of seal,
: front side pressure of seal,
B: seal width,
: wetted length of the seal,
: non-wetted length of the seal. The force diagram sketch is shown in
Figure 11.
By calculating the difference between Rt, (total resistance) and other resistance components, total wave-making resistance Rw (including air cushion and hull wave-making resistance) is obtained. In the actual situation, both Raw and Rhw are interacted and mixed. Using Rw is more likely to explain the composition and proportion of the wave-making resistance.
Through data processing, it is worth noting that the test phenomena and resistance characteristic vary with the speed and have strong regularity and have basically the same trend under various working conditions. Taking condition
= 145 kg, Q = 150 m
3/h as a representative sample is feasible. Decomposing the resistance, every component force and its ratio are obtained within the range of speed. Some of the components (e.g., air resistant) have a very small ratio and are omitted.
Figure 12 shows a diagram of the forces ratio situation. And
Figure 13 shows a series of wave snapshots of bow view at different speeds.
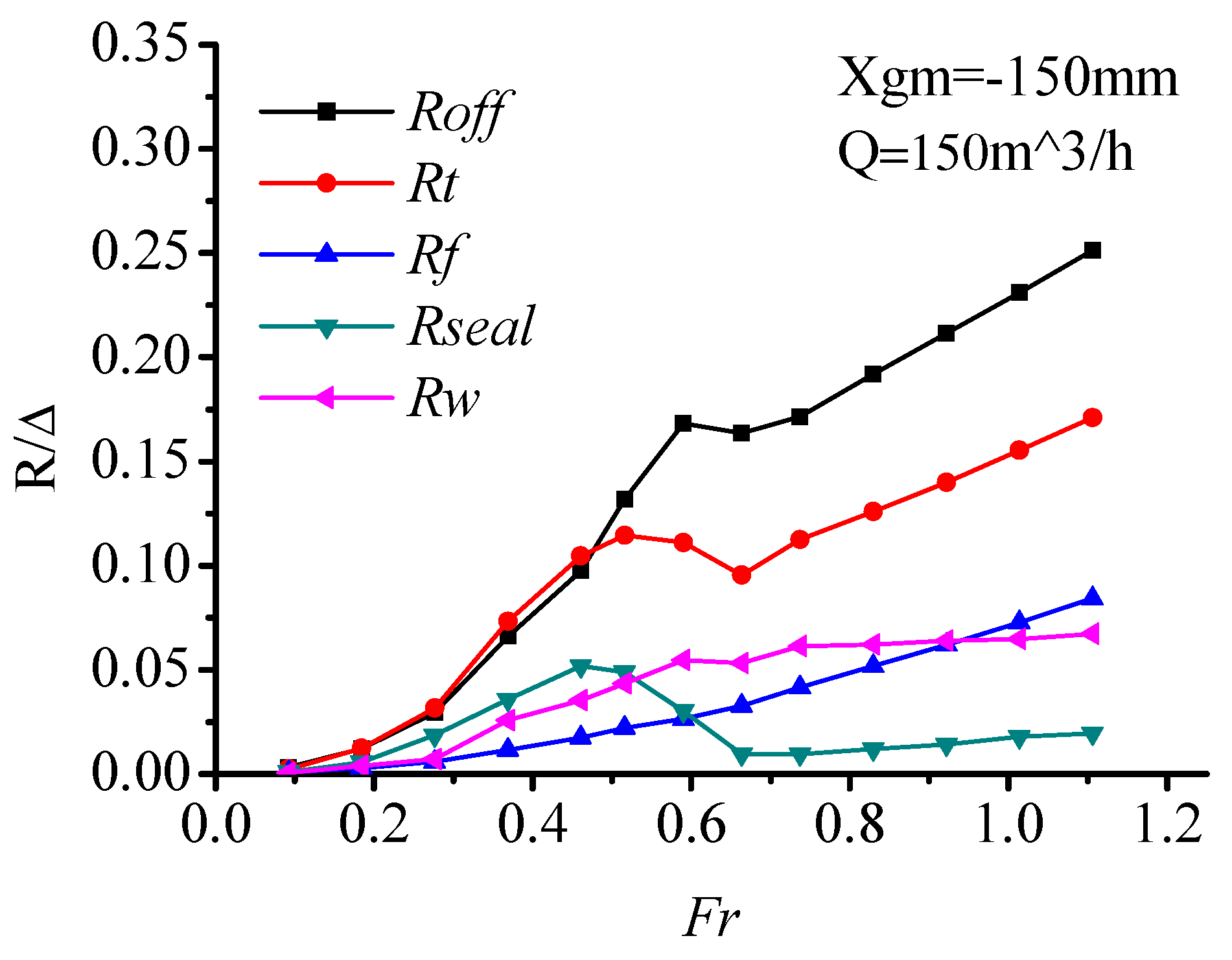
Where Roff is total resistance of hover system off, Rt is total resistance with hover state, Rf is frictional resistance dynamically calculated with a wet surface, Rseal is total resistance of bow and stern seal, Rw is wave-making resistance (including air cushion and hull wave-making resistance).
From
Figure 13, total resistance comparison between
Roff and
Rt at the low-speed segment (
Fr < 0.46),
Roff is slightly less than
Rt. The cause is that the bow seal submerged depth is great at the low-speed hover state, and the impact of decreased hull wetted area cannot cover the friction resistance and wave-making resistance produced by bow air seal. Similarly, the total seal resistance has an increasing trend because of the heave and trim making seal submerged depth increase. At the Froude number of 0.46, the seal immersed maximally, the total seal resistance reached the top until the Froude number of 0.66 where the seal reached the free surface gradually, the total seal resistance decreased to a negligible level. The frictional resistance was similar to that of the displacement ship which increased monotonically with the increase of speed. At low speed, the proportion of friction resistance was small, but with a major proportion at high speed. The wave-making resistance takes a large proportion of total resistance in the full-speed range. And specifically, it is the maximum component at resistance hump, and getting to a stability range after that.
In low-speed segment (Fr ≤ 0.37), with the speed increasing the model trim raised slightly and the gravity center descended obviously, which deepens the immersed depth of the seal. High-speed airflow leaks from the seal slit and its junction with the hull. The water-pushing phenomenon of the bow air seal is obvious. At this moment the seal resistance takes a huge proportion of the total resistance. In resistance peak exceed segment (0.37 ≤ Fr ≤ 0.59), the wave-making length was approximately equal to the length of the air cushion. The bow and stern seals were at the wave crest. The bow seal water-pushing phenomenon was intensified. With the heave and trim change, at the front of demihull, the wave-making was also severe. The wave dashes on the bow seal. With all factors above coupling, the seal resistance is high. During this segment, the wave-making trough in hover chamber was located at midship, it increased the side overflow of the air partly. However, the overflow can be omitted under high displacement working condition. When the Froude number was over 0.59 (Fr > 0.59), the wave-making trough in hover chamber moved to stern seal, and cushion pressure and trim angle meet the maximum, and also explains that with speed increases, the model was in a relatively stable state, with the bow the seal lifted out of the water, hence, the air seal resistance reduced to the minimum. The seal also makes airflow leaking height increase which caused the cushion chamber pressure to decrease obviously. It also caused waves at the bow chine line and stern, generating spatter and breaking waves and energy dissipated.
3.3. Validation and Results of Numerical Method
To evaluate the results of the numerical simulation method, comparisons between the wave phenomenon of numerical simulation and experimental results were carried out. So were the numerical simulation and experimental parameter values. The numerical method showed an accurate simulation of these characteristics with better anastomosis. Taking conditions
Fr = 0.31and
Fr = 1.03 as examples, details are shown in
Figure 14 and
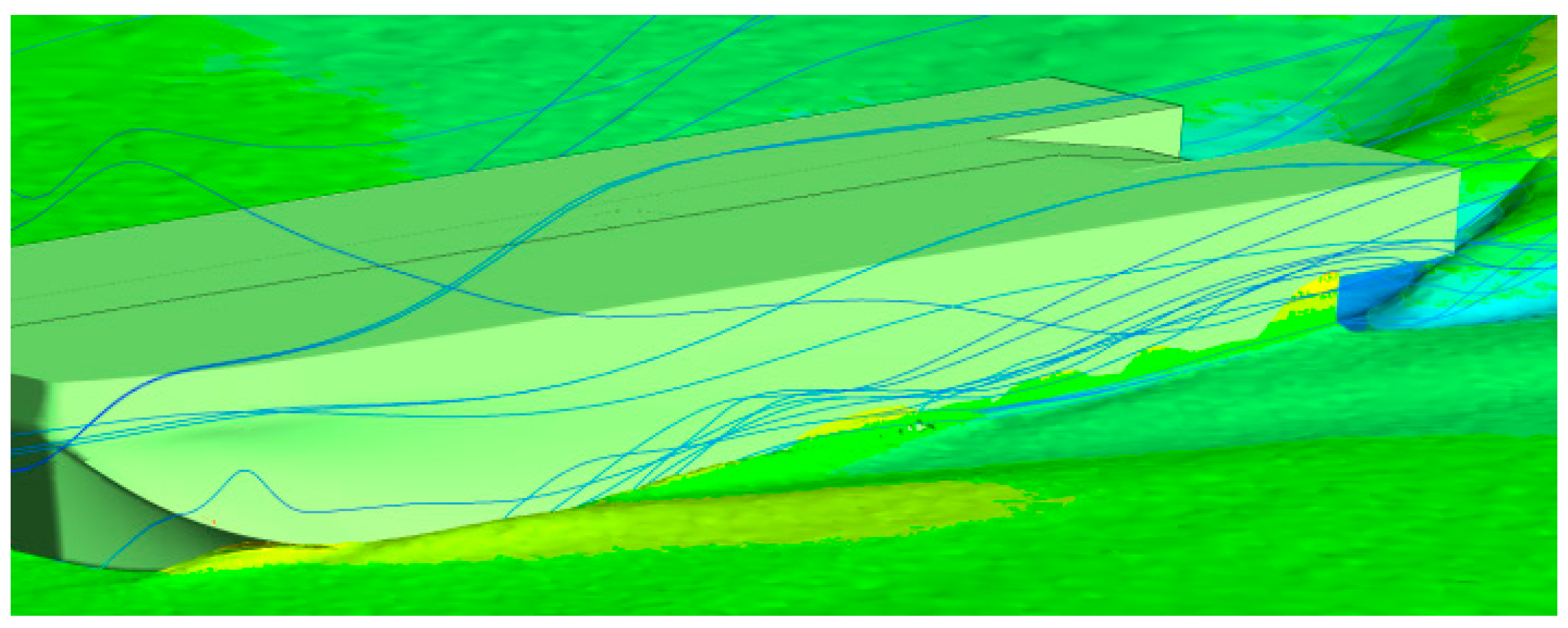
Figure 15. At the Froude number of 0.31, the gravity center and the trim angle were both a small value. Bow seal generated a water-pushing effect and wave at midship side reached a certain height. At the Froude number of 1.03, no significant bow appeared, and the wave peak moved to the stern. A larger wake flow crests formed at the longitudinal mid-section which were all reflected in numerical simulation. In experiment, there were some thin non-airtight slit on the seals and a slit may also exit at the junction with the hull while in the numerical situation, all these junction and slit could be ignored, only demihull side leaks air flow as shown in
Figure 16. Therefore, high-speed airflow can leak from the slits which may cause the wave-making, especially wave-making behind the hull, to be more obvious than the simulating condition.
Figure 14 and
Figure 15 reflect the phenomenon. It is also a reason explaining why the experimental resistance is higher than the numerical result.
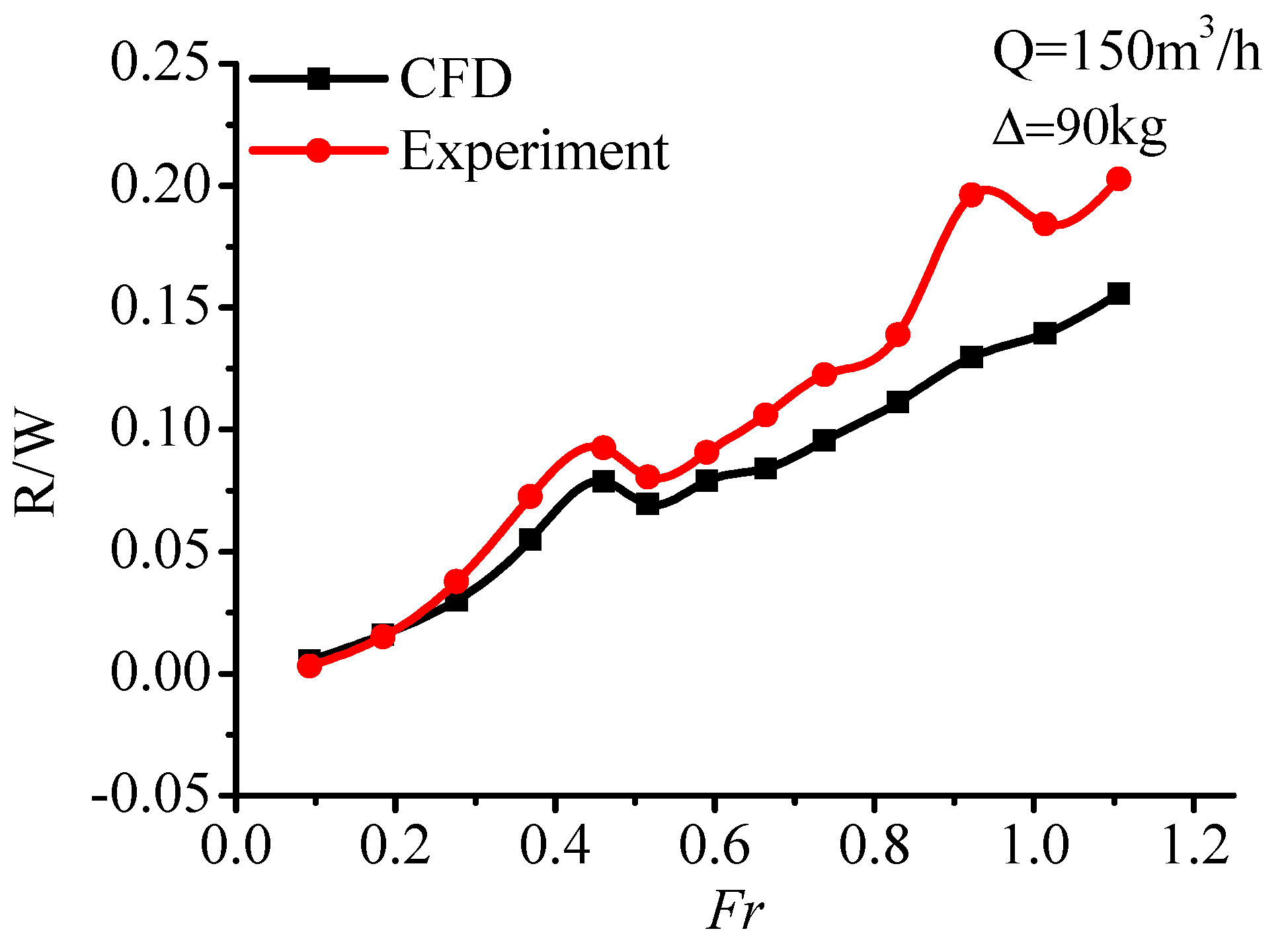
Table 4 shows the comparison of the numerical calculation and model test results (
= 90 kg, Xgm = 150 mm), and calculated R/∆, trim angle, sinkage, and numerical error are summarized in
Figure 17 and
Figure 18 though the numerical simulation fails to simulate the secondary resistance peak under this condition. As shown in
Section 2, this secondary resistance peak does not exist in other working condition experimental data. The error of the numerical simulation resistance increased from the low-speed segment of 6% to the high-speed segment of 33%. However, the numerical simulation resistance prediction under middle or low speed is more accurate. The trend of resistance is basically synchronous in the whole-speed segment. And the numerical simulation predicted the resistance peak at the Froude number of 0.46. It is also an acceptable accuracy compared with other side-wall hovercraft numerical simulation results.
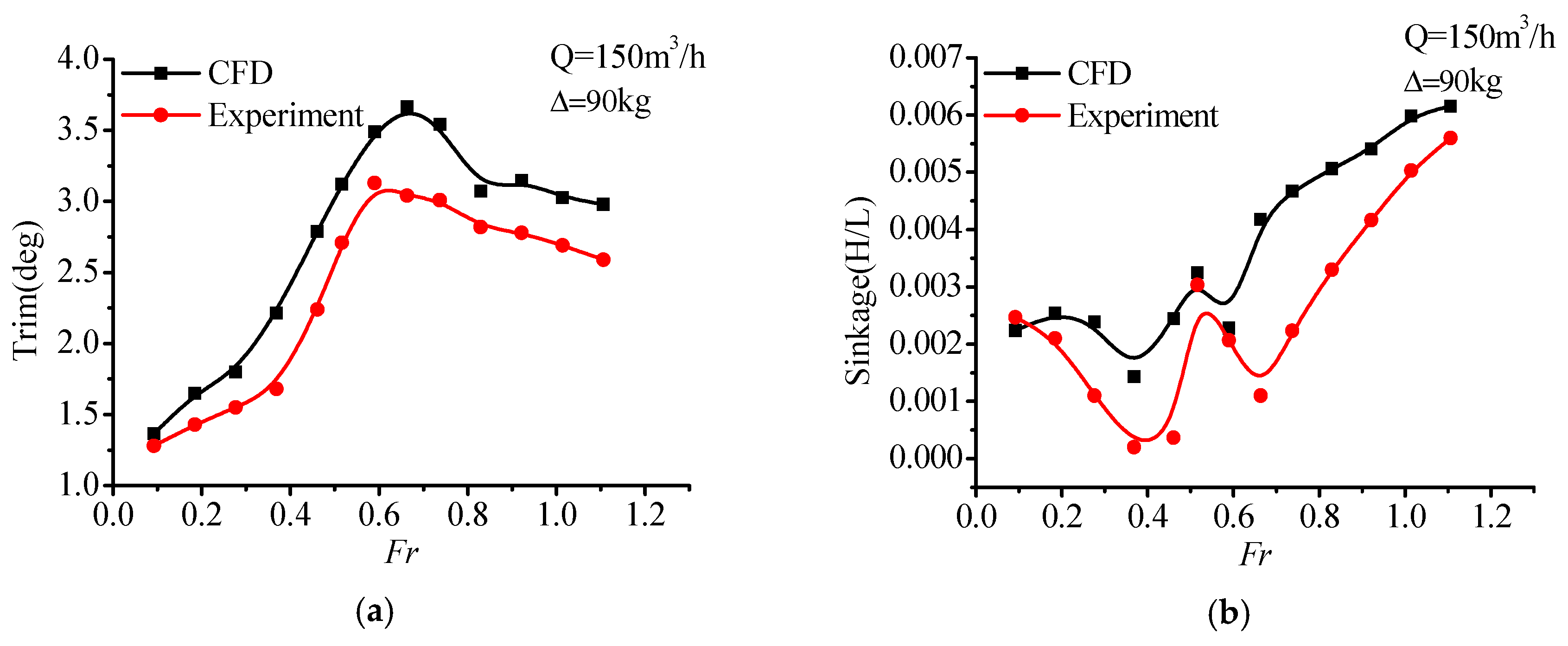
It can be seen in
Figure 18 that, the testing data of trim and sinkage is less than the corresponding simulation results. With increasing speed, in either trim or sinkage line graph, a positive agreement can still be observed between testing data and simulate data. The error of trim angle rages from 7% to 15%, but actually, the value difference is merely 0.63°and 0.37°on average. On the other hand, the value difference is of heave is larger, while the trend also met a good agreement. It seems to be related that the hover system has a lower level air-flow loss in the numerical system. Therefore, the validity of the numerical method is approved. Furthermore, the relatively large error in the high-speed segment will a have a finite impact on the discussion of resistance reduction trend and effect in the following discussion.