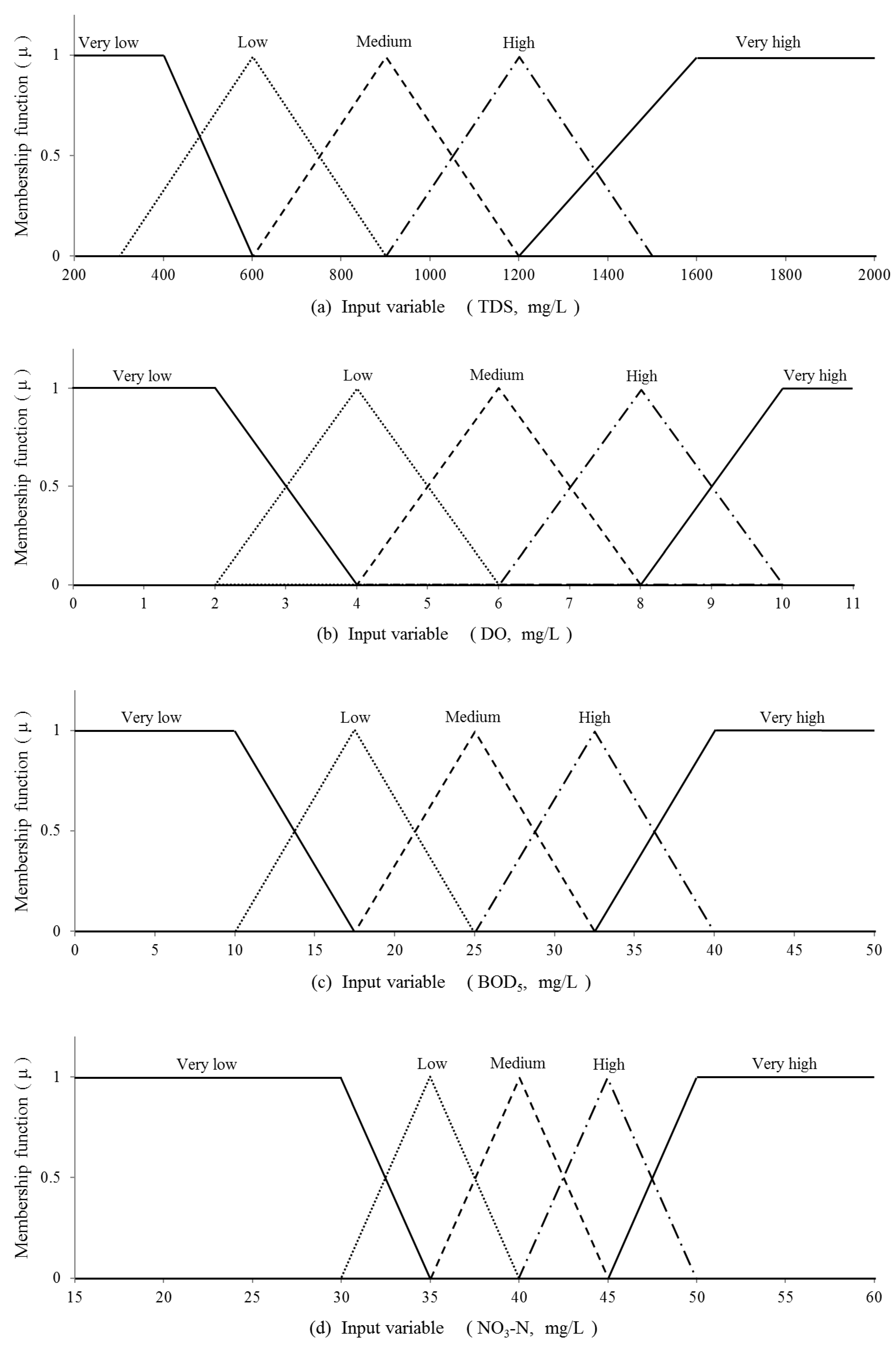
3.1. Water Quality Simulation
The one-dimensional HD and WQ model were applied to simulate water quantity and WQ along the El-Salam Canal. In the calibration process (September 2012–August 2013), the M value which achieved the lowest error in discharge was 40 m
1/3/s. The RMSE and NOF values between the observed and simulated discharge were 1.66 m
3/s and 0.02 for Pump Station No. 1 and 1.10 m
3/s and 0.02 for Pump Station No. 2, respectively. Moreover, for the validation period (September 2013–August 2014), the RMSE values were 2.94 m
3/s and 1.39 m
3/s, with NOF values of 0.04 and 0.02 for the discharges of Pump Stations No. 1 and No. 2, respectively. The model calibration and validation for the discharges of the pump stations (with the low NOF values) evidenced the ability of the model to correctly simulate the processes in the canal and therefore, it seemed reasonable to employ the simulated discharge to investigate the impact of various management scenarios. The TDS, DO, BOD
5 and NO
3-N results from the calibration model (September 2013–August 2014) were calculated at two different locations: (1) after mixing with the Faraskor drain at 1.9 km; and (2) before the downstream of the canal at 86 km from the intake (
Table 5).Overall, the model provided reasonable agreement with observed WQ data along the El-Salam Canal, though TDS at 1.9 km and DO at 86 km showed relatively high NOF values.
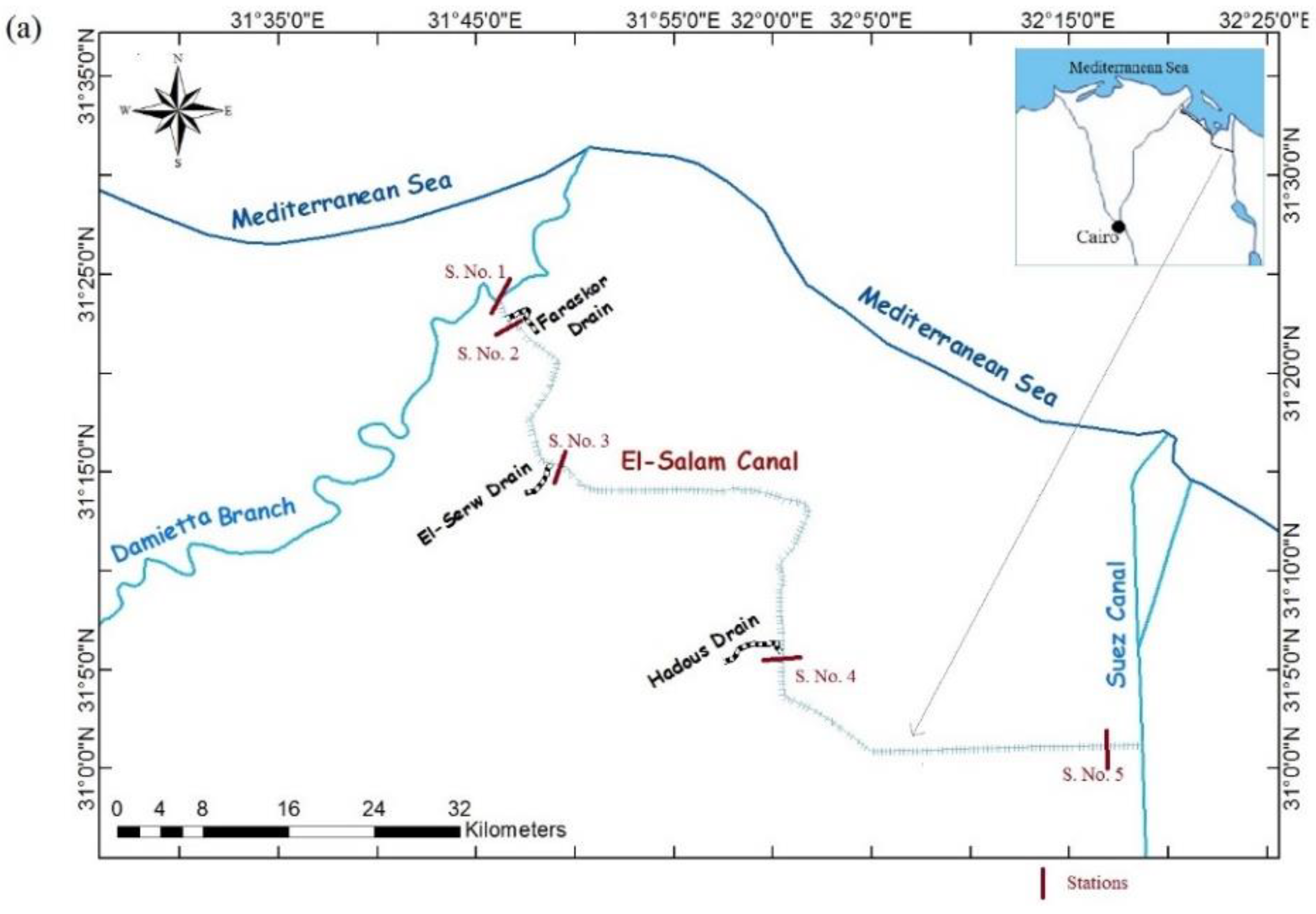
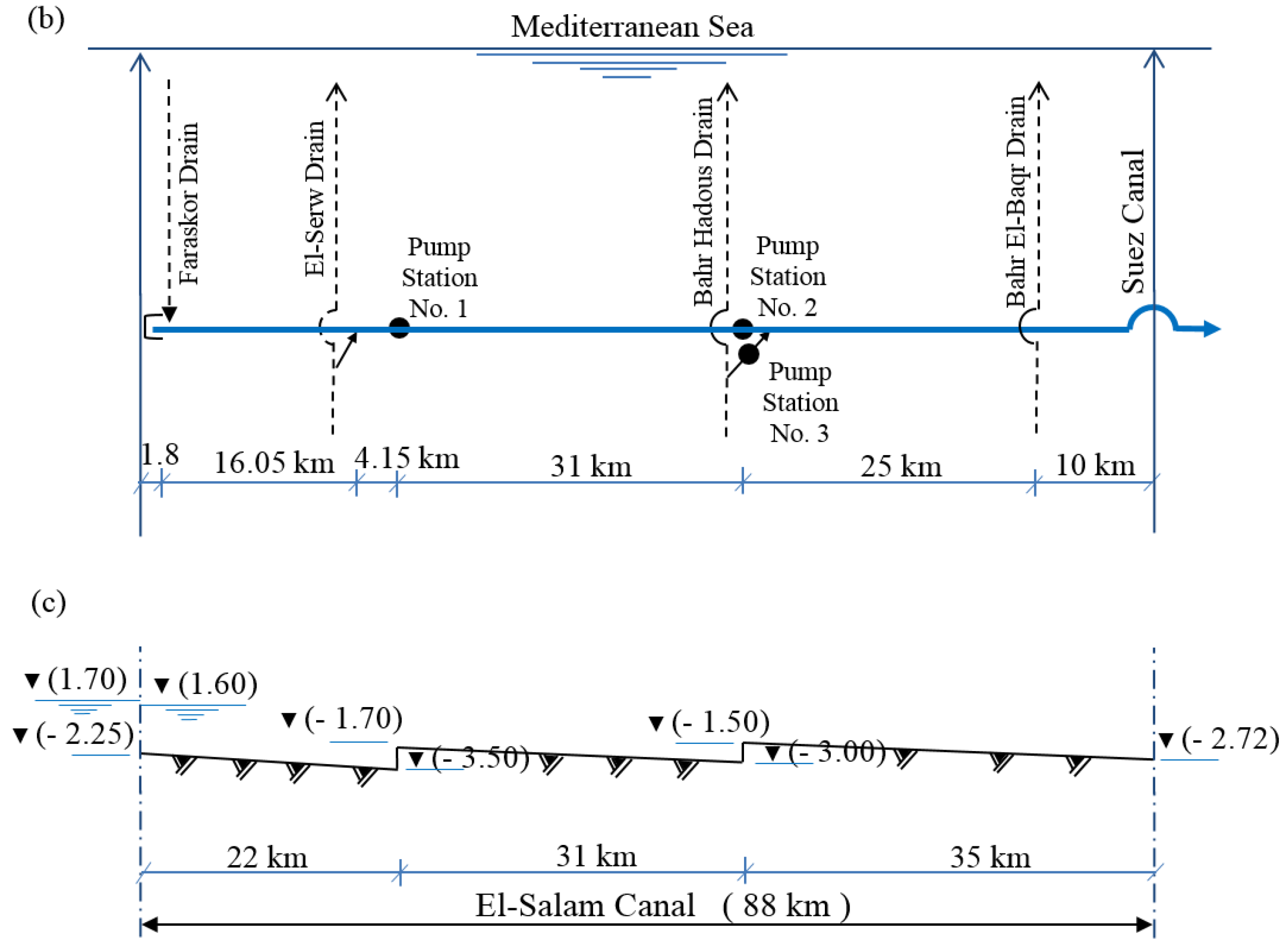
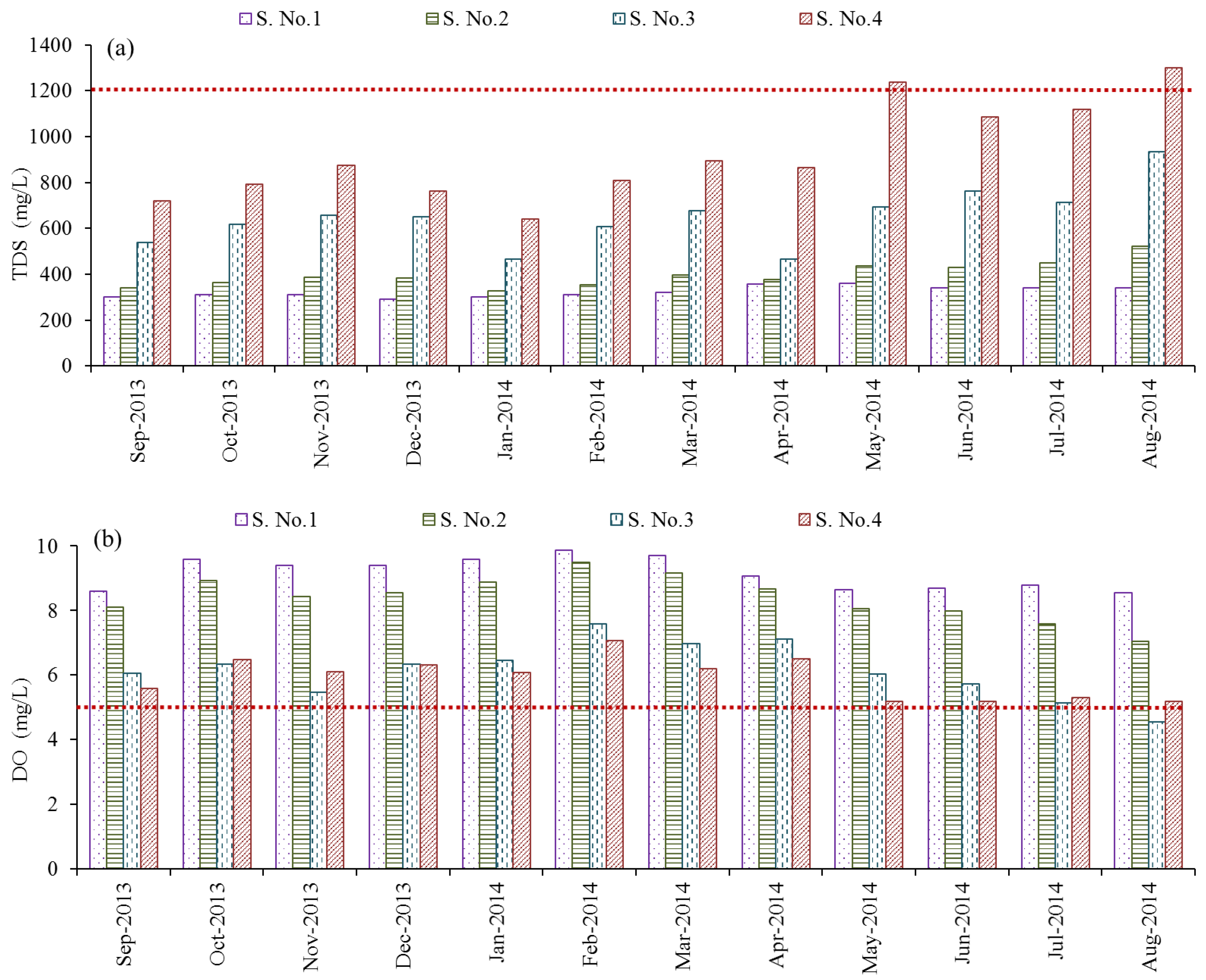
The simulated WQ parameters for the period from September 2013 to August 2014 along the El-Salam Canal at four selected stations (S.) from the intake and after mixing with the agricultural drains, were compared with the Egyptian standards for water reuse in irrigation as shown in
Figure 3a–d. Stations S. No. 1, S. No. 2, S. No. 3, and S. No. 4 were located at 0.0 km, 1.85 km, 18.5 km and 55.0 km, respectively. The TDS values along the El-Salam Canal varied from 292 mg/L to 1300 mg/L, from September 2013 to August 2014 (
Figure 3a). The TDS concentration violated the Egyptian standards (TDS < 1200 mg/L) for direct reuse of water for irrigation after the connection with the Bahr Hadous drain (S. No. 4). The highest TDS values from 1085 mg/L to 1300 mg/L were registered at S. No. 4 in the summer season, particularly from May to August, due possibly to highly polluted water discharged from the Bahr Hadous drain, where the TDS values of ADW were at a maximum of 2420 mg/L. Seepage of salt water from the surrounding region is likely another source that increase TDS in the El-Salam Canal. Seasonal variation in water quantity as well as the fluctuation in mixing ratios of Nile River water with ADW may also have an adverse impact on the level of TDS in the water of the canal. These notions are indeed in agreement with those reported by El Gammal [
37]. Moreover, Hafez et al. [
38] detected high TDS fluctuation and variation in the canal after mixing with the Bahr Hadous drain (34–85%) and the El-Serw drain (31–57%). El-Sheekh et al. [
39] found that electrical conductivity (EC), TDS, salinity, and chloride were maximized at levels of 5616 μs/cm, 10,636 mg/L, 10.9%, and 5.1 g/L, respectively, at the Bahr Hadous drain, and decreased to minimum values of 1933 μs/cm for EC, 2104 mg/L for TDS, 2.6% for salinity, and 1.2 g/L for chlorides at the intake point (i.e., the Nile River). The authors claimed that variations in TDS might have been due to the effect of the ADW being rich in salts at the Bahr Hadous drain.
The simulated DO values varied from 4.5 mg/L to 9.9 mg/L during the period from September 2013 to August 2014 (
Figure 3b). The DO concentration along the El-Salam Canal complied with the Egyptian standards (DO > 5 mg/L) for direct reuse in irrigation except at the El-Serw drain (S. No. 3) in August. Nevertheless, a significant decrease in the DO levels was observed at the El-Serw (S. No. 3) and Bahr Hadous drains (S. No. 4), as shown in
Figure 3b. The DO concentration amounted to 4.5 mg/L in the El-Salam Canal at the connection with the El-Serw drain and 5.1 mg/L at the connection with the Bahr Hadous drain in August. This result is consistent with the results of Hafez et al. [
38], who indicated that the DO levels of Nile River water decreased sharply after the mixing point with the El-Serw and Bahr Hadous drains. One of the plausible reasons for low DO is due to the discharge of domestic wastewater into these drainage canals causing a depletion of oxygen. Indeed, El Gammal [
37] reported that the El-Serw and Bahr Hadous drains receives a significant amount of untreated wastewater that causes severe pollution of the ADW, which subsequently adversely affects the WQ of the El-Salam Canal. Othman et al. [
40] also found that the DO concentration decreased at the connection sites of the drains with the canal. Furthermore, El-Sheekh et al. [
39] found that the maximum annual mean concentration of DO was 6.0 mg/L at the Nile River site, whereas DO was 2.2 mg/L at the Bahr Hadous drain site connection with the canal. However, the relatively higher DO at the Bahr Hadous in this study (5.1 mg/L in 2014) compared to reported value by El-Sheekh et al. [
39] (2.2 mg/L in 2010) is most likely associated with construction of wastewater treatment plants along the drainage systems, which mitigate the effect from pollution source.
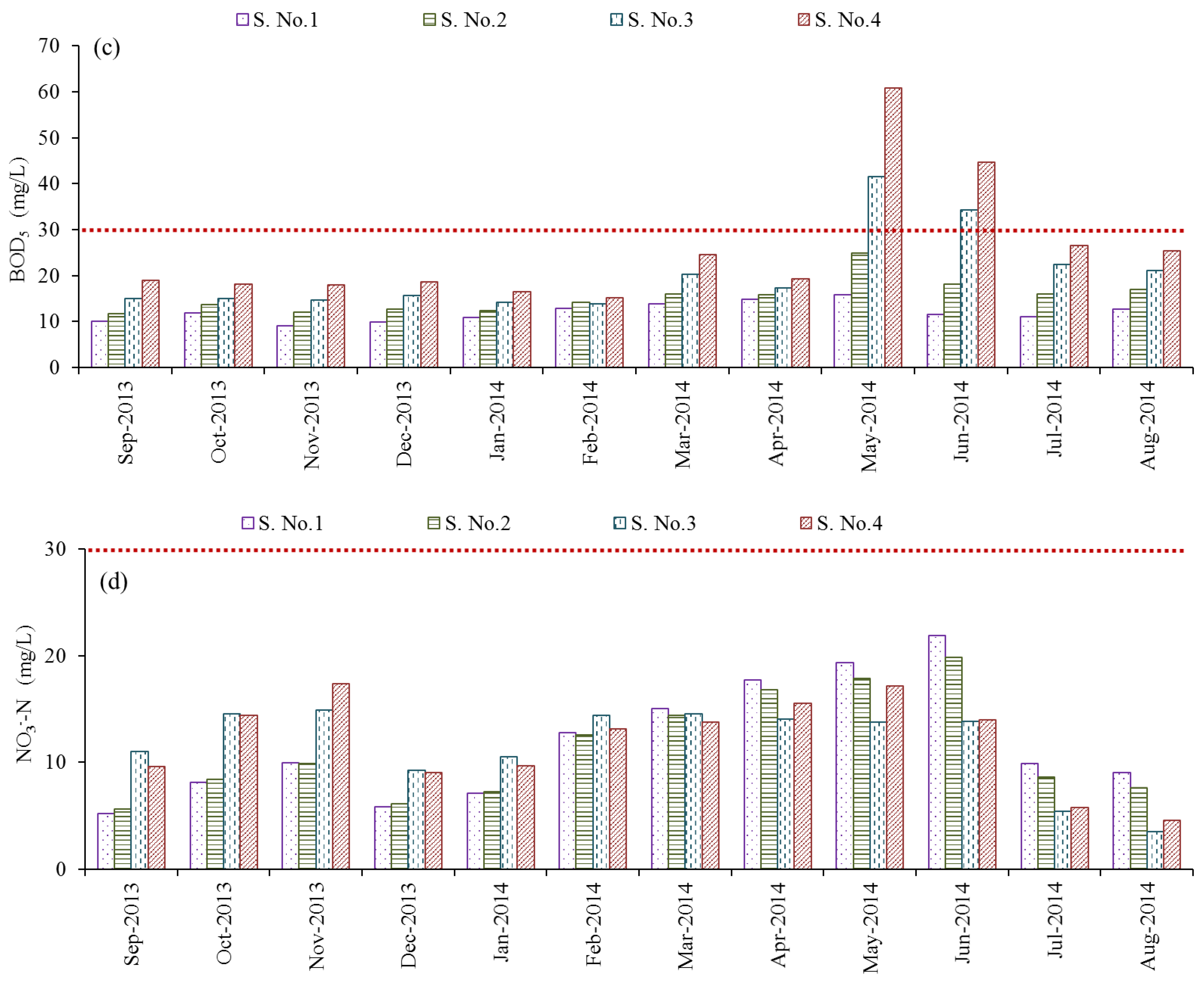
As shown in
Figure 3c, the simulated data for BOD
5 gradually increased from the intake point to the connection sites with the drainage canals. For example, the simulated BOD
5 along the El-Salam Canal exceeded the limit of 30 mg/L for direct reuse of the water in irrigation in May and June 2014; the BOD
5 values further increased downstream at the El-Serw and Bahr Hadous drains. The BOD
5 values were 42 mg/L in May and 34 mg/L in June after mixing with El-Serw drain water (S. No. 3). Moreover, the highest value of BOD
5 was 61 mg/L in May and 45 mg/L in June after mixing with Bahr Hadous drain water (S. No. 4). BOD
5 of the El-Serw drain (21–51 mg/L) and Bahr Hadous drain (30–136 mg/L) were generally higher than that for the main channel of the Nile River (6–34 mg/L). Hafez et al. [
38] noticed that the BOD
5 levels in the canal were high due to the supply of ADW to the canal with the BOD
5 values being recorded as 75 mg/L in June 2004 and 33 mg/L in November 2004 after mixing with El-Serw drain water. The highest value of BOD
5 was 112 mg/L in June 2004 (Bahr Hadous drain), and the lowest value was 43 mg/L in December 2004 after mixing with El-Serw drain water. Therefore, the BOD
5 values of the canal can be affected by the quantity and quality of discharges, as well as seasonal and spatial effects.
In contrast to BOD
5, the results for NO
3-N indicated relatively lower values, which varied from 3.6 to 22 mg/L and complied with the WQ standards for reuse as shown in
Figure 3d. The highest values were observed from April to June 2014 and were most likely due to elevation of the temperature up to 33 °C, which positively affected the nitrification process. These results demonstrate that the canal environment deteriorated after mixing with water from the El-Serw and Bahr Hadous drains. Othman et al. [
40] reported that the NO
3-N values in the El-Salam Canal ranged from 0.01–5.47 mg/L and from 0.07–1.49 mg/L, respectively.
All statistical analyses were performed by Minitab software with a significance level of p < 0.05. The Durbin–Watson test was used to test the WQ data for serial autocorrelation. For the majority of parameters, autocorrelation was insignificant (i.e., D > Du). The results indicated that the WQ parameters were independent over time, but depended on the agriculture seasons. As a consequence of the minimum degree of serial autocorrelation, its effects were neglected in the following statistical analyses.
The WQ data was divided into two groups (winter and summer seasons) according to the irrigation periods, for assessing the seasonal differences of variability for the four stations.
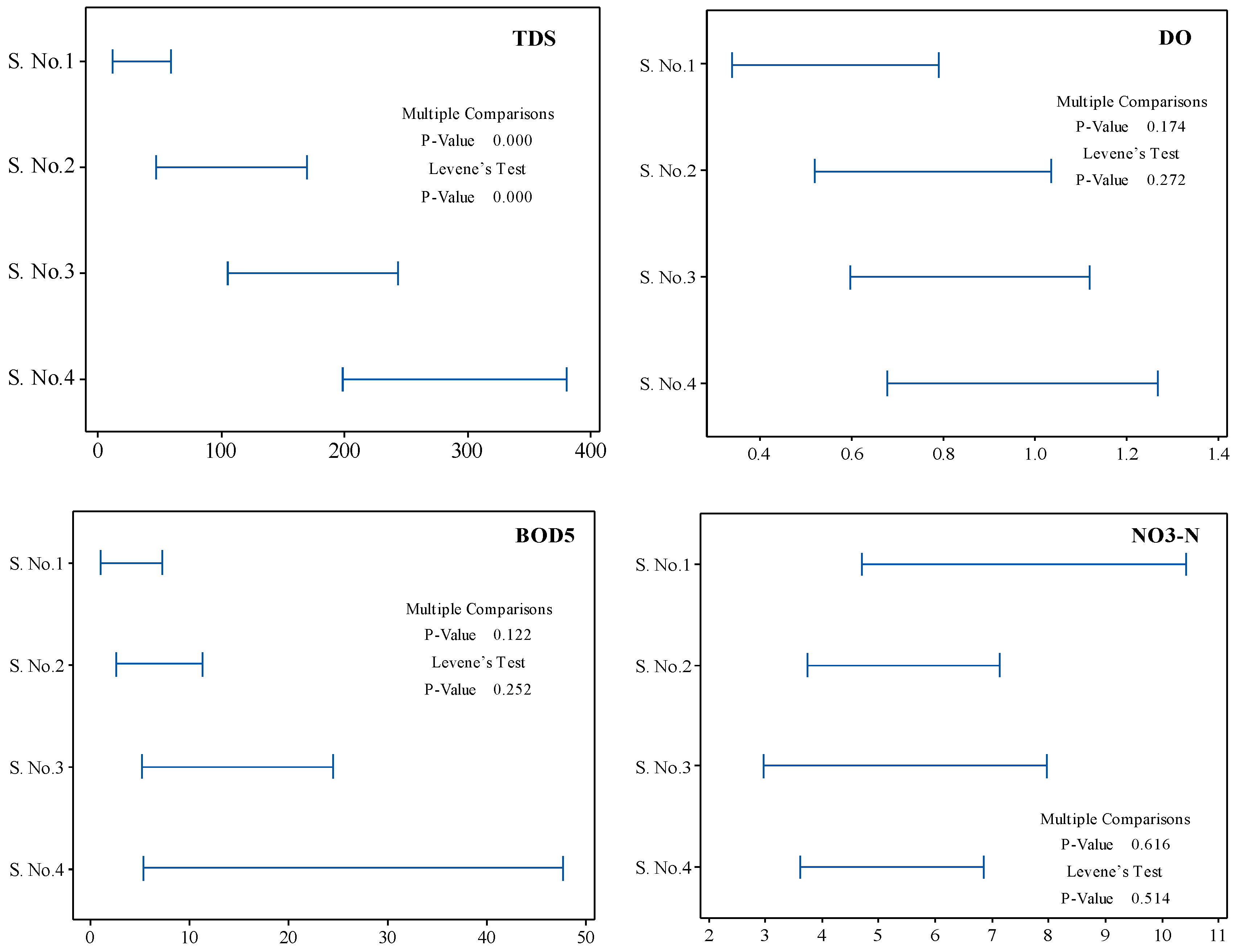
Table 6 displays the results of the homogeneity of variance test, which clearly demonstrated that the ratio of standard deviations or variances is not statistically significant (
p > 0.05), except for BOD
5 at S. Nos. 2–4 (
p < 0.05). These results were confirmed with the simulated outputs in
Figure 3, which illustrated the simulated BOD
5 along the El-Salam Canal exceeded the limit of 30 mg/L for direct reuse of the water in irrigation, with a significant difference especially in May and June 2014.
However, the TDS parameter was the only one that had a significant difference of variances from one station to another (
p < 0.05), as shown in
Figure 4. The result indicated that the TDS values was the most effective parameter for the water quality along the canal, confirming the officials’ concern that the El-Salam Canal be constructed where agricultural drain water can be diluted with fresh water to maintain a TDS less than 1200 mg/L. Moreover, an ANOVA test was applied to illustrate the differences among the four stations for each parameter.
Table 7 shows the results of the ANOVA test that clearly illustrated the significant differences (
p < 0.05) for all parameters in the four stations except for nitrate levels (
p > 0.05). The results indicated that most parameters varied in their spatial variation along the canal after the connection with the drains.
3.2. Water Quality Indices Performance
The WQ indices (FWRI and IWQI) were applied along the El-Salam Canal at the selected four stations over the period from September 2013 to August 2014.
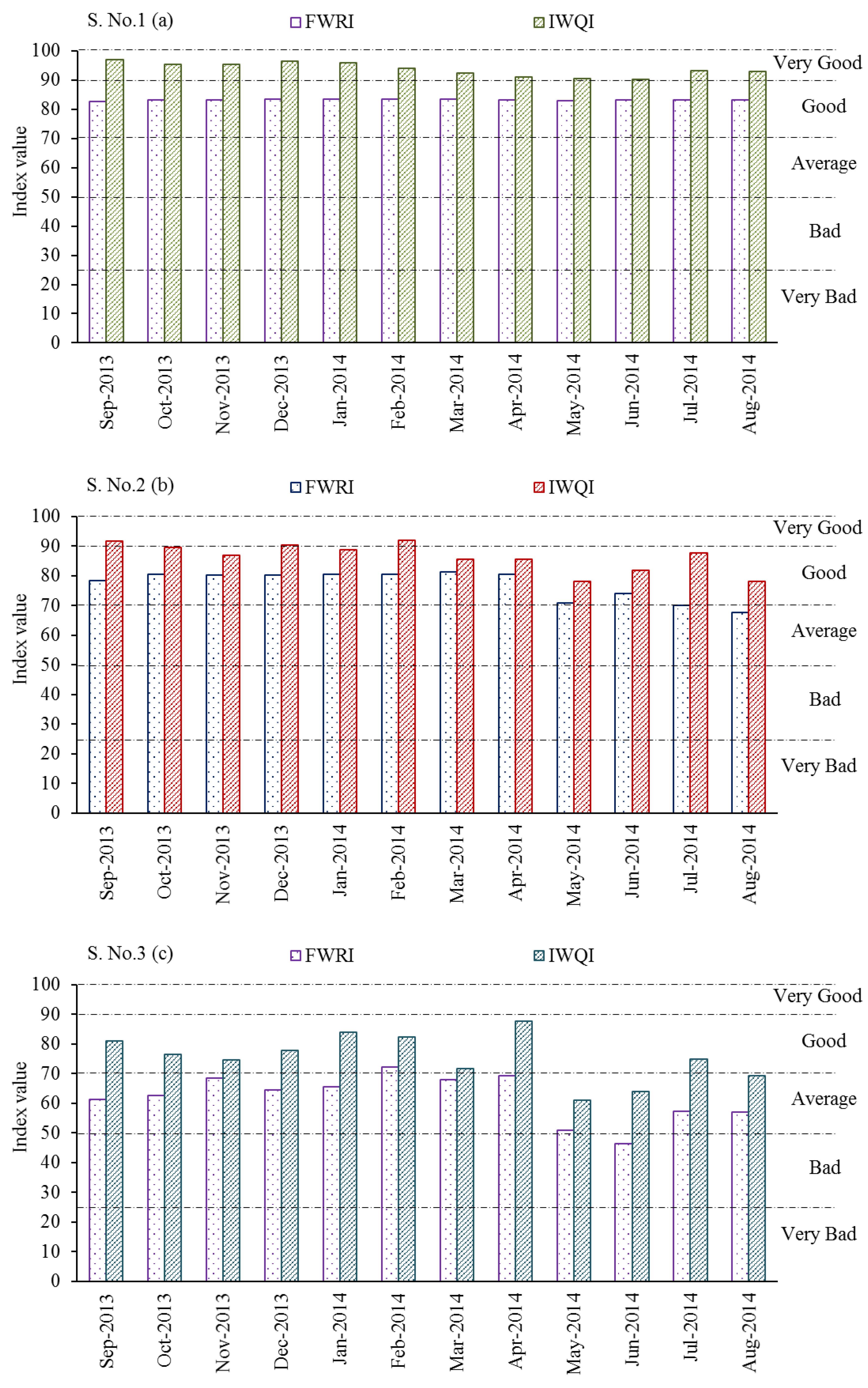
Figure 5a–d shows a comparison of the FWRI with the IWQI at the four stations during the period from September 2013 to August 2014. As shown for S. No. 1 (
Figure 5a), the FWRI and IWQI values had similar trends and the WQ was likely acceptable for irrigation purposes, although the output classes were different. The FWRI values varied from 83.4 to 82.8, indicating that the WQ is in the ‘G’ category. In contrast, the WQ was classified into the ‘VG’ category for the IWQI values, which varied from 96.55 to 90.17.
Moreover, after the connection with the Faraskor drain (S. No. 2), the WQ reduced slightly and ranged between the ‘G’ to ‘A’ categories for the FWRI and the ‘VG’ to ‘G’ categories for the IWQI (
Figure 5b). The FWRI values varied from 81.2 to 67.7 and the IWQI values varied from 91.87 to 78.0. The WQ complied with standards for its safe reuse in agriculture. The results also showed that the annual discharge of drainage water from the Faraskor (8 m
3/s) had little adverse effect on the WQ of the El-Salam Canal. However, the FWRI and IWQI values after the connection with the El-Serw drain (S. No. 3) dropped significantly, probably due to the discharge of 31.1 m
3/s from the El-Serw drain as shown in
Figure 5c. The FWRI values ranged from ‘A’ to ‘B’ and varied from 72.1 to 46.3. The IWQI values decreased slightly; however, they ranged between ‘G’ and ‘A’ and varied from 87.7 to 61.1.
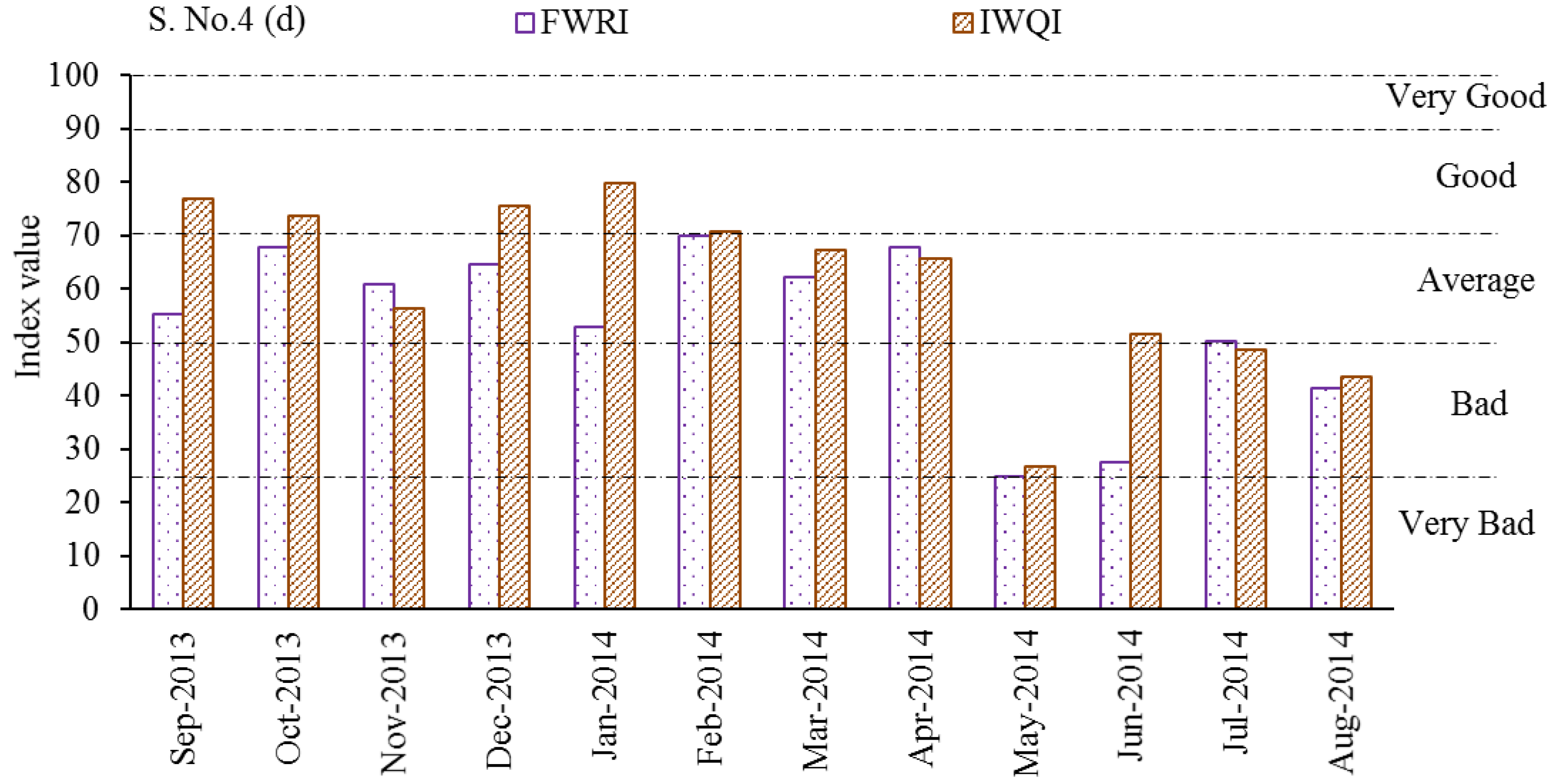
The results in
Figure 5d show the FWRI versus the IWQI values after mixing with the Bahr Hadous drain (39 m
3/s) (S. No. 4); the WQ deteriorated and resulted in a ‘VB’ classification. The FWRI values varied from 70.0 to 24.8 and were classified as ranging between ‘A’ and ‘VB’. In contrast, the IWQI values ranged from ‘G’ to ‘B’ and varied from 79.7 to 26.7. Collectively, as illustrated in
Figure 5, the outputs of the FWRI were sensitive to variations in the WQ parameters compared with the IWQI.
Furthermore, the Z-test of the means was applied to detect whether the differences between the mean FWRI and IWQI outputs for the four stations were significant.
Table 8 displays the statistical properties of the FWRI and IWQI values for the four stations, where the calculated Z (Z
cal) values were associated with the means and between Z-critical values (±1.96 for a 5% significance level). The Z
cal values showed that the mean values between the FWRI and IWQI were significantly different in the three stations with the exception of S. No. 4 (Z
cal > 1.96). As a consequence, the aforementioned analyses consistently indicated that the FWRI and IWQI outputs have different statistical properties and the FWRI values do not preserve the basic statistical properties of the IWQI values.
In order to validate which of the two indices provide the best fit for the real situation of the WQ along the canal, a chi-square test (X
2) was applied comparing the FWRI and IWQI with the official DRI WQ data, which is illustrated in
Table 9. The X
2 test investigates which index is best fitted to the observed WQ data.
Table 10 shows the results of the X
2 test between the FWRI and IWQI outputs with the official classification for the four stations, where all the X
2 values are lower than the critical chi-square value (19.675) with DF = 11. Based on the results, the FWRI and IWQI values can both reasonably explain the current situation. However, the X
2 values for the FWRI were always larger than the IWQI one, which indicated that the FWRI was more relevant to the official classification than the IWQI.
This could be attributed to the method of index calculation, e.g., how each parameter is compared with the standard value in the calculations [
41]. Moreover, the inference rules used for the FWRI calculation not only deal with numerical data, but also apply the expert’s knowledge and experience [
18]. Based on the findings in this study, the FWRI proved its capability and accuracy in the assessment of the ADW for reuse in irrigation compared with those obtained from a simulation model of the canal, and thus it can be applied as a comprehensive approach for the assessment of WQ reuse for irrigation purposes. These results confirm those of Ocampo-Duque et al. [
24], Lermontov et al. [
41] and Gharibi et al. [
18], who studied the development of water quality indices based on fuzzy logic. They reported that this index seems to produce accurate and reliable outcomes, and can therefore be used as an alternative tool for effective water quality assessment.