Modelling Soil Water Dynamics from Soil Hydraulic Parameters Estimated by an Alternative Method in a Tropical Experimental Basin
Abstract
1. Introduction
2. Materials and Methods
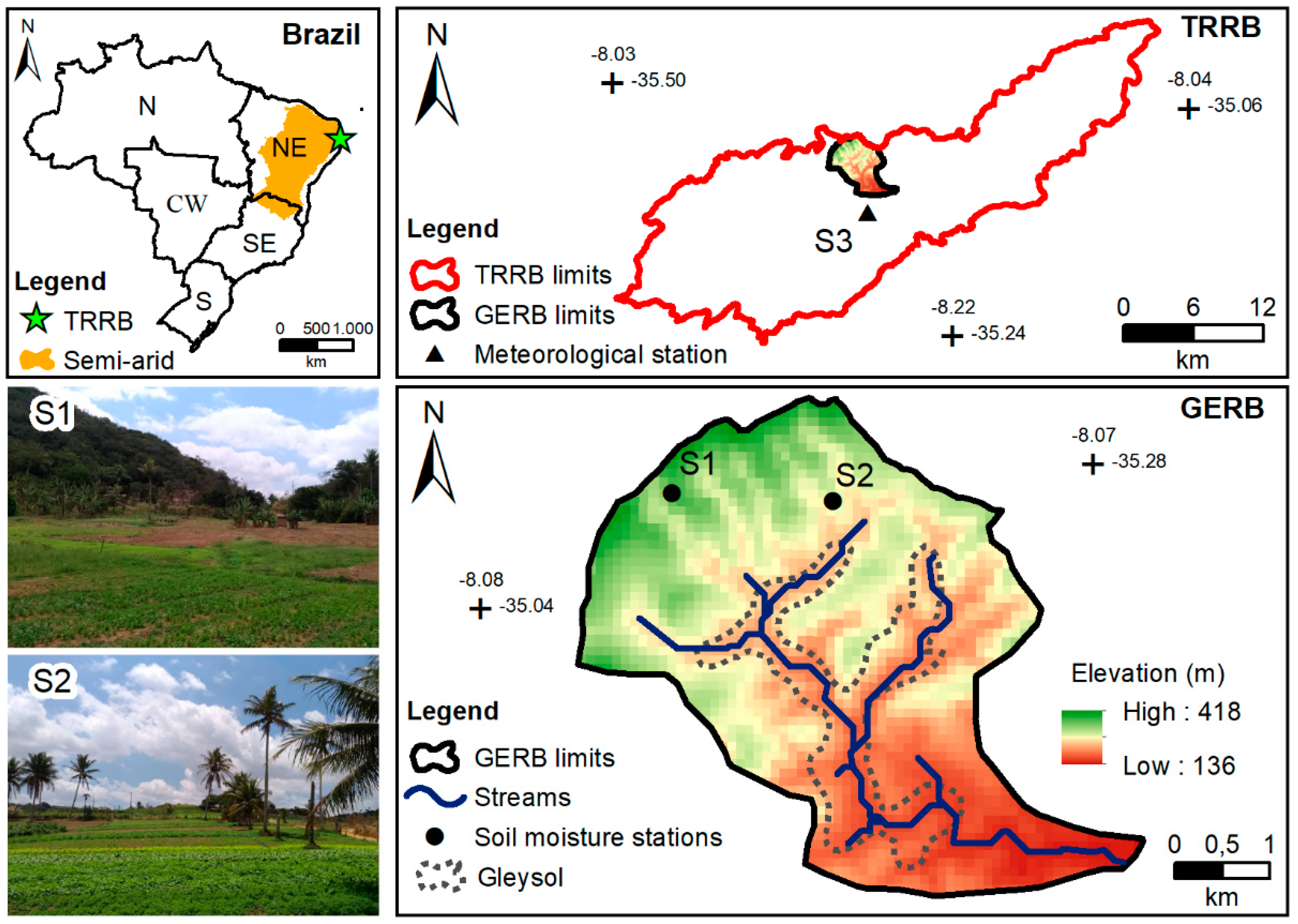
2.1. Study Site Description
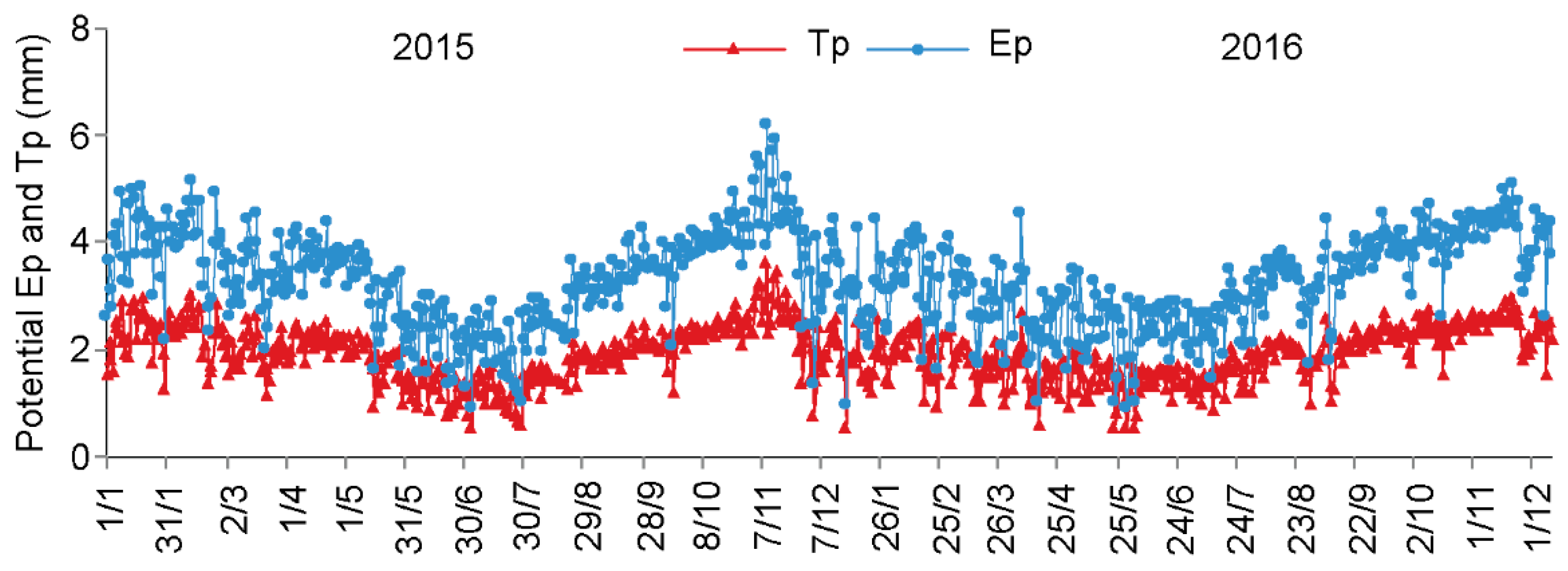
2.2. Data Collection
2.3. Modelling the Unsaturated Water Flow
2.4. Estimation of Soil Hydraulic Parameters Using BEST Methods
2.5. Boundary Condition
2.6. Time and Space Discretisation
2.7. Simulations of Volumetric Water Content and Model Evaluation
3. Results and Discussion
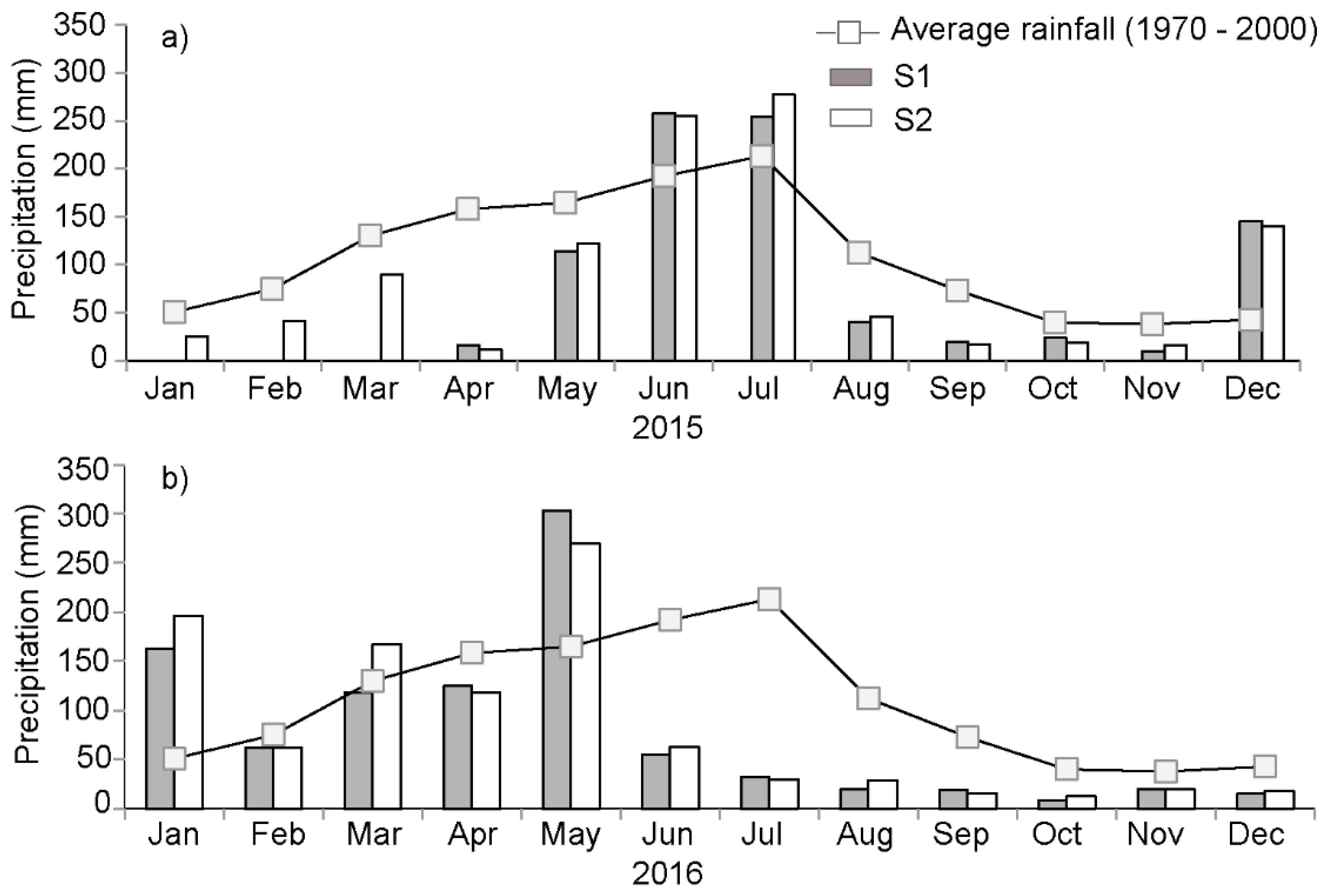
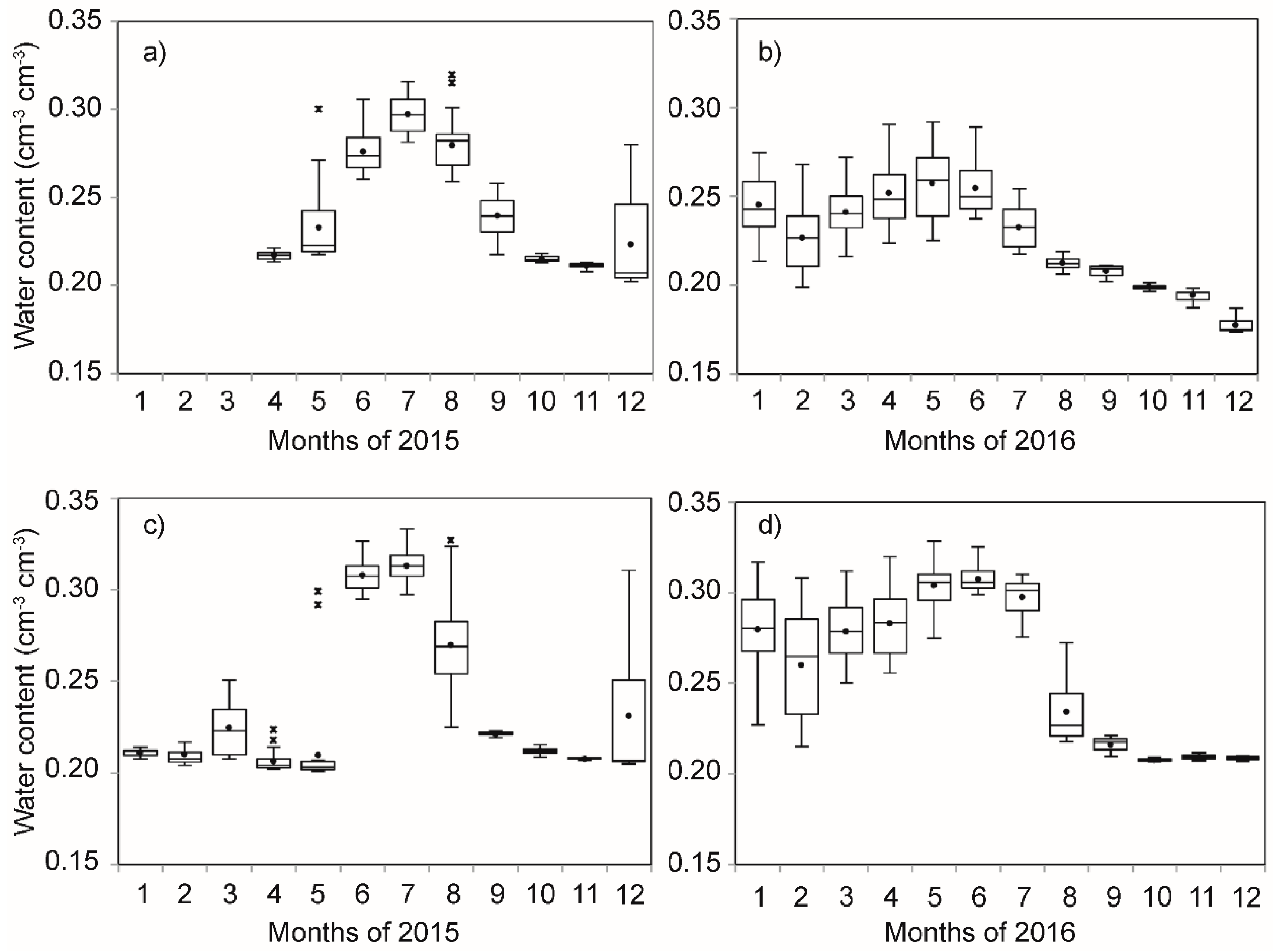
3.1. Rainfall and Soil Moisture Dynamics
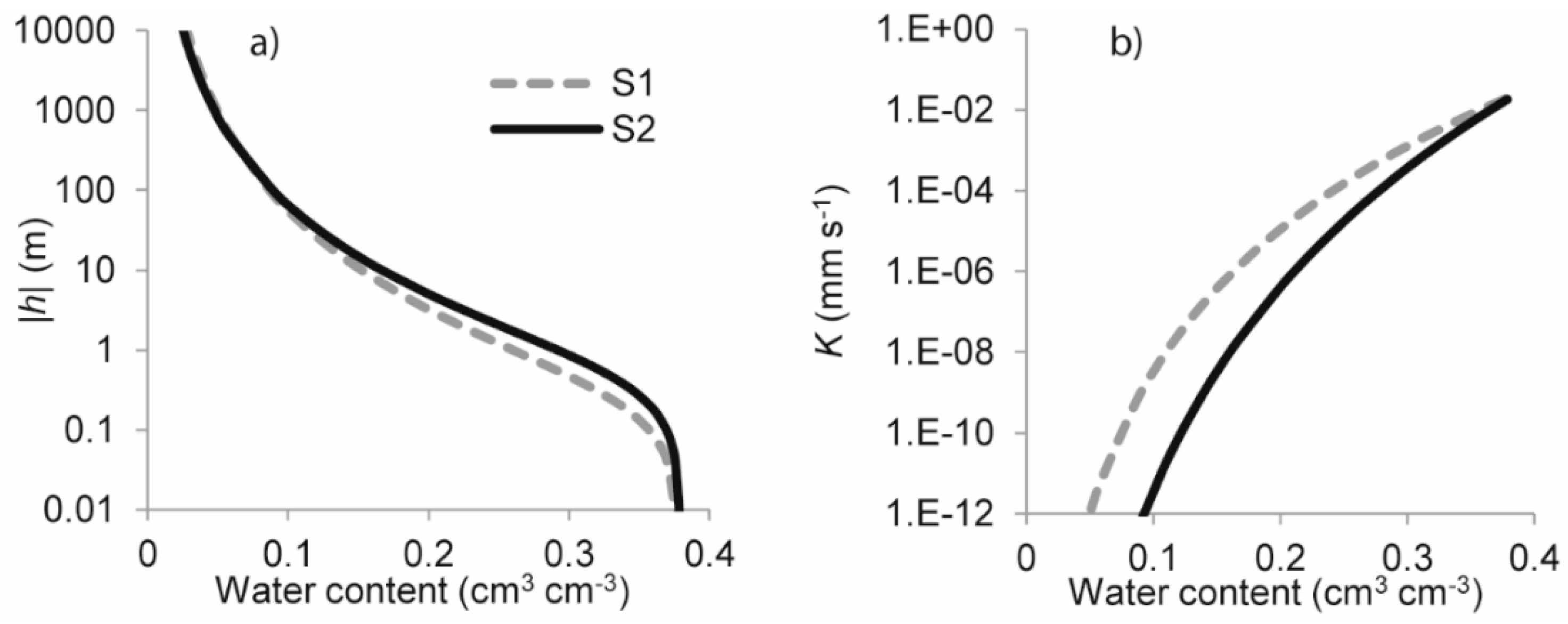
3.2. Hydraulic Characterization of the Sites
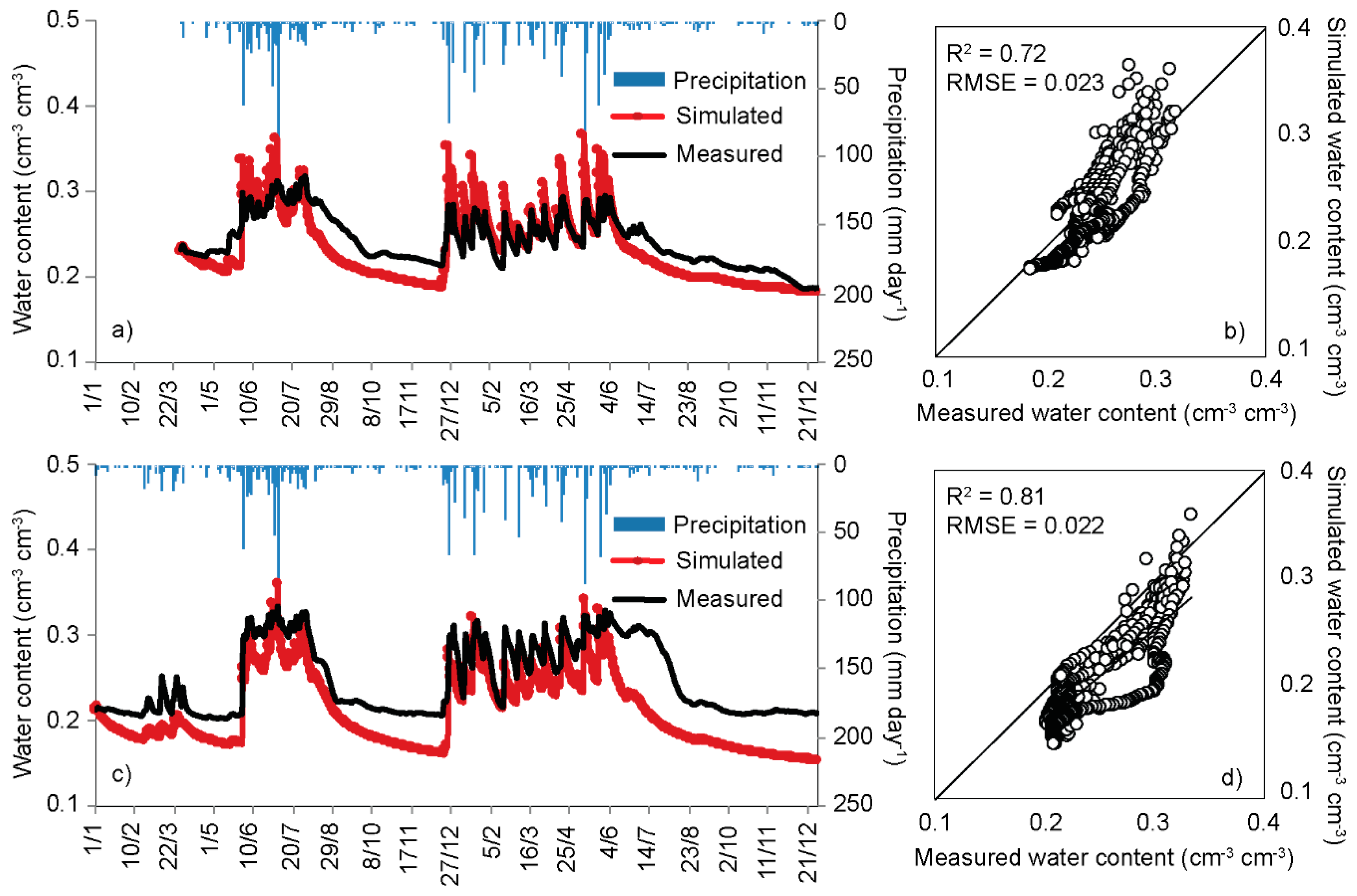
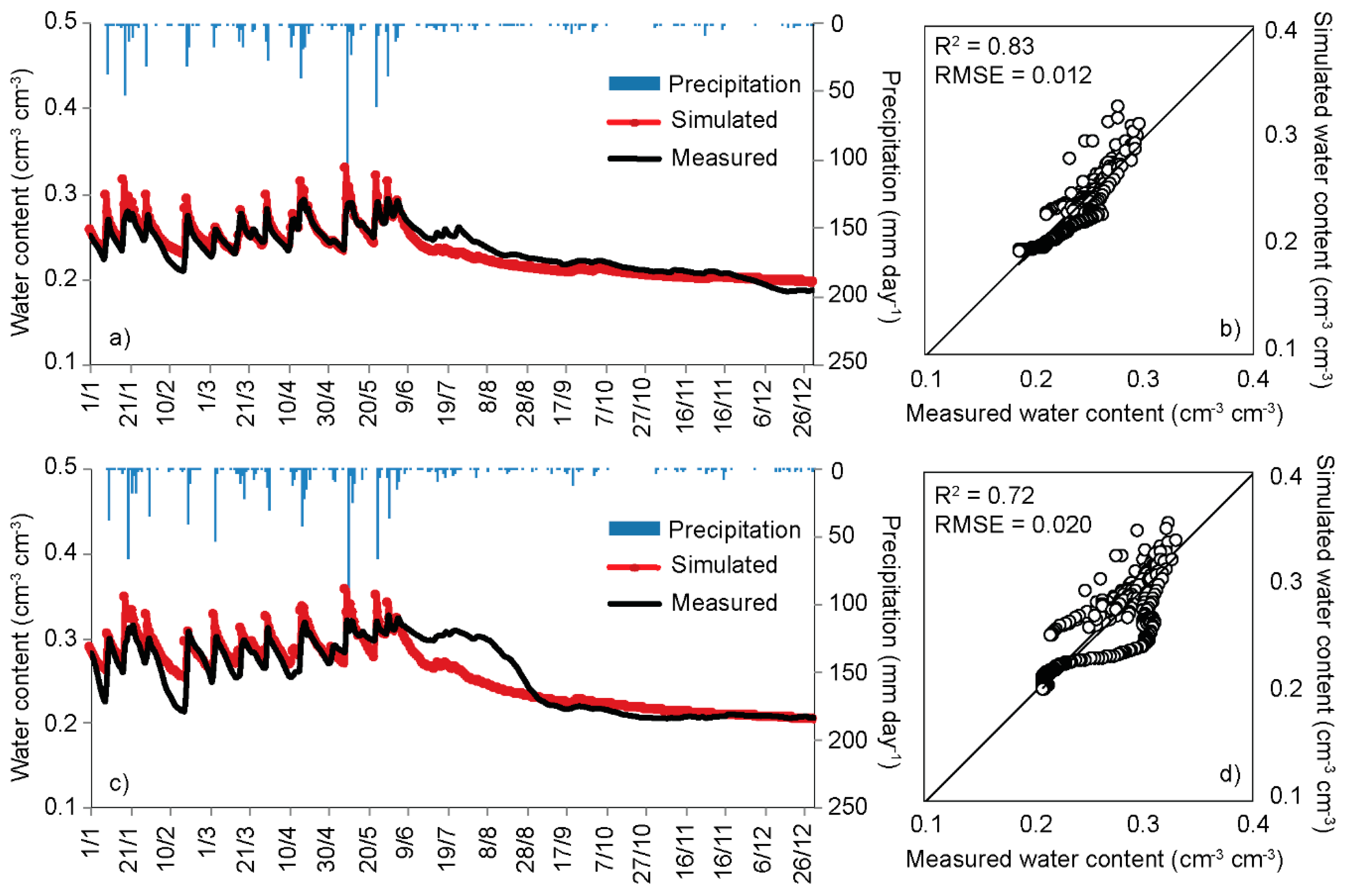
3.3. Simulation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Šípek, V.; Tesar, M. Soil moisture simulations using two different modelling approaches. Die Bodenkult. 2013, 64, 99–103. [Google Scholar]
- Bordoni, M.; Bittelli, M.; Valentino, R.; Chersich, S.; Persichillo, M.G.; Meisina, C. Soil water content estimated by support vector machine for the assessment of shallow landslides triggering: The role of antecedent meteorological conditions. Environ. Model. Assess. 2018, 23, 333–352. [Google Scholar] [CrossRef]
- Zarlenga, A.; Fiori, A.; Russo, D. Spatial variability of soil moisture and the scale issue: A geostatistical approach. Water Resour. Res. 2018, 54, 1765–1780. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; Porporato, A. Ecohydrology of Water-Controlled Ecosystems: Soil Moisture and Plant Dynamics, 1st ed.; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar] [CrossRef]
- Sheikh, V.; van Loon, E.E. Comparing performance and parameterization of a one-dimensional unsaturated zone model across scales. Vadose Zone J. 2007, 6, 638–650. [Google Scholar] [CrossRef]
- Ojha, R.; Morbidelli, R.; Saltalippi, C.; Flammini, A.; Govindaraju, R.S. Scaling of surface soil moisture over heterogeneous fields subjected to a single rainfall event. J. Hydrol. 2014, 516, 21–36. [Google Scholar] [CrossRef]
- Dirmeyer, P.A.; Gao, X.; Zhao, M.; Guo, Z.; Oki, T.; Hanasaki, N. GSWP-2: Multimodel analysis and implications for our perception of the land surface. Bull. Am. Meteorol. Soc. 2006, 87, 1381–1397. [Google Scholar] [CrossRef]
- Li, S.; Liang, W.; Zhang, W.; Liu, Q. Response of soil moisture to hydro-meteorological variables under different precipitation gradients in the Yellow River basin. Water Resour. Manag. 2016, 30, 1867–1884. [Google Scholar] [CrossRef]
- Melo, O.R.; Montenegro, A.A.A. Dinâmica temporal da umidade do solo em uma bacia hidrográfica no semiárido pernambucano. Rev. Bras. Recur. Hídr. 2015, 20, 430–441. [Google Scholar] [CrossRef]
- Huang, X.; Shi, Z.H.; Zhu, H.D.; Zhang, H.Y.; Ai, L.; Yin, W. Soil moisture dynamics within soil profiles and associated environmental controls. Catena 2016, 136, 189–196. [Google Scholar] [CrossRef]
- Negm, A.; Capodici, F.; Ciraolo, G.; Maltese, A.; Provenzano, G.; Rallo, G. Assessing the performance of thermal inertia and Hydrus models to estimate surface soil water content. Appl. Sci. 2017, 7, 975. [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Massari, C.; Camici, S.; Tarpanelli, A. Soil moisture for hydrological applications: Open questions and new opportunities. Water 2017, 9, 140. [Google Scholar] [CrossRef]
- Chen, M.; Willgoose, G.R.; Saco, P.M. Spatial prediction of temporal soil moisture dynamics using HYDRUS-1D. Hydrol. Process. 2014, 28, 171–185. [Google Scholar] [CrossRef]
- Tavakoli, M.; De Smedt, F. Validation of soil moisture simulation with a distributed hydrologic model (WetSpa). Environ. Earth Sci. 2013, 69, 739–747. [Google Scholar] [CrossRef]
- Legates, D.R.; Mahmood, R.; Levia, D.F.; DeLiberty, T.L.; Quiring, S.M.; Houser, C.; Nelson, F.E. Soil moisture: A central and unifying theme in physical geography. Prog. Phys. Geogr. 2011, 35, 65–86. [Google Scholar] [CrossRef]
- Escorihuela, M.J.; Quintana-Seguí, P. Comparison of remote sensing and simulated soil moisture datasets in Mediterranean landscapes. Remote Sens. Environ. 2016, 180, 99–114. [Google Scholar] [CrossRef]
- Espejo-Pérez, A.J.; Brocca, L.; Moramarco, T.; Giráldez, J.V.; Triantafilis, J.; Vanderlinden, K. Analysis of soil moisture dynamics beneath olive trees. Hydrol. Process. 2016, 30, 4339–4352. [Google Scholar] [CrossRef]
- Zribi, M.; Le Hégarat-Mascle, S.; Ottlé, C.; Kammoun, B.; Guerin, C. Surface soil moisture estimation from the synergistic use of the (multi-incidence and multi-resolution) active microwave ERS Wind Scatterometer and SAR data. Remote Sens. Environ. 2003, 86, 30–41. [Google Scholar] [CrossRef]
- She, D.; Liu, D.; Xia, Y.; Shao, M. Modeling effects of land use and vegetation density on soil water dynamics: Implications on water resource management. Water Resour. Manag. 2014, 28, 2063–2076. [Google Scholar] [CrossRef]
- Chen, B.; Liu, E.; Mei, X.; Yan, C.; Garré, S. Modelling soil water dynamic in rain-fed spring maize field with plastic mulching. Agric. Water Manag. 2018, 198, 19–27. [Google Scholar] [CrossRef]
- Van Dam, J.C.; Huygen, J.; Wesseling, J.G.; Feddes, R.A.; Kabat, P.; van Walsum, P.E.V.; Groenendijk, P.; van Diepen, C.A. Theory of SWAP Version 2.0: Simulation of Water Flow, Solute Transport and Plant Growth in the Soil-Water-Atmosphere-Plant Environment; Technical Document 45; Wageningen Agricultural University and DLO Winand Staring Centre: Wageningen, The Netherlands, 1997. [Google Scholar]
- Avissar, R. Which type of soil-vegetation-atmosphere transfer scheme is needed for general circulation models: A proposal for a higher-order scheme. J. Hydrol. 1998, 212–213, 136–154. [Google Scholar] [CrossRef]
- Verburg, K.; Ross, P.J.; Bristow, K.L. SWIM v2.1 User Manual; Divisional Report No. 130; CSIRO Division of Soils: Canberra, Australia, 1996.
- Leonard, R.A.; Knisel, W.G.; Still, D.A. GLEAMS: Groundwater loading effects of agricultural management systems. Trans. ASAE 1987, 30, 1403–1418. [Google Scholar] [CrossRef]
- Vanclooster, M.; Viaene, P.; Diels, J.; Christiaens, K. WAVE: A mathematical model for simulating water and agrochemicals in the soil and vadose environment. In Reference and User’s Manual, Release 2.1; Institute for Land and Water Management, Katholieke Universiteit Leuven: Leuven, Belgium, 1996. [Google Scholar]
- Richards, L.A. Capillary conduction of liquids through porous mediums. J. Appl. Phys. 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Tinet, A.J.; Chanzy, A.; Braud, I.; Crevoisier, D.; Lafolie, F. Development and Evaluation of an Efficient Soil-Atmosphere Model (FHAVeT) based on the Ross fast solution of the Richards equation for bare soil conditions. Hydrol. Earth Syst. Sci. 2015, 19, 969–980. [Google Scholar] [CrossRef]
- Šimůnek, J.; Šejna, M.; Saito, H.; Sakai, M.; van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the One-Dimensional Movement of Water, heat, and Multiple Solutes in Variably-Saturated Media Version 4.17; University of California Riverside: Riverside, CA, USA, 2013; pp. 1–342. [Google Scholar]
- Da Silva, J.R.L.; Montenegro, A.A.A.; Monteiro, A.L.N.; Silva, P.V. Modelagem da dinâmica de umidade do solo em diferentes condições de cobertura no semiárido pernambucano. Rev. Bras. Cienc. Agrar. 2015, 10, 293–303. [Google Scholar] [CrossRef]
- Lai, X.; Liao, K.; Feng, H.; Zhu, Q. Responses of soil water percolation to dynamic interactions among rainfall, antecedent moisture and season in a forest site. J. Hydrol. 2016, 540, 565–573. [Google Scholar] [CrossRef]
- Li, Y.; Šimůnek, J.; Wang, S.; Yuan, J.; Zhang, W. Modeling of soil water regime and water balance in a transplanted rice field experiment with reduced irrigation. Water 2017, 9, 248. [Google Scholar] [CrossRef]
- Wang, H.; Tetzlaff, D.; Soulsby, C. Modelling the effects of land cover and climate change on soil water partitioning in a boreal headwater catchment. J. Hydrol. 2018, 558, 520–531. [Google Scholar] [CrossRef]
- Gabiri, G.; Burghof, S.; Diekkrüger, B.; Leemhuis, C.; Steinbach, S.; Näschen, K. Modeling spatial soilwater dynamics in a tropical floodplain, East Africa. Water 2018, 10, 191. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T. Using the HYDRUS-1D and HYDRUS-2D codes for estimating unsaturated soil hydraulic and solute transport parameters. In Characterization and Measurement of the Hydraulic Properties of Unsaturated Porous Media; van Genuchten, M.T., Leij, F.J., Wu, L., Eds.; University of California: Riverside, CA, USA, 1999; pp. 1523–1536. [Google Scholar]
- Kato, C.; Nishimura, T.; Imoto, H.; Miyazaki, T. Predicting soil moisture and temperature of andisols under a monsoon climate in Japan. Vadose Zone J. 2011, 10, 541–551. [Google Scholar] [CrossRef]
- Honari, M.; Ashrafzadeh, A.; Khaledian, M.; Vazifedoust, M.; Mailhol, J.C. Comparison of HYDRUS-3D soil moisture simulations of subsurface drip irrigation with experimental observations in the south of France. J. Irrig. Drain. Eng. 2017, 143, 1–8. [Google Scholar] [CrossRef]
- Siltecho, S.; Hammecker, C.; Sriboonlue, V.; Clermont-Dauphin, C.; Trelo-Ges, V.; Antonino, A.C.D.; Angulo-Jaramillo, R. Use of field and laboratory methods for estimating unsaturated hydraulic properties under different land uses. Hydrol. Earth Syst. Sci. 2015, 19, 1193–1207. [Google Scholar] [CrossRef]
- Haverkamp, R.; Ross, P.J.; Smettem, K.R.J.; Parlange, J.Y. Three-dimensional analysis of infiltration from the disc infiltrometer: 2. Physically based infiltration equation. Water Resour. Res. 1994, 30, 2931–2935. [Google Scholar] [CrossRef]
- Braud, I.; De Condappa, D.; Soria, J.M.; Haverkamp, R.; Angulo-Jaramillo, R.; Galle, S.; Vauclin, M. Use of scaled forms of the infiltration equation for the estimation of unsaturated soil hydraulic properties (the Beerkan method). Eur. J. Soil Sci. 2005, 56, 361–374. [Google Scholar] [CrossRef]
- Coutinho, A.P.; Lassabatere, L.; Montenegro, S.; Antonino, A.C.D.; Angulo-Jaramillo, R.; Cabral, J.J.S.P. Hydraulic characterization and hydrological behaviour of a pilot permeable pavement in an urban centre, Brazil. Hydrol. Process. 2016, 30, 4242–4254. [Google Scholar] [CrossRef]
- Lassabatère, L.; Angulo-Jaramillo, R.; Soria Ugalde, J.M.; Cuenca, R.; Braud, I.; Haverkamp, R. Beerkan estimation of soil transfer parameters through infiltration experiments—BEST. Soil Sci. Soc. Am. J. 2006, 70, 521. [Google Scholar] [CrossRef]
- Kanzari, S. Spatio-Temporal variability of the soil hydraulic properties—Effect on modelling of water flow and solute transport at field-scale. In Recent Advances in Environmental Science from the Euro-Mediterranean and Surrounding Regions; Kallel, A., Ksibi, M., Ben Dhia, H., Khélifi, N., Eds.; Springer: Cham, Switzerland, 2018; pp. 1279–1281. [Google Scholar] [CrossRef]
- Lai, J.; Ren, L. Estimation of effective hydraulic parameters in heterogeneous soils at field scale. Geoderma 2016, 264, 28–41. [Google Scholar] [CrossRef]
- Nascimento, Í.V.; de Assis Júnior, R.N.; de Araújo, J.C.; de Alencar, T.L.; Freire, A.G.; Lobato, M.G.R.; da Silva, C.P.; Mota, J.C.A.; Nascimento, C.D.V. Estimation of van Genuchten equation parameters in laboratory and through inverse modeling with Hydrus-1D. J. Agric. Sci. 2018, 10, 102. [Google Scholar] [CrossRef]
- Graham, S.L.; Srinivasan, M.S.; Faulkner, N.; Carrick, S. Soil hydraulic modeling outcomes with four parameterization methods: Comparing soil description and inverse estimation approaches. Vadose Zone J. 2018, 17. [Google Scholar] [CrossRef]
- Montenegro, S.M.G.L.M.; Ragab, R. Impact of possible climate and land use changes in the semi arid regions: A case study from north eastern Brazil. J. Hydrol. 2012, 434–435, 55–68. [Google Scholar] [CrossRef]
- Montenegro, A.A.A.; Ragab, R. Hydrological response of a brazilian semi-arid catchment to different land use and climate change scenarios: A modelling study. Hydrol. Process. 2010, 24, 2705–2723. [Google Scholar] [CrossRef]
- Araújo Filho, P.; Cabral, J. Modelagem hidrológica da bacia do riacho Gameleira (Pernambuco) utilizando TOPSIMPL, uma versão simplificada do modelo TOPMODEL. Rev. Bras. Recur. Hídr. 2005, 10, 61–72. [Google Scholar] [CrossRef]
- Paiva, F.M.L.; Montenegro, S.M.G.L.; Salcedo, I.H.; Araújo Filho, P.F.; Srinivasan, V.S.; Silva Filho, S.L.; Azevedo, J.R.G.; Silva, R.M.; Silva, L.P. Análise do transporte de sedimentos em suspensão num pequeno curso d’água na bacia experimental do riacho Gameleira, PE. In Proceedings of the XIX Simpósio Brasileiro de Recursos Hídricos (SBRH), Maceió, Brazil, 27 November–1 December 2011; Available online: https://abrh.s3.sa-east-1.amazonaws.com/Sumarios/81/e7457e425ff7a2508f2b4bfb293cfbd9_e6315e8645bda4bec9188b7bdc137669.pdf (accessed on 17 December 2018).
- Da Silva, R.M.; Paiva, F.M.D.L.; Montenegro, S.M.G.D.L.; Augusto, C.; Santos, G. Aplicação de Eqsuações de Razão de Transferência de Sedimentos na Bacia do rio Gameleira com Suporte de Sistemas de Informação Geográfica. In Proceedings of the XVIII Simpósio Brasileiro de Recursos Hídricos (SBRH), Campo Grande, Brazil, 22–26 November 2009; Available online: https://abrh.s3.sa-east-1.amazonaws.com/Sumarios/110/c9e2c8a28e3027a52b5b34e91b6f9b14_705324c4dd596d1379d42fc4fe927d8f.pdf (accessed on 17 December 2018).
- Furtunato, O.M.; Montenegro, S.M.G.L.; Antonino, A.C.D.; de Oliveira, L.M.M.; de Souza, E.S.; Moura, A.E.S.S. Variabilidade espacial de atributos físico-hídricos de solos em uma bacia experimental no estado de Pernambuco. Rev. Bras. Recur. Hídr. 2013, 18, 135–147. [Google Scholar] [CrossRef]
- Oliveira, L.M.M.; Montenegro, S.M.G.L. Evapotranspiração de referência na bacia experimental do riacho Gameleira, PE, utilizando-se lisímetro e métodos indiretos. Rev. Bras. Ciênc. Agrár. 2008, 81, 58–67. [Google Scholar] [CrossRef]
- Moura, A.R.C.; Montenegro, S.M.G.L.; Antonino, A.C.D.; de Azevedo, J.R.G.; da Silva, B.B.; de Oliveira, L.M.M. Evapotranspiração de referência baseada em métodos empíricos em bacia experimental no estado de Pernambuco - Brasil. Rev. Bras. Meteorol. 2013, 28, 181–191. [Google Scholar] [CrossRef][Green Version]
- Alvares, C.A.; Stape, J.L.; Sentelhas, P.C.; de Moraes Gonçalves, J.L.; Sparovek, G. Köppen’s climate classification map for Brazil. Meteorol. Z. 2013, 22, 711–728. [Google Scholar] [CrossRef]
- WRB, I.W.G. World Reference Base for Soil Resources 2006: A Framework for International Classification, Correlation and Communication; World Soil Resources Reports; Food and Agriculture Organization: Rome, Italy, 2006. [Google Scholar]
- Braga, R.A.P. Gestão Ambiental Da Bacia Do Rio Tapacurá - Plano de Ação; Universitária-UFPE: Recife, Brazil, 2001; p. 101. [Google Scholar]
- Penman, H.L. Natural evaporation from open water, bare soil, and grass. Proc. R. Soc. Lond. 1948, 193, 120–146. [Google Scholar] [CrossRef]
- Shuttleworth, W.J. Evaporation. In Handbook of Hydrology; Maidment, D.R., Ed.; McGraw Hill: New York, NY, USA, 1993; pp. 4.1–4.53. [Google Scholar]
- McVicar, T.R.; Roderick, M.L.; Donohue, R.J.; Li, L.T.; Van Niel, T.G.; Thomas, A.; Grieser, J.; Jhajharia, D.; Himri, Y.; Mahowald, N.M.; et al. Global review and synthesis of trends in observed terrestrial near-surface wind speeds: Implications for evaporation. J. Hydrol. 2012, 416–417, 182–205. [Google Scholar] [CrossRef]
- Donohue, R.J.; McVicar, T.R.; Roderick, M.L. Assessing the ability of potential evaporation formulations to capture the dynamics in evaporative demand within a changing climate. J. Hydrol. 2010, 386, 186–197. [Google Scholar] [CrossRef]
- Coelho, V.H.R.; Montenegro, S.; Almeida, C.N.; Silva, B.B.; Oliveira, L.M.; Gusmão, A.C.V.; Freitas, E.S.; Montenegro, A.A.A. Alluvial Groundwater Recharge Estimation in Semi-Arid Environment Using Remotely Sensed Data. J. Hydrol. 2017, 548, 1–15. [Google Scholar] [CrossRef]
- Li, Y.; Šimůnek, J.; Jing, L.; Zhang, Z.; Ni, L. Evaluation of water movement and water losses in a direct-seeded-rice field experiment using Hydrus-1D. Agric. Water Manag. 2014, 142, 38–46. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Angulo-Jaramillo, R.; Bagarello, V.; Iovino, M.; Lassabatère, L. Infiltration Measurements for Soil Hydraulic Characterization; Springer International Publishing: New York, NY, USA, 2016; ISBN 978-3-319-31786-1. [Google Scholar] [CrossRef]
- Burdine, N.T. Relative permeability calculations from pore size distribution Data. J. Pet. Technol. 1953, 5, 71–78. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Hydraulic Properties of Porous Media; Hydrology Paper 3; Colorade State University: Fort Collins, CO, USA, 1964. [Google Scholar]
- Fuentes, C.; Haverkamp, R.; Parlange, J.Y. Parameter constraints on closed-form soilwater relationships. J. Hydrol. 1992, 134, 117–142. [Google Scholar] [CrossRef]
- Yilmaz, D.; Lassabatère, L.; Angulo-Jaramillo, R.; Deneele, D.; Legret, M. Hydrodynamic characterization of basic oxygen furnace slag through an adapted BEST method. Vadose Zone J. 2010, 9, 107–116. [Google Scholar] [CrossRef]
- Bagarello, V.; Di Prima, S.; Giordano, G.; Iovino, M. A test of the Beerkan Estimation of Soil Transfer Parameters (BEST) procedure. Geoderma 2014, 221–222, 20–27. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Van Genuchten, M.T.; Leij, F.J.; Yates, S.R. The RETC Code for Quantifying the Hydraulic Functions of Unsaturated Soils; Research Report n. EPA/600/2-91/065; U.S. Salinity Laboratory, USDA-ARS: Riverside, CA, USA, 1991; 93p. [CrossRef]
- Ritchie, J.T. Model for predicting evaporation from a row crop with incomplete cover. Water Resour. Res. 1972, 8, 1204–1213. [Google Scholar] [CrossRef]
- Qu, W.; Bogena, H.R.; Huisman, J.A.; Martinez, G.; Pachepsky, Y.A.; Vereecken, H. Effects of soil hydraulic properties on the spatial variability of soil water content: Evidence from sensor network data and inverse modeling. Vadose Zone J. 2014, 13. [Google Scholar] [CrossRef]
- Vereecken, H.; Huisman, J.A.; Bogena, H.; Vanderborght, J.; Vrugt, J.A.; Hopmans, J.W. On the value of soil moisture measurements in vadose zone hydrology: A review. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Silva, R.M.; Silva, L.P.; Montenegro, S.M.G.L.; Santos, C.A.G. Análise da variedade espaço-temporal e identificação do padrão da precipitação na bacia do rio Tapacurá, Pernambuco. Soc. Nat. 2010, 22, 357–372. [Google Scholar] [CrossRef]
- Souza, E.S.; Antonino, A.C.D.; Angulo-Jaramillo, R.; Netto, A.M. Caracterização hidrodinâmica de solos: Aplicação do método Beerkan. Rev. Bras. Eng. Agrícola Ambient. 2008, 12, 128–135. [Google Scholar] [CrossRef]
- Pirastru, M.; Castellini, M.; Giadrossich, F.; Niedda, M. Comparing the hydraulic properties of forested and grassed soils on an experimental hillslope in a mediterranean environment. Procedia Environ. Sci. 2013, 19, 341–350. [Google Scholar] [CrossRef]
- Van Genuchten, M.T.; Nielsen, D. On describing and predicting the hydraulic properties of unsaturated soils. Ann. Geophys. 1985, 3, 615–627. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J.; van Genuchten, M.T. Rosetta: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Okamoto, K.; Sakai, K.; Nakamura, S.; Cho, H.; Nakandakari, T.; Ootani, S. Optimal choice of soil hydraulic parameters for simulating the unsaturated flow: A case study on the island of Miyakojima, Japan. Water 2015, 7, 5676–5688. [Google Scholar] [CrossRef]

| Site | Soil Type | Depth (cm) | Soil Particle Composition | Bulk Density | Particle Density | ||
|---|---|---|---|---|---|---|---|
| Sand (%) | Silt (%) | Clay (%) | (g cm−3) | ||||
| S1 | Acrisol | 0–10 | 71.61 | 20.06 | 8.33 | 1.54 | 2.62 |
| 10–20 | 71.72 | 18.68 | 9.60 | 1.50 | 2.60 | ||
| 20–30 | 76.14 | 14.11 | 9.75 | 1.51 | 2.58 | ||
| S2 | Acrisol | 0–10 | 67.56 | 24.01 | 8.43 | 1.58 | 2.58 |
| 10–20 | 60.40 | 21.26 | 18.34 | 1.62 | 2.56 | ||
| 20–30 | 65.88 | 23.10 | 11.02 | 1.64 | 2.58 | ||
| Site | BEST Output | RETC Output | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| m | n | η | S (mm s−1/2) | Ks (cm day−1) | θr1 (cm3 cm−3) | θs (cm3 cm−3) | hg (cm) | A (cm−1) | n | |
| S1 | 0.102 | 2.223 | 11.482 | 1.31 | 159.97 | 0.063 | 0.377 | −18.5 | 0.041 | 1.245 |
| S2 | 0.094 | 2.204 | 12.682 | 1.20 | 155.52 | 0.026 | 0.379 | −16.7 | 0.020 | 1.273 |
| Site | θr (cm3 cm−3) | θs (cm3 cm−3) | α (cm−1) | n | Ks (cm day−1) | l |
|---|---|---|---|---|---|---|
| S1 | 0.107 | 0.342 | 0.037 | 1.23 | 234.2 | 0.5 |
| S2 | 0.056 | 0.369 | 0.018 | 1.17 | 243.7 | 0.5 |
| Site | RMSE (cm3 cm−3) | d | NSE |
|---|---|---|---|
| S1 | 0.012 | 0.95 | 0.783 |
| S2 | 0.020 | 0.93 | 0.740 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva Ursulino, B.; Maria Gico Lima Montenegro, S.; Paiva Coutinho, A.; Hugo Rabelo Coelho, V.; Cezar dos Santos Araújo, D.; Cláudia Villar Gusmão, A.; Martins dos Santos Neto, S.; Lassabatere, L.; Angulo-Jaramillo, R. Modelling Soil Water Dynamics from Soil Hydraulic Parameters Estimated by an Alternative Method in a Tropical Experimental Basin. Water 2019, 11, 1007. https://doi.org/10.3390/w11051007
Silva Ursulino B, Maria Gico Lima Montenegro S, Paiva Coutinho A, Hugo Rabelo Coelho V, Cezar dos Santos Araújo D, Cláudia Villar Gusmão A, Martins dos Santos Neto S, Lassabatere L, Angulo-Jaramillo R. Modelling Soil Water Dynamics from Soil Hydraulic Parameters Estimated by an Alternative Method in a Tropical Experimental Basin. Water. 2019; 11(5):1007. https://doi.org/10.3390/w11051007
Chicago/Turabian StyleSilva Ursulino, Bruno, Suzana Maria Gico Lima Montenegro, Artur Paiva Coutinho, Victor Hugo Rabelo Coelho, Diego Cezar dos Santos Araújo, Ana Cláudia Villar Gusmão, Severino Martins dos Santos Neto, Laurent Lassabatere, and Rafael Angulo-Jaramillo. 2019. "Modelling Soil Water Dynamics from Soil Hydraulic Parameters Estimated by an Alternative Method in a Tropical Experimental Basin" Water 11, no. 5: 1007. https://doi.org/10.3390/w11051007
APA StyleSilva Ursulino, B., Maria Gico Lima Montenegro, S., Paiva Coutinho, A., Hugo Rabelo Coelho, V., Cezar dos Santos Araújo, D., Cláudia Villar Gusmão, A., Martins dos Santos Neto, S., Lassabatere, L., & Angulo-Jaramillo, R. (2019). Modelling Soil Water Dynamics from Soil Hydraulic Parameters Estimated by an Alternative Method in a Tropical Experimental Basin. Water, 11(5), 1007. https://doi.org/10.3390/w11051007





