On Solving Nonlinear Moving Boundary Problems with Heterogeneity Using the Collocation Meshless Method
Abstract
1. Introduction
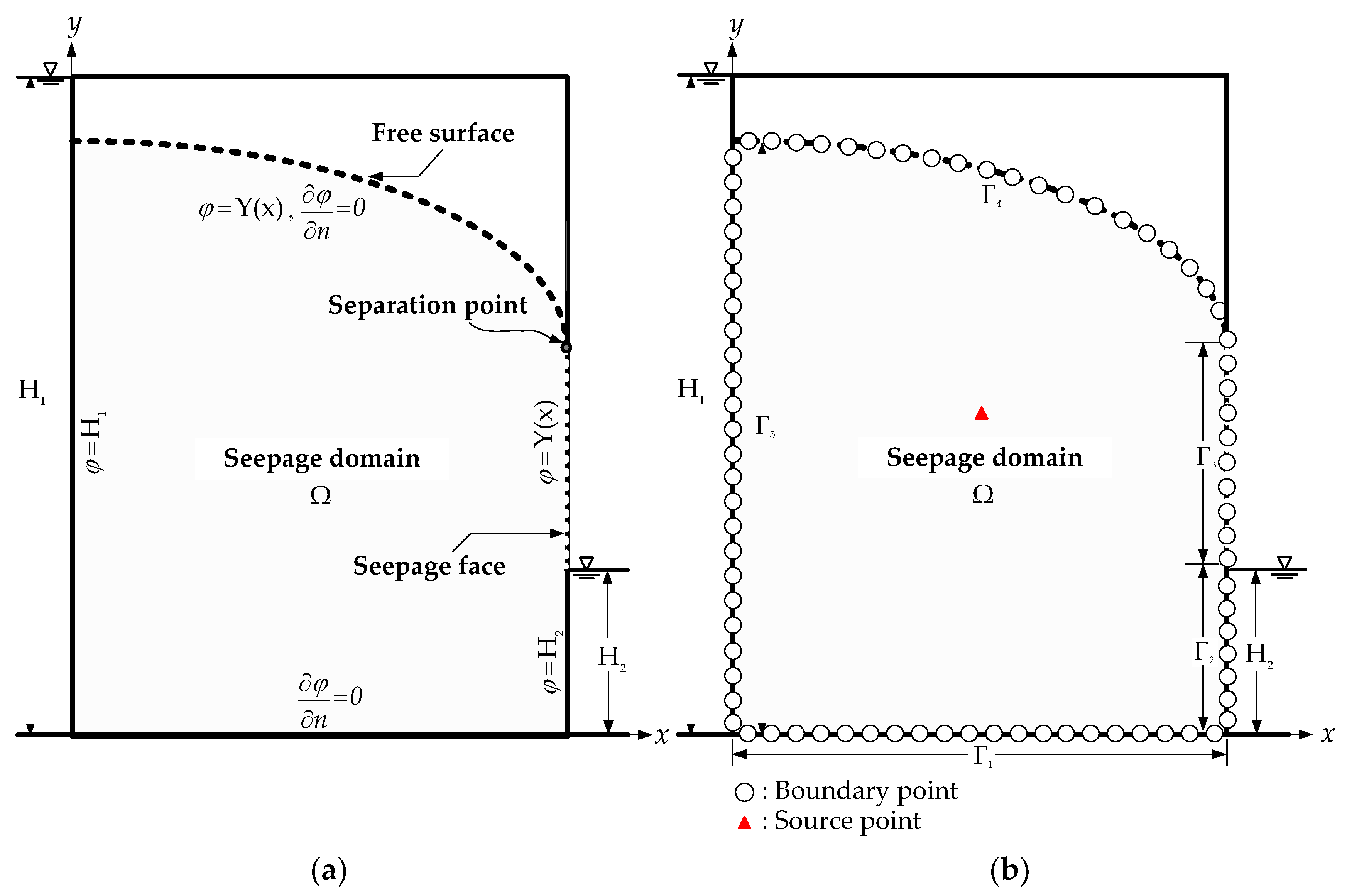
2. Governing Equation and Boundary Conditions
3. The Collocation Trefftz Method
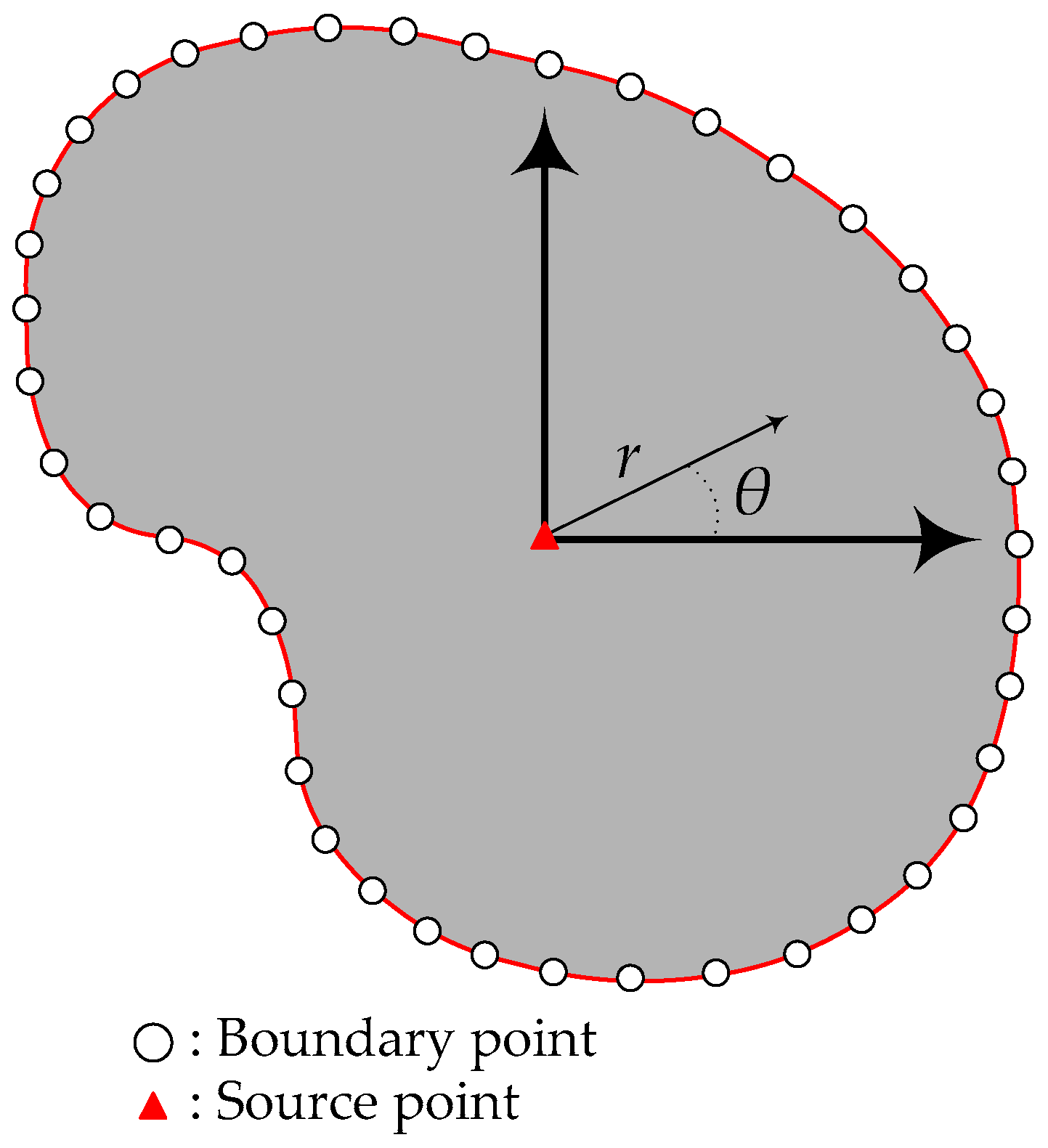
3.1. Formulation of T-Complete Basis Functions
3.2. The Characteristic Length
3.3. The Iterative Scheme for Solving Free Surface
4. Validation Examples
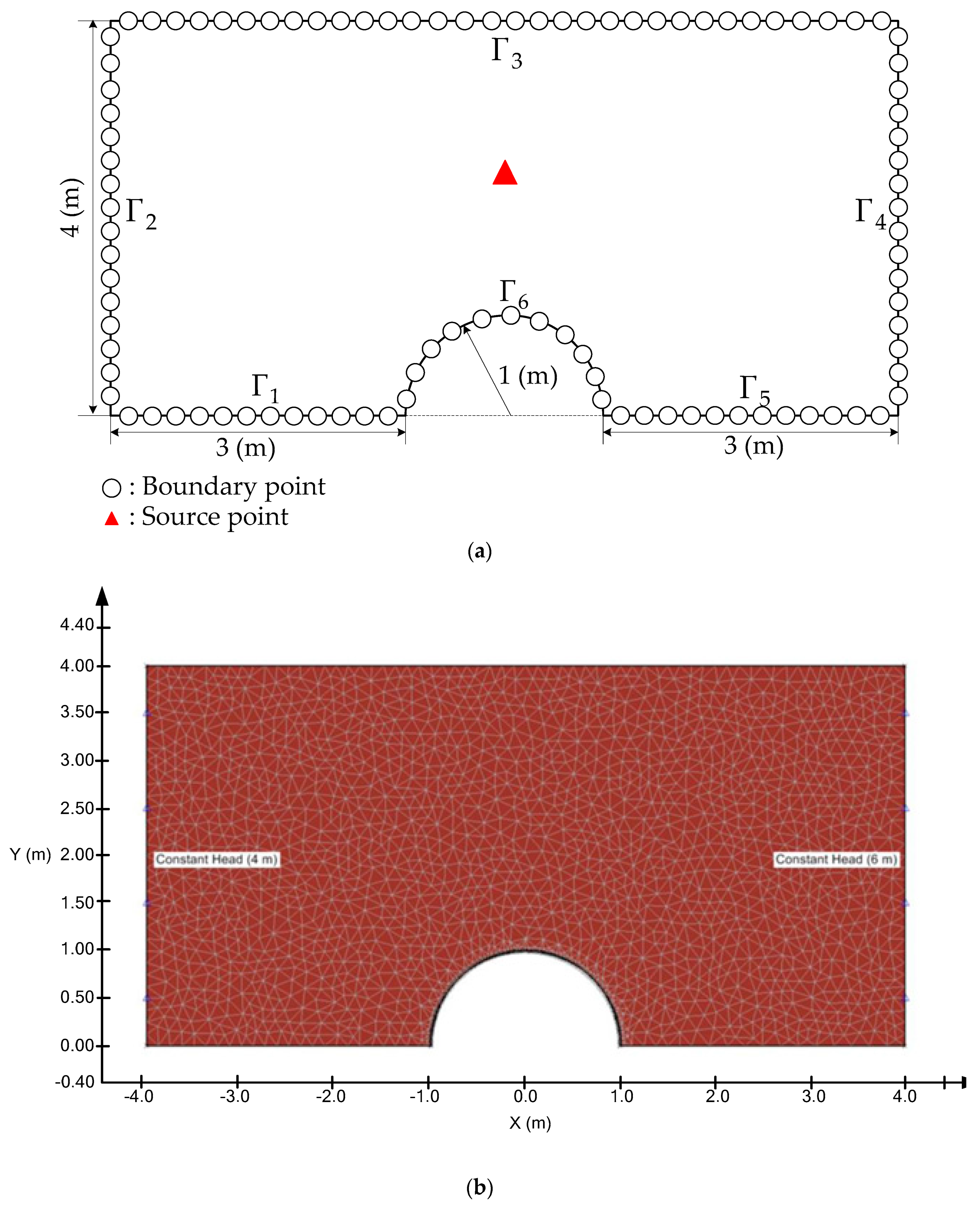
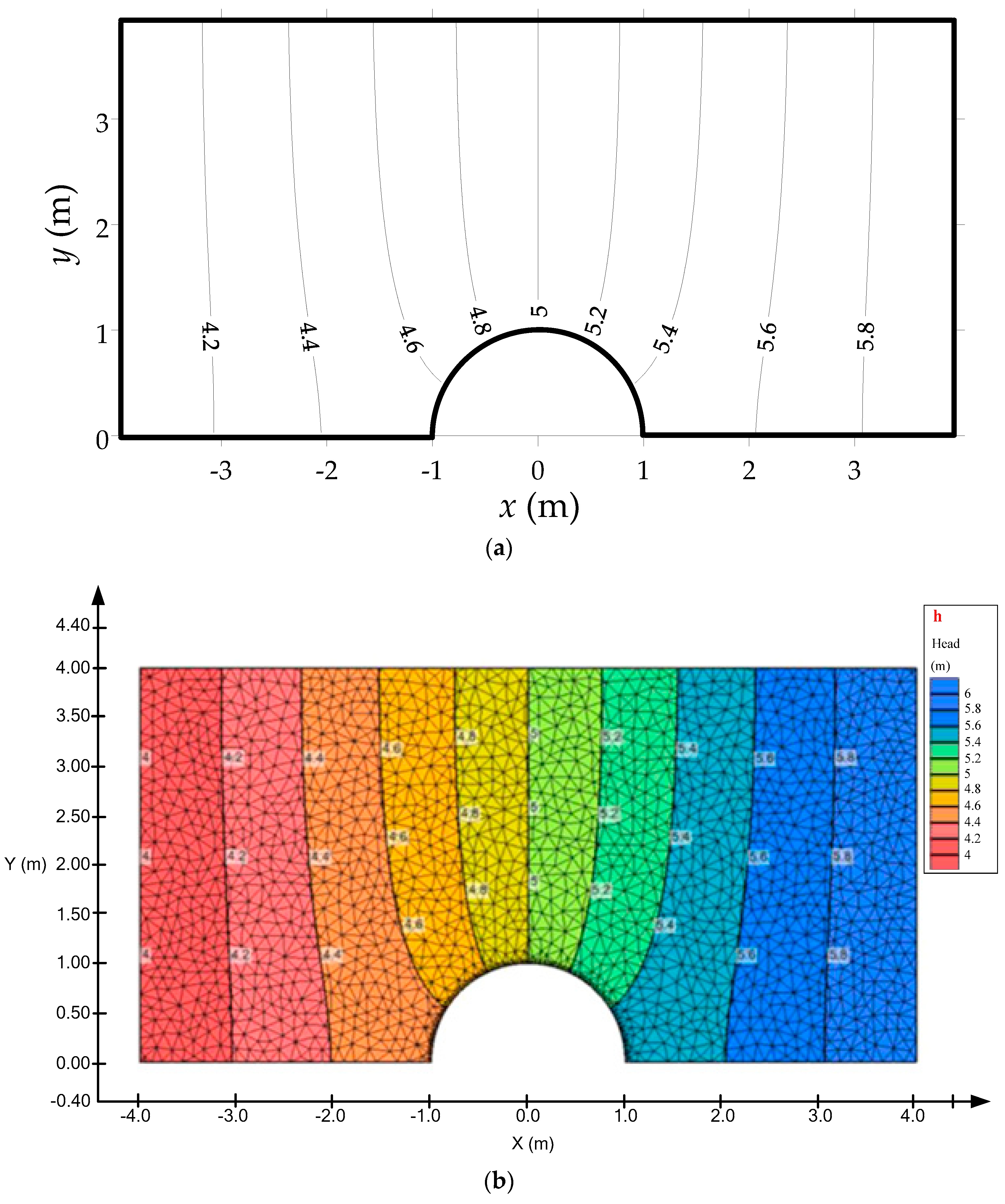
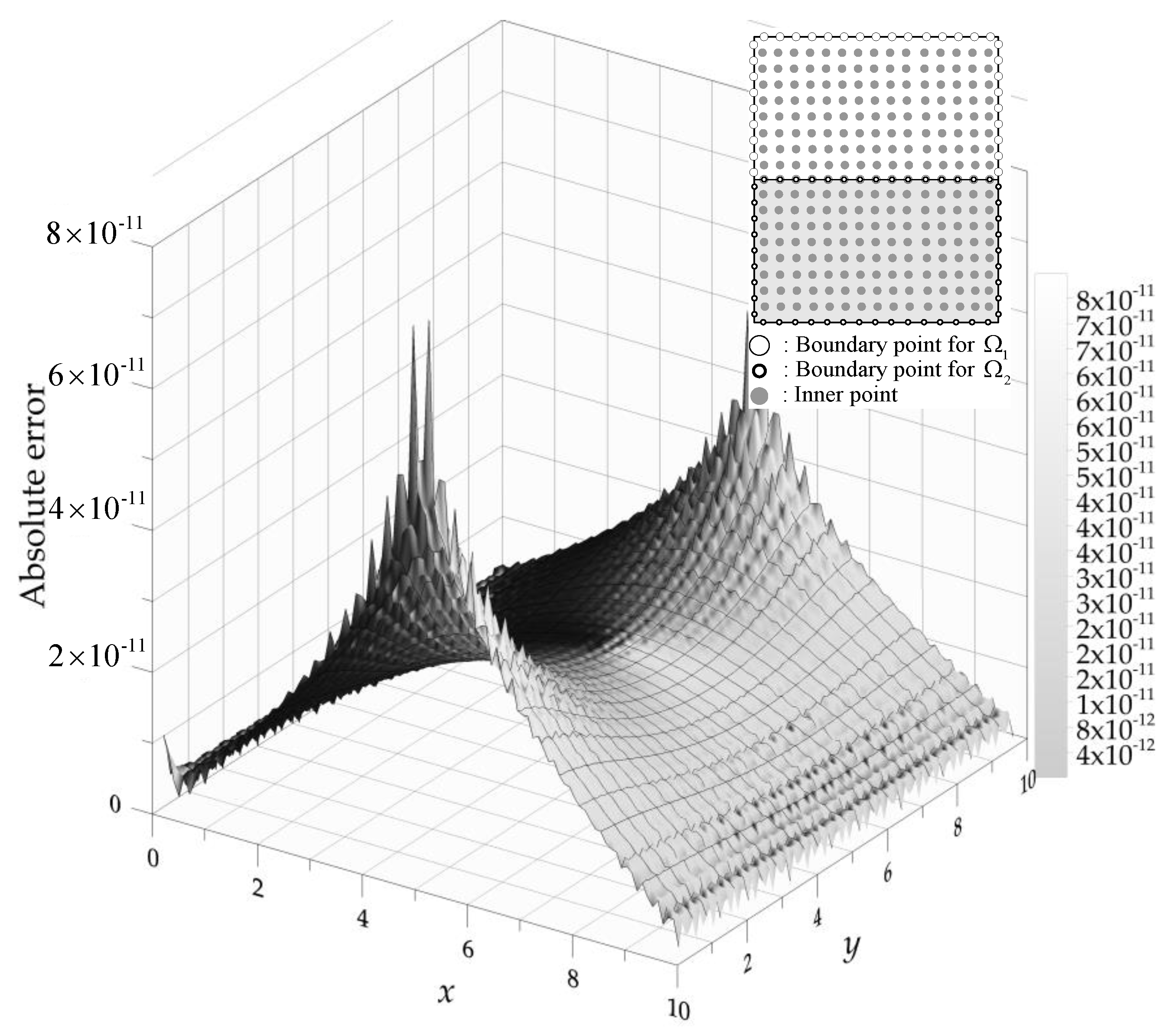
4.1. Laminar Flow around a Cylinder
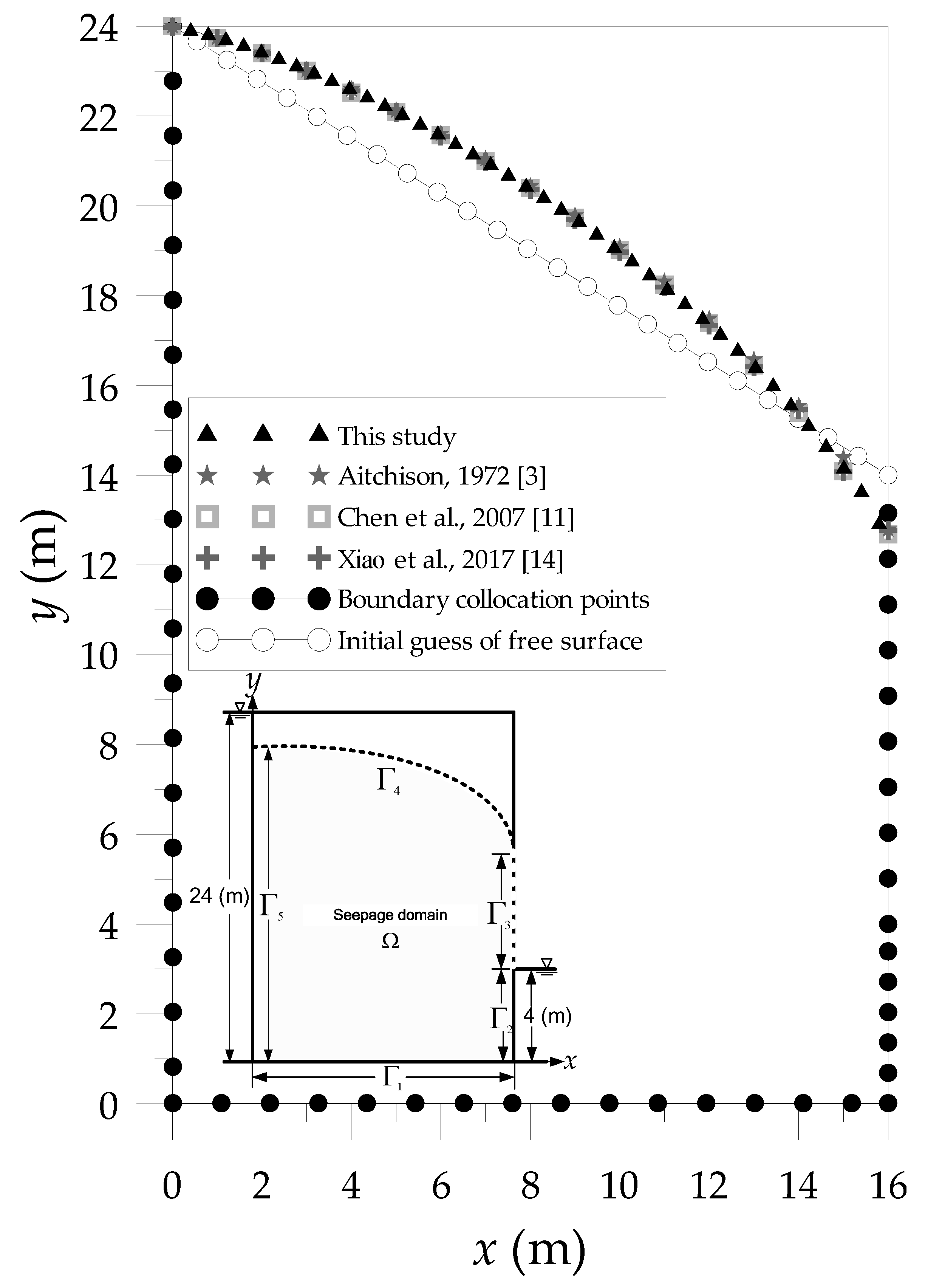
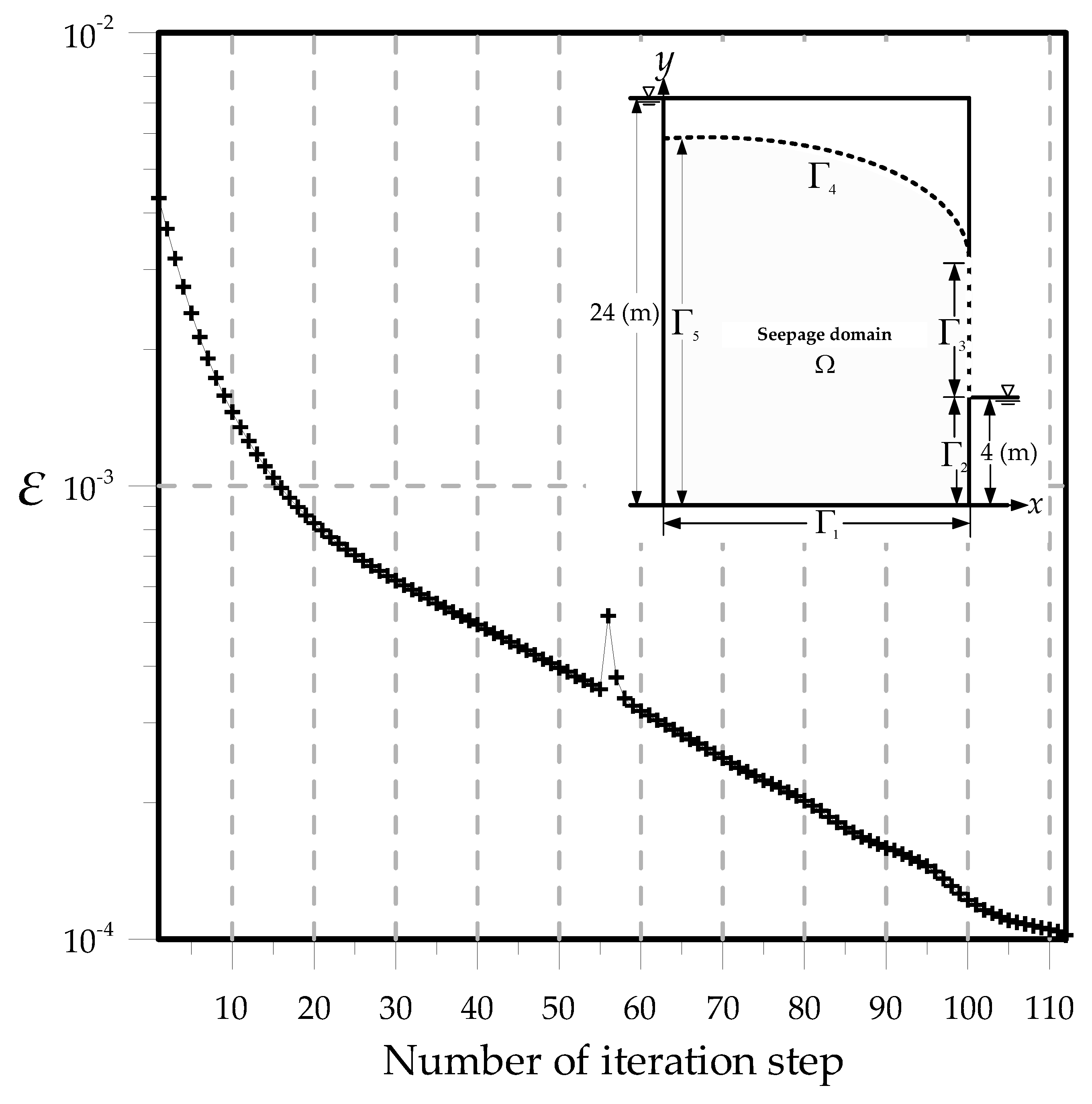
4.2. Nonlinear Moving Surface through a Rectangular Dam
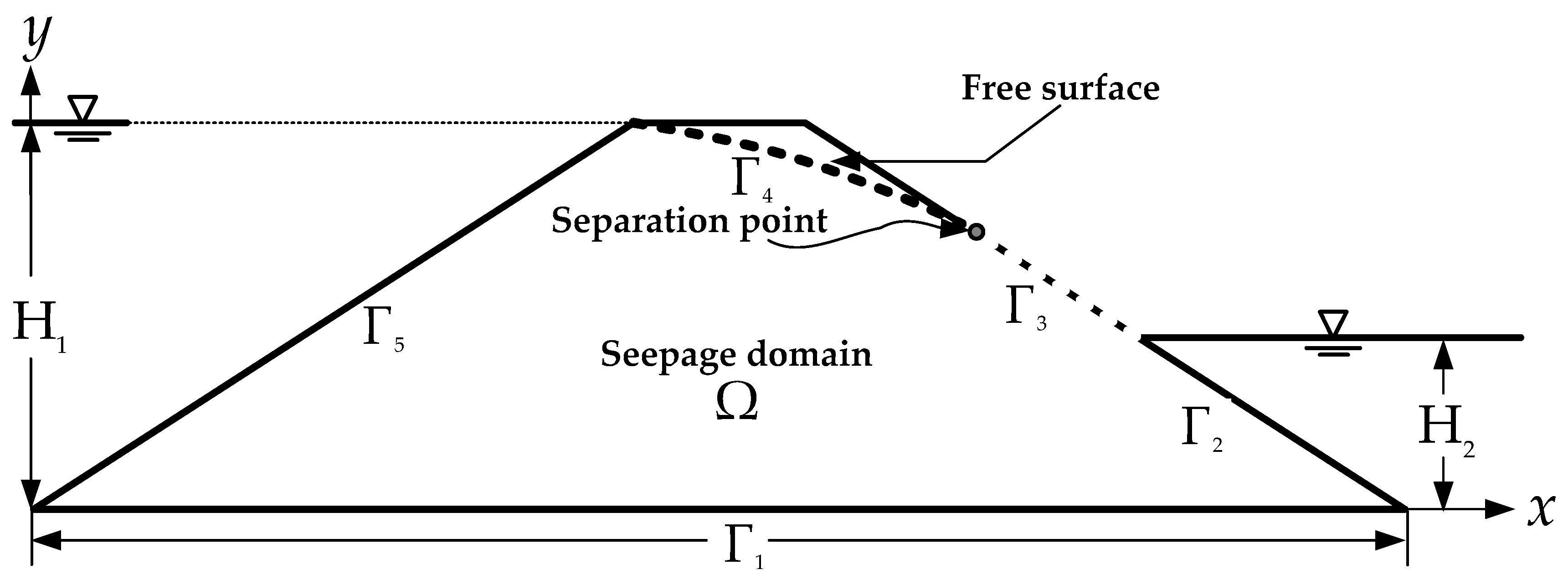
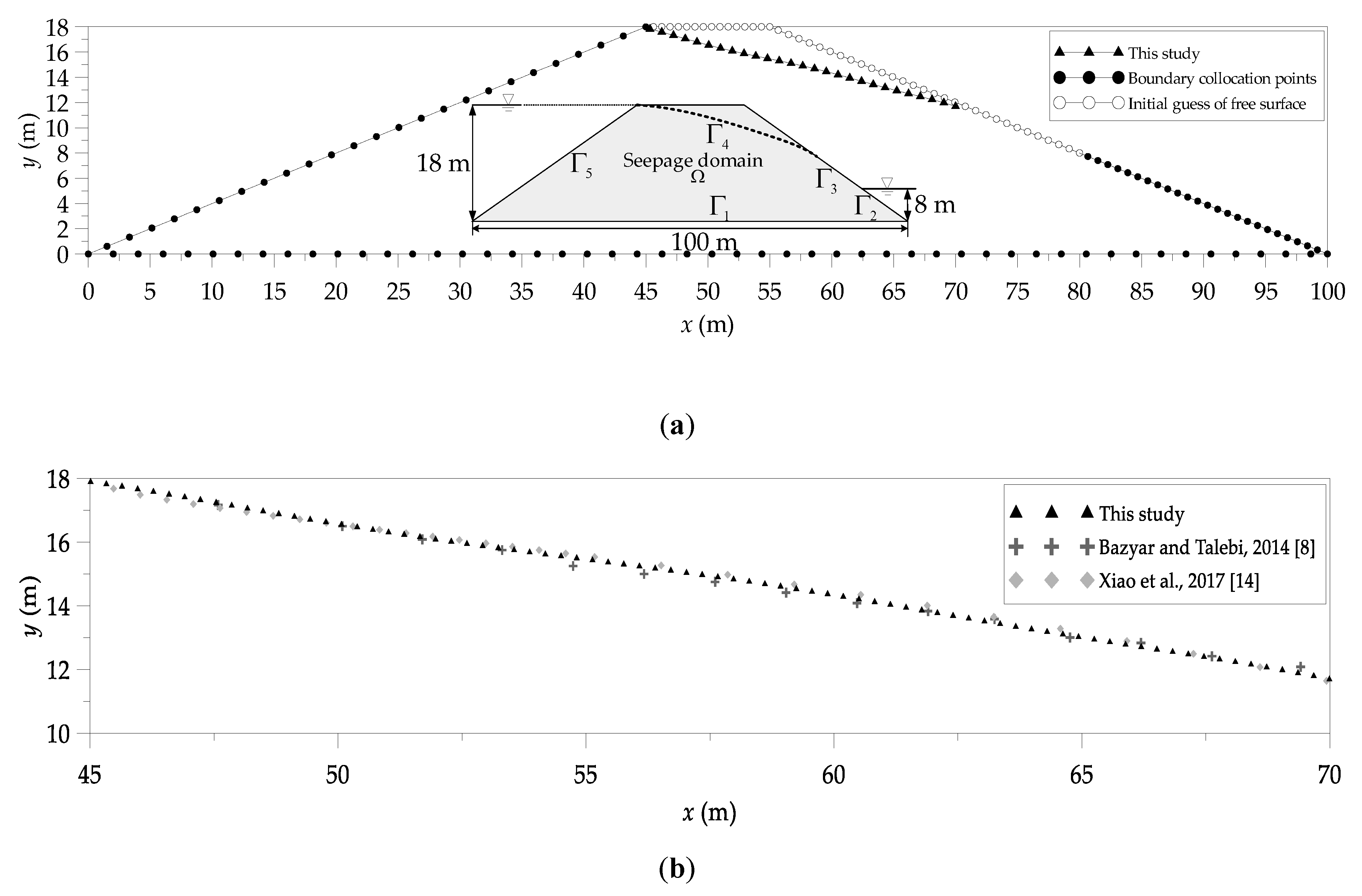
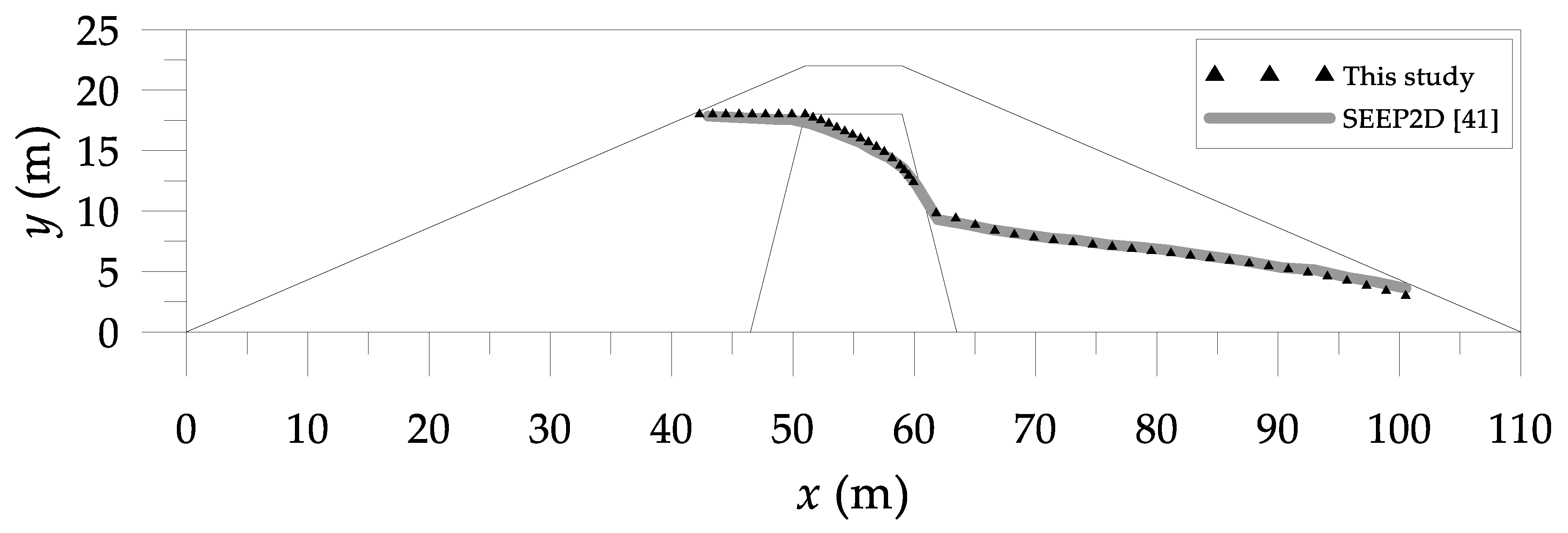
4.3. Nonlinear Moving Surface through an Earth Dam
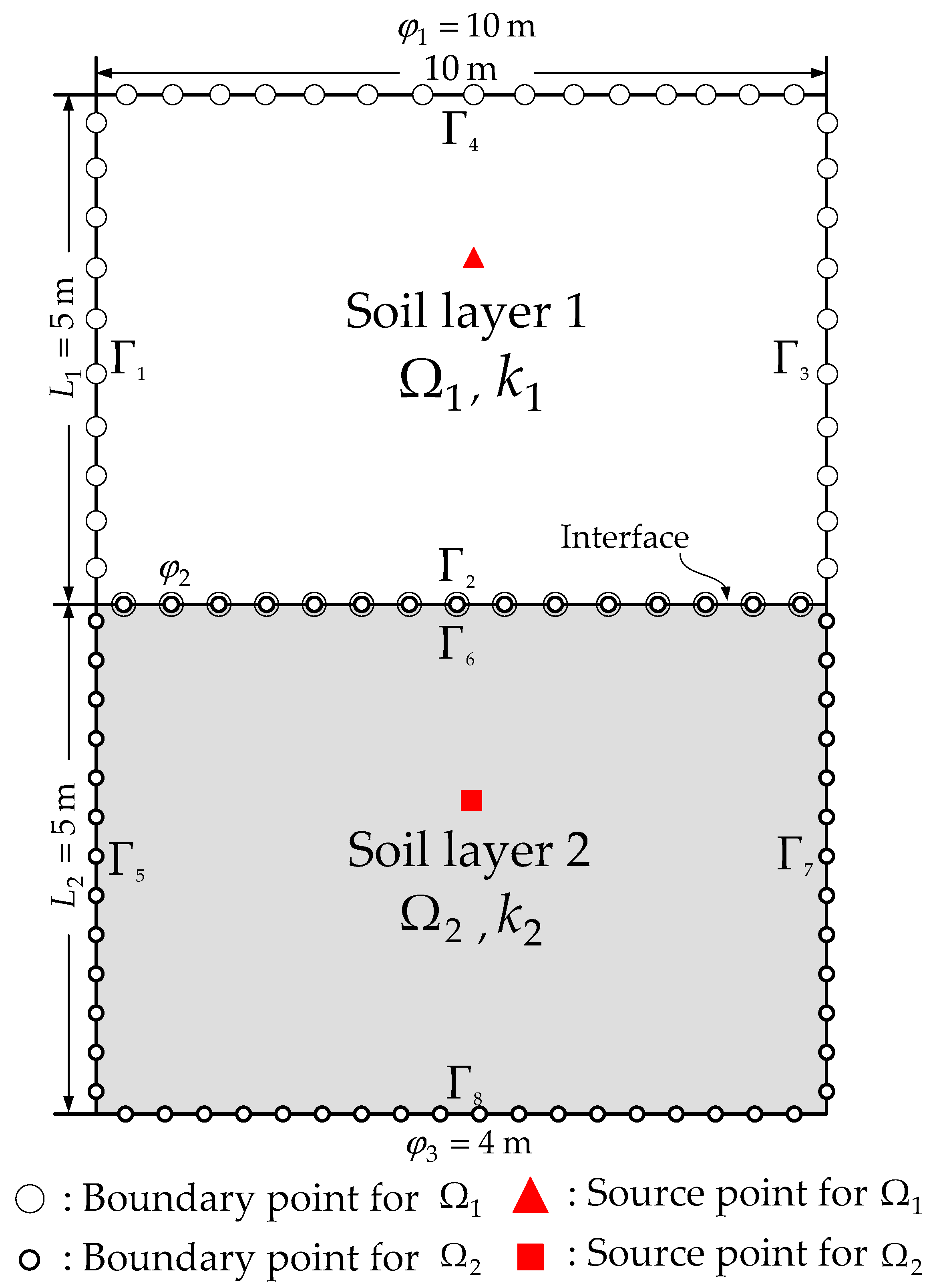
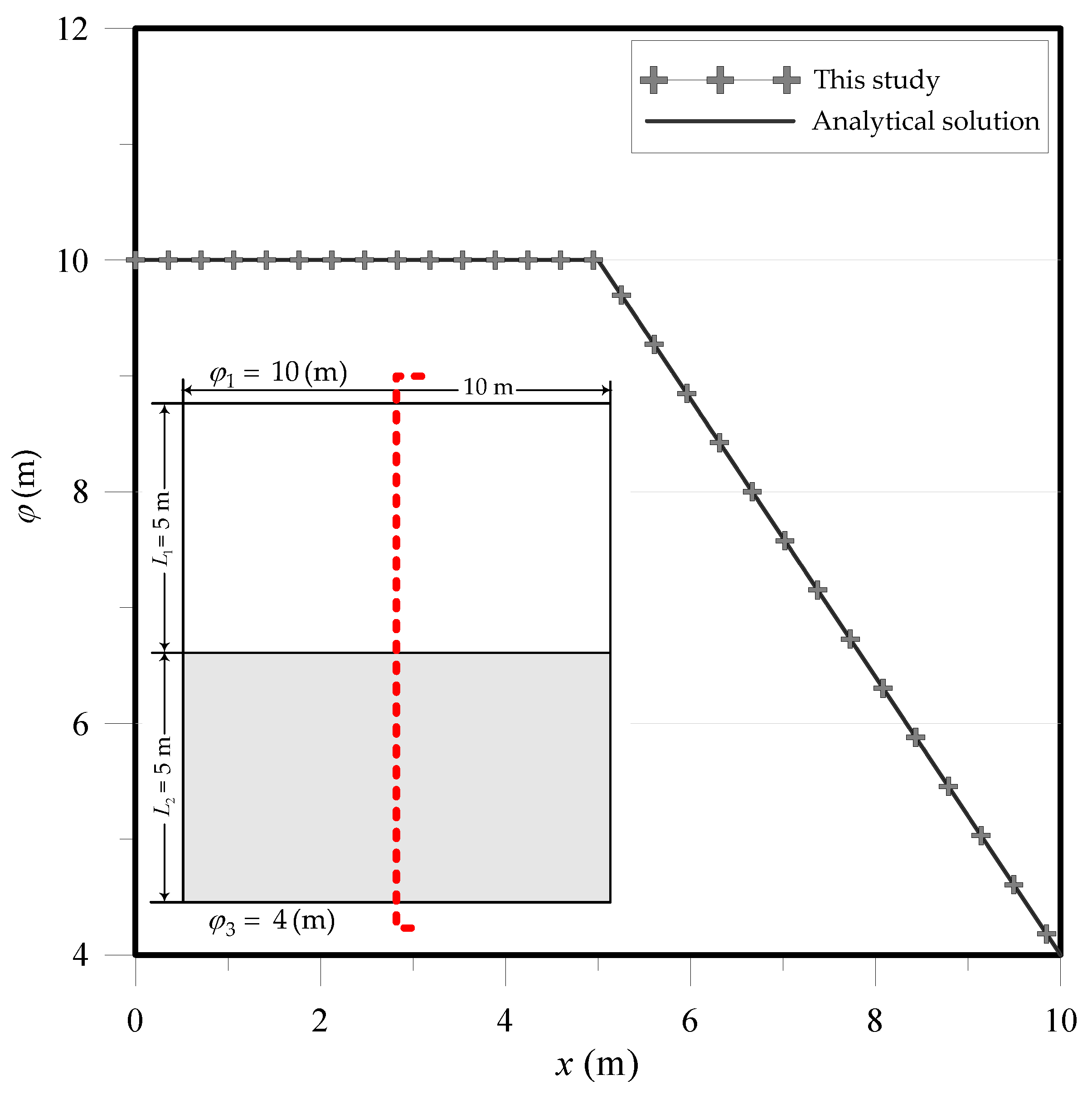
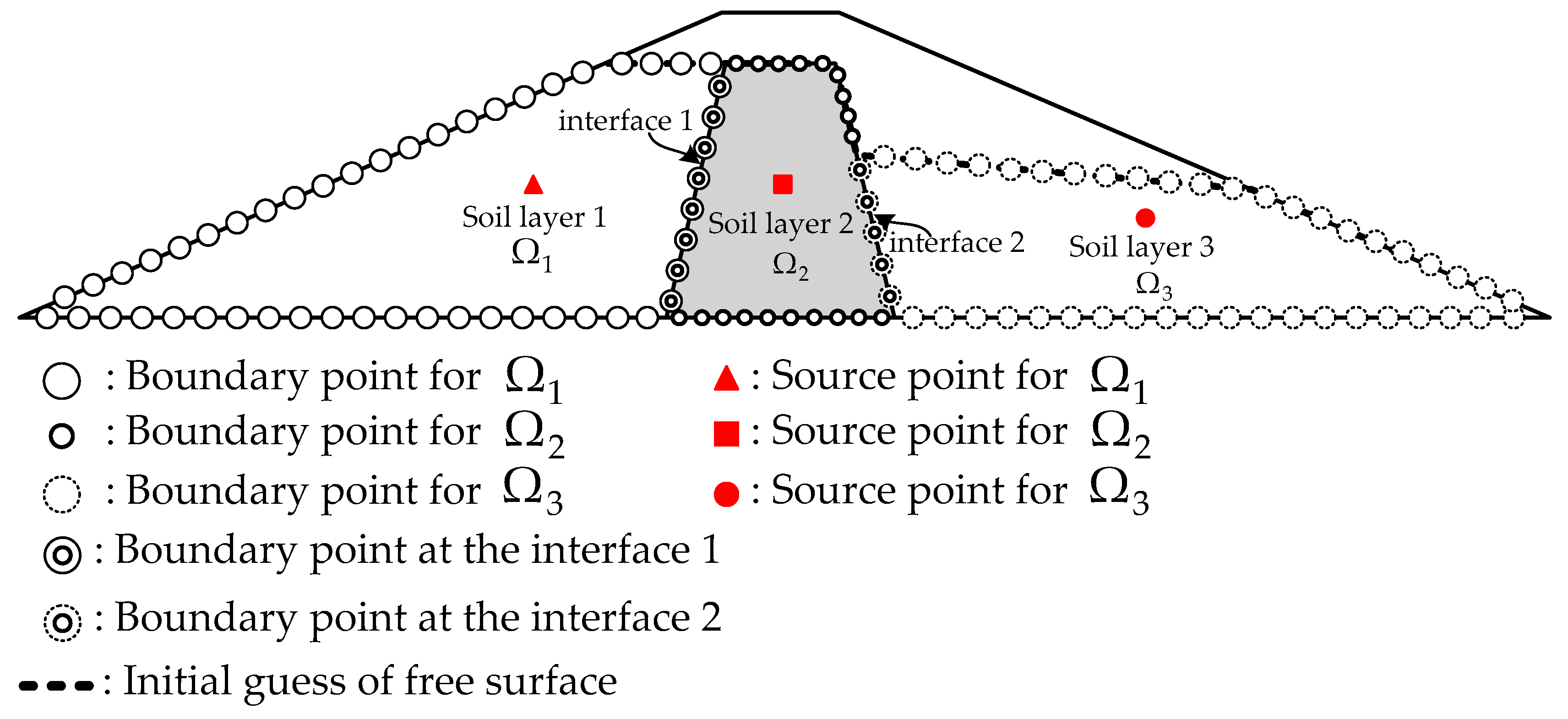
4.4. Flow through Two Layered Soils
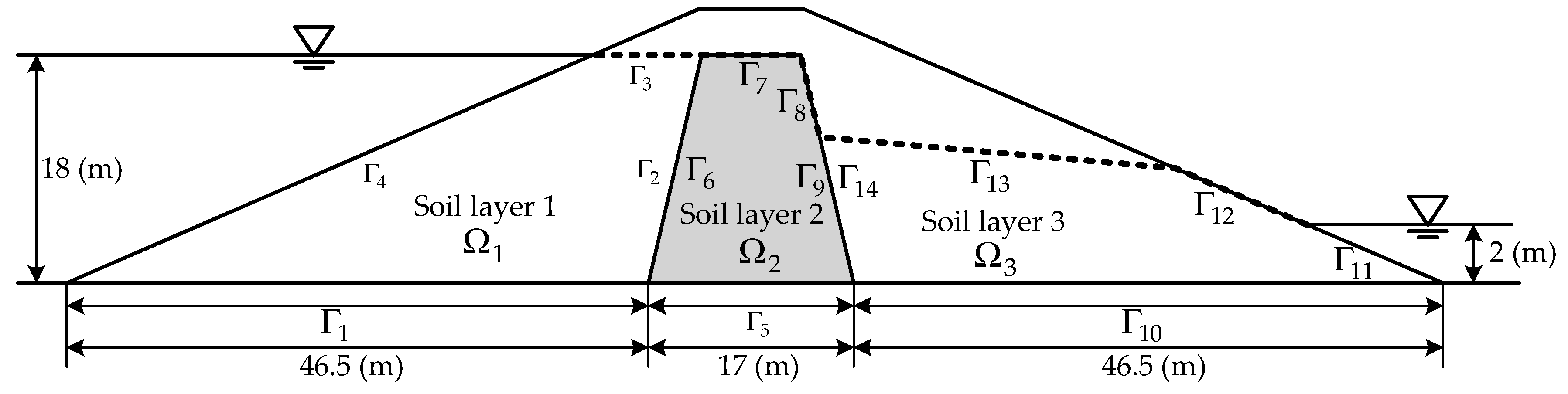
4.5. Nonlinear Moving Surface through a Zoned–Earth Dam
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zheng, H.; Liu, F.; Li, C.G. Primal mixed solution to unconfined seepage flow in porous media with numerical manifold method. Appl. Math. Model. 2015, 39, 794–808. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, M.; Zhou, Q.; Rutqvist, J. A new second-order numerical manifold method model with an efficient scheme for analyzing free surface flow with inner drains. Appl. Math. Model. 2015, 40, 1427–1445. [Google Scholar] [CrossRef]
- Aitchison, J. Numerical treatment of a singularity in a free boundary problem. Proc. R. Soc. Lond. 1972, 330, 573–580. [Google Scholar] [CrossRef]
- Fukuchi, T. Numerical analyses of steady-state seepage problems using the interpolation finite difference method. Soils Found. 2016, 56, 608–626. [Google Scholar] [CrossRef]
- Darbandi, M.; Torabi, S.O.; Saadat, M.; Daghighi, Y.; Jarrahbashi, D. A moving-mesh finite-volume method to solve free-surface seepage problem in arbitrary geometries. Int. J. Numer. Anal. Methods Geomech. 2007, 31, 1609–1629. [Google Scholar] [CrossRef]
- Bresciani, E.; Davy, P.; Dreuzy, J.R. A finite volume approach with local adaptation scheme for the simulation of free surface flow in porous media. Int. J. Numer. Anal. Methods Geomech. 2011, 36, 1574–1591. [Google Scholar] [CrossRef]
- Sauerland, H.; Fries, T.P. The extended finite element method for two-phase and free-surface flows: A systematic study. J. Comput. Phys. 2011, 230, 3369–3390. [Google Scholar] [CrossRef]
- Bazyar, M.H.; Talebi, A. Locating the free surface flow in porous media using the scaled boundary finite-element method. Int. J. Chem. Eng. Appl. 2014, 5, 155–160. [Google Scholar] [CrossRef]
- Bathe, K.J.; Khoshgoftaar, M.R. Finite element free surface seepage analysis without mesh iteration. Int. J. Numer. Anal. Methods Geomech. 1979, 3, 13–22. [Google Scholar] [CrossRef]
- Neuman, S.P.; Witherspoon, P.A. Finite element method of analyzing steady seepage with a free surface. Water Resour. Res. 1970, 6, 889–897. [Google Scholar] [CrossRef]
- Chen, J.T.; Hsiao, C.C.; Chen, K.H. Study of free surface seepage problems using hypersingular equations. Commun. Numer. Methods Eng. 2007, 23, 755–769. [Google Scholar] [CrossRef]
- Rafiezadeh, K.; Ataie-Ashtiani, B. Transient free-surface seepage in three-dimensional general anisotropic media by BEM. Eng. Anal. Bound. Elem. 2014, 46, 51–66. [Google Scholar] [CrossRef]
- Leontiev, A.; Huacasi, W. Mathematical programming approach for unconfined seepage flow problem. Eng. Anal. Bound. Elem. 2016, 25, 49–56. [Google Scholar] [CrossRef]
- Xiao, J.E.; Ku, C.Y.; Liu, C.Y.; Fan, C.M.; Yeih, W. On solving free surface problems in layered soil using the method of fundamental solutions. Eng. Anal. Bound. Elem. 2017, 83, 96–106. [Google Scholar] [CrossRef]
- Pepper, D.W.; Waters, J. A local meshless method for approximating 3D wind fields. J. Appl. Meteorol. Clim. 2016, 55, 163–172. [Google Scholar] [CrossRef]
- Li, Z.C.; Lu, T.T.; Hu, H.Y.; Cheng, A.H.D. Trefftz and Collocation Methods; WIT Press: Southampton, UK; Boston, MA, USA, 2008. [Google Scholar]
- Liu, C.S. A modified Trefftz method for two-dimensional Laplace equation considering the domain’s characteristic length. CMES-Comput. Model. Eng. 2007, 21, 53–65. [Google Scholar]
- Liu, C.S. A highly accurate collocation Trefftz method for solving the Laplace equation in the doubly connected domains. Numer. Meth. Part. Differ. Equ. 2008, 24, 179–192. [Google Scholar] [CrossRef]
- Ku, C.Y.; Xiao, J.E.; Liu, C.Y.; Yeih, W. On the accuracy of the collocation Trefftz method for solving two- and three-dimensional heat equations. Numer. Heat Transf. B-Fundam. 2016, 69, 334–350. [Google Scholar] [CrossRef]
- Ku, C.Y. On solving three-dimensional Laplacian problems in a multiply connected domain using the multiple scale Trefftz method. CMES-Comput. Model. Eng. 2014, 98, 509–541. [Google Scholar]
- Huang, H.T.; Li, Z.C. Global superconvergence of Adini’s elements coupled with the Trefftz method for singular problems. Eng. Anal. Bound. Elem. 2003, 27, 227–240. [Google Scholar] [CrossRef]
- Lee, M.G.; Young, L.J.; Li, Z.C.; Chun, P.C. Combined Trefftz methods of particular and fundamental solutions for corner and crack singularity of linear elastostatics. Eng. Anal. Bound. Elem. 2010, 34, 632–654. [Google Scholar] [CrossRef]
- Kita, E.; Kamiya, N. Trefftz method: An overview. Adv. Eng. Softw. 1995, 24, 3–12. [Google Scholar] [CrossRef]
- Li, Z.C.; Lee, M.G.; Chiang, J.Y.; Liu, Y.P. The Trefftz method using fundamental solutions for biharmonic equations. J. Comput. Appl. Math. 2011, 235, 4350–4367. [Google Scholar] [CrossRef]
- Fu, Z.J.; Qin, Q.H.; Chen, W. Hybrid-Trefftz finite element method for heat conduction in nonlinear functionally graded materials. Eng. Comput. 2011, 28, 578–599. [Google Scholar] [CrossRef]
- Borkowski, M.; Hao, F.; Wang, Y.; Chen, C.S. The scalability of the matrices in direct Trefftz method in 2D Laplace problem. Eng. Anal. Bound. Elem. 2016, 64, 12–18. [Google Scholar] [CrossRef]
- Li, Z.C.; Lee, M.G.; Chiang, J.Y. Collocation Trefftz methods for the Stokes equations with singularity. Numer. Methods Part. Differ. Equ. 2012, 29, 361–395. [Google Scholar] [CrossRef]
- Li, Z.C.; Huang, H.T.; Huang, J.; Ling, L. Stability analysis for the penalty plus hybrid and the direct Trefftz methods for singularity problems. Eng. Anal. Bound. Elem. 2007, 31, 163–175. [Google Scholar] [CrossRef]
- Kong, W.; Wu, X. The Laplace transform and polynomial Trefftz method for a class of time dependent PDEs. Appl. Math. Model. 2009, 33, 2226–2233. [Google Scholar] [CrossRef]
- Ku, C.Y.; Liu, C.Y.; Xiao, J.E.; Yeih, W. Transient modeling of flow in unsaturated soils using a novel collocation meshless method. Water 2017, 9, 954. [Google Scholar] [CrossRef]
- Ku, C.Y.; Kuo, C.L.; Fan, C.M.; Liu, C.S.; Guan, P.C. Numerical solution of three-dimensional Laplacian problems using the multiple scale Trefftz method. Eng. Anal. Bound. Elem. 2015, 50, 157–168. [Google Scholar] [CrossRef]
- Lv, H.; Hao, F.; Wang, Y.; Chen, C.S. The MFS versus the Trefftz method for the Laplace equation in 3D. Eng. Anal. Bound. Elem. 2017, 83, 133–140. [Google Scholar] [CrossRef]
- Fan, C.M.; Liu, Y.C.; Chan, H.F.; Hsiao, S.S. Solutions of boundary detection problem for modified Helmholtz equation by Trefftz method. Inverse Probl. Sci. Eng. 2014, 22, 267–281. [Google Scholar] [CrossRef]
- Fan, C.M.; Chan, H.F.; Kuo, C.L.; Yeih, W. Numerical solutions of boundary detection problems using modified collocation Trefftz method and exponentially convergent scalar homotopy algoithm. Eng. Anal. Bound. Elem. 2012, 36, 2–8. [Google Scholar] [CrossRef]
- Yeih, W.; Liu, C.S.; Kuo, C.L.; Atluri, S.N. Solving the direct/inverse Cauchy problems of Laplace equation in a multiply connected domain, using the generalized multiple-source-point boundary-collocation Trefftz method & characteristic lengths. CMC-Comput. Mater. Contin. 2010, 17, 275–302. [Google Scholar]
- Huang, F.K.; Chuang, M.H.; Wang, G.S.; Yeh, H.D. Tide-induced groundwater level fluctuation in a U-shaped coastal aquifer. J. Hydrol. 2015, 530, 291–305. [Google Scholar] [CrossRef]
- Xiao, J.E.; Ku, C.Y.; Liu, C.Y.; Yeih, W. A novel boundary-type meshless method for modeling geofluid flow in heterogeneous geological media. Geofluids 2018, 2018, 9804291. [Google Scholar] [CrossRef]
- Young, D.L.; Fan, C.M.; Tsai, C.C.; Chen, C.W. The method of fundamental solutions and domain decomposition method for degenerate seepage flow net problems. J. Chin. Inst. Eng. 2006, 29, 63–73. [Google Scholar] [CrossRef]
- Mehl, S. Use of Picard and Newton iteration for solving nonlinear groundwater flow equations. Groundwater 2006, 44, 583–594. [Google Scholar] [CrossRef] [PubMed]
- SoilVision Systems Ltd. SVFLUX Verification Manual; SoilVision Systems Ltd.: Saskatoon, SK, Canada, 2018. [Google Scholar]
- AQUAVEO. SEEP2D Earth Dam; AQUAVEO: Provo, UT, USA, 2016. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ku, C.-Y.; Xiao, J.-E.; Liu, C.-Y. On Solving Nonlinear Moving Boundary Problems with Heterogeneity Using the Collocation Meshless Method. Water 2019, 11, 835. https://doi.org/10.3390/w11040835
Ku C-Y, Xiao J-E, Liu C-Y. On Solving Nonlinear Moving Boundary Problems with Heterogeneity Using the Collocation Meshless Method. Water. 2019; 11(4):835. https://doi.org/10.3390/w11040835
Chicago/Turabian StyleKu, Cheng-Yu, Jing-En Xiao, and Chih-Yu Liu. 2019. "On Solving Nonlinear Moving Boundary Problems with Heterogeneity Using the Collocation Meshless Method" Water 11, no. 4: 835. https://doi.org/10.3390/w11040835
APA StyleKu, C.-Y., Xiao, J.-E., & Liu, C.-Y. (2019). On Solving Nonlinear Moving Boundary Problems with Heterogeneity Using the Collocation Meshless Method. Water, 11(4), 835. https://doi.org/10.3390/w11040835







