Abstract
The increasing occurrence of widespread drought phenomena is a global environmental emergency, especially for the effects of ongoing climate change on groundwater availability. Dry years and extreme temperatures are common drivers of current climate impacts all over the world, including, for example, the freshwater supply for drinking and agriculture purposes, ecosystems, forestry, health, etc. In this frame, to ensure temporal water availability in water-stressed areas, sustainable groundwater management is an increasing challenge. Most groundwater in the South-East Latium Region, Central Italy, as in the whole Apennine Mountains chain, is stored in karst aquifers. In this area important water resources are present, but even here in the last decades they are affected by groundwater depletion as a consequence of occurring drought events, the upward trend in the global average temperature and the increase in groundwater extraction. Due to the lack of flow rate data of springs in many areas of Italy, spring response modeling could be a useful tool for supporting proper water resource management. Several research studies proposed methods based on relationships between spring discharges and rainfall data. The goal of this paper is to propose a simple linear model, based on rainfall-discharge cross correlations, in order to be able to simulate the effects of variation in rainfall on water resource connected Capodacqua di Spigno Spring minimum discharge. The results obtained using the developed model has been compared to an existing method that uses the Standard Precipitation Index (SPI) for the estimation of the minimum annual spring discharge.
1. Introduction
Water crises have become more and more frequent in recent years. Changes in global climate seem to affect the hydrological cycle, altering surface water levels and groundwater recharge to aquifers with various other associated impacts on natural ecosystems and human activities. In this scenario, it seems clear to affirm that climate change can impact groundwater resources by modifying the renewable portion of groundwater storage through changes in recharge [1]. Various studies with different approaches at the river basin level have determined the effect of climate change on water resource systems. The main conclusions of these publications are that there will be less surface runoff and aquifer recharge due to increasing temperatures, and decreasing trends in precipitation rates [2].
During the Mediterranean long dry summer months, karst springs provide fresh high quality water, which has been an important resource for human development in this region since antiquity [3]. Specifically, in Italy, karst carbonate aquifers of the Central Apennines represent the most important groundwater resources [4].
In order to plan a sustainable water resource exploitation, an appropriate water quantitative evaluation is necessary, monitoring spring discharge during the whole hydrological year. When spring flow measurements are not possible to carry out and there is no appropriate knowledge about long time discharge series, spring discharge estimation is recommended. Many approaches have been proposed to analyze the relations between the rainfall time series over the recharge area and the spring outflow [5]. These models, for example, are based on continuous and discrete wavelet analysis [6,7], cross-correlation analysis [8,9,10], or machine learning models [11]. Other studies, concerning karst springs, have employed time-series analysis studying transfer function between rainfall and spring discharge, obtained by black-box models [12] or artificial neural network [13].
Unlike typical hydrologic models, data-driven approaches do not rely directly on explicit physical knowledge of the process, even if they usually are the first step in developing knowledge about system properties, observing relationships between input and output variables. Using various learning algorithms, data-driven approaches provide a flexible way to model complex phenomena such karst spring discharge [14].
The present research concerns the development of a simple estimation model to evaluate spring discharge. The proposed model is grounded on statistical correlations between the series of monthly spring discharge values and the series of monthly rainfall values, referred to in the same time series. Specifically, the present approach is represented by a linear cross-correlation model, where needed input data, after the initial training, is only the rainfall data. The present study represents, therefore, the first results of an approach that tries to disengage from the flow rate values as input, in estimating the karst spring discharge. Even if simple, this model can be a powerful tool in water resource management and planning, especially for minimum flow rates related to long-term rainfall variations.
Afterwards, the model was applied to the Capodacqua di Spigno Spring, calibrating it on the available flow data, related to the years 1973–1977, as part of a scientific technical collaboration between the water agency Acqualatina S.p.A. (i.e., Corporation) and Sapienza University of Rome, aiming to the evaluation of water resources in the area and its sustainable management.
The proposed model is compared to an existing and consolidated forecasting method that uses the Standard Precipitation Index (SPI) for the estimation of the minimum annual spring discharge, a method already widely used in Italy and in many other countries [5,8]. The SPI analysis is often used internationally to study and characterize hydrological drought [15,16,17,18]. The SPI is an indicator of the deviation from the mean of the cumulative rainfall over a specific time-interval, reflecting periods of low (negative SPI) or abundant precipitation (positive SPI). These hydrological conditions are transferred into the aquifers, by lowering or rising groundwater levels and by decreasing and increasing spring discharges [19]. The SPI was designed to quantify the precipitation deficit for multiple timescales. These timescales reflect the impact of drought on the availability of the different water resources. Soil moisture conditions respond to precipitation anomalies on a relatively short scale. Groundwater, streamflow and reservoir storage reflect the longer-term precipitation anomalies [20].
2. Geological and Hydrogeological Setting of the Study Area
In this study, Capodacqua di Spigno Spring, one of the main groundwater outlets in the Southeast Latium Region, has been studied in order to test a method for spring discharge evaluation, on the basis of rainfall data. The Capodacqua di Spigno Spring hydrogeological basin involves the competence territory of Spigno Saturnia, Formia and Esperia municipalities, in the province of Latina (Figure 1).
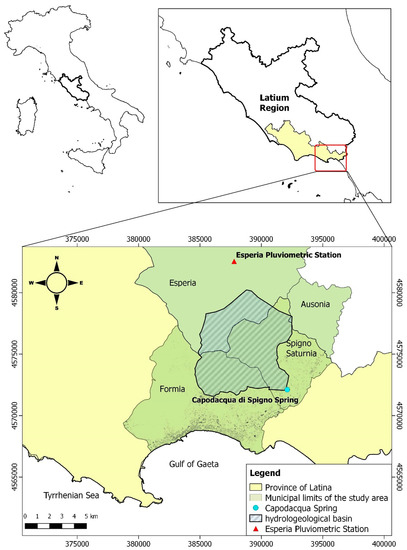
Figure 1.
Territorial framework of the study area (WGS84 coordinates in meters).
The study area is located in the Western Aurunci Mountains, which together with the Lepini and the Ausoni Mountains, belong to the Pre-Apennines of Latium and form the carbonatic platform of the Volsci Ridge, separated from the Apennine ridge by the Latina Valley [21].
The Western Aurunci hydrogeological unit, mostly made of dolomitic limestone and dolomites of Jurassic and Cretaceous age [21,22,23,24] hosts an important karst aquifer, which give rise to many karst springs, including the Capodacqua di Spigno Spring, one of the most important water resources in the Southern Latium Region used for drinking supplies.
The Capodacqua di Spigno Spring, located at an altitude of about 35 m a.s.l. (meters above sea level), is the natural outcrop of groundwater discharging from a hydrogeological basin of about 60 km2 [1]. The spring water comes out from the permeable limestone of La Civita Mountain and Castello Mountain and flows above the upper Miocene clays, at the lowest point of the limestone-clay contact [25].
The altitude of the Capodacqua di Spigno hydrogeological basin ranges from about 100 m a.s.l. to about 1500 m a.s.l., with an average value of 880 m a.s.l. [1]. The general groundwater flow direction of the aquifer is towards the south-east, but there are also important local flows along the two faults that delimit the carbonatic series outcropping, especially the one to the east, which seems to represent the main water conduit towards the spring [26].
Carbonate dissolution strongly influence groundwater flow and evolve into complex networks throughout the limestone matrix. The most important karst landforms are rutted fields, Karren, sinkholes, and swallow holes. The high permeability of the karst surface is responsible of the rapid infiltration of rainfall into the aquifer by the karst depressions (superficial and sub-surficial) originate from the carbonate dissolution processes related to the contact between rainwater and carbonate rocks; i.e., the limestone, the dolomitic limestone and the dolomites, which are part of the Capodacqua di Spigno Spring hydrogeological basin (Figure 2). Although dolomite has a lower solubility than calcite, in the series the two minerals alternate, so in the studied area the superficial karst forms are widespread in the hydrogeological basin, except in those areas with high slopes, usually associated with fault lines.
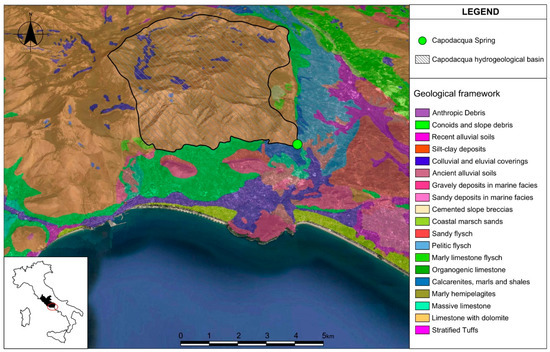
Figure 2.
Geological framework of the study area.
The climatic assessment of the study area has been evaluated on the basis of rainfall monthly time series collected in the Esperia rainfall gauge, the closest to the recharge area of the spring in the northern part of the hydrogeological basin (Figure 1). However, rainfall values from 1998 to 2014 are not available for this Pluviometric Station. Therefore, the rainfall behavior for the longest time series available, i.e., from 1959 to 1988, was studied. The two precipitation time series used to perform, first, the model training (time window 1973–1977) and, afterwards, the validation of the cross-correlation model (time window 2014–2018), were also analyzed.
The Mean Annual Precipitation (MAP) of the time series ranged from 811 to 2103 mm/year in the period 1959–1998. The rainfall seasonal trend (Figure 3) shows that the most important contribution is due to the rainiest season (from November to February), with a trend inversion in the last five years (2014–2018), where it has been registered a deficit mostly due to a reduced contribution rainfall in November and December and a positive increase in February and March.
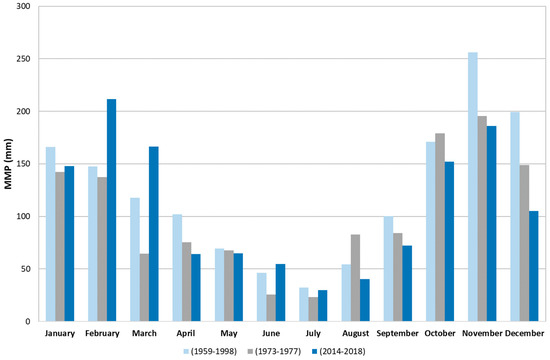
Figure 3.
Mean Monthly Precipitation (MMP) seasonal trend in the study area.
3. Materials and Methods
Based on previous similar approaches [10] the proposed model aims to evaluate spring discharge values using a linear combination of previous monthly rainfall data as input.
More specifically, each contribution is expressed by the rainfall value of the i-th month (from the same month up to the previous n-th month) multiplied by the i-th coefficient. The formula used to simulate spring discharges is the following one:
where:
- Q0 is the spring flow rate referred to the specific month taken into account (L/s);
- k is an amplifying or reducing factor from rainfall to discharge values and is representative of each spring and its hydrogeological basin;
- Pi is the rainfall data (in mm) of the rainfall station representative of the hydrogeological basin related to the specific month, with i varying from the n-th preceding month up to the reference month (i = 0);
- is the incidence coefficient between and the rainfall data series and the spring flow data series at different lag times (for i varying from n to 0) and ranges from 0 to 1;
The number of variables (Pi) in input is related to their specific incidence on the discharge values. This incidence is evaluated assessing the cross-correlation coefficient (Pearson Coefficient) between the monthly spring discharge series and monthly rainfall series, verifying that it is a positive value at different monthly lag time (CPiQ > 0).
Thereby, CPiQ numerically defines how much each single previous monthly rainfall value influences the total spring flow rate related to the specific month considered (Figure 4). Pearson coefficient (CXY) is a measure of the linear correlation between two variables X and Y, expressed as the covariance of the two variables divided by the product of their standard deviations (CXY = σXY/σXσY).
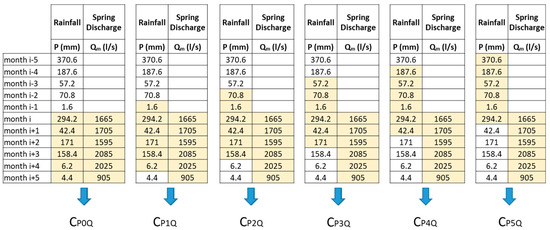
Figure 4.
Graphical representation of the schematic procedure for CPiQ correlation coefficients determination.
So, the spring flow rate is estimated as the sum of different contributions, multiplied by an amplification coefficient (k), which is a scale factor related to the reservoir size, different from spring to spring.
The n value represents the general behaviour of the spring feeding aquifer. In fact, karst aquifers may have three types of groundwater circulation, related to different types of permeability (porosity, cracking and karst conduits).
Karst conduits hydraulic conductivity is associated with a fast circulation of groundwater in the aquifer, which implies an impulsive response of the spring flow to the rainfall inputs.
This phenomenon influences the values of the correlation coefficients, between rainfall data and spring flow values. Springs with a fast response to the hydrological input showed the highest correlation coefficients in those months with shortest lag time (i.e., temporally “closer” to the output specific month). On the contrary, those with a slower response showed the opposite behaviour. This concept is well represented in Figure 5, where CPiQs have been obtained for two test springs in Italy (the Scirca Spring and the San Giovenale Spring), characterized by different groundwater circulation.
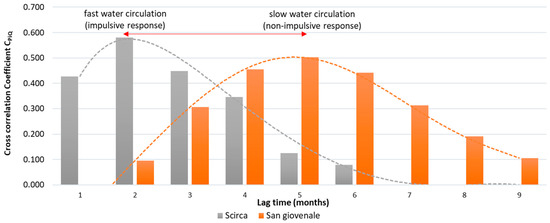
Figure 5.
CPiQ values obtained for two test springs in Italy (Scirca Spring and San Giovenale Spring).
For the Capodacqua di Spigno Spring, the only time series available was 5 years long (1973–1977). In this period, spring discharges values were due to measurements carried out on a monthly basis (Qm). Other measurements were carried out, before 1973, but the discharge time series was not continuous.
Rainfall data (P) taken into account are those collected by the pluviometric station of Esperia, which is the only one located nearby the spring hydrogeological basin and whose data temporally matched spring flow measurements (Table 1).

Table 1.
Rainfall and Capodacqua di Spigno Spring discharges data for the model training period.
4. Results and Discussion
Spring discharge and rainfall data have been previously used for the calibration of the model, which consist in the determination of correlation coefficients (Figure 6).
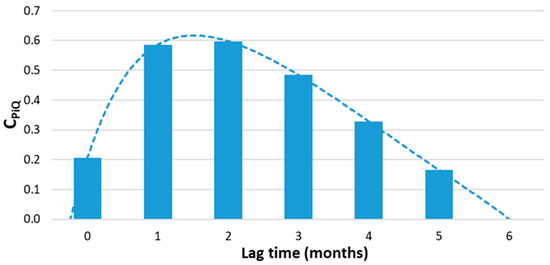
Figure 6.
Cross-correlation coefficients distribution for the Capodacqua di Spigno Spring obtained for the training period (1973–1977).
The time series analyzed for the training was 5 years long (1973–1977). In this period, spring discharge values were available due to measurements carried out on a monthly basis.
Results highlight an impulsive behavior of the Capodacqua di Spigno Spring. The highest values of cross correlation coefficients are referred to i = 1 and i = 2 (respectively equal to 0.59 and 0.60). The spring response to rainfall showed a short lag time, which is typical of “dominant drainage network” karst aquifer behavior, with groundwater circulation mainly occurring in the karst conduits. The amplifying factor from rainfall to discharge values (k), founded through a goal seek, is equal to 5, denoting a large reservoir.
Applying Equation (1) to rainfall data, the estimated flow rates obtained were compared with the measured ones in the same training time window. The blue line represents the measured values (Qm), while the estimated flow rates trend obtained is described by the orange line (Qe) (Figure 7).
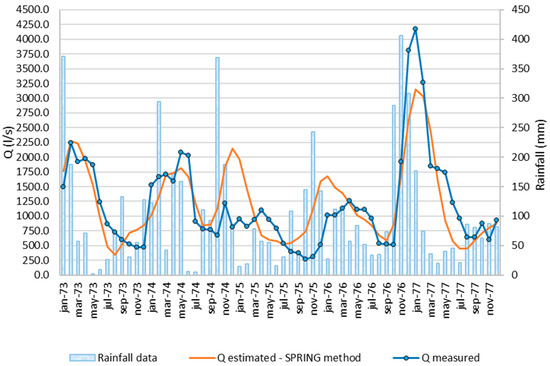
Figure 7.
Training time window: comparison between estimated (Qe) and measured (Qm) discharges for the Capodacqua di Spigno Spring.
Afterwards, Equation (1) was applied to input rainfall data referred to the validation period (2014–2017 only for the minimum annual discharges, 2018 for monthly discharges), in order to study possible spring discharge changes and test the reliability of the model. Two anomalies in spring flow rates, related to the drought events of 2016 and 2017, were successfully described by the estimated flow trend.
In the time window considered (validation time window), the measured flow rate data (Qm) were not available until January 2018 onwards, i.e., when the Department of Civil, Building and Environmental Engineering (DICEA) started quantitative spring monitoring activities. These activities mainly consisted in measurements of the excessing spring flow rate in a discharge channel.
For the previous years (2014–2017), only the withdrawal rates (Qex), recorded by the local water supply agency (Acqualatina S.p.A.) were available. Nevertheless, the withdrawal trend was very useful for assessing the correct estimation of the minimum spring discharges during drought events. In fact, the withdrawal trend, whose values were around 500 L/s, intensively dropped during the drought events of 2016 and 2017 as well as the total spring discharge. For this reason, only in these cases, the flow rate available at the spring may be assumed to be equal to the withdrawal. The phenomenon is well represented by the estimated discharge values, plotted in Figure 8. All values obtained with the proposed method fall upon the Qex values, representing the withdrawal flow rates. Moreover, assuming that the total spring discharge is equal to the sum of excessing flow measurements and the withdrawal values, measurements carried out during 2018 confirms the potentiality of the method: maximum and minimum of the estimation of spring discharge (Qe) show the same trend as collected data (Figure 8).
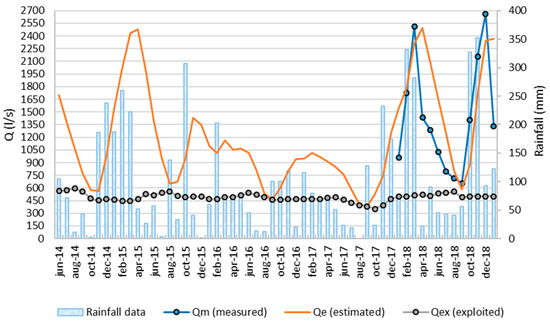
Figure 8.
Validation time window: Comparison between model estimated (Qe), measured (Qm) discharges for the Capodacqua di Spigno Spring and the flow rate exploited (Qex) by the local water supply agency (Acqualatina S.p.A.—i.e., Corporation).
Evaluation of Minimum Spring Discharges Using the Standardized Precipitation Index (SPI)
Finally, minimum discharge values obtained by the proposed model were compared to minimum flow rates estimated using a methodology proposed by Romano et al. (2013) [5] and applied to the case study, using the SPI (Standard Precipitation Index) as input data. This method has been suggested by several Italian regions for minimum spring discharge forecasting. It is indeed indicated in the 2018 guidelines concerning drought and water scarcity indicators [27], drafted by the ISPRA (Italian Environmental Protection Agency) and is internationally recognized.
For the Capodacqua di Spigno Spring, the reference pluviometric station is Esperia, for which an historical series of monthly precipitation of about 30 years was available. Input data have been used in the SPI calculation, for each month of the year, and for different aggregation scales (SPI1, SPI2, SPI24). SPI values were obtained using the “SPI Generator” free software (Version release date: 6 September 2018) made available by the National Drought Mitigation Center – UNL [28].
The minimum annual flow (Qmin) of the total discharge series available (years 1964–1977) was identified. In this case it was not necessary to have a continuous monthly data series, but only the annual minimum values. Correlation coefficients were calculated for each month, between the values of the different SPI and the annual Qmin: The correlation matrix was set up, and the best correlation was consequently identified (Figure 9).
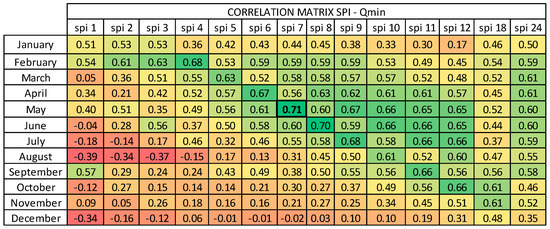
Figure 9.
Correlation matrix SPI (Standard Precipitation Index) - Qmin.
The best correlation found was between the Qmin and SPI7 May, with a R2 of about 0.5. The linear relationship obtained allowed the extension of the Qmin estimation to the validation time window, and hopefully to forecast minimum discharges of the studied spring in future water crises (Figure 10).
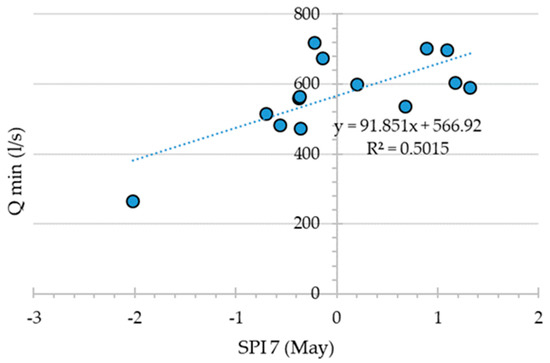
Figure 10.
Relationship between Qmin of the historical discharge series and SPI7 (May).
The minimum annual value spring discharge, estimated by the exposed methodology, were plotted with the total discharge series modeled using Equation (1).
Figure 11 represents the detailed comparison between these two methods: results show that minimum discharge values are comparable. Generally, the Capodacqua di Spigno Spring minimum discharges occur at the end of the summer season (September), with values higher than 500 L/s. The two anomalies, due to drought events (2016–2017) are well represented by the SPI method as well as the proposed model, whose minimum values, match well with the withdrawals recorded by the local water agency Acqualatina S.p.A. for drinking purposes (assumed to be equal to the total spring discharge), which was not enough for satisfying civil water networks supply demands.
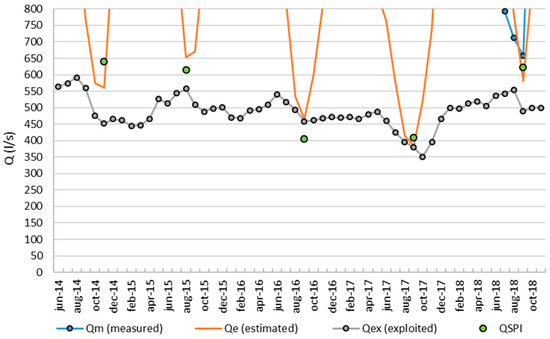
Figure 11.
Validation time window: Detail on minimum discharges estimated using the proposed model and the minimum annual discharge estimated (QSPI) using the methodology proposed by [27].
In the year 2017 the discharge exploited by the Capodacqua di Spigno Spring, during the drought event, dropped to about 380 L/s due to the low supply of the water resource. In this regard, the relative error was calculated between the estimated minimum flow rate and the minimum exploited flow rate, which corresponded to the minimum spring supply. Table 2 shows that for 2017, the discharge estimated with the proposed method (Qe) and with the SPI method (QSPI), compared with the exploited flow rate (Qex), lead to very low relative errors: εe = 1.35% and εSPI = 7.73%, respectively.

Table 2.
Comparison between exploited discharge (Qex), estimate discharge (Qe) and estimated discharge with SPI index (QSPI).
The formulas used to calculate relative errors are the following:
where:
- Qex = exploited discharge;
- Qe = estimated minimum discharge;
- QSPI = estimated minimum discharge with SPI index.
As previously mentioned, for the year 2018, it was possible to compare the estimated flow rates using both methods considered (Qe and QSPI) with the discharge values measured during DICEA monitoring activities. The relative error between the estimated minimum flow rate using both methods is referred to the minimum measured flow rate. Table 3 shows that even for the year 2018, values of error were quite low.

Table 3.
Comparison between total spring minimum discharge (Qt), estimated minimum discharge (Qe) and estimated minimum discharge with the SPI index (QSPI).
The formulas used to calculate relative errors are the following:
where:
- Qe = estimated minimum discharge;
- QSPI = estimated minimum discharge with the SPI index;
- Qt = total spring minimum discharge.
Results showed that the proposed method could provide reliable results on karst spring discharge estimation using a simple linear rainfall-input model, especially referring to minimum values, which are the most important to be monitored for a proper water management. In particular, they showed that it is possible to express spring discharge as a linear combination of monthly rainfall values, properly multiplied by specific coefficients. Coefficients were obtained by cross correlation analyses and numerically define the incidence of previous monthly rainfall data on the spring flow value of the specific month considered.
Due to the lack of spring flow rates monitoring in many areas of Italy, this kind of spring response modeling could become a useful tool for supporting Italian water agencies to face drought issues and planning proper water resource management based on quantitative knowledge of groundwater availability.
In particular, for Capodacqua di Spigno Spring, DICEA will intensify all monitoring activities in order to evaluate the methods reliability and to provide to the local water supply agency (Acqualatina S.p.A.) a hydrogeological model explaining in detail, the behavior of the spring and its feeding aquifer.
Author Contributions
Conceptualization, G.S., F.M.D.F. and S.I.; methodology, F.M.D.F. and S.I.; formal analysis, F.M.D.F., S.I. and G.G.; data curation, F.M.D.F. and S.I.; writing—original draft preparation, G.S., F.M.D.F., S.I. and G.G.; visualization, F.M.D.F. and S.I.; supervision, G.S.
Funding
This research received no external funding.
Acknowledgments
Authors would like to thank Acqualatina S.p.A. for data availability and technical support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sappa, G.; Ferranti, F.; Iacurto, S.; De Filippi, F.M. Effects of climate change on groundwater feeding the Mazzoccolo and Capodacqua di Spigno springs (Central Italy): First quantitative assessments. In Proceedings of the 18th International Multidisciplinary Scientific Geo Conference Surveing Geology and Mining Ecology Management SGEM, Albena, Bulgaria, 30 June–9 July 2018; Volume 18, pp. 219–226. [Google Scholar]
- Hernàndez-Bedolla, J.; Solera, A.; Paredes-Arquiola, J.; Perdo-Monzonìs, M.; Andreu, J.; Sànchez-Quispe, S.T. The assessment of Sustainability Indexes and Climate Change Impacts on Integrated Water Resource Management. Water 2017, 9, 213. [Google Scholar] [CrossRef]
- Bicalho, C.C.; Batiot-Guilhe, C.; Seidel, J.L.; Van Exter, S.; Jourde, H. Geochemical evidence of water source characterization and hydrodynamic responses in a karst aquifer. J. Hydrol. 2012, 450–451, 206–218. [Google Scholar] [CrossRef]
- Sappa, G.; Iacurto, S.; Ferranti, F.; De Filippi, F.M. Groundwater quality assessment in a karst coastal region of the West Aurunci Mountains (Central Italy). Geofluids 2019, 2019, 3261713. [Google Scholar] [CrossRef]
- Romano, E.; Del Bon, A.; Petrangeli, E.; Preziosi, E. Generating synthetic time series of springs discharge in relation to standardized precipitation indices. Case study in Central Italy. J. Hydrol. 2013, 507, 86–99. [Google Scholar] [CrossRef]
- Salerno, F.; Tartari, G. A coupled approach of surface hydrological modelling and Wavelet Analysis for understanding the baseflow components of river discharge in karst environments. J. Hydrol. 2009, 376, 295–306. [Google Scholar] [CrossRef]
- Hadi, S.J.; Tombul, M. Monthly streamflow forecasting using continuous wavelet and multi-genegenetic programming combination. J. Hydrol. 2018, 561, 674–687. [Google Scholar] [CrossRef]
- Fiorillo, F.; Doglioni, A. The Relation between Karst Spring Discharge and Rainfall by the Cross-Correlation Analysis. Hydrogeol. J. 2010, 18, 1881–1895. [Google Scholar] [CrossRef]
- Chiaudani, A.; Di Curzio, D.; Palmucci, W.; Pasculli, A.; Polemio, M.; Rusi, S. Statistical and Fractal Approaches on Long Time-Series to Surface-Water/Groundwater Relationship Assessment: A Central Italy Alluvial Plain Case Study. Water 2017, 9, 850. [Google Scholar] [CrossRef]
- Diodato, N.; Guerriero, L.; Fiorillo, F.; Esposito, L.; Revellino, P.; Grelle, G.; Guadagno, F.M. Predicting Monthly Spring Discharges Using a Simple Statistical Model. Water Resour. Manag. 2014, 28, 969–978. [Google Scholar] [CrossRef]
- Granata, F.; Saroli, M.; De Marinis, G.; Gardano, R. Machine learning Models for Spring Discharge Forecasting. Geofluids 2018, 2018, 8328167. [Google Scholar] [CrossRef]
- Grimaldi, S.; Cristino, G.; Doglioni, A.; Summa, G.; Simeone, V. Data-Driven Analysis of Discharge Variations at Mercure Spring South Italy. Eng. Geol. Soc. Territ. 2015, 5, 655–659. [Google Scholar] [CrossRef]
- Xi, C.; Cai, C.; Quingquing, H.; Zhicai, Z.; Peng, S. Simulation of rainfall-underground outflow responses of a karstic watershed in Southwest China with an artificial neural network. Water Sci. Eng. 2008, 1, 1–9. [Google Scholar]
- Chang, W.; Chen, X. Monthly Rainfall-Runoff Modeling at Watershed Scale: A Comparative Study of Data-Driven and Theory-Driven Approches. Water 2018, 10, 1116. [Google Scholar] [CrossRef]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Gandu, A.W.; Silva, R.F.; Martins, E.S. Drought identification in Cearà state using the standardized precipitation index (SPI). In Proceedings of the VI Simpòsio Internacional de Climatologia, Natal, Brazil, 13–16 October 2015. [Google Scholar]
- Bloomfield, J.P.; Marchant, B.P. Analysis of groundwater drought building on the standardised precipitation index approach. Hydrol. Earth Syst. 2013, 17, 4769–4787. [Google Scholar] [CrossRef]
- Boulos, A.Z.; Bassam, K. Investigation of hydrological drought using Cumulative Standardized Precipitation Index (SPI 30) in the eastern Mediterranean region (Damascus, Syria). J. Earth Syst. Sci. 2016, 125, 969–984. [Google Scholar] [CrossRef]
- Fiorillo, F.; Guadagno, F.M. Karst Spring Discharges Analysis in Relation to Drought Periods, Using the SPI. Water Resour. Manag. 2010, 24, 1867–1884. [Google Scholar] [CrossRef]
- Svoboda, M.; Hayes, M.; Wood, M. Standardized Precipitation Index User Guide; World Meteorological Organization: Geneva, Switzerland, 2012. [Google Scholar]
- Boni, C.; Bono, P. Carta Idrogeologica del Territorio della Regione Lazio—Scala 1:250.000, Regione Lazio, Assessorato alla Programmazione, Ufficio Parchi e Riserve; Università degli Studi di Roma “La Sapienza”: Roma, Italy, 1988. [Google Scholar]
- Rossi, D.; Bigi, S.; Del Castello, M. The structure of the Aurunci Mountains (southern Lazio): A balanced cross-section and its restoration. Ital. J. Geosci. 2002, 1, 151–159. [Google Scholar]
- Celico, P. Schema Idrogeologico dell’Appennino Carbonatico Centro-Meridionale. Memorie e Note dell’Istituto di Geologia Applicata 1978, 14, 1–97. [Google Scholar]
- Accordi, B.; Biasini, A.; Caputo, C.; Devoto, G.; Funiciello, R.; La Monica, G.B.; Lupia Palmieri, E.; Matteucci, R.; Pieruccini, U. Geologia e Dissesti del Territorio Montano della Regione Lazio. Carta della Montagna 1976, 2, 55–101. [Google Scholar]
- Ialongo, N. Studio Idrogeologico Sorgente Mazzoccolo; Relazione Idrogeologica; Technical Report (Unpublished); Amministrazione Comunale di Formia: Formia, Italy, 1983. [Google Scholar]
- Baldi, A.M.; Marzocchi, A.; Ricci, A.; Mencarini, S.; Vecellio, L.; Graziosi, A.; Di Mauro, G. La torbidità alle captazioni idropotabili dei monti Aurunci, Aquifer Vulnerability and Risk. In Proceedings of the 4th Congress on the Protectionand Management of Groundwater, Parma, Italy, 21–23 September 2005. [Google Scholar]
- Mariani, S.; Braca, G.; Romano, E.; Lastoria, B.; Bussettini, M. Linee Guida Sugli Indicatori di Siccità e Scarsità Idrica da Utilizzare Nelle Attività Degli Osservatori Permanenti per gli Utilizzi Idrici—Stato Attuale e Prospettive Future; Thecnical Report; 2018. Available online: http://www.isprambiente.gov.it/files2018/notizie/LineeGuidaPubblicazioneFinaleL6WP1_concopertina.pdf (accessed on 18 April 2019).
- National Drought Mitigation Center—UNL. SPI Generator free software, Version release date: 6 September 2018. Available online: https://drought.unl.edu/droughtmonitoring/SPI/SPIProgram.aspx (accessed on 18 April 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).