A New Multi-Criteria Decision Analysis Methodology for the Selection of New Water Supply Infrastructure
Abstract
1. Introduction
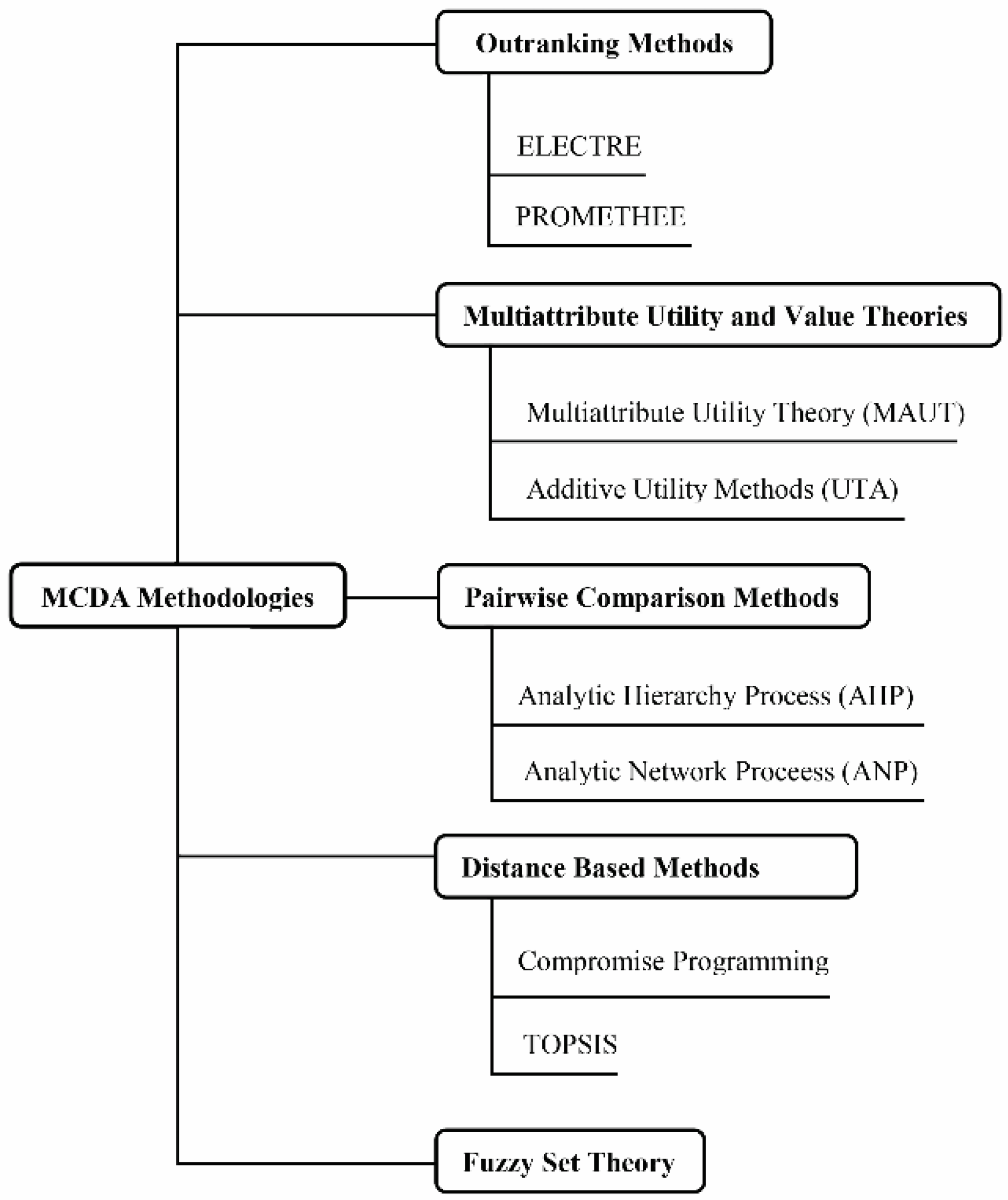
2. Literature Review
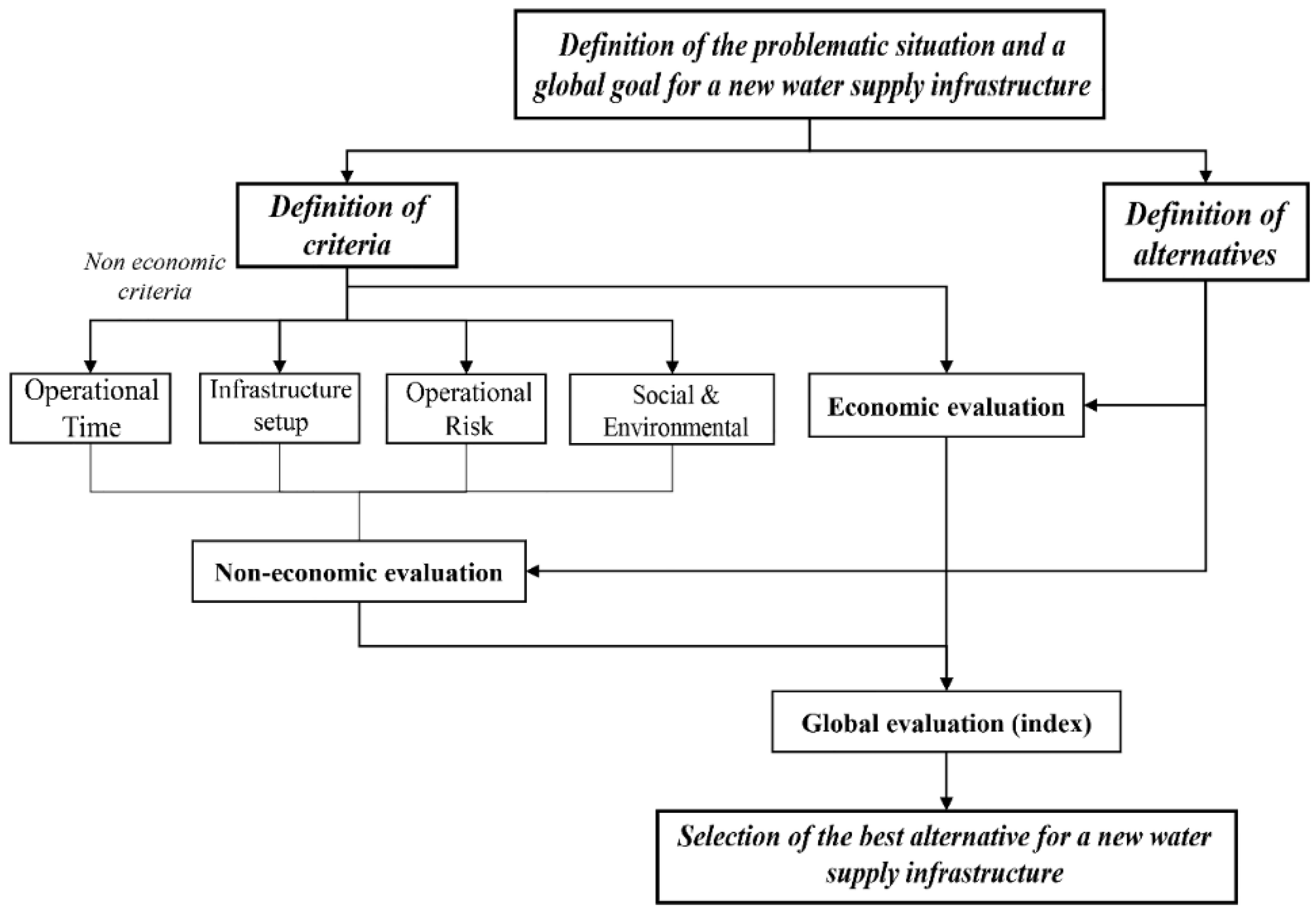
3. Methodology Based on MCDA to Improve the Decision-Making Process for the Selection of New Water Supply Infrastructure
3.1. Definition of the Problematic Situation and a Global Goal for New Water Supply Infrastructure
3.2. Definition of Criteria
Non-economic Criteria
3.3. Economic Evaluation
3.4. Definition of Alternatives
3.5. Non Economic Evaluation
3.6. Global Evaluation
3.7. Selection of the Best Alternative for Water Supply Infrastructure
4. Case Study: City of Santa Marta, Colombia
4.1. Definition of the Problematic Situation and a Global Goal for New Water Supply Infrastructure
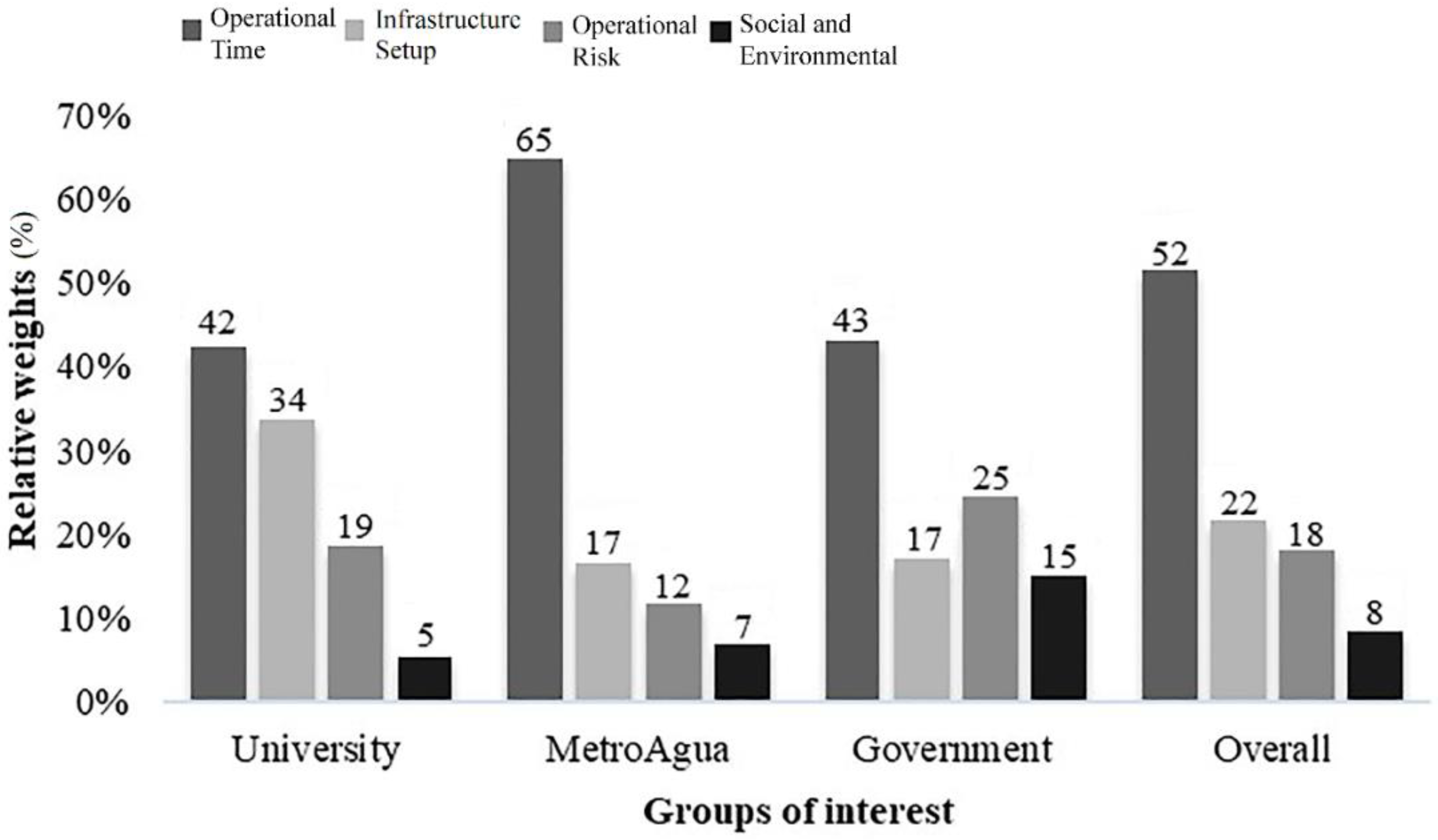
4.2. Definition of Criteria
4.3. Definition of Altermatives
4.4. Non Economic Evaluation
4.5. Economic Evaluation
4.6. Global Evaluation
5. Comparison with Previous Studies
6. Limitations and Future Research
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- United Nations Development Programme. Human Development Report 2006. Beyond Scarcity: Power, Poverty and the Global Water Crisis; United Nations Development Programme: New York, NY, USA, 2006. [Google Scholar]
- United Nations 64/292. The Human Right to Water and Sanitation. Available online: http://www.un.org/es/comun/docs/?symbol=A/RES/64/292&lang=E (accessed on 18 August 2016).
- UNICEF; World Health Organization. Progress on Sanitation and Drinking Water–2015 Update and MDG Assessment; WHO Press: New York, NY, USA, 2015; ISBN 978-92-4-150914-5. [Google Scholar]
- Montgomery, M.A.; Elimelech, M. Water and sanitation in developing countries: Including health in the equation. Environ. Sci. Technol. 2007, 41, 17–24. [Google Scholar] [CrossRef]
- Service, R.F. Desalination Freshens Up. Science (80) 2006, 313, 1088–1090. [Google Scholar] [CrossRef] [PubMed]
- Santos-Pereira, L.; Cordery, I.; Iacovides, I. Coping with Water Scarcity: Adressing the Challenges; Springer Science & Business Media: Paris, France, 2009; ISBN 9788578110796. [Google Scholar]
- WWAP. The United Nations World Water Development Report 2016: Water and Jobs; UNESCO: Paris, France, 2016; ISBN 9789231001468. [Google Scholar]
- Elimelech, M.; Phillip, W.A. The Future of Seawater and the Environment: Energy, Technology, and the Environment. Science (80) 2011, 333, 712–718. [Google Scholar] [CrossRef] [PubMed]
- Food and Agriculture Organization of the United Nations. Coping with Water Scarcity: An Action Framework for Agriculture and Food Security; FAO Publications: Rome, Italy, 2012; ISBN 9789251073049. [Google Scholar]
- Watson, D.; Arrowsmith, C.; Goudey, R. Water availability: A regional water quality problem. Int. J. River Basin Manag. 2003, 1, 321–330. [Google Scholar] [CrossRef]
- Dearmont, D.; McCarl, D.; Tolman, A. Costs of water treatment due to diminished water quality: A case study in Texas. Water Resour. Res. 1998, 34, 849–853. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Q.; Yang, H. Assessing water scarcity by simultaneously considering environmental flow requirements, water quantity, and water quality. Ecol. Indic. 2016, 60, 434–441. [Google Scholar] [CrossRef]
- United Nations Department of Economic and Social Affairs. World Urbanization Prospects: The 2014 Revision; United Nations Department of Economic and Social Affairs: New York, NY, USA, 2015. [Google Scholar]
- OECD. OECD Environmental Outook to 2050: The Consequences of Inaction; OECD: Paris, France, 2012. [Google Scholar]
- Pietrucha-Urbanik, K.; Żelazko, A. Approaches to assess water distribution failure. Period. Polytech. Civ. Eng. 2017, 61, 632–639. [Google Scholar] [CrossRef]
- Pietrucha-Urbanik, K.; Tchórzewska-Cieślak, B. Approaches to failure risk analysis of the water distribution network with regard to the safety of consumers. Water 2018, 10, 1679. [Google Scholar] [CrossRef]
- Bartram, J.; Corrales, L.; Davison, A.; Deere, D.; Drury, D.; Gordon, B.; Howard, G.; Rinehold, A.; Stevens, M. Water Safety Plan Manual (WSP Manual): Step-by-Step Risk Management for Drinking-Water Suppliers; World Health Organization, International Water Association, Eds.; World Health Organization: Geneva, Switzerland, 2009; ISBN 978-92-4-156263-8. [Google Scholar]
- Pietrucha-Urbanik, K.; Tchórzewska-Cieślak, B. Water Supply System operation regarding consumer safety using Kohonen neural network. In Safety, Reliability And Risk Analysis: Beyond The Horizon; Steenbergen, R.D.J.M., van Gelder, P.H.A.J.M., Miraglia, S., Vrouwenvelder, A.C.W.M., Eds.; Taylor & Francis Group: London, UK, 2014; pp. 1115–1120. ISBN 9781138001237. [Google Scholar]
- Shannon, M.A.; Bohn, P.W.; Elimelech, M.; Georgiadis, J.G.; Marinas, B.J.; Mayes, A.M. Science and technology for water purification in the coming decades. Nature 2008, 452, 301–310. [Google Scholar] [CrossRef]
- Eggimann, S.; Mutzner, L.; Wani, O.; Schneider, M.Y.; Spuhler, D.; Moy de Vitry, M.; Philipp, B.; Maurer, M. The potential of knowing more—A review of data-driven urban water management. Environ. Sci. Technol. 2017, 51, 2538–2553. [Google Scholar] [CrossRef]
- Lienert, J.; Scholten, L.; Ehher, C.; Maurer, M. Structured decision-making for sustainable water infrastructure planning and four future scenarios. EURO J. Decis. Process. 2015, 242, 107–140. [Google Scholar] [CrossRef]
- Kang, M.-G.; Lee, G.-M. Multicriteria Evaluation of Water Resources Sustainability in the Context of Watershed Management1. JAWRA J. Am. Water Resour. Assoc. 2011, 47, 813–827. [Google Scholar] [CrossRef]
- Chung, E.S.; Lee, K.S. Prioritization of water management for sustainability using hydrologic simulation model and multicriteria decision making techniques. J. Environ. Manag. 2009, 90, 1502–1511. [Google Scholar] [CrossRef]
- Al-Zu’ bi, Y.; Shatanawi, M.; Al-Jayoussi, O.; Al-Kharabsheh, A. Application of Decision Support System for Sustainable Management of Water Resources in the Azraq Basin—Jordan. Water Int. 2002, 27, 532–541. [Google Scholar] [CrossRef]
- Ennaouri, I.; Fuamba, M. New Integrated Condition-Assessment Model for Combined Storm-Sewer Systems. J. Water Resour. Plan. Manag. 2013, 139, 53–64. [Google Scholar] [CrossRef]
- Ahammed, F.; Alankarage-Hewa, G.; Argue, J.R. Applying multi-criteria decision analysis to select WSUD and LID technologies. Water Sci. Technol. Water Supply 2012, 12, 844–853. [Google Scholar] [CrossRef]
- Martin, C.; Ruperd, Y.; Legret, M. Urban stormwater drainage management: The development of a multicriteria decision aid approach for best management practices. Eur. J. Oper. Res. 2007, 181, 338–349. [Google Scholar] [CrossRef]
- Benzerra, A.; Cherrared, M.; Chocat, B.; Cherqui, F.; Zekiouk, T. Decision support for sustainable urban drainage system management: A case study of Jijel, Algeria. J. Environ. Manag. 2012, 101, 46–53. [Google Scholar] [CrossRef]
- Kim, Y.; Chung, E.-S.; Jun, S.-M.; Kim, S.U. Prioritizing the best sites for treated wastewater instream use in an urban watershed using fuzzy TOPSIS. Resour. Conserv. Recycl. 2013, 73, 23–32. [Google Scholar] [CrossRef]
- Zheng, J.; Egger, C.; Lienert, J. A scenario-based MCDA framework for wastewater infrastructure planning under uncertainty. J. Environ. Manag. 2016, 183, 895–908. [Google Scholar] [CrossRef]
- Hajkowicz, S.; Collins, K. A review of multiple criteria analysis for water resource planning and management. Water Resour. Manag. 2007, 21, 1553–1566. [Google Scholar] [CrossRef]
- Lai, E.; Lundie, S.; Ashbolt, N.J. Review of multi-criteria decision aid for integrated sustainability assessment of urban water systems. Urban Water J. 2008, 5, 315–327. [Google Scholar] [CrossRef]
- Castillo, M. Toma de Decisiones en las Empresas: Entre el arte y la Técnica; Ediciones Uniandes: Bogotá, Colombia, 2006. [Google Scholar]
- Roy, B. Paradigms and challenges. In Multiple Criteria Decision Analysis: State of the Art Surveys; Figueira, J., Greco, S., Ehrgott, M., Eds.; Springer Science + Business Media, Inc.: Boston, MA, USA, 2005; pp. 19–39. ISBN 978-0-387-23067-2. [Google Scholar]
- Figueira, J.; Greco, S.; Ehrgott, M. (Eds.) Multiple Criteria Decision Analysis: State of Art Surveys; Springer Science + Business Media, Inc.: Boston, MA, USA, 2005; ISBN 9788578110796. [Google Scholar]
- Hajkowicz, S.; Higgins, A. A comparison of multiple criteria analysis techniques for water resource management. Eur. J. Oper. Res. 2008, 184, 255–265. [Google Scholar] [CrossRef]
- Kabir, G.; Sadiq, R.; Tesfamariam, S. A review of multi-criteria decision-making methods for infrastructure management. Struct. Infrastruct. Eng. 2014, 10, 1176–1210. [Google Scholar] [CrossRef]
- Scholten, L.; Schuwirth, N.; Reichert, P.; Lienert, J. Tackling uncertainty in multi-criteria decision analysis—An application to water supply infrastructure planning. Eur. J. Oper. Res. 2015, 242, 243–260. [Google Scholar] [CrossRef]
- Okeola, O.G.; Sule, B.F. Evaluation of management alternatives for urban water supply system using Multicriteria Decision Analysis. J. King Saud Univ. Eng. Sci. 2012, 24, 19–24. [Google Scholar] [CrossRef]
- Jaber, J.; Mohsen, M. Evaluation of non-conventional water resources supply in Jordan. Desalination 2001, 136, 83–92. [Google Scholar] [CrossRef]
- Abrishamchi, A.; Ebrahimian, A.; Tajrishi, M.; Mariño, M. A Case study: Application of multicriteria decision making to urban water supply. J. Water Resour. Plan. Manag. 2005, 131, 326. [Google Scholar] [CrossRef]
- Kodikara, P.N.; Perera, B.J.C.; Kularathna, M.D.U.P. Stakeholder preference elicitation and modelling in multi-criteria decision analysis—A case study on urban water supply. Eur. J. Oper. Res. 2010, 206, 209–220. [Google Scholar] [CrossRef]
- Clemen, R.; Reilly, T. Making Hard Decisions with Decision Tools, 2nd ed.; Brooks/Cole: Belmont, CA, USA, 2001. [Google Scholar]
- Zarghami, M.; Szidarovszky, F. Multicriteria Analysis: Applications to Water and Environment Management; Springer-Verlag: Berlin, Germany, 2011; ISBN 3642179371. [Google Scholar]
- Lü, Y.P.; Yang, K.; Che, Y.; Shang, Z.Y.; Zhu, H.F.; Jian, Y.; Lu, Y.P. Cost-efectiveness-based multicriteria optimization for sustainable rainwater utilization: A case study in Shanghai. Urban Water J. 2013, 10, 127–143. [Google Scholar] [CrossRef]
- Saaty, T.L. Mathematical Principles of Decision Making (Principia Mathematica Decernendi); RWS Publications: Pittsburgh, PA, USA, 2010. [Google Scholar]
- Edwards, W.; Miles, R.F., Jr.; Von Winterfeldt, D. (Eds.) Advances in Decision Analysis: From Foundations to Applications; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Cruz, M.G. Modeling, Measuring and Hedging Operational Risk; John Wiley & Sons: New York, NY, USA, 2002. [Google Scholar]
- Zhang, C.; Xu, B.; Li, Y.; Fu, G. Exploring the relationships among reliability, resilience, and vulnerability of water supply using many-objective analysis. J. Water Resour. Plan. Manag. 2017, 143. [Google Scholar] [CrossRef]
- UN-HABITAT. Meeting Development Goals in Small Urban Centres: Water and Sanitation in the World’s Citites; Earthscan: Nairobi, Kenya, 2006; ISBN 9781844073054. [Google Scholar]
- Talavera, D.L.; Nofuentes, G.; Aguilera, J.; Fuentes, M. Tables for the estimation of the internal rate of return of photovoltaic grid-connected systems. Renew. Sustain. Energy Rev. 2007, 11, 447–466. [Google Scholar] [CrossRef]
- Guerrero, T.A.; Furlong, K.; Arias, J. Complicating neoliberalization and decentralization: The non-linear experience of Colombian water supply, 1909–2012. Int. J. Water Resour. Dev. 2016, 32, 172–188. [Google Scholar] [CrossRef]
- Gregory, R.; Failing, L.; Harstone, M.; Long, G.; McDaniels, D.; Ohlson, D. Structured Decision Making: A Practical Guide to Environmental Management Choices; Wiley-Blackwell: New York, NY, USA, 2012. [Google Scholar]
- Marttunen, M.; Lienert, J.; Belton, V. Structuring problems for Multi-Criteria Decision Analysis in Practice: A Literature Review of Method Combinations. Eur. J. Oper. Res. 2017, 263, 1–17. [Google Scholar] [CrossRef]
- Saaty, T.L. The analytic hierarchy and analytic network processes for the measurement of intangible criteria and for decision-making. In Multicriteria Decision Analysis: State of the Art Surveys; Figueira, J., Greco, S., Ehrgott, M., Eds.; Springer Science + Business Media, Inc.: Boston, MA, USA, 2005; pp. 363–419. ISBN 978-0-387-23081-8. [Google Scholar]
- Saaty, R.W. The analytic hierarchy process-what it is and how it is used. Math. Model. 1987, 9, 161–176. [Google Scholar] [CrossRef]
- Saldarriaga, J. SOS: Agua para Santa Marta. Contacto 2015, 10, 5–12. [Google Scholar]
- Saldarriaga, J.; Siabatto, L.; Cotes, L.; Duque, N.; Cifuentes, G.; Madrid, N. Resultados de los Estudios de Abastecimiento de Agua para Santa Marta; Financiera de Desarrollo Territorial S.A. FINDETER: Bogotá, Colombia, 2015. [Google Scholar]
- Giurco, D.P.; Turner, A.; Fane, S.; White, S.B. Desalination for Urban Water: Changing Perceptions and Future Scenarios in Australia. Chem. Eng. Trans. 2014, 42, 13–18. [Google Scholar]
- Giacomoni, M.H.; Berglund, E.Z. Complex Adaptive Modeling Framework for Evaluating Adaptive Demand Management for Urban Water Resources Sustainability. J. Water Resour. Plan. Manag. 2015, 141, 04015024. [Google Scholar] [CrossRef]
- Xiao, Y.; Fang, L.; Hipel, K.W.; Wre, H.D.; Asce, F. Agent-Based Modeling Approach to Investigating the Impact of Water Demand Management. J. Water Resour. Plan. Manag. 2018, 144, 1–12. [Google Scholar] [CrossRef]
- Fielding, K.S.; Spinks, A.; Russell, S.; McCrea, R.; Stewart, R.; Gardner, J. An experimental test of voluntary strategies to promote urban water demand management. J. Environ. Manag. 2013, 114, 343–351. [Google Scholar] [CrossRef]
- Beal, C.D.; Gurung, T.R.; Stewart, R.A. Demand-side management for supply-side efficiency: Modeling tailored strategies for reducing peak residential water demand. Sustain. Prod. Consum. 2016, 6, 1–11. [Google Scholar] [CrossRef]
- Cooley, H.; Phurisamban, R. The Cost of Alternative Water Supply and Efficiency Options in California; Pacific Institute: Oakland, CA, USA, 2016. [Google Scholar]
- Environment Agency (EA). Water Neutrality: An Economic Assessment for the Thames Gateway Development; Environment Agency: Bristol, UK, 2009. [Google Scholar]
- Ho, W.; Ma, X. The state-of-the-art integrations and applications of the analytic hierarchy process. Eur. J. Oper. Res. 2018, 267, 399–414. [Google Scholar] [CrossRef]
- Maleki, H.; Zahir, S. A Comprehensive Literature Review of the Rank Reversal Phenomenon in the Analytical Hierarchy Process. J. Multi-Criteria Decis. Anal. 2013, 20, 141–155. [Google Scholar] [CrossRef]
- Wang, Y.M.; Luo, Y. On rank reversal in decision analysis. Math. Comput. Model. 2009, 49, 1221–1229. [Google Scholar] [CrossRef]
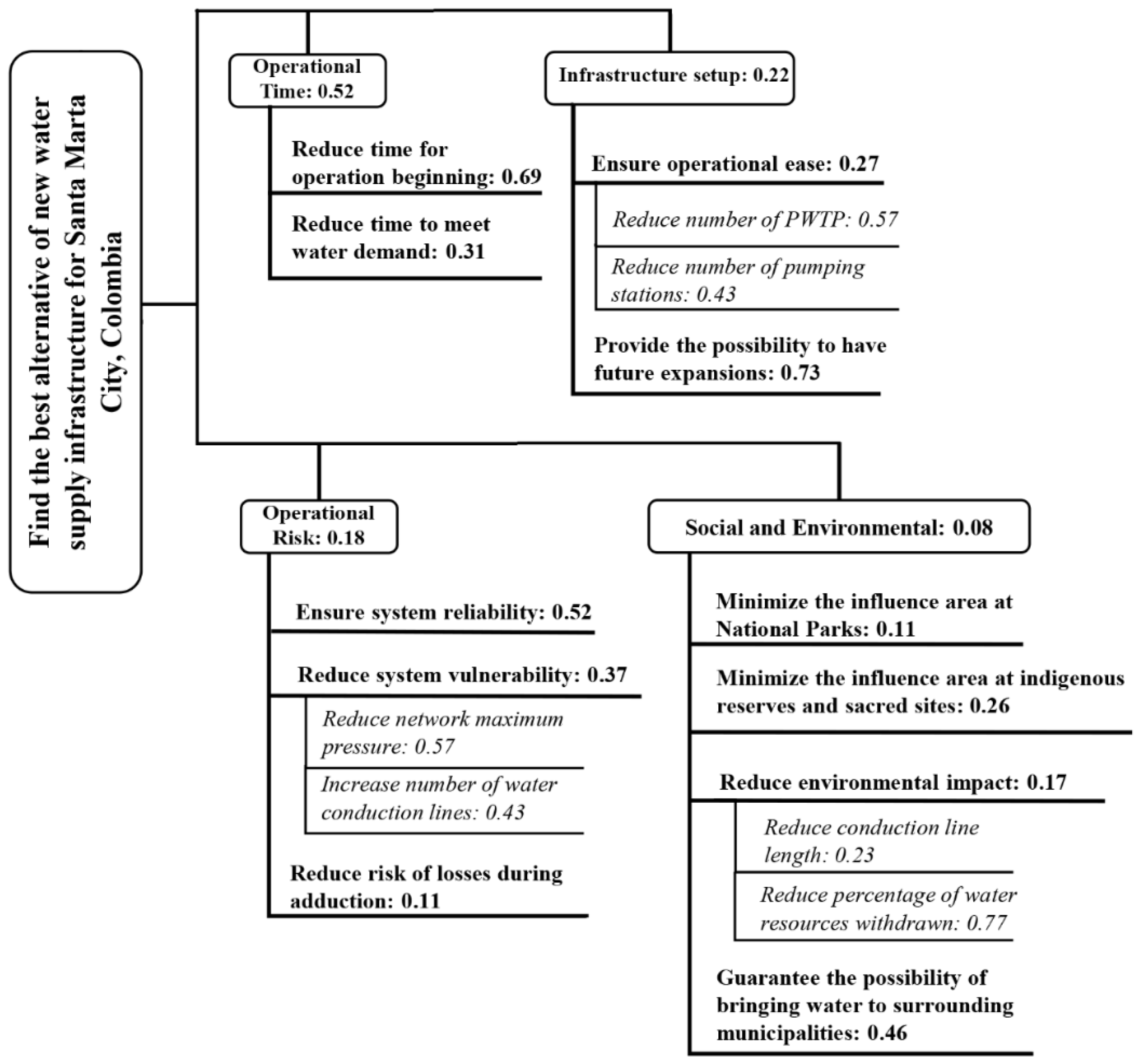
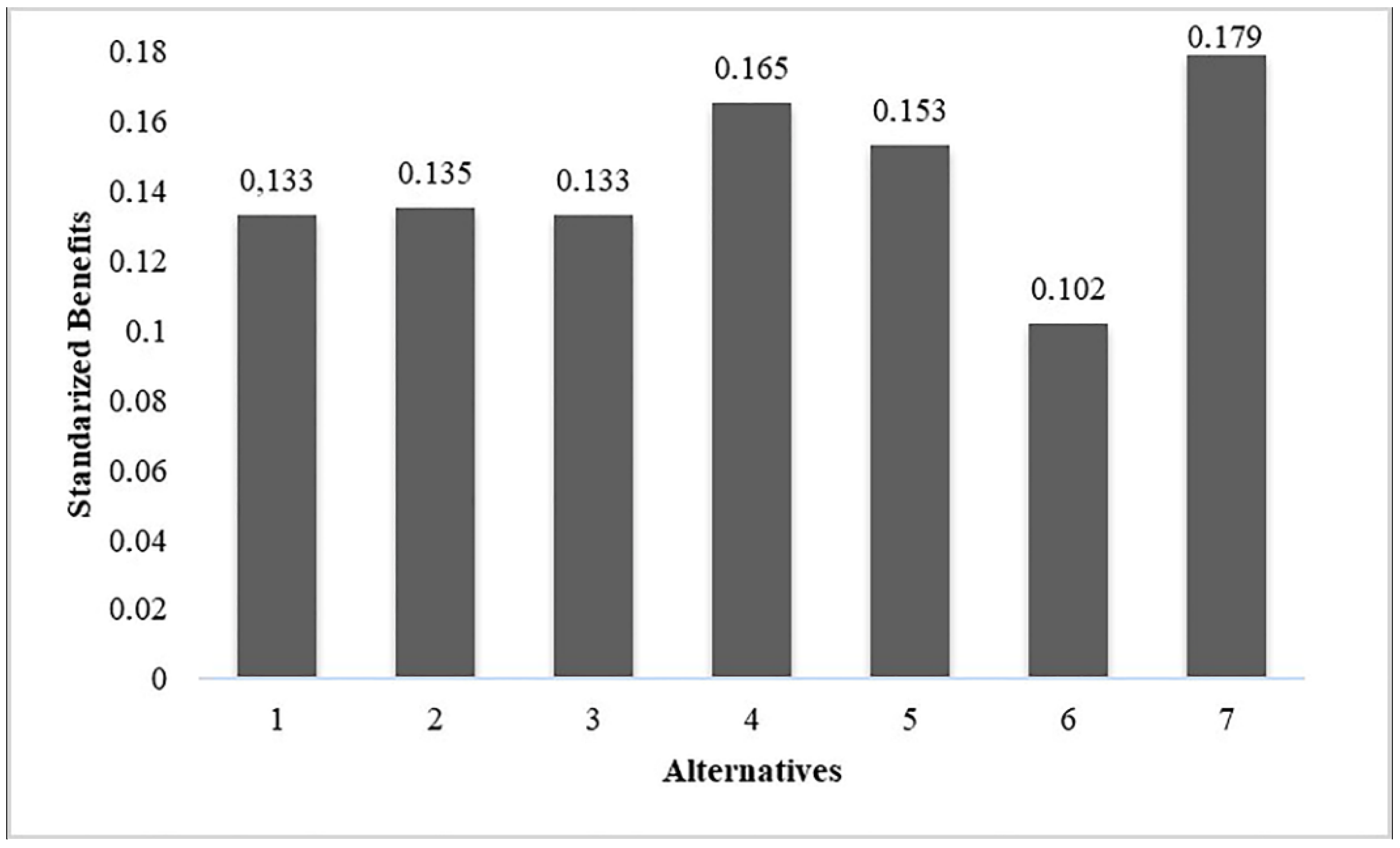
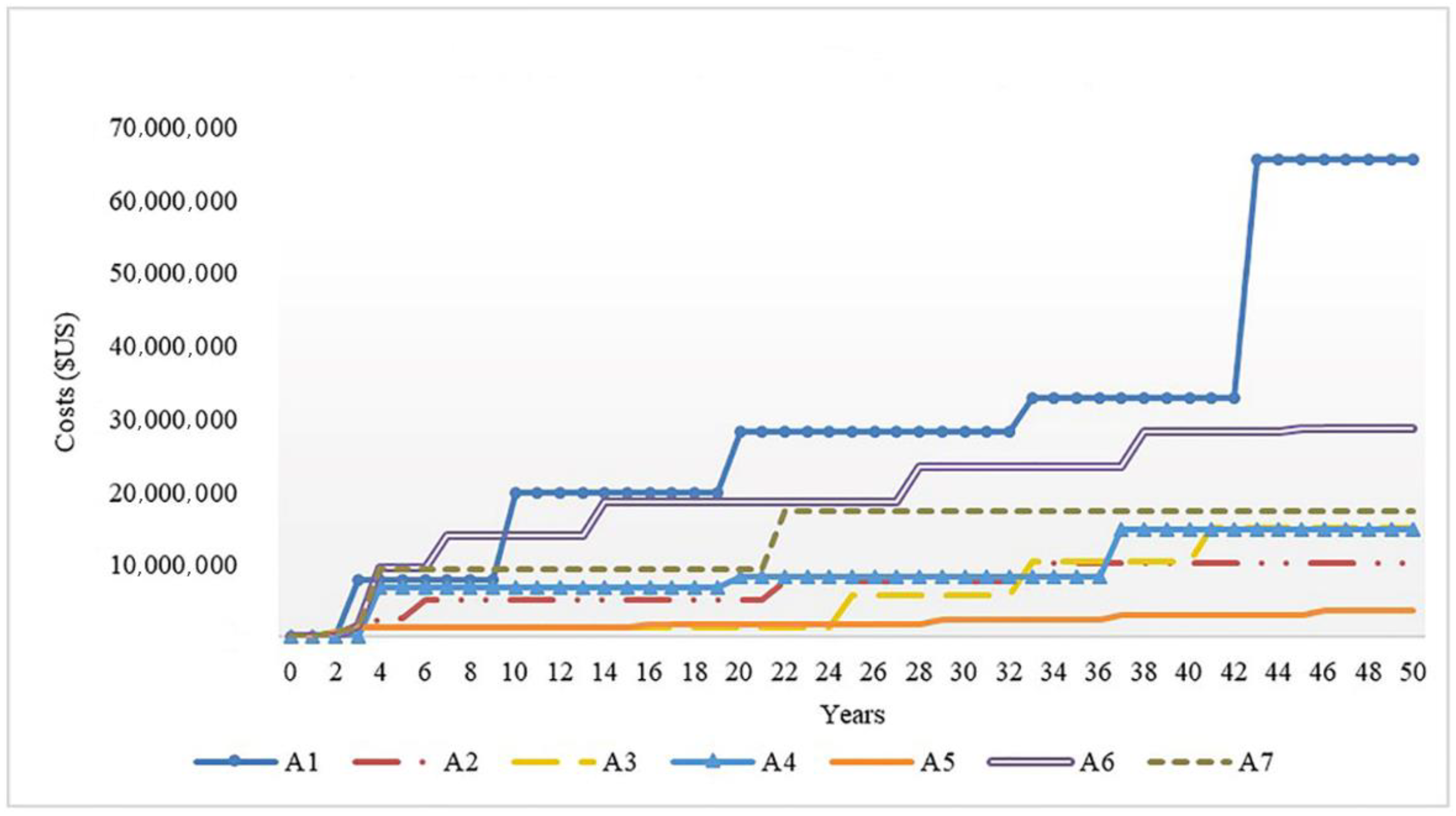
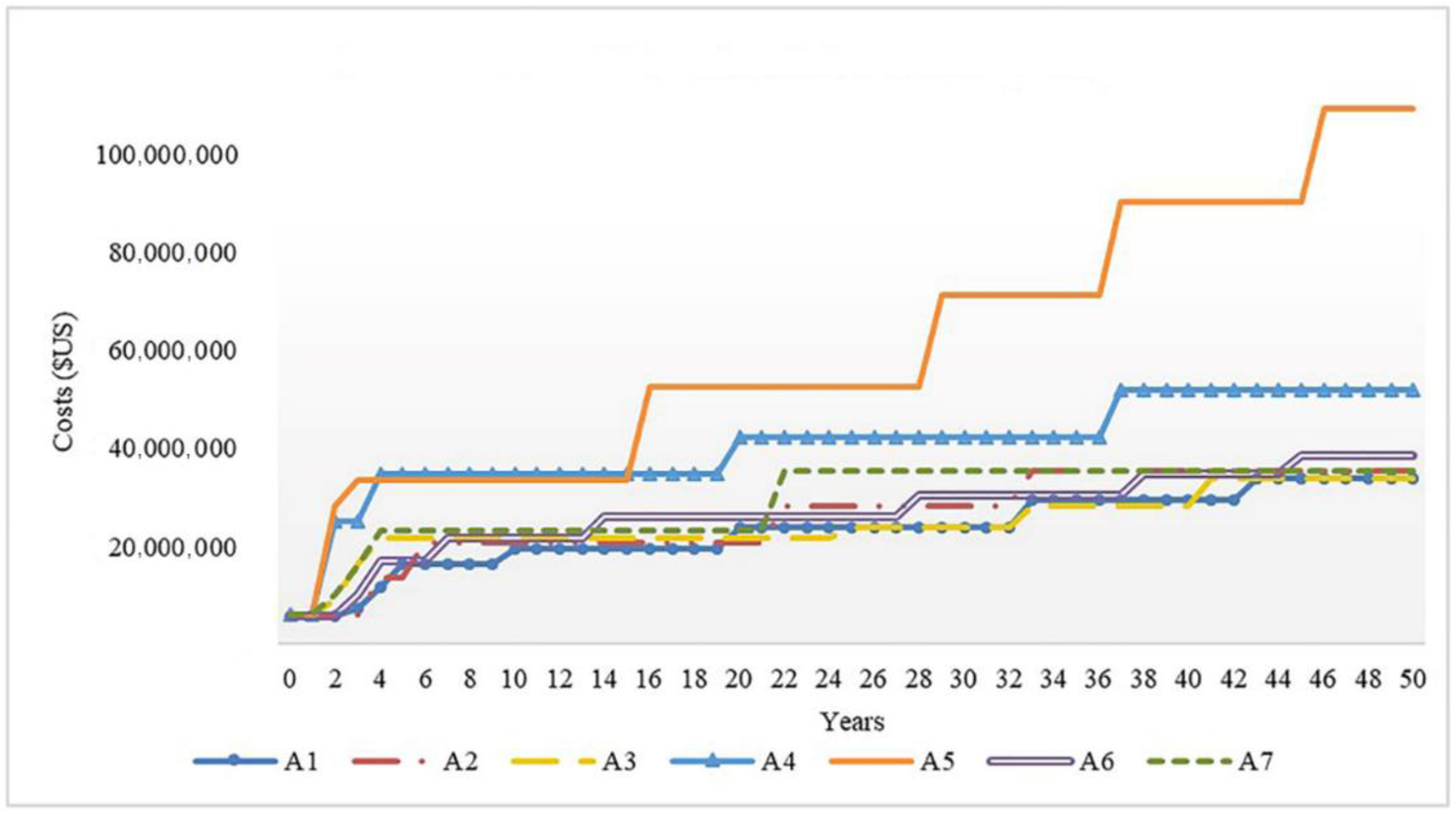
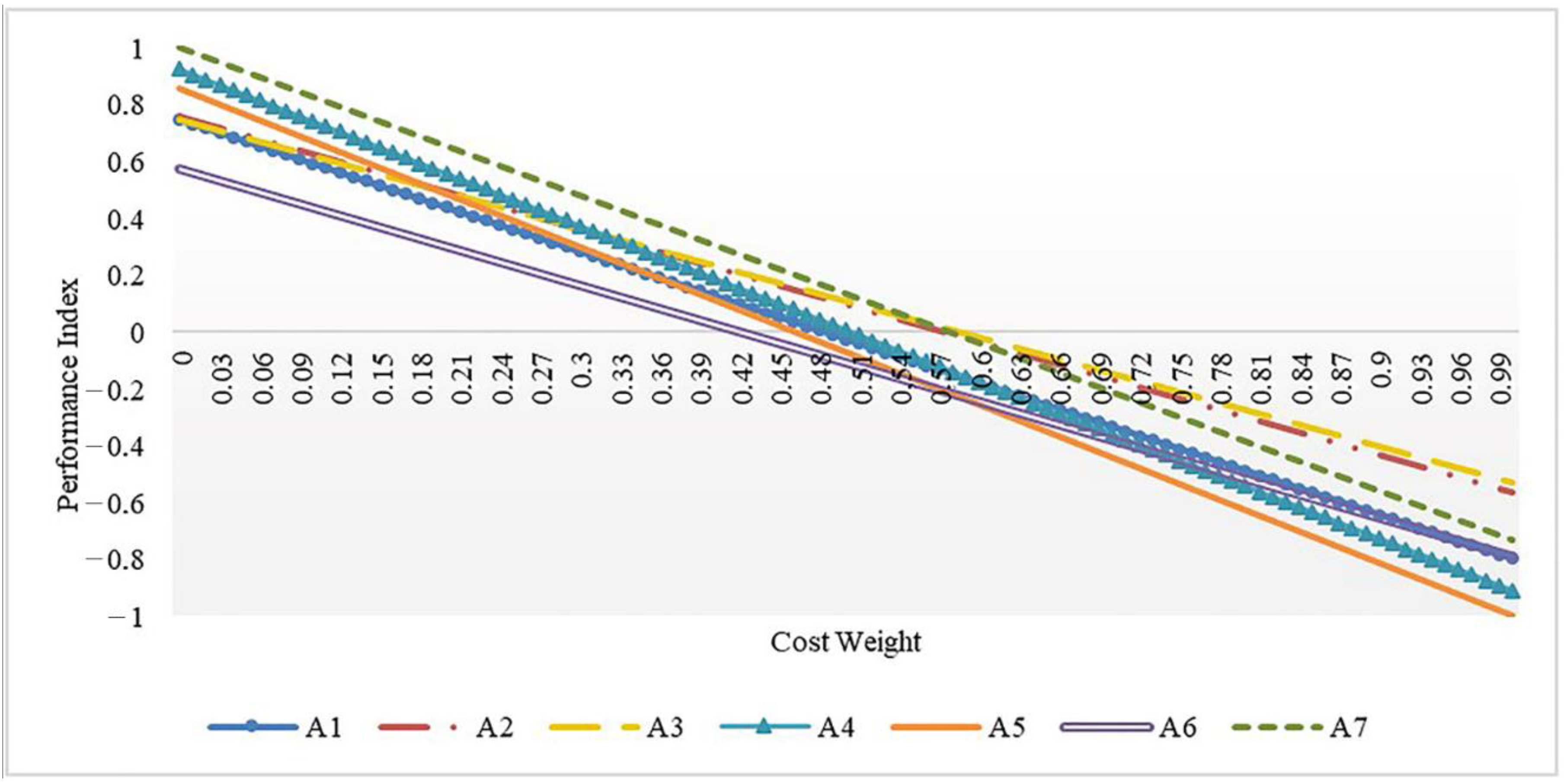

| Goal | Criteria | First Level Sub-Criteria | Second Level Sub-Criteria | Description |
|---|---|---|---|---|
| Find the best alternative of new water supply infrastructure for Santa Marta, Colombia | Operational time | Reduce time for operation beginning | Time in which the first stage of alternative will be in operation | |
| Reduce time to meet water demand | Time in which the demanded water is equal to the water supplied in the city | |||
| Infrastructure setup | Ensure operational ease | Reduce number of potable water treatment plants (PWTP) | Number of PTWP and its required expansions | |
| Reduce number of pumping stations | Number of pumping stations required | |||
| Provide the possibility to have future expansions | Possibility to have additional expansions at the end of the planning horizon | |||
| Operational risk | Ensure system reliability | Related to the water availability and water withdrawals from rivers, this is the relationship between the minimal flow rate of the rivers and the water supply required by the end of the planning horizon | ||
| Reduce system vulnerability | Reduce network maximum pressure | Estimated network pressure | ||
| Increase the number of water conduction lines | Conduction lines required by the alternative | |||
| Reduce the risks of losses during adduction | The risk of water adduction losses is proportional to the accessible area by population to the adduction pipelines | |||
| Social and environmental | Minimize influence area at National Parks | The intersection area between a 100 m influence area of the alternative route and the area of the National Parks | ||
| Minimize influence area at indigenous reserves and sacred sites | The intersection area between a 100 m influence area of the alternative route and the area of indigenous reserves and sacred sites | |||
| Reduce environmental impact | Reduce conduction line length | The impact in the vegetation coverage is proportional to the conduction line length | ||
| Reduce percentage of water withdrawn | This impact is assessed as the ratio between the flow withdrawals and the ecological flows of the respective rivers | |||
| Guarantee possibility of bringing water to surrounding municipalities | Some alternatives have the possibility to supply water to small surrounding municipalities, namely: Ciénaga, Puebloviejo, Tasajera, and Nueva Venecia |
| Alternatives | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | A2 | A3 | A4 | A5 | A6 | A7 | ||||||||
| Time for operation beginning (years) | 3 | 4 | 2 | 2 | 2 | 3 | 2 | |||||||
| Time to meet water demand (years) | 5 | 4 | 3 | 4 | 2 | 4 | 3 | |||||||
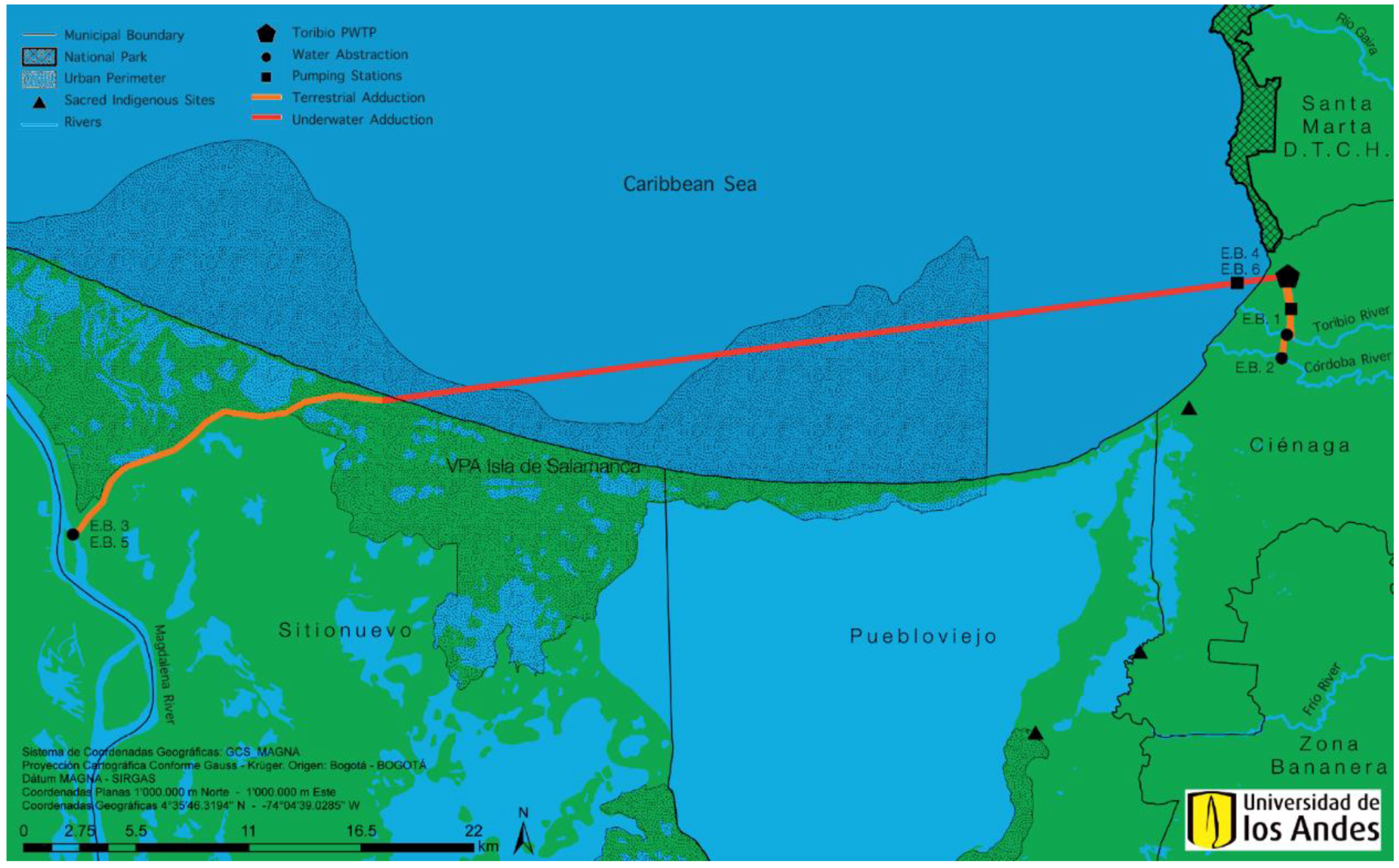
| Water source | Guachacá | Magdalena | Toribio | Guachacá | Magdalena | Caribbean Sea | Toribio | Córdoba | Caribbean Sea | Piedras | Toribio | Toribio | ||
| Buritacá | Guachacá | Córdoba | ||||||||||||
| Don Diego | Córdoba | Buritaca | Buriticá | Magdalena | ||||||||||
| New PTWP | Curval | Toribio | Toribio | Curval | Toribio | Curval | Desalination | Toribio | Curval | Desalination | Curval | Toribio | Toribio | |
| Number of expansions | 7 | 4 | 5 | 2 | 3 | 1 | 1 | 2 | 1 | 5 | 6 | 1 | 4 | |
| New Treatment Capacity at 2064 | New Treatment Capacity per PWTP (m3/s) | 6.4 | 6 | 4.4 | 2 | 5.5 | 0.4 | 1 | 2 | 0.4 | 5 | 7 | 1 | 6 |
| Total Treatment Capacity (m3/s) | 6.4 | 6 | 6.4 | 6.9 | 7.4 | 8 | 6 | |||||||
| Number of pumping stations | 13 | 6 | 12 | 10 | 10 | 15 | 6 | |||||||
| Possibility of future expansions | No | Yes | No | No | No | Yes | Yes | |||||||
| System reliability (-) | 1.9 | 2.0 | 1.4 | 2.0 | 2.0 | 1.3 | 2.0 | |||||||
| Estimated Network Maximum Pressure (PSI) | 341 | 262 | 341 | 270 | 99 | 341 | 259 | |||||||
| Number of conduction lines | 4 | 2 | 5 | 3 | 2 | 6 | 6 | |||||||
| Pipeline length in populated area (Km) | 0.0 | 11.9 | 0.0 | 17.9 | 0.0 | 0.0 | 11.9 | |||||||
| Influence area at National Parks (Ha) | 1.7 | 834.7 | 0.2 | 14.1 | 0.1 | 0.2 | 582.2 | |||||||
| Influence area at indigenous reserves and sacred sites (Ha) | 986.98 | 220.42 | 922.4 | 220.4 | 88.2 | 1048.7 | 88.2 | |||||||
| Conduction line length (Km) | 166.07 | 140.45 | 124.04 | 210.68 | 7.32 | 128.46 | 147.80 | |||||||
| Percentage of water resources withdrawn | 0.14 | 0.00 | 0.59 | 0.00 | 0.50 | 0.64 | 0.50 | |||||||
| Possibility of bringing water to surrounding municipalities | No | Yes | No | Yes | No | No | Yes | |||||||
| Numeric Rating | Definition | Explanation |
|---|---|---|
| 1 | Equal Importance | Two activities contribute equally to the objective |
| 2 | Weak or Slightly More Important | |
| 3 | Moderate Importance | Experience and judgement slightly favour one activity over the other |
| 4 | Moderate to Strong Significance | |
| 5 | Strong Importance | Experience and judgement strongly favour one activity over another |
| 6 | Strong to Very Strong | |
| 7 | Very Strong or Demonstrated Importance | An activity is favoured very strongly over another; its dominance demonstrated in practice |
| 8 | Very Strong to Extreme | |
| 9 | Extreme Importance | The evidence favouring one activity over another is of the highest possible order of affirmation |
| Alternatives | PVC of Treatment (US$) | PVC of Pumping (US$) | PVC of Variable Costs (US$) | Construction Costs (US$) | Total Costs (US$) |
|---|---|---|---|---|---|
| A1 | 321,827,094 | 323,299,388 | 645,126,482 | 47,440,763 | 692,567,245 |
| A2 | 359,423,907 | 86,292,406 | 445,716,313 | 43,313,450 | 489,029,763 |
| A3 | 363,610,315 | 51,672,610 | 415,282,925 | 44,998,266 | 460,281,191 |
| A4 | 608,286,307 | 114,545,941 | 722,832,247 | 67,357,810 | 790,190,057 |
| A5 | 770,633,787 | 26,119,599 | 796,753,386 | 70,747,453 | 867,500,839 |
| A6 | 379,643,598 | 251,435,120 | 631,078,718 | 52,857,836 | 683,936,554 |
| A7 | 424,633,418 | 174,198,263 | 598,831,681 | 38,782,207 | 637,613,888 |
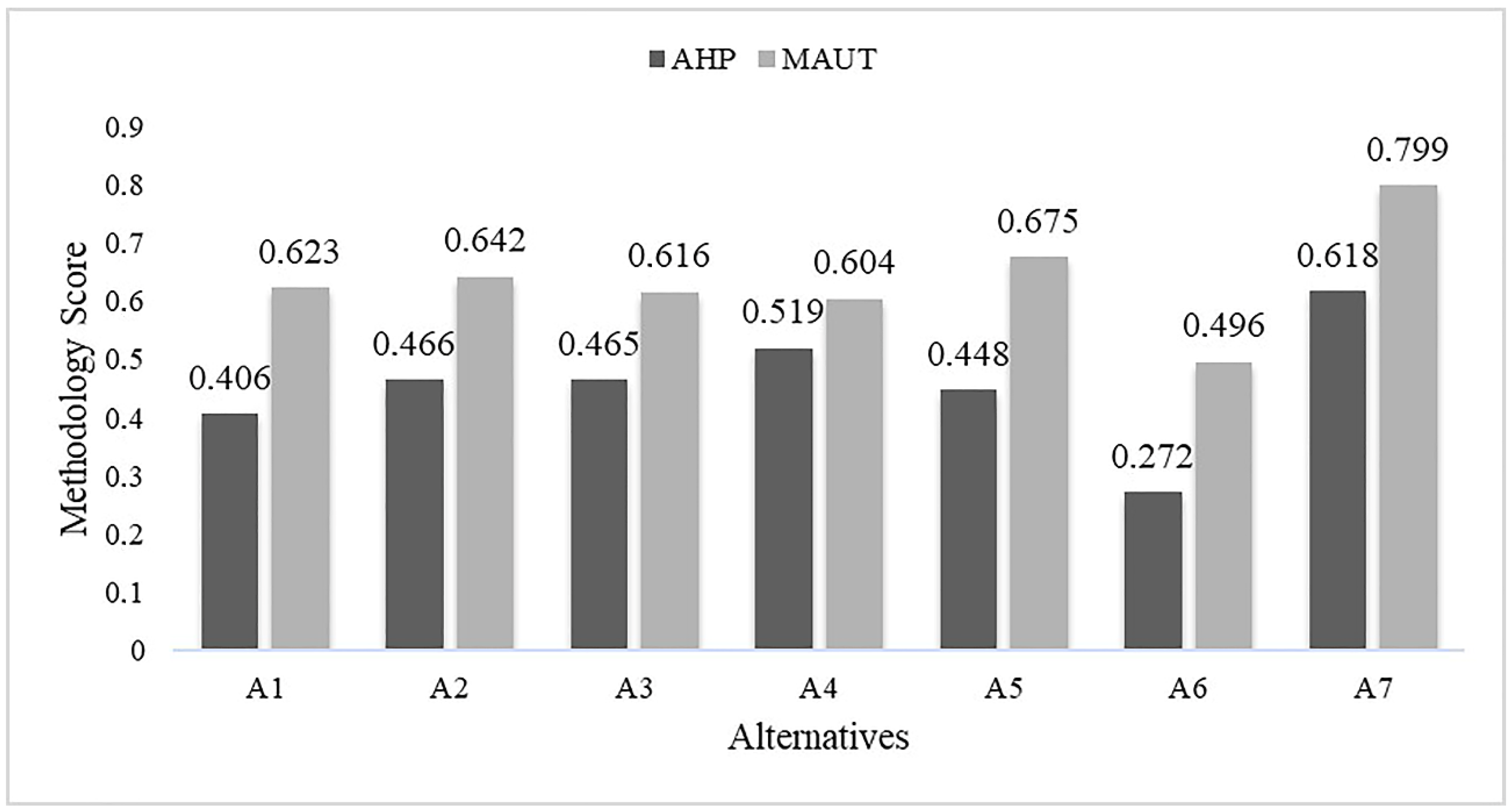
| Rank | Alternative | AHP Performance Index Score |
|---|---|---|
| 1 | A7 | 0.618 |
| 2 | A4 | 0.519 |
| 3 | A2 | 0.466 |
| 4 | A3 | 0.465 |
| 5 | A5 | 0.448 |
| 6 | A1 | 0.406 |
| 7 | A6 | 0.272 |
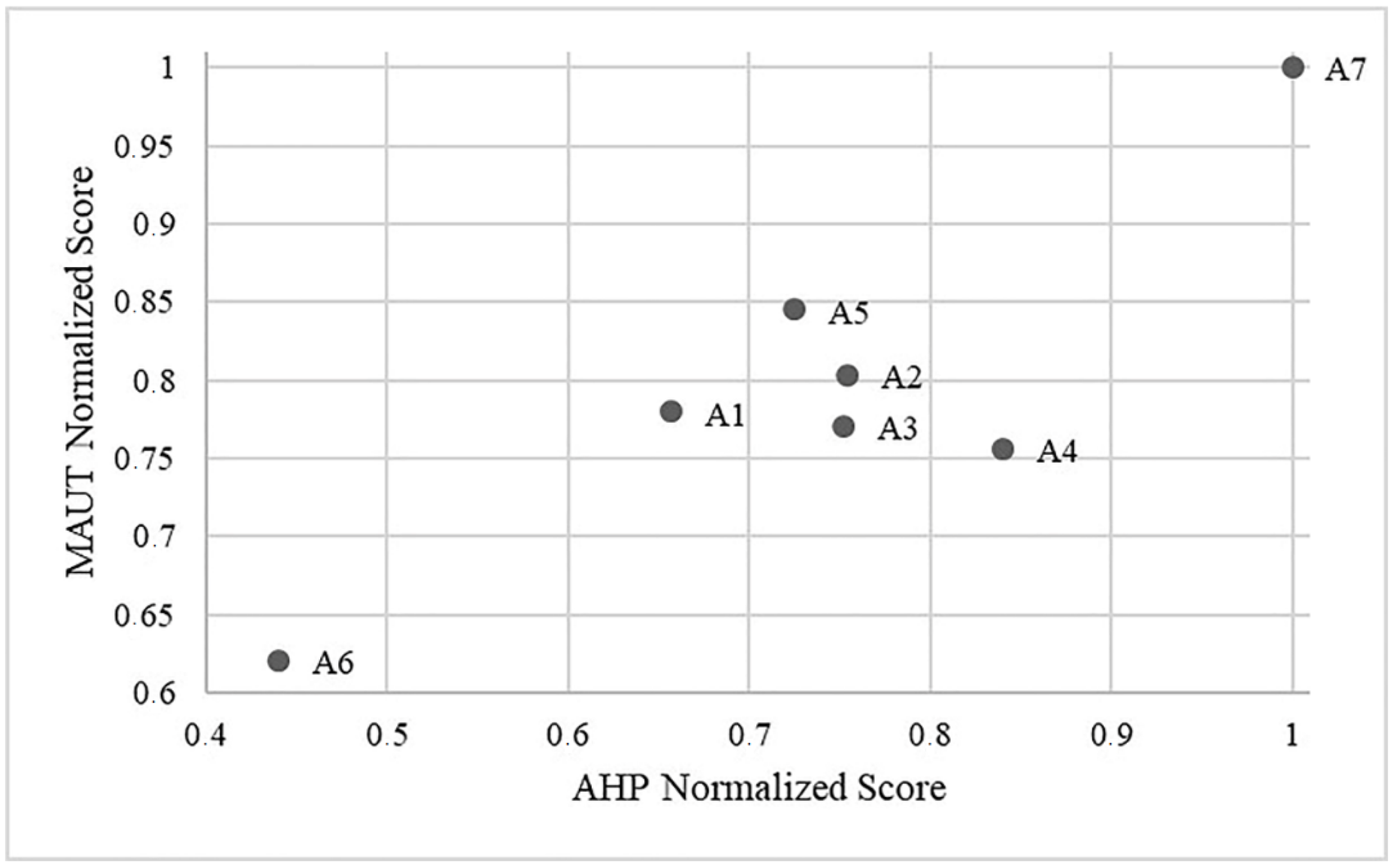
| Rank | AHP | MAUT |
|---|---|---|
| 1 | A7 | A7 |
| 2 | A4 | A5 |
| 3 | A2 | A2 |
| 4 | A3 | A1 |
| 5 | A5 | A3 |
| 6 | A1 | A4 |
| 7 | A6 | A6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amorocho-Daza, H.; Cabrales, S.; Santos, R.; Saldarriaga, J. A New Multi-Criteria Decision Analysis Methodology for the Selection of New Water Supply Infrastructure. Water 2019, 11, 805. https://doi.org/10.3390/w11040805
Amorocho-Daza H, Cabrales S, Santos R, Saldarriaga J. A New Multi-Criteria Decision Analysis Methodology for the Selection of New Water Supply Infrastructure. Water. 2019; 11(4):805. https://doi.org/10.3390/w11040805
Chicago/Turabian StyleAmorocho-Daza, Henry, Sergio Cabrales, Raquel Santos, and Juan Saldarriaga. 2019. "A New Multi-Criteria Decision Analysis Methodology for the Selection of New Water Supply Infrastructure" Water 11, no. 4: 805. https://doi.org/10.3390/w11040805
APA StyleAmorocho-Daza, H., Cabrales, S., Santos, R., & Saldarriaga, J. (2019). A New Multi-Criteria Decision Analysis Methodology for the Selection of New Water Supply Infrastructure. Water, 11(4), 805. https://doi.org/10.3390/w11040805






