Local Meteoric Water Line of Northern Chile (18° S–30° S): An Application of Error-in-Variables Regression to the Oxygen and Hydrogen Stable Isotope Ratio of Precipitation
Abstract
:1. Introduction
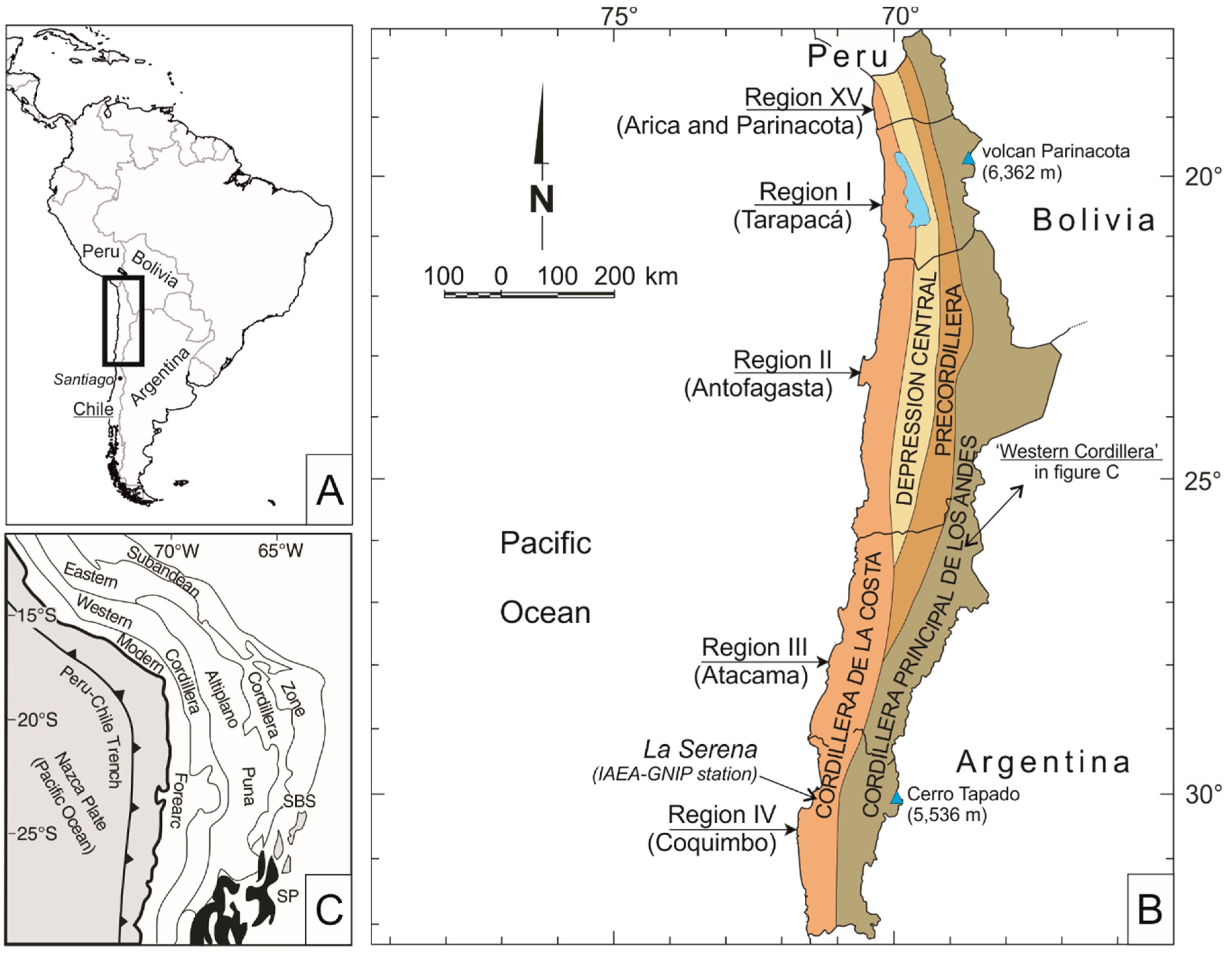
2. Materials and Methods
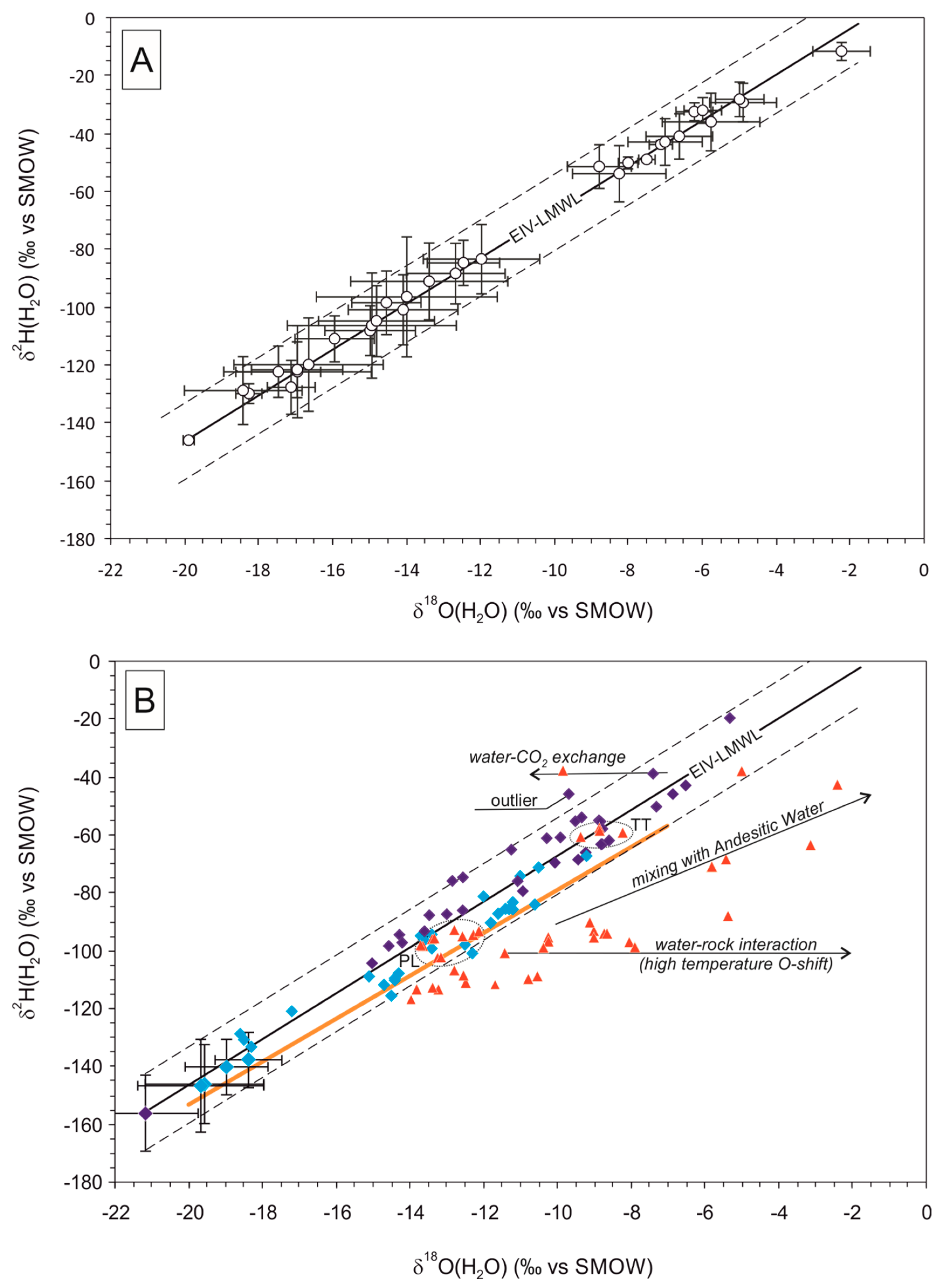
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- NIST/SEMATECH. NIST/SEMATECH e-Handbook of Statistical Methods. Available online: https://www.itl.nist.gov/div898/handbook/index.htm (accessed on 8 February 2019).
- Legendre, P.; Legendre, L. Numerical Ecology, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2012; Volume 24. [Google Scholar]
- Yurtsever, Y.; Gat, J.R. Atmospheric waters. In Stable Isotope Hydrology: Deuterium and Oxygen-18 in the Water Cycle - Technical Report Series N°210; Gonfiantini, R., Ed.; International Atomic Energy Agency: Vienna, Austria, 1981; pp. 103–142. [Google Scholar]
- IAEA. Statistical Treatment of Data on Environmental Isotopes in Precipitation—Technical Report Series n° 331; International Atomic Energy Agency—IAEA: Vienna, Austria, 1992; p. 781. [Google Scholar]
- Harper, W.V. Reduced Major Axis Regression: Teaching Alternatives to Least Squares. In Proceedings of the Ninth International Conference on Teaching Statistics (ICOTS9), Flagstaff, AZ, USA, 13–18 July 2014. [Google Scholar]
- Crawford, J.; Hughes, C.E.; Lykoudis, S. Alternative least squares methods for determining the meteoric water line, demonstrated using GNIP data. J. Hydrol. 2014, 519, 2331–2340. [Google Scholar] [CrossRef]
- Hughes, C.E.; Crawford, J. A new precipitation weighted method for determining the meteoric water line for hydrological applications demonstrated using Australian and global GNIP data. J. Hydrol. 2012, 464, 344–351. [Google Scholar] [CrossRef]
- Argiriou, A.A.; Lykoudis, S. Isotopic composition of precipitation in Greece. J. Hydrol. 2006, 327, 486–495. [Google Scholar] [CrossRef]
- Deming, W.E. Statistical Adjustment of Data; John Wiley & Sons, Inc.: New York, NY, USA, 1943. [Google Scholar]
- Gillard, J. An overview of linear structural models in errors in variables regression. REVSTAT–Stat. J. 2010, 8, 57–80. [Google Scholar]
- Maind. Sigmaplot di Systat Software. Available online: http://www.maind.it/document/SigmaplotStatistica.pdf (accessed on 27 December 2018).
- Francq, B.G.; Govaerts, B.B. Measurement methods comparison with errors-in-variables regressions. From horizontal to vertical OLS regression, review and new perspectives. Chemom. Intell. Lab. Syst. 2014, 134, 123–139. [Google Scholar] [CrossRef]
- Argiriou, A.A.; Salamalikis, V.; Dotsika, E. A Total Weighted Least Squares Method for the Determination of the Meteoric Water Line of Precipitation for Hydrological Purposes. In Perspectives on Atmospheric Sciences; Karacostas, T.S., Bais, A., Nastos, P.T., Eds.; Springer: Cham, Switzerland, 2017; pp. 233–238. [Google Scholar]
- Garreaud, R.D. The climate of northern Chile: Mean state, variability and trends. Rev. Mex. De Astron. Y Astrofísica - Ser. De Conf. 2011, 41, 5–11. [Google Scholar]
- Harrison, S.; Glasser, N.F. The Pleistocene glaciations of Chile. In Developments in Quaternary Sciences; Elhers, J., Gibbard, P.L., Hughes, C.E., Eds.; Elsevier: Amsterdam, The Netherlands, 2011; Volume 15, pp. 739–756. [Google Scholar]
- Yáñez, E.; Lagos, N.A.; Norambuena, R.; Silva, C.; Letelier, J.; Muck, K.P.; San Martin, G.; Benítez, S.; Broitman, B.R.; Contreras, H.; et al. Impacts of climate change on marine fisheries and aquaculture in Chile. In Climate Change Impacts on Fisheries and Aquaculture; Phillips, B.F., Pérez-Ramírez, M., Eds.; John Wiley & Sons: Chichester, UK, 2018; pp. 239–332. [Google Scholar]
- SERNAGEOMIN. Mapa geológico de Chile: Versión digital. Escala 1:1’000’000, 1.0 ed.; Servicio Nacional de Geología y Minería, Subdirección Nacional de Geología: Gobierno de Chile, Santiago, 2003; Publicación Geológica Digital No. 4 (CD-ROM, versión 1, 2003). [Google Scholar]
- DeCelles, P.G.; Carrapa, B.; Horton, B.K.; McNabb, J.; Gehrels, G.E.; Boyd, J. The Miocene Arizaro Basin, central Andean hinterland: Response to partial lithosphere removal. In Geodynamics of a Cordilleran Orogenic System: The Central Andes of Argentina and Northern Chile: Geological Society of America; DeCelles, P.G., Ducea, M.N., Carrapa, B., Kapp, P.A., Eds.; The Geological Society of America: Boulder, CO, USA, 2015; Volume 212, pp. 359–386. [Google Scholar]
- Schilling, F.R.; Trumbull, R.B.; Brasse, H.; Haberland, C.; Asch, G.; Bruhn, D.; Mai, K.; Haak, V.; Giese, P.; Muñoz, M.; et al. Partial melting in the Central Andean crust: A review of geophysical, petrophysical, and petrologic evidence. In The Andes—Active Subduction Orogeny; Oncken, O., Chong, G., Franz, G., Giese, P., Götze, H.J., Ramos, V.A., Strecker, M.R., Wigger, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 459–474. [Google Scholar]
- Geiger, R. Klassifikation der klimate nach W. Köppen. Landolt-Börnstein–Zahlenwerte Und Funkt. Aus Phys. Chem. Astron. Geophys. Und Tech. 1954, 3, 603–607. [Google Scholar]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5. [Google Scholar] [CrossRef]
- Sarricolea, P.; Herrera-Ossandon, M.; Meseguer-Ruiz, Ó. Climatic regionalisation of continental Chile. J. Maps 2017, 13, 66–73. [Google Scholar] [CrossRef]
- Bershaw, J.; Saylor, J.E.; Garzione, C.N.; Leier, A.; Sundell, K.E. Stable isotope variations (δ18O and δD) in modern waters across the Andean Plateau. Geochim. Cosmochim. Acta 2016, 194, 310–324. [Google Scholar] [CrossRef]
- Vuille, M.; Bradley, R.S.; Werner, M.; Healy, R.; Keimig, F. Modeling δ18O in precipitation over the tropical Americas: 1. Interannual variability and climatic controls. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Sánchez-Murillo, R.; Aguirre-Dueñas, E.; Gallardo-Amestica, M.; Moya-Vega, P.; Birkel, C.; Esquivel-Hernández, G.; Boll, J. Isotopic characterization of waters across Chile. In Andean Hydrology; Rivera, D.A., Godoy-Faundez, A., Lillo-Saavedra, M., Eds.; CRC Press: New York, NY, USA, 2018; pp. 205–230. [Google Scholar]
- Fiorella, R.P.; Poulsen, C.J.; Pillco-Zolá, R.S.; Barnes, J.B.; Tabor, C.R.; Ehlers, T.A. Spatiotemporal variability of modern precipitation δ18O in the central Andes and implications for paleoclimate and paleoaltimetry estimates. J. Geophys. Res. Atmos. 2015, 120, 4630–4656. [Google Scholar] [CrossRef]
- Gonfiantini, R.; Roche, M.A.; Olivry, J.C.; Fontes, J.C.; Zuppi, G.M. The altitude effect on the isotopic composition of tropical rains. Chem. Geol. 2001, 181, 147–167. [Google Scholar] [CrossRef]
- Jordan, T.E.; Herrera, L.C.; Godfrey, L.V.; Colucci, S.J.; Gamboa, P.C.; Urrutia, M.J.; González, L.G.; Jacob, F.P. Isotopic characteristics and paleoclimate implications of the extreme precipitation event of March 2015 in northern Chile. Andean Geol. 2019, 46, 1–31. [Google Scholar] [CrossRef]
- Rohrmann, A.; Strecker, M.R.; Bookhagen, B.; Mulch, A.; Sachse, D.; Pingel, H.; Alonso, R.N.; Schildgen, T.F.; Montero, C. Can stable isotopes ride out the storms? The role of convection for water isotopes in models, records, and paleoaltimetry studies in the central Andes. Earth Planet. Sci. Lett. 2014, 407, 187–195. [Google Scholar] [CrossRef]
- Burgener, L.; Huntington, K.W.; Hoke, G.D.; Schauer, A.; Ringham, M.C.; Latorre, C.; Díaz, F.P. Variations in soil carbonate formation and seasonal bias over >4 km of relief in the western Andes (30° S) revealed by clumped isotope thermometry. Earth Planet. Sci. Lett. 2016, 441, 188–199. [Google Scholar] [CrossRef]
- Aravena, R.; Suzuki, O.; Peña, H.; Pollastri, A.; Fuenzalida, H.; Grilli, A. Isotopic composition and origin of the precipitation in Northern Chile. Appl. Geochem. 1999, 14, 411–422. [Google Scholar] [CrossRef]
- Chaffaut, I. Précipitations d’altitude, eaux souterraines et changements climatiques de l’altiplano Nord-Chilien; Universite Paris Sud, U.F.R. Scientifique D’Orsay: Paris, France, 1998. [Google Scholar]
- Chaffaut, I.; Coudrain-Ribstein, A.; Michelot, J.L.; Pouyaud, B. Précipitation d’altitude du nord-Chili, origine des sources de vapeur et données isotopiques. Bull. De L’institut Français D’études Andin. 1998, 27, 367–384. [Google Scholar]
- DGA. Diagnóstico de disponibilidad hídrica en la cuenca del río Lauca, región de Arica y Parinacota; Ministerio de Obras Públicas, Dirección General de Aguas - Arica y Parinacota, XV Región: Arica, Chile, 2015. [Google Scholar]
- Fritz, P.; Suzuki, O.; Silva, C.; Salati, E. Isotope hydrology of groundwaters in the Pampa del Tamarugal, Chile. J. Hydrol. 1981, 53, 161–184. [Google Scholar] [CrossRef]
- Herrera, C.; Pueyo, J.J.; Sáez, A.; Valero-Garcés, B.L. Relación de aguas superficiales y subterráneas en el área del lago Chungará y lagunas de Cotacotani, norte de Chile: Un estudio isotópico. Rev. Geológica De Chile 2006, 33, 299–325. [Google Scholar] [CrossRef]
- IAEA/WMO. Global Network of Isotopes in Precipitation. The GNIP Database. Available online: https://nucleus.iaea.org/wiser (accessed on 15 January 2019).
- Squeo, F.A.; Aravena, R.; Aguirre, E.; Pollastri, A.; Jorquera, C.B.; Ehleringer, J.R. Groundwater dynamics in a coastal aquifer in north-central Chile: Implications for groundwater recharge in an arid ecosystem. J. Arid Environ. 2006, 67, 240–254. [Google Scholar] [CrossRef]
- Troncoso, R.; Castro, R.; Lorca, M.E.; Espinoza, C.; Pérez, Y. Análisis Preliminar de la Composición Isotópica Oxígeno 18 – Deuterio de las Aguas de la Cuenca del Río Copiapó, Región de Atacama: Una Contribución al Conocimiento del Sistema Hidrogeológico. In Proceedings of the XIII Congreso Geológico Chileno, Antofagasta, Chile, 5–9 August 2012; pp. 774–776. [Google Scholar]
- Uribe, J.; Muñoz, J.F.; Gironás, J.; Oyarzún, R.; Aguirre, E.; Aravena, R. Assessing groundwater recharge in an Andean closed basin using isotopic characterization and a rainfall-runoff model: Salar del Huasco basin, Chile. Hydrogeol. J. 2015, 23, 1535–1551. [Google Scholar] [CrossRef]
- Salazar, C.M.; Rojas, L.B.; Pollastri, A. Evaluación de recursos hídricos en el sector de Pica hoya de la Pampa del Tamarugal I region; Ministerio de Obras Públicas, Dirección General de Aguas, CCHEN: Santiago, Chile, 1998; p. 98. [Google Scholar]
- Aravena, R.; Peña, H.; Grilli, A.; Suzuki, O.; Mordeckai, M. Evolución isotópica de las lluvias y origen de las masas de aire en el Altiplano chileno. In Isotope Hydrology Investigations in Latin America; International Atomic Energy Agency—IAEA: Vienna, Austria, 1989; pp. 129–142. [Google Scholar]
- Herrera, C.; Custodio, E.; Chong, G.; Lambán, L.J.; Riquelme, R.; Wilke, H.; Jódar, J.; Urrutia, J.; Urqueta, H.; Sarmiento, A.; et al. Groundwater flow in a closed basin with a saline shallow lake in a volcanic area: Laguna Tuyajto, northern Chilean Altiplano of the Andes. Sci. Total Environ. 2016, 541, 303–318. [Google Scholar] [CrossRef]
- NIST. DATAPLOT Reference Manual - weighted standard deviation. Available online: https://www.itl.nist.gov/div898/software/dataplot/refman2/ch2/weightsd.pdf (accessed on 28 December 2018).
- Taylor, B.N.; Kuyatt, C.E. Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results; National Institute of Standards and Technology—NIST: Gaithersburg, MD, USA, 1994. [Google Scholar]
- Leito, I.; Jalukse, L.; Helm, I. Estimation of Measurement Uncertainty in Chemical Analysis (Analytical Chemistry) Course; University of Tartu: Tartu, Estonia, 2018. [Google Scholar]
- Bell, S. A Beginner’s Guide to Uncertainty of Measurement; National Physical Laboratory: Teddington, UK, 1999. [Google Scholar]
- Williamson, J.H. Least-squares fitting of a straight line. Can. J. Phys. 1968, 46, 1845–1847. [Google Scholar] [CrossRef]
- York, D. Least-squares fitting of a straight line. Can. J. Phys. 1966, 44, 1079–1086. [Google Scholar] [CrossRef]
- York, D. Unified equations for the slope, intercept, and standard error of the best straight line. Am. J. Phys. 2004, 72, 367–375. [Google Scholar] [CrossRef]
- York, D. Least squares fitting of a straight line with correlated errors. Earth Planet. Sci. Lett. 1968, 5, 320–324. [Google Scholar] [CrossRef]
- Originlab. Algorithms (Fit Linear with X Error). Available online: https://www.originlab.com/doc/Origin-Help/Ref-Linear-XErr#Fit_Parameters (accessed on 27 December 2018).
- Systat. Using SigmaStat Statistics in SigmaPlot; Systat Software: San Jose, CA, USA, 2013; p. 470. [Google Scholar]
- Cantrell, C.A. Technical Note: Review of methods for linear least-squares fitting of data and application to atmospheric chemistry problems. Atmos. Chem. Phys. 2008, 8, 5477–5487. [Google Scholar] [CrossRef]
- Sturm, P. bfsl: Best-Fit Straight Line, 0.1.0; CRAN.R-project.org. 2018. Available online: https://cran.r-project.org/web/packages/bfsl/index.html (accessed on 3 February 2019).
- Aravena, R.; Suzuki, O.; Pollastri, A. Coastal fog and its relation to groundwater in the IV region of northern Chile. Chem. Geol. 1989, 79, 83–91. [Google Scholar] [CrossRef]
- Cifuentes, J.L.; Cervetto, M.M.; López, L.A.; Fuentes, F.C.; Feuker, P.; Espinoza, C. Análisis preliminar de Isótopos Estables en aguas subterráneas, superficiales y lluvia de la Pampa del Tamarugal. In Proceedings of the XIV Congreso Geológico Chileno, La Serena, Chile, 4–8 October 2015; pp. 277–280. [Google Scholar]
- DGA. Levantamiento hidrogeológico para el desarrollo de nuevas fuentes de agua en áreas prioritarias de la zona norte de Chile, Regiones XV, I, II y III, Etapa 2; Ministerio de Obras Públicas, Dirección General de Aguas, Departamento de Estudios y Planificación; Pontificia Universidad Católica de Chile, Departamento de Ingeniería Hidráulica y Ambiental: Santiago, Chile, 2009. [Google Scholar]
- López, L.A.; Cifuentes, J.L.; Fuentes, F.C.; Neira, H.A.; Cervetto, M.M.; Troncoso, R.A.; Feuker, P. Hidrogeología de la Cuenca de la Pampa del Tamarugal, Región de Tarapacá; Gobierno de Chile, Servicio Nacional de Geología y Minería: Santiago, Chile, 2017; p. 186. [Google Scholar]
- Durán, L.V.L. Hidrogeoquímica de fuentes termales en ambientes salinos relacionados con salares en los Andes del Norte de Chile; Universidad de Chile: Santigo, Chile, 2016. [Google Scholar]
- Giggenbach, W. The isotopic composition of waters from the El Tatio geothermal field, Northern Chile. Geochim. Cosmochim. Acta 1978, 42, 979–988. [Google Scholar] [CrossRef]
- Godfrey, L.V.; Jordan, T.E.; Lowenstein, T.K.; Alonso, R.L. Stable isotope constraints on the transport of water to the Andes between 22° and 26°S during the last glacial cycle. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2003, 194, 299–317. [Google Scholar] [CrossRef]
- Munoz-Saez, C.; Manga, M.; Hurwitz, S. Hydrothermal discharge from the El Tatio basin, Atacama, Chile. J. Volcanol. Geotherm. Res. 2018, 361, 25–35. [Google Scholar] [CrossRef]
- Peña, H. Mediciones de 180 y 2H en “Penitentes” de Nieve. In Isotope Hydrology Investigations in Latin America; International Atomic Energy Agency—IAEA: Vienna, Austria, 1988; Volume IAEA-TECDOC-502, pp. 143–154. [Google Scholar]
- Cortecci, G.; Boschetti, T.; Mussi, M.; Herrera Lameli, C.; Mucchino, C.; Barbieri, M. New chemical and isotopic data on waters of El Tatio Geothermal Field, Northern Chile. Geochem. J. 2005, 39, 547–571. [Google Scholar] [CrossRef]
- Alpers, C.N.; Whittemore, D.O. Hydrogeochemistry and stable isotopes of ground and surface waters from two adjacent closed basins, Atacama Desert, northern Chile. Appl. Geochem. 1990, 5, 719–734. [Google Scholar] [CrossRef]
- Sinclair, K.E.; MacDonell, S. Seasonal evolution of penitente glaciochemistry at Tapado Glacier, Northern Chile. Hydrol. Process. 2016, 30, 176–186. [Google Scholar] [CrossRef]
- Cervetto, M.M. Caracterización hidrogeológica e hidrogeoquímica de las cuencas: Salar de Aguas calientes 2, Puntas negras, Laguna Tuyajto, Pampa Colorada, Pampa Las Tecas y Salar el Laco, II región de Chile; Universidad de Chile: Santiago, Chile, 2012. [Google Scholar]
- Scheihing, K.; Moya, C.; Struck, U.; Lictevout, E.; Tröger, U. Reassessing Hydrological Processes That Control Stable Isotope Tracers in Groundwater of the Atacama Desert (Northern Chile). Hydrology 2018, 5, 3. [Google Scholar] [CrossRef]
- Tassi, F.; Aguilera, F.; Darrah, T.; Vaselli, O.; Capaccioni, B.; Poreda, R.J.; Huertas, A.D. Fluid geochemistry of hydrothermal systems in the Arica-Parinacota, Tarapacá and Antofagasta regions (northern Chile). J. Volcanol. Geotherm. Res. 2010, 192, 1–15. [Google Scholar] [CrossRef]
- Zaiontz, C. Real Statistics Using Excel. Available online: www.real-statistics.com (accessed on 3 February 2019).
- Boschetti, T.; Cortecci, C.; Barbieri, M.; Mussi, M. New and past geochemical data on fresh to brine waters of the Salar de Atacama and Andean Altiplano, northern Chile. Geofluids 2007, 7, 35–50. [Google Scholar] [CrossRef]
- Verschuuren, G. Excel 2013 for Scientists; Holy Macro! Books: Chicago, IL, USA, 2014; p. 250. [Google Scholar]
- Clark, I. Groundwater Geochemistry and Isotopes; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2015. [Google Scholar]
- Gat, J.R. Isotope Hydrology: A Study of the Water Cycle; Imperial College Press: London, UK; Singapore, 2010. [Google Scholar]
- Francq, B.; Govaerts, B. How to regress and predict in a Bland–Altman plot? Review and contribution based on tolerance intervals and correlated-errors-in-variables models. Stat. Med. 2016, 35, 2328–2358. [Google Scholar] [CrossRef] [PubMed]
- Francq, B.G.; Berger, M. BivRegBLS: Tolerance Intervals and Errors-in-Variables Regressions in Method Comparison Studies, 1.0.0; CRAN.R-project.org. 2017. Available online: https://CRAN.R-project.org/package=BivRegBLS (accessed on 3 February 2019).
- Berger, M.; Francq, B. BivRegBLS: A new R package in method comparison studies with tolerance intervals and (correlated)-errors-in-variables regressions. In Proceedings of the Chimiométrie XVIII, Paris, France, 30 January–1 February 2017. [Google Scholar]
- Lorca, M.E. Hidrogeología e hidrogeoquímica de la cuenca de la Quebrada Paipote, Región de Atacama; Universidad de Chile: Santiago, Chile, 2011. [Google Scholar]
- Aravena, R. Isotope hydrology and geochemistry of northern Chile groundwaters. Bull. De L’institut Français D’études Andin. 1995, 24, 495–503. [Google Scholar]
- Stichler, W.; Schotterer, U.; Fröhlich, K.; Ginot, P.; Kull, C.; Gäggeler, H.; Pouyaud, B. Influence of sublimation on stable isotope records recovered from high-altitude glaciers in the tropical Andes. J. Geophys. Res. Atmos. 2001, 106, 22613–22620. [Google Scholar] [CrossRef]
| Slope | ± | s.e. | Intercept | ± | s.e. | N | R2 | Reference | Year | Ref. [#] | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 7.8 | - | 10.3 | - | 29 | - | Fritz et al. | 1981 | [35] | |||
| 8.2 | ± | 0.17 | 16.6 | ± | 2.2 | 39 | 0.98 | Chaffaut et al. | 1998 | [32,33] | |
| 7.8 | - | 9.7 | - | 129 | - | Aravena et al. | 1999 | [31] | |||
| 7.9 | - | 14 | - | - | - | Herrera et al. | 2006 | [36] | |||
| 7.7 | - | 9.6 | - | - | 0.91 | Squeo et al. | 2006 | [38] | |||
| 7.95 | - | 14.9 | - | - | 0.99 | DGA | 2015 | [34] | |||
| 8.07 | - | 13.5 | - | 23 | 0.98 | Troncoso et al. | 2012 | [39] | |||
| 7.52 | ± | 0.46 | 7.18 | ± | 2.64 | 40 | 0.87 | IAEA/WHO | 2015 | [37] | |
| mean | 7.87 | 11.97 | |||||||||
| std.de. | 0.21 | 3.22 | |||||||||
| ID # | Location | Coordinates | Elevation Meters | δ18O (a.w.m. ± c.s.) | δ2H (a.w.m. ± c.s.) | Na.p. | Precipitation Amount (Mean Value) Millimeters | References | Ref. [#] | |
|---|---|---|---|---|---|---|---|---|---|---|
| Latitude | Longitude | ‰ vs. SMOW | ‰ vs. SMOW | |||||||
| 1 | Apacheta Tapa | −19.5891 | −68.9940 | 4350 | −17.48 ± 1.14 | −122.3 ± 8.9 | 4 | 73.73 | Fritz et al. 1981 | [35] |
| 2 | Chusmiza | −19.7060 | −69.1906 | 3360 | −7.51 ± 0.22 | −48.9 ± 1.0 | 3 | 103.93 | Fritz et al. 1981 | [35] |
| 3 | Alto Mocha | −19.8181 | −69.2987 | 2590 | −7.13 ± 0.31 | −43.7 ± 1.5 | 2 | 33.90 | Fritz et al. 1981 | [35] |
| 4 | Mocha | −19.8436 | −69.2840 | 2200 | −4.91 ± 0.90 | −29.2 ± 6.7 | 2 | 39.65 | Fritz et al. 1981 | [35] |
| 5 | Collacagua | −20.0703 | −68.8259 | 3915 | −15.00 ± 1.22 | −108.1 ± 8.6 | 7 | 82.23 | Fritz et al. 1981 | [35] |
| 6 | Huasco | −20.3144 | −68.8065 | 3800 | −17.13 ± 0.65 | −127.7 ± 9.3 | 3 | 34.63 | Fritz et al. 1981 | [35] |
| 7 | Indio Muerto | −20.3610 | −68.9615 | 4135 | −18.27 ± 0.35 | −129.9 ± 3.4 | 4 | 53.05 | Fritz et al. 1981 | [35] |
| 8 | Tambillos | −20.4672 | −69.1415 | 3300 | −8.02 ± 0.27 | −50.1 ± 2.1 | 3 | 77.13 | Fritz et al. 1981 | [35] |
| 9 | Apacheta Mama * | −20.4734 | −69.1580 | 4115 | −19.90 ± 0.15 | −146.0 ± 1.0 | 1 | 77.00 | Fritz et al. 1981 | [35] |
| 10 | Pumire | −19.0955 | −69.1108 | 4200 | −2.25 ± 0.78 | −11.5 ± 3.1 | 3 | 10.00 | Salazar et al. 1998; Aravena et al. 1989 | [41,42] |
| 11 | Coposa | −20.7089 | −68.6942 | 3460 | −16.66 ± 2.01 | −119.8 ± 16.2 | 9 | 9.17 | Salazar et al. 1998; Aravena et al. 1989 | [41,42] |
| 12 | Collaguasi | −20.9833 | −68.7000 | 4250 | −16.96 ± 1.99 | −122.3 ± 16.0 | 5 | 13.30 | Aravena et al. 1999 | [31] |
| 13 | Ujina | −20.9833 | −68.6000 | 4200 | −11.98 ± 1.57 | −83.3 ± 12.0 | 8 | 18.79 | Aravena et al. 1999 | [31] |
| 14 | Puchuldiza | −19.4000 | −68.9500 | 4150 | −14.55 ± 0.93 | −98.4 ± 11.0 | 15 | 11.88 | Aravena et al. 1999 | [31] |
| 15 | Pampa Lirima | −19.8200 | −68.9000 | 4100 | −16.97 ± 1.23 | −121.6 ± 9.7 | 27 | 9.86 | Aravena et al. 1999 | [31] |
| 16 | Colchane | −19.7003 | −68.8833 | 3965 | −14.95 ± 2.28 | −106.3 ± 18.2 | 4 | 51.90 | Aravena et al. 1999 | [31] |
| 17 | Collacagua | −20.0333 | −68.8500 | 3990 | −12.68 ± 1.34 | −88.3 ± 10.5 | 14 | 15.04 | Aravena et al. 1999 | [31] |
| 18 | Cancosa | −19.8500 | −68.6000 | 3800 | −14.00 ± 2.45 | −96.4 ± 20.7 | 5 | 28.50 | Aravena et al. 1999 | [31] |
| 19 | Huaytane | −19.5433 | −68.6042 | 3720 | −14.10 ± 1.48 | −100.9 ± 12.1 | 5 | 32.20 | Aravena et al. 1999 | [31] |
| 20 | Copaquire | −20.9305 | −68.8922 | 3490 | −12.47 ± 0.98 | −84.6 ± 7.8 | 16 | 5.75 | Aravena et al. 1999 | [31] |
| 21 | Poroma | −19.8667 | −69.1833 | 2880 | −5.00 ± 0.66 | −28.1 ± 6.0 | 9 | 8.01 | Aravena et al. 1999 | [31] |
| 22 | Parca | −20.0167 | −68.8500 | 2570 | −6.64 ± 0.90 | −40.9 ± 7.8 | 4 | 4.88 | Aravena et al. 1999 | [31] |
| 23 | Huatacondo | −20.9167 | −69.0500 | 2460 | −8.26 ± 1.26 | −53.8 ± 9.8 | 12 | 6.21 | Aravena et al. 1999 | [31] |
| 24 | Camina | −19.3116 | −69.4299 | 2380 | −7.02 ± 1.00 | −42.8 ± 8.1 | 4 | 11.50 | Aravena et al. 1999 | [31] |
| 25 | Sillillica | −20.1738 | −68.7377 | 4270 | −15.96 ± 1.07 | −110.9 ± 7.9 | 3 | 95.30 | Uribe et al. 2015 | [40] |
| 26 | Altos del Huasco | −20.3221 | −68.9022 | 3784 | −14.82 ± 1.57 | −104.8 ± 12.3 | 3 | 51.80 | Uribe et al. 2015 | [40] |
| 27 | Diablo Marca | −20.0505 | −68.9962 | 4603 | −18.43 ± 1.59 | −128.8 ± 11.8 | 3 | 78.60 | Uribe et al. 2015 | [40] |
| 28 | Quisquiro | −23.2100 | −67.2500 | 4260 | −13.40 ± 2.12 | −91.1 ± 13.3 | 36 | 14.30 | Chaffaut 1998 | [32] |
| 29 | Tuyajto | −23.9435 | −67.5921 | 4040 | −6.23 ± 0.50 | −32.4 ± 3.1 | 2 | 13.30 | Herrera et al. 2016 | [43] |
| 30 | Pampa Colorada | −23.8588 | −67.4774 | 4426 | −8.80 ± 0.86 | −51.3 ± 7.6 | 3 | 28.50 | Herrera et al. 2016 | [43] |
| 31 | Aguas Calientes-3 | −23.9171 | −67.6971 | 3900 | −6.00 ± 0.51 | −31.9 ± 4.5 | 3 | 21.67 | Herrera et al. 2016 | [43] |
| 32 | La Serena | −29.8981 | −71.2425 | 142 | −5.78 ± 1.32 | −35.9 ± 9.9 | 34 | 43.10 | IAEA/WHO 2015 | [37] |
| Models | N | Slope | Intercept | rmSSEav | t-Value | p | ||
|---|---|---|---|---|---|---|---|---|
| Value | s.e. | Value | s.e. | |||||
| OLSR | 32 | 7.78 | 0.10 | 11.3 | 1.2 | 1.0009 | - | - |
| RMA | 32 | 7.80 | 0.09 | 11.5 | 1.2 | 1.0004 | 0.1318 | 0.896 |
| MA | 32 | 7.82 | 0.10 | 11.7 | 1.2 | 1.0009 | 0.2593 | 0.797 |
| PWLSR | 32 | 7.74 | 0.09 | 10.7 | 1.3 | 1.0054 | 0.3047 | 0.763 |
| PWRMA | 32 | 7.76 | 0.09 | 10.9 | 1.3 | 1.0021 | 0.1810 | 0.858 |
| PWMA | 32 | 7.78 | 0.09 | 11.1 | 1.3 | 1.0000 | 0.0608 | 0.952 |
| Models | N | Slope | Intercept | 95% C.I. Slope | 95% C.I. Intercept | r | GOF | rmSSE | t-Value | p | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Value | s.e. | Value | s.e. | Upper | Lower | Upper | Lower | |||||||
| OLSR | 32 | 7.79 | 0.10 | 11.3 | 1.2 | 7.98 | 7.59 | 13.8 | 8.7 | 0.9977 | 7.1740 | 2.6784 | - | - |
| EIV-a | 32 | 7.93 | 0.15 | 12.3 | 2.1 | 8.24 | 7.63 | 16.7 | 8.0 | 0.9977 | 0.1457 | 0.3817 | 0.8292 | 0.414 |
| EIV-b | 32 | 7.93 | 0.15 | 12.3 | 2.1 | 8.24 | 7.62 | 16.6 | 7.9 | 0.9977 | 0.1457 | 0.3817 | 0.8119 | 0.423 |
| EIV-c | 32 | 7.93 | 0.15 | 12.3 | 2.1 | - | - | - | - | - | 0.1457 | 0.3817 | 0.8289 | 0.414 |
| EIV-d | 32 | 7.93 | 0.06 | 12.3 | 0.8 | - | - | - | - | - | 0.1457 | 0.3817 | 1.3185 | 0.197 |
| EIV-e | 32 | 7.81 | 0.12 | 11.5 | 1.6 | 8.05 | 7.56 | 14.8 | 8.2 | - | - | 0.1256 | 0.901 | |
| Models | t-Value | p | Models | t-Value | p | Models | t-Value | p |
|---|---|---|---|---|---|---|---|---|
| PWLSR | - | - | PWRMA | - | - | PWMA | - | - |
| EIV-a | 1.0843 | 0.287 | EIV-a | 0.9883 | 0.331 | EIV-a | 0.8946 | 0.378 |
| EIV-b | 1.0662 | 0.295 | EIV-b | 0.9705 | 0.340 | EIV-b | 0.8770 | 0.387 |
| EIV-c | 1.0840 | 0.287 | EIV-c | 0.9881 | 0.331 | EIV-c | 0.8944 | 0.378 |
| EIV-d | 1.7481 | 0.091 | EIV-d | 1.5934 | 0.122 | EIV-d | 1.4410 | 0.160 |
| EIV-e | 0.4141 | 0.682 | EIV-e | 0.3029 | 0.764 | EIV-e | 0.1949 | 0.847 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boschetti, T.; Cifuentes, J.; Iacumin, P.; Selmo, E. Local Meteoric Water Line of Northern Chile (18° S–30° S): An Application of Error-in-Variables Regression to the Oxygen and Hydrogen Stable Isotope Ratio of Precipitation. Water 2019, 11, 791. https://doi.org/10.3390/w11040791
Boschetti T, Cifuentes J, Iacumin P, Selmo E. Local Meteoric Water Line of Northern Chile (18° S–30° S): An Application of Error-in-Variables Regression to the Oxygen and Hydrogen Stable Isotope Ratio of Precipitation. Water. 2019; 11(4):791. https://doi.org/10.3390/w11040791
Chicago/Turabian StyleBoschetti, Tiziano, José Cifuentes, Paola Iacumin, and Enricomaria Selmo. 2019. "Local Meteoric Water Line of Northern Chile (18° S–30° S): An Application of Error-in-Variables Regression to the Oxygen and Hydrogen Stable Isotope Ratio of Precipitation" Water 11, no. 4: 791. https://doi.org/10.3390/w11040791
APA StyleBoschetti, T., Cifuentes, J., Iacumin, P., & Selmo, E. (2019). Local Meteoric Water Line of Northern Chile (18° S–30° S): An Application of Error-in-Variables Regression to the Oxygen and Hydrogen Stable Isotope Ratio of Precipitation. Water, 11(4), 791. https://doi.org/10.3390/w11040791





