Abstract
Stormwater urban drainage systems are typically designed in open channel flow. Pipe sewers must have enough capacity to transport maximum design flows for a given frequency of the project rainfall. The classic rational method or related procedures that are based on rational approaches are still currently used to a great extent, particularly for small urban drainage basins, and the pipes are frequently designed in uniform steady flow. Numerical integration of Saint-Venant equations for one-dimensional gradually varied unsteady flow allows the computation of waves’ progression along the pipes for given input surface hydrographs. This paper presents a comprehensive, systematic, simple, and original comparison between the peak flows that are achieved through simulation in unsteady flow using an implicit complete dynamic model, developed in the Laboratory of Hydraulics, Water Resources and Environment of Coimbra University, and those that are obtained with the classic rational method along urban drainage networks. Boundary conditions and some approximations typically considered in the methodologies are analyzed in detail. Classic rational approaches may underestimate the peak and design flows. Practical recommendations for the system design phase when rational approaches are used are also proposed. The need for indispensable requirements for suitable urbanization rules, intelligent management of surface runoff in urban basins, and control measures for the reduction of peak flows entering existing networks is confirmed and reinforced.
1. Introduction
Much research has been and is being currently conducted all over the world in the area of urban drainage systems. See, for instance, Moore et al. [1], that summarize 246 studies published in 2016. It is essential to minimize or mitigate especially the impact of the increasing urban floods, which are due in particular to the increase in the amount of impermeable surfaces in urban agglomerates and global warming, which is causing extreme events that become progressively more intense. Multiple aspects, issues, or measures related to the management or control of stormwater systems have been investigated, ranging from flood incidence analysis [2], or the evaluation of urban hydrologic changes [3], up to flood hazard studies in metro systems [4,5]. Areas of concern include: the reduction of peak flows entering the networks, for example by considering bioretention systems [6,7,8]; detention ponds associated to management strategies [9] and rainwater harvesting systems [10], with potential reuse of the stored rainwater; the creation of conditions at the level of the urban basins allowing controlled surface runoff, particularly similar to those existing prior to urbanization [11,12]; the increase of permeable surfaces in the urban basins, such as through the development of green infrastructures and green roofs [13]; and the mitigation or possible treatment of some pollutants associated with the washing of streets and other impervious surfaces [14].
With deficient planning and urbanization and without suitable measures at the level of the surface basins, it seems likely that the existing stormwater networks and possibly also the future systems will hardly have enough capacity to transport the required peak flows for an actual satisfactory rainfall frequency given that the costs of investment required to create such large infrastructures would be much too high. The occurrence of urban floods seems to be currently recurrent, with the network piping operating under pressure. Extreme precipitation events can cause backwater effects, overflows, and serious drawbacks for the urban populations and surrounding environment. This may be particularly worrying in the case of older combined systems that still co-exist incorrectly in many urban centers [15,16]. These systematic floods may create serious pollution hazards, due to the pollutants transported in the wastewaters that are spread along the urban agglomerates and/or discharged directly into the water bodies without any type of treatment.
Although many methods, possible approximations, engineering procedures, and computational tools are currently available, there is traditionally a general lack of sureness about what exactly the best procedures are for computing the peak volumetric flow rates of stormwater in the phase of urban network design. It does not seem to be easy to relate all variables that influence the formation of the hydrographs and the peak flows in the pipes of a network that collect the surface flows of complex urban drainage basins. Due mainly to its simplicity and effectiveness, the rational method and/or its derivatives are still largely used for relatively small urban drainage basins and are mentioned in the national regulations, manuals of practice, scientific works, reference books, and design guidelines [17,18,19,20,21,22,23,24,25]. Numerous insufficiencies, sometimes contradictory, and some well-reported limitations seem to result from their basic assumptions. Such assumptions are well-known and typically are properly described.
Formulations of kinematic or rational type continue to be referenced or used as expedite and useful tools for evaluating peak flows, particularly in small urban areas. A wide margin of doubts still typically persists in the technical and scientific literature and engineering practice, with indications sometimes contradictory about the real limitations and best usage of the methods. Basic questions may be raised, as for example, if the conventional rational method correctly approximates, overestimates or underestimates the peak flows, should the conventional computed peak flows be maintained, decreased or increased? The complete understanding of the real comparative results that it effectively produces, the elimination of any possible misconceptions, and the best way in which it can be used, are fundamental aspects that do not seem totally and absolutely solved or established.
In the present research work, a simple and new scientific contribution was developed specifically with regard to these important issues. Hydrographs reached in storm sewer networks, operating in open channel unsteady flow for diverse boundary conditions, are simulated extensively and methodically compared with the maximum flows achieved with approaches of rational type. It is well established that Saint-Venant equations for a one-dimensional open-channel gradually varied unsteady flow can be typically integrated by numerical models. The numerical model that solves these equations allows to compute the flow characteristics in the pipes of the networks in any section and at any time, that is, the wave progression, after a stormwater event for input hydrographs that are known or simulated [22,26,27,28,29,30,31,32,33,34,35,36]. An implicit complete dynamic model previously developed in the Laboratory of Hydraulics, Water Resources and Environment of Coimbra University [22,31] was expanded and used in this investigation. Peak flows calculated by means of the classic rational method in any section of a network are thus extensively and systematically compared in this paper with the outcomes that are obtained by computing the wave progression using this implicit hydrodynamic model and inlet hydrographs simplified or approximated for the surface runoff.
The initial hydrodynamic model implemented considers each link separately, sequentially from upstream to downstream, and steady uniform flows, as a simplified assumption both for the downstream boundary condition and for the initial condition in each link that is required for the starting of the dynamic process. These basic simplifications allow simultaneously the optimal design in steady uniform flow (optimal determination of the conduit diameters, and sewer invert elevations) and the simulation in unsteady flow of the urban stormwater networks for surface runoff hydrographs known or simulated. New boundary conditions (and inherent initial conditions) are modeled, implemented on a computer, methodologically explored, and compared in the hydrodynamic model. Additionally, the results achieved with the original implicit hydrodynamic model that was developed in the University of Coimbra are also compared with the results that are obtained applying US Environmental Protection Agency (EPA) software Storm Water Management Model (SWMM), version 5.1 [37], which uses an explicit integration scheme for a dendritic network considered as a whole. All results obtained along the present study and all the simulations are thoroughly discussed, and some approximations usually considered in the classic rational approach are analyzed. Important recommendations, both for peak flow calculations and for the management of urban drainage basins, are suggested.
2. Materials and Methods
2.1. Numerical Modeling in Open Channel Gradually Varied Unsteady Flow
2.1.1. Saint-Venant Equations Succinctly Revisited
With exception to singular points normally located at manholes, or special occurrences as in the case of hydraulic jump, the flow in stormwater sewers normally occurs in gradually varied unsteady flow, with low curvature of trajectories [22]. A system of two differential equations of hydrodynamics, namely the continuity equation and the momentum equation, typically describes these flows mathematically [28,29,30] and is known as the system of Barre de Saint-Venant. This system is based on the assumptions of: (i) a unidirectional open channel flow [expressed in Equation (1) through a volumetric flow rate, Q, and cross-sectional area, A = A(h) varying in space, x, and time, t]; (ii) homogeneous and incompressible fluid; (iii) a practically hydrostatic distribution of pressures in the cross-section; and (iv) a local head loss per unit of pipe length, J, practically equal to that occurring in a steady uniform flow for the same average velocity, U, and water depth, h, in each section x and time t:
If the flow characteristics; average velocity, U; and flow depth, h, are the variables considered, the differential equations may be expressed as:
where hm = hm(h), , and g, respectively, are the average depth of flow, the slope of the channel, and the acceleration of gravity. It should be noted that the lateral inflow is assumed null here, the Boussinesq coefficient is taken approximately equal to 1, and that all geometric variables required in the equations for circular pipes, namely depth of flow, h; liquid cross-sectional area, A; water surface width, b; average depth of flow, hm; and hydraulic radius, Rh, are normally defined using the angle to the center θ in radians.
Currently, this system in both forms is typically solved numerically. This requires: (i) the use of a flow resistance law, like for example the Gauckler-Manning-Strickler equation that is frequently used, assuming fully rough turbulent regimens; (ii) the definition of initial conditions, normally in steady flow, that is, values of Q and A, or values of h and U, along the length of the pipes, before the beginning of the dynamic process that calculates the values of the variables considered in each instant of time, t(j+1), based on the corresponding values that are already known in the previous stage, t(j); and (iii) the definition of generally two boundary conditions in the extremities of each length of the pipe (link) between manholes, outfalls, or entrances of stormwater inflow, that is, equations that allow the determination or that relate in each instant of time to the values of the variables considered in the corresponding sections.
2.1.2. Overview of the Developed Numerical Integration Process
The numerical integration of the Saint-Venant equations, using variables h and U and considering all terms of the equations, that is, a complete dynamic wave model, was performed by finite differences using an implicit method of four points (x(i), t(j)), (x(i+1), t(j)), (x(i), t(j+1)), and (x(i+1), t(j+1)), weighted [27,31,38,39]. Its development and implementation details are presented in Diogo and Diogo et al. [22,31]. The temporal derivatives and the space derivatives are approximated respectively by:
and
with the time weighting factor ψ defined between 0.5 and 1. For ψ = 1, the numerical schema would be totally implicit (and totally explicit if ψ = 0). The expressions used for calculating the variables hx(i), Ux(i), hmx(i), Rhx(i), and J between adjacent times t(j) and t(j+1) are respectively:
where Ks is the inverse of the Manning roughness coefficient, n, which may vary with the flow depth.
Replacing all expressions in the equations of system (2) for a given reach (link), for all points x(i), with i = 1, N − 1, where N is the total number of discrete points into which each reach is subdivided for the execution of the numerical integration and including the two boundary conditions in the extremity nodes (for example, the equation of continuity upstream, and the normal depth, equation of energy, or any other described in Section 2.1.4, downstream) gives a system with 2N equations, with 2N unknowns and , for i = 1, N. This system allows the determination of the characteristics of the flow h and U along the reach at each instant of time t(j+1), after knowing the characteristics of flow at the previous time t(j). An iterative method of successive approximations is used to solve the system at each instant of time in which the initial value of the variables for the first iteration for each discrete point in the space is considered exactly equal to that which occurred at the previous moment at the same point.
2.1.3. Initial Conditions under Steady Flow Modelled and Implemented
Frequently, the initial condition, when t(j) ≤ 0, considers a fictitious steady uniform flow along the pipe with the smallest possible magnitude of the volumetric flow rate, for example of the same order as the infiltration flows. It corresponds to the base of the flood hydrograph (a diagram that gives the volumetric flow rate in a given section over time). In the case of steep slopes (, where represents the critical slope), the uniform flow is supercritical and the control should be performed at the upstream manhole, but the entrance conditions and the subsequent energy equation are frequently ignored in this computation, assuming that the uniform flow continues approximately until the section close of this manhole. On mild slopes (), the uniform flow is subcritical and the control is performed downstream. The depth of flow in the downstream extremity is approximately equal to the downstream control depth, if the latter is above the critical depth, or the critical depth, if the control depth is below, assuming in this last case a free discharge and a hydrostatic distribution of the pressures in the transversal section, that is, ignoring the curvature of the trajectories.
The abovementioned initial conditions in steady flow that were required for the new downstream boundary conditions tested and presented in this paper were modeled and implemented on a computer. The corresponding normal and critical depths of flow and the gradually varied profiles of the steady flows are represented schematically in Figure 1. In practice, due to the curvature of trajectories, it can be observed that the flow depth reached in the end section is lower than critical depth, with a ratio of about 1/1.4 [40], see Figure 1 d), but this fact is rarely mentioned or considered.
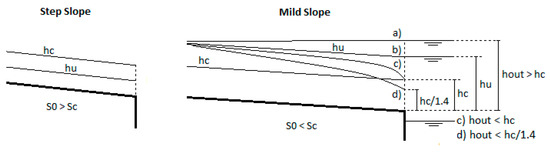
Figure 1.
Initial conditions in the links in steady flow, and downstream boundary conditions in subcritical flow controlled downstream with hout > hc (a, b), and free discharge, hout < hc (c), or alternatively hout < hc/1.4 (d).
2.1.4. Boundary Conditions Modelled and Implemented
In operating conditions below or equal to the design flows, neither the mobilization of storage capacity in the manholes nor the backwater effect through manholes is normally expected or considered. In these circumstances, the first boundary condition that is normally assumed is thus a known inflow hydrograph in the node of the upstream extremity of each link that can be determined through the equation of continuity for each instant of time t(j+1) for all hydrographs estimated or simulated immediately upstream,
where Qin and Qout are all volumetric water flow rates entering and exiting the node, respectively, with U = Q/A(h).
Several alternatives with diverse levels of approximation may be considered for the second boundary condition required in each link. In the general case, it may be an equation of energy in the nodes that depends on the regimen of the flow established and subsequent flow control. In the case of subcritical flow in the reach (link), the energy equation should be established in the downstream node, and if the flow is supercritical in the upstream node,
where the indices in and out refer to each considered pipe entrance in the manhole and the pipe exiting the manhole, respectively, y is the elevation of the internal base of the pipe, and ΔH is the minor head loss or local head loss. In the first case, if no fall is considered in the manhole and if the head loss and changes of kinetic energy can be neglected, the downstream water depth of the node is maintained for the upstream part [41,42,43]. In some circumstances, it may eventually be assumed to be approximately equal to the uniform subcritical water depth of a downstream pipe with the same slope.
In the case of subcritical flow in the link and free discharge at its downstream end or supercritical flow after this node, the flow would be critical in an upstream section that is relatively close to the node (the water depth in steady flow in the section of the fall would be of the order of 70% of the critical depth for the same flow) or exactly in the node if rectilinear trajectories and hydrostatic pressure are assumed approximately. In the case of the existence of hydraulic jump in the link between manholes corresponding to a transition from supercritical flow to subcritical flow, the energy equation needs to be applied in both extremities of the link; that is, an additional boundary condition is thus required [44], and the exact localization and length of the hydraulic jump need to be estimated with some level of approximation.
A possible simplification for the second boundary condition (normally the downstream boundary condition) that is sometimes used independently of the regimen of flow is the condition of steady uniform flow, J = S0, at the downstream end of the reach (the sole downstream boundary condition implemented in the original implicit hydrodynamic model) [22]. That is, an approximation similar to the one that is assumed in the kinematic wave model [27,45]. These simplifications in the upstream hydrograph and in the downstream boundary condition make it possible to consider each link separately and sequentially in the downstream direction. It is then possible to articulate a design hydraulic model in steady uniform flow (that calculates, for each link, the sewer diameters and invert elevations using the peak flow of the input hydrograph in the upstream node of the link), with the simulation model in unsteady flow that calculates the input hydrographs that result from the simulation of the upstream links with sewer pipes already sized and installed. Another approximation mentioned in the literature in the case of free downstream discharge is the consideration of normal depth in the node for supercritical flows or critical depth in the node for subcritical flows [32]. For flow control structures, such as weirs or orifices, the second boundary condition is the discharge law of the hydraulic structure used.
According to the analysis described above, three main downstream boundary conditions for each link considered separately were modeled, implemented and tested: the steady uniform flow or normal depth, the critical condition or critical depth, and a given relative depth (h/D) above the critical depth, reaching typically a maximum of about 0.82 in open channel flow. Two additional boundary conditions, one related to the critical depth (hout = hc/1.4) and another one with a numerical condition somehow connected with the normal depth, both with some nuances, were also implemented and tested as mentioned in the results presented and discussed in Section 3.
2.1.5. Application of the Implemented Hydrodynamic Model
The developed hydrodynamic model was applied to several examples, including a dendritic network, which are presented in Section 3 of this paper, and the peak flows reached were compared to those obtained using a rational approach. New boundary conditions, as described in Section 2.1.4, were considered for a given link and their influence on the peak flows reached is analyzed in detail in Section 3. The results for a dendritic network with the links calculated separately and sequentially by the implemented hydrodynamic model are compared in Section 3.4 with those obtained for the network considered as a whole by the application of the US EPA SWMM version 5.1, which considers an explicit finite differences scheme for the numerical integration of the Saint-Venant equations, defined with variables Q and A [34,35,37].
2.2. Classic Rational Formulation, and Simplified Surface Runoff Hydrographs, Revisited
The classic rational formula, or American formula, initially introduced by Kuickling at the end of the nineteenth century, is currently presented or mentioned practically in all reference texts for urban drainage system projects practice, or in related scientific works, e.g., References [17,18,19,22,27,46,47]. Its essential aspects and some pertinent fundamental hydraulic and hydrologic elements which are important for the comparison developed are briefly summarized or presented here.
The formula is homogeneous and thus independent of the system of units. It assumes as basic concepts that: (i) the maximum direct flow, Qmax(Tr), in a small drainage basin with upstream area Ad for a given frequency which is equal to the inverse of the return period, Tr, occurs when the entire area of the drainage basin is contributing to the flow; and (ii) this flow is a fraction of the average rain for the same frequency (1/Tr) with maximum average intensity I (Tr, Tc), which is constant both in space, along Ad, and in time, during Tc, where Tc is the time of concentration of the basin. Tc is originally defined as the travel time between the point kinematically more distant from the basin and the section for which the maximum flow is being calculated. The formulation may be then expressed as:
C is the runoff coefficient, a non-dimensional coefficient that is the ratio between the maximum direct flow per unit area drained and the maximum average intensity of precipitation that makes such a maximum flow occur, with a duration of Tp = Tc. In other words, in the classic formulation, C is the quotient between the volume of surface runoff, Vs, and the total volume of the precipitation, Vp = I (Tr, Tc) × Tc × Ad, assuming implicitly a hydrograph triangular symmetric of base 2 Tc [46,48,49]. See Figure 2 (1,2a), in which the triangular hydrograph is adapted to include a very small or residual base flow, required for the numerical integration performed. The basic simplifications [19,20] are that the maximum flow occurs when the whole of the drainage basin is contributing to the flow; the assumption of linear relations between the maximum flow and both the area of the drainage basin and the maximum average intensity of precipitation; that the rainfall is constant during Tc and in the physical space of the basin; and that the maximum flow and the maximum rainfall have the same period of return (which is normally defined in urban hydrology as the average time interval in years in which a selected occurrence is equalized or exceeded). The smaller the basin, the more acceptable these approximations, and thus the method loses validity for basins of large dimensions.
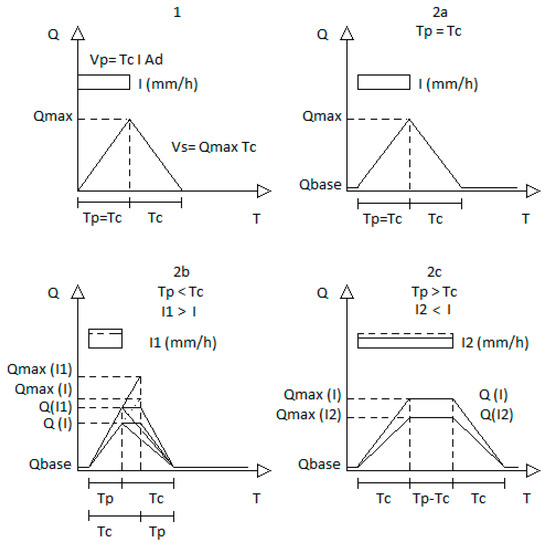
Figure 2.
Classic rational formulation and simplified entrance hydrographs in urban stormwater networks. (A constant minimum/residual volumetric flow rate, Qbase, is assumed in all entrance hydrographs).
If the duration of precipitation Tp is larger than Tc, then the hydrographs are typically assumed by simplification to be approximately trapezoidal, reaching the same maximum flow after Tc, during Tp–Tc, when the intensity of precipitation is maintained (Figure 2c). See, for example, References [27,47,50]. If the duration of precipitation is lower than Tc (see Figure 2b), then there is not a comparable general consensus about the best approximation to be considered for the direct hydrographs shape and for the peak flow that may be reached at Tp, which is lower than Qmax(Tr) for the same intensity of precipitation. It does not look consensual if the shape must be triangular, trapezoidal, or other, and if the peak flow reached must be a fraction of Qmax(Tr) given by Tp/Tc, a fraction given by 2Tp/(Tp + Tc), as proposed by Reference [48], or any other value.
Several authors, such as those in References [23,49,51,52], assumed a trapezoidal shape similar to that represented in Figure 2b (with rising and recession limbs of duration Tp) that may be eventually an acceptable approximation for large runoff coefficients and low capacity of storage in the basins, like in the drainage of roads, for example. However, the observed hydrographs, particularly in natural basins, for example, are known to have an isolated peak for rainfalls of short duration, and C is normally established for Tp ≥ Tc, it being well known that the runoff coefficient increases rapidly with Tp in the beginning of rainfalls. A possible approximation, at least as a minimum limit criterion for the peak flow and direct runoff volume, is to maintain the triangular shape; base of the hydrograph, Tp + Tc; the peak flow as a fraction Tp/Tc of Qmax(Tr); the beginning of the recession limb after Tp; and to reduce C (for Tp ≥ Tc) by (Tp + Tc)/2Tc. Other Engineering approximations maintaining the approximated triangular shape, runoff coefficient, and slope of the rising limb are eventually possible. One conceivable solution is to consider that the duration of the recession limb may be increased and approximated to 2Tc − Tp, instead of Tc. Another alternative is to assume that the duration of the rising limb may be increased and approximated to 2TpTc/(Tp + Tc), instead of Tp, but with the total duration of the hydrograph, Tp + Tc, unchanged, reaching in this case the same peak flow as the one proposed by Reference [48], but not at Tp.
In a typical calculation or design flow, the volumetric coefficient C is frequently estimated in function of the topology and physical characteristics of the basins, such as the type of urbanization, type of soil, percentage of permeable surfaces, and average slope of the basins. The return period in years for the rainfall of the project may vary generally between 1 or 2, and 50 or even 100, being, however, more frequent, under normal circumstances, the selection of return periods of 5 or 10 years. In urban areas, the time of concentration in a given sewer section is normally computed as the sum of two parcels: the inlet time at the upstream extremity of the network, which normally varies between 2 and 30 min, with the range of 5 to 15 min being more frequent; and the time of transportation in sewers until the section under consideration, which may be roughly calculated for a given average velocity in the sewer pipes or computed approximately for the maximum flow.
The rainfall intensity is typically computed using Intensity–Duration–Frequency (IDF) curves, which are previously obtained using empirical correlations for the region under consideration. Although different equation types may be possible, a generic equation sometimes considered for a certain frequency is of the type (Sherman equation):
Frequently, the intensity of precipitation I is expressed in millimeters per hour and the time of precipitation Tp, with Tp = Tc, in minutes [in the SI system I (m/s) = I (mm/h)/(3.6 × 106)] and a, b, and c are constants determined using a suitable adjustment method for the existing records for intense rainfall of short duration in the region. It should be noted that in some correlations, b = 0 or alternatively c = 1. The intensity of precipitation used for computing the maximum or peak flow, that is, the design flow in the rational method, decreases when the time of concentration of the basin in the section of the sewer pipe considered increases, that is, in the downstream direction of the network, given that IDF curves for a given Tr diminish with Tp. The design flow in each section is thus computed for successive lower intensities of precipitation in the downstream direction. For the same area drained in one reach that does not receive any additional lateral inflow along it, the flow then decreases in the downstream direction. Applying Equations (12) and (13) for any reach in these circumstances, for a given Tr and for Tp = Tc, the ratio between the maximum flow in any section of the sewer reach, , and the maximum flow in the upstream extremity of the reach, , with times of concentration and , respectively, may then be expressed by:
may be estimated by , where Lx is the distance between the two sections and U is the average velocity for the maximum computed flow. As a basic approximation just for this specific calculation, this maximum average velocity may be assumed as approximately constant along the considered length and equal to the one that occurs in the upstream extremity of the link [31]. This procedure is typically used, avoiding an iterative process for the time of transportation, rainfall intensity, peak flow, and average velocity, and is comparatively/theoretically on the safety side in the classic rational method. In fact, this approximation produces a faster response and a larger peak flow computed than the one calculated with the iterative method mentioned and is regarded here as an upper limit for the performed comparison. If Manning equation is used, Equation (14) then gives:
where can be calculated by . In all results presented herein, coefficient Ks was considered approximately constant in the transversal section. All basic models presented in this Section were coded in FORTRAN and implemented in micro-computers, additionally or in coordination with the complete hydrodynamic model previously described in Section 2.1.
3. Results and Discussion
3.1. Comparison between the Rational Approach and the Results of Numerical Simulation in a Single Link
The comparison of the peak flows reached in each section of a single sewer link with a length up to 600 m between the rational method using Equation (15) and the simulation in unsteady flow using the four-point implicit integration schema by finite differences, for a symmetric triangular hydrograph of base 2Tc1 and peak flow at full section (equivalent to h/D = 0.82) entering in the upstream manhole (Figure 2a), is presented in Figure 3a,b. The influence of eventual intermediate manholes inside the link in the simulated flows is ignored. IDF curves and their parameters used in this work were determined and proposed by Matos [19] for the Portuguese territory and were adopted by the current Portuguese regulation [21]. These curves are of the mathematical type expressed by Equation (13), with b = 0. The parameters were obtained by regression analysis, using the method of least squares, to a set of maximum average intensities determined statistically, with suitable distribution laws, for several return periods and precipitation duration, and a maximum of 120 years of observations, after 1860 [19]. According to the regulation, c is constant for the entire country and varies between 0.577 and 0.508 for return periods of 2 to 100 years. Parameters a and c used here as base criterion are 290.68 and 0.549, respectively, and correspond to curves for a return period of 10 years and most parts of the Portuguese territory. Two sewer slopes were considered, 0.3 and 0.5%, corresponding to the minimum construction slopes typically considered in ordinary projects in current engineering practice, and five commercial diameters were tested: 0.2, 0.4, 0.6, 1.0, and 2.0 m, respectively.
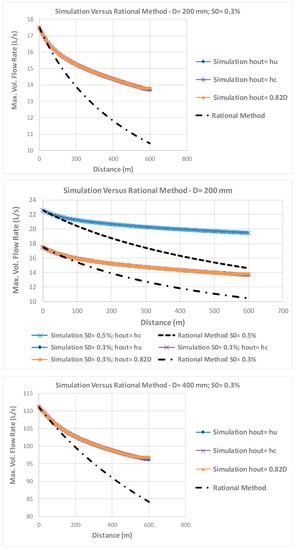
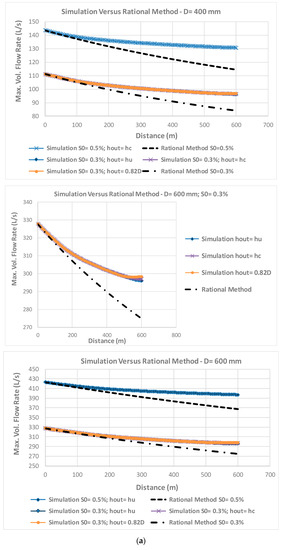
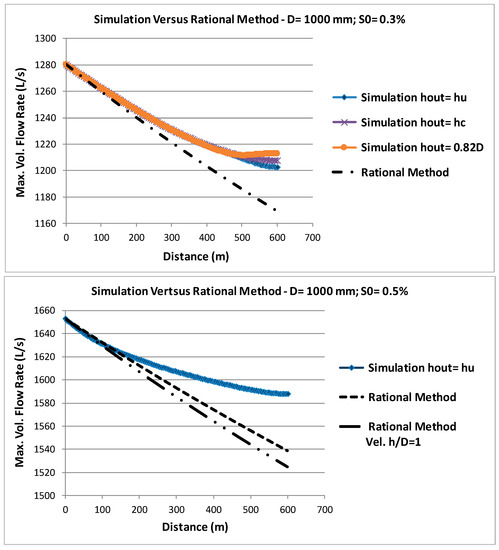
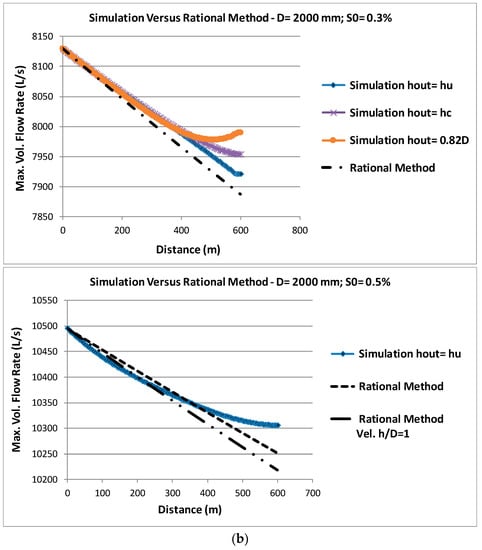
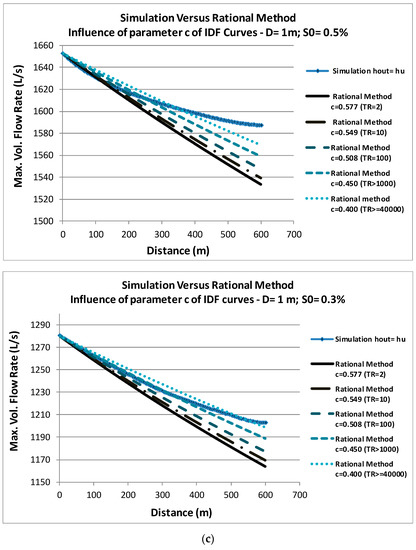
Figure 3.
Simulation in open channel gradually varied unsteady flow versus rational method along a pipe sewer for known input symmetric triangular hydrographs in the upstream extremity for sewer slopes of 0.3 and 0.5%. (a) Diameters of 200, 400, and 600 mm and different downstream boundary conditions. (b) Diameters of 1 and 2 m, different downstream boundary conditions, and two criteria of average velocity in the rational method. (c) Diameter of 1 m and different values of the exponent c of IDF curves in the rational method.
Table 1 presents the peak flows entering the sewer calculated at full section using the Manning equation with n = 1/75 m−1/3 s, for each slope and diameter tested, and the average velocities in the transversal sections for these flows, both fictitious and real, that is, h/D = 1 and h/D = 0.82 (assuming n constant). Table 1 also provides estimates of the magnitudes of the time of concentration at sewer entrances, Tc1, and of the drainage areas served, Ad, considering in this last case the abovementioned coefficients for the IDF curves (with Tr = 10 years) and average limiting values for C in Equation (12).

Table 1.
Volumetric flow rates at full section (peak flow of the symmetric triangular hydrograph of base 2Tc1), average velocities in the transversal section, and estimates of the magnitude of times of concentration and drainage basin areas served for several pipe diameters and sewer slopes of 0.3 and 0.5% with the Manning coefficient n = 1/75 m−1/3 s.
In all simulations in unsteady flow presented herein of the implicit model previously developed and implemented, Ks (assumed constant) was fixed as 75 m1/3 s−1 and the time step and weighting factor used were Δt = 1 s and ψ = 0.55, respectively. All terms of the dynamic equation were normally considered (complete dynamic model). However, in some circumstances of supercritical flows (larger diameters, steeper conduit slopes, and larger flows, e.g., diameters of 1 and 2 m with S0 = 0.5%), local and convective accelerations were neglected in the equation of dynamics (diffusive wave model) in order to meet the convergence requirements of the iterative process by successive approximations.
Three basic downstream flow frontier conditions were tested: normal depth or uniform flow; critical depth; and constant depth set at a maximum value of h = 0.82D in order to always guarantee the condition of open channel flow with some margin of safety (referenced in Figure 3 as hout = hu, hout = hc, and hout = 0.82D, respectively). The differences reached in the peak flows in each section simulated in unsteady flow for the different boundary conditions considered were very small for all diameters and slopes tested and only occur in a short downstream length of the sewer pipes. The reduction in the peak flow is larger for the uniform condition in the downstream extremity and smaller for the maximum depth in this extremity.
Two additional downstream boundary conditions not represented in Figure 3 were also modeled and tested: the critical depth, hc, occurring upstream at a distance of approximately four times hc from the downstream extremity (index/argument N) and/or = and a flow condition in the downstream extremity in each instant of time, , or alternatively , equaling numerically the corresponding flow condition in the previous section (index/argument N − 1) and in the previous instant of time, or , respectively. In the first case, the peak flows found were generally very close to those obtained with the critical condition occurring in the extremity of the link. In the second case, the peak flows were not very far from those obtained when the normal depth is assumed to be the downstream boundary condition. For all boundary conditions tested, the very small differences that were observed between them decrease rapidly for upstream and grow with the diameter increase and with the decrease of the pipe slope. Figure 3a,b shows and highlights such small differences that were found for the tested minimum slope (for S0 = 0.5% they are even minor). The number of points N used in the simulations leading to Figure 3a–c was 121, corresponding to a constant space step Δx = 5 m (600/(N − 1)).
For all situations tested, the peak flows reached in each section considering the rational method are clearly all below the peak flows reached with the simulation for comparable conditions. In other words, the reduction in the peak flow using the conventional rational method is larger than the effects of storing, propagation, and attenuation obtained in sewers with the simulation, and the rational method underestimates the peak flows. The average velocity considered along all sewers for calculating the time of concentration was the maximum in the upstream extremity in real conditions (h/D = 0.82). The comparison with the velocity for the full section (at h/D = 1, the average velocity is slightly lower), which decreases the time of concentration and consequently decreases the peak flows reached along the sewer even more, is shown in Figure 3b for S0 = 0.5% and the larger diameters of 1 and 2 m. In both cases, they were considered constant along the pipe length, which is on the safe side, otherwise the peak flows obtained with the rational method would decrease even more.
All these conclusions were obtained using Portuguese IDF curves of a typical return period of 10 years and were confirmed to remain valid for the whole of the territory for return periods between 2 and 100 years, that is, with c varying between 0.577 and 0.508, respectively, according to the current Portuguese regulation. The decrease in the value of c increases the peak flows reached along the sewers slightly; however, these rational peak flows are always considerably below the maximum peak flows that are simulated in unsteady flow, for the slopes and diameters tested.
To analyze the influence of the exponent c of the IDF curves on the increase of the peak flow along the sewer with the rational method, limiting values of 0.450 and 0.400 were tested for a sewer diameter of 1 m and minimum slopes of 0.5 and 0.3%. In order to realize the magnitude of these values of c for the Portuguese territory, an extrapolation using a logarithmic regression was performed for the return periods established in Reference [21], and the estimation gave return periods of the order of more than 1000 years and about 40,000 years, or more, respectively. The comparison of the different peak flows reached is presented in Figure 3c. This figure shows that, with the exception of the extreme values of c = 0.400 and S0 = 0.3%, the simulation curve (with the normal depth as the downstream boundary condition) is always clearly above the curves of maximum flows obtained by the rational method.
3.2. Comparison between the Rational Approach and the Results of Numerical Simulation in a Branched Network
For comparison between the peak flows obtained in the simulation and those calculated with the rational method, a dendritic network resulting from the three-dimensional optimization of a formulated urban drainage system was selected, tested, and presented in the first author’s doctoral dissertation, completed in 1996 [22]. Starting from the same simplified geometry, represented schematically in Figure 4, and the remaining data, an extensive and thorough analysis has now been developed and is presented in this paper. The figure nodes symbolize fixed position manholes that define the links of the separate stormwater networks. Influences on the simulated flows of aligned intermediate manholes (not represented) that are selected in the optimization and that do not receive lateral inflow are ignored. Table 2 presents the data related to sewers, namely the length, diameter, and slope; the information related to the sub-catchment areas (partial drainage basins) in each node, namely the time of concentration estimated for each surface basin, and useful areas, C × Ad; the entrance surface hydrographs in each node; the base flow of each entrance surface hydrograph considered in the simulations; and the maximum flow and the maximum velocity obtained according to the rational method in each upstream node of the link, calculated for the time of concentration reached in the respective section. The entrance hydrographs are assumed by simplification to be triangular, when Tp ≤ Tc (Figure 2a,b), or trapezoidal, when Tp > Tc (Figure 2c), for different tested precipitation.
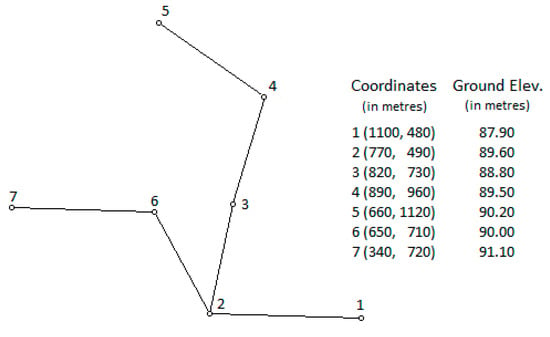
Figure 4.
Simplified plant layout of the tested dendritic network.

Table 2.
Sewers and partial drainage basins data, maximum volumetric flow rates, and base flows of the entrance hydrographs; and rational method maximum volumetric flow rates and maximum average velocities for the simplified dendritic network analyzed.
Durations of 7.5, 9.0, 10.0, 12.5, and 20.4 min, respectively. It should be noted that 20.4 min is the time of concentration in the downstream extremity of the network using the rational method. For the purpose of the comparison performed, when Tp < Tc, the inlet peak flow was assumed to be a fraction Tp/Tc of the maximum surface flow for the same intensity, reached at Tp, and with a hydrograph duration given by Tp + Tc (inferior limit condition for the peak flow and for the total volume of direct runoff).
The separate stormwater network was designed using the conventional rational method, the Manning equation, a coefficient Ks = 75 m1/3 s−1 that was assumed to be constant with flow depth, the pipes aligned through the internal top crown, and a maximum relative water depth of 0.800 (which allows an extra vacant capacity until the maximum capacity reached about h/D = 0.94). The pluvial pipes are concrete. The IDF curves used were for Portuguese territory and had a return period of 10 years [Equation (13), with a = 290.68, b = 0, and c = 0.549].
The comparison between the maximum flows obtained in each section of the network for the different precipitation times tested and the peak flows computed with the classic rational method is represented in Figure 5 and Figure 6a. Figure 6a represents the complete hydrographs simulated in the upstream and downstream sections of the downstream link of the network. The simulation considers each link separately and sequentially and considers the normal depth for each flow rate reached in the extremity as the downstream boundary condition of the link. Along each link of the network in the rational method, similarly to the previous example of a single link, to compute the concentration time in each section, the real velocity at the upstream extremity of the link is considered to be constant (a practice frequently considered in a design situation). The number of points, N, in each link was fixed as 101 (100 space intervals) and due to the convergence requirements in links 7-6 and 2-1 the flow computation was approximated by a diffusive wave model.
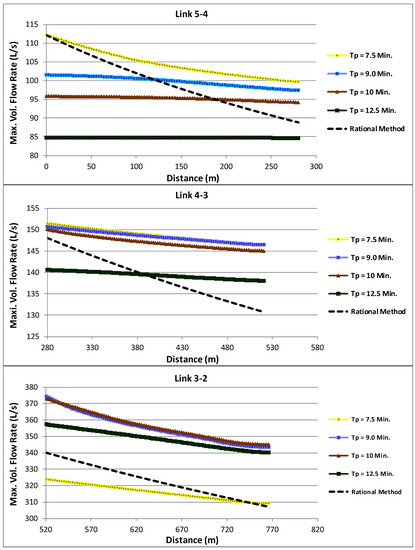
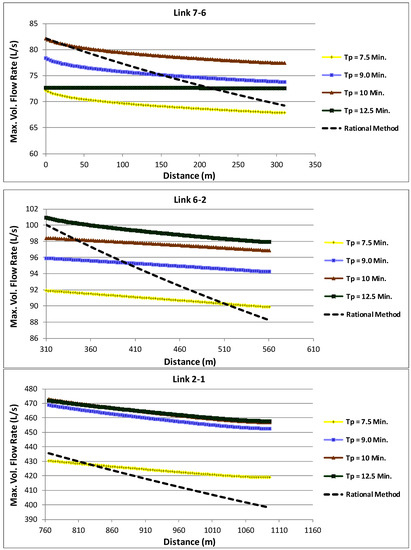
Figure 5.
Comparison of simulation in open channel gradually varied unsteady flow for several times of precipitation with the rational method along a dendritic network.
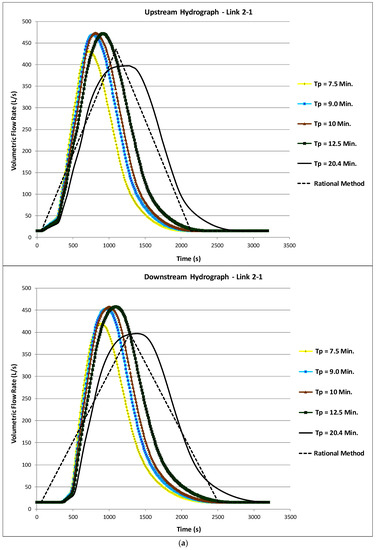
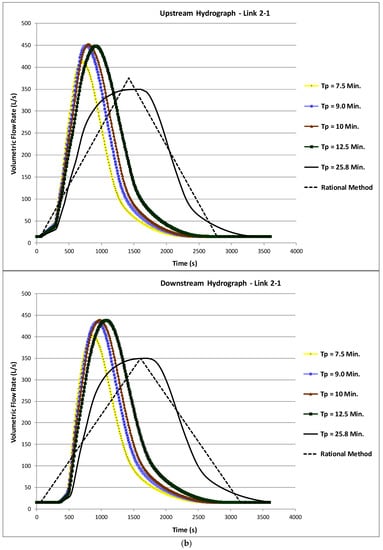
Figure 6.
Upstream and downstream hydrographs in the network downstream link simulated along a dendritic network for several times of precipitation. (a) Base criteria. (b) With a Tc increase in one branch.
The peak flow simulated in unsteady flow in the downstream hydrograph shown in Figure 6a, for Tp = Tc = 20.4 min, is practically equal to the peak flow of the rational method in this section: the sum of the upstream inflows in the column with Tp = 20.4 of Table 2, which gives 398 L/s. Thus, the effects of propagation, attenuation, and cushioning for this precipitation are practically nonexistent, because Tc of each input sub-basin is much less than Tp = 20.4 min, giving entrance trapezoidal hydrographs with a long plateau with corresponding Qmax occurring for a long time (see Figure 2c). Then, if the previously mentioned assumptions of the rational method were valid, particularly the premise that the maximum flow in a given section occurs precisely for Tp = Tc in that section, or, in other words, when the whole of the drainage basin upstream of the section is contributing to forming the flow, the method seems to be an excellent approximation when the time of precipitation is much longer than the time of concentration/entrance of the individual surface sub-basins, as occurred in the downstream section of the network presented here. However, for precipitations of lower duration than Tc of the whole of the basin upstream, and thus more intense, the response of the drainage system upstream is faster and the maximum flows reached in a given section can be clearly higher. Thus, the maximum flow can occur when only part of the upstream basin is draining for the respective section, producing larger peak flows than those computed with the classic formulation, as is extensively shown in Figure 5.
In this example, the two separated sewer branches upstream of node 2, which contain nodes 3, 4, and 5 and nodes 6 and 7, respectively, even with very different geometric and hydraulic characteristics, have practically equal times of concentration at the entrance of node 2: 17.3 and 17.1 minutes, respectively (see Figure 4 and Table 1). To increase the hydraulic arborescent component of the network and analyze its effect on the peak flows reached in link 2-1, the time of concentration of the catchment basin draining to the node of extremity 5 was increased from 7.5 to 12.5 min, maintaining all the geometry of the remaining network and all the remaining data. The times of concentration with the rational method at node 2 entrances are now 22.65 and 17.1 min, respectively, and in the extremities of link 2-1 they change from 17.3 (upstream) and 20.4 min (downstream) to 22.65 (upstream) and 25.8 (downstream) minutes, respectively. The surface hydrographs entering at node 5 change accordingly and now have maximum flows of 67.3, 73.1, 76.6, and 84.75 for precipitation times of 7.5, 9.0, 10.0, and 12.5 min respectively.
Table 2 includes the new peak flows and maximum velocities at the upstream extremities of each node computed with the rational method and the maximum flows in each node of the entrance trapezoidal hydrographs for a precipitation whose duration is equal to the new time of concentration in the downstream extremity of the network (25.8 min). The hydrographs of Figure 6b, when compared to the hydrographs of Figure 6a, show that the differences and the lack of safety with the rational method increased when the compactness of the network decreased.
Any other input surface hydrographs in the nodes can be used as approximation for representing the surface runoff of the urban catchments. It looks somehow obvious that the results and conclusions obtained would be generally analogous with respect to the peak flows reached. Nevertheless, the entrance surface hydrographs that are regarded in this research as simple engineering approximations, just for the comparisons performed, can be eventually measured or adapted to field measurements and laboratorial experiments in further studies. Such studies may eventually include the transport of pollutants and its direct implications on the environment, particularly at the levels local or regional.
3.3. Some Practical Consequences
The parameters or variables used in the rational method when estimating peak flows, particularly in the design of new systems, namely Tc, Tr, the IDF curves, the estimation of I (Tr, Tc), and the runoff coefficient C, should be selected generally in such a way as to allow the increase of conventional predictions. For example, selection of the larger values of C or of higher average velocities in the sewers and faster responses in the drainage basins that decrease Tc conduce increases in I (Tc, Tr) and in the peak flow estimates. Additionally, the eventual increase of impervious surfaces with the increased urbanization of the basins, if no measures are predicted, and the possible increase of the intensity of precipitation and extreme conditions due to global warming and climate change must be taken into consideration when projecting new systems. Controlled flow in channels at surface, green infrastructures, bioretention systems, rainwater harvesting systems, infiltration or detention ponds, and other structures of flow control are gaining increasing popularity.
Due to the swift increase of the maximum flow rates reached when the urban watershed area increases, with the investment costs significantly increased to build the required huge buried infrastructures, the area of the urban basins served by the buried conduits and the extension of the stormwater networks should be as small as possible. This may encourage the appeal to approaches of rational type. Natural depressions, small watercourses or streams, and artificial channels at the urban surface should be used in its maximum bulk and rebuilt or remodeled in order to increase its capacity as much as possible and convey the stormwater flows.
It is very likely that some or even many urban drainage networks have been planned or typically designed for peak flows lower than those that are effectively reached for the same return period of the project rainfall. It is then very important to develop and implement urbanization rules and suitable management practices that make it possible to reduce, at the level of the surface urban basins, the peak flows in the buried pipes of the stormwater networks by cushioning the peak waves at the surface under suitable control conditions, avoiding urban flooding and its potential damages along with both economic and environmental negative impacts.
3.4. Maximum Design Flows and Simulation in Unsteady Flow
An urban drainage system simulation model in unsteady flow requires a previously known geometry of the network in terms of sewer diameters, invert elevations, sewer slopes, and boundary conditions. However, a network cannot be designed without previously knowing the maximum flows that result from the waves’ progression along the network for the project hydrographs or precipitation intensities of the selected rainfall frequency. A possible approximation of kinematic type for a simple design in open channel flow conditions may be given in two interlinked steps:
- (i)
- Calculate or estimate the time of concentration, Tc, which is the sum of the entrance time and the sewer travel time that can be estimated in steady uniform flow for a full or partially filled section, for example, and the intensity of precipitation, I, for Tp = Tc, using IDF curves. Determine the inlet surface hydrographs in each upstream node of the section or node under consideration. If the section or node is not an upstream extremity, calculate the input hydrograph resulting from the simulation in unsteady flow of all upstream links. Add the surface hydrograph of the node and identify the maximum flow reached;
- (ii)
- With the maximum design flow obtained, determine, in steady uniform flow conditions, the diameter, the invert elevations, and the slope of the downstream sewer link. Move to the next node of the sequential process and repeat steps (i) and (ii) successively until the whole of the network has been sized and routed.
In the case of an optimization design problem of a network governed by gravity, the process is performed for each feasible solution in the link, given that different sewer diameters and sewer slopes produce different Tc and different hydrographs (one for each feasible solution) [53].
To evaluate and validate the accuracy of the basic procedure described above, it becomes necessary to analyze the differences between them to consider each link separately and sequentially from upstream to downstream and the real performance or behaviour as a whole of the network already designed. It is generally assumed that the differences are of little practical relevance [22,45], but little information and real data seems to have been normally investigated on this subject.
The hydrographs obtained in the nodes and in the downstream extremities of the links; the peak flows reached in the nodes for the dendritic network described and simulated in Section 3, with known simplified entrance surface hydrographs, using the implemented hydrodynamic model, with each link calculated separately and sequentially; and the US EPA SWMM model, version 5.1, applied for the network as a whole for the same entrance hydrographs, are represented and compared in Figure 7 and Table 3. The base criteria and data of sewers, partial drainage basins, and entrance hydrographs presented in Table 2 were maintained, and two precipitations of duration of 7.5 and 12.5 min were considered in the comparison. Two network geometries that differ only in the alignment of conduits were considered in the SWMM simulations: in SWMM–G1, conduits are aligned by the internal crown (the most frequent design criterion used); and in the second geometry, SWMM–G2, the alignment is performed through the sewer invert elevations. Both profiles, with the lengths, sewer slopes, and diameters of Table 2, begin with invert elevations of 88.765 m and 89.77 m, respectively at the extremity nodes 5 and 7. A free discharge was assumed in the end node 1 at the downstream network extremity in all SWMM simulations.
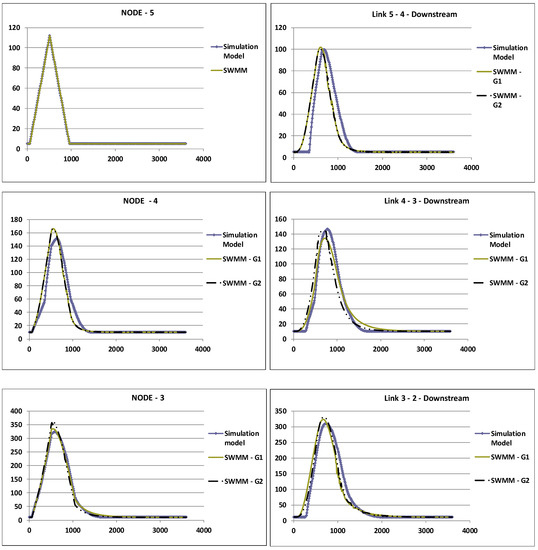
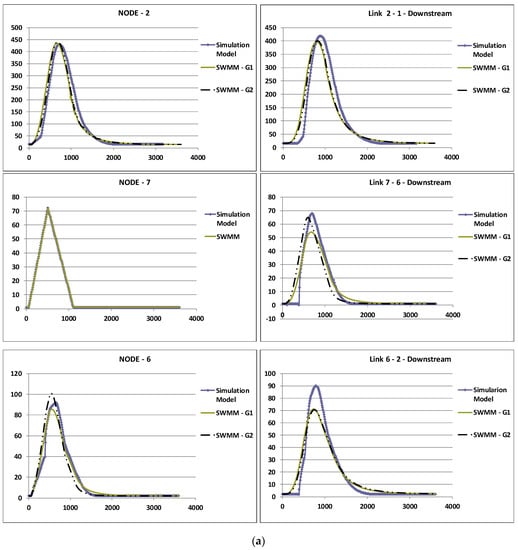
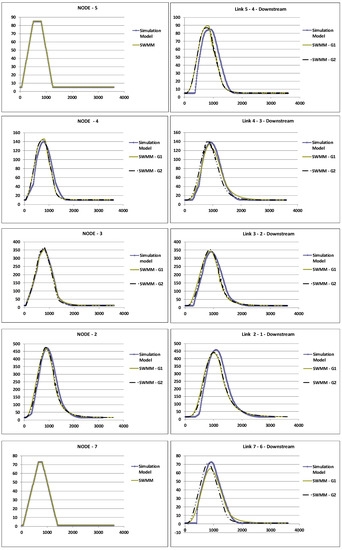
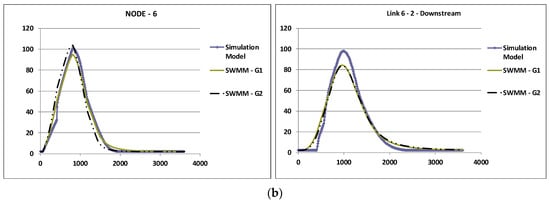
Figure 7.
Comparison of the flow hydrographs in the nodes and in the downstream end of the links for the dendritic network tested with respect to (i) the implicit simulation model considering each link separately and the normal depth as the link downstream boundary condition; (ii) the SWMM explicit model for the network as a whole considering a free discharge and the conduits aligned by the internal crown, SWMM–G1; and (iii) aligned by the invert elevation, SWMM–G2. (a) Precipitation of 7.5 min. (b) Precipitation of 12.5 min. Graph axes: horizontal—time (s); vertical—volumetric flow rate (L/s).

Table 3.
Comparison of the maximum volumetric flow rates obtained in each link for the test network and for periods of precipitation of 7.5 and 12.5 min, applying the simulation model considering each link separately and the normal depth as the link downstream boundary condition, and those obtained using SWMM for the network as a whole considering a free discharge and the conduits aligned by the internal crown, SWMM–G1, and by the invert elevation, SWMM–G2.
The simulation options selected for the running of the dynamic wave of SWMM were the defaults except for the time step of the routing, which was set as 1 s, the normal flow criteria for supercritical flows, which was based only on the Froude number; the minimal node surface area in manholes, which was neglected; the number of trials in each time step, which was increased to 20; and the tolerance for the head convergence, which was decreased to 0.0005 m. See the manual for SWMM Version 5.1 [37].
The hydrographs in Figure 7a,b (which differ with regard to the time of precipitation) show both similar behaviors between the implicit simulation model and the explicit SWMM model for the network considered as a whole and that the maximum flows reached are in general relatively close (see also Table 3). The biggest differences found are reached in link 6-2 and seem to be mainly related to the SWMM results due to the fall that occurs at the confluence in junction 2. However, all differences reached are generally lower than 10%, and in the SWMM model, the reduction in the maximum flows is bigger when the sewers are aligned by the sewer crown than when they are aligned by the sewer invert (and the falls are minimized).
According to the results obtained in this example, the assumption considered is confirmed as an acceptable approximation. In fact, it does not appear to introduce significant differences from the real operational conditions in open channel flow that is and should be normally the considered flow condition in a design situation. Additionally, the hydraulic design of sewerage systems (pluvial sewers and sanitary sewers) is typically performed in order to not allow backwater through manholes, which is generally a criterion that is on the safe side.
4. Summary and Conclusions
Maximum design flows in stormwater networks that are designed in open channel flow using the classic rational method for a given frequency of the project rainfall should be generally increased and not decreased. For that purpose, the upper bound of the average velocity, resulting in a faster response, a lower time of concentration, and a higher intensity of precipitation must be considered, together with the use of the upper limit for the estimated value of C that is normally established in the technical literature.
The basic principles of the rational method are normally limited to small drainage basins. However, if the precipitation was constant in time and space of the drainage basins and the maximum flow occurred effectively for Tp = Tc, then the rational method would be an excellent approximation when the time of concentration of the section considered is significantly larger than the entrance time of the urban surface drainage sub-basins. Nevertheless, for rainfalls shorter and therefore more intense for the selected frequency, the peak flows obtained in any sewer section can be undoubtedly superior than those calculated with the classic approach, i.e., the maximum flow may arise when only a partial area of the upstream watershed is contributing to the volumetric flow rate observed in the corresponding sewer section.
This insufficiency observed is substantively amplified due to the existing and predictable increase of extreme rainfall events caused by global warming and climate change and due to the general increase of population and subsequent urbanization. The planning and management of new and existing urban drainage systems need to consider and implement extensively and urgently urbanization rules and appropriate flow control management practices on the urban surface watersheds, in order to decrease drastically the peak flows that reach the buried pipes conveying stormwater, avoiding the current and predictable flooding in the urban agglomerates with its associated destructions and impacts of social, economic and environmental systems.
Except for the continuity equation, other boundary conditions of sewer networks that are normally considered in unsteady flow simulation introduce limited differences in the maximum flows calculated and reached. Simulation models in unsteady flow and design models in steady uniform flow can be used together with success in the design of urban drainage networks.
Author Contributions
A.F.D. conceived and planned the research work, devised and implemented the investigation details, and wrote the paper; A.F.D. and J.A.d.C. conceived, implemented and applied the details of the numerical integration and of the general hydrodynamic model; J.A.d.C. worked on the formal analysis, validation, and revised the contents and format of the paper.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Moore, T.L.; Rodak, C.M.; Vogel, J.R. Urban stormwater characterization, control, and treatment. Water Environ. Res. 2017, 89, 1876–1927. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Smith, J.A.; Yang, L.; Baeck, M.L.; Chaney, M.; Veldhuis, M.-C.T.; Deng, H.; Liu, S. The complexities of urban flood response: Flood frequency analyses for the Charlotte metropolitan region. Water Resour. Res. 2017, 53, 7401–7425. [Google Scholar] [CrossRef]
- Guan, M.; Sillanpää, N.; Koivusalo, H. Modelling and assessment of hydrological changes in a developing urban catchment. Hydrol. Process. 2015, 29, 2880–2894. [Google Scholar] [CrossRef]
- Lyu, H.M.; Sun, W.J.; Shen, S.L.; Arulrajah, A. Flood risk assessment in metro systems of mega-cities using a GIS-based modeling approach. Sci. Total Environ. 2018, 626, 1012–1025. [Google Scholar] [CrossRef] [PubMed]
- Lyu, H.M.; Shen, S.L.; Zhou, A.; Yang, J. Perspectives for flood risk assessment and management for mega-city metro system. Tunnel. Undergr. Space Technol. 2019, 84, 31–44. [Google Scholar] [CrossRef]
- Stewart, R.D.; Lee, J.G.; Shuster, W.D.; Darner, R.A. Modelling hydrological response to a fully-monitored urban bioretention cell. Hydrol. Process. 2017, 31, 4626–4638. [Google Scholar] [CrossRef]
- Winston, R.J.; Dorsey, J.D.; Hunt, W.F. Quantifying volume reduction and peak flow mitigation for three bioretention cells in clay soils in northeast Ohio. Sci. Total Environ. 2016, 553, 83–95. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, Y. Stormwater capture efficiency of bioretention systems. Water Resources Management. 2014, 28, 149–168. [Google Scholar] [CrossRef]
- Hixon, L.F.; Dymond, R.L. Comparison of stormwater management strategies with an urban watershed model. J. Hydrol. Eng. 2015, 20, 04014091. [Google Scholar] [CrossRef]
- Campisano, A.; Modica, C. Rainwater harvesting as source control option to reduce roof runoff peaks to downstream drainage systems. J. Hydroinform. 2016, 18, 23–32. [Google Scholar] [CrossRef]
- Wella-Hewage, C.S.; Hewa, G.A.; Pezzaniti, D. Can water sensitive urban design systems help to preserve natural channel-forming flow regimes in an urbanised catchment? Water Sci. Technol. 2016, 73, 78–87. [Google Scholar] [CrossRef] [PubMed]
- Chenevey, B. Development and Its Impact on the Water Balance of an Urban Watershed. Master’s Thesis, University of Cincinnati, Cincinnati, OH, USA, 2013. [Google Scholar]
- Stovin, V.; Vesuviano, G.; Kasmin, H. The hydrological performance of a green roof test bed under UK climatic conditions. J. Hydrol. 2012, 414–415, 148–161. [Google Scholar] [CrossRef]
- Jefferson, A.J.; Bhaskar, A.S.; Hopkins, K.G.; Fanelli, R.; Avellaneda, P.M.; McMillan, S.K. Stormwater management network effectiveness and implications for urban watershed function: A critical review. Hydrol. Process. 2017, 31, 4056–4080. [Google Scholar] [CrossRef]
- Diogo, A.F.; Oliveira, M.C. A simplified approach for the computation of steady two-phase flow in inverted siphons. J. Environ. Manag. 2016, 166, 294–308. [Google Scholar] [CrossRef] [PubMed]
- Diogo, A.F.; Barros, L.T.; Santos, J.; Temido, J.S. An effective and comprehensive model for optimal rehabilitation of separate sanitary sewer systems. Sci. Total Environ. 2018, 612, 1042–1057. [Google Scholar] [CrossRef] [PubMed]
- ASCE; WPCF. Design and construction of sanitary and storm sewers. In ASCE—Manuals and Reports on Engineering Practice; No. 37; ASCE: Washington, DC, USA, 1969. [Google Scholar]
- ASCE; WEF. Design and construction of urban stormwater management systems. In ASCE—Manuals and Reports on Engineering Practice; No. 77; ASCE: Virginia, NV, USA, 1992. [Google Scholar]
- Matos, M.R. Métodos de Análise e de Cálculo de Caudais Pluviais em Sistemas de Drenagem Urbana. Tese para Obtenção do Grau de Especialista, LNEC, Lisboa. 1987. Available online: http://livraria.lnec.pt/eng/php/livro_ficha.php?cod_produc_tirag=5398956 (accessed on 10 April 2019).
- Ben-Zvi, A. Toward A New Rational Method. J. Hydraul. Eng. 1989, 115, 1241–1255. [Google Scholar] [CrossRef]
- MOPTC. Regulamento Geral dos Sistemas Públicos e Prediais de Distribuição de Água e de Drenagem de Águas Residuais. Decreto Regulamentar no. 23/95 de 23 de Agosto, Diário da República—I Série-B. 1995, pp. 5284–5319. Available online: https://dre.pt/application/file/a/431921 (accessed on 10 April 2019).
- Diogo, A.F. Optimização Tridimensional de Sistemas Urbanos de Drenagem. Ph.D. Thesis, Faculdade de Ciências e Tecnologia da Universidade de Coimbra, Coimbra, Portugal, 1996. [Google Scholar]
- Dhakal, N.; Fang, X.; Cleveland, T.; Thompson, D. Revisiting modified rational method. In Proceedings of the World Environmental and Water Resources Congress 2011: Bearing Knowledge for Sustainability, Palm Springs, CA, USA, 22–26 May 2011; pp. 751–762. [Google Scholar]
- NYC Environmental Protection (New York City Department of Environmental Protection) in Consultation with the New York City Department of Buildings. Guidelines for the Design and Construction of Stormwater Management Systems. 2012. Available online: http://www.nyc.gov/html/dep/pdf/green_infrastructure/stormwater_guidelines_2012_final.pdf (accessed on 25 November 2017).
- NC DEQ (North Carolina Department of Environmental Quality). Stormwater Design Manual—B. Stormwater Calculations; 2017. Available online: https://deq.nc.gov/sw-bmp-manual (accessed on 11 November 2017).
- Amein, M.; Chu, H.-L. Implicit numerical modeling of unsteady flows. J. Hydraul. Divis. 1975, 101, 717–731. [Google Scholar]
- Froise, S.; Burges, S.J. Least-cost design of urban-drainage networks. J. Water Resour. Plan. Manag. Divis. 1978, 104, 75–92. [Google Scholar]
- Sousa, E.R. Técnicas de simulação em sistemas de drenagem de águas pluviais. In Seminário 290; LNEC: Lisboa, Portugal, 1983; Volume 2, pp. 91–134. [Google Scholar]
- Almeida, A.B. Análise hidráulica de colectores de águas pluviais. In Seminário 290; LNEC: Lisboa, Portugal, 1983; Volume 2, pp. 27–89. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Diogo, A.F.; Sousa, E.R.; Graveto, V.M.; Santos, F.S. Modelação hidráulica em colectores de sistemas urbanos de drenagem. In VII Encontro Nacional de Saneamento Básico; DEC/FCTUC: Coimbra, Portugal, 1996; Volume 1, pp. 177–186. [Google Scholar]
- Ji, Z. General hydrodynamic model for sewer/channel network systems. J. Hydraul. Eng. 1998, 124, 307–315. [Google Scholar] [CrossRef]
- Carmo, J.S.A. Modelação em Hidráulica Fluvial e Ambiente, 2nd ed.; Imprensa da Universidade de Coimbra: Coimbra, Portugal, 2009. [Google Scholar]
- Rossman, L.A. Storm Water Management Model, Quality Assurance Report: Dynamic Wave Flow Routing; National Risk Management Research Laboratory, Office of Research and Development, U.S. Environmental Protection Agency (US EPA): Washington, DC, USA, 2006.
- Rossman, L.A. Storm Water Management Model User's Manual, Version 5.0; National Risk Management Research Laboratory, Office of Research and Development, U.S. Environmental Protection Agency (US EPA): Washington, DC, USA, 2010.
- Liu, H.; Wang, H.; Liu, S.; Hu, C.; Ding, Y.; Zhang, J. Lattice Boltzmann method for the Saint-Venant equations. J. Hydrol. 2015, 524, 411–416. [Google Scholar] [CrossRef]
- EPA (US Environmental Protection Agency). Storm Water Management Model User's Manual Version 5.1; EPA: Washington, DC, USA, 2015.
- Fread, D.L. Technique for implicit dynamic routing in rivers with tributaries. Water Resour. Res. 1973, 9, 918–926. [Google Scholar] [CrossRef]
- Ponce, V.M.; Simons, D.B.; Indlekofer, H. Convergence of four-point implicit water wave models. J. Hydraul. Divis. 1978, 104, 947–958. [Google Scholar]
- Quintela, A.C. Hidráulica, 8th ed.; Fundação Calouste Gulbenkian: Lisboa, Portugal, 2002. [Google Scholar]
- Sen, D.J.; Garg, N.K. Efficient algorithm for gradually varied flows in channel networks. J. Irrigation Drain. Eng. 2002, 128, 351–357. [Google Scholar] [CrossRef]
- Islam, A.; Raghuwanshi, N.S.; Singh, R.; Sen, D.J. Comparison of gradually varied flow computation algorithms for open–channel network. J. Irrigation Drain. Eng. 2005, 131, 457–465. [Google Scholar] [CrossRef]
- Zhu, D.; Chen, Y.; Wang, Z.; Liu, Z. Simple, robust, and efficient algorithm for gradually varied subcritical flow simulation in general channel networks. J. Hydraul. Eng. 2011, 137, 766–774. [Google Scholar] [CrossRef]
- Djordjević, S.; Prodanović, D.; Walters, G.A. Simulation of transcritical flow in pipe/channel networks. J. Hydraul. Eng. 2004, 130, 1167–1178. [Google Scholar] [CrossRef]
- Cembrowicz, R.G.; Krauter, G.E. Design of cost optimal sewer networks. In Proceedings of the Fourth International Conference on Urban Storm Drainage, Lausanne, Switzerland, 31 August–4 September 1987; pp. 367–372. [Google Scholar]
- Costa, P.C. O método racional generalizado. Princípios conceptuais, domínio de aplicação e resultados. In Seminário 290; LNEC: Lisboa, Portugal, 1983; Volume 1, pp. 129–160. [Google Scholar]
- Guo, J.C.Y. Rational Hydrograph Method for Small Urban Watersheds. J. Hydrol. Eng. 2001, 6, 352–356. [Google Scholar] [CrossRef]
- Chien, J.S.; Saigal, K.K. Urban Runoff by Linearized Subhydrograph Method. J. Hydraul. Divis. 1974, 100, 1141–1157. [Google Scholar]
- Bennis, S.; Crobeddu, E. New Runoff Simulation Model for Small Urban Catchments. J. Hydrol. Eng. 2007, 12, 540–544. [Google Scholar] [CrossRef]
- Guo, J.C.Y. Storm Hydrographs from Small Urban Catchments. IWRA Int. J. 2000, 25, 481–487. [Google Scholar]
- Walesh, S.G. Discussion of Urban Runoff by Linearized Subhydrograph Method by Chien and Saigal 1974. J. Hydraul. Divis. 1975, 101, 1447–1449. [Google Scholar]
- Dhakal, N.; Fang, X.; Thompson, D.B.; Cleveland, T.G. Modified rational unit hydrograph method and applications. Proc. Inst. Civ. Eng. Water Manag. 2014, 167, 381–393. [Google Scholar] [CrossRef]
- Diogo, A.F.; Walters, G.A.; Sousa, E.R.; Graveto, V.M. Three-Dimensional Optimization of Urban Drainage Systems. Comput.-Aided Civ. Infrastruct. Eng. 2000, 15, 409–425. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).