Abstract
The optimized design of water quality monitoring networks can not only minimize the pollution detection time and maximize the detection probability for river systems but also reduce redundant monitoring locations. In addition, it can save investments and costs for building and operating monitoring systems as well as satisfy management requirements. This paper aims to use the beneficial features of multi-objective discrete particle swarm optimization (MODPSO) to optimize the design of water quality monitoring networks. Four optimization objectives: minimum pollution detection time, maximum pollution detection probability, maximum centrality of monitoring locations and reservation of particular monitoring locations, are proposed. To guide the convergence process and keep reserved monitoring locations in the Pareto frontier, we use a binary matrix to denote reserved monitoring locations and develop a new particle initialization procedure as well as discrete functions for updating particle’s velocity and position. The storm water management model (SWMM) is used to model a hypothetical river network which was studied in the literature for comparative analysis of our work. We define three pollution detection thresholds and simulate pollution events respectively to obtain all the pollution detection time for all the potential monitoring locations when a pollution event occurs randomly at any potential monitoring locations. Compared to the results of an enumeration search method, we confirm that our algorithm could obtain the Pareto frontier of optimized monitoring network design, and the reserved monitoring locations are included to satisfy the management requirements. This paper makes fundamental advancements of MODPSO and enables it to optimize the design of water quality monitoring networks with reserved monitoring locations.
1. Introduction
River systems play a crucial role in the sustainable development of a community. Water quality is influenced simultaneously by both anthropogenic and natural activities. However, overexploitation and increasing pollution of this vital resource are threatening our ecosystems and even the life of future generations. In the most recent 50 years, with the rapid development of world economy, on the one hand, we need more clean water, and on the other hand, industry and living activities create more and more pollutants to freshwater sources. Wastewater treatment plants can only treat part of pollution water [1,2]. It is estimated that 280 billion Yuan is lost each year in China for freshwater pollution events [3]. Water quality monitoring has become one of the routine efforts for environmental protection all over the world. There are many considerations when we design a water quality monitoring network, such as monitoring locations, water quality parameters, monitoring frequency and identification of monitoring objectives. Monitoring water quality remains a very complicated process [4]. The problem of planning and optimizing water quality monitoring programs (WQMPS) has been addressed since the 1940s, and many papers have been published on this subject [5,6,7,8,9].
The use of computer science and communication technology has significantly grown in recent years. More water quality parameters can be remotely detected and transmitted by automatic monitoring stations resulting in a much higher monitoring frequency, with more monitoring data and better monitoring efficiency. However, the costs of building and operating an automatic monitoring station are very high. The successful water quality monitoring relies on the availability of a low cost and highly efficient monitoring network to collect appropriate and reliable data. Optimization design of water quality monitoring networks can not only help us build a cost-effective and logistically adaptable monitoring network, but also increase the pollution detection probability, decrease the pollution detection time and save the construction and operating costs, which is essential for the sustainable development of water quality monitoring networks. Different monitoring objectives generally determine the level of detail, the cost, and the necessary approach used to design the monitoring network [10]. So, the purpose of the water quality monitoring network should be identified before determining the optimization objectives of a monitoring network.
Many researchers have studied the optimal design of water quality monitoring networks for river systems. Quyang used a single objective genetic algorithm (GA) to design an optimal monitoring network based on a geometric analysis and applied it to a hypothetical river system [11]. However, only the spatial distribution of the monitoring stations was considered as an optimization objective in this algorithm. Practical river systems are complex and other factors such as flow rate, river depth and width should also be considered while designing the monitoring network. Telci argued that the design of an optimal water quality monitoring network should mainly focus on two objectives of minimum pollution detection time and maximum detection reliability [12]. The optimal placement of monitoring devices was calculated using the GA under relatively simple discrete uniform distributions on spill events. They also applied this methodology to the Altamaha river basin to identify the optimal monitoring locations in the river system [13]. However, the Pareto frontier (seeing Section 3.2) of the optimization results was not mentioned in this paper resulting in difficulties for evaluating all the optimization results. Park used a stochastic discrete optimization via a simulation algorithm and a penalty function with memory to obtain the optimal locations of a finite number of monitoring positions [14]. The algorithm can minimize the expected detection time of a contaminant spill event and guarantee a higher detection probability. However, the penalty value significantly increases the detection time of a deployment solution when the pollution detection probability is less than 100%. Chang selected seven criteria to evaluate the suitability of the water quality monitoring design and used fuzzy theory to improve the objectivity in the data classification and ranking [7]. However, it is difficult for researchers to collect detailed information and data (e.g., percentage of farmland and built-up area, and green cover ratio) to satisfy all the criteria of the algorithm.
To the best of our knowledge, most of the literature tried to find the globally optimal solution for water quality monitoring networks without the consideration of reserving particular monitoring locations before optimizing. Some monitoring locations are definitely determined in advance whether they are included in the optimal deployment solutions or not. For example, a stream junction at an intersection of two cities is crucial for special management requirements. We should deploy monitoring devices at theses stream junctions so that the government can evaluate the pollutant discharging between two cities and take economic sanction measures. However, current multi-objective evolution algorithms cannot support this particular management requirement. There is no guarantee that these particular monitoring locations can be included in the final optimal deployment solutions. Besides, we argue that the priorities of monitoring locations should also be considered in the optimal design of water quality monitoring networks.
In this paper, we revise the multi-objective discrete darticle swarm optimization (MODPSO) algorithm and develop a novel optimization algorithm for the optimized design of water quality monitoring network. Our algorithm can include all the reserved monitoring locations into the final optimized monitoring network while still having maximum pollution detection probability, minimum pollution detection time and maximum closeness centrality.
2. Related Technologies
2.1. SWMM
Hydrodynamic simulation analysis based on dynamic models is a scientific, objective and supportive methodology for related strategy planning. The storm water management model (SWMM) is a dynamic rainfall-runoff simulation model used for single event or long-term (continuous) simulation of runoff quantity and quality from primarily urban areas. It can track the quantity and quality of runoff generated within each sub-catchment, and the flow rate, flow depth and quality of water in each pipe or channel during a simulation period [15]. The latest version is SWMM 5, which is extended to the simulation of low impact development utilities [16]. The SWMM is widely used for dynamically simulating storm water runoff and drainage systems in urban areas. Here we use SWMM to simulate the hydraulic model, pollution events and pollutants transporting along the river system.
2.2. Pareto Frontier
The main difficulty in considering multi-objective optimization is that there is no accepted definition of optimum in this case, and therefore it is difficult to compare one solution with another one [17]. In addition, the objectives to be optimized are generally in conflict with each other. For example, assume we distribute some apples to children A and B. Each child wants all the apples. If we give all the apples to child A, then it is a best solution to child A but a worst solution to child B. We aim to find good trade-off solutions among the objectives. We define a multi-objective optimization problem as follows [18].
Definition 1 (Multi-objective optimization problem).
Let F be a set of m objective functions {}, , the MOP is defined as follows.
subject to
where x is a vector of n decision variables, y represents an m-dimensional objective vector, and are the lower and upper bound of . Constraint (3) represents bounds with variables that help define the decision variable space or decision space . Objective functions constitute a multi-dimensional space called the objective space, termed as . Vector g is composed of k constraint functions which shape the feasible region. Solutions that do not satisfy constraint functions and/or variable bounds are called infeasible solutions, while solutions that meet all constraints in (2) and (3) are feasible solutions. The set of all feasible solutions is known as the feasible region. The domain of each is . For each solution x∈ there exists a point y in the objective space. Thus, defines the feasible objective space :
Many multi-objective optimization algorithms use Pareto dominance in order to compare solutions. In a minimization context, the Pareto dominance relation over a set of objectives is defined as follows.
Definition 2 (Pareto dominance relation).
If , it is said that solution x dominates solution over , denoted by . If , it is said that solution is non-dominated regarding x over objective set , denoted by . In case that and , it is simply said that x dominates , denoted as .
Definition 3 (Pareto optimality).
A solution is said to be non-dominated considering objectives regarding a set , if and only if for which . If x is non-dominated regarding considering , it is called a Pareto optimal solution for the given subspace of objectives, while, if it is said that it is a Pareto optimal solution of the problem or simply a Pareto optimal solution.
Pareto optimal solutions form the so-called Pareto set, defined as follows.
Definition 4 (Pareto set).
For a given MOP with a set of objectives F, the Pareto set considering objectives is defined as:
The corresponding vectors of in the objective space defined by form the Pareto front, termed as . When , the sets and are called the Pareto set and the Pareto frontier of the problem respectively.
Definition 5 (Pareto frontier).
The corresponding objective vector set of the Pareto set is called the Pareto frontier.
According to the definition of Pareto frontier, we can know that Pareto frontier is a set of nondominated solutions, being chosen as optimal if no objective can be improved without sacrificing at least one other objective. The Pareto frontier is usually used to evaluate the performance of multi-objective algorithms and obtain the optimal solutions for particular optimization issues.
2.3. MOPSO Algorithm
Particle swarm optimization (PSO) is a heuristic search technique that simulates the movements of a flock of birds which aim to find food [19]. The relative simplicity of the PSO is a natural candidate to be extended for multi-objective optimization [20]. Consequently, lots of proposals of multi-objective particle swarm optimization (MOPSO) were proposed in the literature and it has become one of the popular evolution algorithms in recent years [21]. The Pareto frontier was used in MOPSO to handle multi-objective functions to improve the PSO algorithm to be able to deal with multi-objective optimization problems [20]. The algorithm uses a secondary repository of particles to guide their flight and a particular mutation operator to enrich exploratory capabilities. Compared to other multi-objective evolutionary algorithms known to date, MOPSO has a highly competitive performance and can be considered as a viable alternative to solve multi-objective optimization problems [22]. Literature research shows that it can cover the full Pareto frontier of all the potential solutions with low computational time. The velocities and positions of particles during the computing iteration are updated by the following equations:
where V denotes the particle’s velocity, w is an inertia weight constant, and are uniformly distributed random variables within range [0, 1], is the best position that the particle i has had, is the best position in all current particles, and and are positive constant coefficients for acceleration. The pseudocode of MOPSO is shown in Algorithm A1 in Appendix A.
The classical MOPSO is a robust algorithm to get globally optimal results for continuous definition domains. However, The MOPSO cannot be applied to discrete problems directly, which is a significant limitation because many optimization problems are set in a space featuring discrete variables [23]. Some attempts have been made to design multi-objective discrete particle swarm optimization (MODPSO) algorithms, and several methodologies have been proposed [24,25,26,27].
2.4. Closeness Centrality
In river network simulations, graph theory and network analysis are usually used to model river systems [28,29,30]. Centrality is one of the most important indicators in graph theory and widely used in social networks, urban networks and so on [31,32]. It can identify the importance of vertexes in a graph or network and summarize a node’s involvement in or contribution to the cohesiveness of the network [10]. We can use the centrality to denote the priority of each monitoring location.
There are several measures to denote the centrality such as degree, betweenness, closeness and eigenvector. Closeness is based on the length of the average shortest path between a node and all other nodes in the network. It is widely used to denote the centrality of a connected network. As we know that a river network is also a typical connected network. So, we use the closeness as an evaluation criterion to represent the centrality of each location to all the other potential monitoring locations. Equation (9) shows the definition of closeness for vertices x.
where is the distance between vertices x and y. N is the number of nodes in the network.
3. Methodology
3.1. Main Process of Our Algorithm
The main process of our algorithm is shown in Figure 1. Firstly, we create a hypothetical river network in SWMM. Secondly, pollution events with different pollution detection thresholds are simulated and pollution detection time for each potential monitoring location are calculated. Thirdly, we set several optimization objectives for water quality monitoring networks. Fourthly, we develop an optimized algorithm based on the MODPSO and the optimization objectives we proposed. Finally, we input the pollution detection time into our optimization algorithm to obtain optimized water quality monitoring networks.
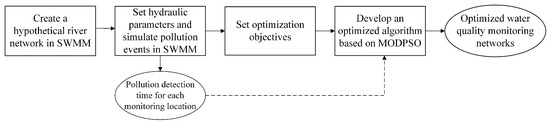
Figure 1.
Main process of our algorithm.
3.2. Hydrodynamic Simulations
3.2.1. Hypothetical River Network
To compare our study results with the achievements given by the literature, we use the same hypothetical river network introduced in [11,12,13] to simulate pollution events, which is as Figure 2 shows. It has eleven catchments numbered from A to K with six inlet locations of 1, 3, 5, 8, 10 and 11, five intermediate locations of 2, 4, 6, 7 and 9, as well as one outlet location of 12. To obtain steady water flows when a pollution event occurs, we simulate water flows with a constant flow rate of 283.168 L/s for each inlet location, which is the same as in Telci’s paper. As we know that pollution events can occur at any locations randomly. We assume that pollution events at inlet locations have a same pollutant concentration of 10 mg/L and last for one hour resulting in a total of 10.19 kg of pollutant spilling for each pollution event. The characteristics of the hypothetical river network are shown in Table 1, which is the same as Telci [12] used.
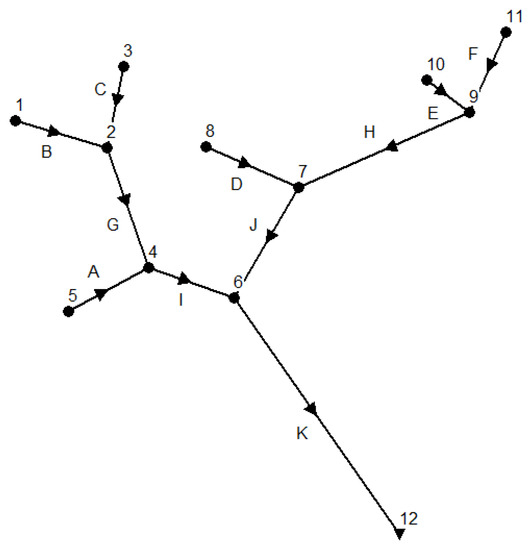
Figure 2.
Hypothetical river network.

Table 1.
Hydraulic characteristics of the river network.
3.2.2. SWMM Simulations
To confirm whether different pollution detection thresholds can affect the design of water quality monitoring networks or not, we set the pollution detection threshold to 0.01 mg/L, 1 mg/L and 2 mg/L respectively and run hydraulic simulations in the SWMM. Table 2, Table 3 and Table 4 show the simulation results of pollution detection time for each potential monitoring location. The `_’ in tables represents an infinite value, which means the pollution event cannot be detected at a monitoring location. For example, the first row in Table 2 demonstrates a scenario that a pollution event occurs at location 1 and can be detected at locations 1, 2, 4, 6 and 12. The pollution detection time for these locations is 0 (detected immediately), 27, 81, 118 and 198 min, respectively. However, the pollution event cannot be detected at locations 3, 5, 7, 8, 9, 10 or 11 because the polluted water flow cannot reach these locations.

Table 2.
Pollution detection time with a detection threshold of 0.01 mg/L.

Table 3.
Pollution detection time with a detection threshold of 1 mg/L.

Table 4.
Pollution detection time with a detection threshold of 2 mg/L.
We can see from Table 3 and Table 4 that when the pollution detection threshold is increased from to and separately, the pollution detection time for each potential monitoring location is also increased. It is because higher pollution concentration requires more time in pollution events. When we set the pollution threshold to (Table 4), some pollution events (e.g., pollution events at locations 6 and 12) cannot be detected. It is because diluted by the upstream water flows, the pollution concentrations at some downstream locations are smaller than the pollution detection threshold. For example, due to the dilution of upstream water flows, when a pollution event occurs at location 6 (or 12), the maximum pollution concentration at location 6 (or 12) is only . It is smaller than the pollution detection threshold of and cannot be detected at any monitoring location.
3.3. Optimization Objectives
Currently, most of the literature only considered optimization objectives such as maximum pollution detection probability and minimum pollution detection time in the design of water quality monitoring networks and tried to obtain globally optimal solutions [11,12,13,33,34]. However, we argue that reserving some particular monitoring locations in advance to satisfy management requirements is also essential and should be achieved in the optimization algorithm. Furthermore, we use the closeness centrality in graph theory to denote the priority of each monitoring location. Four optimization objectives are simultaneously considered in our algorithm.
3.3.1. Minimum Pollution Detection Time
Assume that n monitoring devices will be deployed out of m potential monitoring locations () in a river system. It means that n particular monitoring locations will be selected to deploy monitoring devices from m potential monitoring locations. The total number of potential deployment solutions T is:
where m is the number of potential monitoring locations, n is the number of available monitoring devices. For a given optimized deployment solution , where is the index of a selected monitoring location, and . Let be the pollution detection time at monitoring location i when a pollution event occurs at location j. The minimum pollution detection time for location j is:
where . For a definite optimized deployment solution S, the set of minimum pollution detection time for all potential locations is . Let be the mean value of all minimum pollution detection time at all m potential monitoring locations for a given solution , is:
Let be the minimum mean pollution detection time for all potential deployment solutions, we can get the following equation:
where T is the total number of deployment solutions shown in Equation (10). The first optimization objective is to find a deployment solution which has the minimum mean pollution detection time as Equation (13) shows.
3.3.2. Maximum Pollution Detection Probability
Let be the ratio of successful pollution detection scenarios to all potential detection scenarios for a given deployment solution . The pollution detection probability is:
where , m is the number of potential monitoring locations, if the pollution event at location i can be detected by the deployment solution , or if the pollution event cannot be detected. Let be the maximum pollution detection probability of all the potential deployment solutions:
where T is the total number of potential deployment solutions. The second optimization objective is to find a deployment solution which has a maximum pollution detection probability as Equation (15) shows.
3.3.3. Maximum Closeness Centrality of Monitoring Locations
Let be the length from potential monitoring location i to potential monitoring location j and m be the total number of potential monitoring locations. We can get the closeness centrality for a potential monitoring location i according to the closeness definition in Equation (9).
The total of closeness centrality for a potential deployment solution is as follows.
where n is the number of monitoring devices deployed in a river network, is a monitoring location in a deployment solution .
The third optimization objective is to maximize the total closeness centrality of optimized deployment solutions shown in Equation (18).
where T is the total number of potential deployment solutions.
3.3.4. Reservation of Monitoring Locations
For the sake of management requirements, some particular monitoring locations should be determined beforehand whether they are in the optimal deployment solution or not. On the contrary, some monitoring locations should be excluded in advance because of the difficulty for deployment, little worth of monitoring and so on. It is easy to exclude these particular monitoring locations from the set of potential monitoring locations beforehand. However, current optimization algorithms cannot support the reservation of monitoring locations. One of the most important criteria which is used to evaluate an optimization algorithm in the literature is whether the algorithm can obtain globally or approximate globally optimal solutions or not. There is no guarantee to include all the reserved monitoring locations in final optimization solutions. Therefore, a special approach should be developed to satisfy the requirement of including the reserved monitoring locations in the final optimization results.
Let I be the set of reserved monitoring locations and E be the set of excluded monitoring locations. Our fourth optimization objective is to include all the reserved monitoring locations in set I in the final optimized deployment solutions while excluding all the monitoring locations in set E.
where is the set of final optimal monitoring locations defined in Equation (11).
3.4. Improved Algorithm of MODPSO
On the one hand, we can find from Equation (10) that when we increase the value of m and/or n, the number of potential deployment solutions will also be increased exponentially. Assume we will deploy 20 monitoring devices within 100 potential monitoring locations, the number of deployment solutions is about . It is hard to obtain optimal deployment solutions within a reasonable time by an enumeration search method. On the other hand, these optimization objectives above usually conflict with each other, which means we aim to find some good trade-off solutions among these objectives [15,21]. So, an optimization algorithm should be used here to save the computing time and converge to optimal results within a reasonable period. We integrate the four optimization objectives proposed above into the algorithm of MODPSO. Furthermore, some procedures of the MODPSO such as particle initialization and velocity updating are redesigned and improved to satisfy the optimization requirements.
3.4.1. Particle Design and Swarm Initialization
Assume we select n locations out of m potential monitoring locations along a river network () to deploy water quality monitoring devices. Each potential monitoring location is named from 1 to m respectively resulting in a location set . Each particle in a swarm denotes a deployment solution with n monitoring locations. Therefore, each particle has n positions and each position represents a monitoring location in set S. Particle P can be defined as a vector with n positions shown in Equation (20).
where represents the number of a monitoring location.
Assume we will create k initial particles. n positions of each particle are initialized by random integer values from 1 to m generated by a random integer function. The initial velocity of each position is set to 0. The initialization procedure is as Algorithm A2 in Appendix A shows.
3.4.2. Velocity and Position Updating
We can know from Equations (7) and (8) that each position in a particle has its velocity. When the velocity of a position is changed during computing iterations, the value of the position is also updated, which means we get a new monitoring location. When all positions in the particle are updated, we can get all new positions for the particle. It means we obtain a new monitoring solution for further evaluation by a cost function (seeing Section 3.4.4).
Equations (7) and (8) show that the original velocity and position in the MOPSO are both real values. However, we use integers to denote monitoring locations in a particle. Algorithm A3 in Appendix A shows a new function we developed to update particle’s velocities and positions with integers.
To explore all the domain space, the step of velocity should be constrained in each iteration. We let be the maximum velocity during calculation. A function is used to calculate a new integer value of velocity for each particle based on particles of and . Because the new velocity may be out of the boundary of , we use and functions to restrict the velocity scope. Figure 3 shows the velocity updating process. When particle’s velocities are calculated, the particle’s positions will be updated based on the new velocities. As we know that particle’s positions should be restricted in . If the previous velocity and position are too large or too small, the particle’s position may also be out of boundary. In case of that, the velocity’s direction will be reversed to update the position in a backward direction next time. The and functions are also used to restrict the position boundary.
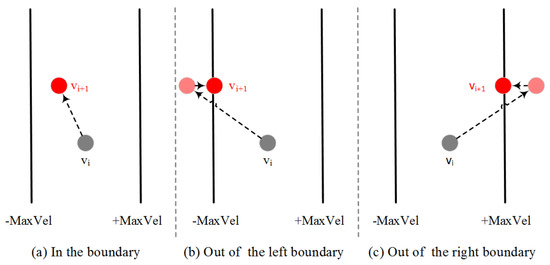
Figure 3.
Velocity updating process.
3.4.3. Reserved Monitoring Locations
As we mentioned in Section 3.3.4, one of the optimization objectives is including all the reserved monitoring locations in final optimized deployment solutions. In a real deployment environment, the reserved monitoring locations for particular management requirements are usually not globally optimal monitoring locations. However, the MODPSO is a heuristic algorithm, and the particle’s velocity and position are updated automatically during the computing iterations based on Equations (7) and (8). Particles with reserved locations are usually dominated by other particles with globally optimal monitoring locations and will be automatically eliminated from the Pareto frontier during optimization iterations. Current algorithms have no guarantee to obtain final optimized solutions with all the reserved monitoring locations. We develop a new approach to guide the update of particle’s positions.
A binary matrix is defined here to denote the reserved monitoring locations. We use “0” to indicate a non-reserved location and “1” to identify a reserved location. For example, the matrix means that there are totally nine potential monitoring locations in a river network, and locations 4 and 6 should be reserved as monitoring locations beforehand. During the velocity computing procedure, if a position in a particle is reserved in the binary matrix, it means that this position should be reserved in the final optimized deployment solutions. We set the velocity of this position to 0, which means the position will not be changed in subsequent computing iterations. We improve the initialization procedure to let all initial particles contain reserved monitoring locations. Algorithm A4 in Appendix A shows the new initialization procedure.
When the binary matrix M is defined, we can obtain the amount and location number of reserved locations from the binary matrix M before particle initialization. Then, these location numbers are used to initialize the values of the first few positions in each particle. At last, we initialize the remain positions in each particle with random integers between 1 to m. We can see from the new initialization procedure that all the reserved locations are included in initial particles.
To keep reserved locations in particles during iterations of computing new velocities and positions for each particle, we slightly improve the velocity and position updating procedure. When the new velocities of a particle are calculated, we ignore all the reserved locations at first few positions of a particle based on the reserved location matrix M, and only the other positions are calculated and updated. By this way, all the reserved locations are retained during the iterations. Algorithm A5 in Appendix A shows the detailed procedure.
3.4.4. Dominance Evaluation
As we mentioned above, four optimization objectives should be simultaneously considered. However, the objective of reserved monitoring locations can be achieved by using the binary matrix. So, only three optimization objectives of maximum pollution detection probability, minimum pollution detection time and maximum closeness centrality of monitoring locations should be calculated in the cost function for dominance evaluation.
Assume we deploy n monitoring devices in the hypothetical river network shown in Figure 2. It means that each particle is composed of n different positions and each position represents a monitoring location. The main procedure of the cost function is: first, we decompose a particle into n separate integers, which represent the number of n monitoring locations respectively. Second, we search each row in the pollution detection time table and get the minimum pollution detection time for each potential pollution event. Then, we calculate the mean pollution detection time and the pollution detection probability for this particle. Third, we calculate the centrality of these monitoring locations. However, the MODPSO always uses the minimum value to calculate the Pareto frontier. So, the cost function will return a matrix with three elements of minimum pollution detection time, the reciprocal of maximum pollution detection probability and the reciprocal of maximum centrality for monitoring locations. As the centrality of each location is determined by the structure of the river network. We can calculate centrality for all the potential monitoring locations based on Equation (16) in advance and save in the matrix . After the calculation of pollution detection time, pollution detection probability and centrality, the cost function can return a matrix as follows:
where is the pollution detection time, is the pollution detection probability and is the closeness centrality. The matrix will be used to evaluate the dominance of each particle (seeing Algorithm A1) in Appendix A.
The pseudocode of the cost function is as Algorithm A6 in Appendix A shows. It should be noted that in the cost function, if a pollution event cannot be detected in a deployment scenario ( = ‘_’), we will not count it into the mean pollution detection time but will calculate it into the pollution detection probability, which is different from Telci’s paper. They use a penalty value for a non-detection scenario which significantly increase the final pollution detection time when the pollution detection probability is less than 100%.
4. Simulations and Analysis
To make a deep understanding about how optimization objectives and dynamic characteristics of a river network affect the optimized design of water quality monitoring networks, we carry out several simulations in this section. We assume that only three monitoring devices will be deployed out of twelve potential monitoring locations showed in Figure 2. In addition, an enumeration search method is also developed to verify the correctness of our algorithm.
4.1. Simulation with Two Objectives of Maximum Pollution Detection Probability and Minimum Pollution Detection Time
To compare our algorithm to the literature and confirm its correctness, we only consider two optimization objectives of maximum pollution detection probability and minimum pollution detection time in this simulation, which is the same as Telci’s paper. We run our algorithm several times based on the pollution detection time in Table 2. Simulation results show that though the main particles are quite different from each other, their Pareto frontiers are the same. Figure 4 shows four Pareto frontiers with eight non-dominated particles in four different sub-diagrams. The mean pollution detection time, pollution detection probability and optimized monitoring locations for non-dominated particles are shown in Table 5.
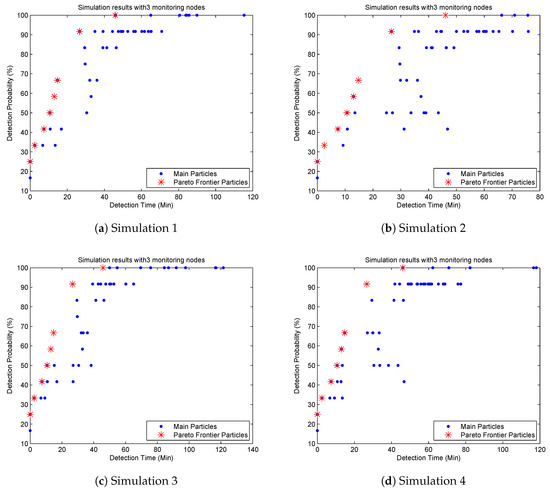
Figure 4.
Pareto frontier with three monitoring nodes and a detection threshold of 0.01 mg/L.

Table 5.
Pollution detection time and pollution detection probability in Pareto frontier with a detection threshold of 0.01 mg/L.
Table 5 indicates that if we deploy three monitoring devices at locations 6, 9 and 12 respectively, all the pollution events can be detected, which is the same as the result in Telci’s paper. If monitoring devices are deployed at locations 2, 6 and 9, the pollution detection probability will be slightly decreased to 91.7% while the mean pollution detection time is also reduced from 45.8 min to 26.6 min. It is the second best solution in the Pareto frontier. However, the second highest detection probability in Telci’s paper is 83%, and the monitoring locations are 4, 7 and 9, which also can be found in Figure 4. However, it is not a non-dominated particle in our algorithm. Based on this observation, we confirm that our algorithm can get a better Pareto frontier and more detailed optimized deployment solutions than the GA algorithm used in the literature.
Telci used a penalty for non-detected pollution scenarios resulting in a much higher pollution detection time for scenarios with non-100% pollution detection probability. We argue that it is not reasonable, because the mean detection time represents how long the pollution event will be detected if it is detectable by the current monitoring network. On the contrary, if a pollution event cannot be detected, the detection probability will be decreased to denote this non-detected scenario. So these non-detected pollution events are not considered in our algorithm when calculating the mean pollution detection time, which results in a smaller mean pollution detection time than in Telci’s paper.
Compared Table 5 to Figure 4, we find that there are 27 different monitoring deployment solutions mapping to eight non-dominated particles. It is because some deployment solutions have the same mean detection time and detection probability, and they map to the same non-dominated particle in Figure 4.
We also develop an enumeration search method to get three optimized monitoring locations within 12 potential locations based on the pollution detection time in Table 2. Figure 5 shows the Pareto frontier of enumeration search results. We can find from Figure 4 and Figure 5 that the enumeration search method gets more particles than the MODPSO. It is because the enumeration search method lists all the combination solutions. However, both the MODPSO and the enumeration search method get the same Pareto frontier with eight Pareto particles. Based on this observation we can confirm that the MODPSO can get the full Pareto frontier and is suitable to be used for the optimized design of water quality monitoring networks.
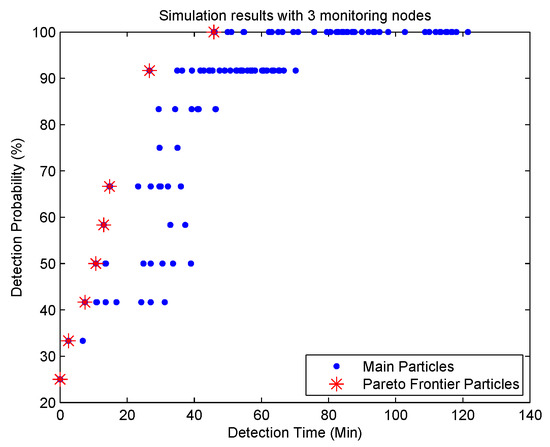
Figure 5.
Enumeration search results.
To understand the effect of dynamic hydrodynamic parameters of a river network to the optimized design of monitoring networks, we set the pollution detection threshold to and , respectively, and get optimized monitoring locations shown in Table 6 and Table 7. Compared Table 5 to Table 6 we can find that when we increase the pollution detection threshold from to , the selected monitoring locations and pollution detection probabilities are almost the same but the pollution detection time is slightly increased. When we increase the pollution detection threshold to , some pollution events cannot be detected (seeing pollution detection time for locations 6 and 12 in Table 4), and the selected monitoring locations and detection probabilities are also changed. Based on this observation, we confirm that the pollution detection threshold can affect the optimized design of water quality monitoring network. We should consider the actual requirement of pollution detection threshold carefully before designing a water quality monitoring network.

Table 6.
Pollution detection time and pollution detection probability in Pareto frontier with a detection threshold of .

Table 7.
Pollution detection time and pollution detection probability in Pareto frontier with a detection threshold of .
4.2. Simulation with Three Objectives of Maximum Pollution Detection Probability, Minimum Pollution Detection Time and Maximum Centrality
In this section, we verify the impact of the maximum centrality to the optimized design of water quality monitoring networks. We still use the pollution detection time in Table 2 and consider three objectives of maximum pollution detection probability, minimum pollution detection time and maximum centrality simultaneously. For the simplicity of calculation, we let the catchment E, which has the shortest length in Table 1 be the standard measurement unit of 1. We obtain a length matrix for all these catchments. Based on the length matrix V, Equations (16) and (17), we calculate the centrality of the hypothetical river network in Figure 2 and obtain a closeness centrality vector for all the potential monitoring locations as Equation (22) shows.
We can find from the centrality matrix that the closer to the center of the river network, the higher centrality value the monitoring location has. For example, the monitoring location 6 in Figure 2 is the center point of the graph. Its centrality value is , which is the highest value in the matrix. However, the MODPSO uses minimum value to calculate the Pareto frontier. So we use a reciprocal of the original centrality value for the optimization computing but convert again to the original value when we obtain the final optimization results. Figure 6 and Table 8 show the Pareto frontier of this simulation.
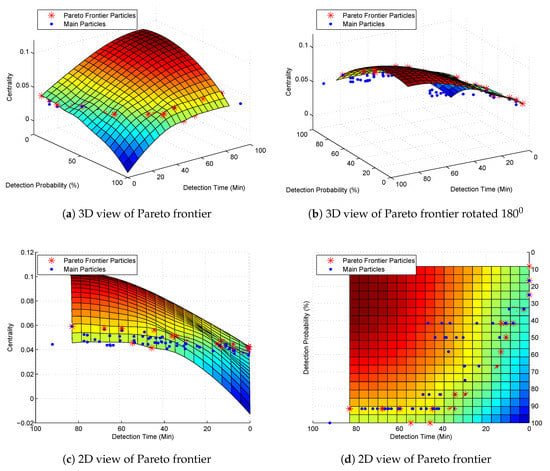
Figure 6.
Pareto frontier with three optimization objectives.

Table 8.
Pollution detection time, pollution detection probability and centrality in Pareto frontier.
Subgraphs (a) and (b) in Figure 6 show that all the other main particles are under the surf of the Pareto frontier particles. Subgraph (c) shows that particles with slightly higher centrality values have larger pollution detection time. It is because if a particle’s centrality is higher, the monitoring locations will locate in the middle of the graph resulting in a higher pollution detection time than those particles uniformly distributing monitoring locations through the river network. From subgraph (d) we can find that the objectives of minimum pollution detection time and maximum pollution detection probability collide with each other.
4.3. Simulation with All Four Optimization Objectives
In this section, we consider all the four optimization objectives mentioned above. We assume the reserved monitoring locations are 4 and 5 respectively and we still use the pollution detection time in Table 2. The Pareto frontiers are shown in Figure 7 and optimization results are shown in Table 9 and Table 10 respectively.
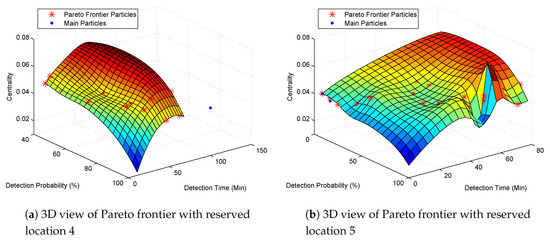
Figure 7.
Pareto frontier with four optimization objectives.

Table 9.
Pollution detection time, pollution detection probability and centrality in Pareto frontier with reserved monitoring location 4.

Table 10.
Pollution detection time, probability and centrality in Pareto frontier with reserved monitoring location 5.
We can find that the Pareto frontier in Figure 7a is quite different from the Pareto frontier in Figure 7b. When location 4 is reserved, we can obtain a 100% pollution detection probability with monitoring locations of 4, 7 and 12. The pollution detection time is 46.1 min and the closeness centrality is 0.0447 (Table 9). If we want a deployment solution with higher centrality, we can deploy monitoring devices at locations 4, 6 and 12, which still has a 100% pollution detection probability while the pollution time is increased to 62.3 min. If a slightly lower pollution detection probability is acceptable, then monitoring locations 4, 6 and 9 are the best locations with a much higher centrality of 0.05 and much lower pollution detection time of 34.9 min. When the reserved location is 5, we can also obtain a 100% pollution detection probability. However, the monitoring locations are changed to 5, 6 and 12 with a higher pollution detection time of 70.9 min and a lower centrality of 0.0423.
Compared Table 5 to Table 9 and Table 10 we find that with a reserved monitoring location, though we can get a 100% pollution detection probability, the pollution detection time is increased respectively. It is because, without reserved monitoring locations, we can obtain a globally optimized solution with higher pollution detection probability and lower pollution detection time. However, we argue that the reservation of monitoring locations is essential for the design of water quality monitoring networks. Due to special management requirements, some particular monitoring locations should be included in the monitoring network in advance whether they are globally optimized monitoring locations or not. So, we should optimize the water quality monitoring network based on reserved monitoring locations.
4.4. Computational Time Analysis with More Potential Monitoring Locations
To confirm the feasibility of using the proposed algorithm to design a real water quality monitoring network, we expand the monitoring network and insert a potential monitoring location every 152.4 m (500 feet) along the river network. Figure 8 shows all the potential monitoring locations numbered from 1 to 57. The red dots along the river network are extra potential monitoring locations. We set the same simulation condition in Section 4.1 and run the simulation for ten times in Matlab2014a with a hardware platform of i5 CPU, 4G memory and 256G SSD. Results show that when we only consider two optimization objectives of minimum pollution detection time and maximum pollution detection probability with a pollution detection threshold of , the computational time for each simulation varies from 5.18 s to 5.46 s and the mean computational time is 5.34 s. It is because the MODPSO is a heuristic algorithm and the dominated particles produced during each simulation are different. So the computational time for each simulation is also slightly different. That is why we use the mean computational time to evaluate the computational time for each simulation. Table 11 shows that when the pollution detection threshold is increased to 1 mg/L and 2 mg/L respectively, the mean computational time is decreased to 5.29 and 5.11 s separately. It is because a higher pollution detection threshold means a lower detection probability when a pollution event occurs, which results in less non-dominated particles and saving the computational time.
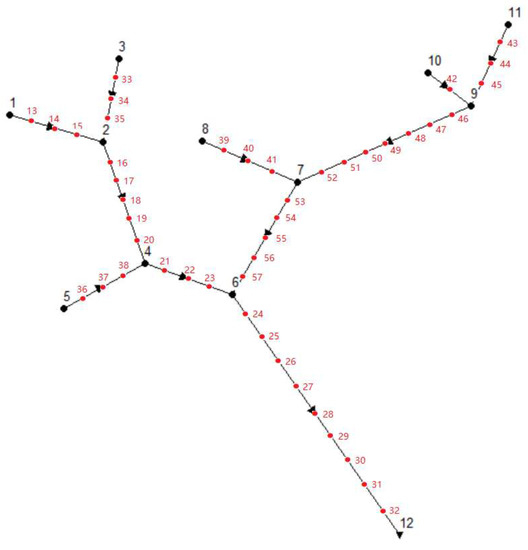
Figure 8.
Hypothetical river network with more potential monitoring locations.

Table 11.
Computational time for different simulations.
However, from a mathematical point of view, we can know there are only 220 combinations when we select three optimized locations out of 12 potential monitoring locations. The number of combinations is significantly increased to 29,260 when we select three optimized locations out of 57 potential monitoring locations, which is 133 times that of 220 combinations. Compared to their computational time in Table 11 we can know that the computational time for 57 potential monitoring locations is only about three times that of 12 potential monitoring locations. Based on this observation we can know that our algorithm is flexible to be applied for a real monitoring network design, especially when the number of potential monitoring locations is too large to be computed by the enumeration search method.
5. Conclusions and Future Work
We presented an improved MODPSO algorithm for the optimized design of water quality monitoring networks with four optimization objectives of minimum pollution detection time, maximum pollution detection probability, maximum closeness centrality and reserved monitoring locations. We first considered two optimization objectives and got optimized monitoring locations. Results were verified by an enumeration search method to confirm the correctness of our algorithm. A binary matrix was used to denote reserved monitoring locations, guide the particle initialization and make sure that the reserved location’s velocities and positions in particles will not be changed during computing iterations. Simulation results in Section 4.1 showed that our algorithm could obtain a better Pareto frontier than GA. It was also verified that reserved monitoring locations had a significant effect on the optimized design of water quality monitoring networks. The computational performance and flexibility of our algorithm for a complex water quality monitoring network were also confirmed.
It should be noted that there were several assumptions such as the same pollutant concentration for each pollution event and the constant channel width for each segment. However, the hypothetical river network was only used to obtain pollution detection time at each potential monitoring location. We further used the set of pollution detection time to verify the correctness of our algorithm. When we change the hydraulic parameters, we will obtain a different set of pollution detection time as well as a different optimized monitoring network. So, the assumptions will not affect the correctness verification of our algorithm. However, when we apply our algorithm to design a real water quality monitoring network, professional hydraulic and pollution simulation tools should be used to obtain more accurate pollution detection time as well as a better optimized monitoring network.
Unlike other global optimization algorithms in the literature, our approach is a constrained optimization algorithm. It seeks the optimized monitoring solutions based on reserved monitoring locations, and the final results may not be global optimization results but the best results when the reserved locations are included in the monitoring network. When the binary matrix is empty (no reserved monitoring location), our approach becomes a global optimization algorithm and can obtain global optimization results. So it can not only be used to design a new monitoring network with reserved locations or add additional monitoring locations into an existing monitoring network but also can be applied to design a global optimization monitoring network (let the binary matrix M be empty).
In the future, this novel approach will be applied to a real water quality monitoring network to optimize the network design. Further research is planned to explore the feasibility of redesigning the velocity and position calculation procedure to prevent a particle with the same positions, which can further improve computational performance. Another future work is to regard define reserved monitoring locations as optimization constraints for optimization algorithms to verify if these reserved monitoring locations can be optimized as a resulting optimal design.
Author Contributions
These authors contributed equally to this work.
Funding
This work was partly funded by Natural Science Foundation of Suzhou City (SYG201837) and Nantong University-Nantong Joint Research Center for Intelligent Information Technology (KFKT2017A06).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
| Algorithm A1 Pseudocode of MOPSO |
| procedure MOPSO Step 1. Initialization (1) Initialize all parameters (e.g., size of population and repository, maximum number of iterations, lower and upper bounds of search space) (2) For each do (a) Initialize the particle’s position randomly (b) Initialize with its initial position (c) Initialize particle’s velocity = 0 (3) Calculate non-domination particles using cost function (4) Initialize with a particle selected from non-domination particles using a roulette wheel selection. Step 2. Repeat until the termination criteria is satisfied or to the maximum number of iterations (5) For each do (a) Calculate particle’s new velocity using Equation (7) (b) Calculate particle’s new position using Equation (8) (c) Update particle’s (d) Calculate non-domination particles using cost function (e) = a particle selected from non-domination particles using a roulette wheel selection. Step 3. Output non-domination particles. end procedure |
| Algorithm A2 Pseudocode of MODPSO initialization |
| procedureInitialization(k)
fori = 1 to k do for j = 1 to n do end for end for end procedure |
| Algorithm A3 Pseudocode of velocity and position updating |
| procedureVel_Pos_Updating(k)
fori = 1 to k do for j = 1 to n do if then end if end for end for end procedure |
| Algorithm A4 Pseudocode of MODPSO initialization with reserved locations |
| procedureInitWithReservedLocations(k) fori = 1 to k do for t = 1 to R do end for for j = to n do end for end for end procedure |
| Algorithm A5 Pseudocode of velocity and position updating with reserved locations |
| procedureNew_Vel_Pos_Updating(k) fori = 1 to k do for to n do if then end if end for end for end procedure |
| Algorithm A6 Pseudocode of cost function |
| procedureCost(p) Array for each in do for each l in do end for if then end if end for for each l in do end for return end procedure |
References
- Skoczko, I.; Struk-Sokolowska, J.; Ofman, P. Modelling Changes in the Parameters of Treated Sewage Using Artificial Neural Networks. Rocz. Ochr. Srodowiska 2017, 19, 633–650. [Google Scholar]
- Skoczko, I.; Ofman, P.; Szatylowicz, E. Using Artificial Neural Networks for Modeling Wastewater Treatment in Small Wastewater Treatment Plant. Rocz. Ochr. Srodowiska 2016, 18, 493–506. [Google Scholar]
- Yang, Y. How to Look at the GDP Receiving Much Attention. Revolution 2015, 12, 26–32. [Google Scholar]
- Behmel, S.; Damour, M.; Ludwig, R.; Rodriguez, M.J. Water quality monitoring strategies—A review and future perspectives. Sci. Total Environ. 2016, 571, 1312–1329. [Google Scholar] [CrossRef] [PubMed]
- Park, S.Y.; Choi, J.H.; Wang, S.; Park, S.S. Design of a water quality monitoring network in a large river system using the genetic algorithm. Ecol. Model. 2006, 199, 289–297. [Google Scholar] [CrossRef]
- Chilundo, M.; Kelderman, P. Design of a water quality monitoring network for the Limpopo River Basin in Mozambique. Phys. Chem. Earth 2008, 33, 655–665. [Google Scholar] [CrossRef]
- Chang, C.L.; Lin, Y.T. A water quality monitoring network design using fuzzy theory and multiple criteria analysis. Environ. Monit. Assess. 2014, 186, 6459–6469. [Google Scholar] [CrossRef]
- Storey, M.V.; Van der Gaag, B.; Burns, B.P. Advances in on-line drinking water quality monitoring and early warning systems. Water Res. 2011, 45, 741–747. [Google Scholar] [CrossRef]
- Lambrou, T.P.; Anastasiou, C.C.; Panayiotou, C.G.; Polycarpou, M.M. A low-cost sensor network for real-time monitoring and contamination detection in drinking water distribution systems. IEEE Sens. J. 2014, 14, 2765–2772. [Google Scholar] [CrossRef]
- Borgatti, S.P.; Everett, M.G. A graph-theoretic perspective on centrality. Soc. Netw. 2006, 28, 466–484. [Google Scholar] [CrossRef]
- Ouyang, H.T.; Yu, H.; Lu, C.H.; Luo, Y.H. Design optimization of river sampling network using genetic algorithms. J. Water Resour. Plan. Manag. 2008, 134, 83–87. [Google Scholar] [CrossRef]
- Telci, I.T.; Nam, K.; Guan, J.; Aral, M.M. Real time optimal monitoring network design in river networks. In World Environmental and Water Resources Congress 2008: Ahupua’A 2008; ASCE: Reston, VA, USA, 2008; pp. 1–10. [Google Scholar]
- Telci, I.T.; Nam, K.; Guan, J.; Aral, M.M. Optimal water quality monitoring network design for river systems. J. Environ. Manag. 2009, 90, 2987–2998. [Google Scholar] [CrossRef] [PubMed]
- Park, C. Discrete Optimization via Simulation with Stochastic Constraints. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2013. [Google Scholar]
- Rossman, L.A. Storm Water Management Model User’s Manual, Version 5.0; National Risk Management Research Laboratory, Office of Research and Development, US Environmental Protection Agency: Cincinnati, OH, USA, 2010; p. 276.
- Xing, W.; Li, P.; Cao, S.B.; Gan, L.L.; Liu, F.L.; Zuo, J.E. Layout effects and optimization of runoff storage and filtration facilities based on SWMM simulation in a demonstration area. Water Sci. Eng. 2016, 9, 115–124. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Maulik, U.; Bandyopadhyay, S.; Coello, C.A.C. A survey of multiobjective evolutionary algorithms for data mining: Part I. IEEE Trans. Evol. Comput. 2014, 18, 4–19. [Google Scholar] [CrossRef]
- Kalyanmoy, D. Multi Objective Optimization Using Evolutionary Algorithms; John Wiley and Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Eberhart, R.C.; Shi, Y. Comparison between genetic algorithms and particle swarm optimization. In International Conference on Evolutionary Programming; Springer: Berlin/Heidelberg, Germany, 1998; pp. 611–616. [Google Scholar]
- Reyes-Sierra, M.; Coello, C.C. Multi-objective particle swarm optimizers: A survey of the state-of-the-art. Int. J. Comput. Intell. Res. 2006, 2, 287–308. [Google Scholar]
- Coello, C.C.; Lechuga, M.S. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the 2002 Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1051–1056. [Google Scholar]
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Ezzeldin, R.; Djebedjian, B.; Saafan, T. Integer discrete particle swarm optimization of water distribution networks. J. Pipeline Syst. Eng. Pract. 2013, 5, 04013013. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997; Volume 5, pp. 4104–4108. [Google Scholar]
- Chen, W.N.; Zhang, J.; Chung, H.S.; Zhong, W.L.; Wu, W.G.; Shi, Y.H. A novel set-based particle swarm optimization method for discrete optimization problems. IEEE Trans. Evol. Comput. 2010, 14, 278–300. [Google Scholar] [CrossRef]
- Aminbakhsh, S.; Sonmez, R. Discrete particle swarm optimization method for the large-scale discrete time–cost trade-off problem. Expert Syst. Appl. 2016, 51, 177–185. [Google Scholar] [CrossRef]
- Venkatesan, S.P.; Kumanan, S. A multi-objective discrete particle swarm optimisation algorithm for supply chain network design. Int. J. Logist. Syst. Manag. 2012, 11, 375–406. [Google Scholar] [CrossRef]
- Cui, Z.; Koren, V.; Cajina, N.; Voellmy, A.; Moreda, F. Hydroinformatics advances for operational river forecasting: Using graphs for drainage network descriptions. J. Hydroinformat. 2011, 13, 181–197. [Google Scholar] [CrossRef]
- Phillips, J.D.; Schwanghart, W.; Heckmann, T. Graph theory in the geosciences. Earth-Sci. Rev. 2015, 143, 147–160. [Google Scholar] [CrossRef]
- Heckmann, T.; Schwanghart, W.; Phillips, J.D. Graph theory—Recent developments of its application in geomorphology. Geomorphology 2015, 243, 130–146. [Google Scholar] [CrossRef]
- Freeman, L.C. Centrality in social networks conceptual clarification. Soc. Netw. 1978, 1, 215–239. [Google Scholar] [CrossRef]
- Nathan, E.; Sanders, G.; Bader, D.A. Numerically approximating centrality for graph ranking guarantees. J. Comput. Sci. 2018, 26, 205–216. [Google Scholar] [CrossRef]
- Strobl, R.; Robillard, P.D. Network design for water quality monitoring of surface freshwaters: A review. J. Environ. Manag. 2008, 87, 639–648. [Google Scholar] [CrossRef] [PubMed]
- Loaiciga, H.A. An optimization approach for groundwater quality monitoring network design. Water Resour. Res. 1989, 25, 1771–1782. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).