1. Introduction
Worldwide, floods cause over one-third of overall economic losses due to natural hazards. These losses are particularly severe in urban environments. Moreover, the severity and frequency of floods are expected to increase over the 21st century [
1]. Therefore, there is a compelling need for resilience against extreme events, such as floods. To mitigate these extreme events, priority adaptation guidelines, measures, and policy recommendations must clearly indicate what can be done to adapt to natural hazards linked to climate change. Most settlements are not adapted to inundations [
2], and because they are often located close to rivers or coastlines, valuable and vulnerable land uses are exposed to floods. Due to urban developments in floodplains, space for the rivers shrinks and water levels increase [
3].
Traditionally, floods have been controlled with artificial, engineered infrastructures (i.e., dykes and dams) [
4]. Rather than attempting to preserve the existing urban structure, however, more flexible measures are sometimes required in which adaptive cities are revamped by (the threat of) flood events [
3]. Combining flood adaptation measures with public space design can serve multiple purposes, including water depuration, recreation, or microclimatic melioration [
5]. Natural water retention measures (NWRMs) and ecosystem-based adaptations, including green roofs, development of buffer zones, rain gardens, and the deployment of rainwater wells and barrels (e.g., using rainwater for washing machines, toilets, maintenance), can be employed in urban residential areas [
6,
7,
8,
9].
Nonetheless, these priority adaptation guidelines can also provide technical measures, e.g., inserting gates where needed, building sluices to prevent ingress of water into drains, raising floor levels in vulnerable town centre properties, installing breakwaters, implementing self-closing barriers at underground car parks, etc.
To determine the balance between these flexible and robust measures and where these measures need to be applied, first, a priority adaptation (road) map is needed.
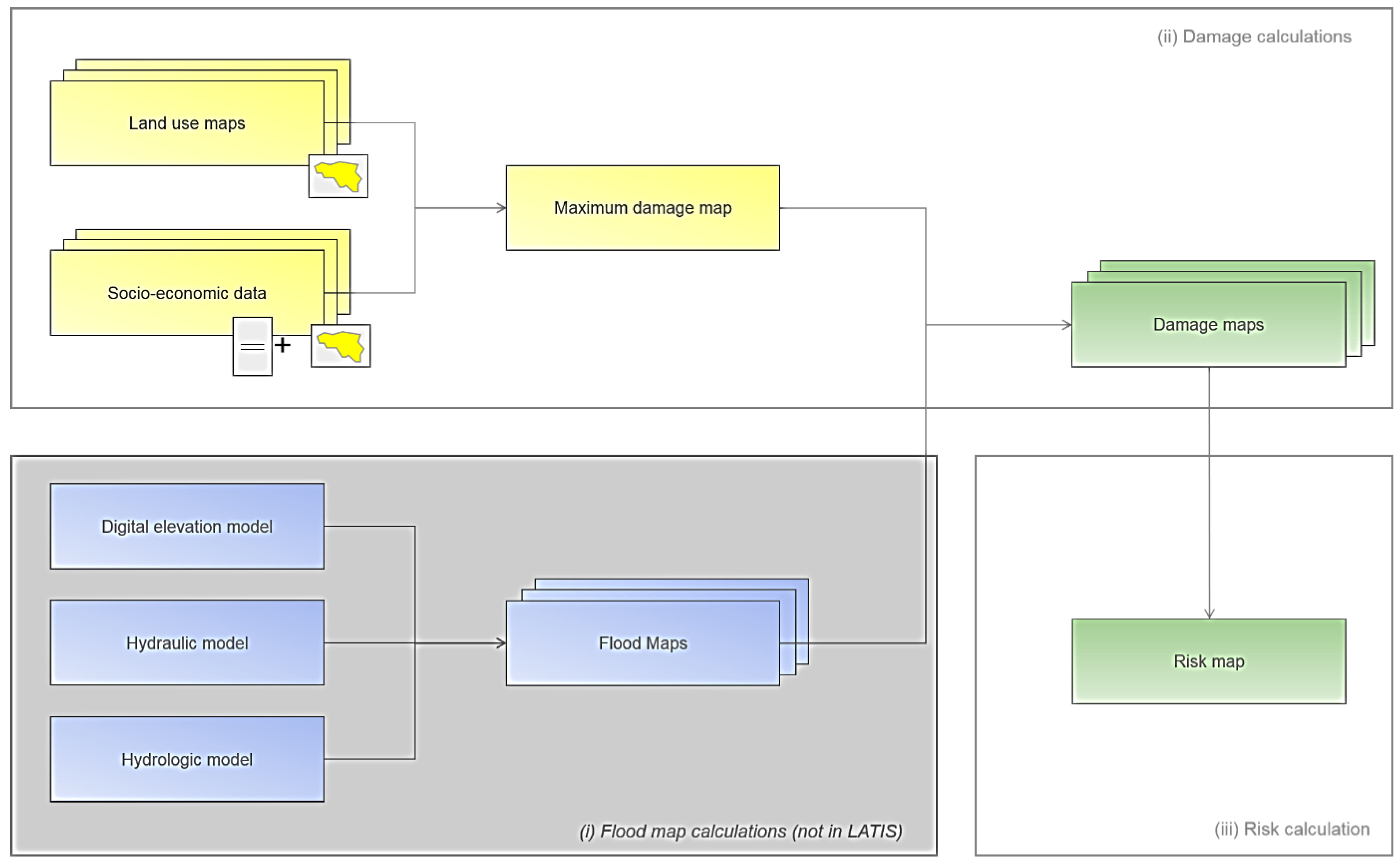
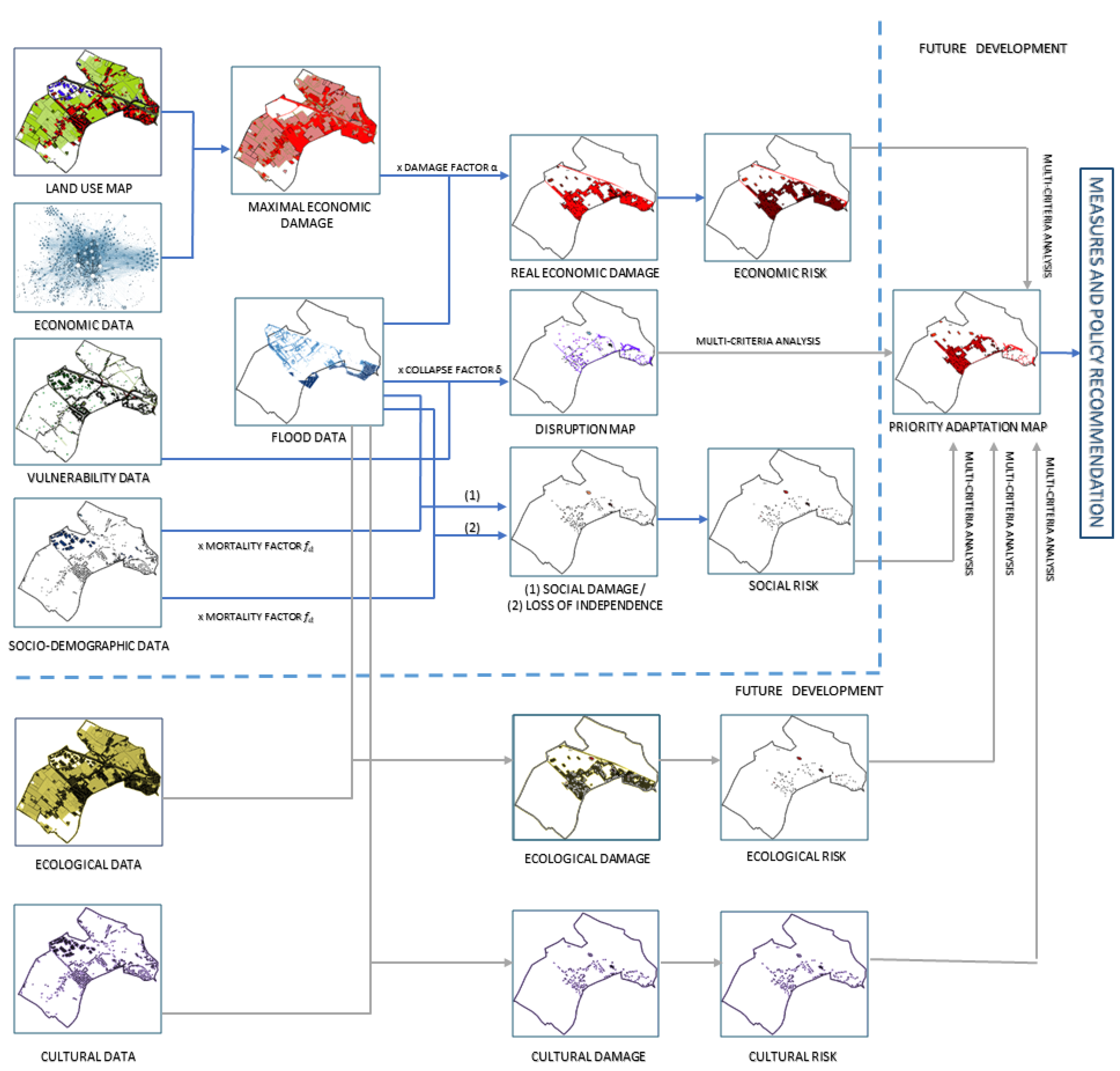
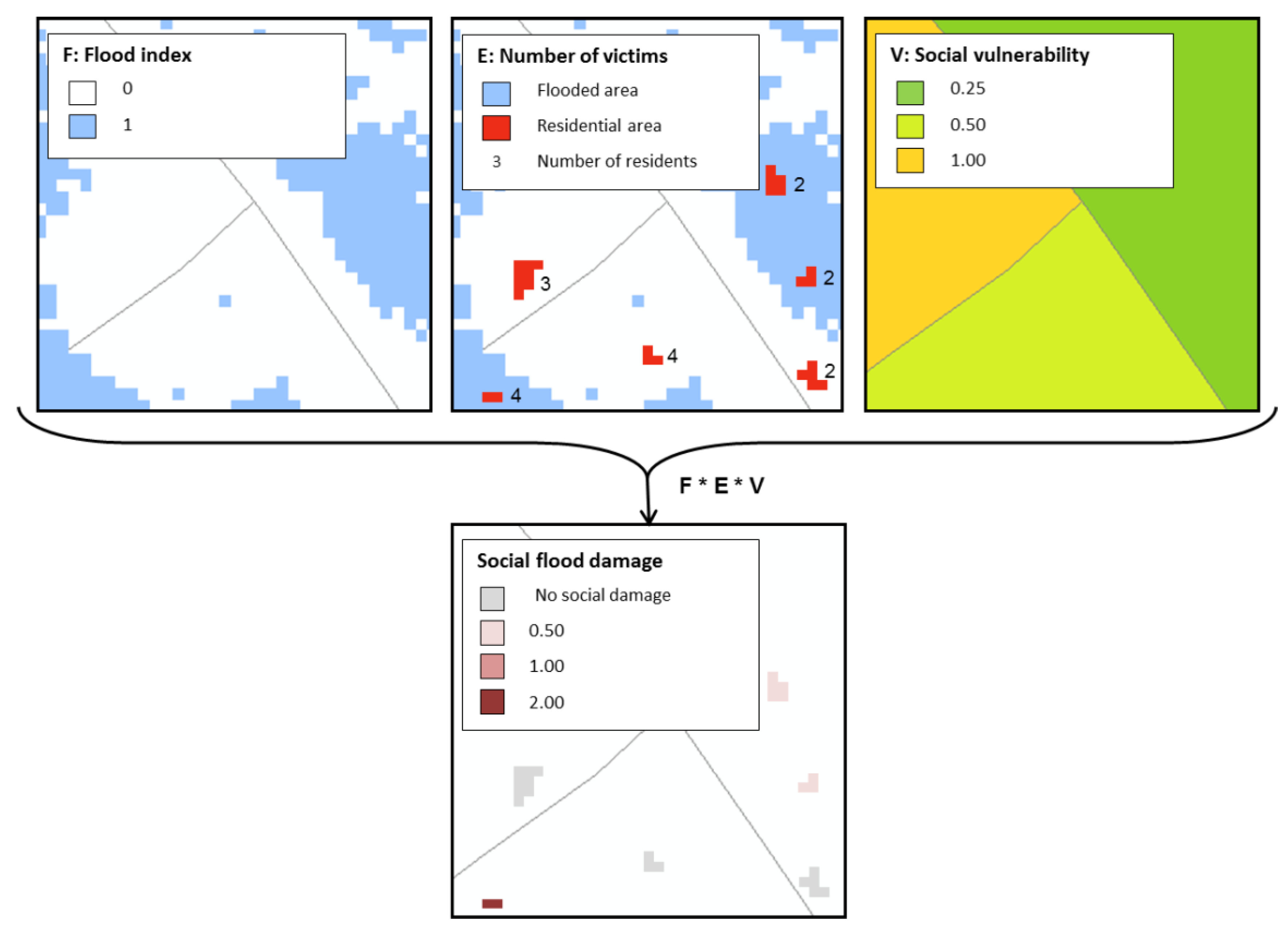
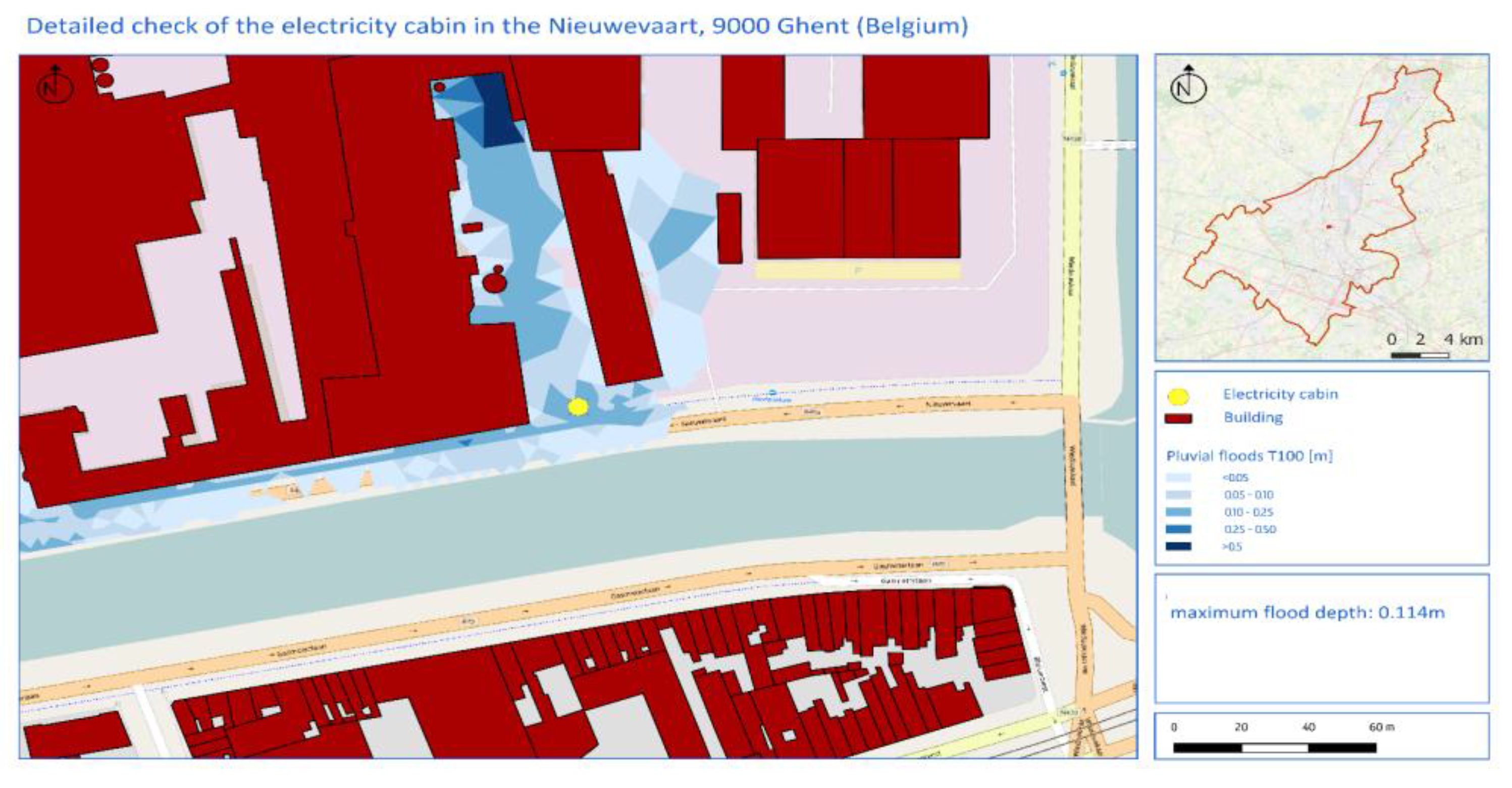
Since 2002, Ghent University, in collaboration with Flanders Hydraulics Research, developed a methodology that computes the socio-economic impact of floods, which is determined based on land use information, socio-economic data, and damage functions (see
Figure 1).
The economic risk and the risk for victims can be measured by considering the expected damage or number of victims for different return periods with a risk formula [
10]. Through the years, the development of the social, ecologic, and cultural impact assessment was added to this existing methodology. Because of the lack of server performance and computing power back in 2003, the LATIS tool was developed with a raster approach and programmed in C#.Net that used the GIS (geographic information system) technology of IDRISI (raster-GIS) [
10].
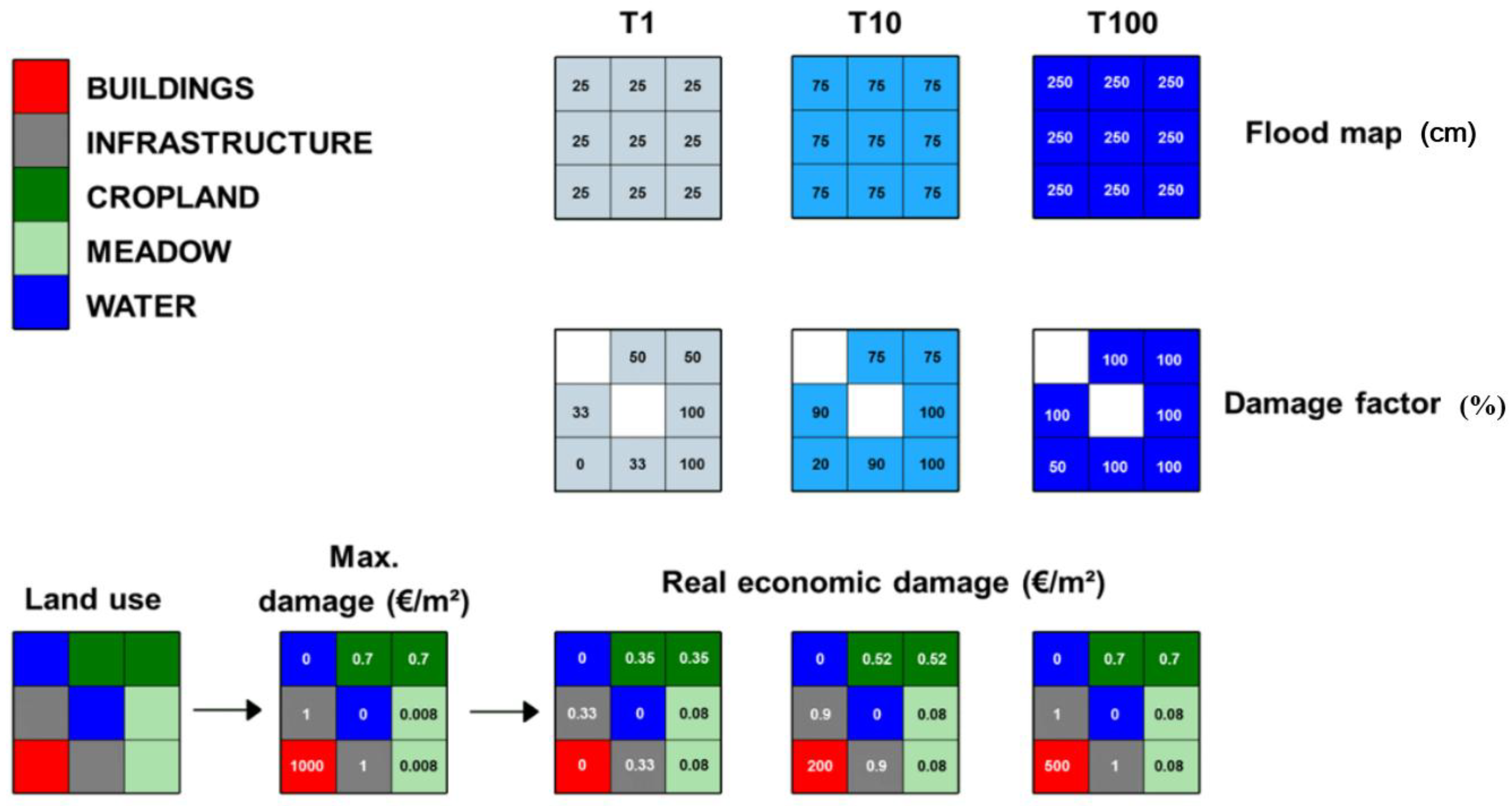
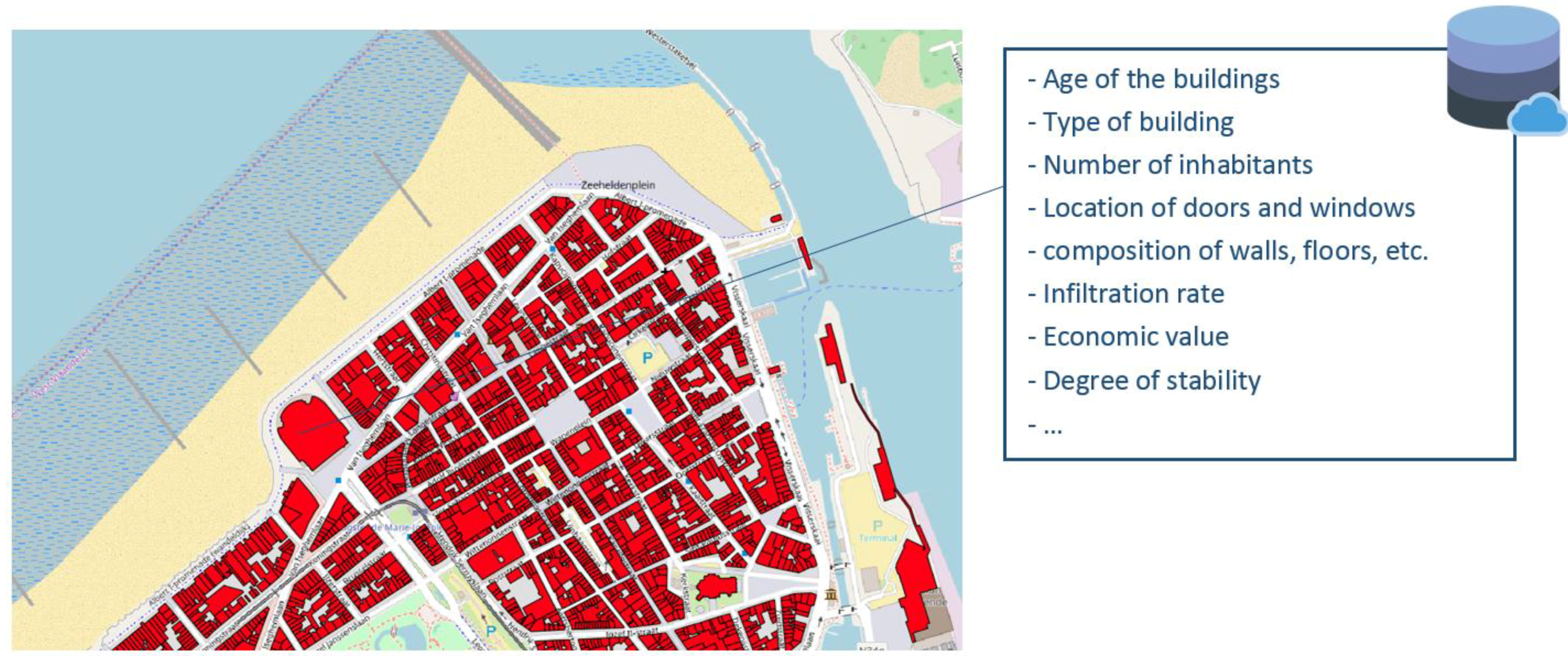
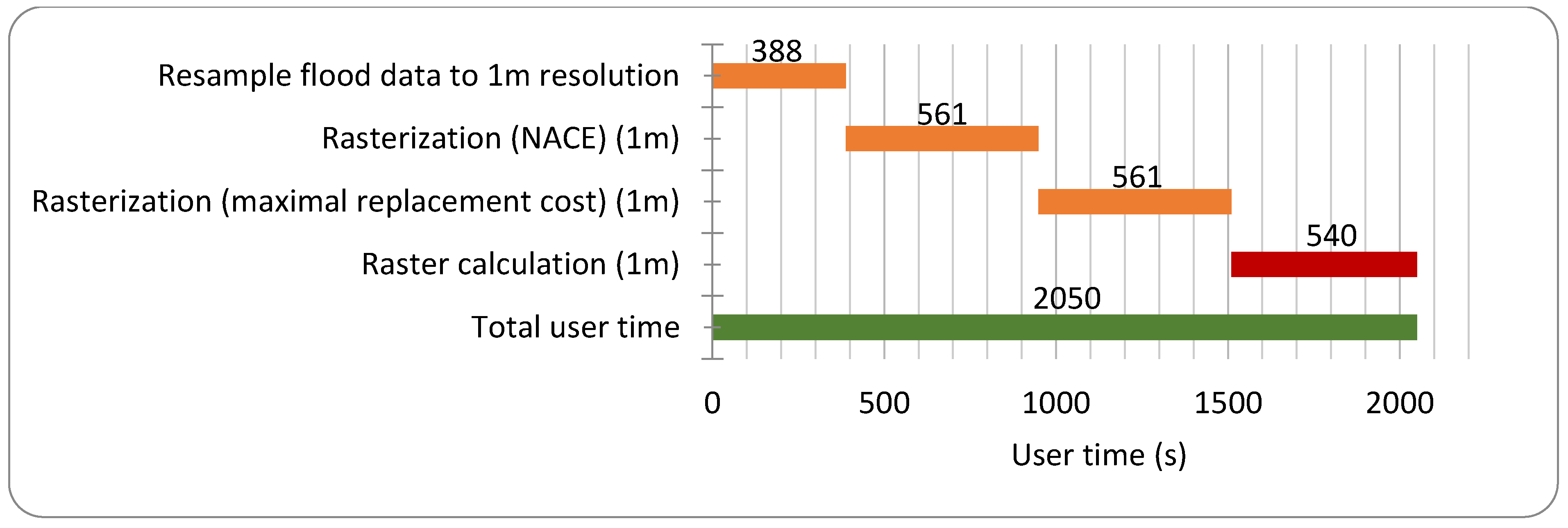
To calculate the economic damage resulting from floods with a raster approach (see
Figure 2), land use data is converted in raster files in which every land use category is translated into an estimated economic replacement value (or maximum economic damage) by using the Standard Method [
11].
Like the flood impact assessment tool LATIS in Flanders, Belgium, many other flood impact assessment tools use the raster approach to calculate socio-economic damage resulting from floods. For example, Delft-FIAT in the Netherlands requires raster files to run its script. Therefore, the tool comes with a free available pre-processing Python script based on the Geospatial Data Abstraction Library (GDAL) library to convert all land use and object data from vector files to raster data with the required Delft-FIAT settings [
13]. A widely used variant of this tool is the HIS-SSM/SSM-2017 tool, also developed for the Netherlands [
14], in which all data is standardized by converting the vector files into raster files with a resolution of 5, 25, 50, or 100 m [
15]. The same applies to Flemo for Germany [
16,
17], HAZUS for the USA, and the CORFU tool for Europe and Asia [
18,
19], where all input variables are processed to be available as raster datasets with a cell size relatively equal to the water depth raster file.
To calculate the socio-economic damage, either the default source data that is included with the specific damage assessment tool (e.g., LATIS, HAZUS, etc.) can be used, or the user can choose to upload their own data that is, for example, more applicable to their assessment study (e.g., more detailed data, emphasis on other flood parameters, etc.). In reference to Flanders, the source data of the LATIS tool has a resolution of 5 m by default and can immediately be used for an assessment of a specific flood event.
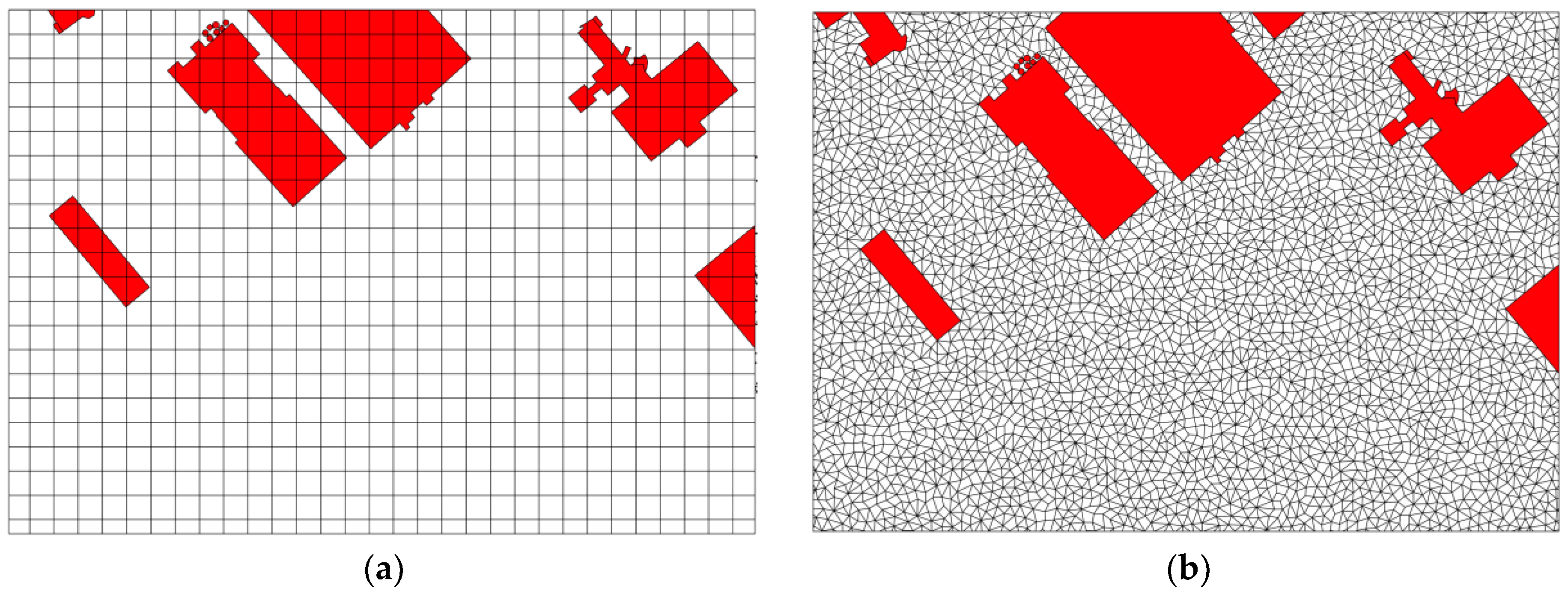
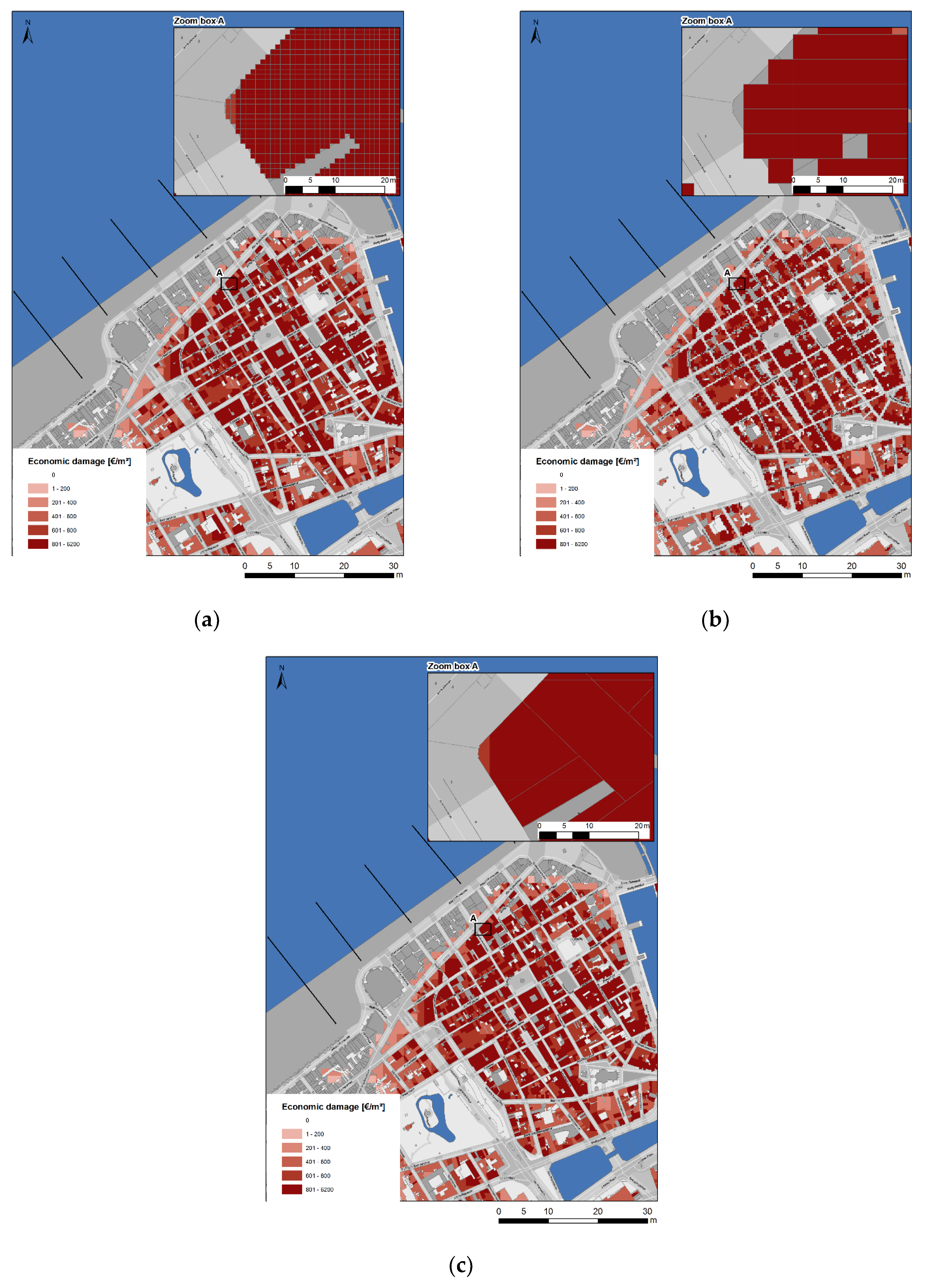
Regardless of differences in methodology, there are a number of disadvantages that come with the raster approach to flood impact assessment tools (see
Figure 3). Chen et al. show that parcel areas and buildings are overestimated when they are represented by large raster cells (larger or equal than 5 m) because, in many cases, only a portion of a cell is occupied by it, while the whole cell area is used to represent this small parcel or building [
19]. In fact, this spatial error applies to all land use and objects that need to be converted from vector data to raster data. Although it is possible to differentiate separate objects when the cell size is not too big, parcel boundaries do not align with the cell boundaries when polygons are converted to raster format. Smaller grid cells reduce this error but increase the computation load and the data storage requirements. Citing Bai et al., “Rasterization is a conversion process accompanied with information loss, which includes the loss of features’ shape, structure, position, attribute and so on” [
20].
Additionally, a raster consists essentially of a matrix of cells (or pixels) organized into rows and columns (a grid), where each cell contains one and only one value representing information (e.g., water depth). Of course, there are a few exceptions to the rule that one grid cell in a raster can only store one value. For example, by using the FD8 algorithm [
21], it allows the raster to use combinations of base-2 numbers to store multiple flow directions towards up to eight different neighbours. Nevertheless, this FD8 algorithm is mostly used in rather specialized and limited case due to its complexity. A second scenario would be to store data in the three bands of 8-bit data (the colour composites red, green, and blue) as a single value and then parse the values when the image is read. However, this limits the data from the three data sources to a narrow numerical range (integers from 0 to 255). The last scenario is to use raster formats that allow multiple bands (e.g., BIL, BSQ, BIP, TIFF, etc.). The standard procedure to combine multiple raster files is when all combined raster files still exist. Consequently, the simplest raster GIS way to store multiple values is by using multiple raster files. Yet, a key issue is storing multi-values of one and the same category with the use of raster files (e.g., when multiple companies are settled in one building). It can be concluded that there are multiple drawbacks when a flood impact assessment tool is developed with a raster approach.
Before the flood impact can be assessed, reliable and accurate flood maps are required. To date, there are many 2D depth-averaged flood simulation models (e.g., TELEMAC-2D [
22], MIKE21 [
23], DIVAST [
24,
25]). Hereby, a depth-integrated solution is considered to be sufficiently accurate in shallow water comparisons [
26]. These depth-averaged tools have a wide range of applications [
27,
28,
29,
30]. Yet in floods with a significant variance in pressure over the water column, a three-dimensional model is required. Three-dimensional models (e.g., TRIVAST [
29], EFDC [
31], TIDE3D [
32], and TELEMAC-3D [
33]) also solve the Navier–Stokes set of equations [
34], but work with multiple layers over the depth and can, thus, model pressure and speed gradients over the depth. These flood simulation models have been constrained by the scarcity of detailed and accurate digital elevation models (DEMs). Luckily, accuracy has improved over the years because of the emergence of new data capture techniques, particularly in the field of aerial digital photogrammetry [
35] and airborne remote sensing, including interferometric synthetic aperture radar (SAR) [
36] and light detection and ranging (LiDAR) [
37].
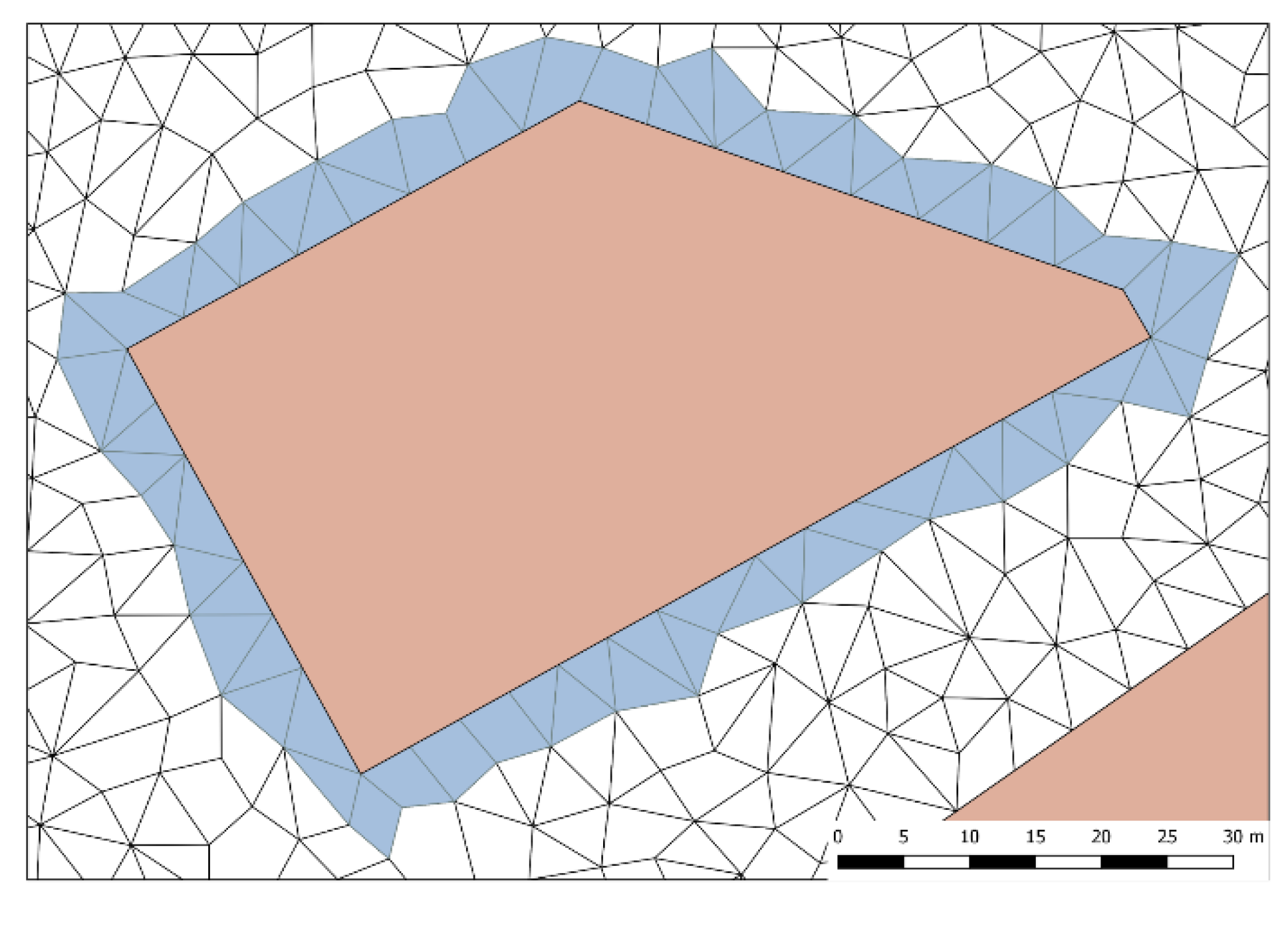
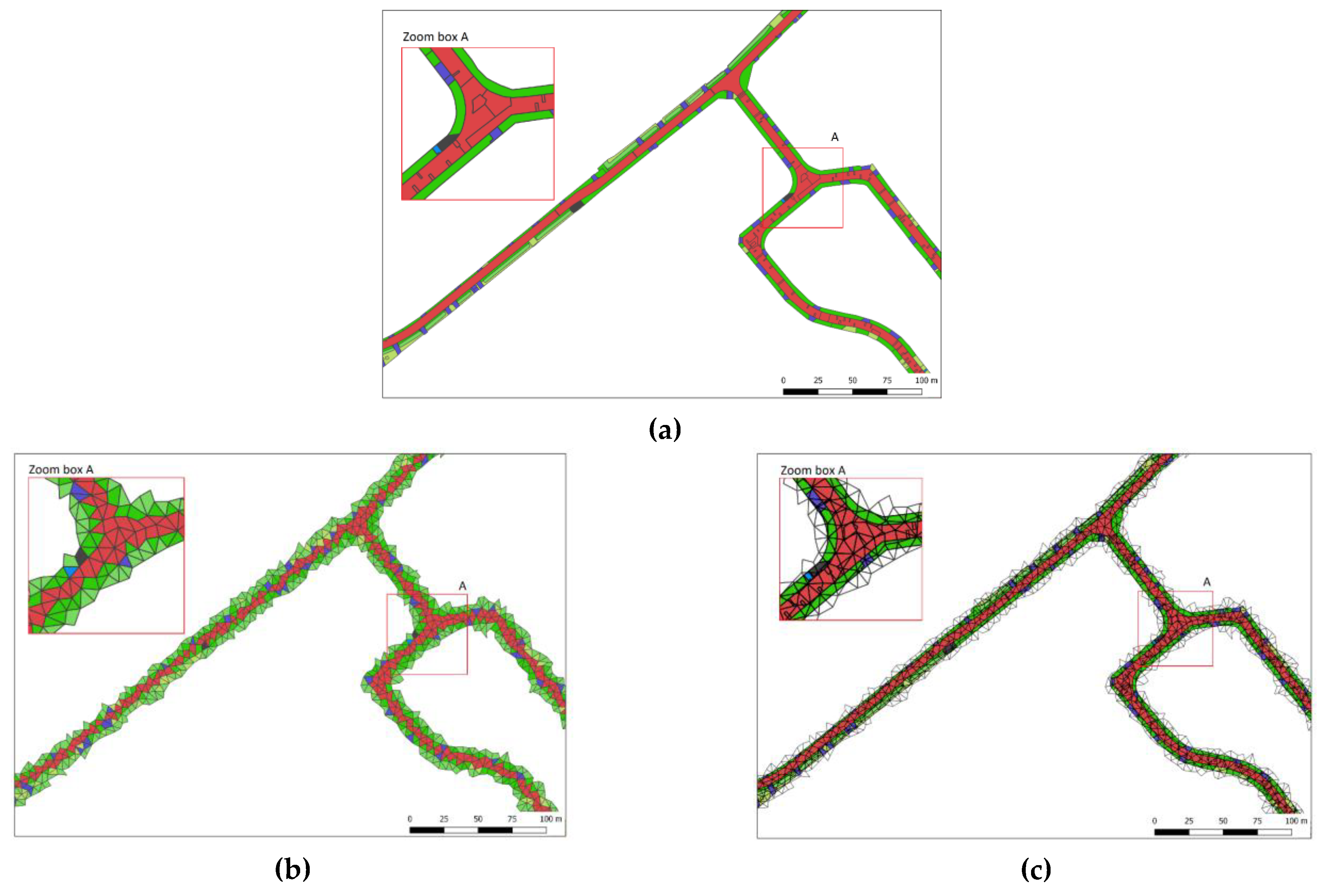
DEM can be represented as raster, TIN, or unstructured meshes (eventually with localized refinements) to calculate and simulate flood inundation [
38] (see
Figure 4).
A raster-based structure makes it possible to represent the complex topographical elevation as highly predefined, discrete areas [
39]. The grid cell resolution indicates the size of the grid cell in which small grid cells are defined by a high resolution. DEM accuracy decreases with coarser resolutions [
40]. As a result, a high resolution allows a better representation of complex topography with a greater accuracy [
41]. It has been shown that a low resolution of DEM has a tremendous impact on slope algorithm calculations (the calculated maximum slope becomes larger as the DEM resolution becomes finer), as complex topographies are flattened due to its averaging [
42,
43,
44,
45]. The resolution of DEM also has a significant impact on hydraulic and hydrological modelling, such as horizontal and vertical flow direction and velocity [
41,
46,
47], erosion and sedimentation modelling [
42], catchment areas derived from DEM [
46], computation of soil water content [
48], etc. Even relatively small changes in DEM resolution have considerable effects on the predicted inundation extent and the timing of flood inundation [
49].
Attention should be paid when raster data with a low spatial resolution is combined with raster data of a relatively much higher spatial resolution (e.g., raster data with a resolution of 1 km combined with raster data with a resolution of 10 m). The output will most likely be unidentifiable, as the scales of analysis are far too disparate to result in interpretable and/or meaningful conclusions. Therefore, it is recommended to calculate the socio-economic impact of floods on the basis of flood data with a spatial resolution that is relatively equal to the land use data.
Analogous to the impact of the resolution of raster-based DEM, the size of unstructured meshes has an enormous impact on the accuracy of hydraulic modelling [
50]. The advantage of unstructured meshes is in its ability to easily vary cell size throughout the changes of the terrain in which unstructured meshes can describe the terrain more accurately than raster-based DEM with a comparable resolution [
51,
52]. Consequently, the unpredictable randomness of unstructured, irregular meshes makes it impossible to convert this data type into a raster file without considerable error.
Because the accuracy of the output of hydraulic simulation models is dependent on the accuracy of the input of the digital elevation model, the unstructured mesh-based hydraulic simulation model output has a greater accuracy than a raster-based hydraulic simulation model output with a comparable resolution (unless there is only a raster-based digital terrain model available). Therefore, by immediately calculating flood impact using the unstructured mesh data type instead of immediately converting the hydraulic simulation into a raster, no loss of accuracy will occur.
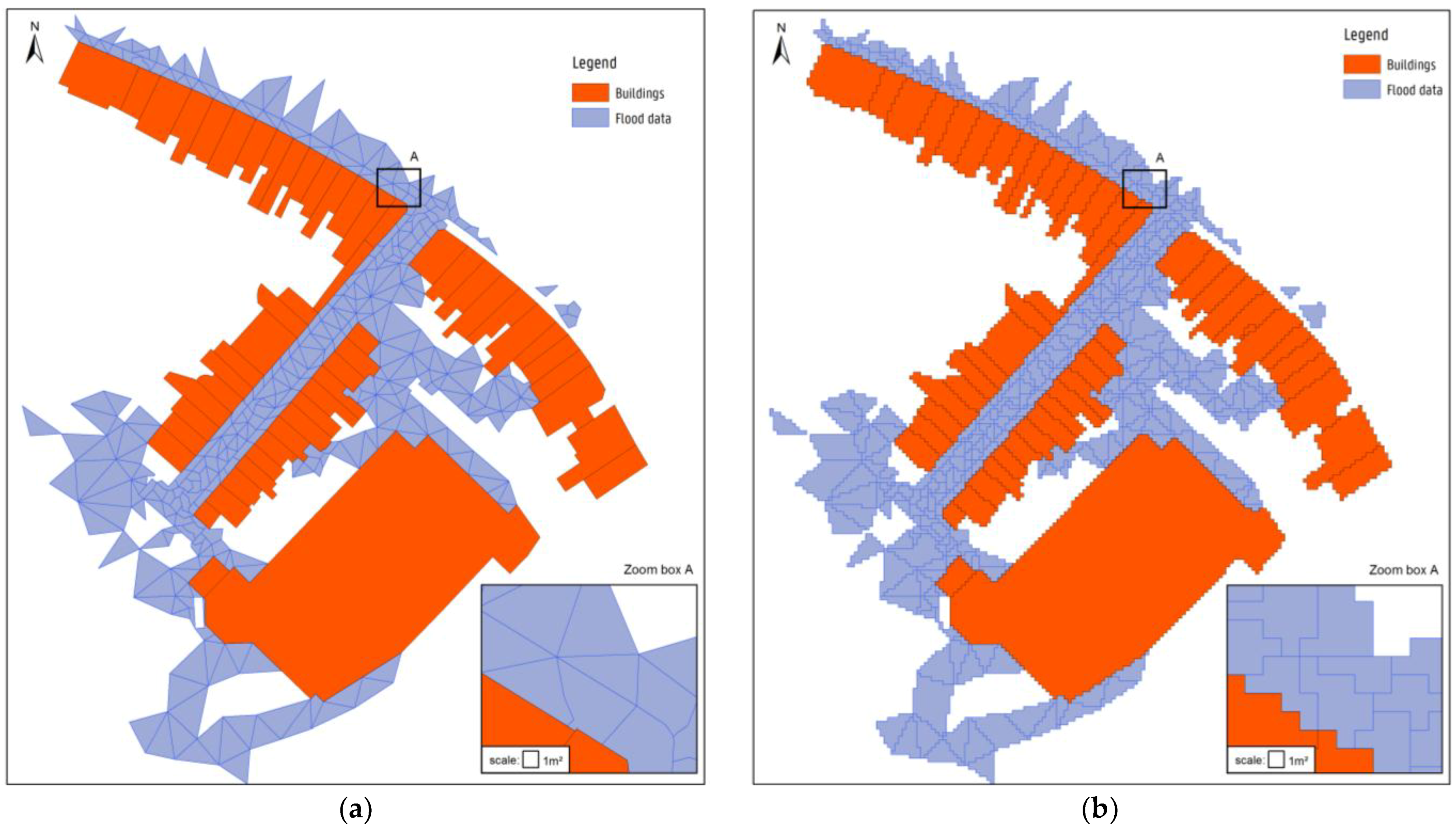
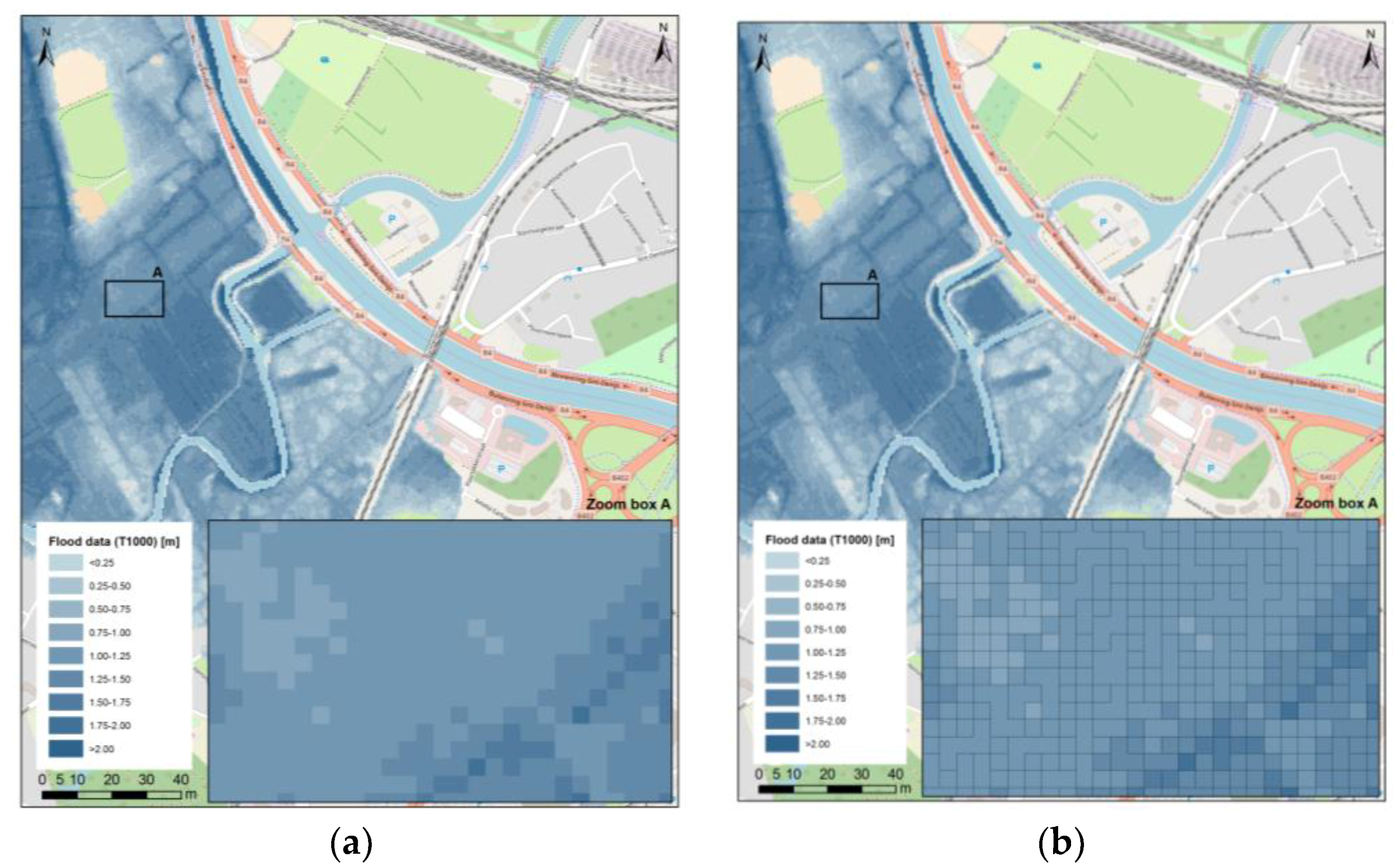
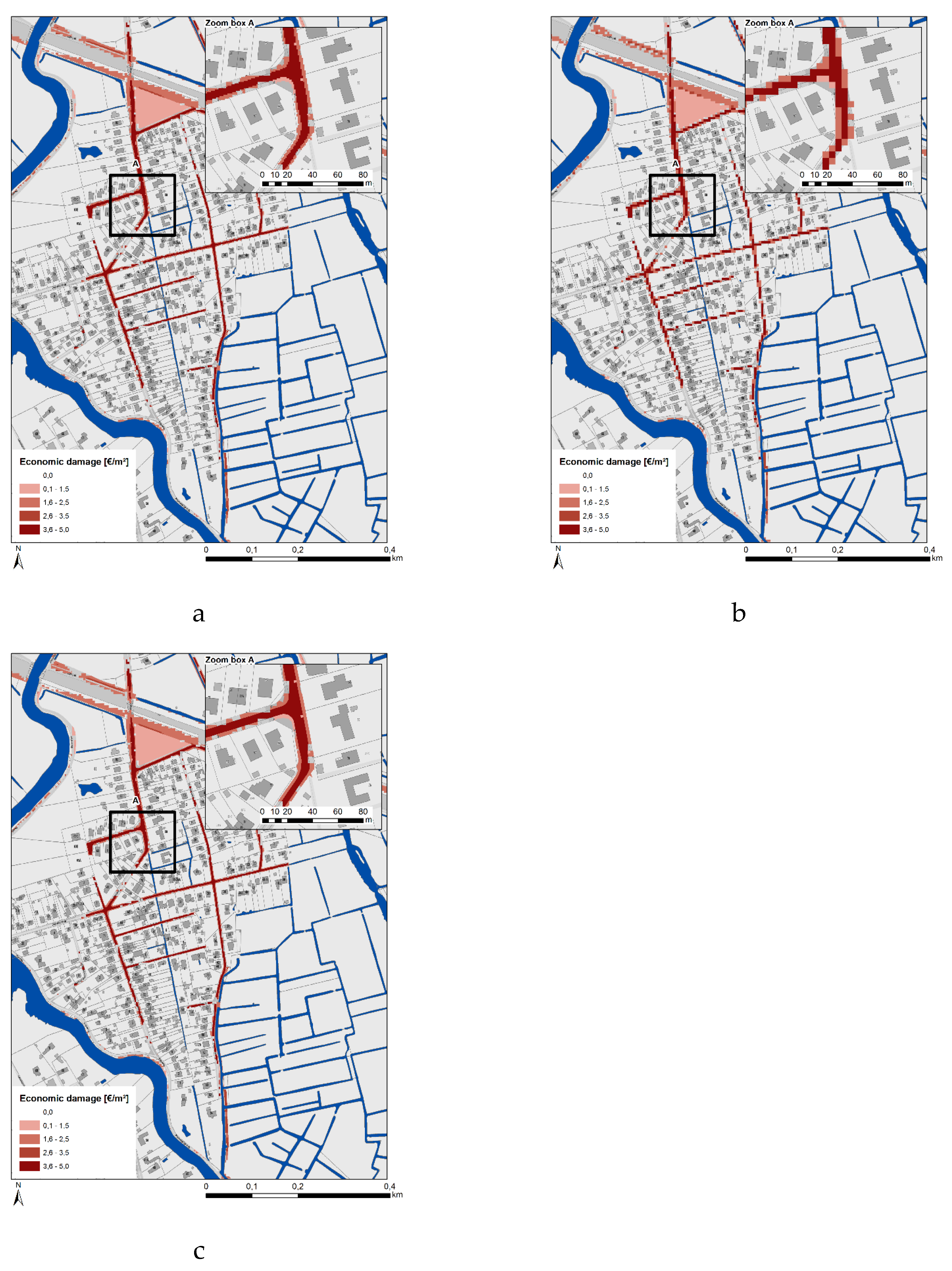
Additionally, more and more hydraulic simulation models are modelling floods by taking buildings, infrastructures, and other objects into account as obstacles for water flow instead of assuming a permeability of 100% for these objects. As a result, the flood boundaries correspond to the boundaries of the objects on the terrain (see
Figure 5a). After converting these unstructured mesh-based flood data into raster-based flood data, there is no overlap of grid cells of the flood data with the object (see
Figure 5b). One exception is in the unlikely case of the equal occurrence of land use (e.g., buildings) and flood data in one raster cell.
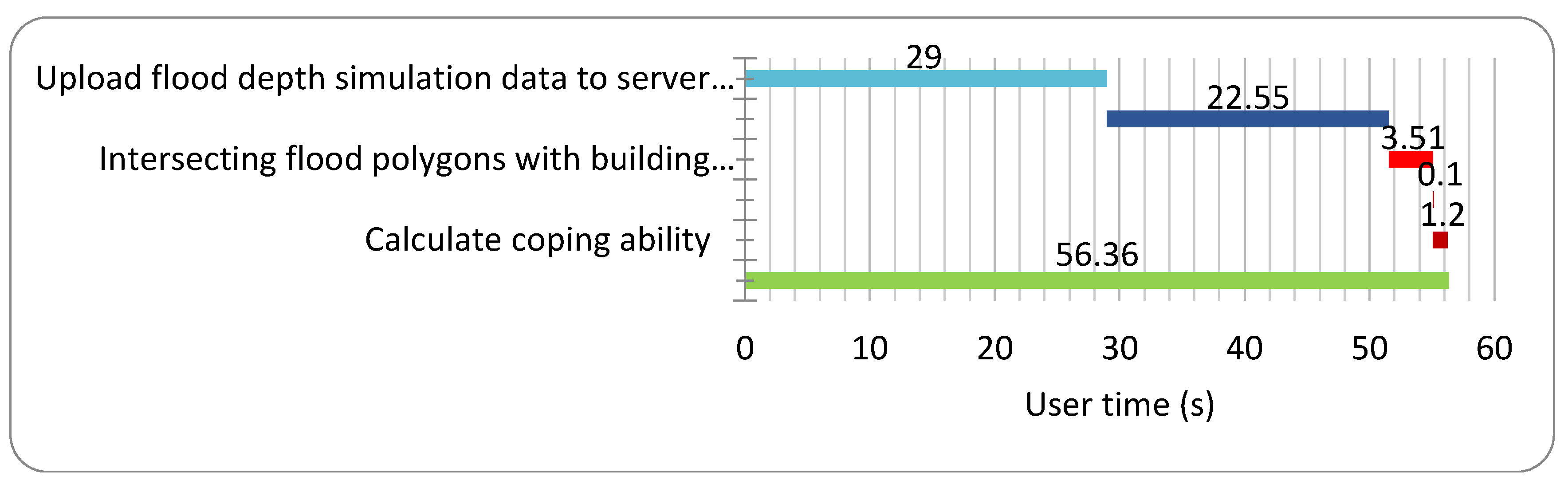
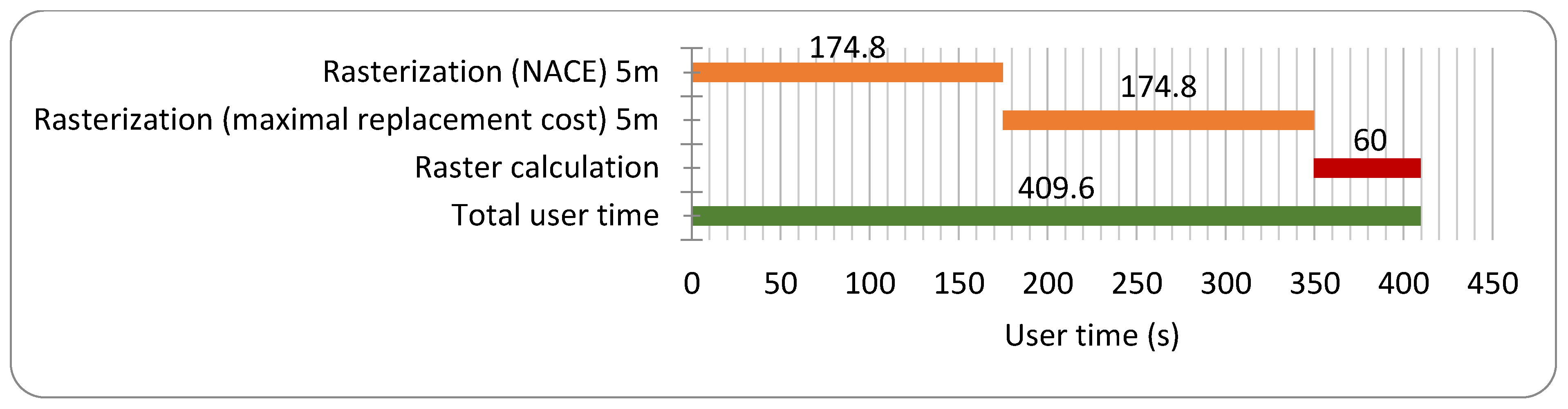
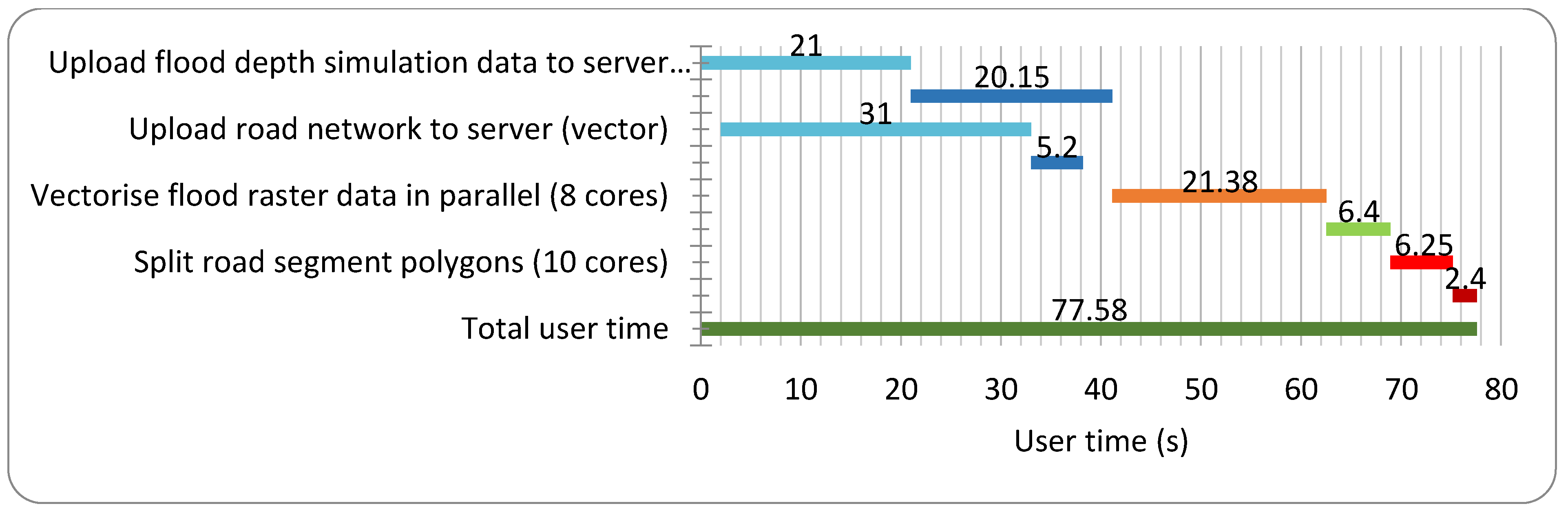
Because of this, a new flood impact assessment tool (FLIAT) is needed that can compute the impact of floods using both a vector approach and a raster approach (when needed), which can handle multiple data sets in a fluent way. Hereby, it is not necessary to run the FLIAT tool with additional data or by using more detailed data compared with the current damage assessments. Nevertheless, this FLIAT tool can be used in detailed flood impact studies, for example when a (societal) cost-benefit analysis of individual measures (or a group of measures in a limited area) is made. The FLIAT tool helps engineers, environmental agencies, and local governments accurately detect and define the priority protection zones, in terms of socio-economic damage and social disruption resulting from flood events, on the basis of the uploaded flood simulation data (or occurred flood events) of a specific region. FLIAT can be used in cost-benefit analyses of, for example, sewerage and road construction projects and the construction of (coastal) protection infrastructures, and this makes the tool valuable as a decision-making tool for priority adaptation guidelines, measures, and policy recommendations. This paper will explore a suitable methodology for calculating the impact of floods with a vector approach and describes the development of the FLIAT prototype [
53]. In
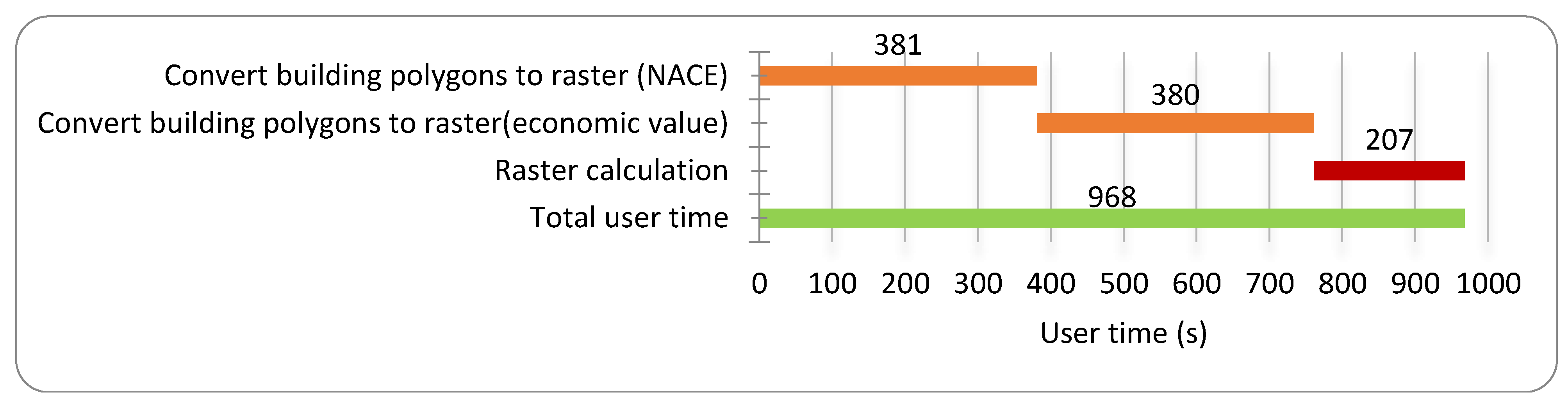
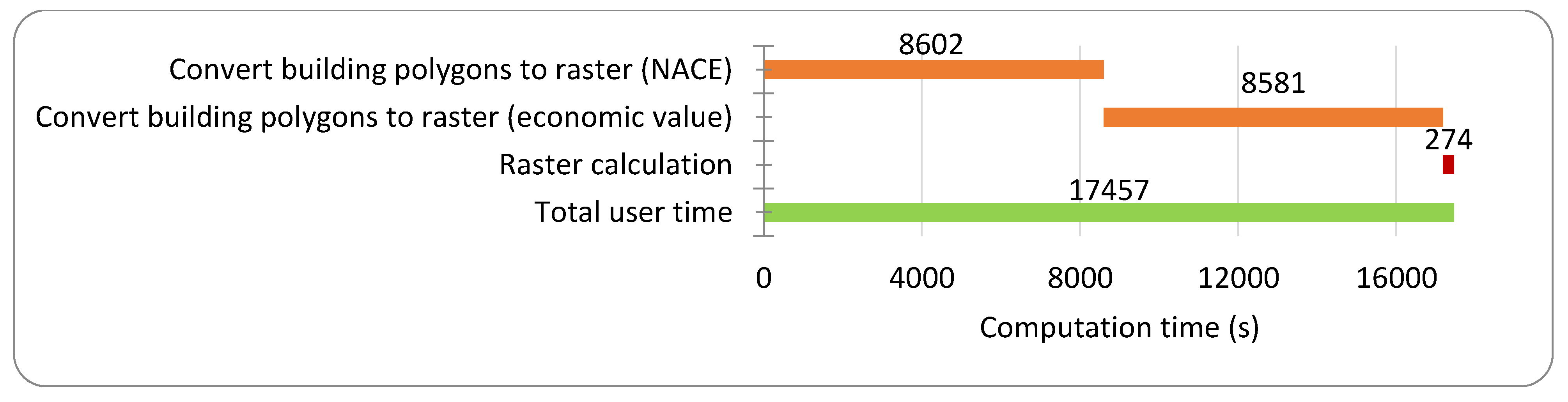
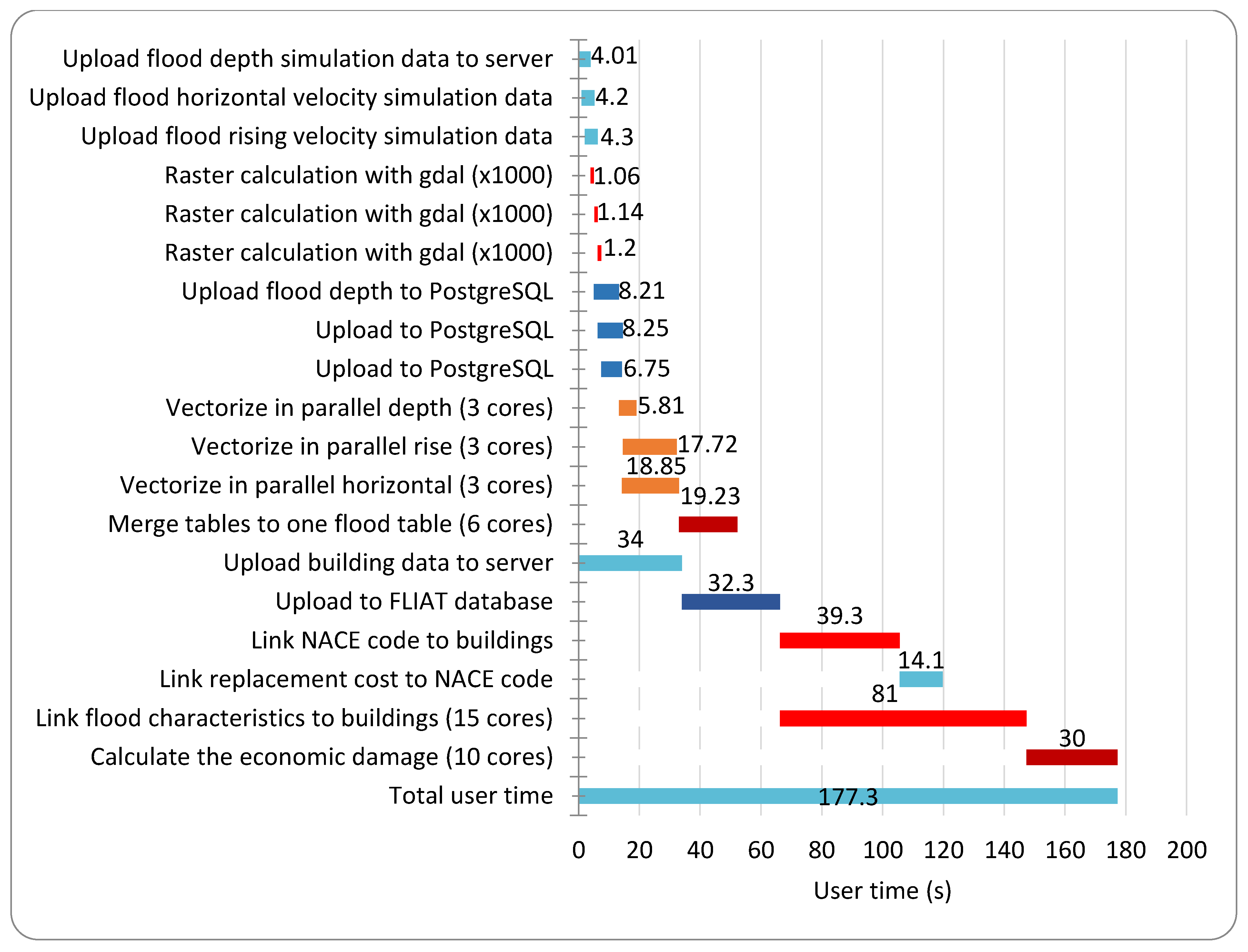
Section 3, case studies of a river flood and a pluvial flood in the city of Ghent and a coastal flood at the Belgian coast are worked out with the proposed FLIAT vector-based approach and the raster approach in order to compare the performance of both approaches, including running speed and accuracy.