1. Introduction
Low probability and high impact extremes in hydrology, such as storms, play an important role in characterizing the hydrologic system and affecting water infrastructure design [
1,
2,
3,
4]. Capturing and defining these extremes is still a difficult task in hydrology because of the complexity of natural systems, as well as their variability in both space and time [
5,
6]. Compared to the prohibitive physical process-based models requiring intensive data that are typically not available for many study sites, statistical analysis of hydrological extremes is an attractive tool to interpret these extreme events within and across systems from simple measurements [
7,
8,
9,
10].
There are two major challenges when applying basic statistics to analyze hydrologic extremes. First, hydrologic processes in the water cycle are interconnected, while basic statistical analysis of extremes often does not consider multiple systems and tends to oversimplify the complexity of the correlated processes like precipitation and groundwater table fluctuations [
11,
12]. Understanding how the subtle properties of one system’s extreme events can affect the other interconnected systems requires more in-depth analysis and use of advanced statistical techniques. Second, these basic statistical techniques often rely on assumptions or major simplifications of properties for water systems, such as stationarity in both space and time, which may not always be valid for real world dynamics [
13,
14,
15]. These issues motivated this study.
One example of the assumption/simplification used by basic statistical studies in hydrological extremes is the well-known Gumbel distribution. Statistics of extremes is one of the historical topics in hydrology, including for example probability density functions (PDFs) developed for analyzing the distribution of hydrologic extremes [
13]. One of the fundamental distributions used in hydrology is the Gumbel distribution, a case of the generalized extreme value distribution where the shape parameter is 0, proposed by Gumbel to fit the frequency of floods [
16]. This distribution was developed before many advances in statistics and computing, and it has been widely used for decades by hydrologists. To apply this theory, data must be assumed to be homogenous, meaning that there should be no change in climate or basin characteristics during both the observation period and any period that predictions are made. This assumption, however, may not be valid considering the intrinsic evolution of the dynamic, natural systems [
13,
17,
18]. One promising way to overcome the assumption of the homogeneous system is non-stationary statistics [
19,
20].
This study aims to fill two knowledge gaps when analyzing the distribution, memory, and correlation embedded in the hydrological extremes. First, we will identify the PDF that can define the overall distribution pattern of real-world hydrological extremes. Several studies [
21,
22] found that various random processes in hydrology usually follow a one-sided distribution with a heavy tail. This finding motivated us to test two physically meaningful PDFs, the stretched Gaussian distribution and the α-stable distribution, in capturing the hydrological extremes and comparing them with the classical Gumbel distribution. All three of the distributions allow for a one-sided, heavy tailed PDF, which is a common occurrence in natural water systems [
23,
24,
25]. Each distribution has different parameters, and they can all be conveniently computed and parameterized for series. Since the extremes of water systems are often needed to determine the infrastructure design and management plans, improving the prediction using the most reasonable distribution as a model can greatly improve water management practices [
26].
Second, we will evaluate the non-stationary statistics for hydrological extremes. One example of a non-stationary statistic is the Hurst exponent, first developed to quantify the long-term persistence of water storage of reservoirs by Hurst [
27]. Peng et al. [
28] introduced detrended fluctuation analysis (DFA) to investigate long-range correlation (also called memory) of a series that contains significant noise, such as DNA nucleotides, financial series, seismic analysis, and hydraulic data [
28,
29,
30,
31,
32]. Peng et al.’s contribution [
28] allowed for a time-scale local Hurst exponent (TSLHE) to be calculated, defining a non-stationary statistic. Zhang and Schilling [
32] applied DFA to investigate the scaling behavior of hydraulic head and base flow, which is related to the groundwater recharge and can be used to determine the fractal dimension and Hurst exponent of the series. Zhou et al. [
33] used a multi fractal DFA (MF-DFA) method to show that river discharge in the Yangtze basin was non-stationary and had different correlation properties depending on the measurement location in the watershed. Tong et al. [
34] used the Hurst exponent to quantify the variation of droughts in both space and time. These successful applications motivated us to apply the TSLHE to explore the evolution of hydrological extreme properties.
Different from most of the previous works, this study tries to evaluate and correlate surface and subsurface hydrological extreme events. We will investigate the effects that extreme storm events, of different properties, have on the fluctuations in surface and subsurface water systems. To the best of our knowledge, these fluctuations have not been compared to different storm properties. With potential changes in climate, the storm properties are expected to evolve in time [
35,
36,
37]. These fluctuations are correlated to the properties over time and compared across systems and storm properties. The memory of the water series is also investigated using the TSLHE, which is correlated to the storm properties. Finally, we will investigate the distributions that fit each of the different data sets and storm properties.
The rest of this study is organized in four sections.
Section 2 briefly introduces the study site and the data sources used for statistical analysis. Methods are then described, including the calculations of storm properties, the Hurst exponent, and the distributions used to fit the time series data.
Section 3 presents the results of statistical analysis for both the surface water and groundwater.
Section 4 discusses the statistical results, and
Section 5 draws the main conclusions.
2. Study Site and Methodologies
2.1. Background of the Study Site and Data Source
The study site was the Lake Tuscaloosa watershed in Tuscaloosa, northern Alabama, USA. The lake has been the primary source of drinking water for the city of Tuscaloosa (200,000 consumers in 2014) since 1970. Lake Tuscaloosa has an approximate volume of 150,000,000 m
3 and a surface area of 23.82 km
2 [
38]. The lake is fed by four major streams which have U.S. Geological Survey (USGS) gauge stations—North Creek, Binion Creek, Bush Creek, and Carroll Creek—which represent most of the surface flow into the lake, as well as many smaller streams that do not significantly contribute to the lake. North and Binion Creeks have the highest discharge and the best coverage of measurements, and hence they are used as the streams for this study. The lake sits primarily in the Pottsville Formation, a Pennsylvanian aged sandstone interbedded with shale and siltstone, as well as the lower Coker Formation, a Cretaceous unit with sand and gravel beds. The lake is partially fed by groundwater from these aquifers, as are the streams that flow into it [
39].
The study site has a humid subtropical climate, typical of the Deep South weather region of the U.S., with abundant rain (with an average precipitation of 1336.04 mm/year) and rare measurable snowfall. The local climate is affected significantly by the Gulf of Mexico which brings relatively warmer and moist air. This causes precipitation during fall, winter, and spring seasons, when the warmer/moist air from the south interacts with the cooler/drier air from the north of the southeastern U.S. Extreme weather conditions, such as hurricanes, can occur in the spring and fall, especially in April. For example, two tornadoes (EF3 and EF4, where “EF” stands for the Enhanced Fujita scale for tornado intensity/damage) in a span of twelve days hit the city of Tuscaloosa in 15–27 April, 2011 killing more than fifty people and causing considerable infrastructure damage [
40]. Therefore, study of extreme hydrological events in this area is particularly important.
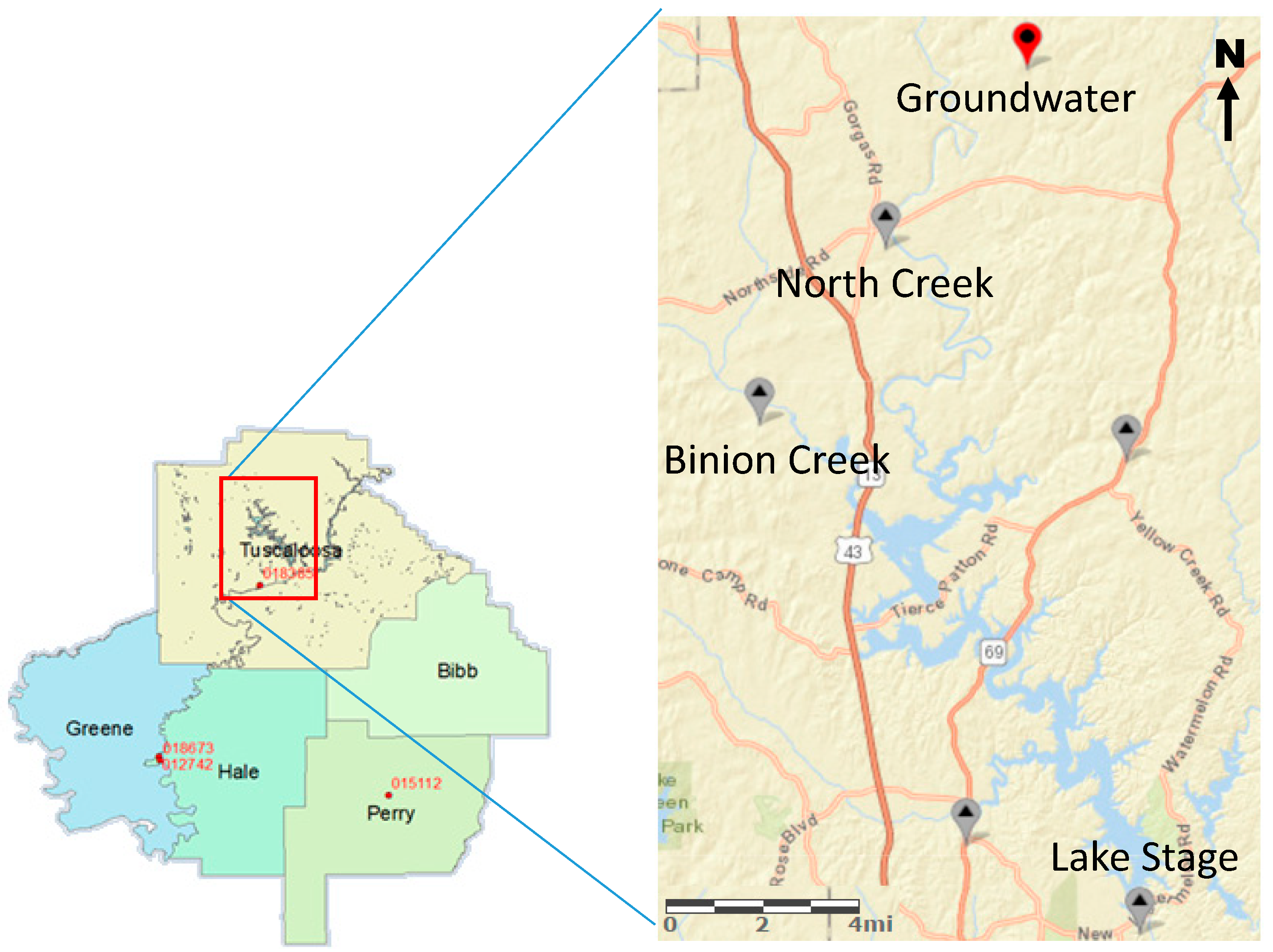
The locations of measurement stations are shown in
Figure 1. The primary precipitation station is ~13 km southwest of the lake, at the Tuscaloosa Municipal Airport, and is assumed to be consistent with rainfall in the watershed, as is the case for rain dominated systems with little topographic variation [
41]. The additional precipitation stations shown in
Figure 1 are used as a supplement to the primary station as discussed in the next section. The data were taken from the USGS National Water Information System (NWIS) for terrestrial water and National Centers for Environmental Information (NCEI) from National Oceanic and Atmospheric (NOAA) for precipitation. Data from the USGS were at a daily resolution and from NOAA at an hourly resolution.
Both the surface and subsurface records were relatively abundant to support reasonable statistical analysis in this study. The data with the longest period of record was the North Creek discharge, with the earliest record from 1938 to the present (i.e., a record of ~80 years with a daily resolution). Precipitation also had a long period of record, starting in 1958 and continuing to 2005. Lake stage and Binion Creek were recorded from 1982 and 1986, respectively. Groundwater data were recorded from 1979 to the present. Groundwater had an average depth from the land surface of approximately 13 m and was generally low in the winter. The vadose zone was comprised mostly of soils, which tended to be loam type soils that are often rich in clay minerals as is typical in the southeast U.S.
2.2. Storm Properties
A complete data series of hourly precipitation was built first, so that there were no missing values. The stations in Perry and Hale counties were first determined to be reasonable analogs by annual statistics. The storm properties were then calculated using the method proposed by Jiang et al. [
42]. We briefly review the methodology here, and further details can be found in that reference [
42].
Four properties were calculated for each storm, including storm duration, intensity, total precipitation, and inter-storm period. Storm duration was the number of consecutive hours of precipitation for a single storm which ended when there were six consecutive hours of no precipitation. Intensity was the average rainfall per hour in a single storm. Total precipitation was the amount of precipitation that fell during that storm. Inter-storm period was the number of consecutive hours with no precipitation that occurred between storms.
There are different possible values that can be used to define the inter-storm periods that have been used in the literature. For this study, six hours was chosen as the minimum value for an inter-storm period as it was a frequently used minimum in previous work [
36,
43,
44]. This minimum threshold for an inter-storm period also allowed for direct comparison to our previous work since it used the same minimum value for the inter-storm period [
42].
To explore the extremes of these properties, the data set was filtered so that the 95th percentile of each property was isolated. These extreme data points were then analyzed against groundwater head fluctuations and fitted with the distributions separately, as well as the entire set of storm properties for further comparison. The distributions used are discussed later in this section.
2.3. Hurst Exponent
The Hurst exponent is a measure of the memory of a time series, meaning how strong the influence of past values is on future values. The Hurst exponent was originally developed to optimize the dam’s size in the 1950s when evaluating the reservoir storage [
27]. It has since been improved and used in many signal processing applications [
28,
29,
30,
31,
32]. This study used the method proposed by Habib et al. [
45] to calculate a time-scale local Hurst exponent using the following four equations:
Here Equation (1) gives the scaling function (F(S)) which is approximately equal to scale (S) raised to the Hurst exponent (H). Equation (2) develops a cumulative sum (Y) where Xk is a specific value and 〈x〉 is the series mean. Equation (3) determines the variance (F2) of each section by subtracting a best fit polynomial of order n (Pn). Finally, Equation (4) finds the (square root of the) average variance for all segments which defines the scaling function. Different values of Hurst exponents H represent different properties in a system. In this study, the calculated H is between 0 and 1. The range of 0 < H < 0.5 represents an anti-persistent series where high values are usually followed by low, and the range of H > 0.5 represents persistent series where high values are followed by high. It is also noteworthy that we used a window of 30 samples as our scale (S) when calculating the TSLHE.
2.4. Random Variable Distributions for Hydrological Processes
Here we introduce the three distributions for random hydrological variables. First, the Gaussian distribution, also known as the exponentially modified Gaussian distribution, can be used to capture the distribution for processes with a heavy tail in one direction. This distribution is defined by the following function with a stability index (
α), location parameter (
D), and scale parameter (
T):
This distribution is closely related to the normal (Gaussian distribution) except that it is modified by the stability index α, which controls the tailing behavior of the distribution.
The stable distribution is defined by the following function with a stability index (
α), skewness parameter (
β), scale parameter (
γ), and location parameter (
δ):
Here the stability index α controls the overall shape (i.e., pattern) of the distribution, with α = 2 reducing the distribution to a Gaussian distribution. The skewness parameter β controls the skewness of the distribution with a negative β resulting in a skewness to the left (representing extreme minimums), and a positive one causing a skewness to the right (representing extreme maximums). The other parameters do not affect the overall shape of the distribution, except for the overall expansion (by the scale parameter γ) and shift (by the location parameter δ).
The widely used Gumbel distribution is also used here as a control and comparison. The following equation gives the PDF of the Gumbel distribution with a location parameter (
µ) and scale parameter (
β) as the only two parameters for the distribution:
where
Another commonly used extreme value distribution is the Log-Pearson Type 3 distribution. This distribution is commonly used to fit a frequency distribution data, often when determining flood occurrence [
46]. The distribution is based on three parameters, which are location (
µ), scale (
β), and skewness (
γ). We introduced this function on the measurement data series since we did not find a single most effective distribution among the first three listed above. The distribution is defined by the following PDF:
where
Γ(x) represents the Gamma function.
The distributions mentioned above were parameterized in MATLAB or R using convenient optimization toolboxes that estimated the best fit parameters from the data. The Gumbel distribution was parameterized using the “evfit” function which estimated a maximum likelihood estimate of the parameters of the type one extreme value distribution (Gumbel) within a 95% confidence interval. The stretched Gaussian distribution was parameterized using the “exgauss_fit” function, which also used a maximum likelihood method but was bounded by a simple algorithm. The stable distribution was parameterized using the “stblfit” function which used Koutrouvelis’ method, an iterative, regression method which used an initial estimate of parameters and repeated using weighted regression runs until convergence criteria was met. The Log-Pearson distribution was parameterized using the “fisdist” function in R, which also used a maximum likelihood estimator method. We used the root mean square error (RSME) as a quantitative metric to determine goodness of fit and compare across different distributions.
3. Results
3.1. Temporal Variation of Precipitation Properties and Their Extremes
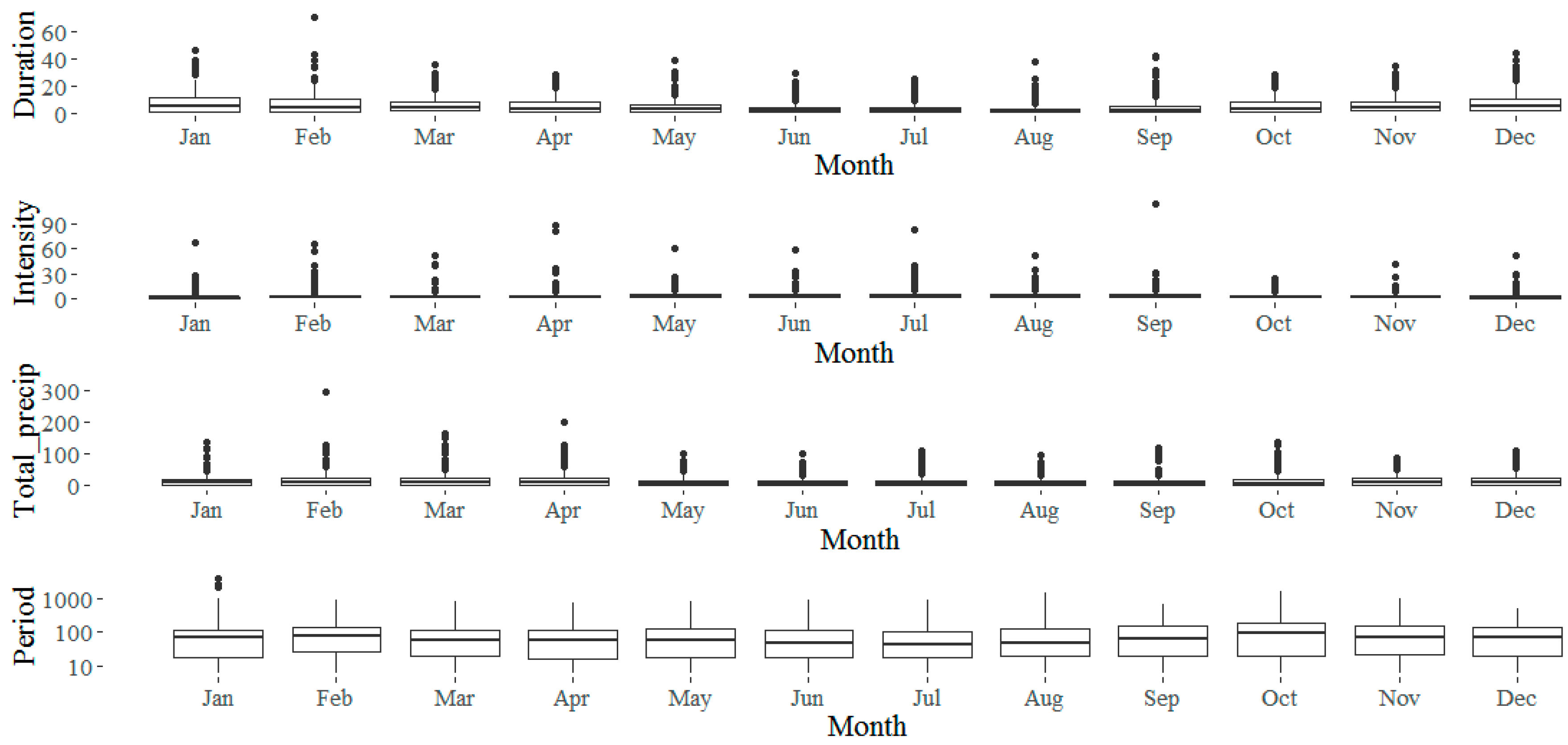
First, the seasonal distribution of storm properties was investigated. Box plots for each property are depicted for each month to show subtle temporal variations (
Figure 2). Duration and total precipitation had similar trends with highs coming in the winter season and lows in the summer. Particularly, February was on average the wettest month (
Figure 2), which was consistent with the local weather conditions. These two properties both tended to have their extremes come during winter months (especially February) when the average values were higher. Intensity had the opposite trend with the most intense precipitation coming in spring/fall and less intense storms in the winter. Intensity extremes had a random pattern with most extremes events occurring in spring and fall, such as April and September, which are the typical seasons for land-falling hurricanes. Inter-storm period did not have a significant trend annually for either average or extreme values, but did have its three largest values all occurring in January, the winter season.
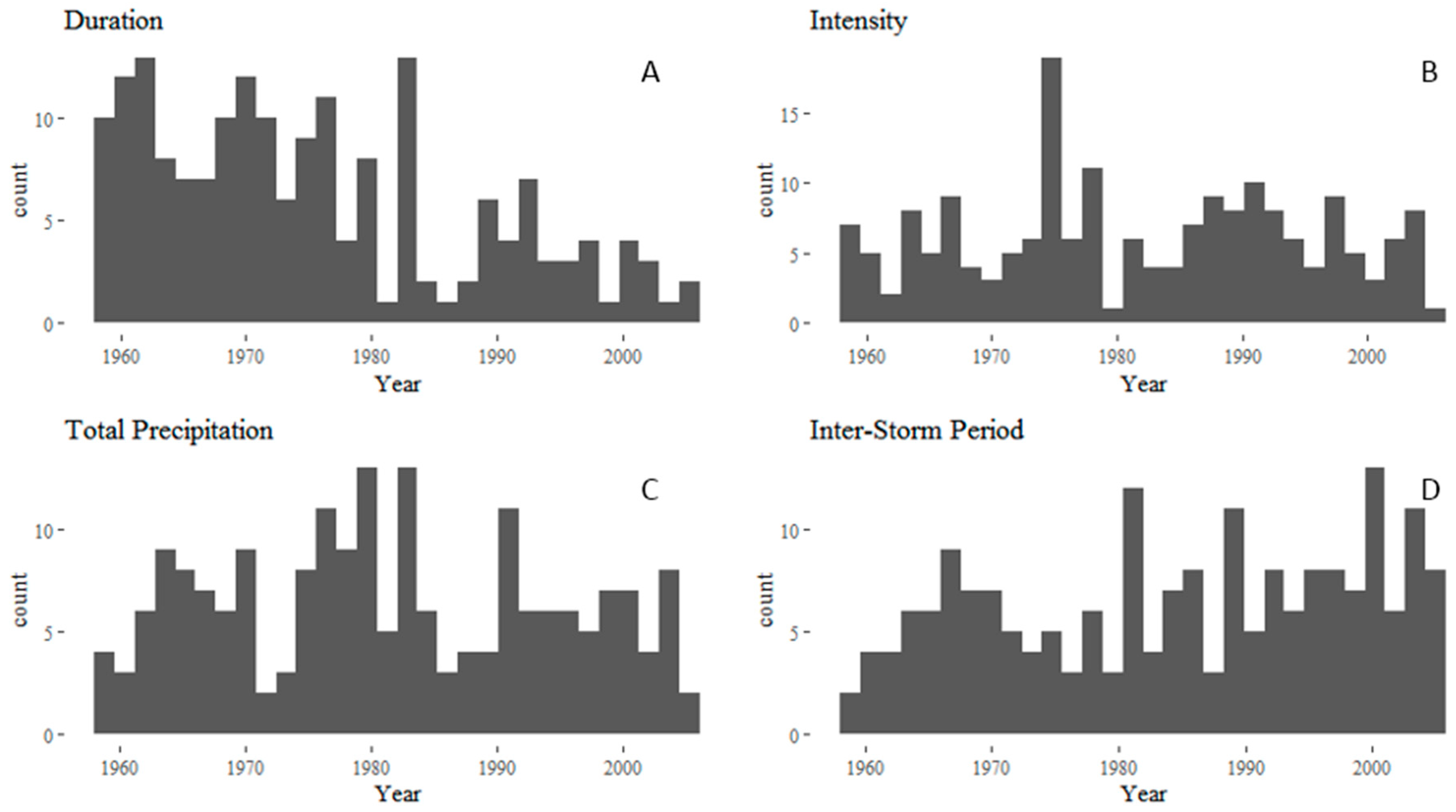
Evolution of the distribution for all storm properties was then evaluated to show when the extremes of precipitation occurred in the area (
Figure 3). Many of the duration extremes occurred in the start of the study period and their occurrence rate slowly declined with time. Inter-storm period had the opposite behavior with many of the extreme values coming in the most recent portion of the study period. Total precipitation and intensity had less obvious changes in the occurrence of their extremes. Extreme events of intensity became more frequent over the study period, with the plot of intensity extremes occurrence vs. time increasing slightly with time (
Figure 3).
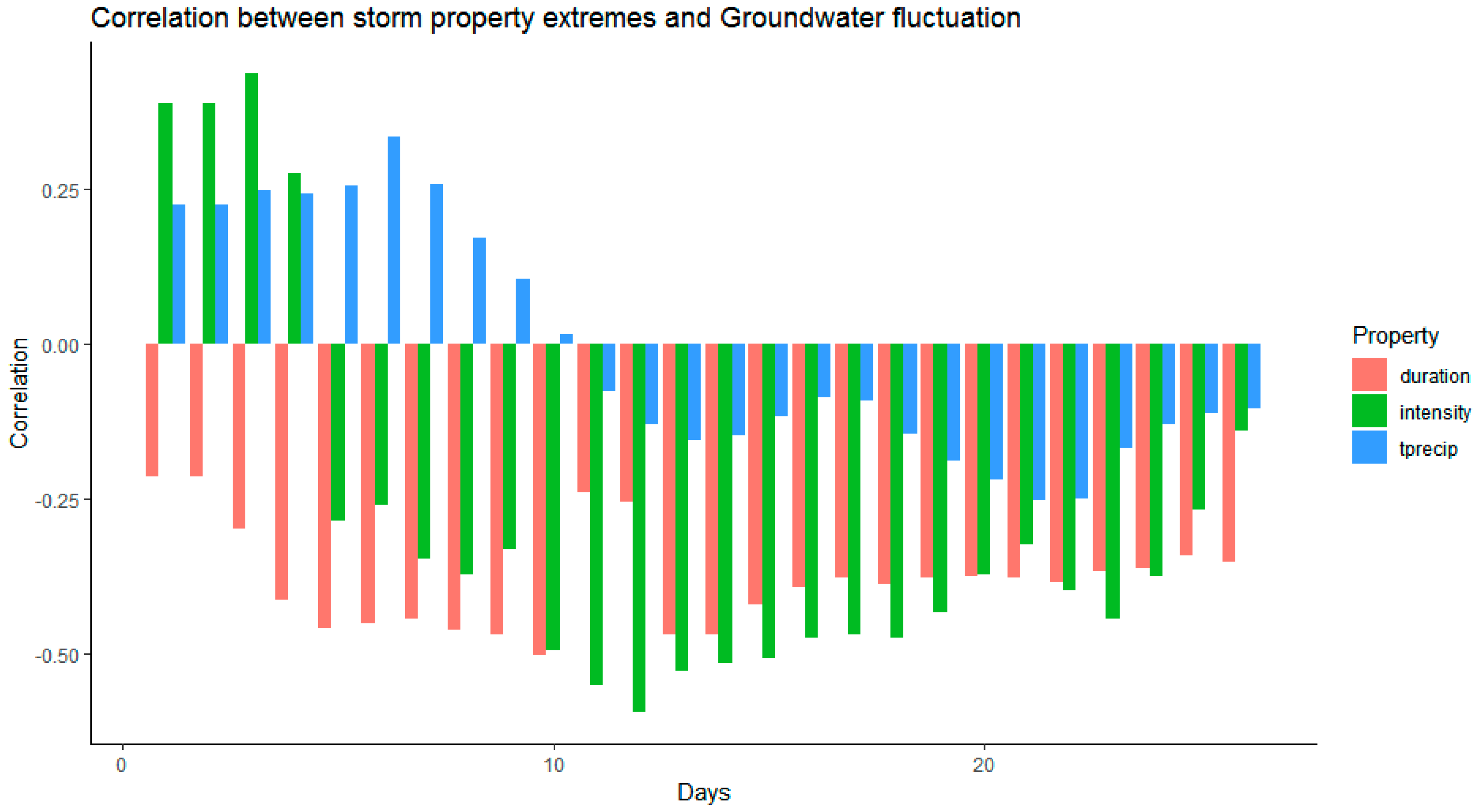
3.2. Correlation between Storm Properties and River/Groundwater
Figure 4 shows the correlation between the extreme values of precipitation characteristics (duration, intensity, and total precipitation), which are taken as the 95th percentile of each unique property compared to the fluctuation of groundwater head. Since groundwater fluctuation was measured using depth to groundwater surface, a decrease in depth to water corresponded to an increase in water storage in the aquifer since the water table was closer to the surface. The strongest correlation of all the studied storm properties was with intensity, with a maximum correlation coefficient of −0.6 at 12 days after the end of a rainfall event. Duration shows a relatively weaker correlation, but it is more consistent with peaks at −0.5 at 10 days. Total precipitation was weakly correlated to increased groundwater storage, peaking much after the other two storm properties mentioned above, at −0.25 at 21 days.
Due to the high frequency of precipitation at the study site (the average number of days with rainfall ≥0.25 mm is 111.3 days per year at the study site), the inter-storm period was often too short to effectively capture the effects of the interval arrival period between storms. Most of the inter-storm periods were usually only a few days long (13 days was the 95th percentile of inter-storm periods) and only 17 dry periods longer than 31 days were recorded over the entire precipitation record (~60 years).
Since surface water recharging to groundwater is a slow acting process (involving relatively slow infiltration through the ~13 m thick vadose zone), with other results showing ~13 days for peak influence for a storm to occur, these short periods only capture the effects of the previous precipitation event on groundwater head.
Stream discharge, however, cannot be correlated to storm properties in this study, because river response (within minutes to hours) to precipitation was faster than our measurement resolution (daily). We could not find a strong correlation at any time period measurable within the resolution of our data. This was likely due to the issue of storms ending in the middle of the day. This makes it difficult to correlate to fluctuations in river stages that occur within the first hours after a storm ends, since the next river measurements after the storm may occur as much as 23 h after the storm actually ends.
Due to these issues, the small sample size of usable inter-storm periods, and the rapid fluctuation in stream discharge, the results were not presented here or found to be significant at the site. Further investigations for inter-storm periods in more arid areas may provide meaningful and interesting insights. High resolution (ideally hourly) stream discharge data are needed to better correlate these fluctuations.
3.3. Time-Scale Local Hurst Exponent
Time-scale local Hurst exponents for all of the surface water data sets were also calculated and compared to those for extreme values.
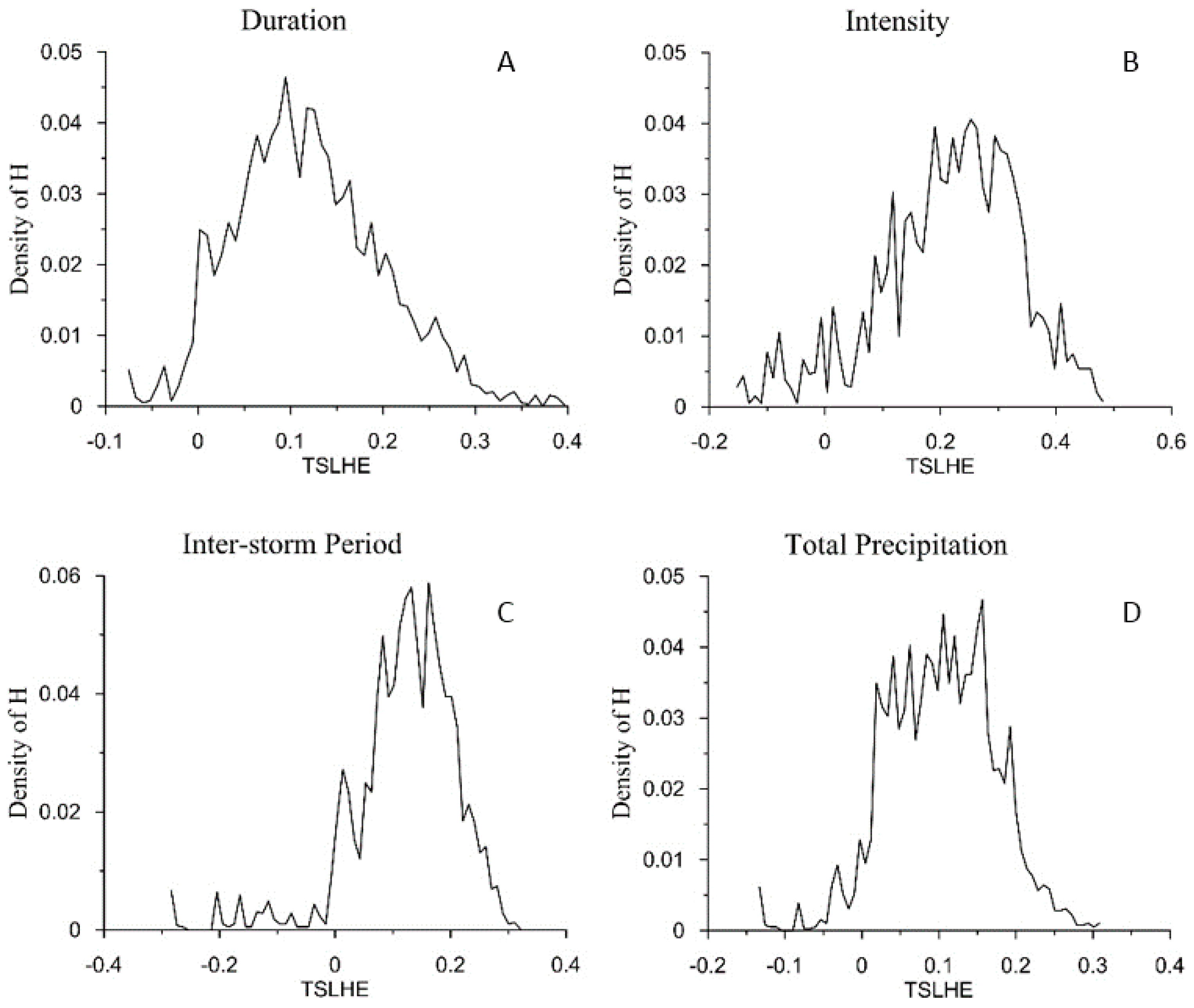
Figure 5 shows the distribution of TSLHE for the four precipitation properties. The modes of each data set are listed in
Table 1. The Hurst exponent revealed the memory present in each system. Streams tended to have a mode of
H slightly above 0.5, indicating that they have memory and that high values (in stream discharge) likely follow high values. Hence, streamflow discharge time series have at least some impact of memory in their behavior. Groundwater head fluctuation had a mode of
H very close to 1 (~0.963), indicating a highly persistent system with strong memory. This follows the expected trend of groundwater being a slowly evolving system that cannot rapidly transition from high to low values and vice versa.
The storm properties however exhibited different behaviors. The storm properties are also a time series that can be analyzed using DFA techniques in the TSLHE. All of the storm properties showed strongly anti-persistent TSLHE values with modes between H = 0.09 and H = 0.25 with maximum values never reaching 0.5 or the minimum threshold for some persistence. The TSLHE values for terrestrial water systems showed no significant correlation to storm properties for either the extreme values or the entire data sets.
3.4. Distribution Fittings
Below are the results from the distribution fittings using the three PDFs introduced in
Section 2.4.
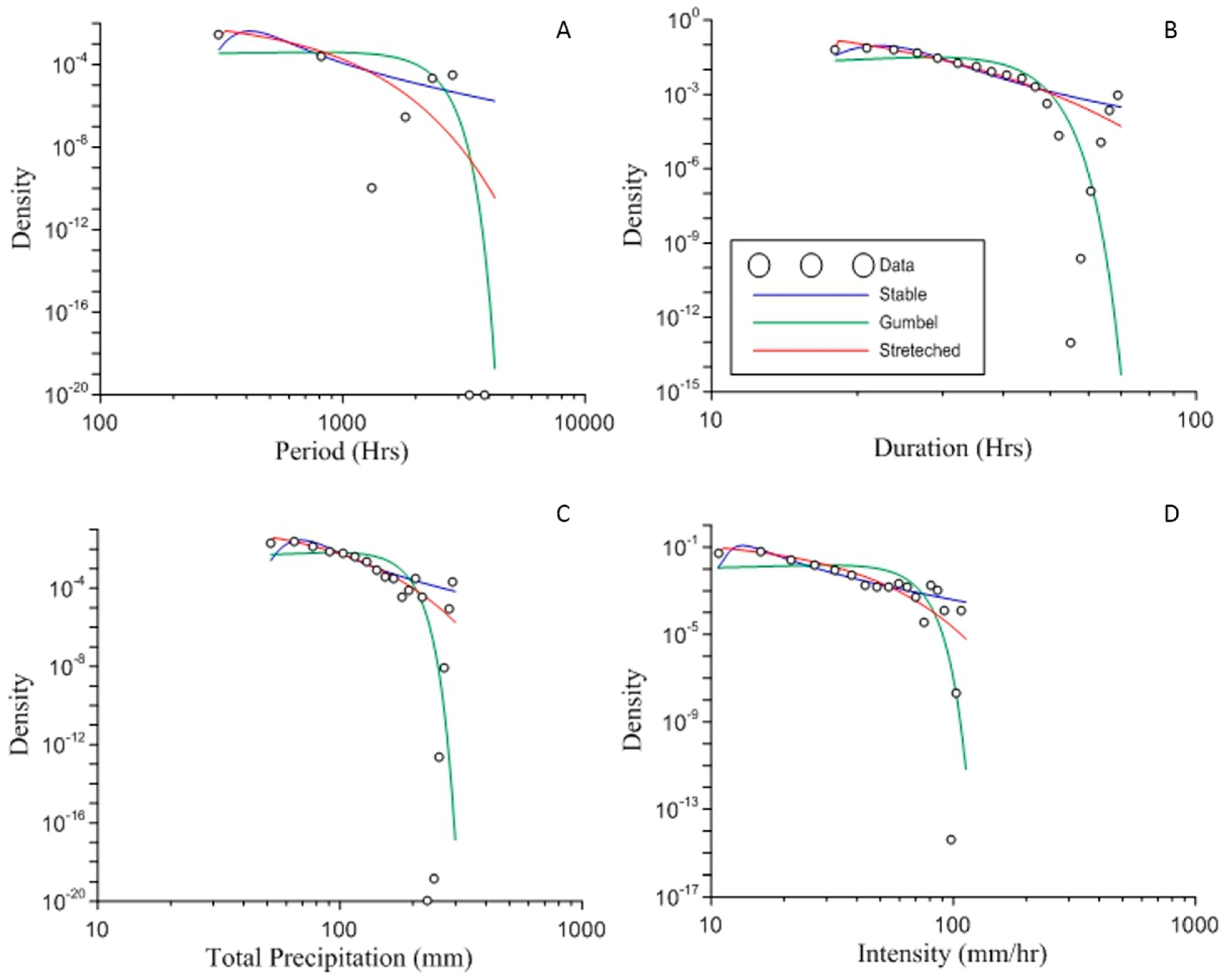
Figure 6 shows the graphical representation of the three distributions which fitted the actual data points for the extreme values of precipitation properties.
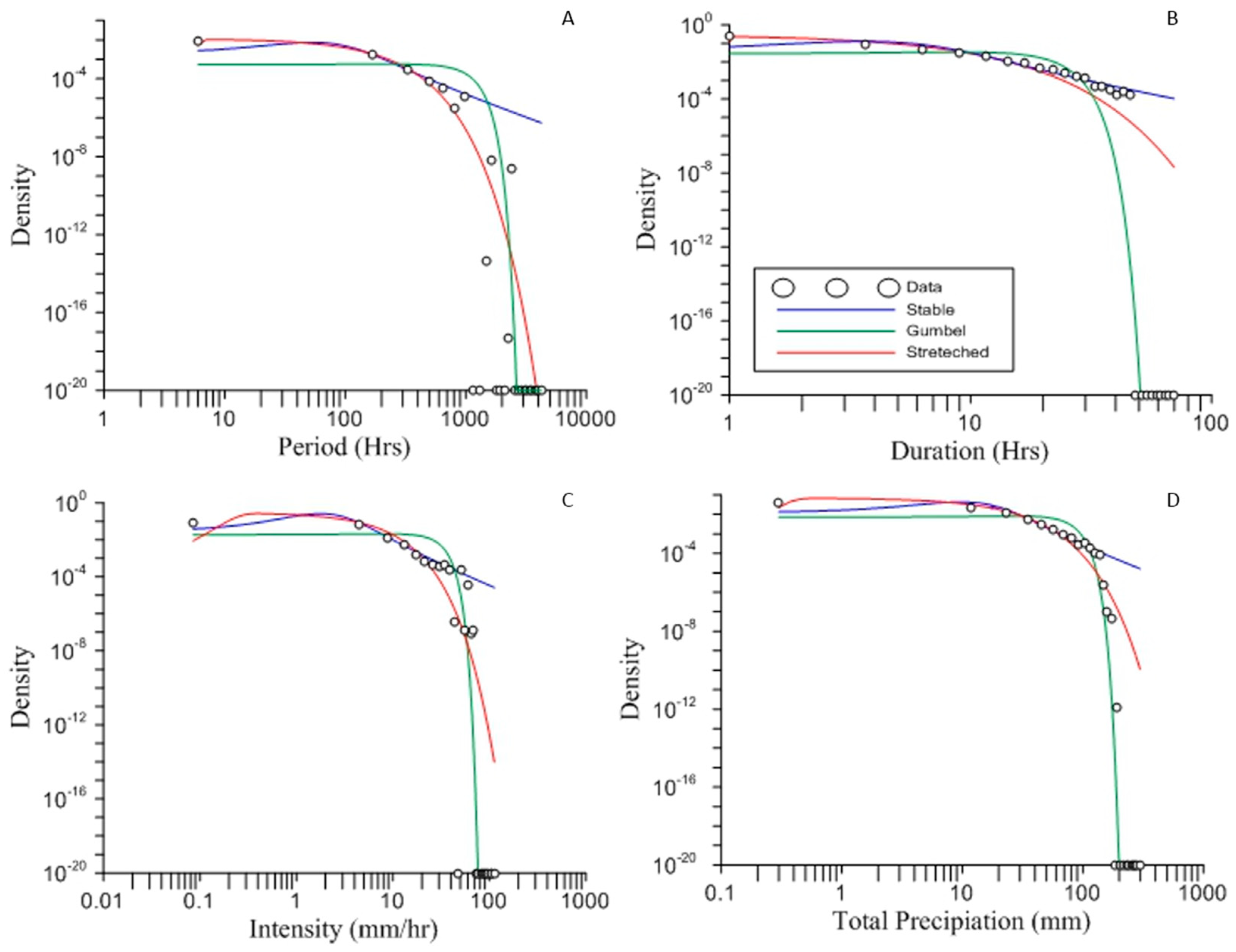
Figure 7 shows the graphs of the fittings of the full storm property value data sets to the three distributions.
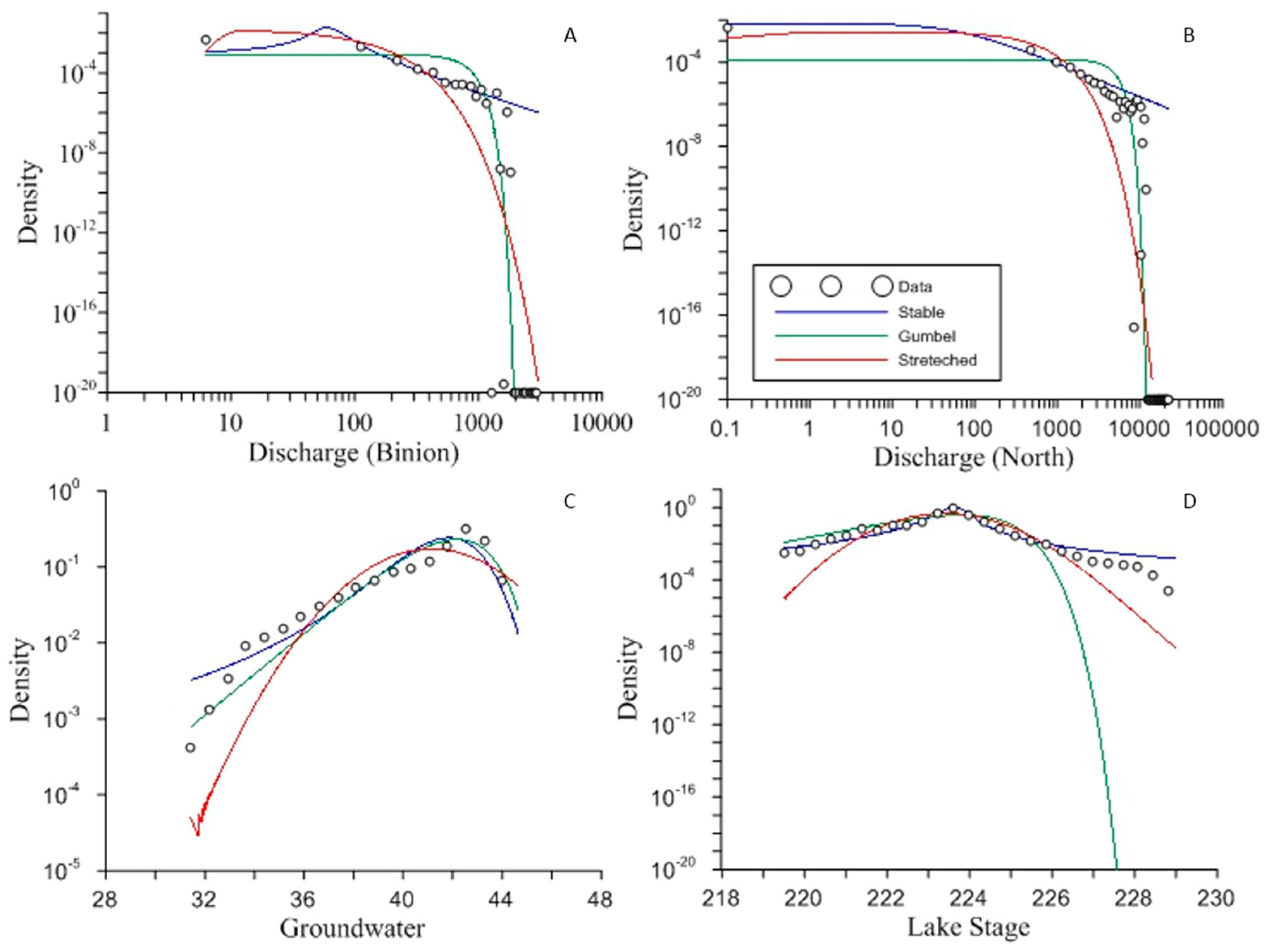
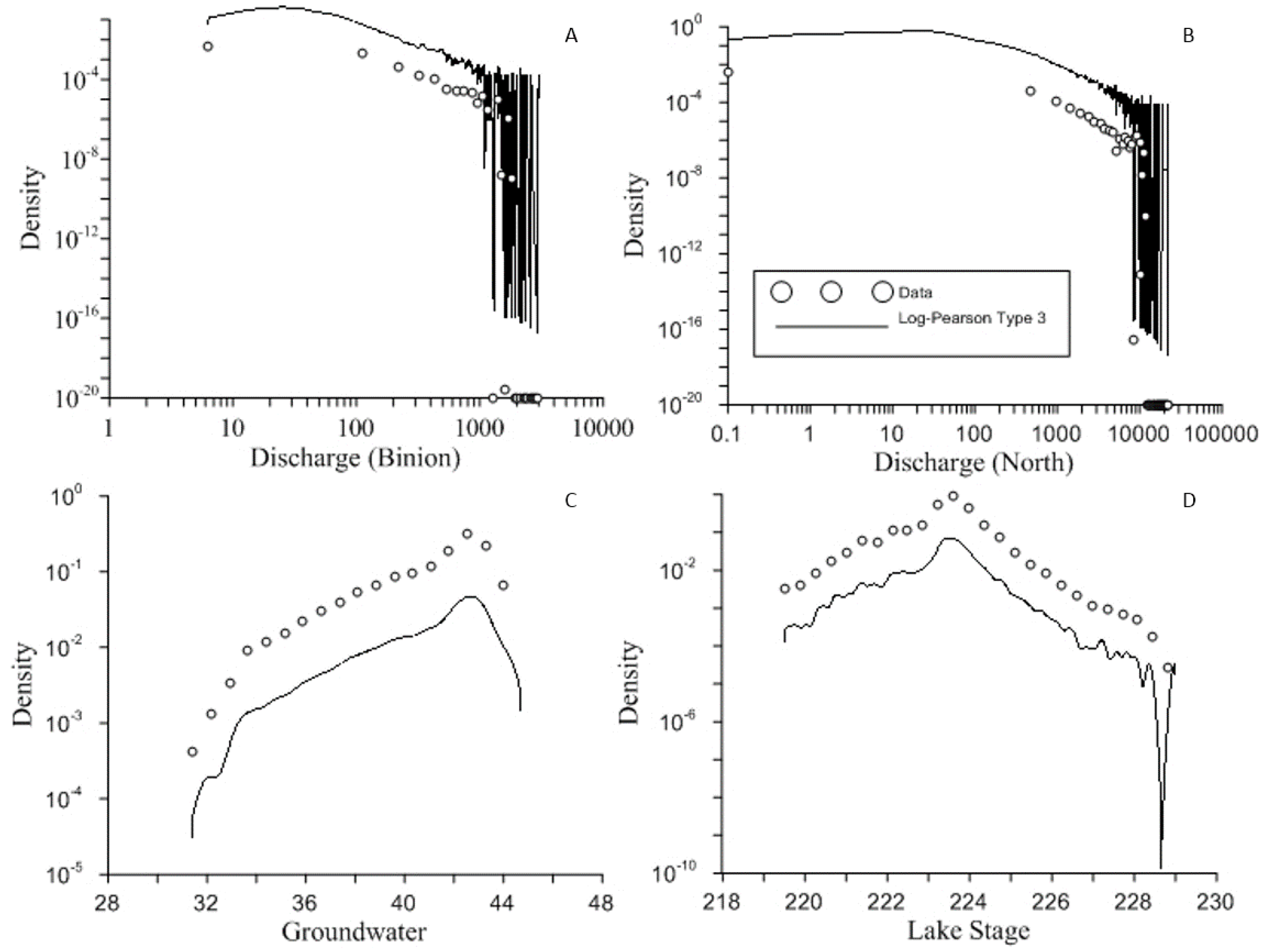
Figure 8 shows fitting results for lake stage, groundwater head fluctuation, and stream discharge using the Gumbel, Stretched Gaussian and Stable distributions.
Figure 9 shows these same series but fits the log-Pearson type 3 distribution.
Table 2 and
Table 3 show the root mean square error (RMSE) for each distribution compared to the storm properties and surface water/groundwater systems.
Table 4 and
Table 5 show the distribution parameters for the different direct measurements, the storm property full series, and the extremes.
4. Discussion
4.1. Surface Water
The distribution for all storm properties were compared to the time in the study period. Occurrence of extreme events over time were plotted to show the changes in precipitation behavior in the area. Many of the duration extremes occurred in the start of the study period and slowly declined with time. Inter-storm period had the opposite behavior, with many of the extreme values coming in the most recent portion of the study period. This would indicate that the region was experiencing shorter storms with longer dry spells in between, but does not necessarily indicate a dryer climate, since intensity is increasing, and total precipitation extremes are generally varying without a stable pattern. Changing climate was likely the driver for these changes, creating more intense, shorter storms, with longer dry periods in between. Furthermore, more intensive climate modeling is needed to fully investigate trends in storm properties. Current research suggests that these properties are changing but there is not a scientific consensus for a projection, and projections are variable in both space and time.
4.2. Storm Propertires Correlated with Groundwater Head Fluctutations
For the fluctuations of groundwater table, the strongest average correlation of any storm property was with intensity, with a maximum correlation coefficient of 0.5 at 10 days after the end of a rainfall event. There are two likely causes for this high correlation between storm duration and groundwater head fluctuation. First, a longer storm allows more time for a higher percentage of precipitation to infiltrate into the aquifer, instead of flowing away as overland flow/surface runoff and eventually discharging into streams and lakes, or evaporating. Second, the extreme values of storm duration occur more frequently in the winter months when there is lower evapotranspiration (ET) and withdrawal from the aquifer is lower during this time since there is less water used for irrigation.
Intensity had the next strongest correlation with groundwater head fluctuation. The highest correlation coefficient for intensity was actually higher than for storm duration; however, across the period where fluctuations were analyzed, there was generally a weaker correlation, and for the first four days the correlation was positive indicating a decrease in water supply. This transition time showed that there was a lag between the precipitation event and the first portion of precipitation to infiltrate to the water table. The peak correlation was at 12 days after the precipitation event ended and the correlation was −0.595, representing the point where the groundwater table reached its highest level after a precipitation event. Intensity tended to be higher in the summer months, so this explains the initial positive decrease in water level. This is because there is higher ET in the summer and there is some water withdrawal for irrigation in the area. After the peak correlation, the correlation slowly decreased, representing the return from the peak increase at 12 days.
Interestingly, total precipitation had the weakest correlation with groundwater head fluctuation of the three properties analyzed with a peak correlation coefficient of −0.253 at 20 days after precipitation events. There is a positive correlation (indicating a decrease in groundwater storage) for the first 10 days, peaking at six days after precipitation, transitioning to a negative correlation (increased GW storage) after day 10. The high total precipitation likely exceeded the infiltration capacity of the soils and a significant portion of the precipitation was discharged into surface water systems or as overland flow. Extreme values of total precipitation are less temporally dependent than the other variables, and generally the winter months have higher total precipitation.
4.3. Time-Scale Local Hurst Exponents and System Memory
The TSLHE values for groundwater head fluctuation, lake stage, and river discharge all showed that they were persistent or semi-persistent series since their modes were above H = 0.5. Groundwater was the slowest evolving system so that likely caused it to have the highest value, followed by lake stage. The lake stage was faster evolving than groundwater, but slower than river discharge, leading to the increase in total correlation. The TSLHE also showed that precipitation properties do not have memory acting on them and are actually anti-persistent across all values, and reverse more frequently than white noise would. This may be because a major storm would use much of the available atmospheric moisture and result in following storms being weaker and not as intense or long lasting.
4.4. Distribution Evaluation
For the distribution fittings of storm properties, the stretched Gaussian distribution performed the best across all of the data series except for the extreme values of duration where the tempered stable distribution was found to be the more effective. The Gumbel distribution was consistently the least effective distribution for capturing storm properties, often overestimating low values and underestimating the extremes of precipitation. The stretched Gaussian produced a RMSE of approximately half the RMSE of the stable distribution for the values where it was most effective. The stretched Gaussian is effective in these data sets because it mixes the properties of the standard Gaussian distribution, which captures the small, more frequent values, and the power law distribution, which is able to capture the extreme values. The stable distribution generally overestimates the lower, more frequent values and underestimates the extreme values, but remains a viable option for fitting these data. The different data sets all had differing parameters for the distribution, however, there was no major trend across all sets. Generally, the extreme events and full data sets for storm properties have similar parameters for each distribution.
For the measured data from lake stage, groundwater head fluctuations, and stream discharge there were varying results in distribution effectiveness. First the Gumbel, stable and stretched Gaussian distributions were tested. The Gumbel distribution was the best of these distributions to fit the values of depth to groundwater. The depth to groundwater surface had the narrowest range of all the systems, and hence the Gumbel distribution was able to effectively capture it. The stable distribution was the most effective of these three distributions for lake stage. Lake stage had a negative tail and very sharp peak value, likely due to its quick response to storm events. This peak and light negative tail allowed the stable distribution to fit it most effectively. The two creeks had different results. The larger creek, North Creek, was best fit by the stable distribution as it had a weaker tail compared to the smaller creek. Binion Creek had a heavier tail of extreme values and was captured most effectively by the stretched Gaussian distribution.
Since there was not a single distribution that proved most effective in capturing these different values, we also tested the Log-Pearson Type 3 distribution to try to find a single most effective distribution. The Log-Pearson gave the best RSME value for both lake stage and for the depth to groundwater measurements. Both of these measurement series had a much more “normal” shape (i.e., closer to standard Gaussian behavior, and weaker tailing behavior), suggesting that the Log-Pearson Type 3 distribution may perform better on series without large tails. The Log-Pearson also exhibited erratic behavior at the extreme values of river discharge since there were values that did not occur in our data sets (i.e., a density of 0) which caused the density curve to change values rapidly. Since these series were from different parts of the water cycle, and controlled by different processes, there may not be a single distribution that will most effectively capture all of them. There are a variety of different extreme value distributions that could possibly be used to effectively capture these series more effectively, such as the generalized extreme value, two-component extreme value, or generalized Pareto distributions, which will be evaluated for details in a future study.
5. Conclusions
This study conducted statistical analysis to reveal the distribution, memory, and correlation in surface and subsurface water observed in the Lake Tuscaloosa watershed in Tuscaloosa, AL. Three main conclusions are obtained.
First, statistical analysis shows that precipitation properties can be correlated to groundwater head fluctuations and different properties can have an influence on the motion of water. Duration was more closely related to the fluctuation of groundwater head than any of the other studied properties, and had a peak correlation at 10 days after the end of the precipitation event for the ~13 m deep well. Intensity had a stronger peak correlation to groundwater head fluctuation at 12 days but was more variable and had a worse average correlation than duration. Total precipitation was weakly correlated compared to the other two properties indicating that it had the least control over recharge.
Second, the surface and groundwater series are found to be persistent from the TSLHE values. Groundwater followed by lake stage was the most persistent. The TSLHE for stream discharge was very close to the values for white noise. Precipitation properties were anti-persistent, with the values entirely constrained in the anti-persistent range of TSLHE for all properties and hourly values. This was the expected result since the most persistent series were the slowest evolving with more volatile systems being heavily anti-persistent. TSLHE itself was not distributed with any meaningful relationship to storm properties and was likely driven by annual processes.
Third, the stretched Gaussian distribution was found to be the most effective distribution in capturing the storm properties for both the extreme values and the entire data sets. This distribution was likely most effective due to its mix of properties of the Gaussian and power law distributions. In other words, it allows to capture the peak frequency values as well as the lower frequency extreme values that are vital to understanding a system like the water cycle. For the surface and groundwater distributions, however, there was not a clear best distribution, since the different systems had different best RSME values, and the stream discharge best distributions differed between the two streams. Further analysis with more data is needed to resolve the best distribution, which may not be any of those tested here, for these different systems.