Using Desalinated Water for Irrigation: Its Effect on Field Scale Water Flow and Contaminant Transport under Cropped Conditions
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Physical Domain and its Parametrization
2.2. The Flow and Transport Scenarios and their Implementation
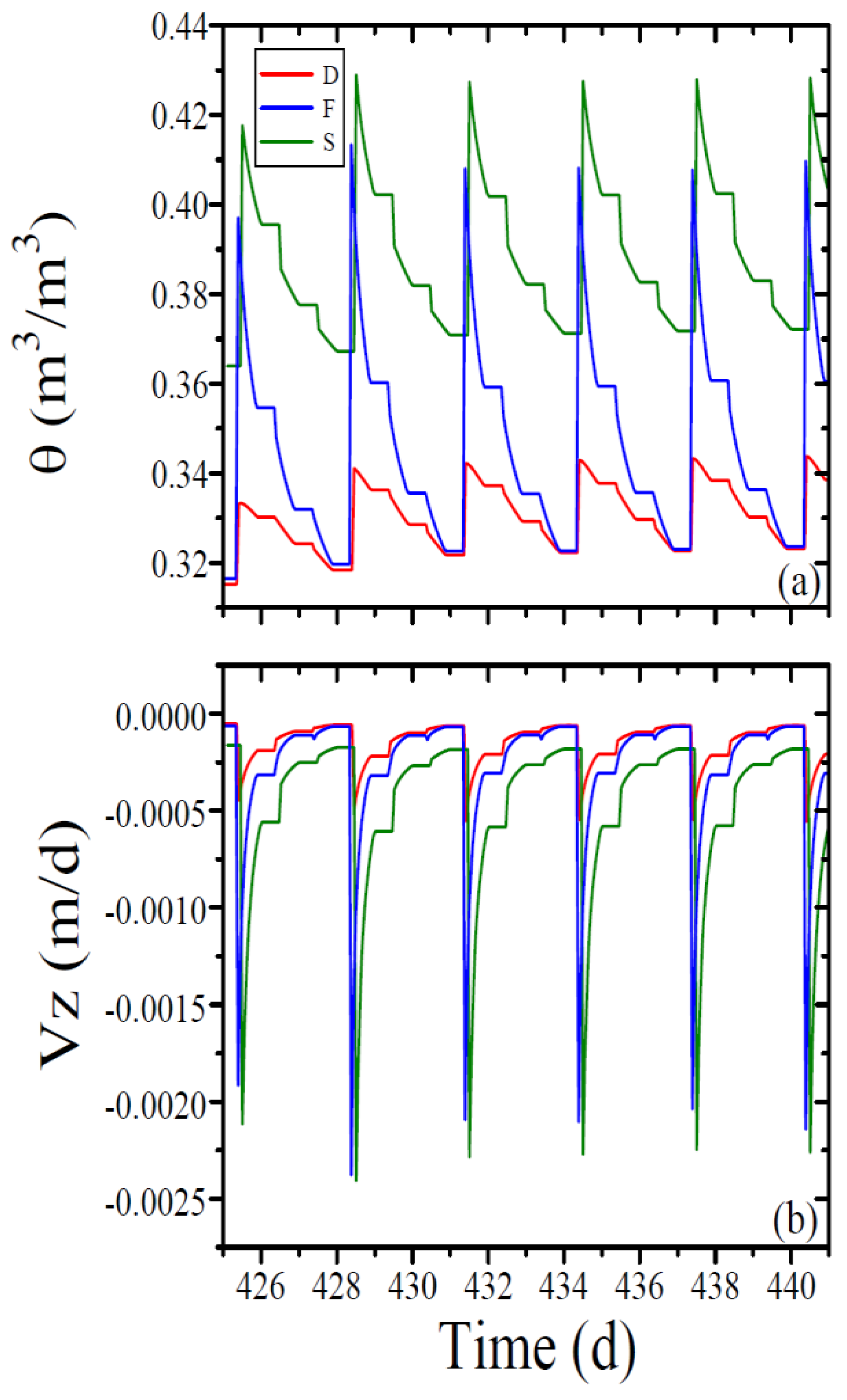
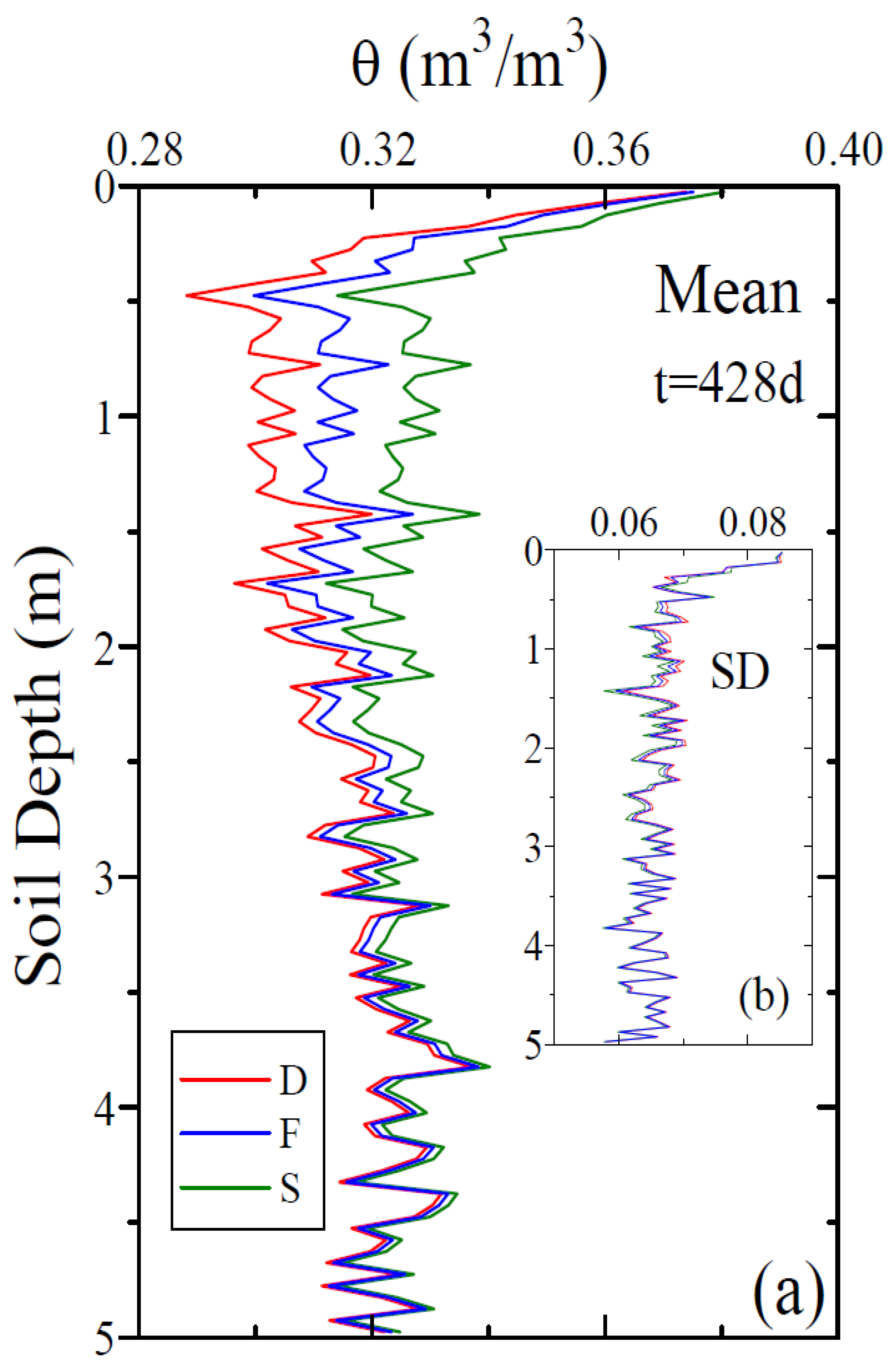
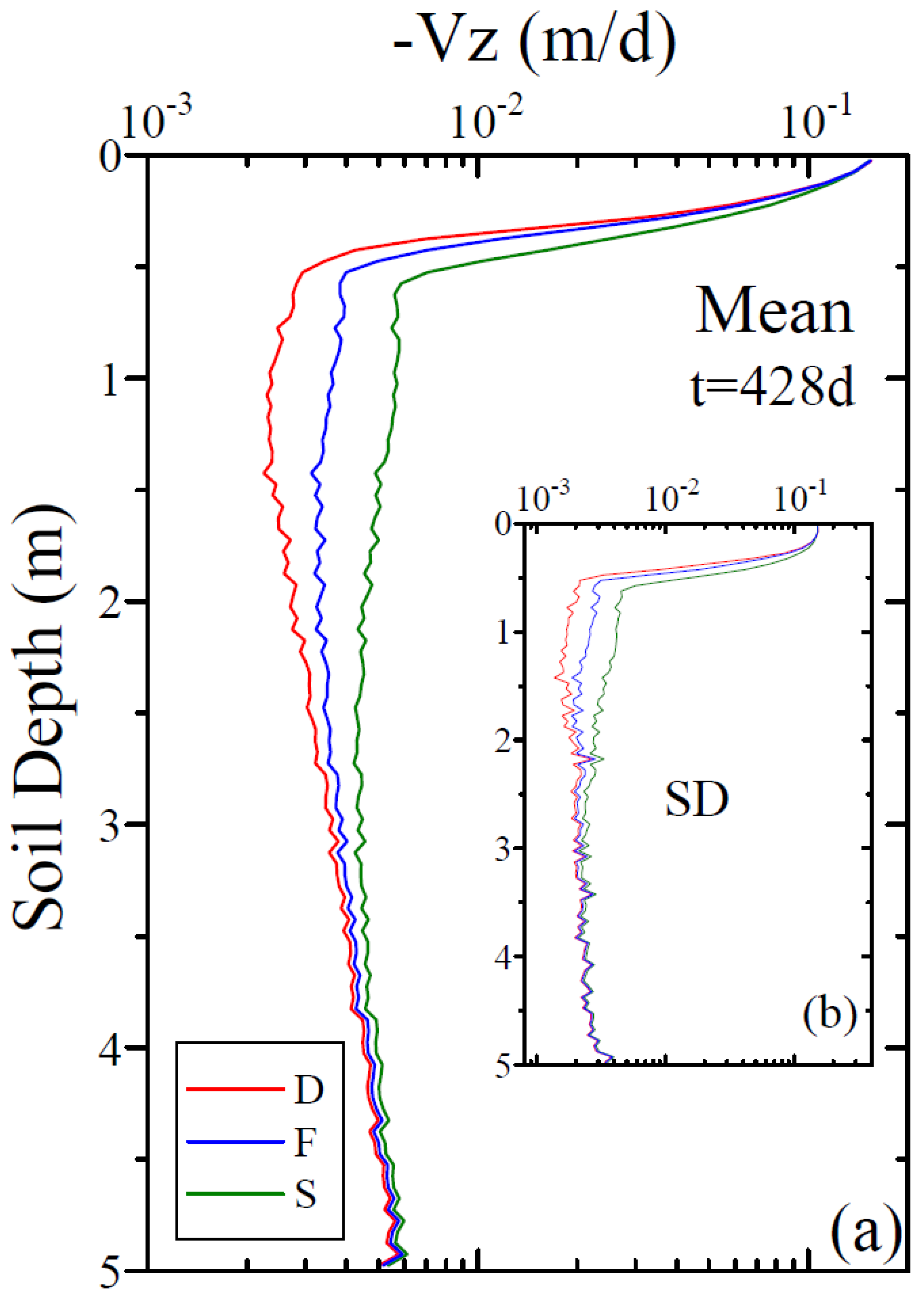
3. Results
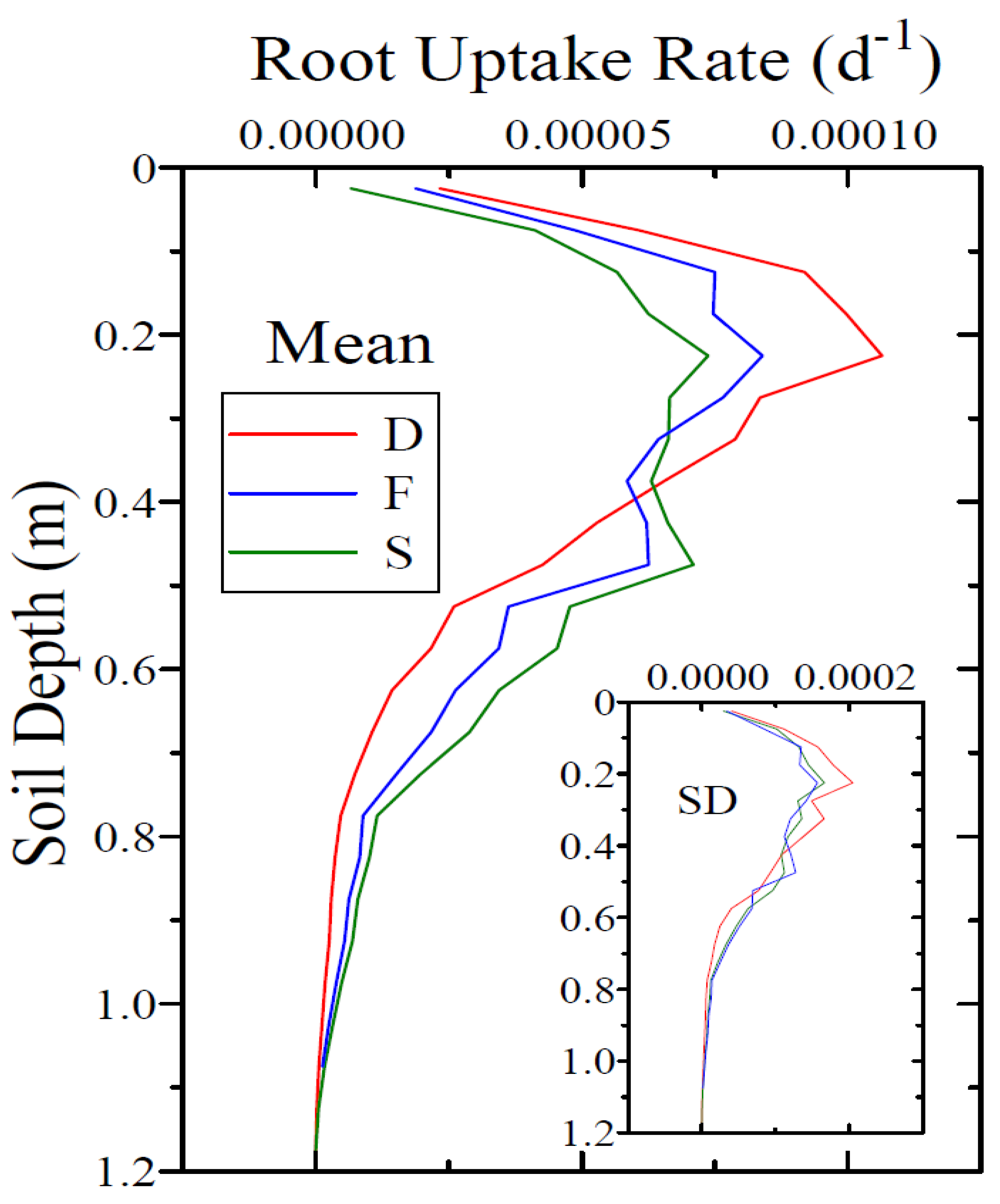
3.1. Water Uptake by the Trees’ Roots
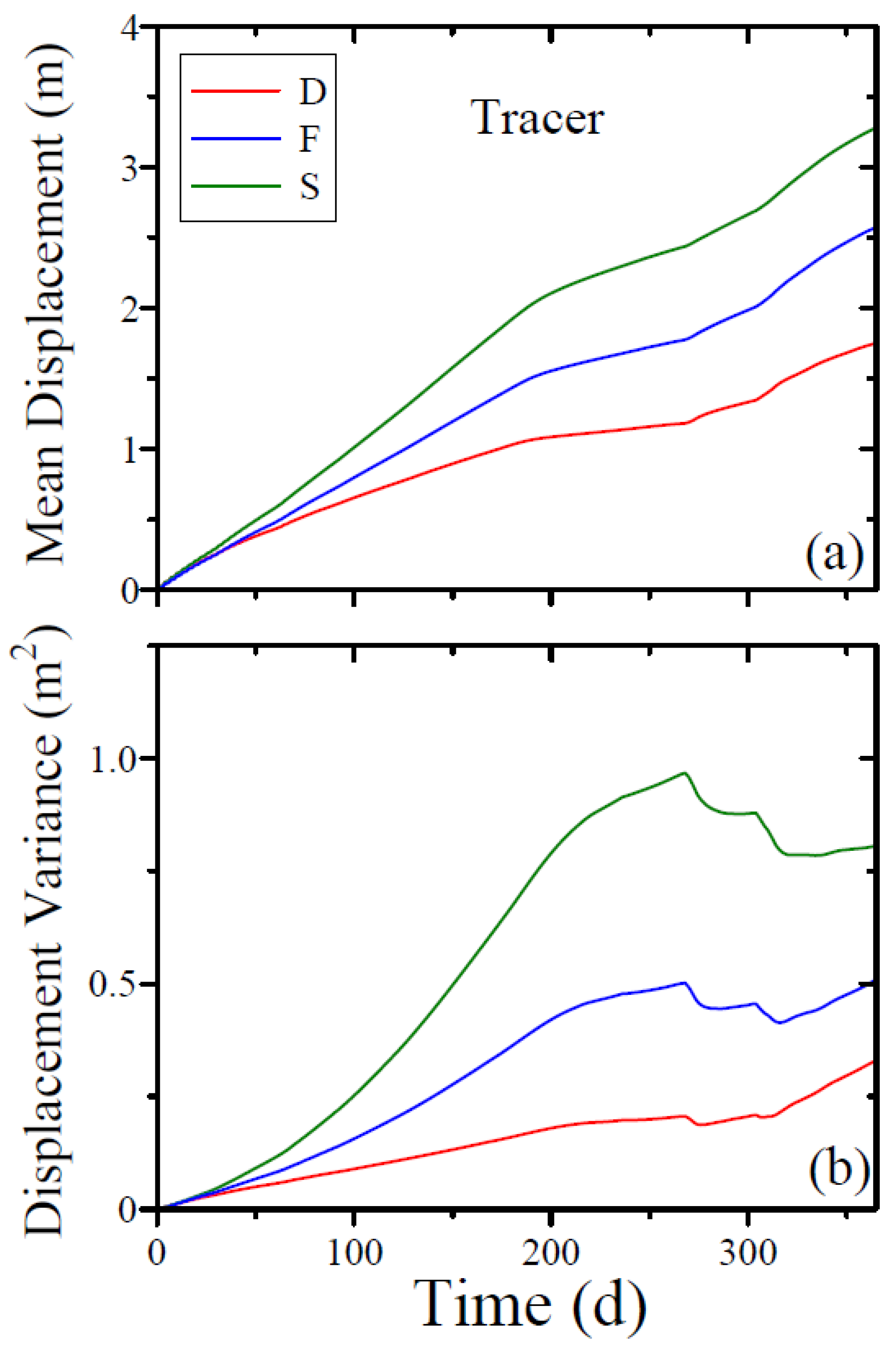
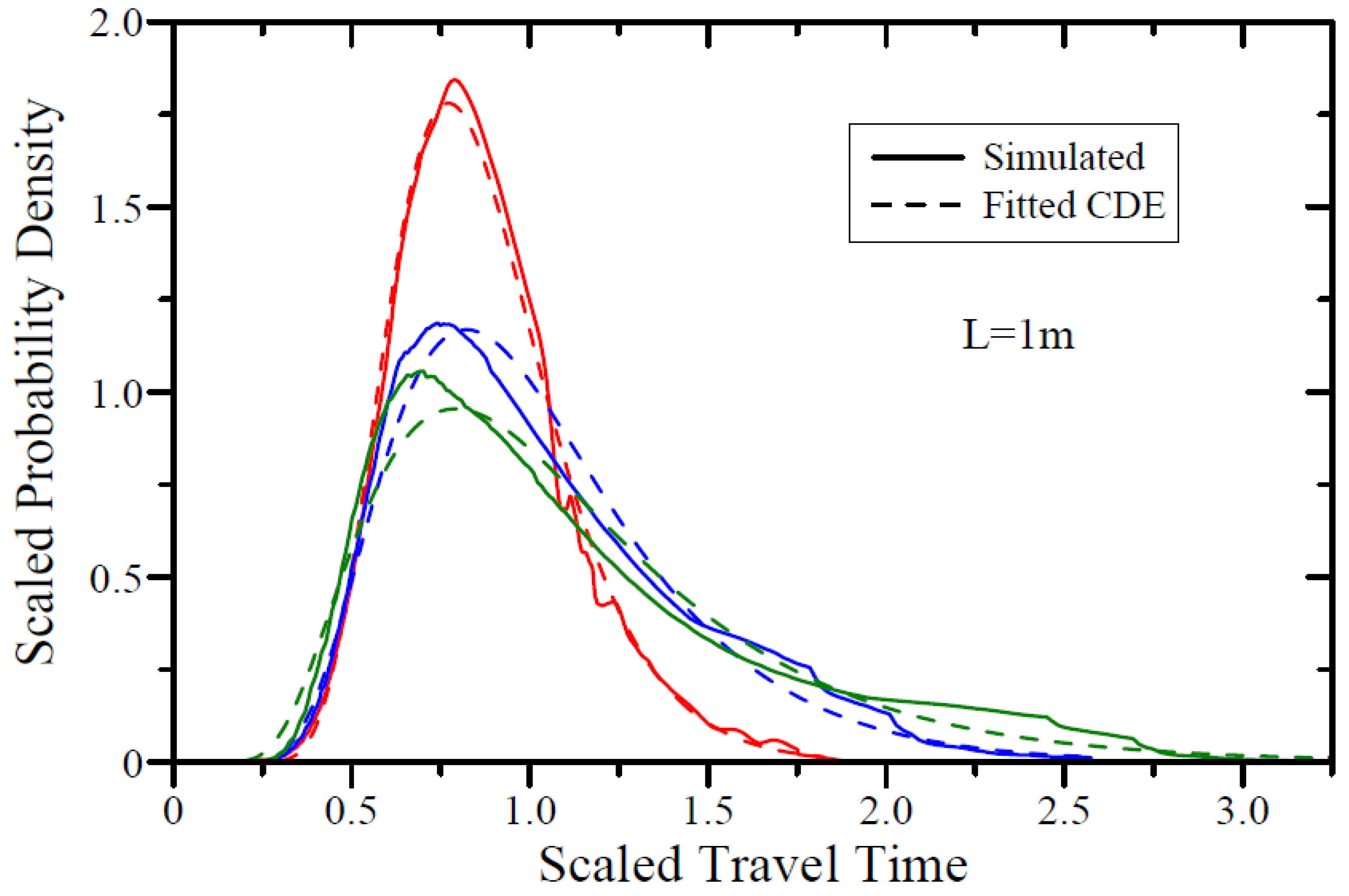
3.2. Movement, Spread, and Breakthrough of a Pulse of a Solute Tracer
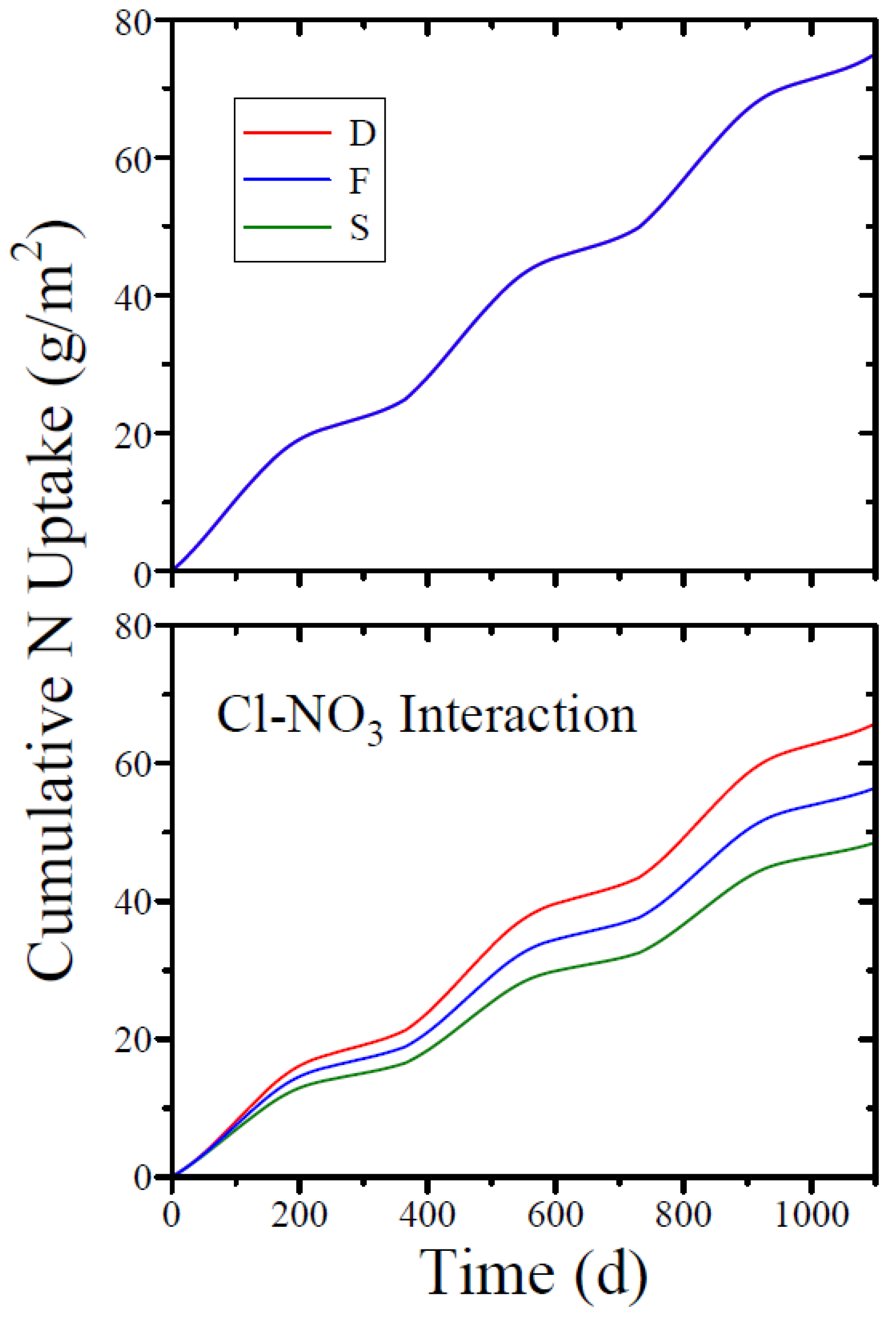
3.3. Nitrogen Uptake by the Trees’ Roots
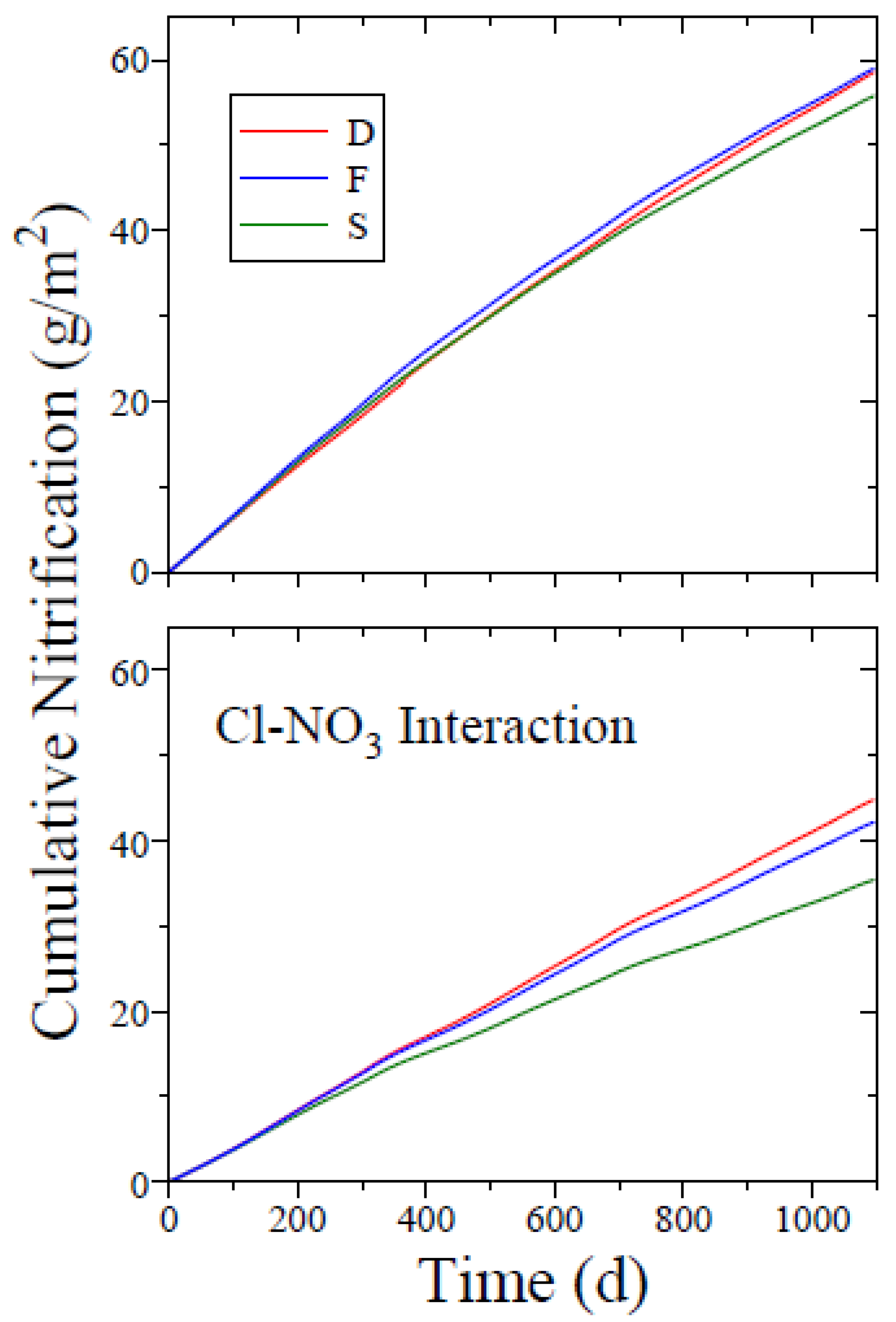
3.4. Nitrification, Denitrification, and Volatilization
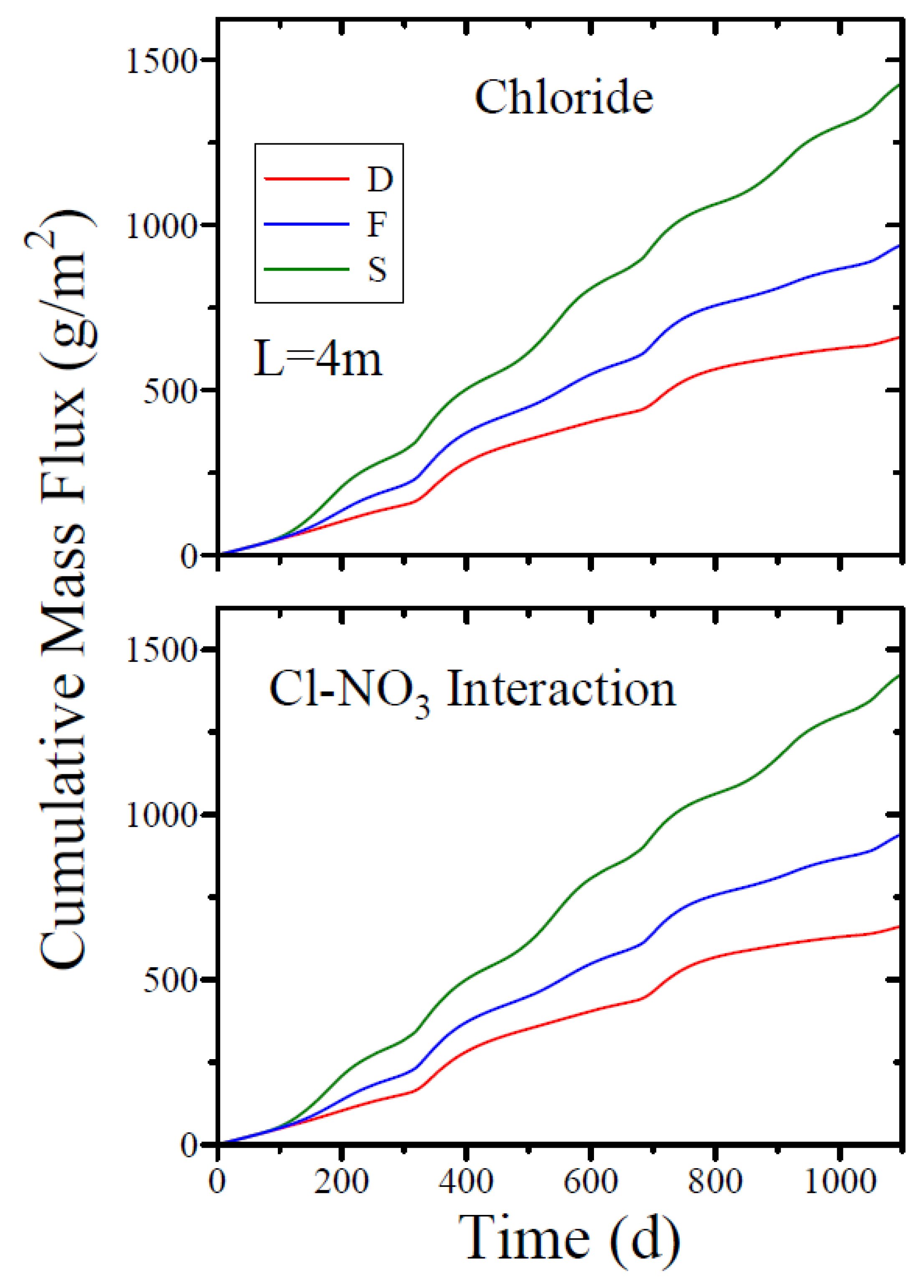
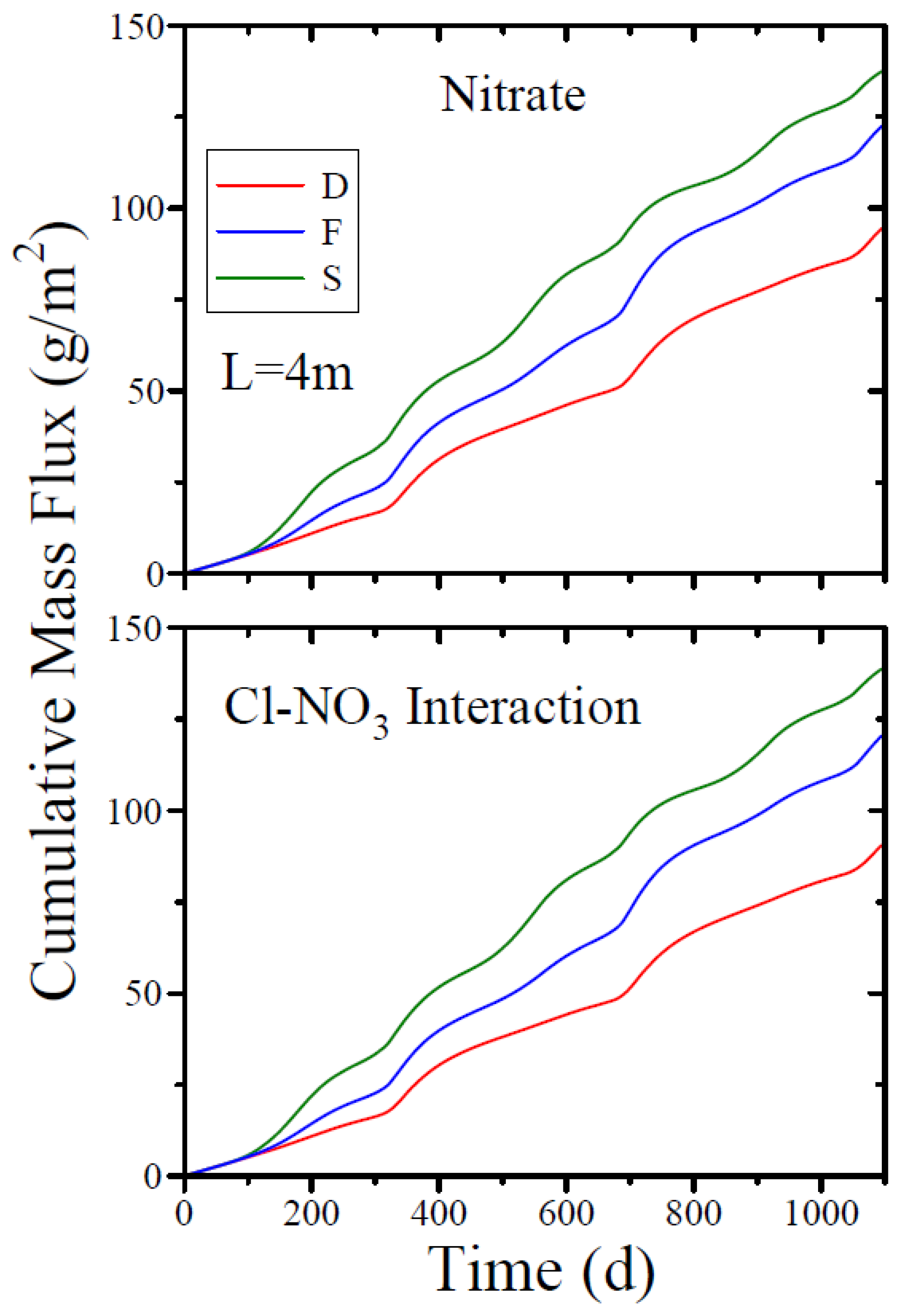
3.5. Contaminant Leaching
4. Discussion
5. Summary and Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gao, L.; Yoshikawa, S.; Iseri, Y.; Fujimori, S.; Kanae, S. An Economic Assessment of the Global Potential for Seawater Desalination to 2050. Water 2017, 9, 763. [Google Scholar] [CrossRef]
- Hanasaki, N.; Yoshikawa, S.; Kakinuma, K.; Kanae, S. A seawater desalination scheme for global hydrological models. Hydrol. Earth Syst. Sci. 2016, 20, 4143–4157. [Google Scholar] [CrossRef]
- Stanhill, G.; Kurtzman, D.; Rosa, R. Estimating desalination requirements in semi-arid climates: A Mediterranean case study. Desalination 2015, 355, 118–123. [Google Scholar] [CrossRef]
- Israel Water Authority. Consumption of Potable Water in 2017 (in Hebrew). 2018. Available online: http://www.water.gov.il/Hebrew/ProfessionalInfoAndData/Allocation-Consumption-and-production/20172/shafirim_mavo_2017.pdf (accessed on 31 March 2019).
- Israeli Government Decision Number 3866, 2018. A Strategic Plan for Dealing with Drought Periods in the Years 2018–2030 (in Hebrew). 2018. Available online: https://www.gov.il/he/Departments/policies/dec3866_2018 (accessed on 31 March 2019).
- Israel Water Authority. Data on Freshwater Consumption for Agriculture from the National Water System (in Hebrew). 2018. Available online: http://www.water.gov.il/Hebrew/ProfessionalInfoAndData/Allocation-Consumption-and-production/DocLib7/agriculture-consumption-2015-2016.pdf (accessed on 31 March 2019).
- Shlezinger, M.; Amitai, Y.; Akriv, A.; Gabay, H.; Shechter, M.; Leventer-Roberts, M. Association between exposure to desalinated sea water and ischemic heart disease, diabetes mellitus and colorectal cancer; A population-based study in Israel. Environ. Res. 2018, 166, 620–627. [Google Scholar] [CrossRef]
- Lehmann, O.; Eckhaus, O.; Lahav, O.; Birnhack, L. Replenishing Mg(II) to desalinated water by seawater nanofiltration followed by magnetic separation of Mg(OH)2(s)Fe3O4 particles. Desalin. Water Treat. 2016, 57, 19903–19916. [Google Scholar] [CrossRef]
- Ganot, Y.; Holtzman, R.; Weisbrod, N.; Russak, A.; Katz, Y.; Kurtzman, D. Geochemical processes during managed aquifer recharge with desalinated seawater. Water Resour. Res. 2018, 54, 978–994. [Google Scholar] [CrossRef]
- Negev, I.; Guttman, J.; Kloppmann, W. The Use of Stable Water Isotopes as Tracers in Soil Aquifer Treatment (SAT) and in Regional Water Systems. Water 2017, 9, 73. [Google Scholar] [CrossRef]
- Ganot, Y.; Holtzman, R.; Weisbrod, N.; Nitzan, I.; Katz, Y.; Kurtzman, D. Monitoring and modeling infiltration–recharge dynamics of managed aquifer recharge with desalinated seawater. Hydrol. Earth Syst. Sci. 2017, 21, 4479–4493. [Google Scholar] [CrossRef]
- Yermiyahu, U.; Tal, A.; Ben-Gal, A.; Bar-Tal, A.; Tarchitzky, J.; Lahav, O. Rethinking desalinated water quality and agriculture. Science 2007, 318, 920–921. [Google Scholar] [CrossRef]
- Lahav, O.; Kochva, M.; Tarchitzky, J. Potential drawbacks associated with agricultural irrigation with treated wastewaters from desalinated water origin and possible remedies. Water Sci. Technol. 2010, 61, 2451. [Google Scholar] [CrossRef] [PubMed]
- Ben-Gal, A.; Yermiyahu, U.; Cohen, S. Fertilization and Blending Alternatives for Irrigation with Desalinated Water. J. Environ. Qual. 2010, 38, 529–536. [Google Scholar] [CrossRef] [PubMed]
- Russo, D.; Laufer, A.; Silber, A.; Assouline, S. Water uptake, active root volume and solute leaching under drip irrigation: A numerical study. Water Resour. Res. 2009, 45, W12413. [Google Scholar] [CrossRef]
- Kurtzman, D.; Shapira, R.; Bar-Tal, A.; Fine, P.; Russo, D. Nitrate fluxes to groundwater under citrus orchards in Mediterranean climate observations, calibrated models, simulations and agro-hydrological conclusions. J. Contam. Hydrol. 2013, 151, 93–104. [Google Scholar] [CrossRef] [PubMed]
- Massa, D.; Mattson, N.S.; Lieth, H.J. Effects of saline root environment (NaCl) on nitrate and potassium uptake kinetics for rose plants: A Michaelis–Menten modeling approach. Plant Soil 2009, 318, 101–115. [Google Scholar] [CrossRef]
- Russo, D.; Bouton, M. Statistical analysis of spatial variability in unsaturated flow parameters. Water Resour. Res. 1992, 28, 1911–1925. [Google Scholar] [CrossRef]
- Russo, D.; Russo, I.; Laufer, A. On the spatial variability of parameters of the unsaturated hydraulic conductivity. Water Resour. Res. 1997, 33, 946–956. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Mishra, S.; Parker, J.C.; Singhal, N. Estimation of soil hydraulic properties and their uncertainties from particle size distribution data. J. Hydrol. 1989, 108, 1–18. [Google Scholar] [CrossRef]
- Russo, D.; Zaidel, J.; Fiori, A.; Laufer, A. Numerical analysis of flow and transport from a multiple—Source system in a partially saturated heterogeneous soil. Water Resour. Res. 2006, 42, W06415. [Google Scholar] [CrossRef]
- Russo, D. On the control of solute mass fluxes and concentrations below fields irrigated with low-quality water: A numerical study. Water Resour. Res. 2017, 53, 8925–8940. [Google Scholar] [CrossRef]
- Perkins, T.K.; Johnston, O.C. A review of diffusion and dispersion in porous media. Soc. Petrol. Eng. J. 1963, 3, 70–84. [Google Scholar] [CrossRef]
- Lotse, E.G.; Jarbo, J.D.; Simmons, K.E.; Baker, D.E. Simulation of nitrogen dynamics and leaching from soil with dual pore system. J. Contam. Hydrol. 1992, 10, 183–196. [Google Scholar] [CrossRef]
- Nye, P.; Tinker, P.B. Solute Movement in the Soil-Root System; Blackwell Scientific Publications: Hoboken, NJ, USA, 1977. [Google Scholar]
- Russo, D.; Laufer, A.; Shapira, R.H.; Kurtzman, D. Assessment of solute fluxes beneath an orchard irrigated with treated sewage water: A numerical study. Water Resour. Res. 2013, 49, 657–674. [Google Scholar] [CrossRef]
- Fried, M.; Broashard, H. The Soil—Plant System; Academic Press: New York, NY, USA, 1967. [Google Scholar]
- Xu, G.; Magen, H.; Tarchitzky, J.; Kafkafi, U. Advances in chloride nutrition of plants. Adv. Agron. 2000, 68, 97–150. [Google Scholar]
- Neuman, S.P.; Feddes, R.A.; Bresler, E. Finite element analysis of two-dimensional flow in soils considering water uptake by roots, 1. Theory. Soil Sci. Soc. Am. Proc. 1975, 39, 224–230. [Google Scholar] [CrossRef]
- Russo, D.; Zaidel, J.; Laufer, A. Numerical analysis of flow and transport in a three-dimensional partially saturated heterogeneous soil. Water Resour. Res. 1998, 34, 1451–1468. [Google Scholar] [CrossRef]
- Russo, D.; Zaidel, J.; Laufer, A. Numerical analysis of flow and transport from trickle sources on a spatially heterogeneous hillslope. Vadose Zone J. 2005, 4, 838–847. [Google Scholar] [CrossRef]
- Jury, W.A.; Sposito, G. Field calibration and validation of solute transport models for the unsaturated zone. Soil Sci. Soc. Am. J. 1985, 49, 1331–1441. [Google Scholar] [CrossRef]
- Weissman, G.; Bell, G.; Dahan, O. The deep unsaturated zone under the Gilat field experiment, chapter 4 in: Reducing nitrate fluxes to groundwater under agricultural land in the desalination era (in Hebrew). A report submitted to the Chief Scientist of the Israeli Ministry of Agriculture for project no. 20-13-0013. 2019. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Russo, D.; Kurtzman, D. Using Desalinated Water for Irrigation: Its Effect on Field Scale Water Flow and Contaminant Transport under Cropped Conditions. Water 2019, 11, 687. https://doi.org/10.3390/w11040687
Russo D, Kurtzman D. Using Desalinated Water for Irrigation: Its Effect on Field Scale Water Flow and Contaminant Transport under Cropped Conditions. Water. 2019; 11(4):687. https://doi.org/10.3390/w11040687
Chicago/Turabian StyleRusso, David, and Daniel Kurtzman. 2019. "Using Desalinated Water for Irrigation: Its Effect on Field Scale Water Flow and Contaminant Transport under Cropped Conditions" Water 11, no. 4: 687. https://doi.org/10.3390/w11040687
APA StyleRusso, D., & Kurtzman, D. (2019). Using Desalinated Water for Irrigation: Its Effect on Field Scale Water Flow and Contaminant Transport under Cropped Conditions. Water, 11(4), 687. https://doi.org/10.3390/w11040687




