Mathematical Model of Ammonium Nitrogen Transport to Runoff with Different Slope Gradients under Simulated Rainfall
Abstract
1. Introduction
2. Materials and Methods
2.1. Soil and Slope Preparation
2.2. Rainfall Simulation
2.3. Experimental Procedure
2.4. Theoretical Analysis
2.4.1. Governing Equation
2.4.2. Solution of the Surface Runoff Equation
2.4.3. Solution of the Solute Transport Equation
2.5. Data Analysis
3. Results and Discussions
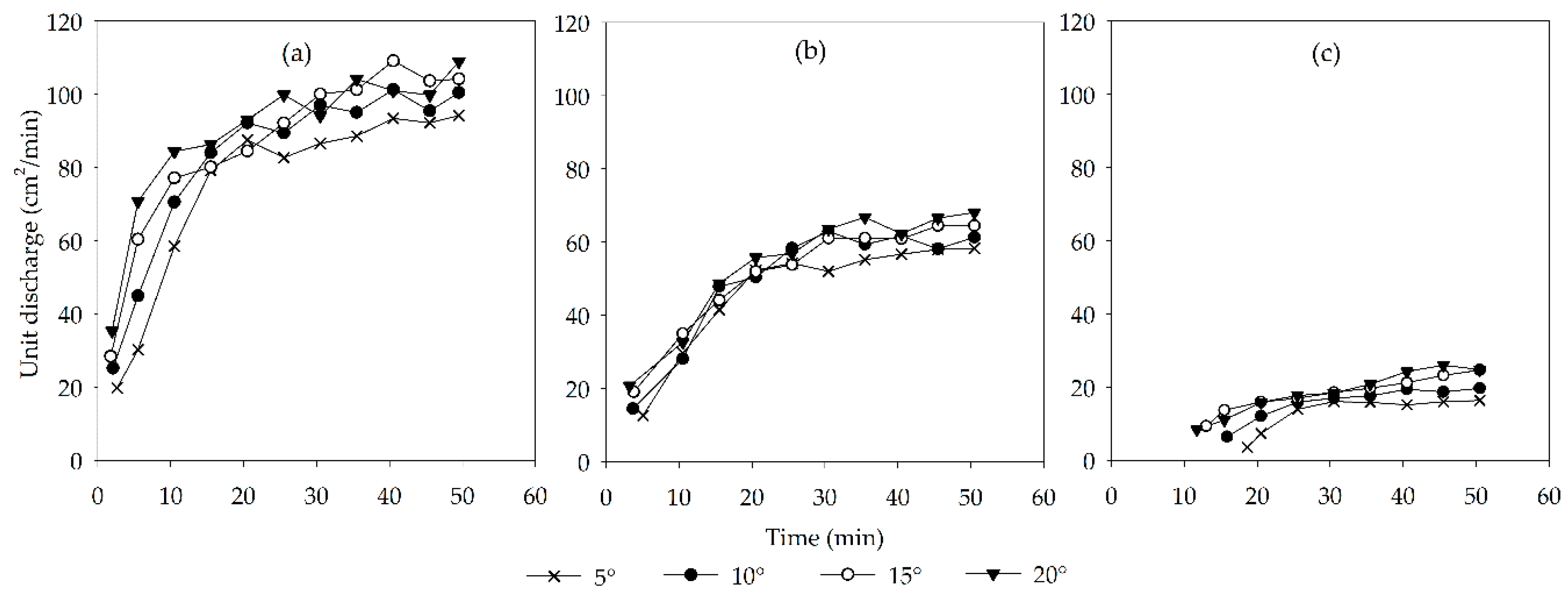
3.1. Effects of Slope Gradient and Rainfall Intensity on Runoff Process
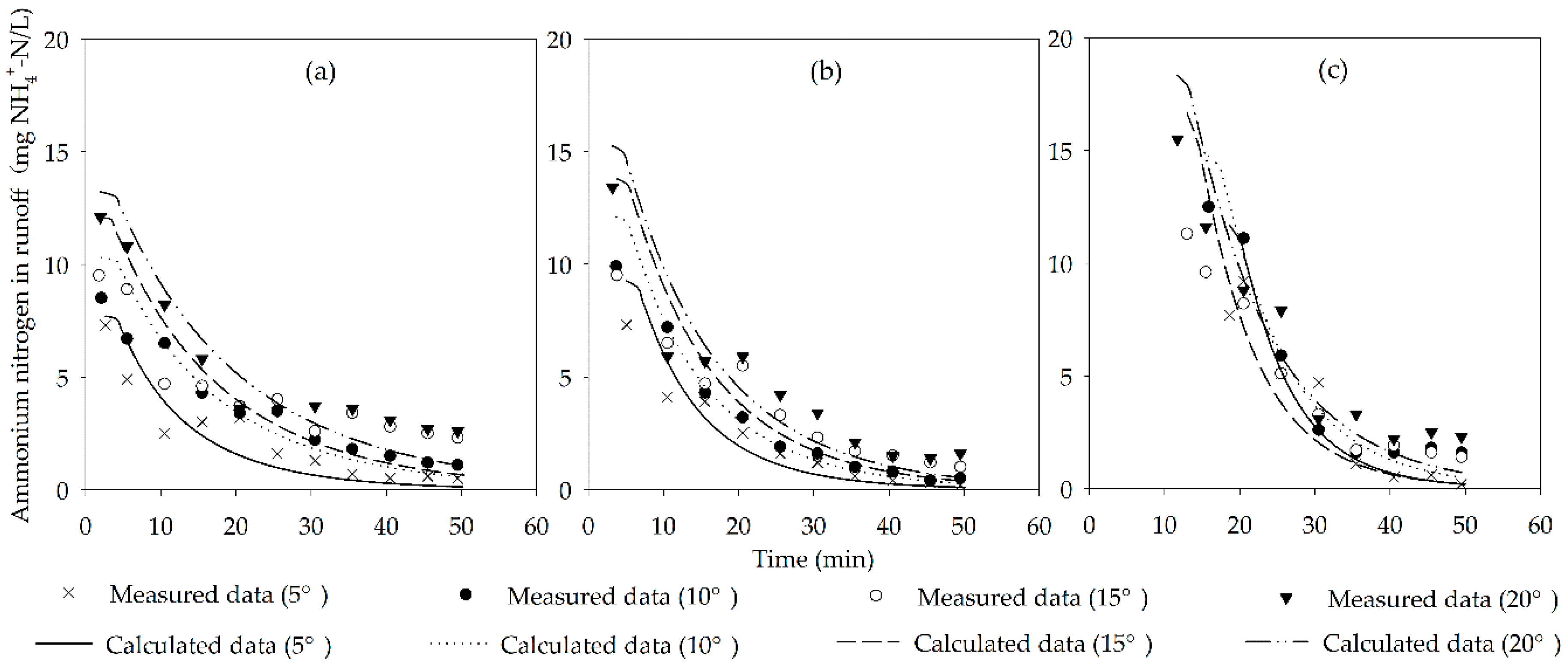
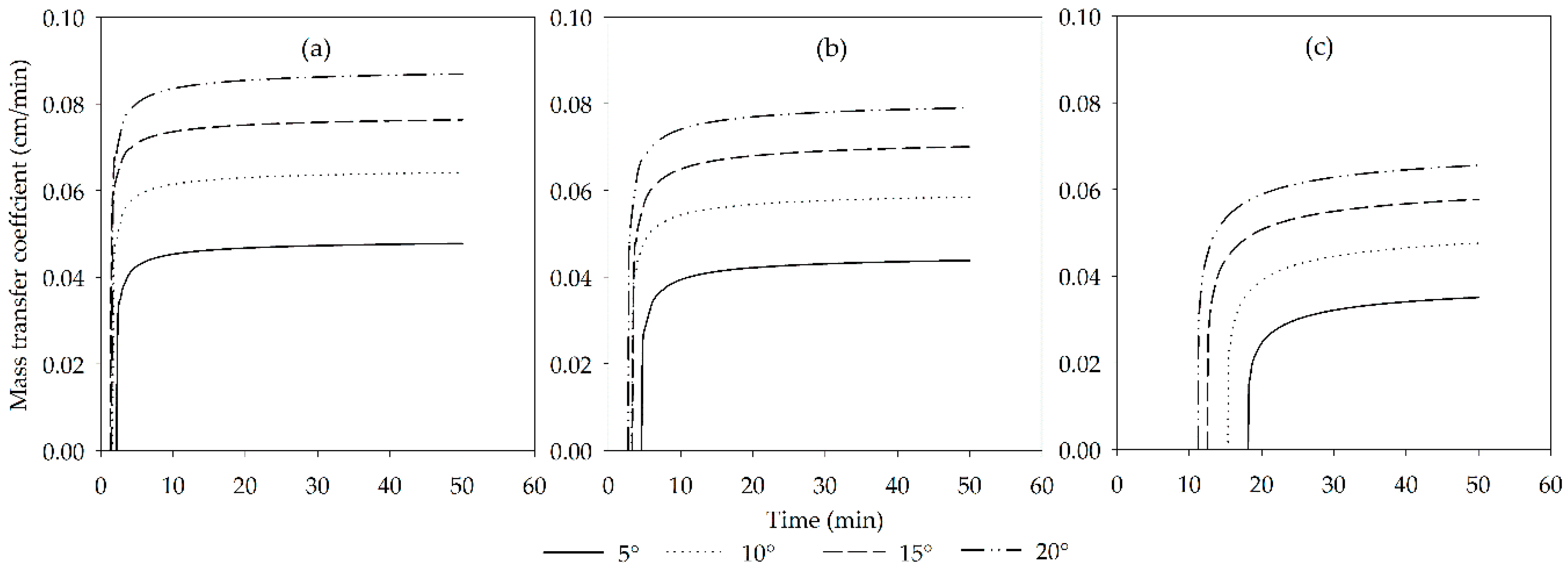
3.2. Effects of Slope Gradient and Rainfall Intensity on the Transport of Ammonium Nitrogen
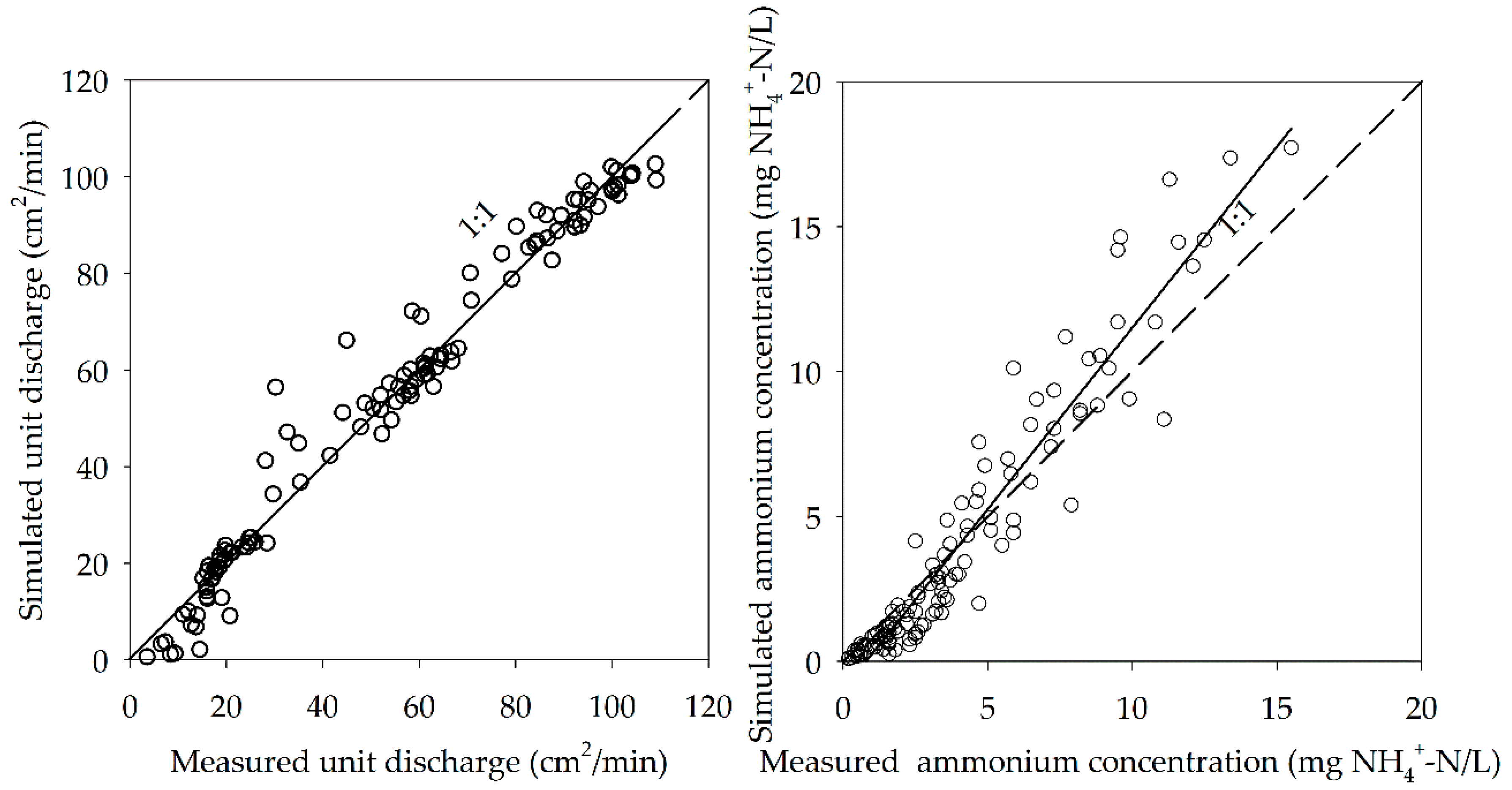
3.3. Parameter Estimation
3.4. Modeling Runoff Processes and Ammonium Nitrogen Concentration in Overland Flow
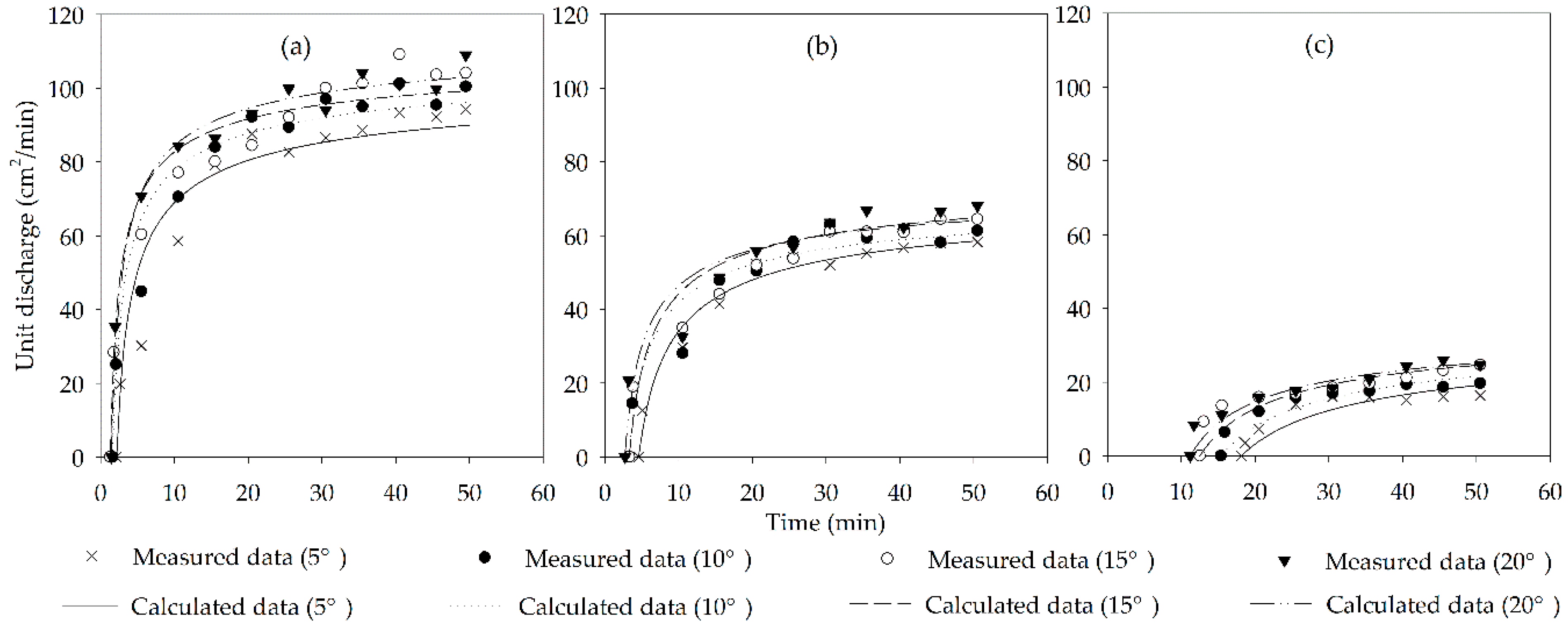
3.4.1. Modeling Runoff Processes
3.4.2. Modelling Ammonium Nitrogen Concentrations in Runoff.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vadas, P.A.; Powell, J.M. Monitoring nutrient loss in runoff from dairy cattle lots. Agric. Ecosyst. Environ. 2013, 181, 127–133. [Google Scholar] [CrossRef]
- Ramos, M.; Benito, C.; Martínez-Casasnovas, J. Simulating soil conservation measures to control soil and nutrient losses in a small, vineyard dominated, basin. Agric. Ecosyst. Environ. 2015, 213, 194–208. [Google Scholar] [CrossRef]
- Parris, K. Impact of agriculture on water pollution in OECD countries: Recent trends and future prospects. Int. J. Water Resour. Dev. 2011, 27, 33–52. [Google Scholar] [CrossRef]
- Sharpley, A.; Moyer, B. Phosphorus forms in manure and compost and their release during simulated rainfall. J. Environ. Qual. 2000, 29, 1462–1469. [Google Scholar] [CrossRef]
- Wilson, G.; McGregor, K.; Boykin, D. Residue impacts on runoff and soil erosion for different corn plant populations. Soil Tillage Res. 2008, 99, 300–307. [Google Scholar] [CrossRef]
- Howarth, R.W.; Sharpley, A.; Walker, D. Sources of nutrient pollution to coastal waters in the United States: Implications for achieving coastal water quality goals. Estuaries 2002, 25, 656–676. [Google Scholar] [CrossRef]
- Kleinman, P.J.; Srinivasan, M.; Dell, C.J.; Schmidt, J.P. Role of rainfall intensity and hydrology in nutrient transport via surface runoff. J. Environ. Qual. 2006, 35, 1248. [Google Scholar] [CrossRef]
- Snyder, J.K.; Woolhiser, D.A. Effects of infiltration on chemical transport into overland flow. Trans. ASAE 1985, 28, 1450–1457. [Google Scholar] [CrossRef]
- Wallach, R.; Shabtai, R. Surface runoff contamination by chemicals initially incorporated below the soil surface. Water Resour. Res. 1993, 29, 697–704. [Google Scholar] [CrossRef]
- Srinivasan, M.; Kleinman, P.; Sharpley, A.; Buob, T.; Gburek, W. Hydrology of small field plots used to study phosphorus runoff under simulated rainfall. J. Environ. Qual. 2007, 36, 1833. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Wang, Q.; Wu, L.; Zhao, G.; Liu, Y.; Zhang, P. A mathematical model for soil solute transfer into surface runoff as influenced by rainfall detachment. Sci. Total Environ. 2016, 557, 590–600. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Wu, L.; Chenc, W.; Wang, Q. Solute Transfer from the Soil Surface to Overland Flow: A Review. Soil Sci. Soc. Am. J. 2011, 75, 1214. [Google Scholar] [CrossRef]
- Ahuja, L.; Sharpley, A.; Yamamoto, M.; Menzel, R. The depth of rainfall-runoff-soil interaction as determined by 32P. Water Resour. Res. 1981, 17, 969–974. [Google Scholar] [CrossRef]
- Steenhuis, T.; Walter, M. Closed form solution for pesticide loss in runoff water. Trans. ASAE 1980, 23, 0615–0620. [Google Scholar] [CrossRef]
- Ahuja, L.; Lehman, O. The extent and nature of rainfall-soil interaction in the release of soluble chemicals to runoff. J. Environ. Qual. 1983, 12, 34–40. [Google Scholar] [CrossRef]
- Havis, R.; Smith, R.; Adrian, D. Partitioning solute transport between infiltration and overland flow under rainfall. Water Resour. Res. 1992, 28, 2569–2580. [Google Scholar] [CrossRef]
- Walton, R.; Volker, R.; Bristow, K.L.; Smettem, K. Solute transport by surface runoff from low-angle slopes: Theory and application. Hydrol. Process. 2000, 14, 1139–1158. [Google Scholar] [CrossRef]
- Yang, T.; Wang, Q.J.; Liu, Y.L.; Zhang, P.Y.; Wu, L.S. A comparison of mathematical models for chemical transfer from soil to surface runoff with the impact of rain. Catena 2016, 137, 191–202. [Google Scholar] [CrossRef]
- Wallach, R.; Jury, W.A.; Spencer, W.F. Transfer of chemicals from soil solution to surface runoff: A diffusion-based soil model. Soil Sci. Soc. Am. J. 1988, 52, 612–618. [Google Scholar] [CrossRef]
- Chen, X.R.; Jia, J.D.; Gao, W.L.; Ren, Y.Z.; Tao, S. Selection of an index system for evaluating the application level of agricultural engineering technology. Pattern Recogn. Lett. 2018, 109, 12–17. [Google Scholar] [CrossRef]
- Gao, B.; Walter, M.T.; Steenhuis, T.S.; Hogarth, W.L.; Parlange, J.-Y. Rainfall induced chemical transport from soil to runoff: Theory and experiments. J. Hydrol. 2004, 295, 291–304. [Google Scholar] [CrossRef]
- Hairsine, P.; Rose, C. Rainfall detachment and deposition: Sediment transport in the absence of flow-driven processes. Soil Sci. Soc. Am. J. 1991, 55, 320–324. [Google Scholar] [CrossRef]
- Walker, J.D.; Walter, M.T.; Parlange, J.-Y.; Rose, C.W.; Tromp-van Meerveld, H.; Gao, B.; Cohen, A.M. Reduced raindrop-impact driven soil erosion by infiltration. J. Hydrol. 2007, 342, 331–335. [Google Scholar] [CrossRef]
- Walter, M.T.; Gao, B.; Parlange, J.-Y. Modeling soil solute release into runoff with infiltration. J. Hydrol. 2007, 347, 430–437. [Google Scholar] [CrossRef]
- Li, J.; Tong, J.; Xia, C.; Hu, B.X.; Zhu, H.; Yang, R.; Wei, W. Numerical simulation and experimental study on farmland nitrogen loss to surface runoff in a raindrop driven process. J. Hydrol. 2017, 549, 754–768. [Google Scholar] [CrossRef]
- Wallach, R.; Jury, W.A.; Spencer, W.F. The concept of convective mass transfer for prediction of surface-runoff pollution by soil surface applied chemicals. Trans. ASAE 1989, 32, 0906–0912. [Google Scholar] [CrossRef]
- Yang, T.; Wang, Q.J.; Su, L.J.; Wu, L.S.; Zhao, G.X.; Liu, Y.L.; Zhang, P.Y. An Approximately Semi-Analytical Model for Describing Surface Runoff of Rainwater Over Sloped Land. Water Resour. Manag. 2016, 30, 3935–3948. [Google Scholar] [CrossRef]
- Philip, J. The theory of infiltration: 1. The infiltration equation and its solution. Soil Sci. 1957, 83, 345–358. [Google Scholar] [CrossRef]
- Jiang, F.S.; Huang, Y.H.; Wang, M.K.; Lin, J.S.; Gan, Z.; Ge, H.L. Effects of Rainfall Intensity and Slope Gradient on Steep Colluvial Deposit Erosion in Southeast China. Soil Sci. Soc. Am. J. 2014, 78, 1741. [Google Scholar] [CrossRef]
- Poesen, J. The Role of Slope Angle in Surface Seal Formation. In International Geomorphology 1986, Part II; Wiley: Hoboken, NJ, USA, 1987; pp. 437–448. [Google Scholar]
- Ribolzi, O.; Patin, J.; Bresson, L.M.; Latsachack, K.O.; Valentin, C. Impact of slope gradient on soil surface features and infiltration on steep slopes in northern Laos. Geomorphology 2014, 127, 53–63. [Google Scholar] [CrossRef]
- Assouline, S.; Ben-Hur, M. Effects of rainfall intensity and slope gradient on the dynamics of interrill erosion during soil surface sealing. Catena 2006, 66, 211–220. [Google Scholar] [CrossRef]
- Wei, W.; Jia, F.; Lei, Y.; Chen, L.; Zhang, H.; Yang, Y. Effects of surficial condition and rainfall intensity on runoff in a loess hilly area, China. J. Hydrol. 2014, 513, 115–126. [Google Scholar] [CrossRef]
- Walton, R.; Volker, R.; Bristow, K.L.; Smettem, K. Experimental examination of solute transport by surface runoff from low-angle slopes. J. Hydrol. 2000, 233, 19–36. [Google Scholar] [CrossRef]
- Tao, W.; Wu, J.; Wang, Q. Mathematical model of sediment and solute transport along slope land in different rainfall pattern conditions. Sci. Rep. 2017, 7, 44082. [Google Scholar] [CrossRef]
- Peng, W.; Zhang, Z.; Zhang, K. Hydrodynamic characteristics of rill flow on steep slopes. Hydrol. Process. 2015, 29, 3677–3686. [Google Scholar] [CrossRef]
- Xiao, S.Q.; Yao, M.W.; Gao, W.B.; Su, Z.; Yao, X. Significantly enhanced dielectric constant and breakdown strength in crystalline@amorphous core-shell structured SrTiO3 nanocomposite thick films. J. Alloy Compd. 2018, 762, 370–377. [Google Scholar] [CrossRef]
- Weast, R.C. CRC Handbook of Chemistry and Physics, 55th Ed. (1974–1975) ed; CRC Press: Cleveland, OH, USA, 1974. [Google Scholar]
- Gao, B.; Walter, M.T.; Steenhuis, T.S.; Parlange, J.Y.; Nakano, K.; Rose, C.W.; Hogarth, W.L. Investigating ponding depth and soil detachability for a mechanistic erosion model using a simple experiment. J. Hydrol. 2003, 277, 116–124. [Google Scholar] [CrossRef]
- Proffitt, A.P.B.; Rose, C.W.; Hairsine, P.B. Rainfall Detachment and Deposition: Experiments with Low Slopes and Significant Water Depths. Soil Sci. Soc. Am. J. 1991, 55, 325–332. [Google Scholar] [CrossRef]
- Zhang, X.C.; Norton, L.D. Coupling mixing zone concept with convection-diffusion equation to predict chemical transfer to surface runoff. Trans. ASAE 1999, 42, 987–994. [Google Scholar] [CrossRef]
- Yang, T.; Wang, Q.; Xu, D.; Lv, J. A method for estimating the interaction depth of surface soil with simulated rain. Catena 2015, 124, 109–118. [Google Scholar] [CrossRef]
- Dong, W.; Wang, Q. Modeling Soil Solute Release into Runoff and Transport with Runoff on a Loess Slope. J. Hydrol. Eng. 2013, 18, 527–535. [Google Scholar] [CrossRef]
- Dong, W.; Song, C.; Qiang, F.; Wang, Q.; Cao, C. Modeling soil solute release and transport in runoff on a loessial slope with and without surface stones. Hydrol. Process. 2018, 32, 1391–1400. [Google Scholar] [CrossRef]
- Rumynin, V.G. Overland Flow Dynamics and Solute Transport; Springer Nature Switzerland AG: Basel, Switzerland, 2015; Volume 26. [Google Scholar] [CrossRef]
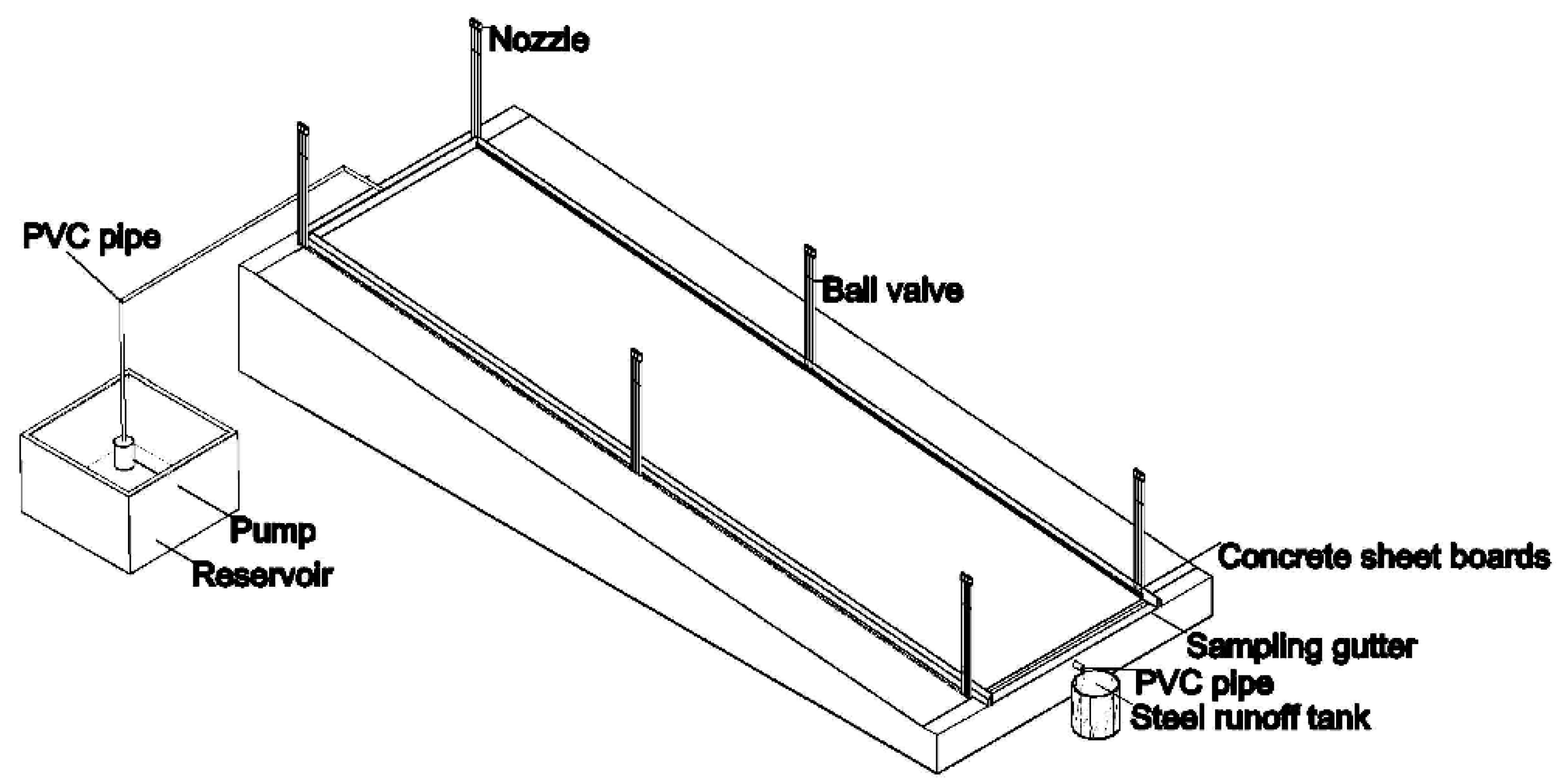

| Soil Type | Soil Texture (%) | Soil Bulk Density (g/cm3) | pH | Organic Matter (g kg−1) | Initial Soil Water Content (cm3/cm3) | Saturated Soil Water Content (cm3/cm3) | Initial Ammonium Nitrogen Concentration of Soil Solution (mg NH4+-N/L) | ||
|---|---|---|---|---|---|---|---|---|---|
| Sand/% (2.0–0.02 mm) | Silt/% (0.02–0.002 mm) | Clay/% (<0.002mm) | |||||||
| Sandy | 89.55 ± 0.39 | 5.43 ± 0.43 | 5.02 ± 0.27 | 1.45 ± 0.09 | 8.40 ± 0.16 | 2.81 ± 0.07 | 0.207 ± 0.03 | 0.50 ± 0.07 | 45.6 ± 2.25 |
| Rainfall Intensity (mm/h) | Slope Gradient | Total Runoff (m3) | Total Ammonium Nitrogen Losses (mg NH4+-N) |
|---|---|---|---|
| 75 | 5 | 1.82 | 2768 |
| 10 | 2.01 | 5563 | |
| 15 | 2.11 | 7485 | |
| 20 | 2.18 | 9356 | |
| 50 | 5 | 1.09 | 1468 |
| 10 | 1.18 | 2252 | |
| 15 | 1.21 | 3341 | |
| 20 | 1.28 | 4141 | |
| 25 | 5 | 0.23 | 457 |
| 10 | 0.28 | 868 | |
| 15 | 0.35 | 1162 | |
| 20 | 0.37 | 1584 |
| Designed Rainfall Intensities | Slope Gradient | tp (min) | S (cm/min1/2) | c | R2 | RMSE (cm2/min) |
|---|---|---|---|---|---|---|
| 75 | 5 | 2.15 | 0.26 | 0.15 | 0.94 | 8.12 |
| 10 | 1.60 | 0.22 | 0.12 | 0.96 | 6.89 | |
| 15 | 1.28 | 0.20 | 0.10 | 0.96 | 6.52 | |
| 20 | 1.45 | 0.21 | 0.06 | 0.99 | 3.93 | |
| 50 | 5 | 4.57 | 0.25 | 0.10 | 0.98 | 2.95 |
| 10 | 3.17 | 0.21 | 0.11 | 0.93 | 5.32 | |
| 15 | 3.28 | 0.21 | 0.05 | 0.95 | 4.58 | |
| 20 | 2.70 | 0.19 | 0.08 | 0.92 | 5.99 | |
| 25 | 5 | 18.15 | 0.25 | 0.13 | 0.87 | 2.75 |
| 10 | 15.35 | 0.23 | 0.10 | 0.92 | 2.55 | |
| 15 | 12.50 | 0.21 | 0.05 | 0.89 | 3.44 | |
| 20 | 11.20 | 0.20 | 0.06 | 0.94 | 2.40 |
| Designed Rainfall Intensity (mm/h) | Slope Gradient | hm (cm) | R2 | RMSE (mg/L) |
|---|---|---|---|---|
| 75 | 5 | 0.20 | 0.89 | 0.92 |
| 10 | 0.30 | 0.96 | 1.04 | |
| 15 | 0.31 | 0.92 | 1.63 | |
| 20 | 0.38 | 0.96 | 1.14 | |
| 50 | 5 | 0.14 | 0.95 | 0.89 |
| 10 | 0.18 | 0.99 | 0.73 | |
| 15 | 0.20 | 0.92 | 1.73 | |
| 20 | 0.22 | 0.92 | 1.56 | |
| 25 | 5 | 0.07 | 0.90 | 1.67 |
| 10 | 0.10 | 0.96 | 1.07 | |
| 15 | 0.08 | 0.94 | 2.45 | |
| 20 | 0.12 | 0.96 | 1.78 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, W.; Yang, P.; Ao, C.; Ren, S.; Xu, Y. Mathematical Model of Ammonium Nitrogen Transport to Runoff with Different Slope Gradients under Simulated Rainfall. Water 2019, 11, 675. https://doi.org/10.3390/w11040675
Xing W, Yang P, Ao C, Ren S, Xu Y. Mathematical Model of Ammonium Nitrogen Transport to Runoff with Different Slope Gradients under Simulated Rainfall. Water. 2019; 11(4):675. https://doi.org/10.3390/w11040675
Chicago/Turabian StyleXing, Weimin, Peiling Yang, Chang Ao, Shumei Ren, and Yao Xu. 2019. "Mathematical Model of Ammonium Nitrogen Transport to Runoff with Different Slope Gradients under Simulated Rainfall" Water 11, no. 4: 675. https://doi.org/10.3390/w11040675
APA StyleXing, W., Yang, P., Ao, C., Ren, S., & Xu, Y. (2019). Mathematical Model of Ammonium Nitrogen Transport to Runoff with Different Slope Gradients under Simulated Rainfall. Water, 11(4), 675. https://doi.org/10.3390/w11040675





