A 40-Year Analysis of the Hydrological Drought Index for the Tigris Basin, Turkey
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data
3. Methods
3.1. Streamflow Naturalization
3.2. Normality Tests of Data Series
3.3. Streamflow Drought Index (SDI)
4. Results and Discussions
5. Summary and Conclusions
- (1)
- The results of the K–S test showed that log-normal distribution was better than normal distribution at the 0.05 significance level.
- (2)
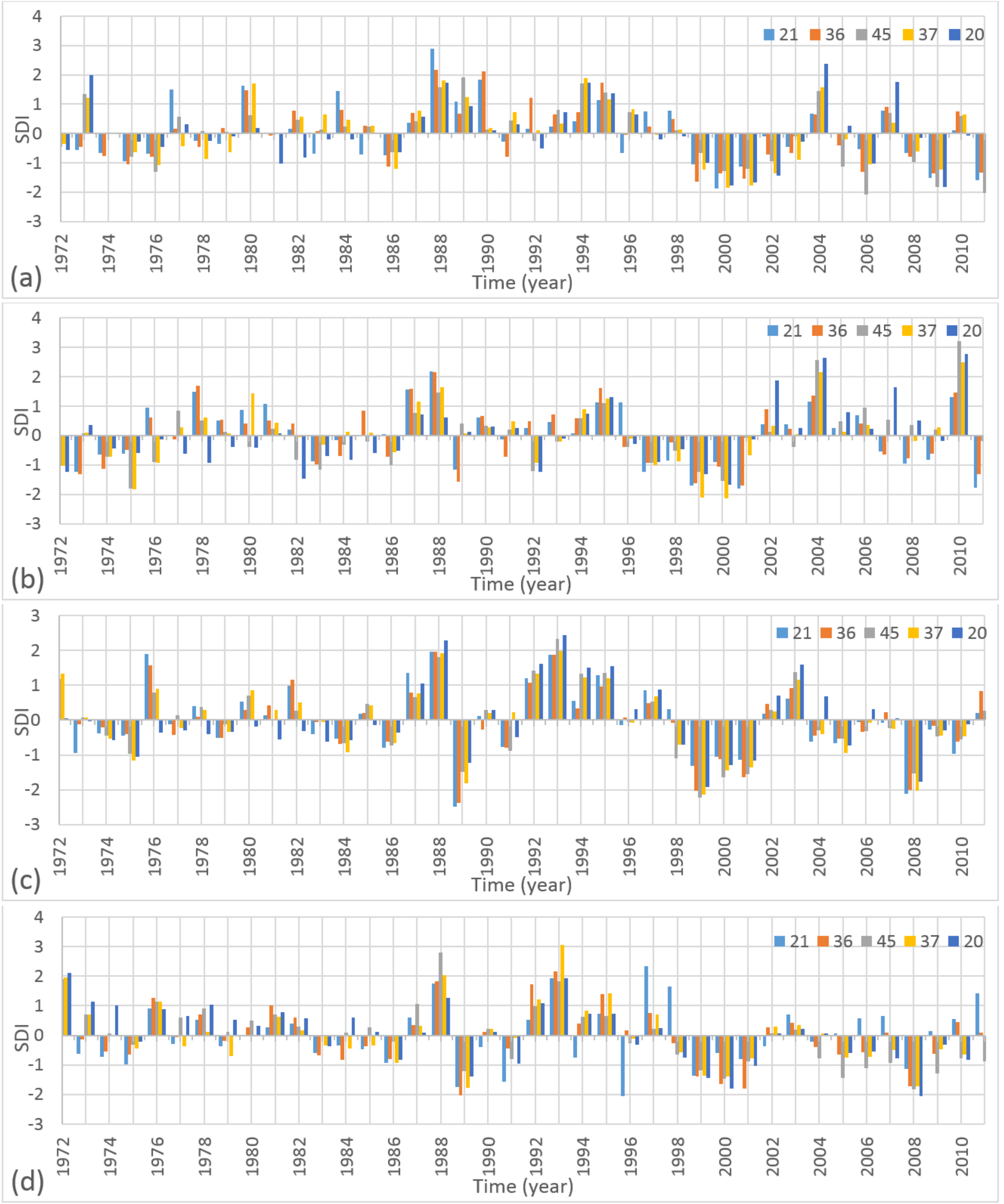
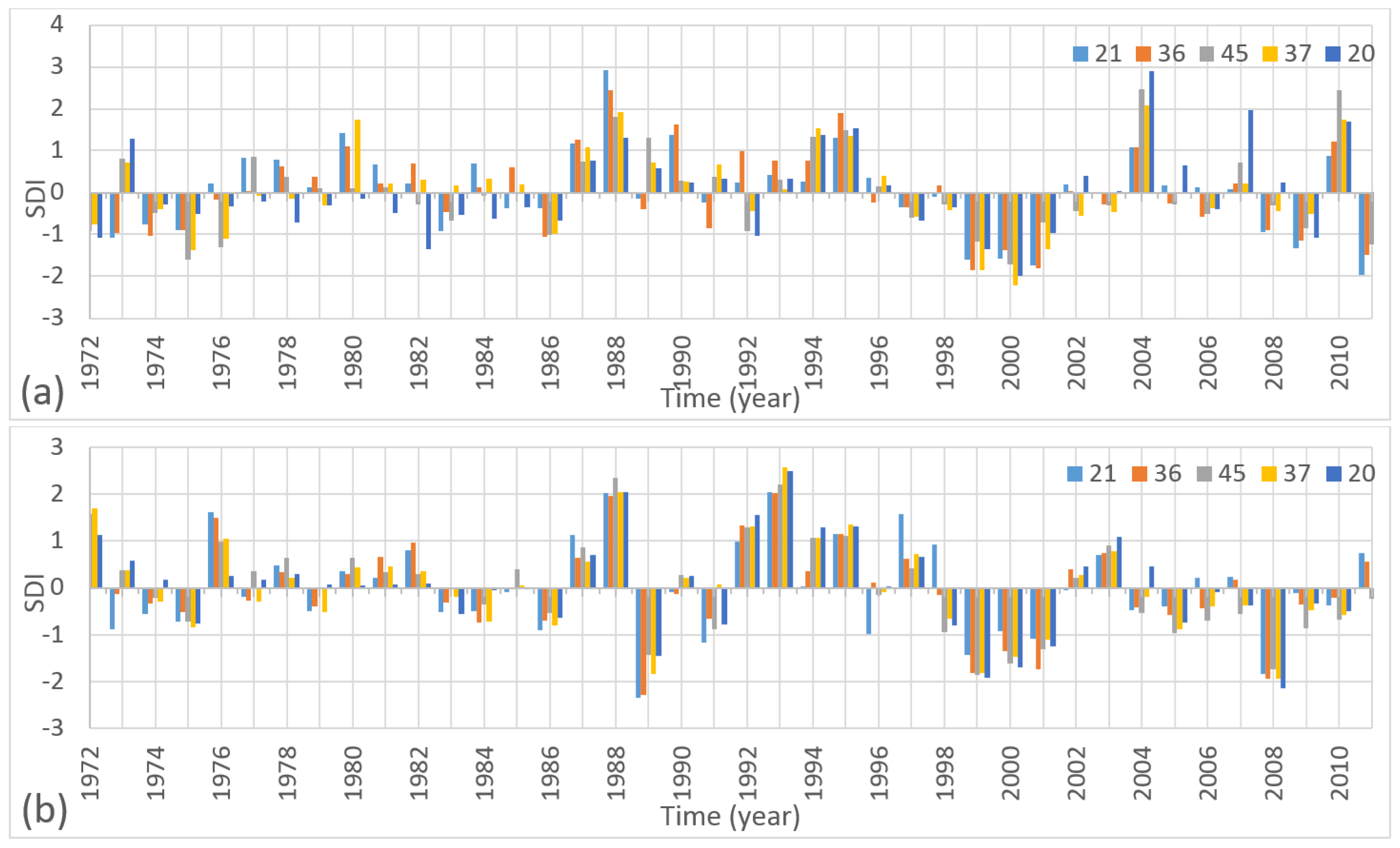
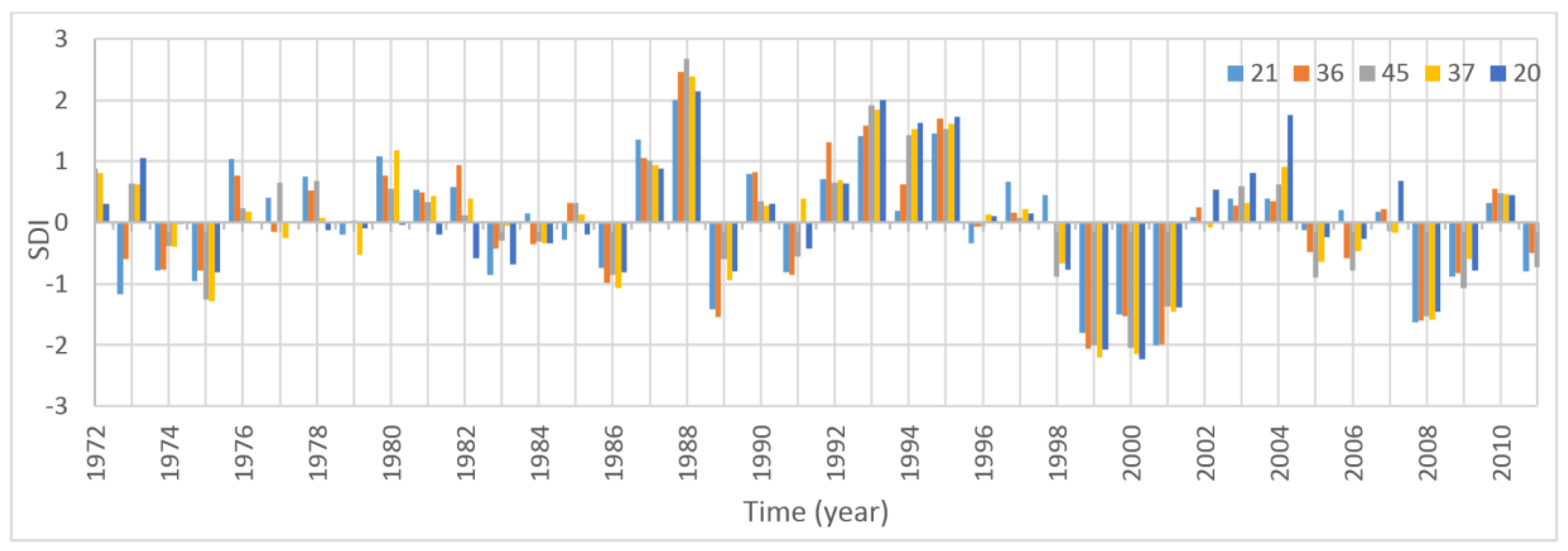
- Almost all stations experienced at least one severe drought during the study period. For yearly (12-month) periods, severe and moderate drought conditions mostly occurred after 1999.
- (3)
- The SDI-6 series showed a more remarkable decrease during the April–September period as compared with the October–March period. During the April–September period, evaporation was very high. A decrease in streamflow and water losses through evaporation resulted in reduced use of irrigation water, because the requirement for crop irrigation was the highest between May and September in the study region.
- (4)
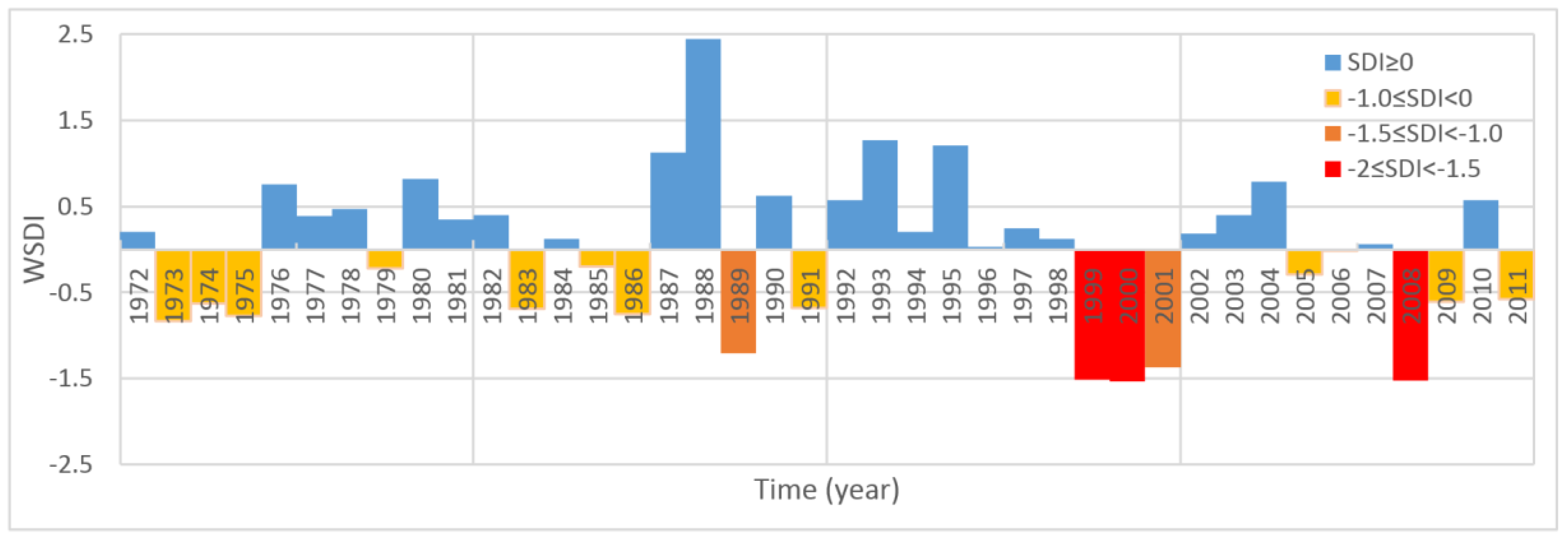
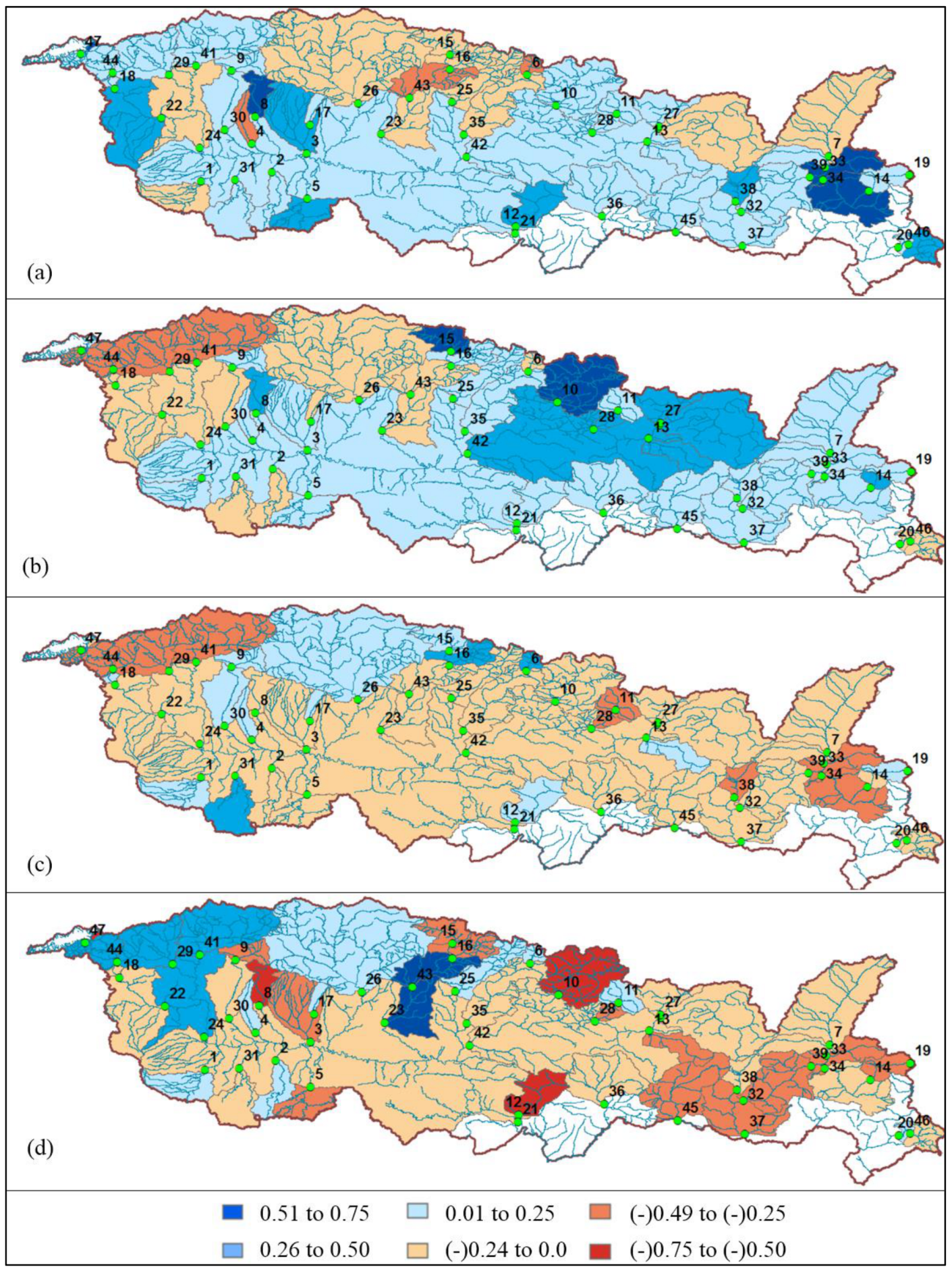
- The WSDI findings confirmed the SDI-12 results of the selected stations. According to the WSDI results, the intensity and frequency of drought conditions increased in every 10-year period. This outcome has been verified using the maps of averaged SDI-12 values over the Tigris Basin. In these maps, we noticed that areas further south experienced drought earlier in the time domain than areas further north.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Manfreda, S.; Iacobellis, V.; Gioia, A.; Fiorentino, M.; Kochanek, K. The Impact of Climate on Hydrological Extremes. Water 2018, 10, 802. [Google Scholar] [CrossRef]
- Van Loon, A.F.; Laaha, G. Hydrological drought severity explained by climate and catchment characteristics. J. Hydrol. 2015, 526, 3–14. [Google Scholar] [CrossRef]
- Nalbantis, I. Evaluation of a Hydrological Drought Index. Eur. Water 2008, 23, 67–77. [Google Scholar]
- Hayes, M.; Svoboda, M.; Wall, N.; Widhalm, M. The Lincoln Declaration on Drought Indices: Universal Meteorological Drought Index Recommended. Bull. Am. Meteorol. Soc. 2011, 92, 485–488. [Google Scholar] [CrossRef]
- Thomas, A.C.; Reager, J.T.; Famiglietti, J.S.; Rodell, M. A GRACE-based water storage deficit approach for hydrological drought characterization. Geophys. Res. Lett. 2014, 41, 1537–1545. [Google Scholar] [CrossRef]
- Wada, Y.; van Beek, L.P.H.; Wanders, N.; Bierkens, M.F.P. Human water consumption intensifies hydrological drought worldwide. Environ. Res. Lett. 2013, 8, 034036. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Glantz, M.H. Understanding: The Drought Phenomenon: The Role of Definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- Vasiliades, L.; Loukas, A.; Liberis, N. A Water Balance Derived Drought Index for Pinios River Basin, Greece. Water Resour. Manag. 2011, 25, 1087–1101. [Google Scholar] [CrossRef]
- Tabari, H.; Nikbakht, J.; Hosseinzadeh Talaee, P. Hydrological Drought Assessment in Northwestern Iran Based on Streamflow Drought Index (SDI). Water Resour. Manag. 2013, 27, 137–151. [Google Scholar] [CrossRef]
- Wable, P.S.; Jha, M.K.; Shekhar, A. Comparison of Drought Indices in a Semi-Arid River Basin of India. Water Resour. Manag. 2019, 33, 75–102. [Google Scholar] [CrossRef]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35, L02405. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; López-Moreno, J.I.; Beguería, S.; Lorenzo-Lacruz, J.; Azorin-Molina, C.; Morán-Tejeda, E. Accurate Computation of a Streamflow Drought Index. J. Hydrol. Eng. 2012, 17, 318–332. [Google Scholar] [CrossRef]
- Nalbantis, I.; Tsakiris, G. Assessment of Hydrological Drought Revisited. Water Resour. Manag. 2009, 23, 881–897. [Google Scholar] [CrossRef]
- Tigkas, D.; Vangelis, H.; Tsakiris, G. Drought and climatic change impact on streamflow in small watersheds. Sci. Total Environ. 2012, 440, 33–41. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Xiong, L.; Dong, L.; Zhang, J. Effects of the Three Gorges Reservoir on the hydrological droughts at the downstream Yichang station during 2003–2011. Hydrol. Process. 2013, 27, 3981–3993. [Google Scholar] [CrossRef]
- Al-Faraj, F.A.M.; Scholz, M.; Tigkas, D. Sensitivity of Surface Runoff to Drought and Climate Change: Application for Shared River Basins. Water 2014, 6, 3033–3048. [Google Scholar] [CrossRef]
- Rimkus, E.; Stonevičius, E.; Korneev, V.; Kažys, J.; Valiuškevičius, G. Aliaksandr Pakhomau Dynamics of meteorological and hydrological droughts in the Neman river basin. Environ. Res. Lett. 2013, 8, 045014. [Google Scholar] [CrossRef]
- Arabzadeh, R.; Kholoosi, M.M.; Bazrafshan, J. Regional Hydrological Drought Monitoring Using Principal Components Analysis. J. Irrig. Drain. Eng. 2016, 142, 04015029. [Google Scholar] [CrossRef]
- Kermen, E.; Gül, O. Comparing two streamflow-based Drought Indices. In Proceedings of the 4th International Conference Water Resources and Wetlands, Tulcea, Romania, 5–9 September 2018; pp. 190–195. [Google Scholar]
- Ljubenkov, I.; Kalin, K.C. Evaluation of drought using standardised precipitation and flow indices and their correlations on an example of Sinjsko polje. Građevinar 2016, 68, 135–143. [Google Scholar]
- Kubiak-Wójcicka, K.; Bąk, B. Monitoring of meteorological and hydrological droughts in the Vistula basin (Poland). Environ. Monit. Assess. 2018, 190, 691. [Google Scholar] [CrossRef]
- Bąk, B.; Kubiak-Wójcicka, K. Impact of meteorological drought on hydrological drought in Toruń (central Poland) in the period of 1971–2015. J. Water Land Dev. 2017, 32, 3–12. [Google Scholar] [CrossRef]
- Leelaruban, N.; Padmanabhan, G.; Oduor, P. Examining the Relationship between Drought Indices and Groundwater Levels. Water 2017, 9, 82. [Google Scholar] [CrossRef]
- Barker, L.J.; Hannaford, J.; Chiverton, A.; Svensson, C. From meteorological to hydrological drought using standardised indicators. Hydrol. Earth Syst. Sci. 2016, 20, 2483–2505. [Google Scholar] [CrossRef]
- Mazzarella, A.; Giuliacci, A.; Liritzis, I. On the 60-month cycle of multivariate ENSO index. Theor. Appl. Climatol. 2010, 100, 23–27. [Google Scholar] [CrossRef]
- Wang, A.-H.; Zeng, X. Impacts of internal climate variability on meteorological drought changes in China. Atmos. Ocean. Sci. Lett. 2018, 11, 78–85. [Google Scholar] [CrossRef]
- Reddy, R.S.; Neralla, V.R.; Godson, W.L. The solar cycle and Indian rainfall. Theor. Appl. Climatol. 1989, 39, 194–198. [Google Scholar] [CrossRef]
- Wood, C.A.; Lovett, R.R. Rainfall, drought and the solar cycle. Nature 1974, 251, 594. [Google Scholar] [CrossRef]
- Guttman, N.B. On the Sensitivity of Sample L Moments to Sample Size. J. Clim. 1994, 7, 1026–1029. [Google Scholar] [CrossRef]
- Quesada-Montano, B.; Wetterhall, F.; Westerberg, I.K.; Hidalgo, H.G.; Halldin, S. Characterising droughts in Central America with uncertain hydro-meteorological data. Appl. Clim. 2018. [Google Scholar] [CrossRef]
- Kibaroglu, A.; Scheumann, W. Euphrates-Tigris Rivers System: Political Rapprochement and Transboundary Water Cooperation. In Turkey’s Water Policy; Kramer, A., Kibaroglu, A., Scheumann, W., Eds.; Springer: Berlin/Heidelberg, German, 2011; pp. 277–299. ISBN 978-3-642-19635-5. [Google Scholar]
- Lovejoy, S.; Schertzer, D.; Ladoy, P. Fractal characterization of inhomogeneous geophysical measuring networks. Nature 1986, 319, 43. [Google Scholar] [CrossRef]
- Hameed, M.; Ahmadalipour, A.; Moradkhani, H. Apprehensive Drought Characteristics over Iraq: Results of a Multidecadal Spatiotemporal Assessment. Geosciences 2018, 8, 58. [Google Scholar] [CrossRef]
- Chenoweth, J.; Hadjinicolaou, P.; Bruggeman, A.; Lelieveld, J.; Levin, Z.; Lange, M.A.; Xoplaki, E.; Hadjikakou, M. Impact of climate change on the water resources of the eastern Mediterranean and Middle East region: Modeled 21st century changes and implications. Water Resour. Res. 2011, 47, W06506. [Google Scholar] [CrossRef]
- Özdoğan, M. Climate change impacts on snow water availability in the Euphrates-Tigris basin. Hydrol. Earth Syst. Sci. 2011, 15, 2789–2803. [Google Scholar] [CrossRef]
- Bozkurt, D.; Sen, O.; Hagemann, S. Projected river discharge in the Euphrates–Tigris Basin from a hydrological discharge model forced with RCM and GCM outputs. Clim. Res. 2015, 62, 131–147. [Google Scholar] [CrossRef]
- Voss, K.A.; Famiglietti, J.S.; Lo, M.; de Linage, C.; Rodell, M.; Swenson, S.C. Groundwater depletion in the Middle East from GRACE with implications for transboundary water management in the Tigris-Euphrates-Western Iran region. Water Resour. Res. 2013, 49, 904–914. [Google Scholar] [CrossRef] [PubMed]
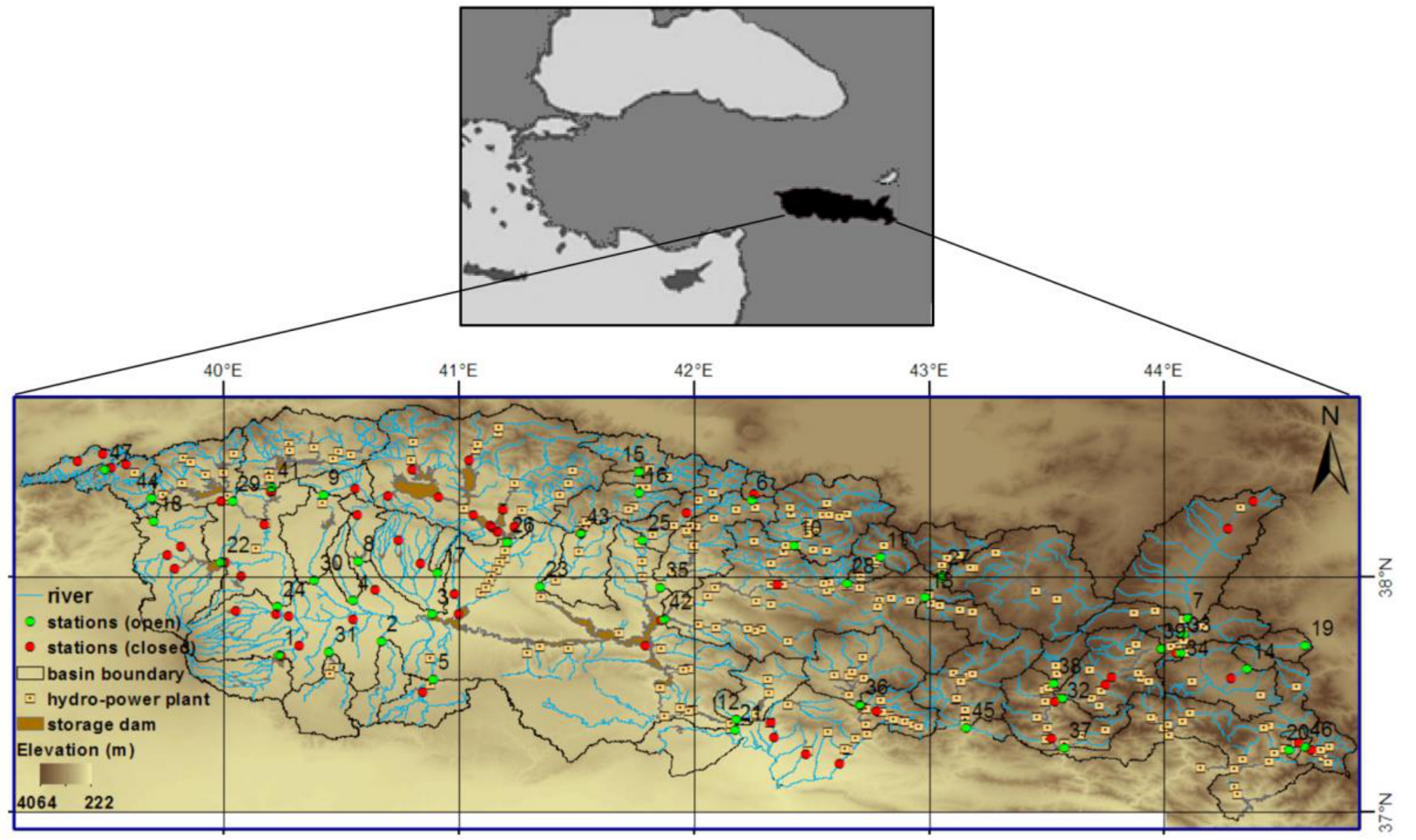
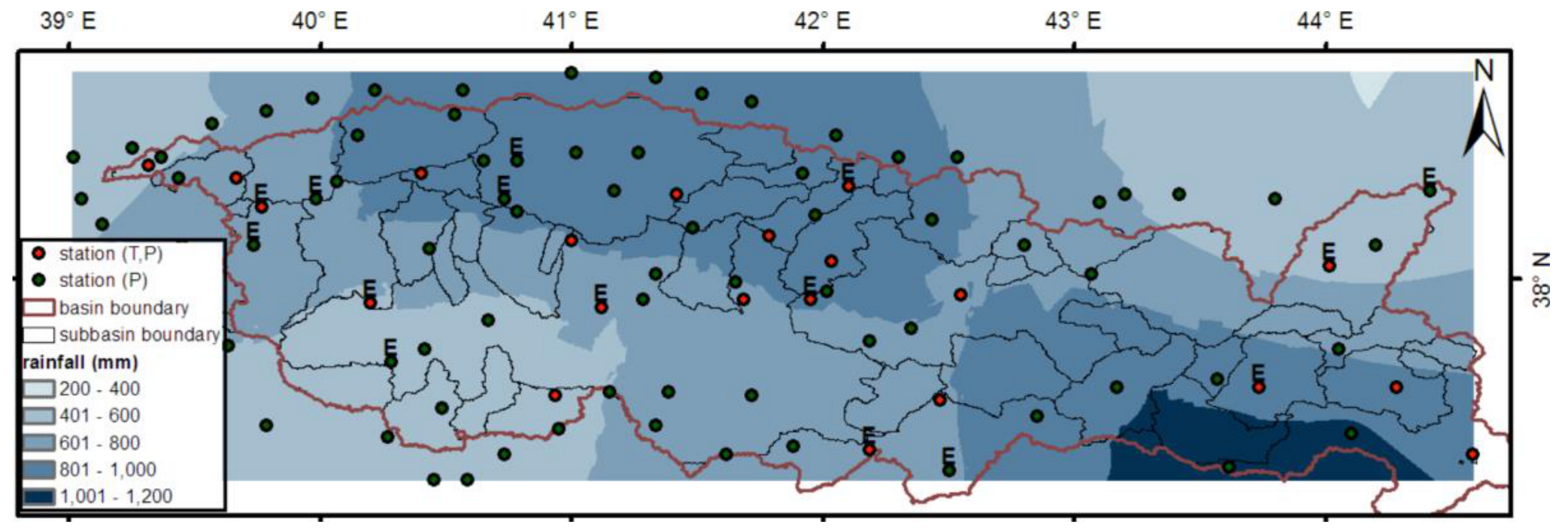

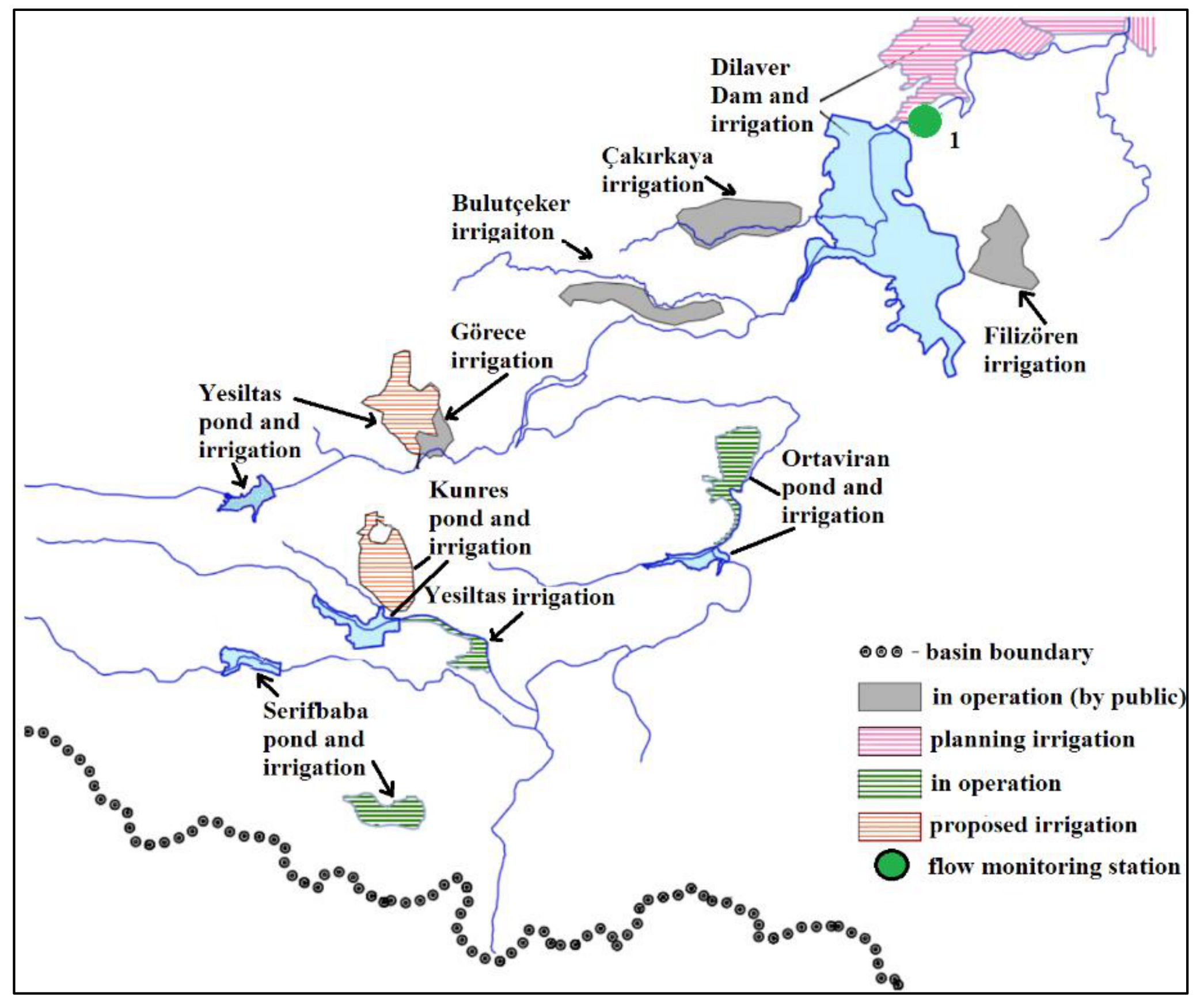

| Station No | Lon. (E) | Lat. (N) | Elevation (m) | Intermediate Basin Area (km2) |
|---|---|---|---|---|
| 1 | 40°14′ | 37°40′ | 702 | 648 |
| 2 | 40°40′ | 37°44′ | 1500 | 407 |
| 3 | 40°53′ | 37°51′ | 525 | 902 |
| 4 | 40°33′ | 37°54′ | 520 | 240 |
| 5 | 40°53′ | 37°34′ | 775 | 576 |
| 6 | 42°15′ | 38°20′ | 1594 | 126 |
| 7 | 44°6′ | 37°50′ | 1813 | 2070 |
| 8 | 40°34′ | 38°4′ | 738 | 305 |
| 9 | 40°26′ | 38°21′ | 800 | 292 |
| 10 | 42°25′ | 38°8′ | 1000 | 1264 |
| 11 | 42°48′ | 38°5′ | 1540 | 253 |
| 12 | 42°11′ | 37°24′ | 400 | 650 |
| 13 | 42°59′ | 37°55′ | 1350 | 614 |
| 14 | 44°21′ | 37°37′ | 1928 | 130 |
| 15 | 41°46′ | 38°27′ | 1200 | 425 |
| 16 | 41°46′ | 38°22′ | 909 | 358 |
| 17 | 40°55′ | 38°1′ | 594 | 158 |
| 18 | 39°42′ | 38°15′ | 852 | 52 |
| 19 | 44°36′ | 37°43′ | 1720 | 244 |
| 20 | 44°32′ | 37°16′ | 1090 | 101 |
| 21 | 42°10′ | 37°21′ | 370 | 9982 |
| 22 | 39°59′ | 38°4′ | 724 | 1524 |
| 23 | 41°21′ | 37°58′ | 545 | 1043 |
| 24 | 40°14′ | 37°53′ | 570 | 1390 |
| 25 | 41°47′ | 38°10′ | 910 | 640 |
| 26 | 41°12′ | 38°9′ | 597 | 4105 |
| 27 | 43°3′ | 38°1′ | 1612 | 426 |
| 28 | 42°39′ | 37°58′ | 1250 | 253 |
| 29 | 40°2′ | 38°20′ | 695 | 798 |
| 30 | 40°23′ | 37°59′ | 595 | 684 |
| 31 | 40°27′ | 37°41′ | 657 | 668 |
| 32 | 43°34′ | 37°29′ | 1072 | 1109 |
| 33 | 44°5′ | 37°46′ | 1725 | 434 |
| 34 | 44°4′ | 37°41′ | 1694 | 1006 |
| 35 | 41°51′ | 37°58′ | 530 | 1044 |
| 36 | 42°42′ | 37°28′ | 780 | 1127 |
| 37 | 43°34′ | 37°17′ | 775 | 1212 |
| 38 | 43°32′ | 37°33′ | 1627 | 290 |
| 39 | 43°59′ | 37°42′ | 1425 | 521 |
| 40 | 43°3′ | 37°60′ | 1482 | 2029 |
| 41 | 40°12′ | 38°23′ | 689 | 1504 |
| 42 | 41°52′ | 37°49′ | 465 | 3909 |
| 43 | 41°31′ | 38°11′ | 630 | 625 |
| 44 | 39°42′ | 38°20′ | 843 | 287 |
| 45 | 43°10′ | 37°22′ | 935 | 1217 |
| 46 | 44°36′ | 37°17′ | 1338 | 296 |
| 47 | 39°30′ | 38°27′ | 1263 | 101 |
| Description | Criterion |
|---|---|
| Non-drought | 0.0 ≤ SDI |
| Mild drought | −1.0 ≤ SDI < 0.0 |
| Moderate drought | −1.5 ≤ SDI < −1.0 |
| Severe drought | −2.0 ≤ SDI < −1.5 |
| Extreme drought | SDI < −2.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ozkaya, A.; Zerberg, Y. A 40-Year Analysis of the Hydrological Drought Index for the Tigris Basin, Turkey. Water 2019, 11, 657. https://doi.org/10.3390/w11040657
Ozkaya A, Zerberg Y. A 40-Year Analysis of the Hydrological Drought Index for the Tigris Basin, Turkey. Water. 2019; 11(4):657. https://doi.org/10.3390/w11040657
Chicago/Turabian StyleOzkaya, Arzu, and Yeliz Zerberg. 2019. "A 40-Year Analysis of the Hydrological Drought Index for the Tigris Basin, Turkey" Water 11, no. 4: 657. https://doi.org/10.3390/w11040657
APA StyleOzkaya, A., & Zerberg, Y. (2019). A 40-Year Analysis of the Hydrological Drought Index for the Tigris Basin, Turkey. Water, 11(4), 657. https://doi.org/10.3390/w11040657





