The Role of Hydraulic Hysteresis on the Hydrological Response of Pyroclastic Silty Covers
Abstract
1. Introduction
- investigation of the wetting/drying paths of an instrumented reconstituted ash layer exposed to weather forcing over four consecutive years;
- selection of a suitable model for analysis of the hydraulic hysteresis and calibration of the parameters required to simulate the soil behavior;
- analysis of the role of the hydraulic hysteresis of a virtual slope in response to a critical event, and comparison with the results obtained by the usual non-hysteretic approaches.
2. Materials and Methods
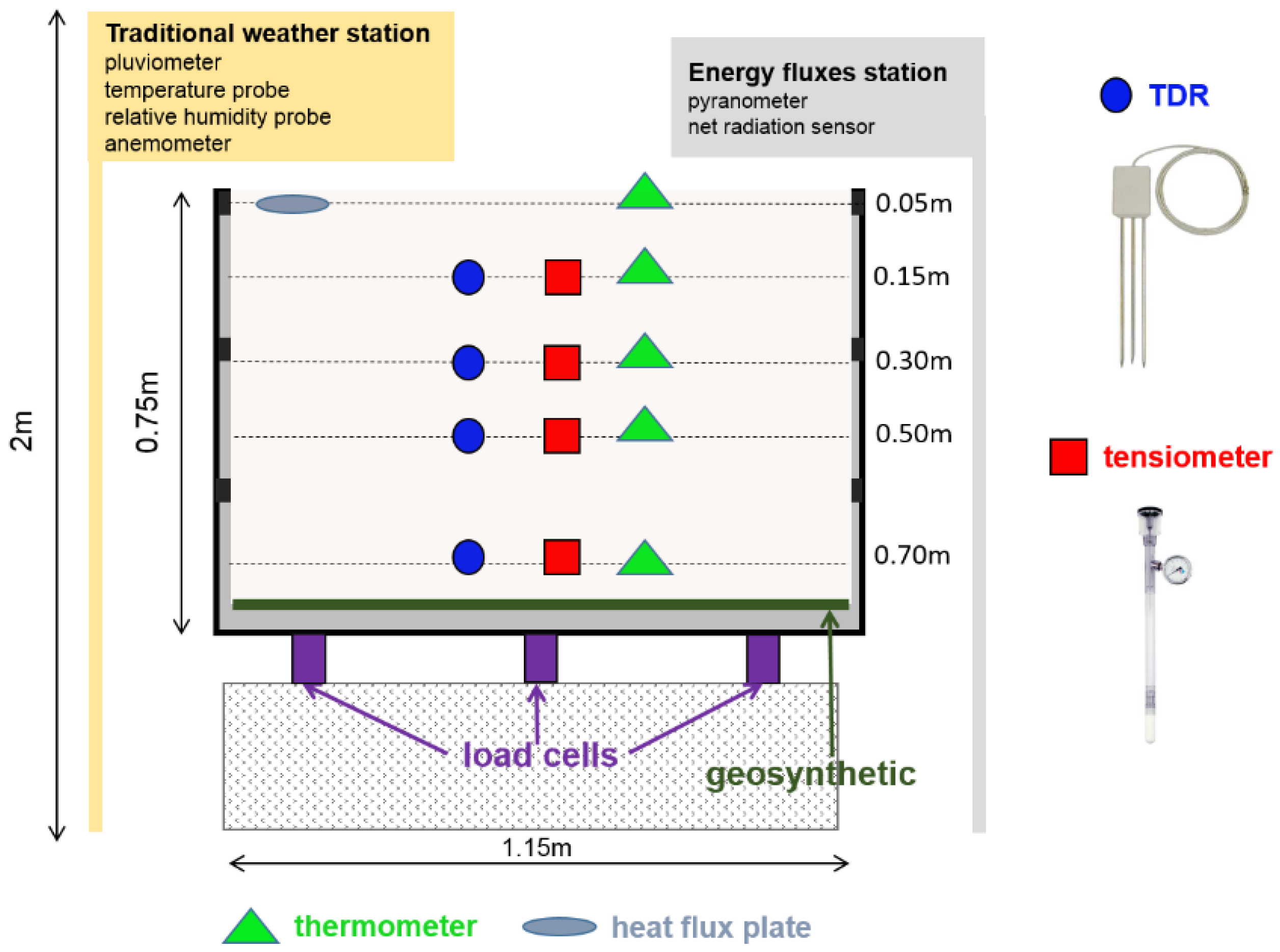
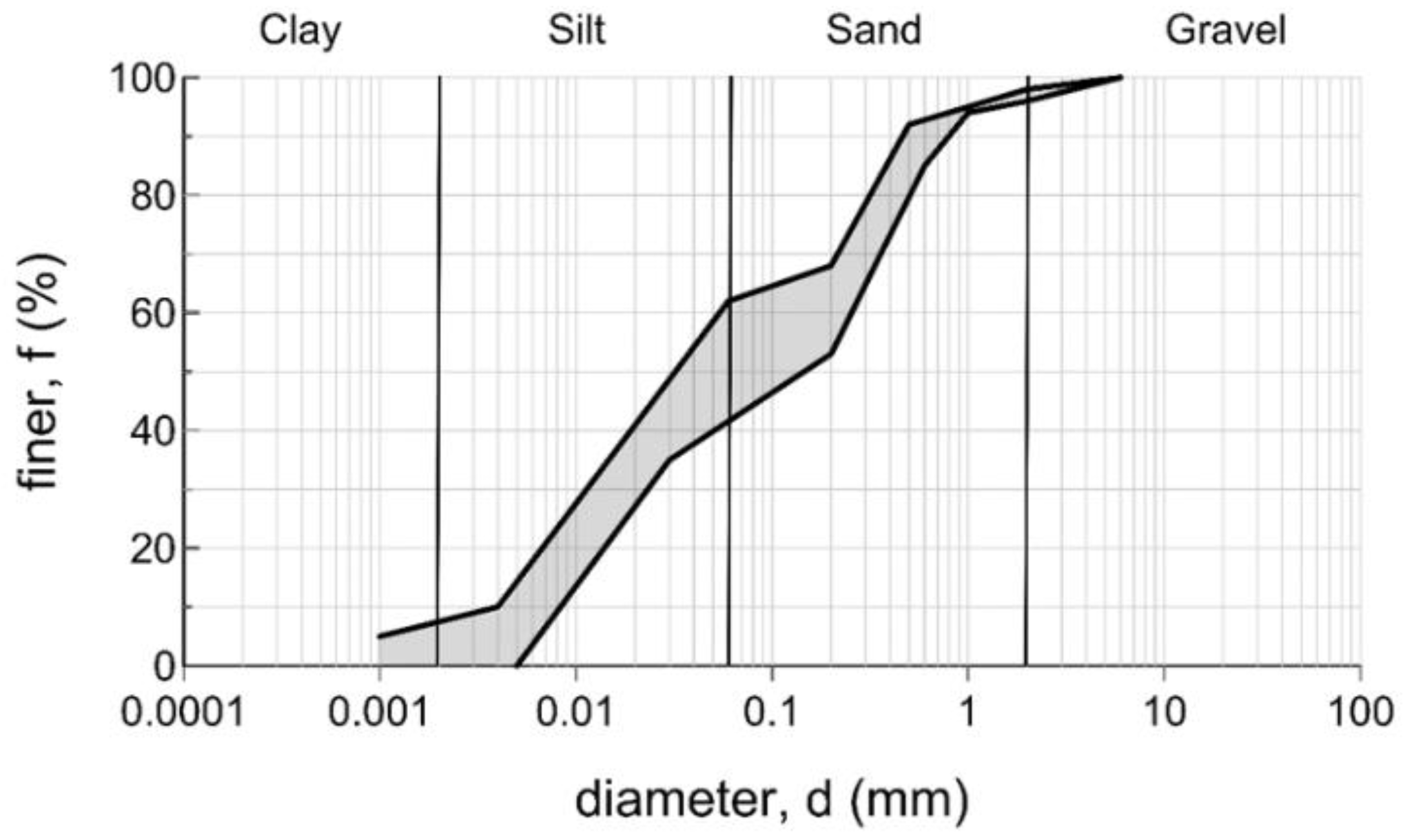
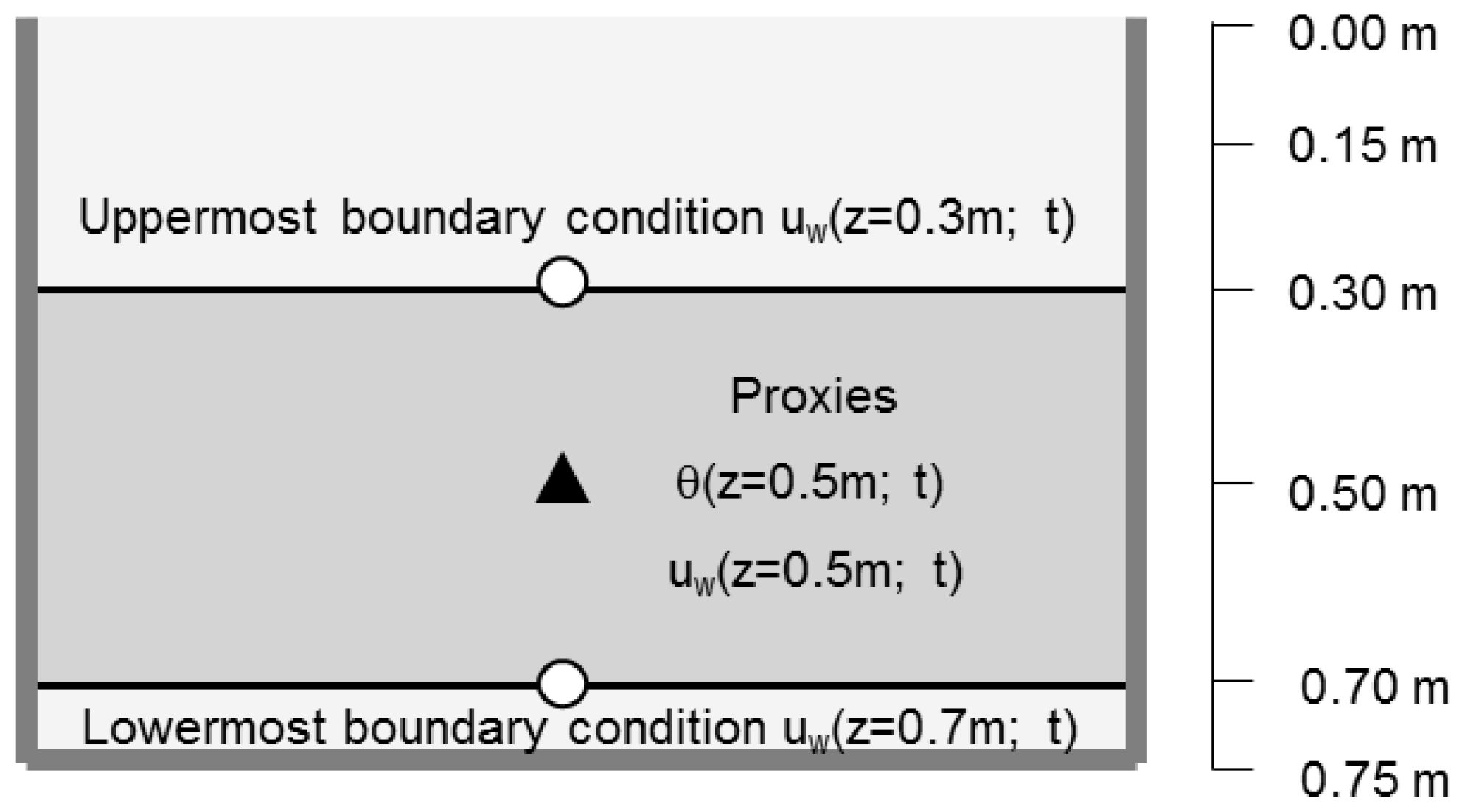
2.1. Test Device and Investigated Soil
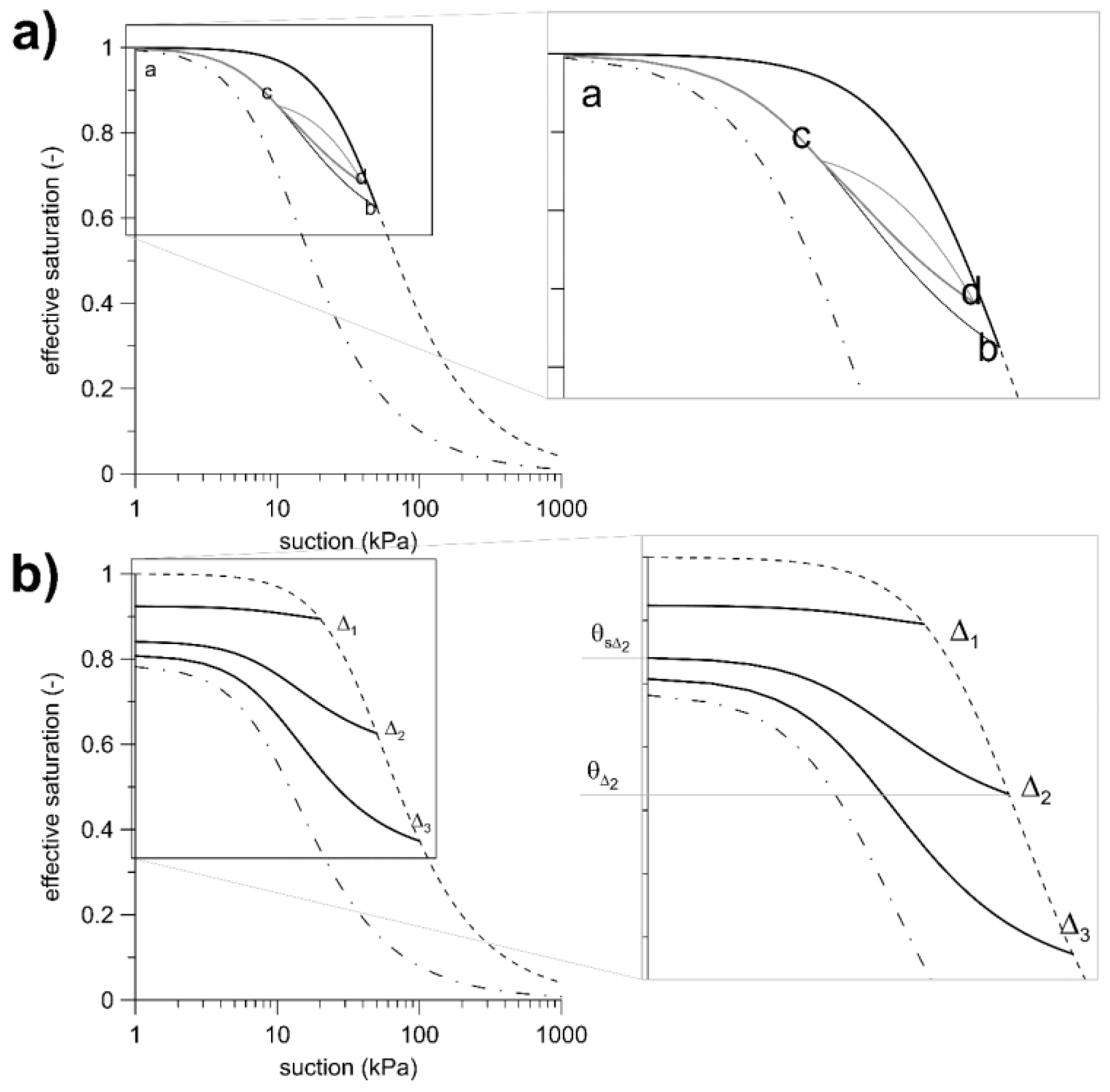
2.2. Modeling Approaches
3. Results and Discussion
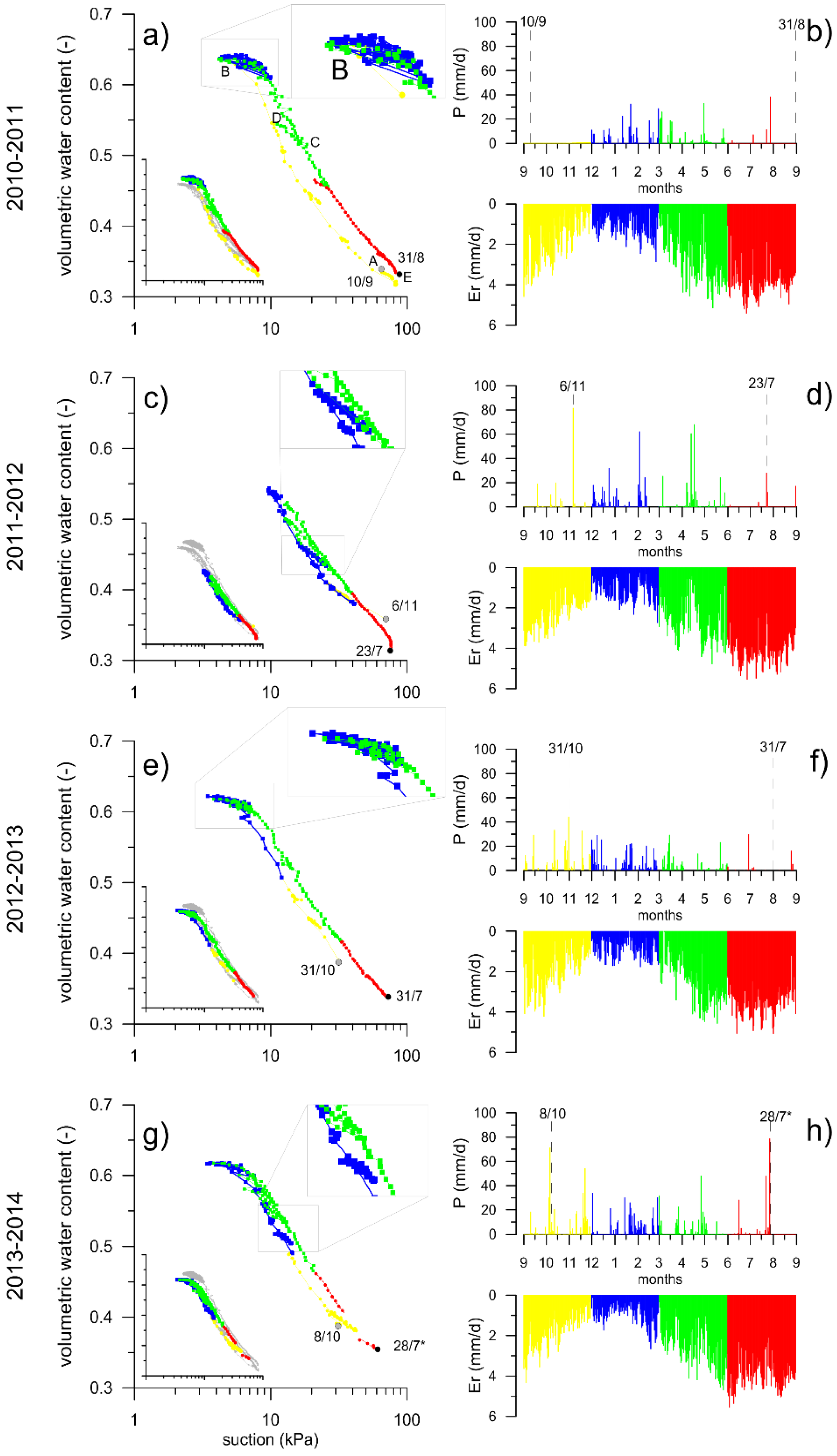
3.1. Lysimeter Results
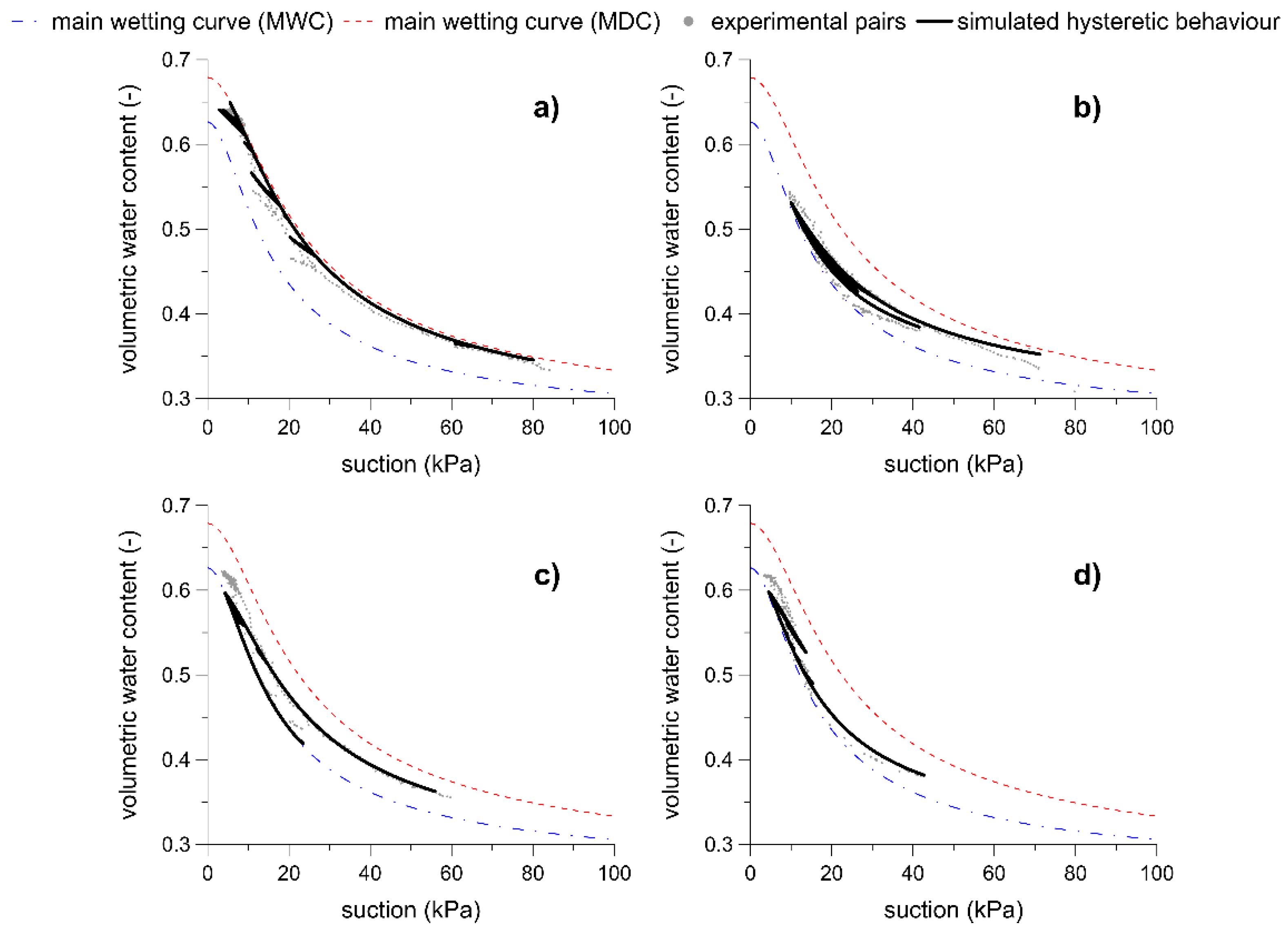
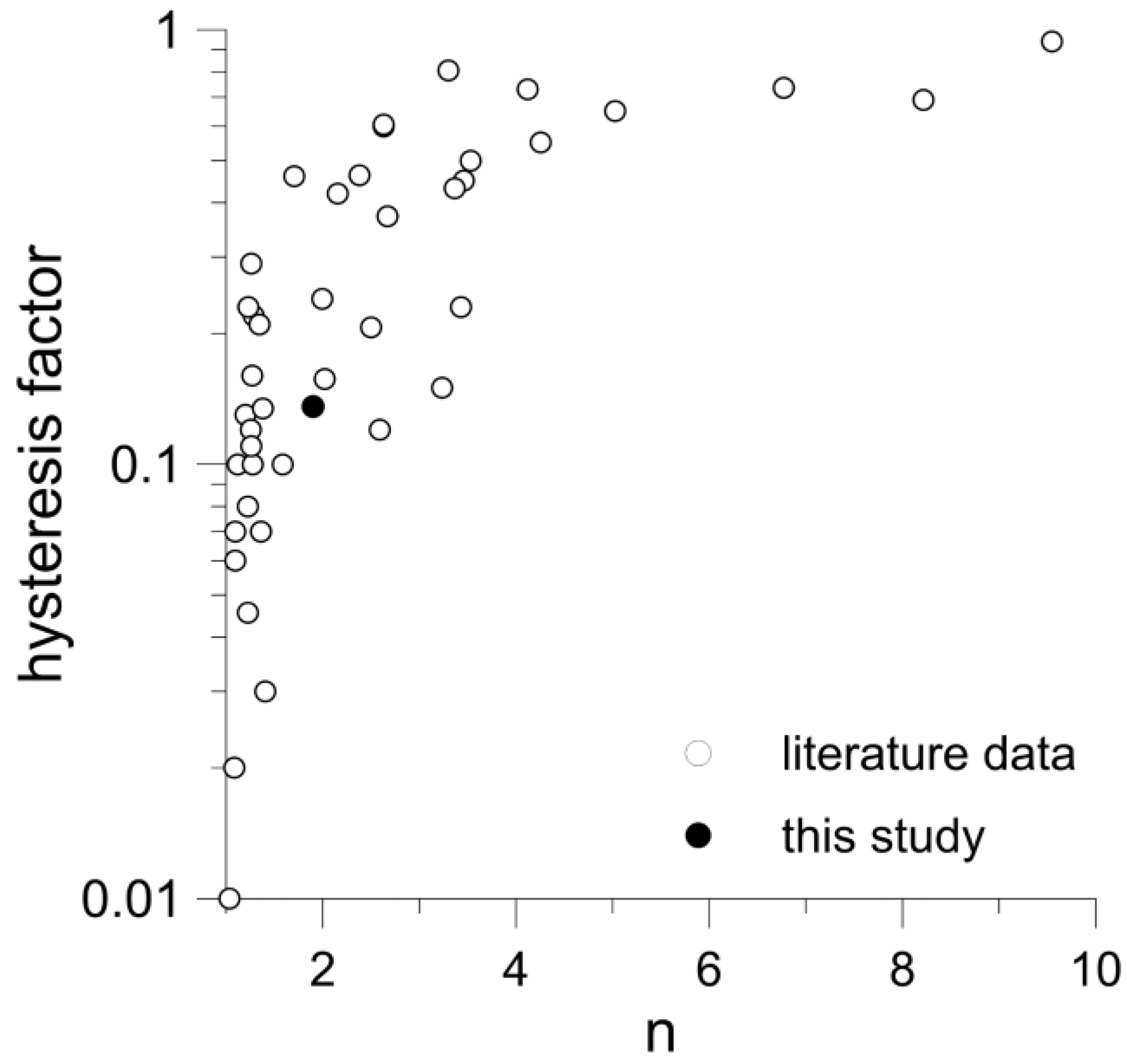
3.2. Model Calibration and Validation
3.3. Numerical Experiments on the Effects of Hydraulic Hysteresis in Landslide Triggering
3.3.1. Investigated Scenarios and Organization of Obtained Results
- (1)
- (2)
- the lowermost boundary condition is modeled as a seepage surface, which behaves as an impervious boundary when suction remains higher than zero, and as a draining surface when it vanishes; this is the condition that has been recognized, through special targeted experiments, at the contact between ash and pumice layers [44];
- (3)
- two alternative hypotheses are adopted for the initial conditions: (A) constant piezometric head and (B) constant volumetric water content; the latter obviously results in an initial non-equilibrated suction profile;
- (4)
- a persistent 100 mm/day constant rainfall, slightly higher (~1.2 × 10−6 m/s) than the hydraulic conductivity of fully saturated soil, is imposed at the uppermost boundary condition; this is a realistic scenario in the considered geomorphological context, where such a daily rainfall intensity occurs every 2–3 years.
- -
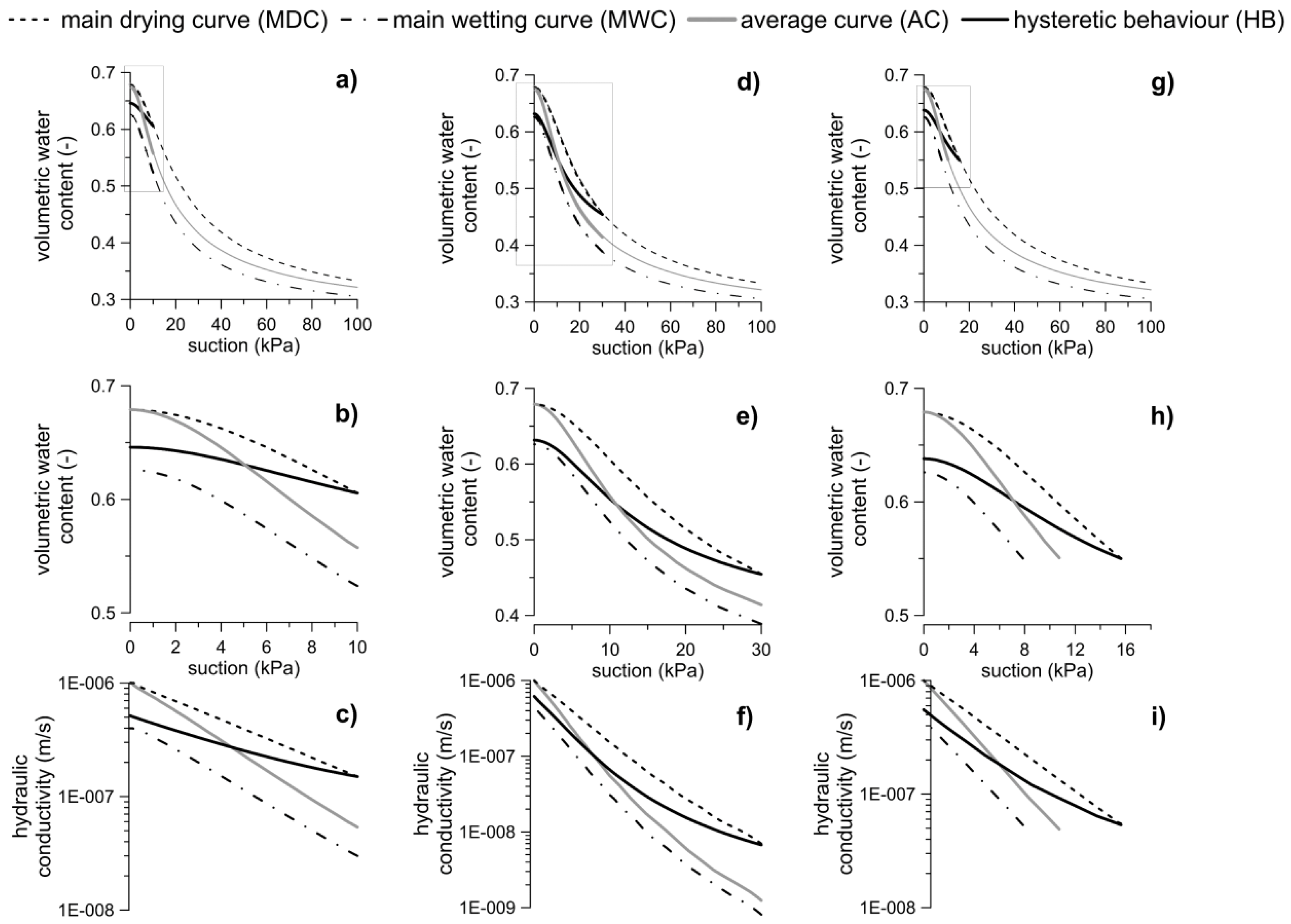
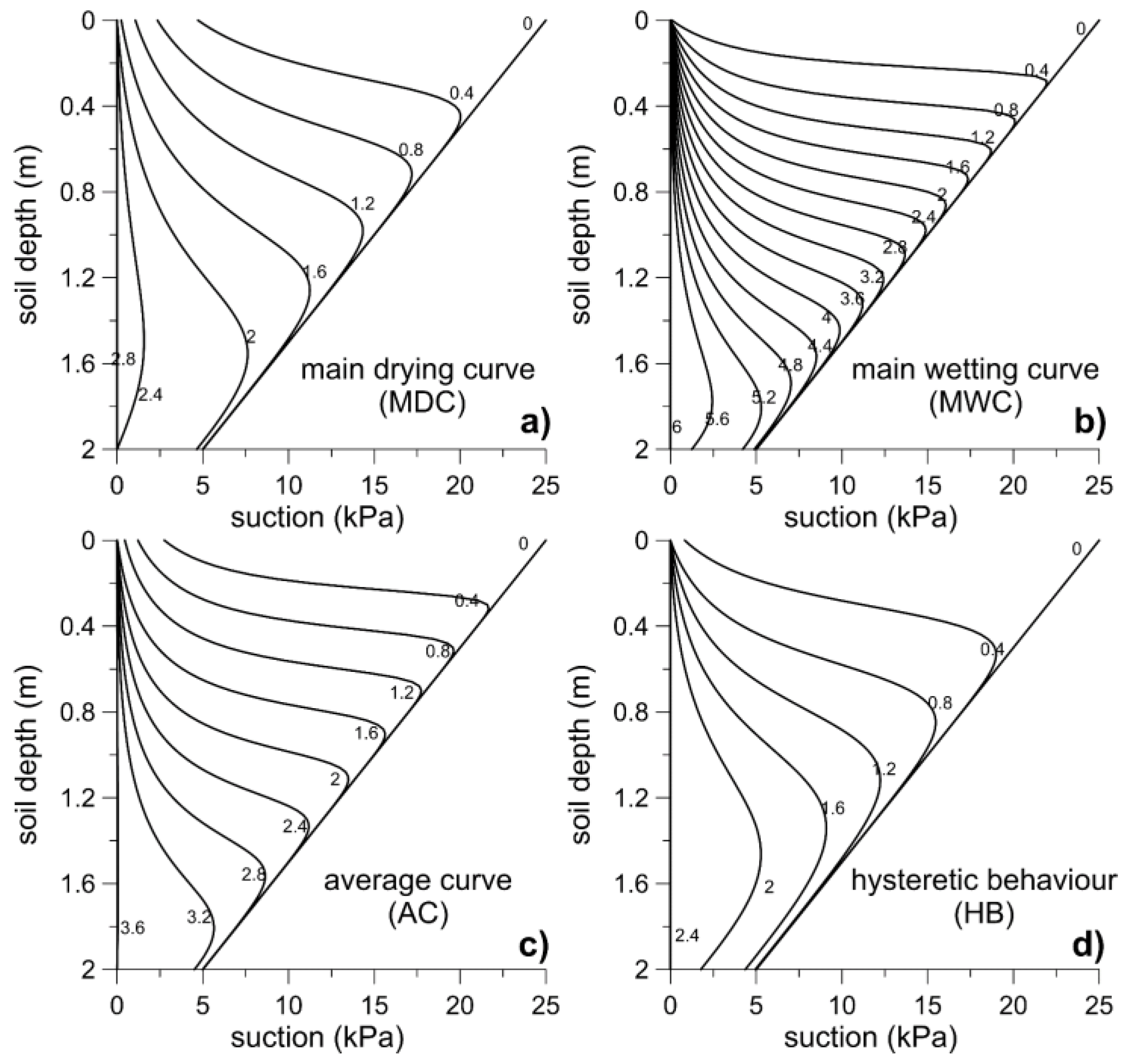
- full hysteretic soil behavior (HB);
- -
- main drying curve (MDC);
- -
- main wetting curve (MWC);
- -
- the curve obtained by averaging the experimental results of Rianna et al. [12] at a depth of 50 cm (AC).
3.3.2. Case A: Persistent Rainfall; Hydrostatic Initial Suction Profile
3.3.3. Case B: Persistent Rainfall; Uniform Initial Volumetric Water Content
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
- Pagano, L.; Picarelli, L.; Rianna, G.; Urciuoli, G. A simple numerical procedure for timely prediction of precipitation–induced landslides in unsaturated pyroclastic soils. Landslides 2010, 7, 273–289. [Google Scholar] [CrossRef]
- Rianna, G.; Pagano, L.; Urciuoli, G. Rainfall patterns triggering shallow flowslides in pyroclastic soils. Eng. Geol. 2014, 174, 22–35. [Google Scholar] [CrossRef]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef]
- Cascini, L.; Guida, D.; Romanzi, G.; Nocera, N.; Sorbino, G. A preliminary model for the landslides of May 1998 in Campania Region. In Proceedings of the International Symposium on The Geotechnics of Hard Soils—Soft Rocks, Naples, Italy, 12–14 October 1998; Evangelista, A., Picarelli, L., Eds.; 1998; Volume 3, pp. 1623–1652. [Google Scholar]
- Olivares, L.; Picarelli, L. Shallow flowslides triggered by intense rainfalls on natural slopes covered by loose unsaturated pyroclastic soils. Geotechnique 2003, 532, 283–287. [Google Scholar] [CrossRef]
- Nocentini, M.; Tofani, V.; Gigli, G.; Fidolini, F.; Casagli, N. Modeling debris flows in volcanic terrains for hazard mapping: The case study of Ischia Island (Italy). Landslides 2015, 12, 831–846. [Google Scholar] [CrossRef]
- Picarelli, L.; Evangelista, A.; Rolandi, G.; Paone, A.; Nicotera, M.V.; Olivares, L.; Scotto di Santolo, A.; Lampitiello, S.; Rolandi, M. Mechanical properties of pyroclastic soils in Campania Region. In Proceedings of the 2nd International Workshop on Characterisation and Engineering Properties of Natural Soils, Singapore, 29 November–1 December 2006; Tan, T.S., Phoon, K.K., Height, D.W., Leroueil, S., Eds.; Taylor & Francis Group: London, UK, 2006; Volume 4, pp. 2331–2384. [Google Scholar]
- Nicotera, M.V.; Papa, R.; Urciuoli, G. An experimental technique for determining the hydraulic properties of unsaturated pyroclastic soils. Geotech. Test. J. 2010, 33, 263–285. [Google Scholar]
- Pirone, M.; Papa, R.; Nicotera, M.V.; Urciuoli, G. In situ monitoring of the groundwater field in an unsaturated pyroclastic slope for slope stability evaluation. Landslides 2015, 12, 259–276. [Google Scholar] [CrossRef]
- Damiano, E.; Olivares, L.; Picarelli, L. Steep–slope monitoring in unsaturated pyroclastic soils. Eng. Geol. 2012, 137, 1–12. [Google Scholar] [CrossRef]
- Rianna, G.; Pagano, L.; Urciuoli, G. Investigation of soil–atmosphere interaction in pyroclastic soils. J. Hydrol. 2014, 510, 480–492. [Google Scholar] [CrossRef]
- Comegna, L.; Damiano, E.; Greco, R.; Guida, A.; Olivares, L.; Picarelli, L. Field hydrological monitoring of a sloping shallow pyroclastic deposit. Can. Geotech. J. 2016, 53, 1125–1137. [Google Scholar] [CrossRef]
- Olivares, L.; Picarelli, L. Modelling of flowslides behaviour for risk mitigation. In Proceedings of the 6th International Conference on Physical Modelling in Geotechnics, Hong Kong, China, 4–6 August 2006; Taylor & Francis: London, UK, 2006; Volume 1, pp. 99–112. [Google Scholar]
- Cascini, L.; Cuomo, S.; Pastor, M.; Sorbino, G.; Piciullo, L. SPH run–out modelling of channelized landslides of the flow type. Geomorphology 2014, 214, 502–513. [Google Scholar] [CrossRef]
- Pirone, M.; Papa, R.; Nicotera, M.V.; Urciuoli, G. Evaluation of the Hydraulic Hysteresis of Unsaturated Pyroclastic Soils by in Situ Measurements. Proced. Earth Planet. Sci. 2014, 9, 163–170. [Google Scholar] [CrossRef]
- Comegna, L.; Damiano, E.; Greco, R.; Guida, A.; Olivares, L.; Picarelli, L. Investigation on the hydraulic hysteresis of a pyroclastic deposit. In Proceedings of the International Workshop on Volcanic Rocks and Soils, Ischia, Italy, 24–25 September 2015; pp. 161–162. [Google Scholar]
- Basile, A.; Ciollaro, G.; Coppola, A. Hysteresis in soil water characteristics as a key to interpreting comparisons of laboratory and field measured hydraulic properties. Water Resour. Res. 2003, 39, 1355. [Google Scholar] [CrossRef]
- Comegna, L.; Rianna, G.; Lee, S.; Picarelli, L. Influence of the wetting path on the mechanical response of shallow unsaturated sloping covers. Comput. Geotech. 2016, 73, 164–169. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed form equation for predicting the hydraulic conductivity. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Viaene, P.; Vereecken, H.; Diels, J.; Feyen, J. A statistical analysis of six hysteresis models for the moisture retention characteristic. Soil Sci. 1994, 157, 345–355. [Google Scholar] [CrossRef]
- Pham, H.Q.; Fredlund, D.G.; Barbour, S.L. A study of hysteresis models for soil-water characteristic curves. Can. Geotech. J. 2005, 42, 1548–1568. [Google Scholar] [CrossRef]
- Bashir, R. Quantification of Surfactant Induced Unsaturated Flow in the Vadose Zone. Ph.D. Thesis, McMaster University, Hamilton, ON, Canada, 2007. [Google Scholar]
- Parker, J.C.; Lenhard, R.J. A model for hysteretic constitutive relations governing multiphase flow: 1. Saturation–pressure relations. Water Resour. Res. 1987, 23, 2187–2196. [Google Scholar] [CrossRef]
- Scott, P.; Farquhar, G.; Kouwen, N. Hysteretic effects on net infiltration. In Advances in Infiltration; ASCE: Reston, VA, USA, 1983; pp. 163–170. [Google Scholar]
- Kool, J.B.; Parker, J.C. Development and evaluation of closed–form expressions for hysteretic soil hydraulic properties. Water Resour. Res. 1987, 23, 105–114. [Google Scholar] [CrossRef]
- Werner, A.D.; Lockington, D.A. Artificial pumping errors in the Kool– Parker scaling model of soil moisture hysteresis. J. Hydrol. 2006, 325, 118–133. [Google Scholar] [CrossRef]
- Land, C.S. Calculation of Imbibition Relative Permeability for Two– and Three–Phase Flow from Rock Properties. Soc. Pet. Eng. J. 1968, 8, 149–156. [Google Scholar] [CrossRef]
- Lenhard, R.J.; Parker, J.C. A Model for Hysteretic Constitutive Relations Governing Multiphase Flow 2. Water Resour. Res. 1987, 23, 2197–2206. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Requirements. Irrigation and Drainage Paper No. 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Rianna, G.; Reder, A.; Pagano, L. Estimating actual and potential bare soil evaporation from silty pyroclastic soils: Towards improved landslide prediction. J. Hydrol. 2018, 562, 193–209. [Google Scholar] [CrossRef]
- Pagano, L.; Reder, A.; Rianna, G. Effects of vegetation on hydrological response of silty volcanic covers. Can. Geotech. J. 2018. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H.; Fredlund, M.D. Unsaturated Soil Mechanics in Engineering Practice; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Hopmans, J.W.; Šimůnek, J.W.; Romano, N.; Durner, W. Inverse Methods. In Methods of Soil Analysis—Part 4—Physical Methods; Dane, J.H., Topp, G.C., Eds.; SSSA Book Ser. 5; SSSA: Madison, WI, USA, 2014; pp. 963–1008. [Google Scholar]
- Šimunek, J.; Šejna, M.; Saito, H.; Sakai, M.; van Genuchten, M.T. The Hydrus–1D Software Package for Simulating the Movement of Water, Heat, and Multiple Solutes in Variably Saturated Media. Version 4.17. Hydrus Software Series 3; Department of Environmental Sciences, University of California Riverside: Riverside, CA, USA, 2013. [Google Scholar]
- Likos, W.J.; Lu, N.; Godt, J.W. Hysteresis and Uncertainty in Soil Water–Retention Curve Parameters. J. Geotech. Geoenv. Eng. 2014, 140, 04013050. [Google Scholar] [CrossRef]
- Gebrenegus, T.; Ghezzehei, T.A. An index for degree of hysteresis in water retention. Soil Sci. Soc. Am. J. 2011, 75, 2122–2127. [Google Scholar] [CrossRef]
- Yang, C.; Sheng, D.; Carter, J.P. Effect of Hydraulic Hysteresis on Seepage Analysis for Unsaturated Soils. Comput. Geotech. 2012, 41, 36–56. [Google Scholar] [CrossRef]
- Huang, H.C.; Tan, Y.C.; Liu, C.W.; Chen, C.H. A novel hysteresis model in unsaturated soil. Hydrol. Process. 2005, 19, 1653–1665. [Google Scholar] [CrossRef]
- Reder, A.; Rianna, G.; Pagano, L. Physically based approaches incorporating evaporation for early warning predictions of rainfall–induced landslides. Nat. Hazards Earth Syst. Sci. 2018, 18, 613–631. [Google Scholar] [CrossRef]
- Di Crescenzo, G.; Santo, A. Debris slides–rapid earth flows in the carbonate massifs of the Campania region (Southern Italy): Morphological and morphometric data for evaluating triggering susceptibility. Geomorphol. 2005, 66, 255–276. [Google Scholar] [CrossRef]
- Reder, A.; Pagano, L.; Picarelli, L.; Rianna, G. The role of the lowermost boundary conditions in the hydrological response of shallow sloping covers. Landslides 2017, 14, 861–873. [Google Scholar] [CrossRef]
- Feddes, R.A.; Bresler, E.; Neuman, S.P. Field test of a modified numerical model for water uptake by root systems. Water Resour. Res. 1974, 10, 1199–1206. [Google Scholar] [CrossRef]

| Hydraulic Characterization | θs | θr | α (1/kPa) | N | ks (m/s) |
|---|---|---|---|---|---|
| MDC | 0.679 | 0.260 | 0.07 | 1.9 | 1.00 × 10−6 |
| MWC | 0.626 | 0.260 | 0.10 | 1.9 | 3.00 × 10−7 |
| AC | 0.679 | 0.288 | 0.11 | 1.9 | 1.00 × 10−6 |
| Hydraulic Characterization | Δθ | kav (m/s) |
|---|---|---|
| HB | 0.04 | 3.90 × 10−7 |
| MDC | 0.07 | 2.25 × 10−7 |
| MWC | 0.11 | 1.00 × 10−7 |
| AC | 0.12 | 2.39 × 10−7 |
| Hydraulic Characterization | Δθ | kav (m/s) | NST (Days) |
|---|---|---|---|
| HB | 0.09 | 1.72 × 10−7 | 3.0 |
| MDC | 0.13 | 2.34 × 10−7 | 2.8 |
| MWC | 0.08 | 1.55 × 10−7 | 3.5 |
| AC | 0.13 | 2.22 × 10−7 | 2.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rianna, G.; Comegna, L.; Pagano, L.; Picarelli, L.; Reder, A. The Role of Hydraulic Hysteresis on the Hydrological Response of Pyroclastic Silty Covers. Water 2019, 11, 628. https://doi.org/10.3390/w11030628
Rianna G, Comegna L, Pagano L, Picarelli L, Reder A. The Role of Hydraulic Hysteresis on the Hydrological Response of Pyroclastic Silty Covers. Water. 2019; 11(3):628. https://doi.org/10.3390/w11030628
Chicago/Turabian StyleRianna, Guido, Luca Comegna, Luca Pagano, Luciano Picarelli, and Alfredo Reder. 2019. "The Role of Hydraulic Hysteresis on the Hydrological Response of Pyroclastic Silty Covers" Water 11, no. 3: 628. https://doi.org/10.3390/w11030628
APA StyleRianna, G., Comegna, L., Pagano, L., Picarelli, L., & Reder, A. (2019). The Role of Hydraulic Hysteresis on the Hydrological Response of Pyroclastic Silty Covers. Water, 11(3), 628. https://doi.org/10.3390/w11030628








