4.1. Statistical Verification of Data
Taking into account the increasing frequency of human interference in the natural water environment, which is affecting changes in the river regime, research into the invariance of hydrological conditions in the studied catchments is necessary for the considered measurement period. Therefore, statistical verification of the
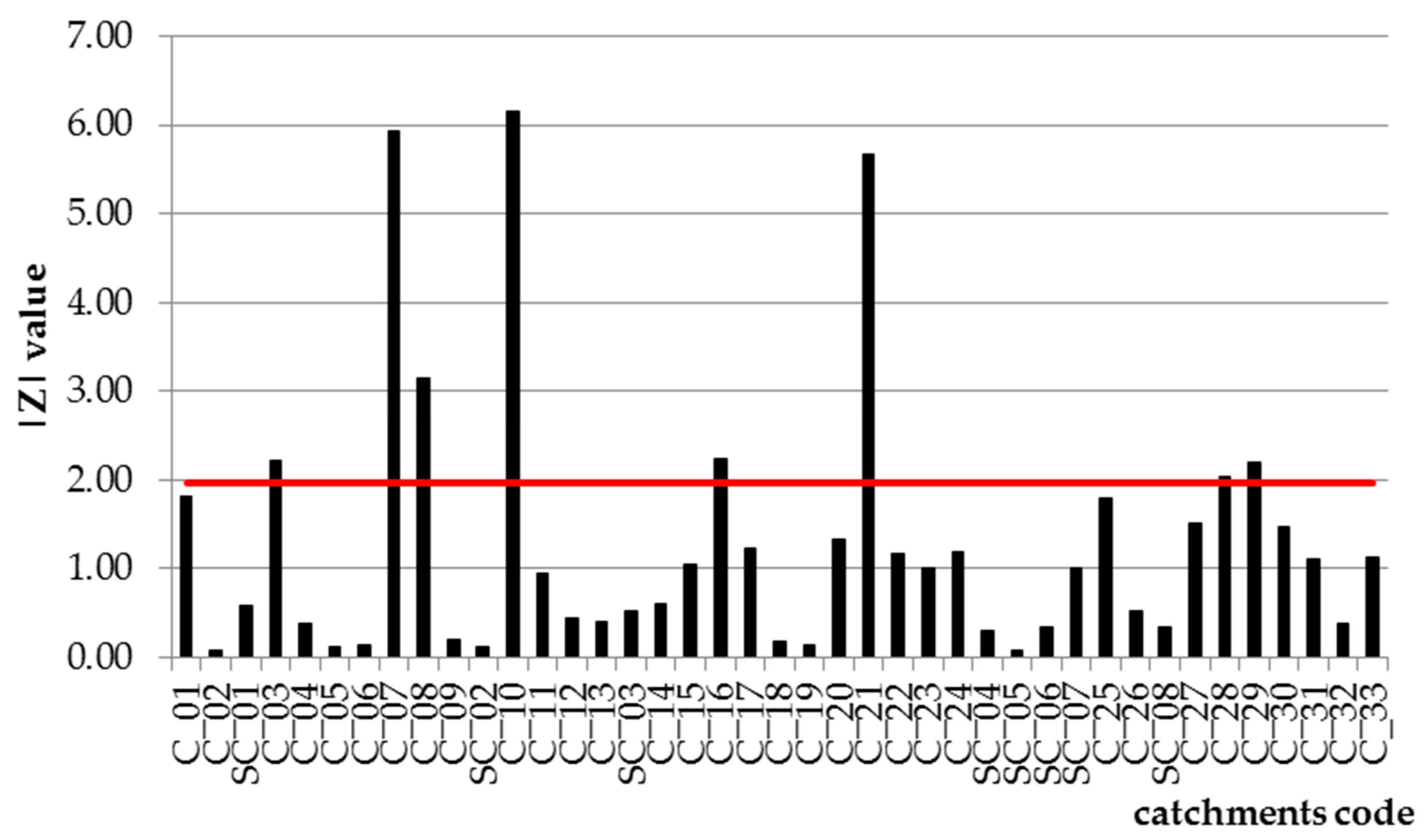
Qmax flow observation series versus the homogeneity and independence of data was carried out, using the Mann–Kendall test to examine the significance of the trend. The results of the analysis are presented in
Figure 2.
Based on the obtained results, it was found that the majority of the studied rivers did not show statistically significant trends of the
Qmax flows. This is evidenced by the size of normalized statistics |
Z|, for which most values were lower than the critical value of this test for the significance level of α = 0.05 (
Zcrit = 1.96). The following catchment areas constitute exceptions: Bystra-Kamesznica (C_03), Skawica-Zawoja (C_07), Stryszawka-Sucha (C_08), Raba-Rabka (C_10), Kirowa Woda-Kościelisko Kiry (C_16), Grajcarek-Szczawnica (C_21), San-Dwernik (C_28), and Czarny-Polana (C_29), for which the values of |
Z| are bigger than
Zcrit. Such results are attributed to the response of these catchments to the course of heavy rainfall of very strong intensity that occurred in Central and Eastern Europe in 1997 and 2010, causing flash floods in the upper Vistula basin [
33]. In addition, as stated by Wyżga et al. [
34], in recent years in the basin of the upper Vistula there had been changes in land use, which resulted in the modified occurrence of floods. For the remaining catchments, there were no statistically significant trends observed. This means that the studied variables are independent and that they derive from the same general population. Therefore, in the analysed multi-year period, no factor has appeared that would significantly affect the course of processes shaping flood flows from these catchments.
Similar research results related to the analysis of changes in the flood flows from the catchments of the upper Vistula river basin are presented in the papers [
35,
36], where in the majority of the studied cases there were also no statistically significant trends found in the observation series of flood flows in the upper Vistula basin. Bearing in mind that the observation series adopted for further analysis should meet the requirements of a simple random sample, the following catchments were excluded from further research: Bystra-Kamesznica, Skawica-Zawoja, Stryszawka-Sucha, Raba-Rabka, and Grajcarek-Szczawnica. On the other hand, catchments where a slight deviation from the assumed
Zcrit was recorded were included in further analyses.
4.3. Determining the Form of the Equation for Calculating the Peak Flows in the Catchments of the Upper Vistula River Basin
The preliminary selection of physiographic and meteorological characteristics describing
Qmed flows in the upper Vistula basin was made on the basis of the correlation matrix analysis, conducted for the initially determined values of these factors. It should be emphasized that due to the nature of statistical significance, it follows that if a significant number of determinations of correlation coefficients are performed, then statistically significant values may occur relatively frequently. There is no universal way to identify true (actual) correlations. Therefore, all results for which the strength of the correlation relationship is insufficient should be treated with caution. They should be verified in a subjective way, intuitively assessing the impact of these characteristics on the variable under study. With this in mind, final selection was made from the group of predictors (see
Table 1) for the construction of the model in its final form: surface area of the catchment
A, height difference in the catchment area Δ
H, river network density
D, arable land index
Sfr, built-up index
Sfu, soil imperviousness index
N, and annual normal precipitation
P. According to Węglarczyk [
39], the number of predictors describing the dependent variable should not be overly high. This is due to the fact that each independent variable, in addition to information about the forecasted value, carries with it a certain degree of uncertainty, resulting from the observation series of this particular feature. Hence the need to determine the optimum number of independent variables, based on the quality of the model.
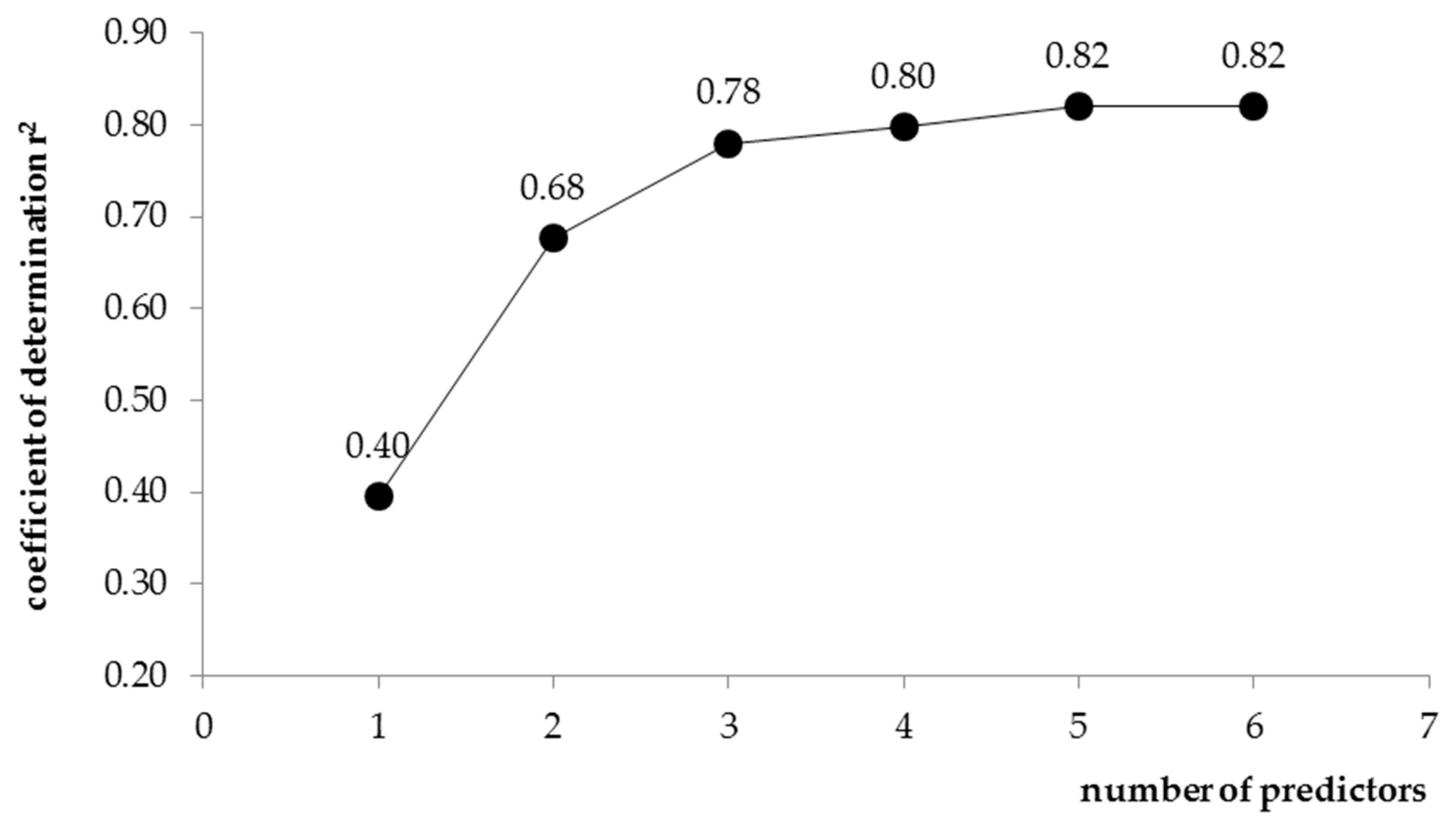
Figure 4 summarizes the values of statistics for a given number of independent variables of the analysed formula.
Based on the data presented in
Figure 4, it was found that the values of the determination coefficient
r2 increase significantly with the addition of further independent variables to the equation. This results from the very essence of this coefficient, as it is a non-decreasing function of the number of independent variables in multiple regression models. On the other hand, a markedly smaller increase in this characteristic was recorded after taking into account the fifth predictor in the equation. Furthermore, the addition of a sixth independent variable did not provide a significant improvement in the quality of the model. Therefore, as the final configuration of the formula for calculating the
Qmed flows in the entire upper Vistula basin, a five-parameter form of the exponential equation was adopted:
where:
A—catchment area (km2);
ΔH—height difference in the catchment area (m a.s.l.);
D—river network density (km·km−2);
N—Boldakov’s soil imperviousness index (%);
P—annual normal precipitation in the catchment (mm).
While making the substantive verification of the established model form, it was found that it is logical. This is evidenced by the values of regression coefficients n for the predictors describing particular equations. When analysing Formula (22) in detail, it is concluded that the flow of Qmed increases with the increase of the catchment’s surface area, as well as the height difference of the catchment area, the density of the river network, the value of the soil imperviousness index, and the amount of normal annual precipitation within the catchment.
Statistical verification of the established model forms was made on the basis of the significance of the linear regression of the model, the significance of partial regression coefficients, the evaluation of redundancy between independent variables, the assumption of homoscedasticity of residuals, the lack of autocorrelation of residuals, the normality of distribution of residuals, and the evaluation of the expected value of a random component.
Table 2 presents the results concerning the analysis of the significance of the linear regression of the model, and the significance of partial regression coefficients.
Based on the values summarized in
Table 2, it has been found that the model form for calculating
Qmed in the entire upper Vistula basin is characterized by a statistically significant value of the
F statistic, for which the
p-value is less than the assumed significance level of α = 0.05. In turn, statistically significant values of
pi partial regression coefficients occur for the catchment area and river network density. Bearing in mind the analysis regarding the determination of the optimum number of predictors in the equations, it was decided that statistically insignificant parameters should be retained, because their removal decreases the quality of the examined models, reflected by a marked decrease in the value of the determination coefficient
r2.
The evaluation of the redundancy of variables is based on the so-called tolerance factor. In cases when the value of that factor was higher than 0.1, it was concluded that there is no collinearity of independent variables. The results of this analysis are summarized in
Table 3.
When analysing the values listed in
Table 3, it was found that the tolerance for all variables is high (above 0.1). In addition, the values of coefficient
r2c differ significantly from one. Thus, independent variables do not show redundancy in regression equations, which indicates the lack of their collinearity. Furthermore, the relatively high values of semi-partial correlations in the studied equation forms, for independent variables, indicate relatively high correlations with the dependent variable.
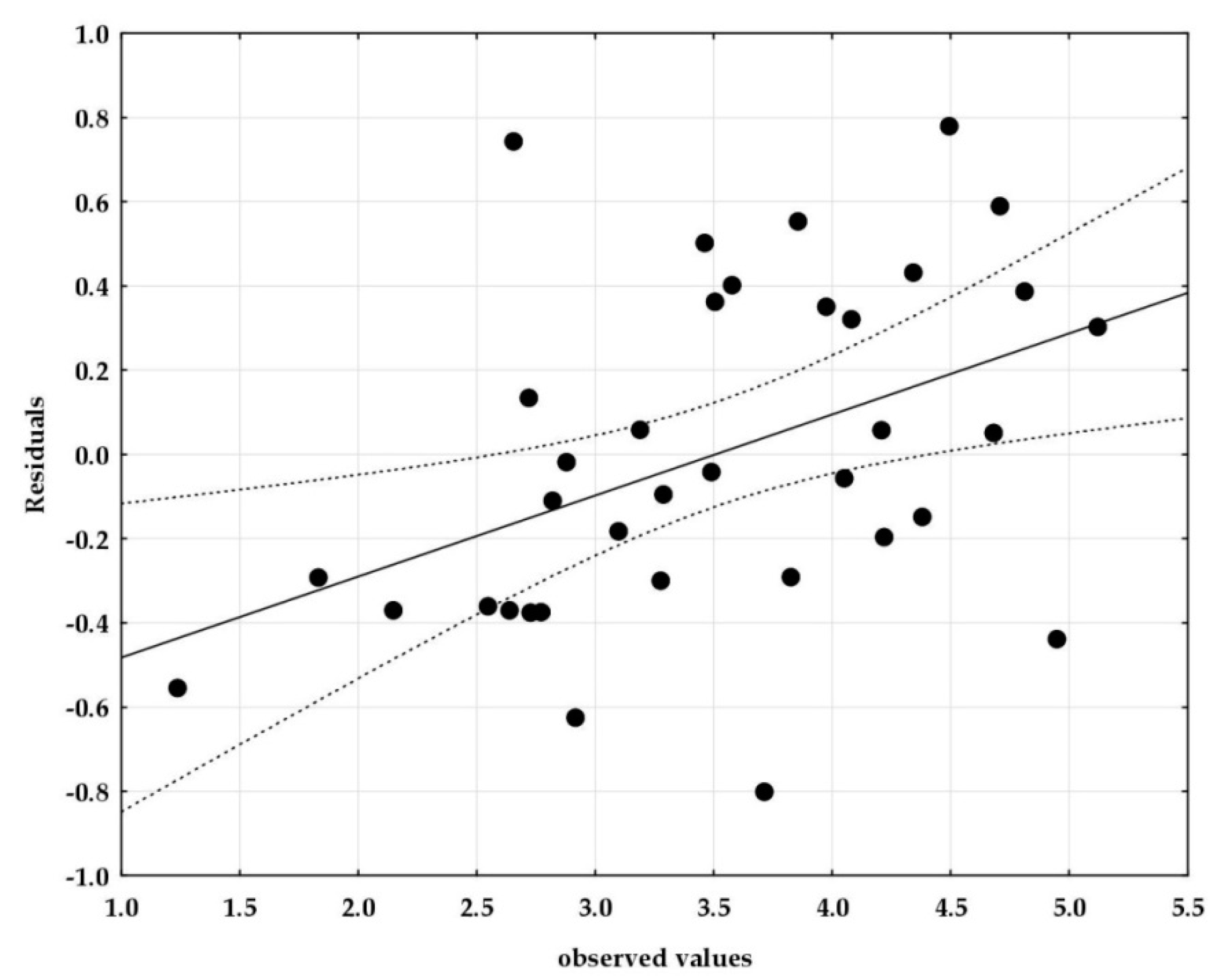
The assumption of constancy of the variance of the random component for individual values of independent variables (homoscedasticity) was verified using the scatter plots.
Figure 5 is a graph of predicted values relative to residual values.
When analysing the values summarized in
Figure 5, we noted the lack of heteroscedasticity (violation of the assumption of homoscedasticity) of the random variables being analysed. Points on the graph are arranged in the form of an evenly distributed cloud, and there are no clear systems of the points that form individual groups. Therefore, there is no reason to reject the assumption of constancy of the random component variance, for individual independent variables.
To verify the autocorrelation of the residuals of the models, the Durbin-Watson statistics were used. The results of the analysis are summarized in
Table 4. Based on the results as seen in
Table 4, the hypothesis was adopted that the random elements were not correlated.
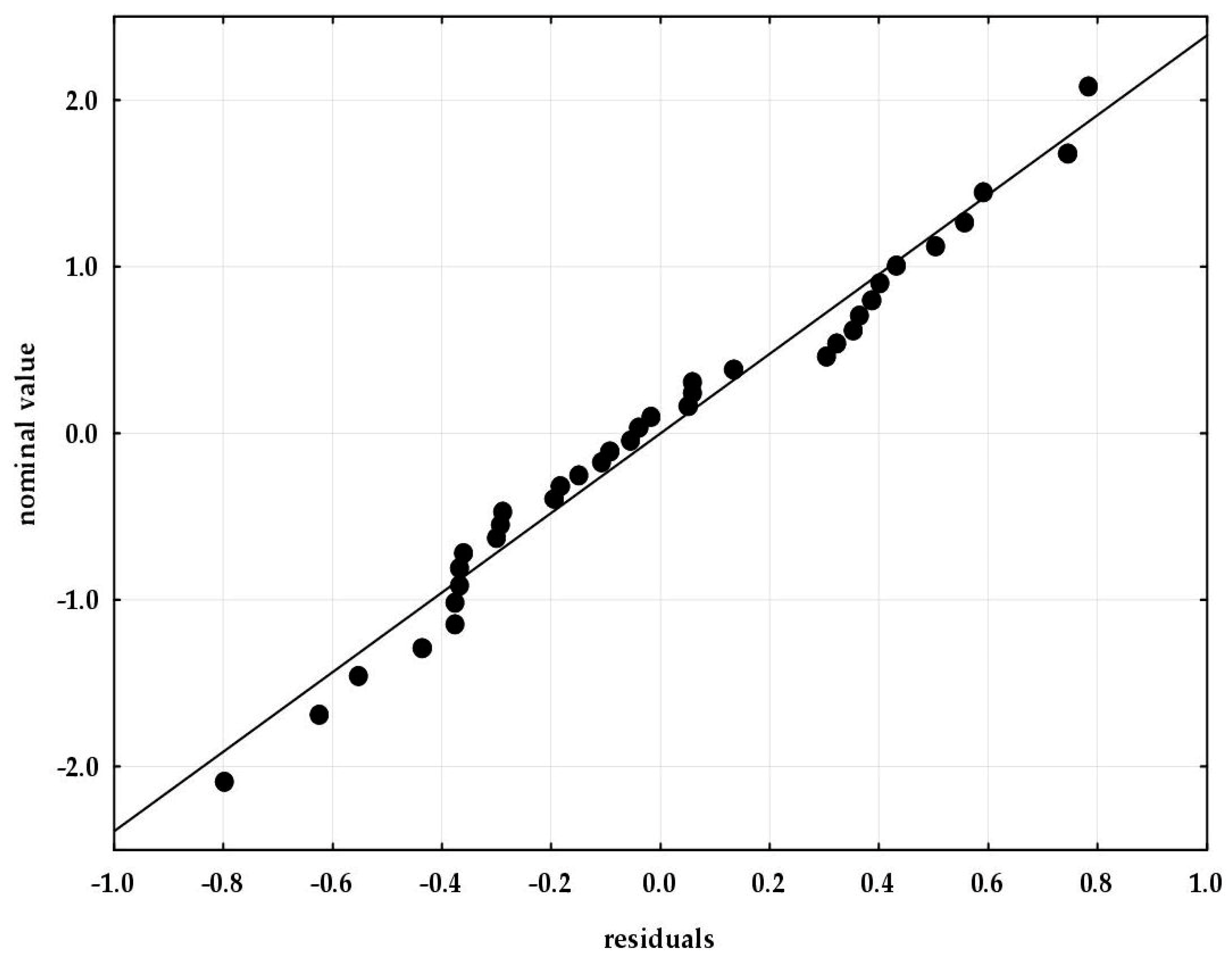
The normality of the distribution of residues was verified using the normality plot.
Figure 6 presents a chart of nominal (expected) values relative to residual values obtained by applying the tested form of the empirical model. Based on the normality plot of the residuals, it was found that for the analysed equation, most points are arranged along a straight line. Hence the inference that in these cases the distribution of residues is consistent with the normal distribution.
The verification of the assumption about the zero value of the expected random component
εi was made based on the analysis of average residuals for the studied forms of equations. The results are summarized in
Table 5.
Based on the results summarized in
Table 5, it was found that the average values of the residuals for the developed model are 0; therefore, the hypothesis with a zero value for the random component
εi is true. This means that the distortions (random components) do not show any tendency of the empirical values of the dependent variable deviating from the theoretical values in any direction (either plus or minus).
Verification of the determined correlation for the forecast of
Qmed flows in the catchments of the upper Vistula basin was made on the basis of independent hydrometric material for the following catchments: Przemsza-Piwoń, Skawinka-Radziszów (non-Carpathian catchments) and Stradomka-Stradomka, Niedziczanka-Niedzica, Jasiołka-Zboiska (Carpathian catchments). Additionally, the confidence interval was estimated by applying the Formulas (6) and (7), for the significance level of α = 0.05. The results are shown in
Table 6.
Based on the results summarized in
Table 6, it was found that the obtained form of the empirical model produces satisfying results. This is evidenced by the small differences between
Qmed and
. Therefore, it is recommended that Formula (22) be used in the ungauged basins of the upper Vistula river basin. This will eliminate the problem related to the choice of the appropriate regional equation if the river flows through several physiographic regions, and above all, through both Carpathians and non-Carpathian areas. Such rivers may demonstrate characteristics acquired in the upper course, even though their water gauge profile is far beyond the region’s reach. Regarding the analysis we have conducted, concerning the determination of the lower and upper boundaries of the confidence interval for the determined form of the empirical model, it can be stated that for the confidence level of 95%, the predicted
Qmed values remain within the range described by Equation (6).
4.4. Determination of Dimensionless Quantiles’ Values for the Calculation of Peak Annual Flows with a Defined Frequency of Occurrence
Determination of the values of dimensionless
μT quantiles was meant to facilitate the determination of
QT flows, based on Formula (22). To determine the quantile values of
μT, firstly, the best-fit probability distribution function to calculate the
QT was indicated. Then the statistical distributions recommended in Poland were subjected to analysis: Pearson type III (PIII), Weibull, and log-normal.
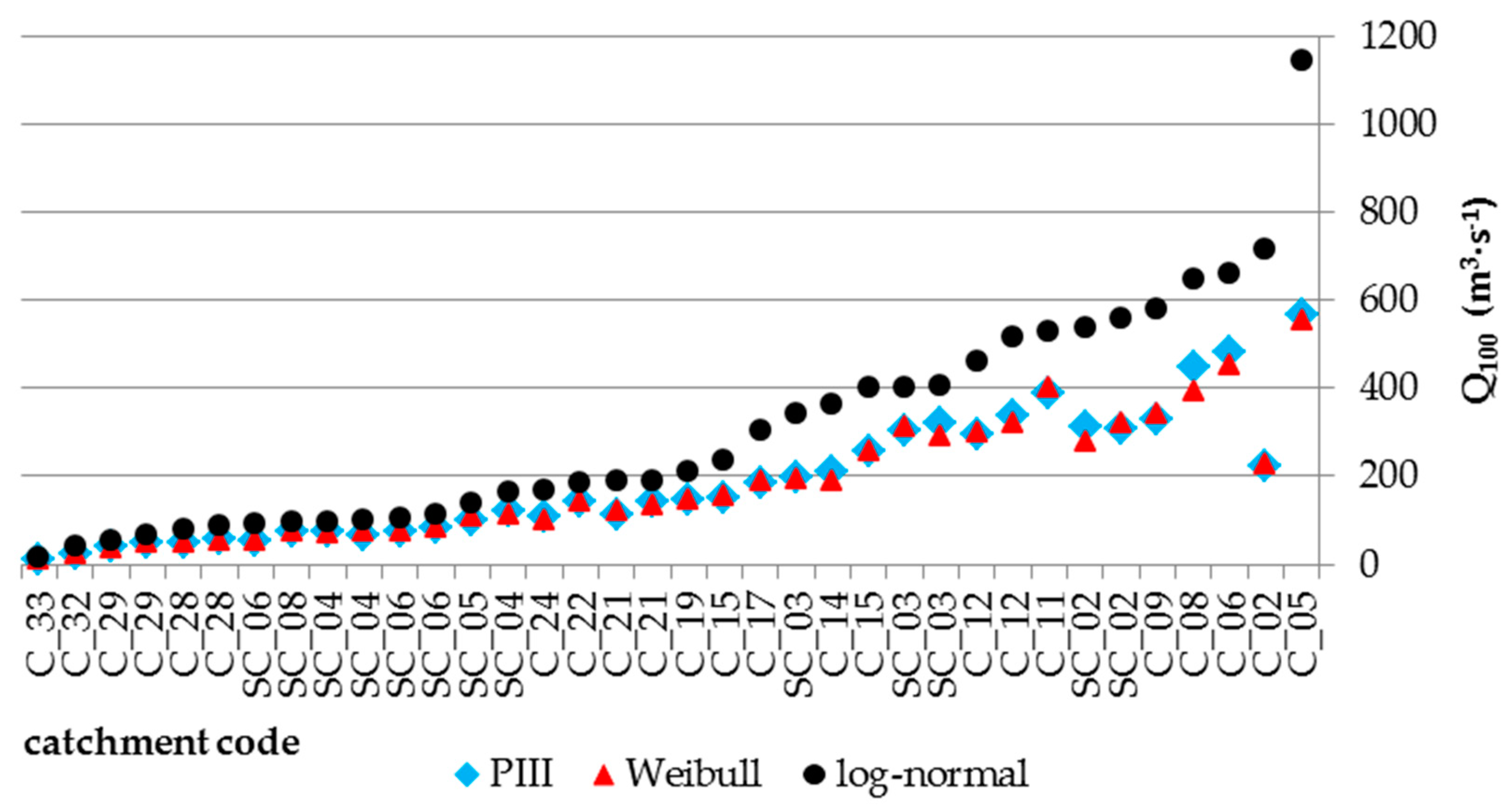
Figure 7 presents
Q100 values determined by the studied probability distributions.
Based on the results summarized in
Figure 7, it was found that the highest
Q100 values were obtained by means of the log-normal distribution. However, for the Pearson distribution type III and for the Weibull distribution, these values remained at similar levels. Obtaining the highest
Q100 quantile values using the log-normal function is justified by the properties of this particular model. The log-normal function is fat-tailed to the right, which means that with the same row of the upper quantile, e.g.,
p ≤ 0.2, it generates much higher quantile values compared to other probability distributions [
14]. Furthermore, the effects of the flood regime may also influence such results. The peak flows are rare (occurring once a year). However, their values are significant, and they stand out clearly from other data. Therefore, fat-tailed distributions can effectively describe empirical sequences of such variables.
The selection of the theoretical function best fitting the empirical distribution of the
Qmax variable was made using the Akaike’s information criterion (AIC) ranking method. The results of the calculations are summarized in
Table 7.
Based on the results summarized in
Table 7, it was found that in a majority of cases (58% of all the studied catchments) the log-normal distribution best approximates the empirical
Qmax sequences. However, for the Pearson distribution type III and for the Weibull distribution, the best fit was obtained in 9 and in 6 research catchments, respectively. Bearing in mind the obtained results and the sum of ranks, log-normal was adopted as the recommended statistical distribution for estimating
QT quantiles in the upper Vistula basin. Kuczera obtained similar results, as quoted in his paper [
40], where the author pointed out that the best theoretical distribution for the approximation of
Qmax flows is the log-normal distribution. Strupczewski et al. [
41] also found that the log-normal distribution best describes the empirical distributions of the analysed random variables.
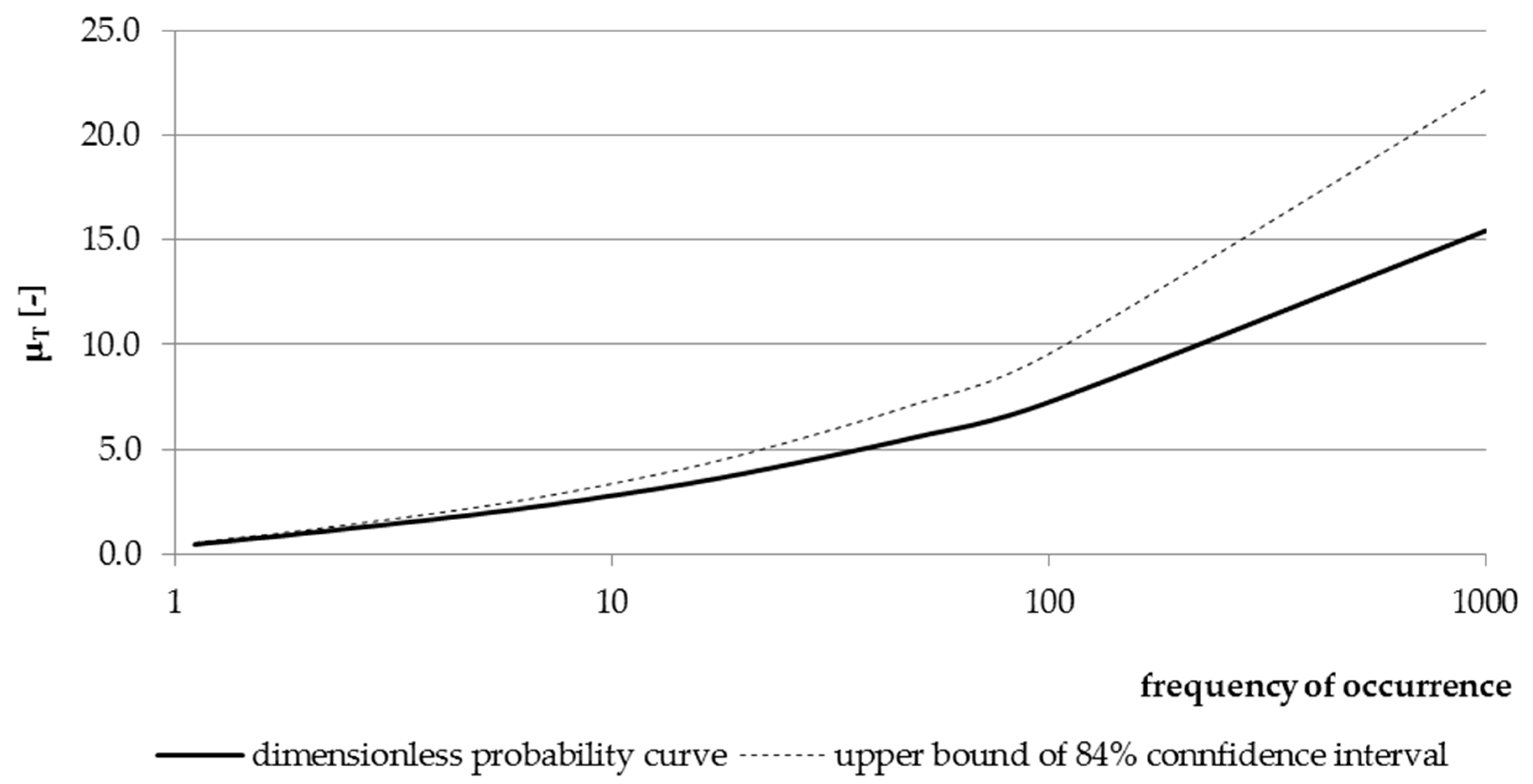
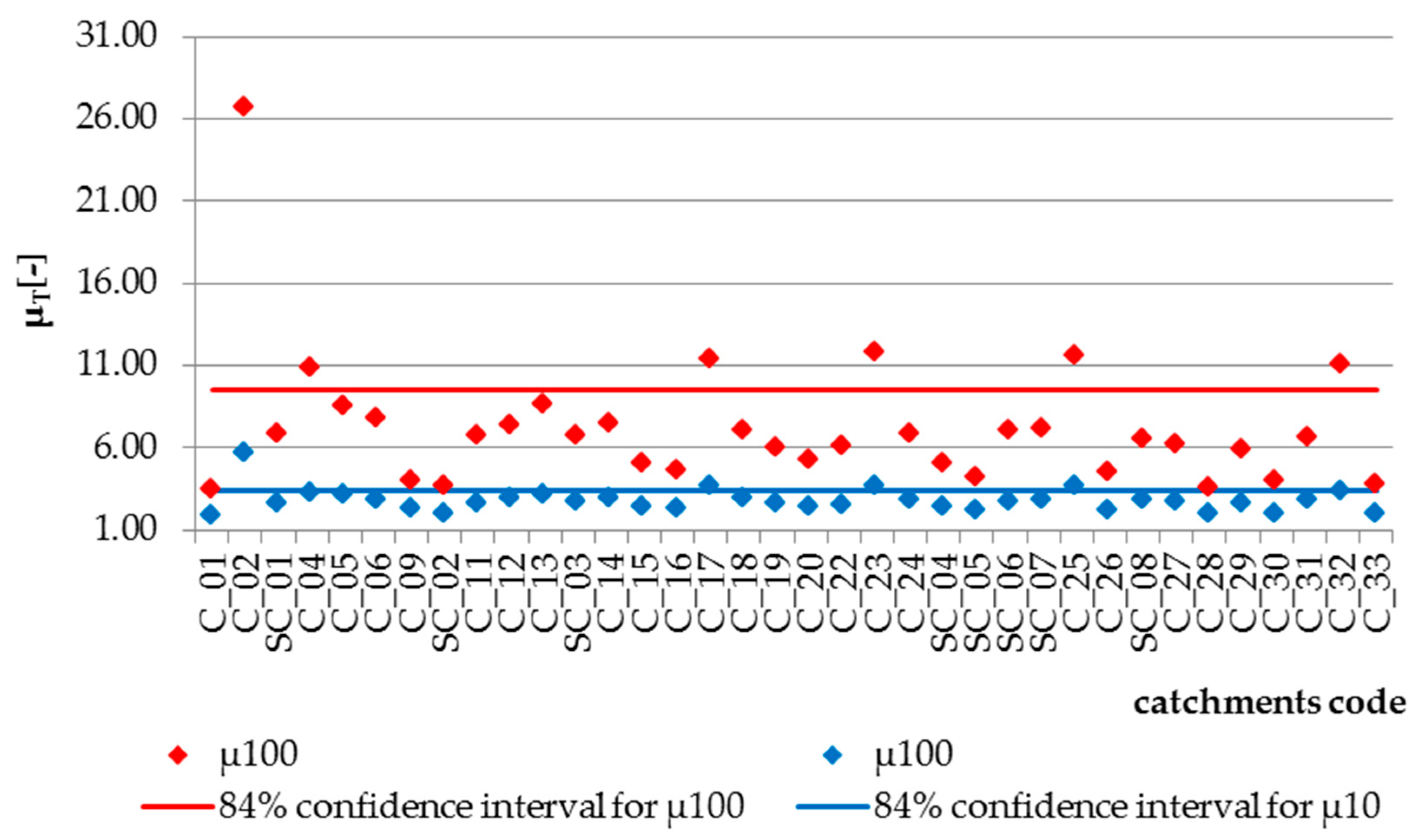
Based on the recommended statistical distribution, a non-dimensional probability curve was determined (see
Figure 8). The curve was verified based on the results summarized in
Figure 9. Verification of the non-dimensional probability curve, subject to log-normal distribution, produced satisfactory results. In the total number of 36 tested catchments of the entire upper Vistula basin, the
Q10/
Qmed quantile was outside the upper boundary of the confidence interval 4 times (11%), and the
Q100/
Qmed quantile, 6 times (17%). According to the definition of the upper boundary at 84% of the confidence interval, for 36 cases outside this limit, there may be 5 observations (16% of 36 cases). With a small number of observations, such a result can be considered acceptable. Therefore, the log-normal distribution was assumed as the basis for determining
QT quantiles using the determined empirical correlation.
Bearing in mind the calculations we have carried out, the final form of the empirical model for estimating
QT flows in the catchments of the ungauged upper Vistula basin was obtained as follows:
where:
Qmed—median annual flow, determined by Formula (22) (m3·s−1);
μT—dimensionless value of distribution quantile for the assumed frequency of occurrence, taken from
Figure 8 (-).
Thus, the developed empirical formula is recommended for use in catchments whose surface areas range from 50 to 600 km2.
As a complement to the conducted research, verification of the established formula (23) for estimating
QT quantiles was performed against the currently used empirical formulas in the upper Vistula basin: Punzet’s and the spatial equation of regression (SER). The results of the verification are presented in
Figure 10. Based on the obtained results, it was found that compared to the Punzet and SER formula, the values obtained with Formula (23) present the lowest
MAPE value for each
QT quantile. Standard error of estimating
QT using the Punzet formula is 46%; when using the area regression equation, it is 39%, and when using formula (23) it is 21%. Therefore, it is concluded that the developed equation can be a viable alternative to the currently used empirical formulas for calculating
QT in ungauged catchments of the upper Vistula basin.