1. Introduction
One drainage basin attribute of particular importance for this research is drainage density. Drainage density,
, is defined as the total length of channels per unit area [
1], and it describes the drainage spacing and distribution in a catchment [
2]. It can be said that the ratio that defines drainage density also represents the quantity of rivers in the catchment needed to drain the basin [
3]. According to Marani et al. [
4], drainage density, in practice, is defined by the statistical distribution and correlation structure of the lengths of un-channelled pathways. According to Prabu and Baskaran [
5], drainage density is expressed as the distance between the streams and reflects the soil structure in the catchment.
This parameter is not constant over time; it evolves as the drainage system in a catchment evolves [
6]. This attribute of a drainage basin provides a useful numerical measure of landscape dissection and runoff potential to hydrologists and geomorphologists.
During recent decades, drainage density has been analysed in relation to many parameters, such as soil erosion and soil erodibility [
7], as well as sediment yield [
8]. In 1945, Horton [
1] defined an un-channelled slope as a “belt of no erosion” with insufficient overland flow strength to induce erosion. Later, Montgomery and Dietrich [
9,
10], as well as Dietrich et al. [
11], confirmed his hypothesis. It is known that bare soils are much more erodible or prone to soil erosion. Catchments with such characteristics have a higher drainage density and greater runoff production, which leads to large flood peaks and volume [
12]. In his research, Luoto [
13] highlighted the importance of soil erodibility and its effect on drainage density and pointed out the relatively weak effects of other parameters, such as relief and bedrock geology, on drainage density. In addition, catchments with greater drainage density are prone to higher sediment yield values [
14]. According to Tucker and Bras [
15], a threshold for runoff erosion can influence landscape morphology and drainage density. A detachment-limited model was developed by Horward [
16], where the controlling factors defining the relationship between drainage density and mean erosion rate are the dominant hillslope transport processes and the presence or absence of a threshold for runoff erosion. The relationship between drainage density and climatically driven erosional processes indicate that drainage density, as a catchment characteristic, can provide insight into signature processes and landscape history in a catchment. Analyses that compare erosion rates and drainage density can potentially be used to make conclusions about tectonic and geomorphic history [
17].
A negative correlation between drainage density and slope angle is found in quickly eroding areas, whereas the correlation between these two parameters is positive in areas prone to slow erosion processes [
16]. The relationship between slope angle and drainage density is found to be more directly related to the stages of channelisation, although previous research indicates it is connected to dominant erosion types [
18].
According to the review research of Gregory and Walling [
8], drainage density is often used (i) in relation to catchment characteristics, such as soil type or shape of the catchment, (ii) as an input or output of the drainage basin system and (iii) in relation to past and future conditions. This parameter has been recognised as one of the most important characteristics of natural terrain and is currently a frequent topic in hydrology and geomorphology.
In many studies, drainage density is often extracted as one of the areal parameters in morphometric analyses [
5,
19,
20,
21,
22,
23]. Drainage morphometry is found to be extremely important in understanding the physical properties of soil in the catchment, the catchment landforms and erosion processes [
19].
According to Strahler [
24], an important aspect of catchment characteristics can be obtained from quantitative drainage system analysis. Morphometric analysis of the drainage catchment and river network are the foundation to understanding hydrogeological behaviour, climate, and geology and geomorphology in the catchment [
20].
Drainage density has been found to correlate with valley density, channel head source area, relief, climate, vegetation, soil and rock properties, and landscape evolution processes [
19]. Analysis by Pal and Saha [
21] showed a high correlation between drainage density and the following parameters: length of overland flow, number of stream junctions in the basin, and the infiltration coefficient and drainage texture [
21]. Low drainage diversity was related to low drainage density.
Weak and impermeable subsurface materials, sparse vegetation and high relief are related to higher drainage density values, while coarse drainage texture is related to low drainage density values. Areas with high drainage density have high runoff, coarse drainage texture and higher erosion potential [
24].
Ansari and Yusuf [
20] conducted morphometric analysis on three sub-catchments in the Fatehabad Area of the Agra District in Uttar Pradesh. They found that areas with low density have high permeable sub-soil material and dense vegetation cover.
High rainfall is associated with higher runoff and an increase in drainage patterns. Areas with a permeable subsurface and higher infiltration rates result in less runoff and a reduction in drainage patterns [
20].
The definitions of drainage and relief are essential for understanding spatial differences within the catchment [
21]. Drainage and relief characteristics are often conducted on sub-catchment levels or grid levels [
21].
Measuring drainage density is extremely difficult, and it relies on good topographic maps at a detailed scale [
17,
25]. As an alternative to drainage density, the parameter of potential drainage density is often obtained from a digital elevation model (DEM). The distinction between the two is the fact that the actual drainage density can be measured on site and is based on a real drainage network map. In contrast, the potential drainage density is derived from a DEM and does not take into consideration the loss of surface runoff due to infiltration into the ground. For this reason, the potential drainage density is always higher or equal to the actual drainage density in the analysed area [
25].
In recent decades, GIS and remote sensing technologies, along with accessible data from various sources, has enabled more sophisticated image processing and spatial data analysis [
26].
According to various researchers [
19,
20], remote sensing of satellite data is a very effective technique for morphometric analysis at the catchment-scale and is time-saving and fairly accurate. Researchers found this method relevant for catchment determination and river network extraction from digital elevation models (DEMs) [
19]. Geographic information systems (GIS), remote sensing, spatial information technologies, and global positioning systems (GPS), either individually or combined, can be used for solving problems related to the planning and management of land, soil and water [
19].
Today, digital elevation data are available from various sources: Google Earth Images, advanced spaceborne thermal emission and reflection radiometer (ASTER), Shuttle Radar Topographic Mission (SRTM), and the United States Geological Survey (USGS), among many others. These named databases provide low resolution elevation data, despite some specific analyses for local-scale applications requiring high resolution data. For such analysis, Lidar data, which are based on airborne laser scanning, are appropriate [
26].
Ahmadi et al. [
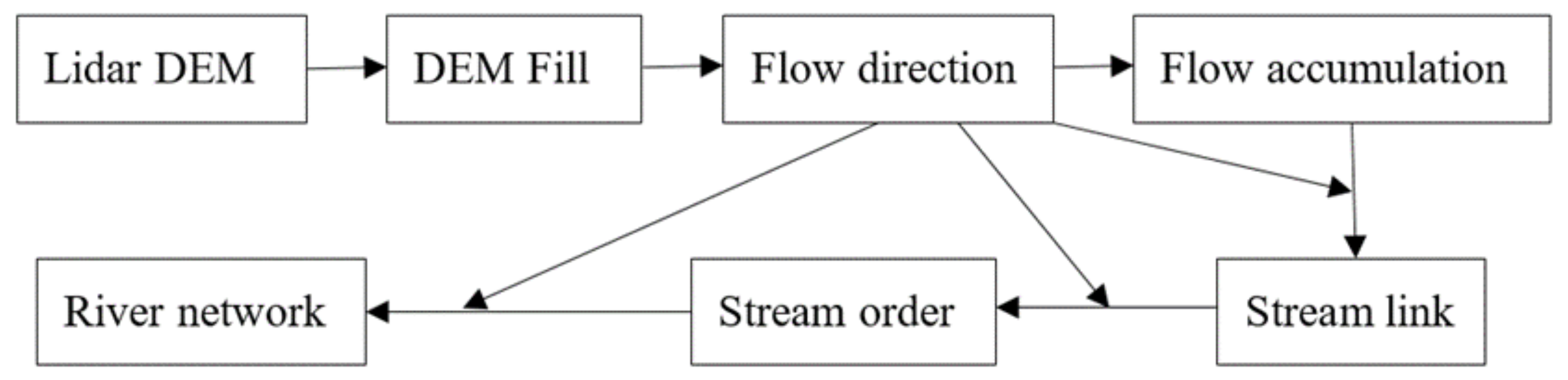
26] used four different digital elevation models (ASTER—advanced spaceborne thermal emission and reflection radiometer, SRTM—Shuttle Radar Topographic Mission, digital topography and topographic maps) to define catchment boundaries and river networks. The DEM analysis was conducted in GIS software. The methods applied included sink filling, flow direction and flow accumulation analysis. The final model output was a river network map. The model was verified by combining field surveys and GPS. The authors concluded that the accuracy of the model results depends on the quality of the DEMs. The ASTER DEM had fewer errors and was recommended for future use in hydrology and land use analysis in other research [
26].
Rai et al. [
19] used remotely sensed satellite data to determine the river catchment and river network extraction from an ASTER DEM. They generated various morphometric parameters, including drainage density, for seven sub-catchments of the Kanhar River catchment in India. For the derivation of river networks, they used various geoprocessing tools within a GIS environment.
An update of the drainage patterns for the Upper Vaigai River sub-catchment in South India was conducted using satellite remote sensing data. A new drainage map was later used as an input for morphometric analysis, which included various different parameters such as drainage density. The analysis combined remote sensing and GIS [
5].
In recent years, various different papers reflected upon river network extractions from DEMs [
22,
27,
28,
29,
30,
31,
32,
33]. They found that the derivation of topographic characteristics and river networks from DEMs using GIS and remote sensing technologies is faster and less subjectable than using traditional methods.
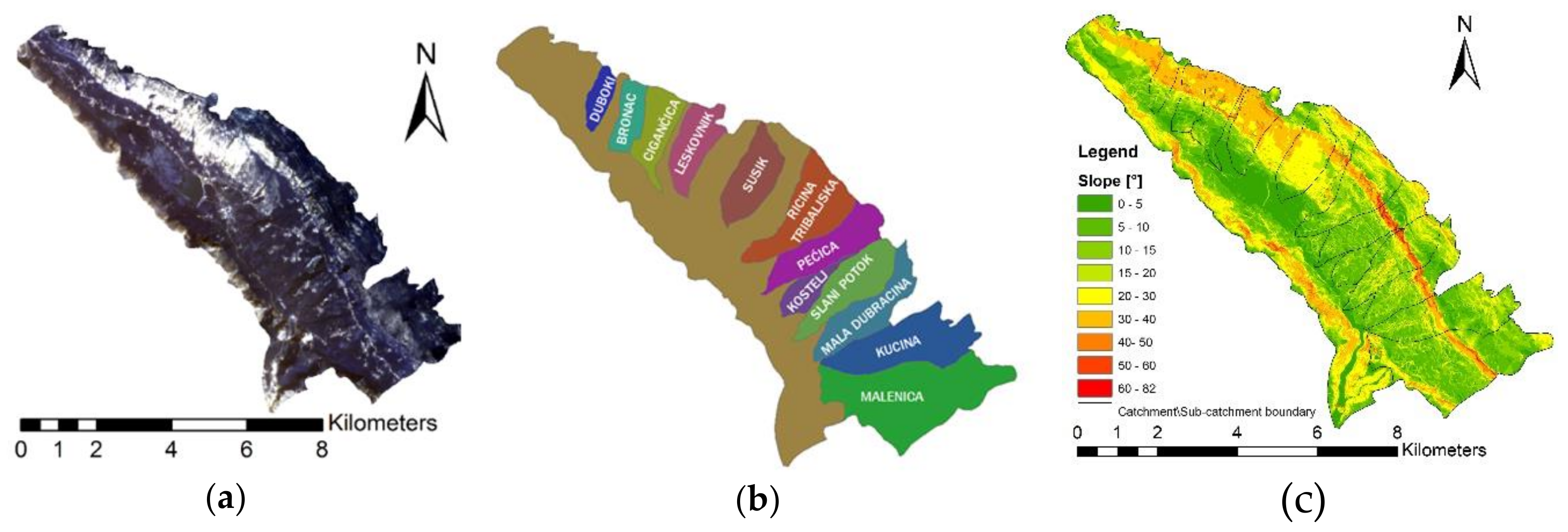
This paper analyses the possibilities to improve the precision and obtain better outputs for the Erosion Potential Method (EPM) by deriving drainage density maps with higher detail and spatial variability. For this purpose, four different approaches are used to derive drainage density maps for the case study: the Dubračina catchment, Croatia. The approaches have different assumptions and allow different spatial variabilities. The first two approaches are commonly applied in the EPM. The third and fourth approaches are used in the EPM for the first time and allow greater detail and precision than the first two approaches. The output of the third case scenario is actual drainage density based on a topographic map, and the output of the fourth approach is potential drainage density and is based on a river network map derived from a Lidar-generated DEM. The results are discussed, and the differences between each drainage density map are compared, as well as the effects on the sediment delivery ratio used in the EPM.
3. Results and Discussion
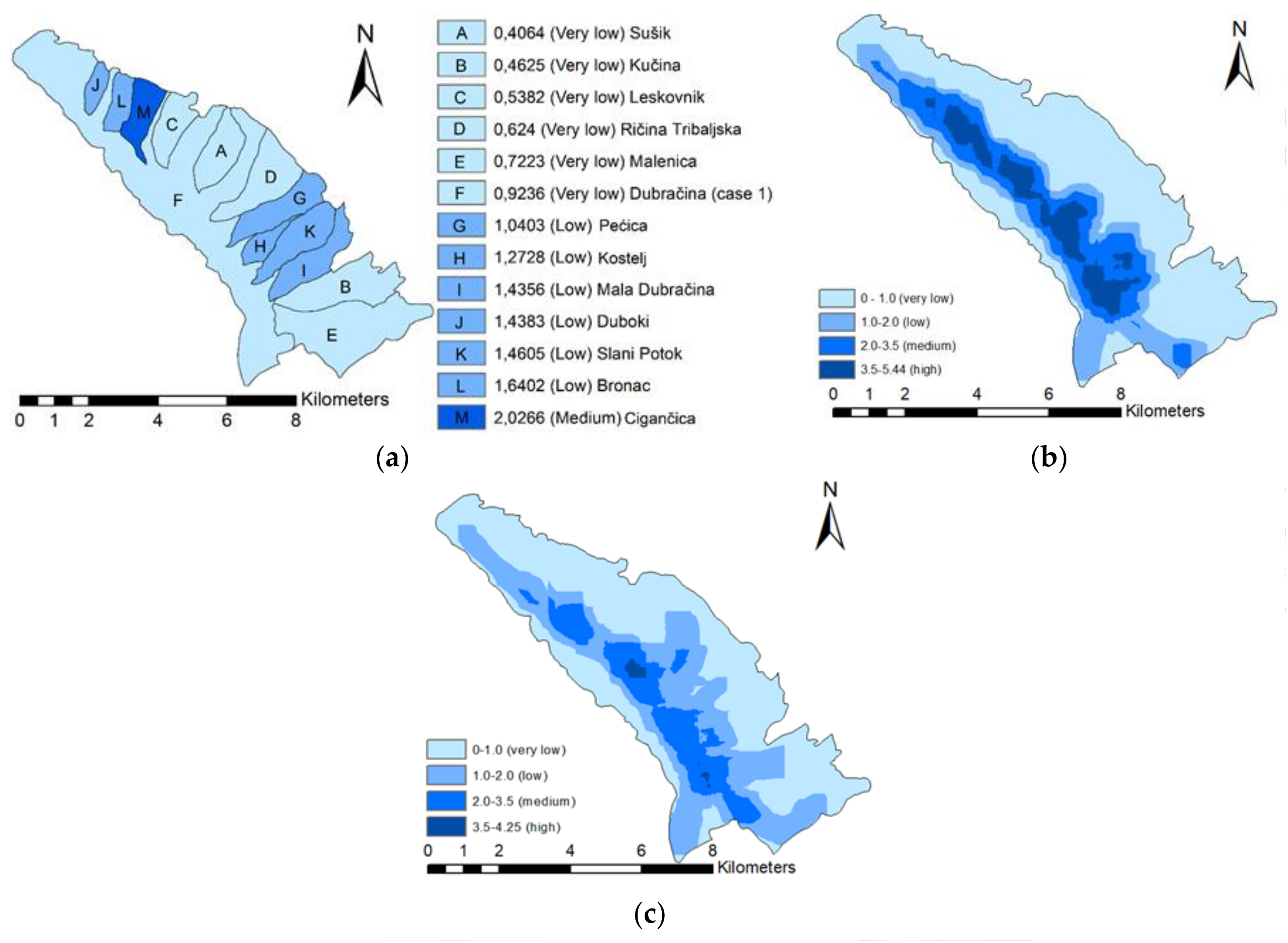
The drainage density value (0.923 km/km
2) obtained in the first case scenario corresponds to the very low drainage density class in Ravi Shankar and Mohan’s [
38] drainage density classification and is homogenous throughout the entire catchment.
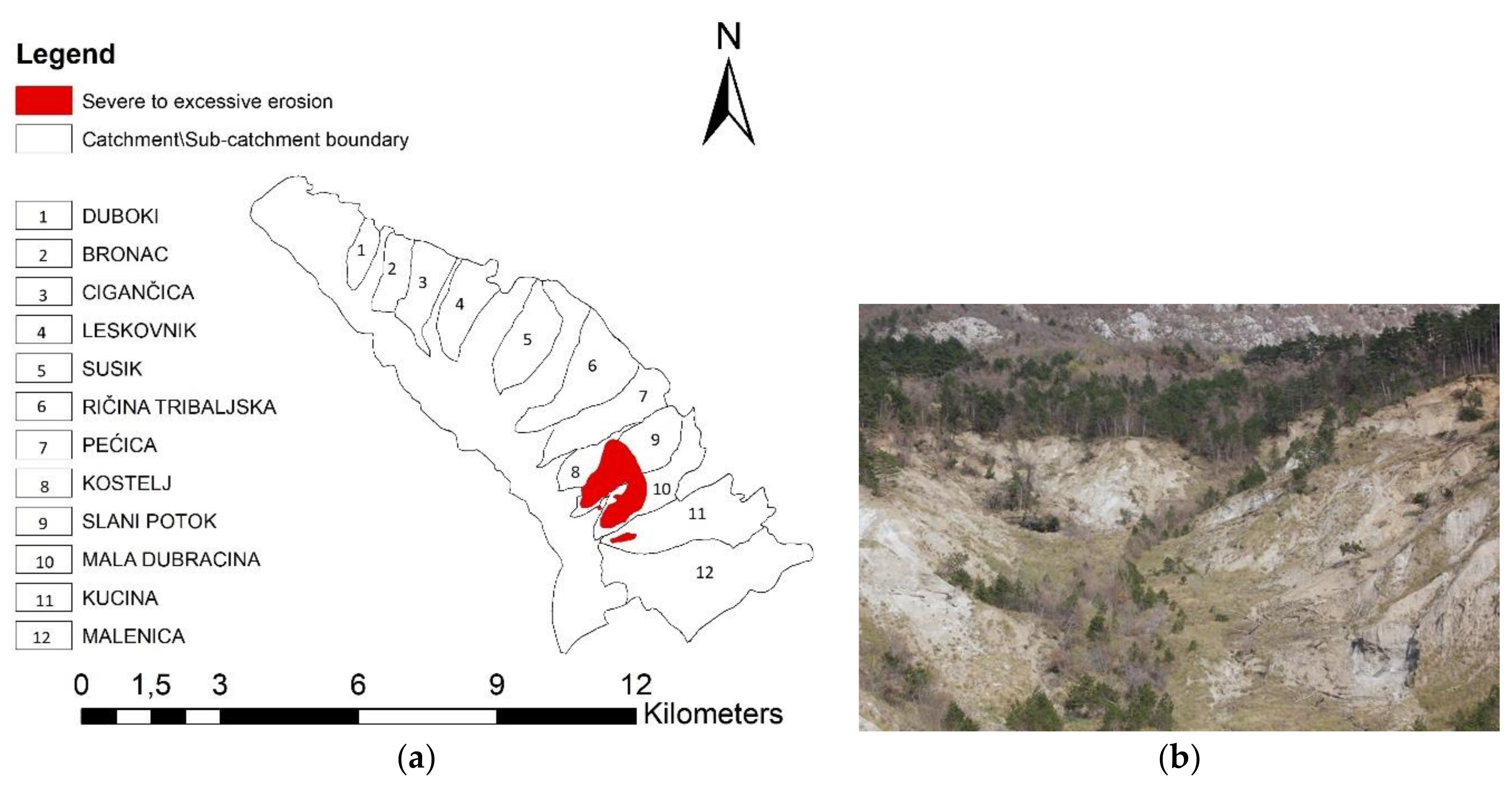
In the second case scenario (
Figure 5), using the same classification, five sub-catchments within the Dubračina catchment have very low drainage densities (Sušik, Kučina, Leskovnik, Ričina and Malenica), while the six other sub-catchments have low values (Pećica, Kostelj, Mala Dubračina, Duboki, Slani Potok and Bronac), and only the Cigančica sub-catchment has a medium drainage density. It is known that low values for drainage density can indicate different characteristics, such as higher infiltration rates, lower surface flow velocities and/or lower values of sediment yield transported through river networks, all of which do not necessarily relate to the Slani potok and Mala Dubračina sub-catchments, which are two of the most severely affected sub-catchments by erosion processes (
Figure 2).
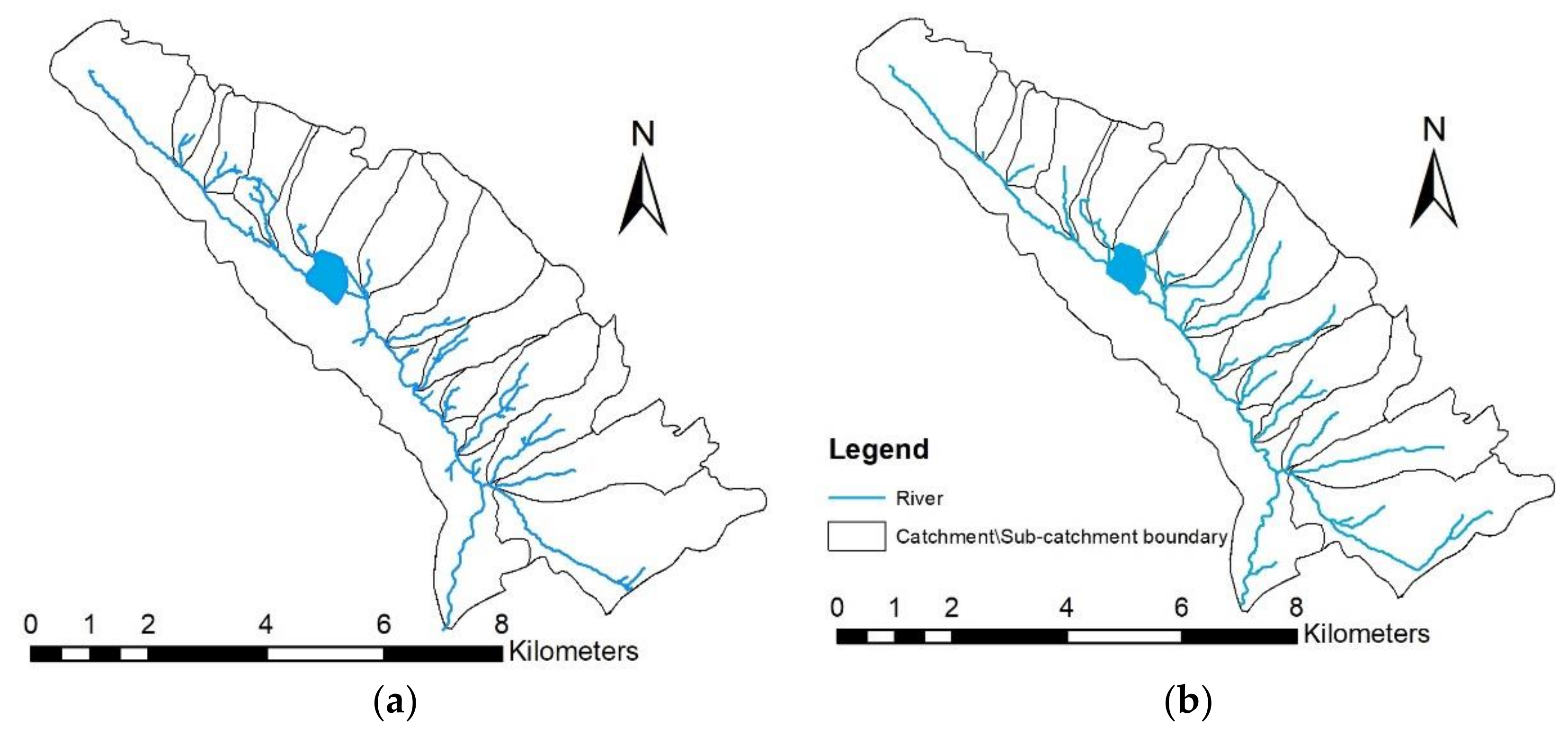
Differences in spatial variability and drainage density values for the second, third and fourth case scenarios can be seen in
Figure 5. Since the first case scenario represents a homogenous drainage density for the entire catchment, and current technological possibilities provide much more detailed and accurate maps, this case is disregarded from further analysis in this paper. Between the three other cases, the third and fourth case scenarios provide the most spatially variant maps and are the most complex maps to derive. In cases three and four, the obtained drainage density maps provide the most realistic spatial variance for this parameter, with lower drainage density values along the edges of the catchment and higher values concentrated along the river and tributary intersections where higher surface velocity, lower infiltration rates and higher values for sediment yield transport are expected. The difference between the third and fourth case scenarios is mainly at the river intersections, where the third case scenario results in higher drainage density values. The basic statistical analysis and comparison between the third and fourth case scenarios are given in
Table 4 and
Table 5.
Overall, the mean values for drainage density in fourth case scenario are lower for most sub-catchments, with the exception of five (Kostelj, Malenica, Kučina, Ričina Tribaljska and Sušik). For these sub-catchments, the maximum values are lower than in the third case scenario.
The statistical analysis,
t-test with 95% confidence (two-tailed test), was conducted with a purpose to define if the difference between drainage density maps (case scenarios II to IV) is significant. The null hypothesis assumes that the two data sets (drainage density maps) are likely to have come from distribution with equal population means. Comparison was made in the pairs II–III, II–IV and III–IV case scenarios. Analysis has shown no significant change between the scenarios (
Table 6).
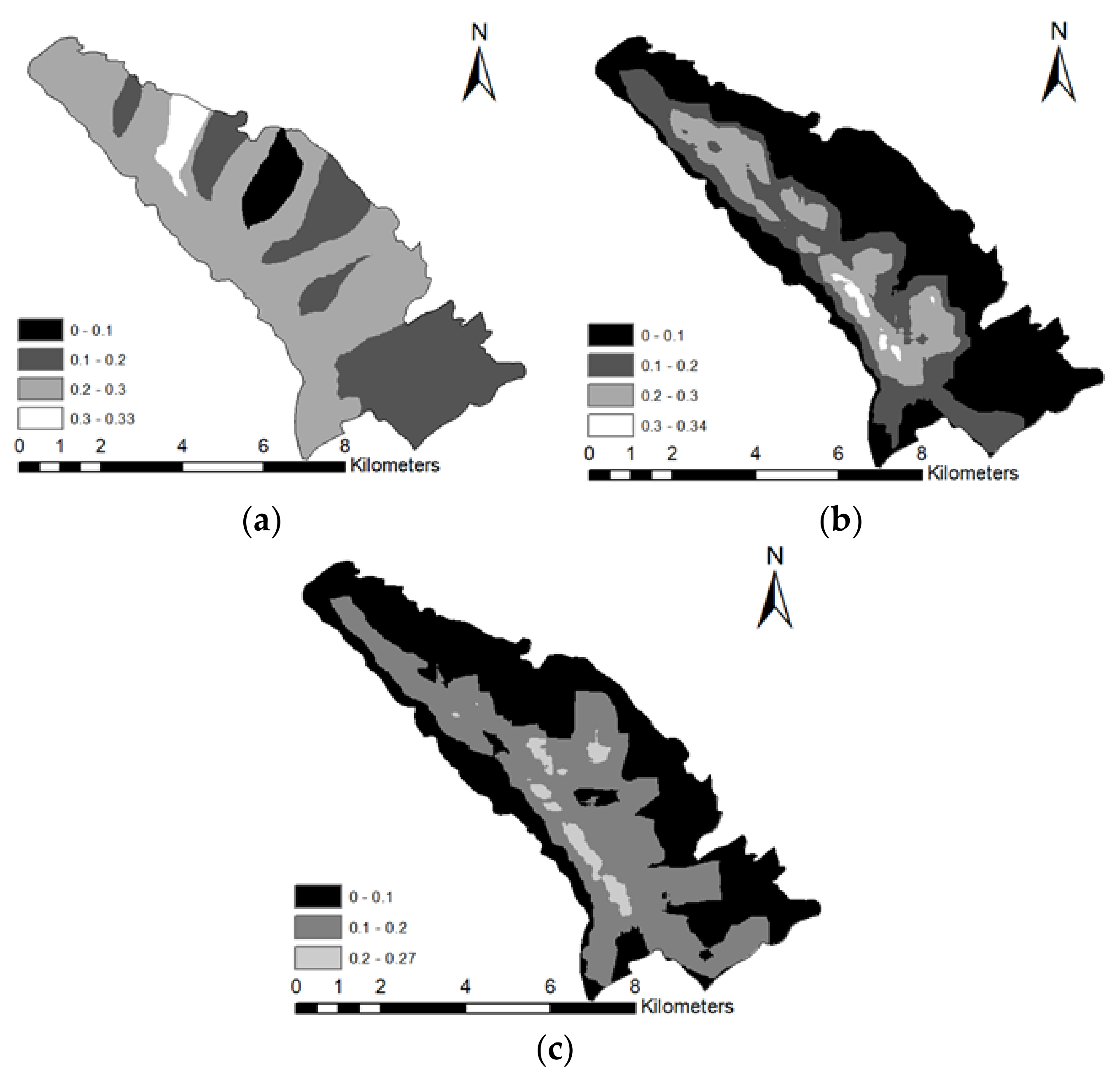
The question is, how do these four different drainage density derivation approaches affect the sediment delivery ratio in EPM? The main model parameter that is dependent on the drainage density parameter is the sediment delivery ratio ξ. This parameter was calculated for three case scenarios (
Table 7 and
Table 8,
Figure 6) using Equation (6) and previously derived drainage maps shown in
Figure 5 (case scenario II–IV) as input data.
The range of values for the second and third case scenarios do not differ much, but the spatial variation of the parameter is different, as can be seen in
Figure 6, and it follows the same variation pattern as drainage density. Mean values for the fourth case scenario differ somewhat from the third case scenario, but the spatial distribution remains similar. It can be observed that all four case scenarios provide different values, but the third and fourth case scenarios are the most similar in values and spatial distribution. Therefore, the third and fourth case scenarios provide the best spatial variability for the drainage density parameter. This method was used in previous research by Dobos and Daroussin [
25] and was approved and defined as an appropriate method for deriving drainage density maps. Thus, both case scenarios are considered appropriate input data for the EPM application in the Dubračina catchment.
The statistical analysis,
t-test, was conducted once again, this time for the sediment delivery ratio, using the same assumptions and same pair comparisons (
Table 9).
For the pairs II–III and II–IV, a significant change was found between derived datasets. But no significant change was found for the III–IV pair comparison.
4. Conclusions
The first case scenario provided no spatial variability and as such cannot be considered comparable to other case scenarios. Also, due to its homogenous characteristics throughout the catchment, it is considered less reliable and precise. For the derivation of drainage density for the III. and IV. case scenario, some modifications were made to the original methodology proposed by Dobos and Daroussin [
25]. In both case scenarios, square neighbourhood windows were used opposite to the circle neighbourhood. In the third case scenario, actual drainage density was calculated using topographic maps as input data. The fourth case scenario used high resolution Lidar data as input data to derive potential drainage density map. However, according to Dobos and Daroussin [
25], potential drainage density should always be higher or equal to actual drainage density, which is not the case in our analysis. The reason for that may be found in high resolution input data for the IV. case scenario. The topographic map for the Dubracina catchment is approximately 10 years older than the Lidar data, so some changes in the drainage patterns are expected to occur in this time period. This area, as it was mentioned before, is characterised by gully type of erosion and has intensive rainfall, all of which affects drainage patterns. For future analysis, detailed field observations and measurement should be conducted.
No significant difference was found between drainage density maps but they effect the sediment delivery ratio used in EPM. A significant change in sediment delivery ratio was found between II and III case scenarios and II and IV case scenarios. However, the change between drainage density maps was not considered significant; its effect on EPM parameter (sediment delivery ratio) should not be neglected.
The drainage density map, derived using the Dobos and Daroussin [
25] methodology, has provided more realistic model input data with more detailed spatial variance of this parameter. The methods used in the third and fourth case scenarios have been applied for the first time in the EPM in the Dubračina catchment. Until now, drainage density that was used as input data in the EPM had a maximum spatial variability on the sub-catchment level, or was a unique value for the entire catchment. For this reason, the Dobos and Daroussin [
25] modified methodology, used to derive drainage density maps for this case study, is considered an improvement in the accuracy and precision of the EPM.