1. Introduction
Reliable prediction of runoff in large catchments has been a subject of interest in hydrologic sciences for some time and is significant for sustainable management of water resources, design of water infrastructure, and flood risk management [
1,
2,
3]. Understanding the complex relationships between rainfall and runoff processes is essential to accurately predicting surface runoff [
4]. This can be achieved by hydrological modeling which, besides simulating surface runoff, also aids in understanding, predicting, and managing water resources and modeling impacts of climate and land use changes on the surface water balance [
5].
The Semi-distributed Soil Water Assessment Tool (SWAT) hydrological model [
6] is one of the most useful tools for simulating runoff, sediment and water quality of agricultural watersheds over the last decades [
7]. The SWAT model, which requires numerous input parameters, e.g. soil, land-use, topography, meteorological data, should be calibrated and validated at monitoring stations to reduce the error between measured and predicted outputs, before applying the model for specific analyses or predictions [
8,
9]. However, the performance of hydrological models in predicting streamflow relies heavily on the quality and spatial distribution of the input rainfall observations [
10,
11,
12]. Although rain gauges as reference instruments provide accurate measurements of rainfall, because of the variability of rainfall in time and space, they do not often provide adequate spatial representation of rainfall, especially in poorly gauged basins [
13].
Using remotely-sensed rainfall products, which are nowadays available at various resolutions (temporal and spatial) and with increased accuracy, is an alternative to the use of rain gauge-observed data. Some recent studies used satellite-derived rainfall in hydrological modeling [
14,
15,
16,
17,
18,
19]. For instance, Stisen and Sandholt [
20] evaluated the performance of five satellite-based rainfall products with different spatial resolutions as input into the MIKE SHE model for runoff simulation of four sub-basins of the Senegal River basin in West Africa. They showed a significant improvement in runoff prediction performance when the model is recalibrated using bias-corrected satellite rainfall data with rain gauge observations. Thiemig et al. [
21] investigated the suitability of satellite-derived rainfall estimates as forcing data for the LISFLOOD hydrological model, applying two different bias-correction methods to correct the bias in the satellite-based rainfall estimates.
Among the satellite-based rainfall predictions, the TRMM Multi-Satellite Precipitation Analysis (TMPA) products [
22] are still the most widely used in various research studies and applications [
23,
24]. For example, Dinku et al. [
25] evaluated the TMPA-3B43 rainfall products with nine other satellite-based rainfall using a rain gauge network over Ethiopia. Their results showed that TMPA-3B43 performs very well with a Bias value less than 10% and a relative root-mean-square error of about 25% at the monthly time scale.
Another approach, overcoming some of the known deficiencies of classical measurements of rainfall, like rain gauge data, is a recently developed method called SM2RAIN proposed by Reference [
26], which provides an area-integrated time-accumulated rainfall measurement from soil moisture (SM) data based on the inversion of the soil water balance equation. Brocca et al. [
27] carried out a thorough analysis of the physical consistency of the SM2RAIN algorithm, its hypothesis, and performance, using in-situ SM observations as input. For this purpose, different formulations of the SM2RAIN algorithm were applied to 10 sites across Europe. The results showed that SM2RAIN performed very well in the synthetic experiments with a correlation coefficient between synthetically generated and simulated data, at daily time step, higher than 0.940 and an average bias lower than 4%. However, generally, the temporal and spatial scale of ground SM measurements, especially in developing countries, is limited and insufficient. Hence, satellite SM observations, which use images retrieved from either passive or active microwave sensors, can be used due to their ease of operation, global coverage, and good accuracy [
28].
However, the derivation of accurate and reliable SM from satellite remote sensing still represents a challenging task because of uncertainty of inexact instrument calibration, errors in the retrieval algorithms, noise in the microwave signal, and data transmission failure [
29,
30].
Nowadays, satellite SM products are available at different spatial and temporal resolution (e.g. References [
31,
32]). Two space-borne satellite missions, such as Soil Moisture and Ocean Salinity (SMOS) mission launched by the European Space Agency (ESA) in 2009 [
33] and Soil Moisture Active Passive (SMAP) launched by the National Aeronautics and Space Administration (NASA) in 2015 [
34], were placed in orbit and dedicated specifically to measure SM. Advanced Microwave Scanning Radiometer—Earth Observing System (AMSR-E) on board of the NASA’s AQUA satellite is one of the most commonly used sensor for SM retrieval over the last years, as it has been available from years 2002–2011 (e.g. References [
35,
36]). However, because of the rather shallow remotely sensed depth of the bare soil layer for AMSR-E SM (<1 cm), attenuation of the electromagnetic signal is further increased by dense vegetation, snow-covered, and frozen soils [
37].
SM estimation based on both active and passive microwave sensors was evaluated in several studies (e.g. References [
38,
39,
40]). For instance, Rahmani et al. [
28] extracted surface SM from SMOS and the active + passive ESA Climate Change Initiative SM products to investigate the correlation between surface SM products and monthly precipitation and temperature data observations in six different regions of Iran, with the final purpose of drought monitoring. The results reveled that the agreement between all surface SM products was quite satisfactory with correlation coefficients higher than 0.5. Babaian et al. [
41] evaluated the accuracy of different simulated surface soil moisture data (using observed van Genuchten-Mualem hydraulic parameters and those obtained with parametric transfer functions) along with retrieved soil moisture content (using ENVISAT/ASAR active microwave and the inversion algorithm of IEM estimates) in the Zanjanrood River sub-basin of northwestern Iran. The findings indicated the feasibility of using spectral data to predict VGM hydraulic parameters and soil water dynamics at the larger scales. Al-Yaari et al. [
42] evaluated two passive (SMOS) and active (ASCAT) satellite microwave products at the global scale with respect to SM simulations from MERRA-Land. They found that ASCAT SM product is prone to larger random errors in Iran.
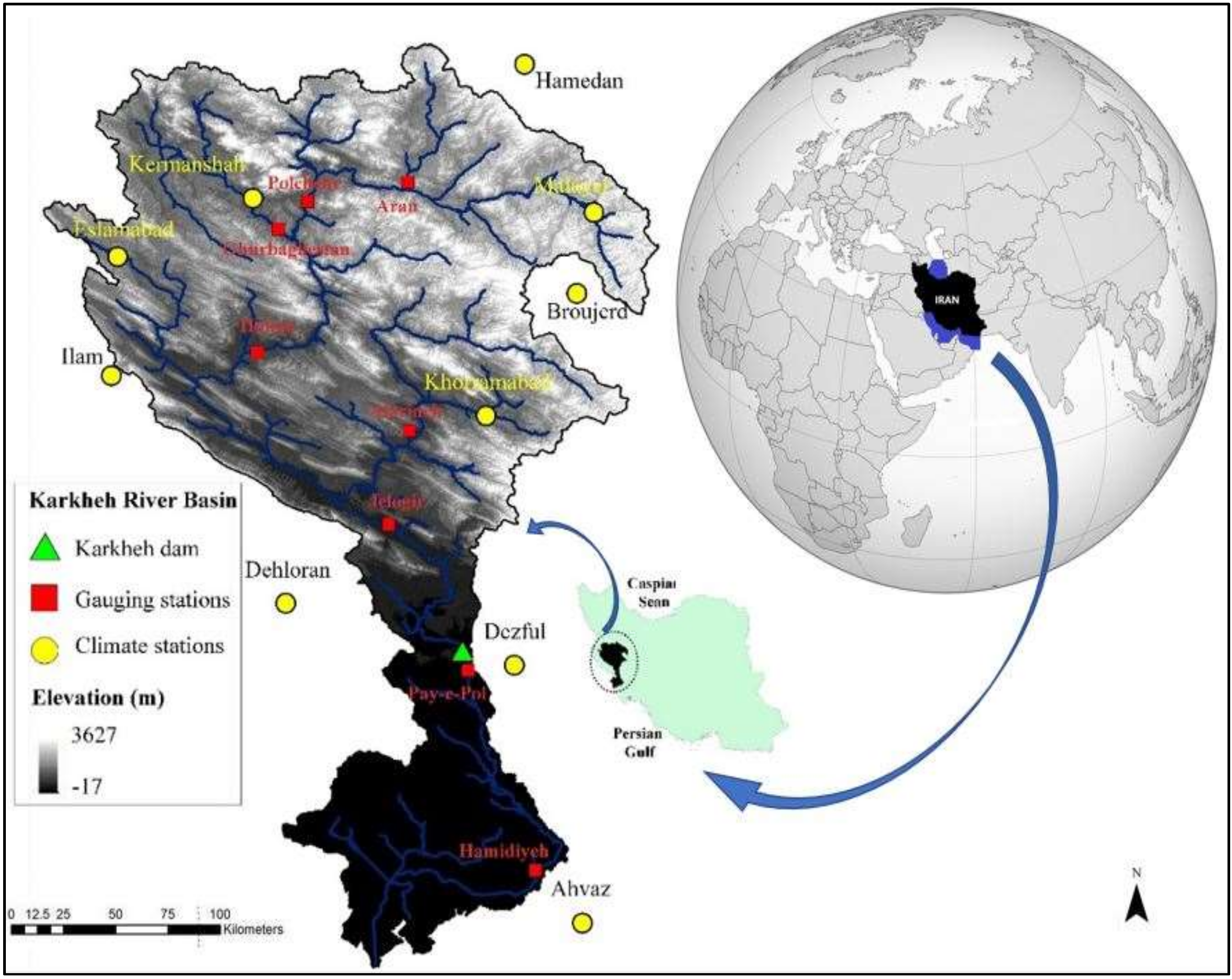
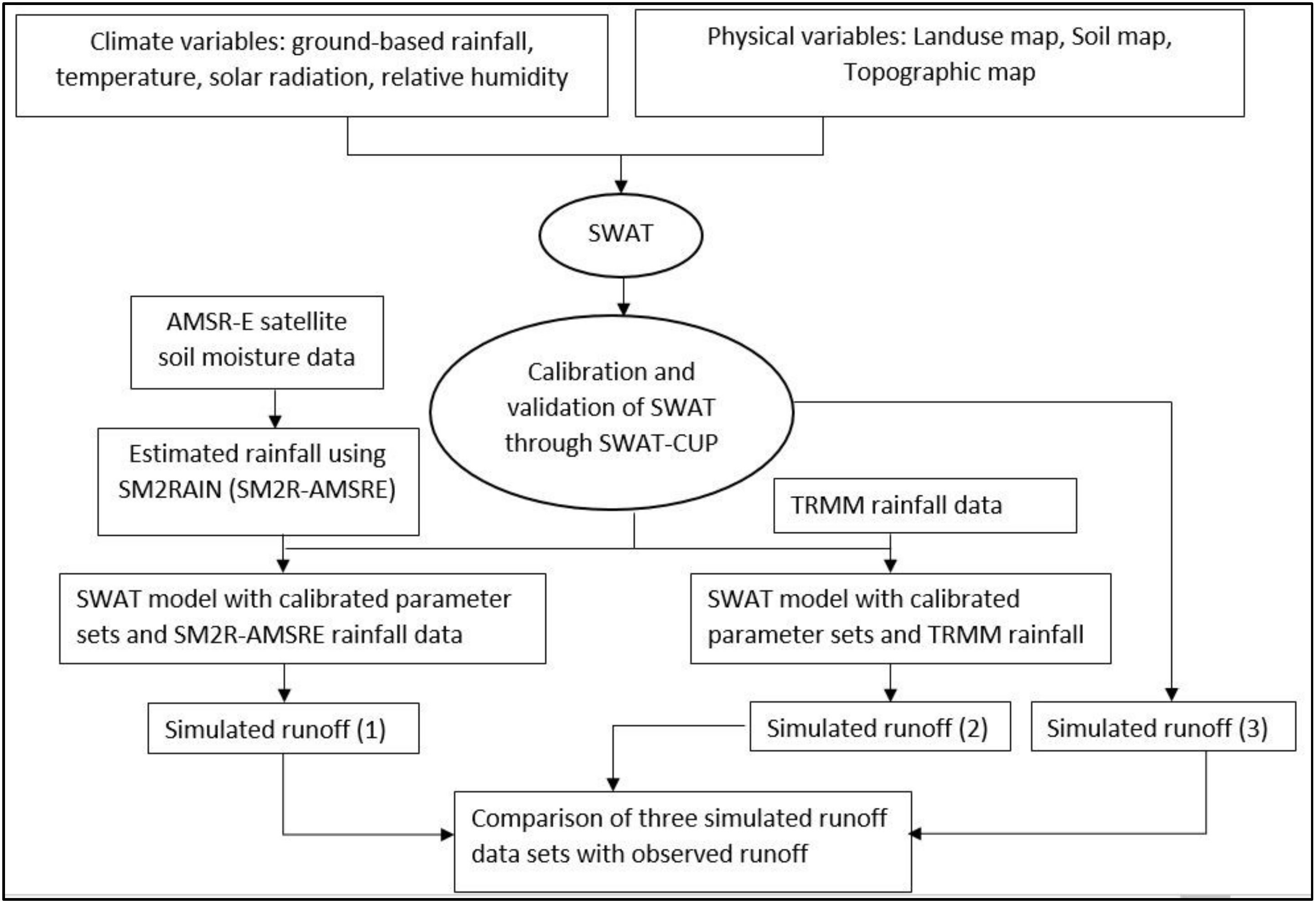
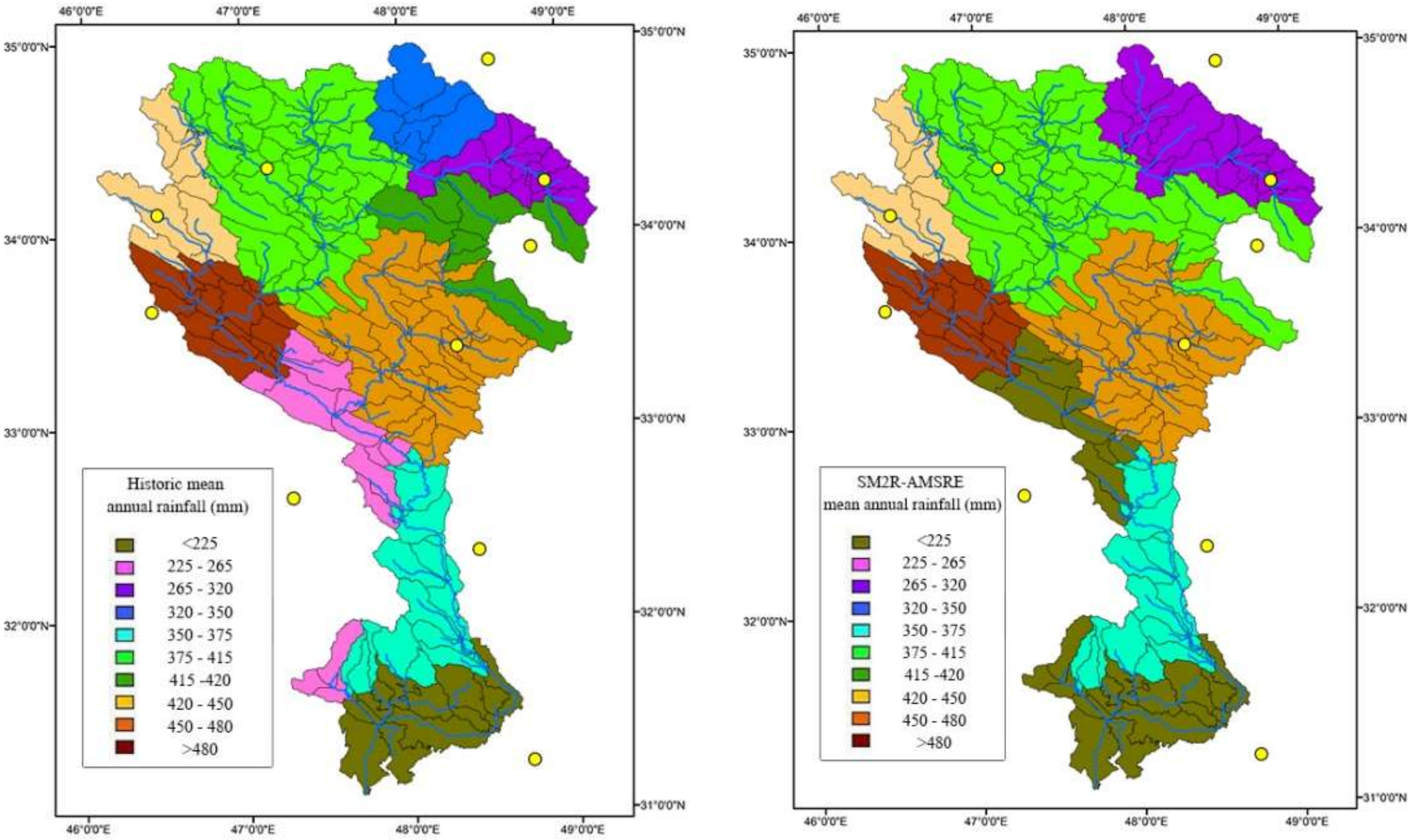
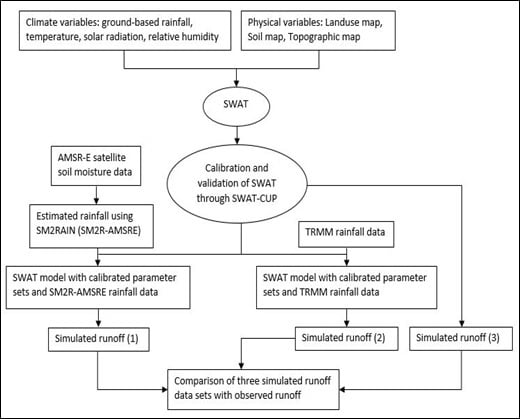
The objective of this work is twofold. First, we aim to evaluate the accuracy of rainfall estimates obtained from SM2RAIN. For this purpose, the AMSR-E SM product generated by implementing the standard NASA algorithm is used as input into the SM2RAIN algorithm to estimate rainfall, called SM2R-AMSRE, at 10 different sites in the Karkheh river basin (KRB). The lack of in-situ SM measurements in Iran, but the availability of AMSR-E SM data over the modeling time period (2003–2006), are the main reasons for choosing the AMSR-E SM product for this study. Moreover, the quality of the SM2RAIN rainfall estimations was evaluated further by comparing them with TRMM-satellite- predicted rainfall for two versions of the seven TRMM-TMPA-products, daily near-real-time (3B42RT) and research-grade (3B42) after bias correction with in-situ rainfall.
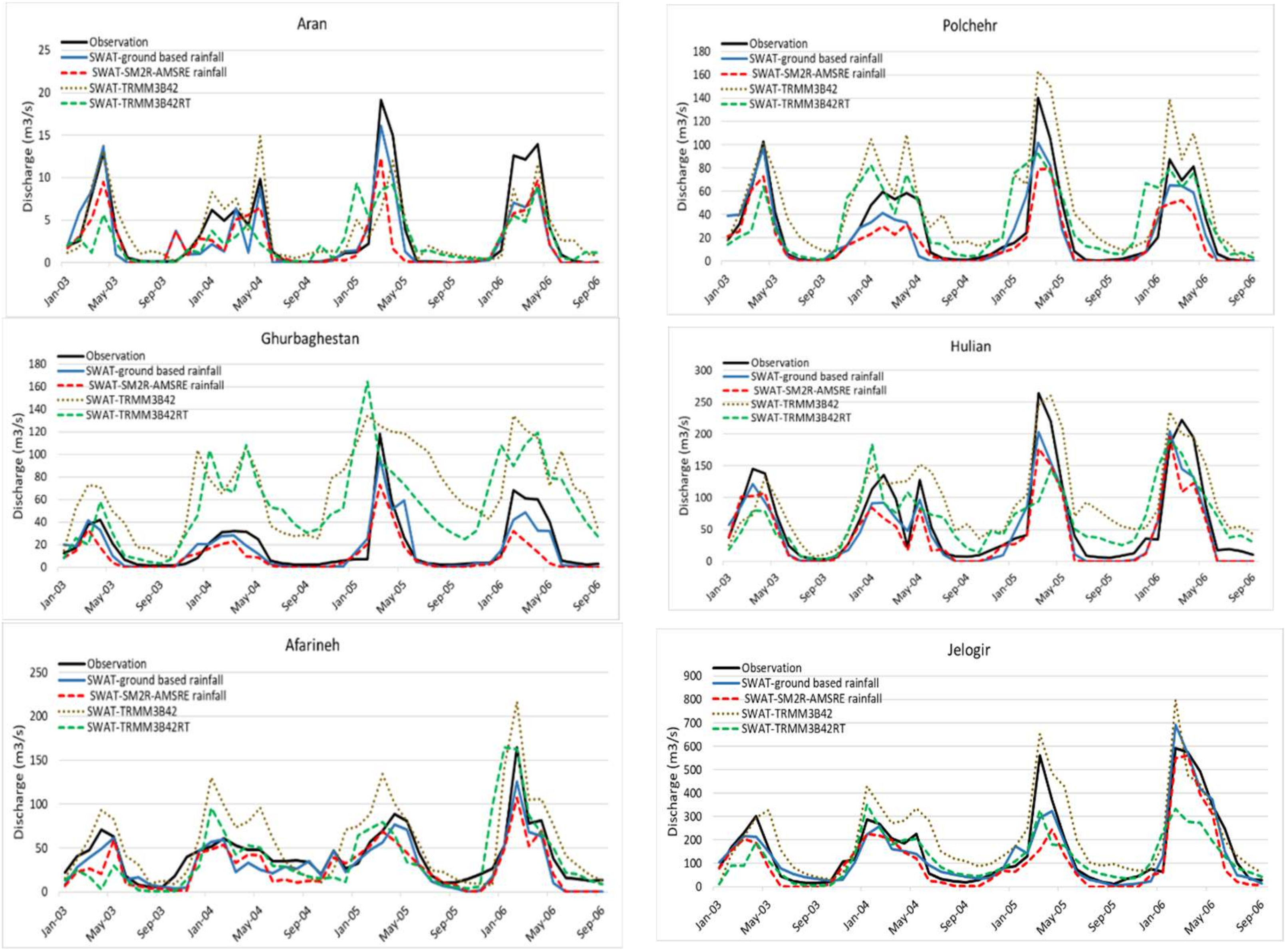
Second, we aim to assess the suitability of SM2R-AMSRE as input for the calibrated-SWAT model for monthly streamflow simulation at six gauging stations of the KRB. Similarly, the two bias-corrected versions of TMPA- products were employed in the calibrated-SWAT model as well to predict the monthly surface runoff at the same gauging stations. Model performances were assessed by comparing observed and predicted monthly runoff obtained through ground-based, SM2RAIN-estimated, and satellite-based rainfall inputs.
4. Conclusions
The estimation of river discharge in poorly gauged basin is fundamental for flood risk mitigation and water resources management. Among the different hydrological variables that have an impact on water discharge, rainfall is considered the most important. The recently developed SM2RAIN algorithm [
51] can be used for rainfall estimation from satellite soil moisture observations and it has been successfully applied to many regions (e.g. Reference [
59]). However, the use of SM2RAIN-derived rainfall for river discharge estimation is less explored [
18,
60,
61].
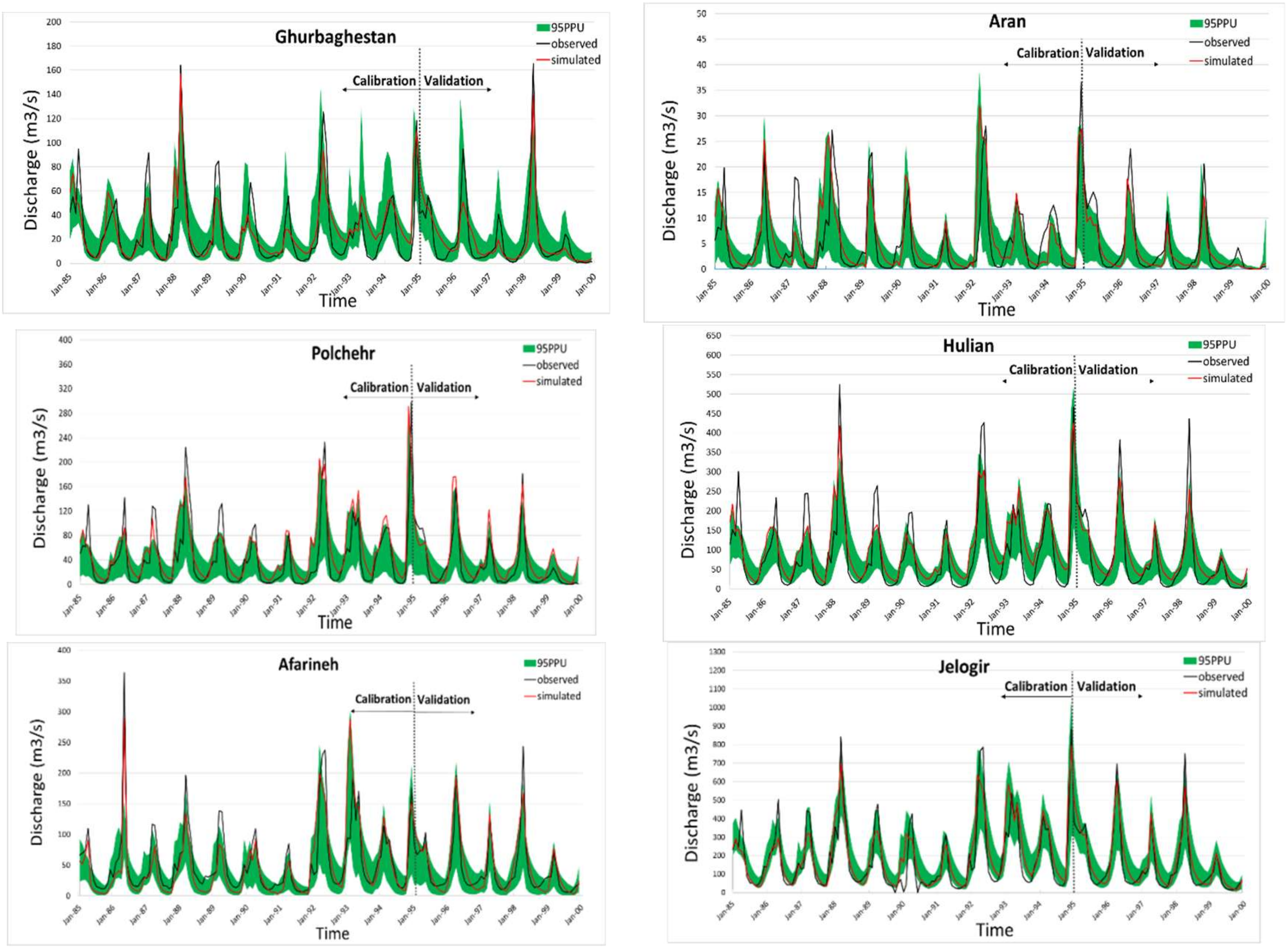
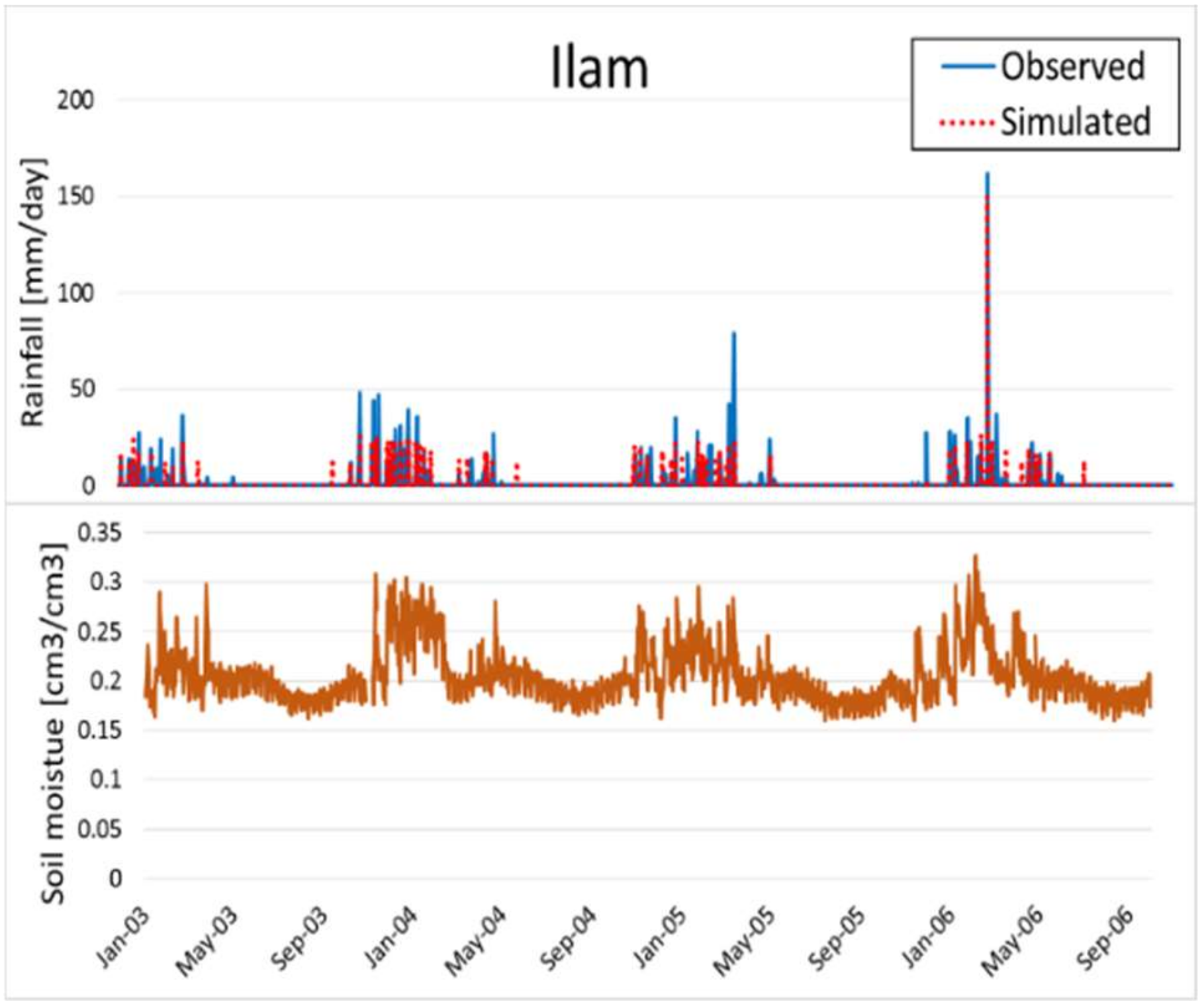
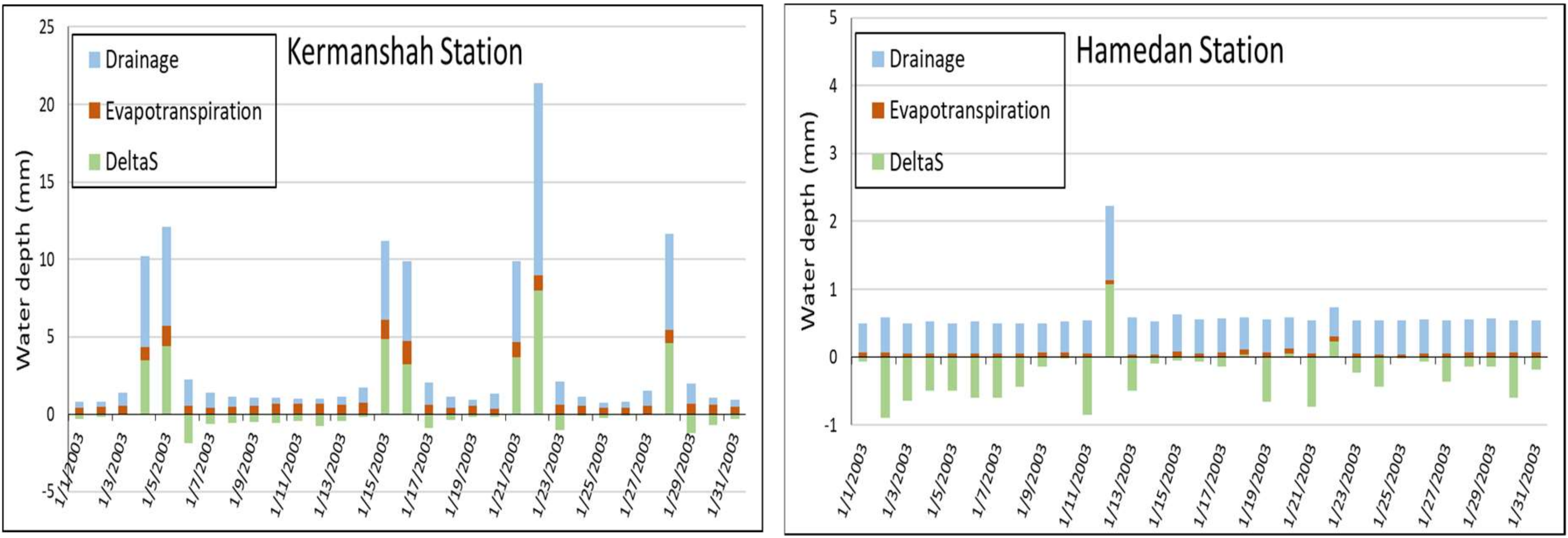
In this study, the SM2RAIN algorithm is successfully applied in the semi-arid Karkheh river basin in Iran to convert AMSR-E satellite SM product to daily rainfall at 10 meteorological stations. Good correlations
R, ranging from 0.58–0.88, between the satellite-derived and the observed ground-based rainfall are obtained. Then, the SM2R-AMSRE rainfall are used as input into a previously calibrated-SWAT model to estimate the monthly river discharge at six gauging stations in the basin. Good agreement with the observations, with
R2—values ranging between 0.72–0.87, are obtained, which is slightly less than the range obtained with the SWAT model using ground-based rainfall as input (
R2~0.83–0.89). Indeed, there is a small but systematic underestimation of the SWAT- SM2R-AMSRE simulated streamflow, owing to the fact that the SM2R-AMSRE rainfall estimated with the SM2RAIN algorithm is also smaller than the ground-based one, which in turn, is due to the possibility of saturation of the satellite-retrieved soil moisture level. In spite of these restrictions, the overall good performance of the SM2RAIN algorithm for rainfall and river discharge (via SWAT) estimation in the Karkheh basin here opens new possibilities for discharge estimation throughout Iran, also by using more recent and more versatile satellite SM products, as started to be investigated by [
62].
Furthermore, the two well-known TRMM-satellite-based rainfall products, TMPA-3B42 and TMPA-3B42RT, are assessed at the KRB climate stations after bias correction and compared with both ground-based and SM2E-AMSRE predictions. The results show that these TMPA-products predict the observed rainfall consistently less accurately than the SM2RAIN model. Similarly to SWAT- SM2R-AMSRE- simulated streamflow, the two TMPA-products are used as input into the previously calibrated-SWAT model. Expectedly, these SWAT-TMPA versions simulate the monthly runoff also less well than the SWAT- SM2R-AMSRE version, indicating again that using SM2R-AMSRE rainfall data in a hydrological model is a viable approach in basins with limited ground-based rainfall data.
The results of the present study indicate that with the use of AMSR-E SM products in the SM2RAIN algorithm as well as in the corrected version of TRMM satellite products, rainfall for poorly gauged regions can be fairly predicted. Moreover, these results show that physically based SM2RAIN model is at least in this application is more correlated with in-situ rainfall than TRMM rainfall satellite products that leads better prediction of runoff.
The methodology is applied to a watershed where the density of rain gauge stations is sparse, so conclusions from this study may provide evidence for the utilization of different rainfall and runoff estimation for water resources assessment of the KRB. The outputs of this study will help hydrologists to understand the efficiency and application of different rainfall estimation at the watershed scale.