Assessment of Water Quality Parameters Using Temporal Remote Sensing Spectral Reflectance in Arid Environments, Saudi Arabia

Abstract

Remote sensing applications in water resources management are quite essential in watershed characterization, particularly when mega basins are under investigation. Water quality parameters help in decision making regarding the further use of water based on its quality. Water quality parameters of chlorophyll a concentration, nitrate concentration, and water turbidity were used in the current study to estimate the water quality parameters in the dam lake of Wadi Baysh, Saudi Arabia. Water quality parameters were collected daily over 2 years (2017–2018) from the water treatment station located within the dam vicinity and were correspondingly tested against remotely sensed water quality parameters. Remote sensing data were collected from Sentinel-2 sensor, European Space Agency (ESA) on a satellite temporal resolution basis. Data were pre-processed then processed to estimate the maximum chlorophyll index (MCI), green normalized difference vegetation index (GNDVI) and normalized difference turbidity index (NDTI). Zonal statistics were used to improve the regression analysis between the spatial data estimated from the remote sensing images and the nonspatial data collected from the water treatment plant. Results showed different correlation coefficients between the ground truth collected data and the corresponding indices conducted from remote sensing data. Actual chlorophyll a concentration showed high correlation with estimated MCI mean values with an R² of 0.96, actual nitrate concentration showed high correlation with the estimated GNDVI mean values with an R² of 0.94, and the actual water turbidity measurements showed high correlation with the estimated NDTI mean values with an R² of 0.94. The research findings support the use of remote sensing data of Sentinel-2 to estimate water quality parameters in arid environments.

1. Introduction

There are many changes in the water body that take place when flowing water stops at the lowest elevation point on land. The flowing water transfers and holds the temperature from one location to the next, so all drainages that recharge a natural reservoir or an artificial dam will affect the water at the destination [1]. Moreover, thermal changes in the water body are associated with chemical changes which influence the organism cycle at the lagoon. Again, small streams and other channels that end at a lagoon will carry any small particles in its path and transfer all these pollutants to the lagoon [2]. As the water stays in the dam or in a pond, more recharge streams will contaminate it and move more sediment to the dam. Hence, over a long period, the change in the water quality will be larger than the change within a short time. In the case of water at a dam, all water supplies from that dam will be contaminated [3].

The amount of decline in water quality is connected to the retention time of the dam’s water and its storage capacity in relation to the amount of water charging the dam during the year. Water in a small pond behind a run-of-river dam will undergo very little or no deterioration; that stored for many months or even years behind a major dam may be lethal to most life in the reservoir and in the river for many kilometers below the dam [4].

Sinking organic materials will consume oxygen in the water. Then, undesirable materials, like carbon dioxide and methane, are released into the dam water. This procedure can take a decade or so, although, in the tropics it may take many decades or even centuries for most of the organic matter to molder [5]. One of the large events that caused great harm to the environment and the surrounding people happened at Brokopondo Dam in 1964.

Normal bacteria can change the water quality because of cyanobacteria concentrations. Cyanobacteria produce a greenish floating matter over the surface of the water body—bloom—which pollutes the water and is associated with respiratory problems and skin irritation issues [6]. Also, a high concentration of such bacteria leading to a slight aberrance in the amount of nitrogen will cause a strong and horrific smell. Discovering harmful blooms over the surface of the water body while in the early stages is very important for protecting the water quality and to control the water source [7].

Digital pictures are easier to use than older images, also, they allow researchers to work with bigger areas than before. In addition, digital images can be saved onto small hard drives and used later with most standard computers carrying the appropriate software. In fact, digital images have opened the doors for many kinds of developments, such as watershed modeling, ship tracking, accurate weather forecasting, flood analyzing, and other beneficial examples of gained knowledge [8]. At the same time, other scientists working on wave bands were trying to study the effects of each band on different objects. Sensors were also developed to detect invisible bands [9].

In recent times, the Environmental Protection Agency (EPA) has been developing and offering an application that monitors the water surface and provides a reasonable water quality parameter and is available for normal users. The current observation application uses satellite data that comes from the European Space Agency (ESA). The ESA gets images and data by using the ocean land color instrument (OCLI), USGS Landsat satellite, and the medium resolution imaging spectrometer (MODIS). Sentinel-2 provides data with a high spatial resolution and has been used in conjunction with developed models to detect chlorophyll and dissolved organic matter. A recent study on Sentinel-2 shows that the most accurate algorithm to acquire the highest reflectance from dissolved organic matter (DOM) comes from bond 5 and bond 3. Bond 4 and 5 were used to develop a model to detect chlorophyll with low root mean squared error [10]. Furthermore, Sentinel-2 with an onboard multispectral imager MSI was proven, in more than one study, to be more accurate than the moderate-resolution imaging spectroradiometer. MSI has been used to detect suspended particulate matter in the water body and its results were acceptable within a wavelength range of 560 to 780 nm [11].

In this study, the goal is to monitor the water quality, therefore, the focus will be on the highest reflectance percentage from the chlorophyll, nitrogen, and water turbidity. Sentinel-2 provides data with high spatial resolution and has developed models for detecting such parameters. Regression analysis is practiced in the current research to define the relationship between the actual and the estimated water quality parameters.

2. Materials and Methods

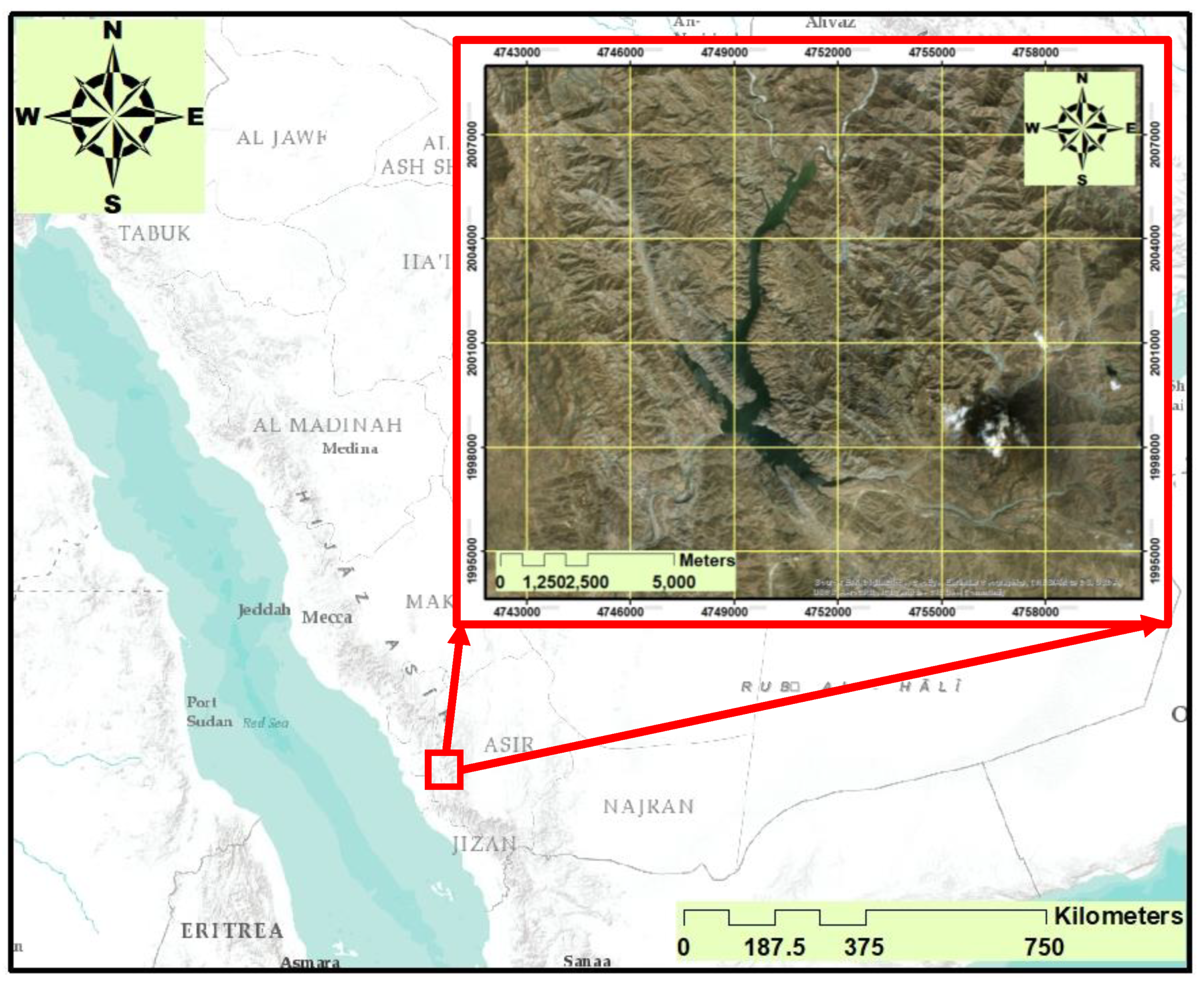
2.1. Study Area Description

Baysh Dam is a gravity dam on Wadi Baysh around 35 km upper east of Baysh in the Jizan Region of southwestern Saudi Arabia (Figure 1). The dam has numerous reasons to incorporate surge control, water system, and groundwater revive. The Baysh Dam was constructed between 2003 and 2009, and is owned and operated by the Ministry of Water and Electricity. The Baysh Dam is 120 m high from the foundation level, with no sunlight reaching the bottom of the dam’s lake. The total reservoir capacity of the dam is 192 million cubic meters. The dam normally requires a long time to be clear of the effects of organic materials. Sinking organic materials will consume oxygen in the water. Then, undesirable gases, like carbon dioxide and methane, are released into the dam water. This procedure can take a decade or so, although, in the tropics it may take many decades or even centuries for most of the organic matter to molder.

2.2. Water Sample Collection

Regular water sample collections were initiated during the middle of each climatic season. From 2017 to 2018, following the complete random sampling (CRS) technique [12], a total of 120 water samples were collected and transferred to the laboratory to perform the designated colorimetry test [13], nitrate concentration (mg/L) test [14], and turbidity test (NTU) [15]. For the restricted part of the lake, water quality parameters were collected from the water treatment plant located at the vicinity of the dam lake.

2.3. Remote Sensing Data

Routine collection of Sentinel-2 data began in January 2017 and continued until the end of December 2018 on a sensor revisit resolution (16 days) which resulted in total of 52 images. The Sentinel-2 instrument is made of 12 spectral bands with a 10 m resolution of visible bands (VI), 20 m resolution of vegetation red edge (VRE) bands, and short-wave infrared (SWIR) bands, in addition to three bands related to coastal aerosols and water vapor of 60 m resolution. Three different remotely sensed indices were obtained to represent three different water quality parameters, maximum chlorophyll index (MCI), green normalized difference vegetation index (GNDVI), and normalized difference turbidity index (NDTI).

2.3.1. Maximum Chlorophyll Index

Maximum chlorophyll index (MCI) was used to exploit the height of the measurements in a certain spectral band above a baseline which passes through three bands B4 (665 nm), B5 (705 nm), and B6 (740 nm) [16,17]. The MCI for floating vegetation and inland water bodies is estimated using the algorithm of Matthews et al. [18] considering the top of atmosphere (TOA) condition:

$$\mathrm{MCI}= R_{rs}\left({\lambda }_2\right)-R_{rs}\left({\lambda }_1\right)\left[\frac{{\lambda }_2-{\lambda }_1}{{\lambda }_3-{\lambda }_1}{R}_{rs}\left({\lambda }_3\right)-R_{rs}\left({\lambda }_1\right)\right],$$

(1)

where R_rs can be obtained based on a field measurement as follows [19]:

$$R_{rs}\left(\lambda \right)=R_{P}X\left\{\left[L_w\left(\lambda \right)-\rho X{L}_{sky}\left(\lambda \right)\right]/\pi X{L}_P\right\},$$

(2)

where Rp is the standard reflectance panel, Lw(λ) is the radiance of water-viewing, Lsky(λ) is sky-measured radiance, ρ is the air–water interface reflectance, and Lp is the radiance reference panel.

2.3.2. Green Normalized Difference Vegetation Index

The green normalized difference vegetation index is based on two-band combinations of the red-edge region of the spectrum [20]. GNDVI is very sensitive to the change in chlorophyll content, which is tidally related with the nitrogen content at the dam lake. The nitrogen index was created and found from the following equation [21]:

(NIR − Green)/(NIR + Green).

(3)

The normalized difference vegetation index was used to detect nitrogen content using the following equation:

(NIR − (690 nm~710 nm))/(IR + (690 nm~710 nm)).

(4)

After many studies, it was found that using the green ray for detection of nitrogen content was more effective than the normal vegetation index. Therefore, GNDVI uses the following equation [22]:

GNDVI = ((NIR − (540 nm~570 nm))/(NIR + (540 nm~570 nm)).

(5)

The wavelength which was used in the previous equation was shifted to the green edge in order to get a clearer result from satellite images [22], where NIR is the near-infrared band of Sentinel-2.

2.3.3. Normalized Difference Turbidity Index

Lacaux et al. [23] developed an algorithm to estimate the water turbidity using remote sensing data specifically for ponds and inland waters, and it can be estimated as follows:

$$\mathrm{NDTI}=\frac{\mathrm{Red}-\mathrm{Green}}{\mathrm{Red}+\mathrm{Green}},$$

(6)

where R is the red band of Sentinel-2, and G is the green band of Sentinel-2.

2.4. Data Normalization and Regression Analysis

In order to establish a regression analysis between the actual and estimated water quality parameters, a data normalization procedure is essential task to omit the unit’s dimension from the two datasets. Data normalization can be achieved as follows [24]:

$$f\left(\chi , \mu , \sigma \right)=\frac{1}{\sqrt{2\pi \sigma }}{e}^{-\left(\frac{{\left(\pi -\mu \right)}^2}{2{\sigma }^2}\right)}.$$

(7)

The basic equation for Pearson’s correlation is defined as follows [25]:

$$r=\frac{n\left(\sum xy\right)-\left(\sum x\right)\left(\sum y\right)}{\sqrt{\left[n\sum x^2\right]\left[n\sum y^2-{\left(\sum y\right)}^2\right]}},$$

(8)

where N is number of pairs of scores, ∑xy is sum of the products of paired scores, ∑x is sum of x scores, ∑y is sum of y scores, ∑x₂ is sum of squared x scores, and ∑y₂ is sum of squared y scores.

The intention behind performing the regression analyses is to envisage the regression potentials between the actual and the remotely sensed estimated water quality parameters. Therefore, the actual parameters will be plotted against the estimated parameters and root mean square error (RMSE) values are used to obtain the best fit. RMSE is obtained as follows [26]:

$$\mathrm{RMSE}=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^n{\left(P_i-O_i\right)}^2}{n}},$$

(9)

where P is the predicted value; O is the observed values.

Zonal statistics under arc environment were exercised and resulted in four different statistic types (mean, P 90 “majority”, maximum, and minimum values of the input raster) which were used in the regression analysis to identify the best fit.

3. Results and Discussion

Multiple empirical regression analyses were exercised in order to evaluate and realize the coherent relationships between the actual water quality parameter concentrations collected in situ and the corresponded water quality parameters in reflectance values estimated from remote sensing data.

The in-situ water quality parameters were taken daily by the dam authority for routine analysis, therefore, there was no time difference between the in-situ sampling and remote sensing data acquisition.

Statistical analyses that included calculations of the average, maximum, and minimum values, and linear and nonlinear regressions were performed. Pearson correlation analysis was used to investigate the strength of the association between the two variables with a correlation coefficient (r). Significance levels were reported to be significant (p < 0.05) or not significant (p > 0.05) with a t-test, which provides evidence of an association between the two variables.

Statistical analyses were performed using the mean values of in situ measurements against the mean, P 90 (majority), maximum, and minimum values of remote sensing data to evaluate the analysis consistencies in linear and nonlinear regressions. The variables’ association strength was examined for subsequent Person correlation with p < 0.05 for a significant association and p > 0.05 for no significant association. Figure 2, Figure 3 and Figure 4 demonstrates the linear regression analysis of MCI, GNDVI, and NDTI, respectively.

Regression results showed that mean pixel values were the best for presenting a coherent association between the actual water parameters and the remotely sensed estimated ones in each of the investigated water quality parameters (MCI, GNDVI, and NDTI). RMSE expressed in

Table 1. Summary of fit analysis.

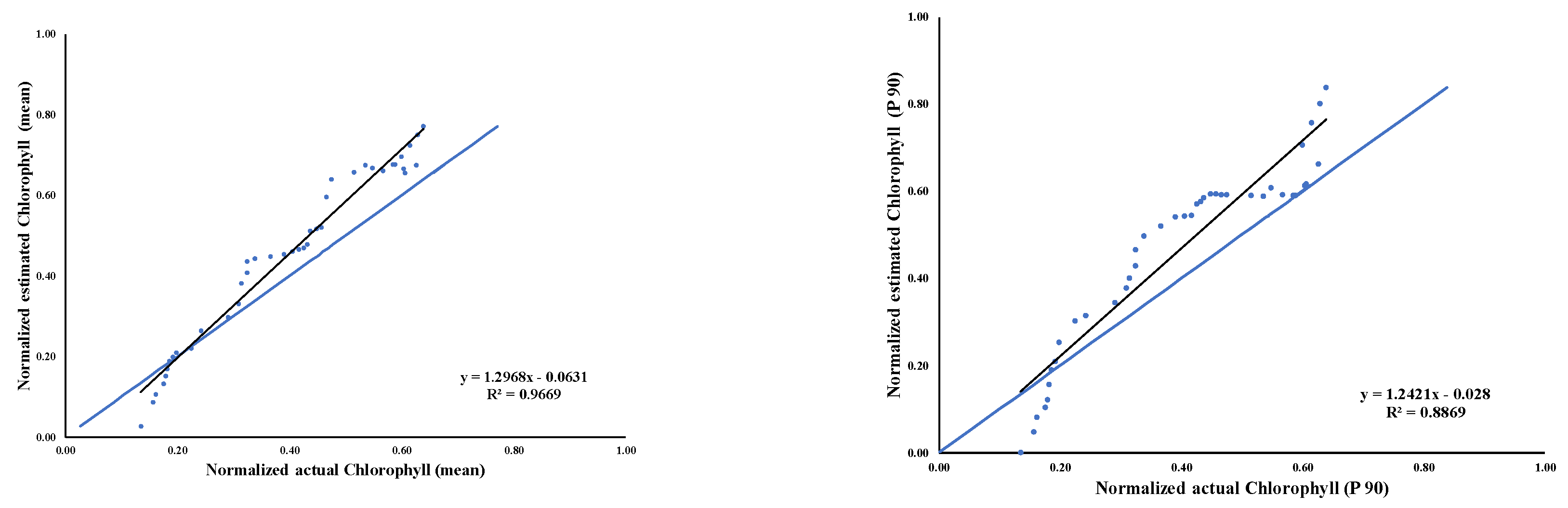
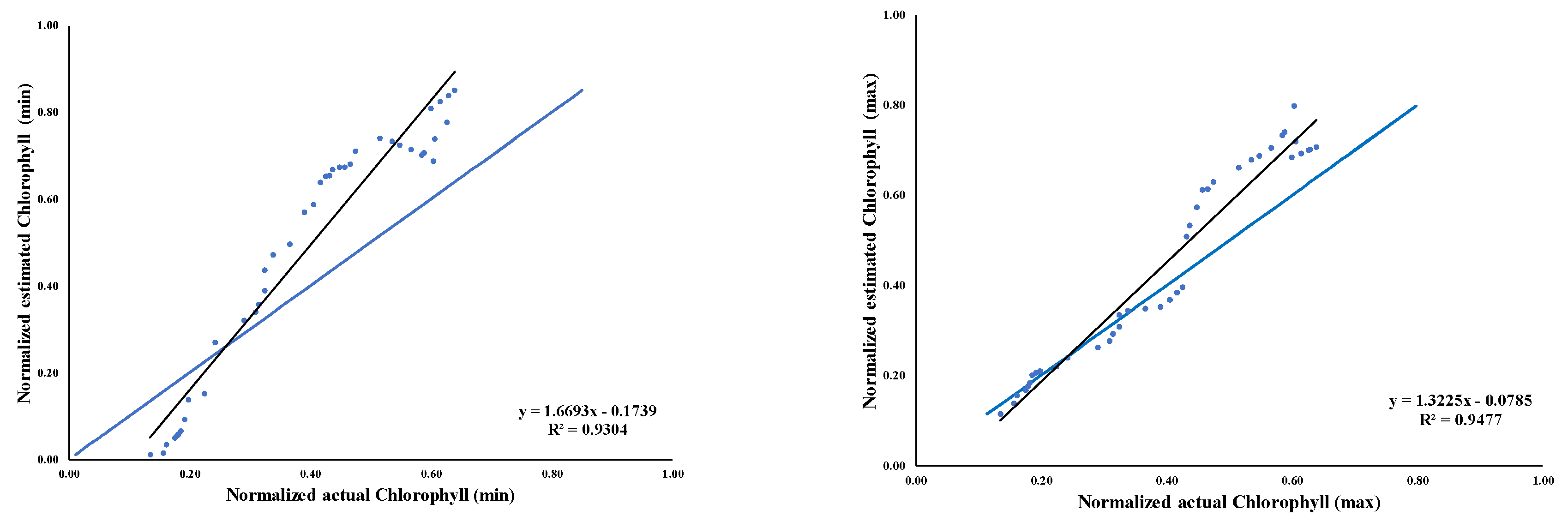
Header	MCI
	Mean	P 90	Min	Max
RSquare	0.966900	0.886912	0.930364	0.947727
RSquare Adj	0.966051	0.884012	0.928579	0.946386
Root Mean Square Error	0.039628	0.073256	0.075427	0.051299
Mean of Response	0.452561	0.465951	0.489893	0.447380
	GNDVI
RSquare	0.940660	0.920928	0.917046	0.096571
RSquare Adj	0.939138	0.918900	0.914919	0.073406
Root Mean Square Error	0.068546	0.076428	0.090124	0.014555
Mean of Response	0.492012	0.520620	0.510049	0.420685
	NDTI
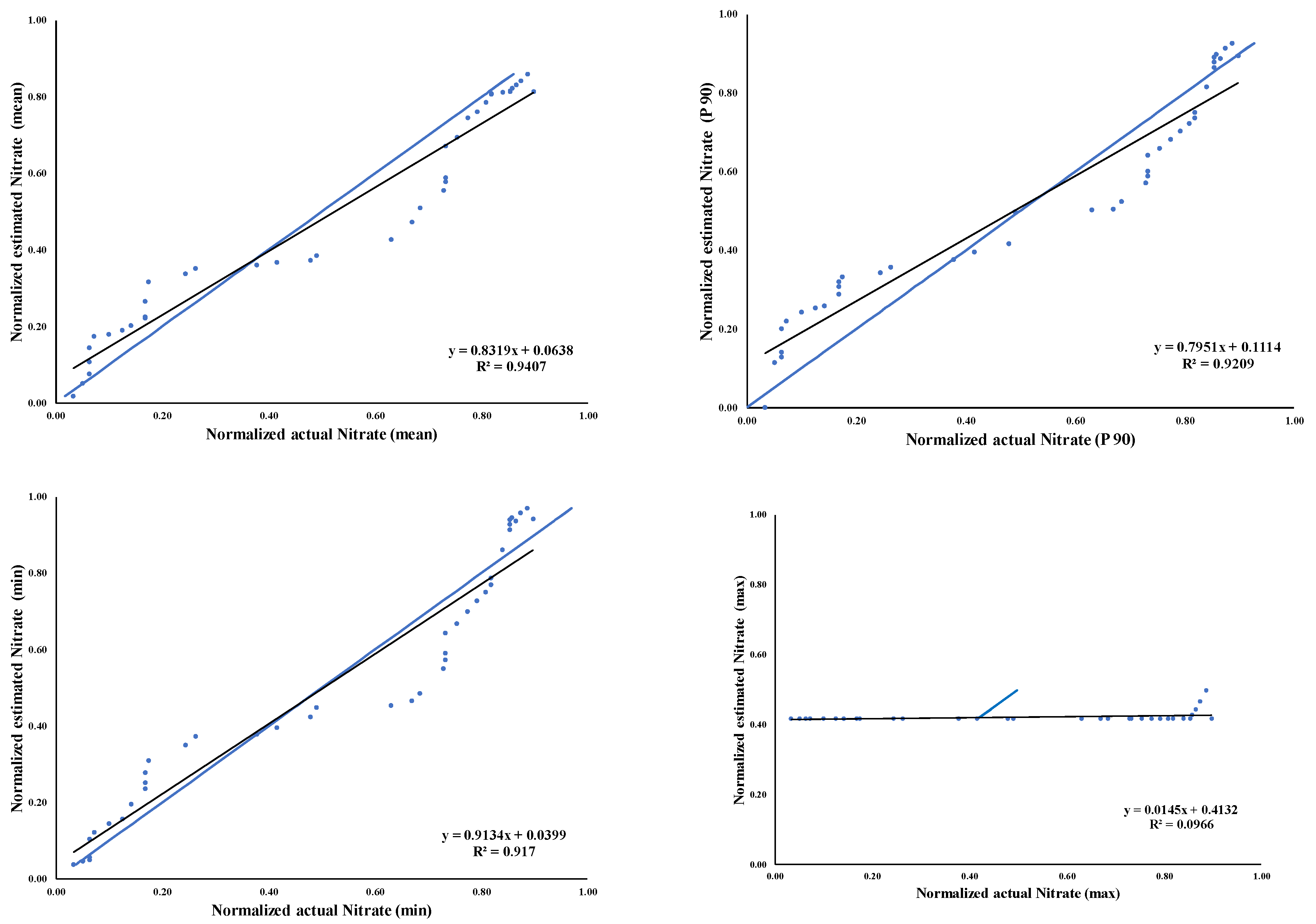
RSquare	0.941958	0.921015	0.942222	0.736541
RSquare Adj	0.940470	0.918990	0.940741	0.729786
Root Mean Square Error	0.077774	0.062725	0.075304	0.156997
Mean of Response	0.513581	0.413256	0.504930	0.532880

confirms the robust association between the mean value of the in-situ water quality measurements and the conducted values from remote sensing data based on the summary of the fit analysis [27,28].

Multi variance analysis shows a strong correlation between the mean in situ readings and the mean image values of estimated MCI, GNDVI, and NDTI (Figure 5, Figure 6 and Figure 7).

Table 2. The correlation coefficient of the water quality parameters.

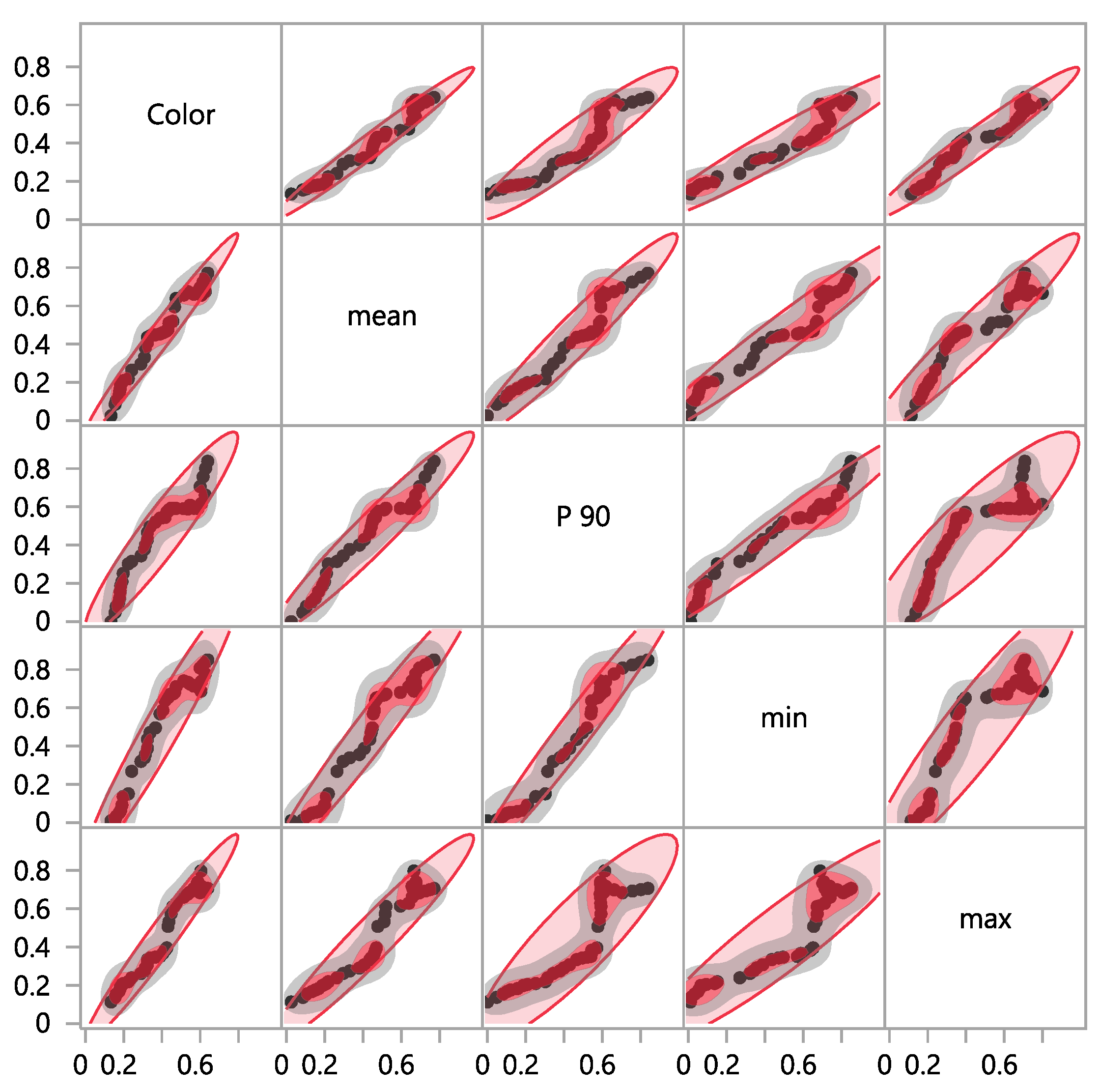
Header	Color	Mean	P 90	Min	Max
Color	1.0000	0.9833	0.9418	0.9646	0.9735
Mean		1.0000	0.9648	0.9748	0.9607
P 90			1.0000	0.9786	0.8863
Min				1.0000	0.9271
Max					1.0000
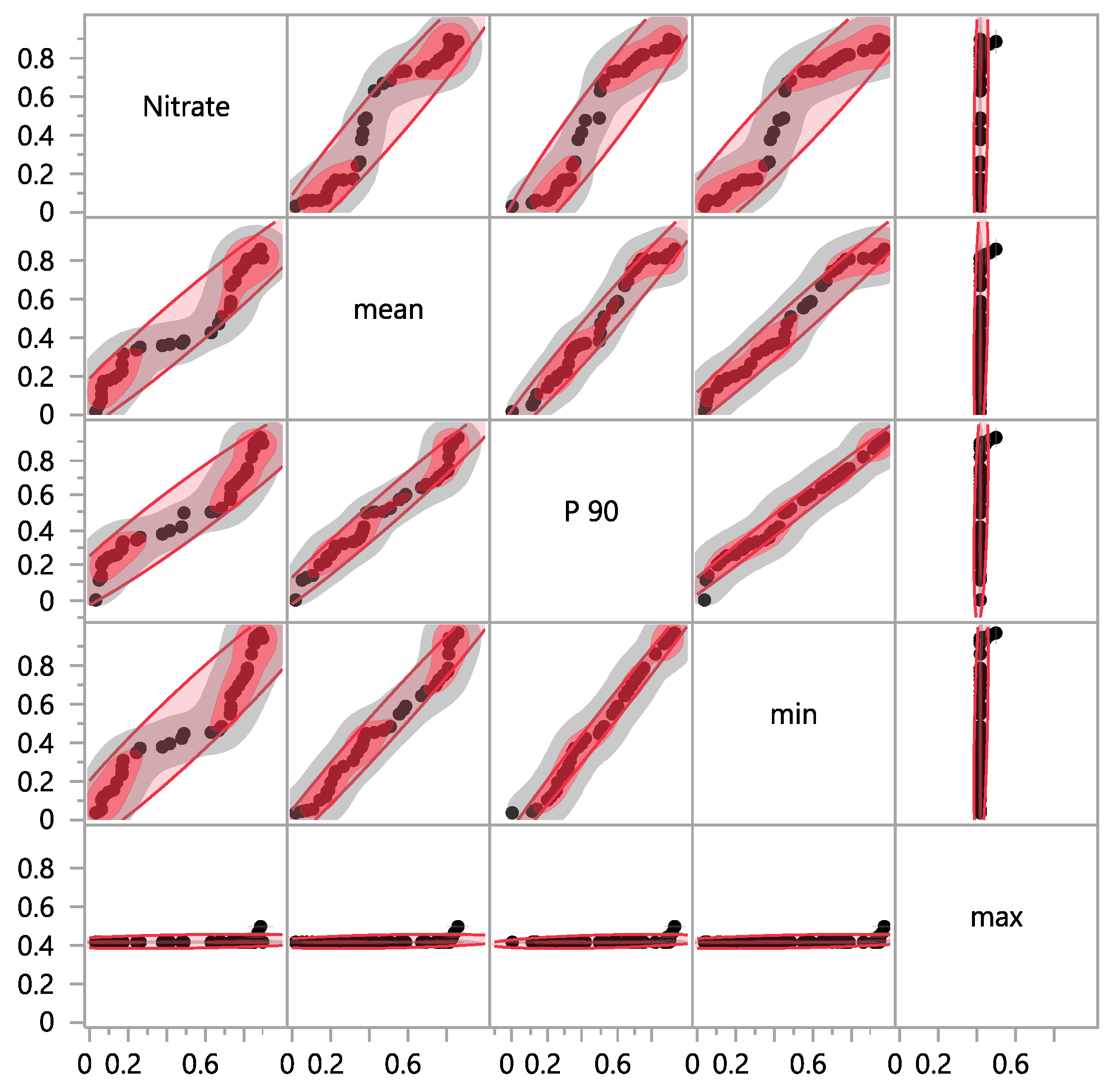
	Nitrate	Mean	P 90	Min	Max
Nitrate	1.0000	0.9699	0.9596	0.9576	0.3108
Mean		1.0000	0.9859	0.9874	0.3553
P 90			1.0000	0.9951	0.4076
Min				1.0000	0.4040
Max					1.0000
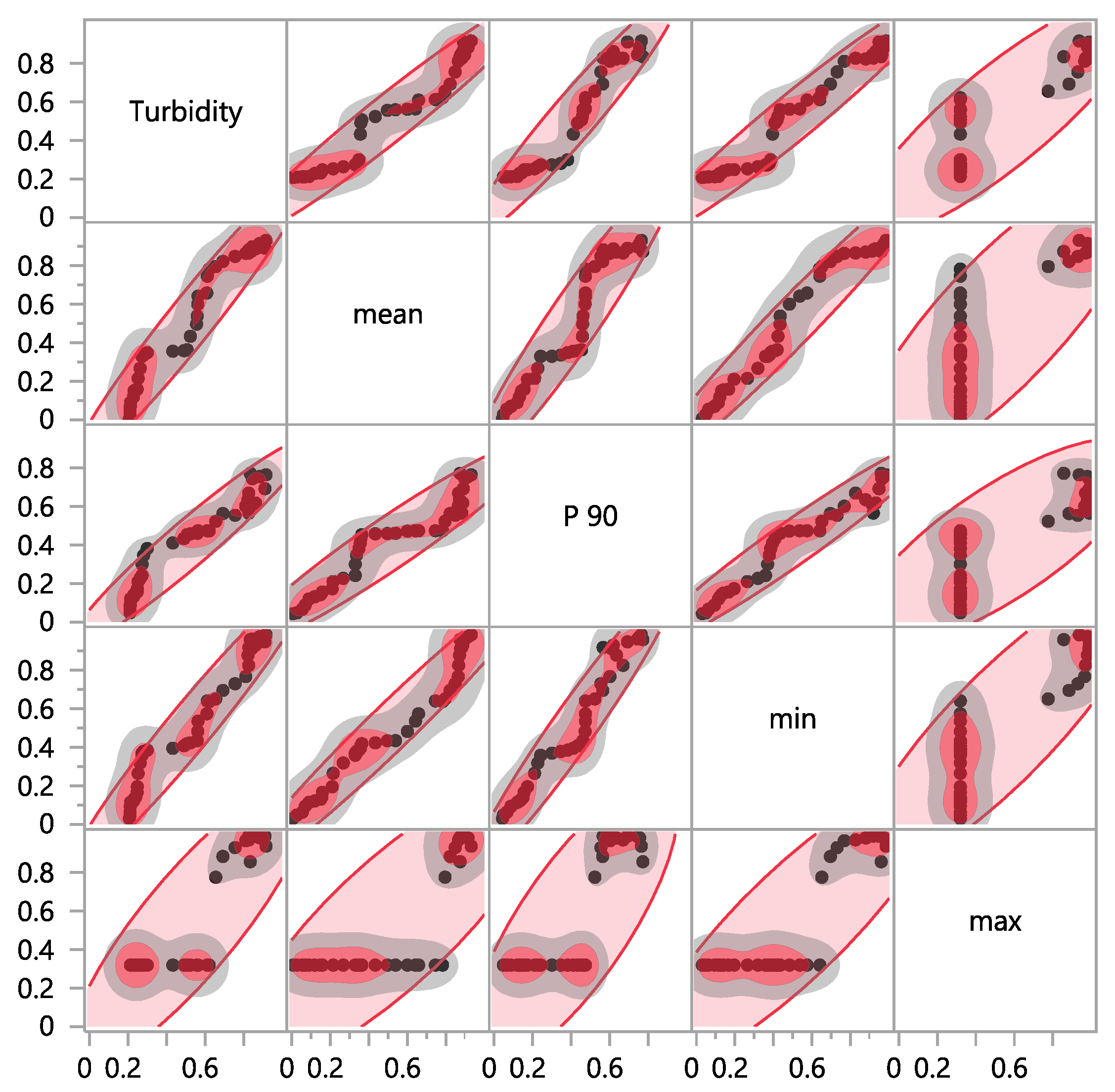
	Turbidity	Mean	P 90	Min	Max
Turbidity	1.0000	0.9707	0.9597	0.9705	0.8582
Mean		1.0000	0.9559	0.9771	0.8206
P 90			1.0000	0.9676	0.7770
Min				1.0000	0.8616
Max					1.0000

expresses the correlation coefficient of the water quality parameters under investigation.

The minimum and maximum pixel did not show a strong association with in situ measurements. The reason behind this weak relationship is that both minimum and maximum pixel values were considered as the analysis range anomalies [29].

There was no significant difference between the in-situ surface water sampling across different climatic conditions and the subsurface measurements taken by the dam authority, which might be understood as reaching the saturation level of the investigated water quality parameters [30]. Therefore, this leads to water being classified as of a low quality that cannot be safely or directly used [31].

The temporal analysis of the estimated remotely sensed indices ensured regression stability [7] based on robust linear coherence between the actual and estimated water quality parameters examined in the current research study.

While Van Wagtendonk et al. [32] failed to establish a strong association using Landsat data, red-edge bands of Sentinel-2 proved to be efficiently reliable for estimating water quality parameters specified in inland water [33].

According to Gitelson et al. [34], Odermatt et al. [35], and Vesali et al. [36] estimation of chlorophyll concentration underwater turbidity conditions was satisfactorily conducted using several models based on accurate spectral measurements. However, developing complex models seems to be difficult, due to the broad bandwidth of Operational Land Imager (OLI) data. This requires the development of a different method that is applicable to OLI data.

Nevertheless, complex models for chlorophyll estimations based on Landsat OLI data are hard to develop because of Landsat OLI broad bandwidth in the near-infrared and thermal infrared regions [37]. Previously, scholarly work of Walthall et al. [38] and Adam et al. [39] reported weaknesses in the association of middle infrared and chlorophyll concentrations in water using Landsat ETM+ data. This was explained by the penetration limitations of Landsat ETM+ bands in deep water [40,41].

Estimation of N concentration in agricultural crops and its spatial distribution has been the goal of several scholarly works because of its importance to soil fertilization [42,43]. However, estimation of dissolved N is confined to a limited number of earth observation sensors equipped specifically with the red-edge region of the spectrum [44].

Regression analysis between the actual N concentration and the estimated index was exercised on four different zonal statistic types. The mean and the P 90 values were more coherent than the actual data with a correlation coefficient of 0.9699 and 0.9596, respectively, while maximum and minimum values were less representative of the actual N concentration. The increase in the dissolved N in the dam lake is a sign of pollution pressure to the water quality on the catchment scale [45,46]. However, the N concentration is monitored by the local authority at the outflow, disregarding only the separation distribution of the pollutant which can be assessed using remote sensing data [47,48].

Water turbidity as a sign of sedimentation processes was initially considered by Carpenter [49] utilizing Landsat Thematic Mapper data. The algorithm was consequently developed to consider the change in the central bandwidth of the recent sensors as Doxaran [50] reported using Satellite Probatoire de l’Observation de la Terre (SPOT) images. The duality of the bands at 645 and 850 nm of suspended particulate matter proved to be effective in turbidity detection, especially in inland water [51]. Similarly, Sentinel-2 central band wavelengths in the near-infrared region cover the designated bands for suspended particulate detection, making the sensor capable of estimation of water turbidity in a precise manner [52,53].

4. Conclusions

The routine monitoring of water quality parameters is costly and requires constant laboratory supplies and efforts. The implemented methodologies, as well as the comprehensive assessments, answered the questions concerning the feasibility of using a linear empirical approach to estimate the designated water quality parameters across temporal remote sensing data. Estimation of chlorophyll, nitrogen content, and water turbidity were successfully achieved utilizing remote sensing data acquired from Sentinel-2. Red-edge bands of Sentinel-2 are the keystone feature of the sensor for estimating the addressed water quality parameters in a reliable manner. Moreover, the mean values of the raster data showed a high correlation with the actual data from the conducted laboratory examinations. Therefore, a consistent empirical model could be determined.