Assessment of the Decadal Impact of Wildfire on Water Quality in Forested Catchments
Abstract
1. Introduction
- Lack of studies showing >5 years post-wildfire impact on WQ;
- lack of studies with adequate pre- and post-wildfire data;
- past studies predominantly use least-square regression models for change detection without accounting for auto-correlation in the data, and therefore hypothesis testing is erroneous;
- past studies rely on simple discharge-WQ models to detect change due to wildfire.
- Assess the medium-term impacts of wildfire on WQ in the forest catchments around Sydney based on a 10 years pre-wildfire and 10 years post-wildfire dataset;
- present an approach using LMM to detect change based on sparse (as compared to discharge) WQ observations to address the shortcomings identified previously.
2. Materials and Methods
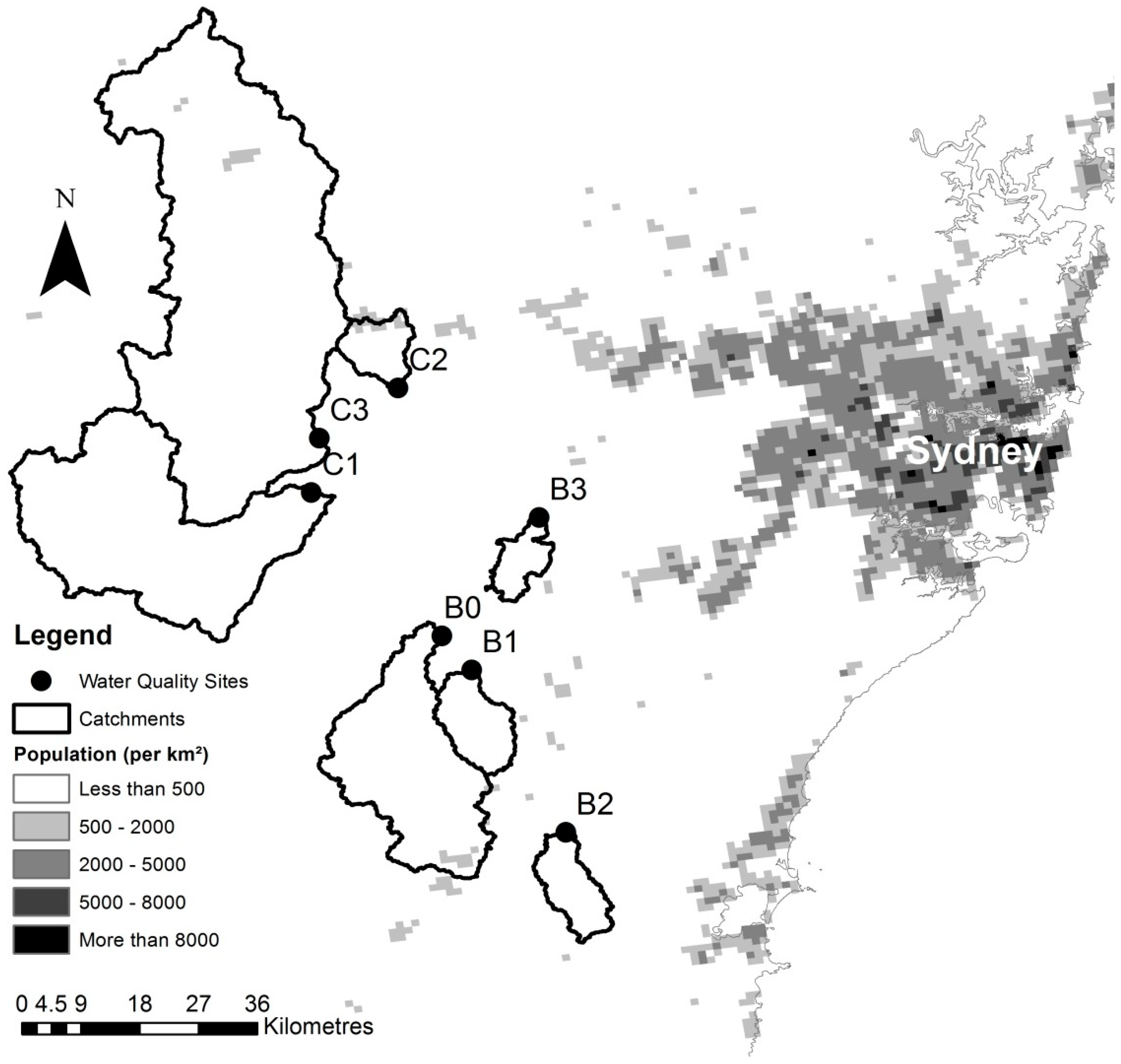
2.1. Study Area
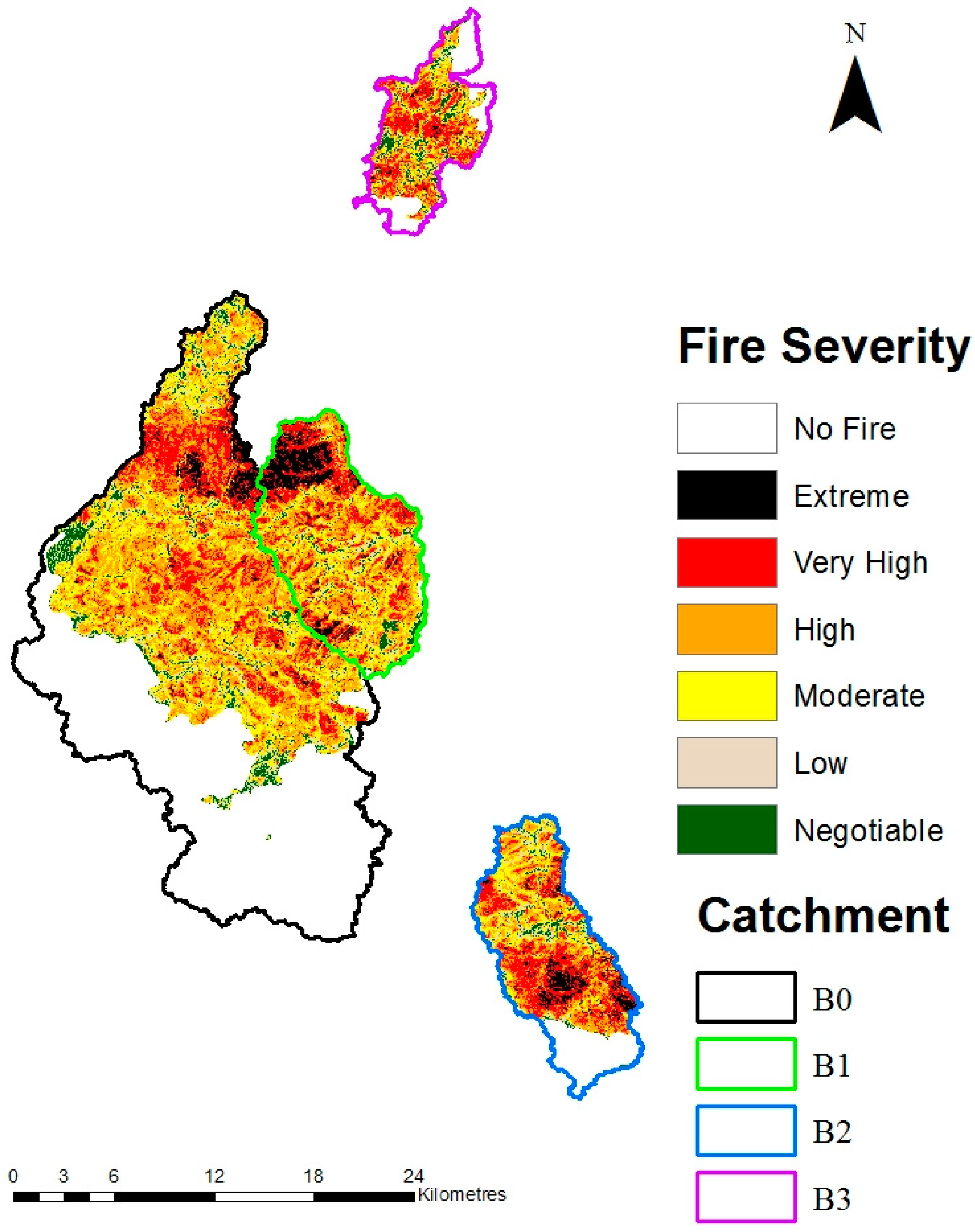
2.2. Wildfire Severity
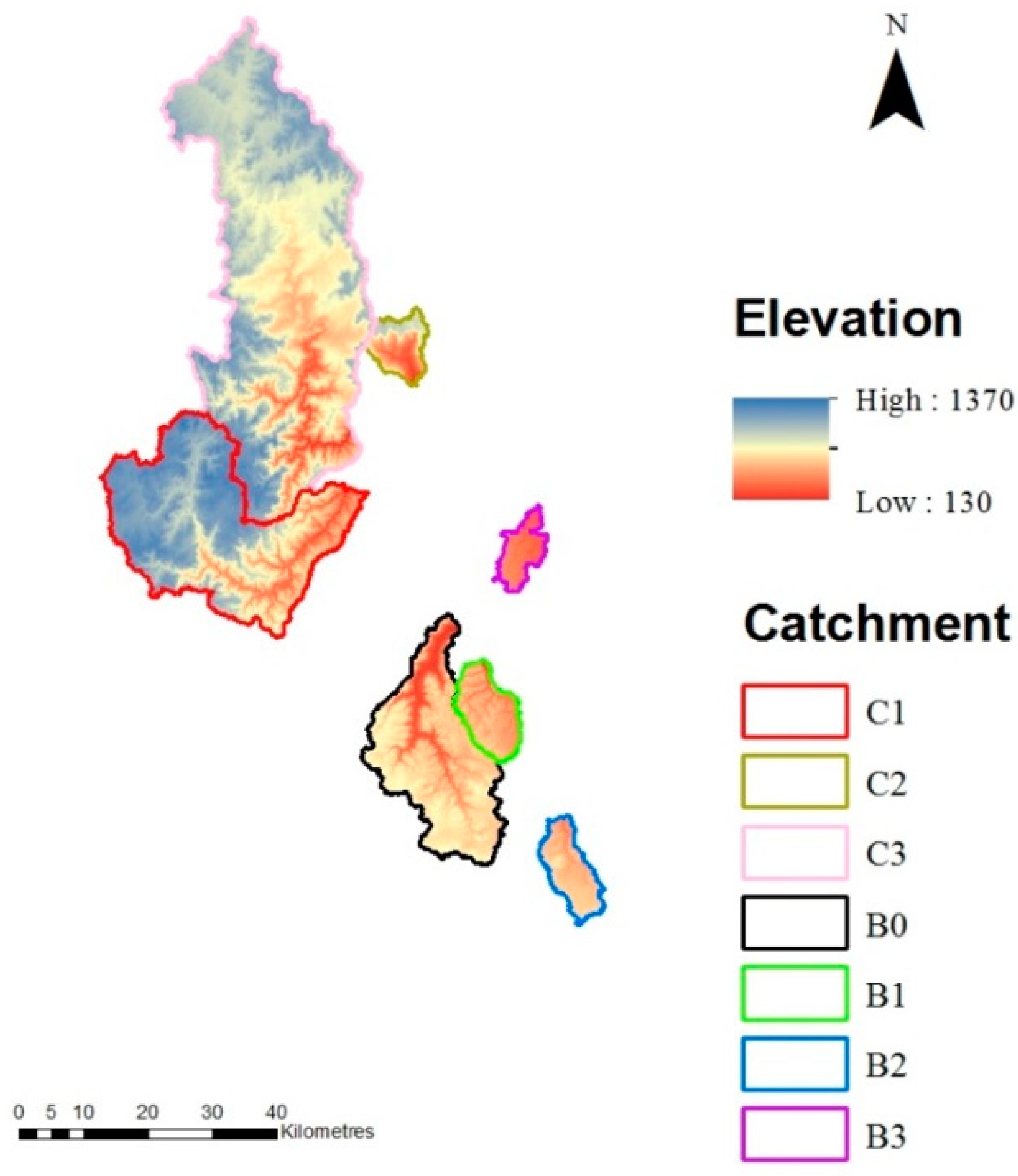
2.3. Catchment Terrain
2.4. Change Detection Method
2.5. Assessment of Model Quality
3. Results
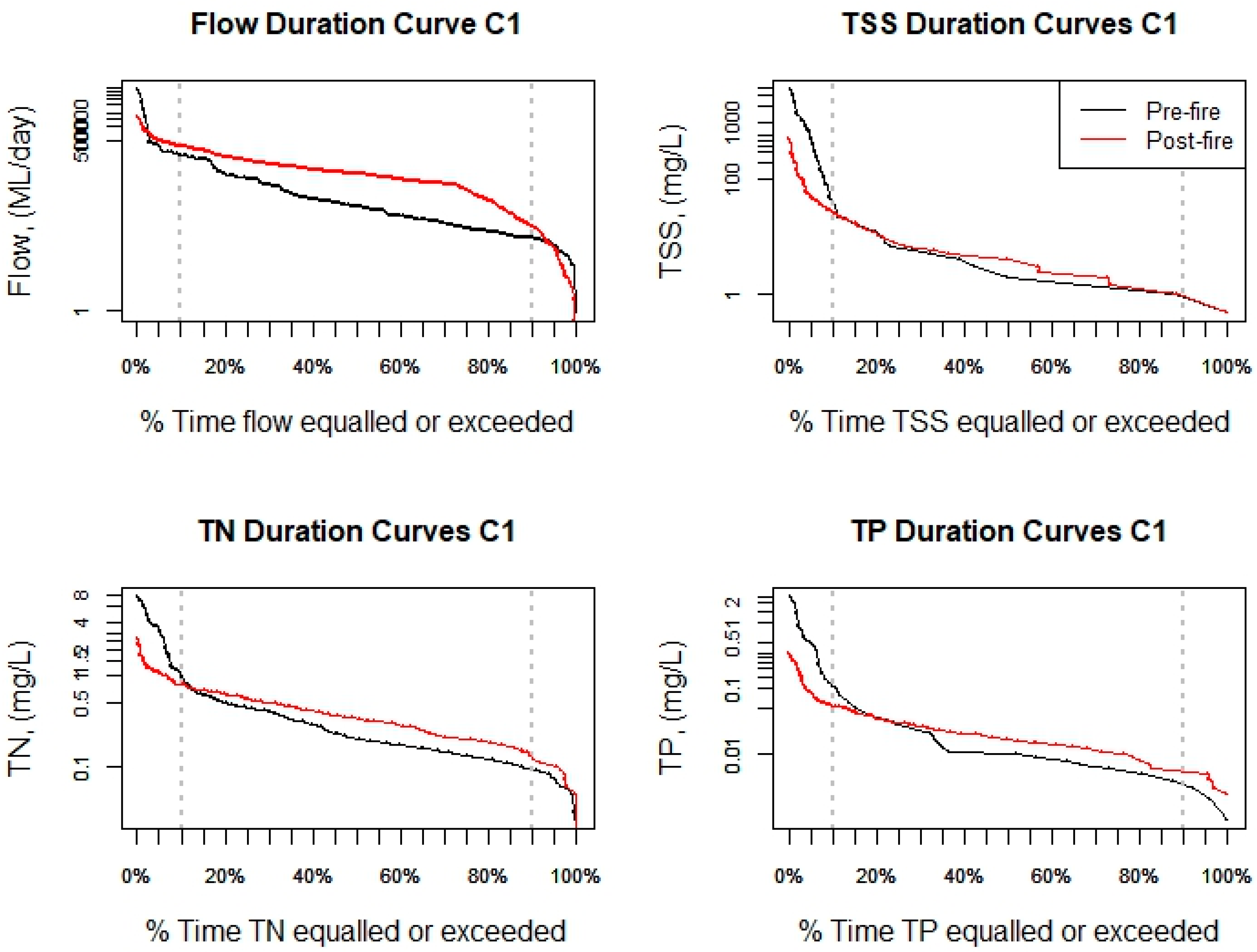
3.1. Exploratory Data Analysis
3.2. Linear Mixed Modelling
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shakesby, R.A.; Doerr, S.H. Wildfire as a hydrological and geomorphological agent. Earth-Sci. Rev. 2006, 74, 269–307. [Google Scholar] [CrossRef]
- Ice, G.G.; Neary, D.G.; Adams, P.W. Effects of wildfire on soils and watershed processes. J. For. 2004, 102, 16–20. [Google Scholar]
- Crouch, R.L.; Timmenga, H.J.; Barber, T.R.; Fuchsman, P.C. Post-fire surface water quality: Comparison of fire retardant versus wildfire-related effects. Chemosphere 2006, 62, 874–889. [Google Scholar] [CrossRef] [PubMed]
- Lane, P.N.J.; Feikema, P.M.; Sherwin, C.B.; Peel, M.C.; Freebairn, A.C. Modelling the long term water yield impact of wildfire and other forest disturbance in eucalypt forests. Environ. Model. Softw. 2010, 25, 467–478. [Google Scholar] [CrossRef]
- Neary, D.G.; Ice, G.G.; Jackson, C.R. Linkages between forest soils and water quality and quantity. For. Ecol. Manag. 2009, 258, 2269–2281. [Google Scholar] [CrossRef]
- Lucas, C. Bushfire Weather in Southeast Australia: Recent Trends and Projected Climate Change Impacts; Bushfire Cooperative Research Centre: Melbourne, Australia, 2007. [Google Scholar]
- Lane, P.N.J.; Sheridan, G.J.; Noske, P.J. Changes in sediment loads and discharge from small mountain catchments following wildfire in South Eastern Australia. J. Hydrol. 2006, 331, 495–510. [Google Scholar] [CrossRef]
- Smith, H.G.; Sheridan, G.J.; Lane, P.N.J.; Nyman, P.; Haydon, S. Wildfire effects on water quality in forest catchments: A review with implications for water supply. J. Hydrol. 2011, 396, 170–192. [Google Scholar] [CrossRef]
- Kuczera, G.; Parent, E. Monte carlo assessment of parameter uncertainty in conceptual catchment models: The metropolis algorithm. J. Hydrol. 1998, 211, 69–85. [Google Scholar] [CrossRef]
- Drewry, J.J.; Newham, L.T.H.; Greene, R.S.B.; Jakeman, A.J.; Croke, B.F.W. A review of nitrogen and phosphorus export to waterways: Context for catchment modelling. Mar. Freshw. Res. 2006, 57, 757–774. [Google Scholar] [CrossRef]
- Wood, P.J.; Armitage, P.D. Biological effects of fine sediment in the lotic environment. Environ. Manag. 1997, 21, 203–217. [Google Scholar] [CrossRef]
- Townsend, S.A.; Douglas, M.M. The effect of a wildfire on stream water quality and catchment water yield in a tropical savanna excluded from fire for 10 years (Kakadu National Park, North Australia). Water Res. 2004, 38, 3051–3058. [Google Scholar] [CrossRef]
- Moody, J.A.; Martin, D.A. Post-fire, rainfall intensity–peak discharge relations for three mountainous watersheds in the western USA. Hydrol. Process. 2001, 15, 2981–2993. [Google Scholar] [CrossRef]
- Neary, D.G.; Ryan, K.C.; DeBano, L.F. Wildland Fire in Ecosystems: Effects of Fire on Soils and Water; U.S. Department of Agriculture, Forest Service: Ogden, UT, USA, 2005.
- Onda, Y.; Dietrich, W.E.; Booker, F. Evolution of overland flow after a severe forest fire, point reyes, California. Catena 2008, 72, 13–20. [Google Scholar] [CrossRef]
- Heath, J.T.; Chafer, C.J.; Bishop, T.F.; Van Ogtrop, F.F. Wildfire effects on soil carbon and water repellency under eucalyptus forest in eastern australia. Soil Res. 2015, 53, 13–23. [Google Scholar] [CrossRef]
- Johansen, M.P.; Hakonson, T.E.; Whicker, F.W.; Breshears, D.D. Pulsed redistribution of a contaminant following forest fire. J. Environ. Qual. 2003, 32, 2150–2157. [Google Scholar]
- Kuczera, G. Prediction of water yield reductions following a bushfire in ash-mixed species eucalypt forest. J. Hydrol. 1987, 94, 215–236. [Google Scholar] [CrossRef]
- Bladon, K.D.; Silins, U.; Wagner, M.J.; Stone, M.; Emelko, M.B.; Mendoza, C.A.; Devito, K.J.; Boon, S. Wildfire impacts on nitrogen concentration and production from headwater streams in southern alberta‘s rocky mountains. Can. J. For. Res. 2008, 38, 2359–2371. [Google Scholar] [CrossRef]
- Oliver, A.A.; Reuter, J.E.; Heyvaert, A.C.; Dahlgren, R.A. Water quality response to the angora fire, lake tahoe, California. Biogeochemistry 2012, 111, 361–376. [Google Scholar] [CrossRef]
- Bartley, R.; Speirs, W.J.; Ellis, T.W.; Waters, D.K. A review of sediment and nutrient concentration data from australia for use in catchment water quality models. Mar. Pollut. Bull. 2012, 65, 101–116. [Google Scholar] [CrossRef] [PubMed]
- Lessels, J.; Bishop, T. A simulation based approach to quantify the difference between event-based and routine water quality monitoring schemes. J. Hydrol. Reg. Stud. 2015, 4, 439–451. [Google Scholar] [CrossRef]
- Lark, R.M.; Cullis, B.R. Model-based analysis using reml for inference from systematically sampled data on soil. Eur. J. Soil Sci. 2004, 55, 799–813. [Google Scholar] [CrossRef]
- Salavati, B.; Oudin, L.; Furusho-Percot, C.; Ribstein, P. Modeling approaches to detect land-use changes: Urbanization analyzed on a set of 43 us catchments. J. Hydrol. 2016, 538, 138–151. [Google Scholar] [CrossRef]
- Ravichandran, S. Hydrological influences on the water quality trends in tamiraparani basin, South India. Environ. Monit. Assess. 2003, 87, 293–309. [Google Scholar] [CrossRef]
- Drewry, J.; Newham, L.; Croke, B. Suspended sediment, nitrogen and phosphorus concentrations and exports during storm-events to the Tuross Estuary, Australia. J. Environ. Manag. 2009, 90, 879–887. [Google Scholar] [CrossRef]
- Lessels, J.S.; Bishop, T.F. Using the precision of the mean to estimate suitable sample sizes for monitoring total phosphorus in australian catchments. Hydrol. Process. 2015, 29, 950–964. [Google Scholar] [CrossRef]
- Mast, M.A.; Clow, D.W. Effects of 2003 wildfires on stream chemistry in glacier national park, montana. Hydrol. Process. 2008, 22, 5013–5023. [Google Scholar] [CrossRef]
- Malmon, D.V.; Reneau, S.L.; Katzman, D.; Lavine, A.; Lyman, J. Suspended sediment transport in an ephemeral stream following wildfire. J. Geophys. Res. Earth Surf. 2007, 112. [Google Scholar] [CrossRef]
- Kunze, M.D.; Stednick, J.D. Streamflow and suspended sediment yield following the 2000 bobcat fire, colorado. Hydrol. Process. Int. J. 2006, 20, 1661–1681. [Google Scholar] [CrossRef]
- Hauer, F.R.; Spencer, C.N. Phosphorus and nitrogen dynamics in streams associated with wildfire: A study of immediate and longterm effects. Int. J. Wildland Fire 1998, 8, 183–198. [Google Scholar] [CrossRef]
- Winter, J.; Watts, M. Christmas fires 2001, commemorative edition. Bushfire Bull. 2002, 23, 1–160. [Google Scholar]
- Lessels, J.; Bishop, T. Estimating water quality using linear mixed models with stream discharge and turbidity. J. Hydrol. 2013, 498, 13–22. [Google Scholar] [CrossRef]
- Shakesby, R.A.; Wallbrink, P.J.; Doerr, S.H.; English, P.M.; Chafer, C.J.; Humphreys, G.S.; Blake, W.H.; Tomkins, K.M. Distinctiveness of wildfire effects on soil erosion in south-east australian eucalypt forests assessed in a global context. For. Ecol. Manag. 2007, 238, 347–364. [Google Scholar] [CrossRef]
- Heath, J.T.; Chafer, C.J.; van Ogtrop, F.F.; Bishop, T.F.A. Post-wildfire recovery of water yield in the sydney basin water supply catchments: An assessment of the 2001/2002 wildfires. J. Hydrol. 2014, 519 Pt B, 1428–1440. [Google Scholar] [CrossRef]
- Ribeiro, P.J., Jr.; Diggle, P.J. Geor: A package for geostatistical analysis. R News 2001, 1, 14–18. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2015. [Google Scholar]
- Wang, Y.-G.; Kuhnert, P.; Henderson, B. Load estimation with uncertainties from opportunistic sampling data–a semiparametric approach. J. Hydrol. 2011, 396, 148–157. [Google Scholar] [CrossRef]
- van Dijk, A.I.; Beck, H.E.; Crosbie, R.S.; de Jeu, R.A.; Liu, Y.Y.; Podger, G.M.; Timbal, B.; Viney, N.R. The millennium drought in southeast australia (2001–2009): Natural and human causes and implications for water resources, ecosystems, economy, and society. Water Resour. Res. 2013, 49, 1040–1057. [Google Scholar] [CrossRef]
- South Eastern Australian Climate Initiative. Climate Variability and Change in South-Eastern Australia: A Synthesis of Findings from Phase 1 of the South Eastern Australian Climate Initiative (seaci); CSIRO Australia: Canberra, Australia, 2010.
- Sheridan, G.J.; Lane, P.N.; Noske, P.J. Quantification of hillslope runoff and erosion processes before and after wildfire in a wet eucalyptus forest. J. Hydrol. 2007, 343, 12–28. [Google Scholar] [CrossRef]
- Gallaher, B.; Koch, R.; Mullen, K. Quality of Storm Water Runoff at Los Alamos National Laboratory in 2000 with Emphasis on the Impact of the Cerro Grande Fire; Los Alamos National Laboratory LA-13926; Los Alamos National Laboratory: Los Alamos, NM, USA, 2002; p. 166.
- Hicke, J.A.; Allen, C.D.; Desai, A.R.; Dietze, M.C.; Hall, R.J.; Hogg, E.H.T.; Kashian, D.M.; Moore, D.; Raffa, K.F.; Sturrock, R.N. Effects of biotic disturbances on forest carbon cycling in the United States and canada. Glob. Chang. Biol. 2012, 18, 7–34. [Google Scholar] [CrossRef]
- Abramson, L. Post-Fire Sedimentation and Flood Risk Potential in the Mission Creek Watershed of Santa Barbara; University of California: Santa Barbara, CA, USA, 2009. [Google Scholar]
- Feikema, P.M.; Sheridan, G.J.; Argent, R.M.; Lane, P.N.J.; Grayson, R.B. Estimating catchment-scale impacts of wildfire on sediment and nutrient loads using the e2 catchment modelling framework. Environ. Model. Softw. 2011, 26, 913–928. [Google Scholar] [CrossRef]
- Lane, P.N.J.; Sheridan, G.J.; Noske, P.J.; Sherwin, C.B. Phosphorus and nitrogen exports from se Australian forests following wildfire. J. Hydrol. 2008, 361, 186–198. [Google Scholar] [CrossRef]
- Sheridan, G.; Lane, P.; Noske, P.; Feikema, P.; Sherwin, C.; Grayson, R. Impact of the 2003 Alpine Bushfires on Streamflow: Estimated Changes in Stream Exports of Sediment, Phosphorus and Nitrogen Following the 2003 Bushfires in Eastern Victoria; Murray-Darling Basin Commission: Canberra, Australia, 2007.
- Hopmans, P.; Bren, L.J. Long-term changes in water quality and solute exports in headwater streams of intensively managed radiata pine and natural eucalypt forest catchments in South-Eastern Australia. For. Ecol. Manag. 2007, 253, 244–261. [Google Scholar] [CrossRef]
- Porporato, A.; D’Odorico, P.; Laio, F.; Rodriguez-Iturbe, I. Hydrologic controls on soil carbon and nitrogen cycles. I. Modeling scheme. Adv. Water Resour. 2003, 26, 45–58. [Google Scholar] [CrossRef]
- Hart, S.C.; DeLuca, T.H.; Newman, G.S.; MacKenzie, M.D.; Boyle, S.I. Post-fire vegetative dynamics as drivers of microbial community structure and function in forest soils. For. Ecol. Manag. 2005, 220, 166–184. [Google Scholar] [CrossRef]
| Study | Description | Pre-Wildfire Data/Post-Wildfire Data | Method 1 | Limitation |
|---|---|---|---|---|
| Lane, Sheridan and Noske [7] | Severe wildfire burnt over 1 million ha of forested land in Australia | 10 years/2 years post-wildfire | ANCOVA (with control) 2 | Long term impact were hard to compare due to the high variations in climate and the effect of logging. |
| Bladon, Silins, Wagner, Stone, Emelko, Mendoza, Devito and Boon [19] | The effect of wildfire on post-wildfire nitrogen concentration with 3 burnt catchments and 2 unburnt catchments | NA/3 years | ANCOVA (with control) | Lack of pre-wildfire WQ data and there is a shortage in assessing the initial wildfire effect on WQ and recovery of the catchments. |
| Mast and Clow D.W [28] | Post-wildfire WQ change after a wildfire in Glacier National Park, USA | 5 years/4 years | Compare average concentration | No control (unburnt) catchment studed. Result effected by snow melt event (first flow released during long period of time). |
| Townsend and Douglas [12] | The effect of a wildfire on stream WQ and catchment water yield in a tropical savanna (North Australia) excluded from wildfire for 10 years | 3 years/10th year post-wildfire | ANCOVA (No control) | Only the WQ 10 years post-wildfire was described, no earlier observation was compared with pre-wildfire data. |
| Malmon, et al. [29] | Sediment change post-wildfire in New Mexico | 2 years/3 years | ANCOVA (No control) | Only 2 years pre-wildfire data was used in the study. |
| Kunze and Stednick [30] | Sediment change post-wildfire in 2 burnt catchments in Colorada, USA. | NA/3 years | ANCOVA (with control) | No available pre-wildfire data. First year post-wildfire, WQ and quantity data were collected only after events. |
| Oliver, Reuter, Heyvaert and Dahlgren [20] | Analyisis the WQ change post a severe wildfire in lake Tahoe basin, USA | 10 years/2 years | ANCOVA | Pre-wildfire sample collected monthly and during events, no information on daily or annual discharge. |
| Hauer and Spencer [31] | Phosphorus and nitrogen concentration change after wildfire in Columbia | NA/5 years | Compare average concentration | Lack of pre-wildfire data Limited data were collected at some sites due to funding limit. |
| Catchment | Area (km2) | % Burnt | % Grass Land | % Forest | % Urban | Annual Rainfall (mm) | Mean Flow (ML/day) |
|---|---|---|---|---|---|---|---|
| C1 | 719 | 0 | 9 | 90 | 0 | 932 | 3,445,519 |
| C2 | 72 | 0 | 0 | 85 | 14 | 1263 | 341,462 |
| C3 | 1447 | 0 | 25 | 73 | 1 | 886 | 2,968,759 |
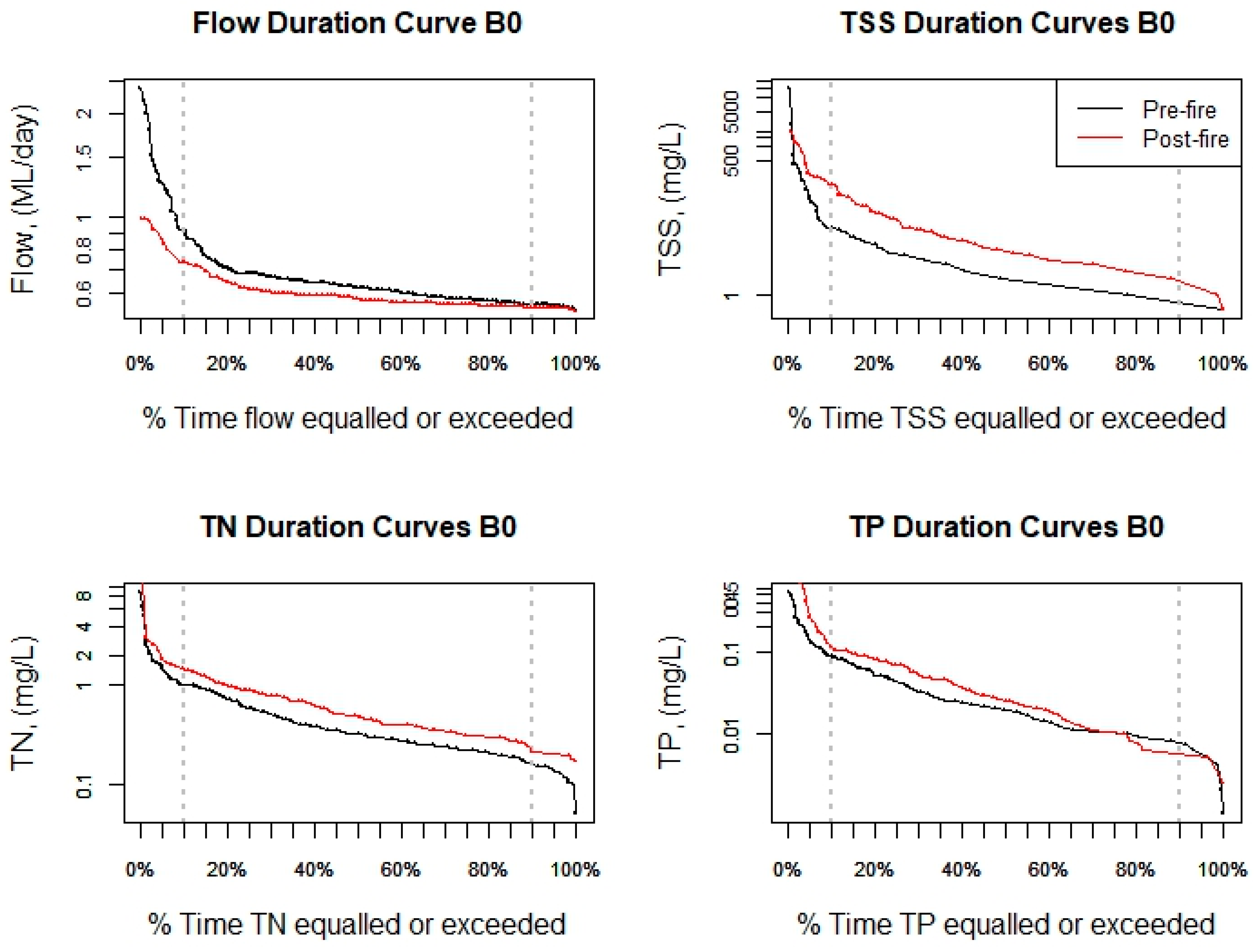
| B0 | 436 | 57 | 12 | 86 | 1 | 857 | 576,706 |
| B1 | 104 | 100 | 2 | 97 | 0 | 824 | 137,954 |
| B2 | 88 | 83 | 4 | 95 | 0 | 1182 | 420,889 |
| B3 | 56 | 79 | 29 | 69 | 1 | 694 | 240,910 |
| Flow (ML/day) | TSS (mg/L) | TN (mg/L) | TP (mg/L) | Available Data | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Catchment | Pre/Post-wildfire | Min | Max | Median | Min | Max | Median | Min | Max | Median | Min | Max | Median | |
| C1 | pre | 0.88 | 65,000 | 181.51 | 0.5 | 3829 | 1.00 | 0.03 | 7.52 | 0.20 | 0.001 | 2.42 | 0.01 | 244 |
| post | 0.23 | 16,673.89 | 908.45 | 0.5 | 532 | 4.00 | 0.005 | 2.25 | 0.31 | 0.003 | 0.34 | 0.02 | 536 * | |
| C2 | pre | 5.66 | 6238.66 | 31.51 | 0.5 | 1316 | 3.00 | 0.2 | 15.8 | 1.13 | 0.001 | 1.5 | 0.16 | 220 |
| post | 1.736 | 2202.96 | 87.48 | 0.5 | 536 | 6.00 | 0.005 | 2.08 | 0.36 | 0.002 | 0.39 | 0.01 | 284 | |
| C3 | pre | 11.11 | 101,778.8 | 191.10 | 0.5 | 2807 | 1.00 | 0.06 | 7.84 | 0.18 | 0.001 | 0.92 | 0.01 | 213 |
| post | 3.28 | 8879.39 | 646.18 | 0.5 | 2149 | 5.00 | 0.05 | 13.2 | 0.30 | 0.002 | 1.92 | 0.01 | 331 | |
| B0 | pre | 0.54 | 2.39 | 0.62 | 0.5 | 15110 | 1.00 | 0.05 | 6.3 | 0.32 | 0.001 | 0.53 | 0.02 | 288 |
| post | 0.53 | 0.99 | 0.56 | 0.5 | 1998 | 7.00 | 0.17 | 11.8 | 0.42 | 0.003 | 2.3 | 0.02 | 126 | |
| B1 | pre | 1.57 | 6828.59 | 6.77 | 0.5 | 97 | 1.00 | 0.005 | 9.4 | 0.10 | 0.001 | 0.26 | 0.004 | 218 |
| post | 0.34 | 1126.86 | 5.48 | 0.5 | 3950 | 1.00 | 0.05 | 21.2 | 0.20 | 0.003 | 2.45 | 0.005 | 69 * | |
| B2 | pre | 3.43 | 7491.3 | 21.80 | 1 | 149 | 1.00 | 0.03 | 0.79 | 0.16 | 0.001 | 0.17 | 0.009 | 157 |
| post | 1.54 | 4067 | 55.77 | 0.5 | 35 | 1.25 | 0.005 | 0.95 | 0.17 | 0.001 | 0.06 | 0.008 | 381 | |
| B3 | pre | 0 | 14,299.22 | 9.565 | 0.5 | 803 | 4.0 | 0.05 | 6.8 | 0.42 | 0.001 | 0.73 | 0.01 | 233 |
| post | 0 | 1184.46 | 32.29 | 0.5 | 496 | 7.0 | 0.005 | 2.65 | 0.44 | 0.003 | 0.5 | 0.02 | 351 | |
| Catchment | Pre-Wildfire | 1–5 years Post-Wildfire | 6–10 years Post-Wildfire |
|---|---|---|---|
| C1 | 912.79 | 796.50 | 1111.44 |
| C2 | 1214.06 | 1080.18 | 1556.01 |
| C3 | 851.94 | 757.99 | 1091.89 |
| B0 | 903.51 | 697.83 | 914.69 |
| B1 | 869.25 | 671.38 | 880.01 |
| B2 | 1246.38 | 962.65 | 1261.80 |
| B3 | 670.72 | 592.18 | 849.14 |
| TSS | TN | TP | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Catchment | Mean SSPE | ME | RMSE | Lin’s CCC | Mean SSPE | ME | RMSE | Lin’s CCC | Mean SSPE | ME | RMSE | Lin’s CCC |
| C1 | 0.96 | −0.03 | 0.94 | 0.79 | 0.96 | −0.03 | 0.43 | 0.85 | 0.96 | −0.04 | 0.61 | 0.83 |
| C2 | 1.02 | 0.00 | 1.12 | 0.76 | 0.97 | 0.01 | 0.59 | 0.81 | 1.03 | 0.00 | 0.87 | 0.84 |
| C3 | 0.99 | −0.03 | 0.97 | 0.76 | 1.03 | −0.02 | 0.55 | 0.78 | 0.99 | −0.01 | 0.69 | 0.73 |
| B0 | 0.98 | −0.01 | 1.04 | 0.81 | 0.96 | −0.01 | 0.51 | 0.73 | 0.90 | −0.01 | 0.69 | 0.78 |
| B1 | 0.98 | −0.01 | 0.89 | 0.74 | 0.97 | −0.01 | 0.87 | 0.71 | 0.97 | 0.00 | 0.84 | 0.70 |
| B2 | 1.00 | 0.01 | 0.73 | 0.65 | 1.05 | −0.01 | 0.48 | 0.74 | 0.98 | 0.00 | 0.54 | 0.70 |
| B3 | 1.00 | −0.03 | 0.93 | 0.77 | 0.96 | −0.03 | 0.43 | 0.77 | 0.94 | −0.01 | 0.53 | 0.81 |
| TSS | Log Flow | Event Direction | Event Distance | DF50 | DF75 | DF90 | DF95 | DF99 | Wildfire |
|---|---|---|---|---|---|---|---|---|---|
| C1 | |||||||||
| C2 | |||||||||
| C3 | |||||||||
| B0 | |||||||||
| B1 | |||||||||
| B2 | |||||||||
| B3 |
| TN | Log Flow | Event Direction | Event Distance | DF50 | DF75 | DF90 | DF95 | DF99 | Wildfire |
|---|---|---|---|---|---|---|---|---|---|
| C1 | |||||||||
| C2 | |||||||||
| C3 | |||||||||
| B0 | |||||||||
| B1 | |||||||||
| B2 | |||||||||
| B3 |
| TP | Log Flow | Event Direction | Event Distance | DF50 | DF75 | DF90 | DF95 | DF99 | Wildfire |
|---|---|---|---|---|---|---|---|---|---|
| C1 | |||||||||
| C2 | |||||||||
| C3 | |||||||||
| B0 | |||||||||
| B1 | |||||||||
| B2 | |||||||||
| B3 |
| Catchment | TSS | TN | TP |
|---|---|---|---|
| C1 | X | X | X |
| C2 | X | 0.37 | 0.1 |
| C3 | 1.46 | X | X |
| B0 | 3.32 | 1.35 | X |
| B1 | 1.84 | 2.88 | 2.45 |
| B2 | X | 0.7 | 1.13 |
| B3 | 1.32 | X | X |
| Average for control *,1 | 1.23 | 1 | 1 |
| Average for burned * | 1.87 | 1.48 | 1.40 |
| Net change (burnt-control) | 0.64 | 0.48 | 0.40 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, M.; Bishop, T.F.A.; Van Ogtrop, F.F. Assessment of the Decadal Impact of Wildfire on Water Quality in Forested Catchments. Water 2019, 11, 533. https://doi.org/10.3390/w11030533
Yu M, Bishop TFA, Van Ogtrop FF. Assessment of the Decadal Impact of Wildfire on Water Quality in Forested Catchments. Water. 2019; 11(3):533. https://doi.org/10.3390/w11030533
Chicago/Turabian StyleYu, Mengran, Thomas F.A. Bishop, and Floris F. Van Ogtrop. 2019. "Assessment of the Decadal Impact of Wildfire on Water Quality in Forested Catchments" Water 11, no. 3: 533. https://doi.org/10.3390/w11030533
APA StyleYu, M., Bishop, T. F. A., & Van Ogtrop, F. F. (2019). Assessment of the Decadal Impact of Wildfire on Water Quality in Forested Catchments. Water, 11(3), 533. https://doi.org/10.3390/w11030533





