1. Introduction
In hydrosystem design, performance evaluation, and simulation, the problems often involve multiple random variables that are correlated with a mixture of non-normal marginal distributions. Under this condition, it is generally difficult, if not impossible, to establish an analytical joint probability distribution for these variables. In comparison with univariate distributions, there are relatively few analytical multivariate distribution functions under special combinations of parametric marginal distributions, and most of them are of the same type, which can be found in [
1,
2]. Examples of using analytical multivariate distributions in hydrology are bivariate Gamma distribution [
3] and bivariate generalized extreme distribution [
4]. Their use is somewhat limited to many practical problems because of different marginal distributions.
Due to the difficulty in establishing a truly multivariate joint distribution model for problems involving mixtures of several correlated, non-normal variables, approximated approaches, such as copula or normal transform, are often used by preserving marginal distributions or moments, including the correlation features among the variables. However, one should realize that, unlike using a true multivariate joint distribution function, preservation of the marginal distributions and dependence structure represents the retention of partial information of the concerned multivariate random variables in the analysis [
5].
The concept of copula is one type of approximated multivariate approaches that has recently received tremendous attention and applications by researchers in various disciplines, including in hydrology [
6]. Some examples of applying copula in multivariate hydrologic modeling can be found in analyzing floods [
7,
8], droughts [
9,
10,
11,
12], dam safety [
13], and extreme rainfalls [
14,
15]. Most of the copula-based applications deal with bivariate problems and some trivariate problems under some restrictive conditions on correlation structures [
8]. Applications of copula to higher dimension multivariate problems are rare primarily because there are only a few copula families that are rather restrictive in describing the dependence structure. Recently, the introduction of vine copulas has shown the advantage of overcoming the limitation of currently used copulas in multivariate analysis [
16,
17,
18,
19]. A copula-based approach is parametric by nature in that analytical marginal distribution models for the involved variables are specified.
Alternatively, another viable scheme in treating multivariate problems involving correlated non-normal random variables is to apply a NORTA (normal-to-anything) algorithm [
20]. By a NORTA algorithm, normal transformation of an individual non-normal variable is made by preserving its marginal probability content in the normal variable domain as
with
, respectively, being the cumulative distribution functions (CDFs) of the standard normal variable
Z and the original variable
X. In addition, a relationship must be established to allow the determination of an equivalent correlation coefficient,
, of a pair of normal transformed variables,
, from the correlation coefficient,
, of the corresponding random variables,
, in the original space. Once the correlation matrix of standard normal variables
Z’s,
, is obtained from that of the non-normal variables
X’s,
, appropriate orthogonal transformation can be implemented to transform the original correlated variables into uncorrelated standard normal space for analysis.
The determination of
from
is made through the Nataf transform [
21], which requires solving an implicit non-linear equation in the form of a double integration involving marginal distributions of a pair of random variables,
, under consideration:
where
, and
= bivariate standard normal joint probability density function (PDF). Lebrun and Dutfoy [
22] provide an insightful analysis of Nataf transform and uncover that it is a special modeling of dependence structure using Gaussian copula. To facilitate practical engineering applications, a set of empirical equations for 10 commonly used distribution functions has been established to relate
to
and their distribution properties [
23]. Such empirical relations were applied to reliability analysis of engineering systems [
5,
24]. Later, computationally more efficient methods based on root finding and linear search [
25], the false position method [
26], and the artificial neural network method [
27] were proposed to solve Equation (1) for
from the known
and marginal PDFs of
.
The above mentioned schemes (i.e., copula, NORTA, and Nataf transform) all require the stipulation of marginal PDFs. The stipulation of a distribution function implies knowing the complete statistical information of the random variable, including its moments of all orders. This ideal situation is attainable only when one has a large amount of data, which generally is not the case in practice. Therefore, to relax the information requirement without having to specify the distribution functions, third-order polynomial normal transform (TPNT) can be used. By TPNT, each individual non-normal random variable is related to a 3rd-order polynomial function of the corresponding standard normal variable [
28]. The polynomial coefficients are determined by matching the statistical moments or quantiles of the individual random variables. The multivariate version of TPNT was first proposed by Vale and Maurelli [
29] to simultaneously consider statistical moments and correlation coefficients. A multivariate TPNT procedure has been applied to different fields including, but not limited to, Monte Carlo simulation for generating multivariate random variates [
24,
30,
31,
32,
33], wind power modeling [
34], load computation in power network planning [
35], and reliability analysis [
36,
37].
It should be noted that the great majority of multivariate TPNT applications are done under the assumption of known marginal statistical moments (i.e., product-moments and L-moments) and correlation coefficients. However, in real-life hydrologic applications, the amount of available data generally is not sufficiently large to reliably ascertain the true marginal probability distribution functions, statistical moments, and correlation coefficients. Therefore, the sample statistical moments and correlation coefficients used could be subject to sampling errors. In this study, a procedure is proposed to (1) optimally estimate multivariate TPNT coefficients by explicitly incorporating sampling errors associated with the sample moments and correlation coefficients, and (2) comply with a one-to-one monotonicity increasing relation between quantiles of the original and normal transformed variables. The procedure is illustrated by analyzing annual maximum rainfall data series involving seven different durations to establish at-site rainfall intensity–duration–frequency (IDF) and depth–duration–frequency (DDF) relationships.
2. Methods
2.1. Third-Order Polynomial Normal Transform (TPNT)
2.1.1. Univariate TPNT
By TPNT, a univariate non-normal random variable,
, is approximated by the standard normal variable,
, in the form of a 3rd-order polynomial functional relation as [
28]
where
denotes the 3rd-order polynomial transform with
a0,
a1,
a2, and
a3 being the transformation coefficients. The TPNT coefficients can be determined by several methods of varying mathematical complexity. By preserving the first four product-moments, the TPNT coefficients are related to the first four product moments of the standardized variable,
, as [
28]
in which
= skew coefficient;
= kurtosis of the original random variable
X. Alternatively, the TPNT coefficients in Equation (2) can also be related to the first four L-moments as [
38]
in which
= the
mth order L-moment [
39] of the original non-normal random variable,
X. Other than the above two moment-matching methods, TPNT coefficients can also be determined by the quantile-based least square method and the Fisher–Cornish asymptotic expansion (FC) method [
40]. Chen and Tung [
41] investigated the performance of different methods in determining the TPNT coefficients with regard to their accuracy and robustness in capturing the probabilistic features of the random variable
X under the condition that the population distribution is known. It was found that, among the various methods for estimating TPNT coefficients, the L-moment based method is computational simplistic and can yield a satisfactory performance under a wide range of distribution conditions. The product-moment method can also yield a satisfactory normal transformation provided that accurate estimations of skew coefficient and kurtosis in Equations (3)–(6) can be made. However, when the statistical moments are to be estimated from finite data, the sample L-moments have been proven to be more stable and robust than those of product-moments [
42], especially when the sample size is not large.
By referring to Equations (3)–(6), one also realizes that determining TPNT coefficients based on the product-moments requires solving a system of non-linear equations. It is expected that solving Equations (3)–(6) would be more difficult than solving L-moments based on Equations (7)–(10), which is linear. Sometimes, the solution to the system of non-linear equation may not be attainable. According to Equations (7)–(10), TPNT coefficients can be easily obtained in terms of L-moments as
In the transformation process, it is necessary to preserve probability content in both original space and standard normal space, i.e.,
. This implies that quantiles of the two variables should satisfy the following relationship:
where
=
pth-order quantiles of random variable
X and standard normal random variable,
Z, respectively, that is,
and
. Furthermore, inherently embedded in Equation (15) is a requirement of one-to-one monotonically increasing relations between
. This, then, requires that TPNT coefficients must comply with the following conditions:
It should be noted that the TPNT coefficients obtained from solving Equations (3)–(6), Equations (7)–(10), or other methods mentioned above do not guarantee the compliance of the monotonicity condition stipulated in Equation (16). This is especially a major concern when sample statistics are used in determining TPNT coefficients.
2.1.2. Multivariate TPNT
The TPNT coefficients can be determined by preserving the statistical moments of individual random variables. Specifically, L-moments are used herein to determine the multivariate TPNT coefficients due to simple, linear functional relationships between the TPNT coefficients and the L-moments as shown in Equations (11)–(14). Furthermore, sample L-moments have several desirable sampling properties over the product-moments as proven by Hosking [
42]. In the context of fitting the first four L-moments of a total of
N correlated variables, Equations (7)–(10) can be re-written as
in which
= the
mth order L-moment of the
jth random variable
Xj for
j = 1, 2, …,
N.
In addition to preserving marginal statistical moments of involved variables, multivariate TPNT must also simultaneously preserve the statistical dependence between random variables in the transformation. The correlation coefficient of any two correlated random variables,
, is imbedded in their 2nd-order cross-product moment of which Vale and Maurelli [
29] had shown the explicit expressions in terms of TPNT coefficients as
in which
= correlation coefficient of random variables
and its equivalent
in normal space;
= mean and standard deviation of random variable
, respectively. The correlation coefficient in the original scale,
, is related to its counterpart in the normal space,
, in a 3rd-order polynomial relationship through TPNT coefficients.
Upon the determination of TPNT coefficients for the two concerned random variables, the correlation coefficient in the normal space,
, corresponding to that in the original space,
, can be obtained by finding the real root of Equation (21). The mathematical relations between the two correlation coefficients are [
20]
Equation (21) is used repeatedly to solve for for all pairs of correlated random variables to establish the correlation matrix in multivariate normal space.
2.2. Optimization Framework for Determining Multivariate TPNT Coefficients
2.2.1. Objective Function
To determine the multivariate TPNT coefficients that best preserve the known values of L-moments, the least-square criterion is used in the study by which the objective function can be expressed as
where
= a decision variable defining the deviation between the
mth-order TPNT-based L-moments computed by the left-hand side of Equations (17)–(20) and the known values,
, of the
jth random variable,
Xj. Of course, other forms of objective function, such as minimizing the sum of absolute deviations, can be used.
2.2.2. Constraints
Several constraints are essential to make sure that multivariate TPNT coefficients obtained are able to preserve the known statistical features and mathematical relationships of concerned random variables.
(a) Preservation of L-moments for the individual variable Xj:
The deviation
in the objective function defining the degree of preserving the known values of the first-four L-moments of individual variable
Xj can be written, according to Equations (17)–(20), as
Note that the value of is unrestricted-in-sign, meaning that its value can be negative, zero, and positive, depending on the relative magnitudes of TPNT-based L-moments and those of the known values.
In reality, statistical properties of a random variable are estimated from a finite number of sample data. Consequently, sample L-moments of random variables,
Xj, are subject to uncertainty. In practice, two approaches are used to estimate sample L-moments: plotting position-based estimators and unbiased estimators. This study adopts the latter by which the first four unbiased estimators of L-moments,
, can be computed respectively as [
42]
in which
= sample estimator of the
mth-order L-moment,
;
= the
ith ranked sample (ascending order) in a data of size
n.
Suppose that the sampling distributions of sample L-moments are derived or approximated. Proper bounds can then be incorporated into Equations (24)–(27) for determining the suitable and probabilistically plausible TPNT coefficients for all
N random variables
X1,
X2, …,
XN. Assuming that the lower and upper bounds of the L-moments can be determined from their corresponding sampling distributions, constraint Equations (24)–(27) then can be modified as
for
j = 1, 2, …,
N. In Equations (32)–(35),
are, respectively, the upper and lower bounds containing the unknown population
mth-order L-moment of random variable
Xj,
. The derivation of bounds for unknown population L-moments is described in
Section 2.3.1.
(b) Preservation of the monotonic probability–quantile relationship for individual variable
Xj:
(c) Preservation of the correlation between all pairs of different variables, Xj and Xk:
Based on Equation (21), any pair of two correlated random variables
must satisfy the following equation.
where
= cross-product moment of variables,
Xj and
Xk, defined in Equation (21), which are functions of the corresponding TPNT coefficients
and
;
and
= correlation coefficients of random variables,
, and their normal equivalents,
, respectively;
,
= mean and standard deviation of random variable
, respectively.
Similarly, constraint Equation (37) on correlation coefficients can be modified as
in which
= lower and upper bounds, respectively, of the unknown population correlation coefficient,
, between the random variables
Xj and
Xk (see
Section 2.3.2);
= equivalent correlation coefficient of the random variables in the standard normal domain;
= TPNT-based estimation of mean and standard deviation of random variables
Xj which can be computed according to Equations (3) and (4) as
Equation (38) can alternatively be expressed as
In summary, by considering sampling errors of sample L-moments and correlation coefficients, the optimization model to determine the most plausible TPNT coefficients for establishing multivariate relationships can be summarized as follows:
The objective function is expressed in Equation (23) or its variations, which is subject to the following constraints:
Equations (32)–(35) for preserving plausible L-moments (8 × N constraints);
Equation (36) for complying with a probability–quantile monotonic relationship (2 × N constraints);
Equations (41) and (42) for preserving plausible correlation coefficient (N × (N − 1) constraints); and
unrestrictive-in-sign of polynomial coefficients and deviations .
2.3. Determination of Bounds for L-Moments and Correlation Coefficients
2.3.1. Bounds for L-Moments
To determine the bounds for L-moments, the sampling distributions corresponding to the sample L-moments are needed. For independent random samples of size
n from a distribution function
having the
mth-order population L-moment
, Hosking [
39] showed that the statistic
, with
being the sample L-moment of order
m, is unbiased, having a sampling distribution asymptotically converge to the normal distribution with the mean zero and variance
. Therefore, the variance of the
mth-order sample L-moment,
, has the variance of
. For the first four orders of sample L-moment, the value of
can be computed by
in which
. To estimate the values of
based on the ranked sample observations, the double integration stated in Equations (43)–(46) can be carried out numerically as
in which
= the
ith ranked sample in ascending order, i.e.,
;
= estimated cumulative probability for the
ith ranked sample, i.e.,
, by using the well-known Weibull plotting position formula,
. Makkonen [
43] has shown that the Weibull plotting position formula [
44] provides the best estimate for the underlying non-exceedance probability. The superiority of the Weibull formula gets more pronounced with a decreasing sample size. By adopting the normality distribution assumption, the
α-confidence interval for the unknown population
can be obtained as
in which
, a standard normal quantile with an exceedance probability of
, with
being the inverse standard normal CDF.
2.3.2. Bounds for Correlation Coefficients
To quantify the lower and upper bounds of a correlation coefficient, Fisher transform is often used by which the sampling distribution of the inverse hyperbolic tangent function of sample correlation approximately follows a normal distribution as [
45,
46]
in which
= sample and population correlation coefficients, respectively;
n = number of sample pairs. With a specified confidence level
, the corresponding lower and upper bounds for the unknown population coefficient
can be obtained as
where the hyperbolic tangent function is defined as
.
2.4. Solution Algorithm
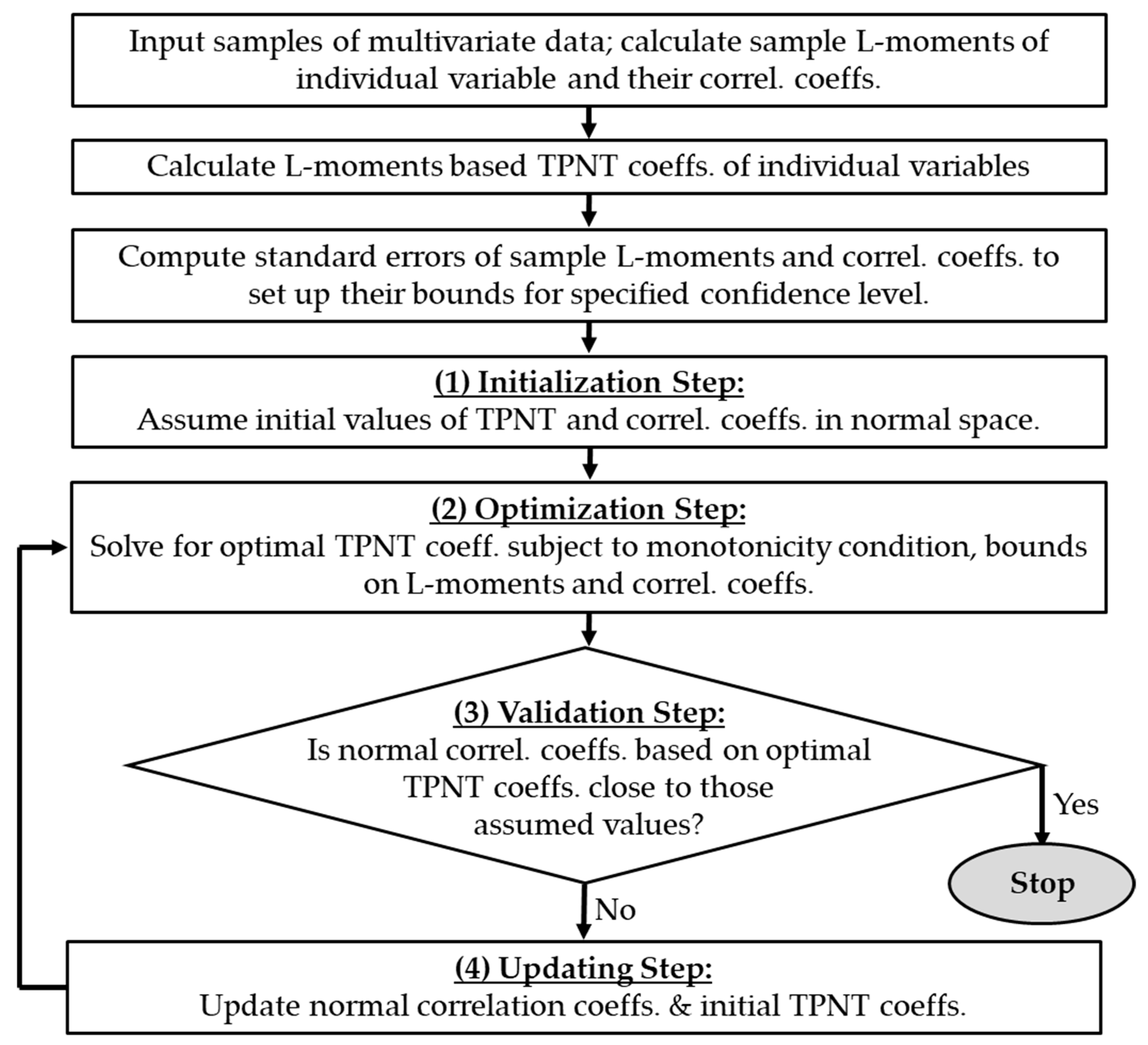
A recursive procedure is proposed to solve the above optimization models for determining multivariate TPNT coefficients. The procedure consists of four steps of initialization, optimization, validation, and updating. Solution algorithm for determining multivariate TPNT coefficients considering sampling errors of L-moments and correlation coefficients is detailed below and outlined in
Figure 1.
Step (1): Initialization—Since the problem involves a nonlinear optimization model, an initial solution would be needed. One straightforward and sound initial solutions for the TPNT coefficients, , are those provided by Equations (11)–(14) for all variables j = 1, 2, …, N. The initial TPNT coefficients obtained this way will automatically satisfy the constraint Equations (24)–(27). However, they do not necessarily comply with the monotonicity constraint Equation (36). As for the initial normal correlation coefficients, rather than arbitrarily choosing a set of initial correlation coefficients, let in which is the sample correlation coefficient between random variables . Alternatively, obtain a feasible set of initial by solving the 3rd-order polynomial function of in Equation (21) according to the initially assumed TPNT coefficients, .
Step (2): Optimization—Based on the initially adopted TPNT coefficients, , and the normal transformed correlation coefficients , solve the optimization model with objective function Equation (23) and constraint Equations (32)–(35), (36), and (41)–(42) for the optimal TPNT coefficients for random variable
Step (3): Validation—From the optimal feasible TPNT coefficients
for
j = 1, 2, …,
N obtained from Step (2), determine the equivalent normal variates corresponding to the sample data by solving the 3rd-order polynomial function:
where
= unknown normal variate corresponding to the
ith observation of the
jth random variable
under the optimal set of TNPT coefficients
. From the normal-transformed data series of two different variables,
and
, the corresponding correlation coefficient,
, in the normal space is calculated.
Step (4): Updating—Compare the discrepancies between the initialized and validated for all different pairs of concerned random variables. If the discrepancy in any pair of durations is judged to be significant, update the initial normal correlation as and TPNT coefficients , and the process from Steps (2)–(4) is repeated. Otherwise, the optimal solutions are obtained and the iteration stops.
With regard to the optimization step presented in Step (2), the sequential quadratic programming (SQP) algorithm is implemented [
47]. The SQP tackles a nonlinear optimization problem by successively finding the approximated optimum solution to the quadratic programming (QP) representation of the original problem. The approximated solution is improved iteratively by solving the QP problem. Boggs and Tolle [
48] elaborated some useful properties of the SQP algorithm. The subroutine “sqp.m” in Matlab is used in this study to solve the optimization model.
3. Numerical Example
In this section, at-site rainfall intensity–duration–frequency (IDF) and depth–duration–frequency (DDF) relations are established to demonstrate the proposed multivariate TPNT method and examine its general performance. Rainfall IDF relations are widely used in the planning, design, and management of hydrosystem infrastructures, such as stormwater sewer systems and detention basins [
49,
50]. Such relations at a given location involves at-site frequency analysis of annual maximum rainfall intensity (or depth) data of several selected durations. The conventional approach in rainfall frequency analysis chooses a proper parametric probability distribution model to individually fit the observed annual maximum rainfall data of different durations. The choice of a distribution model for the rainfall intensity–frequency relations is largely statistical without much physical justification [
51].
By the conventional approach, resulting rainfall intensity–frequency curves of different durations could sometimes intersect within the probability range of practical application. The crossover phenomenon often occurs when data record length is relatively short. According to the physical reality, rainfall intensity–frequency curves of different durations should not crossover or intersect. Porras and Porras [
52] attributed the occurrence of crossover of rainfall IDF curves to short record data of questionable representation in which a significant amount of sampling errors existed in the estimated rainfall quantiles by frequency analysis. One other plausible reason for the possible crossover of IDF curves is that frequency analysis of rainfall data is performed separately for each duration without considering the inter-correlations that are intrinsically embedded in rainfall data of different durations. Haktanir [
53] earlier pointed out that rainfall frequency analysis of different durations in the process of establishing IDF relationships should not be performed independently of each other, but did not propose a mechanism to handle the correlation directly. Recently, Gräler et al. [
54] applied D-vine copula, along with the generalized extreme value distributions, to derive rainfall IDF relationships based on rainfalls of five durations. You and Tung [
55], under the TPNT framework, developed a constrained least square model to simultaneously considering rainfall data of seven durations for establishing at-site rainfall IDF relations. However, their model does not explicitly take into account the correlation among rainfall data of different durations.
The multivariate TPNT-based model presented above was applied to establish at-site rainfall IDF relations using annual maximum hourly rainfall data of various durations at a raingauge in Zhongli City of Taoyuan County, Taiwan. Annual maximum rainfall intensity data cover the record period of 1988–2015, but the year 1992 was excluded from the analysis due to long periods of registers with technical issues. Hence, only 27-year data (
n = 27) with seven (
N = 7) durations (i.e., 1, 2, 6, 12, 24, 48, and 72 h) are used in this illustration (see data in
Table 1). The sample values of the mean, standard deviation, and first-four L-moments of rainfall data of different durations are tabulated in
Table 2. Furthermore, the standard error values corresponding to the first four sample L-moments, according to Equations (47)–(50), are listed in
Table 3. The sample correlation coefficients of all rainfall intensity pairs of different durations in the original and normal-transformed domains are shown in
Table 3 and
Table 4, respectively. Based on the information given in
Table 2 and
Table 4, one is able to define the lower and upper bounds for the L-moments and correlation coefficients according to the desired confidence level,
α, by Equations (51) and (53), respectively.
Table 5 lists the values of correlation coefficients in normal-transformed space,
, provided by the solution to constraint Equations (41) and (42) in the optimization model.
Under different constraint types and confidence levels for the L-moments and correlation coefficients, the corresponding optimal multivariate TPNT coefficients can vary. With the confidence level of
α = 90% for both L-moments and correlation coefficients,
Table 6a–d list the optimal TPNT coefficients under four different constraint types, including “LM” for L-moments by Equations (32)–(35), “Mono” for monotonicity by Equation (36), “Corr” for correlation by Equations (41) and (42), and “NC” for no-crossover by Equation (56). Once the optimal TPNT coefficients associated with each rainfall duration are obtained from solving the multivariate TPNT model, the rainfall IDF relations, according to Equation (15), can be established as
where
= estimated
t-h,
T-year rainfall intensity;
, , , and
= optimum TPNT coefficients corresponding to rainfall of duration
t (h);
zT is the standard normal quantile corresponding to return period
T-year having an annual exceedance probability of
.
4. Results and Discussions
By varying the value of
zT for different return periods in Equation (55), in conjunction with the optimal TPNT coefficients listed in
Table 6a–d, one can establish IDF curves as shown in
Figure 2 and
Figure 3. Part (a) of
Table 6 and
Figure 2,
Figure 3 and
Figure 4 (denoted by “LM”) shows the results from considering only the bounding constraints of L-moments, Equations (32)–(35). In fact, the optimal TPNT coefficients corresponding to each duration can be obtained separately from the exact solutions using sample L-moments in Equations (11)–(14). Note that the TPNT coefficients obtained from each rainfall duration at this stage do not necessarily comply with a one-to-one monotonic increasing relation of rainfall quantile and probability. This can be clearly seen in
Table 6a for 1 and 2 h rainfalls for which the two monotonicity constraints are violated (shown by *). Part (b) (denoted by “LM/Mono”) shows the results by considering both L-moment constraints, Equations (32)–(35), and the monotonicity constraints, Equation (36), for each rainfall duration. In this case, both results presented in Parts (a) and (b) in
Table 6 and
Figure 2,
Figure 3 and
Figure 4 can be obtained separately by treating rainfall data of different durations without considering their inter-correlations. Results in Part (c), denoted by “LM/Mono/Corr,” were obtained by incorporating correlation constraints of rainfall data with different durations, Equations (41) and (42), in determining the multivariate TPNT coefficients.
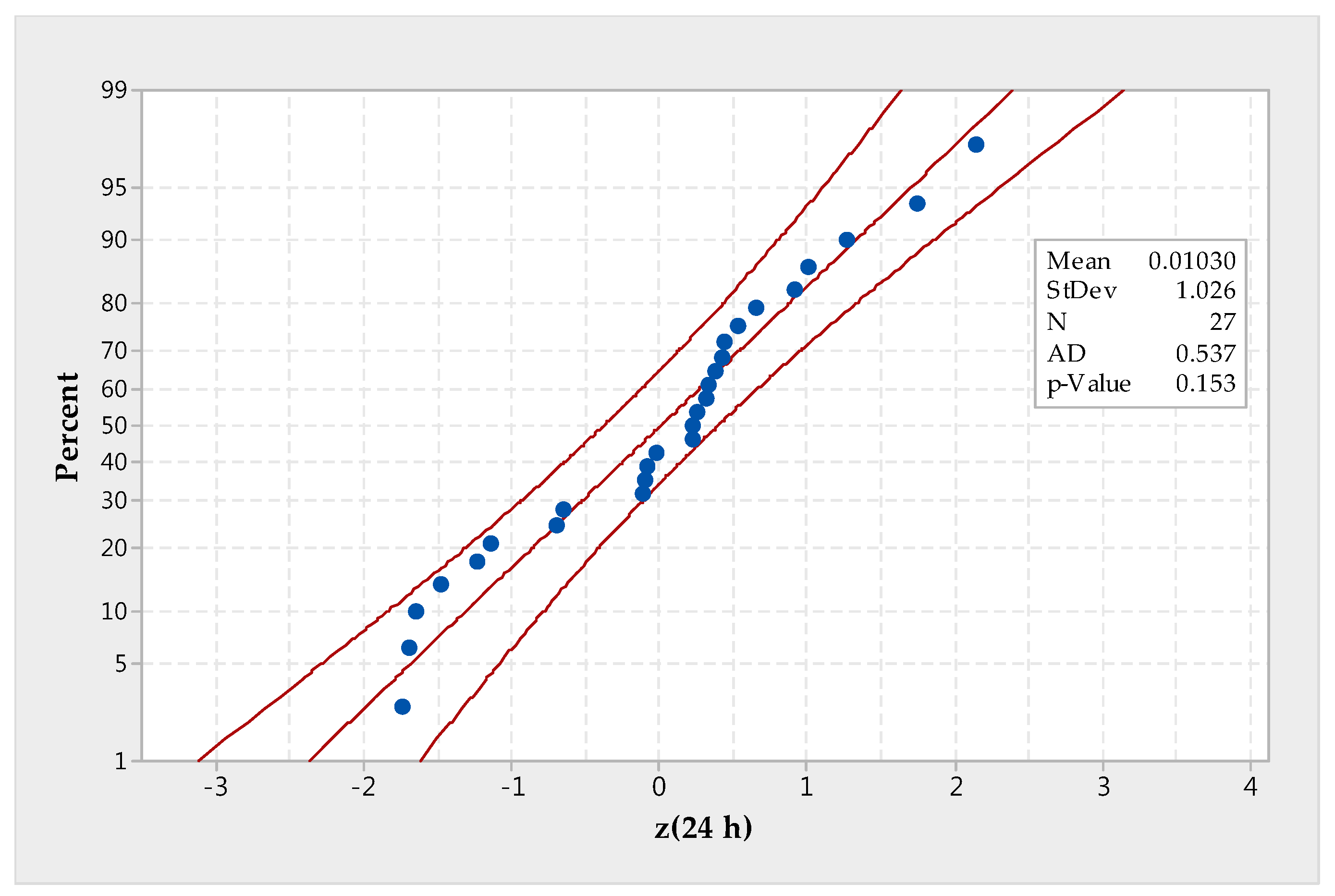
To show the degree of goodness-of-fit of normal transformed rainfall data by the proposed multivariate TPNT procedure, a normal probability plot of 24 h rainfall data (after normal transformation) with the fitted line and 95% confidence band are shown in
Figure 5 as an example. The goodness-of-fit test shown in
Figure 5 was achieved by the Anderson–Darling test [
56] by which the test statistic is 0.535 with a
p-value of 0.155.
Figure 5 represents the worst case among the seven durations considered. The range of
p-value varies from 0.155 (for 72 h) to 0.933 (for 2 h), which are higher than the generally adopted significance level of 0.05. This indicates that the normal transform by the proposed multivariate TPNT procedure is quite adequate.
Note that the solution obtained up to this stage does not necessarily comply with the physical reality that rainfall intensity (depth) of a given return period is a decreasing (an increasing) function of duration. In other words, rainfall intensity/depth–frequency curves of different durations should not intersect or crossover each other. However, in the process of establishing rainfall IDF/DDF relationships, one does not know in advance if any two resulting two curves would intersect before the statistical model is developed. Therefore, a special set of intersections avoidance constraints are imposed in establishing the IDF curves:
where
= upper limit of selected rainfall return period below which no crossover of IDF curves is permitted to occur;
= standard normal quantile obtainable from
. Hence, additional
N − 1 no-crossover (NC) constraints are included in the optimization model to solve for multivariate TPNT coefficients. Part (d) results (denoted by “LM/Mono/Corr/NC”) show the rainfall IDF relations considering the NC constraints.
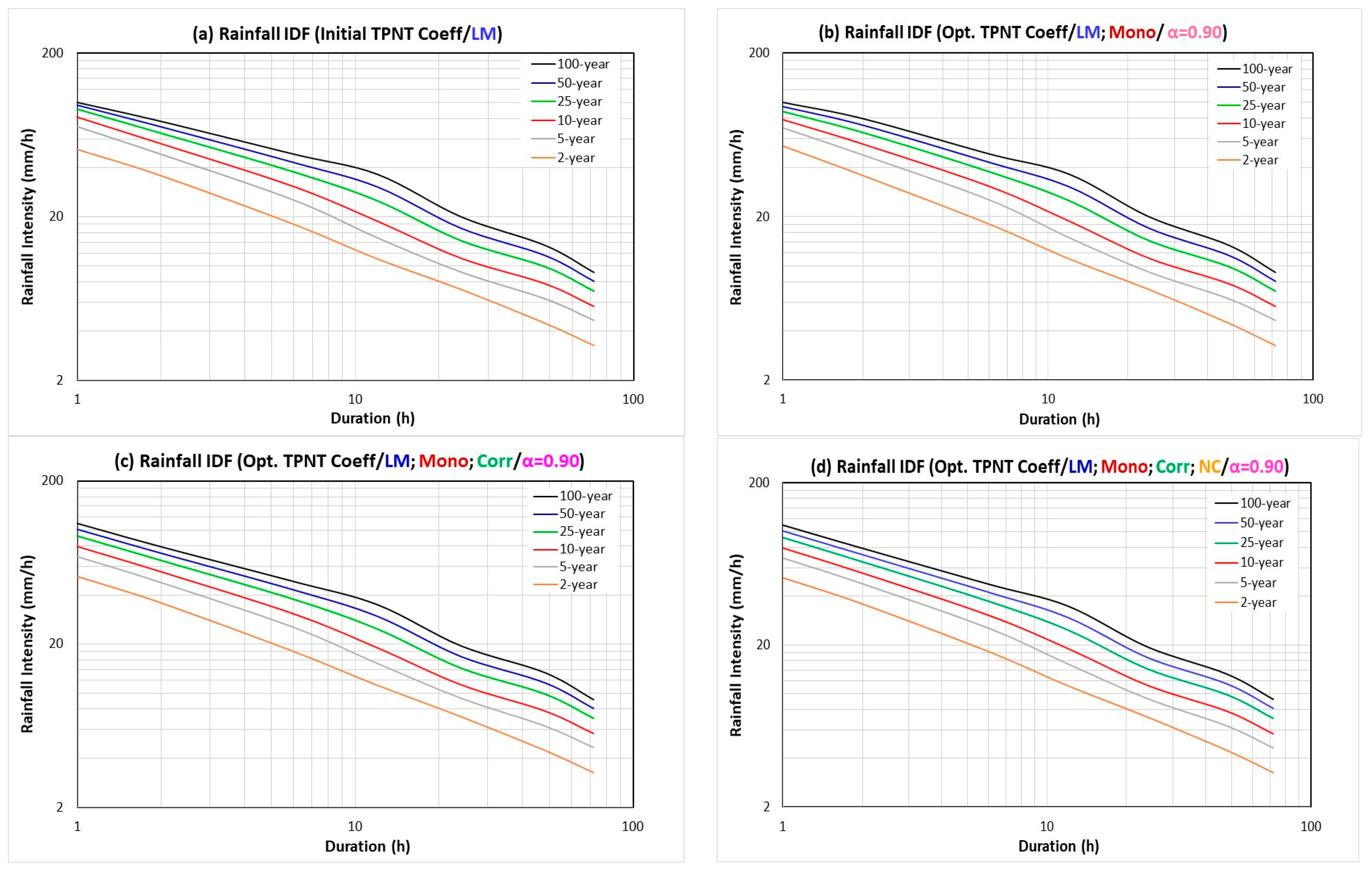
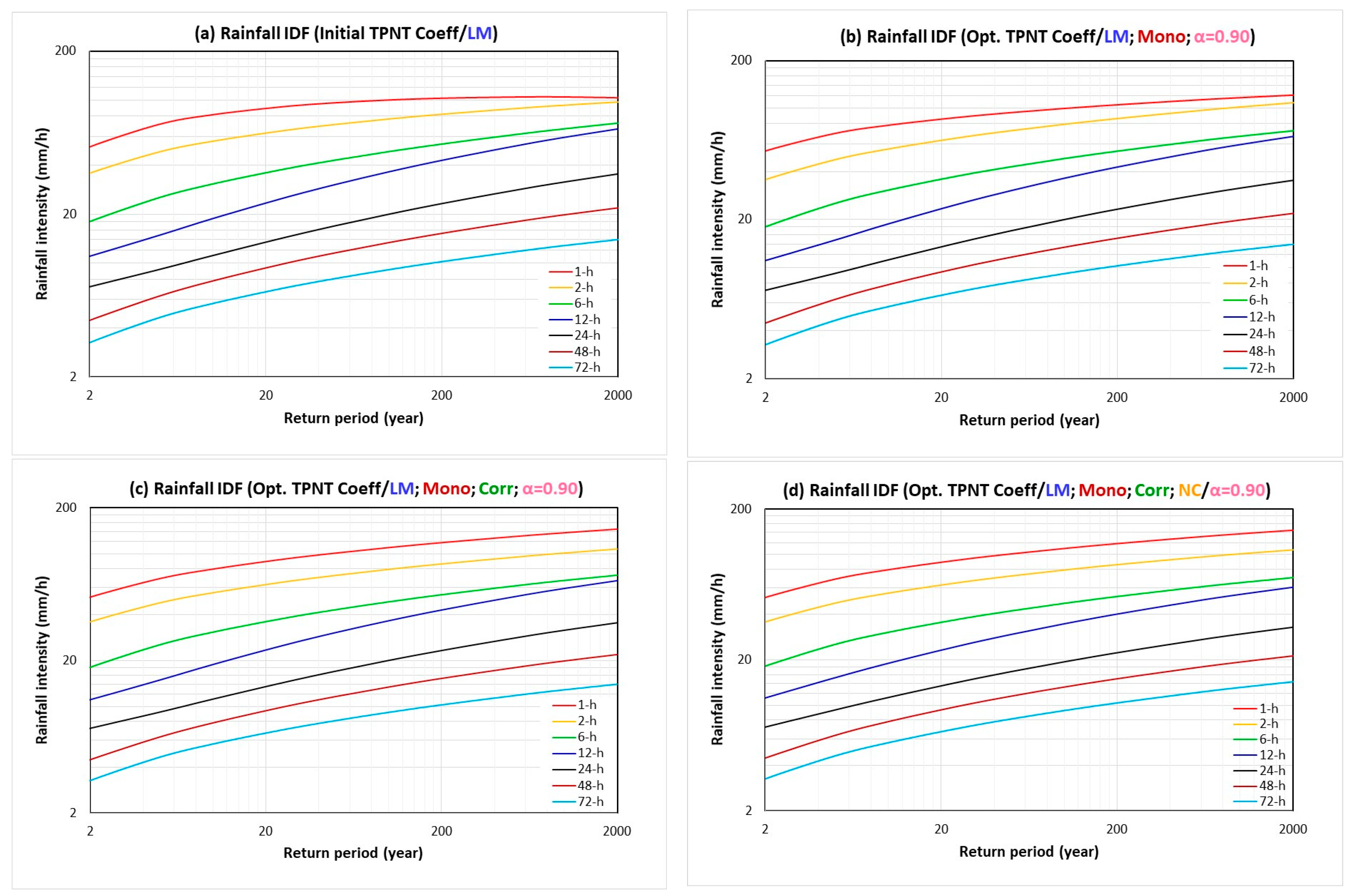
Figure 2 shows the rainfall intensity–duration curves corresponding to various frequencies. For this particular data set, by only preserving sample L-moments,
Figure 2a reveals two unusual features for those curves when return period is high (say, ≥100 years). They are (1) curves that tend to converge together for rainfall duration in the vicinity of 1 h and (2) the relatively pronounced undulation of curves for medium and long duration. These features are indications of possible anomalies that should not appear in a reasonable rainfall IDF relation. The convergence of rainfall intensity–duration curves in
Figure 2a, shown in a different form in intensity–frequency relation as
Figure 3a, reveal that the 1 h curve (in red) clearly does not satisfy the monotonicity condition according to Equation (36), which requires a rainfall intensity quantile value to increase continuously with a return period (see also
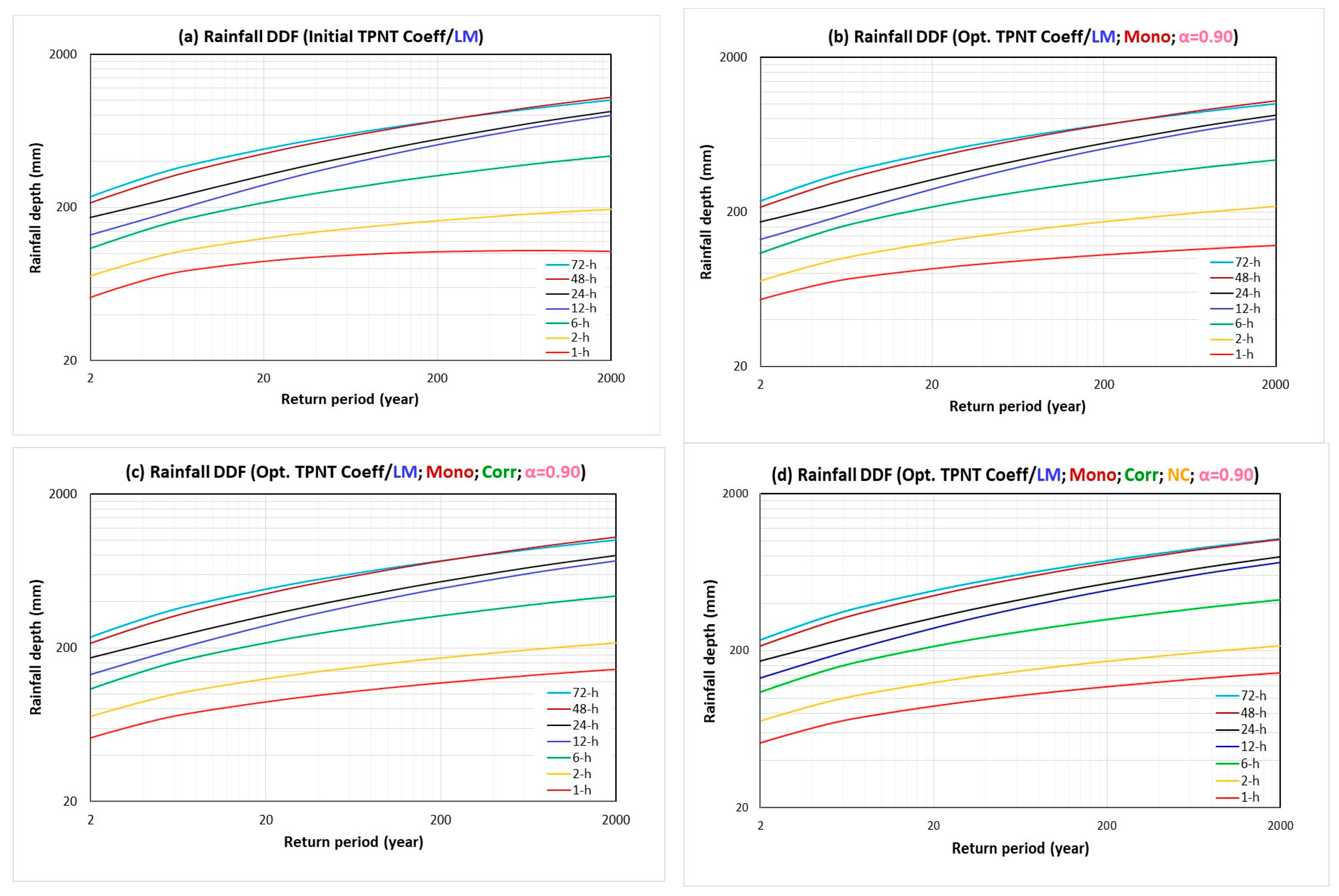
Table 4a). In fact, the 2 h intensity–frequency curve (in gold) also mildly violates the monotonicity requirement as the curve starts to bend down for high return periods. The violation of the monotonicity condition can also be observed in the form of the depth–frequency curve for a 1 h duration (see
Figure 4a). In this circumstance, the non-monotonicity of the 1 h rainfall intensity–frequency relation produces a crossover with the 2 h curve shown in
Figure 3a.
Interestingly,
Figure 3a also reveals that 6 and 12 h rainfall intensity–frequency curves have a strong tendency to intersect as rainfall frequency increases. This tendency to intersect could be attributed to a relatively large undulation of intensity–duration curves in the range of 6–12 h when rainfall frequency increases (see
Figure 2a). From 6 to 12 h, the gradient of intensity–duration curves flatten out for larger return periods. The empirical results show some evidence of improvement (in terms of a decrease in undulation, for large frequencies) when more constraints are considered. However, the improvement is not significantly enough to remove undulation. In practical engineering applications, the undulation of rainfall IDF curves such as those shown in
Figure 2a–d is removed by fitting the estimated rainfall intensity–duration data by an empirical IDF model, such as Sherman’s equation [
57].
It is clear that, by considering the monotonicity constraint, Equation (36), the crossover tendency of intensity–duration curves (see
Figure 2b) in the vicinity of 1–2 h disappears (see also
Table 6b), as does that of the 1 h and 2 h intensity–frequency curves in
Figure 3b. Correspondingly, the concave down appearance of the 1 h depth–frequency curve and, to a lesser extent, the 2 h curve is corrected (see
Figure 4b).
Notice that joint consideration of complying with L-moments and the monotonicity condition does not truly take into account the inter-correlations of rainfall intensity or depth with different durations. The appearance of undulation in the rainfall intensity–duration curves for medium and long durations (≥6 h), which satisfy the monotonicity condition, is not affected. Hence, the crossover tendency of 6 and 12 h intensity–frequency curves (see
Figure 3b) and the actual intersection of 48 and 72 h depth–frequency curves (see
Figure 4b) remain unchanged.
With further consideration of inter-correlations of rainfalls of different durations, Equations (41) and (42), the resulting rainfall IDF and DDF curves are shown in Part (c) of
Figure 2,
Figure 3 and
Figure 4.
Figure 2c shows that the rainfall intensity–duration curves in the range of short duration for a high return period completely remove the crossover tendency. Both
Figure 3c and
Figure 4c show that rainfall intensity–frequency and depth–frequency curves for 1 and 2 h are parallel to each other. Still, the 48 and 72 h rainfall depth–frequency curves intersect (see
Figure 4c).
For illustration, this application artificially select
= 5000-year in Equation (56) as the limiting frequency below which rainfall depth–frequency or intensity–frequency curves of any two durations are not allowed to intersect. The obvious results of imposing no-crossover constraint is that the 48 h rainfall depth–frequency curve in
Figure 4d would not intersect with the 72 h curve.
As for the effect of confidence level, numerical results indicate that a feasible solution for TPNT coefficients may not exist when the confidence levels for the unknown true L-moments and correlation coefficients are too low. This is expected because the width of confidence interval shrinks toward the sample L-moments and correlation coefficients as the confidence level reduces. At a certain confidence level, the corresponding width of the confidence band might be too restrictive for the optimization model to find feasible TPNT coefficients that simultaneously satisfy the monotonicity constraints. How low the limiting confidence level is depends on the problem. In this numerical example, the limiting confidence level is about 70%, below which no feasible solution can be found for multivariate TPNT coefficients. On the other hand, a reasonable confidence interval allows one to obtain a suitable set of TPNT coefficients to approximate multivariate relations.