Abstract
One-third of the global population depends on groundwater for drinking, which is an even larger proportion for arid regions. The integration of isotopic and geophysical applications has been very useful in understanding the process of groundwater recharge. The aim of this study is to define a conceptual model that describes groundwater functions within an aquifer located in a semi-arid region by identifying recharge patterns based on the isotopic characteristics of: Rainfall, surface water, shallow and deep groundwater, and incorporating regional geophysical data. We demonstrated that rainfall was affected by sub-cloud evaporation and altitude. Shallow and deep modern groundwater samples were clustered and exhibited similar evolution from rainfall. However, different groups recharged from different precipitation sources compared to the local one. In the current study, we analyzed the isotopic evolution of deep groundwater over a 10-year period, which was mainly affected by the incorporation of different flows with different isotopic signatures and the hydrodynamics of the area. We performed two geoelectrical sections in the study area to improve the understanding of the hydrogeological setting and water movement patterns. The new conceptual model should help stakeholders in the context of water management policies for the study area.
1. Introduction
Arid and semiarid regions represent >30% of the global terrestrial surface area and receive <400 mm yr−1 of rainfall. In these regions, aquifers represent the principal water supply; in many cases, groundwater may be a fossil resource [1,2,3,4]. The study of water resources in arid and semiarid regions has become important due to their increasing demand, and groundwater depletion [5]. Many studies indicate that infiltration through streambeds during flood events is the main form of recharge, whereby water losses by infiltration into alluvial channels during floods initiate the recharge process into groundwater [2,6]. Similarly, recharge likely occurs in only small portions of the basins in arid and semiarid regions, such as depressions and ephemeral stream channels [7,8,9,10]. Identifying the relationship between groundwater–surface water (GW–SW) systems is crucial when developing programs and policies for managing water resources [11]. The main factors controlling groundwater recharge on catchment-scale are: (1) Basin morphology and stream channel position within a landscape; (2) hydraulic conductivity of the porous medium connecting stream channels to adjacent alluvial aquifers; and, (3) the relation between the stream stage and water table levels in the adjacent aquifer [11,12].
Hydrogeological studies based only on hydraulic analyses are not sufficient for characterizing a GW–SW system and projecting its sustainability. Therefore, combining hydrogeochemical and isotopic methods could bridge this gap, and provide insights for determining water recharge sources and residence times for its sustainable exploitation [5]. Techniques for estimating groundwater recharge are generally classified into physical, tracer, and numerical modeling approaches [13]. According to several investigations (e.g., [14,15]), the tracer technique most successfully estimated recharge, especially in dry regions.
The stable oxygen and hydrogen isotopes are environmental isotopes that exist ubiquitously in natural waters; they represent a novel tracer technique employed in hydrology for investigating water composition and circulation in the whole water cycle. Stable isotopic compositions in water are affected by meteorological process (e.g., temperature, humidity, etc.) and geographical factors (latitude, longitude, and altitude), and to a lesser extent by reactions with geologic material, making them suitable for investigating groundwater provenance [16,17]. 18O and 2H are considered conservative tracers when the δ values are minimally affected by evaporation processes and past climate regime effects on signatures are ignored [16]. Compared to 18O and 2H, 16O and 1H have higher vapor pressure values, which facilitates their separation from the liquid phase leading to heavy water isotopes—18O and 2H—enrichment [18]. Stable oxygen and hydrogen isotopes are useful for identifying groundwater recharge from streams. In regions where streams have headwaters at high elevations, stable isotopes are often depleted in stream water relative to the local rainfall in adjacent basins. If streams retain the headwaters’ depleted isotopic signature, stable-isotope signature differences between streams and local rainfall can be used to determine the relative contribution of these two groundwater recharge sources [3].
Conversely, the necessity of understanding the geological complexity of aquifers has prompted the execution of geophysical surveys that combine this information with isotope data analysis. Geophysical investigations are essential for groundwater evaluation, which can address groundwater potentiality by providing a spatially extensive, non-invasive/non-destructive subsurface investigative method. Geophysical methods have been mainly applied in groundwater and vadose zone hydrology to map geological structures, delineate aquifer boundaries, map fractures zones, etc. These methods have been often used for mapping aquifer geometry, and are considered the most promising and suitable for groundwater prospecting [19,20,21,22]. They have been widely used groundwater-related studies in arid and semiarid regions, for example in the estimation and monitoring of groundwater levels [23,24], general exploration of groundwater [21,25,26], and groundwater potentiality [27]. Furthermore, geophysics has been increasingly used for characterizing the groundwater and surface water interface (e.g., [28,29,30]).
This study recognizes the need for understanding the structural complexity of the study area’s geological setting. Previous work has addressed the definition of potential groundwater pattern flows in the area (e.g., [7,31,32,33]); however, the studies did not integrate geophysical surveys. In fact, only a few studies reported in the literature have simultaneously integrated geophysical and isotopic data (e.g., [34]). The aim of our current study was to investigate the evolution of water from rainfall to surface water and groundwater, in fractured and alluvial aquifers named Calera, Benito Juarez, and Chupaderos, in the state of Zacatecas, Mexico. We integrated isotopic and geophysical data. Patterns of recharge to aquifers were identified based on the isotopic characteristics of: Rainfall, surface water (storage water and streamflow), and groundwater; a conceptual model was built by incorporating regional geophysical data. Herein, we present a continuation of the study presented by Gonzalez-Trinidad et al. [7]—groundwater isotopic information presented by Navarro-Velasco [35] was also included. Stable isotopes were used to: (1) Establish an improved Local Water Meteoric Line (LMWL) for the study site; and (2) asses affectation on the isotopic composition of rainfall and surface water, and their significance to aquifers’ recharge. The geophysics studio, through transient electromagnetic (TEM) measurements, was used to: (1) Build a conceptual model of groundwater flow patterns based on the analysis of isotopic water composition, and (2) define a geological cross-section of the study area.
2. Study Site
The state of Zacatecas is located at the central-northern part of Mexico; it is characterized by low rainfall rates and consequently low surface runoff. Therefore, groundwater resources are vital for the local population; supplying drinking water, an irrigation source, and sustaining the oasis ecosystems in the region. The climate in Zacatecas is mostly semiarid and half of the population lives in rural areas. The study area mostly encompasses three administrative aquifers: Calera, Benito Juarez, and Chupaderos; zone topography presents low relief. Most water samples and geophysical data for this study were taken from the Calera aquifer, which is therefore most relevant. According to the National Commission of Water [36], over 130 thousand hectares of this zone are annually irrigated with 330 hm³. This process leads to a decline in annual groundwater levels from 1 to 5 m, largely due to rudimentary and outdated irrigation systems with <45% efficiencies. Figure 1 shows the study area where the water sampling and geophysical survey were performed. Piezometric elevations of deep groundwater with an elevation interval of 20 m were constructed using 2017 static water level data from 84 observation wells, distributed in and around the three aquifers. Important seasonal and long-term changes were documented in the Calera aquifer, water table changes from 1980 to 1994 showed ~5 m depletions in areas near the aquifer boundaries. Most irrigation wells are located in central-north of the valley where major depletions of 15 m were recorded in the same period; the average depletion rate was 0.4–1.15 m yr−1 [32].
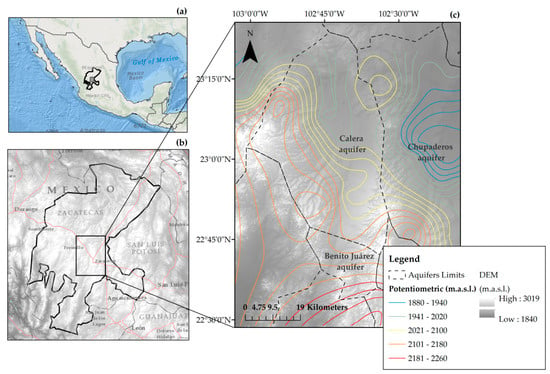
Figure 1.
Study area showing the location of Mexico (a) with the Mexican State of Zacatecas (b), and a digital elevation model (DEM) showing the extent of Calera, Benito Juarez, and Chupaderos Aquifers (c).
3. Hydrogeological Setting
The Calera horst-graben structure developed over a long stage during the Late Tertiary and Early Quaternary periods; normal faults had three main trends: (i) North–South; (ii) Northwest–Southeast; and (iii) Northeast–Southwest. These trends uplifted peripheral Tertiary volcanic mountains, central area settlements, and the deposition of basin fill sediments (alluvial material interbedded with tuffs), with a maximum thickness of 400 m. From the Late Tertiary period, mountains underwent a rapid uplift, the Tertiary Fractured Volcanic Unit was represented by the following: (i) Rhyolite lava flows with porphyritic texture with quartz, sanidine, and plagioclase in a glassy matrix, biotite and clay as an accessory and secondary mineral; and (ii) tuffs and ignimbrites with a felsic nature [31]. The lithology of the aquifer rocks is polymictic conglomerates from the Quaternary period merged to igneous and metamorphic fractured rocks from the Triassic and Cretaceous periods by tectonic movements [33]. The Calera Aquifer is considered an unconfined aquifer in a granular medium, filling a regional graben, with ~2087 km2 horizontal extent. Saturated thickness estimation of the Calera Aquifer indicated a maximum saturated thickness of 38–570 m from the north to central area, respectively, corresponding to the aquifer’s sedimentary fill. Hydraulic conductivity varied from 10−8 to 10−5 m s−1, specific yield from 0.01 to 0.3, and the aquifer’s reported average representative specific yield was 0.13 [37]. The abstraction wells within the area (~2035) were identified mainly tapping the Basin Fill Sediments; approximately 67% of the extracted groundwater was used for irrigation and 32% for human consumption. The aquifer basement varied in elevation from ~1620 m above sea level (m.a.s.l.) in the South–Central area to ~2125 m.a.s.l. in the West–Central area. Three flow patterns were reported in the aquifer: (1) Moving South to North, (2) crossing from West to East, and (3) traveling Northwest to Northeast (possibly regional) [31]. Figure 2 shows the geological map of the study area.
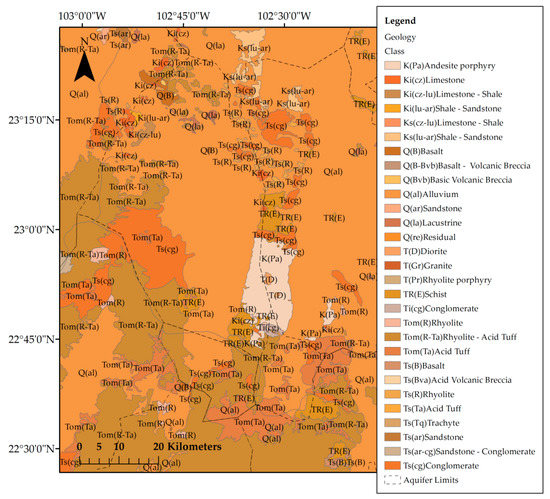
Figure 2.
Geological setting map of the study area.
4. Methods
4.1. Sampling of Stable Isotopes and Collected Data
In this study, we followed the same criteria used by Gonzalez-Trinidad et al. [7] to define sampling locations, which was in accordance with the IAEA (International Atomic Energy Agency). A hundred and forty-four water samples were taken from Gonzalez-Trinidad et al. [7]: 115 groundwater and 29 rainfall samples. We further added 123 newly collected samples: 14 rainfall (the total amount of rainfall in the 4-months rainy season, from June to August, in the same locations of Gonzalez-Trinidad et al. [7]), 37 surface water bodies, 3 stream runoff, and 69 shallow groundwater samples, which were mainly collected from the Chupaderos aquifer for the same season in 2017. The water’s isotopic composition was measured using a GV–Isoprime isotope-ratio mass spectrometer, with ±0.33‰ and ±1.78‰ precision for δ18O and δ2H, respectively. 18O and 2H were expressed in δ notation relative to the Vienna Standard Mean Ocean Water (VSMOW). In addition, 35 groundwater samples collected by Navarro-Velasco [35] were considered. Groundwater was sampled through wells at 65–125 m below the ground’s surface (depth) in all sampling periods, whereas shallow groundwater was sampled through shallow wells at 3–10 m below the surface. This shallow water corresponds to perched aquifers settled in the area’s vadose zone above the regional water table shown in Figure 1. All in all, we used a total of 302 water samples and their locations are shown in Figure 3. All 43 rainwater isotope data were used to determine the improved local meteoric water line. Data are presented in the Supplementary File.
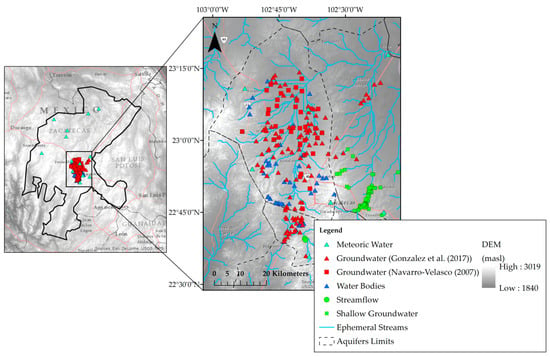
Figure 3.
Sampling locations of groundwater, rainfall, streamflow water, and shallow groundwater in the study area.
4.2. Bivariate Data Analysis
The BiDASys (bivariate data analysis system) software [38] was used to apply ordinary and uncertainty weighted least-squares linear regression models (OLR and UWLR). Rosales Rivera et al. [38] and Verma [39] reported that the UWLR should be considered as a better alternative because the use of uncertainty has a probability connotation with a strict confidence level of 99%, which was used in the present study. The OLR and UWLR were used to estimate the new LMWL, and several regressions with the different sampled sources of water.
4.3. Geophysical Data Acquisition
Aquifers are regularly characterized by low electrical resistivity, which correlates with differences between rocks (density, shape, and porosity), water content, and temperature. Geological units are also affected by differences in humidity percentages [25]; therefore, they were separated into different geoelectrical units [21,26]. The transient electromagnetic method (TEM) is sensitive to bulk resistivity (conductivity) of the studied medium. Quantitative interpretation of resistivity is based on the modified Archie’s Law [40], which establishes that in saturated geologic materials, with conductive water in the pores, bulk electrical resistivity depends on the porosity and resistivity of the pore fluid.
The TEM data were measured using the TerraTEM conductivity meter of Monex Geoscope PTY LTD. TEMIX XL4 and WinGLINK programs were used for processing and inversion of TEM data. Data were inverted by applying Occam´s inversion technique developed by Constable et al. [41]. The final output was a set of cross-sections describing the electrical parameters of the subsurface medium and their corresponding geological material in the study area. In total, 54 VES (vertical electrical soundings) points were placed in two profiles crossing the Calera aquifer (Figure 4); the cross-sections were traced in both West–East (25 VES along the profile) and North–South (29 25 VES along the profile) directions. Data for the 54 TEM stations were acquired using a single loop configuration with a loop-side length of 200 m × 200 m reaching a depth of 500 m. The same loops were used for transmitting and receiving electromagnetic signals. The TEM survey was done between March and August 2017.
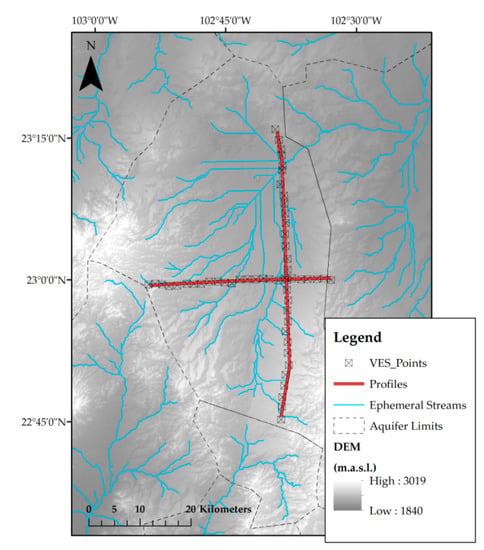
Figure 4.
Location map of the VES (vertical electrical sounding) using a square transmitter of 200 m × 200 m.
5. Results and Discussion
5.1. Isotopic Composition of Water
The summary of collected water samples and stable isotopes are presented in Table 1.

Table 1.
Summary of collected water samples and stable isotope.
OLR and UWLR regressions for all water sources are shown in Table 2 and Table 3, respectively. The grouping (for shallow and deep groundwater) and number of discordant values observed, the R, and R2 values are also presented (Table 2 and Table 3). A better fit was obtained using UWLR with lower values of uncertainties compared to those for OLR, which was consistent with reports by Rosales-Rivera et al. [38]. UWLR showed an improved local meteoric water line (LMWL) to be δ2H = 5.0918(±0.2647) δ18O − 10.5123(±2.4577), with R2 = 0.9003—values within the brackets represent uncertainty values at the strict confidence level of 99% (Figure 5).

Table 2.
Ordinary least-squares linear regression parameters from stable isotopic compositions of all water sources.

Table 3.
Uncertainty weighted least-squares linear regression parameters from stable isotopic compositions of all water sources.
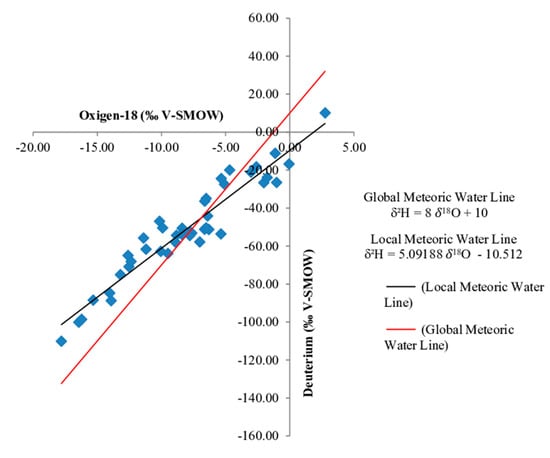
Figure 5.
Plot of local meteoric water line (LMWL) for precipitation samples, and the global meteoric water line (GMWL).
The LMWL slope, as noted by Gonzalez-Trinidad et al. [7], was lower than the global water meteoric line, δ2H = 8 δ18H + 10 [42]; this difference can be attributed to several factors. Since the sampling sites were placed in arid and semiarid areas, the subcloud evaporation was an important factor affecting the stable isotopic composition of liquid precipitation falling through dry air. However, it is possible that at higher elevations, subcloud evaporation is lower than at lower altitude; as reported by Ingraham et al. [4] where 5.5–6.5 rainfall slopes in arid regions were not uncommon. Similarly, lower slopes for arid environments have been reported by several authors [43,44,45]. All meteoric sampling sites were higher than 2000 m.a.s.l. Thus, the “altitude effect” [44]—the progressive depletion in heavy isotopes—could be affecting the isotopic composition of meteoric waters; however, this effect is not a direct cause of the LMWL slope.
The sampled water bodies and streams are ephemeral. Water bodies in arid regions suffer large degrees of evaporation due to long residence times and free-water surface areas in contact with high temperatures, especially during the dry season (Figure 6). This type of water becomes progressively enriched with high rates of continued evaporation (the estimated potential evaporation for the area is 2227 mm yr−1), which renders it isotopically distinct compared to surrounding meteoric water. Isotopic values for water bodies lie on a line (SWL) that probably identifies some evaporation lines (since these do not intersect, the LMWL is not considered as an evaporation line), where the slope = 5.0795 (similar to LMWL), and intercept = −22.9634 (Table 3). In fact, δ18O positive values were found in meteoric and surface waters, reflecting larger durations of residence. Similar positive values in water bodies have been reported in the same arid regions [46,47,48]. Stream runoff samples do not fall in the LMWL. In fact, these values lie under the SWL, but not close to positive values. The isotopic-depleted composition of these three samples may be due to their higher elevation with respect to other water bodies sampling sites [4,49].
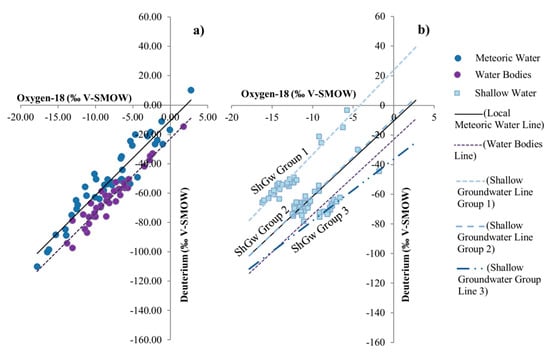
Figure 6.
Stable isotopic composition of meteoric water, surface water (a); and sampled ShGw, LMWL (local meteoric water line), and SWL (surface water line) (b).
Analysis of water sources’ isotopic compositions represents a useful tool for identifying GW–SW interactions, which has been applied in alluvial aquifers with relevant results [7,16,50,51,52]. Shallow groundwater (ShGw) samples, LMWL, and SWL are plotted in Figure 6. ShGw was clustered and plotted following the methodology employed by Gonzalez-Trinidad et al. [7], which consisted of clustering the samples depending on their perpendicular distance from the LMWL. We also performed a hierarchical clustering analysis (HCA); however, it did not explain the recharge process in the study area. In addition, Figure 6 shows UWLR for three groups for comparative analysis against data from previously explained water lines. Figure 7 shows the spatial variation of δ18O and deuterium for the ShGw groups in the study area, with soils classified according to FAO (Food and Agriculture Organization).
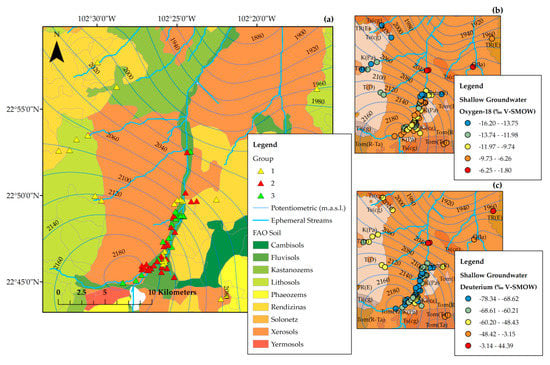
Figure 7.
Spatial distribution of the stable isotopic composition of ShGw sampled in the study area (a); and spatial distribution of Oxygen-18 (b) and Deuterium (c).
The three ShGw groups were analyzed using a soil water approach, which provided relevant information on groundwater recharge [53]. Group 2 lay almost on the LMWL, reflecting the fact that shallow wells recharged directly from local precipitation. Figure 7 shows this group to be in the lowest area (see Figure 1), indicating rapid watershed responses to precipitation that allow rapid infiltration. This type of infiltration could also be due to microtopographic features, which allow the rapid precipitation movement downward into deep soil layers, thereby greatly reducing evaporation [53]. Group 2 settled in fluvisols, which allowed water flux depending on its volume, porosity, as well as sand and clay content [54]. Group 3 lay under LMWL and SWL; with a slope = 4.1607 and an intercept = −36.3241. The stable composition of soil water in arid regions is a function of the isotopic composition of rainfall and evaporation losses. Evaporation flux was predominant in Group 3, and the resultant isotopic signature was dependent on the relative magnitude of rainfall or evaporation contributions, which could be explained by the enrichment in Figure 6. Group 1 elements were widespread at both lower and higher elevations, while Groups 2 and 3 settled at lower elevations. Nevertheless, it can be assumed that there is no difference in isotopic signatures as a function of well location. To analyze the effects of surface water on groundwater, two databases previously reported for the study area were considered; the first one by Gonzalez-Trinidad et al. [7] who reported 115 samples collected in 2014–2015, and the second by Navarro-Velasco [35] involving 35 samples collected in 2007. Figure 8 shows the UWLR for the samples obtained in 2007 with respect to the LMWL, all samples were under the LMWL. Depletion of groundwater in arid and semiarid regions was expected in comparison to local precipitation, the difference in the intercept was in the order of 20‰ δD. This difference suggested that groundwater had undergone some evaporation before or during its underground transit, same evaporated waters were observed in the sampled surface waters and the stream water flow [7,55,56,57]. Arid and semiarid regions are recharged during humid climate or from weather systems traveling in different atmospheric trajectories, resulting in a more depleted hydrogen isotope composition than present day values, which occurs in the study area [4].
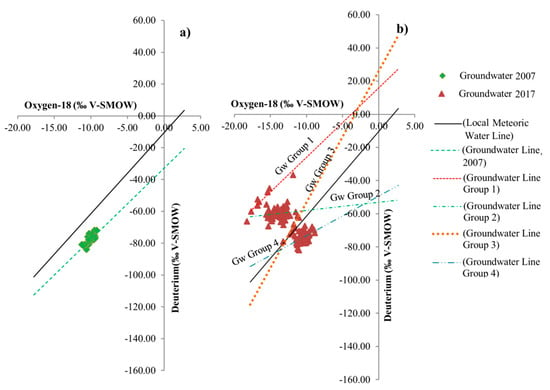
Figure 8.
Stable isotopic composition of groundwater sampled in 2007 (a) and sampled in 2014–2015 (b).
Spatial distribution of the sampling performed in 2014–2015 was practically distributed in the same area where the sampling was performed in 2007, except for those samples settled in Benito Juarez and Chupaderos aquifers (see Figure 2). Sampling performed in 2014–2015 revealed four different clusters (Figure 8), Group 4 and partially group 3 were similar to GW sampled in 2007, while Groups 1 and 2 had similar isotopic signatures ShGw Group 1.
Groundwater Groups 1 and 2 were less depleted in δD, suggesting that this groundwater was recharged by different sampled precipitation, probably faster traveling from the ocean due to their isotopic signature. The isotopic composition of Group 3 plotted on/or close to LMWL, suggesting a meteoric origin, and implying that modern rainfall is the dominant component of that groundwater. Furthermore, the absence of evaporation during infiltration suggested that the surface recharge towards underground networks was rapid, and that the isotopic effect due to evaporation was unimportant [17,57,58]. This preferential infiltration through the unsaturated zone that reaches the groundwater level has been previously reported for arid regions [53]. Group 4 plotted similar to the 2007 samples, suggesting that groundwater had undergone some evaporation before or during its underground transit (previously discussed). The regression line’s slope for Group 4 was lower than that for surface water. Therefore, pools can be considered as a potential source of groundwater. The intercept of LMWL and groundwater lines from Groups 3 and 4 identified the stable isotope composition for the water source prior to recharge. Figure 9 depicts the spatial distribution of the stable isotopic composition of groundwater sampled during 2014–2015.
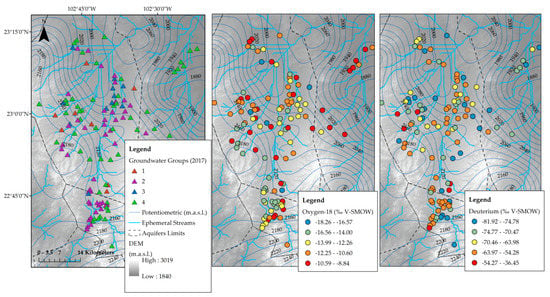
Figure 9.
Spatial distribution of the stable isotopic composition of groundwater sampled during 2014–2015 [7].
Similar to ShGw, deep groundwater does not only reflect recharge by local precipitation events, as most samples did not plot close to LMWL, implying that groundwater can be recharged from a mixture of sources [53]. An insignificant contrast was found between shallow (recent) and deep (old) groundwater, reflecting circulation and mixing of ShGw with deeper groundwater [4,59,60].
Different groups of groundwater were presented in 2014–2015 and 2007. In fact, the former exhibited isotopic signatures similar to those of ShGw; which may be due to several reasons, for example hydrodynamic processes in the vadose zone allow meteoric water evolution into ShGw and finally into deep groundwater through unsaturated zone material (water–rock interaction following the recharge). ShGw represents water sampled from wells settled in perched aquifers, this water may be affected by soil properties and hydrodynamic processes in the ground’s upper layers. Vertical hydraulic conductivity is heterogeneous in the upper layer, and therefore, the infiltration rates are widely different. The water residence time within the evaporation zone in the vadose zone determines its level of exposure to evaporation impacts arising from high ambient temperatures and low humidity—typical in arid areas and, therefore, different levels of fractionation. The relative heterogeneity of groundwater between 2007 and 2014–2015 suggests that the recharge sources are not largely similar in space and/or time, reflecting mixed conditions (young and old groundwater) [61,62,63]. Deuterium excess “d” also reflects different recharge sources. In accordance with Ingraham et al. [4], deep groundwater in arid regions is observed to have lower deuterium excess compared to LMWL, average values of groundwater sampled in 2007 and Group 1 sampled in 2007 had lower d than LMWL (see Table 4), which may be due to: (1) Evaporation occurring during rainfall through an atmosphere of lower humidity, and (2) the sampled meteoric water was initially evaporated from the ocean under more humid conditions than the present day.

Table 4.
Summary of deuterium excess in sampled water.
5.2. Geoelectrical Sections
Four geolectrical units were identified in both profiles, West–East and North–South. These units are discussed for each geoelectrical section (Table 5). Results from the West–South profile are plotted in Figure 10 (Section 1). Section 1 resistivity values were <150 Ωm, regions with higher values were located in the section extremes, while 5–25 Ωm values were presented in the central region. This data indicated the presence of an alluvial deposit with low resistivity values limited by two mountain systems named Sierra de Fresnillo (west) and Sierra de Zacatecas (east) (Figure 3), with different geological compositions (Figure 2) compared to alluvial deposits in the middle profile. Unit U1A was defined as predominant clay material mixed with limestone. Unit 1B was the basin fill sediments (alluvial material interbedded with tuffs) with different particle sizes constituted by gravels, sands, clays, and limestones (Q(al)). Unit 2 was a mixture between unit 1B, with altered and fractured volcanic rocks from a conglomerate of tertiary volcanic mountains. Unit 3 corresponded to the tertiary fractured volcanic unit, which was represented by rhyolite lava flows with a porphyritic texture as well as quartz, sanidine, and plagioclase in a glassy matrix, biotite and clay were also present as accessory and secondary minerals.

Table 5.
Geoelectrical units and their geological correlation.
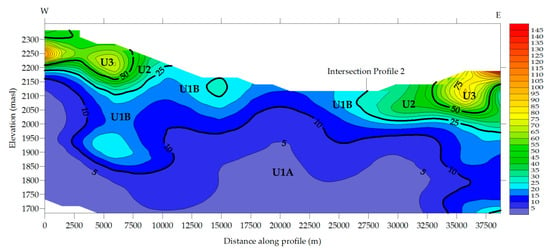
Figure 10.
Two-dimensional time–domain electromagnetic models along West–East Section 1.
Section 2 (Figure 11) had a North–South direction, 12% of the section had values h > 150 Ωm, reaching almost 6000 Ωm. Section 2 had the highest values in its extremes, indicating boundary conditions for the study area in terms of the geological setting. Similar to Section 1, the low resistivity values were in the center region of the area, reflecting the basin fill sediments. Units 1A and 1B corresponded to the same material explained in Section 1; therefore, units U2 and U3 in Section 2 had different origins. Unit 3 in the left side of the profile corresponded to the rhyolite—acid tuff (Tom(R-Ta)), which has several rocky outcrops in that region. Lower values of resistivity in this region may correspond to the conglomerate (Ts(cg)) which is in the upper section compared to rhyolite. Unit 3 in the right side of the section was analyzed under the same approach, although it lacks outcrops, there is an important area covered by extrusive igneous rock (Tom(R-Ta)) south of Benito Juarez aquifer, a region where the section can be projected (see Figure 2).
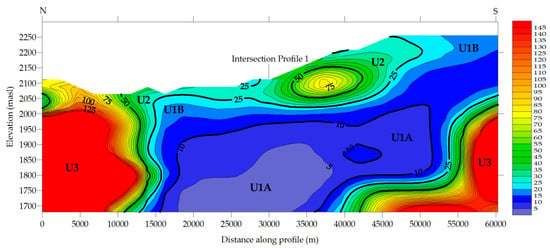
Figure 11.
Two dimensional time–domain electromagnetic models along the North–South Section 2.
5.3. Conceptual Model
Hydrogen and oxygen heavy isotope contents of rainwater decrease with increasing altitude [58,64,65]. The relationship between the altitude of meteoric water stations and 18O ratios is known as the Regional Isotopic Gradient Line (RIGL). The proposed RIGL was elaborated using the annual average isotopic signature of 12 stations at different altitudes [64], between 1660 and 2580 m.s.n.m. (see Supplementary File).
To define the local recharge of groundwater, the 18O ratios versus altitude were plotted together with the new proposed RIGL (Figure 12). The RIGL equation is δ18O = 7.97619 (±3.69416) − 0.00752 (±0.00176) ∗ alt (R2 = 0.6465, R = −0.80405), the calculated depletion was −0.752‰/100 m; even lower values of correlation have been previously reported [58].
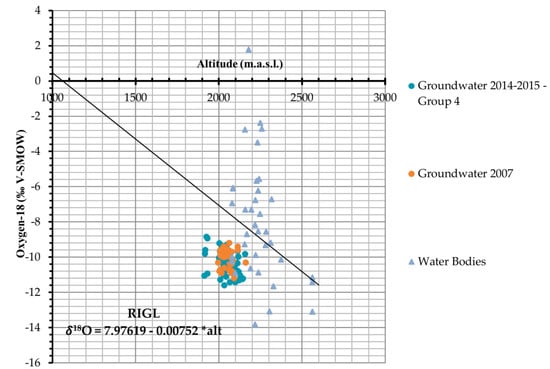
Figure 12.
Estimation of the recharge elevation using δ18O versus elevation, the first RIGL (regional isotopic gradient line) for the region is also presented.
Figure 12 shows Group 4 of groundwater sampled in 2014–2015 and groundwater sampled in 2007, which were recharged from local precipitation. According to References [57,66,67], projecting different points on the line determines the mean elevation effect of different aquifers, if we consider similar assumptions (the gradient has not changed during the course of time). The results indicated that water originates from average altitudes of 2000–2600 m.a.s.l.; foothills in the area can be found between both elevations, where notorious changes in resistivity values at the surface of both geoelectrical sections are also found, which may indicate the fractured medium.
A conceptual model for groundwater recharge was proposed based on the isotopic and geoelectrical data (Figure 13). Geoelectrical Section 1 confirmed water table elevation, starting with ~2180 m.a.s.l. (west) and finishing at ~2000 m.a.s.l. (east), corresponding to the potentiometric lines shown in Figure 1. Section 2 also reflected the water table along the section, with water elevations between 2140 and 2020 m.a.s.l. in the south and north extremes, respectively. Section 2 was used and projected to the Benito Juarez aquifer to build the conceptual model. Groundwater flow followed the slope of the section. Infiltration associated to precipitation, soil water replenishment, and groundwater recharge are complicated processes; most of the recharge from precipitation originates at an average elevation of 2200 m, nevertheless streams and water bodies may be contributing to recharge.
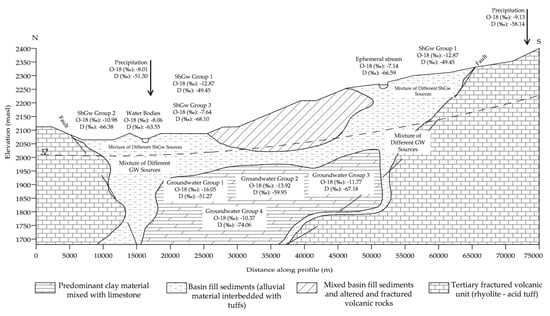
Figure 13.
Conceptual diagram of recharge to the study area.
6. Conclusions
Our study aimed to use stable isotopes and geophysical applications to define a groundwater conceptual model in a semiarid region of Mexico. To define the correlation between δ18O and δ2H, two linear regression models (OLR and UWLR) were used. The results showed that UWLR was the better option. Stable isotopes of precipitation were analyzed in the state of Zacatecas, Mexico and a new LMWL is proposed for the region. The new LMWL shows a lower slope compared to GMWL, mainly due to the subcloud evaporation and altitude effect, which are consistent with similar water lines reported for semiarid regions.
The isotopic compositions of shallow and deep groundwater are similar, due to several factors including the hydrodynamic process in the vadose zone allowing the evolution of meteoric water into groundwater. However, this evolution is a complex process. The ShGw isotopic signature may be affected by hydrodynamic processes of the upper ground layers, soil properties, and mainly fractionation by evaporation. Similarly, groundwater heterogeneity reflects the spatial and temporal complexity of the recharge process, leading to potential mixed conditions (young and old groundwater). Fifty-four VES points were placed in two profiles crossing the Calera aquifer to define the geological setting in the study area and build a conceptual model. The integration of both applications allows a better understanding of groundwater recharge.
Several studies do not include a correct understanding of geological setting in aquifers; however, geophysical applications could bridge this gap. In addition, environmental tracers are a novel technique that helps define groundwater recharge sites. Here, we presented a study where both applications are properly integrated for future research. It is expected that the new conceptual model will help stakeholders in defining water management policies for the study area. In order to support the proposed conceptual model, future research should include an analysis of radioactive isotopes such as radiocarbon and tritium as well as hydrogeochemical data.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4441/11/3/488/s1, File S1: Data.
Author Contributions
P.-G.A. conceived of the subject and wrote the paper; G.-T.J. and B.-C.C. performed the statistical analysis and contributed to writing the paper; J.-F.H. and H.-A.A. contributed to the analysis of isotopic information and its integration into the conceptual model; O.-T.E. and Á.-S.C. elaborated the figures.
Funding
This research received no external funding.
Acknowledgments
The authors thank the Mexican Council for Science and Technology (CONACYT) for financing the scholarship of the main author, Anuard Pacheco-Guerrero. The authors appreciate the help given by Ana Isabel Veyna Gomez, a collaborator from the Water Geochemestry Laboratory at the Autonomous University of Zacatecas. The authors also express their gratitude to the Isotopy Laboratory of the Water Center for Latin America and the Caribbean, Monterrey Institute of Technology and Higher Education, Nuevo León, México, for contributing to the isotopic analysis of all of the new samples.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kpegli, K.A.R.; Alassane, A.; Trabelsi, R.; Zouari, K.; Boukari, M.; Mama, D.; Dovonon, F.L.; Yoxi, Y.V.; Toro-Espitia, L.E. Geochemical processes in Kandi Basin, Benin, West Africa: A combined hydrochemistry and stable isotopes approach. Quat. Int. 2015, 369, 99–109. [Google Scholar] [CrossRef]
- Shanafield, M.; Cook, P.G. Transmission losses, infiltration and groundwater recharge through ephemeral and intermittent streambeds: A review of applied methods. J. Hydrol. 2014, 511, 518–529. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Keese, K.E.; Flint, A.L.; Flint, L.E.; Gaye, C.B.; Edmunds, W.M.; Simmers, I. Global synthesis of groundwater recharge in semiarid and arid regions. Hydrol. Process. 2006, 20, 3335–3370. [Google Scholar] [CrossRef]
- Ingraham, N.L.; Caldwell, E.A.; Verhagen, B.T. Arid Catchments. In Isotope Tracers in Catchment Hydrology; Elsevier: Amsterdam, The Netherlands, 1998; pp. 435–465. ISBN 978-0-444-81546-0. [Google Scholar]
- Ettayfi, N.; Bouchaou, L.; Michelot, J.L.; Tagma, T.; Warner, N.; Boutaleb, S.; Massault, M.; Lgourna, Z.; Vengosh, A. Geochemical and isotopic (oxygen, hydrogen, carbon, strontium) constraints for the origin, salinity, and residence time of groundwater from a carbonate aquifer in the Western Anti-Atlas Mountains, Morocco. J. Hydrol. 2012, 438–439, 97–111. [Google Scholar] [CrossRef]
- Greenbaum, N. Paleofloods and the Estimation of Long Termn Transmission Losses and Recharge to the Lower Nahal Zin Alluvial Aquifer, Negev Desert, Israel. Anc. Floods Mod. Hazards Princ. Appl. Paleoflood Hydrol. 2002, 5, 311–328. [Google Scholar]
- González-Trinidad, J.; Pacheco-Guerrero, A.; Júnez-Ferreira, H.; Bautista-Capetillo, C.; Hernández-Antonio, A. Identifying Groundwater Recharge Sites through Environmental Stable Isotopes in an Alluvial Aquifer. Water 2017, 9, 569. [Google Scholar] [CrossRef]
- Schoener, G. Quantifying Transmission Losses in a New Mexico Ephemeral Stream: A Losing Proposition. J. Hydrol. Eng. 2017, 22, 05016038. [Google Scholar] [CrossRef]
- McCallum, A.M.; Andersen, M.S.; Acworth, R.I. A New Method for Estimating Recharge to Unconfined Aquifers Using Differential River Gauging. Groundwater 2014, 52, 291–297. [Google Scholar] [CrossRef]
- Goodrich, D.C.; Williams, D.G.; Unkrich, C.L.; Hogan, J.F.; Scott, R.L.; Hultine, K.R.; Pool, D.; Goes, A.L.; Miller, S. Comparison of methods to estimate ephemeral channel recharge, Walnut Gulch, San Pedro River basin, Arizona. In Groundwater Recharge in a Desert Environment. AGU Mon: The Southwestern United States; Wiley: Hoboken, NJ, USA, 2004; pp. 77–99. [Google Scholar]
- Yu, M.C.L.; Cartwright, I.; Braden, J.L.; de Bree, S.T. Examining the spatial and temporal variation of groundwater inflows to a valley-to-floodplain river using 222Rn, geochemistry and river discharge: The Ovens River, southeast Australia. Hydrol. Earth Syst. Sci. 2013, 17, 4907–4924. [Google Scholar] [CrossRef]
- Martinez, J.L.; Raiber, M.; Cox, M.E. Assessment of groundwater–surface water interaction using long-term hydrochemical data and isotope hydrology: Headwaters of the Condamine River, Southeast Queensland, Australia. Sci. Total Environ. 2015, 536, 499–516. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Healy, R.W.; Cook, P.G. Choosing appropriate techniques for quantifying groundwater recharge. Hydrogeol. J. 2002, 10, 18–39. [Google Scholar] [CrossRef]
- Li, Z.; Chen, X.; Liu, W.; Si, B. Determination of groundwater recharge mechanism in the deep loessial unsaturated zone by environmental tracers. Sci. Total Environ. 2017, 586, 827–835. [Google Scholar] [CrossRef] [PubMed]
- Allison, G.B.; Gee, G.W.; Tyler, S.W. Vadose-zone techniques for estimating groundwater recharge in arid and semiarid regions. Soil Sci. Soc. Am. J. 1994, 58, 6–14. [Google Scholar] [CrossRef]
- Liu, Y.; Yamanaka, T.; Zhou, X.; Tian, F.; Ma, W. Combined use of tracer approach and numerical simulation to estimate groundwater recharge in an alluvial aquifer system: A case study of Nasunogahara area, central Japan. J. Hydrol. 2014, 519, 833–847. [Google Scholar] [CrossRef]
- Clark, I.D.; Fritz, P. Environmental Isotopes in Hydrogeology; CRC Press/Lewis Publishers: Boca Raton, FL, USA, 1997; ISBN 978-1-56670-249-2. [Google Scholar]
- Sun, H.; Hu, Z.; Zhang, J.; Wu, W.; Liang, S.; Lu, S.; Liu, H. Determination of hydraulic flow patterns in constructed wetlands using hydrogen and oxygen isotopes. J. Mol. Liq. 2016, 223, 775–780. [Google Scholar] [CrossRef]
- Mogaji, K.A.; Omobude, O.B. Modeling of geoelectric parameters for assessing groundwater potentiality in a multifaceted geologic terrain, Ipinsa Southwest, Nigeria—A GIS-based GODT approach. NRIAG J. Astron. Geophys. 2017, 6, 434–451. [Google Scholar] [CrossRef]
- Younis, A.; Soliman, M.; Moussa, S.; Massoud, U.; ElNabi, S.A.; Attia, M. Integrated geophysical application to investigate groundwater potentiality of the shallow Nubian aquifer at northern Kharga, Western Desert, Egypt. NRIAG J. Astron. Geophys. 2016, 5, 186–197. [Google Scholar] [CrossRef]
- Mohamaden, M.I.I.; Hamouda, A.Z.; Mansour, S. Application of electrical resistivity method for groundwater exploration at the Moghra area, Western Desert, Egypt. Egypt. J. Aquat. Res. 2016, 42, 261–268. [Google Scholar] [CrossRef]
- Wattanasen, K.; Elming, S.-Å. Direct and indirect methods for groundwater investigations: A case-study of MRS and VES in the southern part of Sweden. J. Appl. Geophys. 2008, 66, 104–117. [Google Scholar] [CrossRef]
- Song, L.; Zhu, J.; Yan, Q.; Kang, H. Estimation of groundwater levels with vertical electrical sounding in the semiarid area of South Keerqin sandy aquifer, China. J. Appl. Geophys. 2012, 83, 11–18. [Google Scholar] [CrossRef]
- Lopes, D.D.; Silva, S.M.C.P.; Fernandes, F.; Teixeira, R.S.; Celligoi, A.; Dall’Antônia, L.H. Geophysical technique and groundwater monitoring to detect leachate contamination in the surrounding area of a landfill—Londrina (PR—Brazil). J. Environ. Manag. 2012, 113, 481–487. [Google Scholar] [CrossRef] [PubMed]
- Ruthsatz, A.D.; Sarmiento Flores, A.; Diaz, D.; Reinoso, P.S.; Herrera, C.; Brasse, H. Joint TEM and MT aquifer study in the Atacama Desert, North Chile. J. Appl. Geophys. 2018, 153, 7–16. [Google Scholar] [CrossRef]
- Mohamaden, M.I.I.; Ehab, D. Application of electrical resistivity for groundwater exploration in Wadi Rahaba, Shalateen, Egypt. NRIAG J. Astron. Geophys. 2017, 6, 201–209. [Google Scholar] [CrossRef]
- Helaly, A.S. Assessment of groundwater potentiality using geophysical techniques in Wadi Allaqi basin, Eastern Desert, Egypt—Case study. NRIAG J. Astron. Geophys. 2017, 6, 408–421. [Google Scholar] [CrossRef]
- McLachlan, P.J.; Chambers, J.E.; Uhlemann, S.S.; Binley, A. Geophysical characterisation of the groundwater–surface water interface. Adv. Water Resour. 2017, 109, 302–319. [Google Scholar] [CrossRef]
- Singha, K.; Day-Lewis, F.D.; Johnson, T.; Slater, L.D. Advances in interpretation of subsurface processes with time-lapse electrical imaging. Hydrol. Process. 2015, 29, 1549–1576. [Google Scholar] [CrossRef]
- Binley, A.; Hubbard, S.S.; Huisman, J.A.; Revil, A.; Robinson, D.A.; Singha, K.; Slater, L.D. The emergence of hydrogeophysics for improved understanding of subsurface processes over multiple scales: The Emergence of Hydrogeophysics. Water Resour. Res. 2015, 51, 3837–3866. [Google Scholar] [CrossRef] [PubMed]
- Navarro-SolíS, O.; González-Trinidad, J.; Júnez-Ferreira, H.; Cardona, A.; Bautista-Capetillo, C.F. Integrative methodology for the identification of groundwater flow patterns: Application in a semi-arid region of Mexico. Appl. Ecol. Environ. Res. 2016, 14, 645–666. [Google Scholar] [CrossRef]
- Hernández, J.E.; Gowda, P.H.; Howell, T.A.; Steiner, J.L.; Mojarro, F.; Núñez, E.P.; Avila, J.R. Modeling groundwater levels on the Calera aquifer region in Central Mexico using ModFlow. J. Agric. Sci. Technol. B 2012, 2, 52–61. [Google Scholar]
- Hernández, J.E.; Gowda, P.H.; Howell, T.A.; Steiner, J.L.; Mojarro, F.; Peña Nuñez, E.; Avila, J.R. Groundwater Modeling of the Calera Aquifer Region in Central Mexico; ASCE: Reston, VA, USA, 2011; pp. 1009–1018. [Google Scholar]
- Dailey, D.; Sauck, W.; Sultan, M.; Milewski, A.; Ahmed, M.; Laton, W.R.; Elkadiri, R.; Foster, J.; Schmidt, C.; Al Harbi, T. Geophysical, remote sensing, GIS, and isotopic applications for a better understanding of the structural controls on groundwater flow in the Mojave Desert, California. J. Hydrol. Reg. Stud. 2015, 3, 211–232. [Google Scholar] [CrossRef]
- Navarro-Velasco, J.L. Análisis y Determinaciónde Zonas de Recarga en el Acuífero de Calera, Zacatecas, México; Universidad Autónoma de Zacatecas “Francisco García Salinas”: Zacatecas, México, 2007. [Google Scholar]
- Comisión Nacional del Agua (CONAGUA). Actualización de la Disponibilidad Media Anual de Agua Subterránea, Acuífero (3225) Calera; Diario Oficial de la Federación, Government of Mexico: Mexico City, Mexico, 2015.
- Júnez-Ferreira, H.; González, J.; Reyes, E.; Herrera, G.S. A Geostatistical Methodology to Evaluate the Performance of Groundwater Quality Monitoring Networks Using a Vulnerability Index. Math. Geosci. 2016, 48, 25–44. [Google Scholar] [CrossRef]
- Rosales-Rivera, M.; Díaz-González, L.; Verma, S.P. A new online computer program (BIDASys) for ordinary and uncertainty weighted least-squares linear regressions: case studies from food chemistry. Rev. Mex. Ing. Quím. 2018, 17, 507–522. [Google Scholar] [CrossRef]
- Verma, S.P. Geoquimiometría. Rev. Mex. Cienc. Geológicas 2012, 29, 276–298. [Google Scholar]
- Roy, S.; Tarafdar, S. Archie’s law from a fractal model for porous rocks. Phys. Rev. B 1997, 55, 8038. [Google Scholar] [CrossRef]
- Constable, S.C.; Parker, R.L.; Constable, C.G. Occam’s inversion: A practical algorithm for generating smooth models from electromagnetic sounding data. Geophysics 1987, 52, 289–300. [Google Scholar] [CrossRef]
- Craig, H. Isotopic variations in meteoric waters.pdf. Science 1961, 133, 1702–1703. [Google Scholar] [CrossRef] [PubMed]
- Cartwright, I.; Weaver, T.R.; Cendón, D.I.; Fifield, L.K.; Tweed, S.O.; Petrides, B.; Swane, I. Constraining groundwater flow, residence times, inter-aquifer mixing, and aquifer properties using environmental isotopes in the southeast Murray Basin, Australia. Appl. Geochem. 2012, 27, 1698–1709. [Google Scholar] [CrossRef]
- Liebminger, A.; Haberhauer, G.; Papesch, W.; Heiss, G. Correlation of the isotopic composition in precipitation with local conditions in alpine regions. J. Geophys. Res. 2006, 111, D05104. [Google Scholar] [CrossRef]
- Boronina, A.; Balderer, W.; Renard, P.; Stichler, W. Study of stable isotopes in the Kouris catchment (Cyprus) for the description of the regional groundwater flow. J. Hydrol. 2005, 308, 214–226. [Google Scholar] [CrossRef]
- Luo, X.; Jiao, J.J.; Wang, X.; Liu, K.; Lian, E.; Yang, S. Groundwater discharge and hydrologic partition of the lakes in desert environment: Insights from stable 18O/2H and radium isotopes. J. Hydrol. 2017, 546, 189–203. [Google Scholar] [CrossRef]
- Karroum, M.; Elgettafi, M.; Elmandour, A.; Wilske, C.; Himi, M.; Casas, A. Geochemical processes controlling groundwater quality under semi arid environment: A case study in central Morocco. Sci. Total Environ. 2017, 609, 1140–1151. [Google Scholar] [CrossRef] [PubMed]
- Herczeg, A.L.; Barnes, C.J.; Macumber, P.G.; Olley, J.M. A stable isotope investigation of groundwater-surface water interactions at Lake Tyrrell, Victoria, Australia. Chem. Geol. 1992, 96, 19–32. [Google Scholar] [CrossRef]
- Goebel, T.S.; Lascano, R.J.; Paxton, P.R.; Mahan, J.R. Rainwater use by irrigated cotton measured with stable isotopes of water. Agric. Water Manag. 2015, 158, 17–25. [Google Scholar] [CrossRef]
- Keesari, T.; Sharma, D.A.; Rishi, M.S.; Pant, D.; Mohokar, H.V.; Jaryal, A.K.; Sinha, U.K. Isotope investigation on groundwater recharge and dynamics in shallow and deep alluvial aquifers of southwest Punjab. Appl. Radiat. Isot. 2017, 129, 163–170. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Tang, C.; Chen, J.; Song, X.; Li, F.; Sakura, Y. Spatial characteristics of water quality, stable isotopes and tritium associated with groundwater flow in the Hutuo River alluvial fan plain of the North China Plain. Hydrogeol. J. 2008, 16, 1003–1015. [Google Scholar] [CrossRef]
- Gaye, C.B.; Edmunds, W.M. Groundwater recharge estimation using chloride, stable isotopes and tritium profiles in the sands of northwestern Senegal. Environ. Geol. 1996, 27, 246–251. [Google Scholar] [CrossRef]
- Tan, H.; Liu, Z.; Rao, W.; Wei, H.; Zhang, Y.; Jin, B. Stable isotopes of soil water: Implications for soil water and shallow groundwater recharge in hill and gully regions of the Loess Plateau, China. Agric. Ecosyst. Environ. 2017, 243, 1–9. [Google Scholar] [CrossRef]
- Souza, R.; Souza, E.; Netto, A.M.; de Almeida, A.Q.; Júnior, G.B.; Silva, J.R.I.; de Sousa Lima, J.R.; Antonino, A.C.D. Assessment of the physical quality of a Fluvisol in the Brazilian semiarid region. Geoderma Reg. 2017, 10, 175–182. [Google Scholar] [CrossRef]
- Abadi Berhe, B.; Erdem Dokuz, U.; Çelik, M. Assessment of hydrogeochemistry and environmental isotopes of surface and groundwaters in the Kütahya Plain, Turkey. J. Afr. Earth Sci. 2017, 134, 230–240. [Google Scholar] [CrossRef]
- Ako, A.A.; Shimada, J.; Hosono, T.; Ichiyanagi, K.; Nkeng, G.E.; Eyong, G.E.T.; Roger, N.N. Hydrogeochemical and isotopic characteristics of groundwater in Mbanga, Njombe and Penja (Banana Plain)—Cameroon. J. Afr. Earth Sci. 2012, 75, 25–36. [Google Scholar] [CrossRef]
- Bouragba, L.; Mudry, J.; Bouchaou, L.; Hsissou, Y.; Krimissa, M.; Tagma, T.; Michelot, J.L. Isotopes and groundwater management strategies under semi-arid area: Case of the Souss upstream basin (Morocco). Appl. Radiat. Isot. 2011, 69, 1084–1093. [Google Scholar] [CrossRef] [PubMed]
- Dogramaci, S.; Skrzypek, G.; Dodson, W.; Grierson, P.F. Stable isotope and hydrochemical evolution of groundwater in the semi-arid Hamersley Basin of subtropical northwest Australia. J. Hydrol. 2012, 475, 281–293. [Google Scholar] [CrossRef]
- Carucci, V.; Petitta, M.; Aravena, R. Interaction between shallow and deep aquifers in the Tivoli Plain (Central Italy) enhanced by groundwater extraction: A multi-isotope approach and geochemical modeling. Appl. Geochem. 2012, 27, 266–280. [Google Scholar] [CrossRef]
- Petitta, M.; Primavera, P.; Tuccimei, P.; Aravena, R. Interaction between deep and shallow groundwater systems in areas affected by Quaternary tectonics (Central Italy): A geochemical and isotope approach. Environ. Earth Sci. 2011, 63, 11–30. [Google Scholar] [CrossRef]
- Addai, M.O.; Yidana, S.M.; Chegbeleh, L.-P.; Adomako, D.; Banoeng-Yakubo, B. Groundwater recharge processes in the Nasia sub-catchment of the White Volta Basin: Analysis of porewater characteristics in the unsaturated zone. J. Afr. Earth Sci. 2016, 122, 4–14. [Google Scholar] [CrossRef]
- Ahmed, A.; Clark, I. Groundwater flow and geochemical evolution in the Central Flinders Ranges, South Australia. Sci. Total Environ. 2016, 572, 837–851. [Google Scholar] [CrossRef]
- Bestland, E.; George, A.; Green, G.; Olifent, V.; Mackay, D.; Whalen, M. Groundwater dependent pools in seasonal and permanent streams in the Clare Valley of South Australia. J. Hydrol. Reg. Stud. 2017, 9, 216–235. [Google Scholar] [CrossRef]
- Gonfiantini, R.; Roche, M.-A.; Olivry, J.-C.; Fontes, J.-C.; Zuppi, G.M. The altitude effect on the isotopic composition of tropical rains. Chem. Geol. 2001, 181, 147–167. [Google Scholar] [CrossRef]
- Dansgaard, W. Stable isotopes in precipitation. Tellus 1964, 4, 438–467. [Google Scholar]
- N’da, A.B.; Bouchaou, L.; Reichert, B.; Hanich, L.; Ait Brahim, Y.; Chehbouni, A.; Beraaouz, E.H.; Michelot, J.-L. Isotopic signatures for the assessment of snow water resources in the Moroccan high Atlas mountains: Contribution to surface and groundwater recharge. Environ. Earth Sci. 2016, 75, 755. [Google Scholar] [CrossRef]
- Paternoster, M.; Liotta, M.; Favara, R. Stable isotope ratios in meteoric recharge and groundwater at Mt. Vulture volcano, southern Italy. J. Hydrol. 2008, 348, 87–97. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).