Quantification of Stream Drying Phenomena Using Grid-Based Hydrological Modeling via Long-Term Data Mining throughout South Korea including Ungauged Areas
Abstract
1. Introduction
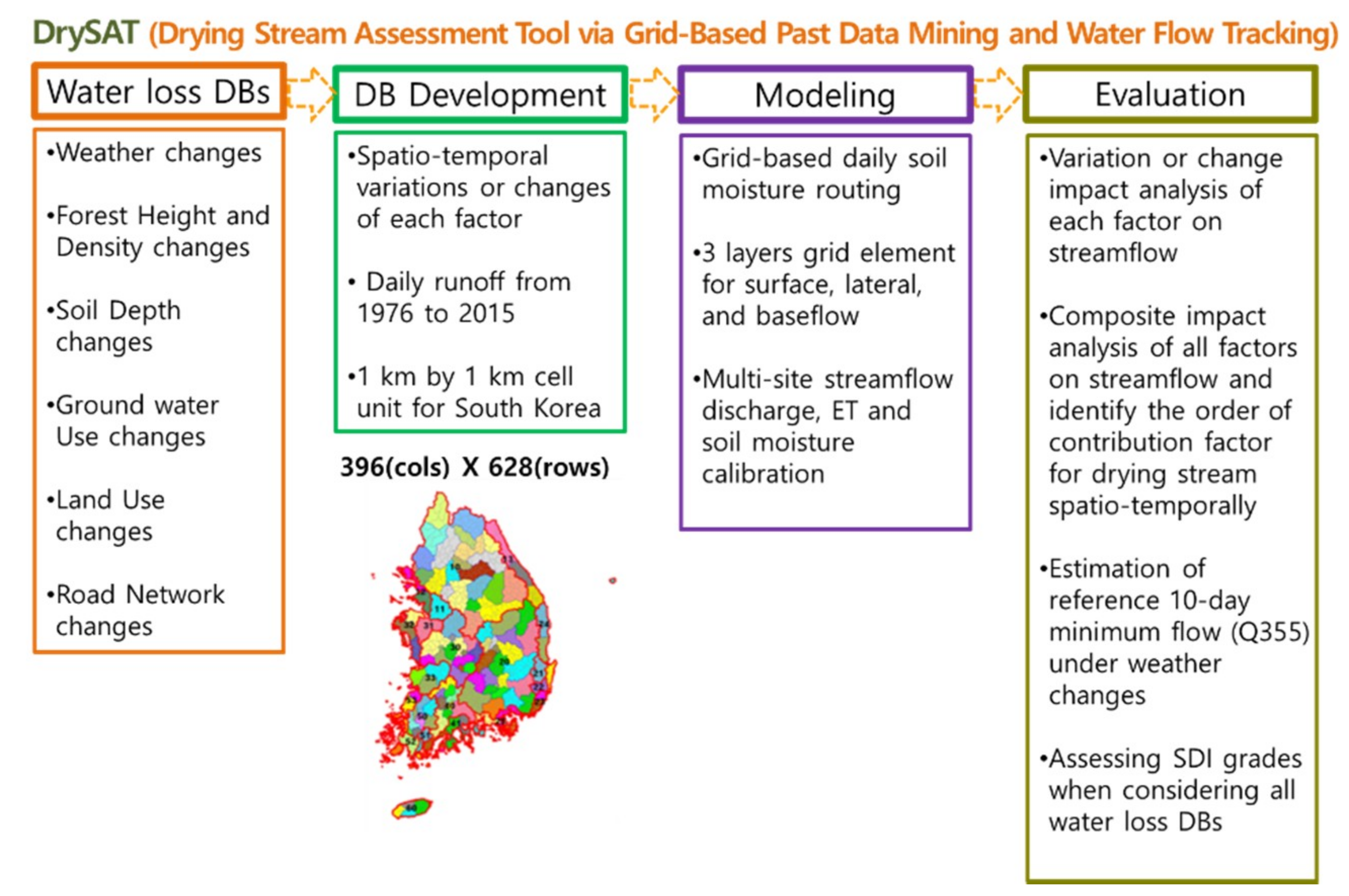
2. Materials and Methods
2.1. Causes of Stream Drying Phenomena
2.2. Description of Grid-Based Continuous Hydrologic Model
2.3. Stream Drying Phenomena Definition
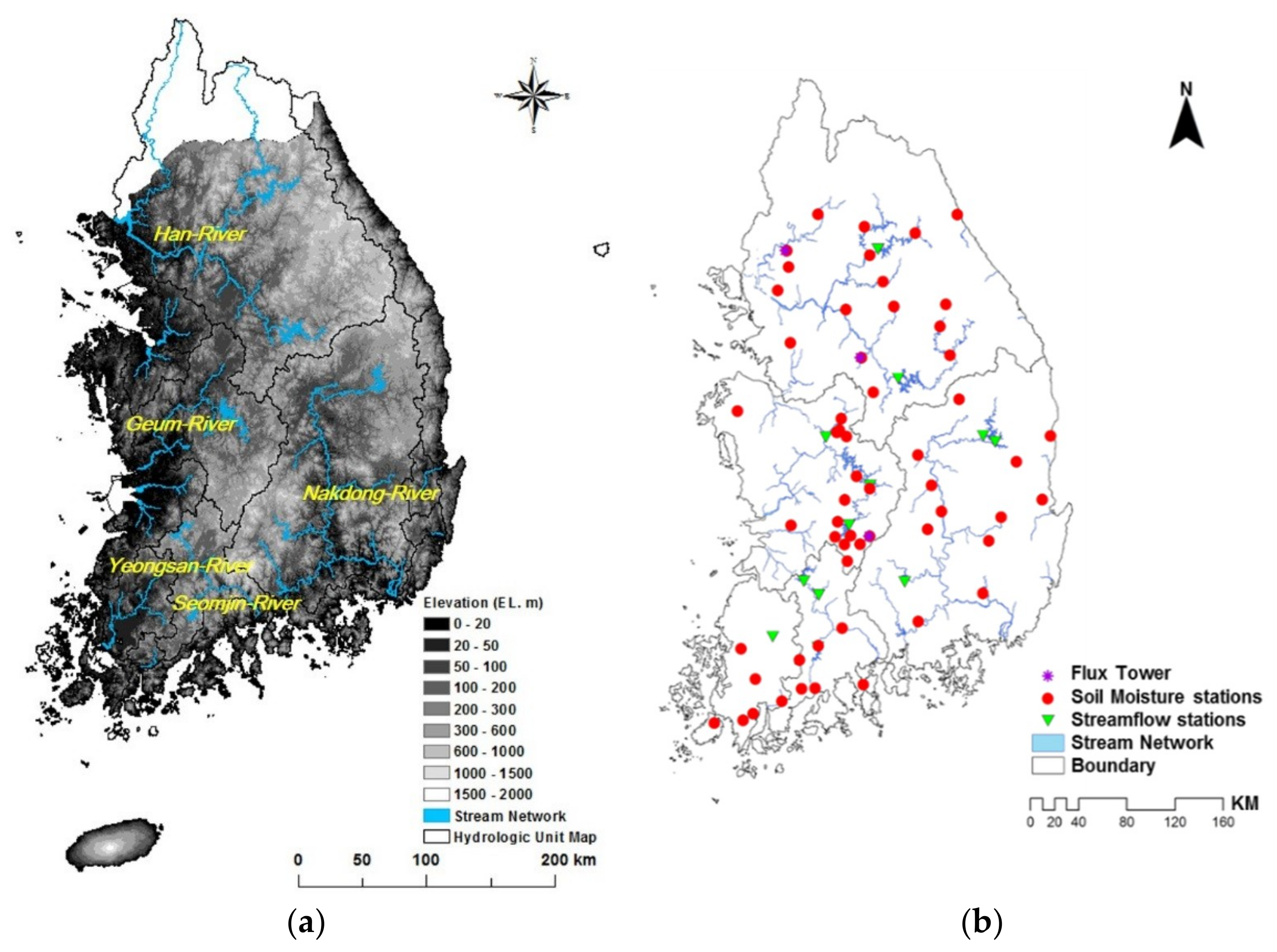
2.4. Description of the Study Area
3. Results and Discussion
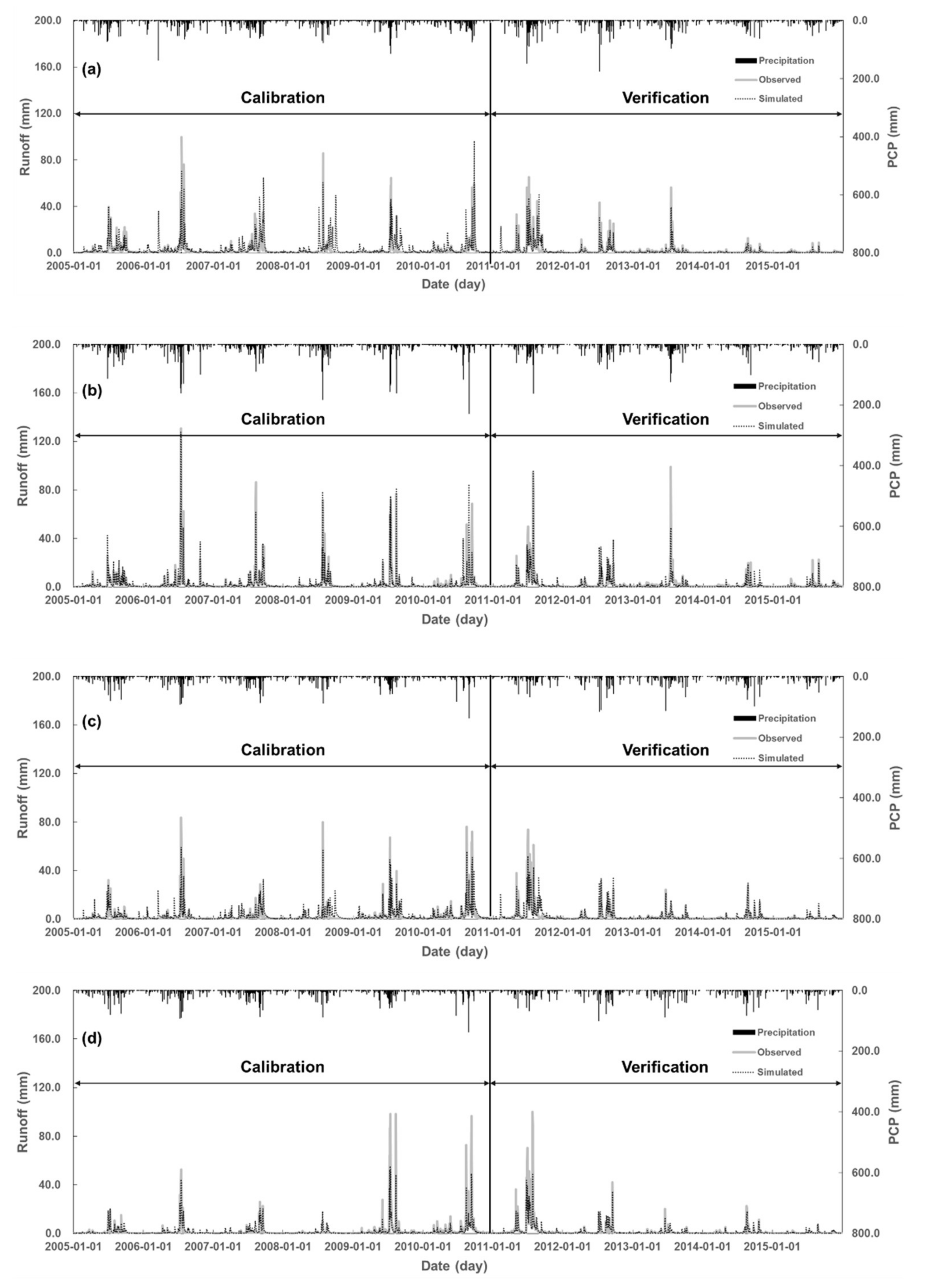
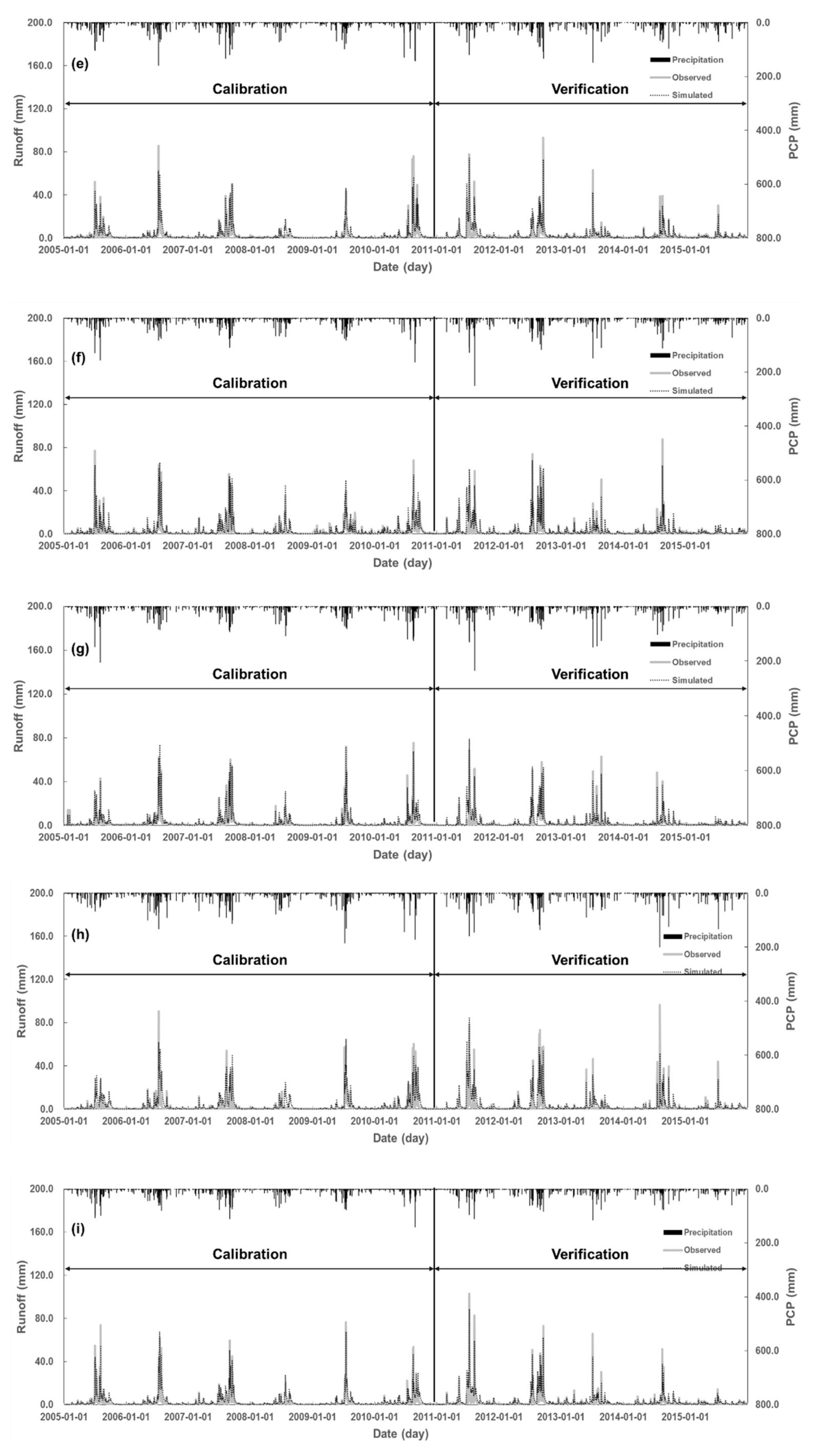
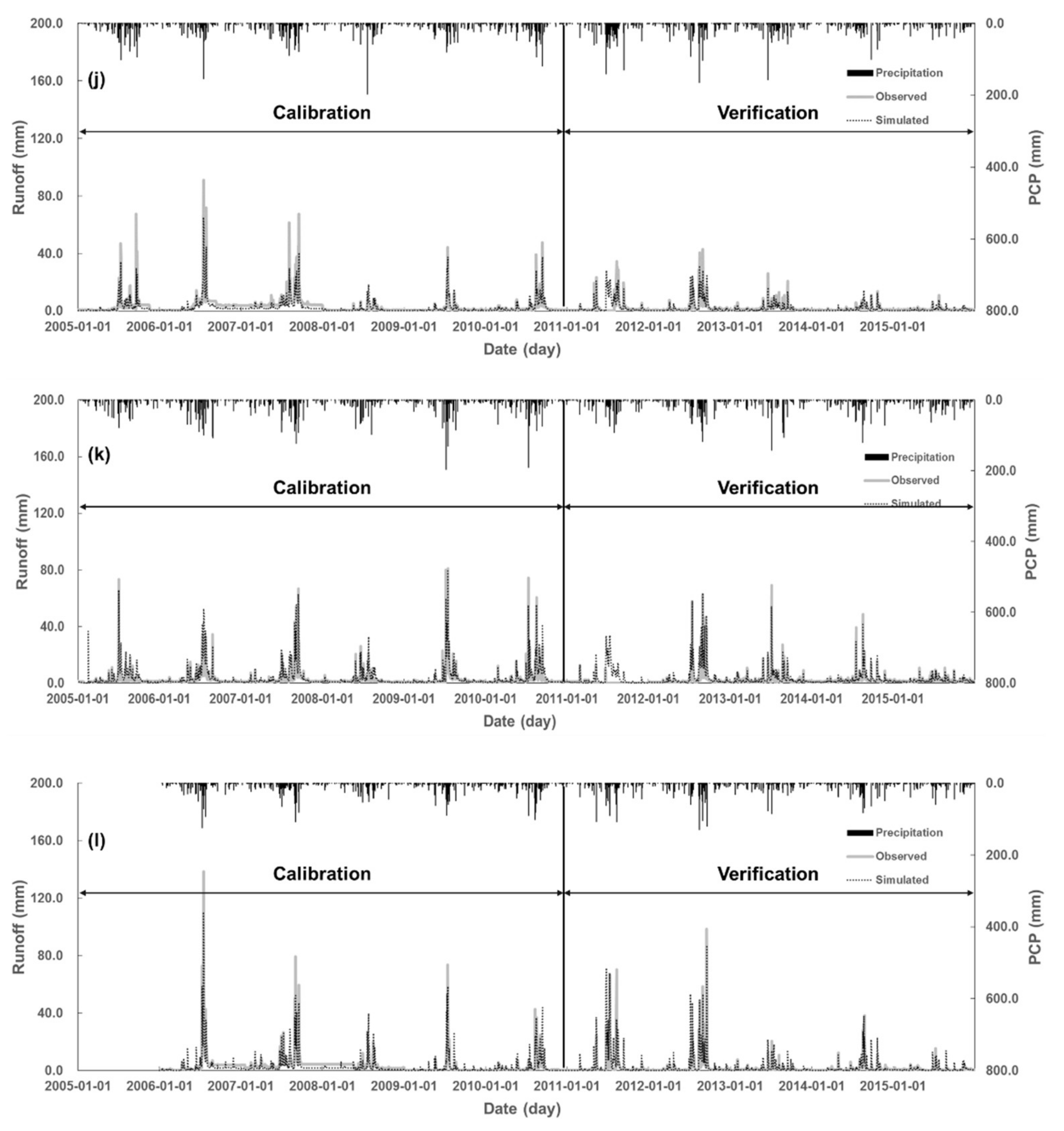
3.1. Calibration and Validation of the Model
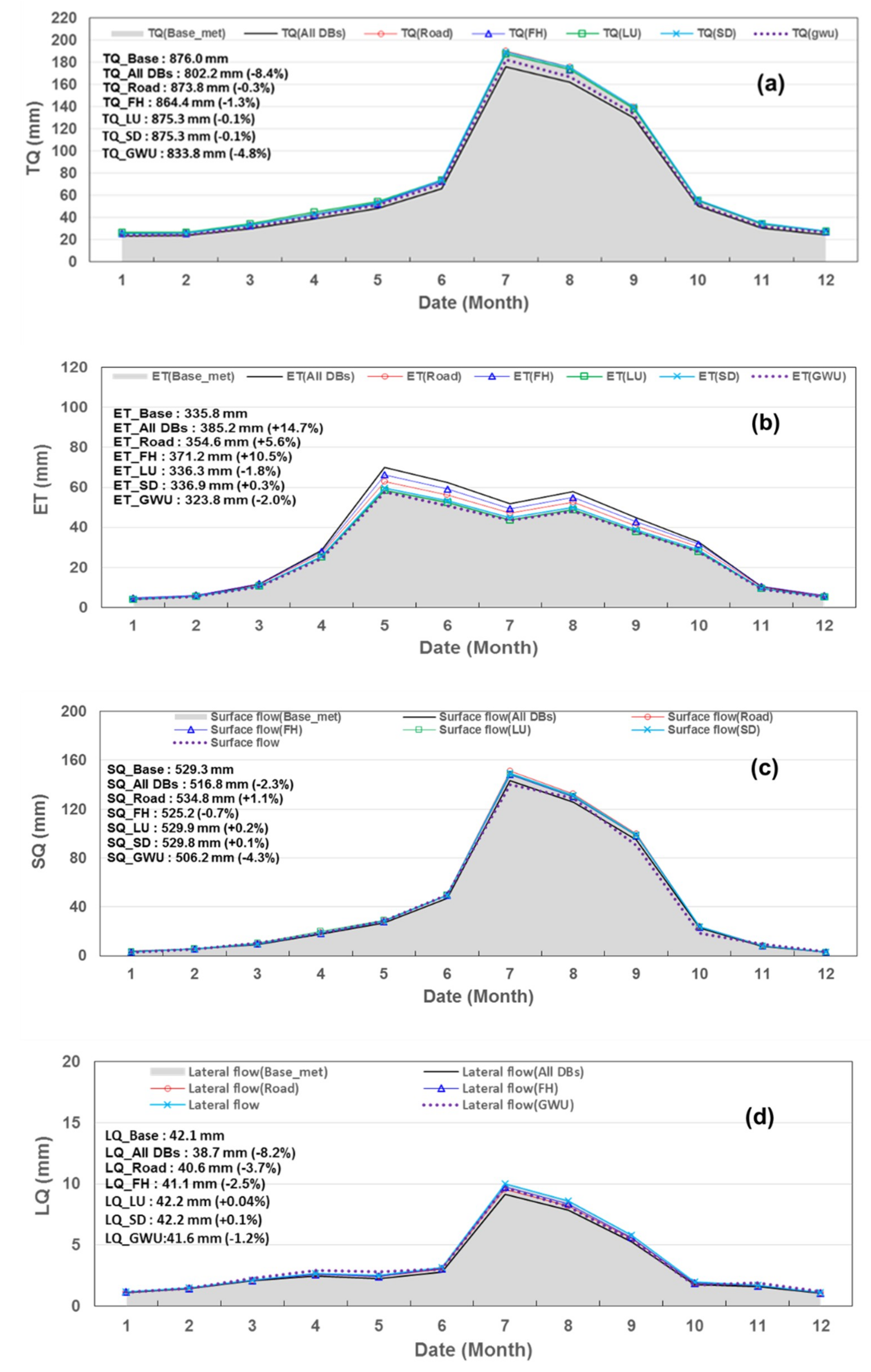
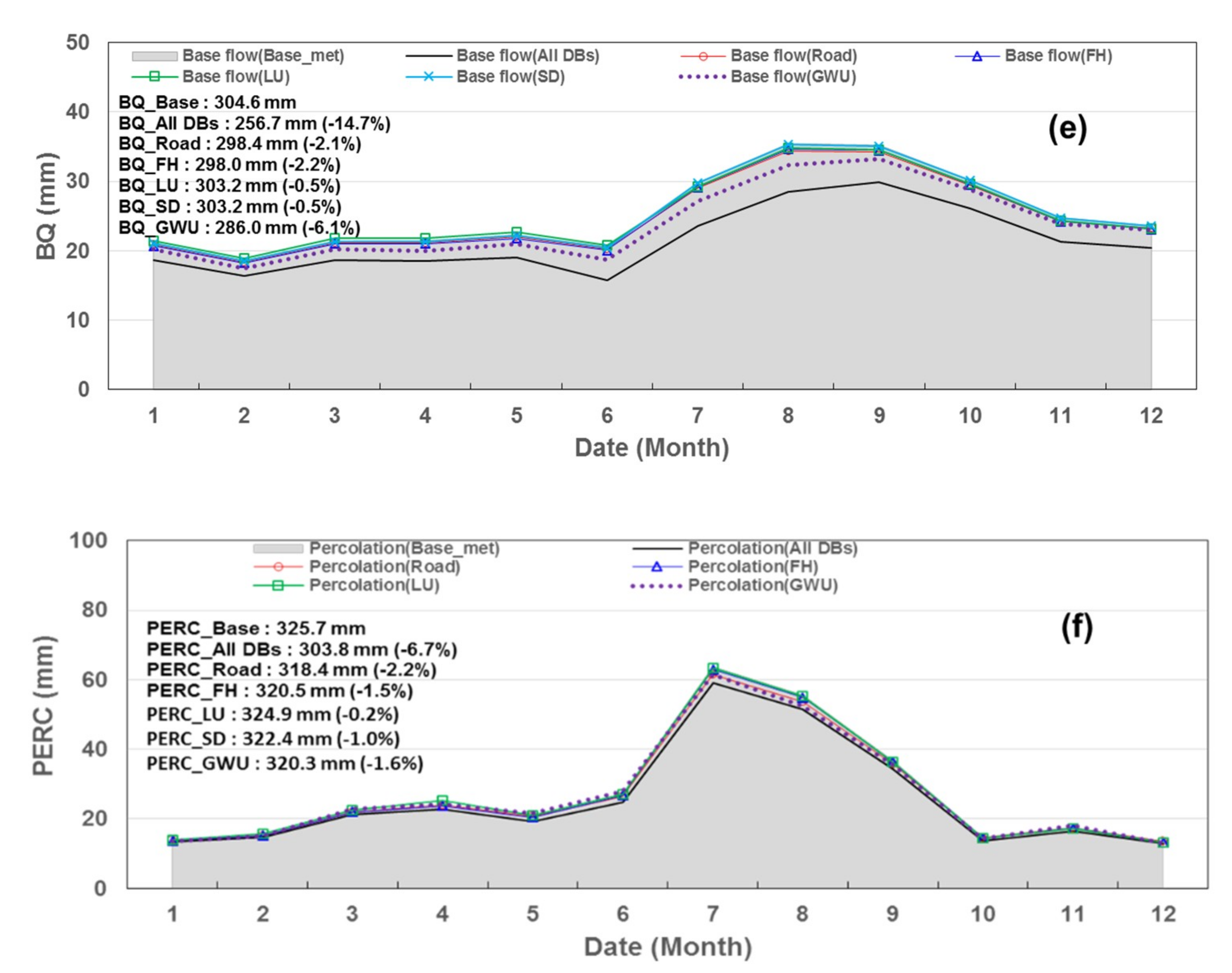
3.2. Water Balance Analysis
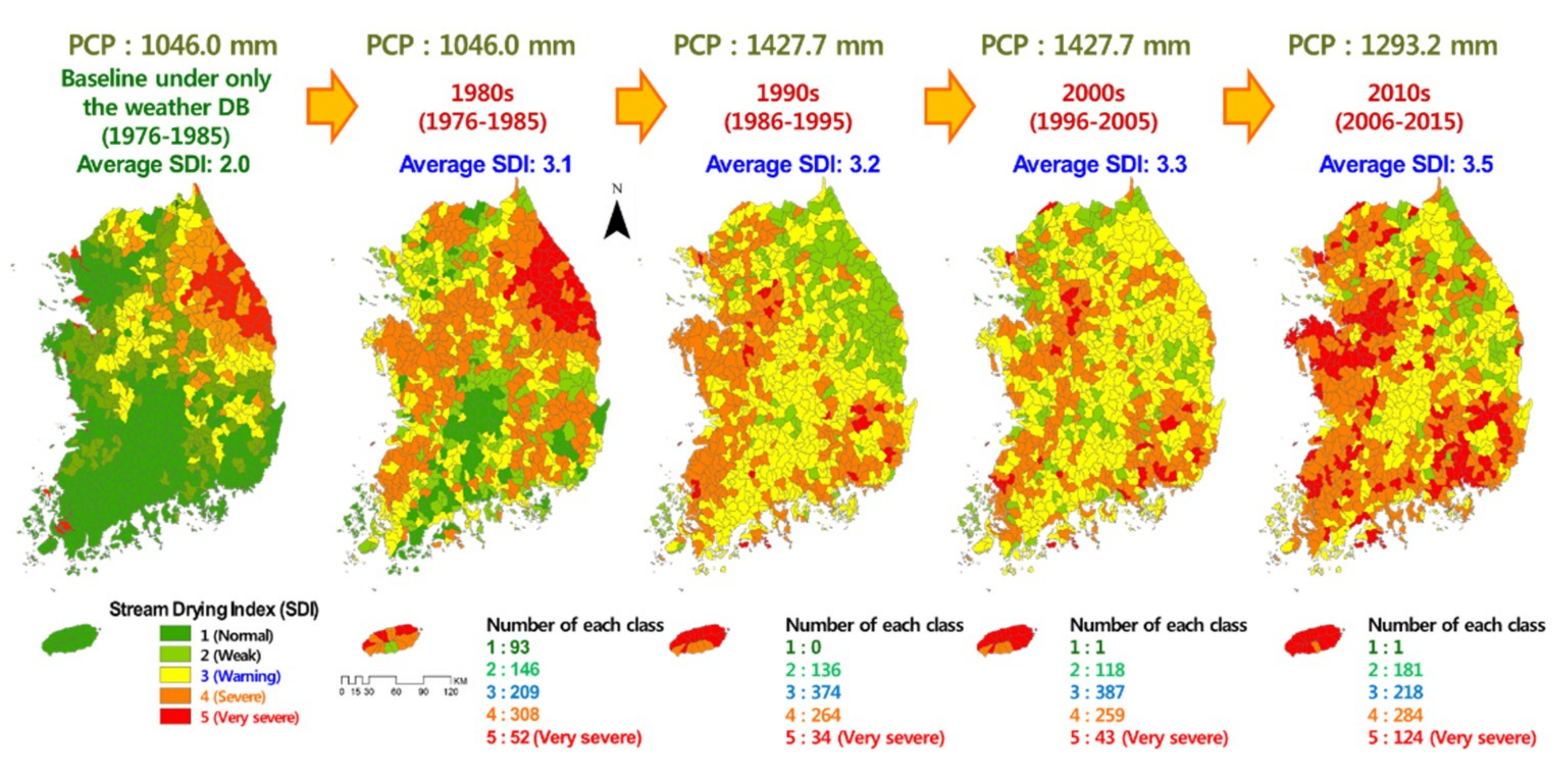
3.3. Comparison of the Stream Drying Index (SDI) Results
3.4. Verification for Severity Assessment of the Model Results
4. Conclusions
- (1)
- The stream drying phenomena were defined with the method using the 10-day minimum flow (reference Q355) by applying only the weather DB. Additionally, the DBs that can affect the stream drying phenomena were defined as water loss DBs. Then, the water loss DBs were spatially distributed from 1976 to 2015.
- (2)
- The modified DrySAT-WFT model was calibrated and verified with the TQ, ET, and SM. To quantify these phenomena, this study used the average reference Q355 values over 40 years. The progress of the phenomena was able to be analyzed by the SDI. The SDI grades were determined by counting days less than the reference Q355 value. The reference Q355 values from the 1980s (1976–1985), 1990s (1986–1995), 2000s (1996–2005), and 2010s (2006–2015) were 0.37, 0.53, 0.48, and 0.44 mm, respectively. Since the 1990s, the Q355 value has decreased by 16.9%. The lowest Q355 value was observed in the 1980s, which was affected by extreme droughts from 1976 to 1982.
- (3)
- The DrySAT-WFT model simulated the hydrological components of the water balance by each water loss DB, including the application of all DBs. As a result, the change ratios of TQ were −4.8% for GWU, −1.3% for FH, −0.3% for RN, −0.1% for LU and −0.1% for SD. Overall, the TQ decreased by −8.4%. The change ratios of ET were −2.0% for GWU, +10.5% for FH, +5.6% for RN, −1.8% for LU and +0.3% for SD. Overall, ET increased by +14.7%.
- (4)
- By applying all DBs, the SDI was evaluated in all watersheds. The SDI increased in the recent period (2006–2015). Under the changing weather DB conditions, the average SDI was 2.0 in all watersheds. The drying stream maintained a weak SDI grade. From the baseline, the stream drying progress increased to grades of 3.1 (1976–1985), 3.2 (1986–1995), 3.3 (1996–2005) and 3.5 (2006–2015) in all water loss DBs.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Equations of Grid-Based Continuous Hydrologic Model
Appendix A.1. SM Routing Equation
Appendix A.2. NRCS-CN Equation
Appendix A.3. Lateral Flow Equation
Appendix A.4. Penman-Monteith Equation
Appendix A.5. The Dynamic Resistance Equation
Appendix B. Algorithms and Water Loss Databases (DBs) for the Stream Drying Phenomena
Appendix B.1. Groundwater Use (GWU)
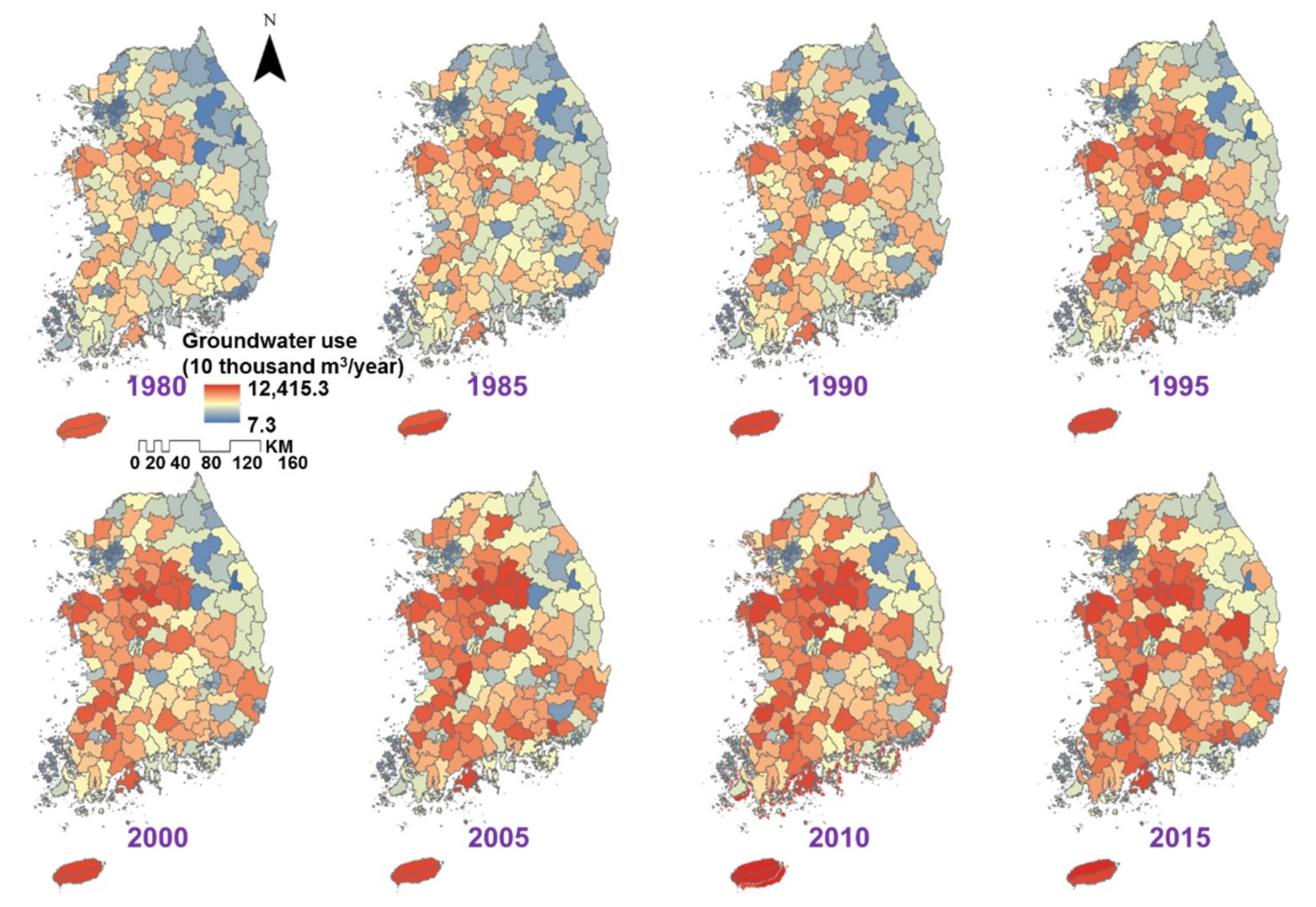
Appendix B.2. Forest Height (FH)
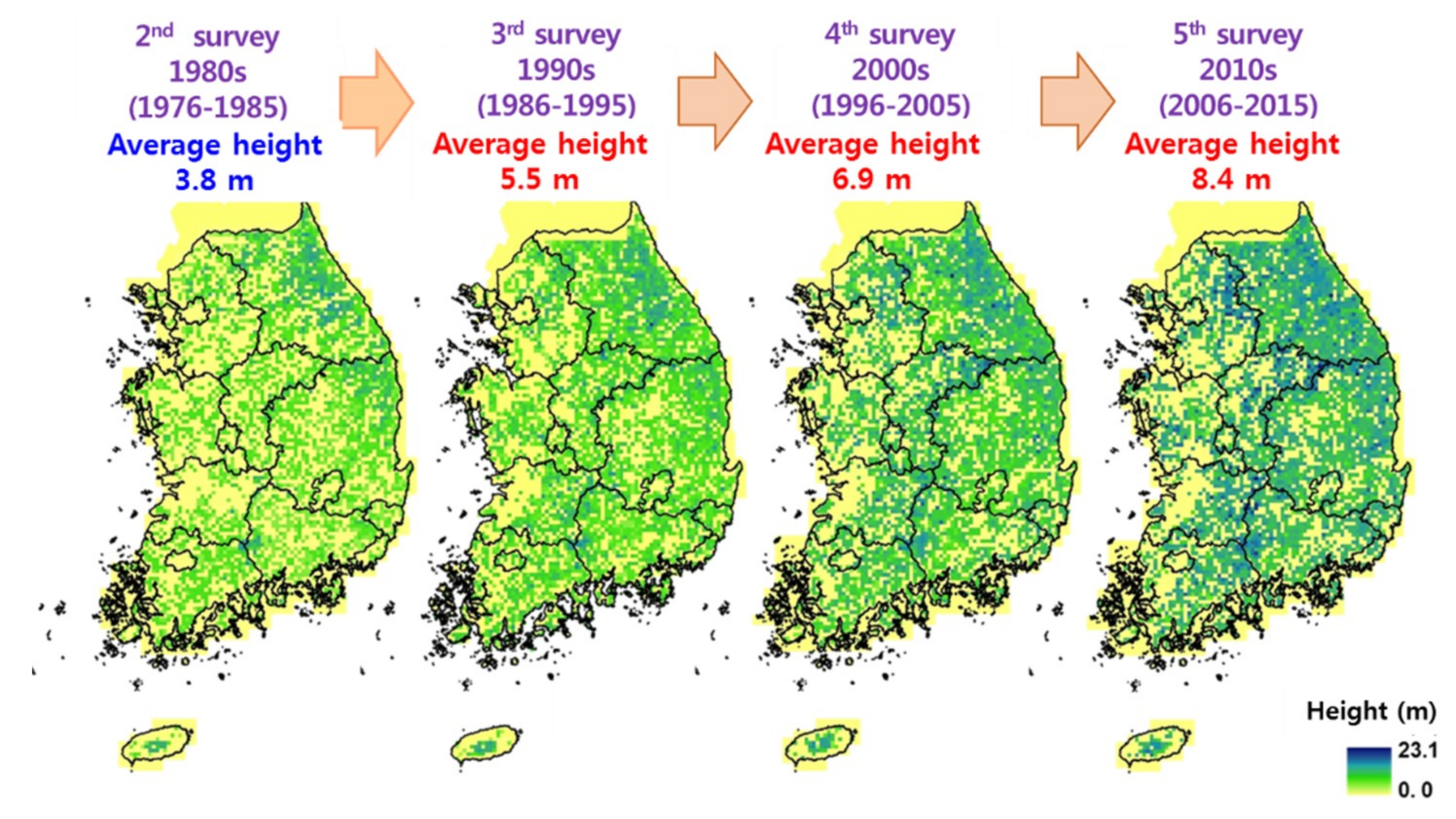
Appendix B.3. Soil Depth (SD)
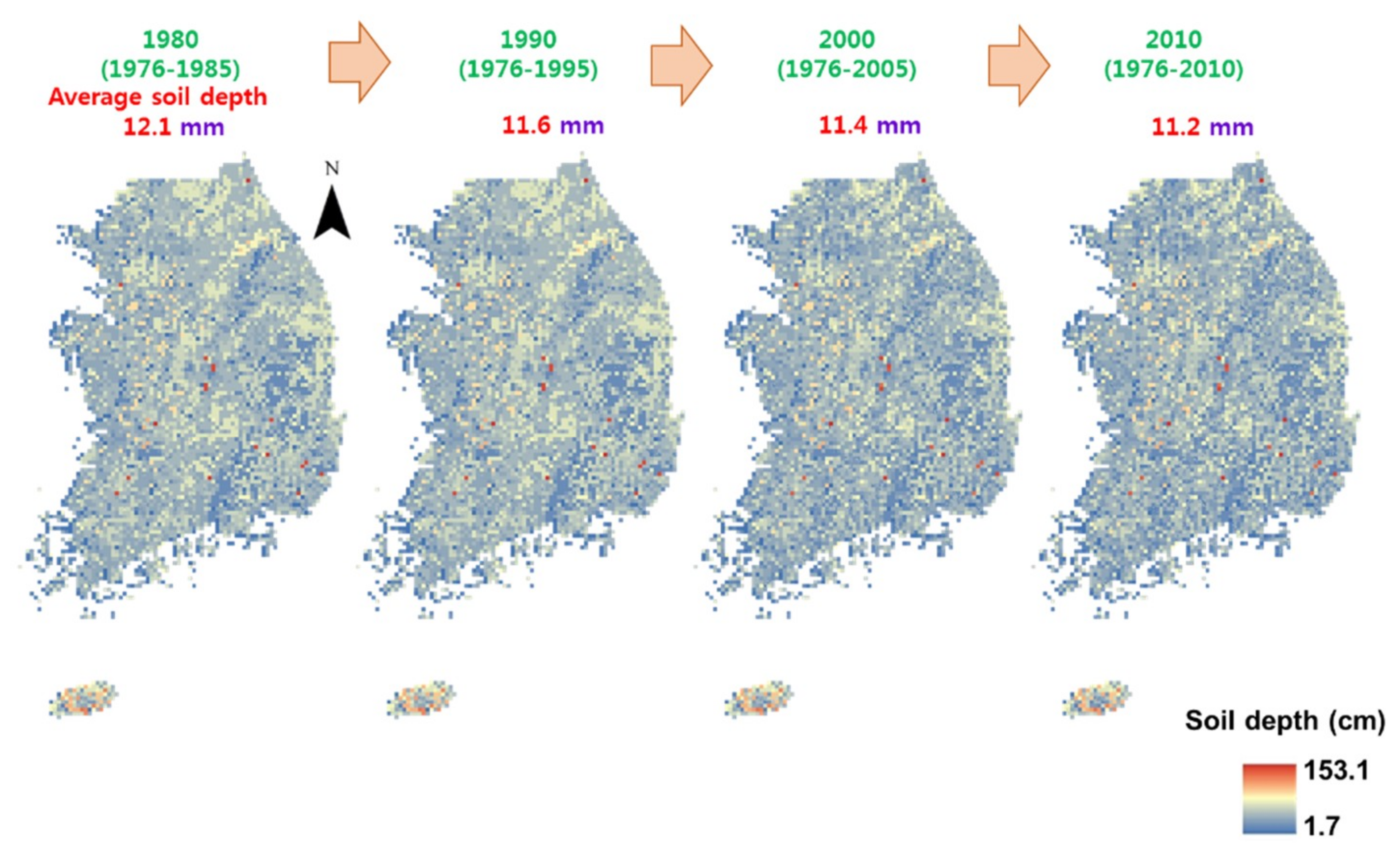
Appendix B.4. Land Use (LU)
Appendix B.5. Road Network (RN)
References
- Lake, P. Disturbance, patchiness, and diversity in streams. J. N. Am. Benthol. Soc. 2000, 19, 573–592. [Google Scholar] [CrossRef]
- Matthews, W.J.; Marsh-Matthews, E. Effects of drought on fish across axes of space, time and ecological complexity. Freshw. Biol. 2003, 48, 1232–1253. [Google Scholar] [CrossRef]
- Dekar, M.P.; Magoulick, D.D. Factors affecting fish assemblage structure during seasonal stream drying. Ecol. Freshw. Fish 2007, 16, 335–342. [Google Scholar] [CrossRef]
- Sophocleous, M. Managing water resources systems: Why “safe yield” is not sustainable. Groundwater 1997, 35, 561. [Google Scholar] [CrossRef]
- Rural Research Institute. A Study on Causative Factors of Drying Streams in Rural Area; Rural Research Institute: Tehran, Iran, 2006. [Google Scholar]
- K-water. Establishment of Quantitative Soundness Evaluation System in National Rivers (Korean); K-water: Seoul, South Korea, 2008. [Google Scholar]
- Lee, Y.G. Estimation of Spatial Evapotranspiration for South Korea by Modifying Meso-Scale SEBAL Model. Master’s Thesis, Konkuk University, Seoul, South Korea, 2016. [Google Scholar]
- Jung, K.S.; Cho, H.S.; Kim, J.Y.; Shim, M.P. Analysis of drying streams characteristics using a GIS. J. Korea Water Resour. Assoc. 2003, 36, 1083–1095. [Google Scholar] [CrossRef]
- Ministry of Science and ICT. Technology of Sustainable Surfacewater Development (Korean); Ministry of Science and ICT: Gwacheon, Gyeonggi-do, South Korea, 2003. [Google Scholar]
- Barron, O.; Barr, A.; Donn, M.J. Effect of urbanisation on the water balance of a catchment with shallow groundwater. J. Hydrol. 2013, 485, 162–176. [Google Scholar] [CrossRef]
- Kim, S.J.; Chae, H.S.; Yoo, C.S.; Shin, S.C. Stream discharge prediction via a grid based soil water routing with paddy fields 1. Jawra J. Am. Water Resour. Assoc. 2003, 39, 1143–1155. [Google Scholar] [CrossRef]
- Kim, S.J.; Kwon, H.J.; Park, G.A.; Lee, M.S. Assessment of land-use impact on streamflow via a grid-based modelling approach including paddy fields. Hydrol. Process. 2005, 19, 3801–3817. [Google Scholar] [CrossRef]
- Farokhnia, A.; Morid, S.; Byun, H.R. Application of global SST and SLP data for drought forecasting on Tehran plain using data mining and ANFIS techniques. Theor. Appl. Climatol. 2011, 104, 71–81. [Google Scholar] [CrossRef]
- Cho, Y.A. Watershed water quality evaluation model using data mining as an alternative to physical watershed models. Water Sci. Technol. Water Supply 2016, 16, 703–714. [Google Scholar] [CrossRef]
- Granata, F.; Gargano, R.; De Marinis, G. Support Vector Regression for Rainfall-Runoff Modeling in Urban Drainage: A Comparison with the EPA’s Storm Water Management Model. Water 2016, 8, 69. [Google Scholar] [CrossRef]
- Granata, F.; Saroli, M.; de Marinis, G.; Gargano, R. Machine Learning Models for Spring Discharge Forecasting. Geofluids 2018, 2018, 8328167. [Google Scholar] [CrossRef]
- Intaraprasong, T.; Zhan, H. A general framework of stream–aquifer interaction caused by variable stream stages. J. Hydrol. 2009, 373, 112–121. [Google Scholar] [CrossRef]
- Bakker, M.; Anderson, E.I. Steady flow to a well near a stream with a leaky bed. Groundwater 2003, 41, 833–840. [Google Scholar] [CrossRef]
- Theis, C. The effect of a well on the flow of a nearby stream. Trans. Am. Geophys. Union 1941, 22, 734–738. [Google Scholar] [CrossRef]
- Glover, R.E.; Balmer, G.G. River depletion resulting from pumping a well near a river. Trans. Am. Geophys. Union 1954, 35, 468–470. [Google Scholar] [CrossRef]
- Hantush, M.S. Wells near streams with semipervious beds. J. Geophys. Res. 1965, 70, 2829–2838. [Google Scholar] [CrossRef]
- Jenkins, C.T. Techniques for computing rate and volume of stream depletion by Wells. Groundwater 1968, 6, 37–46. [Google Scholar] [CrossRef]
- Hunt, B. Unsteady stream depletion from ground water pumping. Groundwater 1999, 37, 98–102. [Google Scholar] [CrossRef]
- Hunt, B. Unsteady stream depletion when pumping from semiconfined aquifer. J. Hydrol. Eng. 2003, 8, 12–19. [Google Scholar] [CrossRef]
- Hunt, B. Stream depletion for streams and aquifers with finite widths. J. Hydrol. Eng. 2008, 13, 80–89. [Google Scholar] [CrossRef]
- Landsberg, J.J.; Gower, S.T. Applications of Physiological Ecology to Forest Management; Academic Press: San Diego, CA, USA, 1997. [Google Scholar]
- Langford, K.J. Change in yield of water following a bushfire in a forest of Eucalyptus regnans. J. Hydrol. 1976, 29, 87–114. [Google Scholar] [CrossRef]
- Hornbeck, J.W.; Adams, M.B.; Corbett, E.S.; Verry, E.S.; Lynch, J.A. Long-term impacts of forest treatments on water yield: A summary for northeastern USA. J. Hydrol. 1993, 150, 323–344. [Google Scholar] [CrossRef]
- Cornish, P.M. The effects of logging and forest regeneration on water yields in a moist eucalypt forest in New South Wales, Australia. J. Hydrol. 1993, 150, 301–322. [Google Scholar] [CrossRef]
- Vertessy, R.A.; Watson, F.G.R.; O′Sullivan, S.K. Factors determining relations between stand age and catchment water balance in mountain ash forests. For. Ecol. Manag. 2001, 143, 13–26. [Google Scholar] [CrossRef]
- Vertessy, R.A.; Benyon, R.G.; O’Sullivan, S.K.; Gribben, P.R. Relationships between stem diameter, sapwood area, leaf area and transpiration in a young mountain ash forest. Tree Physiol. 1995, 15, 559–568. [Google Scholar] [CrossRef] [PubMed]
- Vertessy, R.A.; Hatton, T.J.; Reece, P.; O’Sullivan, S.K.; Benyon, R.G. Estimating stand water use of large mountain ash trees and validation of the sap flow measurement technique. Tree Physiol. 1997, 17, 747–756. [Google Scholar] [CrossRef] [PubMed]
- Jayasuriya, M.D.A.; Dunn, G.; Benyon, R.; O’Shaughnessy, P.J. Some factors affecting water yield from mountain ash (Eucalyptus regnans) dominated forests in South-East Australia. J. Hydrol. 1993, 150, 345–367. [Google Scholar] [CrossRef]
- Köstner, B.M.M.; Schulze, E.D.; Kelliher, F.; Hollinger, D.; Byers, J.; Hunt, J.; McSeveny, T.; Meserth, R.; Weir, P. Transpiration and canopy conductance in a pristine broad-leaved forest of Nothofagus: An analysis of xylem sap flow and eddy correlation measurements. Oecologia 1992, 91, 350–359. [Google Scholar] [CrossRef] [PubMed]
- Antrop, M. Landscape change and the urbanization process in Europe. Landsc. Urban Plan. 2004, 67, 9–26. [Google Scholar] [CrossRef]
- Haase, D. Effects of urbanisation on the water balance – a long-term trajectory. Environ. Impact Assess. Rev. 2009, 29, 211–219. [Google Scholar] [CrossRef]
- Trinh, D.G.; Chui, T.F.M. Assessing the hydrologic restoration of an urbanized area via an integrated distributed hydrological model. Hydrol. Earth Syst. Sci. 2013, 17, 4789–4801. [Google Scholar] [CrossRef]
- Tromp-van Meerveld, H.J.; McDonnell, J.J. On the interrelations between topography, soil depth, soil moisture, transpiration rates and species distribution at the hillslope scale. Adv. Water Resour. 2006, 29, 293–310. [Google Scholar] [CrossRef]
- Ahn, S.R.; Kim, S.J. Assessment of climate change impacts on the future hydrologic cycle of the Han river basin in South Korea using a grid-based distributed model. Irrig. Drain. 2016, 65, 11–21. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Aseessment Tool (SWAT) Theoretical Documentation Version 2009. Texas Water Reosurces Institute Technical Report No. 406; Texas A&M University: College Station, TX, USA, 2011. [Google Scholar]
- Beven, K. On subsurface stormflow: Predictions with simple kinematic theory for saturated and unsaturated flows. Water Resour. Res. 1982, 18, 1627–1633. [Google Scholar] [CrossRef]
- Bo, X.; Qing-Hai, W.A.N.G.; Jun, F.; Feng-Peng, H.A.N.; Quan-Hou, D.A.I. Application of the SCS-CN model to runoff estimation in a small watershed with high spatial heterogeneity. Pedosphere 2011, 21, 738–749. [Google Scholar]
- De Winnaar, G.; Jewitt, G.P.W.; Horan, M. A GIS-based approach for identifying potential runoff harvesting sites in the Thukela River basin, South Africa. Phys. Chem. Earth 2007, 32, 1058–1067. [Google Scholar] [CrossRef]
- Mishra, S.K.; Pandey, R.P.; Jain, M.K.; Singh, V.P. A rain duration and modified AMC-dependent SCS-CN procedure for long duration rainfall-runoff events. Water Resour. Manag. 2008, 22, 861–876. [Google Scholar] [CrossRef]
- Sloan, P.G.; Moore, I.D. Modeling subsurface stormflow on steeply sloping forested watersheds. Water Resour. Res. 1984, 20, 1815–1822. [Google Scholar] [CrossRef]
- Grismer, M.E.; Orang, M.; Snyder, R.; Matyac, R. Pan evaporation to reference evapotranspiration conversion methods. J. Irrig. Drain. Eng. 2002, 128, 180–184. [Google Scholar] [CrossRef]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. A 1948, 193, 120–145. [Google Scholar]
- Hammer, G.L.; Goyne, P.J. Determination of regional strategies for sunflower production. In Proceedings of the International Sunflower Conference Surfers paradise, Surfers Paradise, Queensland, 14–18 March 1982; pp. 48–52. [Google Scholar]
- Jones, C.A.; Kiniry, J.R.; Dyke, P.T. CERES-Maize: A Simulation Model of Maize Growth and Development; Texas A&M University Press: College Station, TX, USA, 1986. [Google Scholar]
- Ministry of Land, Infrastructure, and Transport (MLIT). A Study on Evaluation and Improvement of Drying Stream (Korean); MLIT: Tokyo, Japan, 2009. [Google Scholar]
- Jung, C.G.; Kim, S.J. Evaluation of land use change and groundwater use impact on stream drying phenomena using a grid-based continuous hydrologic model. Paddy Water Environ. 2017, 15, 111–122. [Google Scholar] [CrossRef]
- Baik, J.; Choi, M. Evaluation of remotely sensed actual evapotranspiration products from COMS and MODIS at two different flux tower sites in Korea. Int. J. Remote Sens. 2015, 36, 375–402. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models: Part I. A discussion of principles. J. Hydrol. 1970, 10, 283–290. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Am. Soc. Agric. Biol. Eng. 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M.; Bernhardt, G. A comprehensive surface-groundwater flow model. J. Hydrol. 1993, 142, 47–69. [Google Scholar] [CrossRef]
- Hong, W.Y.; Park, G.; Jeong, I.K.; Kim, S.J. Development of a grid-based daily watershed runoff model and the evaluation of its applicability. J. Korean Soc. Civ. Eng. 2010, 30, 459–469. [Google Scholar]
- Verhoef, A.; Feddes, R.A. Preliminary Review of Revised FAO Radiation and Temperature Methods Land and Water Division; FAO: Rome, Italy, 1991. [Google Scholar]
- Scanlon, B.R.; Reedy, R.C.; Stonestrom, D.A.; Prudic, D.E.; Dennehy, K.F. Impact of land use and land cover change on groundwater recharge and quality in the Southwestern US. Glob. Chang. Biol. 2005, 11, 1577–1593. [Google Scholar] [CrossRef]
- Burroughs, E.R.; Marsden, M.A.; Haupt, H.F. Volume of snowmelt intercepted by logging roads. J. Irrig. Drain. Div. Am. Soc. Civ. Eng. 1972, 98, 1–12. [Google Scholar]
- Megahan, W.F. Subsurface flow interception by a logging road in mountains of central Idaho. In National Symposium on Watershed in Transition; American Water Resources Association: Middleburg, VA, USA, 1972; pp. 350–356. [Google Scholar]
- Megahan, W.F.; Clayton, J.L. Tracing subsurface flow on roadcuts on steep, forested slopes1. Soil Sci. Soc. Am. J. 1983, 47, 1063–1067. [Google Scholar] [CrossRef]
- Harr, R.D.; Harper, W.C.; Krygier, J.T.; Hsieh, F.S. Changes in storm hydrographs after road building and clear-cutting in the Oregon Coast Range. Water Resour. Res. 1975, 11, 436–444. [Google Scholar] [CrossRef]
- King, J.G.; Tennyson, L.C. Alteration of streamflow characteristics following road construction in North Central Idaho. Water Resour. Res. 1984, 20, 1159–1163. [Google Scholar] [CrossRef]
- Jones, J.A.; Grant, G.E. Peak flow responses to clear-cutting and roads in small and large basins, Western Cascades, Oregon. Water Resour. Res. 1996, 32, 959–974. [Google Scholar] [CrossRef]
- Wemple, B.C.; Jones, J.A.; Grant, G.E. Channel network extension by logging roads in two basins, western cascades, oregon. Jawra J. Am. Water Resour. Assoc. 1996, 32, 1195–1207. [Google Scholar] [CrossRef]
- Jones, J.A. Hydrologic processes and peak discharge response to forest removal, regrowth, and roads in 10 small experimental basins, Western Cascades, Oregon. Water Resour. Res. 2000, 36, 2621–2642. [Google Scholar] [CrossRef]
- Wemple, B.C.; Jones, J.A. Runoff production on forest roads in a steep, mountain catchment. Water Resour. Res. 2003, 39, 1220–1228. [Google Scholar] [CrossRef]
- Negishi, J.N.; Sidle, R.C.; Ziegler, A.D.; Noguchi, S.; Rahim, N.A. Contribution of intercepted subsurface flow to road runoff and sediment transport in a logging-disturbed tropical catchment. Earth Surf. Process. Landf. 2008, 33, 1174–1191. [Google Scholar] [CrossRef]
| SDI | Stream Drying Progression | Condition | Comments |
|---|---|---|---|
| 1 | D ≤ 10 | Normal | - |
| 2 | 10 < D ≤ 30 | Weak | Monitor |
| 3 | 30 < D ≤ 50 | Warning | Monitor carefully |
| 4 | 50 < D ≤ 90 | Severe | Requires short-term improvement |
| 5 | 90 < D | Very severe | Requires long-term improvement |
| Parameters | Definition | Unit | Calibrated Values | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CJ | SY | AD | IH | HC | SJ | YD | JA | OSC | MHC | MR | CG | |||
| inf_rt | Soil infiltration ratio | % | 0.02 | 0.02 | 0.01 | 0.01 | 0.1 | 0.08 | 0.2 | 0.35 | 0.3 | 0.3 | 0.2 | 0.1 |
| per_rt | Soil percolation ratio | % | 0.3 | 0.2 | 0.2 | 0.2 | 0.3 | 0.35 | 0.4 | 0.4 | 0.25 | 0.15 | 0.2 | 0.3 |
| surlag | Surface runoff lag coefficient | - | 4 | 4 | 5 | 5 | 4.5 | 3 | 4 | 3 | 2.5 | 2.5 | 2.5 | 2 |
| slp_l | Lateral flow recession curve slope | degree | 0.3 | 0.3 | 0.3 | 0.3 | 0.2 | 0.25 | 0.4 | 0.4 | 0.2 | 0.3 | 0.3 | 0.25 |
| time_l | Lateral flow lag time | day | 6 | 6 | 8 | 8 | 7 | 7 | 6 | 5 | 4 | 6 | 5 | 5 |
| slp_b | Baseflow recession curve slope | degree | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.3 | 0.3 | 0.3 | 0.2 | 0.35 | 0.35 | 0.2 |
| time_b | Baseflow basin lag time | day | 7 | 7 | 10 | 10 | 7 | 7 | 8 | 9 | 9 | 10 | 7 | 8 |
| CANMX | Maximum canopy storage | mm | 7 | 7 | 7 | 7 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| Basins | State Survey (Middle Watersheds) | DrySAT Results (Standard Watersheds) | Accuracy (%) | ||||
|---|---|---|---|---|---|---|---|
| 4 Grades | 5 Grades | Total | 4 Grades | 5 Grades | Total | 4 and 5 Grades | |
| Han-river | 3/30 | 5/30 | 8/30 | 87/258 | 33/258 | 120/258 | 21/69 |
| (10.0%) | (16.7%) | (26.6%) | (33.7%) | (12.8%) | (46.5) | (30.4%) | |
| Nakdong-river | 10/42 | 12/42 | 22/42 | 75/265 | 40/265 | 115/265 | 88/124 |
| (23.8%) | (28.6%) | (52.4%) | (28.3%) | (15.1%) | (43.4) | (71.0) | |
| Geum-river | 4/20 | 6/20 | 10/20 | 64/137 | 30/137 | 94/137 | 32/44 |
| (20.0%) | (30.0%) | (50.0%) | (46.7%) | (21.9%) | (68.6) | (72.7%) | |
| Seomjin-river | 3/10 | 3/10 | 6/10 | 30/73 | 10/73 | 40/73 | 22/32 |
| (30.0%) | (30.0%) | (60.0%) | (41.1%) | (13.7%) | (54.8) | (68.8%) | |
| Youngsan-river | 4/10 | 2/10 | 6/10 | 8/14 | 2/14 | 10/14 | 14/32 |
| (40.0%) | (20.0%) | (60.0%) | (57.1%) | (14.3%) | (71.4) | (43.8%) | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, C.; Lee, J.; Lee, Y.; Kim, S. Quantification of Stream Drying Phenomena Using Grid-Based Hydrological Modeling via Long-Term Data Mining throughout South Korea including Ungauged Areas. Water 2019, 11, 477. https://doi.org/10.3390/w11030477
Jung C, Lee J, Lee Y, Kim S. Quantification of Stream Drying Phenomena Using Grid-Based Hydrological Modeling via Long-Term Data Mining throughout South Korea including Ungauged Areas. Water. 2019; 11(3):477. https://doi.org/10.3390/w11030477
Chicago/Turabian StyleJung, Chunggil, Jiwan Lee, Yonggwan Lee, and Seongjoon Kim. 2019. "Quantification of Stream Drying Phenomena Using Grid-Based Hydrological Modeling via Long-Term Data Mining throughout South Korea including Ungauged Areas" Water 11, no. 3: 477. https://doi.org/10.3390/w11030477
APA StyleJung, C., Lee, J., Lee, Y., & Kim, S. (2019). Quantification of Stream Drying Phenomena Using Grid-Based Hydrological Modeling via Long-Term Data Mining throughout South Korea including Ungauged Areas. Water, 11(3), 477. https://doi.org/10.3390/w11030477






