Abstract
An experimental soil tank (12 m long × 1.5 m wide × 1.5 m deep) equipped with a spatially distributed instrument network was designed to conduct the artificial rainfall-runoff experiments. Soil moisture (SM), precipitation, surface runoff (SR) and subsurface runoff (SSR) were continuously monitored. A total of 32 rainfall-runoff events were analyzed to investigate the non-linear patterns of rainfall-runoff response and estimate the impact of antecedent soil moisture (ASM) on runoff formation. Results suggested that ASM had a significant impact on runoff at this plot scale, and a moisture threshold-like value which was close to field capacity existed in the relationship between soil water content and event-based runoff coefficient (φe), SSR and SSR/SR. A non-linear relationship between antecedent soil moisture index (ASI) that represented the initial storage capacity of the soil tank and total runoff was also observed. Response times of SR and SM to rainfall showed a marked variability under different conditions. Under wet conditions, SM at 10 cm started to increase prior to SR on average, whereas it responds slower than SR under dry conditions due to the effect of water repellency. The predominant contributor to SR generation for all events is the Hortonian overland flow (HOF). There is a hysteretic behavior between subsurface runoff flow and soil moisture with a switch in the hysteretic loop direction based on the wetness conditions prior to the event.
1. Introduction
Nonlinearity in the spatially and temporally complicated hydrologic responses, is widely discussed in the hydrology community [1,2,3]. The typical nonlinearity in the runoff response is the combined effects of the surface runoff process, the antecedent soil moisture condition, and the way precipitation intensity affects the subsurface process. Regarding interactions of antecedent wetness conditions, various rainfall features (e.g., intensity and duration) and topography properties (e.g., soil type and soil depth) [4,5], non-linear behavior is frequently discussed as influencing surface and subsurface runoff generation processes at hillslope [6,7] and catchment scales [8]. One widely discussed nonlinear phenomenon is the rainfall-runoff threshold behavior, that is common in environmental systems, and by definition produces nonlinearity [9].
Soil moisture (SM) has great influences on the rainfall-runoff responses [5,10,11,12,13,14] and is non-linearly related to runoff generation [4,15]. Antecedent soil moisture (ASM) is the most studied factor controlling the nonlinear behavior [1,15,16,17,18,19,20]. Early work by Western and Grayson [16] showed that SR was a threshold process controlled by catchment wetness conditions, with runoff coefficients abruptly increasing when a certain moisture threshold was exceeded. Similar results for the relationship between near surface soil water content and runoff were also found by Detty and McGuire [3]; Zehe et al. [13]; Radatz et al. [15]; Tromp-van Meerveld and McDonnell [17]; James and Roulet [19]; Zhao et al. [20]; Norbiato et al. [21]; Latron and Gallart [22]; and Penna et al. [1] with varying values of the moisture threshold. Meanwhile, Zhang et al. [23] found no prominent relation between measured runoff ratio and ASM in four semi-arid watersheds. Based on the research results reported in the literature, we know that wetness conditions play a critical role in surface and subsurface runoff generation. But the physics behind the moisture threshold, e.g., how it is related to the field capacity, is still not clear.
SM also has significant impact on the response time in headwater catchments, which is defined as the time slot between the start of precipitation and first response of SM at different depths, surface runoff (SR), subsurface runoff (SSR) and groundwater. Montgomery and Dietrich [24] argued that patterns of ASM and vadose zone characteristics control response times of runoff generation by subsurface storm flow for a humid steep catchment. For a forested catchment where SR is unlikely to occur due to high infiltration rates and porosities, Blume et al. [25] investigated response times of soil moisture, groundwater and stream flow at the event scale in the wet and dry season separately, and found that both SM and groundwater reacted slower than stream flow. Penna et al. [1] showed that during dry conditions below the SM threshold value (approximately 45%), stream flow reacted and peaked prior to SM at an alpine headwater catchment scale whereas during wet periods the reverse occurred. However, Meyles et al. [26] observed that lag times in a small headwater catchment in UK were poorly related to antecedent conditions and were predominantly a function of the characteristics of rainstorms. Actually, response times are controlled by dominant runoff processes [27].
The essence of the nonlinearity in rainfall-runoff response is the runoff generation mechanisms. The spatial variability of ASM, soil properties, topography, and rainfall will result in different surface runoff generation mechanisms [28]. Runoff occurs at a certain SM value when precipitation exceeds the effective infiltration capacity of the soil, known as infiltration excess or Hortonian overland flow (HOF) [29]. Saturation excess overland flow (SOF) occurs when the soil becomes saturated, and any additional rainfall that falls (irrespective of intensity) becomes overland flow [30]. SM variability limits the predictability of hydrologic response, assuming perfect knowledge on the nature of the processes [11]. Even within a particular watershed, the dominant runoff producing mechanism might vary with storm characteristics and antecedent conditions [27]. Zhao [31] stated that HOF would occur under dry soil conditions and high intensity rainfall, and SOF primarily in humid regions. Castillo et al. [4] noted that SOF was more dependent on ASM than HOF and was affected by the spatial variations of soil characteristics within the catchment. Haga et al. [32] analyzed the lag time between peak rainfall and peak discharge in a forested catchment. They found that for events with short lag time (<2 h) SOF was dominant whereas for events with longer lag time (>24 h) saturated subsurface flow above the soil bedrock interface was the principal runoff generation process. It is believed that in humid, well-vegetated areas with shallow soils, such as in the northeastern USA, the predominant runoff generating mechanism is SOF on variable source areas [33]. To quantify SM influenced on runoff-generating mechanisms and explore the effect of dominant runoff processes on runoff formation, Leitinger et al. [34] conducted the sprinkling experiments at three hillslope scales and pointed out that pre-rain-event SM could be deemed as a precondition to generate runoff formation. When the dominant runoff mechanism was HOF, as pre-rain-event SM increased, time to runoff reduced and consequently to a prolonged runoff-generating period and a higher runoff coefficient that was defined to be the ratio of runoff intensity and the rainfall rate at a given time. Meanwhile, at the HOF/SOF-dominate site, increased pre-rain-event SM conditions led to a pronounced increase of runoff coefficient. In addition, soil water repellency is regularly observed in humid temperate climates as well as in arid and semiarid regions of the world [35]. Water repellent behavior is triggered below a certain soil moisture content [36,37]; and the switch between hydrophilic and hydrophobic conditions are strongly controlled by antecedent soil moisture conditions [35]. Above the critical soil water content, a soil behaves as a wettable porous medium, below as a water repellent one [38]. This change in state may lead to significant change of hydrological behavior, however no observational evidence in runoff about such kind of behavior being reported so far.
Most of the aforementioned research has been carried out at catchment and hillslope scales, whereas experimental plot scale studies focusing on the nonlinearity in rainfall-runoff processes with continuous monitoring of high-resolution SM, SR and SSR observations (such as Zhao et al. [20,39]) are rare. Virtual experiments are able to simplify the complexities in the nature and allow the experimentalists to use visualization as an expositive part of the approach [40]. Investigating the effects of SM on runoff at plot and hillslope scales under field and laboratory conditions can be useful for studying runoff formation and identification of hydrological processes of catchments, especially those are ungauged or areas with poor data quality. In this study, we conduct simulated rainfall-runoff experiments with high-resolution (30s) SM, precipitation, SR and SSR measurements in a big soil tank. The main objective of this research is to: (i) explore for evidence of non-linear behavior between antecedent wetness conditions and surface, subsurface flow at a plot scale; (ii) characterize response times based on rainfall, SM in near surface soil layers and surface water dynamics during the specific period; (iii) investigate the rainfall-runoff generation mechanisms under different initial wetness conditions.
2. Indoor Rainfall-Runoff Experiments
2.1. Experiment Setups
The experiment was conducted in a soil tank which is located in the State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University, Jiangsu Province, China. The experimental runoff soil tank was 12 m long, 1.5 m wide and 1.5 m deep with a slope of 0.03 which represents a gentle slope in a flat area (Figure 1). The tank was filled with a coarse sand layer of 5 cm at the bottom, and a loamy sand soil layer of 140 cm above the sand layer. A steel plate in the center divides the tank into two equal parts, and only the left side with no vegetation was used in the experiment.

Figure 1.
Structure of experimental soil tank. The left side of the soil tank with no vegetation is used in the present study. There are 3 rain gauges, 4 groundwater well and 6 groups of soil moisture (SM) sensors connected to data loggers.
A rainfall simulator is installed twenty meters above the soil tank, which can simulate rainfall covering the entire soil tank with different intensities. The width of the whole plot (including the right and left side) is 3 m, but the area wetted is 8 m wide. Thus, the soil tank could be surely wetted during the artificial rain.
The soil bulk density, porosity, particle size, wilting moisture content and so forth of the 140-cm-thick homogeneous loamy sand soil layer were measured directly (listed in Table 1). Specifically, particle size analysis was conducted by the Laser Particle Size Analyzer. Then, using USDA classification system based on grain size to determine the soil texture. Soil bulk density was determined by cutting rings (100 cm3) from undisturbed soil cores collected from each transect at 10, 30 cm depths. Saturated hydraulic conductivity (Ks) was measured by Cheng et al. [41] via single-ring infiltrometer experiment and numerical modelling jointly. Saturated water content was set equal to the maximum SM measured by sensors during the consecutive rainfall experiments. The water content of air-dried soil was deemed as the content of wilting point.

Table 1.
Soil characteristics in the soil tank.
2.2. Experimental Measurements and Processes
Six groups of SM sensors (10HS capacitance sensors, produced by Onset Computer Corporation, Bourne, MA, USA) were equipped to measure volumetric SM at 10, 30, 60, 100 cm depths, shown in Figure 1. The six groups of SM sensors were horizontally and evenly located away from the top boundary of the plot. The sensors were connected to H21-002 data-loggers and the volumetric SM was continuously measured with high temporal resolution of 30 s during the artificial precipitation as well as after rainfall ceased.
10HS sensor is one of the most recent developments using the capacitance technique [42]. Previous studies indicated that the calibration of the sensors achieved performance results similar to that of Time Domain Reflectometers [43]. 24 soil cores collected at the four investigated depths was used to calibrate the sensors, using cutting ring method. The procedure for calibrating capacitance sensors and additional details on instrumentation could be found in Starr and Palineanu [44]. Its absolute volumetric SM error is approximately ±3–4% (as given by the manufacturer). Accuracy of the sensors increases to ±1–2% after the calibration [43].
Three tipping bucket rain gauges (HOBO RG3-M, produced by Onset Computer Corporation, Bourne, MA, USA) were used to observe the rainfall characteristics with a resolution of 0.2 mm located on specific sites (Figure 1). To calibrate the rain gauges and capture the spatial pattern of simulated rainfall, 100 cups were used as a 25 × 4 grid on the soil surface of the soil tank (Figure 2). IDW method was used to interpolate the measurement of rainfall cups, and the scaling factor of three rain gauges were estimated so as to get spatial average rainfall over the soil tank during the rainfall simulations.

Figure 2.
Spatial distribution of simulated rainfall over the soil tank from the upside (left) to the downside (right). (Note: black circles are locations of the cups, and circles with cross are rain gauges).
A hole of 6 cm diameter paralleled to the soil surface was drilled and connected to a tube to measure surface runoff (SR). There are four small holes at the bottom of the downslope side of the soil tank to drain out the subsurface runoff (SSR) (or interflow). SR and SSR (strictly speaking, it is interflow) were both measured continuously (including the rising limb and the recessing limb of the hydrograph) during rainfall-runoff events at the outlet of the soil tank with tipping buckets with a capacity of 200 mL (Figure 3). Another tipping bucket was used to measure SSR at the bottom of the soil tank. Because there is a coarse sand layer at the bottom of the soil tank which made the soil water drain out of the soil tank easily, thus, groundwater was not considered in this study.

Figure 3.
(a) Device for collecting surface runoff (SR). The umbrella is used to prevent the rainfall from splashing into the tipping bucket. (b) Device for collecting subsurface runoff (SSR). There are four small holes at the bottom of the soil tank, also one hole at the bottom of the rectangular collection tank.
To avoid data missing in case of the failure of tipping bucket and estimating the proportion of sediment in SR, two big buckets with the same volume were set below the tipping buckets for several events. Sediment of the collected water by the buckets were weighed with an electronic scale (50 kg range, with a 0.01 g resolution) respectively. The proportion of sediment was about 4%. Moreover, the hydrographs for SR were quite noisy in the rainfall-runoff events because of the relatively low stability of the instruments with high measurement frequency [45]. Therefore, the tipping buckets were calibrated under several different velocities of flow.
In comparison with catchment scale experiment, one advantage of the soil tank experiments is the obvious separation of SR and SSR. However, because of short time interval (mostly one day) between rainfall events, there were overlaps of SSR between adjacent events, thus, the SSR separation for adjacent events is necessary. The comparison of the SSR recession curves of different events indicates that recession curves match each other well, therefore, to simplify the separation of subsurface runoff, the same recession curve is used for all the events, which is obtained by measuring the SSR of the final rainfall-runoff event continuously until the end of the generation of SSR. The SSR of each event is estimated as the area surrounded by the recession curve of the previous event, and the rising limb of SSR and the recession curve of the present event. For instance, the SSR of Event 2 is area surrounded the recession curve of Event 1, and the rising limb of SSR during Event 2 and the recession curve of Event 2, as shown in Figure 4.
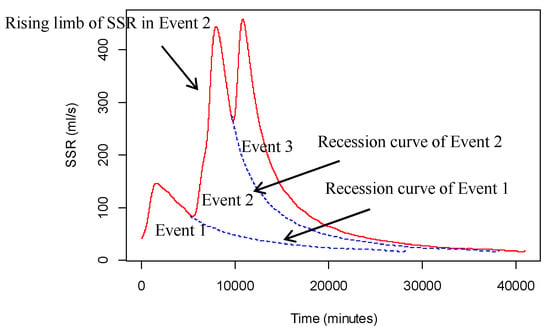
Figure 4.
A schematic diagram of the separation of subsurface runoff (SSR) for different events.
2.3. Data Obtained
Over forty rainfall-runoff events were conducted in total. However, due to the problem of instrument failure, only 32 rainfall-runoff events (Table 2) were selected for further analysis. Considering the stability of the rainfall simulator, rainfall rate of the majority events was set at about 0.8 mm min−1. Precipitation, discharge (SR and SSR) and volumetric SM data were aggregated to a 2-min interval. Event-based runoff coefficient (φe) is the ratio between event-flow volume (mm) and total rainfall (mm) for one rainfall-runoff event [46,47]. The SM varies approximately from 20% to 40% and the SM at the topmost layer varies the most.

Table 2.
Description of the 32 rainfall events.
Precipitation with relatively high kinetic energy may make the surface soil strongly sealed. Microtopography and sedimentary seal conditions determined a complicated interaction of the soil surface [48], to disentangle this problem, a surface tillage with rake to reduce sedimentary seal conditions and made the soil surface smooth was used (Figure 1).
There were two assumptions made in this study: (1) there was no unsaturated lateral flow in the soil layers because the soil tank was homogeneously textured with high sand content and non-layered, so that soil water only moved vertically except at the bottom of the soil tank; (2) evapotranspiration is not considered since evapotranspiration was minimal during the rainfall events, and the surface of soil tank was covered with a plastic film to minimize evaporation losses after each rainfall event. Meanwhile, the experiments were conducted indoor in the laboratory, we did not consider the impacts of other meteorological factors, such as wind speed, daily solar radiation and so forth.
3. Results and Discussion
We investigate the rainfall-runoff response from three aspects, i.e., precipitation, soil moisture (SM) and response time. When investigating the effects of precipitation on the rainfall-runoff relationship, the effects of SM is also considered jointly by investigating the impacts of antecedent soil moisture (ASM) and antecedent storage index (ASI). ASM is the arithmetic average of SM at depths of 10, 30, 60 and 100 cm of all the six instrumented soil profiles during the 60 min before the rainfall event [49,50,51]. ASI is calculated for each event by the arithmetic mean of values at the six transects and used to reflect initial water storage of the soil layer (0–1400 mm) in this soil tank, given by
where VWCi is the volumetric water content of the soil at the measurement point, D is the thickness of the soil (1400 mm). We use SM prior to a rainfall event integrating with the depth interval represented by each 10HS SM sensor in each soil horizon to estimate ASI at the measured depths of 0–100 cm. The SM at 100–140 cm is assumed to be equal to SM at the depth of 100 cm. ASI provides a foundation to quantify the initial wetness conditions on the subsurface water dynamics in each soil profile and control the differences in saturation deficit between events [32].
3.1. Relation between Rainfall Rate and SR Depths
Rainfall rate variations within event are not considered in our experiments, because rainfall rate in each event is set as to be uniform. Relationships among variables such as precipitation intensities among events and precipitation duration are considered; however, the relationships are not as strong as with antecedent wetness conditions. As shown in Figure 5, the correlation between rainfall rate and SR in this study is weak, mostly because precipitation intensities vary not much among events, mostly around 0.8 mm min−1, but we can find a general tendency that SR increases with the increase of rainfall rate. We focus our attention on three special points at the lower boundary and upper boundary in Figure 5, labelled with their event IDs. At the lower boundary, event 25, 10 and 23 have ASM of 29.5%, 35.8% and 26.8%, respectively, representing dry conditions, whereas at the upper boundary, event 6, 12 and 1 have ASM of 35.9%, 37.8% and 40.0%, respectively, representing comparatively wet conditions. Comparing the points in dry conditions or wet conditions, we can find that given a specific antecedent wetness, SR increases with the increase of rainfall intensity.
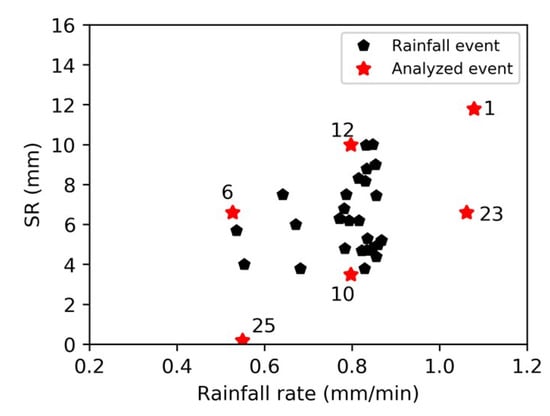
Figure 5.
The relationship between rainfall rate and SR (Surface Runoff).
According to HOF theory, SR occurs when rainfall rate exceeds the infiltration capacity. As displayed in Table 2, the saturated hydraulic conductivity is 0.47 mm/min, which is less than the rainfall intensity in our experiments. Therefore, we know that the observed SR is HOF. Meanwhile, the infiltration capacity tends to decrease as the soil moisture content of the surface layers increase, therefore SR increases with the increases of rainfall intensity and soil wetness.
3.2. Relation between SM and Runoff
The scatter plots of ASM at different depths vs. event-based surface runoff coefficient (φe) are presented in Figure 6a–d. Obviously, φe is positively related to ASM at 10, 30, 60, 100 cm and one discernible feature is that there is a threshold-like value of ASM at ~35% on average, below which φe is increase slowly with the varying of ASM, whereas above the threshold-like value φe increases sharply (Figure 6). As the infiltration capacity tends to decrease as the soil moisture content of the surface layers increases and more runoff in the form of HOF will be generated.
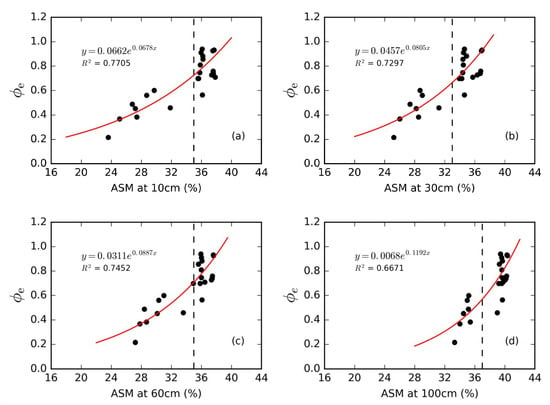
Figure 6.
Relationship between φe (Event-based runoff coefficient) and ASM (Antecedent Soil Moisture) at different depths: (a) 10 cm; (b) 30 cm; (c) 60 cm; (d) 100 cm. The vertical line highlights the significant change.
To investigate the impacts of antecedent wetness on the composition of runoff, we also plot the scatter plot of profile ASM vs. SSR in Figure 7 and profile ASM vs. the ratio of subsurface runoff to surface runoff (SSR/SR) in Figure 8. A visual inspection of Figure 7; Figure 8 reveals that there is a tendency that SSR and SSR/SR increase with the increase of ASM at different depths, and the threshold-like behavior is also observed in such an increase.
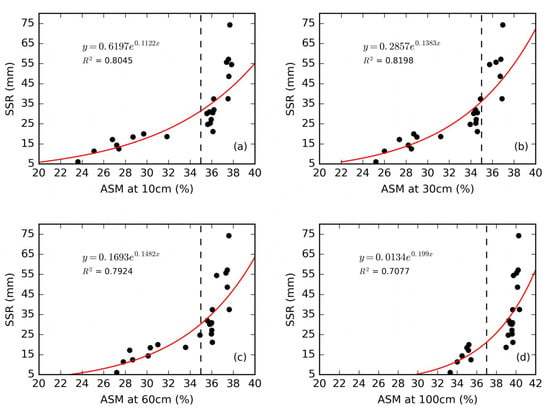
Figure 7.
Relationship between SSR (Subsurface Runoff) and ASM (Antecedent Soil Moisture) at different depths: (a) 10 cm; (b) 30 cm; (c) 60 cm; (d) 100 cm. The vertical line highlights the significant change.
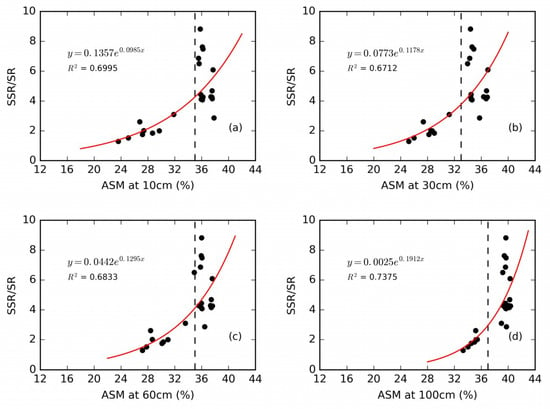
Figure 8.
Relationship between the ratio of subsurface runoff to surface runoff (SSR/SR) and ASM (Antecedent Soil Moisture) at different depths: (a) 10 cm; (b) 30 cm; (c) 60cm; (d) 100 cm. The vertical line highlights the significant change.
It has been argued recently that some non-linear systems evolve to a “critical” state, generally characterized by proximity to a threshold [9]. As the limited experimental data points in this study are incapable of capturing the threshold behavior, we recognize the significant change as threshold-like behavior [9,19]. As shown in Figure 6, the threshold-like values for ASM at depths of 10, 30, 60 cm are similar (around 33–35%), while the threshold-like value at 100 cm depth is slightly higher (37%) than that in upper soil layers. The arithmetic mean of the threshold-like values at four depths is ~35%, which is close to the field capacity.
The threshold-like behavior in the rainfall-runoff response has been reported for various types of land surface at various scales. For instance, Norbiato et al. [21] showed that when a certain moisture value was exceeded, event-based runoff coefficient (φe) is highly sensitive to SM. Similarly, as noted by Zehe et al. [13], based on the long-term monitoring with two TDR clusters, average initial SM explained 92% variability in the runoff coefficients of frost-free period rainfall-runoff events at a forested site in the Ore Mountains; a SM threshold of approximately 30% was observed between soil moisture and runoff coefficients/surface flow for silt loam soil in artificial rainfall simulation experiments by Zhao et al. [20]; Western and Grayson [16] and Penna et al. [1] found that SR was strongly controlled by ASM in a small headwater catchment with silty clay loam soil, ranging from 41% to 46% and 45%, respectively, below which no runoff occurred; James and Roulet [19] found the ASM threshold of sandy loam for runoff ratio was 22–23%, Radatz et al. [15] observed an ASM threshold of 39% for silt loam. In our present study, the ASM threshold of ~35%, for loamy sand soil are observed. However, there are insufficient data to fully demonstrate the threshold and the data can suggest an exponential relation as well [6].
The threshold-like value of ASM (0.35) is close to but a little bit less than the field capacity (0.38) in our experiments. Theoretically, after soil water content reach field capacity, any additional water will move rapidly driven by gravity, leading to the generation of interflow. That is the major runoff generation mechanism described in Xinanjiang model [31]. Two possible causes that the ASM threshold is less than the field capacity in our present study are the existence of large pores in the soil layer and the spatial heterogeneity of rainfall. In the presence of large pores, even when the soil moisture is below field capacity, water filled in the large pores can move rapidly through the pores and also generate interflow. The spatial heterogeneity of rainfall (i.e., concentration of rainfall in the center of the soil tank) would make some parts of the soil tank reach the field capacity while other parts not; therefore, the average ASM threshold is less the field capacity when interflow is generated. Many studies have reported the effects of the field capacity on soil water movement. For instance, Blume et al. [25] found that all water in excess of field capacity is being transported quickly to greater depths, SM increases most for dry antecedent conditions; Zehe and Blöschl [11] showed a threshold SM value of 32% which is on the order of the field capacity for the soils in the Weiherbach catchment; Redding and Devito [52] and Meyles et al. [26] noted when the SM increased above the field capacity, the hydraulic conductivity increased significantly and thus lateral subsurface flow generated; Leitinger et al. [34] displayed a predominant pre-rain-event SM threshold which is close to the field capacity (35% and 32% by volume). The field capacity can be deemed as an essential indicator in rainfall-runoff generation processes, and the threshold-like behavior between SSR and ASM underlines the influence of SM on runoff generation processes.
The relationship between total runoff depths and PG (i.e., gross precipitation), and ASI (i.e., antecedent soil moisture index) are also investigated (Figure 9a,c). By visual inspection of the relationship between ASI and total runoff, a clear non-linear behavior is evident (Figure 9b), and the threshold-like value is ~520 mm. This pattern suggests a critical point above which minor changes in ASI were associated with large changes in total runoff, moreover, below which large changes in ASI were associated with minor changes in total runoff.
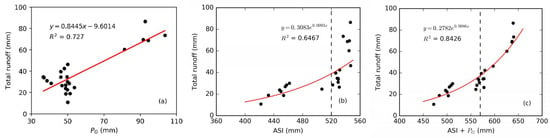
Figure 9.
Total runoff (Subsurface runoff + Surface runoff) plotted against three variables, i.e., (a) PG (gross precipitation), (b) ASI (Antecedent soil moisture index) and (c) the sum of ASI and PG.
Previous studies have explored the non-linear threshold-like behavior between the sum of ASI and PG and stormflow, and it is found that total stormflow response thresholds vary interannually due to seasonal variation of vegetation-climate interactions [2,3,32,53]. Whipkey [54] displayed a relation between total flow and precipitation in his early trench flow studies in the northeast United States. Quickflow volumes against total precipitation from Mosley [55] and Detty and McGuire [3] for catchments suggested a linear correlation and a non-linear correlation. In our soil tank experiment, linear total runoff depths response to precipitation and non-linear behavior between the sum of ASI and PG presented, also the threshold-like behavior between ASI and total runoff depths. Due to the differences in the physical properties of the soil tank and natural catchments, what we observed here is a threshold-like step change in the rainfall-runoff response.
The threshold-like pattern is often recognized as a transition between different “dynamic regimes” [56], e.g., the transition between wet and dry conditions [1], the switch between hydrophobic and hydrophilic conditions [57], and the switch between well mixed matrix flow and preferential flow paths in the subsurface [50] which leads to a rapid expansion of the runoff contributing area [3]. Once precipitation infiltrates into the soil and the SM of the topmost layer (0–10 cm) reaches the field capacity, it will be transported quickly to the deeper ones (e.g., 10–30 cm) [26,34]. In instances where the pores in soil is being filled and the soil storage capacity (the storage threshold-like value was ~520 mm) reaches, the higher hydraulic conductivity and the increase in interflow will be observed. Generally, soil storage capacity relates to moisture surpluses or deficits, and depends on soil thickness, field capacity and initial water content [58]. In this soil tank, when ASM exceeds 35% that is close to the field capacity, runoff increases sharply. The runoff response probably reflects a transition of rainfall-runoff transformation, that is, below the storage threshold-like value, the storage deficits are replenished by rainfall, whereas above the storage threshold-like value, rainfall will be increasingly transferred to SR and SSR. The same is true of the moisture threshold-like value. Thus, the field capacity and storage capacity are essential for understanding the runoff generation processes.
3.3. Response Times
According to the definition by Blume et al. [25], response time is deemed as the time period between the beginning of precipitation and the first response of SM and flow, and the beginning of precipitation and the peak occurrence. An increase of 0.2% in SM time series, and an increase of 1 mL/s in runoff time series are used in the present study to identify the first response of SM and SR to rainfall events. Figure 10 shows the response times of SM and SR for 30 (except event 1 and 25) rainfall-runoff episodes listed in Table 2. S10, S30, S60 and S100 are the response times of SM at 10, 30, 60 and 100 cm depths, SF is the response time of SR; P10, P30 and PSF are the peak times of the 10, 30 cm depth SM and SR (Figure 10). Because S60 and S100 are too long to tell the start and peak time of changes, we only present S10, S30, SF, P10, P30 and PSF in Figure 10. Because the rainfall intensity variations within event and among events are low and do not influence signigicantly response times, they are not considered in our analysis. The concentration time is negligible because the tank length is only 12 m long, and the travel time is mostly less than 20 s.
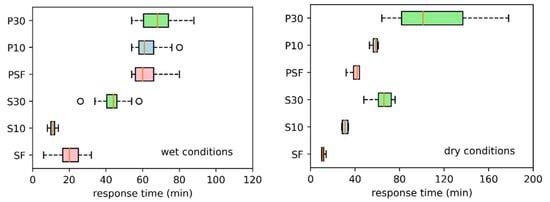
Figure 10.
Response times in SM and SR for 30 of 32 events. The notches represent 50% confidence limit of the median values. Whiskers describe the highest and lowest nonoutlier data. Different variables are presented in different colors.
To analyze the dependence of the response times on ASM, all selected events are classified into dry and wet antecedent moisture conditions according to the ASM threshold-like value (35%). As shown in Figure 10, the response times have a marked variability under different conditions. During wet conditions, SM at 10 cm on average responded quicker than SR on average, but SM at 30 cm responded slower. SF varies over large ranges. Near surface SM and SR peak at approximately the same time. Conversely, the response of SM at 10 cm to rainfall is slightly slower than SR.
Precipitation with relatively high kinetic energy left the soil tank surface strongly sealed, crusts may affect the infiltration rate and soil hydraulic conductivity of uppermost layer [59,60]. Microtopography is another essential influencing factor. Considering these factors, we slightly tilled the uppermost layer with rake to reduce sedimentary seal conditions and made the soil surface smooth (Figure 1). A new problem arising from the surface tillage is that, infiltration rate is susceptible to the disturbed soil which results in the manmade macropores and the physicochemical dispersion of soil particles [61]. It is worth mentioning that the preferential flow through macropores can increase runoff yield and increase with antecedent wetness conditions [44]. Nevertheless, almost all of S30 reacted slower than SF, which may indicate that the existence of the preferential flow between the near surface soil layers (0–30 cm) is nearly negligible. Measured infiltration rate is 0.47 mm/min in condition of no surface tillage [41], which is smaller than the designed rainfall rate. Actually, as soon as raindrops fall on the slightly tilled soil surface, the soil is compacted.
Such kind of phenomenon for dry and wet conditions were also reported in the literature, for example, Penna et al. [1] found that during wet periods, SM reacted and peaked prior to streamflow whereas the opposite occurred during dry conditions, and similar results were illustrated by Zhao et al. [20]. Our explanation for this phenomenon is that, although the initial infiltration rate is higher under dry conditions, the infiltrated water would be absorbed by the dry soil, and the hydraulic connections between the top layer and lower layers are not fully established due to stronger effects of water repellency under dry conditions than under wet conditions [62], which make the infiltrated water move down much slower, therefore S10 under dry conditions is much longer than that under wet conditions.
On the other hand, in our experiment the SM never reaches the status of saturation, and rainfall intensity is higher than the saturated hydraulic conductivity, therefore there is no doubt that the SR is dominantly generated in the form of infiltration-excess flow, or Hortonian overland flow. As shown by the response time of more than 5 min for all events, we know that the initial infiltration rates of the soil surface are larger than rainfall rates under all conditions at the beginning of each event, and no surface runoff is generated initially, especially during dry conditions, the special treatment has a little bit effect on the experimental results. But under dry conditions, poor hydraulic connections make the lower layer act as a relative impermeable layer. Such kind of relative impermeable layer can be detected by the variation of top layer soil moisture possibly due to the exhibition of water repellency. If the surface of a soil is water repellent and it starts raining, water will not infiltrate into the soil immediately, instead, it will first pond on the soil surface and, if there are any microtopographical or macrotopographical contours, then flow to the lower depressions [38]. From the pictures took during each rainfall event, we can clearly see such kind of ponding before the start of surface runoff.
As shown in Figure 11a, under dry condition (Event 28), after rainfall start, SR occurs first, then SM increases. Near surface SM quickly rebounds to previous levels, possible reasons are the reduced storage deficits and also the higher hydraulic conductivity. A special feature that needs to be noticed is the presence of a peak of SM at 10 cm, which indicates the existence of a relative impermeable layer. The effects of the relative impermeable layer, together with a high initial infiltrate rate, blocks much water from moving down. That makes the surface soil moisture increase fast, and the infiltration rate of the surface soil go down quickly to the constant infiltration rate which is below the rainfall rate, leading to the generation of Hortonian flow. At the same time, the water repellency breaks down, and soil water moves down at the constant infiltration rate. Under wet condition, water repellency may still present, as shown by the existence of the peak of SM at 10 cm, but weaker than that in the dry conditions. Therefore, the response time of surface runoff SF under dry conditions is shorter than that under wet conditions.
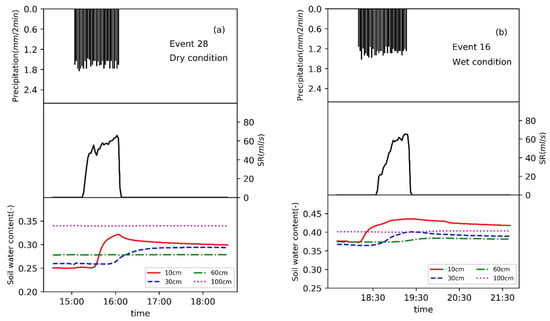
Figure 11.
Two examples of the variation of rainfall, surface runoff (SR) and soil water content at soil moisture profile SM4 with selected period: (a) Event 28 with relatively dry initial conditions (25.1%); (b) Event 16 with relatively wet initial conditions (39.4%).
Furthermore, it was reported that there is a hysteretic behavior between streamflow/subsurface flow and soil moisture [1,63,64], and such hysteretic relation between the soil moisture and runoff switches from clockwise to anticlockwise response in dry and wet conditions [1,63]. Figure 12 shows the typical hysteretic behavior in SSR with the respect to the SM at 30 cm two typical episodes with wet and dry condition. The SSR we plot in Figure 12 is not the SSR observed simultaneously with SM, instead, it is observation of SSR which is generated resulted from the pulse of the precipitation in each precipitation event (about 3 h for the wet event, and 4 h for the dry event after the start of rainfall). During the wet antecedent condition, SSR has more amount of flow when it rise than when it falls, leading to hysteretic loops with a clockwise direction, and the rising of SSR is slow in the rising limb (Figure 12a); While for the event with dry antecedent condition, the reverse situation about SSR occurs, resulted in a hysteretic behavior with an anticlockwise direction. The directions of hysteretic loops are opposite to the hysteretic behavior between streamflow and soil moisture reported by Penna et al. [1] and Graff [63]. The reason behind this needs further investigation.
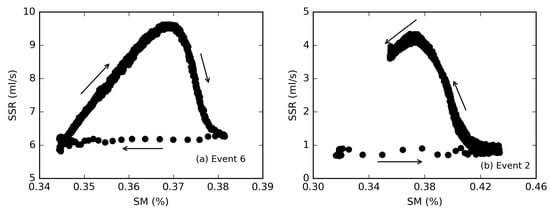
Figure 12.
Hysteretic behavior in SSR (Subsurface runoff) with the respect to the SM (soil moisture) at 30 cm during (a) an event with wet condition and (b) an event with dry condition.
4. Conclusions
An experimental soil tank (12 m long × 1.5 m wide × 1.5 m deep) equipped with a spatially distributed instrument network was designed to conduct the artificial rainfall-runoff experiments. Precipitation, discharge (SR and SSR) and volumetric SM data were collected at the soil tank and aggregated to a 2-min interval. What had been shown in this study was that the SM data offered insights into hydrological responses and runoff generation processes by analyzing 32 rainfall-runoff events that conducted by the artificial rainfall experiments under the homogeneous loamy sand soil. The main conclusions can be summarized as follows:
1. There displayed non-linear relationships between SM at surface (0–30 cm) and deep (60–100 cm) depths and runoff. Above the threshold-like value (~35%) which close to field capacity, a notable φe and SSR/SR increases occurred. The threshold-like behavior between SSR/SR and ASM will play a guiding role in the study of hydrograph separation A clear threshold-like behavior between ASI and total runoff was also found. The non-linear patterns proved the hydrologically active on both SR and SSR exerted by antecedent wetness conditions.
2. Analysis of response times showed a marked variability under different conditions. Under wet conditions SM at 10 cm started to increase prior to SR on average, whereas the response of SM at 10 cm to rainfall was slower than SR under dry conditions due to the effect of water repellency. The predominant contributor to runoff generation for all events was the HOF. There is a hysteretic behavior between subsurface runoff flow and soil moisture with a switch in the hysteretic loop direction based on the wetness conditions prior to the event.
One limitation of the study is that no mathematical modelling is used to interpret the experimental data. We will consider this aspect as a second step in the future.
Author Contributions
W.W. designed the experiment, S.S. conducted the experiment and processed the data, they wrote the paper and revised the paper jointly.
Funding
This research is financially supported by the China National Key Research and Development Program (Project No. 2017YFC0406101), the National Natural Science Foundation of China (Project No. 41830752), and the 111 Project (Grant No. B08048).
Acknowledgments
We are grateful to Wei Cui who helped a lot in conducting the experiment and processing the data, and Yongyu Xie who gave a lot of technical support during the experiments. We are also very grateful to the reviewers for their valuable and constructive comments that significantly improved the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Penna, D.; Tromp-van Meerveld, H.J.; Gobbi, A.; Borga, M.; Dalla Fontana, G. The influence of soil moisture on threshold runoff generation processes in an alpine headwater catchment. Hydrol. Earth Syst. Sci. 2011, 15, 689–702. [Google Scholar] [CrossRef]
- Scaife, C.I.; Band, L.E. Nonstationarity in threshold response of stormflow in southern Appalachian headwater catchments. Water Resour. Res. 2017, 53, 6579–6596. [Google Scholar] [CrossRef]
- Detty, J.M.; McGuire, K.J. Threshold changes in storm runoff generation at a till-mantled headwater catchment. Water Resour. Res. 2010, 46, W07525. [Google Scholar] [CrossRef]
- Castillo, V.M.; Gómez-Plaza, A.; Martínez-Mena, M. The role of antecedent soil water content in the runoff response of semiarid catchments: A simulation approach. J. Hydrol. 2003, 284, 114–130. [Google Scholar] [CrossRef]
- Zehe, E.; Becker, R.; Bárdossy, A.; Plate, E. Uncertainty of simulated catchment runoff response in the presence of threshold processes: Role of initial soil moisture and precipitation. J. Hydrol. 2005, 315, 183–202. [Google Scholar] [CrossRef]
- Tromp-van Meerveld, H.J.; Mcdonnell, J.J. Threshold relations in subsurface stormflow: 1. A 147-storm analysis of the Panola hillslope. Water Resour. Res. 2006, 42, W02410. [Google Scholar] [CrossRef]
- Weiler, M.; Mcdonnell, J.J. Conceptualizing lateral preferential flow and flow networks and simulating the effects on gauged and ungauged hillslopes. Water Resour. Res. 2007, 43, W03403. [Google Scholar] [CrossRef]
- Zehe, E.; Sivapalan, M. Threshold behaviour in hydrological systems as (human) geo-ecosystems: Manifestations, controls, implications. Hydrol. Earth Syst. Sci. 2009, 13, 1273–1297. [Google Scholar] [CrossRef]
- Phillips, J.D. Sources of nonlinearity and complexity in geomorphic systems. Prog. Phys. Geogr. 2003, 27, 1–23. [Google Scholar] [CrossRef]
- Bronstert, A.; Bárdossy, A. The role of spatial variability of soil moisture for modelling surface runoff generation at the small catchment scale. Hydrol. Earth Syst. Sci. 1999, 3, 505–516. [Google Scholar] [CrossRef]
- Zehe, E.; Blöschl, G. Predictability of hydrologic response at the plot and catchment scales: Role of initial conditions. Water Resour. Res. 2004, 40, W10202. [Google Scholar] [CrossRef]
- Blöschl, G.; Zehe, E. On hydrological predictability. Hydrol. Process. 2005, 19, 3923–3929. [Google Scholar] [CrossRef]
- Zehe, E.; Graeff, T.; Morgner, M.; Bauer, A.; Bronstert, A. Plot and field scale soil moisture dynamics and subsurface wetness control on runoff generation in a headwater in the Ore Mountains. Hydrol. Earth Syst. Sci. 2010, 14, 873–889. [Google Scholar] [CrossRef]
- McGuire, K.J.; McDonnell, J.J. Hydrological connectivity of hillslopes and streams: Characteristic time scales and nonlinearities. Water Resour. Res. 2010, 46, W10543. [Google Scholar] [CrossRef]
- Radatz, T.F.; Thompson, A.M.; Madison, F.W. Soil moisture and rainfall rate thresholds for runoff generation in southwestern Wisconsin agricultural watersheds. Hydrol. Process. 2013, 27, 3521–3534. [Google Scholar] [CrossRef]
- Western, A.W.; Grayson, R.B. The Tarrawarra data set: Soil moisture patterns, soil characteristics, and hydrological flux measurements. Water Resour. Res. 1998, 34, 2765–2768. [Google Scholar] [CrossRef]
- van Meerveld, I.T.; McDonnell, J.J. Comment to “Spatial correlation of soil moisture in small catchments and its relationship to dominant spatial hydrological processes, Journal of Hydrology 286: 113–134”. J. Hydrol. 2005, 303, 307–312. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T. Empirical and conceptual approaches for soil moisture estimation in view of event-based rainfall-runoff modeling. In Proceedings of the 10th Conference of the Euromediterranean, Network of Experimental and Representative Basins (ERB), Turin, Italy, 13–17 October 2004. [Google Scholar]
- James, A.L.; Roulet, N.T. Investigating hydrologic connectivity and its association with threshold change in runoff response in a temperate forested watershed. Hydrol. Process. 2007, 21, 3391–3408. [Google Scholar] [CrossRef]
- Zhao, N.; Yu, F.; Li, C.; Zhang, L.; Liu, J.; Mu, W.; Wang, H. Soil moisture dynamics and effects on runoff generation at small hillslope scale. J. Hydrol. Eng. 2015, 20, 05014024. [Google Scholar] [CrossRef]
- Norbiato, D.; Borga, M.; Merz, R.; Blöschl, G.; Carton, A. Controls on event runoff coefficients in the eastern Italian Alps. J. Hydrol. 2009, 375, 312–325. [Google Scholar] [CrossRef]
- Latron, J.; Gallart, F. Runoff generation processes in a small Mediterranean research catchment (Vallcebre, Estern Pyrenees). J. Hydrol. 2008, 358, 206–220. [Google Scholar] [CrossRef]
- Zhang, Y.; Wei, H.; Nearing, M.A. Effects of antecedent soil moisture on runoff modeling in small semiarid watersheds of southeastern Arizona. Hydrol. Earth Syst. Sci. 2011, 15, 3171–3179. [Google Scholar] [CrossRef]
- Montgomery, D.R.; Dietrich, W.E. Runoff generation in a steep, soil-mantled lanscape. Water Resour. Res. 2002, 38, 1168. [Google Scholar] [CrossRef]
- Blume, T.; Zehe, E.; Bronstert, A. Use of soil moisture dynamics and patterns at different spatio-temporal scales for the investigation of subsurface flow processes. Hydrol. Earth Syst. Sci. 2009, 13, 1215–1233. [Google Scholar] [CrossRef]
- Meyles, E.W.; Williams, A.G.; Ternan, J.L.; Anderson, J.M.; Dowd, J.F. The influence of grazing on vegetation, soil properties and stream discharge in a small Dartmoor catchment, southwest England, UK. Earth Surf. Process. Landf. 2006, 31, 622–631. [Google Scholar] [CrossRef]
- Dunne, T. Field studies of hillslope flow processes. In Hillslope Hydrology; Kirkby, M.J., Ed.; Wiley: Chichester, UK, 1978; pp. 227–293. [Google Scholar]
- Xie, Z.; Su, F.; Liang, X.; Zeng, Q.; Hao, Z.; Guo, Y. Applications of a surface runoff model with Horton and Dunne runoff for VIC. Adv. Atmos. Sci. 2003, 20, 165–172. [Google Scholar]
- Minet, J.; Laloy, E.; Lambot, S.; Vanclooster, M. Effect of high-resolution spatial soil moisture variability on simulated runoff response using a distributed hydrologic model. Hydrol. Earth Syst. Sci. 2011, 15, 1323–1338. [Google Scholar] [CrossRef]
- Dunne, T.; Black, R.D. Partial area contributions to storm runoff in a small New England watershed. Water Resour. Res. 1970, 6, 1296–1311. [Google Scholar] [CrossRef]
- Zhao, R.-J.; Zuang, Y.-L.; Fang, L.-R.; Liu, X.-R.; Zhang, Q.-S. The Xinanjiang model. In Proceedings of the Oxford Symposium, Oxford, UK, 15–18 April 1980; pp. 351–356. [Google Scholar]
- Haga, H.; Matsumoto, Y.; Matsutani, J.; Fujita, M.; Nishida, K.; Sakamoto, Y. Flow paths, rainfall properties, and antecedent soil moisture controlling lags to peak discharge in a granitic unchanneled catchment. Water Resour. Res. 2005, 41, W12410. [Google Scholar] [CrossRef]
- Schneiderman, E.M.; Steenhuis, T.S.; Thongs, D.J.; Easton, Z.M.; Zion, M.S.; Neal, A.L.; Mendoza, G.F.; Todd Walter, M. Incorporating variable source area hydrology into a curve-number-based watershed model. Hydrol. Process. 2007, 21, 3420–3430. [Google Scholar] [CrossRef]
- Leitinger, G.; Ruggenthaler, R.; Markart, G.; Klebinder, K.; Schöberl, F.; Hammerle, A. Quantification of soil moisture effects on runoff formation at the hillslope scale. J. Irrig. Drain. Eng. 2015, 141, 5015001. [Google Scholar]
- Dekker, L.W.; Oostindie, K.; Ritsema, C.J. Exponential increase of publications related to soil water repellency. Aust. J. Soil Res. 2005, 43, 403–441. [Google Scholar] [CrossRef]
- Dekker, L.W.; Ritsema, C.J. How water moves in a water repellent sandy soil: 1. Potential and actual water repellency. Water Resour. Res. 1994, 30, 2507–2517. [Google Scholar] [CrossRef]
- Dekker, L.W.; Doerr, K.; Oostindie, K.; Ziogas, A.K.; Ritsema, C.J. Water repellency and critical soil water content in a dune sand. Soil Sci. Soc. Am. J. 2001, 65, 1667–1674. [Google Scholar] [CrossRef]
- Dekker, L.W.; Ritsema, C.J.; Oostindie, K.; Morre, D.; Wesseling, J.G. Methods for determining soil water repellency on field-moist samples. Water Resour. Res. 2009, 45, W00D33. [Google Scholar] [CrossRef]
- Zhao, N.N.; Yu, F.L.; Li, C.Z.; Wang, H.; Liu, J.; Mu, W.B. Investigation of Rainfall-Runoff Processes and Soil Moisture Dynamics in Grassland Plots under Simulated Rainfall Conditions. Water 2014, 6, 2671–2689. [Google Scholar] [CrossRef]
- Weiler, M.; McDonnell, J. Virtual experiments: A new approach for improving process conceptualization in hillslope hydrology. J. Hydrol. 2004, 285, 3–18. [Google Scholar] [CrossRef]
- Cheng, Q.B.; Chen, X.; Zhao, L.L.; Ling, M.H. Dynamic coupled modeling and infiltration experiment on soil water in saturated and unsaturated zones. J. Hohai Univ. 2009, 37, 284–289. (In Chinese) [Google Scholar]
- Kargas, G.; Soulis, K.X. Performance analysis and calibration of a new low-cost capacitance soil moisture sensor. J. Irrig. Drain. Eng. 2012, 138, 632–641. [Google Scholar] [CrossRef]
- Czarnomski, N.M.; Moore, G.W.; Pypker, T.G.; Licata, J.; Bond, B.J. Precision and accuracy of three alternative instruments for measuring soil water content in two forest soils of the Pacific Northwest. Can. J. For. Res. 2005, 35, 1867–1876. [Google Scholar] [CrossRef]
- Starr, J.L.; Paltineanu, I.C. Methods for Measurement of Soil Water Content: Capacitance Devices; Agricultural Research Service (ARS), U.S. Department of Agriculture: Washington, DC, USA, 2002.
- Kirstetter, G.; Hu, J.; Delestre, O.; Darboux, F.; Lagrée, P.Y.; Popinet, S.; Fullana, J.M.; Josserand, C. Modeling rain-driven overland flow: Empirical versus analytical friction terms in the shallow water approximation. J. Hydrol. 2016, 536, 1–9. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G. A regional analysis of event runoff coefficients with respect to climate and catchment characteristics in Austria. Water Resour. Res. 2009, 45, W01405. [Google Scholar] [CrossRef]
- Blume, T.; Zehe, E.; Bronstert, A. Rainfall-runoff response, event-based runoff coefficients and hydrograph separation. Hydrol. Sci. J. 2007, 52, 843–862. [Google Scholar] [CrossRef]
- Langhans, C.; Govers, G.; Diels, J.; Leys, A.; Clymans, W.; Van de Putte, A.; Valckx, J. Experimental rainfall-runoff data: the concept of infiltration capacity needs re-thinking. In Proceedings of the EGU General Assembly 2009, Vienna, Austria, 19–24 April 2009; p. 4496. [Google Scholar]
- Gao, X.; Wu, P.; Zhao, X.; Shi, Y.; Wang, J.; Zhang, B. Soil moisture variability along transects over a well-developed gully in the Loess Plateau, China. Catena 2011, 87, 357–367. [Google Scholar] [CrossRef]
- Qiu, Y.; Fu, B.J.; Wang, J.; Chen, L.D. Spatiotemporal prediction of SM using multiple-linear regression in a small catchment of The Loess Plateau, China. Catena 2003, 54, 173–195. [Google Scholar] [CrossRef]
- Yi, C.Q.; Fan, J. Application of hydrus-1d model to provide antecedent soil water contents for analysis of runoff and soil erosion from a slope on the loess plateau. Catena 2016, 139, 1–8. [Google Scholar]
- Redding, T.E.; Devito, K.J. Lateral flow thresholds for aspen forested hillslopes on the Western Boreal Plain, Alberta, Canada. Hydrol. Process. 2008, 22, 4287–4300. [Google Scholar] [CrossRef]
- Sidle, R.C.; Tsuboyama, Y.; Noguchi, S.; Hosoda, I.; Fujieda, M.; Shimizu, T. Seasonal hydrologic response at various spatial scales in a small forested catchment, Hitachi Ohta, Japan. J. Hydrol. 1995, 168, 227–250. [Google Scholar] [CrossRef]
- Whipkey, R. Subsurface stormflow from forested slopes. Int. Assoc. Sci. Hydrol. Bull. 1965, 10, 74–85. [Google Scholar] [CrossRef]
- Mosley, M.P. Streamflow generation in a forested watershed, New Zealand. Water Resour. Res. 1979, 15, 795–806. [Google Scholar] [CrossRef]
- Lindenmaier, F.; Zehe, E.; Helms, M.; Evdakov, O.; Ihringer, J. Effect of soil shrinkage on runoff generation in micro and mesoscale catchments. In Proceedings of the Symposium S7, 7th IAHS Scientific Assembly, Foz do Iguacu, Brazil, 3–9 April 2005; pp. 305–317. [Google Scholar]
- Zehe, E.; Elsenbeer, H.; Lindenmaier, F.; Schulz, K.; Blöschl, G. Patterns of predictability in hydrological threshold systems. Water Resour. Res. 2007, 43, W07434. [Google Scholar] [CrossRef]
- Langhans, C.; Govers, G.; Diels, J.; Leys, A.; Clymans, W.; Van de Putte, A.; Valckx, J. Experimental rainfall-runoff data: Reconsidering the concept of infiltration capacity. J. Hydrol. 2011, 399, 255–262. [Google Scholar] [CrossRef]
- Morin, J.; Keren, R.; Benjamini, Y.; Ben-Hur, M.; Shainberg, I. Water infiltration as affected by soil crust and moisture profile. Soil Sci. 1989, 148, 53–59. [Google Scholar] [CrossRef]
- Cantón, Y.; Domingo, F.; Solé-Benet, A.; Puigdefábregas, J. Hydrological and erosion response of a badlands system in semiarid SE Spain. J. Hydrol. 2001, 252, 65–84. [Google Scholar] [CrossRef]
- Agassi, M.; Shainberg, I.; Morin, J. Effect of electrolyte concentration and soil sodicity on infiltration rate and crust formation. Soil Sci. Soc. Am. J. 2010, 45, 848–851. [Google Scholar] [CrossRef]
- Doerr, S.H.; Thomas, A.D. The role of soil moisture in controlling water repellency: New evidence from forest soils in Portugal. J. Hydrol. 2000, 231–232, 134–147. [Google Scholar] [CrossRef]
- Gräff, T. Soil Moisture Dynamics and Soil Moisture Controlled Runoff Processes at Different Spatial Scales: From Observation to Modeling. Ph.D. Thesis, University of Potsdam, Berlin-Brandenburg, Germany, 2011. [Google Scholar]
- Hrnčíř, M.; Šanda, M.; Kulasová, A.; Císlerová, M. Runoff formation in a small catchment at hillslope and catchment scales. Hydrol. Process. 2010, 24, 2248–2256. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).