Water Price Prediction for Increasing Market Efficiency Using Random Forest Regression: A Case Study in the Western United States
Abstract
:1. Introduction
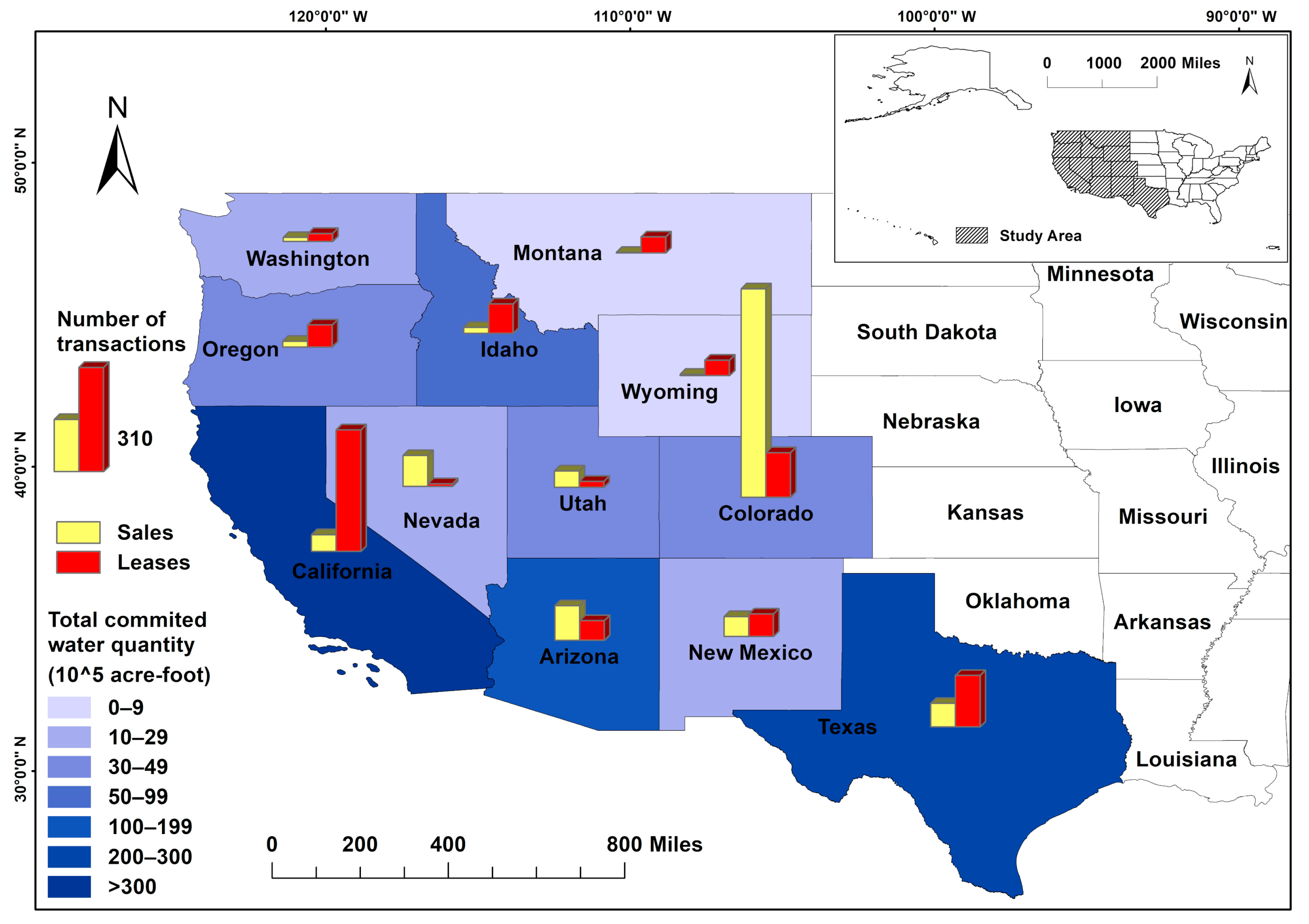
2. Study Area and Data
3. Methods
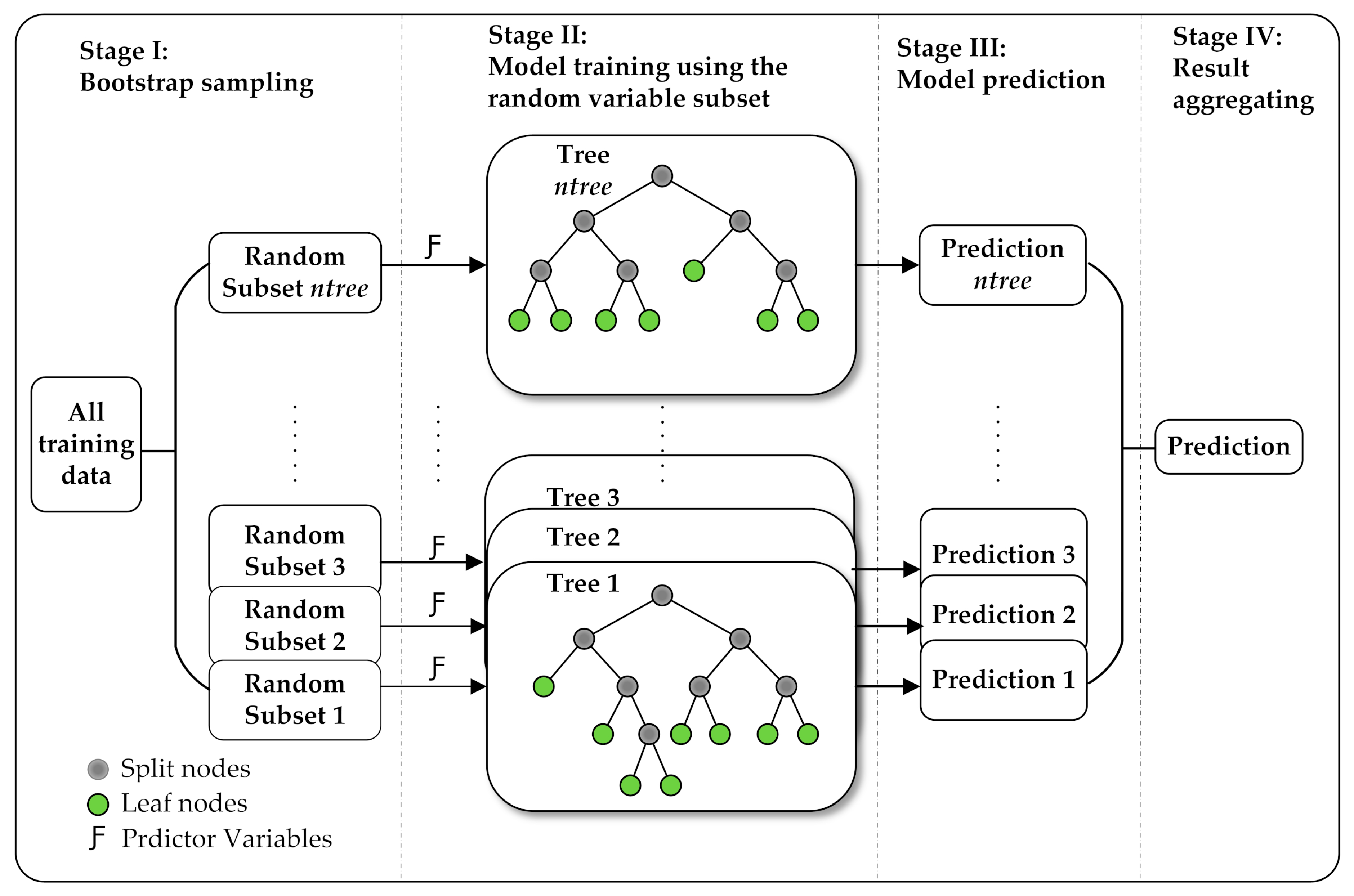
3.1. Random Forest Regression
- (1)
- Use the bootstrap method to produce ntree subset samples from the original training dataset, where ntree is the number of trees to grow.
- (2)
- Grow regression trees on each bootstrap sample, during which, randomly draw a subset containing mtry predictor variables at each splitting node and determine the optimal split based on this subset of variables only. This process is conducted recursively until a stopping criterion (nodesize) is reached.
- (3)
- Obtain regression predictions over ntree decision trees. For each individual tree, the prediction is the mean of the dependent variable values at the corresponding leaf nodes.
- (4)
- Compute the final prediction by averaging ntree predictions in the forest.
3.2. Model Hyperparameter Optimization
- (1)
- For each round of CV, tune hyperparameters using the grid search method to minimize the OOB error within the training dataset.
- (2)
- Assign the hyperparameter combinations with the lowest OOB errors to each of the k models and test their performances using their corresponding validation datasets. The hyperparameter combination that has the best model performance is the final model configuration.
3.3. Variable Importance Metrics
3.4. Model Performance Indices
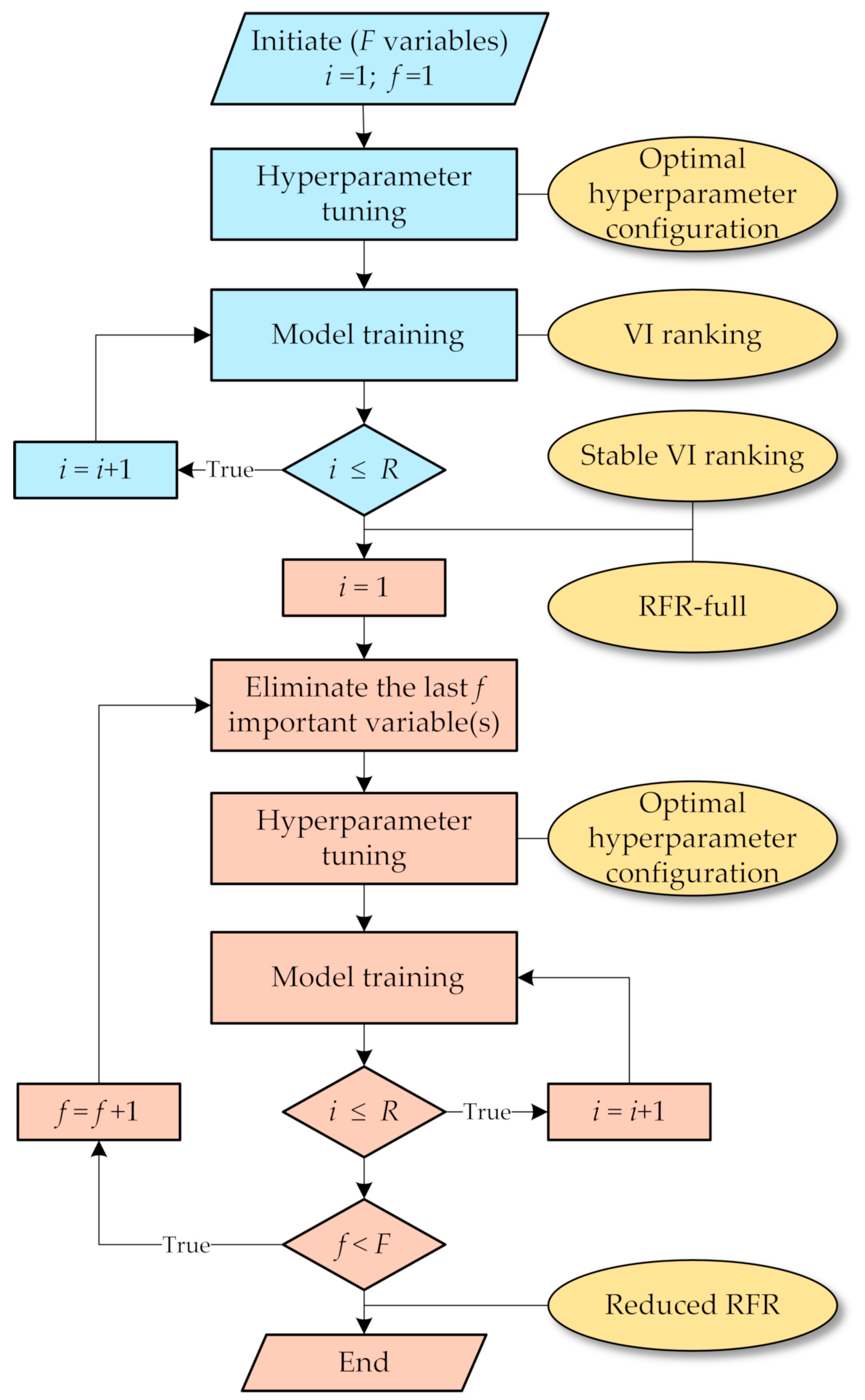
3.5. Stepwise Model Selection
- (1)
- Obtain the optimal hyperparameter configuration of RFR-full as described in Section 3.2. Compute the VI scores of the F variables based on the optimal hyperparameters. Average VI scores over R replications to acquire a stable VI ranking.
- (2)
- Build a stepwise series of F−1 RFR models by iteratively eliminating the last f important variable(s). That is, according to the finalized ranking, discard the least important variable in the first round (when f = 1), and continue to remove the next important variable until a series of RFR models with F−1, F−2,…, 1 variables are constructed. For each model, an optimal hyperparameter set is selected and the model is trained R times.
- (3)
- Evaluate the series of RFR models by averaging their performances over the R runs. The optimal RFR reduced model is the one with the highest predictive performance.
4. Results and Discussion
- (1)
- The full variable set RFR model (RFR-full);
- (2)
- The optimal reduced RFR developed based on the PVI metric (RFR-red-P);
- (3)
- The optimal reduced RFR developed based on the NVI metric (RFR-red-N);
- (4)
- A single decision tree model (DT), which was used as a baseline model. It was programmed based on the R part package in the R computer language.
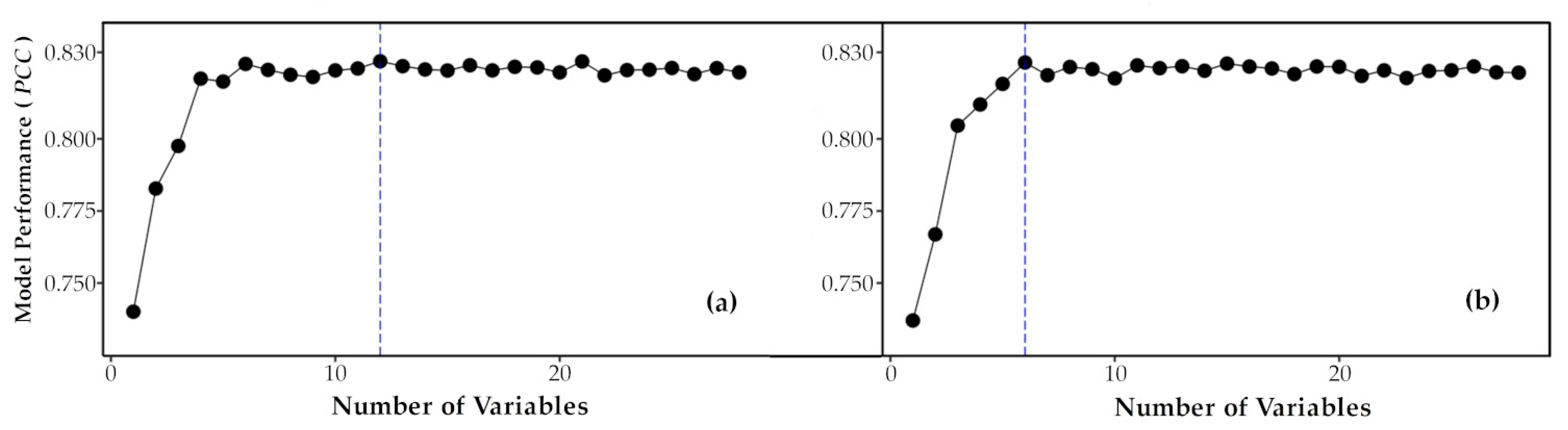
4.1. Optimal Numbers of Variables
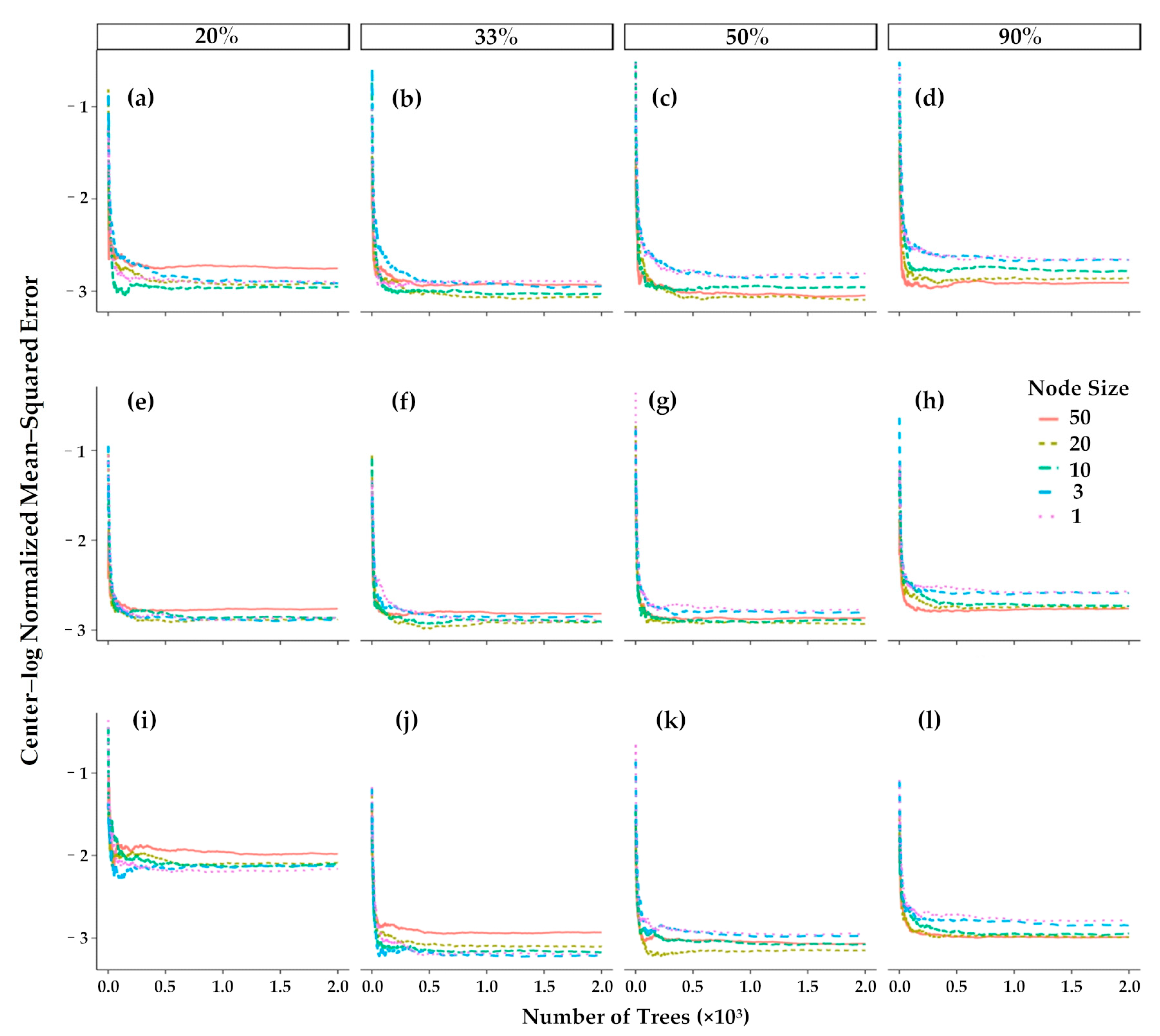
4.2. Optimal Hyperparameters
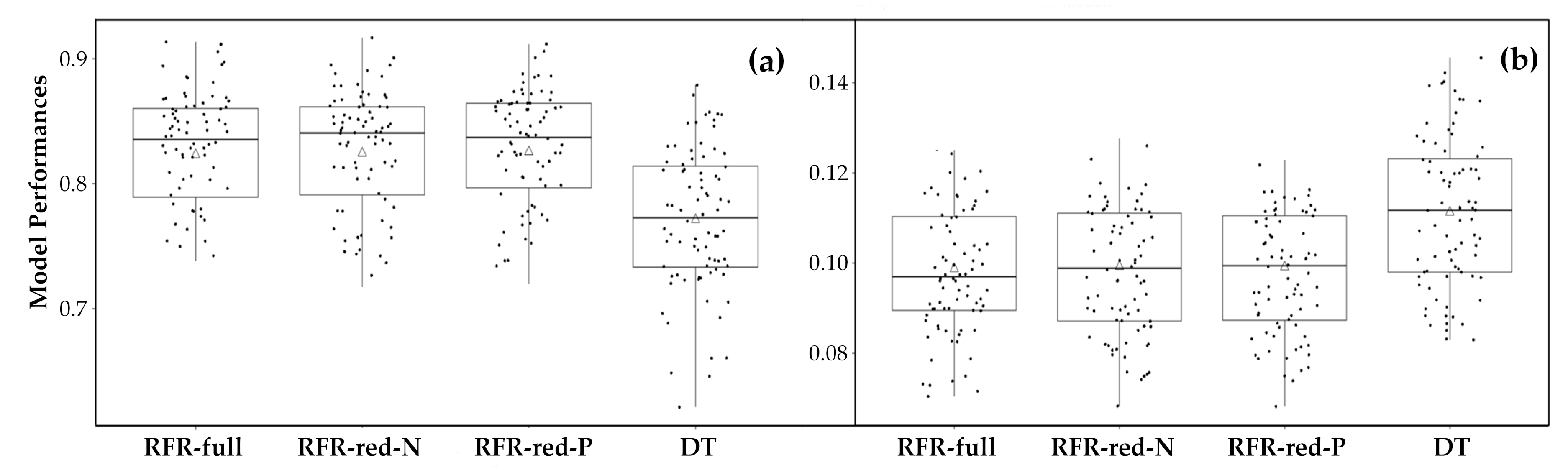
4.3. Model Performances
4.3.1. Predictive Accuracy
4.3.2. Model Reliability
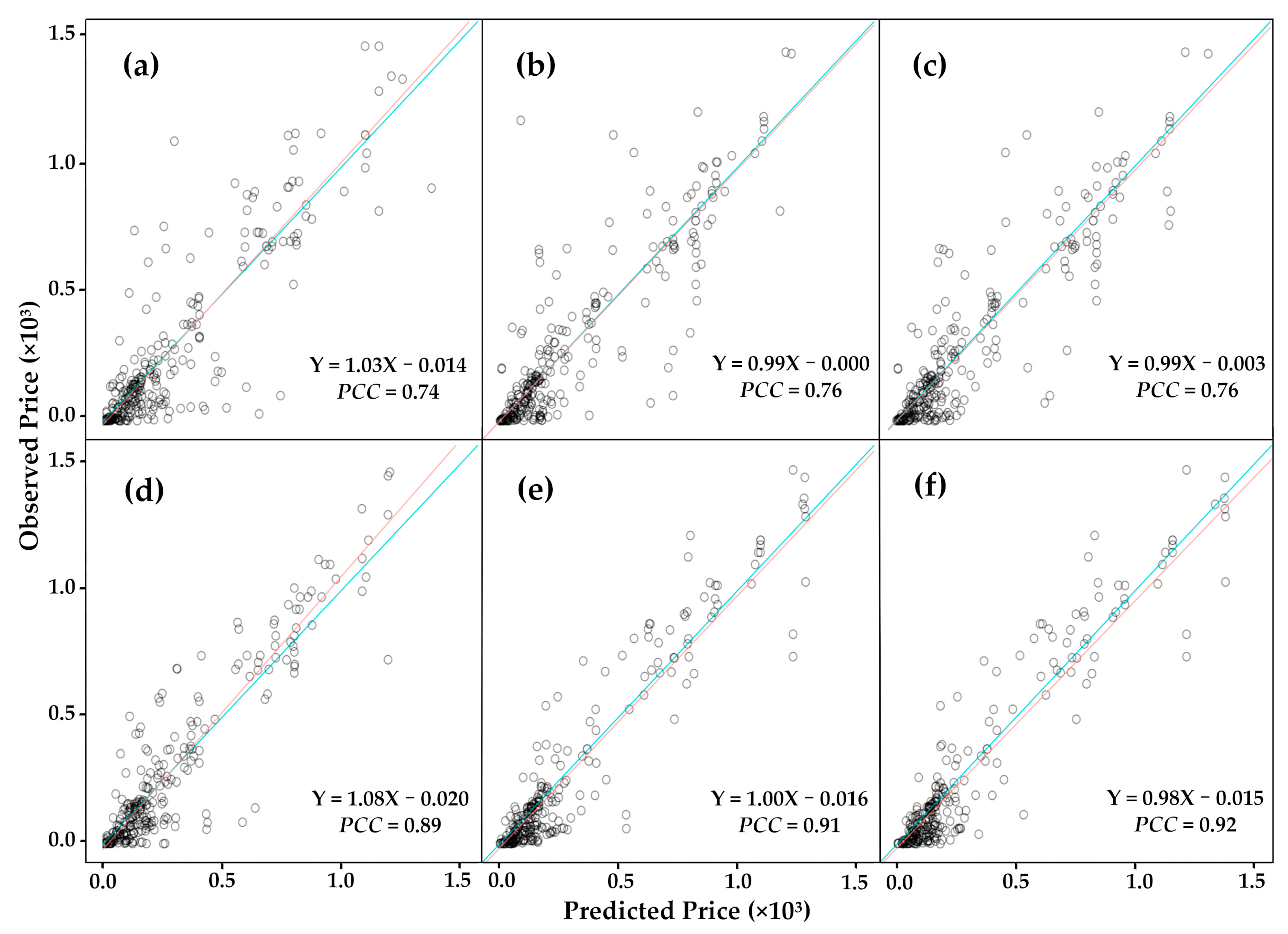
4.3.3. Consistency and Bias between Observations and Predictions
4.3.4. Model Generalization
4.4. Relative Importance of Individual Variables
5. Conclusions and Suggestions
- (1)
- Despite the large price variance (the CoV of water price is over 214% in this study) and different market structures (i.e., the ratio between leases and sales) across the western states, the RFR models showed good predictive capability for water price while producing plausible VI rankings. This demonstrates the great potential of the RFR algorithm in capturing the complex and nonlinear relationships between water price and a large number of determinants that the traditional regression modeling often fails to address adequately. The RFR models are also able to include many correlated variables, whereas adding to many correlated variables can cause the serious issue of multicollinearity in traditional regression modeling. Moreover, the RFR models not only beat the DT baseline model, but also avoided overfitting, which the baseline model suffered from in the generalization process.
- (2)
- The BVE procedure can improve the overall model accuracy to some degree, which reflects the advantage of filtering out variables with low to moderate VI. However, the improvement was not significant as the RFR algorithm is robust to including low informative variables. Despite the algorithm’s ability to handle noisy variables, we do not suggest using as many predictor variables as possible for RFR modeling. The pre-selection of variables with hypothesized pertinence to water rights price, based on the researchers’ knowledge and data availability, is an essential part of RFR modeling. Potential predictor variables such as seniority and quality of water rights, water storage, water consumption, prices of relevant commodities, etc. can also be taken into account for future studies.
- (3)
- There remain a few limitations in this paper. First, The RFR models may result in higher predictive power if trained with finer spatial resolution data (e.g., county or sub-basin levels), particularly for those variables that have high spatial variations within states. But because we were not able to acquire the precise geographic locations of each transaction, the dataset assembled for this study lacked specificity to some degree. Second, many informal transactions, of which the price can be determined by different factors, were not recorded by the Water Strategist [10]. Nevertheless, the recorded water trade data still allowed us to conduct empirical analysis about state-level impacts on water price. Another minor limitation of this study is the assumption on the optimal latency of the hydrologic variables, of which the lagging information with longer or shorter periods may improve the predictive performances of the models. However, as it is beyond the scope of this paper, we suggest separate studies be conducted in examining the optimal lag-time of these predictors for water price prediction.
- (4)
- As water markets are heterogeneous, future studies, using the RFR-based models, focusing on price prediction for specific regional or local water markets are suggested, which can generate more valuable price information at lower scales. With continued data acquisition, the models presented in this study can be further improved and commercialized for use of water market participants in making water trade decisions, water administrators in water management or policy makers in policy implication analysis, and could ultimately make a contribution to higher economic and water use efficiency.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Grafton, R.Q.; Libecap, G.; McGlennon, S.; Landry, C.; O’Brien, B. An Integrated Assessment of Water Markets: A Cross-Country Comparison. Rev. Environ. Econ. Policy 2011, 5, 219–239. [Google Scholar] [CrossRef]
- Deng, X.; Song, X.; Xu, Z. Transaction Costs, Modes, and Scales from Agricultural to Industrial Water Rights Trading in an Inland River Basin, Northwest China. Water 2018, 10, 1598. [Google Scholar] [CrossRef]
- Qureshi, M.E.; Whitten, S.M.; Mainuddin, M.; Marvanek, S.; Elmahdi, A. A biophysical and economic model of agriculture and water in the Murray-Darling Basin, Australia. Environ. Model. Softw. 2013, 41, 98–106. [Google Scholar] [CrossRef]
- Skurray, J.H.; Roberts, E.J.; Pannell, D.J. Hydrological challenges to groundwater trading: Lessons from south-west Western Australia. J. Hydrol. 2012, 412–413, 256–268. [Google Scholar] [CrossRef]
- Brookshire, D.S.; Colby, B.; Ewers, M.; Ganderton, P.T. Market prices for water in the semiarid West of the United States. Water Resour. Res. 2004, 40, W4S–W9S. [Google Scholar] [CrossRef]
- Brooks, R.; Harris, E. Efficiency gains from water markets: Empirical analysis of Watermove in Australia. Agric. Water Manag. 2008, 95, 391–399. [Google Scholar] [CrossRef]
- Chong, H.; Sunding, D. Water Markets and Trading. Annu. Rev. Env. Resour. 2006, 31, 239–264. [Google Scholar] [CrossRef]
- Anderson, T.L.; Scarborough, B.; Watson, L.R. Tapping Water Markets, 1st ed.; Routledge: New York, NY, USA, 2012; pp. 1–9. ISBN 978-1617261008. [Google Scholar]
- Nguyen-Ky, T.; Mushtaq, S.; Loch, A.; Reardon-Smith, K.; An-Vo, D.A.; Ngo-Cong, D.; Tran-Cong, T. Predicting water allocation trade prices using a hybrid Artificial Neural Network-Bayesian modelling approach. J. Hydrol. 2017. [Google Scholar] [CrossRef]
- Edwards, E.C.; Libecap, G.D. Water Institutions and the Law of One Price. In Handbook on the Economics of Natural Resources; Edward Elgar Publishing: Cheltenham, UK, 2015; pp. 442–473. [Google Scholar]
- De Mouche, L.; Landfair, S.; Ward, F.A. Water Right Prices in the Rio Grande: Analysis and Policy Implications. Int. J. Water Resour. Dev. 2011, 27, 291–314. [Google Scholar] [CrossRef]
- Payne, M.T.; Smith, M.G.; Landry, C.J. Price Determination and Efficiency in the Market for South Platte Basin Ditch Company Shares. J. Am. Water Resour. Assoc. 2014, 50, 1488–1500. [Google Scholar] [CrossRef]
- Bjornlund, H.; Rossini, P. Fundamentals Determining Prices and Activities in the Market for Water Allocations. Int. J. Water Resour. Dev. 2005, 21, 355–369. [Google Scholar] [CrossRef]
- Bjornlund, H.; Rossini, P. Fundamentals Determining Prices in the Market for Water Entitlements: An Australian Case Study. Int. J. Water Resour. Dev. 2007, 23, 537–553. [Google Scholar] [CrossRef]
- Brennan, D. Price formation on the Northern Victorian water exchange. In Proceedings of the 48th Conference of the Australian Agricultural and Resource Economics Society, Melbourne, Australia, 11–12 February 2004. [Google Scholar]
- Brown, T.C. Trends in water market activity and price in the western United States. Water Resour. Res. 2006, 42, W9402. [Google Scholar] [CrossRef]
- Li, X.; Maier, H.R.; Zecchin, A.C. Improved PMI-based input variable selection approach for artificial neural network and other data driven environmental and water resource models. Environ. Model. Softw. 2015, 65, 15–29. [Google Scholar] [CrossRef]
- Maier, H.R.; Jain, A.; Dandy, G.C.; Sudheer, K.P. Methods used for the development of neural networks for the prediction of water resource variables in river systems: Current status and future directions. Environ. Model. Softw. 2010, 25, 891–909. [Google Scholar] [CrossRef]
- Yang, T.; Asanjan, A.A.; Welles, E.; Gao, X.; Sorooshian, S.; Liu, X. Developing reservoir monthly inflow forecasts using Artificial Intelligence and Climate Phenomenon Information. Water Resour. Res. 2017, 53, WR020482. [Google Scholar] [CrossRef]
- Khan, S.; Dassanayake, D.; Mushtaq, S.; Hanjra, M.A. Predicting water allocations and trading prices to assist water markets. Irrig. Drain. 2010, 59, 388–403. [Google Scholar] [CrossRef]
- Panchal, G.; Ganatra, A.; Shah, P.; Panchal, D. Determination of Over-Learning and Over-Fitting Problem in Back Propagation Neurl Network. Int. J. Soft Comput. 2011, 2, 40–51. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cavallo, D.P.; Cefola, M.; Pace, B.; Logrieco, A.F.; Attolico, G. Contactless and non-destructive chlorophyll content prediction by random forest regression: A case study on fresh-cut rocket leaves. Comput. Electron. Agric. 2017, 140, 303–310. [Google Scholar] [CrossRef]
- Booth, A.; Gerding, E.; Mcgroarty, F. Automated trading with performance weighted random forests and seasonality. Expert Syst. Appl. 2014, 41, 3651–3661. [Google Scholar] [CrossRef]
- Ballings, M.; Van den Poel, D.; Hespeels, N.; Gryp, R. Evaluating multiple classifiers for stock price direction prediction. Expert Syst. Appl. 2015, 42, 7046–7056. [Google Scholar] [CrossRef]
- Zhang, J.; Cui, S.; Xu, Y.; Li, Q.; Li, T. A novel data-driven stock price trend prediction system. Expert Syst. Appl. 2018, 97, 60–69. [Google Scholar] [CrossRef]
- Liu, D.; Li, Z. Gold Price Forecasting and Related Influence Factors Analysis Based on Random Forest. In Proceedings of the Tenth International Conference on Management Science and Engineering Management, Baku, Azerbaijan, 30 August–4 September 2016. [Google Scholar] [CrossRef]
- Liu, C.; Hu, Z.; Li, Y.; Liu, S. Forecasting copper prices by decision tree learning. Resour. Policy 2017, 52, 427–434. [Google Scholar] [CrossRef]
- Gaillard, P.; Goude, Y.; Nedellec, R. Additive models and robust aggregation for GEFCom2014 probabilistic electric load and electricity price forecasting. Int. J. Forecast. 2016, 32, 1038–1050. [Google Scholar] [CrossRef]
- Chen, F.; Howard, H. An alternative model for the analysis of detecting electronic industries earnings management using stepwise regression, random forest, and decision tree. Soft Comput. 2016, 20, 1945–1960. [Google Scholar] [CrossRef]
- Antipov, E.A.; Pokryshevskaya, E.B. Mass appraisal of residential apartments: An application of Random forest for valuation and a CART-based approach for model diagnostics. Expert Syst. Appl. 2012, 39, 1772–1778. [Google Scholar] [CrossRef]
- Lessmann, S.; Voß, S. Car resale price forecasting: The impact of regression method, private information, and heterogeneity on forecast accuracy. Int. J. Forecast. 2017, 33, 864–877. [Google Scholar] [CrossRef]
- Yang, T.; Gao, X.; Sorooshian, S.; Li, X. Simulating California reservoir operation using the classification and regression-tree algorithm combined with a shuffled cross-validation scheme. Water Resour. Res. 2016, 52, 1626–1651. [Google Scholar] [CrossRef]
- He, X.; Zhao, T.; Yang, D. Prediction of monthly inflow to the Danjiangkou reservoir by distributed hydrological model and hydro-climatic teleconnections. J. Hydroelectr. Eng. 2013, 32, 4–9. [Google Scholar]
- Papacharalampous, G.; Tyralis, H. Evaluation of random forests and Prophet for daily streamflow forecasting. Adv. Geosci. 2018, 45, 201–208. [Google Scholar] [CrossRef]
- Herrera, M.; Torgo, L.; Izquierdo, J.; Pérez-García, R. Predictive models for forecasting hourly urban water demand. J. Hydrol. 2010, 387, 141–150. [Google Scholar] [CrossRef]
- Chen, G.; Long, T.; Xiong, J.; Bai, Y. Multiple Random Forests Modelling for Urban Water Consumption Forecasting. Water Resour. Manag. 2017, 31, 4715–4729. [Google Scholar] [CrossRef]
- Feng, Q.; Liu, J.; Gong, J. Urban Flood Mapping Based on Unmanned Aerial Vehicle Remote Sensing and Random Forest Classifier—A Case of Yuyao, China. Water 2015, 7, 1437–1455. [Google Scholar] [CrossRef]
- Muñoz, P.; Orellana-Alvear, J.; Willems, P.; Célleri, R. Flash-Flood Forecasting in an Andean Mountain Catchment—Development of a Step-Wise Methodology Based on the Random Forest Algorithm. Water 2018, 10, 1519. [Google Scholar] [CrossRef]
- Wu, J.; Chen, Y.F.; Yu, S.N. Research on drought prediction based on random forest model. China Rural Water Hydropower 2016, 17, 17–22. [Google Scholar]
- Eccel, E.; Ghielmi, L.; Granitto, P.; Barbiero, R.; Grazzini, F.; Cesari, D. Prediction of minimum temperatures in an alpine region by linear and non-linear post-processing of meteorological models. Nonlinear Process. Geophys. 2007, 14, 211–222. [Google Scholar] [CrossRef]
- Karthick, S.; Malathi, D.; Arun, C. Weather prediction analysis using random forest algorithm. Int. J. Pure Appl. Math. 2018, 118, 255–262. [Google Scholar]
- Ibarra-Berastegi, G.; Saénz, J.; Ezcurra, A.; Elías, A.; Diaz Argandoña, J.; Errasti, I. Downscaling of surface moisture flux and precipitation in the Ebro Valley (Spain) using analogues and analogues followed by random forests and multiple linear regression. Hydrol. Earth Syst. Sci. 2011, 15, 1895–1907. [Google Scholar] [CrossRef]
- He, X.; Chaney, N.W.; Schleiss, M.; Sheffield, J. Spatial downscaling of precipitation using adaptable random forests. Water Resour. Res. 2016, 52, 8217–8237. [Google Scholar] [CrossRef]
- Brewer, J.; Glennon, R.; Ker, A.; Libecap, G.D. Water markets in the west: Prices, trading and contractual form. Econ. Inq. 2008, 46, 91–112. [Google Scholar] [CrossRef]
- Donohew, Z. Property rights and western United States water markets. Aust. J. Agric. Resour. Econ. 2009, 53, 85–103. [Google Scholar] [CrossRef]
- Hansen, K.; Howitt, R.; Williams, J. An Econometric Test of Water Market Structure in the Western United States. Nat. Resour. J. 2015, 55, 127–152. [Google Scholar]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995. [Google Scholar] [CrossRef]
- Zhong, S.; Xie, X.; Lin, L. Two-layer random forests model for case reuse in case-based reasoning. Expert Syst. Appl. 2015, 42, 9412–9425. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Hjerpe, A. Computing Random Forests Variable Importance Measures (VIM) on Mixed Continuous and Categorical Data. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2016. [Google Scholar]
- Fox, E.W.; Hill, R.A.; Leibowitz, S.G.; Olsen, A.R.; Thornbrugh, D.J.; Weber, M.H. Assessing the accuracy and stability of variable selection methods for random forest modeling in ecology. Environ. Monit. Assess. 2017, 189, 316. [Google Scholar] [CrossRef]
- Lujan-Moreno, G.A.; Howard, P.R.; Rojas, O.G.; Montgomery, D.C. Design of experiments and response surface methodology to tune machine learning hyperparameters, with a random forest case-study. Expert Syst. Appl. 2018, 109, 195–205. [Google Scholar] [CrossRef]
- Bernard, S.; Heutte, L.; Adam, S. Influence of Hyperparameters on Random Forest Accuracy. In Proceedings of the 8th International Workshop, MCS 2009, Reykjavik, Iceland, 10–12 June 2009. [Google Scholar] [CrossRef]
- Yang, T.; Asanjan, A.A.; Faridzad, M.; Hayatbini, N.; Gao, X. An enhanced artificial neural network with a shuffled complex evolutionary global optimization with principal component analysis. Inform. Sci. 2017, 418–419, 302–316. [Google Scholar] [CrossRef]
- Biau, G. Analysis of a Random Forests Model. J. Mach. Learn. Res. 2010, 13, 1063–1095. [Google Scholar]
- Piñeiro, G.; Perelman, S.; Guerschman, J.P.; Paruelo, J.M. How to evaluate models: Observed vs. predicted or predicted vs. observed? Ecol. Model. 2008, 216, 316–322. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning, 1st ed.; MIT Press: Cambridge, MA, USA, 2016; ISBN 9780262035613. [Google Scholar]
- Libecap, G.D. Institutional path dependence in climate adaptation: Coman’s some unsettled problems of irrigation. Am. Econ. Rev. 2011, 101, 64–80. [Google Scholar] [CrossRef]
- Ghosh, S. Droughts and water trading in the western United States: Recent economic evidence. Int. J. Water Resour. Dev. 2018, 35, 145–159. [Google Scholar] [CrossRef]
- Mideksa, T.K. The economic impact of natural resources. J. Environ. Econ. Manag. 2013, 65, 277–289. [Google Scholar] [CrossRef]
- Mehrara, M.; Baghbanpour, J. Analysis of the Relationship between Total Natural Resources Rent and Economic Growth: The Case of Iran and MENA Countries. Int. J. Appl. Econ. Stud. 2015, 3, 1–7. [Google Scholar]
- Lach, D.; Ingram, H.; Rayner, S. Maintaining the status quo: How institutional norms and practices create conservative water organizations. Texas Law Rev. 2005, 83, 2027–2053. [Google Scholar]
- Grafton, R.Q.; Libecap, G.D.; Edwards, E.C.; O’Brien, R.B.; Landry, C. Comparative assessment of water markets: Insights from the Murray–Darling Basin of Australia and the Western USA. Water Policy 2012, 14, 175–193. [Google Scholar] [CrossRef]
- Payne, M.T.; Smith, M.G. Price determination and efficiency in the market for water rights in New Mexico’s Middle Rio Grande Basin. Int. J. Water Resour. Dev. 2013, 29, 588–604. [Google Scholar] [CrossRef]
- Colby, B.G.; Crandall, K.; Bush, D.B. Water Right Transactions: Market Values and Price Dispersion. Water Resour. Res. 1993, 29, 1565–1572. [Google Scholar] [CrossRef]
- Li, D.; Wrzesien, M.L.; Durand, M.; Adam, J.; Lettenmaier, D.P. How much runoff originates as snow in the western United States, and how will that change in the future? Geophys. Res. Lett. 2017, 44, 6163–6172. [Google Scholar] [CrossRef]

| Predictor Name | Predictor Description |
|---|---|
| Transaction Attributes | |
| Direction | Prior and destination purposes of transferred water rights |
| Duration | Length of a contract (perpetual for sales) |
| Quantity | Committed volume of water sold in acre-foot |
| State | The state in which a transaction was made |
| Economics & Demographic | |
| PerCapIn | Per capita income |
| PopGrow | Population growth rate |
| RealGDP | Real gross domestic product |
| IPI-Constrct | National total construction index |
| IPI-Other | National industry production index excluding constructions |
| CrpProdn | Value of crop production |
| FarmIn | Net farm income |
| Meteorological & Hydrologic | |
| PrecipWtr | Mean precipitable water |
| Precip | Mean precipitation |
| MeanTemp | Mean temperature |
| MaxTemp | Mean of monthly maximum temperatures |
| MinTemp | Mean of monthly minimum temperatures |
| SnowDep | Snow depth |
| SWE | Snow water equivalent |
| CDD | Cooling degree days |
| HDD | Heating degree days |
| PDSI | Palmer drought severity index |
| PHDI | Palmer hydrological drought index |
| PMDI | Palmer modified drought index |
| P Z-index | Palmer Z-index |
| Land Uses | |
| UrbLnd | Size of urban land use |
| IndusLnd | Size of industry land use |
| CrpLnd | Size of total cropland |
| EnvLnd | Size of environmental land use |
| GrassLnd | Size of grassland for pasture |
| Models | ntree | mtry | nodesize |
|---|---|---|---|
| RFR-full | 1876 | 15 (50%) | 20 |
| RFR-red-N | 452 | 4 (33%) | 20 |
| RFR-red-P | 109 | 2 (33%) | 3 |
| Models | PCC | R2 | NRMSE | |||
|---|---|---|---|---|---|---|
| Mean 1 | Maximum 2 | Mean 1 | Maximum 2 | Mean 1 | Minimum 2 | |
| RFR-full | 0.832 | 0.900 | 0.692 | 0.810 | 0.093 | 0.069 |
| RFR-red-N | 0.836 | 0.912 | 0.699 | 0.832 | 0.094 | 0.066 |
| RFR-red-P | 0.841 | 0.920 | 0.707 | 0.846 | 0.091 | 0.065 |
| DT (baseline) | 0.736 | 0.805 | 0.541 | 0.648 | 0.118 | 0.089 |
| Models | PCC | R2 | NRMSE |
|---|---|---|---|
| RFR-full | 6.21% | 11.90% | 15.03% |
| RFR-red-N | 6.31% | 12.75% | 15.91% |
| RFR-red-P | 6.44% | 12.62% | 15.88% |
| DT (baseline) | 7.63% | 13.09% | 16.33% |
| Models | Test b (Slope) = 1 | Test a (Intercept) = 0 | ||
|---|---|---|---|---|
| t Statistic | p-Value | t Statistic | p-Value | |
| RFR-full | −1.270 | 0.201 | 0.360 | 0.720 |
| RFR-red-N | 0.698 | 0.487 | −0.305 | 0.761 |
| RFR-red-P | 0.794 | 0.430 | 0.614 | 0.541 |
| Models | PCC | R2 | NRMSE |
|---|---|---|---|
| RFR-full | 0.875 | 0.766 | 0.083 |
| RFR-red-N | 0.908 | 0.824 | 0.067 |
| RFR-red-P | 0.917 | 0.841 | 0.063 |
| DT (baseline) | 0.116 | 0.013 | 0.364 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Lian, J.; Bin, L.; Hua, K.; Xu, K.; Chan, H.Y. Water Price Prediction for Increasing Market Efficiency Using Random Forest Regression: A Case Study in the Western United States. Water 2019, 11, 228. https://doi.org/10.3390/w11020228
Xu Z, Lian J, Bin L, Hua K, Xu K, Chan HY. Water Price Prediction for Increasing Market Efficiency Using Random Forest Regression: A Case Study in the Western United States. Water. 2019; 11(2):228. https://doi.org/10.3390/w11020228
Chicago/Turabian StyleXu, Ziyao, Jijian Lian, Lingling Bin, Kaixun Hua, Kui Xu, and Hoi Yi Chan. 2019. "Water Price Prediction for Increasing Market Efficiency Using Random Forest Regression: A Case Study in the Western United States" Water 11, no. 2: 228. https://doi.org/10.3390/w11020228
APA StyleXu, Z., Lian, J., Bin, L., Hua, K., Xu, K., & Chan, H. Y. (2019). Water Price Prediction for Increasing Market Efficiency Using Random Forest Regression: A Case Study in the Western United States. Water, 11(2), 228. https://doi.org/10.3390/w11020228






