Numerical Study on the Hydrodynamic Characteristics of Submarine Pipelines under the Impact of Real-World Tsunami-Like Waves
Abstract
1. Introduction
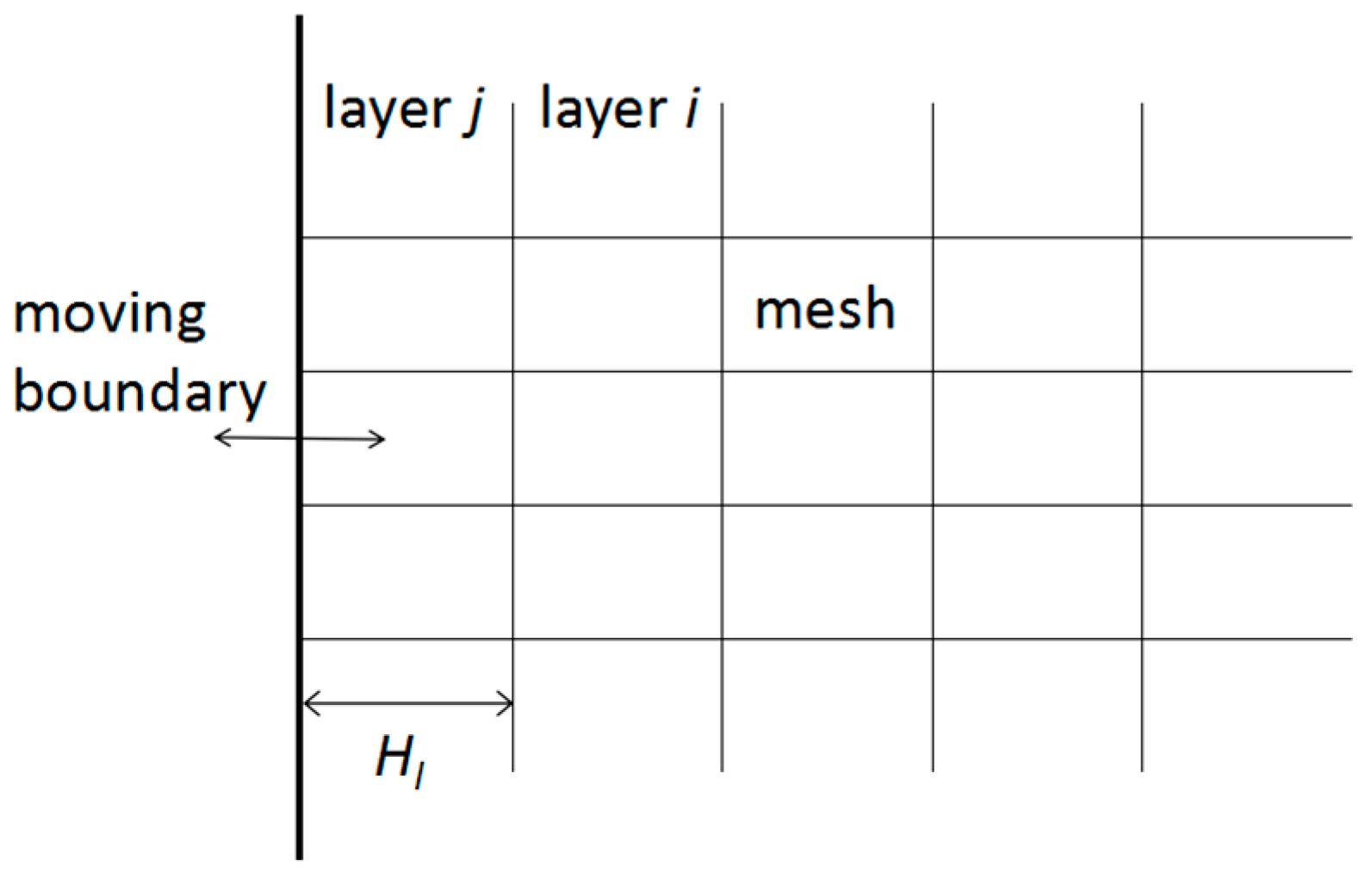
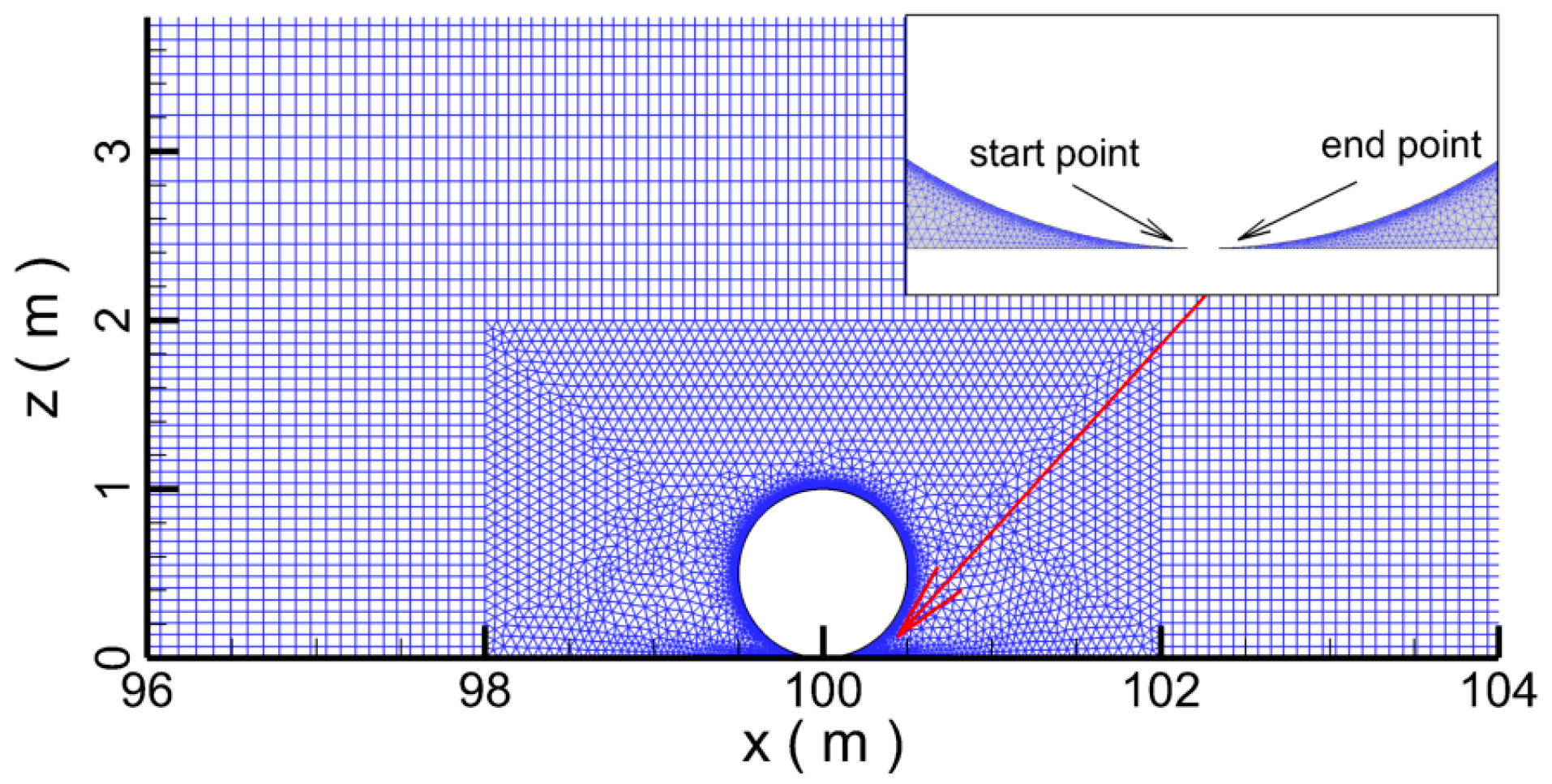
2. Numerical Model
2.1. Governing Equations
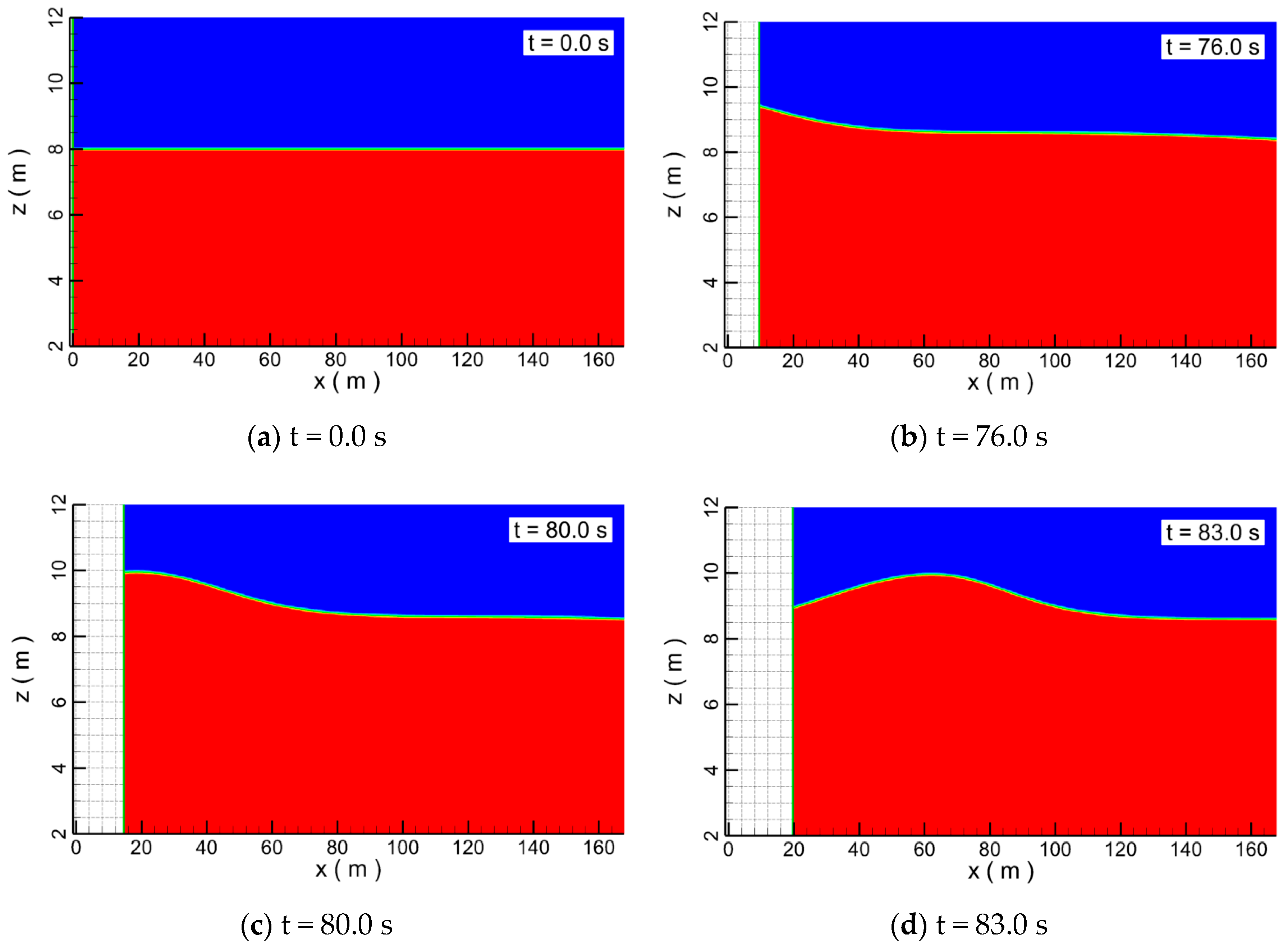
2.2. Wave Generation Method
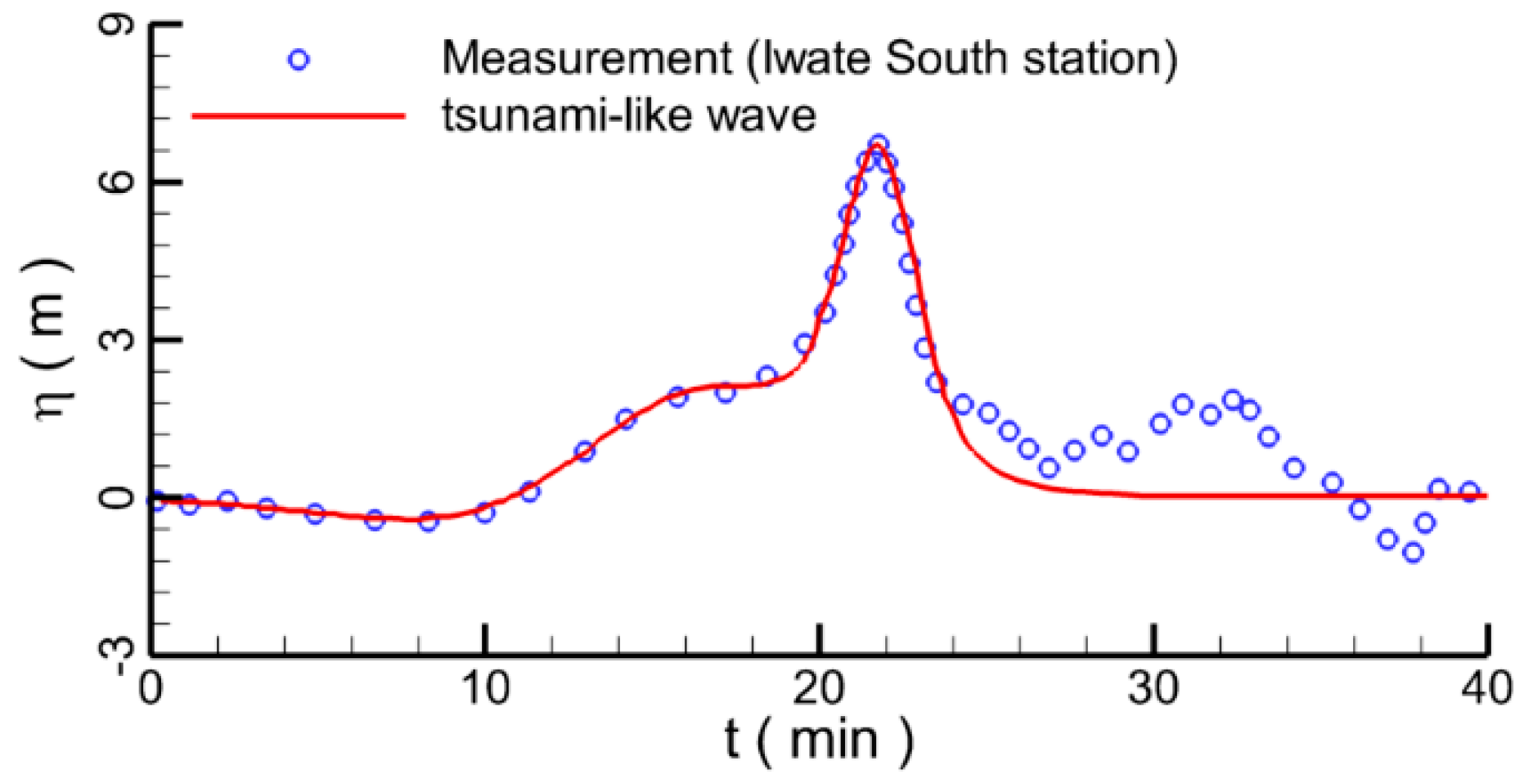
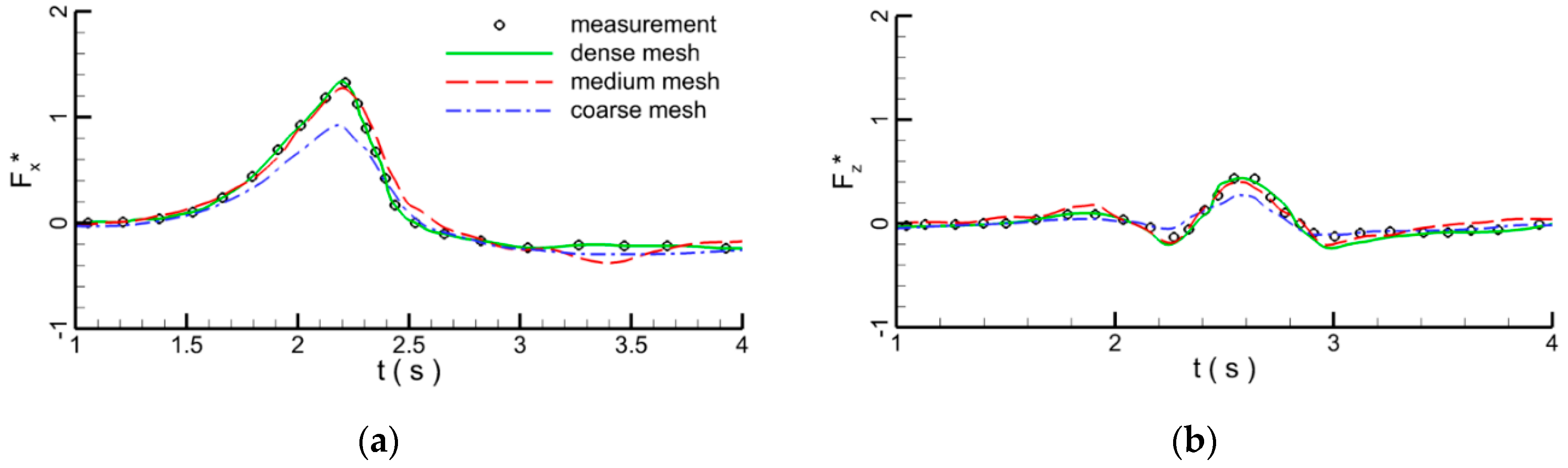
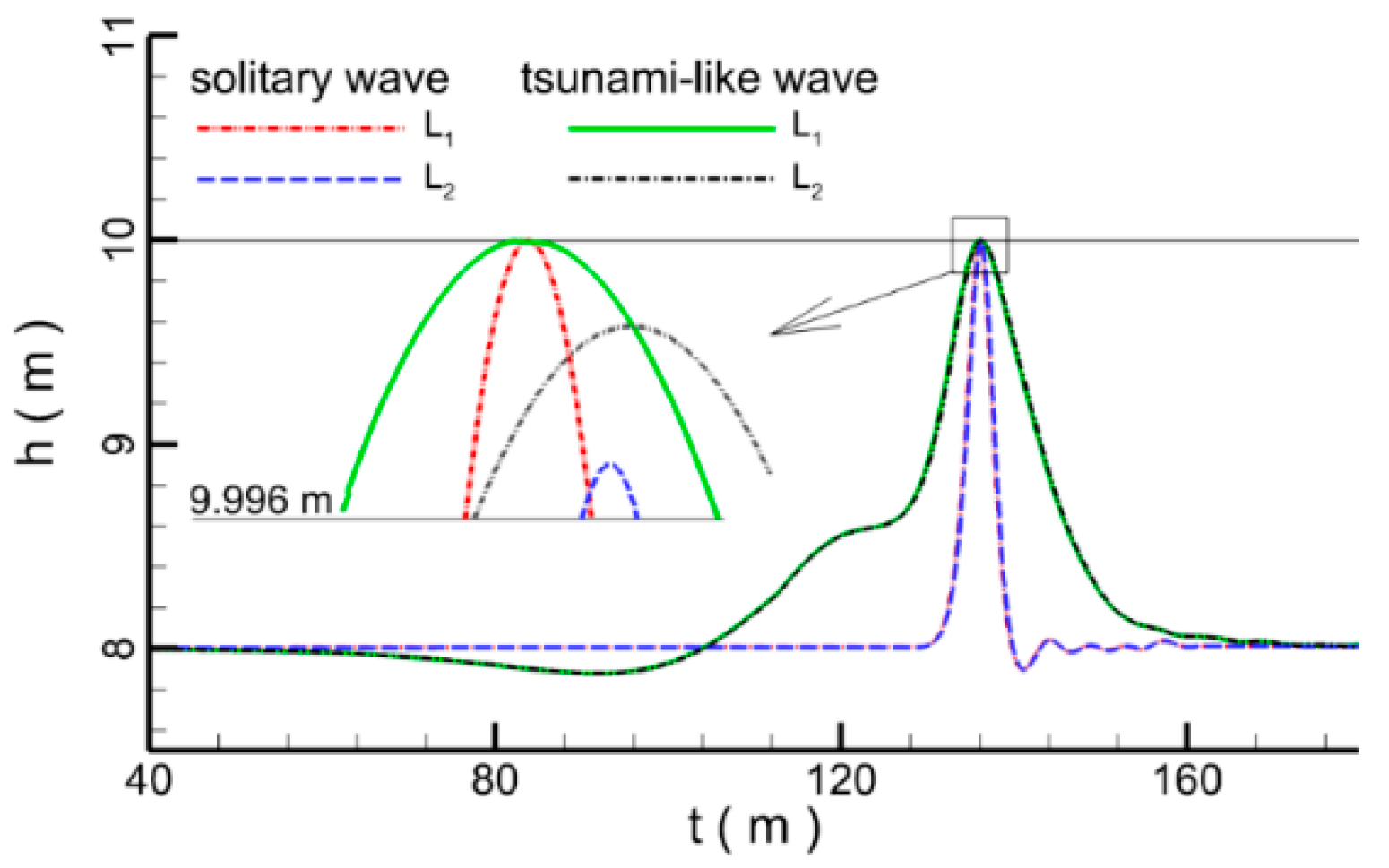
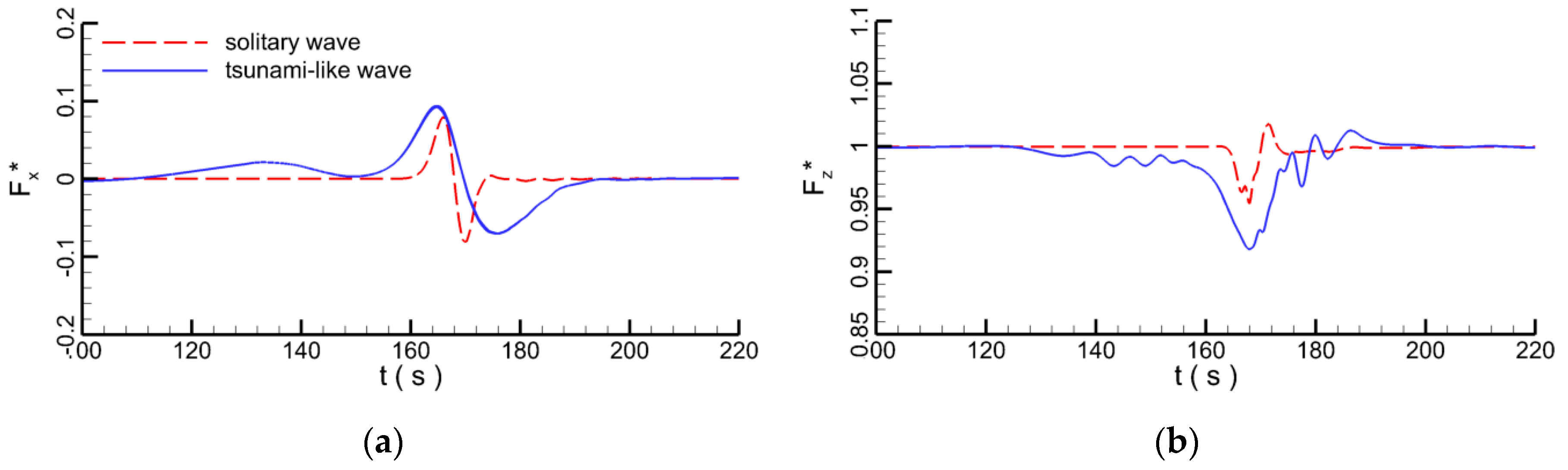
3. Model Validation
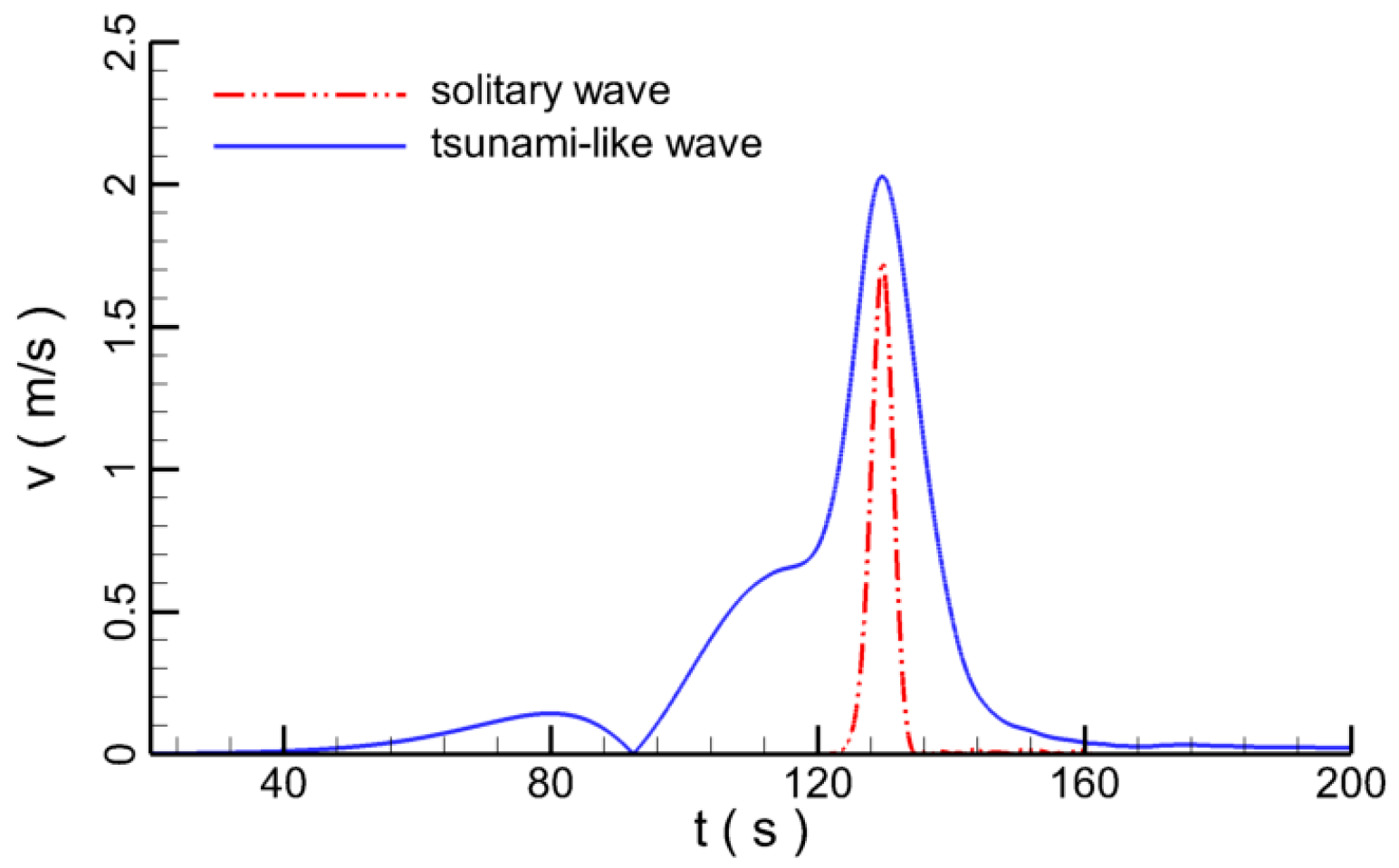
4. Results and Discussions
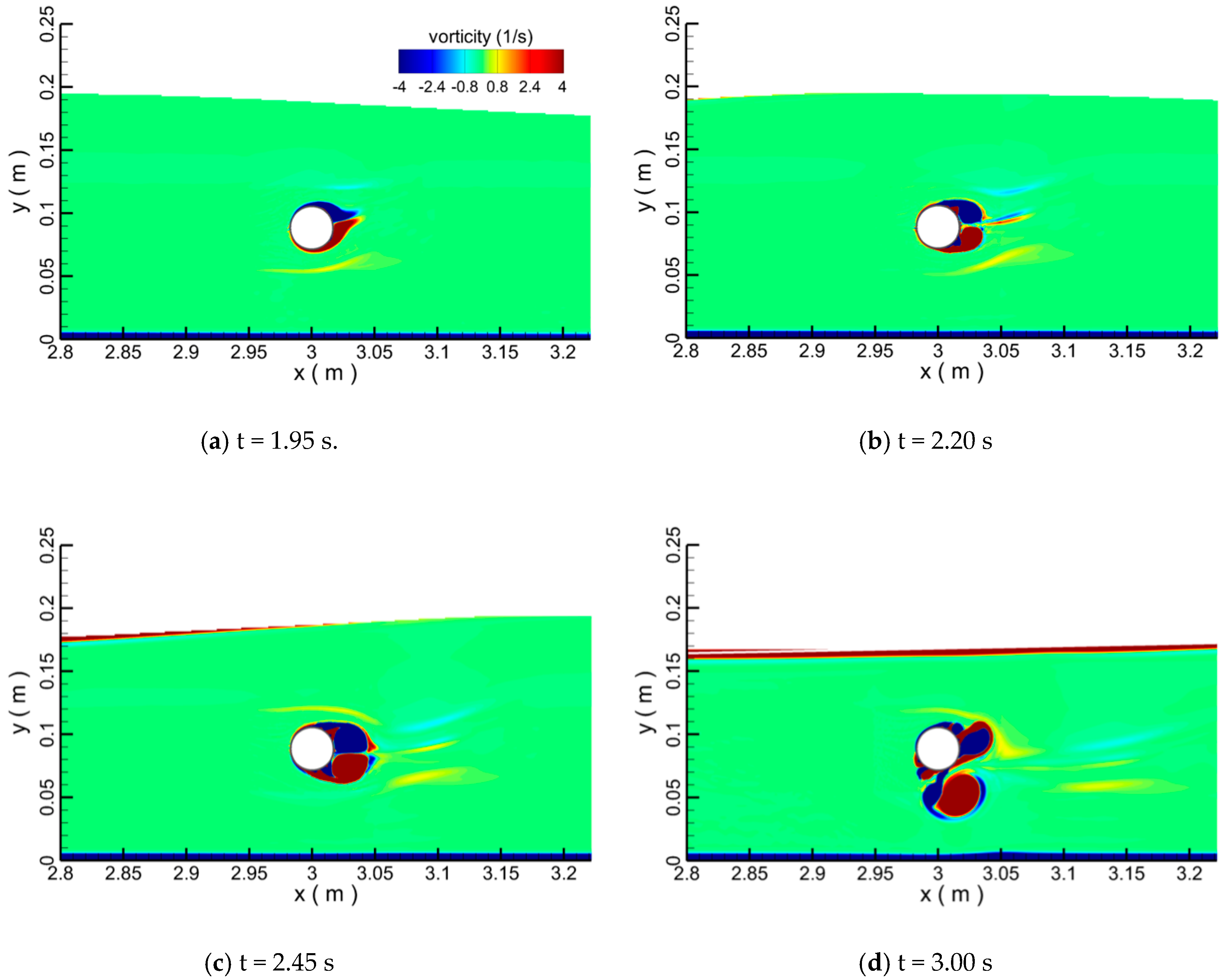
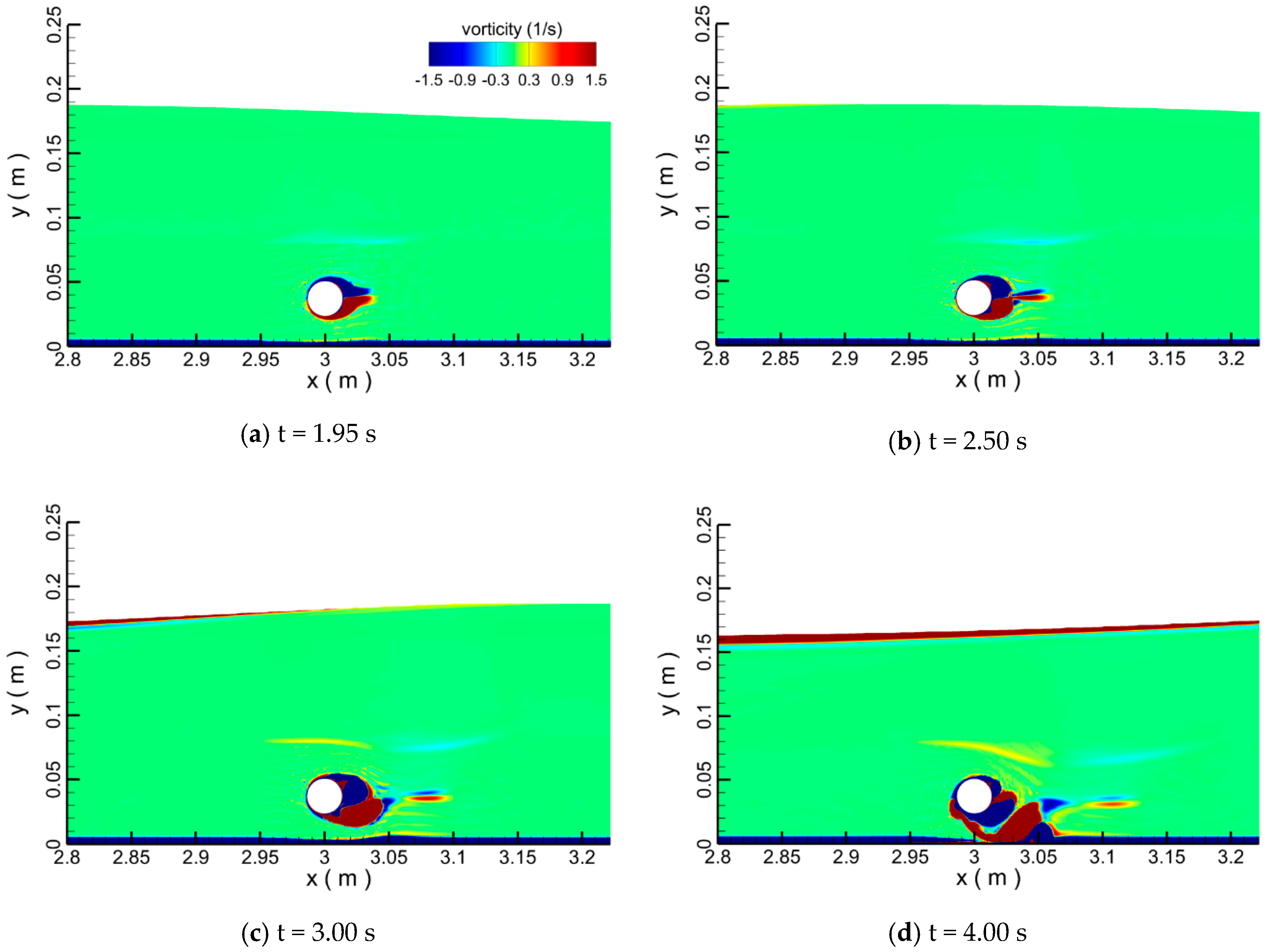
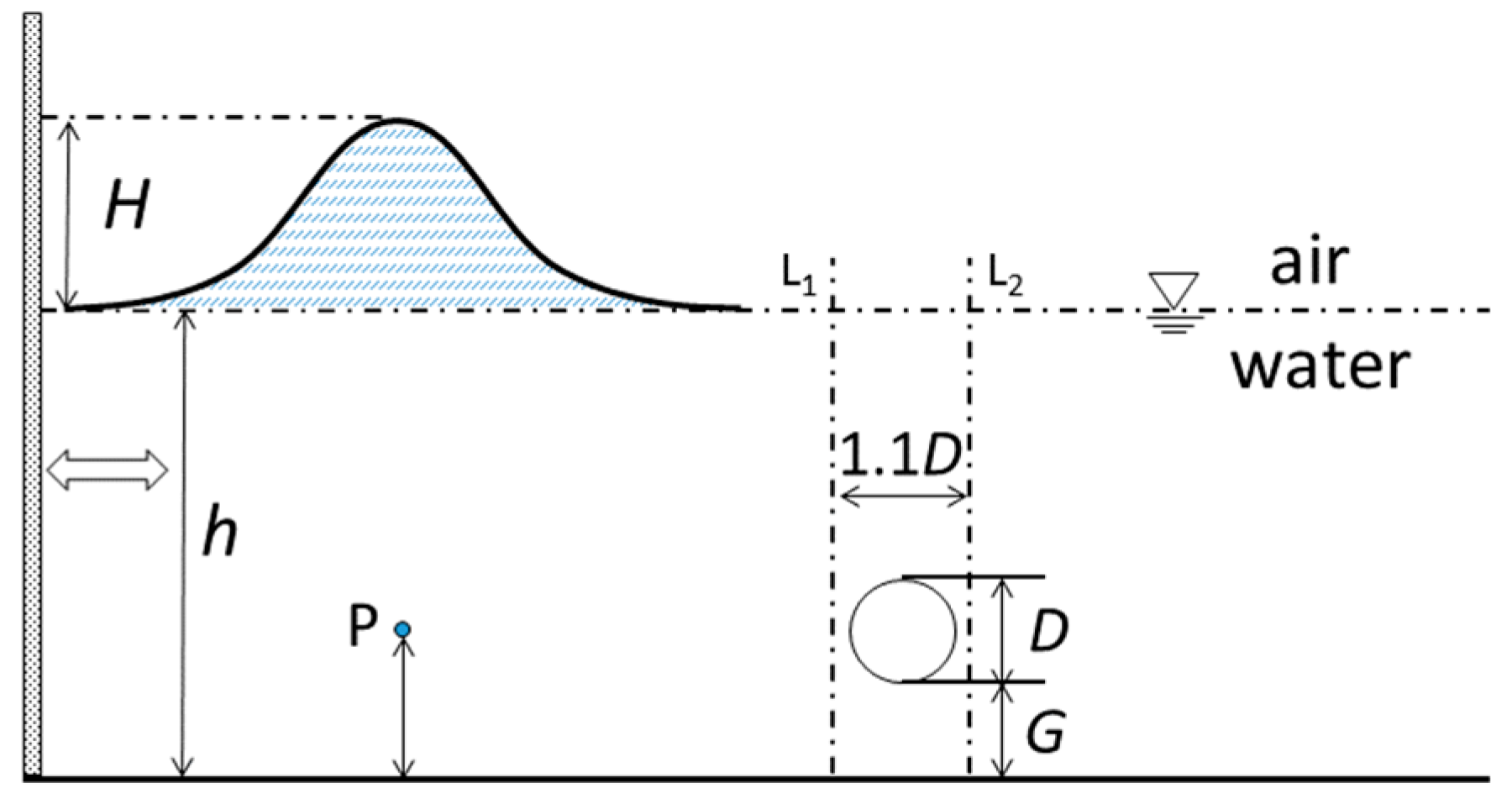
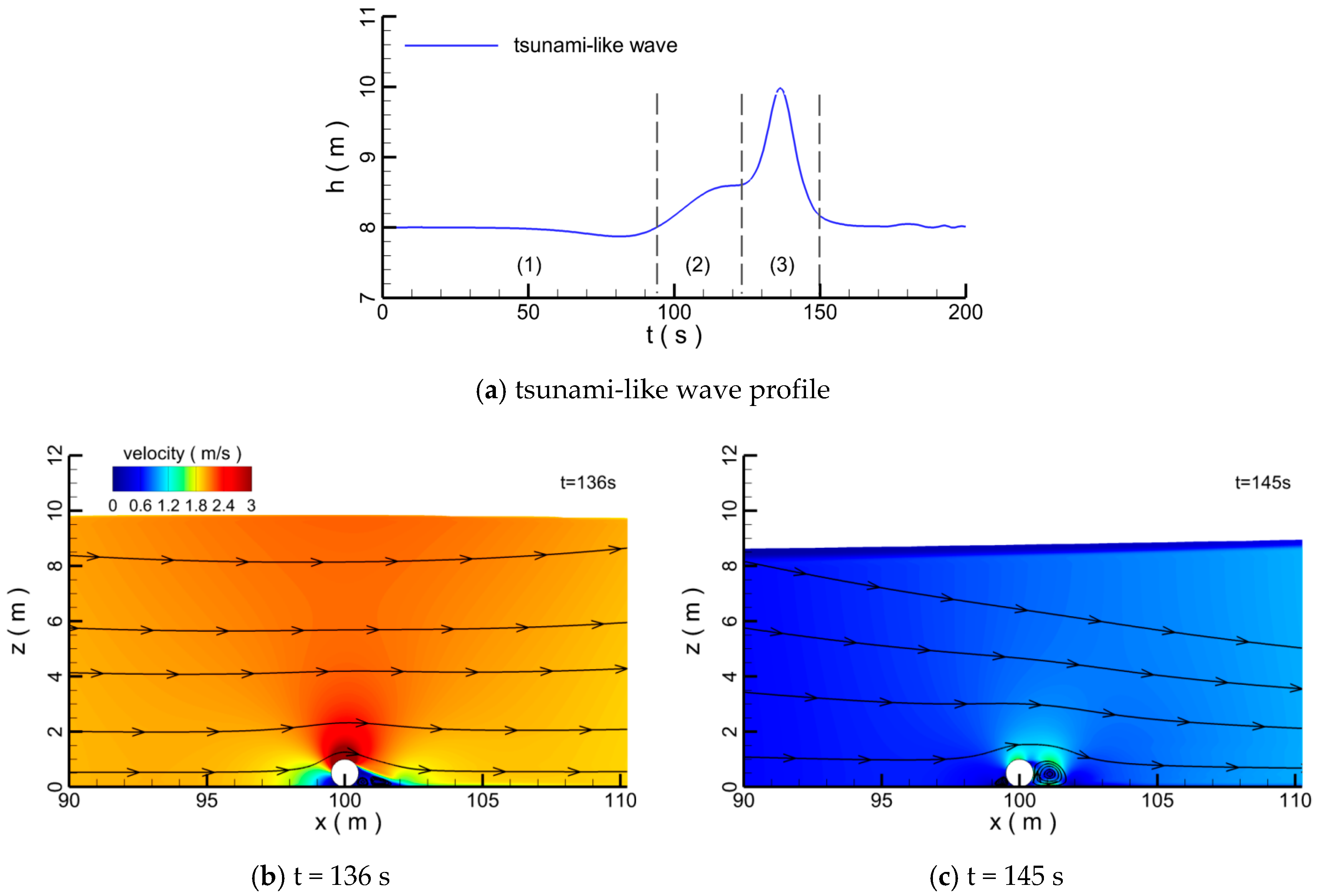
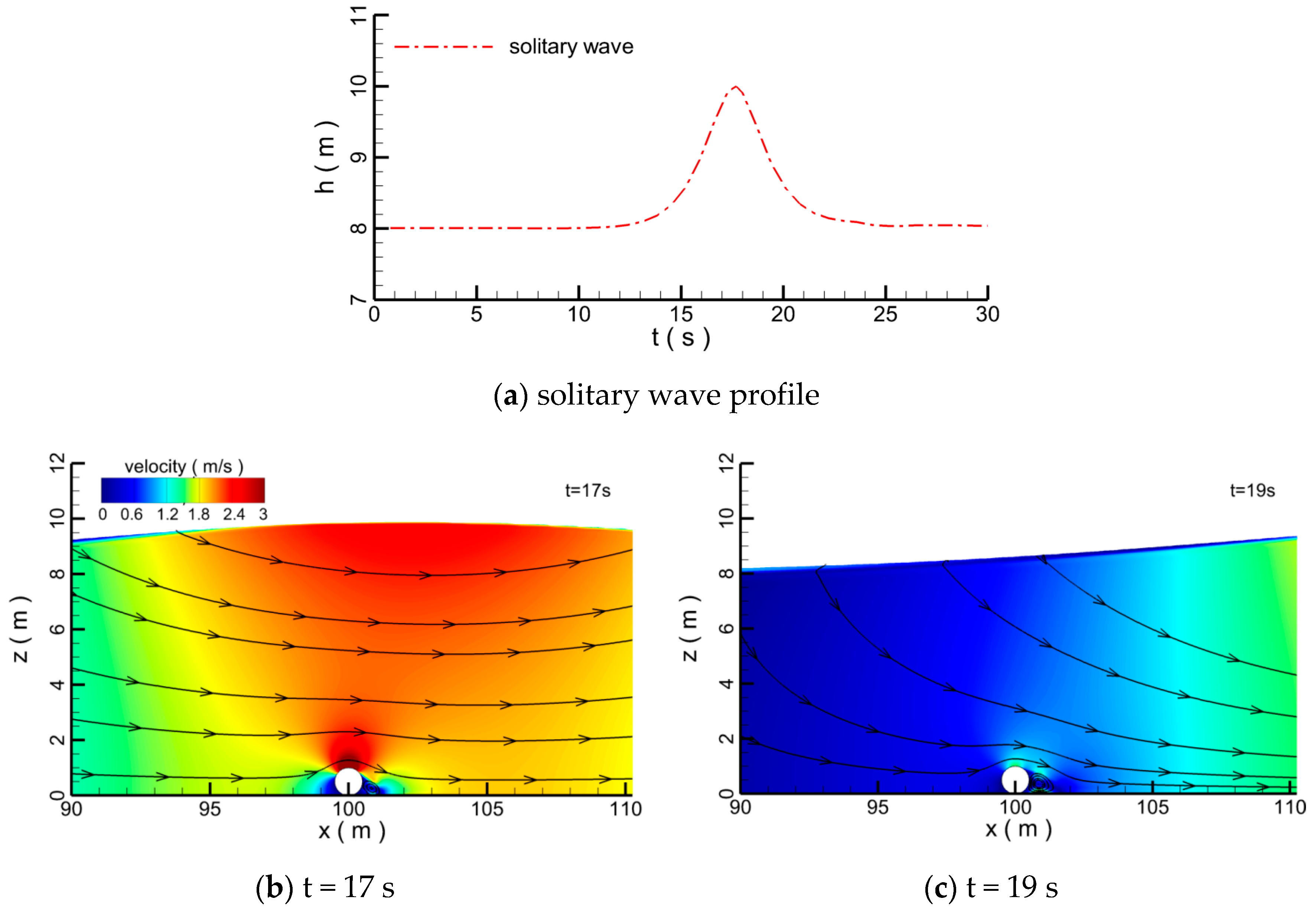
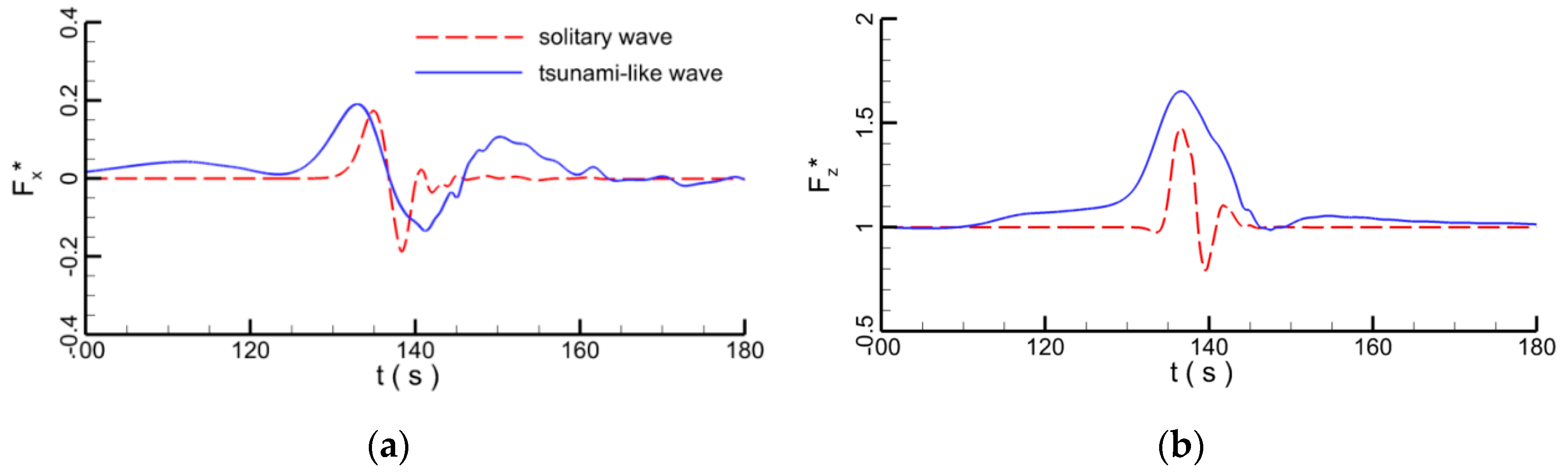
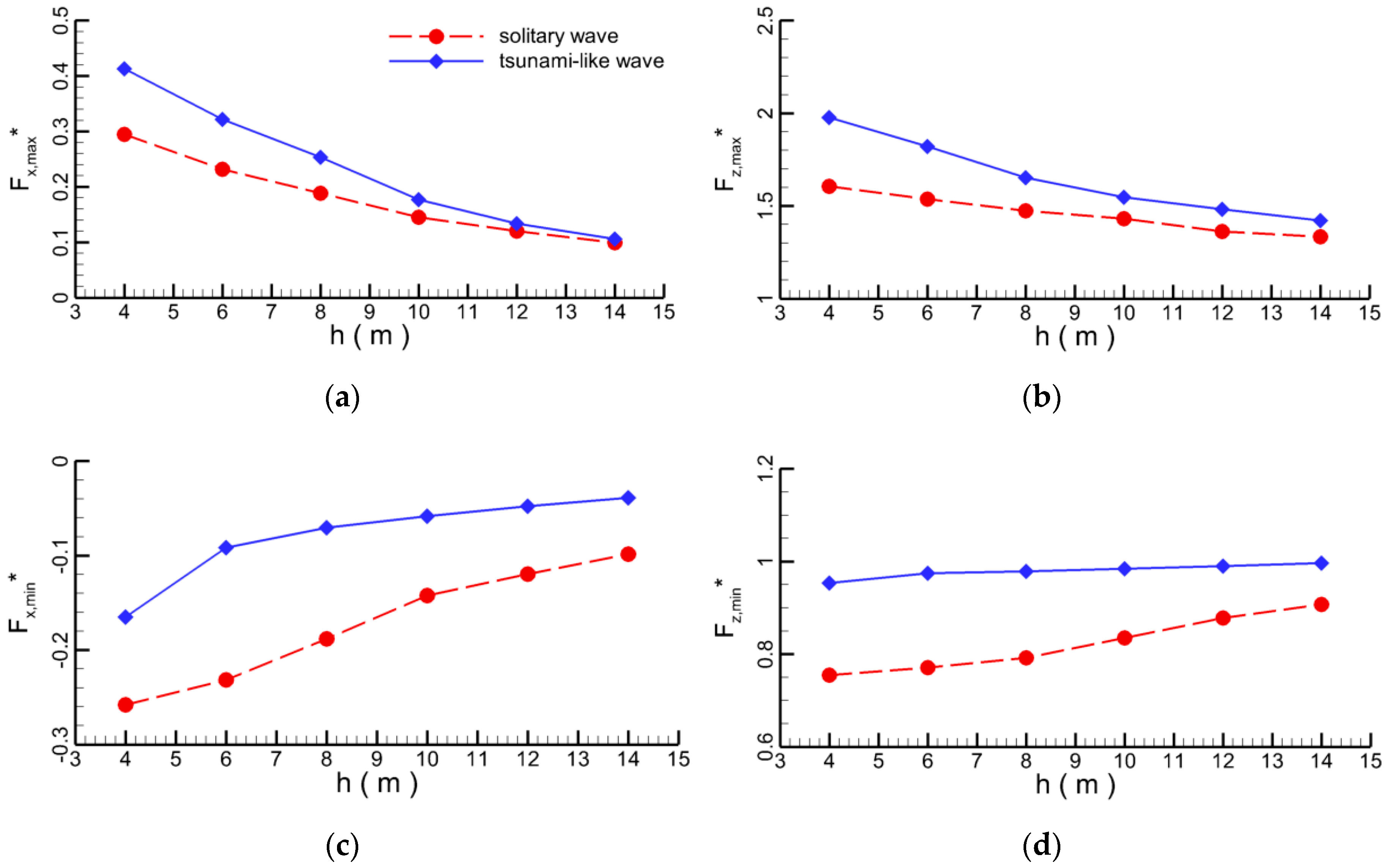
4.1. Single Pipeline
- (1)
- the leading-depression wave portion;
- (2)
- the preceding elevated wave portion;
- (3)
- the secondary elevated wave portion.
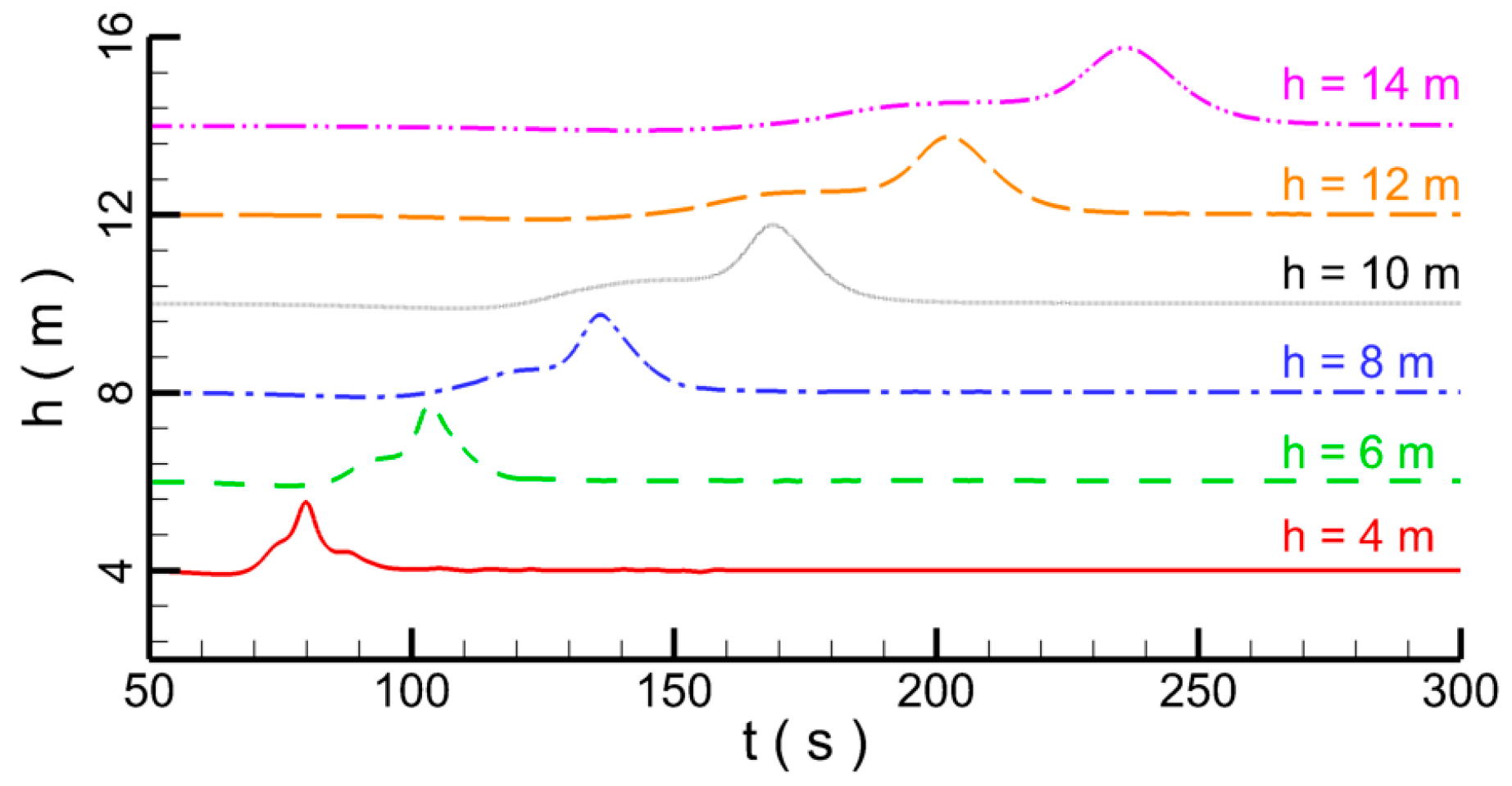
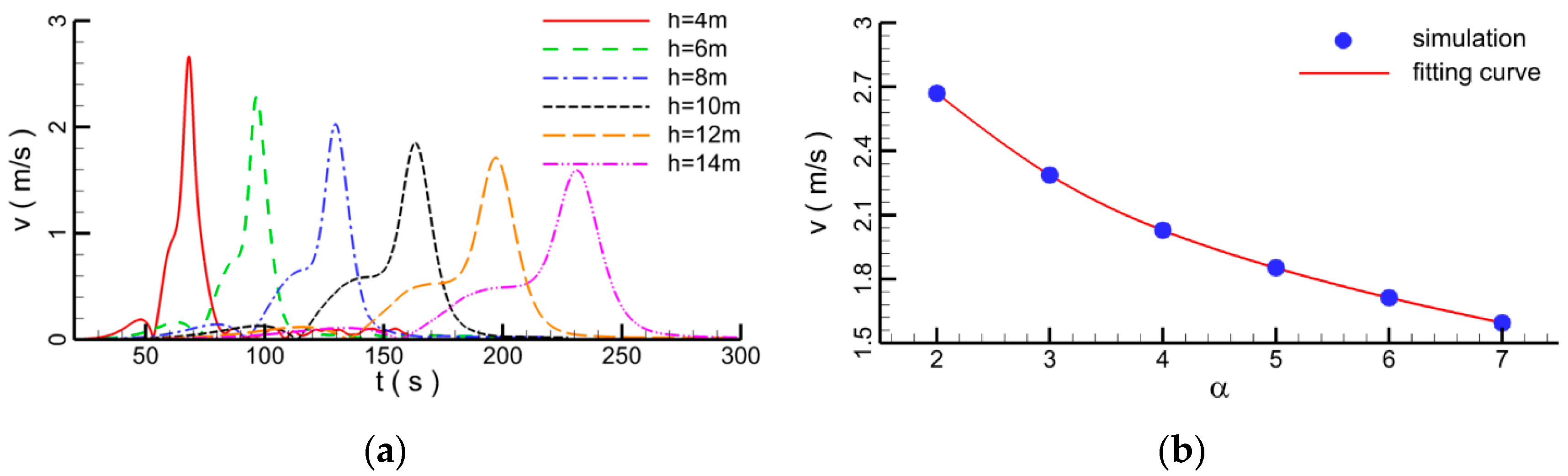
4.1.1. Effect of Water Depth
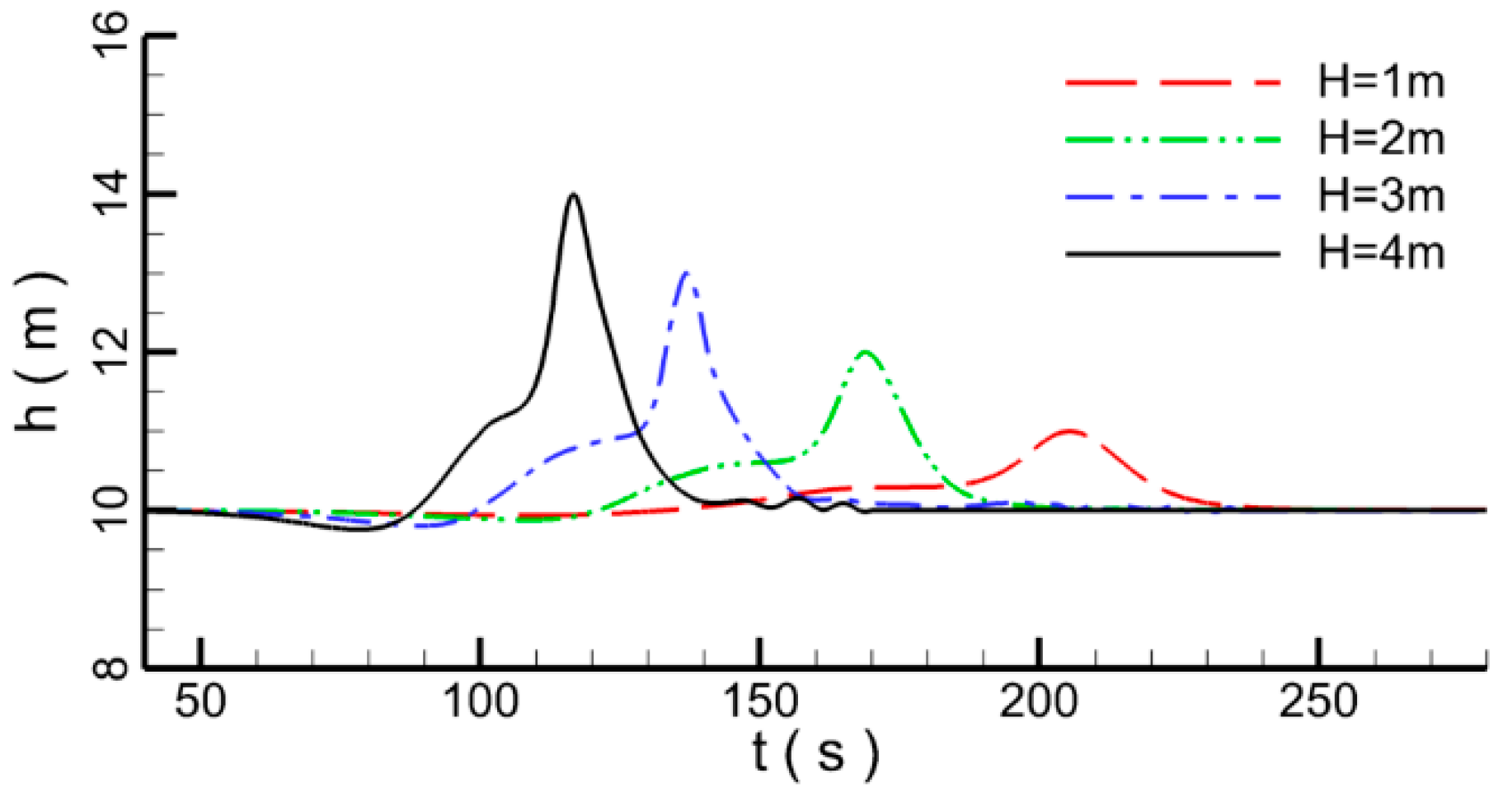
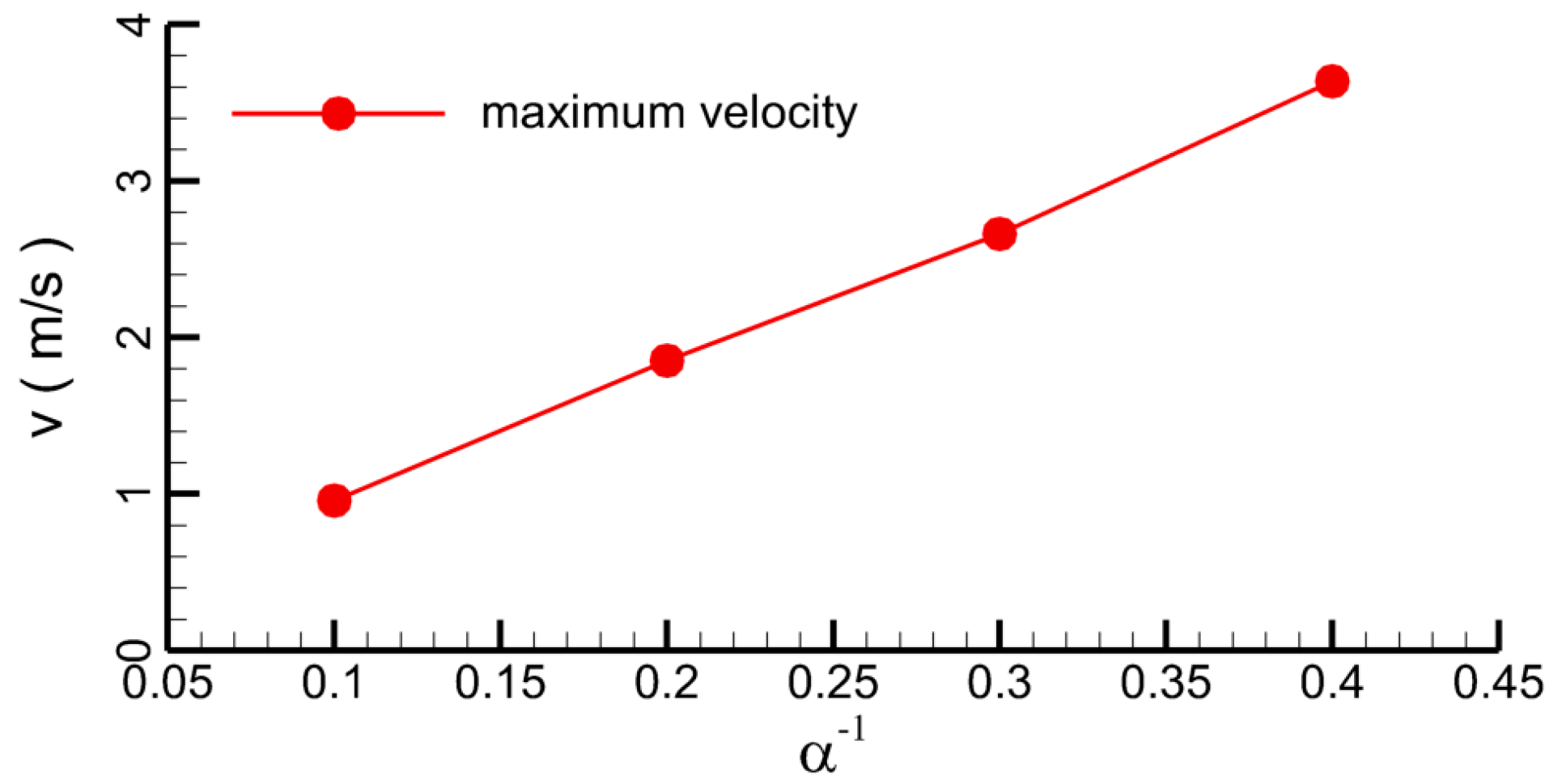
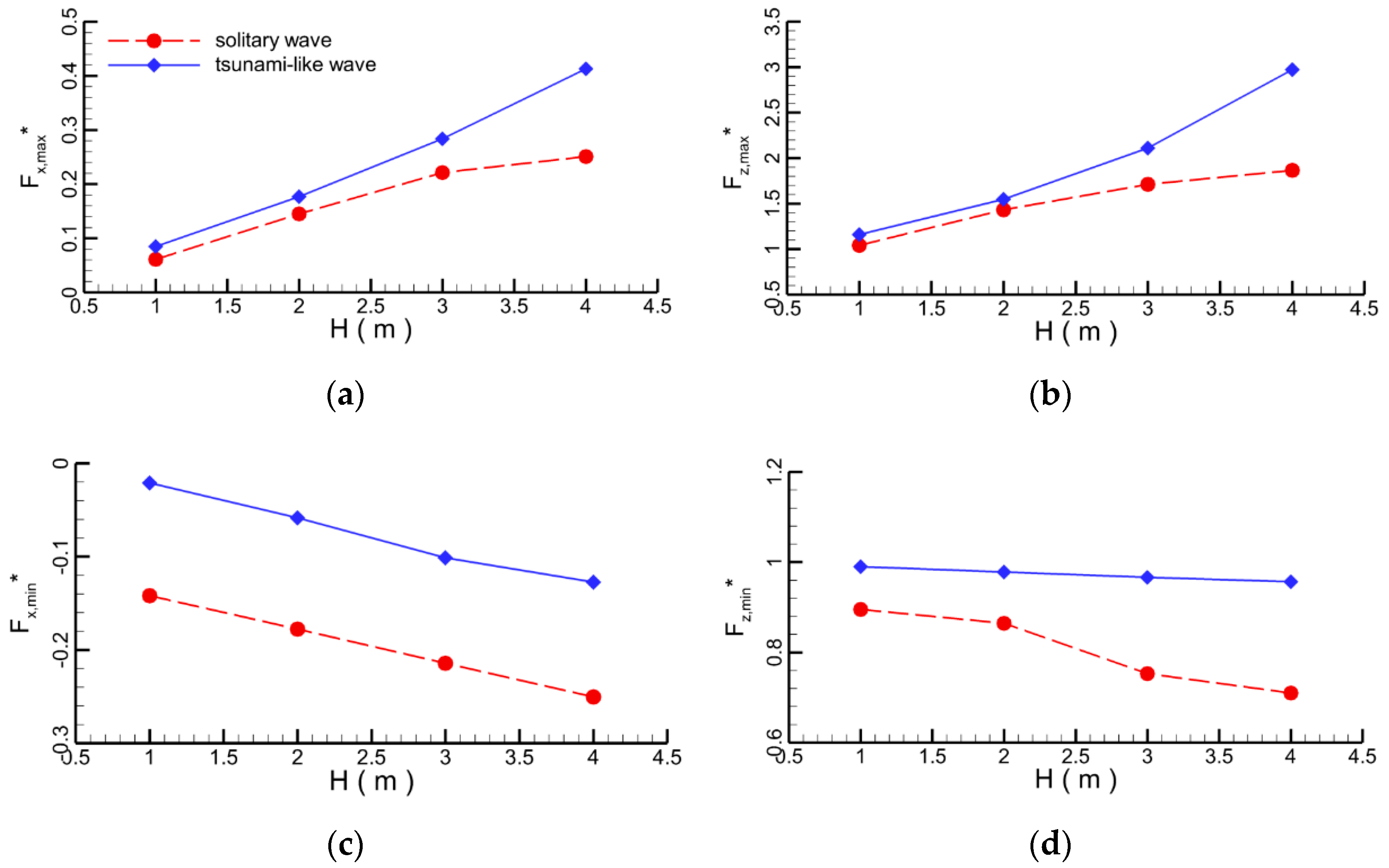
4.1.2. Effect of Wave Height
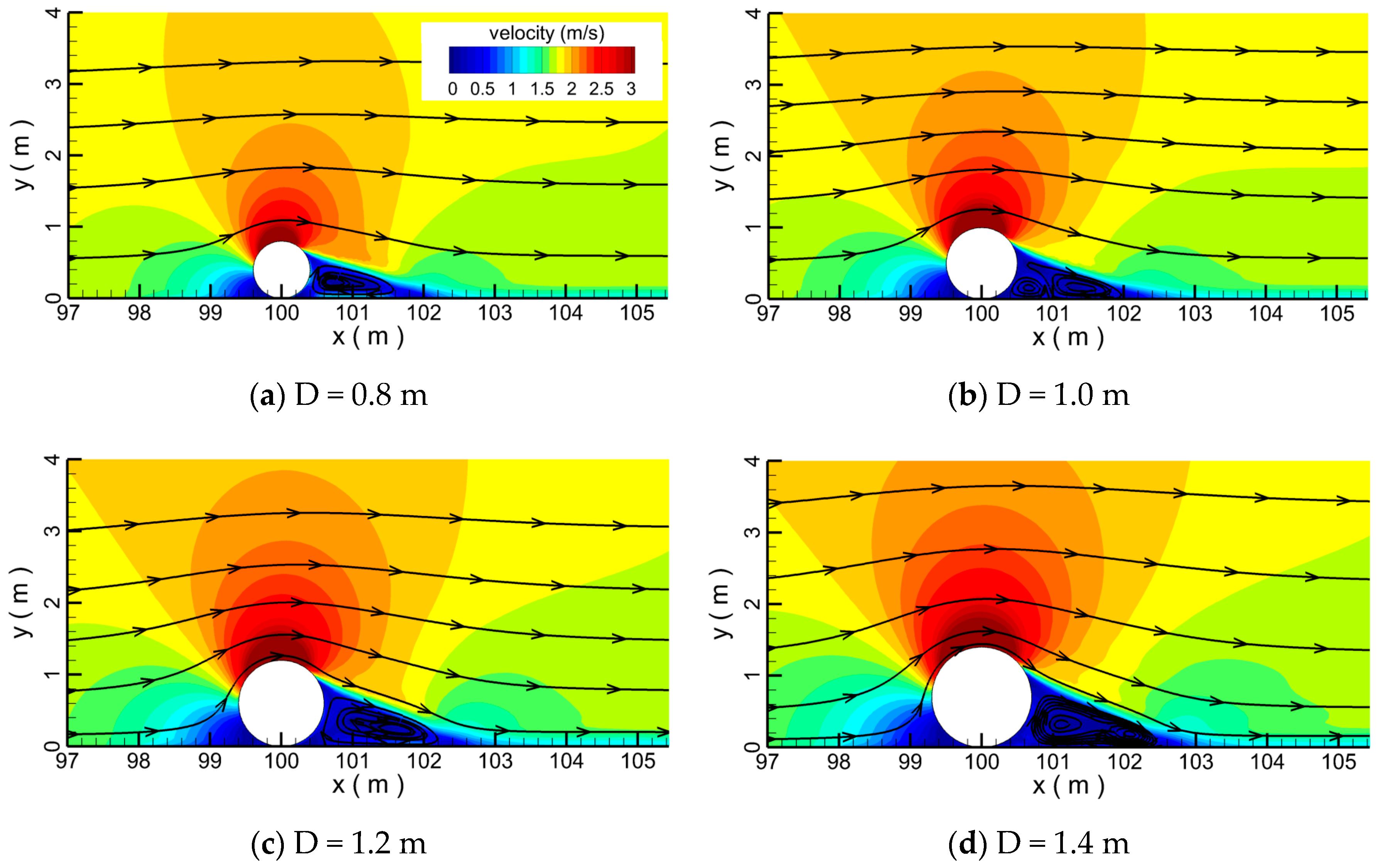
4.1.3. Effect of Pipe Diameter
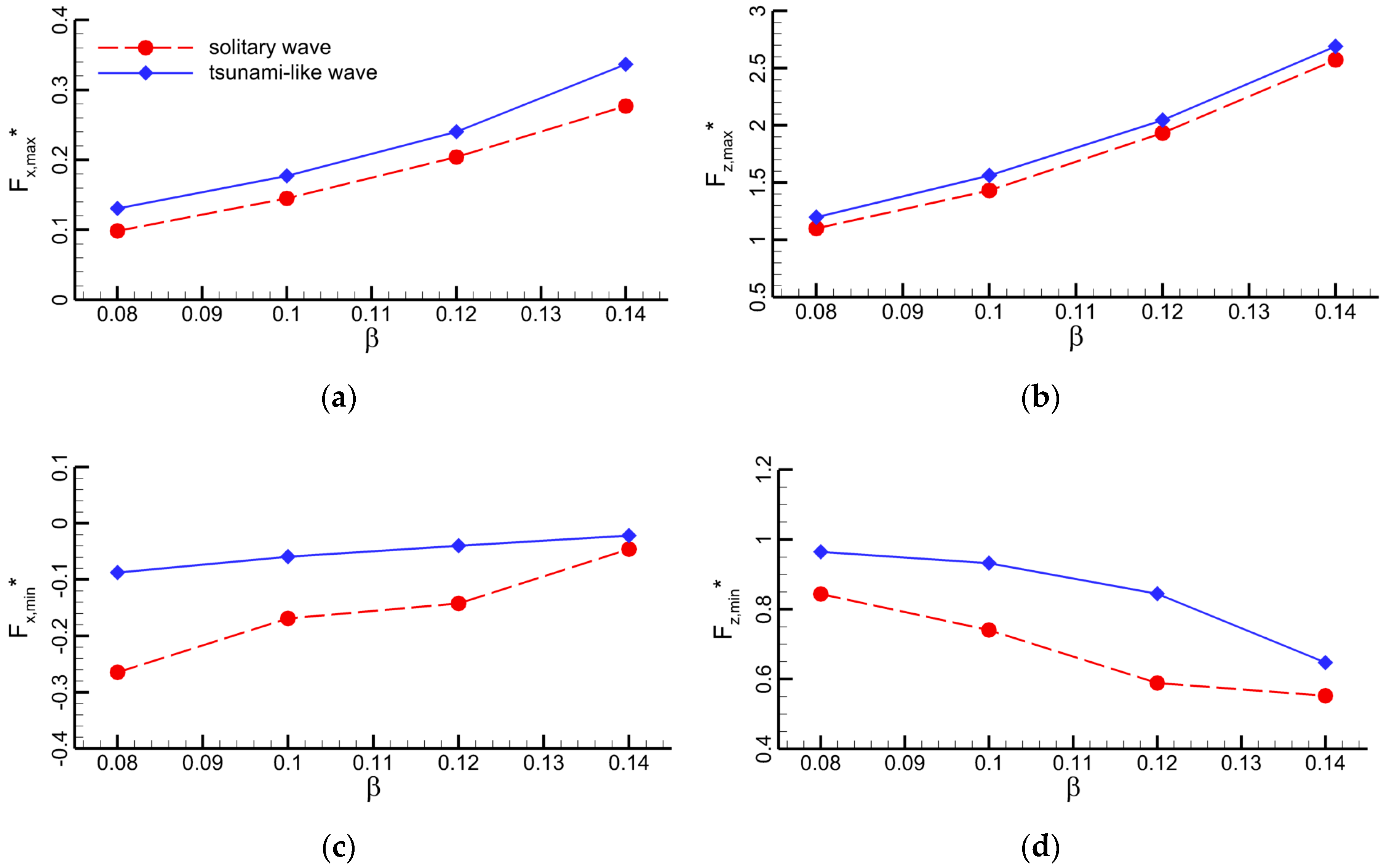
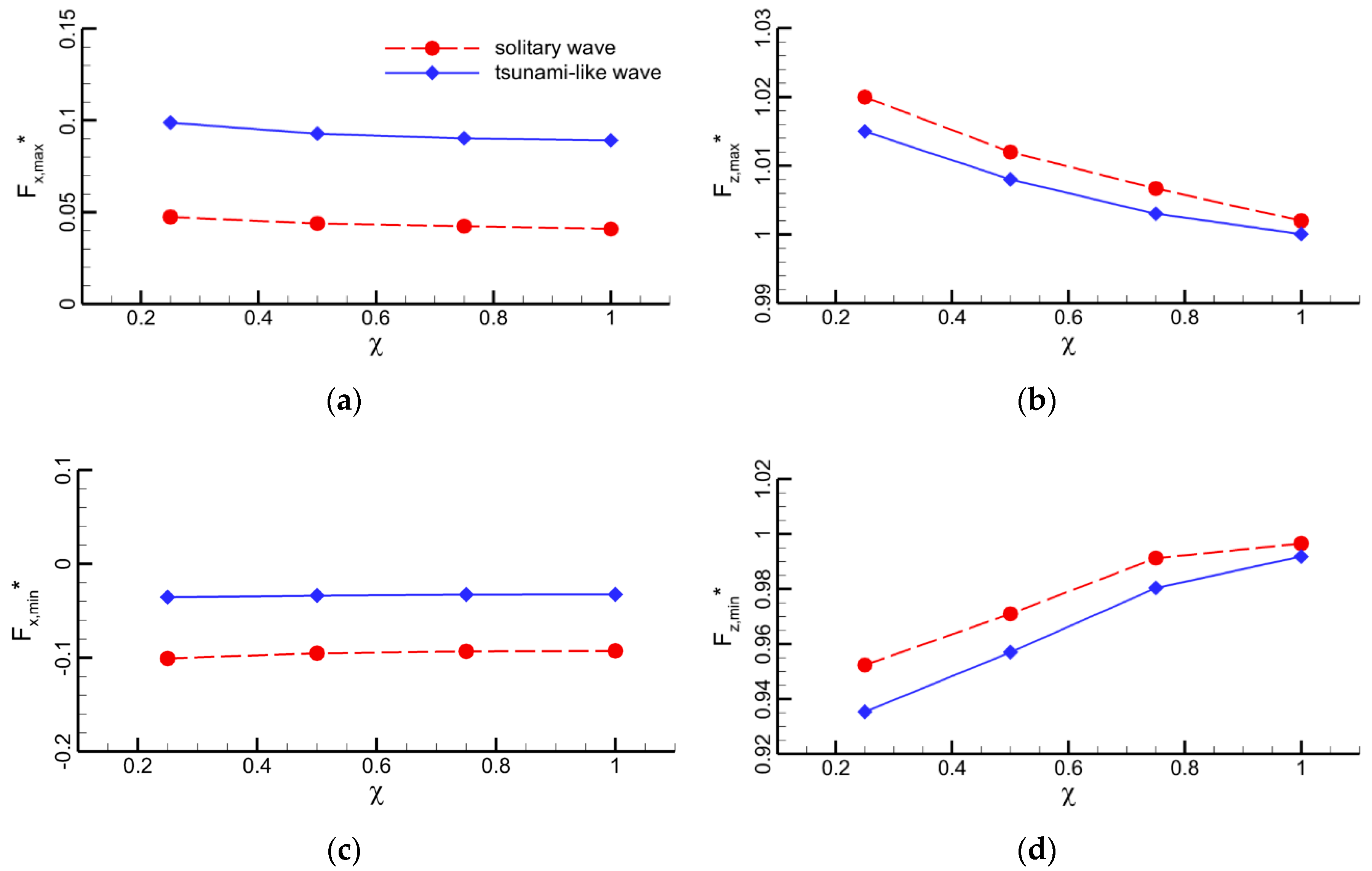
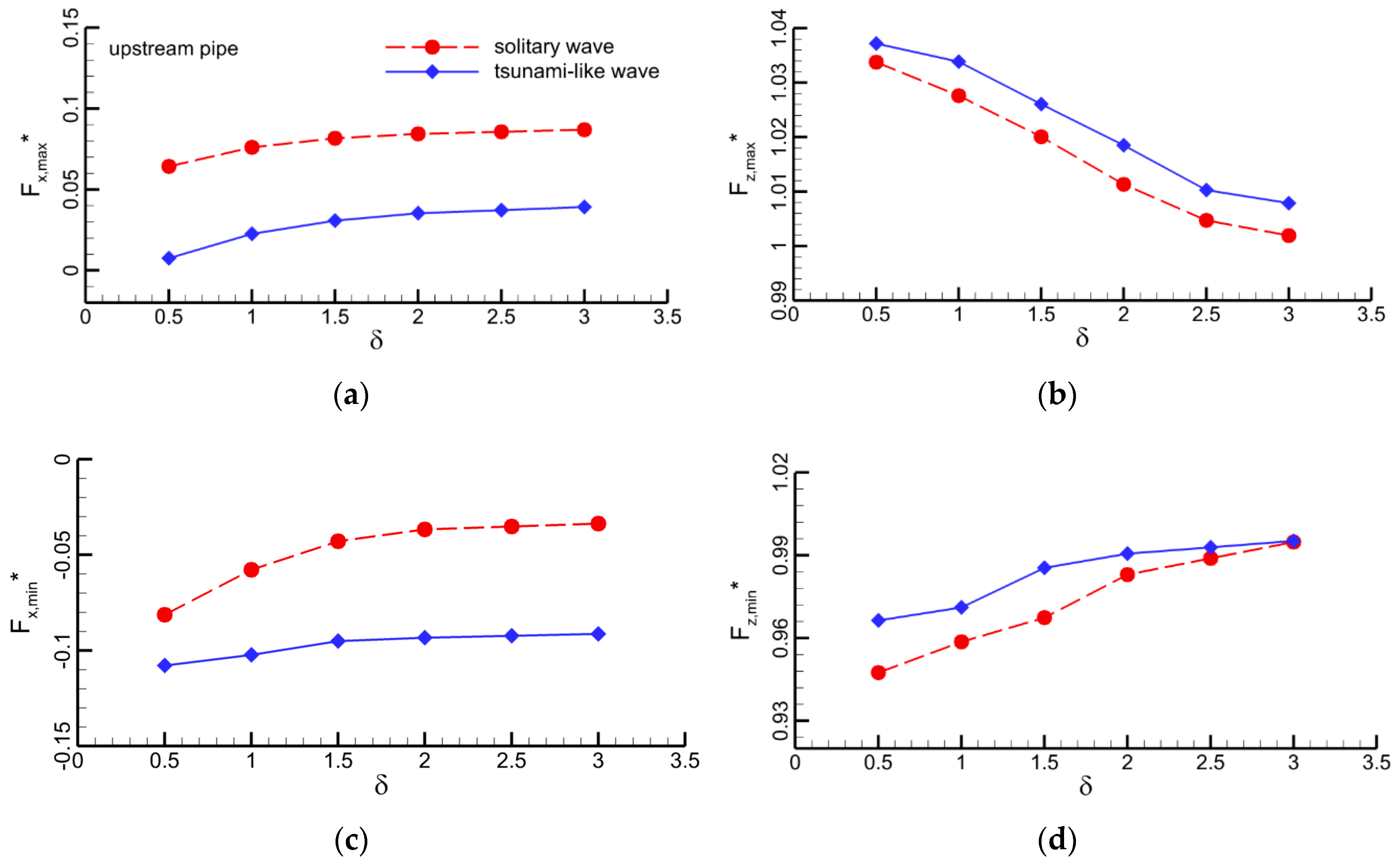
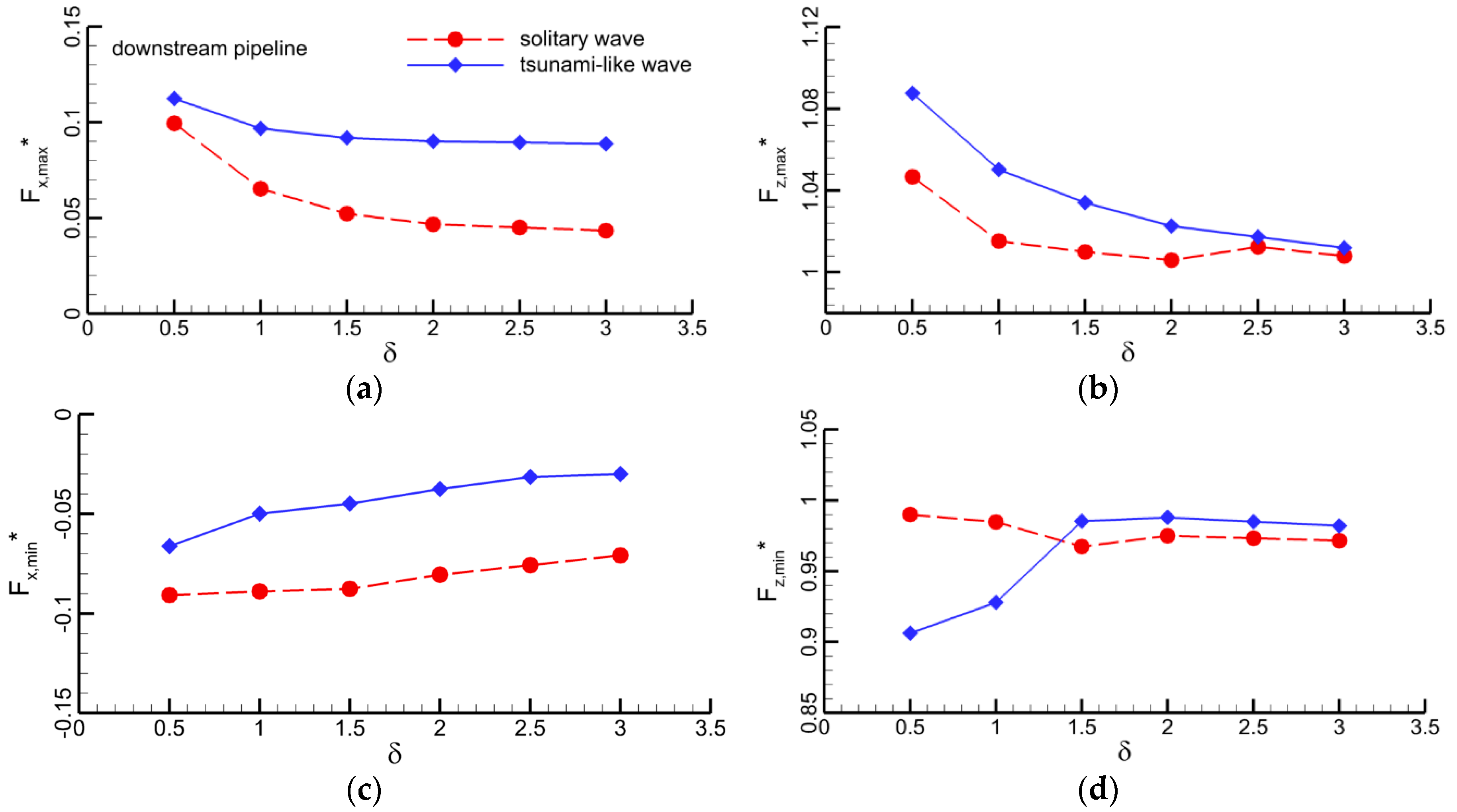
4.1.4. Effect of Gap-Ratio
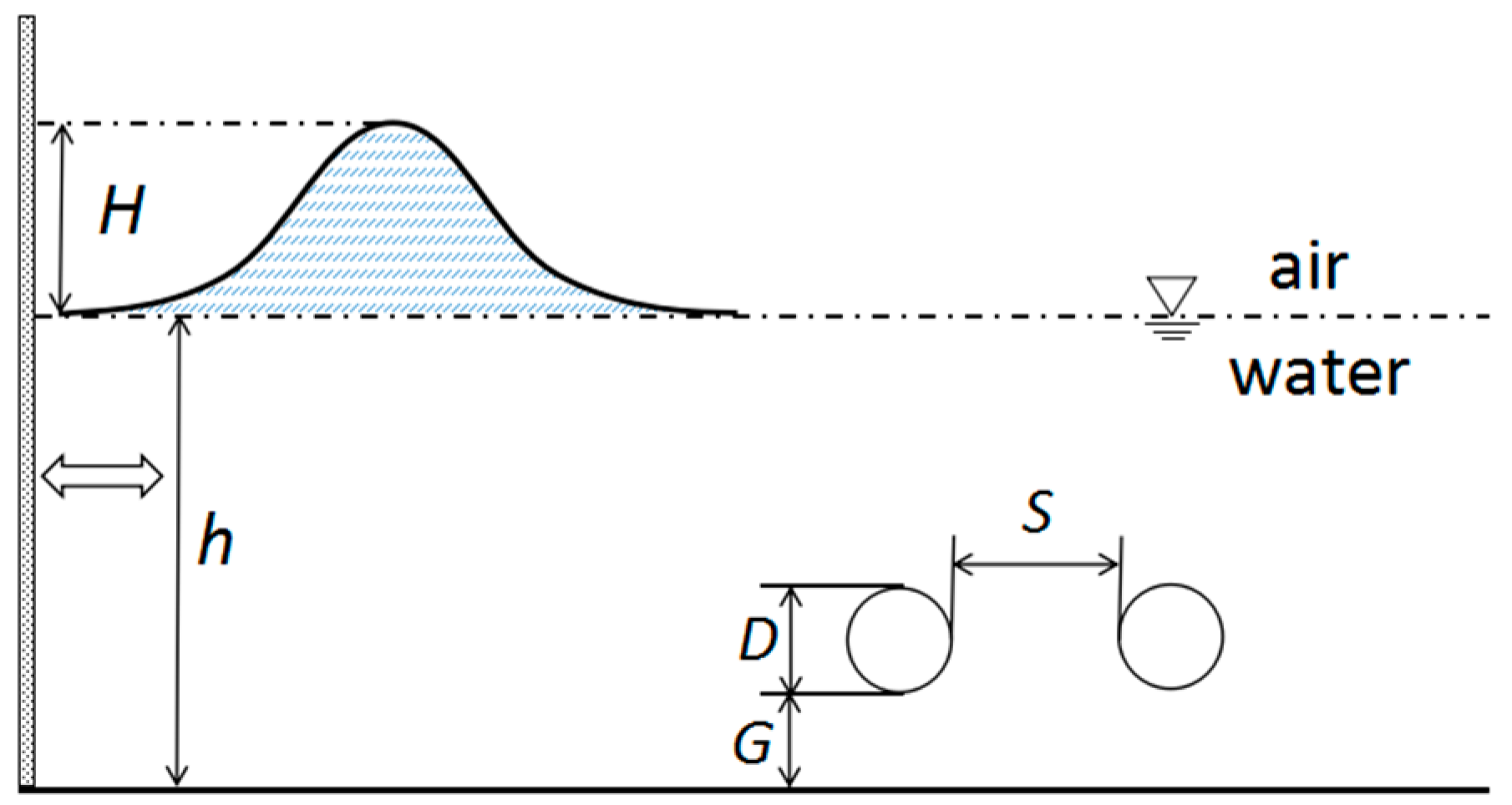
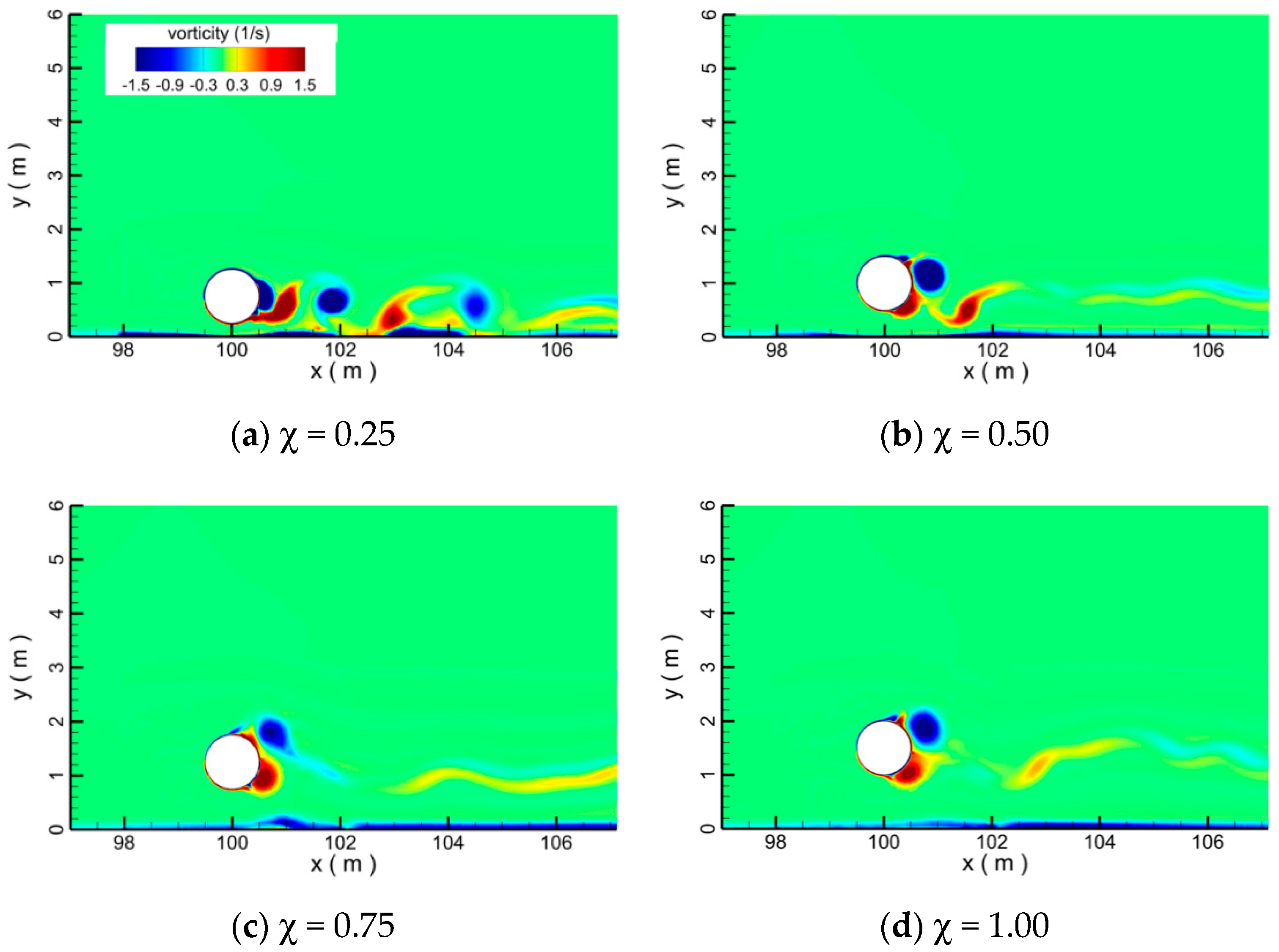
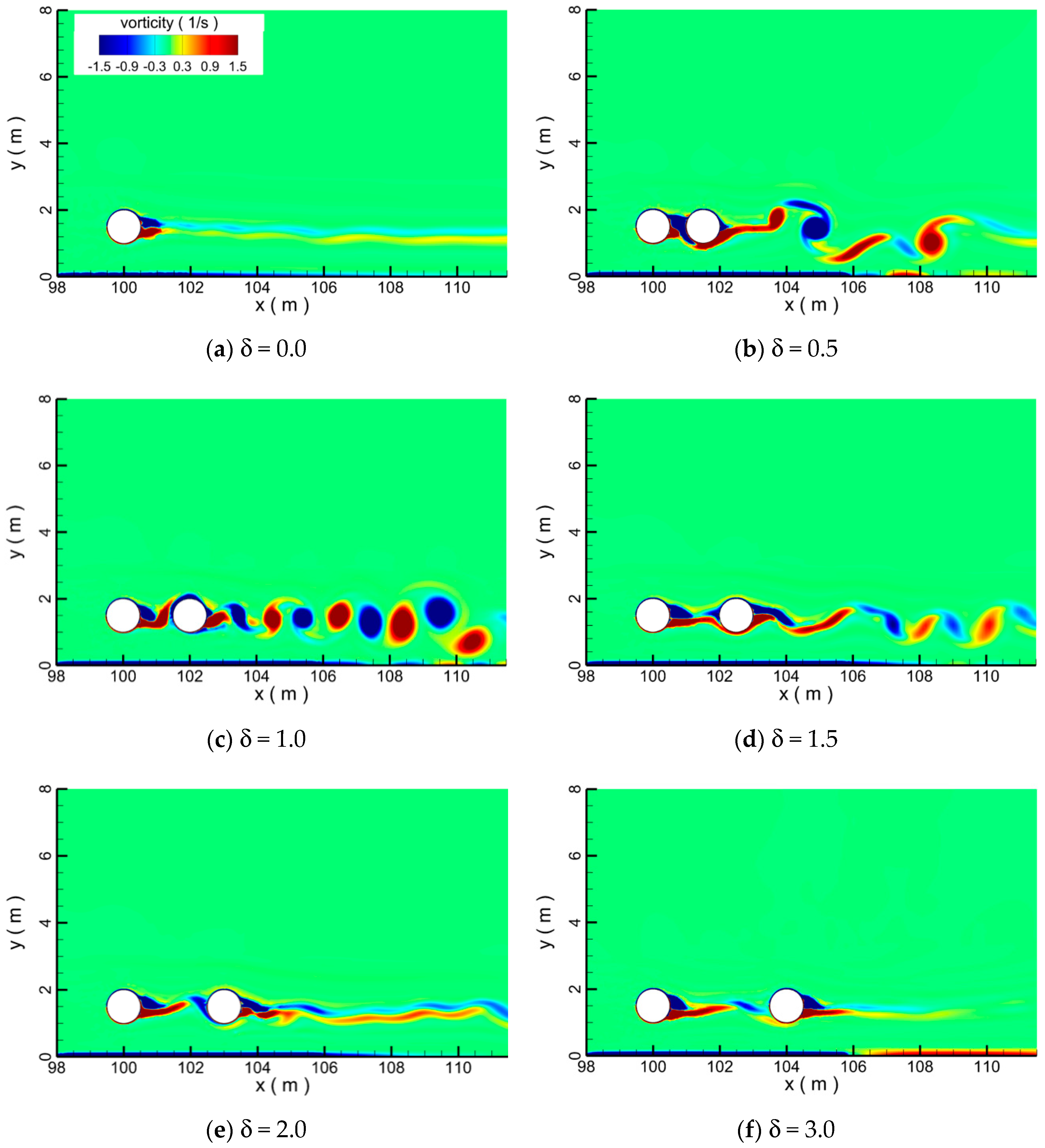
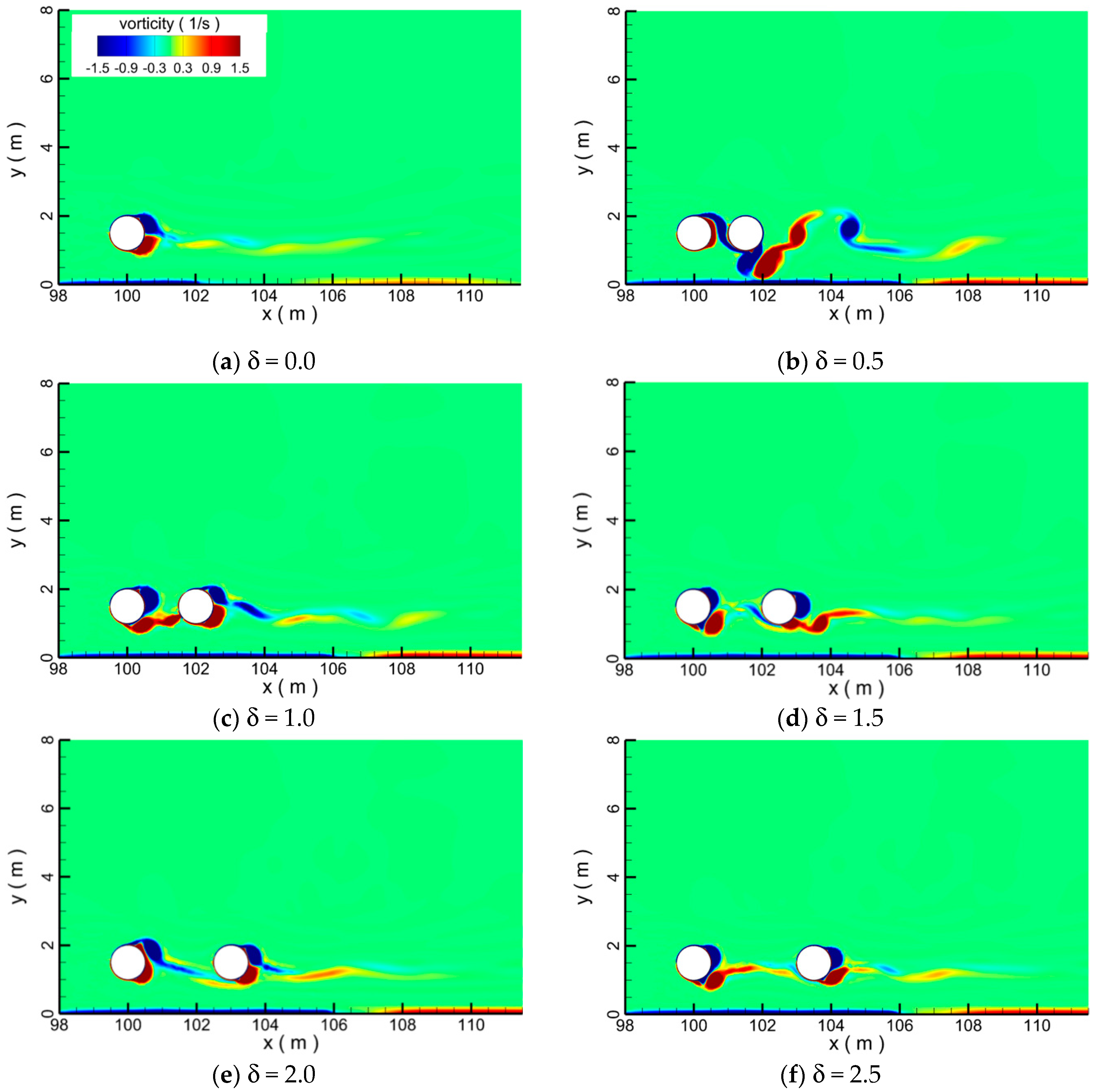
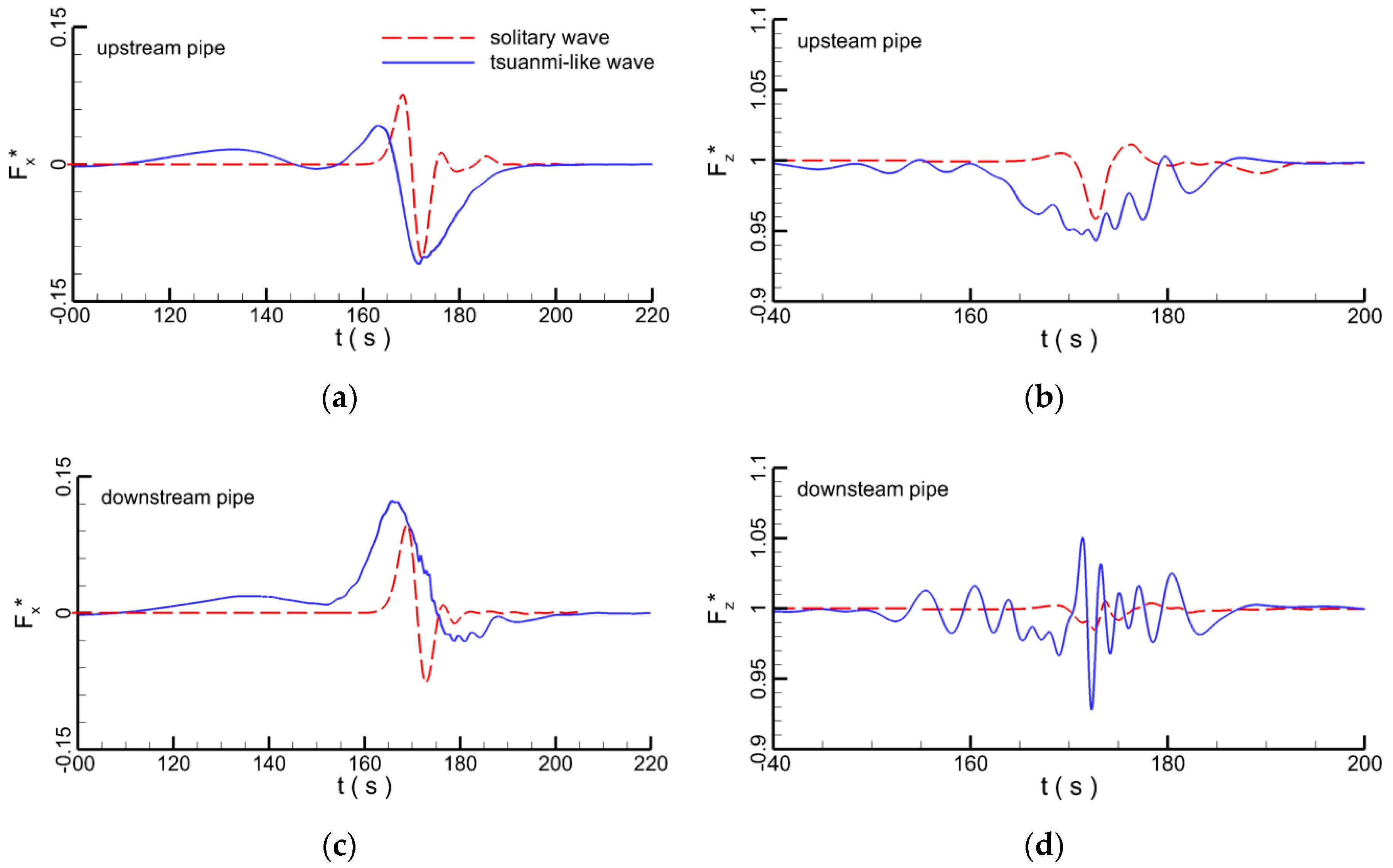
4.2. Pipelines in Tandem Arrangement
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fang, N.; Chen, G.M.; Zhu, H.W.; Meng, H.X. Statistical analysis of leakage accidents of submarine pipeline. Oil Gas Storage Transp. 2014, 33, 99–103. [Google Scholar]
- Tong, F.F.; Cheng, L.; An, H.; Griffiths, T. The hydrodynamic forces on a circular cylinder in proximity to a wall with intermittent contact in steady current. Ocean Eng. 2017, 146, 424–433. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsoe, J.; Gravesen, H.; Bruschi, R. Response of Marine Pipelines in Scour Trenches. J. Waterway Port Coast. Ocean Eng. 1989, 115, 477–496. [Google Scholar] [CrossRef]
- Zhao, E.J.; Shi, B.; Qu, K.; Dong, W.B.; Zhang, J. Experimental and Numerical Investigation of Local Scour around Submarine Piggyback Pipeline under Steady Currents. J. Ocean Univ. China 2018, 17, 244–256. [Google Scholar] [CrossRef]
- Subbiah, K.; Cheong, H.F.; Shankar, N.J. Regular and random wave pressures around large diameter submarine pipeline near ocean bed. J. Hydraul. Res. 1991, 29, 49–66. [Google Scholar] [CrossRef]
- Gao, F.P.; Gu, X.Y.; Jeng, D.S.; Teo, H.T. An experimental study for wave-induced instability of pipelines: The breakout of pipelines. Appl. Ocean Res. 2002, 24, 83–90. [Google Scholar] [CrossRef]
- Haley, J.F.; Swan, C.; Gibson, R. An Experimental Investigation of Wave Impact Loads on a Slender Horizontal Cylinder. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014; American Society of Mechanical Engineers: New York, NY, USA, 2014; p. V08BT06A041. [Google Scholar]
- Gao, N.; Yang, J.; Li, X.; Zhao, W. Wave forces on horizontal cylinder due to nonlinear focused wave groups. In Proceedings of the Twenty-fifth International Ocean and Polar Engineering Conference, Kona, HI, USA, 21–26 June 2015; International Society of Offshore and Polar Engineers: Houston, TX, USA, 2015. [Google Scholar]
- Chern, M.-J.; Odhiambo, E.A.; Horng, T.-L.; Borthwick, A.G.L. Numerical simulation of vibration of horizontal cylinder induced by progressive waves. Fluid Dyn. Res. 2016, 48, 015508. [Google Scholar] [CrossRef]
- Ong, M.C.; Kamath, A.; Bihs, H.; Afzal, M.S. Numerical simulation of free-surface waves past two semi-submerged horizontal circular cylinders in tandem. Mar. Struct. 2017, 52, 1–14. [Google Scholar] [CrossRef]
- Liang, D.F.; Gotoh, H.; Khayyer, A.; Chen, J.M. Boussinesq mdelling of solitary wave and N-wave runup on coast. Appl. Ocean Res. 2013, 42, 144–154. [Google Scholar] [CrossRef]
- Hsiao, S.C.; Lin, T.C. Tsunami-like solitary waves impinging and overtopping an impermeable seawall: Experiment and RANS modeling. Coast. Eng. 2010, 57, 1–18. [Google Scholar] [CrossRef]
- Limura, K.; Norio, T. Numerical simulation estimating effects of tree density distribution in coastal forest on tsunami mitigation. Ocean Eng. 2012, 54, 223–232. [Google Scholar]
- Synolakis, C.E. The run-up of solitary waves. J. Fluid Mech. 1987, 185, 523–545. [Google Scholar] [CrossRef]
- Gedik, N.; Irtem, E.; Kabdasli, S. Laboratory investigation on tsunami run-up. Ocean Eng. 2005, 32, 513–528. [Google Scholar] [CrossRef]
- Goseberg, N.; Wurpts, A.; Schlurmann, T. Laboratory-scale generation of tsunami and long waves. Coast. Eng. 2013, 79, 57–74. [Google Scholar] [CrossRef]
- Francesco, A.; Tripepi, G.; Meringolo, D.D.; Veltri, P. Solitary wave-induced forces on horizontal circular cylinders: Laboratory experiments and SPH simulations. Coast. Eng. 2017, 129, 17–35. [Google Scholar]
- Madsen, A.; Schäffer, H.A. Analytical solutions for tsunami run-up on a plane beach: Single waves, N-waves and transient waves. J. Fluid Mech. 2010, 645, 27–57. [Google Scholar] [CrossRef]
- Madsen, A.; Fuhrman, D.R.; Schäffer, H.A. On the solitary wave paradigm for tsunamis. J. Geophys. Res. 2008, 113, 286–292. [Google Scholar] [CrossRef]
- Chan, I.C.; Liu, L.F. On the run-up of long waves on a plane beach. J. Geophys. Res. 2012, 117, 72–82. [Google Scholar] [CrossRef]
- Qu, K.; Ren, X.Y.; Kraatz, S. Numerical investigation of tsunami-like wave hydrodynamic characteristics and its comparison with solitary wave. Appl. Ocean Res. 2017, 63, 36–48. [Google Scholar] [CrossRef]
- Stefan, L.; Oumeraci, H. Solitary waves and bores passing three cylinders-effect of distance and arrangement. Coast. Eng. Proc. 2014, 1, 39. [Google Scholar]
- Istrati, D.; Buckle, I.; Lomonaco, P.; Yim, S. Deciphering the Tsunami Wave Impact and Associated Connection Forces in Open-Girder Coastal Bridges. J. Mar. Sci. Eng. 2018, 6, 148. [Google Scholar] [CrossRef]
- Zhao, E.J.; Mu, L.; Shi, B. Numerical Study of the Influence of Tidal Current on Submarine Pipeline Based on the SIFOM–FVCOM Coupling Model. Water 2018, 10, 1814. [Google Scholar] [CrossRef]
- Rhie, T.M.; Chow, A. Numerical study of the turbulent flow past an isolated airfoil with trailing-edge separation. AIAA J. 1983, 21, 1525–1532. [Google Scholar] [CrossRef]
- Gomes, M.N.; Olintoa, C.R.; Rochaa, L.A.O.; Souzaa, J.A.; Isoldi, L.A. Computational modeling of a regular wave tank. Therm. Eng. 2009, 8, 44–50. [Google Scholar]
- Hafsia, Z.; Haj, M.B.; Lamloumi, H.; Maalel, K. Comparison between Moving Paddle and Mass Source Methods for Solitary Wave Generation and Propagation over A Steep Sloping Beach. Eng. Appl. Comput. Fluid Mech. 2009, 3, 355–368. [Google Scholar] [CrossRef]
- Qu, K.; Ren, X.Y.; Kraatz, S.; Zhao, E.J. Numerical analysis of tsunami-like wave impact on horizontal cylinders. Ocean Eng. 2017, 145, 316–333. [Google Scholar] [CrossRef]
- Sibley, P.O. The Solitary Wave and the Forces It Imposes on a Submerged Horizontal Circular Cylinder: An Analytical and Experimental Study. Ph.D. Thesis, City University London, London, UK, 1991. [Google Scholar]
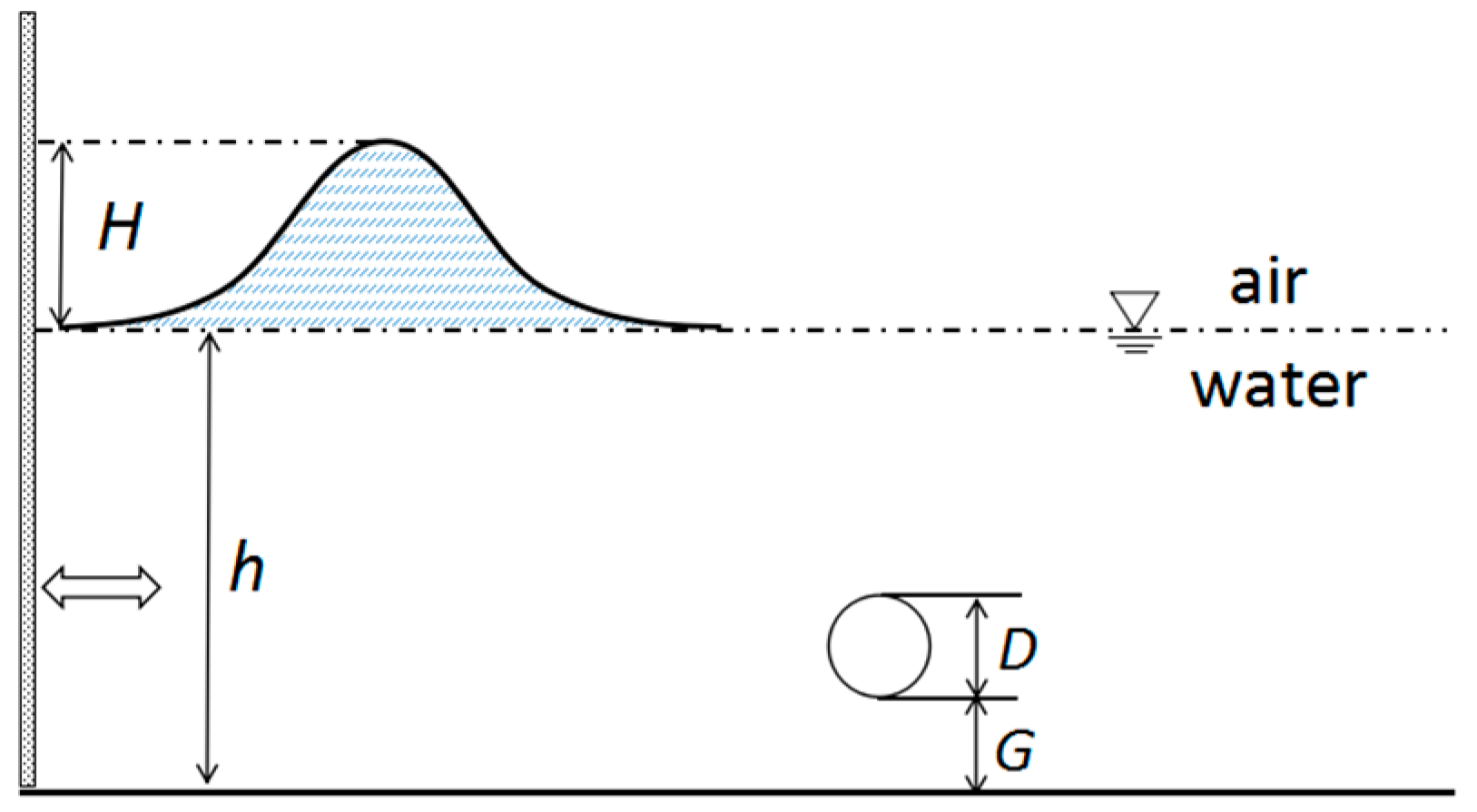

| Run | h (m) | H (m) | D (m) | G (m) |
|---|---|---|---|---|
| 1 | 0.17 | 0.034 | 0.034 | 0.0714 |
| 2 | 0.16875 | 0.03105 | 0.027 | 0.023625 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, E.; Qu, K.; Mu, L.; Kraatz, S.; Shi, B. Numerical Study on the Hydrodynamic Characteristics of Submarine Pipelines under the Impact of Real-World Tsunami-Like Waves. Water 2019, 11, 221. https://doi.org/10.3390/w11020221
Zhao E, Qu K, Mu L, Kraatz S, Shi B. Numerical Study on the Hydrodynamic Characteristics of Submarine Pipelines under the Impact of Real-World Tsunami-Like Waves. Water. 2019; 11(2):221. https://doi.org/10.3390/w11020221
Chicago/Turabian StyleZhao, Enjin, Ke Qu, Lin Mu, Simon Kraatz, and Bing Shi. 2019. "Numerical Study on the Hydrodynamic Characteristics of Submarine Pipelines under the Impact of Real-World Tsunami-Like Waves" Water 11, no. 2: 221. https://doi.org/10.3390/w11020221
APA StyleZhao, E., Qu, K., Mu, L., Kraatz, S., & Shi, B. (2019). Numerical Study on the Hydrodynamic Characteristics of Submarine Pipelines under the Impact of Real-World Tsunami-Like Waves. Water, 11(2), 221. https://doi.org/10.3390/w11020221







