Numerical Study of the Influence of Tidal Current on Submarine Pipeline Based on the SIFOM–FVCOM Coupling Model
Abstract
1. Introduction
2. Solver for Incompressible Flow on Overset Meshes–Unstructured Grid Finite Volume Coastal Ocean Model (SIFOM–FVCOM) Modeling System
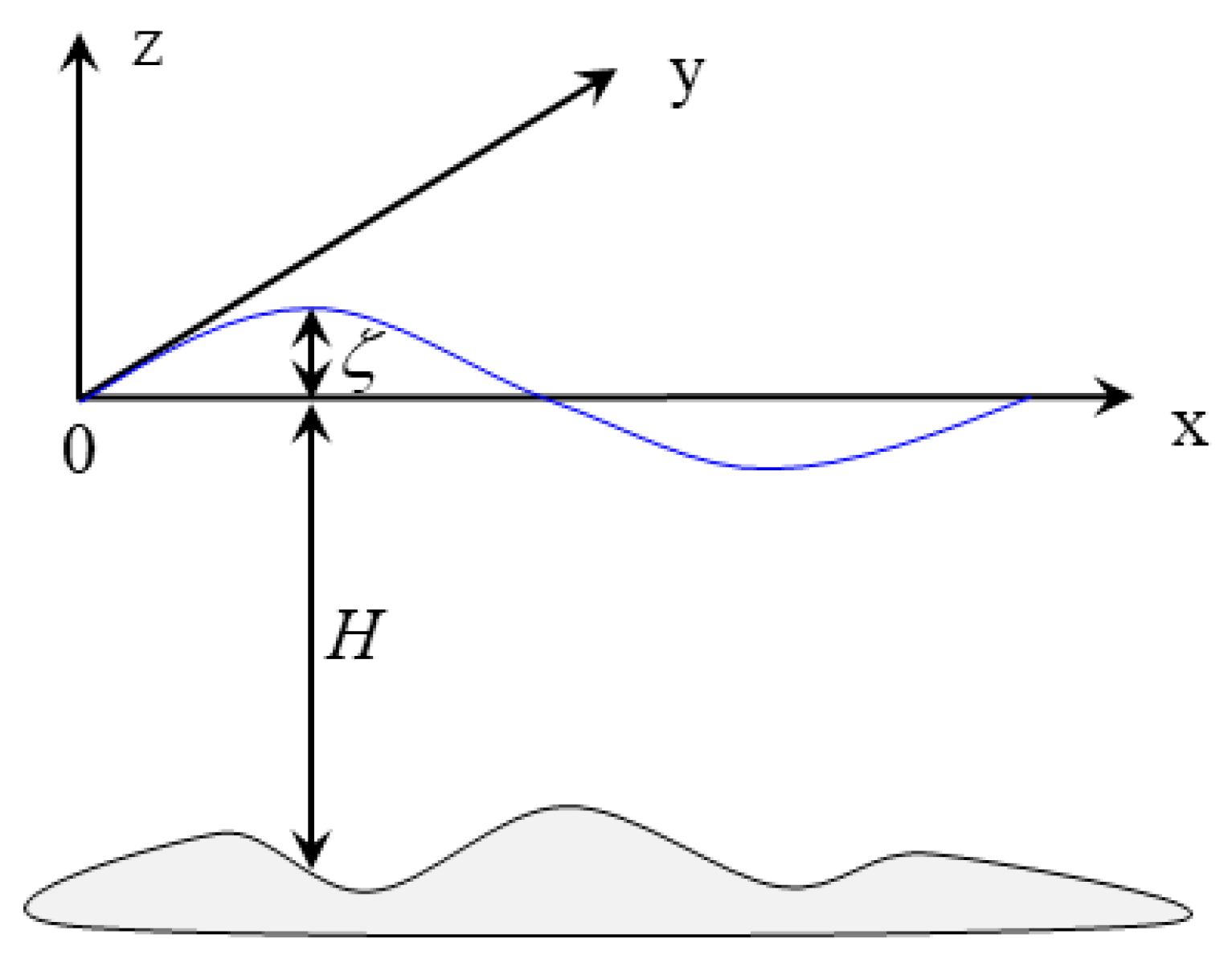
2.1. SIFOM Modeling
2.2. FVCOM Modeling
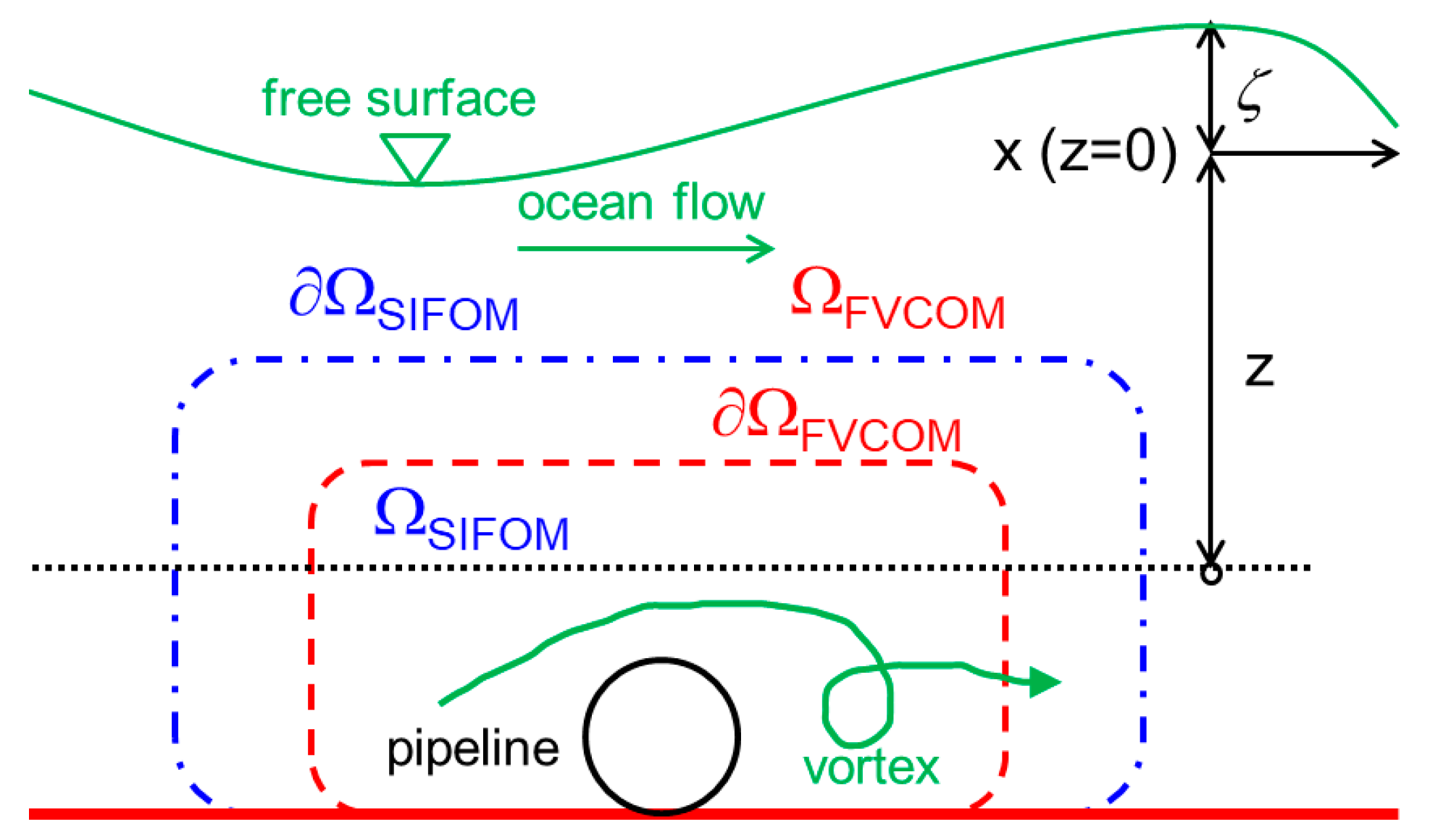
2.3. Coupling Strategy of SIFOM–FVCOM Modeling
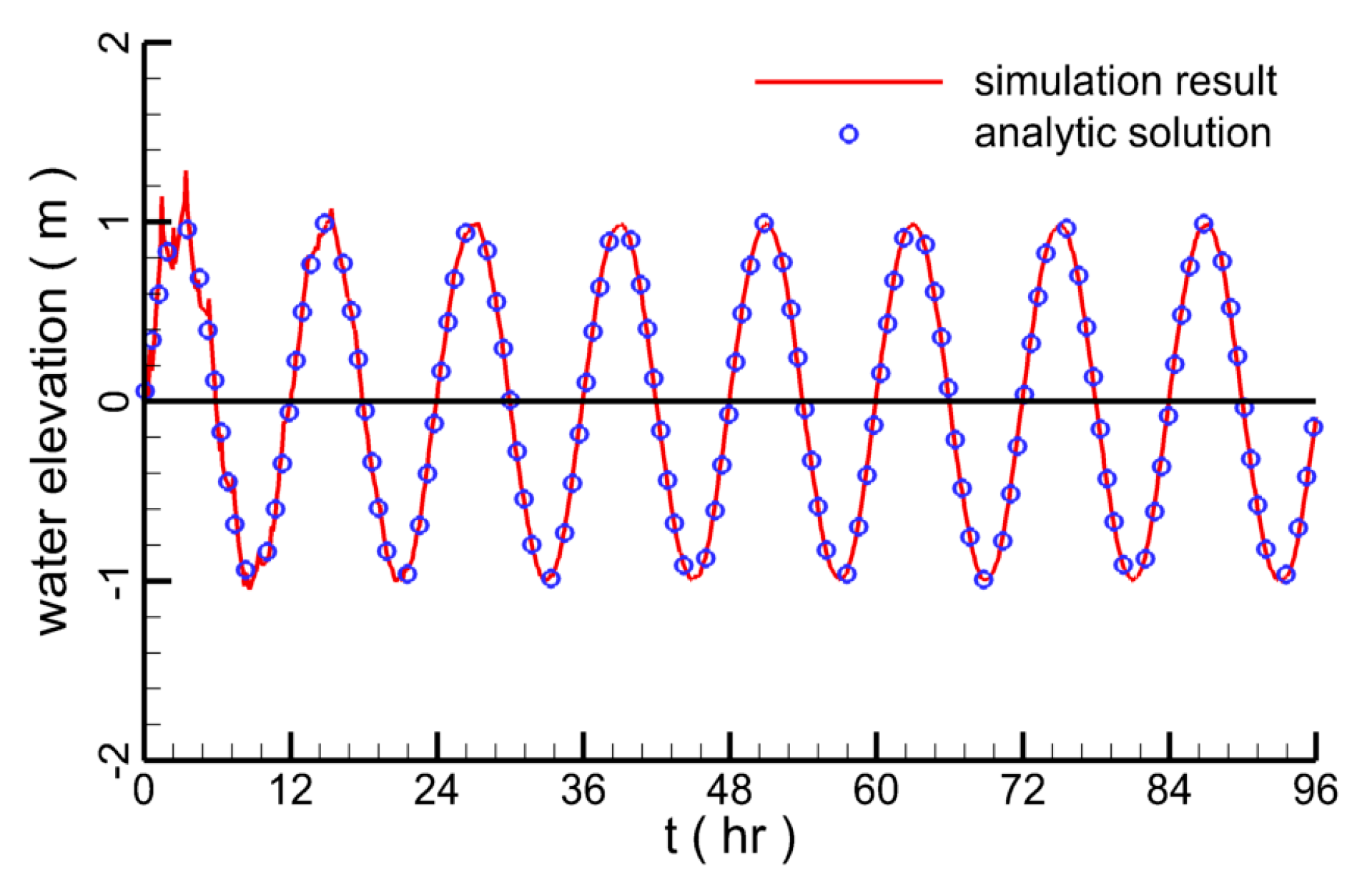
3. Modeling System Validation
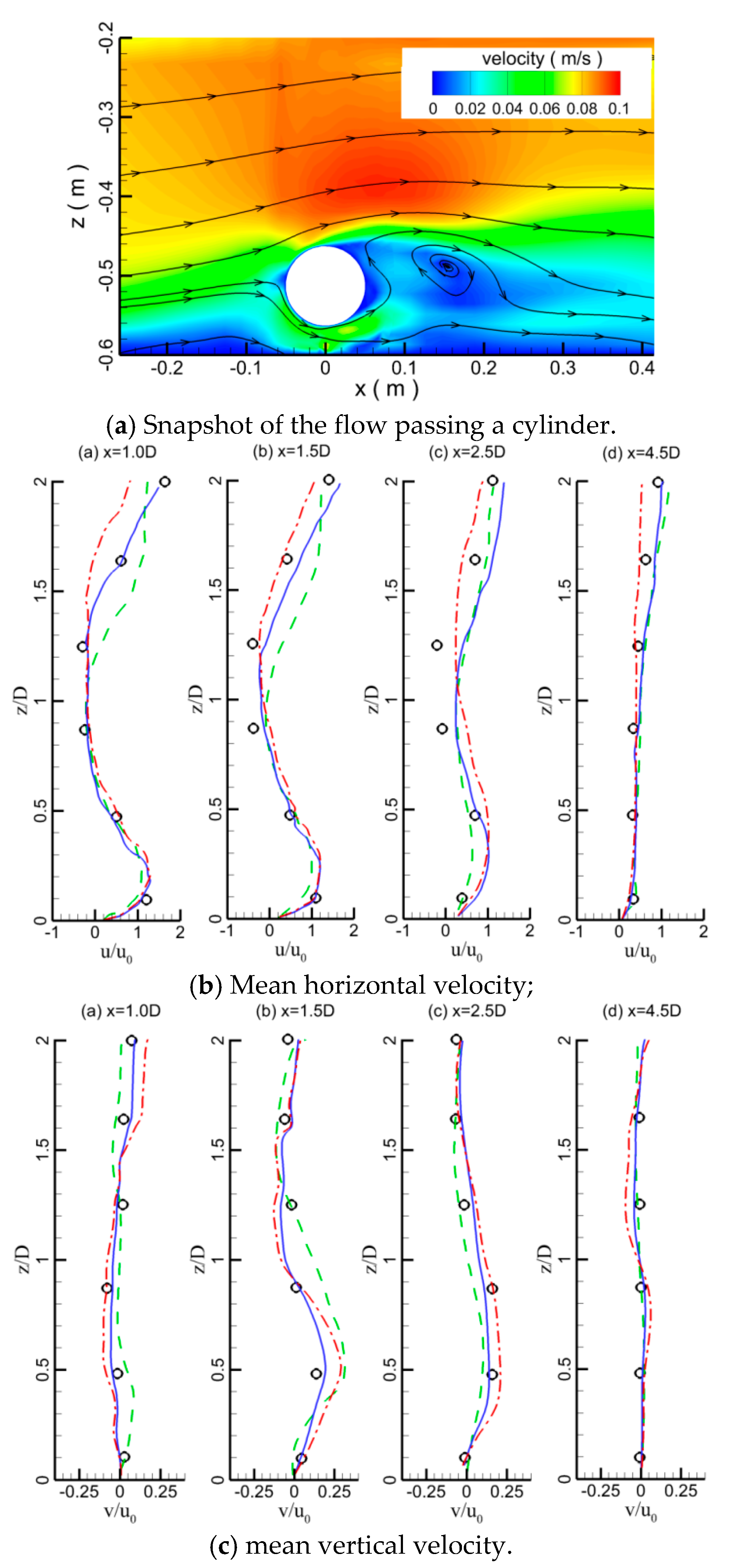
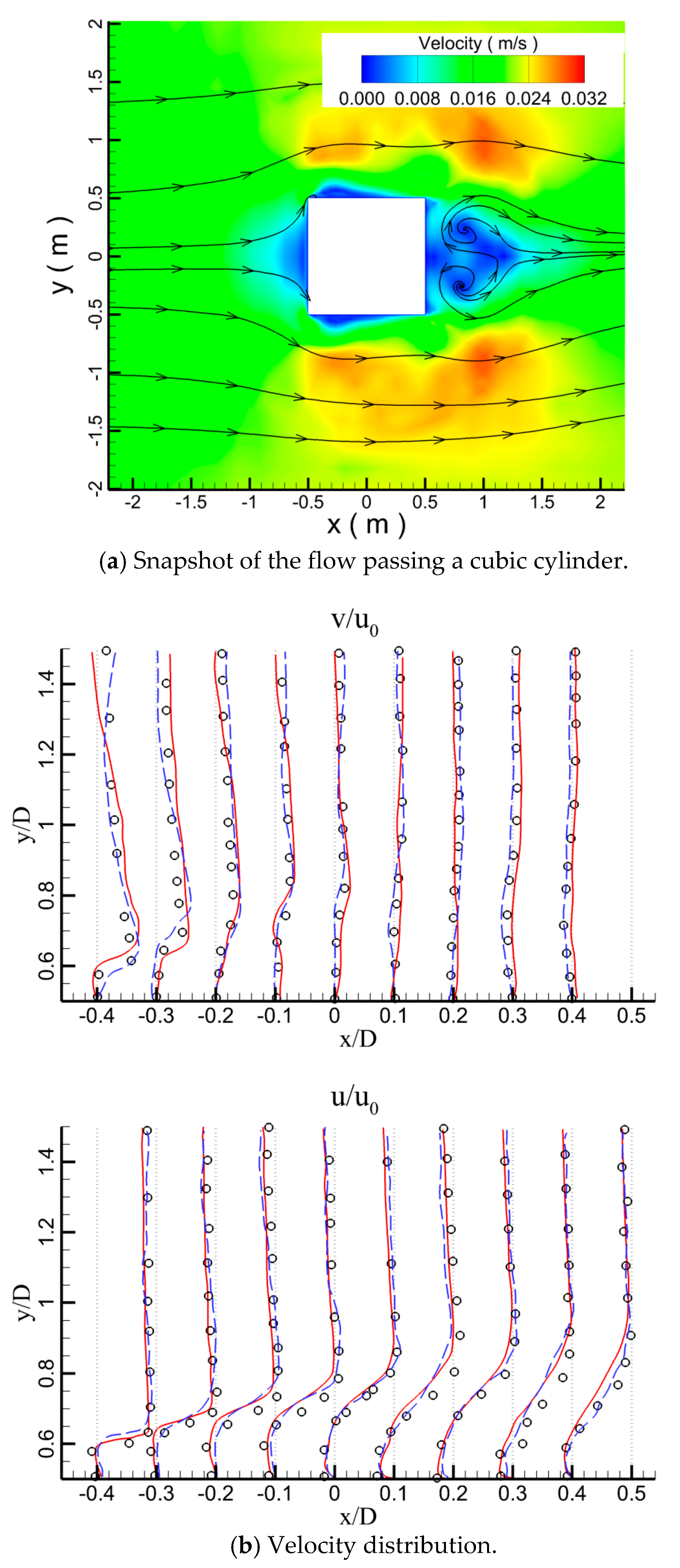
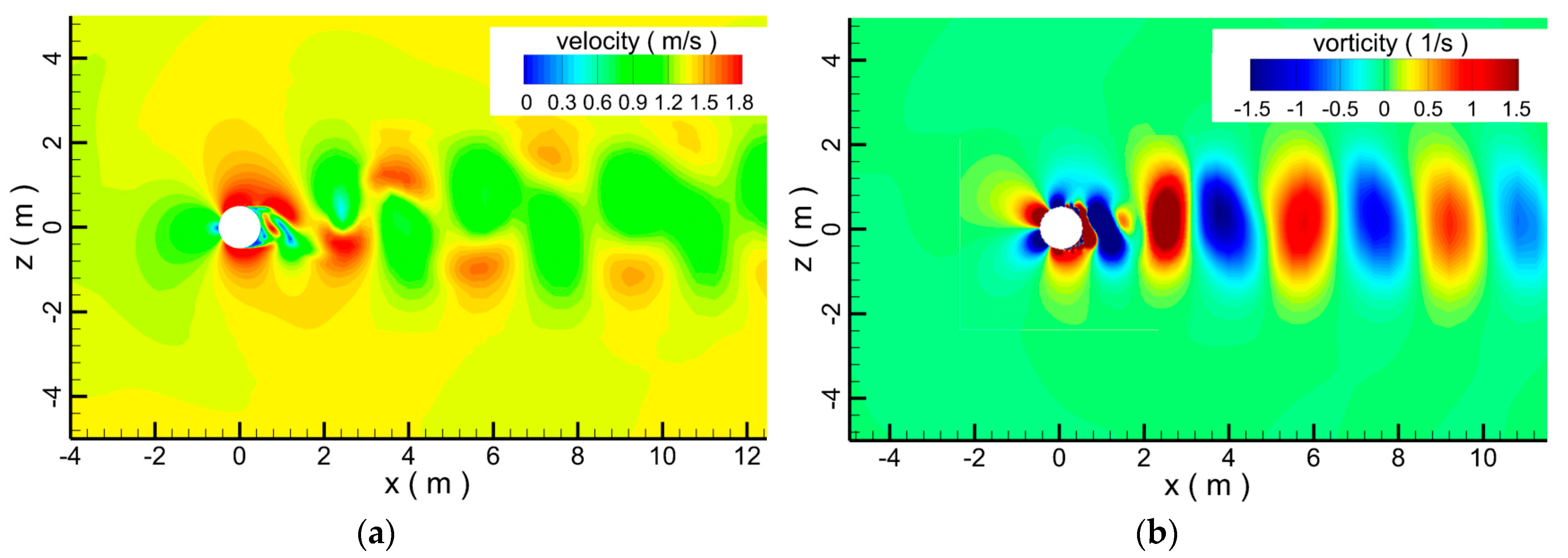
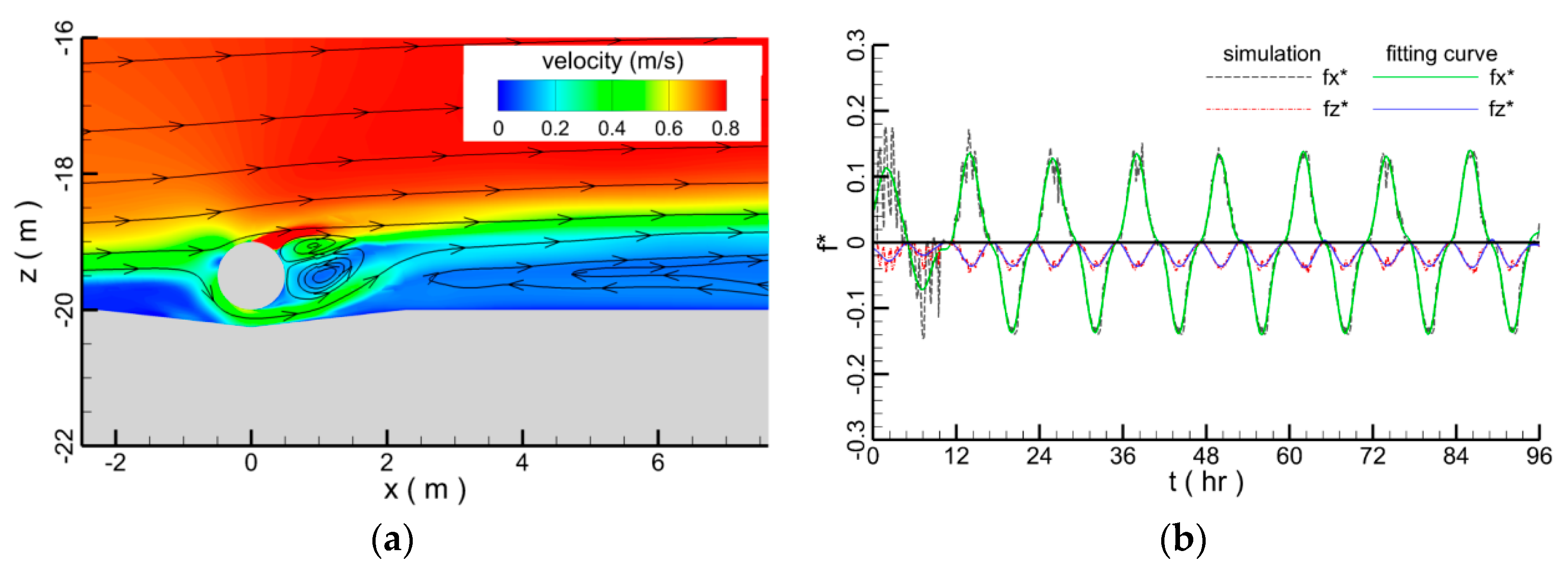
3.1. Validation on Flow Velocity and Vortex
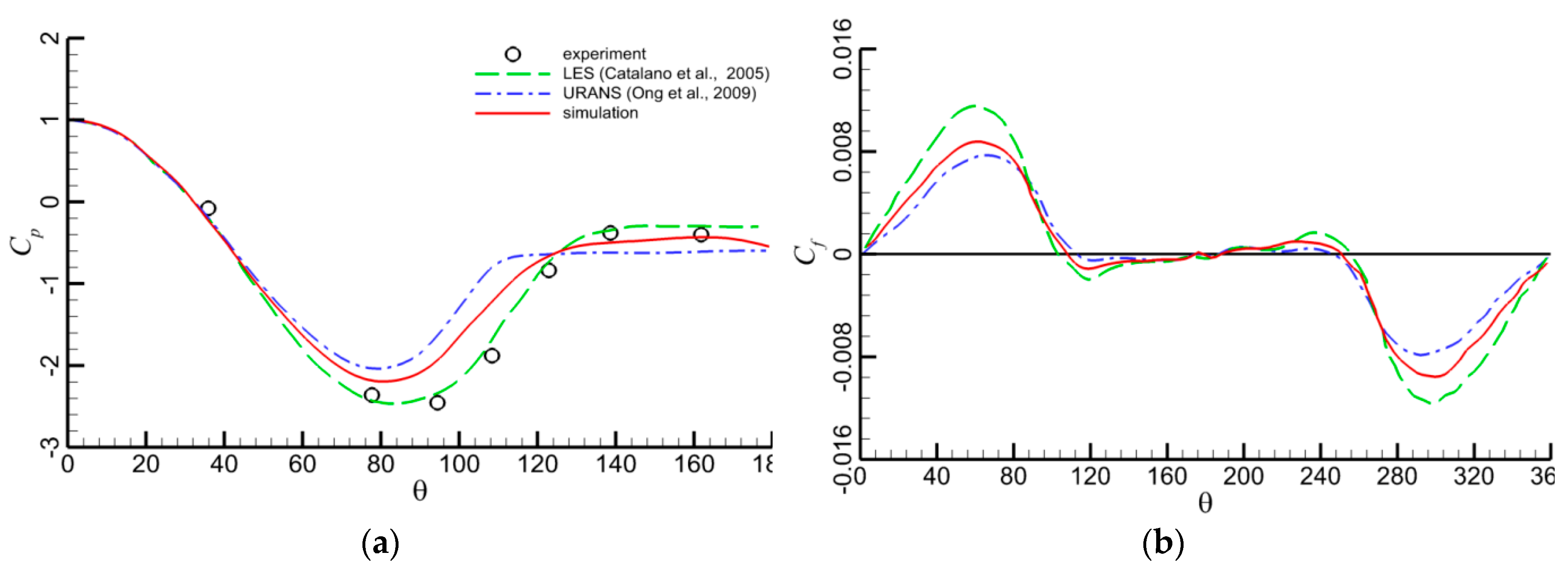
3.2. Validation on Force
4. Results and Discussions
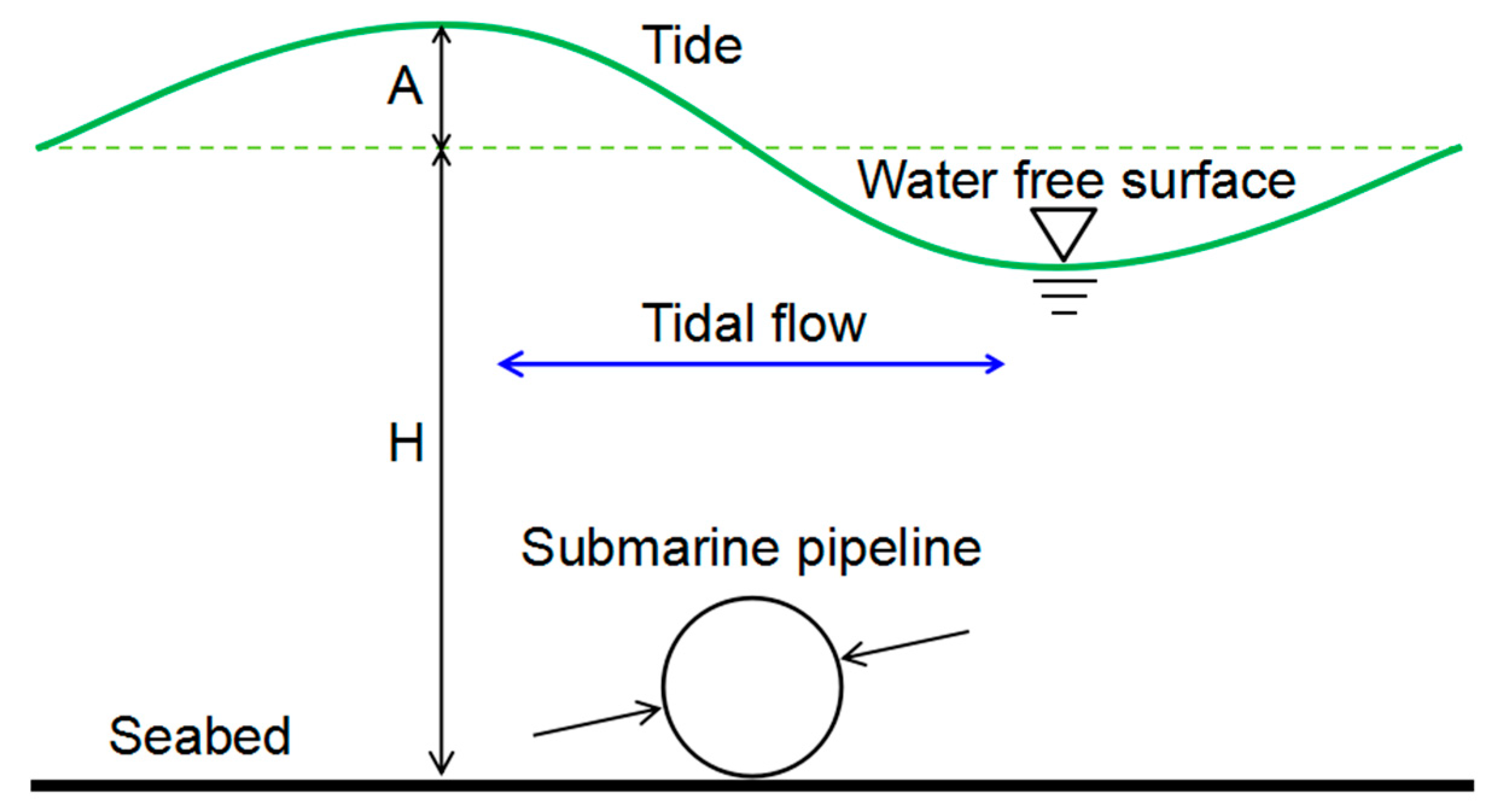
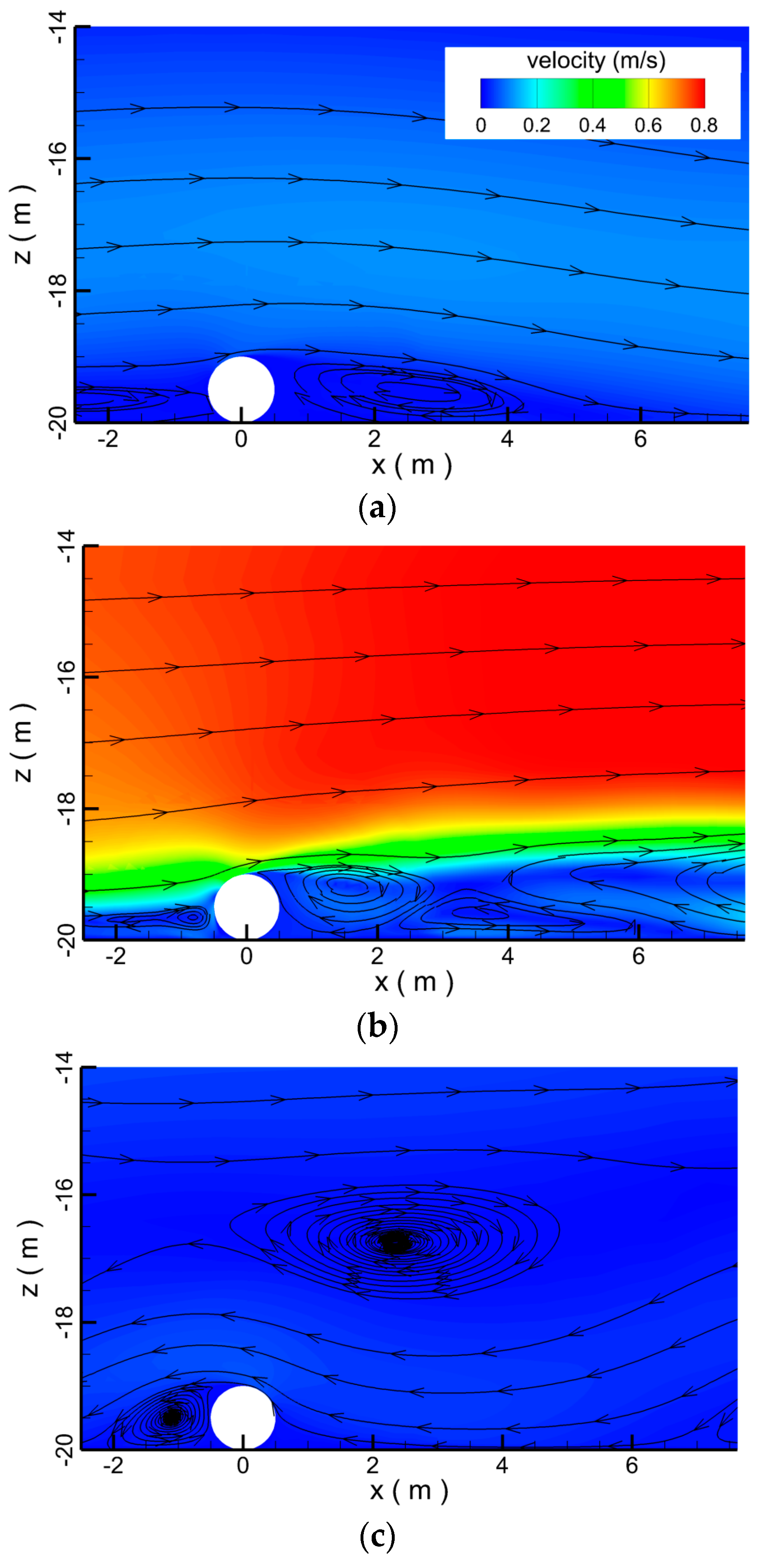
4.1. Hydrodynamics around Submarine Pipeline with No Scour
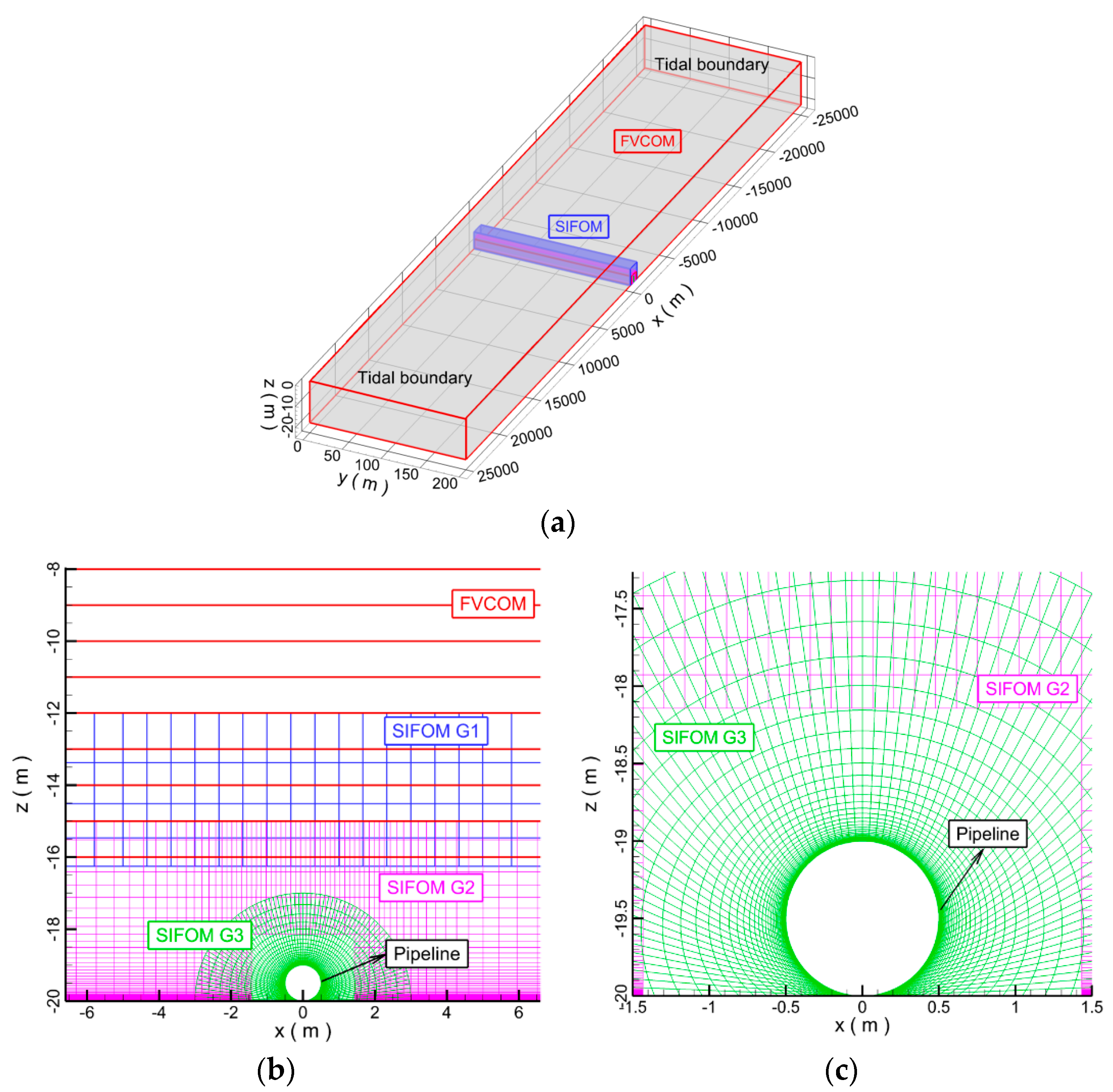
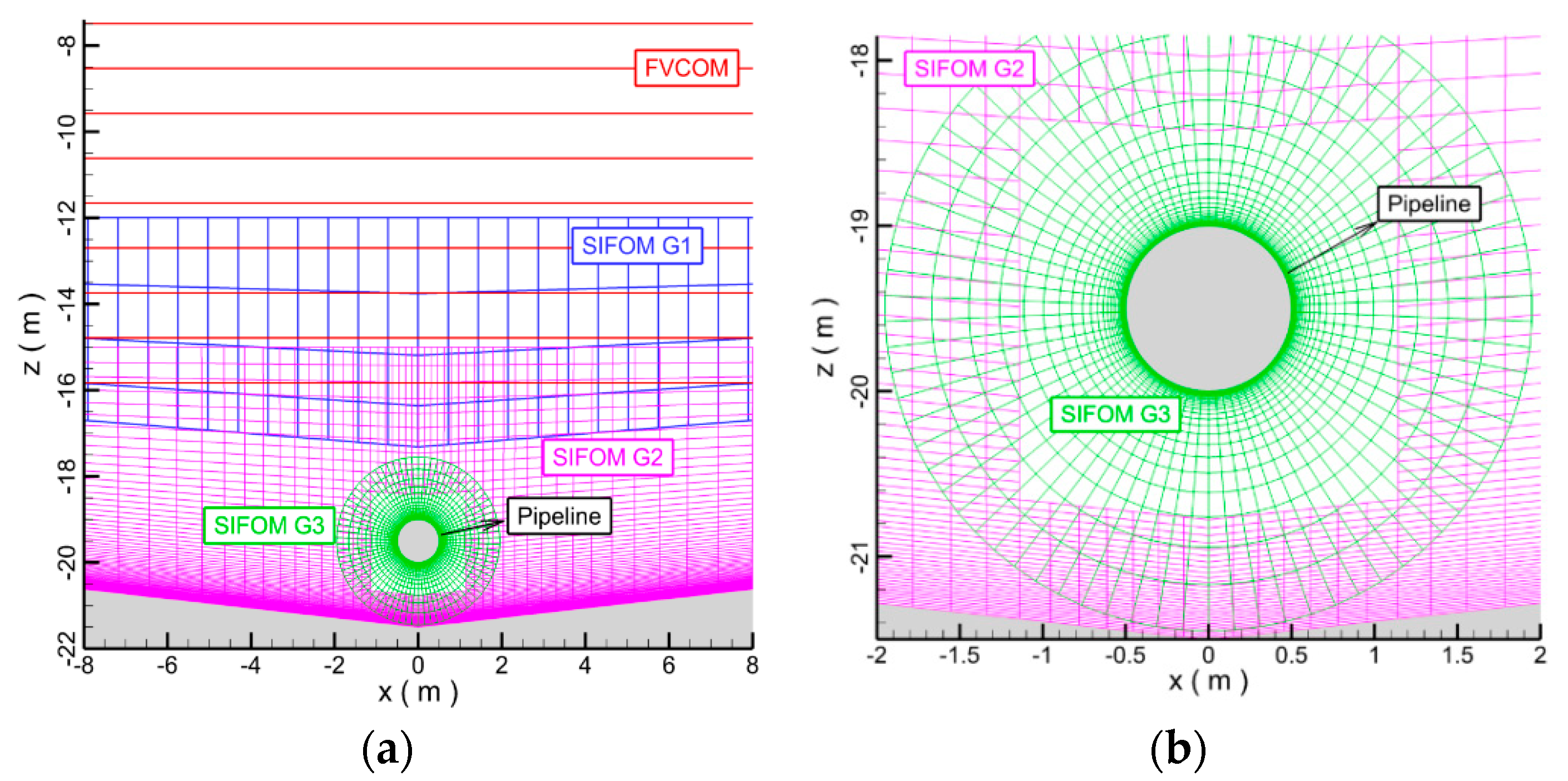
4.1.1. The Mesh and Calculation Setting
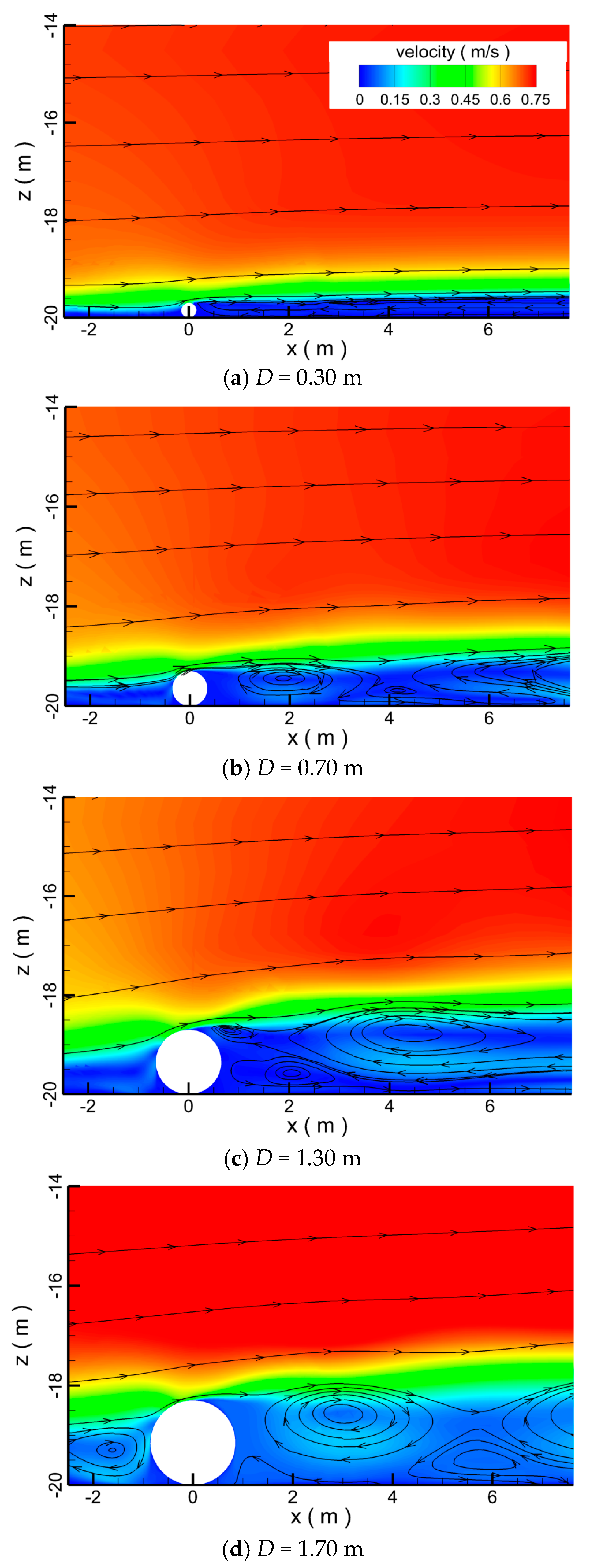
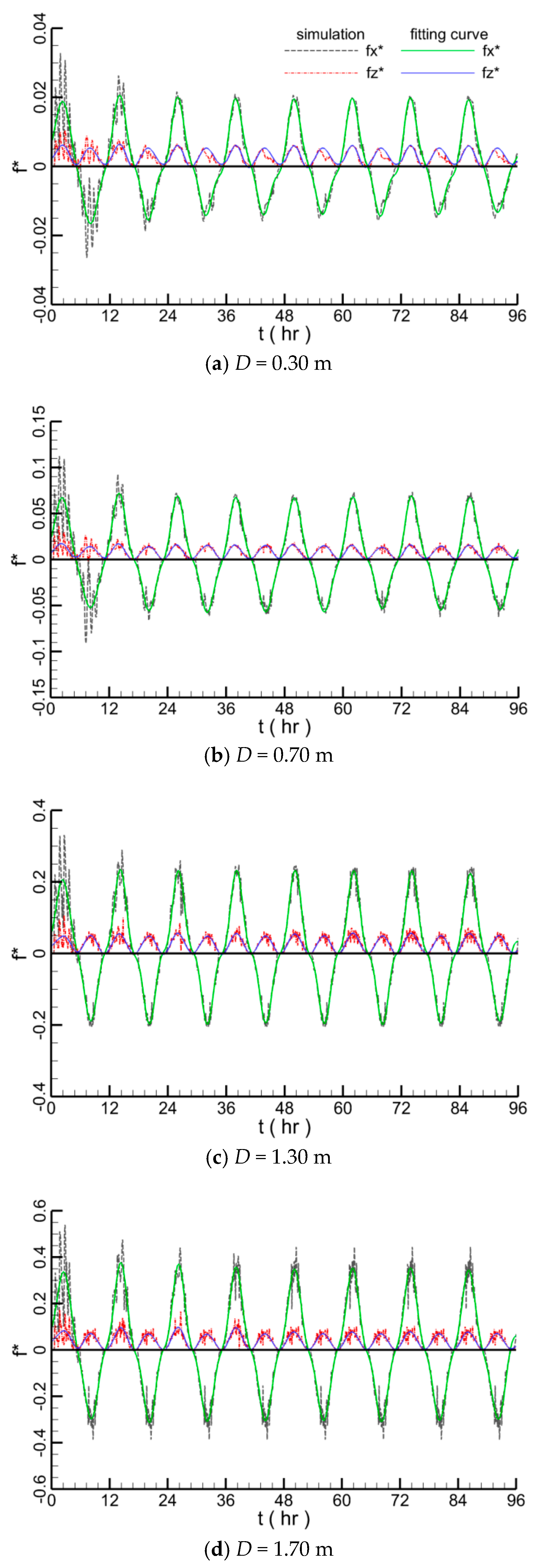
4.1.2. Effect of Pipeline Diameter
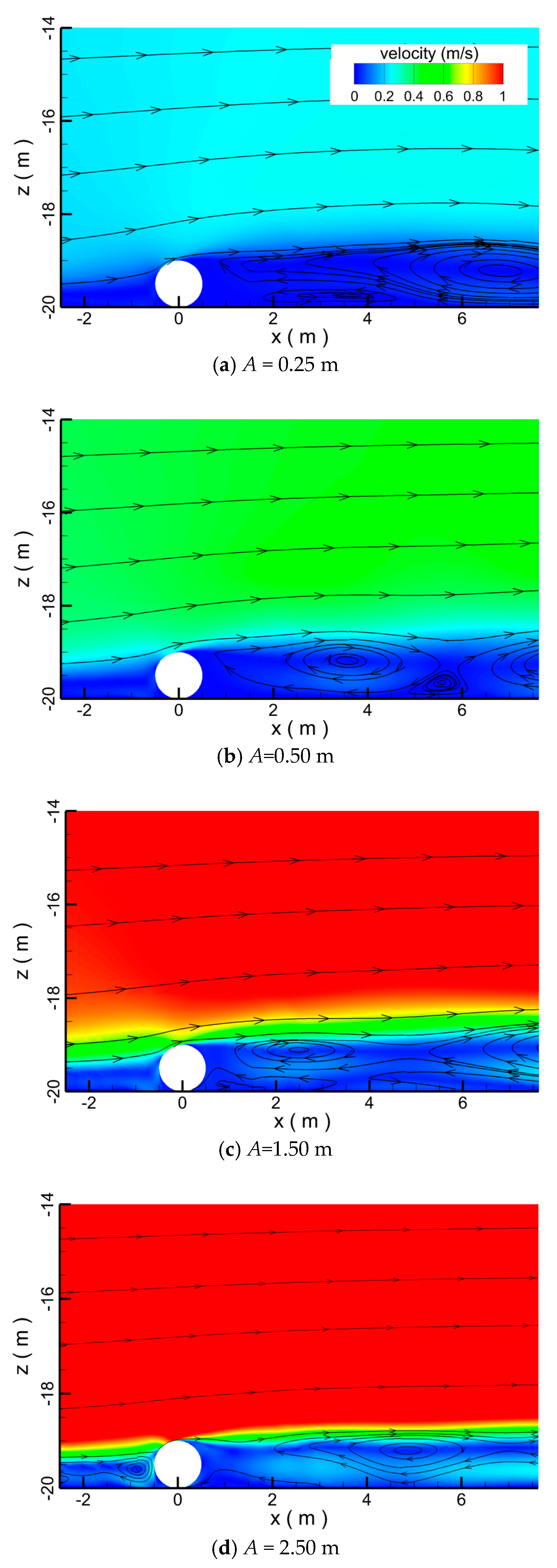
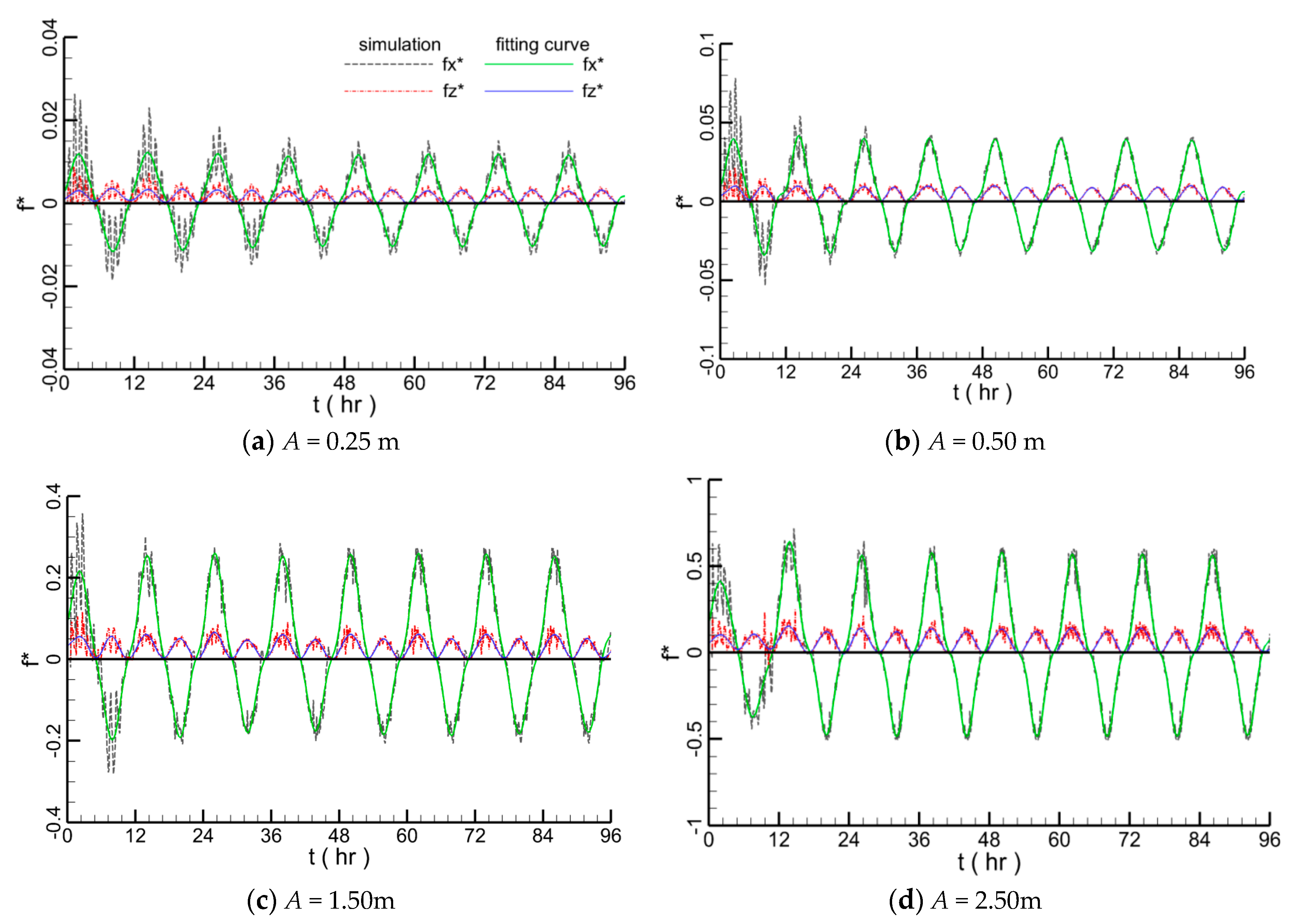
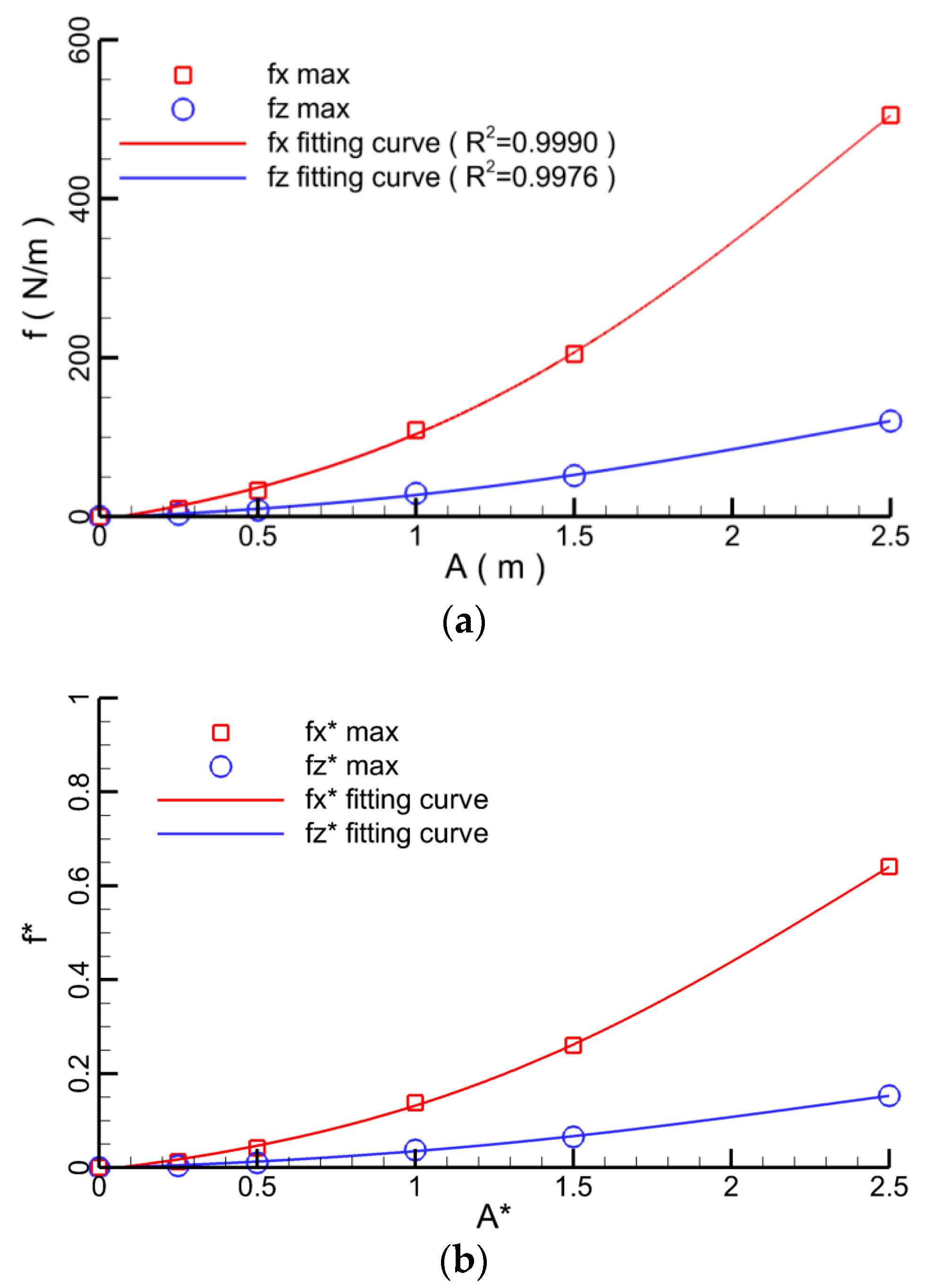
4.1.3. Effect of Tidal Amplitude
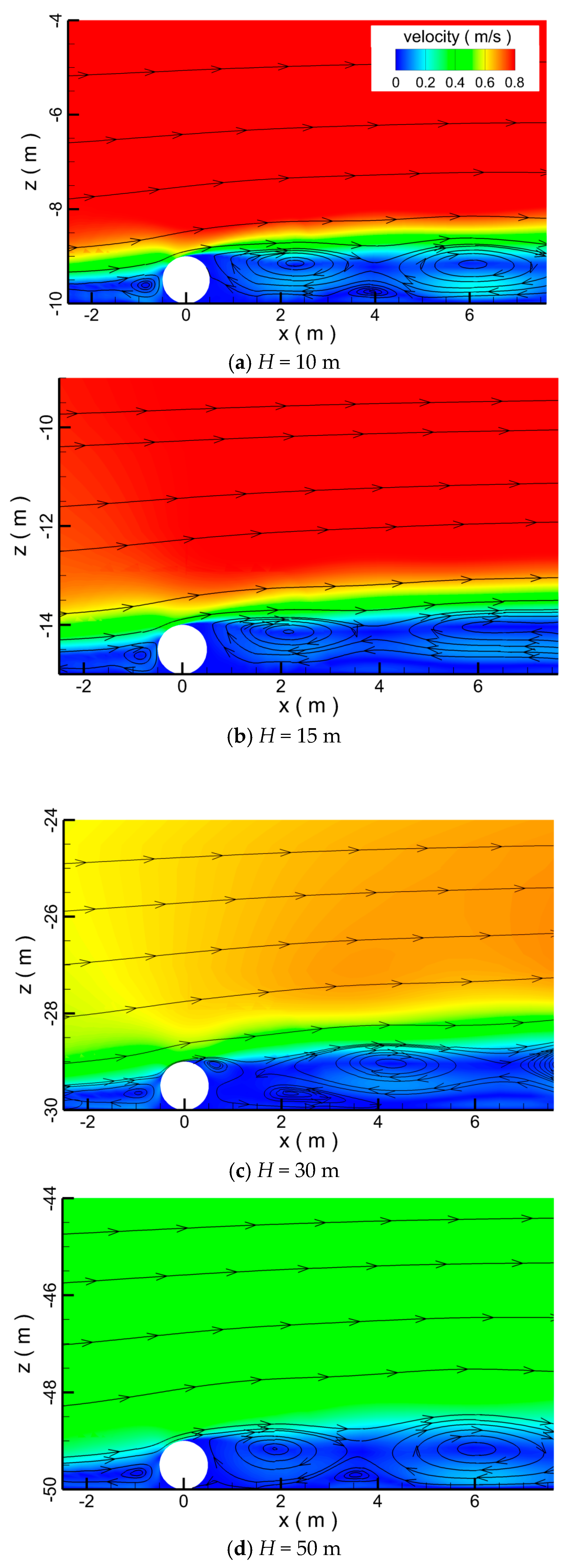
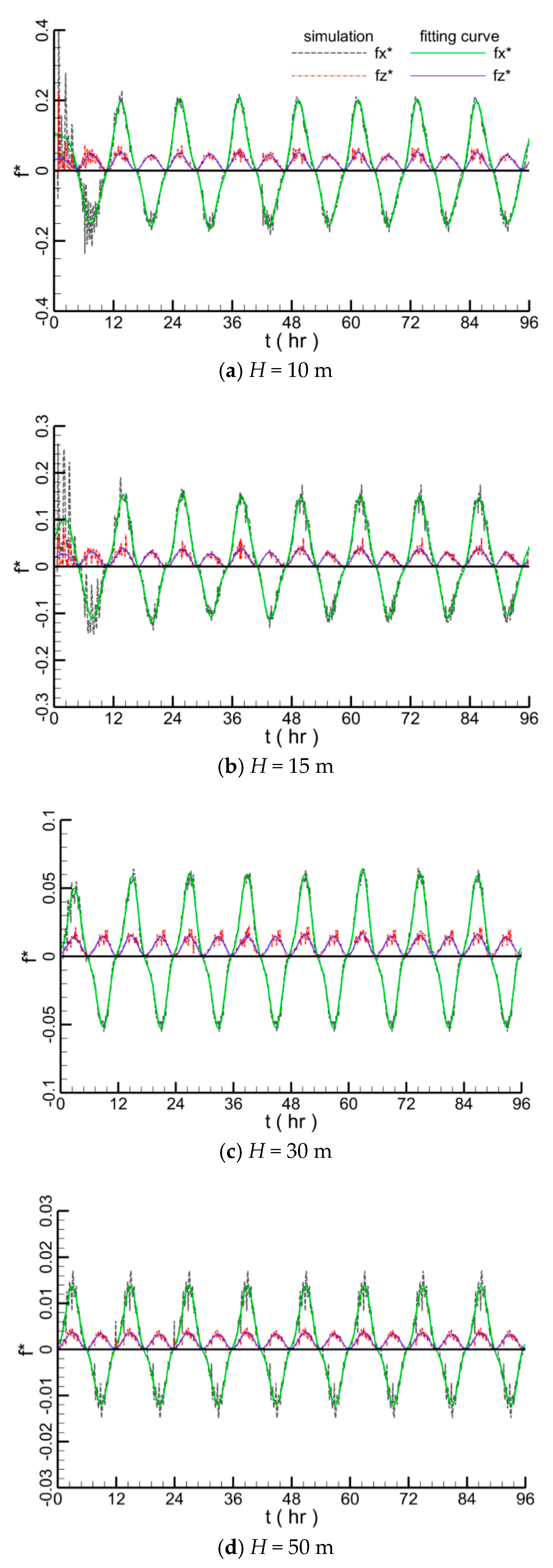
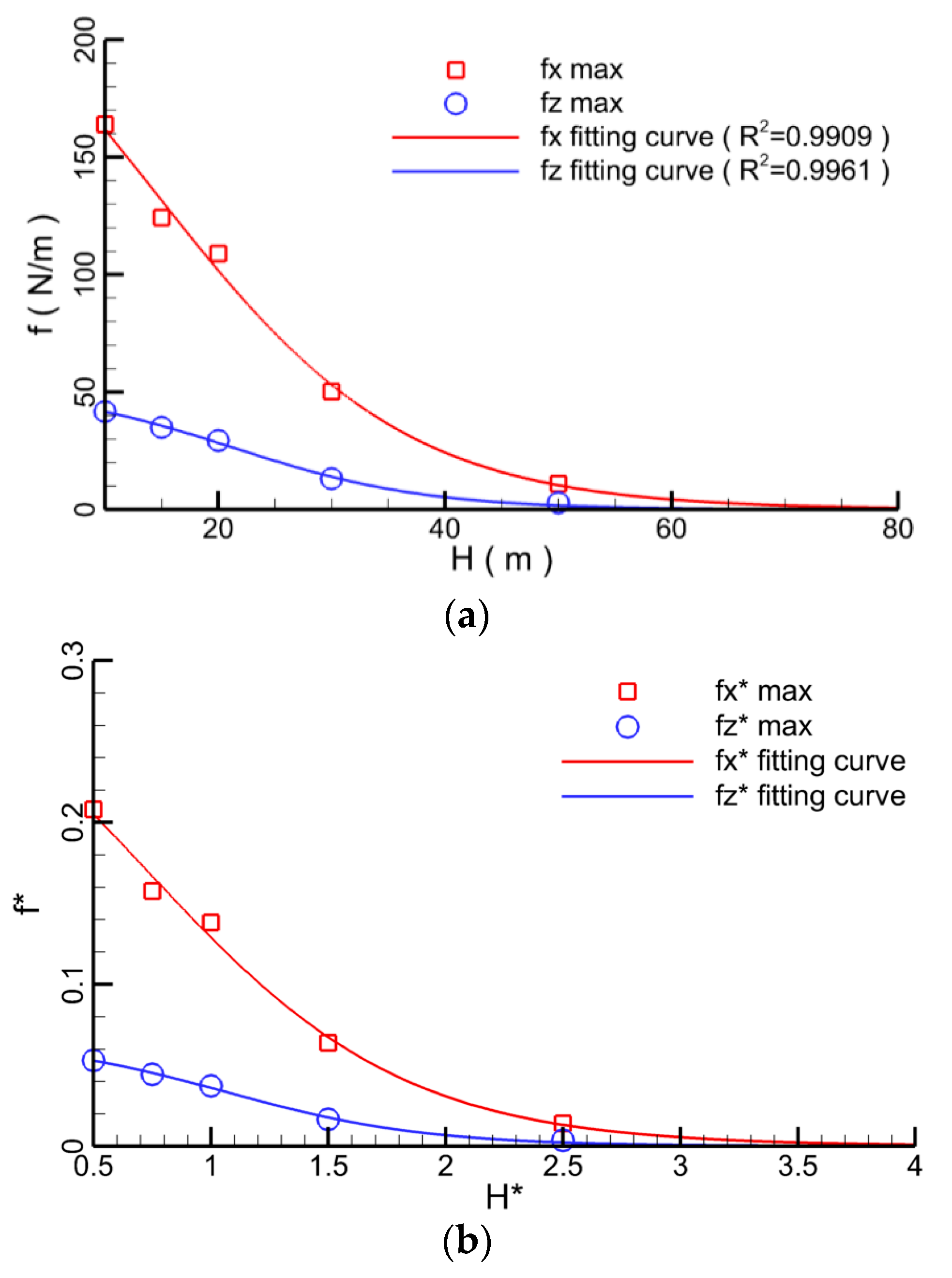
4.1.4. Effect of Water Depth
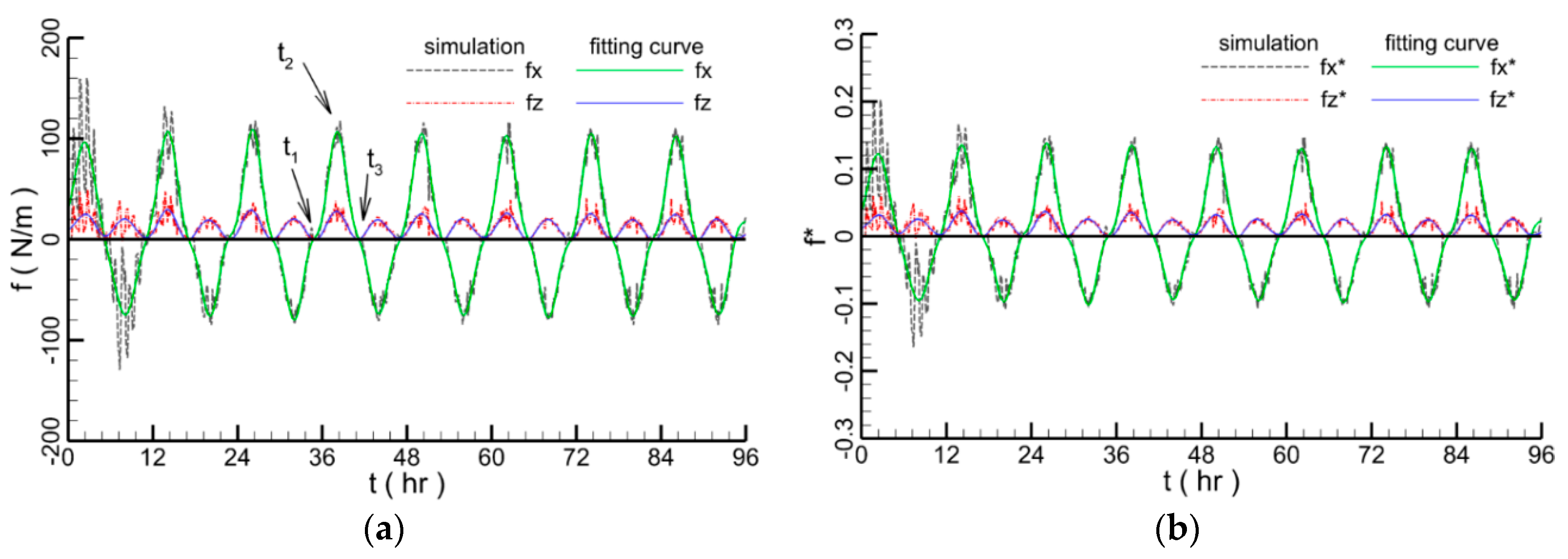
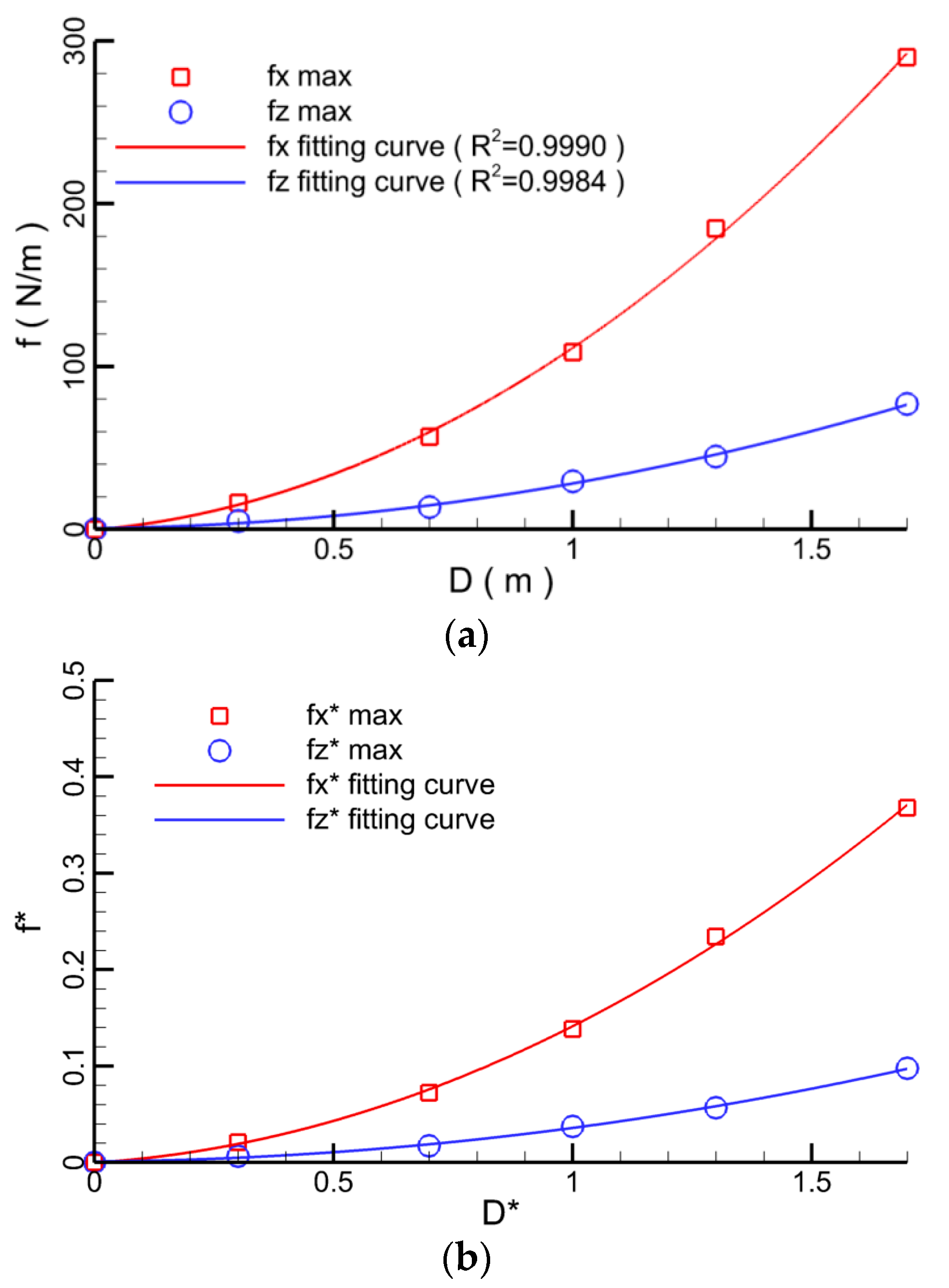
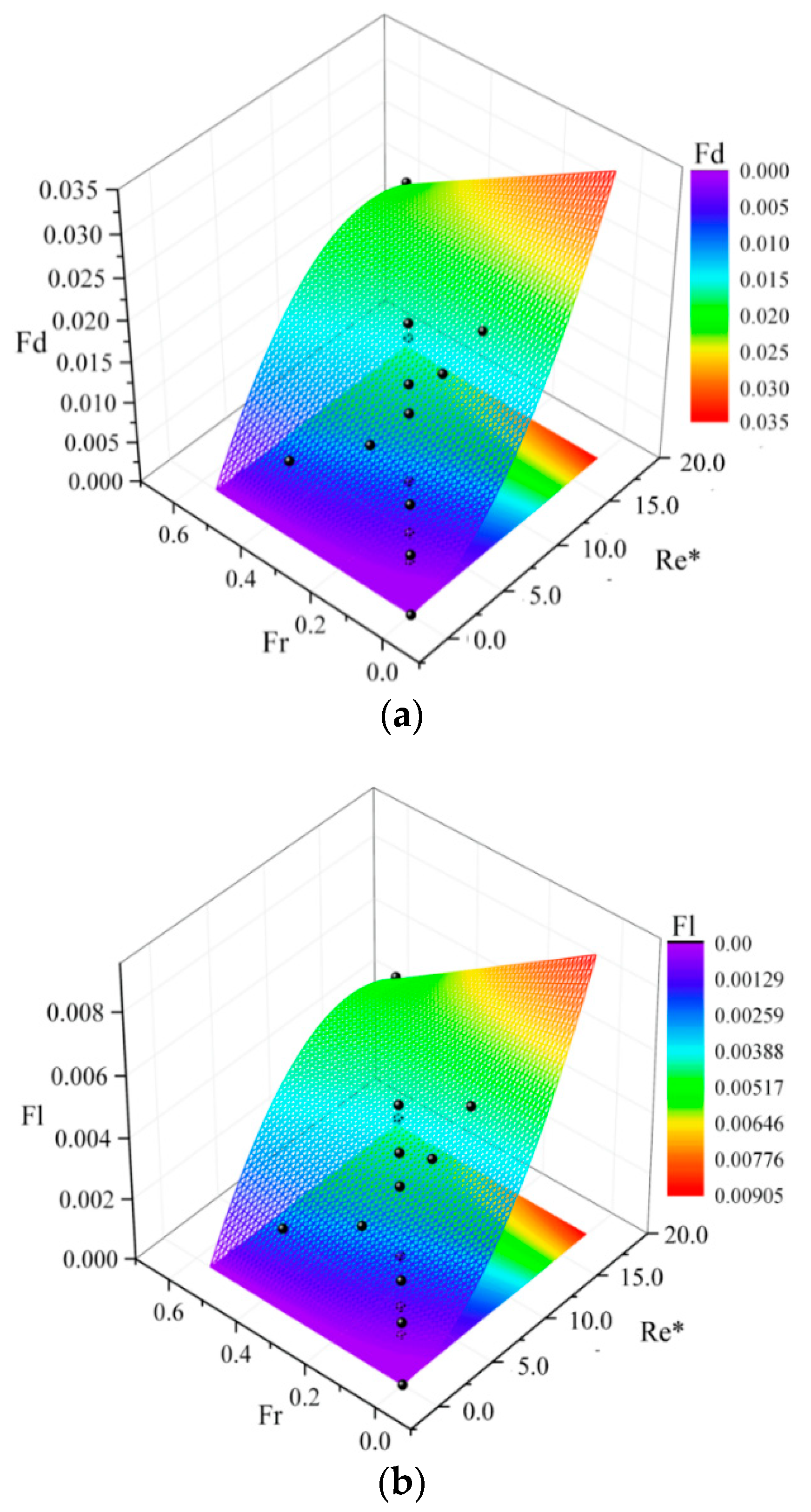
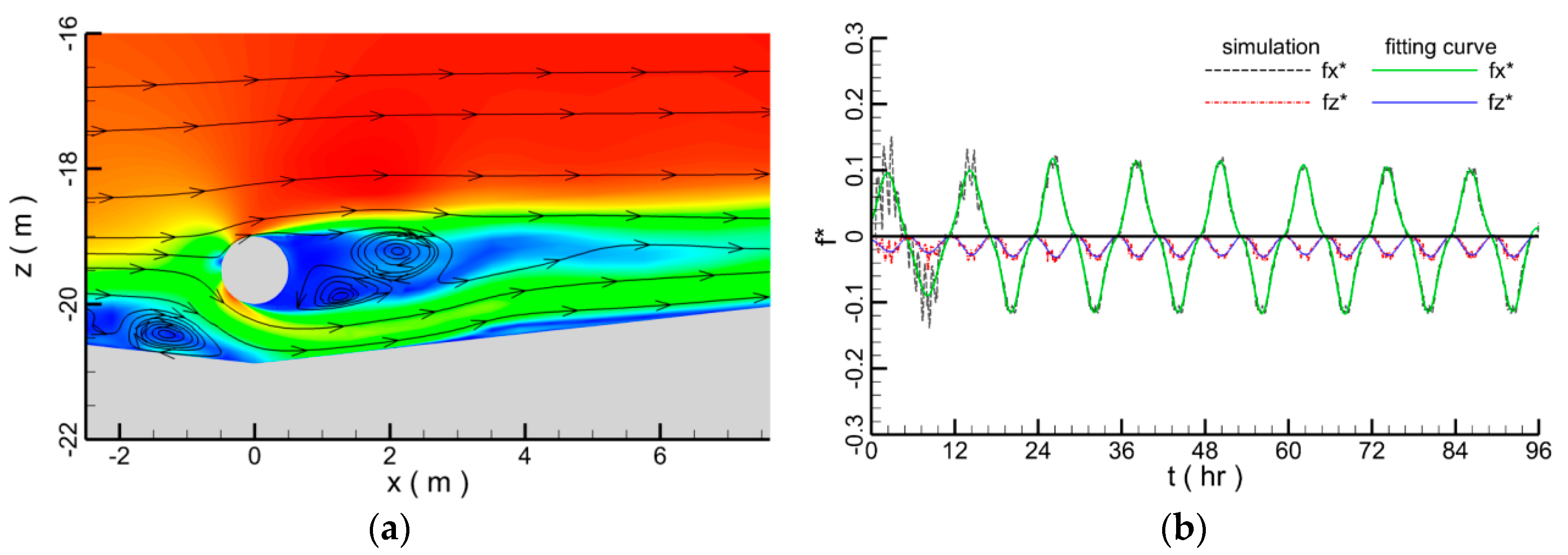
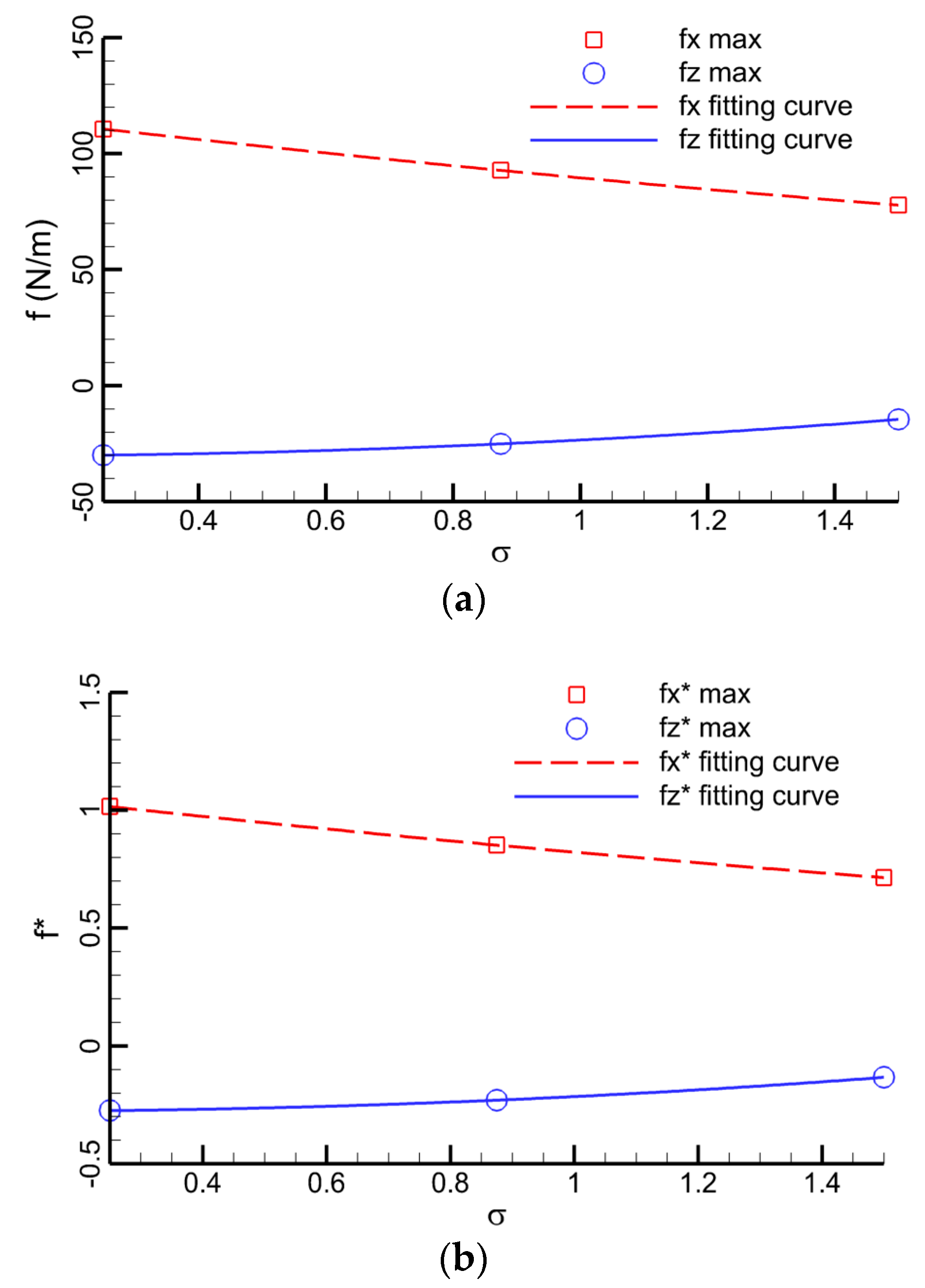
4.1.5. Hydrodynamic Forces on the Submarine Pipeline
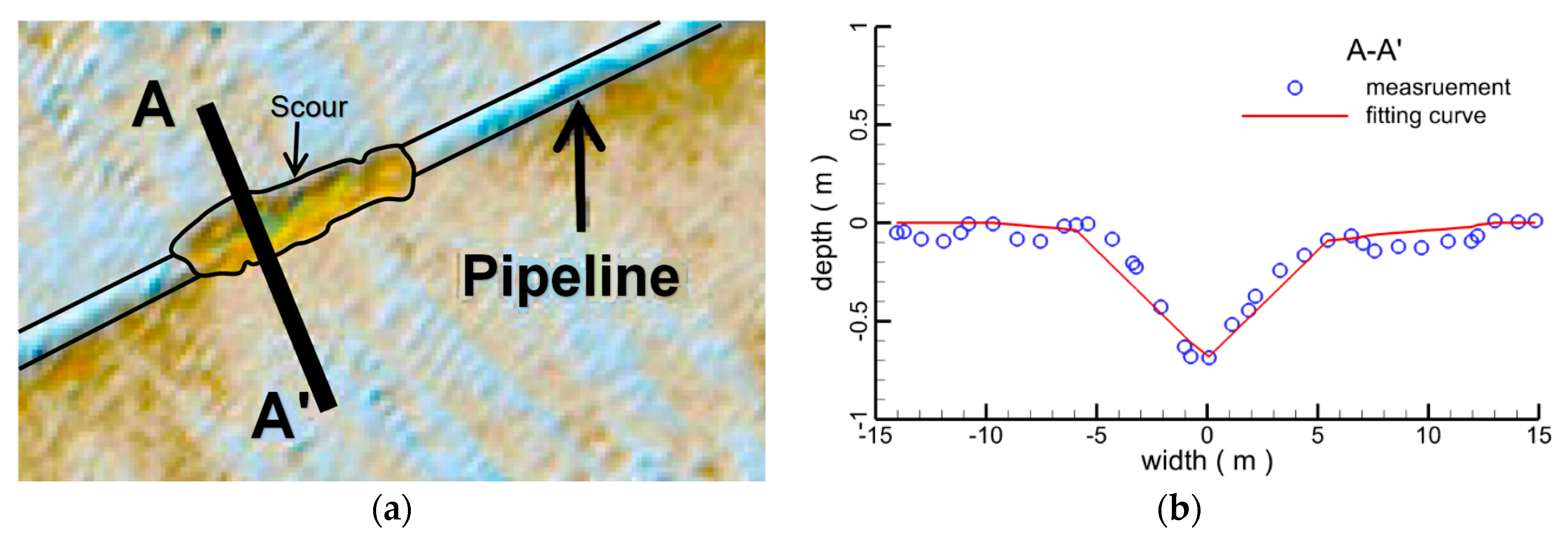
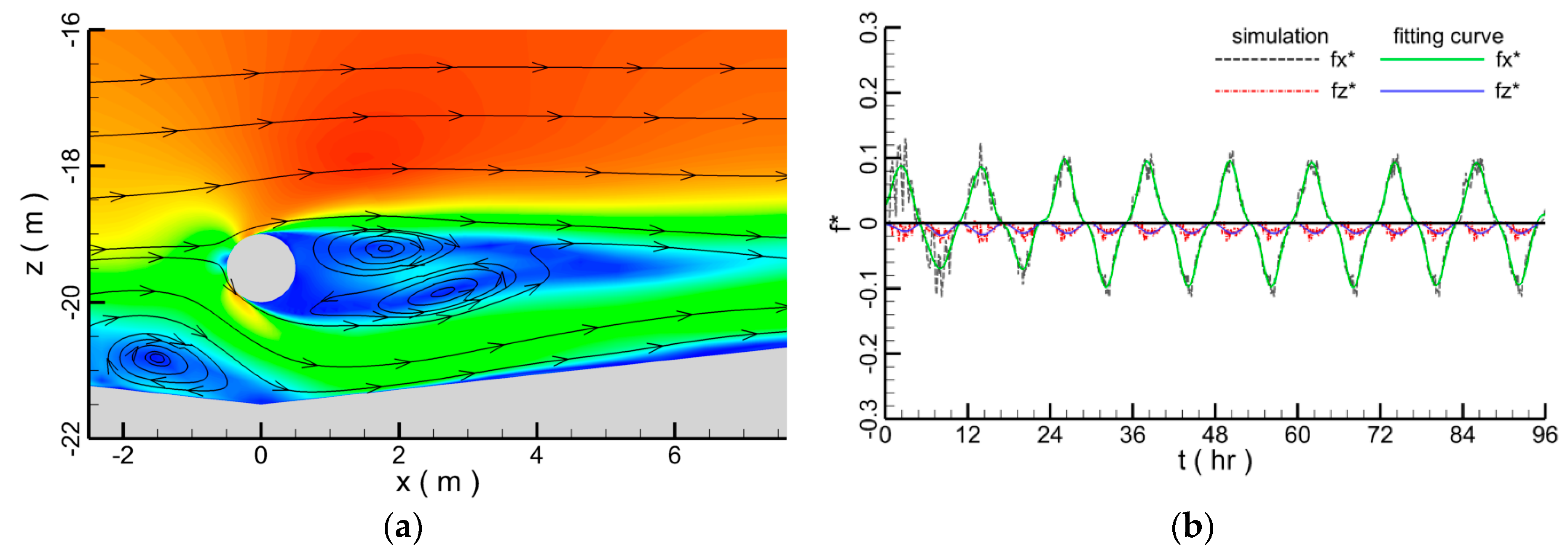
4.2. Hydrodynamics around Submarine Pipeline with Scour
5. Conclusions
Author Contributions
Funding
Acknowledgment
Conflicts of Interest
Appendix A
References
- Shankar, N.J.; Cheong, H.F.; Subbiah, K. Forces on a smooth submarine pipeline in random waves—A comparative-study. Coast. Eng. 1987, 11, 189–218. [Google Scholar] [CrossRef]
- Al-Dakkan, K.; Alsaif, K. On the design of a suspension system for oil and gas transporting pipelines below ocean surface. Arab. J. Sci. Eng. 2012, 37, 2017–2033. [Google Scholar] [CrossRef]
- Kok, N.J. Lift and Drag Forces on a Submarine Pipeline in Steady Flow. Ph.D. Thesis, University of Cape Town, Cape Town, South Africa, 1988. [Google Scholar]
- Li, X.; Li, M.G.; Zhou, J. Experimental study of the hydrodynamic force on a pipeline subjected to vertical seabed movement. Ocean Eng. 2013, 72, 66–76. [Google Scholar] [CrossRef]
- Yang, B.; Gao, F.P.; Wu, Y.X.; Li, D.H. Experimental study on vortex-induced vibrations of submarine pipeline near seabed boundary in ocean currents. China Ocean Eng. 2006, 20, 113–121. [Google Scholar]
- Mattioli, M.; Alsina, J.M.; Mancinelli, A.; Miozzi, M.; Brocchini, M. Experimental investigation of the nearbed dynamics around a submarine pipeline laying on different types of seabed: The interaction between turbulent structures and particles. Adv. Water Res. 2012, 48, 31–46. [Google Scholar] [CrossRef]
- Mattioli, M.; Mancinelli, A.; Brocchini, M. Experimental investigation of the wave-induced flow around a surface-touching cylinder. J. Fluid Struct. 2013, 37, 62–87. [Google Scholar] [CrossRef]
- Pierro, A.; Tinti, E.; Lenci, S.; Brocchini, M.; Colicchio, G. Investigation of the dynamic loads on a vertically-oscillating circular cylinder close to the sea bed: The role of viscosity. J. Offshore Mech. Arct. Eng. 2017, 139, 061101. [Google Scholar] [CrossRef]
- Ong, M.C.; Utnes, T.; Holmedal, L.E.; Myrhaug, D.; Pettersen, B. Numerical simulation of flow around a smooth circular cylinder at very high Reynolds numbers. Mar. Struct. 2009, 22, 142–153. [Google Scholar] [CrossRef]
- Cheng, L.; Chew, L.W. Modelling of flow around a near-bed pipeline with a spoiler. Ocean. Eng. 2003, 30, 1595–1611. [Google Scholar] [CrossRef]
- Chiew, Y.M. Mechanics of local scour around submarine pipelines. J. Hydraul. Eng. 1990, 116, 515–529. [Google Scholar] [CrossRef]
- Brors, B. Numerical modeling of flow and scour at pipelines. J. Hydraul. Eng. 1999, 125, 511–523. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsoe, J. Wave scour around a large vertical circular cylinder. J. Waterw. Port Coast. Ocean Eng. 2001, 127, 125–134. [Google Scholar] [CrossRef]
- Myrhaug, D.; Ong, M.C.; Føien, H.; Gjengedal, C.; Leira, B.J. Scour below pipelines and around vertical piles due to second-order random waves plus a current. Ocean Eng. 2009, 36, 605–616. [Google Scholar] [CrossRef]
- Zhou, X.L.; Wang, J.H.; Zhang, J.; Jeng, D.S. Wave and current induced seabed response around a submarine pipeline in an anisotropic seabed. Ocean Eng. 2014, 75, 112–127. [Google Scholar] [CrossRef]
- Postacchini, M.; Brocchini, M. Scour depth under pipelines placed on weakly cohesive soils. Appl. Ocean Res. 2015, 52, 73–79. [Google Scholar] [CrossRef]
- Zhao, M.; Vaidya, S.; Zhang, Q.; Cheng, L. Local scour around two pipelines in tandem in steady current. Coast. Eng. 2015, 98, 1–15. [Google Scholar] [CrossRef]
- Lam, K.Y.; Wang, Q.X.; Zong, Z.A. Nonlinear fluid-structure interaction analysis of a near-bed submarine pipeline in a current. J. Fluid Struct. 2002, 16, 1177–1191. [Google Scholar] [CrossRef]
- Lin, Z.B.; Guo, Y.K.; Jeng, D.S.; Liao, C.C.; Rey, N. An integrated numerical model for wave-soil-pipeline interactions. Coast. Eng. 2016, 108, 25–35. [Google Scholar] [CrossRef]
- Zhao, E.J.; Shi, B.; Qu, K.; Dong, W.B.; Zhang, J. Experimental and Numerical Investigation of Local Scour around Submarine Piggyback Pipeline under Steady Currents. J. Ocean Univ. China 2018, 17, 244–256. [Google Scholar] [CrossRef]
- Sabag, S.R.; Edge, B.L.; Soedigdo, I. Wake II model for hydrodynamic forces on marine pipelines including waves and currents. Ocean Eng. 2000, 27, 1295–1319. [Google Scholar] [CrossRef]
- Fringer, O.B.; Gerritsen, M.; Street, R.L. An unstructured-grid, finite-volume, nonhydrostatic, parallel coastal ocean simulator. Ocean Model. 2006, 14, 139–173. [Google Scholar] [CrossRef]
- Tang, H.S.; Qu, K.; Wu, X.G. An overset grid method for integration of fully 3D fluid dynamics and geophysics fluid dynamics models to simulate multiphysics coastal ocean flows. J. Comput. Phys. 2014, 273, 548–571. [Google Scholar] [CrossRef]
- Leonard, B.P. A stable and accurate convective modelling procedure based on quadratic upstream interpolation. Comput. Methods Appl. Mech. Eng. 1979, 19, 59–98. [Google Scholar] [CrossRef]
- Tang, H.S.; Keen, T.R.; Khanbilvardi, R. A model-coupling framework for nearshore waves, currents, sediment transport, and seabed morphology. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 2935–2947. [Google Scholar] [CrossRef]
- Chen, C.S.; Liu, H.D.; Beardsley, R.C. An unstructured, finite-volume, three-dimensional, primitive equation ocean model: Application to coastal ocean and estuaries. J. Atmos. Ocean. Technol. 2003, 20, 159–186. [Google Scholar] [CrossRef]
- Xu, J.S.; Pu, J.J.; Li, G.X. Field Observations of Seabed Scours around a Submarine Pipeline on Cohesive Bed. In Advances in Computational Environment Science; Lee, G., Ed.; Springer: Berlin, Germany, 2012; Volume 142, pp. 23–33. [Google Scholar]
- Jensen, B.L. Large-scale vortices in the wake of a cylinder placed near a wall. In Proceedings of the 2nd International Conference on Laser Anemometry-Advances and Applications, Strathclyde, UK, 21–23 September 1987; pp. 153–163. [Google Scholar]
- Liang, D.F.; Cheng, L. Numerical modeling of flow and scour below a pipeline in currents. Part I. Flow simulation. Coast. Eng. 2005, 52, 25–42. [Google Scholar] [CrossRef]
- Lyn, D.; Rodi, W. The flapping shear layer formed by flow separation from the forward corner of a square cylinder. J. Fluid Mech. 1994, 267, 353–376. [Google Scholar] [CrossRef]
- Catalano, P.; Wang, M.; Iaccarino, G.; Moin, P. Numerical simulation of the flow around a circular cylinder at high Reynolds number. Int. J. Heat Fluid Flow 2003, 24, 463–469. [Google Scholar] [CrossRef]
- White, F.M. Fluid Mechanics, 7th ed.; McGraw Hill Press: New York, NY, USA, 2009. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, E.; Mu, L.; Shi, B. Numerical Study of the Influence of Tidal Current on Submarine Pipeline Based on the SIFOM–FVCOM Coupling Model. Water 2018, 10, 1814. https://doi.org/10.3390/w10121814
Zhao E, Mu L, Shi B. Numerical Study of the Influence of Tidal Current on Submarine Pipeline Based on the SIFOM–FVCOM Coupling Model. Water. 2018; 10(12):1814. https://doi.org/10.3390/w10121814
Chicago/Turabian StyleZhao, Enjin, Lin Mu, and Bing Shi. 2018. "Numerical Study of the Influence of Tidal Current on Submarine Pipeline Based on the SIFOM–FVCOM Coupling Model" Water 10, no. 12: 1814. https://doi.org/10.3390/w10121814
APA StyleZhao, E., Mu, L., & Shi, B. (2018). Numerical Study of the Influence of Tidal Current on Submarine Pipeline Based on the SIFOM–FVCOM Coupling Model. Water, 10(12), 1814. https://doi.org/10.3390/w10121814






